Abstract
Free energy perturbation (FEP) simulations have been widely applied to obtain predictions of the relative binding free energy for a series of congeneric ligands binding to the same receptor, which is an essential component for the lead optimization process in computer-aided drug discovery. In the case of several congeneric ligands forming a perturbation map involving a closed thermodynamic cycle, the summation of the estimated free energy change along each edge in the cycle using BAR (Bennett acceptance ratio) usually will deviate from zero due to systematic and random errors, which is the hysteresis of cycle closure. In this work, the advanced reweighting techniques UWHAM (binless weighted histogram analysis method) and LWHAM (locally weighted histogram analysis method) are applied to provide statistical estimators of the free energy change along each edge in order to eliminate the hysteresis effect. As an example, we analyze a closed thermodynamic cycle involving four congeneric ligands which bind to HIV-1 integrase, a promising target which has emerged for antiviral therapy. We demonstrate that compared with FEP and BAR, more accurate and hysteresis-free estimates of free energy differences can be achieved by using UWHAM to find a single estimate of the density of states based on all of the data in the cycle. Furthermore, by comparison of LWHAM results obtained from the inclusion of different numbers of neighboring states with UWHAM estimation involving all the states, we show how to determine the optimal neighborhood size in the LWHAM analysis to balance the tradeoffs between computational cost and accuracy of the free energy prediction. Even with the smallest neighborhood, LWHAM can improve the BAR free energy estimates using the same input data as BAR. We introduce an overlapping states matrix that is constructed by using the global jump formula of LWHAM and plot its heat map. The heat map provides a quantitative measure of the overlap between pairs of alchemical/thermodynamic states. We explain how to identify and improve the FEP calculations along the edges that most likely cause large systematic errors by using the heat map of the overlapping states matrix and by comparing the BAR and UWHAM estimates of the free energy change.
Graphical Abstract
Introduction
Ranking the binding affinities for a series of congeneric ligands binding to the same receptor is a central component in the lead optimization process of drug discovery.1 Nowadays, quantitative prediction of the relative binding affinities of the congeneric ligands can be achieved based on the free energy perturbation (FEP) method in conjunction with molecular dynamics simulations.2–8 Significant progress in the development of new methodology, improvement of the force field and increase of the computer speed has lead to higher accuracy estimates of the relative binding free energy using FEP.9–11 Compared with popular methods like docking and MM-GBSA,12,13 FEP is rooted in a rigorous statistical mechanical framework, which involves the calculation of the alchemical free energy to convert the reference ligand into the target ligand in both the bound state around the receptor and the unbound state in pure water.14–16 In FEP calculations, the optimal way to construct the mutation paths among several congeneric ligands can be achieved by using algorithms such as LOMAP,17 which results in a single graph or perturbation map consisting of one or more closed cycles.18,19 Based on the fundamental law of thermodynamics, the total free energy change in a closed thermodynamic cycle should sum to zero. However, hysteresis of cycle closure is usually observed in practice, which means that the total free energy change in the closed cycle may deviate from zero due to insufficient sampling arising from at least one edge of the cycle.
In this study, two advanced reweighting techniques UWHAM (binless weighted histogram analysis method)20–22 and LWHAM (locally weighted histogram analysis method)23,24 are implemented to analyze the simulation data generated at states along multiple edges in order to estimate the free energy change along each edge. Compared with the Bennett Acceptance Ratio (BAR)25–27 approach involving analysis of the data from pairs of adjacent states, UWHAM (also called MBAR28) is an extension to include data from all states in the closed cycle, with the solution as the maximum likelihood free energy estimators along each edge given the contributions from all the data. In this way, it is guaranteed that there is no hysteresis in the closed cycle since UWHAM solves for a single density of states. The UWHAM method can be considered to not only generalize BAR but also remove the necessity of discretizing observations into bins in the original WHAM (weighted histogram analysis method),29which therefore provides the estimate of density of states for each data point and increases the statistical precision. Furthermore, estimating the density of states provides a connection with the potential distribution theorem.30,31 LWHAM is based on serial tempering32–34 and its extensions24,35 to resample data obtained from multi-ensemble simulations. The advantage of LWHAM is that a proper neighborhood size can be chosen in the analysis, so that the unnormalized density functions for each data point only need to be locally evaluated at the states within a chosen neighborhood of each state for reweighting, which can be computationally much less expensive as compared with UWHAM. On the other hand, the variability in free energy estimation is, to a large extent, affected by the degree of overlap between different ensembles. LWHAM is expected to yield similar statistical efficiency to that of UWHAM, because LWHAM is constructed to effectively exploit the overlaps between pairs of adjacent ensembles which often represent the majority of overlaps between all ensembles considered.
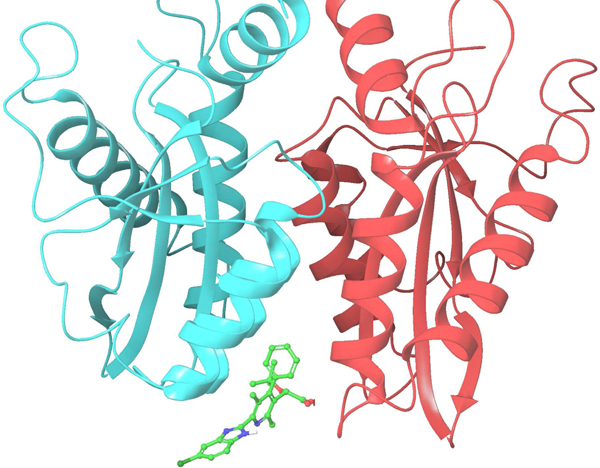
The target protein we studied in this work is HIV-1 integrase. HIV-1 integrase not only catalyzes the integration of viral DNA into the host chromosomes, but also plays an important role in virus particle maturation.36 Due to the multifunctional nature of HIV-1 integrase, it serves as an attractive drug target. In this work, we study ligands known to bind to the allosteric binding site which is located at the dimer interface of the HIV-1 integrase catalytic core domain (CCD) as shown in Figure 1.37–40 Structure-based drug design of ALLINIs has been facilitated by the crystal structure of the HIV-1 integrase CCD bound with the integrase-binding domain (IBD).41 Quinoline-based allosteric HIV-1 integrase inhibitors (ALLINIs) have been identified through both the in silica screening method using the cocrystal structure40 and high-throughput screening methods using HIV-1 integrase 3’– processing reactions39. We apply the FEP method to calculate the relative binding affinities of a series of quinoline-based ALLINIs binding to HIV-1 integrase. The four congeneric ligands in the series form a rectangular perturbation map as shown in Figure 2. We use this closed thermodynamic cycle to demonstrate the advantages of using reweighting techniques like UWHAM and LWHAM to analyze the free energy difference map when there is hysteresis, as we found to be the case for the thermodynamic cycle involving the four ligands shown in Fig.2. UWHAM and LWHAM both use all of the data sampled from each of the states along the closed cycle to construct an estimate of a single density of states for the map. LWHAM is an approximation to UWHAM which associates each state with all other states within a preselected neighborhood. We examine the optimal neighborhood size which balances computational cost and accuracy for ligand binding FEP simulations of the kind which are the focus of this work. Finally, we introduce a new analytic tool - the overlapping states matrix - which can be used to quantitate and visualize the extent to which the states of the thermodynamic cycle overlap. The overlapping states matrix can be used to choose the optimal neighborhood for LWHAM reweighting and to identify states in the cycle that may be less converged, and where additional simulation time is best focused to improve estimates of free energy differences along some edges of the cycle.
Figure 1:
ALLINI binding to the dimer interface of the HIV-1 integrase CCD
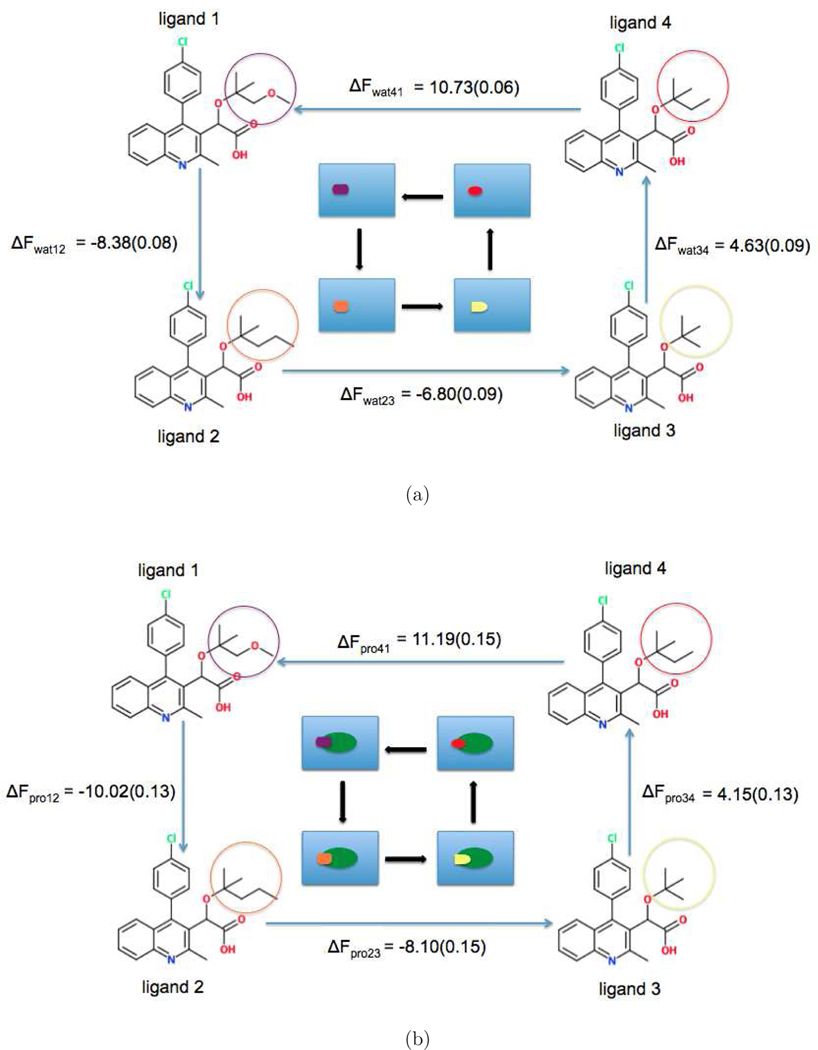
Figure 2:
(a) Free energy change along each edge in the unbound state, Δ = −8.38 – 6.80 + 4.63 + 10.73 = 0.18(kcal/mol) (b) Free energy change along each edge in the bound state, Delta = −10.02 – 8.10 + 4.15 + 11.19 = −2.78(kcal/mol)
Method
Simulation Setup
All MD simulations were performed in GROMACS package version 5.1.242–44. FEP involves estimating the relative binding free energy among ligands based on alchemically transforming one ligand to another in both the bound and unbound states. In order to apply the UWHAM/LWHAM approach to estimate the free energy change along each edge, one needs to obtain the potential energy for a series of configurations generated at one simulation state under different Hamiltonians of other simulation states in the closed cycle of the perturbation map. This requires a special treatment with a further modification of the dual topology in the FEP transformation45,46. In the system involving ligand 1, ligand 2, ligand 3 and ligand 4 in Figure 2, the topology file used for the FEP simulations contains the topological information for all four ligands of interest. This topology can be decomposed into five sets, including the shared set and four distinct sets. The shared set includes the topology of the same atoms that are shared by the four ligands of interest, and the four distinct sets include the topology of the unique atoms of the four ligands, respectively. At the beginning of the FEP transformation from ligand 1 to ligand 2, the atoms described by the shared set and distinct set from ligand 1 have full interactions with the environment, while the atoms described by the distinct set from ligand 2, distinct set from ligand 3 and distinct set from ligand 4 have no interactions with the environment except the linkage with the shared part of the ligand. In the case of the bound state, the environment refers to the receptor and the solvent; while in the case of the unbound state, the environment refers to only the pure solvent. Then as the transformation proceeds along the edge from ligand 1 to ligand 2, the interactions between the atoms described by the distinct set from ligand 1 and the environment are decreased from the full effect to zero and simultaneously the interactions between the atoms described by the distinct set from ligand 2 and the environment are increased from zero to full effect using 31 states with different coupling parameter λ values. Throughout the process, atoms described by the shared set have full interaction with the environment; atoms described by the distinct set from ligand 3 and distinct set from ligand 4 have no interactions with the environment. Therefore, at the end of this transformation, the atoms described by the shared set and distinct set from ligand 2 have full interactions with the environment, while the atoms described by the distinct set from ligand 1, distinct set from ligand 3 and distinct set from ligand 4 have no interactions with the environment except the linkage with the shared part of the ligand. In GROMACS, the 31 λ-states involved in the transformation are chosen by varying the coul-lambdas and vdw-lambdas in the mdp file. First, the Van der Waals (VdW) interactions of ligand 2 with the surrounding are turned on using 11 λ-states; then the electrostatic interactions of ligand 2 are turned on while simultaneously the electrostatic interactions of ligand 1 with the surrounding are turned off using 10 λ-states; the last step involves turning off the VdW interactions of ligand 1 with the surroundings using 10 λ-states. Similarly, this process can be applied to the transformations along each of the other edges. In this way, a closed thermodynamic cycle involving simulations of a total of 120 λ-states was constructed to represent the FEP transformations.
For the FEP perturbations of the ligands corresponding to the unbound state in solution, the ligand molecule was solvated in a cubic TIP3P47,48 water box with dimensions 4.6 nm × 4.6 nm ×4.6 nm using the “gmx solvate” tool in GROMACS. This ensures that each atom of the ligand was at least 1.0 nm away from the edge of the box. In this way, a total of 3226 water molecules were contained in the box with one additional Na+ to neutralize the system. For the bound state perturbations, the ligand was located in the allosteric binding site of HIV-1 integrase based on the crystal structure of the complex with PDB code 4TSX49. The protein in the complex was prepared using the Protein Preparation Wizard50 and the protonation states were assigned assuming a pH of 751. The complex was solvated using 15456 TIP3P water molecules and 3 Cl- with the box size of 8.0 nm × 8.0 nm ×8.0 nm. The protein molecules were modeled by the Amber ff99sb-ILDN force field52, and the ligands were described by the Amber GAFF parameters set53. The partial charges of the ligands were obtained using the AM1-BCC method54. For each individual λ-state, energy minimization was performed first, followed by 100 ps of equilibration under the NVT ensemble and 1 ns of equilibration under the NPT ensemble. Finally, a 10 ns production MD simulation under the NPT ensemble was performed. Temperature was maintained at 300 K by the leapfrog stochastic dynamics integrator (Langevin dynamics) with time constant of ps55. For the constant pressure simulations during the equilibrium period, the pressure was kept constant by the Berendsen pressure barostat with a pressure relaxation time of 0.5 ps56. For the constant pressure simulations during the production period, the pressure was kept constant by the Parrinello-Rahman pressure barostat with a pressure relaxation time of 2.0 ps57. The time step for the MD simulations was 2 fs with the LINCS algorithm used to constrain bond lengths involving hydrogen atoms58. The long-range electrostatic interaction was treated using the smooth particle-mesh Ewald approach59,60 with a real-space cutoff of 1.0 nm and a spline order of 4. Trajectory files and energy files were both saved every 2 ps.
We also performed another set of perturbation simulations in the bound states using the parallel Hamiltonian replica exchange conformational sampling method61–63. With this scheme, the ligands were less likely to become trapped in low-energy conformations when the ligand interacts strongly with the receptor at the end points in the cycle and the simulations are better converged. The results obtained from Hamiltonian replica exchange serve as benchmark calculations. The length of the production simulation based on Hamiltonian replica exchange was also 10 ns for each λ-state.
To apply the reweighting techniques UWHAM and LWHAM for computing free energies from multiple ensembles with different potentials, one needs to build up a matrix which contains the potential energy for each individual data point evaluation at each of 120 λ-states, not just at the λ-state observed to be associated with the data point in the simulations. This can be achieved by post processing of the simulation trajectory with the “-rerun” option in GROMACS.
UWHAM
Under the canonical ensemble, one could perform M parallel simulations at M states. These simulations could either be independent or coupled. Each state is characterized by a specific combination of thermodynamic parameters and potential energy functions, which we describe collectively as “λ-state”. Suppose is the ith configuration observed at the αth λ-state, the probability of observing at the γth λ-state is
| (1) |
where is the Boltzmann’s factor of at the γth λ-state; is the coordinates of the configuration is the inverse temperature of the γth λ-state; is the potential energy of the configuration at the γth λ-state; and is the partition function of the γth λ-state. The likelihood of the observed data is proportional to
| (2) |
where uαi is the energy coordinate of the configuration Xαi that in general may be written as the sum of of a reference energy plus perturbations. Nα is the total number of observations observed at the αth λ-state; and Ω(uαi) is the density of states. Let and (uαi) denote estimates of the partition function of the αth λ-state and the density of states of uαi, respectively based on finite samples of the states using all the simulation data. They satisfy the equation
| (3) |
Maximizing the log likelihood function yields
| (4) |
The above two equations are the UWHAM equations21,28. Since the UWHAM estimates do not depend on the original λ-state at which each observation was observed, the UWHAM equations can be simplified as
| (5) |
| (6) |
where is the total number of observations.
LWHAM
The UWHAM equations can be solved stochastically by applying the serial tempering (ST) protocol to resample the raw data (ST-SWHAM).22–24,64 Like serial tempering simulations, ST-SWHAM runs by cycles and each cycle consists of a move and a jump process. In the move process, we randomly select an observation ui with uniform probability from all the observations observed at the state that is resampled in the current cycle. In the jump process, we randomly choose one state (e.g. the αth state) to resample in the next cycle according to the probability
| (7) |
where ζ and π0 are both vectors that contain M components; ζκ = −ln Zκ is the estimate of the unitless free energy of the κth state, and ζ0 is fixed at is the proportion of the raw data observed at the κth state during the multi-state simulations. Suppose πκ is the observed proportion of the κth state resampled during the ST-SWHAM analysis. The values of ζ are adjusted iteratively according to the differences between the vectors π0 and π. It can be shown that the estimates of free energies ζ are the solutions of the UWHAM equations when each pair of πκ and agree with each other.23 The jump process described by Eq.(7) is referred to as a global jump because any state can be chosen to resample in the next cycle. As can be seen from Eq.(7), each jump process requires calculations of M exponential functions, where M is the total number of states. The computational cost of using ST-SWHAM with the global jump proposal can be prohibitive when the total number of states M is large.
Recently, we introduced a much faster stochastic solver that provides an approximate solution of the UWHAM equations.23,24 In this approximate algorithm, only the states in a preselected neighborhood of the state resampled in the current cycle can be chosen for the next cycle, and hence the exponential functions of the potential functions only associated with the neighborhood states at ui need to be evaluated. This can be substantially less costly than evaluations of all M exponential functions. Therefore, it is referred to as Local WHAM (LWHAM) with stochastic solution or simply LWHAM. Suppose the γth state is resampled in the current cycle, the procedure of performing one jump in LWHAM is as follows:
randomly select one state in the neighborhood of the γth state with uniform probability to jump to. Suppose the trial state is the αth state,
- accept the αth state as the next state according to the Metropolis probability
where p(α|ui;ζ, π0) and p(γ|ui;ζ,π0) are defined by Eq.(7); Γ(α,γ) is the probability of selecting the αth state as the trial state when resampling the γth state in the current cycle. Namely, Γ(α,γ) = 1/nγ, where nγ is the total number of neighbors of the γth state if the αth state is one of the γth state’s neighbors; Γ(α,γ) = 0 otherwise.(8)
Although only the states within a preselected neighborhood are resampled in the next cycle after one local jump, the states outside of the neighborhood can be resampled if multiple jumps are performed in one cycle. Similarly as in the ST-SWHAM algorithm for UWHAM described above, the values of ζ are adjusted iteratively according to the differences between the vectors π0 and π during the LWHAM analysis. As the number of jumps per cycle increases, the result of LWHAM converges to the result of the ST-SWHAM using the global jump proposal and therefore converges to the UWHAM result. The global jump described by Eq.(7) is the infinite jump limit in serial tempering simulations, which is analogous to the infinite swapping limit in replica exchange simulations.65
Variance Estimation
In order to calculate the standard errors of free energy estimates from multiple simulation states, we propose a method called the fractional replication method. This method involves dividing the simulation data from each state into nonoverlapping blocks, similarly as in (nonoverlapping) block bootstrap,66,67 but this method is expected to be applicable with a larger block length and hence a smaller number (such as 3 or 4) of blocks than typically used with block bootstrap. In fact, existing statistical theory indicates that the optimal block length is of order n1/3 for a stationary series of length n.68 The practical performance of block bootstrap can also be sensitive to different choices of the block length, which will be demonstrated in our numerical experiment (see Supporting Information).
We describe the proposed method in a system with M states, denoted as λ1, λ2… λM, for example, M = 31 alchemical states along the edge between ligands 1 and 2. Suppose that the simulation data from each state are divided into 4 nonoverlapping blocks, which are sufficiently large such that the averages from consecutive blocks are approximately uncorrelated. For the αth state , denote the four blocks as λα(1),…,λα(4), and the original dataset as λα(1234). Let be an estimate of the free energy change between states λ1 and λM, obtained by, for example, BAR, using all M original datasets λα(1234) for α = 1,…,M. For any indices 1 ≤ j1,…,jM ≤ 4, let be the estimate of the free energy change based on a fractional replication of the original datasets, which is defined as a combined dataset of the blocks from the M states. Then the variance of is estimated as S/3 and the standard error of is where
| (9) |
In practice, the summation over all possible 4M combinations is too costly. For a Monte Carlo approximation, S is estimated by averaging over, for example, 200 combined datasets, which are constructed by randomly selecting 1 ≤ jα ≤ 4 for α = 1,…,M.
The variance estimate (9) is similar to that used in the method of balanced repeated replications69,70 for estimating the variance of a nonlinear statistic in stratified random sampling, where orthogonal replications are employed instead of random replications as above. Note that the variance estimate of could be S/4, because the variance of is that of multiplied by 4 according to different sample sizes. However, the estimate S/3 is used, to adjust the degree of freedom due to centering by similarly as in the common definition that the sample variance of is , where .
The fractional replication method can also be applied to calculate standard errors of UWHAM estimates of free energy differences using simulation data from all M = 120 alchemical states along the four edges in the thermodynamic cycle. For any two states for which the free energy change is estimated, the formula (9) is used, where is the UWHAM estimate using all the 120 original datasets, and is the UWHAM estimate using a combined dataset including the blocks from the M states. For a Monte Carlo approximation, the average in (9) can be estimated by using 200 combined datasets randomly selected from a total of 4120 combinations.
The proposed method can be further employed to calculate the standard error for the difference between two alternative estimates of a free energy difference, such as the BAR estimate and UWHAM estimate, denoted as and . For this purpose, formula (9) is used, with replaced by and replaced by , where indicates a combined dataset of the blocks from all M = 120 states along the four edges. Note that actually depends only on the blocks from the particular edge to which BAR is applied. Similarly as above, the average in Eq.(9) can be approximated by using, for example, 200 randomly selected combined datasets.
Results and Discussion
Results from BAR and UWHAM
We first calculated the change of free energy along each edge based on BAR to evaluate the hysteresis of cycle closure in both the unbound and bound states. The free energy change along each edge in the unbound state is shown in Figure 2a. The hysteresis is the summation of free energy change along each edge to form the closed thermodynamic cycle, which is expressed as = −8.38 − 6.80 + 4.63 + 10.73 = 0.18 (kcal/mol). With consideration of the standard errors associated with the free energy estimations along each edge by using fractional replication methods, the value of hysteresis shows no significant difference from zero. In this case, the source of this small difference comes from the unbiased errors arising from the random fluctuations in the sampling of the configurational space. In Figure 2b, it shows the free energy change along each edge in the bound state with hysteresis as = −10.02−8.10+ 4.15 + 11.19 = −2.78 (kcal/mol). Based on the model proposed by Wang et al.71 (also see the supporting information), if we assume the hysteresis is Gaussian distributed with mean 0 then the standard deviation. The fact that indicates that it is highly unlikely that the calculations are converged and there should be some systematic errors coming from the incomplete sampling of the configurational space in the case of bound state of the perturbations.
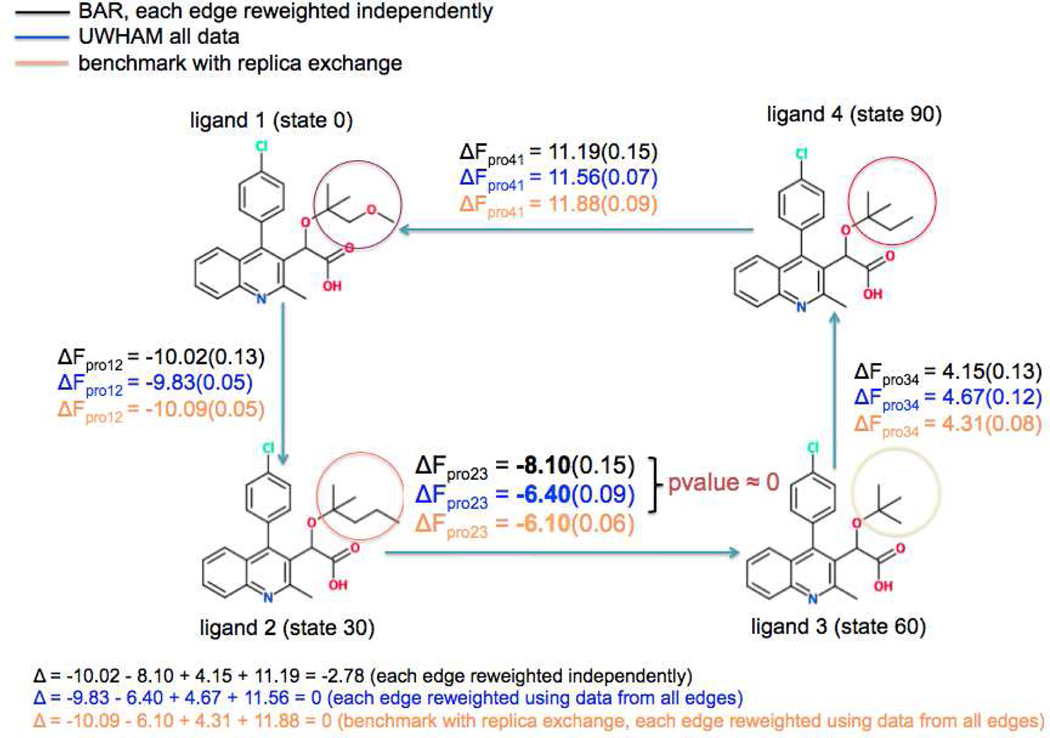
In order to tackle the problem of large hysteresis effects and improve the reliability of the free energy predictions, we applied the UWHAM analysis to estimate the free energy change along each edge in the bound state with results summarized in Figure 3. Along each edge, the value with black indicates the result from BAR, while the value with blue represents the estimation from UWHAM. Tests of statistical hypotheses were performed along each edge with the null hypothesis as ΔFBAR = ΔFUWHAM and alternative hypothesis as ΔFBAR ≠ ΔFUWHAM. P-value was computed based on P-value = , where Z is standard normal, and SED is the standard error for the difference between UWHAM and BAR estimates based on fractional replication method as discussed in the Method section. The calculated P-values are smaller than 0.05 along the edges of ligand 2 to ligand 3, ligand 3 to ligand 4 and ligand 4 to ligand 1, which indicates strong evidence against the null hypothesis. Hence, we can conclude that the differences between the predictions from BAR and UWHAM are statistically significant along these edges. On the other hand, the calculated P-value along the edge of ligand 1 to ligand 2 is 0.11, which suggests that the evidence against the null hypothesis is not as strong as that from the other three edges.
Figure 3:
Comparison of free energy change along each edge in the bound state estimated from BAR and UWHAM
To serve as the benchmark for the comparisons between the two reweighting methods, we further adopted a better converged dataset from replica exchange simulations and obtained the free energy estimations using UWHAM as shown in orange. We observe that the largest discrepancy between the calculations from BAR and benchmark lies in the edge of ligand 2 to ligand 3 with a discrepancy of 2.00 kcal/mol. Such a large bias from the benchmark indicates the existence of a sampling issue arising from this edge. Interestingly, we observed that this edge of transformation from ligand 2 to ligand 3 has the largest perturbation in terms of ligand structures, which involves growing two heavy atoms in the environment. In the other edges of the thermodynamic cycle, the perturbations of ligand structures are smaller. The underlying rationale for the poorly converged simulation datasets generated along the edge of ligand 2 to ligand 3 is that it involves a larger perturbation of the local environment by the structural change to the ligand in this mutation, associated with higher barriers between free energy basins which are only rarely crossed at some states. In order to overcome this quasi-ergodicity problem, we apply UWHAM to include all the λ-states in the thermodynamic cycle with additional information arising from states along the alternative mutation pathway consisted of the other three edges. As we expect, ΔFpro23 estimated from UWHAM of all the states agrees with the benchmark results better, which suggests that the UWHAM approach to reweighting data points across all of the λ-states under study in the cycle to estimate the free energy change along each edge is a superior method to use in the case of several ligands forming a closed cycle perturbation map, compared with analyzing each edge using BAR separately. We have also considered another example for the FEP calculations involving three congeneric ligands forming a perturbation path of closed triangle as shown in the Supporting Information. Interestingly, the free energy estimation along the edge with the largest discrepancy between BAR and benchmark are also improved by applying UWHAM to include all the λ-states in the triangular cycle. Such an improvement may be a more general result based on the two examples in our study. It is not however true that the UWHAM estimate will always be a better estimate than the BAR estimate along all the edges. When there are significant discrepancies between the BAR and UWHAM estimates along more than one edge, it is not clear how to choose the best estimate - BAR or UWHAM. Instead the discrepancy between UWHAM and BAR can be used as a guide to decide where to focus additional simulations. Nevertheless, for the two examples we studied the discrepancy between the UWHAM and BAR estimates is much greater along one of the edges than the others, and we conjecture that for cases like this, the conclusion that UWHAM provides the better estimate will apply.
Results from LWHAM - Determination of the Optimal Neighborhood Size
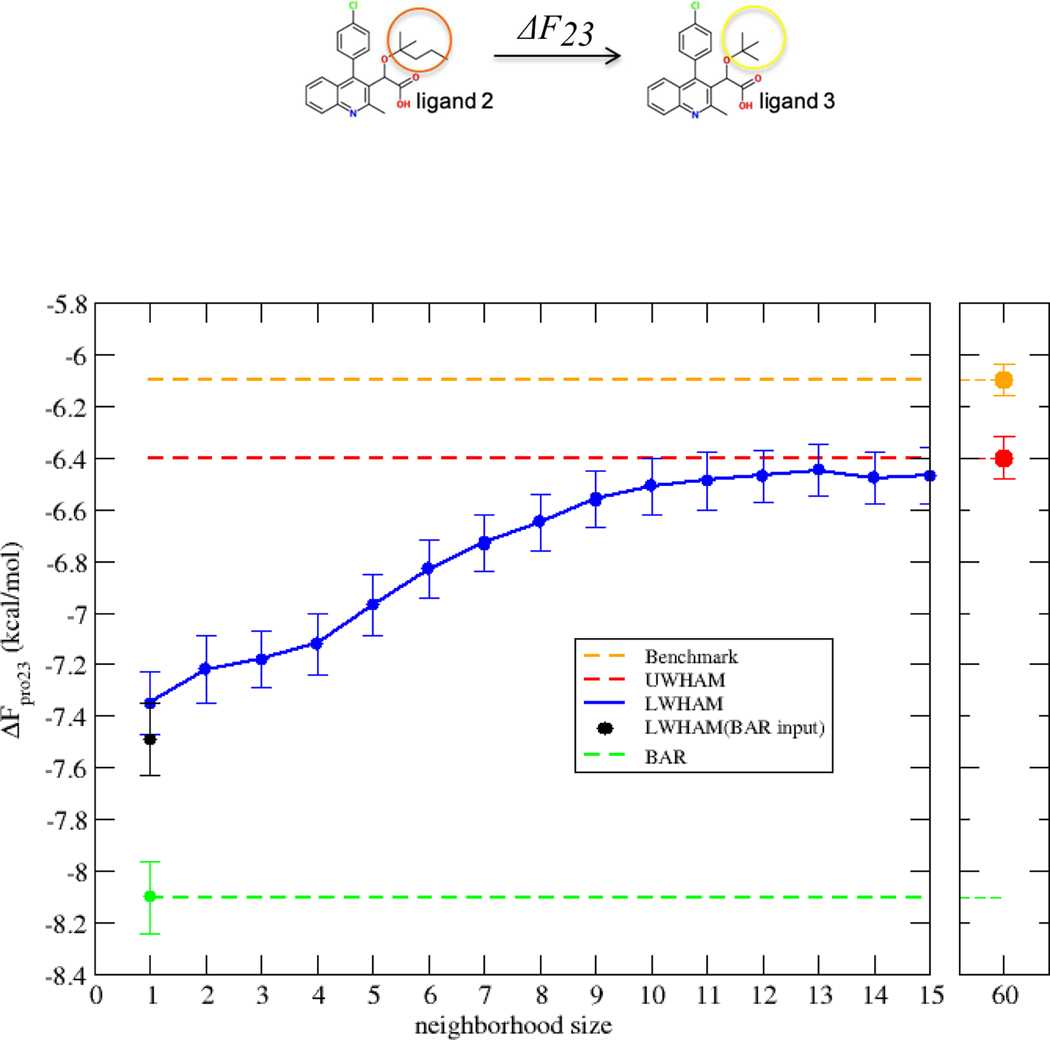
As has been discussed,71 FEP calculations for several congeneric ligands binding to the same receptor usually involve the buildup of multiple cycle closures which correspond to a network of mutation paths. One can foresee that as the network of the perturbation paths grows more complicated, more λ-states are required to connect all the nodes. We note that the computational cost of UWHAM grows quadratically as the number of thermodynamic states under study increases.23 A more feasible and effective way to analyze simulations from a large number of ensembles is based on LWHAM. A key question for applying LWHAM to estimate the free energy change along each edge is to determine the optimal neighborhood size in the analysis. In this study, we use the edge defined by the transformation of ligand 2 to ligand 3 in the bound state as an example to demonstrate the choice of optimal neighborhood size. Figure 4 displays the comparison of LWHAM results obtained from different neighborhood sizes with UWHAM and BAR results. The red horizontal line indicates the result from the UWHAM approach; the green horizontal line indicates the result from the BAR approach; the orange horizontal line indicates the result from the benchmark. The blue line with dots indicates the results from the LWHAM approach, with each dot representing the free energy estimation provided by LWHAM using a different neighborhood size. Here a neighborhood size of n includes both n states from the left and right of the reference state, i.e. the neighborhood is 2 × n. LWHAM results obtained from different neighborhood sizes always lie between the two horizontal lines representing the results from UWHAM and BAR. When the neighborhood size was set to ±1, the calculated ΔFpro23 from LWHAM is close to the result by reweighting with BAR. But it is an improvement over BAR because for LWHAM with n = ±1 both adjacent states, i + 1 and i − 1 contribute to estimate of the density of states for state i, whereas using BAR leads to two different estimates of the density of states for state i. As the neighborhood size increases in the LWHAM analysis to include more and more states, the calculated ΔFpro23 gradually reaches a plateau value approaching the result obtained by reweighting all the states using UWHAM. This indicates that configurations from neighboring states within a certain range make a significant contribution to the free energy estimation, while the additional contribution from configurations generated at states further away with little overlap to the reference states becomes negligible. Therefore, an advantage of applying LWHAM compared with UWHAM reweighting is that a neighborhood size can be chosen such that LWHAM involves reweighting observations only across neighboring states which contribute significantly to the free energy estimate instead of all states in the cycle, which can be much less computationally expensive.
Figure 4:
Comparison of LWHAM results obtained from different neighborhood size with UWHAM, BAR and benchmark results. The neighborhood (2 × n) is twice the value of the neighborhood size (n) indicated on the abscissa.
Figure 4 shows that for this example when the neighborhood size of ±12 is chosen in the LWHAM analysis, the prediction of is a very close to the result from UWHAM with consideration of the standard errors, while LWHAM only requires 10% ~ 20% of the computational time compared with UWHAM. The timing of UWHAM and LWHAM and their convergence behavior as the amount of simulation data increase have been studied on selected systems22,23. In summary, these results demonstrate the potential that LWHAM serves as a fast and accurate approximation to UWHAM to incorporate information from multiple neighboring simulations for estimating binding free energies.
LWHAM Reweighting Using BAR Input Data
Another appealing advantage of applying LWHAM is that LWHAM analyses do not require full biasing matrices as inputs. As mentioned in Section [Simulation Setup], when constructing the biasing matrix for UWHAM, we need to evaluate the potential energy of each configuration using the Hamiltonian function of each state. Therefore, UWHAMing all data requires the binding complex in FEP simulations includes all the ligands in the perturbation map. Suppose the simulations and analyses are accomplished for a perturbation map and more ligands are desired to add into the map. We have to redesign and rerun the simulation at each state in the original perturbation map to include the additional ligands so that UWHAM can be applied for the new perturbation map. On the other hand, inputs for BAR analyses contain much less information. Suppose we plan to analyze a perturbation map using BAR. The binding complex simulated at each edge only includes two ligands; the potential energies of each configuration are evaluated using the Hamiltonian functions of the original state at which the configuration is collected and the nearest neighbors in the same edge; and more ligands can be added to the perturbation map without rerunning any simulations at the states in the original map.
The complexity of inputs of LWHAM depends on the neighborhood size. When the neighborhood contains every state in the perturbation map, the inputs of LWHAM are the same as the inputs of UWHAM. However, when the neighborhood size decreases to one, the inputs of LWHAM are as simple as the inputs of BAR except for the state at the vertices in the perturbation map. If we plan to analyze the perturbation map shown by Fig.3 using BAR, we usually run two simulations at each vertex state. For example, the binding complex in the first simulation at the 60th state includes ligand 3 and ligand 2, where ligand 3 is real and ligand 2 is virtual. We then evaluate the potential energy for each configuration generated from this simulation using the Hamiltonian functions of the 59th state and the 60th state, which belong to the leg at the bottom. The binding complex of the other simulation at the 60th state includes ligand 3 and ligand 4, where ligand 3 is real and ligand 4 is virtual. We evaluate the potential energy for each configuration generated from the second simulation using the Hamiltonian functions of the 60th state and the 61th state, which belong to the leg at the right hand side. If we plan to analyze the same perturbation map using LWHAM and the neighborhood size is one, we run a single simulation at the 60th state, in which the binding complex includes ligand 2, 3, and 4. The ligand 3 is real and both ligand 2 and 4 are virtual. Then we evaluate the potential energy for each configuration generated from this single simulation using the Hamiltonian functions of the 59th, the 60th, and the 61th state to construct the input file for LWHAM.
Here we introduce an approximate approach to apply LWHAM using the inputs of BAR analyses directly. Again, let’s use the perturbation map shown by Fig.3 and the 60th state as examples. Suppose the simulations are set up to be analyzed by BAR, and two simulations are run at each vertex state. Although the Hamiltonian functions of the two simulations run at the 60th state (that we mentioned above) are the same, the raw data cannot be mixed together for the LWHAM analysis. For the configurations generated by the simulation with ligand 3 and ligand 2, it is not possible to evaluate their potential energies using the Hamiltonian function of the 61th state without manipulating the configurations because ligand 4 is not included in the original simulation; and for the configurations generated by the simulation with ligand 3 and ligand 4, it is not possible to evaluate their potential energies using the Hamiltonian function of the 59th state either. However, these two simulations can be treated as simulations run at two different states even though their Hamiltonian functions are the same. In other words, we split each state at the vertices into two states, and there are no biases between these two split states. After this simple revision of the perturbation map, we can run LWHAM analyses using the inputs to BAR directly. We applied this approach to the the perturbation map shown by Fig.3, and the free energy differences calculated for edges are listed in Table. 1. The results are close to the LWHAM estimates reported in Fig.4 when the neighborhood size is one. There is a side effect of this revision of the perturbation maps: the physical state of each ligand is now represented by two states and the free energy difference between them is nonzero. In this case, the largest difference between the two split states is ~ 0.02kcal/mol. We use the average free energy value of the two split states for the physical state of each ligand during the calculation of relative binding affinities.
Table 1:
Free energy changes along each edge in the bounding state, ΔF(kcal/mol), estimated by LWHAM using the BAR inputs compared with the results estimated by UWHAM and BAR.
| pro12 | pro23 | pro34 | pro41 | |
|---|---|---|---|---|
| LWHAM | −9.22 ± 0.11 | −7.49 ± 0.14 | 4.79 ± 0.12 | 11.92 ± 0.14 |
| UWHAM | −9.83 ± 0.05 | −6.40 ± 0.09 | 4.67 ± 0.12 | 11.56 ± 0.07 |
| BAR | −10.02 ± 0.13 | −8.10 ± 0.15 | 4.15 ± 0.13 | 11.19 ± 0.15 |
Heat Map of the Overlapping States Matrix
In addition to the benefits of applying LWHAM discussed above, LWHAM (or ST-SWHAM) can also provide information to optimize FEP simulations. Suppose we apply ST-SWHAM with the global jump proposal (Eq.(7)) to analyze a raw data set. The average probability of jumping from the γth state to the αth state is
| (10) |
where ui ∈ γ denotes that ui is one of the observations collected at the γth state; p(α|ui;ζ,π0) is defined by Eq.(7) and Nγ is the total number of observations collected at the γth state. The distribution Pγα(ζ, π0) is normalized to unity:
| (11) |
where M is the total number of states. When the ST-SWHAM analysis converges, the probability Pγα(ζ, π0) can be rewritten as
| (12) |
where , , and are the UWHAM maximum likelihood estimates of free energies, partition functions and density of states, respectively.
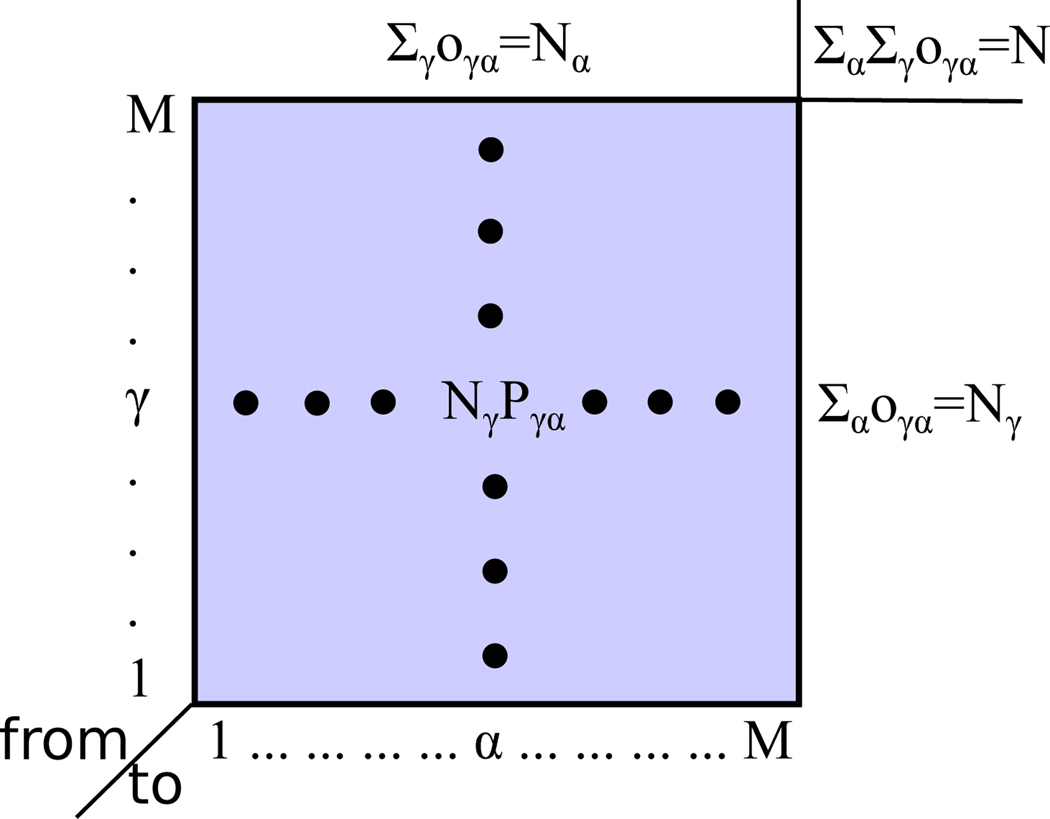
Next let’s consider a matrix O that is defined by the following equation
| (13) |
Fig.5 shows an illustration of the matrix O. On one hand, the sum of the matrix elements at the γth row is Nγ; and the sum of all matrix elements is
| (14) |
where N is the total number of observations. We can interpret the rows of this matrix as follows. Consider that this matrix represents N ST-SWHAM cycles that contain N global jumps. During these N cycles, each data point in the raw data ensemble is resampled once on average because observations are chosen uniformly to resample when the ST-SWHAM analysis converges. Nγ of the total N jumps start from the γth state; and oγα of those jumps starting from the γth state end at the αth state. On the other hand, the sum of the matrix elements at the αth column is also Nα due to the UWHAM equations
| (15) |
Figure 5:
Illustration of the overlapping states matrix.
Similarly, this implies that Nα of the total N jumps end at the αth states; and oγα of those jumps ending at the αth state start from the γth state. When the length of the simulation at each state is sufficiently long, the matrix O converges to a symmetric matrix,
| (16) |
Namely, the detailed balance condition is satisfied. This can be seen by rewriting the matrix element oγα as
| (17) |
where the labels (γ,α) appear symmetrically on the right hand side of Eq.(17). The approximation becomes exact when the simulation at each state converges.
Furthermore, rewriting Eq.(13) as
| (18) |
shows that the matrix elements oγα at the αth column are proportional to the contributions of the observations of the γth state to the partition function of the αth state. If the observations observed at the γth state make a large contribution to the partition function of the αth state, the probability of observing those configurations at the αth state is large. Therefore, the column elements of the matrix O provide a quantitative measure of the overlap between pairs of alchemical/thermodynamic states. Analogous to adjusting the spacing between states in replica exchange simulations based on acceptance ratios to achieve better sampling, we can improve FEP simulations based on the overlap between states to obtain better estimates of the binding affinity differences along the edges of the thermodynamic cycle.
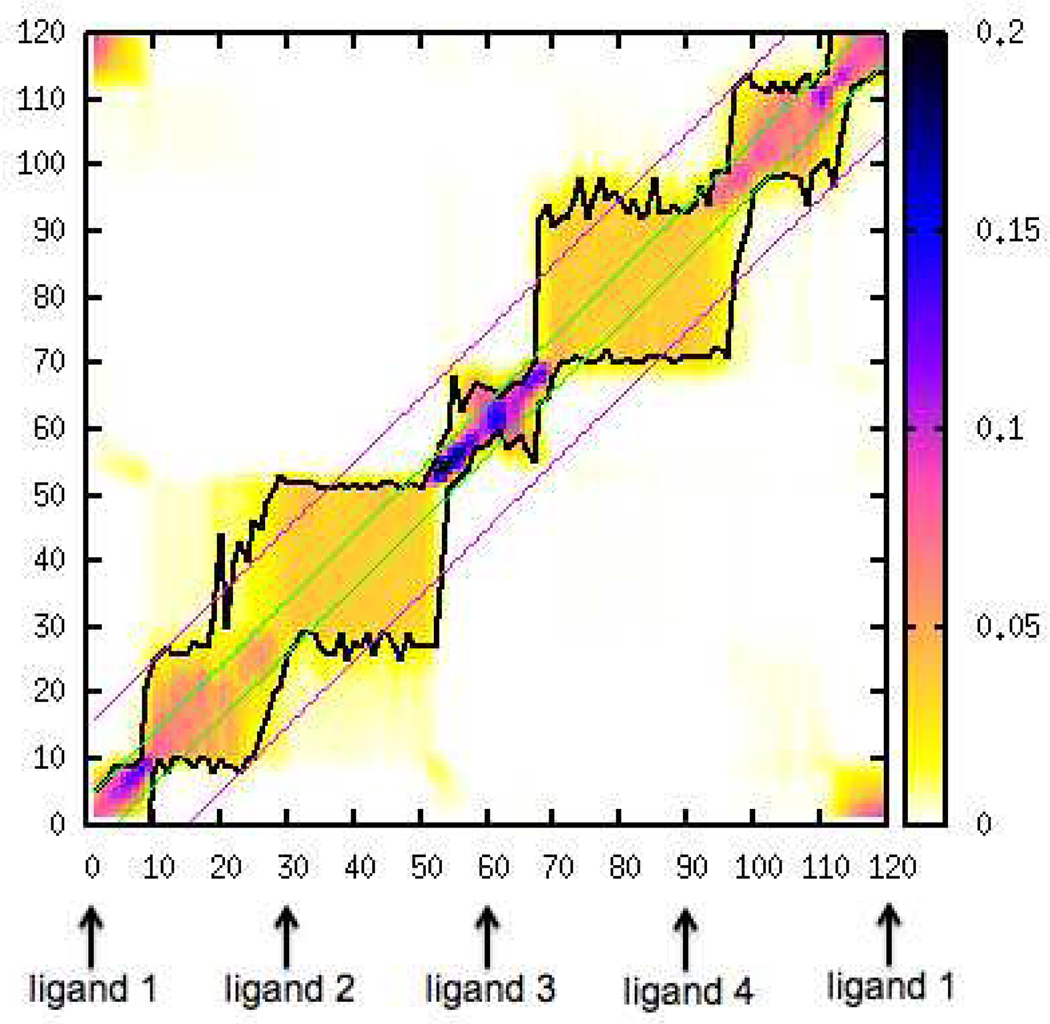
Fig.6 shows the heat map that represents the overlapping states matrix constructed from our FEP simulations of 120 states that form the closed cycle. Because the number of observations at every state is the same, the elements of the matrix are simplified to Pγα instead of NγPγα; and the sums of elements in rows or in columns are normalized to unity. The black lines in Fig.6 indicate upper and lower boundaries within which the neighbors (including itself) contribute 85% of the partition function.
Figure 6:
Heat map of the overlapping state matrix. The black lines indicate the boundaries of 85% of the total contribution of the partition function of each diagonal state; the green lines indicate the neighborhood size of 4 for each state; the pink lines indicate the neighborhood size of 15 for each state. The raw data set obtained from state 61 shows the narrowest overlap with its neighbors; and the raw data set obtained from state 25 shows the widest overlap with its neighbors.
Looking at the overlap matrix heat map it is apparent that the extent to which each of the 120 alchemical/thermodynamic states overlaps with its neighbors varies substantially. The raw data generated at states numbered 30–50 and 70–90 have wider overlaps with their neighbors compared with the raw data generated at other states. In this region, the contribution of each state to its own partition function, which is represented by the diagonal element of the overlapping state matrix, is around 5%. The raw data generated at states numbered 50–70 have much narrower overlaps with their neighbors. In this region, the contribution of each state to its own partition function is as high as 15 ~ 20%. As illustrated in Fig.3 we convert one hydrogen atom in a methyl group of the ligand to a methyl group from state 60 to 90; we convert the same hydrogen atom to a ethyl group from state 60 to 30. The heat map of overlapping states indicates that our choice of spacing between states causes narrow overlaps at the alchemical states that are adjacent to the physical state of the small ligand (ligand 3, state 60), and wide overlaps at the alchemical states that are adjacent to the physical states of the large ligand (ligand 2 and 4, state 30 and 90, respectively). Narrow overlap suggests that the majority in the weighted configuration ensemble (partition function) for that state are those configurations sampled at a small number of neighboring states and itself, which should be avoided because more overlaps with simulations at other states can decrease the probability of systematic errors. A likely reason for this is as follows. Suppose the simulation at one state does not converge because basins in the free energy landscape centered on that state are separated by high barriers. However, those basins are possibly well sampled at neighboring states where the landscape is less rugged. Applying UWHAM or LWHAM on the raw data will lead to improvements to the estimates for the unconverged state. Examples can be found in our previous work.23,64 As described in Sec. [Simulation Setup], the states numbered 60–70, which have the narrowest overlaps with their neighbors, are the states at which we switch on the Vdw interactions between the ligand 4 and the environment — water and the receptor. (Note that the Vdw interactions between different ligands are always turned off.) In other words, the simulations from state 60 to state 70 gradually create a larger size cavity in the solvated protein receptor environment. This corresponds to one of the largest alchemical perturbations of the ligand excluded volume from the full thermodynamic cycle. We expect to obtain better binding affinity estimates if the number of the states in this region is increased.
There are alternative methods to measure the overlap between pairs of states. Along with ST-SWHAM, we proposed another algorithm called RE-SWHAM that can solve the UWHAM equations stochastically by applying the replica exchange (RE) protocol instead of serial tempering to resample the raw data.64 One can construct a matrix of exchange acceptance ratios to measure the overlap between pairs of states simultaneously when running RE-SWHAM analyses. We also note a previous study by Klimovich, Shirts and Mobley who proposed to calculate a similar overlapping matrix (referred to as the KSM matrix)72, which is defined by
| (19) |
The element aγα of the KSM matrix represents the average probability of observing a configuration at the αth state using all the configurations generated at all the states weighted by their (UWHAM) probability of observation of the γth state. Note the element oγα of our overlapping states matrix represents the average probability of observing a configuration at the αth state using the configurations that are actually collected at the γ state during the FEP simulations. We can modify the KSM matrix by multiplying a factor Nα to each column and obtain a new matrix
| (20) |
Apparently, our overlapping matrix and the modified KSM matrix become the same when the simulation at each state converges, which is clear through a simple comparison between Eq.(17) and Eq.(20). In this study, we measure overlaps by using the matrix defined by Eq.(13) for the following reasons. First, the matrix elements oγα have a clear physical meaning — they are proportional to the contribution of the observations collected at the γth state to the partition function of the αth state. More importantly, the asymmetry of the matrix O is an indicator of the lack of convergence of the FEP simulations. This information is lost when forcing the detailed balance condition satisfied by taking the average of all data weighted by their UWHAM weights. Last but not the least, constructing a matrix defined by Eq.(20) is as computationally time consuming as solving the UWHAM equations exactly. For large data ensembles, it is convenient to analyze the data by LWHAM and construct an approximation of the overlapping states matrix O based on jump probabilities during the LWHAM analysis.
Conclusion
In this study, we have applied the analysis tools UWHAM and LWHAM to compute the free energies for data ensembles generated by multi-state simulations in FEP simulations of protein-ligand binding involving a closed perturbation map. When UWHAM is applied, it leads to the unique and best estimate of the density of states since measurements have been taken at all the simulation states in the thermodynamic cycle. Hence, it is guaranteed that there is no hysteresis of cycle closure for the ligand binding free energy predictions. This does not mean the UWHAM estimates are exact, only that the signed errors in the estimates are constrained to cancel. In the example we focus on, the simulations at some states along the edge of ligand 2 to ligand 3 are far from convergence, as indicated by the estimation of ΔFpro23 with BAR exhibiting considerable bias from the benchmark, while this can be improved by UWHAM or LWHAM to include the contributions from neighboring λ-states with lower barriers that can be more easily crossed.
To avoid the requirements of large memory and computational power to solve the UWHAM equations involving the weighting from all states, we pointed out that LWHAM can be used to effectively extract information from adjacent λ-states for free energy estimation based on a neighborhood criteria. To determine an optimal neighborhood size, we suggested plotting the estimate of the free energy change for an FEP transformation as a function of neighborhood size using LWHAM, and then looking for a plateau, as illustrated in Figure 4. We also described an approach that applies LWHAM using the smallest neighborhood size, ±1, to obtain the relative binding affinities using the same inputs as BAR but which removes the hysteresis and can lead to improved free energy estimates. By using the global jump formula of ST-SWHAM, we constructed the overlapping states matrix (jump probabilities matrix) to measure the extent of configurational space overlap. This overlapping states matrix serves as a useful tool to identify locations where additional λ-states can be added nearby to achieve better sampling.
Supplementary Material
Acknowledgement
This work was supported by NIH grants (GM30580 and R35GM132090), an NSF grant (1665032), and an NIH computer equipment grant (OD020095). This work also used Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation (ACI-1053575). Di Cui also gratefully acknowledges the support from Haoping Yu.
Footnotes
Supporting Information Available
Free energy change along each edge in a triangular cycle. Gaussian statistics analysis method. Block bootstrap analyses. This information is available free of charge via the Internet at http://pubs.acs.org.
References
- (1).Jorgensen WL. Efficient Drug Lead Discovery and Optimization. Acc. Chem. Res 2009, 42, 724–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Wang L. et al. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc 2015, 137, 2695–2703. [DOI] [PubMed] [Google Scholar]
- (3).Cournia Z; Allen B; Sherman W. Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model 2017, 57, 2911–2937. [DOI] [PubMed] [Google Scholar]
- (4).Chipot C; Rozanska X; Dixit SB. Can free energy calculations be fast and accurate at the same time? Binding of low-affinity, non-peptide inhibitors to the SH2 domain of the src protein. J. Comput.-Aided Mol. Des. 2005, 19, 765–770. [DOI] [PubMed] [Google Scholar]
- (5).Lybrand TP; McCammon JA; Wipff G. Theoretical calculation of relative binding affinity in host-guest systems. Proc. Natl. Acad. Sci. U. S. A 1986, 83, 833–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Jorgensen WL; Ravimohan C. Monte Carlo simulation of differences in free energies of hydration. J. Chem. Phys 1985, 83, 3050–3054. [Google Scholar]
- (7).Zwanzig RW. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys 1954, 22, 1420–1426. [Google Scholar]
- (8).König G; Hudson PS; Boresch S; Woodcock HL. Multiscale Free Energy Simulations: An Efficient Method for Connecting Classical MD Simulations to QM or QM/MM Free Energies Using Non-Boltzmann Bennett Reweighting Schemes. J. Chem. Theory Comput 2014, 10, 1406–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Wang L; Berne BJ; Friesner RA. On achieving high accuracy and reliability in the calculation of relative protein-ligand binding affinities. Proc. Natl. Acad. Sci. U. S. A 2012, 109, 1937–1942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Harder E. et al. OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. J. Chem. Theory Comput 2016, 12, 281–296. [DOI] [PubMed] [Google Scholar]
- (11).Harvey MJ; Giupponi G; Fabritiis GD. ACEMD: Accelerating Biomolecular Dynamics in the Microsecond Time Scale. J. Chem. Theory Comput 2009, 5, 1632–1639. [DOI] [PubMed] [Google Scholar]
- (12).Friesner RA; Banks JL; Murphy RB; Halgren TA; Klicic JJ; Mainz DT; Repasky MP; Knoll EH; Shelley M; Perry JK; Shaw DE; Francis P; Shenkin PS. Glide: A New Approach for Rapid, Accurate Docking and Scoring. 1. Method and Assessment of Docking Accuracy. J. Med. Chem 2004, 47, 1739–1749. [DOI] [PubMed] [Google Scholar]
- (13).Genheden S; Ryde U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discovery 2015, 10, 449–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Chodera JD; Mobley DL; Shirts MR; Dixon RW; Branson K; Pande VS. Alchemical Free Energy Methods for Drug Discovery: Progress and Challenges. Curr. Opin. Struct. Biol 2011, 21, 150–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Christ CD; Mark AE; van Gunsteren WF. Basic ingredients of free energy calculations: A review. J. Comput. Chem 2010, 31, 1569–1582. [DOI] [PubMed] [Google Scholar]
- (16).Michel J; Essex JW. Prediction of protein–ligand binding affinity by free energy simulations: assumptions, pitfalls and expectations. J. Comput.-Aided Mol. Des. 2010, 24, 639–658. [DOI] [PubMed] [Google Scholar]
- (17).Liu S; Wu Y; Lin T; Abel R; Redmann JP; Summa CM; Jaber VR; Lim NM; Mobley DL. Lead optimization mapper: automating free energy calculations for lead optimization. J. Comput.-Aided Mol. Des. 2013, 27, 755–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Michel J; Tirado-Rives J; Jorgensen WL. Energetics of Displacing Water Molecules from Protein Binding Sites: Consequences for Ligand Optimization. J. Am. Chem. Soc 2009, 131, 15403–15411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Steiner D; Oostenbrink C; Diederich F; Zurcher M; van Gunsteren WF. Calculation of binding free energies of inhibitors to plasmepsin II. J. Comput. Chem 2011, 32, 1801–1812. [DOI] [PubMed] [Google Scholar]
- (20).Tan Z. On a Likelihood Approach for Monte Carlo Integration. J. Am. Stat. Assoc 2004, 99, 1027–1036. [Google Scholar]
- (21).Tan Z; Gallicchio E; Lapelosa M; Levy RM. Theory of binless multi-state free energy estimation with applications to protein-ligand binding. J. Chem. Phys 2012, 136, 144102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Zhang BW; Arasteh S; Levy RM. The UWHAM and SWHAM Software Package. Sci. Rep 2019, 9, 2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Tan Z; Xia J; Zhang BW; Levy RM. Locally weighted histogram analysis and stochastic solution for large-scale multi-state free energy estimation. J. Chem. Phys 2016, 144, 034107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Tan Z. Optimally Adjusted Mixture Sampling and Locally Weighted Histogram Analysis. J. Comput. Graph. Stat 2017, 26, 54–65. [Google Scholar]
- (25).Bennett CH. Efficient estimation of free energy differences from Monte Carlo data. Comput. Phys 1976, 22, 245 – 268. [Google Scholar]
- (26).Shirts MR; Pande VS. Comparison of efficiency and bias of free energies computed by exponential averaging, the Bennett acceptance ratio, and thermodynamic integration. J. Chem. Phys 2005, 122, 144107. [DOI] [PubMed] [Google Scholar]
- (27).Lu N; Singh JK; Kofke DA. Appropriate methods to combine forward and reverse free-energy perturbation averages. J. Chem. Phys 2003, 118, 2977–2984. [Google Scholar]
- (28).Shirts MR; Chodera JD. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys 2008, 129, 124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Ferrenberg AM; Swendsen RH. Optimized Monte Carlo data analysis. Phys. Rev. Lett 1989, 63, 1195–1198. [DOI] [PubMed] [Google Scholar]
- (30).Widom B. Some Topics in the Theory of Fluids. J. Chem. Phys 1963, 39, 2808–2812. [Google Scholar]
- (31).Beck TL; Paulaitis ME; Pratt LR. The Potential Distribution Theorem and Models of Molecular Solutions; Cambridge University Press: Cambridge, 2006. [Google Scholar]
- (32).Marinari E; Parisi G. Simulated Tempering: A New Monte Carlo Scheme. Europhys. Lett 1992, 19, 451–458. [Google Scholar]
- (33).Lyubartsev AP; Martsinovski AA; Shevkunov SV; Vorontsov-Velyaminov PN. New approach to Monte Carlo calculation of the free energy: Method of expanded ensembles. J. Chem. Phys 1992, 96, 1776–1783. [Google Scholar]
- (34).Geyer CJ; Thompson EA. Annealing Markov Chain Monte Carlo with Applications to Ancestral Inference. J. Am. Stat. Assoc 1995, 90, 909–920. [Google Scholar]
- (35).Chodera JD; Shirts MR. Replica exchange and expanded ensemble simulations as Gibbs sampling: Simple improvements for enhanced mixing. J. Chem. Phys 2011, 135, 194110. [DOI] [PubMed] [Google Scholar]
- (36).Jurado KA; Wang H; Slaughter A; Feng L; Kessl JJ; Koh Y; Wang W; Ballandras-Colas A; Patel PA; Fuchs JR; Kvaratskhelia M; Engelman A. Allosteric integrase inhibitor potency is determined through the inhibition of HIV-1 particle maturation. Proc. Natl. Acad. Sci. U. S. A 2013, 110, 8690–8695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Patel D; Antwi J; Koneru PC; Serrao E; Forli S; Kessl JJ; Feng L; Deng N; Levy RM; Fuchs JR; Olson AJ; Engelman AN; Bauman JD; Kvaratskhelia M; Arnold E. A New Class of Allosteric HIV-1 Integrase Inhibitors Identified by Crystallographic Fragment Screening of the Catalytic Core Domain. J. Biol. Chem 2016, 291, 23569–23577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Sharma A; Slaughter A; Jena N; Feng L; Kessl JJ; Fadel HJ; Malani N; Male F; Wu L; Poeschla E; Bushman FD; Fuchs JR; Kvaratskhelia M. A New Class of Multimerization Selective Inhibitors of HIV-1 Integrase. PLoS Pathog. 2014, 10, 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Fader LD. et al. Discovery of BI 224436, a Noncatalytic Site Integrase Inhibitor (NCINI) of HIV-1. ACS Med. Chem. Lett 2014, 5, 422–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Christ F; Voet A; Marchand A; Nicolet S; Desimmie BA; Marchand D; Bardiot D; Van der Veken NJ; Van Remoortel B; Strelkov SV; De Maeyer M; Chaltin P; Debyser Z. Rational design of small-molecule inhibitors of the LEDGF/p75-integrase interaction and HIV replication. Nat. Chem. Biol 2010, 6, 442–448. [DOI] [PubMed] [Google Scholar]
- (41).Cherepanov P; Ambrosio ALB; Rahman S; Ellenberger T; Engelman A. Structural basis for the recognition between HIV-1 integrase and transcriptional coactivator p75. Proc. Natl. Acad. Sci. U. S. A 2005, 102, 17308–17313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Berendsen H; van der Spoel D; van Drunen R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun 1995, 91, 43–56. [Google Scholar]
- (43).Hess B; Kutzner C; van der Spoel D; Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput 2008, 4, 435–447. [DOI] [PubMed] [Google Scholar]
- (44).Pronk S; Pall S; Schulz R; Larsson P; Bjelkmar P; Apostolov R; Shirts MR; Smith JC; Kasson PM; van der Spoel D; Hess B; Lindahl E. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Hansen N; van Gunsteren WF. Practical Aspects of Free-Energy Calculations: A Review. J. Chem. Theory Comput 2014, 10, 2632–2647. [DOI] [PubMed] [Google Scholar]
- (46).Pearlman DA. A Comparison of Alternative Approaches to Free Energy Calculations. J. Phys. Chem 1994, 98, 1487–1493. [Google Scholar]
- (47).Jorgensen WL; Chandrasekhar J; Madura JD; Impey RW; Klein ML. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys 1983, 79, 926–935. [Google Scholar]
- (48).Jorgensen WL; Jenson C. Temperature dependence of TIP3P, SPC, and TIP4P water from NPT Monte Carlo simulations: Seeking temperatures of maximum density. J. Comput. Chem 1998, 19, 1179–1186. [Google Scholar]
- (49).Slaughter A; Jurado KA; Deng N; Feng L; Kessl JJ; Shkriabai N; Larue RC; Fadel HJ; Patel PA; Jena N; Fuchs JR; Poeschla E; Levy RM; Engelman A; Kvaratskhelia M. The mechanism of H171T resistance reveals the importance of Nδ-protonated His171 for the binding of allosteric inhibitor BI-D to HIV-1 integrase. Retrovirology 2014, 11, 100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Schrodinger Suite< 2018 Protein Preparation Wizard; Schrodinger,LLC: New York, 2018. [Google Scholar]
- (51).Olsson MHM; SÞndergaard CR; Rostkowski M; Jensen JH. PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pKa Predictions. J. Chem. Theory Comput 2011, 7, 525–537. [DOI] [PubMed] [Google Scholar]
- (52).Lindorff-Larsen K; Piana S; Palmo K; Maragakis P; Klepeis JL; Dror RO; Shaw DE. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins: Struct., Funct., Bioinf 2010, 78, 1950–1958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA. Development and testing of a general amber force field. J. Comput. Chem 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- (54).Jakalian A; Jack DB; Bayly CI. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem 2002, 23, 1623–1641. [DOI] [PubMed] [Google Scholar]
- (55).Gunsteren WFV; Berendsen HJ. C. A Leap-frog Algorithm for Stochastic Dynamics. Mol. Simul 1988, 1, 173–185. [Google Scholar]
- (56).Berendsen HJC; Postma JPM; van Gunsteren WF; DiNola A; Haak JR. Molecular dynamics with coupling to an external bath. J. Chem. Phys 1984, 81, 3684–3690. [Google Scholar]
- (57).Parrinello M; Rahman A. Polymorphic Transitions In Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys 1981, 52, 7182–7190. [Google Scholar]
- (58).Hess B; Bekker H; Berendsen HJC; Fraaije JGEM LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem 1997, 18, 1463–1472. [Google Scholar]
- (59).Essmann U; Perera L; Berkowitz ML; Darden T; Lee H; Pedersen LG. A smooth particle mesh Ewald method. J. Chem. Phys 1995, 103, 8577–8593. [Google Scholar]
- (60).Darden T; York D; Pedersen L. Particle mesh Ewald: An N.log(N) method for Ewald sums in large systems. J. Chem. Phys 1993, 98, 10089–10092. [Google Scholar]
- (61).Jang S; Shin S; Pak Y. Replica-Exchange Method Using the Generalized Effective Potential. Phys. Rev. Lett 2003, 91, 058305. [DOI] [PubMed] [Google Scholar]
- (62).Gallicchio E; Lapelosa M; Levy RM. Binding Energy Distribution Analysis Method (BEDAM) for Estimation of Proteinï¿œ H RLigand Binding Affinities. J. Chem. Theory Comput 2010, 6, 2961–2977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Liu P; Kim B; Friesner RA; Berne BJ. Replica exchange with solute tempering: A method for sampling biological systems in explicit water. Proc. Natl. Acad. Sci. U. S. A 2005, 102, 13749–13754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Zhang BW; Xia J; Tan Z; Levy RM. A Stochastic Solution to the Unbinned WHAM Equations. J. Phys. Chem. Lett 2015, 6, 3834–3840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Zhang BW; Dai W; Gallicchio E; He P; Xia J; Tan Z; Levy RM. Simulating Replica Exchange: Markov State Models, Proposal Schemes, and the Infinite Swapping Limit. J. Phys. Chem. B 2016, 120, 8289–8301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Chernick M. Bootstrap Methods: A Guide for Practitioners and Researchers, 2nd ed.; Wiley: Hoboken,NJ, 2008. [Google Scholar]
- (67).Carlstein E. The Use of Subseries Values for Estimating the Variance of a General Statistic from a Stationary Sequence. Ann. Statist 1986, 14, 1171–1179. [Google Scholar]
- (68).Lahiri SN. Theoretical comparisons of block bootstrap methods. Ann. Statist 1999, 27, 386–404. [Google Scholar]
- (69).Mccarthy PJ. Pseudoreplication half samples. Review of International Statistical Institute 1969, 37, 239–264. [Google Scholar]
- (70).Gurney M; Jewett RS. Constructing orthogonal replications for variance estimation. J. Am. Stat. Assoc 1975, 70, 819–821. [Google Scholar]
- (71).Wang L; Deng Y; Knight JL; Wu Y; Kim B; Sherman W; Shelley JC; Lin T; Abel R. Modeling Local Structural Rearrangements Using FEP/REST: Application to Relative Binding Affinity Predictions of CDK2 Inhibitors. J. Chem. Theory Comput 2013, 9, 1282–1293. [DOI] [PubMed] [Google Scholar]
- (72).Klimovich PV; Shirts MR; Mobley DL. Guidelines for the analysis of free energy calculations. J. Comput.-Aided Mol. Des. 2015, 29, 397–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.