Nonparametric Bayes Models of Fiber Curves Connecting Brain Regions

Abstract

In studying structural inter-connections in the human brain, it is common to first estimate fiber bundles connecting different regions relying on diffusion MRI. These fiber bundles act as highways for neural activity. Current statistical methods reduce the rich information into an adjacency matrix, with the elements containing a count of fibers or a mean diffusion feature along the fibers. The goal of this article is to avoid discarding the rich geometric information of fibers, developing flexible models for characterizing the population distribution of fibers between brain regions of interest within and across different individuals. We start by decomposing each fiber into a rotation matrix, shape and translation from a global reference curve. These components are viewed as data lying on a product space composed of different Euclidean spaces and manifolds. To nonparametrically model the distribution within and across individuals, we rely on a hierarchical mixture of product kernels specific to the component spaces. Taking a Bayesian approach to inference, we develop efficient methods for posterior sampling. The approach automatically produces clusters of fibers within and across individuals. Applying the method to Human Connectome Project data, we find interesting relationships between brain fiber geometry and reading ability. Supplementary materials for this article, including a standardized description of the materials available for reproducing the work, are available as an online supplement.

1. Introduction

There has been dramatically increasing interest in recent years in connectomics, which studies functional and structural inter-connections in the humanbrain (Jbabdi et al. 2015; Glasser et al. 2016; Park and Friston 2013; Fornito, Zalesky, and Breakspear 2013). This interest has been spurred by the development of new imaging technologies, which allow researchers to noninvasively peer into the human brain and obtain data on connections. The focus of this article is on structural connectomes, corresponding to fiber bundles that are estimated from diffusion magnetic resonance imaging (dMRI) and structural MRI (Smith et al. 2012; Girard et al. 2014). Focusing on two regions of interest (ROIs), Figure 1 shows the fiber connections for four individuals.

Figure 1.

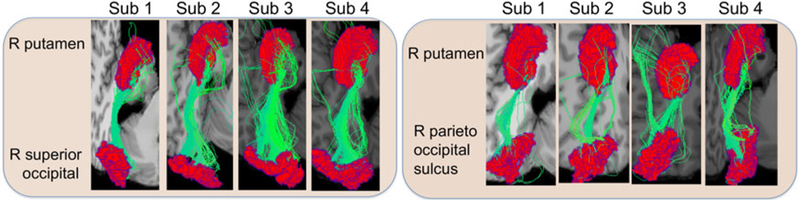
Examples of fiber curves connecting two different pairs of regions in four subjects.

Fiber connections in each individual’s brain can be viewed as a type of object data. The current literature on statistical analysis of fiber tracts reduces the complex object data to simple summary statistics prior to analysis. For example, an adjacency matrix consisting of a count of fibers in each ROI pair (de Reus and van den Heuvel 2013; Fornito, Zalesky, and Breakspear 2013) is the most common connectome representation. The adjacency matrix is further reduced to a binary form (Durante, Dunson, and Vogelstein 2017; Durante and Dunson 2018) or to topological features of the network (Cheng et al. 2012; Fornito, Zalesky, and Breakspear 2013) to simplify the analysis. Representing the connectome as an adjacency matrix is appealing in its simplicity, but leads to an enormous loss of information. The rich geometric information of tracts is totally discarded. However, geometric features of the brain, such as brain size, shape, and cerebral cortex folding patterns, have been found to be related to cognition (Cachia et al. 2014; Rushton and Ankney 1996; Toro et al. 2008) and progression of neurodegenerative diseases (Cornea et al. 2017; Bachman et al. 2014; Querbes et al. 2009). As illustrated in Figure 1, there are varying numbers, locations and shapes of fiber connections; such geometric differences may be important in detecting and understanding group differences (Eden et al. 2015; Zhang, Allen et al. 2018). As we illustrate later in the article, utilizing geometry of fiber curves instead of simply the count, we can better distinguish subjects with good versus poor oral reading ability.

Clearly, the data represented in Figure 1 are functional data, and hence it is natural to think of applying functional data analysis (FDA) methodology (Gu, Pati, and Dunson 2014; Ramsay 2006; Srivastava, Wu et al. 2011; Müller 2008; Yang et al. 2016, 2017). However, most FDA methods are developed for much simpler cases in which there is a single function $y_i:\mathcal{T}\to \Re$ for each individual, with $T\subset \Re .$ For example, y_i may represent a growth curve with age for individual i (Srivastava, Wu et al. 2011; Müller 2008). There is also a rich literature on more elaborate FDA models for curve data (Wang, Chiou, and Mueller 2015), for example, allowing multivariate, hierarchical (Rodriguez, Dunson, and Gelfand 2009), spatial and temporal dependence structures (Yao, Müller, and Wang 2005). Even in more complex cases, the majority of the focus has been on one-dimensional curves $y_i:\mathcal{T}\to \Re ,$ using a rich variety of representations ranging from spline expansions to functional principal components analysis (FPCA) to Gaussian process-based models.

Fiber tracts correspond to many three-dimensional curves snaking through ${\Re }^3$ having different intersection points with two nonregularly shaped ROIs. There is clear clustering and heterogeneity among individuals. It is not obvious how to define a model for these data to sufficiently and flexibly capture the important characteristics without discarding too much information or becoming computationally intractable. There is a rich literature on nonparametric Bayesian models for functional data, which induce clustering (Rodríguez, Dunson, and Gelfand 2009) and can even allow joint modeling of functional predictors with a response (Bigelow and Dunson 2009), but these methods focus on the case in which a single function y_i is observed for each individual.

We propose a novel approach, which characterizes each fiber curve in terms of its rotation, shape, and translation from a global reference curve. This allows us to define a nonparametric model for the fiber curve data through a dual representation of the data on a product space. We define a mixture of product kernels motivated by Bhattacharya and Dunson (2010b, 2012), who showed that Dirichlet process mixtures of product kernels having support on different manifolds can lead to consistent density estimation. They did not consider data consisting of rotation matrices or allow nested dependence, as we obtain due to nesting of the fibers within each individual’s brain.

Section 2 describes the basic data structure and representation of fiber curves. Section 3 proposes a product mixture model for fiber connections in an individual’s brain, and Section 4 proposes a nested Dirichlet process model for modeling fiber curves for a population of individuals. Section 5 summarizes analyses of human brain connectomics data. Section 6 discusses the results.

2. Fiber Curves Extraction and Representation

2.1. Data Description

We use a state-of-the-art tractography algorithm (Smith et al. 2012; Girard et al. 2014) to generate the fiber tracts relying on two steps. First, high angular resolution diffusion imaging (HARDI) techniques are used to estimate the fiber orientation distribution function (ODF) at each location (Descoteaux et al. 2009) (implemented in dipy (Garyfallidis et al. 2014)). Next, streamlines following the principal directions of the fiber ODF are constructed by probabilistic tractography algorithms under local continuity constraints. Anatomical structure information is used to guide selection of where to start and stop the streamlines (Smith et al. 2012; Girard et al. 2014). The final constructed three-dimensional curves are assumed to represent the most likely pathways through the diffusion profile delineated by the fiber ODF. We refer to these curves as fibers, though they may not exactly correspond to anatomical fibers in the brain.

Let T_j denote the jth subject’s tractography dataset. In general, T_j contains millions of fiber curves indicating how different regions of the brain are connected. Let y_ji represent a single fiber curve in T_j; the data on y_ji output by the tractography algorithm consist of hundreds of points along a curve, but we view $y_{ji}:[0,1]\to {\Re }^3$ as a parameterized curve that can be accurately approximated by spline interpolation of these data points. Figure 2(a) shows one example of the tractography dataset we generated for an individual’s brain.

Figure 2.

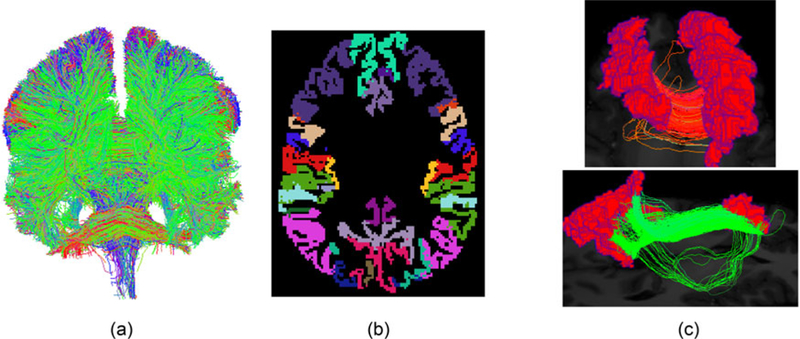
(a) One example of the whole tractography dataset for a brain. (b) The Desikan–Killiany parcellation of the cortical region. (c) Fiber curves connecting a pair of regions.

Directly analyzing all fibers in T_j is not realistic for several reasons. The data are huge (millions of fibers in each subject) and current statistical methods are ineffective in handling such big data for a sample of subjects. Second, the streamline datasets are usually in subject-specific spaces with different coordinate systems, and it is hard to directly compare any two tractography datasets.

In this article, we group each fiber in T_j based on the different anatomical regions it connects, and focus our analysis on fibers connecting two specific regions. To achieve this, each individual’s brain is first parcellated into different meaningful anatomical regions based on an existing template (Desikan et al. 2006). Figure 2(b) shows a parcellation of the brain using the Desikan–Killiany atlas. Then fiber curves connecting each pair of regions are extracted, as illustrated in Figure 2(c).

Our goal is to build a flexible but parsimonious Bayesian model to characterize the distribution of fiber curves connecting two ROIs within each individual and across a population of individuals. The extracted fibers $\left\{y_{ji},i=1,\dots ,n_j\right\}$ connecting r_a (ROI a) and r_b (ROI b) in subject j have some special properties, for example, y_ji’s always start from one region and end at another one (due to the preprocessing in Zhang, Descoteaux et al. (2018)) and they are smooth and follow similar white matter pathways. These properties make the underlying functional space ${\mathrm{\Omega }}_{\left(r_a,r_b\right)}$ much smaller comparing with Ω, where Ω is the entire functional space ${\mathcal{L}}^2\left([0,1],{\Re }^3\right)$ and ${\mathrm{\Omega }}_{\left(r_a,r_b\right)}$ is the functional space for fiber curves connecting r_a and r_b for all subjects in our dataset. To build an efficient model on the correct space parsimoniously, we consider a variance decomposition for fibers in ${\mathrm{\Omega }}_{\left(r_a,r_b\right)}.$

2.2. Variation Decomposition

When we treat a fiber y as a three-dimensional curve, there are five factors contributing to the variance: (1) translation, (2) rotation, (3) scaling, (4) reparameterization, and (5) shape, with (1)–(4) being shape-preserving transformations (Srivastava, Klassen et al. 2011). The shape of a fiber represents appearance after removing these shape-preserving transformations. Letting ${\mathcal{L}}^2\left([0,1],{\Re }^3\right)$ be a fiber, a translation of y is represented as y + a, where $a\in {ℝ}^3.$ The rotation of y is represented as O * y, where O ϵ SO(3) is a rotation matrix. Scaling represents the length of the fiber. Reparameterization of f is represented as $y(\gamma (s)),s\in [0,1],$ where γ is a warping function in $\mathrm{\Gamma },$ the set of all orientation-preserving diffeomorphisms of [0,1]. Reparameterization of f does not change the shape, it only changes the point-wise correspondence between fibers. In other words, if we let $g(s)=y(\gamma (s)),$ g passes through the same path as y, but g(s) is different from y(s) if y(s) ≠ s. The reparameterization component performs the role of aligning fibers (Kurtek et al. 2012), and reduces variability of the remaining shape component.

Figure 3 illustrates the shape components for 200 simulated fiber curves. As additional shape-preserving components are removed, the remaining shape part has decreasing cross-sectional variance at each point s ϵ [0,1]. Since fibers connecting two ROIs usually have similar lengths, we do not remove scaling. The reparameterization component does not contribute to the geometric appearance of fibers, and hence is removed in an alignment phase prior to statistical analysis.

Figure 3.

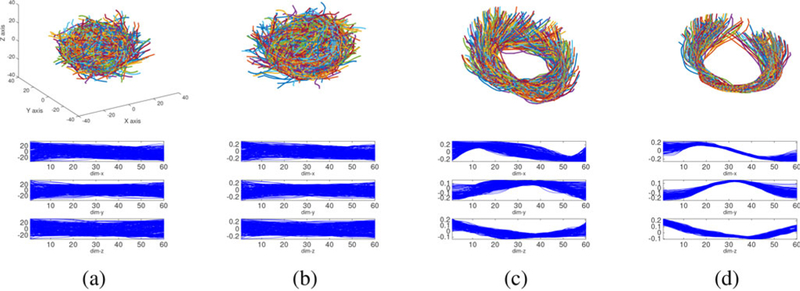
Shape components after removing different shape-preserving transformations. (a) Simulated raw three-dimensional curves. (b) Shape after removing translations and scalings. (c) Shape after removing translations, rotations, and scalings. (d) Shape after removing translations, rotations, scalings, and reparameterizations.

2.3. Estimating Manifold Components From Curves

As a preliminary step before defining a Bayesian model, we extract each component in the variance decomposition by using elastic shape analysis (Srivastava, Klassen et al. 2011). Given a set of fiber curves $\left\{y_1,\dots ,y_n\right\}$ in the connection (r_a, r_b), to separate the translation, we center each fiber by $y_i^c(\cdot )=y_i(\cdot )-{\mathit{c}}_i^{(1)},$ where ${\mathit{c}}_i^{(1)}={\int }_0^1{y}_i(s)\left|{\dot{y}}_i(s)\right|ds/L_{y_i},$ in which ${\dot{y}}_i(s)=d{y}_i\left(s\right)/ds$ and L_y is the length of fiber y. To separate rotation and reparameterization, we represent each fiber y as its square-root velocity function (SRVF) q(s), defined as $q(s)=\dot{y}(s)/\sqrt{\Vert \dot{y}(s)\Vert }.$ A rotation of y by O ϵ SO(3) is denoted as O * y and its SRVF becomes O * q. A reparameterization of y by $\gamma \in \mathrm{\Gamma }$ is denoted as $y(\gamma (s)),$ and its SRVF is denoted as $(q,\gamma )=(q\circ \gamma )\sqrt{\dot{\gamma }},$ where $\circ$ denotes the composition of two functions.

To align all fibers by separating the rotation and reparameterization, we estimate a template fiber first, denoted as $y_{\mu },$ and then align all fibers to the template. We formulate the calculation of $y_{\mu }$ and individual alignment as an iterative procedure: first initialize the mean function $y_{\mu }$ and its SRVF q_μ and then iteratively solve for

$$\begin{gathered} \left({\mathbf{O}}_i,{\gamma }_i\right)=\underset{\mathbf{O}\in SO(3),\gamma \in \mathrm{\Gamma }}{\text{argmin}}\Vert q_{\mu }-\mathbf{O}*\left(q_i,\gamma \right)\Vert ,\text{and} \\ {q}_{\mu }=n^{-1}\sum _{i=1}^n{\mathbf{O}}_i*\left(q_i,{\gamma }_i\right) \end{gathered}$$ (1)

for i = 1,..., n until convergence. We optimize O_i through Procrustes analysis and ${\gamma }_i$ through dynamic programming (Srivastava, Klassen et al. 2011). As the output of this iterative algorithm, for each fiber y_i, we obtain the best rotation O_i, reparameterization γ_i, to the template y_μ, and the shape part $g\text{(}s)={\mathbf{O}}_i*y_i\left({\gamma }_i(s)\right).$ To better model the rotation component and avoid an arbitrary reference point for the embedding to be introduced later, we apply a global rotation O_μ to each O_i so that the sample mean of the new rotated {O_i} is the identify matrix, where O_μ is the Karcher mean of the original rotations (estimated using the algorithm in Rentmeesters and Absil (2011)).

To efficiently represent shape, we use FPCA to learn basis functions for the aligned fiber curves $\{{\varphi }_l:[0,1]\to {\Re }^3,l=1,\dots ,T\}.$ A discretization method similar to the one introduced in Chapter 8.4 of Ramsay and Silverman (2005) (or in Chapter 4.3 of Srivastava and Klassen (2016) and Zhang, Klassen, and Srivastava (2018)) is used to estimate $\left\{{\varphi }_l\right\}$ from training data. For the connection (r_a, r_b), we obtain a low-dimensional structure consisting of $L_{\left(r_a,r_b\right)}=\left\{y_{\mu },\left\{{\varphi }_l,l=1,\dots ,T\right\}\right\}.$ Letting g be the shape part of fiber $y\in {\mathrm{\Omega }}_{\left(r_a,r_b\right)},$ we can represent g as $g(s)\approx y_{\mu }(s)+{\sum }_{l=1}^T{x}_l{\varphi }_l(s),$ where x_l represents the coefficient corresponding to ϕ_l. For notational convenience, we let ${\mathit{c}}^{(2)}={\left[x_1,x_2,\dots ,x_T\right]}^{\prime }\in {\Re }^T.$

We decompose fiber curve $y\in {\mathrm{\Omega }}_{\left(r_r,r_b\right)}\text{as}y:=\{{\mathit{c}}^{(1)},{\mathit{c}}^{(2)},\mathbf{O},\gamma \},$ where c⁽¹⁾, c⁽²⁾, O, and γ are the translation, shape, rotation, and reparameterization components, respectively. The fiber path can be estimated using $\widehat{y}(s)\approx {\mathbf{O}}^T*(y_{\mu }+{\sum }_{l=1}^T{\mathit{c}}^{(2)}(l){\varphi }_l)+{\mathit{c}}^{(1)}.$ The difference between the recovered path $\widehat{y}$ and the original path y depends on the number of basis functions. We did not include γ because γ does not change the geometric appearance of y but only changes its parameterization.

3. Model for One Individual

3.1. Product Kernel Mixture Model

In this section, we model fiber curves {y_i} for $i=1,\dots ,n$ from a connection in a single subject. After the decomposition, each fiber y_i is represented as $y_i:=\left\{{\mathit{c}}_i^{(1)},{\mathit{c}}_i^{(2)},{\mathit{c}}_i^{(3)}\right\},$ where ${\mathit{c}}_i^{(3)}={\mathbf{O}}_i.$ Each of the ${\mathit{c}}_i^{(m)}$ has a different Euclidean or manifold support. Letting ${\mathit{c}}_i^{(m)}\in {\mathcal{Y}}_m,$ we have $y_i\in \mathcal{Y}={\otimes }_{m\in I}{\mathcal{Y}}_m,I=\{1,\dots ,M\}.$ Our goal is to specify a joint model in which y_i ~ f, with f a probability measure characterizing the joint distribution. Let $\mathcal{B}(\mathcal{Y})$ denote an appropriate σ-algebra of $\mathcal{Y},$ with f assigning probability f(B) to each $B\in \mathcal{B}(\mathcal{Y}).$

Initially, we focus on modeling one component ${\mathit{c}}_i^{(m)}$ using a mixture model with

$$f_m(\mathit{c})={\int }_{{\mathrm{\Theta }}_m}{\mathcal{K}}_m\left(\mathit{c};{\theta }^{(m)}\right)dP\left({\theta }^{(m)}\right),\mathit{c}\in \mathcal{B}\left({\mathcal{Y}}_m\right),$$ (2)

where ${\mathcal{K}}_m\left(\cdot ;{\theta }^{(m)}\right)$ is a parametric probability measure on $\left\{{\mathcal{Y}}_m,\mathcal{B}\left({\mathcal{Y}}_m\right)\right\},$ and P is a probability measure over $\{{\mathrm{\Theta }}_m,\mathcal{B}{(\mathrm{\Theta })}_m)\}.$ A nonparametric Bayesian approach is realized by choosing P as a random probability measure and assigning an appropriate prior through

$$P=\sum _{h=1}^K{\pi }_h{\delta }_{{\theta }_h},{\theta }_h~P_0^m$$ (3)

where $P_0^m$ is a base measure on $\left\{{\mathrm{\Theta }}_m,\mathcal{B}\left({\mathrm{\Theta }}_m\right)\right\}$ and ${\delta }_{\theta }{}_{{}_h}$ denotes a degenerate distribution with all its mass at θ_h. Equation (3) contains a broad class of priors, including Dirichlet process and Poisson-Dirichlet process. In the Dirichlet process case, K = ∞ and π_h is generated through a stick-breaking process (Sethuraman 1994).

To jointly model the different components of y_i, we apply a product kernel mixture (Bhattacharya and Dunson 2010a; Banerjee, Murray, and Dunson 2013). In particular, supposing that $y_i{}^{\underset{\sim }{\text{iid}}}f,$

$$f\left(y_i\right)={\int }_{\mathrm{\Theta }}\prod _{m=1}^M{\mathcal{K}}_m\left({\mathit{c}}_i^{(m)};{\theta }^{(m)}\right)dP(\theta ),\theta =\left\{{\theta }^{(1)},\dots ,{\theta }^{(M)}\right\},$$ (4)

where ${\mathcal{K}}_m$ is a parametric density on ${\mathcal{Y}}_m,$ and P is a mixing measure with the form,

$$P=\sum _{h=1}^K{\pi }_h{\delta }_{{\theta }_h},{\theta }_h=\left\{{\theta }_h^{(1)},{\theta }_h^{(2)},\dots ,{\theta }_h^{(M)}\right\}~P_0=\prod _{m=1}^M{P}_0^m.$$ (5)

Under this model, the conditional likelihood for fiber $y:=\left\{{\mathit{c}}^{(1)},\dots ,{\mathit{c}}^{(M)}\right\}$ given $\pi =\left\{{\pi }_1,\dots ,{\pi }_k\right\}$ and θ can be written as

$$f(y|\pi ,\theta )=\sum _{h=1}^K{\pi }_h\prod _{m=1}^M{\mathcal{K}}_m\left({\mathit{c}}^{(m)};{\theta }_h^{(m)}\right).$$ (6)

Introducing a cluster index $S_i\in \{1,\dots ,k\}$ for fiber i, we have ${\mathit{c}}_i^{(m)}~{\mathcal{K}}_m\left(\cdot ;{\theta }_{S_i}^{(m)}\right)$ independently for $m=1,\dots ,M,$ and $\text{Pr}\left(S_i=h\right)={\pi }_h,$ for $h=1,\dots ,K.$ This conditional independence structure given the cluster indices of the fibers facilitates computation, while still allowing a flexible dependence structure between the different components marginally. The remaining task is to specify the ${\mathcal{K}}_m\left({\mathit{c}}_i^{(m)};{\theta }^{(m)}\right)$ for each component.

3.2. Kernel Density for Each Component

We describe the intrinsic space of each component m and define a parametric distribution ${\mathcal{K}}_m$ having appropriate support. We have M = 3 corresponding to the translation (m = 1), shape (m = 2), and rotation (m = 3) components.

Translation component:

The translation component c⁽¹⁾ is a vector in ${\Re }^3.$ We simply use a multivariate normal distribution for c⁽¹⁾,

$$\begin{gathered} {\mathcal{K}}_1\left({\mathit{c}}^{(1)};\mathit{\mu },\mathbf{\Sigma }\right)=\frac{1}{\sqrt{{(2\pi )}^3\left|\mathbf{\Sigma }\right|}} \\ \times \exp \left\{-\frac{1}{2}{\left({\mathit{c}}^{(1)}-\mathit{\mu }\right)}^T{\mathbf{\Sigma }}^{-1}\left({\mathit{c}}^{(1)}-\mathit{\mu }\right)\right\}. \end{gathered}$$

FPCA coefficient component:

Let ${\mathit{c}}^{(2)}\in {\Re }^T$ denote the shape component corresponding to the coefficients of the FPCA basis functions. Similar to the translation component, we assign a multivariate normal distribution for c⁽²⁾,

$$\begin{gathered} {\mathcal{K}}_2\left({\mathit{c}}^{(2)};\mathit{\mu },\Sigma \right)=\frac{1}{\sqrt{{(2\pi )}^T\left|\Sigma \right|}} \\ \times \exp \left\{-\frac{1}{2}{\left({\mathit{c}}^{(2)}-\mathit{\mu }\right)}^T{\Sigma }^{-1}\left({\mathit{c}}^{(2)}-\mathit{\mu }\right)\right\}. \end{gathered}$$

The rotation component:

The rotation matrix c⁽³⁾ is an element of the special orthogonal group $\text{SO}(3)=\{\mathbf{X}\in O(3)|\text{det}(\mathbf{X})=1\}.$ The most common parametric distribution on SO(3) is the matrix Fisher distribution, also known as the Langevin distribution (Downs 1972; Khatri and Mardia 1977; Jupp and Mardia 1979). Bingham, Nordman, and Vardeman (2009) and Qiu, Nordman, and Vardeman (2014) proposed a more flexible class of uniform axis random spin (UARS) distributions, which improves upon the flexibility of the Langevin. We carefully considered both choices, but faced computational and stability problems in conducting inferences, particularly as the number of fibers increases.

To address these problems, we define a simple Gaussian like parametric distribution based on an embedding in the Lie algebra of SO(3). Let I₃ denote the identity element of SO(3). The tangent space at I₃, T_I3 (SO(3)), forms a Lie algebra, which is usually denoted as $\mathfrak{s}\mathfrak{o}\left(3\right)$. The exponential map, exp : $\mathfrak{s}\mathfrak{o}(3)\to \text{SO}(3),$ provides a mapping from the tangent space T_I3 (SO(3)) to SO(3). The inverse of the exponential map is called the log map. $\mathfrak{s}\mathfrak{o}(3)$ is a set of 3 × 3 skew-symmetric matrices. We use the following notation to denote any matrix ${\mathbf{A}}_{\mathit{v}}\in \mathfrak{s}\mathfrak{o}(3):{\mathbf{A}}_{\mathit{v}}=\left[{\mathit{v}}_1,{\mathit{v}}_2,{\mathit{v}}_3\right],$ where ${\mathit{v}}_1={\left[0,v_1,-v_2\right]}^{\prime },$ ${\mathit{v}}_2={\left[-v_1,0,v_3\right]}^{\prime },$ ${\mathit{v}}_3={\left[v_2,-v_3,0\right]}^{\prime }$ and $\mathit{v}={\left[v_1,v_2,v_3\right]}^{\prime }.$ The exponential map is given by Rodrigues’ formula: exp(A_v) = I₃ when α = 0, and exp $\left({\mathbf{A}}_{\mathit{v}}\right)={\mathbf{I}}_3+\frac{\sin (\alpha )}{\alpha }{\mathbf{A}}_{\mathit{v}}+\frac{1-\cos (\alpha )}{{\alpha }^2}{{\mathbf{A}}_{\mathit{v}}}^2$ when $\alpha \in (0,\pi ),$ where $\alpha =\sqrt{\frac{1}{2}tr\left({{\mathbf{A}}_{\mathit{v}}}^T{\mathbf{A}}_{\mathit{v}}\right)}=\Vert \mathit{v}\Vert \in [0,\pi ).$ The log map of X ϵ SO(3) is a matrix in $\mathfrak{s}\mathfrak{o}(3),$ given by log(X) = 0 when α = 0, $\alpha =0,\log (\mathbf{X})=\frac{\alpha }{2\sin (\alpha )}\left(\mathbf{X}-{\mathbf{X}}^T\right)$ when $|\alpha |\in (0,\pi ),$ where α satisfies $tr(\mathbf{X})=2\cos (\alpha )+1.$

We define a mapping Φ to embed an element in $\mathfrak{s}\mathfrak{o}(3)$ to ${\Re }^3$ $\Phi :\mathfrak{s}\mathfrak{o}(3)\to {\Re }^3,\varphi \left({\mathbf{A}}_{\mathit{v}}\right)=\mathit{v}.$ Let $\varphi (\mathbf{X}):=\Phi (\log (\mathbf{X}))\in {\Re }^3$ be the embedded vector for the element X ϵ SO(3) in ${ℝ}^3.$ We define a trivariate normal distribution on this embedding space

$$\begin{array}{l}{\mathcal{K}}_3(\mathbf{X};\mathit{\mu },\Sigma )=\frac{1}{\sqrt{{(2\pi )}^3\left|\Sigma \right|}}\\ \times \exp \left\{-\frac{1}{2}(\varphi (\mathbf{X})-\mathit{\mu }){\Sigma }^{-1}{(\varphi (\mathbf{X})-\mathit{\mu })}^T\right\}.\end{array}$$

This embedded Gaussian kernel has substantial practical advantages over alternative intrinsic parametric kernels we attempted to implement. Centering the sampled rotation matrices using the technique introduced in Section 2.3 makes their Karcher mean be I₃, and therefore, the embedding is performed on the tangent space of the identity.

3.3. Prior Specification and Posterior Inference

To complete a Bayesian specification of the model, we choose a prior for the cluster probabilities: $\mathit{\pi }={\left[{\pi }_1,\dots ,{\pi }_K\right]}^{\prime }~\text{Dir}\left(\frac{\alpha }{K},\dots ,\frac{\alpha }{K}\right),$ where K is an upper bound on the number of clusters. In the limit as $K\to \infty ,$ this choice leads to a Dirichlet process mixture model. In addition, Rousseau and Mengersen (2011) motivated a similar choice of prior as being effective at favoring deletion of redundant mixture components not needed to characterize the data. If K is chosen to be too small, then none of the clusters will be unoccupied, and the analysis should be repeated for larger K. Posterior sampling of the proposed mixture model is standard, and the details are presented in Section 1 in the supplementary materials.

4. Model for a Population of Individuals

Section 3 proposes a flexible mixture model for the distribution of fibers connecting two ROIs in a single brain; in this section, we generalize the model to accommodate multiple individuals. This generalization is challenging because (1) fibers in each individual have their own coordinate system inherited from the MRI scan; (2) there are different numbers and appearances of fibers for different individuals. Although (1) can potentially be addressed via image alignment before tractography or tractogram alignment after tractography (Garyfallidis et al. 2015), such multiple-subject alignment can be suboptimal and challenging, especially in the nonlinear case. Our variation decomposition makes the shape component invariant to misalignment, and thus bypasses this issue when the inference is performed only based on the shape component. Issue (2) can be solved by using a hierarchical Bayesian model to allow differences between individuals while encouraging borrowing of information.

Let $\left\{y_{ji}\right\}$ for $j=1,\dots ,J$ and $i=1,\dots ,n_j$ be a collection of fiber curves for the same pair of brain regions in n subjects, where n_j represents the number of fiber curves in the jth subject. We have $y_{ji}=\{\begin{array}{l}{\mathit{c}}_{ji}^{(1)},\dots ,{\mathit{c}}_{ji}^{(M)}\}\hfill \end{array},$ so that the fibers are represented by their different geometric components. In addition, let w_j denote a scalar summary of the strength of connection between the brain regions for individual j, which is usually set as the number of fibers, n_j.

4.1. Nested Dirichlet Process Model

Generalizing the model in Section 3 to multiple individuals, we have distributions f_j, for subject $j=1,\dots ,J,$ and require a model for an unknown distribution of distributions, $f_j~Q,$ with Q unknown. One natural possibility is a hierarchical Dirichlet process (HDP) mixture (Teh et al. 2006), which would induce clusters of fibers, with these clusters having different weights for each individual. This model assumes that white matter pathways (each pathway represents a cluster) connecting two ROIs are shared by all individuals, but the proportions of fiber curves in each pathway are different. However, we found that this model has poor performance, as our data (illustrated in Figure 1) show that many subjects have completely different white matter bundles. This motivates us to instead use the nested Dirichlet process (NDP) (Rodríguez, Dunson, and Gelfand 2008), which clusters subjects based on their fiber curve distribution, with subjects in a cluster having similar clusters of fibers.

Our NDP model has the following form

$$\begin{gathered} f_j\left(y_{ji}\right)=\int \prod _{m=1}^M{\mathcal{K}}_m\left({\mathit{c}}_{ji}^{(m)};{\theta }^{(m)}\right)d{G}_j(\theta ),\theta =\left\{{\theta }^{(1)},\dots ,{\theta }^{(M)}\right\}, \\ {G}_j(·)~\sum _{h=1}^{\infty }{\pi }_h^{*}{\delta }_{G_h^{*}}(·),G_h^{*}(·)=\sum _{l=1}^{\infty }{\omega }_{lh}^{*}{\delta }_{{\theta }_{lh}^{*}}, \end{gathered}$$ (7)

where ${\theta }_{lh}^{*}=\left\{{\theta }_{lh}^{(1)*},\dots ,{\theta }_{lh}^{(M)*}\right\}$ and ${\theta }_{lh}^{*}~{\prod }_{m=1}^M{P}_0^m,{\omega }_{lh}^{*}=u_{lh}^{*}{\prod }_{s=1}^{l-1}\left(1-u_{sh}^{*}\right),{\pi }_h^{*}=v_h^{*}{\prod }_{s=1}^{h-1}\left(1-v_s^{*}\right)$, $v_h^{*}~$ beta(1, α), and $u_{lh}^{*}~$ beta(1, β). The collection of individual-specific mixing measures $\left\{G_j\right\}$ are drawn from an NDP, $\left\{G_j\right\}~\text{NDP}\left(\alpha ,\beta ,P_0\right),$ where $P_0={\prod }_{m=1}^M{P}_0^m$ is the base measure.

Under this structure, the prior probability that two individuals are assigned to the same brain structure cluster is 1/(1 + α), while the prior probability of clustering two fibers together within a brain is 1/(1 + β). The model can be used for any combination of the components of variability in the fiber curves; for example, one can use only the shape component or a combination of different components to estimate f_j. In applying these models to brain connectomics data, we will assess how clustering performance depends on which components are included. Section 2 in the supplementary materials shows an extension to include information on strength for connection; length of connection can also be easily incorporated.

4.2. Posterior Inference

Following Rodríguez, Dunson, and Gelfand (2008), we propose a blocked Gibbs sampling algorithm. An approximation of the stick-breaking process is used, with the infinite sums in (7) replaced by finite sums of K (for G_j) and L (for $G_h^{*}$) elements. Let ${\zeta }_j,$ for $j=1,\dots ,J,$ be the membership indicator of individuals and let ${\xi }_{ji},$ for $i=1,\dots ,n_j,$ be the membership indicator of fiber curves for the jth subject. Sampling proceeds via the following steps:

1. Sample the membership indicator for the jth individual ($j=1,\dots ,J)$ from a multinomial

   $$P\left({\zeta }_j=h|-\right)\propto {\pi }_h^{*}\prod _{i=1}^{n_j}\sum _{l=1}^L{w}_{lh}^{*}\prod _{m=1}^M{\mathcal{K}}_m\left({\mathit{c}}_{ji}^{(m)}|{\theta }_{lh}^{{(m)}^{*}}\right).$$
2. Sample the membership indicator ${\xi }_{ji},$ for $j=1,\dots ,J$ and $i=1,\dots ,n_j,$ with

   $$P\left({\xi }_{ji}=l|-\right)\propto w_{l{\zeta }_j}^{*}\prod _{m=1}^M\mathcal{K}\left(c_{ji}^{(m)}|{\theta }_{l{\zeta }_j}^{(m)*}\right).$$

3. Sample ${\pi }_h^{*}$ by first sampling $\left(u_h^{*}|-\right)~$ beta $(1+m_h,\alpha +{\sum }_{s=h+1}^K{m}_s),h=1,\dots ,K-1,$ and $u_K^{*}=1,$ where m_h is the number of subjects assigned to cluster h, and then let ${\pi }_h^{*}=u_h^{*}{\prod }_{s=1}^{h-1}\left(1-u_s^{*}\right).$

4. Sample $w_{lh}^{*}$ by first sampling $\left(v_{lh}^{*}|-\right)~\text{beta}(1+n_{lh},\beta +{\sum }_{s=l+1}^L{n}_{sh}),l=1,\dots ,L-1,h=1,\dots ,K$ and $v_{LK}^{*}=1,$ where n_lh is the number of observations assigned to atom l of distribution h, and then $w_{lh}^{*}=v_{lh}^{*}{\prod }_{s=1}^{l-1}\left(1-v_{sh}^{*}\right).$

5. Sample the parameters ${\theta }_{lh}^{(m)*}$ for $l=1,\dots ,L,h=1,\dots ,K$ and $m=1,\dots ,M$ from

   $$P\left({\theta }_{lh}^{(m)*}|-\right)\propto P_0^m\left({\theta }_{lh}^{(m)*}\right)\left(\prod _{\left\{i,j|{\zeta }_j=h,{\xi }_{ij}=l\right\}}{\mathcal{K}}_m\left({\mathit{c}}_{ji}^{(m)}|{\theta }_{lh}^{(m)*}\right)\right),$$

   where $P_0^m(\cdot )$ is the conjugate prior for parameters in ${\mathcal{K}}_m\left(\cdot |{\theta }^{(m)}\right).$ If no observation is assigned to the lhth cluster, we draw ${\theta }_{lh}^{(m)*}$ from the prior $P_0^m.$
6. Sample the concentration parameters α and β: we choose conjugate priors,α ~ gamma(a_α, b_α) and β ~ gamma(a_β, b_β). The posterior samples for α and β are constructed as

   $$\begin{gathered} P(\alpha |-)~\text{gamma}\left(a_{\alpha }+(K-1),b_{\alpha }-\sum _{h=1}^{K-1}\log \left(1-{\mu }_h^{*}\right)\right), \\ P(\beta -)~\text{gamma}\left(a_{\beta }+K(L-1),b_{\beta } \\ -\sum _{l=1}^{L-1}\sum _{h=1}^K\log (1-v_{lh}^{*})\right). \end{gathered}$$

We will evaluate the performance of this Gibbs sampler through application to human brain connectome data.

5. Application to Human Brain Connectome Data

We consider two datasets: a test-retest dataset and the Human Connectome Project dataset.

Test-retest dataset:

This dataset contains 3 scans for each subject taken at one month intervals. A total of 15 acquisitions, from 5 healthy participants, were used for our analysis. In each scan, a dMRI image and an anatomical T1-weighted image were acquired on a 1.5 Tesla SIEMENS Magnetom. The dMRI image has a 2 mm isotropic resolution and was acquired along 64 uniformly distributed directions. The T1 image has a 1 mm isotropic resolution.

Human Connectome Project (HCP) dataset:

The dMRI images in HCP have isotropic voxel size of 1.25 mm, and 270 diffusion weighted scans. HCP has processed the diffusion image and T1 image such that they have the same resolution and lie in the same space (aligned). See Van Essen et al. (2012) for more details. A subset of 50 subjects was used in our analyses.

The tractography data for each subject were generated using the probabilistic method of Girard et al. (2014) with the recommended optimal parameters. About 1 million fiber curves for each subject were generated. Under the Desikan–Killiany atlas, the brain cortical bands were segmented into 68 anatomical regions (34 regions per hemisphere). Fiber curves connecting any pair of regions were extracted. Before applying our method to each connection, outlying fiber curves that do not follow major white matter pathways (false positives caused by the fiber tracking algorithm) were removed using the method proposed in Zhang, Descoteaux et al. (2018).

5.1. Component Estimation

For connection (r_a, r_b), to learn a low-dimensional structure $L_{\left(r_a,r_b\right)}$ representing the shape component, we use 30 subjects from HCP as the training data and learn a basis using FPCA (our numerical experiments indicate that 30 subjects are adequate for estimating the FPCA basis, and using more training data does not significantly change the estimated FPCA basis). We focus on two connections: (1) between right paracentral lobule (r_pl) and left postcentral gyrus (l_pg); (2) between right paracentral lobule (r_pl) and left posterior cingulate cortex (l pcc). Figure 4 illustrates these connections in a subject in the test-retest dataset.

Figure 4.

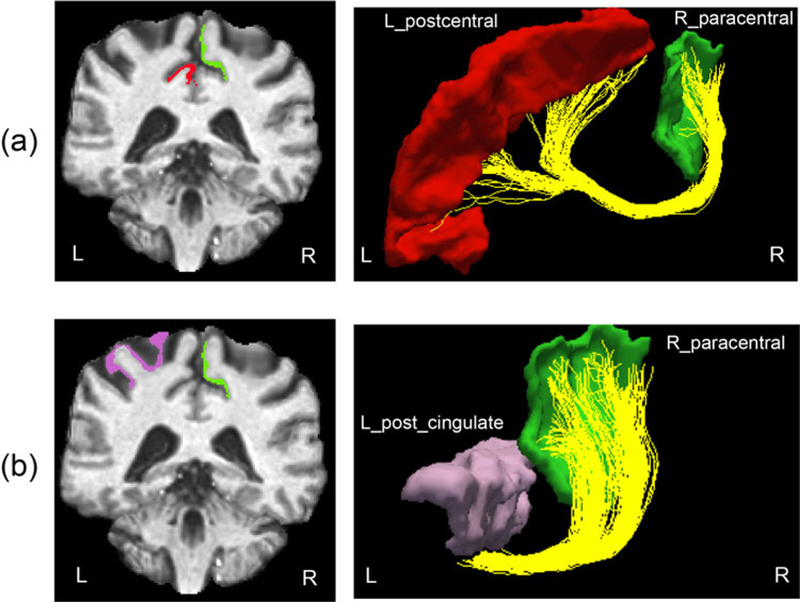
Example of two connections we used in this paper: (a) between r_pl and l_pg and (b) between r_pl and l_pcc.

Using the method introduced in Section 2.3, we estimated three components c⁽¹⁾, c⁽²⁾, and c⁽³⁾ for all fibers. For ${\mathit{c}}^{(2)}\in {\Re }^T,$ we set T = 3, so we use three coefficients (on three major FPCA basis functions) to represent a fiber. Using a larger T will increase representation precision, but for balancing representation accuracy and computational cost, we set T = 3 (refer to more details in Section 3 in the supplementary materials. In Figure 5, we plot the estimated components for fiber curves in the two connections. For the connection (r_pl, l_pg), the fiber curves start from the right paracentral lobule, group into a bundle, traverse the corpus callosum, and then split into two bundles to connect the left postcentral gyrus region. The split makes the fiber curves have two distinct shapes. For the connection (r_pl, l_pcc), there are a few distinct pathways, differing in both shape and location. In Figure 5(d), we plot the recovered fiber curves using c⁽¹⁾, c⁽²⁾, and c⁽³⁾. The color along the curves indicates the discrepancy (with a unit of mm) between the original fiber and the recovered fiber. These fibers were recovered from images with an isotropic resolution of 2 mm. In Figure 2 of the supplementary materials, we plot the histograms of cross-sectional distances between the raw and recovered fibers, where we observe that the major pathways can be recovered well with only nine parameters. The biggest discrepancies generally focus on the starting and ending points, which are either in gray matter or in interface of gray matter and white matter. Diffusion in these regions is close to isotropy (Descoteaux et al. 2009) and accurate fiber reconstruction is intrinsically difficult.

Figure 5.

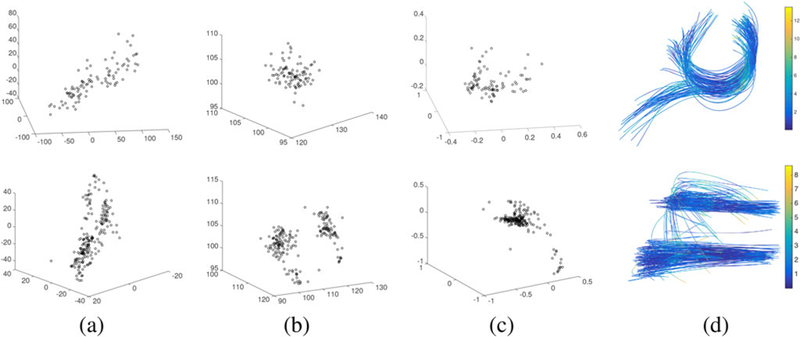
Decomposed components and the recovered fiber curves. (a–c) The shape, translation, and rotation components, respectively. (d) The recovered fiber curves using these components. Colors indicate the difference (in unit of mm) between the recovered and original fibers. Most recovery errors (89% in the first row and 99% in the second row) are less than 2 voxels.

5.2. Simulation Study

The proposed model for representing and modeling fiber curves is similar to random effects models for functional data (Yang et al. 2016, 2017), but we use nonparametric Bayesian tools for characterizing the random effects distributions, leading to clustering. We estimate the random effects through the variance decomposition in Section 2.3 (the two-step procedure leads to some under-estimation of uncertainty, but in Section 3 of the supplementary materials we show that this under-estimation is mild). We conduct a simulation study to evaluate our approach and compare with existing random effect models for functional data. Data were generated to mimic fiber curves in the corpus callosum, while introducing clustering effects and different deviations between clusters. We generated two clusters of fibers by combining simulated shapes, rotations and translations. The shapes were simulated from a mixture of two Gaussians; the rotations and translations were from Gaussians. Figure 6 column (a) shows two examples of the simulated data (each of them contains 70 fibers), where in the first row the deviation between the two clusters of fibers is smaller than the second row (the L₂ distances between the means of the two clusters are 0.3 and 0.8 in row one and two, respectively).

Figure 6.

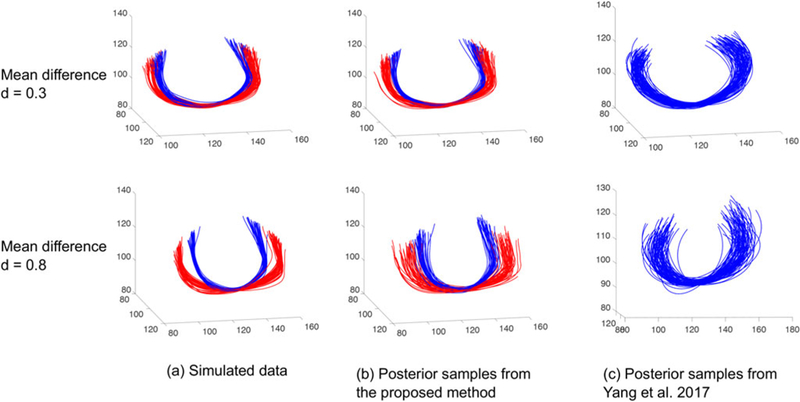
Comparison of the proposed nonparametric Bayesian model with the parametric model for functional data in Yang et al. (2017). (a) Simulated 70 fiber curves with two classes (each color represents a class). (b) Posterior samples from the proposed model. (c) Posterior samples from Yang et al. (2017).

The nonparametric mixture model defined in (4) was used to model the simulated fibers. We decomposed the fibers into multivariate data with T = 3 for the shape component. The data were centered and rescaled such that each coordinate has unit variation. The prior specification and posterior sampling procedure are described in Section 3.3. We assigned a normal-inverse-Wishart NIW $\left({\mu }_0^{(m)},{\lambda }_0^{(m)},{\Phi }_0^{(m)},v_0^{(m)}\right)$ for $P_0^m\left({\theta }^{(m)}\right)\left({\theta }^{(m)}=\left\{{\mu }^{(m)},{\Sigma }^{(m)}\right\}\right),$ where ${\mu }_0^{(m)}={[0,0,0]}^T,{\lambda }_0^{(m)}=1,{\Phi }_0^{(m)}={\mathbf{I}}_3,$ and $v_0^{(m)}=5$ for $m=1,2,3,$ implying that $E\left({\mu }^{(m)}|{\Sigma }^{(m)}\right)={[0,0,0]}^T$ and $E\left({\Sigma }^{(m)}\right)={\mathbf{I}}_3.$ The above hyper-parameter values will be used in all our analyses, including for the real data. The inference is based on 10,000 samples from the MCMC sampler after a burn in of 1000 samples. After post-processing to fix the label switching issue (Stephens 2000; Jasra, Holmes, and Stephens 2005), trace plots (illustrated in Figure 8 in the supplementary materials) suggest that this burn-in is sufficient and there is no evidence of lack of convergence.

As a comparison, we applied the random effect model for functional data in Yang et al. (2017). Each fiber is represented by $y_i(t)=z_i(t)+{ϵ}_i(t),$ where ${ϵ}_i(t)~N\left(0,{\delta }_{ϵ}^2\right)$ represents the measurement noise, and $z_i\text{(}t\text{)}$ represents the ground truth fiber. Yang et al. represent $z_i\text{(}t\text{)}$ as a linear combination of basis functions $\left\{b_k(\cdot )\right\}$ with coefficients $\left\{{\zeta }_{ik}\right\}$ for $k=1,\dots ,K.$ Letting ${\mathit{\zeta }}_i={\left[{\zeta }_{i1},{\zeta }_{i2},\dots ,{\zeta }_{iK}\right]}^T$ and assuming ${\mathit{\zeta }}_i~N\left({\mathit{\mu }}_{\zeta },{\mathbf{\Sigma }}_{\zeta }\right),$ a Bayesian hierarchical model is used to fit the data and estimate the distribution of $\mathit{\zeta }.$ Since fiber curves are in ${\Re }^3,$ we performed the inference using Yang et al. (2017) for each coordinate independently and let K = 5 (fibers cannot be represented well with fewer parameters). While our model used 9 parameters to represent each fiber, Yang et al. used 15.

A good model is expected to fit the data well and produce similar random samples to the training data. We generated 70 randomly sampled fibers from the posterior predictive distributions. The results are presented in Figure 6, where the second column shows our results and the third column shows the results of Yang et al. (2017). The colors in Figure 6 represent data from different classes. The random effect model in Yang et al. (2017) only uses one Gaussian to capture the distribution of fibers and there is no clustering information to display. Our model captures the structure and variation of the data better than Yang et al. (2017). In addition, because of our efficient representation, it took about 30 sec to run 10,000 MCMC samples with a 2.9 GHz Intel Core i7 CPU, while Yang et al.’s method took 240 sec. A post-clustering using K-means was performed using ${\mathit{\zeta }}_i$ to compare with our clustering result. We used the Rand index (RI; Rand 1971) and adjusted Rand index (ARI; Hubert and Arabie 1985) to measure the accuracy of clustering. We achieved (1,1) in both examples for (RI, ARI), while Yang et al.’s method achieved (0.49, –0.01) and (1,1) in the two examples.

5.3. Modeling Brain Connection

We first consider a single subject scenario with data from connections (r_pl, l_pg) and (r_pl, l_pcc). While Figures 3 and 5 in the supplementary materials summarize the posterior results of each $\left\{{\mathit{c}}_i^{(m)}\right\},$ Figure 7 shows the results of modeling all three components together for the connection (r_pl, l_pg). Column (a) shows posterior samples of number of clusters and (b) shows the pairwise probability heat map according to the posterior samples. We reordered the fiber curves such that fibers with similar shapes are close to each other. We used the mode of the posterior distribution on number of clusters k as the final cluster number and map the heat map matrix into a membership matrix that has k clusters. To quantitatively evaluate the clustering results, we manually clustered the fibers in each connection to assign “ground truth” labels (see Section 5 in the supplementary materials). Table 1 quantifies agreement between the manual and model-based clustering. We see that the shape contains most of the information, followed by the rotation and translation. Combining all components together gives us better clustering results.

Figure 7.

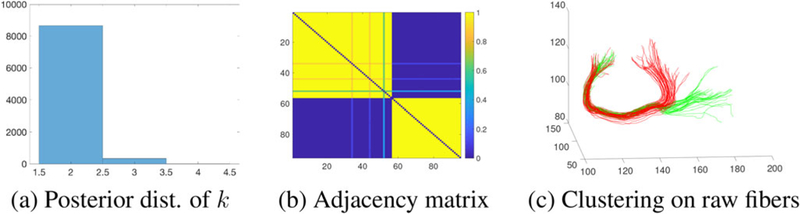
Joint model result for the connection (r_pl, l_pg).

Table 1.

Quantitative evaluation of clustering result for connections (r_pl, l_pg) and (r_pl,l_pcc).

	r_pl, l_pg					r_pl,l_pcc
	Shape	Trans.	Rot.	All		Shape	Trans.	Rot.	All
RI	0.9265	0.6656	0.8694	1.0		0.8626	0.8284	0.6501	0.8762
ARI	0.8533	0.3393	0.7391	1.0		0.7088	0.6119	0.3565	0.7384

Next, we study the connections in a set of individuals using the test-retest dataset. Figure 8 shows fiber curves of the connection (r_pl, l_pg) from three subjects in three different scans. Routinely, each connection is reduced to either a binary number or a scalar number (e.g., the count of fibers) for brain network analysis. However, as all subjects have at least one fiber in the connection, the usual 0–1 representation of the connection would show no heterogeneity; the rich information about the connection is totally discarded. From Figure 8, we see that although the counts do vary, they change erratically across scans from the same subject. The variation within subjects for different scans is not smaller than the variation between subjects, which is mainly caused by noise introduced by image acquisition and preprocessing.

Figure 8.

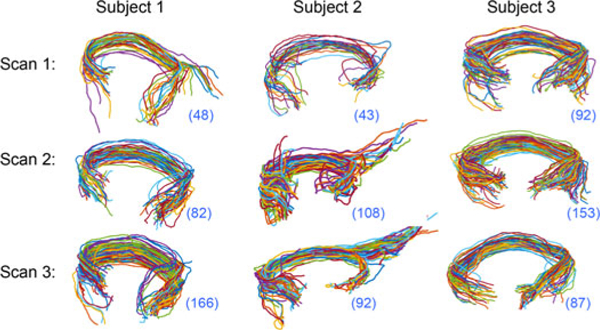
Fiber curves connecting r_pl and l_pg in 9 scans of 3 subjects in the test-retest dataset. The number in the bottom left bracket shows the number of fibers.

To assess whether shape provides a more discriminative and reproducible summary of a connection, we applied our NDP model to fibers in the test-retest dataset to cluster individual brain scans. Due to potential misalignment between subjects, our analysis indicates that using all three components is not a good choice. We merged rotation to shape, and decomposed each fiber curve into only translation $c^{(1)}\in {\Re }^3$ and shape $c^{(2)}\in {\Re }^3$ to simplify our model. We set $P_0={\prod }_{m=1}^M{P}_0^m,$ where $P_0^m~\text{NIW}\left({[0,0,0]}^T,1,{\mathbf{I}}_3,5\right),\alpha ,\beta ~$ gamma(3,3), K = 9 and L = 15, a priori. The prior on α and β implies that E(α) = 1 and E(β) = 1, which is a common choice in the literature. K and L are upper bounds on the cluster number of subjects and curves, respectively. The results that follow are based on 5000 MCMC samples with a burn-in of 500. As a comparison, we clustered subjects according to their fiber counts by the rounded kernel mixture model of Canale and Dunson (2011), using their recommended priors, collecting 10,000 posterior draws, and discarding the first 1000.

With all 5 subjects and their 15 scans from the test-retest dataset, we extracted 45 between-hemisphere connections that have more than 30 fiber curves. We compared clustering results using geometric information or only fiber count. For connections with very rich fibers, we randomly subsampled them to have an upper limit of n curves (n = 400 in our experiments; our numerical study indicated that this subsampling does not greatly affect the clustering results and the fitted distributions of fibers; refer to Figure 12 in the supplementary materials for more details). Table 2 shows results for 16 connections, with the remaining results in Sections 7 and 8 in the supplementary materials (including a detailed analysis for connections in Figure 8). The ROIs are indexed by numbers and their names are provided in the supplementary materials. These results provide evidence that shape provides the most useful summary of a connection: (1) shape can be reproduced robustly, (2) it is much more informative than other features (e.g., the widely used count); (3) using the whole fiber curves (shape and translation) is not a good idea due to registration issues and the relatively limited information in the translation component (a preregistration of tractography data using Garyfallidis et al. (2015) and O’Donnell et al. (2012) may improve the clustering results for shape and translation).

Table 2.

Comparison of clustering results of using geometric information and count.

RI/ARI	(2,61)	(3,61)	(7,43)	(7,58)	(7,62)	(9,58)	(9,62)	(11,47)
Shape	0.91/0.72	1.0/1.0	0.87/0.51	0.90/0.50	0.90/0.47	0.91 /0.72	0.91 /0.72	0.84/0.51
Trans.	0.90/0.64	0.74/0.31	0.65/0.18	0.71 /0.18	0.81 /0.30	0.66/0.30	0.60/0.16	0.52/0.15
Shape and trans.	0.70/0.3	0.74/0.4	0.74/0.23	0.54/0.12	0.82/0.28	0.66/0.30	0.62/0.13	0.70/0.30
Count	0.64/0.23	0.58/0.19	0.49/0.16	0.63/0.21	0.49/0.16	0.14/0	0.45/0.01	0.58/0.19
RI/ARI	(13,55)	(13,47)	(16,50)	(16,55)	(16,56)	(16,57)	(16,61)	(22,50)
Shape	0.82/0.35	1.0/1.0	0.91 /0.72	0.86/0.51	0.83/0.53	0.91 /0.72	0.90/0.64	0.74/0.4
Trans.	0.61/0.14	0.83/0.53	0.49/0.16	0.61/−0.04	0.75/0.37	0.49/0.16	0.78/0.25	0.58/0.19
Shape and trans.	0.70/0.21	0.74/0.40	0.74/0.40	0.47/0.11	0.52/0.15	0.74/0.40	0.58/0.19	0.66/0.30
Count	0.62/0.21	0.58/0.19	0.50/0.04	0.49/0.16	0.14/0	0.58/0.19	0.60/0.18	0.58/0.19

NOTE: The ROIs are indexed by numbers and their names are provided in Table 2 in the supplementary materials.

5.4. Relationship Between Fiber Geometry and Cognition

The HCP provides rich trait measures of each subject, enabling study of relationships between fiber geometry and traits. In this section, we study the relationship between geometry of fibers and the oral reading recognition ability (Van Essen et al. 2013). We first focused on a set of 20 subjects to identify ROI pairs that have potential geometry differences between people having high and low reading scores (refer to Section 10 in the supplementary materials for more details). Among the 20 subjects, 10 have very low reading scores (67.4 ± 3.3) and 10 have very high scores (134.9 ± 2.6) (Section 10 in the supplementary materials contains more details on how these subjects were selected). Similar to Section 5.3, we applied our NDP model to study distributions of the shape component in the 45 between-hemisphere connections. Labels of 0 and 1 are assigned to subjects with lowand high scores, respectively. We use the RI to evaluate the subject-level clustering result, measuring similarity between unsupervised clustering and the ground truth labels. We also compared with the clustering results using fiber count.

Based on the shape component, among the 45 connections, there are 3 (6.7%) connections having RI scores greater than 0.6, and 29 (64.4%) between 0.5 and 0.6. For the count, there is only 1 (2.2%) connection having RI score greater than 0.6, and 10 (22.2%) between 0.5 and 0.6. In Figure 9(a) and (b), we show ROI pairs that obtained the highest RI scores with the count feature and the shape feature and their heat maps of clustering results. While the best RI score is 0.62 on the connection (11,47) for the count feature, the best RI score is 0.64 on the connection (24,58) for the shape feature. From the heat maps, we can see that the clustering with shape on (24,58) is clearer and closer to the “ground truth” than the count on (11,47). We also display the result with the shape feature on (11,47) in Figure 9(c). Although its RI score is lower than the count, we observe a more interesting result: there is a big cluster of subjects with high reading scores; the clusters for subjects with low reading scores are very small; subjects with high and low scores are barely clustered together (they have distinct fiber geometry).

Figure 9.

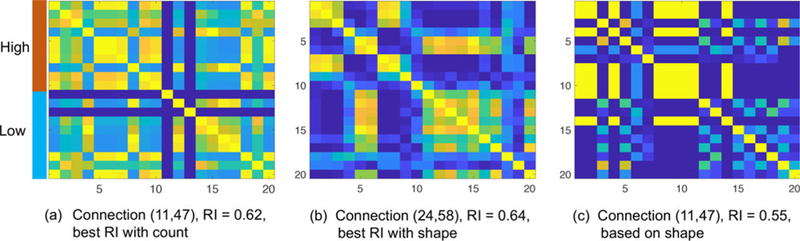
Pairwise probability of clustering 20 HCP subjects with high and low reading scores. (a, b) Connections and pairwise probabilitymatrices with the best RI scores under the shape and count feature. (c) Connection (11, 47) and pairwise probability matrix with the shape feature.

Based on the RI score in the last experiment, we selected three connections {(24,58), (7,58), (27,51)} to conduct a more comprehensive experiment. In this experiment, instead of unsupervised clustering, we slightly modify our NDP model to generate a supervised classifier to classify subjects based on their fiber shape distributions. More specifically, for N subjects from two groups (with good and poor reading abilities) with m of them as testing data and N − m as training data, we fit NDP models separately on the training data for each group. The NDP model clusters subjects and pools fiber curves within each cluster to estimate a mixture distribution. Therefore, for each group, we will have a set of mixture distributions to describe the distribution of shapes of fibers in that group. We allocate each subject in the test data to the group that maximizes the likelihood of that subject’s data. With the subset of 20 subjects, we conducted leave one out cross-validation (m = 1), holding out a different subject each time and averaging the results. The mean classification rates are 0.65, 0.75, and 0.65, respectively, for connections (24,58), (7, 58), (27,51) with the shape feature. As a comparison, the count feature achieves 0.35, 0.5, and 0.5. In another experiment, we identified N = 100 subjects with 50 having good reading scores and 50 having poor reading scores. We let m = 10 and repeated the classification experiment 10 times, the mean classification rates achieved by shape features are 0.60, 0.66, and 0.62, respectively, for the three connections.

These results indicate the geometry of fibers is different in subjects with high and low reading scores, and therefore, geometry can potentially be used to explain part of the cognitive variation in the brain. It is very interesting to find that the discriminative ability of fiber geometry is better than the count feature in distinguishing subjects with high and low reading scores. The count feature has been studied in the literature (Zhang, Allen et al. 2018) and is discovered to be strongly associated with many traits. To further examine our results, we visually checked the 20 subjects’ T1 brain images and observed that: in general, people with very low reading scores tend to have smaller brains with less complex gyrus and sulcus folding patterns than people with high reading scores. Some examples of their T1 images and reading scores are shown in Figure 13 in the supplementary materials. This observation is consistent with existing literature (Cachia et al. 2014; Rushton and Ankney 1996; Toro et al. 2008) and at least partially explains why geometry of fibers can distinguish people with different reading abilities.

6. Discussion

We have presented a novel framework to nonparametrically model the geometric information of fiber curves connecting two brain regions. Geometry is decomposed into three com ponents: shape, rotation, and translation. Our decomposition not only encourages a low-dimensional representation of the shape component but also overcomes the misalignment issue across multiple brain scans. Relying on a flexible hierarchical mixture model, we obtain an accurate and efficient approach to characterize variation in fiber curves, leading to clustering of fibers within and across individuals according to fiber geometry. These clustering results provide new insights about how to better use the tractography dataset for brain connectome analysis. The shape component is the most discriminative feature to distinguish different subjects and can be reliably reproduced in repeated scans. Using the shape component, we can distinguish people with low/high reading abilities better than the count feature, indicating that fiber geometry can be a candidate feature to explain the cognitive variation in the brain.

As a first step toward incorporating geometric information in brain structural connectome analysis, our results suggest many interesting future directions. One thread is to more intensively investigate the reproducibility of the tractography dataset from a geometric object perspective. Most previous analyses focus on analyzing arbitrarily thresholded binary networks or count weighted networks. As we have illustrated, these features discard shape information and are highly sensitive to errors in tractography processing pipelines. Fiber shapes appear to be significantly more robust and informative. A comprehensive study of the reproducibility of all brain connections using their geometric information can let us know which fiber bundles can be reliably reproduced. We can assign reliability scores to every connection according to their reproducibility and give more weights to the connections with high reproducibility scores in future network analysis. This step will be fundamental in improving the reproducibility of findings in structural brain network analysis. In addition, as the future work, some steps of the proposed method maybe improved. For example, due to the different complexity of different connections, we can adaptively choose the model parameters (e.g., the number of coefficients for the shape component) to more efficiently model each connection. To link geometry to traits, instead of dichotomizing trait scores and perform classification analysis, a better usage of the continuous traits is to develop a regression type analysis.