Multi-State Multi-Configuration Quantum Chemical Computation of the Two-Photon Absorption Spectra of Bovine Rhodopsin

Abstract

Recently, progress in IR sources, has led to the discovery that humans can infrared (IR) light. This is hypothesized due to two-photon absorption (TPA) events promoting the retina dim-light rod photoreceptor rhodopsin to the same excited state populated via one-photon absorption (OPA). Here, we combine quantum mechanics/molecular mechanics and extended multi-configuration quasi-degenerate perturbation theory calculations to simulate the TPA spectrum of bovine rhodopsin (Rh) as a model for the human photoreceptor. The results show that the TPA spectrum of Rh has an intense S₀→S₁ band but shows also S₀→S₂ and S₀→S₃ transitions whose intensities, relative to the S₀→S₁ band, is significantly increased when compared to the corresponding bands of the OPA spectrum. In conclusion, we show that IR light in the 950 nm region can be perceived by rod photoreceptors supporting the two-photon origin of the IR perception. We also found that the same photoreceptor can perceive red (i.e. close to 680 nm) light provided that TPA induces population of S₂.

Graphical Abstract

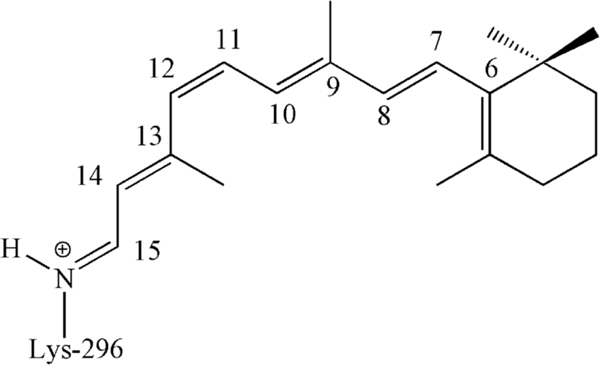
The vertebrate dim-light (scotopic) photoreceptor rhodopsin belongs to a large group of proteins forming the so-called G protein-coupled receptor (GPCR) family. More specifically, rhodopsin features the common hollow α-helical transmembrane structure of GCPR, but hosts an 11-cis-retinal chromophore (rPSB11) antagonist covalently connected to the protein via a protonated Schiff base linkage.^1–2 (see Scheme 1). The light-induced (i.e. photochemical) isomerization of the rPSB11 chromophore to its all-trans isomer (rPSBAT), is the first step of the so called rhodopsin photocycle ultimately leading to the production of the protein biologically active Meta-II state.³

Scheme 1.

Chemical structure of rPSB11.

For a long time, it has been thought that humans cannot perceive infrared (IR) radiation. However, in the 1970s it was discovered that the human retina perceives IR light in the 800–1355 nm range.^4–5 Second harmonic generation⁶ in the eye, fluorescence and two-photon absorption (TPA)⁷ were suggested as IR perception mechanisms. Several electrophysiological studies with lower vertebrate photoreceptors revealed a nonlinear optical processes leading to rhodopsin activation.^8–9 Although these studies imply that human visual perception might not be limited to the visible part of the electromagnetic spectrum, they did not explain how IR perception is allowed at the molecular level. Thus, their implications for photoreceptor activation, including human photoreceptors, has remained unidentified.

In 2014, Palczewski and coworkers¹⁰ provided evidence that humans can detect IR light at wavelengths around 950–1000 nm and that this is perceived as visible light. The study indicates that IR irradiation causes the photoisomerization of the rPSB11 chromophore suggesting that IR laser beams could be used to scan the retina and detect eye problems in their early stages—before they become insurmountable, where the using of visible-wavelength lasers might damage the retina.

The present paper is focused on the possibility of computing, rather than measuring, the TPA spectra of rhodopsins using quantum chemistry. To this aim, a theoretical exploration of the TPA properties of Rh using a quantum mechanics/molecular mechanics (QM/MM) model based on multi-state multi-configurational second order perturbation (MS-MC-PT2) level of QM theory, is carried out. To do so we focus on the structurally resolved bovine rhodopsin (Rh)¹ dim-light photoreceptor whose amino acid sequence and wavelength of absorption maximum (λ_max) are very close to those of human rhodopsin (93% identity and 498^11–12 vs. 496^13–14 nm respectively).

More specifically:

1. We construct ten isolated QM/MM models of Rh based on a previously reported Automatic Rhodopsin Modelling (ARM) protocol^15–16 (see section S1 in the supporting information (SI), for computational details) and the XMCQDPT2 (i.e. extended multi-configuration quasi-degenerate perturbation theory) implementation of the MS-MC-PT2 theory and use it to determine the λ_max and intensity (oscillator strength) of the OPA spectra. To assess the model accuracy, we compare the computed and experimental OPA features of Rh.

2. By focusing on two previously investigated molecules, trans-stilbene and a related stilbenoid,^17–19 we evaluate the reliability of XMCQDPT2 for the simulation of TPA spectra.

3. Finally, by using the constructed QM/MM model we compute the Rh TPA spectra and compare it with the available experimental data. The possible photochemical response of the TPA transition is then qualitatively evaluated using semi-classical trajectories.

OPA properties of the XMCQDPT2/cc-pVTZ//CASSCF/6–31G(d)/AMBER QM/MM model of Rh.

The absorption spectrum of Rh shows three peaks in UV-Vis region.²⁰ The two principal peaks are located at 498¹¹ and 280^20–21 nm (57.4 and 102.1 kcal/mol, respectively). The long-wavelength peak is attributed to the S₀→S₁ transition²² and short-wavelength intense peak attributed to aromatic amino acids.²⁰ However, the latter peak is also presents in the spectra of rPSB11 in 1,2-dichloroethane solvent²¹ with lower intensity. The band at 498 nm corresponds to the lowest π-π* transition of the chromophore. There is a weaker peak at 340^{12, 20, 23–24} nm (84.1 kcal/mol) assigned to the S₀→S₂ transition²² which is only seen in rPSB11.²⁰

In Table 1 we report the calculated average vertical excitation energies ⟨ΔE_S1−S0⟩, ⟨ΔE_S2−S0⟩ and ⟨ΔE_S3−S0⟩ computed using the constructed 8-root state average XMCQDPT2/cc-pVTZ//CASSCF/6–31G(d)/AMBER Rh models (the right side of the “//” indicate the level employed for geometry optimization and the left side that used for the energy and property calculations) and compare them to the experimental values obtained by converting wavelengths into vertical excitation energy values. Such excitations involve the ground state (S₀) and the first three singlet excited states (i.e. S₁, S₂ and S₃).

Table 1.

Computed OPA spectroscopic properties of Rh with different approaches. Transition energies (vertical excitation energies) are given in kcal/mol (nm in parentheses).

	Vertical (i.e. Franck-Condon) excitation			Oscillator Strength
Method	S0 → S1	S0 → S2	S0 → S3	S0 → S1	S0 → S2	S0 → S3
XMCQDPT21	60.1 (475 nm)	84.3 (339 nm)	88.8 (322 nm)	0.88	0.20	0.20
XMCQDPT22	60.2 (475 nm)	84.3 (339 nm)	88.5 (323 nm)	0.87	0.20	0.21
XMCQDPT23	60.3 (474 nm)	84.3 (339 nm)	-	0.87	0.18	-
XMCQDPT24	63.7 (449 nm)	86.4 (331 nm)	-	0.84	0.26	-
CASPT2 (IPEA=0)5	57.5 (497 nm)	83.6 (342 nm)	-	0.60	0.38	-
Experiment	57.4 (498 nm)	84.0 (340 nm)		-	-	-

^1.Average (10 models) 8-root SA with the cc-pVTZ basis set

^2.8-root SA of the representative model (model-6) with the cc-pVTZ basis set

^3.3-root SA of the representative model (model-6) with the cc-pVTZ basis set

^4.3-root SA of the representative model (model-6) with the 6–31G(d) basis set

^5.3-root SA with the 6–31G(d) basis set calculated with MOLCAS.

The results show that the ⟨ΔE_S1−S0⟩ value is 60.1±0.5 kcal/mol (λ_max = 475±4 nm) differs from the experimental value for less than 3.0 kcal/mol. After looking at the distribution of the positive charge along the chromophore backbone (see Scheme S1 and Table S2 in the SI) in S₀ and S₁, we see that the positive charge, initially located on the −N=C₁₅– moiety, moves forward towards the β-ionone ring and conclude that S₁ has character in agreement with previous studies.^{22, 25–26} The ⟨ΔE_S2−S0⟩ value is 84.3±0.4 (λ_max = 339±2 nm) that differs from the experimental data of only 0.2 kcal/mol. Such kind of differences are also displayed by the corresponding values of the 10 uncorrelated QM/MM models (see Section S1 and Table S3 in the SI), which present errors in the 2.3 to 3.6 kcal/mol and 0.0 to 1.0 kcal/mol range, respectively. Notice that for ΔE_S1–S0 these errors are close to the ca. 3.0 kcal/mol blue-shifted error previously documented for ARM generated QM/MM rhodopsin models.¹⁵ Further assessment of the accuracy of the XMCQDPT2 method, the effect of basis set and variation in the number of contributing roots in the state averaging have been documented in section S4 of the SI. It is also worth to mention that a comprehensive investigation on the S₀→S₃ transition, and the effect of the protein environment on the S₀→S₂ and S₀→S₃ transitions have been reported in section S5 of the SI.

TPA properties of trans-stilbene and a D-π-A stilbenoid.

The gas-phase trans-stilbene (see Scheme S2A in the SI) and its acceptor–π–donor (A–π–D) derivative 4-dimethylamino-4’-nitrostilbene (hereafter referred to as ACCD. See Scheme S2B in the SI) chromophores were used as benchmarks to validate the protocol for TPA spectra simulation. We selected ACCD because it features a non-centrosymmetric π-conjugation similar to rPSB11. The TPA cross section is related to the imaginary part of the second hyperpolarizability. Hence, our protocol is based on the Sum-Over-State (SOS) approach and accordingly, the equations “F1” and “D2” in Fortrie et al. ²⁷ have been used to calculate the TPA line-shape as a function of the frequency ω, i.e. the excitation wavelength. Here, the SOS was approximated using eleven intermediate electronic states (12-root single point calculation, based on previous computations on conjugated chromophores of similar size,²⁸ see section S1 in the SI). In our protocol, two absorbed photons in TPA are degenerate and therefore, the calculated λ_{max, TPA} and σ_TPA values for trans-stilbene (see Figure S4A for the simulated spectra) can be defined as the values corresponding to the maximum of its TPA spectra as in previous studies^{17–19, 29} (see Table 2). All calculated data reveal that while the obtained gas-phase λ_max,TPA values match the experimental value measured in solution (toluene¹⁷ and chloroform²⁹) reasonably well, the calculated σ_TPA by different methods, displays a substantial discrepancy (for more discussion see section S1 of the SI) which potentially may arise from the prediction of the transition dipole moments by different computational methods. In fact, comparing with experimental values, our computed TPA properties (λ_max,TPA = 480 nm and σTPA= 32 GM) are in good agreement with the values reported by Wergifosse et. al,²⁹ (λ_max,TPA = 486 nm and σTPA= 32 GM) rather than the values reported by Brédas et. al,¹⁷ (λ_max,TPA = 514 nm, and σ_TPA=12 GM). Furthermore, comparing to those computed with other methods,^18–19,29 XMCQDPT2 calculations shows the best agreement with the experimental data reported by Wergifosse et. al.²⁹

Table. 2.

Calculated and experimental OPA and TPA data for trans-stilbene, ACCD and Rh. λ_OPA and λ_TPA (nm) are, respectively, the lowest one-photon absorption wavelength and the two-photon resonance wavelength. σ_TPA (GM; 10⁻⁵⁰ cm⁴s/photon-molecule) is the TPA cross section. For the choice of Γ_mn value see page 11 in the SI.

		Theoretical Results				Experimental Results
		λmax,OPA(nm)	Λmax,TPA (nm)	σTPA GM (a.u.)	Γmn(eV)		λmax,OPA (nm)	λmax,TPA (nm)	σTPA GM
trans-stilbene	this work	292	480	32(2033)	0.2	ref (17)	297	514	12
	ref (17)a	278	466	27	0.1
	ref (19)b	267	469;425	280;54	0.25	ref (29)	302	486	32
	ref (18)c	471	397–514	117–129	0.2
	ref (29)d	273	432	43	0.2
ACCD	this work	332	664	141(9106)	02	ref (30)	452 (335)f	909	191
	ref (31)e	404–481	-	70–149	0.2–0.4
	ref (33)e	451	-	149	-	ref (32)	451	930	114
	ref (34)	279	~550	~30	0.248
Rh	this work	475	950	472 (30373)	0.2	ref (10)	498g	950–1050h 909i	260j
	ref (10)	-	1014	2.1	-

^aTheoretical data from the INDO-MRD-CI method.

^bTheoretical data from the CI-CNDO/S method.

^cTheoretical data from the ATDA formalism.

^dTheoretical data from the EOM-EE-CCSD method.

^eTheoretical data from the TDDFT method.

^fThe value in parentheses is measured in the vacuum.

^gThe value is extracted from ref (¹¹).

^hThe value is extracted from ref (¹⁰).

ⁱThe value is extracted from ref (³⁵).

^jThe value is extracted from ref (³⁶) for ChR2.

The TPA spectra of trans-stilbene (see Figure S4A) show a peak centered at the λ_max,TPA = 480 nm corresponds to the S₀→S₄ transition. According to our calculations, appreciable transition dipole moments from S₀ are found only for S₀→S₁ (5.7 Debye) and S₀→S₃ (5.0 Debye) pointing to this fact that the most intense TPA transition of S₀→S₄ could happen via the intermediate states S₁ or S₃ (i.e. S₀→S₁→S₄ or S₀→S₃→S₄, respectively). Inspection of the computed quantities and comparison with the results of the Brédas et. al,¹⁷ corroborate the dominant contribution of the S₀→S₁→S₄ transition in TPA spectra with the transition dipole moments of 5.7 Debye for S₀→S₁ and 2.5 Debye for S₁→S₄, analogous to that reported in Brédas et. al¹⁷ (i.e. 7.1 and 3.1 Debye for S₀→S₁ and S₁→S₄, respectively). In contrast, TDDFT prediction by Nayyar et. al ¹⁸ overestimates the S₁→S₄ transition dipole moment by a factor of ~2.6 (8.2 Debye). This leads to the overestimation of the σ_TPA by a factor of ~5 (note that their reported σ_TPA values are in the order of hundred). In conclusion, our gas-phase trans-stilbene study indicates that XMCQDPT2 predicts σ_TPA in good agreement with experimental data due to the reasonable values obtained for the transition energies and transition dipole moments.

To understand the effect of molecular geometry on the TPA properties of trans-stilbene, the spectra of the MP2/cc-pVTZ optimized structure²⁸ was calculated (Figure S5). The result shows a maximum at 486 nm with the σ_TPA of 29 GM, and hence, indicates a small effect of the geometry on the transition energies, dipole moments and, consequently, TPA properties of trans-stilbene. The geometry of ACCD was then optimized at the MP2/ccpVTZ and the gas-phase TPA spectra of ACCD was calculated using the same procedure used for trans-stilbene due to the complexity of considering the solvent effect. The corresponding TPA spectra are shown in Figure S4B. One of the spectral characteristics of such D-π-A molecules is the absence of symmetry rules governing optical absorption properties of centrosymmetric molecules and therefore, any excited state becomes both one- and two-photon allowed. Furthermore, these D-π-A molecules (also known as push-pull molecules) show, in general, larger TPA cross section with respect to trans-stilbene.

The calculated OPA vertical excitation energy (λ_max,OPA = 332 nm, see Table 2) of ACCD, corresponding to the S₀→S₁ transition, is in good agreement with the OPA gas-phase measurements (i.e. in a supersonic jet expansion.³⁷ See Table 2, value in parentheses). This indicates the reliability of our protocol in predicting the OPA properties of D-π-A chromophores. However, this value is far from that of experimental OPA spectra (λ_max,OPA = 452 nm) in DMSO solvent ^{30, 32} pointing to a solvatochromic effect whose simulation would require an effort going beyond the scope of the present work. Such effect is expected to cause substantial structural and property (such as absorption spectra, hyperpolarizabilities and TPA cross sections) variation. In fact, DFT-based QM/MM calculations ^{31, 33} have showed that, in contrast with the case of trans-stilbene in an apolar solvent, a polar solvent (such as DMASO and water) induced geometrical changes are important to accurately predict the OPA and TPA spectra of ACCD. Thus, in principle, when comparing our calculated results to the experiment, it would be important to consider the effects of the medium.^{31, 33} However, we noticed that when comparing the changes in the experimental λmax,TPA and σ_TPA values going from trans-stilbene to ACCD (486 to 909 nm and 32 to 191 GM, respectively), our XMCQDPT2-based methodology provide the same trend (480 to 664 nm and 32 to 141 GM, respectively). We take this as supportive for the protocol qualitative validity for TPA spectra simulation. It is also worth mentioning that our calculated σ_TPA value for ACCD is comparable with the value obtained by QM/MM studies probing the solvatochromic effect (see Table 2).^{31, 33}

TPA properties of Rh.

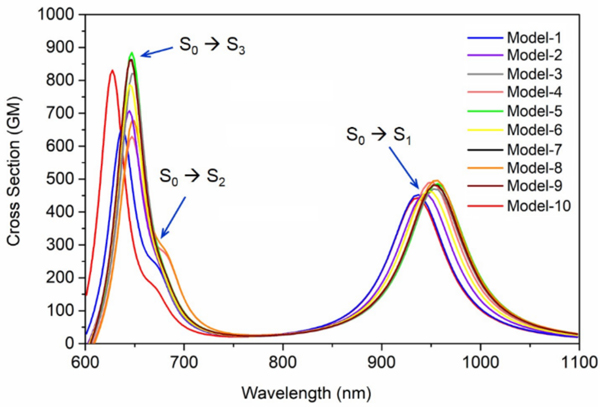
The predicted σ_TPA and λ_max,TPA values from 10 uncorrelated XMCQDPT2/cc-pVTZ//CASSCF/6–31G(d)/AMBER models of Rh, have allowed to simulate the TPA band presented in Figure 1. The simulated spectra reflect the blue shift of the OPA spectra of Rh with respect to the gas-phase chromophore^38–40 (Figure S6). The data predict an average TPA cross section of 472 GM at λ_max,_TPA = 950 nm, for the TPA corresponding to the S₀→S₁ transition. The calculated σ_TPA value is comparable with the relatively high value reported for the close system channelrhodopsin 2 (ChR2) which is ~ 260 GM at 920 nm.³⁶ The predicted λ_max,TPA value matches the value predicted in a previous theoretical study, reporting an absorption between 950–1150 nm with a ∼1000 nm maximum¹⁰ and demonstrating the consistency of such value with experimental electrophysiology data on the sensitivity to IR light of rods and, possibly, cones photoreceptor cells. However, our σ_TPA value is different from that computed in the same study. A fact that may be attributed to the use of TDDFT to compute the transition dipole moments or to the choice of macroscopic conversion pre-factor. Additionally, analyzing the important orbitals involved in TPA transitions (see section S8 in the SI for details), in consistent with the charge distribution on the rPSB11 chromophore (Table S2 in the SI) corroborates the charge transfer character of S₀→S₁ transition induced by TPA. Accordingly, considering the incorrect description of charge-transfer excitations as one of the hallmark failures of TDDFT,⁴¹ shows the superiority of our protocol for reliable prediction of the TPA properties of Rh.

Figure 1.

TPA of Rh (rPSB11 embedded in the protein cavity) obtained from 10 QM/MM models at the XMCQDPT2 level of theory (XMCQDPT2/cc-pVTZ//CASSCF/6–31G(d)/AMBER models). The color code matches Figure S3.

As mentioned above, the computed λ_max,TPA (~1000 nm) corresponds to the energy gap of 60.2 kcal/mol results in electronic excitation of the rPSB11 chromophore to its S₁ state. The S₀→S₁ vertical excitation corresponds to a π→π* transition which is also responsible for the rapid 11-cis to all-trans photo-isomerization of rPSB11.⁴² Therefore, as concluded in Palczewska et. al,¹⁰ our calculations is consistent with an effective Rh IR light perception and with the hypothesis that OPA and TPA result in the same photoisomerization process, producing rPSBAT and therefore activating the Rh photocycle and, in turn, visual perception.¹⁰ This appears to be a straightforward conclusion when considering the computational and experimental evidence in favor of a barrierless nature of the S₁ double-bond isomerization path and the results of semi-classical trajectory simulations as well as time-resolved absorption spectroscopy experiments.^{22, 43}

OPA and TPA calculations of our Rh QM/MM model demonstrate that while the second excitation (S₀→S₂) of the Rh is weak in the OPA spectra (see the oscillator strengths in Table 1), it is somehow more intense in TPA (Figure 1). As also evident from Table 1, these observations match well with the reported OPA^{12, 20, 23–24} experimental spectra which shows a weak peak at the β band of the Rh corresponding to the S₀→S₂ transition. In our study, the calculated average λ_max,TPA of the Rh models, related to the S₀→S₂ transition, is located at 678 (2 × λ_max,_OPA = 339) nm with the average cross section of 231 GM.

We compared our Rh computed TPA spectra with the corresponding experimental spectra reported by Birge et al.³⁵ In such study, the S₁ and S₂ states appear close to each other being assigned to a ~490 nm (as appeared in the OPA experiment) and ~440 nm (appeared in the TPA experiment) values, respectively.³⁵ Based on their experiment, the λ_max,_TPA is 909 nm (11000 cmwhich is far from our predictions for the λ _max,TPA of S₀→S₂ but matches well with the λ _max,TPA of S₀→S₁. Furthermore, previously experimental studies showed a low-intensity band at 340 nm which can be assigned to the S₀→S₂ transition.^{12, 20} This assignment is supported by gas-phase^{40, 44} and our QM/MM calculations, which is observed well separated transitions to the S₁ and S₂ states, challenging the S₂ assignment by Birge et al.³⁵

The calculated average λ_max,_TPA of our Rh models related to the S₀→S₃ transition, is located at 644 (2 × λ_max,_OPA = 322) nm and shows an average σ_TPA of 771 GM. Similar to the S₀→S₂ transition, the S₀→S₃ OPA transition is weak (i.e. it has a small oscillator strength) but, obviously, predicted to be strongly allowed in TPA. Furthermore, while both S₀→S₂ and S₀→S₃ transitions are predicted to have the same intensity in OPA (i.e. same oscillator strength), the later has a higher s_TPA (771 GM vs. 231 GM). This could be explained in terms of dipole and transition dipole moments used in the Sum-Over-State (SOS) approach (see section S1, equation 2 in the SI). After looking at the transition dipole moments (see section S8, SI), it was found that the most important contributions to the S₀→S₂ and S₀→S₃ transitions in the TPA spectrum of Rh are S₀→S₁→S₂ and S₀→S₁→S₃, respectively. The related transition dipole moments are 9.4, 5.0, and 7.5 Debye for S₀→S_1, S₁→S₂ and S₁→S₃ transitions, respectively. The higher transition dipole moment of S₁→S₃ by the factor of ~1.5 with respect to the S₁→S₂ leads to the larger σ_TPA of S₀→S₃. Looking at the transition diploe moments provides the explanation for different intensity of S₀→S₂ and S₀→S₃ transitions in OPA and TPA. This value for both OPA transitions corresponds to 3.8 Debye (note to the same oscillator strength), which is much smaller than the transition dipole moments responsible for the two-photon transitions (9.4, 5.0, and 7.5 Debye for S₀→S_1, S₁→S₂ and S₁→S₃ transitions, respectively). This also has been justified on the bases of molecular orbital excitations in the section S8 of SI.

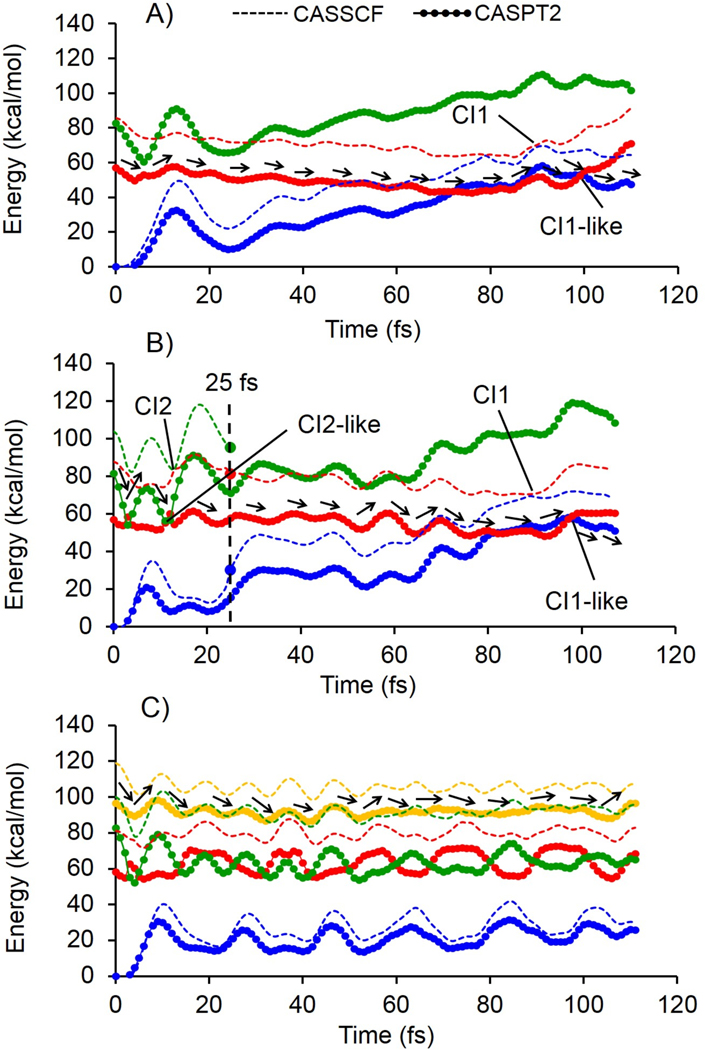
The dynamics triggered by the population of the S₁, S₂ and S₃ potential energy surfaces has been investigated by computing the corresponding FC trajectories at the CASSCF/6–31G(d)/AMBER level of theory (see section S1 in the SI, for computational details) which are surface-hop trajectories starting from the S₀ equilibrium structure of our QM/MM representative model (i.e. model-6) with zero initial velocities. The analysis of the geometrical progression along the CASSCF-driven FC trajectories is provided in the SI (see Figure S8). In order to qualitatively account for the effect of dynamic electron correlation and to be consistent with the above spectral analysis, the energy profiles are also recomputed using the CASPT2//CASSCF/6–31G(d)/AMBER level of theory (Figure 2). As shown in the Figure 2, the shape of the CASPT2 and CASSCF energy profiles for the excited state progression of Rh are similar. However, as expected, the CASPT2 energies are red-shifted due to the inclusion of dynamic electron correlation. FC trajectories provide an approximate description of the motion of the center of the excited state population and, in the present context, are used to provide qualitative evidence that the reactive S₁ state gets populated after TPA to the S₂ and S₃ states. Accordingly, we begin by showing that, with the constructed QM/MM model, the FC trajectory of Rh computed at the two-root state-average CASSCF/6–31G(d)/AMBER level and corrected by three-root state-average CASPT2 level, starting on S₁, reaches the reactive S₁/S₀ conical intersection on a ca. 100 fs timescale (Figure 2A), CI1 and CI1-like points in CASSCF and CASPT2 profiles, respectively) as previously documented with other models for the OPA process.^{26, 45} This is taken as an evidence that the rPSB11 chromophore in the adopted Rh model undergoes isomerization and that the primary photocycle intermediate bathorhodopsin is produced upon decay and relaxation on the S₀ potential energy surface upon IR irradiation. In order to demonstrate that the reactivity is maintained also when populating the S₂ state, we computed the FC trajectory at the same level of theory but employing three-root state-average orbitals in both CASSCF and CASPT2 calculations and starting on S₂ (see Figure 2B). The results indicate that S₁ is populated after ~15 fs (CI2 and CI2-like in CASSCF and CASPT2 profiles, respectively) upon decay from S₂ to S₁. To provide evidence for a reactive populated region of S₁, we stop the trajectory 10 fs after S₁ population and restart it from the same geometry and velocities and level of theory but with the more accurate two-root state average CASSCF wavefunction. The S₁ population reaches the reactive S₁/S₀ conical intersection on a ca. 100 fs timescale (Figure 2B), CI1 and CI1-like points in CASSCF and CASPT2 profiles, respectively).

Figure 2.

Relative CASSCF (solid lines) and CASPT2 (solid line + circles) semi-classical energy profiles. A) Photoisomerization after population of the S₁ state. B) Photoisomerization after population of the S₂ state. The large full circles and dashed vertical line indicate the change in methodology from three-root to two-root state average in CASSCF energy profiles. C) Photoisomerization after population of the S₃ state. CI and CI-like points referred to predicted conical intersection by CASSCF and CASPT2 level of theory, respectively. The stream of black arrows shows the reactive path at each trajectory.

Finally, in order to assess the reactivity of the TPA excitation to S₃ we compute a FC trajectory at the three-root state-average level (from the second to the fourth root) starting from S₃. We show that the S₃ doesn’t decay after ~110 fs (see Figure 2C). Accordingly, in contrast with TPA excitation to S₂ and S₁, we see that excitation to S₃ does not yield a fast decay to the S₁ state and hence, a fast S₁-like reactivity (the lack of progress along the isomerization coordinate is documented in the SI, Figure S8C). A much longer dynamics would be required to establish if this state is bounded (i.e. emissive) or if simply reacts on a much longer timescale.

We have simulated the TPA spectra of the dim-light visual receptor Rh, using a set of QM/MM models constructed via a semi-automatic protocol. Such models allow to use MS-MC-PT2 theory to consistently calculate OPA and TPA spectral properties, ultimately leading to an effective XMCQDPT2/cc-pVTZ//CASSCF/6–31G(d)/AMBER protocol, then validated by comparing computed and experimental quantities for trans-stilbene in its C₂ non-centrosymmetric equilibrium geometry and its polar D-π-A derivative ACCD. The comparison shows that the protocol yields transition dipole moments and transition energies and, hence, σ_TPA values comparable with experimental data.

The calculated energies and transition dipole moments of the 10 Rh models, allowed to predict an average σ_TPA of 472 GM at λ_max,_TPA = 950 nm, for the S₀→S₁ transition. This fully support the hypothesis that a cattle eye and, most likely, the human eye can detect IR light which is then perceived as visible light. However, the computed σ_TPA value appears to be different from that reported in Palczewska et. al.,¹⁰ a fact that may be attributed to the use of TDDFT to calculate the transition dipole moments or to the choice of the macroscopic conversion pre-factor.

While the S₀→S₂ OPA transition of Rh is very weak, its intensity is increased in the TPA spectrum. More specifically, the computed average σ_TPA is 231 GM at λ_max,_TPA = 678 nm. Such S₀→S₂ λ_max,_TPA value appears quite different with respect to the experimentally derived value reported by Birge et al. possibly due to the wrong assignment of the S₂ state as shown in this paper and also pointed out by Andersen et al.^{40, 44} in the study of the gas-phase rPSB chromophore. On the other hand, while a possible contribution to the assignment of intermolecular charge transfer states (e.g. between the retinal chromophore and a conjugated cavity side chain) cannot be excluded, our QM/MM model is unable to deal with such event that will have to be investigated in future work by trying to extend the model QM subsystem.

The capability of two-photon excitation microscopy (TPM) to detect retinal disfunctions has been successfully confirmed in vivo by Palczewska et. al.,^46–47 thus showing the potential of two-photon imaging for monitoring early retinoid changes. Due to the possibility of increasing the intrinsic fluorescence of the retinal chromophore via suitable mutations or by using microbial rhodopsins, large cross section values in our calculations asserted that rPSB11 could be turned into a fluorescent probe⁴⁸ for two-photon microscopy for in vivo imaging and monitoring in the red and infrared light regime with the least light-induced damage of living cells. Furthermore, in agreement with the previous experimental studies ^49–50 which approve the applicability of near-infrared (NIR) laser (via TPA) to investigate the activation of channelrhodopsin, our model and predicted TPA properties are promising for the computational investigation of rhodopsins (e.g. ChR2) useful in optogenetics.

In conclusion, our calculations show that ca. 950 nm light can be perceived by the green-blue light absorbing Rh photoreceptor at the TPA level, thus supporting the two-photon origin of the IR perception. We also provide evidence, by using semi-classical trajectory calculations, that via TPA Rh can also perceive (see) red light (i.e. close to 678 nm), as population of S₂ ultimately leads to chromophore isomerization through a conventional S₁ path. However, TPA population of S₃ may not lead to chromophore isomerization with the same speed of S₂ and S₁ population. Therefore, it is likely that TPA-based perception of a wavelength of 643 nm (ca. orange light) cannot be detected with the same type of mechanism or occur through a significantly slower reaction channel.

ABBREVIATIONS

TPA

Two Photon Absorption

OPA

One photon Absorption

Rh

Bovine Rhodopsin

XMCQDPT2

Extended Multi-Configuration Quasi-Degenerate Second Order Perturbation Theory

QM/MM

Quantum Mechanic/Molecular Mechanic

rPSB11

11-cis-retinal chromophore

ChR2

Channelrhodopsin-2

DFT

Density Functional Theory

TDDFT

Time Dependent Density Functional Theory