MANTIS: Model-Augmented Neural neTwork with Incoherent k-space Sampling for efficient MR parameter mapping

Abstract

Purpose:

To develop and evaluate a novel deep learning-based image reconstruction approach called MANTIS (Model-Augmented Neural neTwork with Incoherent k-space Sampling) for efficient MR parameter mapping.

Methods:

MANTIS combines end-to-end convolutional neural network (CNN) mapping, incoherent k-space undersampling, and a physical model as a synergistic framework. The CNN mapping directly converts a series of undersampled images straight into MR parameter maps using supervised training. Signal model fidelity is enforced by adding pathway between the undersampled k-space and estimated parameter maps to ensure that the parameter maps produced synthesized k-space consistent with the acquired undersampling measurements. The MANTIS framework was evaluated on the T₂ mapping of the knee at different acceleration rates and was compared with two other CNN mapping methods and conventional sparsity-based iterative reconstruction approaches. Global quantitative assessment and regional T₂ analysis for the cartilage and meniscus were performed to demonstrate the reconstruction performance of MANTIS.

Results:

MANTIS achieved high-quality T₂ mapping at both moderate (R=5) and high (R=8) acceleration rates. Compared to conventional reconstruction approaches that exploited image sparsity, MANTIS yielded lower errors (normalized root mean square error of 6.1% for R=5 and 7.1% for R=8) and higher similarity (structural similarity index of 86.2% at R=5 and 82.1% at R=8) to the reference in the T₂ estimation. MANTIS also achieved superior performance compared to direct CNN mapping and a two-step CNN method.

Conclusion:

The MANTIS framework, with a combination of end-to-end CNN mapping, signal model-augmented data consistency, and incoherent k-space sampling, is a promising approach for efficient and robust estimation of quantitative MR parameters.

INTRODUCTION

Quantitative mapping of magnetic resonance (MR) parameters, such as the spin-lattice relaxation time (T₁) and the spin-spin relaxation time (T₂), have been shown as valuable methods for improved assessment of a range of diseases. Compared to conventional MR imaging, parameter mapping can provide increased sensitivity to different pathologies with more specific information on tissue composition and microstructure. Standard approaches for estimation of MR parameters usually require repeated acquisitions of datasets with varying parameters of imaging, for example, multiple echo times (TEs) for T₂ mapping and various flip angles (FAs) or inversion recovery times (TIs) for T₁ mapping. The corresponding parameter values can then be generated by fitting the acquired images to a physical model on a pixel-by-pixel basis, yielding a parameter map. Due to the need to image an anatomic structure multiple times, parameter mapping usually requires long scan times compared to conventional imaging, limiting its widespread clinical use. Therefore, accelerated parameter mapping is highly-desirable and remains a topic of great interest in the MR research community.

Many approaches can be applied to accelerate data acquisitions, such as parallel imaging utilizing multi-coil sensitivities (1–3), compressed sensing exploiting image sparsity (4), or a combination of both (5,6). Data acquisitions can also be further accelerated by reconstructing undersampled dynamic images in a joint spatial and parametric space (x-p space) to explore spatial-temporal correlations (7), or by additionally incorporate a model into the reconstruction process (8–12). Indeed, the high correlations presented in the parametric dimension offer an efficient way of exploring signal models as prior knowledge for image reconstruction. For example, several methods have been proposed to examine temporal correlations along the parameter dimension to profoundly accelerate data acquisitions (11–13). Other approaches aim to constrain signal evolution in the parametric dimension using an analytical model for further improved reconstruction performance (8,14,15). More recently, MR fingerprinting (MRF) (16), a technique which takes advantage of incoherent signal acquisition schemes in combination with pattern recognition of numerically simulated signal dictionary, has provided fast and artifact-insensitive parameter mapping in several applications (17).

There has been a much recent interest in applying deep learning to a wide variety of MR imaging applications. Deep learning methods have been successfully used for image classification, tissue segmentation, object recognition, and image registration. There have also been recent works describing the use of deep learning in image reconstruction with promising initial results. For example, Hammernik et al. have recently proposed a generalized compressed sensing framework using a variational network for accelerated imaging of the knee (18). This approach aims to learn an optimal regularization function and reconstruction setting for improved reconstruction performance. Other methods attempt to extend the compressed sensing framework using different deep learning architectures and have achieved success for image reconstruction (19,20). Meanwhile, various methods have also been proposed to directly remove aliasing artifacts from undersampled images using a direct end-to-end convolutional neural network (CNN) mapping (21–26). Zhu et al. have also proposed an approach called AUTOMAP to directly estimate artifact-free images from undersampled k-space using the so-called domain-transform learning, which has demonstrated the feasibility of learning mutually correlated information from multiple manifolds (27). While these deep learning methods have focused on highly efficient image reconstruction for conventional static MR imaging, applications of deep learning for dynamic imaging and in particular accelerated parameter mapping have been limited (28–30).

The purpose of this work was to develop and evaluate a novel deep learning-based reconstruction framework called Model-Augmented Neural neTwork with Incoherent k-space Sampling (MANTIS) for efficient and robust MR parameter mapping. Our approach combines end-to-end CNN mapping with k-space consistency using the concept of cyclic loss (19,31) to enforce data and model fidelity further. Incoherent k-space sampling is used to improve reconstruction performance. A physical model is incorporated into the proposed framework so that the parameter maps can be efficiently estimated directly from undersampled images. The performance of MANTIS was demonstrated for T₂ mapping of the knee joint.

THEORY

This section describes details about the MANTIS framework tailored for T₂ mapping. However, such a structure can also be modified to estimate other quantitative MR parameters with corresponding signal models.

Model-Based Reconstruction for Accelerated T₂ Mapping

In model-based reconstruction for accelerated T₂ mapping, an image needs to be estimated from a subset of k-space measurements for the j^th echo first, which can be written as:

$$d_j=E{i}_j+\epsilon$$ [1]

Here ε is the complex Gaussian noise in the measurements (32), d_j is the undersampled k-space data, and i_j is the corresponding image with a size of n_x×n_y to be reconstructed satisfying the T₂ signal behavior at the j^th echo time (te_j) as:

$$i_j=S_j\left({\text{I}}_0,{\text{T}}_2\right)={\text{I}}_0\cdot e^{-T{E}_j/{\text{T}}_2}$$ [2]

where i₀ and t₂represent the proton density image and associated T₂ map, respectively. The encoding matrix E can be expanded as:

$$E=MF$$ [3]

where f is an encoding operator performing Fourier Transform and m is an undersampling pattern selecting desired k-space measurements. A signal-to-noise ratio (SNR) optimized reconstruction of Eq. [1] can be accomplished by minimizing the following least squares errors:

$${\tilde{\text{I}}}_0,{\tilde{\text{T}}}_2=\arg \underset{{\text{I}}_0,{\text{T}}_2}{\min }\sum _{j=1}^t{\Vert E{S}_j\left({\text{I}}_0,{\text{T}}_2\right)-d_j\Vert }_2^2$$ [4]

where ‖·‖₂ denotes the l₂ norm and t is the total number of echoes. Since the system of Eq. [4] can be poorly conditioned at high acceleration rates, the reconstruction performance can be improved by minimizing a cost function that includes additional regularization terms on the to-be-reconstructed proton density image and T₂ map:

$${\tilde{\text{I}}}_0,{\tilde{\text{T}}}_2=\arg \underset{{\text{I}}_0,{\text{T}}_2}{\min }\left(\frac{1}{2}\sum _{j=1}^t{\Vert E{S}_j\left({\text{I}}_0,{\text{T}}_2\right)-d_j\Vert }_2^2+\sum _k{\lambda }_k{R}_k\left({\text{I}}_0,{\text{T}}_2\right)\right)$$ [5]

The regularization penalty r_k (i₀, t₂) (can be selected based on prior knowledge or assumptions about the model considering desired parameters (8–12), with a weighting parameter λ_k controlling the balance between the data fidelity (the left term) and the regularization (the right term). Eq.[5] describes the generalized model-based reconstruction framework that can be implemented for accelerated quantitative T₂ mapping (7,8).

End-to-End CNN Mapping

End-to-end mapping using CNN as a nonlinear mapping function has been shown to be quite successful in recent applications of domain-to-domain translation. The concept behind the mapping method is to use CNN to learn spatial correlations and contrast relationships between input datasets and desirable outputs. Such a network structure has been shown to capable of mapping from one image domain to another image domain representing discrete tissue classes (e.g. image segmentation (33–35)), from artifact or noise corrupted images to artifact-free images (e.g. image restoration and reconstruction (21–26)), from one image contrast to a different image contrast (e.g. image synthesis (36–40)), and from k-space directly to image space (e.g. domain-transform learning (27)). In the current study, end-to-end CNN mapping was performed from the undersampled image domain to the parameter domain, denoted as $i_u\to \left({\tilde{\text{I}}}_0,{\tilde{\text{T}}}_2\right)$, where the undersampled image can be obtained from fully sampled image retrospectively using zero-filling reconstruction:

$$i_u=E^{H}Fi$$ [6]

Here, E^H represents the Hermitian transpose of the encoding matrix E shown in Eq. [3].

To perform parameter mapping using CNN, a deep learning framework is designed that regularizes the estimation by satisfying the constraints of prior knowledge in the training process (i.e., regularization by prior knowledge in the training datasets). Since no particular assumptions are made in the training process, the prior knowledge originates from certain latent features that are learned from the datasets during network training (18,22,29). In another word, the network aims to discover a model that will map the undersampled images directly to the parameter maps that will be estimated. Besides, by implementing the dynamic image series as a combined input (see Methods section), the spatial convolutional filters typically used in the network are implicitly extended into spatial-temporal filters which can characterize hidden features between spatial and dynamic signals in the dataset. The end-to-end CNN mapping from the undersampled images (in domain(i_u)) to the T₂ parameter maps can be expressed as:

$$R_{cnn}\left({\text{I}}_0,{\text{T}}_2\right)={\mathbb{E}}_{i_u\sim domain\left(i_u\right)}\left[{\Vert C\left(i_u|\theta \right)-\left({\text{I}}_0,{\text{T}}_2\right)\Vert }_2\right]$$ [7]

Here, $C\left(i_u|\theta \right):i_u\to \left({\tilde{\text{I}}}_0,{\tilde{\text{T}}}_2\right)$ is a mapping function conditioned on network parameter θ, and the ${\mathbb{E}}_{i_u\sim domain\left(i_u\right)}[\cdot ]$ is an expectation operator of a probability function given i_u belongs to a training dataset domain(i_u). As in most deep learning works, the l₂ norm is typically selected as a loss function to ensure that the mapping is accurate(18,21–25).

MANTIS: Extending End-to-End CNN Mapping with Model-Consistency

Similar to prior studies for CNN-based image reconstruction with a focus on data consistency (19,22), Eq. [7] is inserted into Eq. [5] to replace the original regularization term so that a new objective function (Eq. [8]) can be formulated, in which the CNN-based mapping serves as a regularization penalty term (right term) to the data consistency term (left term).

$$\tilde{\theta }=\arg \underset{\theta }{\min }\left({\lambda }_{data}{\mathbb{E}}_{i_u\sim domain\left(i_u\right)}\left[\sum _{j=1}^t{\Vert E{S}_j\left(C\left(i_u|\theta \right)\right)-d_j\Vert }_2^2\right]+{\lambda }_{cnn}{\mathbb{E}}_{i_u\sim domain\left(i_u\right)}\left[{\Vert C\left(i_u|\theta \right)-\left({\text{I}}_0,{\text{T}}_2\right)\Vert }_2\right]\right)$$ [8]

Here, λ_data and λ_cnn are regularization parameters balancing the model fidelity and CNN mapping, respectively, assuming that there is a training database including the fully-sampled images i and a pre-defined undersampling mask m .

The training process of Eq. [8] is equivalent to training two cyclic losses (19,31) as shown in Figure 1. The first loss term (loss 1) ensures that the reconstructed parameter maps from CNN mapping produce undersampled k-space data matching the acquired k-space measurements. The second loss term (loss 2) provides that the undersampled images generate the same parametric maps as the reference parameter maps (i.e., an objective in normal supervised learning). Note that Eq. [8] is fundamentally different from Eq.[5] concerning the optimization target. While the conventional model-based reconstruction in Eq. [5] is attempting to reconstruct each set $\left({\tilde{\text{I}}}_0,{\tilde{\text{T}}}_2\right)$ matching the acquired k-space data, the new framework in Eq.[8] is trying to estimate a parameter set $\tilde{\theta }$ conditioned on which the CNN mapping optimizes the estimation performance in the current training datasets. The data-consistency term (the left term in Eq.[8]) further ensures that the estimation during the training process is correct in k-space. Once the training process is completed, the estimated parameter set $\tilde{\theta }$ is fixed, and it can be used to efficiently convert new undersampled images to their corresponding parameter maps $\left({\tilde{\text{I}}}_0,{\tilde{\text{T}}}_2\right)$ directly, formulated as:

$${\tilde{\text{I}}}_0,{\tilde{\text{T}}}_2=C\left(i_u|\tilde{\theta }\right),i_u\in domain\left(i_u\right)$$ [9]

Figure 1:

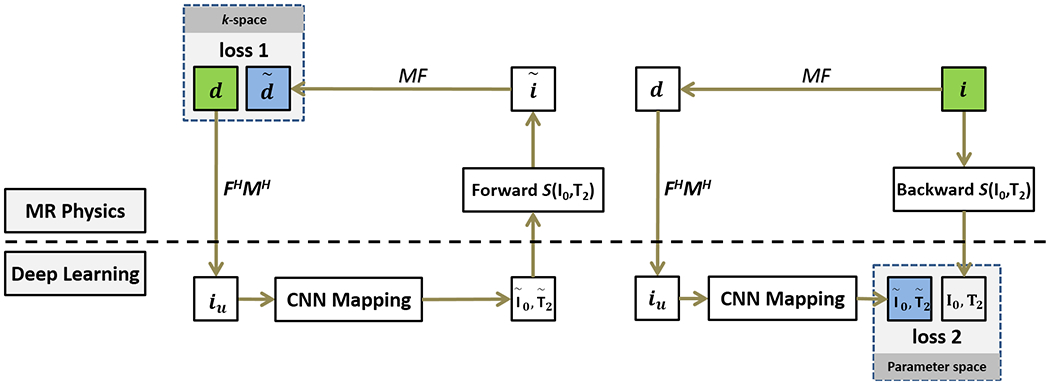
Illustration of the MANTIS framework, which features two loss components. The first loss term (loss 1) ensures that the reconstructed parameter maps from the CNN mapping produce synthetic undersampled k-space data ($\tilde{d}$) matching the acquired k-space measurements (d) in the k-space domain. The second loss term (loss 2) ensures that the undersampled multiecho images produce parameter maps $\left({\tilde{\text{I}}}_0,{\tilde{\text{T}}}_2\right)$ that are same as the reference parameter maps (i₀, t₂) genrated from reference multiecho images. The MANTIS framework considers both the data-driven deep learning component and signal model from the basic MR physics. The notation in this figure follows the main text description.

METHODS

In-Vivo Image Datasets

This retrospective study was performed in compliance with the Health Insurance Portability and Accountability Act (HIPPA) regulations, with approval from our Institutional Review Board, and with a waiver of written informed consent. T₂ mapping images of the knee acquired in 100 symptomatic patients (55 males and 45 females, mean age = 65 years) on a 3T scanner (Signa Excite Hdx, GE Healthcare, Waukesha, Wisconsin) equipped with an eight-channel phased-array extremity coil (InVivo, Orlando, Florida) were retrospectively collected for training the deep neural network. All images were acquired using a multi-echo spin-echo T₂ mapping sequence in sagittal orientation with the following imaging parameters: field of view (FOV) = 16×16cm², repetition time (TR) = 1500ms, echo times (TEs) = [7, 16, 25, 34, 43, 52, 62, 71] ms, flip angle = 90°, bandwidth = 122Hz/pixel, slice thickness = 3-3.2mm, number of slices = 18-20, and acquired image matrix = 320×256 which was interpolated to 512×512 after reconstruction. The images were reconstructed directly on the MR scanner (CartiGram, GE Healthcare, Waukesha, Wisconsin) and were saved as magnitude images into DICOM files after coil combination and thus was considered as a single-coil scenario. These image datasets were treated as “fully sampled” reference in the network training. To evaluate the trained network, T₂ mapping images of the knee were acquired on additional ten symptomatic patients (7 males and three females, mean age = 63 years). For the patient scans, images were reconstructed on the MR scanner and were saved as magnitude images into DICOM files. To demonstrate the generality of MANTIS for true k-space, prospective data was also acquired in one healthy volunteer using the same T₂ mapping sequence with matching imaging parameters, and multi-coil true k-space data saved directly from the scanner. In this case, the fully sampled reference image was processed offline with the coil combination. For the DICOM images, the undersampled multi-echo images were generated by multiplying the reference fully sampled k-space data with the undersampling masks (described in the following subsection) using a zero-filling reconstruction. The fully sampled k-space data was obtained by performing direct Fourier Transform on the reference images. For the multi-coil k-space data, the undersampled images were generated by first undersampling multi-coil k-space data and then performing coil combination of the undersampled multi-coil images.

Implementation of Neural Network

A U-Net architecture (41) was adapted from an image-to-image translation study (42) (https://github.com/phillipi/pix2pix) for the application of MANTIS for mapping the undersampled image datasets directly to corresponding T₂ maps. As illustrated in Figure S1 in the Supporting Information, the U-Net structure consists of an encoder network and a decoder network with multiple shortcut connections between them. The encoder network is used to achieve efficient data compression while probing robust and spatial invariant image features of the input images. The decoder network, designed with a mirrored structure, is applied for restoring image features and increasing image resolution using the output of the encoder network. Multiple shortcut connections are incorporated to concatenate entire feature maps from the encoder to the decoder to enhance mapping performance. This type of network structure has shown promising results for image-to-image translation in many recent studies (23,34,38,40,41).

Network Training

The undersampled images are concatenated from all the eight echoes together, so that the network input has a total of 8 channels, as shown in Figure S1 in the Supporting Information. From the 100 patient image datasets in the training group, 90 patient datasets (1717 concatenated images) were randomly selected for network training, while the remaining 10 patient datasets (195 concatenated images) were used for validation during the training process to choose the best network model. It should be noted that the ten patient datasets used for network training validation were different from the ten patient datasets used for the final evaluation of the best network model.

The input of the framework included the desired undersampling masks for each image (described in the following subsection) and the undersampled multi-echo images. The output of the network was a T₂ map and a proton density (I₀) image directly estimated from the undersampled multi-echo images. The estimated T₂ map and proton density image were then validated against the reference T₂ map and proton density images obtained by fitting the reference multi-echo images to an exponential model (Eq. [2]) using a standard nonlinear least squares fitting algorithm. With the output T₂ map and proton density image from the network, the multi-echo images can be synthesized using (Eq. [2]), from which multi-echo k-space can be generated. The synthetic multi-echo k-space were then compared with the real acquired undersampled multi-echo k-space data with the undersampling masks.

Due to GPU memory limitations, every input two-dimensional (2D) image was down-sampled to a matrix size of 256×256 using bilinear interpolation and then used for generating reference T₂ map and proton density images. This step was performed due to the limited GPU memory in the server and could be avoided if sufficient memory was available. Image normalization was conducted using data from each patient by dividing the images by its maximum magnitude signal intensity. During the training of the network, the network weights were initialized using the initialization scheme suggested by He et al. (43) and were updated using an adaptive gradient descent optimization (ADAM) algorithm (44) with a fixed learning rate of 0.0002. The network was trained in a mini-batch manner with three image slices in a single mini-batch. Total iteration steps corresponding to 200 epochs of the training dataset were carried out for the training, and the best model was selected as the one that provided the lowest loss value in the validation datasets. The parameters in the objective function (Eq. [8]) were empirically selected as λ_data =0.1 and λ_cnn =1. To investigate the influence of different weighting parameters, additional experiments were also performed for λ_cnn =0 (denoted as a relax constraint), λ_cnn =0.1 (denoted as a weak constraint) and λ_cnn =10 (denoted as a strong constraint) while keeping the remaining parameters unmodified.

The entire training process was implemented in standard Python (v2.7, Python Software Foundation, Wilmington, Delaware). The network was designed using the Keras package (45) running Tensorflow computing backend (46) on a 64-bit Ubuntu Linux system. The l₂ norm was implemented using the standard Tensorflow subroutine tf.norm to calculate the value for both real and complex data. All training and evaluation were performed on a computer server with an Intel Xeon W3520 quad-core CPU, 32 GB DDR3 RAM, and one NVidia GeForce GTX 1080Ti graphic card with a total of 3584 CUDA cores and 11GB GDDR5 RAM.

Sampling-Augmented Training Strategy

To improve the robustness of MANTIS against k-space trajectory discrepancy between the training and testing datasets, a sampling-augmented training strategy was applied in our network training. Specifically, a sampling pattern library consisting of different 1D variable-density random undersampling masks (N = 1000 in the current study) was first generated, as shown in Figure 2a. Each mask-set has eight different sampling masks (for introducing temporal incoherence) matching the number of echoes in our datasets, as shown in Figure 2b for one representative example. During the training process, a mask-set was randomly generated from this library for one training iteration, so that the network can learn a wide range of undersampling artifact structures during the training. We hypothesize that such a strategy can improve the robustness of the system against k-space trajectory discrepancy, and thus the trained system can be used to reconstruct undersampled images acquired with different undersampling patterns.

Figure 2:

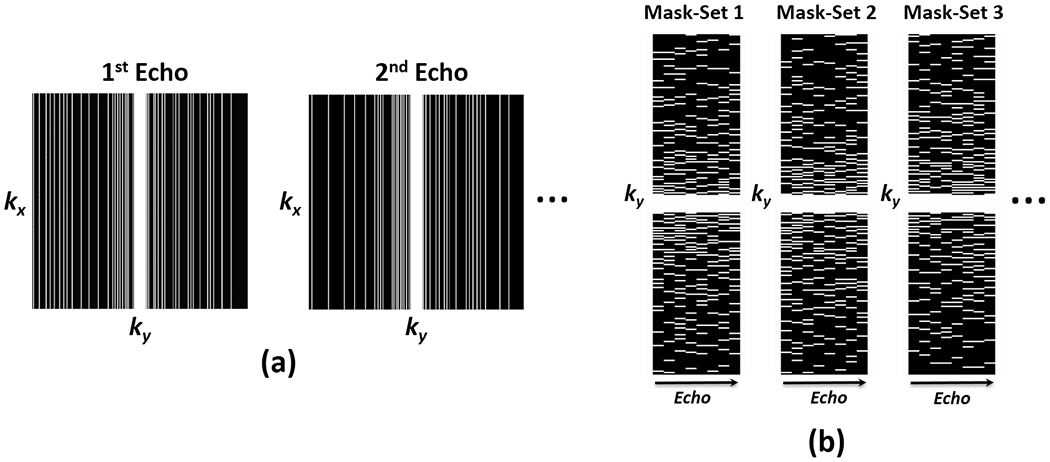
Schematic demonstration of the undersampling patterns used in the study. (a) Representative examples of the applied 1D variable-density random undersampled mask used for 1^st and 2^nd echo image. (b) Example sets of k_y-t 1D variable-density random undersampling masks for eight echo times. The undersampling mask varies along the echo dimension, and the mask-set was randomized for each iteration during the network training to augment the training process.

For each undersampling pattern, 5% of the k-space center was fully sampled, and two different acceleration rates (R) were investigated, including R=5 and R=8.

Evaluation of Reconstruction Methods

The performance of MANTIS was evaluated by comparing with 1) conventional sparsity-based reconstruction approaches using a global low-rank constraint (referred to as GLR hereafter), locally low-rank constraint (referred to as LLR hereafter), a combination of low-rank and sparsity constraint (k-t SLR (47)), and a combination of structure low-rank and sparsity constraint (ALOHA) (48) on the multiecho image-series; 2) direct CNN training using only the loss 2 component in Figure 1 (referred to as “U-Net Mapping” hereafter); and 3) a two-step CNN approach (referred to as “U-Net Imaging + T₂ Fitting” hereafter) where the MANTIS framework was slightly modified to allow direct restoration of the multi-echo images with CNN mapping in loss 2, and then the parameter maps were obtained by fitting the reconstructed multi-echo images with Eq. [2] in the inference.

The GLR and LLR reconstructions were implemented using an iterative soft thresholding (ISTA) algorithm adapted from that proposed by Zhang et al. in Ref (13). The regularization parameters were empirically selected for each reconstruction type separately and were fixed for all reconstructions. For all the datasets, the GLR reconstruction was performed with a total of 50 iterations. Following the reconstruction implemented in Ref (13), the LLR reconstruction was initialized with GLR reconstruction for 20 iterations first, then followed by LLR reconstruction with reduced regularization weight for another 30 iterations. The block size was selected as 8×8 was selected and the reconstruction was implemented with overlapping blocks to minimize the blocky effect. The k-t SLR reconstruction was performed using the source code provided by the original developers in https://research.engineering.uiowa.edu/cbig/content/matlab-codes-k-t-slr with its default parameter setting. The ALOHA reconstruction was performed using the source code provided by the original developers in https://bispl.weebly.com/aloha-for-mr-recon.html with its default parameter setting. For each of the reconstructed image dataset, a T₂ map was estimated by fitting Eq. [2] from the reconstructed images on a pixel-by-pixel basis as described above.

The normalized Root Mean Squared Error (nRMSE) and Structural SIMilarity (SSIM) index, calculated with respect to the reference, were used to assess the overall reconstructed image errors. The nRMSE is defined as:

$$nRMSE=\frac{{\Vert {\text{T}}_2-{\tilde{\text{T}}}_2\Vert }_{2,\text{Φ}}}{{\Vert {\text{T}}_2\Vert }_{2,\text{Φ}}}$$ [10]

where t₂ and ${\tilde{\text{T}}}_2$ were estimated from the reference and accelerated data, respectively, and ‖·‖_{2, Φ} denoted the l₂ norm measured over the knee region Φ.

Regional T₂ Analysis

Region-of-interest (ROI) analysis was performed to compare the mean T₂ values of the cartilage and meniscus from GLR, LLR, k-t SLR, ALOHA, U-Net Mapping, U-Net Imaging + T₂ Fitting, and MANTIS at both R=5 and R=8 with the reference T₂ values from the fully sampled images. A research scientist performed manual segmentation of the patellar, femoral and tibial cartilage and meniscus of the knee in the 10 testing patient datasets with eight years of experience in medical image segmentation under the supervision of an experienced musculoskeletal radiologist using the first echo image and the reference T₂ map. Besides, the cartilage from all the ten patients was further divided into deep and superficial halves for sub-regional T₂ analysis. The agreement was assessed using the Bland-Altman analysis. Differences between the reconstructed and reference T₂ values were evaluated using the non-parametric Wilcoxon signed-rank test for the rank differences between paired measurements. Statistical significance was defined as a p-value less than 0.05.

RESULTS

The average time for the total network training process was ~19.4 hours. Following network training, the average time for reconstructing T₂ maps in all image slices was ~2.1 seconds for each patient dataset.

Evaluation of Reconstruction Methods

Table 1 summarizes the mean nRMSE and SSIM values between the reference T₂ maps and the reconstructed T₂ maps averaged over all the ten testing patient datasets. In general, The U-Net Imaging + T₂ Fitting, U-Net Mapping and MANTIS reconstruction methods were superior to the GLR, LLR, k-t SLR, and ALOHA reconstruction methods at both R=5 and R=8. MANTIS yielded the smallest reconstruction errors and the highest similarity to the reference at both acceleration rates.

Table 1:

nRMSE and SSIM between the reference T₂ maps estimated from the fully sampled images and the reconstructed T₂ maps estimated using undersampling patterns. Results were averaged over the 10 test patient datasets and represent mean value ± standard deviation. MANTIS achieved the highest reconstruction performance with te smallest errors at both R=5 and 8.

Methods	Mean ± SD at R=5		Mean ± SD at R=8
	nRMSE (%)	SSIM (%)	nRMSE (%)	SSIM (%)
GLR	13.5 ± 4.3	72.5 ± 3.7	15.0 ± 3.9	63.2 ± 4.5
LLR	12.2 ± 3.5	70.4 ± 3.1	13.9 ± 3.5	59.2 ± 3.3
k-t SLR	9.8 ± 2.4	77.5 ± 3.3	11.6 ± 2.9	70.5 ± 3.6
ALOHA	8.9 ± 2.1	80.3 ± 3.5	10.9 ± 2.7	72.6 ± 3.8
U-Net Imaging + T2 Fitting	6.5 ± 2.0	83.5 ± 3.1	8.8 ± 2.9	76.2 ± 3.2
U-Net Mapping	6.9 ± 1.8	82.3 ± 2.8	8.5 ± 2.5	78.0 ± 2.5
MANTIS	6.1 ± 1.5	86.2 ± 1.9	7.1 ± 1.8	82.1 ± 2.3

Figure 3 shows representative T₂ maps estimated from different reconstruction methods at R=5 (top row) and R=8 (bottom row), respectively, for a symptomatic patient. The GLR reconstruction generated images with inferior image quality with noticeable artifacts in bone and fatty tissues indicated by the white arrows. Although the LLR reconstruction improved overall image quality with reduced image artifacts, it led to a noticeable smooth appearance due to the exploitation of local sparsity at high acceleration. The k-t SLR performed better than GLR and LLR for restoring image details but remained significant residual artifacts. The ALOHA outperformed other conventional iterative methods for the removal of image streaking artifacts but still led to an oversmooth appearance on the bone region. In contrast, MANTIS generated nearly artifact-free T₂ maps with well-preserved sharpness and texture comparable to the reference T₂ maps. This qualitative observation was also confirmed by the corresponding residual error maps and nRMSE values from the same patient shown in Figure S2 in the Supporting Information. The relevant residual error maps are displayed at the same scale to compare the reconstruction performance qualitatively.

Figure 3:

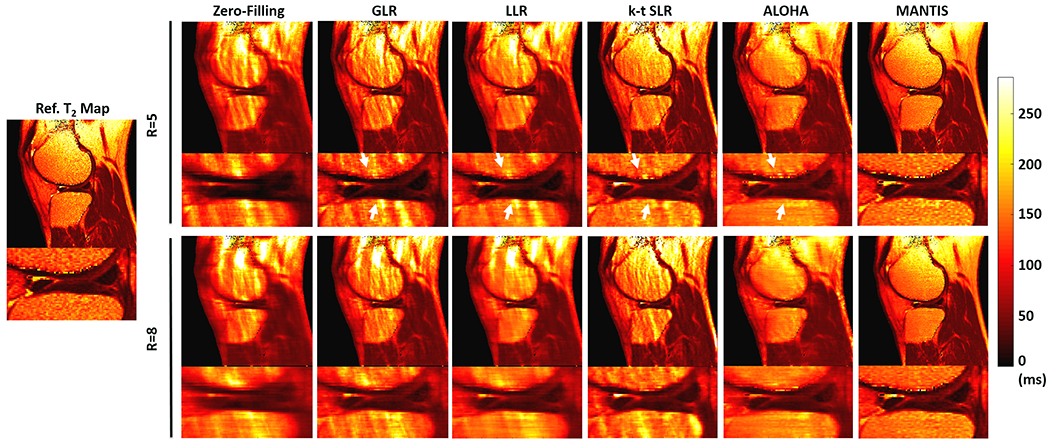
Comparison of T₂ map estimated from MANTIS with T₂ maps produced using different conventional reconstruction methods at R=5 (top row) and R=8 (bottom row) in one patient. MANTIS generated a nearly artifact-free T₂ map with well-preserved sharpness and texture comparable to the reference T₂ maps. Other methods created suboptimal T₂ maps with either reduced image sharpness or residual artifacts, as indicated by the white arrows.

Figure 4 shows representative T₂ maps estimated from different deep learning methods at R=5 for the same patient of Figure 3. The U-Net Mapping produced T₂ maps with reduced image artifacts, but the sharpness and texture details of the reconstructed image were suboptimal as indicated by the white arrows. The U-Net Imaging + T₂ Fitting provided a favorable overall performance similar to MANTIS. However, there were amplified noises indicabed by the white arrows in the deep cartilage layers and meniscus where image SNR is low.

Figure 4:

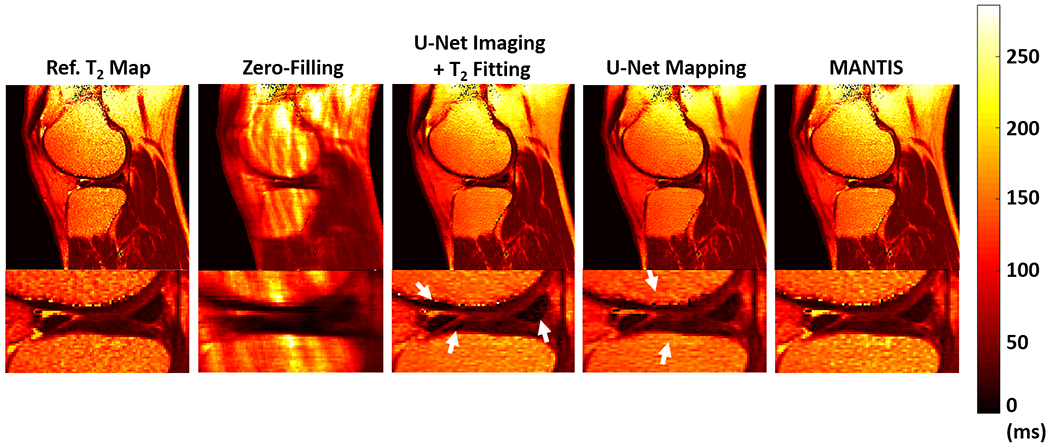
Comparison of T₂ map estimated from MANTIS (direct mapping of the T₂, loss1+loss2) with T₂ maps generated from U-Net Mapping (direct mapping of the T₂, loss2 only) and U-Net Imaging + T₂ Fitting approach at R=5. U-Net Mapping is implemented using the MANTIS framework without the loss 1 (data consistency) component. U-Net Imaging + T₂ Fitting is a two-step approach in which multiecho images are first generated (loss1 + loss2) followed by parameter fitting. MANTIS achieved better performance (more homogeneous tissue structure and realistic appearance) compared to the other two methods particularly in the cartilage and meniscus where the SNR is typically low.

Figure 5 shows the T₂ maps (top row) and proton density I₀ maps (bottom row) reconstructed from MANTIS in the volunteer with raw k-space data with different k-space undersampling patterns at R=5. Due to the applied different undersampling masks, there was a significant difference in image artifacts for the same image from the zero-filling reconstruction. However, regardless the difference of the undersampling masks, MANTIS achieved a favorable reconstruction performance for suppressing the heterogeneous image artifacts and maintaining image quality and sharpness. Incorporation of additional incoherence at the dynamic frame and training phase improved image quality and resulted in a robust MANTIS model.

Figure 5:

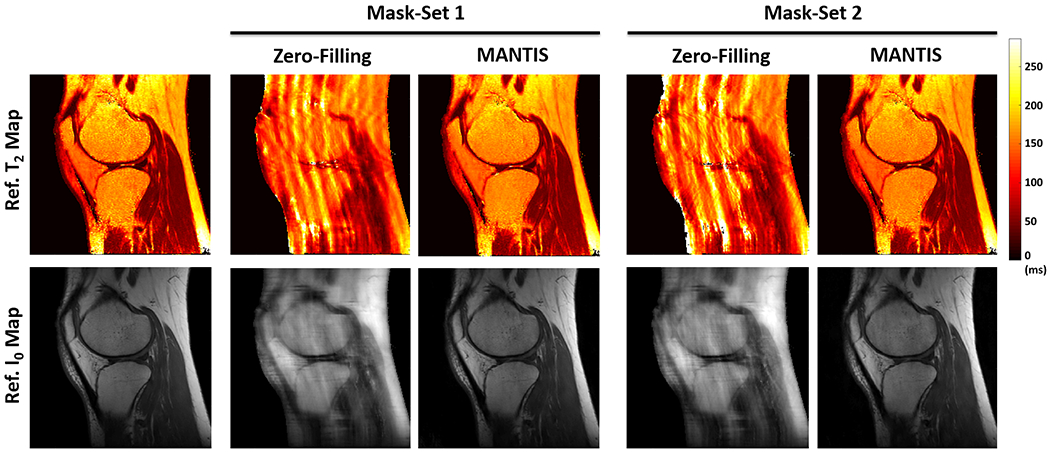
Comparison of T₂ (top row) and I₀ (bottom row) maps reconstructed using MANTIS at different undersampling masks for a prospectively acquired multi-coil k-space data. Although the image artifacts arisen from the different undersampling masks are different, MANTIS was able to remove the heterogeneous artifacts and provided nearly artifact-free T₂ and I₀ maps regardless of pattern of undersampling masks.

Figure 6 shows the T₂ maps reconstructed from MANTIS with different λ_cnn values at R=5. The reconstruction quality is subject to the selection of the weighting parameters. In contrast to the relax constraint (λ_cnn=0), weak constraint (λ_cnn=0.1) and strong constraint (λ_cnn=10) conditions, the default constraint (λ_cnn=1) provided the best reconstruction performance with most magnificent texture and contrast preservation indicated by the white arrows in the figure. Besides, it should be noted that despite there were small residual artifacts in bone, the relax constraint (λ_cnn=0) which used only the data and model consistency loss also achieved great noise and artifact suppression indicating the efficacy of such loss term in MANTIS framework.

Figure 6:

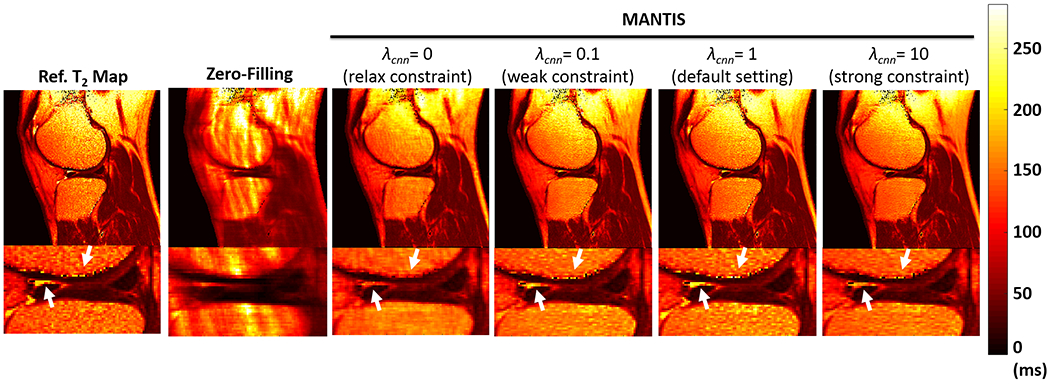
Comparison of T₂ maps reconstructed from MANTIS with different λ_cnn values at R=5. The reconstruction quality is subject to the selection of the weighting parameters. In contrast to the relax, weak, and strong constraint conditions, the default constraint provided the best reconstruction performance with most magnificent texture and contrast preservation indicated by the white arrows.

Lesion Detection

Figure 7 compares T₂ maps between MANTIS and the reference in two representative patients. Figure 7a shows T₂ maps from a 67-year male patient with knee osteoarthritis with superficial cartilage degeneration on the medial femoral condyle and medial tibial plateau. The morphologic abnormalities and increased T₂ relaxation time in the superficial cartilage could be identified in the reconstructed T₂ maps at R=5. While the overall reconstruction quality was reduced at R=8, the high contrast abnormalities could still be reliably identified. Figure 7b shows T₂ maps from a 59-year male patient with a tear of the posterior horn of the medial meniscus. The reference T₂ maps show a heterogeneous increase in T₂ relaxation time at the center of the meniscus extending into the inferior articular surface, which could also be successfully captured on the reconstructed T₂ maps using MANTIS at both R=5 and R=8.

Figure 7:

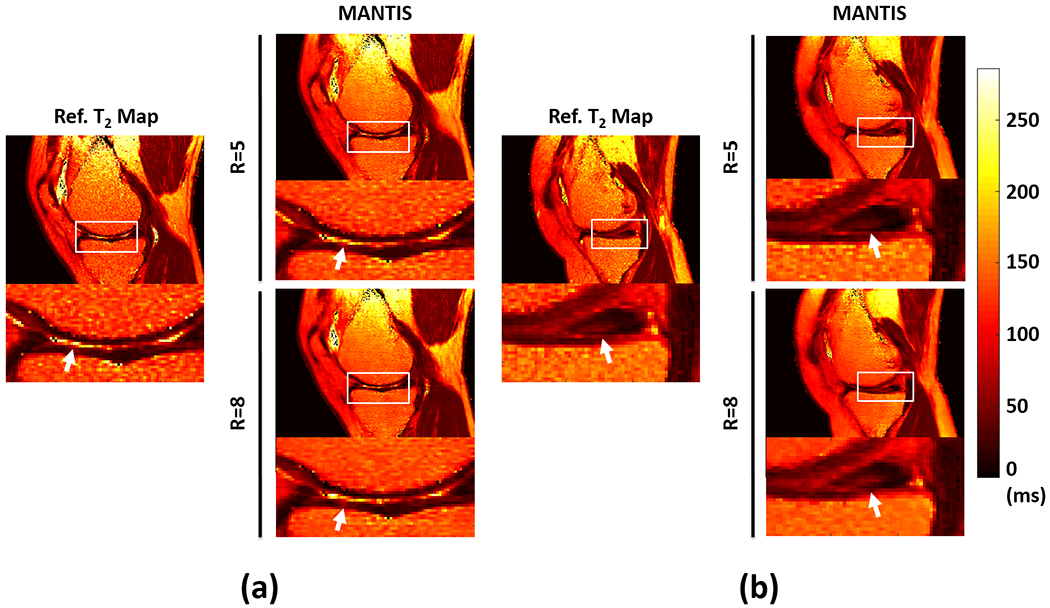
Two representative examples demonstrating the performance of MANTIS in cartilage and meniscus lesion detection. a) Results from a 67-year male patient with knee osteoarthritis and superficial cartilage degeneration on the medial femoral condyle and medial tibia plateau. b) Results from a 59-year male patient with a tear of the posterior horn of the medial meniscus. MANTIS was able to reconstruct high-quality T₂ maps for unambiguous identification of cartilage and meniscus lesions at both R=5 and R=8.

Regional Cartilage and Meniscus T₂ Analysis

Table 2 summarizes the results of the regional T₂ analysis for the ten testing patient datasets at different acceleration rates. MANTIS provided mean T₂ values that agree well with the reference in the patellar, femoral, and tibial cartilage, the deep and superficial half cartilage, and the meniscus. There were significant differences in the estimated T₂ values between the GLR, LLR, k-t SLR, and ALOHA method and the reference (p<0.001) at both R=5 and R=8. In contrast, there was no significant difference between the deep learning-based methods and the reference, with p=0.06 (R=5) for U-Net Imaging + T₂ Fitting, p=0.34 (R=5) and p=0.29 (R=8) for U-Net Mapping and p=0.43 (R=5) and p=0.37 (R=8) for MANTIS, respectively, indicating the best accuracy for MANTIS.

Table 2:

Regional cartilage and meniscus T₂ analysis for the ten testing patient datasets using the different reconstruction methods at acceleration rate R=5 and R=8. MANTIS provided mean T₂ values that agree well with the reference T₂ values for the patellar, femoral, and tibial cartilage, superficial and deep half cartilage, and meniscus.

Methods	T2 values (ms) (mean ± SD) at R=5						T2 values (ms) (mean ± SD) at R=8
	Patellar	Femoral	Tibial	Superficial	Deep	Meniscus	Patellar	Femoral	Tibial	Superficial	Deep	Meniscus
GLR	55.0 ± 3.2	54.7 ± 2.8	48.7 ± 5.9	66.0 ± 3.8	39.6 ± 2.3	37.3 ± 2.8	57.4 ± 3.1	56.8 ± 2.5	49.6 ± 5.5	68.2 ± 3.5	40.9 ± 2.1	38.0 ± 3.4
LLR	52.4 ± 3.4	53.1 ± 2.8	47.1 ± 6.2	63.6 ± 3.9	38.2 ± 2.3	34.7 ± 3.1	52.7 ± 3.3	53.5 ± 2.8	47.4 ± 6.1	64.0 ± 3.9	38.4 ± 2.3	34.9 ± 3.1
k-t SLR	48.1 ± 3.2	52.2 ± 4.2	44.7 ± 8.3	55.8 ± 4.3	33.5 ± 2.6	33.6 ± 3.3	55.0 ± 5.5	54.0 ± 4.0	44.1 ± 8.1	58.7 ± 4.3	35.2 ± 2.6	35.0 ± 3.1
ALOHA	44.3 ± 3.2	48.9 ± 3.7	43.2 ± 6.8	54.5 ± 4.1	32.7 ± 2.5	30.9 ± 3.5	48.8 ± 4.1	49.2 ± 3.3	42.0 ± 7.7	55.8 ± 4.4	33.5 ± 2.7	31.7 ± 3.1
U-Net Imaging + T2 Fitting	42.3 ± 3.4	47.3 ± 3.5	42.4 ± 6.2	53.9 ± 4.1	31.3 ± 1.6	25.8 ± 4.1	44.9 ± 3.7	47.4 ± 3.4	41.7 ± 6.5	54.5 ± 4.2	32.7 ± 2.5	28.8 ± 4.0
U-Net Mapping	41.1 ± 3.7	45.9 ± 3.2	41.5 ± 6.1	53.5 ± 4.4	32.1 ± 2.7	28.0 ± 3.9	42.6 ± 4.4	44.5 ± 3.4	39.1 ± 7.4	52.9 ± 5.0	31.7 ± 3.0	28.4 ± 3.9
MANTIS	40.4 ± 3.7	45.6 ± 3.4	41.7 ± 5.6	53.2 ± 4.1	31.9 ± 2.4	28.3 ± 4.0	41.0 ± 3.9	45.5 ± 3.6	41.1 ± 5.8	53.3 ± 4.3	32.0 ± 2.8	28.7 ± 4.5
Reference	39.6 ± 3.5	46.0 ± 3.4	42.5 ± 5.5	53.4 ± 3.8	32.0 ± 2.3	27.5 ± 4.0	39.6 ± 3.5	46.0 ± 3.4	42.5 ± 5.5	53.4 ± 3.8	32.0 ± 2.3	27.5 ± 4.0

Figures 8 shows the Bland-Altman plots comparing the reference T₂ maps with reconstructed T₂ maps in the cartilage and meniscus at R=5. Compared to GLR, LLR, k-t SLR and ALOHA, deep learning methods achieved greater agreement with the reference T₂ values for cartilage and meniscus, as indicated by the narrower limits of agreements at a ±1.96*standard deviation of the mean differences in the plots. MANTIS achieved further improved agreement compared to U-Net Mapping and U-Net Imaging + T₂ Fitting. The Bland-Altman plots for the sub-regional superficial and deep cartilage is shown in Figure S3 in the Supporting Information. A similar observation that MANTIS archived the best agreement with the reference compared to other approaches was noted.

Figure 8:

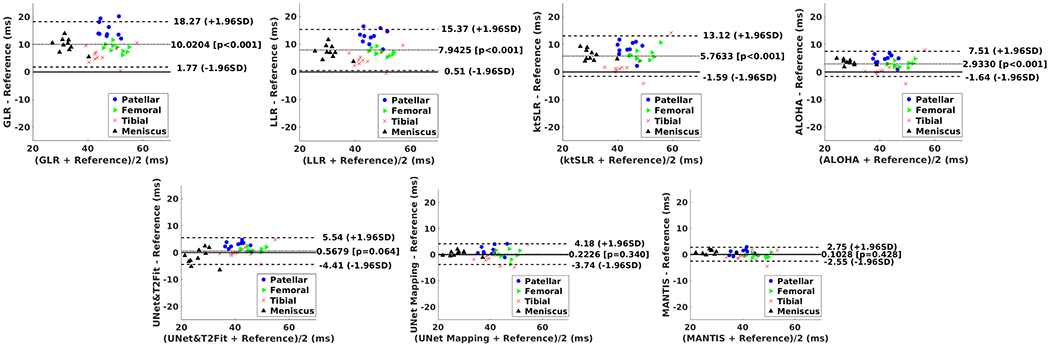
The Bland-Altman analysis for agreement of the regional cartilage and meniscus T₂ values obtained using the reference T₂ maps and the T₂ maps estimated using the different reconstruction methods at R=5.

DISCUSSION

In this work, a deep learning-based reconstruction framework called MANTIS was proposed for efficient T₂ mapping in the knee joint. To the best of our knowledge, MANTIS is the first method for direct reconstruction of parameter mapping from undersampled images using deep learning. The MANTIS pipeline consists of several key components. As the core component of the reconstruction framework, a convolutional encoder-decoder network is designed to directly convert a series of undersampled MR images to a T₂ map and a proton-density image using supervised end-to-end CNN mapping. Meanwhile, time-varying random k-space sampling is employed to ensure proper performance of the CNN mapping by taking advantage of the resulting incoherent undersampling behavior. Furthermore, a signal model is incorporated into MANTIS to enforce data and model consistency for optimal reconstruction performance. The entire reconstruction framework is formulated as a regularized reconstruction approach, in line with a conventional constraint reconstruction pipeline, where the end-to-end CNN mapping serves as a regularizer to the data/model consistency component.

In our study, MANTIS enabled up to eight-fold acceleration with acceptable reconstruction performance and accurate T₂ estimation in the cartilage and meniscus with respect to the fully sampled reference. In addition to global nRMSE and SSIM assessment, a regional T₂ analysis in the cartilage and meniscus was also conducted to further confirm that MANTIS produced accurate T₂ values. Moreover, MANTIS was proven to be highly time-efficient. Although the network was trained up to 20 hours, the training was only needed once, and the trained MANTIS network can be deployed to generate MR T₂ maps directly within seconds. Compared to existing iterative reconstruction approaches that generally take up to hours, the high runtime efficiency in MANTIS holds greater promise towards translation for routine clinical use.

In this work, MANTIS was evaluated with a 1D variable-density undersampling scheme to allows good performance in the CNN mapping step. This was inspired by the compressed sensing theory, in which reduced correlations of aliasing behavior arising from incoherent sampling is more beneficial for distinguishing subtle anatomical structures from undersampling artifacts. Furthermore, the strategy of using randomized undersampling patterns to augment CNN training was shown to increase the robustness of the proposed framework against different undersampling artifacts (Figure 5). This feature is essential, since the robustness of learning-based image reconstruction framework against k-space trajectory discrepancy between the training and testing datasets is of great interest (49). In addition to random Cartesian sampling, we expect that non-Cartesian sampling schemes, such as radial or spiral, are also well-suited for the MANTIS framework. The extension of MANTIS into non-Cartesian sampling is of high interest and can further improve the mapping performance and clinical applicability of the technique.

MANTIS was compared with conventional iterative reconstruction approaches including the GLR, LLR, k-t SLR and ALOHA methods, all of which have previously been demonstrated with good performance in accelerated dynamic MR applications (13,47,48). MANTIS showed improved reconstruction performance at both R=5 and R=8. The suboptimal reconstruction performance of GLR, LLR, and k-t SLR can be attributed to the fact that a high acceleration rate (up to R=8) was beyond the sparsity level of the T₂ mapping image-series (only eight echo images with limited temporal correlations) in our study, particularly with a single-coil setup. It was also observed ALOHA outerperformed standard low-rank constrained reconstruction by exploring structure low rank property in dynamic images. However, as shown in Figure S4 in the Supporting Information, although the reconstructed images had much better improvement compared to the zero-filling images in the conventional iterative methods, the pixel-wise fitted T₂ maps of conventional approaches showed redisual artifacts, suggesting uncertainties during the fitting process and amplified error propagation from reconstructed dynamic images into MR parameter maps (8,50). Besides, MANTIS was also compared with direct U-Net Mapping without the data and model consistency components and a two-step approach with a combination of deep learning image reconstruction first and subsequent T₂ fitting. MANTIS produced superior performance in the nRMSE and SSIM analyses and regional T₂ assessment. Despite favorable overall performance in the two-step approach, this method still show sensitivity to residual image artifiacts and image noises as shown in Figure 4. The results also agree with similar observation from prior model-based reconstruction studies for MR parameter mapping (15,50,51).

Although our current study demonstrated the feasibility of MANTIS for accelerated T₂ mapping of the knee, the approach can be extended to combine other models for various applications. For example, MANTIS can be used for mapping apparent diffusion coefficients (ADC) or intravoxel incoherent motion (IVIM) parameters in diffusion imaging and direct estimation of pharmacokinetic parameters in perfusion imaging. The accuracy of the estimation is dependent on the model employed to generate the reference maps for the network training. We elected to use a simple mono-exponential decay model for reconstructing the T₂ maps for the current feasibility study. Although this mono-exponential model has been shown to be suboptimal for a multi-echo spin-echo sequence (52,53), improvement can be obtained by substituting this simple model with more advanced signal models. For example, Ben-Eliezer et al. have shown that an echo modulation curve algorithm, which is based on Bloch simulations to model the signal evolution in a multi-echo spin-echo sequence, can be used to produce more reliable T₂ parameter estimations (52). Recently, another study has also demonstrated the feasibility of using a spin-echo sequence with different echo times, the current gold standard for T₂ mapping, to generate accurate T₂ maps for subsequent network training (54). Although the method in (54) can be extremely time-consuming, the simulation-based approach (52) is ideal for incorporation into the MANTIS framework to further improve the accuracy of T₂ parameter estimation. This combination is of great interest and is currently underway. Furthermore, MANTIS can also be used for efficient estimation of both T₁ and T₂ simultaneously using the MRF framework. One pilot study has demonstrated the feasibility of mapping images generated from MRF to parameter maps using an end-to-end fully connected neural network (30). Such a mapping strategy can also be combined with the MANTIS framework to promote further acceleration for parameter mapping.

Our study has several limitations. First, the feasibility of MANTIS was demonstrated on images with a reduced matrix size and in a single-coil DICOM image scenario. It would be ideal to train the CNN model using true multi-coil k-space data directly saved from MR scanner. The extension of MANTIS for high-resolution images and multi-coil data is entirely possible provided that appropriate and adequate multi-coil training dataset, better GPU architecture, and increased GPU memory are available. Second, the current study used a U-Net structure and did not compare the usefulness of U-Net with other end-to-end CNN mapping structures. This selection was based on prior studies that have justified the performance of U-Net for a wide range of image reconstruction and analysis tasks (23,26,38). However, it would be more interesting to compare the U-Net with other newly developed deep learning networks for the implementation of the MANTIS framework. The newly developed CNN structures, such as GANCS (20), KIKI-Net (24), and stacked convolutional auto-encoder (25) with proper adaptation, could be further incorporated into the MANTIS framework for providing improved reconstruction performance. In particular, the deep cascaded network (22), readily demonstrated with a superior reconstruction capability for restoring undersampled dynamic MR images could potentially be a great candidate for efficient mapping CNN in the MANTIS framework. Third, the hyperparameters for the network structure and parameters used in the network training process were selected based on heuristic information from previous studies. This is similar to the parameter tuning in constrained reconstruction, where a regularization weight is typically tailored to a specific application. The selection of parameter in MANTIS is also dependent on the application and the quality and the number of training datasets, like other learning-based methods (19,20). Future research involving comprehensive network hyperparameter selection and parameter optimization strategy is needed to validate the optimized performance of the network and the sensitivity of reconstruction results to these parameters. Finally, further investigation of the generalization of MANTIS to different acquisition parameters, image protocols, and MR scanners are also warranted in future studies.

CONCLUSIONS

Our study demonstrated that the proposed MANTIS framework, with a combination of end-to-end CNN mapping, signal model-augmented data consistency, and incoherent k-space sampling, represents a promising approach for efficient T₂ mapping. MANTIS can potentially be extended to other types of parameter mapping such as T₁ relaxation time, diffusion, and perfusion with appropriate models as long as a sufficient number of training datasets are available.

Supplementary Material

Supplementary Material

Supporting Information Figure S1: Illustration of the U-Net implemented in MANTIS for end-to-end CNN mapping. The U-Net structure consists of an encoder network and a decoder network with multiple shortcut connection (e.g., concatenation) between them to enhance mapping performance. The abbreviations for the CNN layers include BN for Batch Normalization, ReLU for Rectified Linear Unit activation, Conv for 2D convolution, and Deconv for 2D deconvolution. The parameters for the convolution layers are labeled in the figure as image size @ the number of 2D filters.

Supporting Information Figure S2: Residual error maps and corresponding nRMSE values from the same patient shown in Figure 3 which compares T₂ maps estimated from the different reconstruction methods at R=5 (top row) and R=8 (bottom row), respectively.

Supporting Information Figure S3: The Bland-Altman analysis for agreement of the sub-regional cartilage (superficial and deep halves) and meniscus T₂ values obtained using the reference T₂ maps and the T₂ maps estimated using the different reconstruction methods at R=5.

Supporting Information Figure S4: Examples of reconstructed first echo images from different conventional iterative reconstruction methods at both R=5 and R=8.