Computational wrapping: A universal method to wrap 3D-curved surfaces with nonstretchable materials for conformal devices

Computational wrapping provides a universal method to wrap arbitrary curved 3D shapes with 2D-based brittle materials.

Abstract

This study starts from the counterintuitive question of how we can render conventional stiff, nonstretchable, and even brittle materials sufficiently conformable to fully wrap curved surfaces, such as spheres, without failure. Here, we extend the geometrical design method of computational origami to wrapping. Our computational wrapping approach provides a robust and reliable method for fabricating conformal devices for arbitrary curved surfaces with a computationally designed nonpolyhedral developable net. This computer-aided design transforms two-dimensional (2D)–based materials, such as Si wafers and steel sheets, into various targeted conformal structures that can fully wrap desired 3D structures without fracture or severe plastic deformation. We further demonstrate that our computational wrapping approach enables a design platform that can transform conventional nonstretchable 2D-based devices, such as electroluminescent lighting and flexible batteries, into conformal 3D curved devices.

INTRODUCTION

The development of new flexible and stretchable materials has recently generated substantial interest in fabricating conformal devices that can conform to the target three-dimensional (3D) surface (1–5). However, the application of such materials for practical conformal electronics remains strictly limited by the inability to provide certain key criteria available in conventional electronic products, such as high conductivity and reliability. While the majority of works involving conformal devices have used soft and stretchable materials, there are a few works that have pioneered conformal devices made of conventional nonstretchable or brittle materials such as silicon and metal. Nevertheless, those pioneered works have used the conventional materials in a limited area of the devices with very thin “patterned structures” such as horseshoe patterns (6–8). In other words, it is still challenging to cover an entire 3D surface with conventional materials used in the advanced devices (9, 10). This study introduces a universal method to use conventional nonstretchable materials to reliably wrap arbitrary 3D curved surfaces, including the human body and curved vehicle interiors, as potential applications. This approach allows us to make conformal devices without sacrificing performance.

Figure 1A shows that wrapping a sphere with a rectangular piece of paper inevitably results in the formation of wrinkles, crumples, and overlaps regardless of the material type, including stretchable sheets. If the material is a substrate or another active layer of a flexible device, then severe material deformation and overlapping can cause the material to fracture or break, as shown in fig. S1 and movie S1. One common way to wrap 3D surfaces with nonstretchable materials is by introducing patterned cuts in the materials. Recent examples of patterned cuts are lattice cut patterns and fractal cut patterns. Cho et al. (11) proposed a fractal cut design approach for planar materials that enabled the production of mechanical metamaterials with a hierarchical auxetic structure. They showed that the fractal cut-designed materials are shape programmable and can effectively cover a sphere. In addition, Konaković et al. (12) suggested computer algorithms for designing complex 3D models using 2D auxetic structures. Both studies overcame the limitations of existing flexible materials by geometrically designing cut patterns. However, when covering complex 3D surfaces, these structures inevitably result in openings that lead to the design and functional limitations in conformal devices, such as suboptimal coverage of printable batteries and undesirable holes in lighting and displays (Fig. 1B). To overcome this problem, we introduce a computational design strategy called “computational wrapping with nonpolyhedral developable nets” to make a 2D nonstretchable material platform to fabricate wearable and conformal devices.

Fig. 1. Reverse engineering computational origami for conformal wrapping.

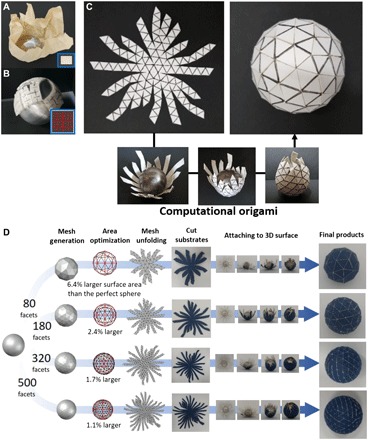
(A) Wrinkles are formed when tightly wrapping a rectangular sheet of paper around a nonzero Gaussian surface. (B) Fractal cut patterns can avoid wrinkles but inevitably lead to openings and uncovered areas. (C) The 2D unfolding of a spherical polyhedron generated automatically by computational origami can wrap a steel ball without leaving uncovered areas. (D) As the number of facets increases, the smoothness and conformability of the mesh naturally improve. The difference in surface area between the perfect sphere and the approximated polyhedra decreases by 5.3% when the number of facets increases from 80 to 500. The Hausdorff distance between the polyhedral surfaces and the perfect sphere also reduces from 7.05 to 1.17% of the radius of the perfect sphere when the number of facets increases from 80 to 500 (see also fig. S4). (Photo credit: Y.-K. Lee, Seoul National University.)

RESULTS AND DISCUSSION

Figure 1C shows a series of snapshots that illustrate the 2D unfolding of a sphere generated automatically by our polyhedral edge unfolding algorithm, which is used to wrap a steel ball. Theoretically, a curved surface can be characterized by the Gaussian curvature, which is the vector product of the maximum and minimum principal curvatures at a point. A 2D material with zero Gaussian curvature at all points, such as a sheet of paper, is called a developable surface. A developable surface cannot be transformed into a nondevelopable 3D surface with positive or negative Gaussian curvatures without tearing, stretching, or compressing the material. This has been mathematically proven by the “Gauss Theorema Egregium,” which states that “To move a surface onto another surface, the Gaussian curvature of all corresponding points must match” (13) (fig. S2). Instead, polyhedral edge unfolding (14, 15) flattens arbitrary surfaces into 2D structures by cutting the surface into developable patches with C⁰ continuity; i.e., the patches are connected without gaps and seams. The computer science community has recently exerted great efforts to algorithmically determine surface cuts that segment a nondevelopable surface into developable surface patches called polyhedral nets (or simply nets) (16–18). Beyond designing valid nets, recent computational methods, including those developed by the authors (19–22), have focused on optimizing net quality and foldability using machine learning techniques that drastically reduce the time and effort needed relative to traditional trial-and-error approaches.

A polyhedron can have multiple possible polyhedral nets (23), especially when the polyhedron is convex. For a given polyhedral sphere, we demonstrate six unfoldings created by six different methods (fig. S3). Figure S3A shows the “steepest edge (SE) unfolding” (16). Given a polyhedron P and a 3D vector $\overrightarrow{\mathit{c}}$, SE unfolding associates each edge e = (v, w) of P with a weight $\frac{<c,v-w>}{\mid v-w\mid },$ where v and w are the end points of e and <, > denotes the inner product between two vectors. Then, for each vertex v, the edge incident to v with the largest weight, i.e., the edge most aligned with $\overrightarrow{\mathit{c}}$, is cut. The SE unfolding can unfold nearly all convex polyhedra with a few randomly selected $\overrightarrow{\mathit{c}}$, creating radially spread unfolded figures. Other methods, such as flat-tree unfolding (fig. S3B) (16) and genetic algorithm (GA) methods (22, 24), are also available to unfold nonconvex polyhedra (fig. S3C). As it is critically important that a conformal device is composed of one or as few pieces as possible, our recently developed GA method can evolve the unfoldings by mutating the edge weights until a net with zero overlaps is found (22). This evolution is controlled by a fitness function f : N → ℝ that evaluates an unfolding. An example of f(N) is defined as follows

$$f(N)=-({\mathrm{\lambda }}_0{\mathrm{\delta }}_0+{\mathrm{\lambda }}_1{\mathrm{\delta }}_1)$$

where δ₀ is the number of overlaps in N, δ₁ is the number of hyperbolic vertices that cause local overlaps in N, and λ₀ and λ₁ are user parameters, which are set to 100 and 1, respectively. The maximum value of f(N) must be 0. In addition, three more unfolding algorithms are presented in fig. S3. Although all of these algorithms can be used depending on the required application, we chose the SE unfolding and GA methods to further illustrate our notion of wrapping a 3D curved surface via computational unfolding methods.

Figure 1D illustrates four different unfolding paper structures that were fabricated from four polyhedral spheres with different resolutions via the computational SE unfolding method. To ensure that the polyhedral sphere can tightly enclose a perfect sphere so that the facets of the polyhedron touch the perfect sphere, the polyhedral sphere must be properly scaled. Consequently, to ensure the enclosure of the perfect sphere, the radius and surface area (4πr²) of the polyhedron with 80 facets are 7.05 and 6.38% larger than those of a perfect sphere, respectively. The difference in the radii of the polyhedral sphere and the perfect sphere decreases to 1.17% when the number of facets increases to 500. The area difference is also reduced as the mesh number increases, resulting in a 1.09% difference for a polyhedron with 500 facets (fig. S4). Consequently, increasing the resolution of meshes for paper polyhedra provides better conformability on the steel ball, as shown in fig. S4D. In many applications of conformal devices, accurate covering and tight wrapping are crucial. In addition, because most real-world objects are smooth and curved, high-resolution meshes are needed to provide the necessary covering accuracy. However, there are still issues in folding the creases to cover the surface, which requires a long folding time during fabrication and possibly causes mechanical fracture or plastic deformation of the materials used, leading to electrical failure in devices. Here, we develop an approach called “computational wrapping,” which goes beyond the conventional computational folding method. By considering conformal device design as a paper wrapping problem instead of a paper folding (origami) problem, we recognize that the operations of attaching and wrapping conformal devices to cover an underlying curved 3D surface are made much easier by bending and pressing a polyhedral net without creases than by creasing and folding, as illustrated in Fig. 2A.

Fig. 2. Concept and physical demonstration of computational wrapping.

(A) When the sum of the folding angles of a net is minimized, the crease lines can be ignored to accommodate flexible but nonstretchable stiff and brittle materials. For 500 meshes, the gaps in the case of a rigid material and the wrinkles in the case of a flexible material are no longer visible, and the difference between the two becomes imperceptible. (B) A nonstretchable stainless steel sheet is cut into a developable net. (C) With a sufficient number of meshes, the stainless steel sheet can be bent and fully wrap a sphere without creasing or folding. (D) Part of the sphere is unfolded with 400 meshes, and the crease lines are removed. (E) A 20-μm-thick brittle Si wafer is cut into an unfolded net with a laser cutter. (F) The cut Si wafer stably wraps both convex and concave frames. (Photo credit: Y.-K. Lee, Seoul National University.)

Paradoxically, we found that in this bending and attaching approach, high-resolution meshes provide us with the needed solution to address the limitations of long fabrication times and mechanical reliability. A mesh with high-resolution tessellation can better represent surfaces with a higher degree of continuity (e.g., G¹ continuity along the branches where facets on both sides of a crease line share a common tangent direction), which is common for many surfaces formed by real materials.

Computationally, this goal is achieved by ensuring that the distance between the wrapped object and the developable surface is smaller than a user-provided value based on the required wrapping tightness and the material properties. For example, a surface with nonzero Gaussian curvature everywhere, such as a perfect sphere, can be enclosed by a developable surface; however, there will always be spaces between these two surfaces. To control the size of this space, we adaptively refine the facet mesh until the two-sided Hausdorff distance between the developable surface formed by the polyhedral net and the wrapped object is bounded. More specifically, we modify the GA fitness function in our edge unfolding method as follows

$$f(N)=\text{min}(-({\mathrm{\lambda }}_0{\mathrm{\delta }}_0+{\mathrm{\lambda }}_1{\mathrm{\delta }}_1),{\sum }_{e_i}{\mathrm{\theta }}_{e_i})$$

where θ_ei is the dihedral angle of a cut edge e_i in the polyhedral net N. This enhanced f(N) further evolves N to minimize the sum of the folding angles, and the net is thus optimized for bending by maximizing f(N). After obtaining a polyhedral paper net with minimal folding angles (Fig. 2A, top), we use the outer cut lines of the net but ignore (erase) all the crease lines; the result is called a nonpolyhedral developable net (Fig. 2A, bottom). The distance between the target shape and the developable surface formed by its nonpolyhedral developable net (referred to as “developable net” hereinafter) is calculated. Our method then determines the areas that require more detailed tessellation, e.g., areas with high Gaussian curvature, and repeats the process (remeshing, unfolding, and distance estimation) until the distance is sufficiently short. Therefore, given a polyhedral net with a high-resolution mesh, because there is a small distance between the perfect sphere and the developable surface formed by its developable net, we can ignore (erase) all the crease lines and simply bend and press the strips of the developable paper net to tightly wrap the sphere, creating controlled and bounded spaces between the net and the sphere without gaps or overlaps between facets (see fig. S4 regarding the required mesh numbers for smooth wrapping). Consequently, this fabrication process can accurately produce highly complex and smooth 3D surfaces and is many times faster than the conventional computational folding method when handling complex shapes because there is no creasing and folding involved in the wrapping procedure. Moreover, we note that the small bending angles of the strips possibly prevent the materials used in conformal devices from being damaged when wrapping an object.

This computational wrapping scheme based on developable nets enables our method to be applied not only to papers but also to metallic and ceramic materials. For the same developable net generated with 500 meshes, a stainless steel sheet can tightly wrap a steel ball, as shown in Fig. 2 (B and C). Moreover, we can even apply our method to brittle Si wafers. We fabricated a computational wrapping pattern for a Si wafer to cover part of a sphere with a diameter of 4 cm, as shown in Fig. 2D. A thin Si wafer with a thickness of 20 μm was cut by laser cutting based on a computed developable net consisting of 400 meshes without crease lines (Fig. 2, D and E). We attached this wafer to both convex and concave surfaces without noticeable gaps, overlaps, or fractures (Fig. 2F). A finite element (FE) analysis of the Si wafer in Fig. 3 provides more quantitative mechanical analysis supporting the assertion that the computational wrapping process for the Si wafer is mechanically reliable. The wrapping process is realized in the FE simulation by compressing the developable net between the sphere and a concave mold of a wrapped part of the sphere (Fig. 3A and movie S2). In the FE simulation, the radius of the sphere is set to 2 cm, replicating the radius of the sphere used in the experiment (Fig. 2G), and the radius of the concave mold is set to the sum of 2 cm and the 2D net thickness. The developable nets with different numbers of meshes are generated by the GA method, and the computational models for the FE simulation are constructed with adaptive meshing (Fig. 3B).

Fig. 3. FE analysis.

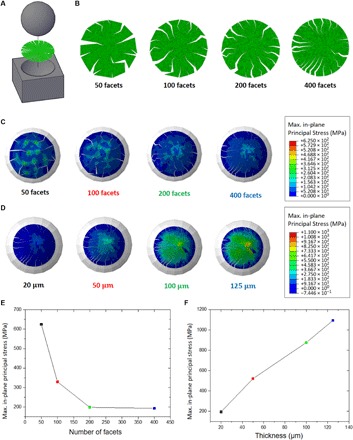
The mechanical reliability of the computational wrapping of the Si wafer shown in Fig. 2F is further investigated through FE simulations for wrapping a part of a sphere. (A) The wrapping process is simulated by compressing the 2D nonpolyhedral developable net between the sphere and a concave mold of a wrapped part of the sphere (see also movie S2). The radius of the sphere in the FE simulation is identical to that used in our experiment (Fig. 2F). (B) The nonpolyhedral developable nets are generated by the GA method. The distributions of the maximum in-plane principal stress for the wrapped Si wafers are analyzed (C) with respect to the number of meshes at a fixed thickness of 20 μm and (D) with respect to the thickness at 400 meshes. Consequently, the maximum in-plane principal stress decreases as the number of meshes increases and increases as the thickness increases (E and F). In both cases, the maximum stress values are much smaller than the fracture strength of the Si wafer.

Figure 3C shows that for the 20-μm-thick Si wafer wrapping the part of the sphere, the maximum in-plane principal stress distribution indicates that the stress decreases as the number of meshes increases from 50, 100, 200, to 400. Consequently, the highest value of the maximum in-plane principal stress in Fig. 3E decreases from 624 MPa for 50 meshes to 193 MPa for 400 meshes. These stress values are much smaller than the fracture strength of the Si wafer, which is approximately 5 GPa (25, 26). This finding clearly indicates that by maximizing f(N), the bending angles of the strips are minimized to ensure minimal stress and strain, thereby preventing the occurrence of fracture or severe plastic deformation. We also simulated the maximum in-plane principal stress distribution in the wrapped Si wafer with 400 meshes under various thicknesses (20, 50, 100, and 125 μm), and the results are shown in Fig. 3D. The residual stress is developed throughout the developable net as the thickness increases to 125 μm. The highest value of the maximum in-plane principal stress is 1.093 GPa, which is still less than the fracture strength of the Si wafer (see fig. S5 for an additional FE analysis of a stainless steel sheet).

The above results have significant practical implications. Most flexible devices are made from 2D brittle substrate materials that can be slightly bent at a small angle only if the aspect ratio is sufficiently large (27). As long as we can make 2D unfolding structures, we can use conventional materials and processes, such as deposition and evaporation to wrap a curved surface with a conformal device. Hence, these structures lead to a significant increase in the applicability of computational origami to real industrial fabrication processes, wherein wrapping can be used instead of folding to fabricate conformal devices. For instance, in this study, we realize a conformal device using commercial electroluminescent lamp (EL) panels. We simply use a laser cutter to cut the commercial EL panels, including the power supply terminals at the end of an edge site, corresponding to the computationally generated developable net of a sphere and an ellipsoid with 500 meshes. The final cut EL panels can be stably and easily attached to the sphere (Fig. 4, A to C) and the ellipsoid (Fig. 4, D and E, and fig. S6). The EL panels consist of top and bottom brittle electrodes with solid interlayers (including an indium tin oxide conductive layer) that can be easily fractured by creasing and folding. However, no catastrophic failures occurred during the fabrication process, and the 3D conformal device exhibited good operation, as shown in Fig. 4 (C and E), because we conformally wrapped the sphere by bending and pressing rather than creasing and folding. In addition to a sphere and an ellipsoid model, a traditional Korean mask was conformably wrapped by EL panels. We used 3D scanning to obtain a 3D model and generate meshes for the most curved region of the mask. For the traditional Korean mask model, a total of 169 meshes are used for the target region, which are unfolded with the SE unfolding method without overlapping (Fig. 4, F and G, and fig. S7). Last, the EL panel with a developable net was conformally attached to the mask, and the panel exhibited good operation without failure. The concept was applied for complex exterior parts of an electric toy vehicle with a nonzero Gaussian surface. We generated the meshes and the corresponding developable net via the GA unfolding method, as shown in fig. S8, and then EL panels were cut and attached to the surfaces to decorate the exterior car parts (Fig. 4, H to J, fig. S8, and movie S3). We also fabricated a conformal primary battery. For battery fabrication, the diversity of the developable net can yield advantages in terms of manufacturing efficiency and printing material waste reduction for screen prints (fig. S9).

Fig. 4. Demonstration of conformal devices.

(A) Cuttable, nonstretchable, commercial EL panels consisting of brittle electrodes are cut with a laser cutter to form developable nets for a sphere. (B) EL panels with a developable net can fully cover a sphere and (C) operate without catastrophic failure. (D and E) The computational wrapping concept is also demonstrated for an ellipsoid model (see fig. S6). (F and G) In addition to a sphere and an ellipsoid, a commercial Korean facial mask can also be conformably covered with EL panels and operated without electrical failure (fig. S7). (H) An electric toy vehicle can also be conformably wrapped with EL panels in the same manner, and the attached EL panels also operate well without failure. The GA unfolding method is used for generating the developable net for parts with nonzero Gaussian surfaces, including (I) the headlights, the edge of the front side bumper, and (J) the edge of the rear side bumper of the electric toy vehicle (fig. S8). (Photo credit: Y.-K. Lee, Seoul National University.)

In summary, we introduced the concept of computational wrapping to transform nonstretchable 2D flexible devices into 3D conformal devices. A surface with nonzero Gaussian curvature, such as a perfect sphere, can be enclosed by a developable surface, but there will always be spaces between these two surfaces. The proposed computational method controls the distance between these two surfaces to ensure sufficiently tight wrapping. Although approximating an arbitrary surface with developable surfaces has also been studied in the past, all existing works break the surface into multiple separated developable surfaces. Our work produces a single connected surface, called nonpolyhedral developable net, which is a conformal wrapping design of a 2D sheet for any 3D surface. Nonpolyhedral developable net enables applications that require connectivity and conductivity between all pairs of points on the surface. In particular, we successfully showed that slightly bending nonstretchable substrates to comply with an underlying object can effectively wrap the desired shape without forming crease lines between adjacent facets. Consequently, stiff or even brittle materials, such as metal sheets or Si wafers, can fully cover and tightly wrap nonzero Gaussian curvature surfaces without catastrophic fractures. We demonstrated that the advantages of wrapping over folding can be applied to make real conformal devices from conventional devices, such as EL lighting devices and batteries. Our universal computational wrapping method provides new insights into the development of conformal devices with arbitrary shapes using efficient algorithms with robust and reliable conventional fabrication processes.

MATERIALS AND METHODS

Computational methods

The nonpolyhedral developable net was generated by our computational algorithm. We implemented the computational unfolding algorithm in C++, and the executable file can be found at http://masc.cs.gmu.edu/wiki/OrigamiSoftware. The 3D surface models for the traditional Korean mask and the electric toy vehicle were obtained by 3D scanning followed by meshing with MeshLab software. The mechanical reliability of computational wrapping was verified through FE simulations [ABAQUS/Explicit (version 6.14)], wherein a part of a sphere was wrapped. The computational models for the FE simulations were constructed with adaptive meshing. The orthotropic values in Voigt notation shown below were used as the mechanical property inputs for the Si wafer

$$\left[\begin{array}{c}{\mathrm{\sigma }}_{11}\\ {\mathrm{\sigma }}_{22}\\ {\mathrm{\sigma }}_{33}\\ {\mathrm{\sigma }}_{23}\\ {\mathrm{\sigma }}_{31}\\ {\mathrm{\sigma }}_{12}\end{array}\right]=\left[\begin{array}{cccccc}165.6& 63.9& 63.9& 0& 0& 0\\ 63.9& 165.6& 63.9& 0& 0& 0\\ 63.9& 63.9& 165.6& 0& 0& 0\\ 0& 0& 0& 79.6& 0& 0\\ 0& 0& 0& 0& 79.6& 0\\ 0& 0& 0& 0& 0& 79.6\end{array}\right]\left[\begin{array}{c}{\mathrm{\epsilon }}_{11}\\ {\mathrm{\epsilon }}_{22}\\ {\mathrm{\epsilon }}_{33}\\ {\mathrm{\gamma }}_{23}\\ {\mathrm{\gamma }}_{31}\\ {\mathrm{\gamma }}_{12}\end{array}\right][\text{GPa}]$$

The wrapping process was simulated by compressing the 2D nonpolyhedral developable net between the sphere and a concave mold of a wrapped part of the sphere (movie S2). The radius of the sphere was set to 2 cm, replicating the radius of the sphere used in our experiment (Fig. 3G), and the radius of the concave mold was set to the sum of 2 cm and the 2D net thickness.

Experimental methods

Cardstock papers, 100-μm-thick stainless steel sheets, and a 20-μm-thick Si wafer were used to demonstrate wrapping a steel ball with nonstretchable materials. The commercial EL lighting panels were used to realize a computationally wrapped conformal device. The cardstock papers and EL lighting panels were cut into developable nets with a cutting plotter (Cricut cutting machine), whereas the stainless steel sheets and Si wafer were cut with a laser cutter. All the developable nets were attached to the 3D curved surfaces with double-sided tape.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/15/eaax6212/DC1