Protein structural changes characterized by high-pressure, pulsed field gradient diffusion NMR spectroscopy

Abstract

Pulsed-field gradient NMR spectroscopy is widely used to measure the translational diffusion and hydrodynamic radius (R_h) of biomolecules in solution. For unfolded proteins, the R_h provides a sensitive reporter on the ensemble-averaged conformation and the extent of polypeptide chain expansion as a function of added denaturant. Hydrostatic pressure is a convenient and reversible alternative to chemical denaturants for the study of protein folding, and enables NMR measurements to be performed on a single sample. While the impact of pressure on the viscosity of water is well known, and our water diffusivity measurements agree closely with theoretical expectations, we find that elevated pressures increase the R_h of dioxane and other small molecules by amounts that correlate with their hydrophobicity, with parallel increases in rotational friction indicated by ¹³C longitudinal relaxation times. These data point to a tighter coupling with water for hydrophobic surfaces at elevated pressures. Translational diffusion measurement of the unfolded state of a pressure-sensitized ubiquitin mutant (VA2-ubiquitin) as a function of hydrostatic pressure or urea concentration shows that R_h values of both the folded and the unfolded states remain nearly invariant. At ca 23 Å, the R_h of the fully pressure-denatured state is essentially indistinguishable from the urea-denatured state, and close to the value expected for an idealized random coil of 76 residues. The intrinsically disordered protein (IDP) α-synuclein shows slight compaction at pressures above 2 kbar. Diffusion of unfolded ubiquitin and α-synuclein is significantly impacted by sample concentration, indicating that quantitative measurements need to be carried out under dilute conditions.

Graphical Abstract

1. Introduction

Pulsed-field gradient (PFG) NMR spectroscopy enables the measurement of translational diffusion of biomolecules in solution [1–4]. Through the Stokes-Einstein equation, the translational diffusion coefficient of a molecule is inversely related to its hydration radius (R_h), which provides insight into size [5, 6], including alterations upon oligomerization [7–12], ligand binding [13], as well as folding and unfolding [14–18]. Translational diffusion coefficients are commonly obtained by recording arrayed 1D or 2D pulsed field gradient (PFG) NMR spectra, from which the signal attenuation caused by diffusion during a fixed delay time is then fit to the Stejskal-Tanner equation [1, 19–23]. PFGs are widely used in modern NMR spectroscopy, and availability of the requisite hardware now enables routine measurement of translational diffusion constants for a wide range of systems, spanning molecules as small as tens of Da [24] to complex protein assemblies [11, 25], amyloid fibrils [26], virus-like particles [27], and phase-separated membrane-less organelles [28, 29]. In addition, pulse sequences have been developed to characterize the diffusion of large proteins [28–31] and those undergoing chemical exchange [32].

PFG translational diffusion measurements also offer insight into structural ensembles populated by denatured, intrinsically disordered, or partially folded proteins [13, 15, 17, 33]. Empirical measurements have established a relationship between the number of amino acids in a fully denatured protein and its expected R_h [33], and comparison to the measured R_h for the protein of interest thus reports on the overall compaction or, in rare cases, expansion of the polypeptide chain. Compaction of the disordered chain can result from the presence of transiently structured elements or weak hydrophobic or electrostatic interactions within the unfolded polypeptide. While studies performed under high denaturant conditions (e.g. 8 M urea or 6 M guanidine hydrochloride) generally yield R_h values that closely follow the empirical relation between chain length and R_h, the magnitude of the change in the structural ensemble populated by unfolded proteins at lower denaturant conditions, approaching the folding threshold, remains controversial: under such conditions, both significantly collapsed and near fully expanded conformations were deduced from Förster resonance energy transfer (FRET) and small-angle X-ray scattering (SAXS) methods [34–37]. Previous solution-state NMR studies demonstrated that R_h of the unfolded state of the N-terminal SH3 domain of drk, which exists in a slow equilibrium with its folded state, is ca 30% larger than its folded state, but ca 10% smaller than the R_h of its fully denatured state in guanidine hydrochloride [17, 38]. Following a recent, renewed debate about discrepancies between the denaturant dependence of the unfolded state measured by SAXS and FRET [39, 40], another group concluded that such differences are consistent with a decoupling of size and shape fluctuations in finite-sized, heteropolymeric disordered systems [41]; i.e., the FRET-derived distance distributions, SAXS-derived radii of gyration, and diffusion-derived R_h contain semi-independent constraints on the ensemble distribution [17].

In comparison to high temperature or addition of denaturing chemicals, elevated hydrostatic pressure represents a relatively benign and often reversible unfolding mechanism [42–45]. Under conditions where there is an appreciably negative volume change between the folded and unfolded states, on the order of ≥ 50–100 mL/mole, a few kilobar of hydrostatic pressure can drive the thermodynamic equilibrium of a folded protein to that of the unfolded state. Hydrophobic cavities (void volume) present in the folded protein but absent in the unfolded state constitute an important component of this volume difference [45, 46], but decreased solvent density at the larger solvent-accessible hydrophobic surface of the unfolded protein may also represent a significant factor [47]. Proteins that unfold at high pressure typically exist in slow exchange with their folded state when studied at intermediate pressures. Under such conditions, PFG NMR can provide simultaneous access to the measurement of translational diffusion coefficients for both the folded and unfolded states that are in equilibrium with one another over a range of pressures. This situation applies for the previously characterized pressure-sensitized double mutant of ubiquitin, V17A/V26A (VA2-ubiquitin [48–50]), used as a model system in the present study.

While high-pressure NMR has been used to study translational diffusion of neat liquids and a handful of small molecules [51–53], relatively little is known about the effect of elevated pressures on the hydrodynamic properties of unfolded proteins. Here, we sought to characterize the impact of increased pressure on the hydrodynamic behavior of three model proteins: the intrinsically disordered protein (IDP) α-synuclein, which remains unfolded at all pressures; the pressure-sensitized VA2-ubiquitin, which can access both folded and unfolded states depending on the pressure; and wild-type (WT) ubiquitin, which remains fully folded at all experimentally accessible pressures. Pressure-induced changes to the viscosity of water become an important factor when performing translational diffusion measurements as a function of pressure. Although the diffusivity of water follows the known pressure dependence of its viscosity (https://webbook.nist.gov/chemistry/fluid/), we find that dioxane and other small hydrophobic molecules show a significant expansion in their R_h values with increasing pressure, and a concomitant decrease in rotational diffusion rate as indicated by ¹³C T₁ times. When using dioxane as an internal reference to derive the R_h of a protein, failure to correct for this effect results in underestimates of the protein R_h. Taking the newly calibrated pressure dependence of the dioxane R_h into account restores accuracy of the internal referencing method. The R_h of α-synuclein and the unfolded chain of VA2-ubiquitin are then found to be nearly independent of pressure up to 2 kbar. At pressures > 2 kbar, a slight compaction of the unfolded chains is observed, whereas WT ubiquitin, which remains fully folded at 3 kbar, shows virtually no change in its R_h at all examined pressures. We compare the high-pressure diffusion data to those collected in the presence of increasing concentrations of urea, and find that the R_h of the unfolded state of VA2-ubiquitin depends minimally on the amount of added urea. Our results suggest that both α-synuclein and the unfolded state of VA2-ubiquitin do not expand significantly between mildly and highly denaturing conditions. However, since NMR diffusion measures an ensemble-averaged property, we cannot rule out a small change in the population of transiently compacted chains as such states would not contribute significantly to the measured signal.

2. Methods

2.1. Protein expression and purification

¹⁵N-labeled VA2-ubiquitin and αS were expressed and purified as described previously [54]. αS lacked the N-terminal acetylation present in mammalian cells. For VA2-ubiquitin, a final HPLC purification step was essential to avoid protease contamination, which otherwise presents a problem at high pressures where VA2-ubiquitin but not the protease unfolds, making VA2-ubiquitin an excellent protease substrate. WT ubiquitin was purchased from Sigma-Aldrich (USA). Both VA2- and WT-ubiquitin NMR samples were prepared in 30 mM sodium phosphate at pH 6.4. αS samples were in 30 mM sodium phosphate, 3 mM EDTA, pH 7.

2.2. R_h determination

Determination of R_h from PFG NMR experiments requires accurate knowledge of the solution viscosity and gradient strength in units of G_●cm⁻¹. With solvent viscosity being strongly dependent on temperature, and non-linearity of the gradient across the sample making the effective gradient strength sensitive to the sample size and position, in particular when Shigemi tubes are used to restrict the sample volume to the most linear region of the applied gradients, the use of an internal standard is often preferred. In this case, the diffusion of a reference molecule of known R_h is determined alongside that of the protein of interest. For measurements carried out in D₂O, diffusion of the residual HDO signal may be used as the internal reference [1], while using a long inter-scan delay to account for the very long T₁ of HDO protons. In H₂O, radiation damping effects can interfere with measurement of the H₂O diffusion rate, making it less suitable as an internal reference. For this reason, a small amount (e.g. 0.1% v/v) of dioxane is commonly used as a reference (R_h = 2.12 Å under ambient conditions) [14]. It conveniently resonates near 3.5 ppm, upfield of most H^α resonances and downfield of most H^β signals and was found not to interact with folded or unfolded proteins. For all our protein diffusion measurements, samples were doped with 0.1% dioxane (v/v), enabling calculation of the hydration radius for the protein (eq 3), as outlined previously [14]:

$$D=\frac{k_{B}T}{6\pi \eta R_h}$$ (1)

$$I_j=I_0{e}^{-{\gamma }^2{G_j}^2{\delta }^2\left(\Delta -\frac{\delta }{3}-\frac{\tau }{2}\right)D}$$ (2)

$${R_h}^{\mathit{\text{unknown}}}=\frac{D_{\mathit{\text{reference}}}}{D_{\mathit{\text{unknown}}}}\times {R_h}^{\mathit{\text{known}}}$$ (3)

where D refers to the diffusion coefficient, k_B to Boltzmann’s constant, T to the temperature, η to the solvent viscosity, I_j to the intensity in spectrum j, I₀ to the intensity in the reference spectrum, γ to the gyromagnetic ratio, G_j to the gradient strength in spectrum j, δ to the total duration of the encoding gradient pulses, τ to the gradient recovery delay, and Δ is defined as the diffusion time including the total duration of the encoding gradients (δ) plus 2τ for the two short gradient recovery delays, as defined in Fig. 1B of reference [23]. D_reference refers to the diffusion coefficient of the molecule of known R_h, with D_unknown and R_h^unknown respectively referring to the diffusion coefficient and hydration radius of the target molecule.

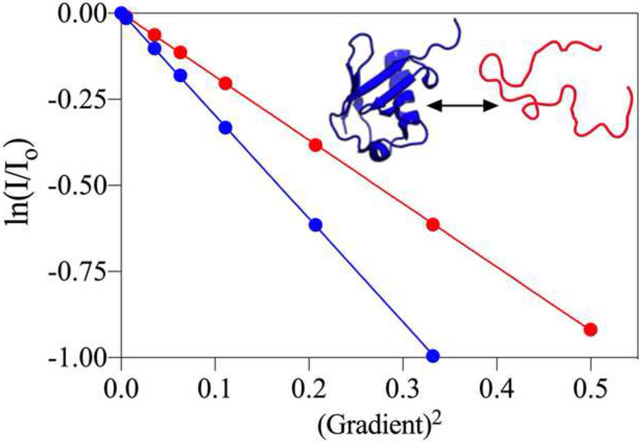
Fig. 1 |.

Pressure-dependence of the translational diffusion of tracer molecules. (a) The relative diffusion (D_x-bar / D_1-bar) at 293 K, plotted as a function of hydrostatic pressure. Symbols correspond to a sample of 95% H₂O, 4% D₂O, 0.25% each (v/v) of dioxane, DMSO, methanol and ethanol, plus 150 mM sodium formate, 20 mM benzene, 50 μM DSS, and 50 mM Tris buffer, pH 6.5. The solid black line depicts the inverse relative solvent viscosity (η_1-bar / η_x-bar), as obtained from the NIST website for water at 293 K (https://webbook.nist.gov/chemistry/fluid/). (b) Relative R_h values (R_h^x-bar / R_h^1-bar) of formate, benzene, dioxane, and ethanol as a function of pressure. R_h at elevated pressures were determined from the diffusion rate after correcting for the increased water viscosity, taken from the NIST website. Solid lines represent best-fit second-order polynomials with the coefficients listed in Table 1. Data for Tris, methanol, and DMSO are shown in SI Fig. S3.

2.2. NMR spectroscopy

All ¹H-detected NMR spectra were recorded on a 700-MHz Bruker Avance-III spectrometer equipped with a room-temperature, triple-axis gradient TXI probe. ¹³C relaxation measurements were carried out on a Bruker 600-MHz Avance-II system, with direct ¹³C detection at 150.9 MHz and using a cryogenic (TCI) probehead. All NMR measurements were carried out using a ceramic NMR tube with a 2.8 mm inner diameter, rated for pressures up to 3000 bar, which was linked to an automatic pump system (Daedalus Innovations, Philadelphia, PA) to regulate the hydrostatic pressure inside the sample cell [55].

To measure self-diffusion coefficients (D), the 1D stimulated echo longitudinal encodedecode pulse sequence with bipolar pulse paired gradients (BPP-LED) [22, 23] was used. BPP gradients [56] strongly reduce eddy current effects and thereby the requisite durations of gradient recovery delays, while also minimizing ¹H–¹H NOE losses during the diffusion delay [23]. In our BPP-LED experiments, simultaneous x- and y-gradients were employed for encoding and decoding, but the BPP pulse pair was slightly imbalanced, with the first gradient set 12.7% higher than the second, oppositely signed gradient [57]. When both x and y gradients are set simultaneously at their maximum value, this corresponds to a strength of 66.8 G/cm when calibrated based on the measured self-diffusion of dioxane in D₂O, using R_h(dioxane) = 2.12 Å, and η_D2O = 1.25 cP at 293 K, 1 bar [58]. Transverse gradients instead of z gradients were employed to minimize convection effects [59]. Encoding and decoding bipolar gradients were applied for 2×1.5 ms, with diffusion delays ranging from 200–400 ms.

For diffusion measurement of the tracer molecules at 293 K, a solution of 95% H₂O, 4% D₂O, and 0.25% each of dioxane, ethanol, methanol, and DMSO (v/v) was prepared, to which 150 mM sodium formate, 20 mM benzene, 50 μM DSS, and 50 mM tris(hydroxymethyl)aminomethane (Tris), pH 6.5 was added. A second sample contained 96% H₂O, 2% D₂O, and 0.5% each of dioxane, ethanol, methanol, and DMSO (v/v). Eight 1D spectra with different encoding and decoding gradient strengths were recorded in an interleaved manner, with the diffusion delay set to 200 ms. The encoding/decoding gradients strengths were set to 2.24, 4.34, 5.75, 6.85, 7.78, 8.65, 9.42, and 10.12% of the maximum value of 66.8 G/cm, with the encoding and decoding gradients slightly imbalanced as described above. Strong detuning of the ¹H channel of the probe was used to prevent radiation damping effects, thereby removing the need for presaturating or otherwise suppressing the H₂O signal. The time domain data were apodized with a 3-Hz exponential line broadening function, zero-filled four-fold, and baseline corrected after Fourier transformation. Data were processed with NMRPipe [50] and analyzed using in-house Python and Nmrglue [60] scripts to automatically extract the attenuation of intensities resulting from translational diffusion (I_grad,/ I₀), where I₀ refers to the intensity in the spectrum with the weakest encoding/decoding gradients and I_grad to the intensities in the spectra with higher gradient strengths. Errors were obtained from the variance-covariance matrix derived from a fit of ln(I_grad,/I₀) versus squared gradient strength.

For 1D PFG NMR diffusion measurements on VA2-ubiquitin, WT ubiquitin, and αS a similar procedure was performed, except for usage of longer diffusion delay, a 7-Hz exponential line broadening function, and data were collected at 288 K. The range of encoding/decoding gradient strengths was adjusted to enable accurate measurement of the diffusion coefficients of both protein and dioxane molecules, and only the data attenuated by less than 10-fold were used for fitting the diffusion decay constants.

2D PFG NMR diffusion data were collected as pseudo-3D spectra, comprising eight interleaved 2D datasets of 40* × 1024* points (where N* indicates N complex data points) with acquisition times of 26 and 113 ms (t₁, t₂). Depending on the population of the unfolded state, either 8, 16, or 64 scans were acquired per FID, yielding total experimental durations of 2.15 h (8 scans), 4.3 h (16 scans), or 17.2 h (64 scans). The diffusion delay (375 ms), maximum x/y gradient strengths, and gradient durations (2×1.5 ms) were set identically to those in the 1D PFG NMR datasets. To decouple ¹⁵N spins during t₂ acquisition, WALTZ-16 decoupling with a 1.39 kHz field was employed. Decreasing the decoupling field to 0.69 kHz had no impact on the measured diffusion coefficient, indicating that potential sample heating and convection from radiofrequency irradiation did not affect the results (Supplementary Fig. S1). 2D data were processed with NMRPipe [61] with the time domain of the indirect dimension extended by 50% using the SMILE program [62], followed by apodization with a cosine-squared window. Spectra were visualized with NMRFAM-Sparky [63], and peak shapes were fit with FuDA [64]. Intensities from resonances that arose from the folded or unfolded states were grouped separately and fit to single exponential decays, with errors in the fitted diffusion coefficient estimated from a standard jackknife procedure.

3. Results and Discussion

3.1. Pressure-dependence of translational and rotational diffusion rates of tracer molecules

Prior high-pressure NMR studies have investigated the self-diffusion of neat liquids and a handful of binary mixtures as a function of pressure [51]. Although hydrophobicity was found to impact the pressure dependence of rotational and translational diffusivity, many of these results were obtained in organic solvents. Less is known about the pressure-dependence of the hydrodynamic properties of molecules in aqueous solutions. Here, we evaluate at high precision the rotational and translational diffusion of six, chemically diverse molecules as a function of hydrostatic pressure. Although one might expect the translational diffusivity of small tracer molecules to simply scale with the pressure dependence of the water viscosity, we find this to apply only for highly polar molecules such as sodium formate and tris(hydroxymethyl)aminomethane (Tris). For more hydrophobic solutes, their diffusivity decreases with pressure by amounts that roughly scale with their hydrophobicity (Fig. 1a). Using the pressure dependence of the water viscosity, which is known at very high accuracy https://webbook.nist.gov/chemistry/fluid/, these diffusion coefficients can be converted into apparent radii of hydration relative to those at 1 bar (Fig. 1b). As can be seen, substantial increases in the apparent Stokes radii, far outside the measurement uncertainty, are observed for all hydrophobic solutes. The largest increase is observed for benzene, which increases in R_h by 11.3% at 3 kbar over atmospheric pressure conditions. Importantly, the R_h of dioxane, which often is used as an internal standard also shows a substantial increase of up to 7.5% at 3 kbar.

The diffusivity of water as a function of pressure at a fixed temperature is also readily extracted from the PFG NMR spectra. Note, however, that strong detuning of the ¹H coil as well as a weak (ca 1 G/cm) gradient along the z-axis during the diffusion delay were needed to prevent radiation damping. At 293 K, the diffusivity of water as a function of pressure shows a maximum near 800 bar, expected on the basis of the known pressure dependence of its viscosity at this temperature (Fig. 1a). Although the agreement is much closer than seen in early NMR PFG studies of water diffusion [65, 66], a small but systematic difference, approaching 1.5% at 3 kbar is reproducibly seen. This difference relative to the pressure dependence of water viscosity does not arise from the presence of 4% D₂O (v/v) and 4% (v/v) tracer molecules (dioxane, methanol, ethanol, and DMSO), as repeating the measurement with 2% D₂O (v/v) and 2% tracer molecules (v/v) yielded indistinguishable results (data not shown). Instead, this difference has been attributed to a break-down of the applicability of the Stokes-Einstein equation for describing translational and rotational diffusion of water at high pressures [67, 68].

All tracer molecules also exhibit a slightly non-linear pressure dependence of their ¹H chemical shift (Supporting Information Fig. S2; Table S1). However, we note that this apparent pressure dependence is small, with the largest value of −0.03 ppm at 3 kbar observed for methanol, and depends strongly on what is used as the reference value. If chemical shifts are referenced to trimethylsilyl propionate (TSP), for example using the procedure of Vajpai et al. [69], significant non-linearity is observed for the solutes, whereas the water chemical shift to a good approximation increases linearly with pressure. On the other hand, when using the methyl signal of IUPAC-recommended 4,4-dimethyl-4-silapentane-1-sulfonic acid (DSS) as an internal reference, with the exception of water, the non-linearities in ¹H chemical shifts are much smaller. To a good approximation, the pressure dependence of both the apparent radii of hydration, as well as the ¹H chemical shifts, can be fitted by second order polynomials, with coefficients reported in Table 1.

Table 1.

Fitted parameters obtained for the pressure dependence of ¹H chemical shifts and R_h values of tracer molecules, measured in 94% H₂O, 293 K, pH 6.5.^a

Molecule	δ0 (ppm)	B1 (10−5 bar−1)	B2 (10−9 bar−2)	Rh,0 (Å)	C1 (10−4 Å)	C2 (10−8 Å)
Formate	8.4402	−0.584 ± 0.003	−0.210 ± 0.013	1.624	−0.040 ± 0.017	−0.284 ± 0.071
Benzene	7.4298	0.035 ± 0.004	0.385 ± 0.015	2.012	0.653 ± 0.019	−0.937 ± 0.078
Dioxane	3.7484	−0.300 ± 0.004	0.083 ± 0.017	2.120	0.497 ± 0.016	−0.844 ± 0.068
Tris	3.7206	−0.613 ± 0.004	0.146 ± 0.015	3.114	0.041 ± 0.019	−0.447 ± 0.078
MeOH	3.3481	−0.898 ± 0.004	0.055 ± 0.016	1.442	0.282 ± 0.017	−0.462 ± 0.069
DMSO	2.7167	0.901 ± 0.006	−0.669 ± 0.026	1.945	0.393 ± 0.013	−0.631 ± 0.055
EtOH-methyl	1.1713	−0.540 ± 0.005	0.173 ± 0.019	1.883	0.166 ± 0.023	−0.177 ± 0.096
Water	4.8326	0.931 ± 0.009	2.049 ± 0.038	0.940	0.221 ± 0.017	−1.437 ± 0.071

^a1H chemical shifts (δ) and the effective R_h (R_h,eff) measured at each pressure are fit to second-order polynomials, δ = δ₀ + B₁(P – P₀) + B₂(P – P₀)² and $R_{\text{h,eff}}=R_{\text{h},0}+C_1\left(\frac{P}{P_0}\right)+C_2{\left(\frac{P}{P_0}\right)}^2$. The coefficients B₁, B₂, C₁, and C₂ are fitting parameters; P stands for pressure; δ for the measured chemical shift; δ₀ for the chemical shift at 1 bar; R_h,eff for the effective R_h; R_h,0 for the R_h at 1 bar; and P₀ = 1 bar. Errors represent one standard deviation from the best-fit value.

We find that the change in translational diffusion rate of the hydrophobic solutes with pressure correlates with a decrease in longitudinal ¹³C relaxation times of these solutes when pressure is increased (Table 2). ¹³C T₁ values are dominated by J (ω_C) spectral density and, considering that the rotational diffusion of these small tracer molecules is far into the fast tumbling limit (ω_Cτ_r « 1), the decrease in ¹³C T₁ with increasing pressure must result from slower rotational diffusion.

Table 2.

¹³C longitudinal relaxation times, T₁, of various tracer molecules in 96% H₂O, 293 K, 14.1 Tesla, at three different pressures.

Carbon nucleus	T1 (s)
	1 bar	1500 bar	3000 bar
Formate	14.8 ± 0.2	14.9 ± 0.2	14.5 ± 0.2
Benzene	10.4 ± 0.2	9.9 ± 0.2	8.8 ± 0.2
Dioxane	5.91 ± 0.02	5.40 ± 0.02	4.67 ± 0.02
Tris-methylene	0.95 ± 0.01	0.99 ± 0.01	0.96 ± 0.01
Tris-quaternary	8.80 ± 0.07	8.92 ± 0.07	8.84 ± 0.05
MeOH	12.35 ± 0.08	13.13 ± 0.08	13.13 ± 0.08
DMSO methyl	5.44 ± 0.04	5.15 ± 0.03	4.78 ± 0.03
EtOH-methyl	7.31 ± 0.03	7.30 ± 0.03	6.91 ± 0.02
EtOH-methylene	10.17 ± 0.03	10.07 ± 0.03	9.40 ± 0.03

3.2. R_h pressure dependence of a folded and a disordered protein

To assess the impact of pressure on the translational diffusion of proteins, we measured these rates as a function of pressure for two proteins under conditions where pressure does not impact the folding-unfolding equilibrium: WT-ubiquitin and αS. The mid-point for pressure denaturation of WT-ubiquitin is ca 5.4 kbar [70] and this protein therefore remains fully folded under the conditions used in our study. The second protein, αS, is intrinsically disordered and the previously reported pressure dependence of its chemical shifts closely follows that observed for short linear peptides [71], pointing to the absence of any significant secondary structure formation with pressure.

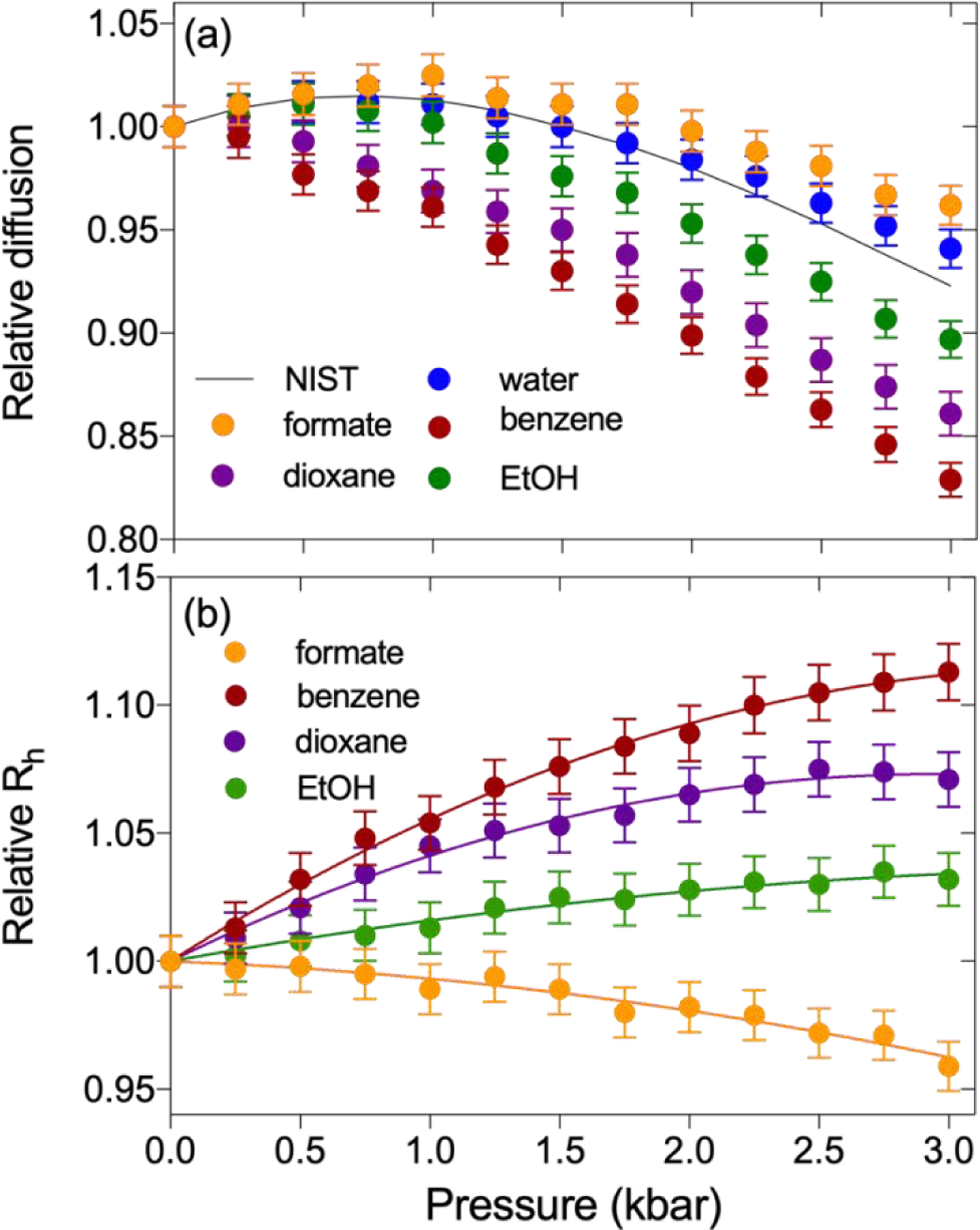
The R_h of αS is rather insensitive to hydrostatic pressure up to ca 2 kbar, but then decreases by ca 3% when the pressure is raised to 3 kbar (Fig. 2a; Supporting Information Table S2). Results also show a small but distinct concentration dependence of the diffusion rate, resulting in an apparent R_h that is ca 1 Å larger at 240 μM than at 120 μM protein concentration. Considering that, at 240 μM αS and using R_h as an approximate radius of the unfolded protein, the apparent volume fraction occupied by αS is only ca 1.7%, the difference in R_h observed at this relatively dilute concentration is larger than expected from obstruction [72]. However, the approximation to consider the protein as an object with a single, constant R_h is clearly an oversimplification. It is likely that obstruction involving extended conformers out of the large ensemble sampled by αS will disproportionately impact the translational diffusion behavior of this IDP. At ca 30 Å, the Stokes radius derived here is smaller than the value originally obtained from gel filtration chromatography (34 Å) [73], and somewhat smaller than the 31.7 Å value derived from NMR diffusion by Baum and co-workers at slightly higher (300 μM) αS concentration [74], while essentially indistinguishable from the value reported more recently by Ruzafa et al. [75], also using NMR diffusion measurements under conditions very similar to ours. We hypothesize that the small, ca 3% decrease in R_h seen at 3 kbar relative to atmospheric conditions may be related to a small shift in the Ramachandran map distribution of random coil residues with pressure, as reflected in the previously noted decrease in ³J_HNHα couplings with pressure [71].

Figure 2 |.

Pressure-dependence of the R_h values of (a) αS and (b) WT-ubiquitin are plotted as a function of hydrostatic pressure. Measurements were carried out at protein concentrations of 0.12 mM (black) and 0.24 mM (grey) αS (pH 7.0), and 0.5 mM WT-ubiquitin (pH 6.5), each in 94% H₂O at 288 K. The midpoint of pressure-induced unfolding of WT-ubiquitin is 5.4 kbar [70], and our measurements therefore pertain to the folded state. The R_h measurements are calibrated relative to a value of 2.12 Å for the R_h of internal dioxane at 1 bar and account for the known pressure dependence of the water viscosity.

For WT-ubiquitin, the translational diffusion rates as a function of pressure (Table S2) are found to scale with the inverse of the water viscosity, resulting in a R_h value that is nearly flat (Fig. 2b). A linear fit of the data as a function of pressure yields a very small decrease from 15.39 Å at 1 bar to 15.18 Å at 3 kbar. Using an average compressibility of folded proteins of ca 15 Mbar⁻¹ [76, 77], a volume compression of ca 4.5% is expected at 3 kbar, or a ca 1.5% reduction in radius, in good agreement with our diffusion measurements. The absence of any significant structural rearrangement of ubiquitin at pressures ≤ 3 kbar is consistent with excellent fits of the backbone residual dipolar couplings, measured at these elevated pressures, to the solution NMR structure derived at 1 bar [78], and with minute but detectable changes in the lengths of its backbone H-bonds [79]. Note that both these H-bond and our RDC and diffusion measurements were carried out at near neutral pH. At pH 4.6, hydrostatic pressure was shown to have a substantially larger impact on ubiquitin structure, as judged by changes in backbone amide chemical shifts and measurement of NOEs [80].

3.3. Diffusion rates for mixtures of folded and unfolded protein by 2D PFG NMR

Having validated that accurate translational diffusion coefficients can be obtained at high pressures, we sought to utilize PFG NMR at intermediate pressures to simultaneously study the diffusion of a protein that populates both the folded and unfolded states. For these experiments, we utilized VA2-ubiquitin, which unfolds with a midpoint near 1.6 kbar at 288 K.

In order to sufficiently resolve signals from the folded and unfolded states of VA2-ubiquitin, we used 2D PFG NMR experiments. Exchange between the folded and unfolded states during the long diffusion delay (375 ms) could adversely impact the extracted diffusion rates of each state. However, by evolving the ¹⁵N t₁ chemical shift evolution right after the gradient encoding, the presence of exchange between the folded and unfolded states, to first order, does not impact the decay of the “diagonal peaks” even if exchange were present [17]. Such exchange would result in ZZ-exchange cross peaks between folded and unfolded species, and the absence of such resonances confirms that the exchange process is slow compared to the 375-ms diffusion delay used in our experiments. Thus, each resonance for folded and unfolded VA2-ubiquitin reports faithfully on the respective state without contamination from exchange. Albeit less sensitive, the 2D dataset has the advantage of yielding a large number of independent intensity measurements, those of the resolved peaks in the 2D NMR spectrum, thereby offering a reliable measure for the statistical uncertainty in the derived diffusion rates.

At 1400 bar, the folded and unfolded species of VA2-ubiquitin are populated at 68% and 32% respectively (Fig. 3a). Diffusion of the unfolded species is considerably slower than for the folded protein, as can be seen from the slower decay of the cross peak of the unfolded G35 resonance compared to A17 of the folded species (Fig. 3b). Well-resolved unfolded ¹H–¹⁵N correlations were obtained for N=12 amides. To prevent a bias in the intensity measurement at the highest gradient strengths, where the signals become vanishingly weak, it is important to fix the position at which the resonance intensity is measured to that of the most intense spectrum, i.e., that with the weakest gradient [81]. To estimate the statistical uncertainty, resolved resonances then were split into two equal sized groups, and the N/2 resonance intensities for each group within a given spectrum were co-added, thereby decreasing the fractional uncertainty of the sum by √(N/2). Repeating this procedure for a large number of random groupings, the root-mean-square of the pairwise difference between the diffusion rates obtained for such pairs of groups is double the uncertainty of the fit obtained when all intensities are used (SI Fig. S6), thereby yielding an estimate for the uncertainty in the diffusion rate. The decay of such sums for both the folded and unfolded species is well fit by exponential functions, as seen from the linearity of the natural logarithm of these summed intensities plotted against the squared values of the gradient strength (Fig. 3c).

Fig. 3.

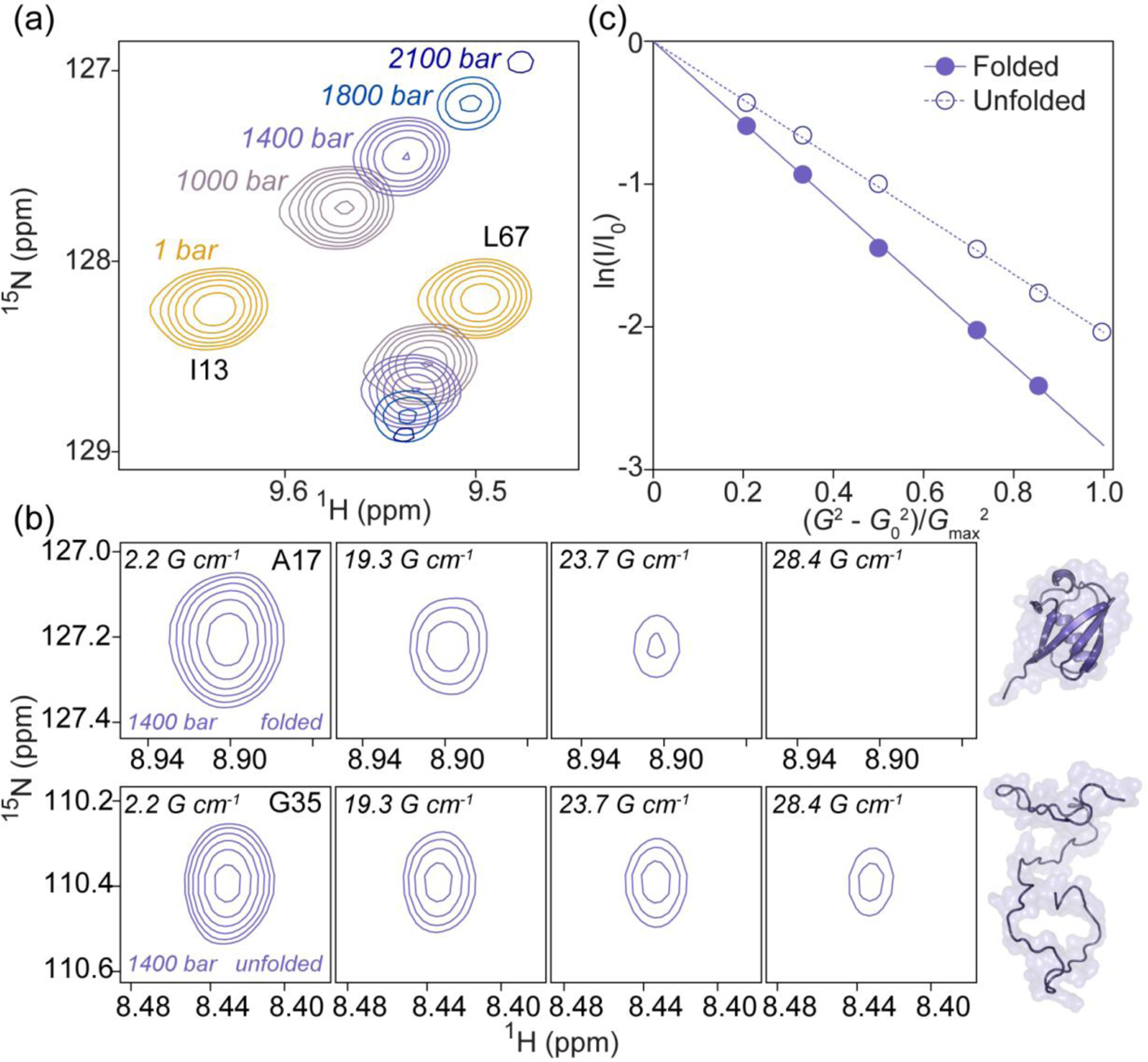
Simultaneous measurement of the diffusion rates of folded and unfolded protein from 2D PFG diffusion experiments. (a) Overlays of a small region of the 2D ¹H–¹⁵N HSQC spectra of ¹⁵N-VA2-ubiquitin recorded at five hydrostatic pressures ranging from 1 bar to 2.1 kbar. Shown are resonances from the folded state (I13, L67) at 1, 1000, 1400, 1800, and 2100 bar. Contours are spaced by factors of 1.4 (b) Example of the decrease in cross peak intensity with increasing gradient strength, G, in 2D PFG NMR spectra of folded (top, A17 resonance) and unfolded (bottom, G35 resonance) VA2-ubiquitin recorded at 1400 bar where spectral intensities of folded and unfolded states are comparable. Corresponding 2D PFG NMR data from the urea-denatured state are shown in Supplementary Figure S6. (c) Intensity decay profiles for the folded (filled) and unfolded (empty circles) states of VA2-ubiquitin at 1400 bar. These are the data from panel B, summed over the N resonances analyzed for each state. The natural logarithm of the intensity decay (I/I₀) is plotted vs normalized gradient strength. G_max = 33.4 G/cm; G₀ = 2.1 G/cm.

3.4. Diffusion measurements on equilibria of folded and unfolded protein by 1D PFG NMR

As described above, 2D PFG NMR diffusion experiments are generally required to achieve sufficient resolution to separate signals from the folded and unfold states. However, as a result of relaxation losses during the relatively long diffusion delay, compounded by the loss associated with the stimulated echo which refocuses only half of the initial magnetization, 2D PFG NMR diffusion experiments are intrinsically of rather low sensitivity. Coupled with the requirement to measure the weakest spectrum, i.e., recorded with the strongest gradient, at adequate signal to noise, and reduced sample volumes available in high pressure measurements that require thick wall sample tubes, 2D PFG measurements at elevated pressures are demanding from a sensitivity viewpoint. Moreover, while for small molecules, conventional 1D DOSY measurements are routinely applied to mixtures of molecules that frequently contain resonances free of overlap between molecular species, for a mixture of folded and unfolded protein, the standard 1D method only works well for the folded fraction of the sample. The unfolded protein typically lacks resonances free of overlap with the folded species.

Thus, we explored the feasibility of faster and more sensitive 1D NMR alternatives. The method outlined below requires a 1D reference spectrum, recorded for the folded state (e.g., 1 bar, 0 M urea), henceforth referred to as the reference spectrum. Except for the number of scans, sample concentrations, and pressure or urea concentration, all experimental parameters were kept constant for the measurements on the mixtures of folded and unfolded protein. An in-house Python script that utilizes the software Nmrglue [60] was then used to automatically execute the steps described below.

First, the reference spectrum is shifted to match the position of a unique, folded resonance in the mixed sample (Fig. 4a), e.g. an upfield methyl or downfield amide signal. This is followed by downscaling of the reference spectrum such that the selected resonance (L50-C^δ2H₃ for our VA2-ubiquitin sample) in the folded reference spectrum matches the intensity in the mixed sample (Fig. 4b), which then allows generation of a difference spectrum (Fig. 4c) that no longer contains a net integral of folded protein resonance intensity. Of course, it is critical that relative resonance intensities in the 1D reference spectrum are the same as those recorded with the 1D BPP-LED experiment for the folded component of the mixed sample. For this reason, the reference spectrum of the fully folded protein is also recorded with the 1D BPP-LED pulse sequence, using a very weak encoding/decoding gradient combination. Even though resonances of the folded protein may have shifted somewhat relative to the reference spectrum, either due to the effect of pressure or weak interactions of denaturant with the folded protein, thereby generating a difference spectrum that contains negative components (Fig. 4c), the integral of the methyl region is minimally affected by such shifting, provided no resonances move outside of the integrated region. Integration regions were chosen to include most of the methyl signals for the artificially reconstructed unfolded state, typically 0.7 – 0.9 ppm, but results were found rather insensitive to the limits of the chosen region. Using this procedure to generate difference spectra for the unfolded state (Fig. 4d) then permits measuring the integrated unfolded protein intensity over the selected methyl region, at rather high sensitivity. The clean, single exponential decay of the integrated intensity with increased gradient strength (Fig. 4e) implies the method is reliable.

Fig. 4.

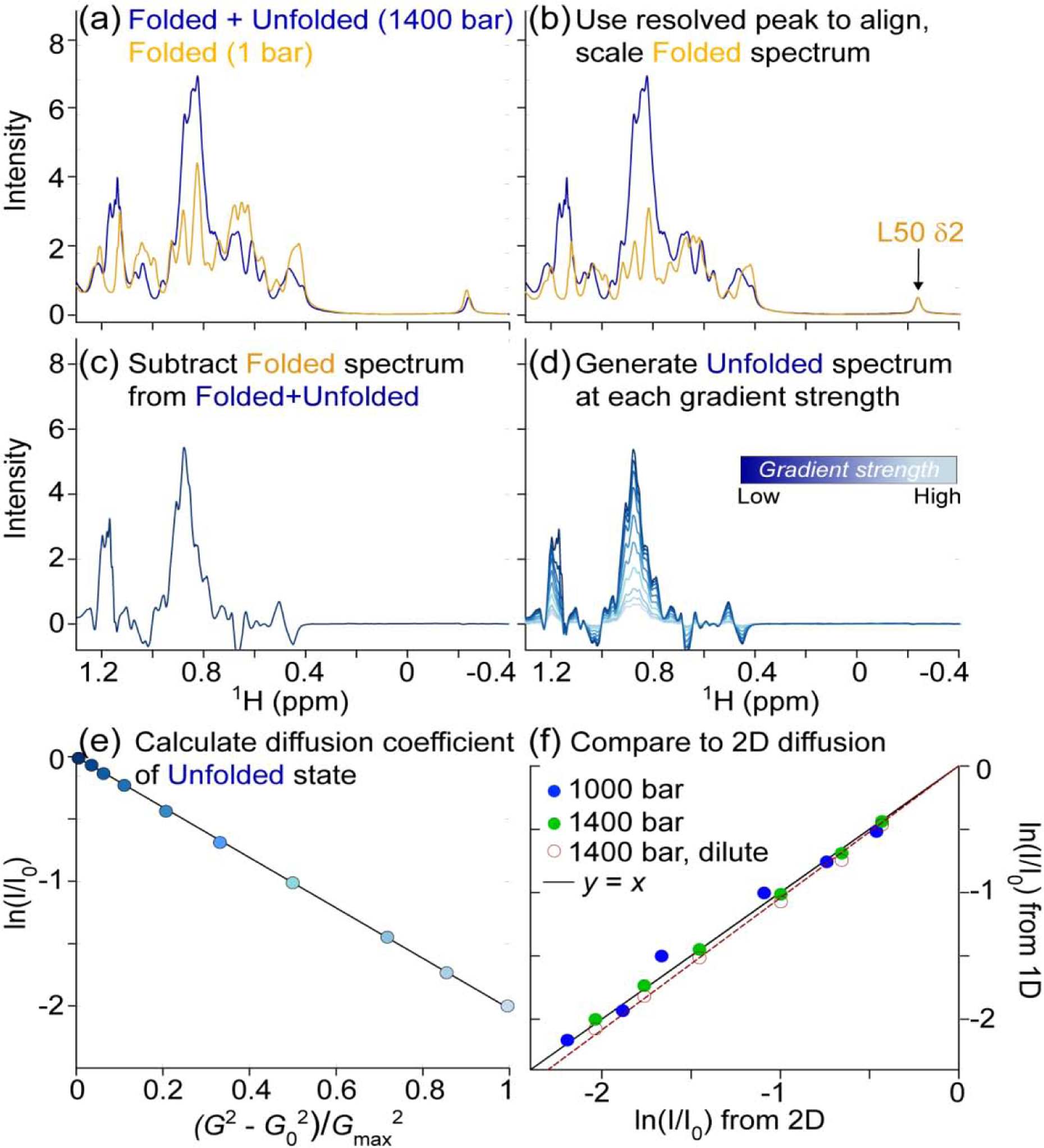
Translational diffusion measurement of unfolded VA2-ubiquitin in 94% H₂O. Total protein concentration is 1.3 mM, pH 6.4. (a) The 1D NMR spectrum at 1400 bar (blue) contains signals from both folded and unfolded protein. The L50 C^δ2H₃ resonance at −0.25 ppm serves as a reference for the folded protein spectrum (orange). (b) The spectrum of the folded state (1 bar) is aligned and scaled such that L50 C^δ2H₃ matches that of the partially unfolded sample. (c) Subtraction of the scaled, folded spectrum then yields an artificial spectrum of the unfolded state. (d) Repeating the procedure for spectra generated at different gradient strengths yields the series of 1D spectra for which integrals over the methyl region are obtained. (e) Plot of the natural logarithm of the integrated methyl resonance intensity, ln(I/I₀), at 1400 bar as a function of the squared gradient strength. G₀ = 2.2 G/cm; G_max = 33.4 G/cm. (f) A correlation plot showing the agreement between ln(I/I₀) values derived from the unfolded state in 2D PFG NMR diffusion data set (x-axis) and those determined from the 1D method outlined above (y-axis). The I/I₀ values from the 1D method were obtained through integration of the ¹H chemical shift region between 0.80 and 0.94 ppm after reconstruction of the spectra of the unfolded state. I/I₀ values from the 2D diffusion datasets were obtained by summing the intensities of N = 12 unfolded resonances at each gradient strength. Data collected at 1000 bar (blue) and 1400 bar (green) are presented, both at 1.3 mM total protein, and the solid line corresponds to y = x. The empty red circles are from a dilute sample (120 μM total) at 1400 bar and the best-fitted diffusion rate of the 120 μM sample is 5% faster than for the 1.3 mM sample (dashed red line).

The 1D measurement and the relatively short longitudinal relaxation times of protein methyl protons enables extensive signal averaging. As such, we also lowered the total concentration of VA2-ubq to 120 μM and collected 1D diffusion data at 1400 bar where the unfolded protein is present at ca 40 μM (Fig. 4f). Notably, this concentration is lower than that required for typical SAXS measurements. Using the 1D difference method described above, we measured the translational diffusion of both the folded and the unfolded state in the dilute sample. The good linearity of the decay when plotted on a log scale against the square of the gradient strength (Fig. 4e) reflects the robustness of the method. The observation of slightly (ca 5%) faster diffusion at 0.12 vs 1.3 mM VA2-ubiquitin concentrations (Fig. 4f) implies that intermolecular interactions come into play when studying the diffusion behavior of unfolded ubiquitin at elevated concentrations (ca 0.4 mM unfolded protein at 1400 bar).

To validate the accuracy of the 1D PFG based diffusion measurements for mixtures of folded and unfolded protein, these measurements were repeated for a limited number of conditions by the more time-consuming 2D method [17, 23]. The diffusion rates, derived from the 2D PFG diffusion measurements for the unfolded fractions of VA2-ubiquitin at 1000 bar and at 1400 bar are in excellent agreement with those derived from the above described 1D method (Fig. 4f), thereby validating consistency of the independent measurements. The larger scatter in the data collected at 1000 bar, where the fraction of unfolded protein is small (ca 4%), is dominated by the signal-to-noise limited precision of the 2D PFG measurement.

3.5. Minimal compaction of the VA2-ubiquitin unfolded state near its unfolding midpoint

To determine whether the R_h of unfolded VA2-ubiquitin decreases when the conditions are such that the folded and unfolded states are comparable in free energy, we measured the diffusion rates across a range of pressures and urea concentrations where both states are appreciably populated. The diffusion rate of the unfolded state is relatively sensitive to protein concentration, and data of Fig. 4f pointed to a small obstruction effect for the unfolded protein when measured at relatively high concentration of 1.3 mM total protein. As the fraction of unfolded protein changes when increasing pressure or urea concentration, the concomitant change diffusion obstruction could lead to an increase in apparent R_h when the fraction of unfolded protein increases (Fig. 5). To avoid this pitfall, we also collected data at 100 μM total protein concentration, where obstruction effects are negligible. With the denaturation mid-point of VA2-ubiquitin near 3.5 M urea, we measured diffusion data in 250 mM urea increments around this concentration. At 4 M urea, where the protein is ca 68% unfolded, the R_h of the unfolded state (23.1 Å) remains very close to the value measured at 7.6 M urea (23.3 Å) (Fig. 5a). Likewise, at 3 M urea where the unfolded state is populated to ca. 27%, R_h only slightly decreases to 22.9 Å, while the experimental uncertainty in the measurement increases due to the lower concentration of the unfolded species (Fig. 5a). Overall, only a 1.6% decrease in R_h between 5 M and 3 M urea was observed, whereas the population of the unfolded state drops from 93% to ca 27% over this range.

Fig. 5.

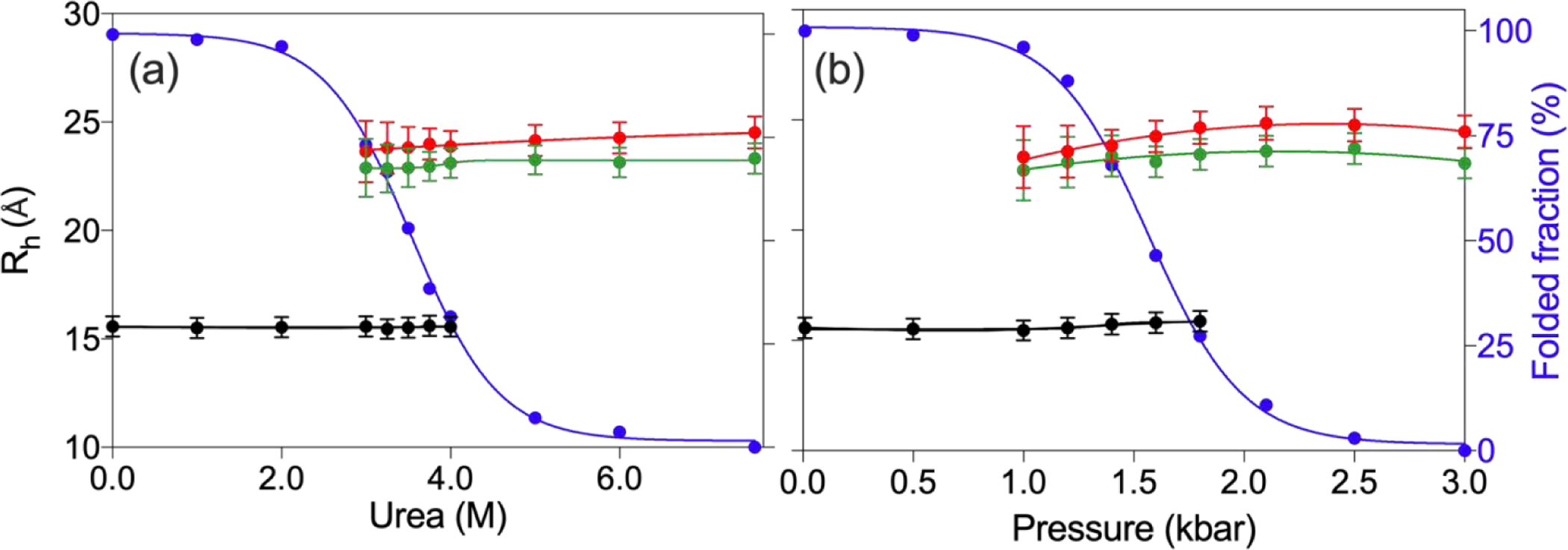
R_h of folded (black) and unfolded (red/green) VA2-ubiquitin under a range of denaturing conditions. (a) R_h values as a function of urea concentration and (b) as a function of hydrostatic pressure. Red and green symbols correspond to high (0.7 mM for urea denaturation; 1.3 mM for pressure unfolding) and dilute (0.1 mM) total protein concentration, respectively. Black symbols correspond to the diffusion of the folded protein at the higher concentration and values are within experimental error from diffusion rates measured at 0.1 mM concentration. Blue symbols correspond to the fraction of folded population. Solvent viscosity as a function of urea concentration for the samples of panel (a), as reflected in the diffusion rate of dioxane, are shown in Fig. S8.

Performing the same experiments on dilute VA2-ubiquitin as a function of pressure yields similar results: comparison of the R_h values measured at 1000 bar (ca. 4% unfolded) and 3000 bar (100% unfolded) shows a ca 1.4% decrease in R_h at the lower pressure, where the folded state is strongly favored (Fig. 5b). Our results therefore indicate that the unfolded state of VA2-ubiquitin shows only a very small degree of collapse when denaturing conditions are adjusted such that both folded and unfolded states are comparably populated. Importantly, our results also show that the pressure-denatured state has a R_h value that is very close to that of the urea-denatured state, confirming that pressure denaturation indeed results in a fully disordered protein with no significant compaction.

At 1 bar, VA2-ubiquitin and the wild-type protein show indistinguishable translational diffusion rates (Supplementary Fig. S5), as expected on the basis of their very similar 3D structures. At 3 kbar, where the folded state of VA2-ubiquitin is no longer appreciably populated, the diffusion-derived R_h of the pressure-denatured chain is 23.0 Å (Fig. 5b). Both the experimentally derived R_h of the folded protein at 1 bar (15.5 Å) and the R_h of the unfolded chain are in good agreement with the empirical equations of Wilkins et al. [14], which predict values of 16.7 and 26.1 Å, respectively for this 76-residue protein. If instead of high pressure, 7.6 M urea is used to denature VA2-ubiquitin, translational diffusion measurements at 1 bar yield R_h = 23.3 Å (Fig. 5a). Using the empirical relation for unfolded chains of Wilkins et al. [14], R_g ≈ 1.06 R_h, between the radius of gyration, R_g, derived from SAXS and the Stokes radius, our value is in good agreement with R_g ≈ 25.2 Å for guanidinium-denatured ubiquitin [82]. However, in contrast to prior SAXS data on urea-unfolded wild-type ubiquitin at pH 2.5 [83], our data show no evidence for the large expansion of the unfolded chain when the urea concentration is raised to 8M. At pH 6.4, we also do not observe the nearly uniform progressive upfield movement of unfolded amide ¹H resonances (referenced relative to internal DSS), previously attributed to urea binding [83].

4. Concluding Remarks

Our work confirms that precise measurement of translational diffusion of proteins at elevated hydrostatic pressures is readily feasible, but that care needs to be exercised when following the common procedure of using an internal reference such as dioxane to derive the radius of hydration. Our results for dioxane and a number of other small hydrophobic molecules indicate that their effective R_h values increase substantially with pressure. The increased R_h with pressure is presumed to be caused by changes in their hydration shell. Prior measurements have clearly established the lower density of water molecules at hydrophobic surfaces [47], sometimes discussed as a solvent clathrate shell that can collapse under pressure [84, 85]. Our results suggest that hydrostatic pressure reduces the void space around the hydrophobic solute, thereby impacting the diffusion behavior of the solute. The higher compressibility of water on the surface of solvent-exposed hydrophobic moieties is potentially an important factor in obtaining a more quantitative understanding of the energetics that form the basis of pressure-induced protein unfolding [47]. The tighter coupling between solvent and solute at elevated pressure is also apparent in the ¹³C T₁ values measured for a set of small hydrophobic molecules, which are all in the fast tumbling limit (ω_cτ_c « 1) and decrease significantly with increasing pressure (Table 2). By contrast, the ¹³C T₁ of the polar formate and Tris molecules, as well as their translational diffusion rates, are minimally impacted by pressure.

Probing the translational diffusion of the folded state of VA2-ubiquitin across a range where both folded and unfolded states are significantly populated reveals minimal variation in the R_h value of the folded state, both for the cases where high pressure and urea are used to induce unfolding of the protein. WT ubiquitin, which requires pressures much higher than 3 kbar to unfold, shows an approximate 1.5% reduction in its R_h at 3 kbar, close to the value expected based on the compressibility of folded proteins [76].

More remarkable is the near-absence of compaction of the unfolded VA2-ubiquitin when conditions start favoring the folded state, provided the measurements are made under dilute conditions. A number of single molecule FRET studies provide strong support for compaction when the concentration of denaturant is reduced [86–90], as did two-focus correlation spectroscopy [91]. Such compaction potentially could be attributed to transient formation of secondary structure elements [92]. Our observations, which show an absence of detectable compaction of unfolded VA2-ubiquitin, suggest that transient sampling of such states does not significantly impact the ensemble-averaged hydration radius of the protein. Similar conclusions were reached for several other systems using small angle X-ray scattering (SAXS) measurements [34, 35]. It is important to point out, however, that our study focuses on just a single denaturant- and pressure-unfoldable protein, and our finding that the unfolded chain does not significantly collapse as the ΔΔG between the folded and unfolded states approaches zero may depend strongly on the system studied.

A prior study found no effect of urea on the SAXS-derived R_g of an intrinsically disordered protein [93]. Interestingly, our results show a slight, gradual decrease in R_h of αS at pressures above 2000 bar. The reason for this decrease is not immediately clear but we speculate that it may correlate with a shift in the population of the Ramachandran map of IDPs with pressure, also reflected in a small decrease of ³J_HNHα couplings with increasing pressure [71]. The latter suggests a small increase in turn-like conformations, thereby potentially decreasing the persistence length of the unfolded chain, resulting in a decreased R_h. Considering the observed increase in R_h when the αS concentration is increased from 120 to 240 μM, we note that in order to prevent significant inter-particle interference, PFG measurements of R_h for unfolded systems need to be carried out at low concentrations, an effect also noted previously [94].

Our results indicate that the addition of urea or increasing pressures do not cause αS or the unfolded state of VA2-ubiquitin to expand. While αS and VA2-ubiquitin provide two proteins of quite different length and sequence composition, a more systematic analysis of the effect of hydrostatic pressure on the translational diffusion of unfolded proteins is warranted. It appears plausible that the effect of hydrostatic pressure on the unfolded state of a protein will depend on its sequence composition, particularly on its level of enrichment with hydrophobic and aromatic residues.

Highlights.

• Changes in hydration radii of small molecules with pressure depend on hydrophobicity

• Diffusion of folded and unfolded proteins can be deconvolved from overlapping 1D NMR spectra

• Pressure- and urea-denatured ubiquitin have very similar hydrodynamic radii

• Translational diffusion of unfolded proteins significantly depends on concentration

• Hydrodynamic radii of folded and unfolded proteins show little dependence on ΔΔG