From Drift to Draft: How Much Do Beneficial Mutations Actually Contribute to Predictions of Ohta’s Slightly Deleterious Model of Molecular Evolution?

Abstract

Since its inception in 1973, the slightly deleterious model of molecular evolution, also known as the nearly neutral theory of molecular evolution, remains a central model to explain the main patterns of DNA polymorphism in natural populations. This is not to say that the quantitative fit to data are perfect. A recent study used polymorphism data from Drosophila melanogaster to test whether, as predicted by the nearly neutral theory, the proportion of effectively neutral mutations depends on the effective population size (N_e). It showed that a nearly neutral model simply scaling with N_e variation across the genome could not alone explain the data, but that consideration of linked positive selection improves the fit between observations and predictions. In the present article, we extended the work in two main directions. First, we confirmed the observed pattern on a set of 59 species, including high-quality genomic data from 11 animal and plant species with different mating systems and effective population sizes, hence a priori different levels of linked selection. Second, for the 11 species with high-quality genomic data we also estimated the full distribution of fitness effects (DFE) of mutations, and not solely the DFE of deleterious mutations. Both N_e and beneficial mutations contributed to the relationship between the proportion of effectively neutral mutations and local N_e across the genome. In conclusion, the predictions of the slightly deleterious model of molecular evolution hold well for species with small N_e, but for species with large N_e, the fit is improved by incorporating linked positive selection to the model.

THE year 2018 saw the celebration of the 50th anniversary of the neutral theory of molecular evolution (called simply the neutral theory thereafter). At 50 years of age, the neutral theory is still shrouded in controversies, some pronouncing it dead and overwhelmingly rejected by facts (Kern and Hahn 2018), while others see it as very much alive and kicking (Nei et al. 2010; Jensen et al. 2019). As a quick glance at major textbooks in population genetics and at the literature would suggest, it seems fair to say that the neutral theory is certainly not totally dead. Even if it undoubtedly did lose some of its initial appeal it continues to play a central role in population genetics, a position well summarized by Kreitman (1996) in his spirited essay “The neutral theory is dead. Long live the neutral theory.” Shortcomings of the neutral theory were already noted in the 1970s and the Neutral Theory has itself evolved. Indeed, its inadequacy to fully explain the data, in particular the constancy of the molecular clock, was already noted in 1973, leading Tomoko Ohta (1973) to propose the nearly neutral theory of molecular evolution. In contrast to the neutral theory, where most mutations are assumed to be neutral or strongly deleterious, the nearly neutral theory assigns much more prominence to the contribution of standing polymorphism of mutations that are weakly selected and effectively neutral (Ohta 1992; Ohta and Gillespie 1996). Weakly selected mutations can be slightly deleterious or slightly beneficial, but as noted by Kreitman (1996), the best developed of the weak selection models primarily considers slightly deleterious mutations and was therefore christened by him “the slightly deleterious model”. This is the model that we will be testing in most of the present paper.

Like the neutral theory, the nearly neutral theory still assumes that “only a minute fraction of DNA changes in evolution are adaptive in nature” (Kimura 1983). Under this view, polymorphism is thought to be mostly unaffected by positive selection, except around the few recently selected beneficial alleles (selective sweeps). This was already at variance with the view put forward by Gillespie (2004) that assigned a greater role to linked positive selection in shaping polymorphism [see also Corbett-Detig et al. (2015)], and is in even stronger contrast with the claim by Kern and Hahn (2018) that “natural selection has played the predominant role in shaping within- and between-species genetic variation,” and that “the ubiquity of adaptive variation both within and between species” leads to the rejection of the universality of the neutral theory. In a far more nuanced assessment of the neutral theory and its contribution, Jensen et al. (2019) argued that the effects of linked selection could readily be incorporated in the nearly neutral framework. The heart of the dispute, either today or in the early days of the nearly neutral theory, is about the degree to which each category of mutation contributes directly and indirectly to genetic variation within and between species.

A core prediction of the nearly neutral theory is that the fraction of mutations affected by selection depends on the effective population size, N_e (Ohta 1973). N_e is a measure of (the inverse of) genetic drift and corresponds to the size of an ideal, typically Wright–Fisher, population generating the same amount of drift as the observed population. The definition of N_e depends on the drift-related process (e.g., inbreeding, variance in allelic frequencies) and the timescale of interest. The coalescent effective population size is relevant for the prediction of polymorphism patterns (Sjödin et al. 2005). N_e can vary among species (because of difference in population size, variance in fecundity, reproductive systems etc.), but also along a genome because linked selection generates variation in the coalescent process if recombination rate and selection targets are not uniformly distributed [reviewed in Ellegren and Galtier (2016)]. The effect of selection against deleterious mutations on linked neutral variants—background selection (Charlesworth et al. 1993)—is often modeled by a simple rescaling of N_e, but in specific situations effects of linked selection are more complex and there is not a single rescaling (Barton 1995; Zeng 2013; Comeron 2017; Cvijović et al. 2018; Torres et al. 2019). In the case of beneficial mutations, for instance, the interference depends both on the beneficial effect of the sweeping mutation and on selection acting at linked sites (Barton 1995; Weissman and Barton 2012).

Evidence that linked positive selection, and not only direct selection on slightly deleterious and beneficial mutations, contributed to the relationship between the fraction of mutations affected by selection and N_e has recently been obtained by Castellano et al. (2018). Using two Drosophila melanogaster genome resequencing data sets, Castellano et al. (2018) tested a prediction of the slightly deleterious model first obtained by Kimura (1979) and then extended by Welch et al. (2008). Welch et al. (2008) showed that if one considers only deleterious mutations, the logarithm of the ratio of nucleotide diversity at nonsynonymous and synonymous amino acid changes is linearly related to the logarithm of the effective population size, and that the slope of this log–log regression line is equal to the shape parameter of the distribution of fitness effects (DFE), β, if the DFE of deleterious mutations is modeled by a γ distribution:

$$ln\left({\mathrm{\pi }}_{\mathrm{N}}/{\mathrm{\pi }}_{\mathrm{S}}\right)\approx -\beta ln\left(N_e\right)+constant$$ (1a)

where π_N is the nucleotide diversity at nonsynonymous sites and π_S is the nucleotide diversity at synonymous sites.

Or, rewriting this expectation by using π_S as a proxy for N_e:

$$ln\left({\mathrm{\pi }}_{\mathrm{N}}/{\mathrm{\pi }}_{\mathrm{S}}\right)\approx -\beta ln\left({\mathrm{\pi }}_S\right)+constant’$$ (1b)

The second equation holds only if variation in π_S solely depends on variation in N_e, and there is no correlation between the mutation rate and N_e. It should also be pointed out that the DFE used here only considers deleterious mutations, as estimated for instance by DFE-α (Eyre-Walker and Keightley 2009). A direct test of this prediction using among-species comparison can be problematic if mutation rates cannot be controlled for. To circumvent this problem, Castellano et al. (2018) used within-genome variation in N_e, under the reasonable assumption that variation in mutation rates are negligible compared to variation in N_e across a genome. They found [see also James et al. (2017)] that the slope was significantly steeper than expected under a simple scaling of N_e and simulations indicated that linked positive selection, but not background selection, could explain this discrepancy. The effect of linked selection on the relationship between π_N/π_S and π_S is twofold. First it increases stochasticity in allele frequencies, or, in other words, decreases the local effective population size. Second, linked selection leads to nonequilibrium dynamics. Genetic diversity will recover faster for deleterious than neutral mutations, altering the relationship between π_N/π_S and π_S (Gordo and Dionisio 2005; Do et al. 2015; Brandvain and Wright 2016; Vigué and Eyre-Walker 2019). More precisely, the more a region is affected by selective sweeps, the lower π_S is and the higher π_N/π_S is compared to the equilibrium expectation: this effect makes the slope steeper compared to the equilibrium expectation.

In the present paper, we first confirmed the observed pattern on the set of 59 species used in Chen et al. (2017). We then used 11 high-quality genomic data sets for which an outgroup was available to test whether the results obtained by Castellano et al. (2018) hold more generally and, in particular, in species with much smaller effective sizes than D. melanogaster, and with different levels of linkage disequilibrium. While we adopted the same general approach as Castellano et al. (2018), our analysis differed from theirs in one important respect. In their study, Castellano et al. (2018) only characterized the DFE of deleterious mutations. Instead, we used a newly developed approach, polyDFE (Tataru et al. 2017), that also considers positive mutations, which is expected to improve the estimation of the shape of the DFE of deleterious mutations, and to disentangle the direct effects of both positive and negative selection.

Materials and Methods

Genomic data and regression of π_N/π_S over π_S

In a first step, we reanalyzed 59 species from Chen et al. (2017), which included 30 animals and 29 plant species. We estimated the DFE using folded site frequency spectra (SFS) with the same method as in Chen et al. (2017) and calculated the slope [regression coefficient of log (π₀/π₄) over log (π₄)] as described in the next paragraph (we used 0-fold degenerated sites for the calculation of genetic diversity at nonsynonymous sites and fourfold degenerated sites for synonymous sites; the same estimates are used in the rest of the paper). For DFE estimation using folded SFS, the model assumes a γ distribution for deleterious mutations and takes demography (or sampling or any departure from equilibrium) into account by introducing n−1 nuisance parameters for an SFS of size n [the corresponding code was provided in Chen et al. (2017)]. In later analyses that required unfolded SFS, we retained 11 species with high-quality genomic data sets and with an available outgroup. These 11 species are given in Table 1. They include both animal and plant species with contrasting levels of nucleotide polymorphism and mating systems. For each of the 11 species, we aligned short reads to the genome using BWA-mem (Li and Durbin 2010) and sorted the alignment using SAMtools. PCR duplicates were removed and insertions/deletions (indels) were realigned using the GATK toolkit (McKenna et al. 2010). HaplotypeCaller was used for individual genotype identification and joint SNP calling was performed across all samples using GenotypeGVCFs. Variant and invariant sites were kept only if genotypes of all individuals were successfully identified (Carson et al. 2014). We collected SNPs in all coding sequence regions, and calculated genetic diversity of fourfold and 0-fold degenerated sites as proxies for polymorphism at synonymous (π_S) and nonsynonymous sites (π_N). Sites were all masked with “N” and excluded from further computation in the following five cases: heterozygous sites in selfing species, sites with more than two variants, variants at sites within 5 bp of a flanking indel, variants sites with GQ < 20, and missing individuals. We applied the same SNP sampling strategy as in James et al. (2017) and Castellano et al. (2018) to remove potential dependency between estimates of π₀/π₄ and π₄. In brief, we first split all synonymous SNPs into three groups (S1, S2, and S3) following a hypergeometric sampling process in R based on the total number of synonymous sites (see equations 3–6 in Castellano et al. 2018). To bin genes and reduce the difference in the number of SNPs in each bin, we ranked genes according to their Watterson’s estimate of nucleotide diversity (θ_S1) and grouped these ranked genes into 20 bins each representing ∼1/20 of the total number of synonymous SNPs. We then used π_S2 to estimate the π₀/π₄ (we summed π over all genes, and scaled by the total length to get π₀ and π₄ for each bin) ratio and π_S3 as an independent estimate of the genetic diversity of each bin.

Table 1. Species and data sets used in the present study.

Species	Reference	Outgroup	Reference	Mating type	AIC	b	βfull	βγ	βmax
A. thaliana	Alonso-Blanco et al. (2016)	A. lyrata	Novikova et al. (2016)	Selfing	231.3, 227.3	0.48	0.32	0.32	0.45
A. lyrata	Novikova et al. (2016)	A. thaliana	Alonso-Blanco et al. (2016)	Outcrossing	247.4, 243.4	0.50	0.35	0.34	0.36
C. rubella	Koenig et al. (2019)	C. grandiflora	Ågren et al. (2014)	Selfing	201.4, 200.3	0.43	0.39	0.26	2.86
C. grandiflora	Ågren et al. (2014)	C. rubella	Koenig et al. (2019)	Outcrossing	321.9, 327.8	0.52	0.30	0.27	0.36
S. habrochaites	Aflitos et al. (2014)	S. lycopersicon	Aflitos et al. (2014)	Selfing	141.5, 148.1	0.21	0.23	0.13	3.61
S. huaylasense	Aflitos et al. (2014)	S. lycopersicon	Aflitos et al. (2014)	Outcrossing	87.1, 121.5	0.54	0.31	0.15	3.89
S. propinquum	Mace et al. (2013)	S. bicolor	Mace et al. (2013)	Selfing	163.8, 159.8	0.37	0.26	0.26	0.34
Z. mays (teosinte)	Chia et al. (2012)	T. dactyloides	Chia et al. (2012)	Outcrossing	208.1, 204.1	0.29	0.19	0.18	0.45
P. trichocarpa	Evans et al. (2014)	P. nigra	Faivre-Rampant et al. (2016)	Outcrossing	318.9, 319.6	0.42	0.22	0.16	2.21
D. melanogaster	Huang et al. (2014)	D. simulans	Stanley and Kulathinal (2016)	Outcrossing	422.7, 535.5	0.70	0.41	0.33	0.51
H. timareta	Martin et al. (2013)	H. melpomene	Martin et al. (2013)	Outcrossing	208.2, 204.2	0.44	0.21	0.21	2.78

Note: AIC values were estimated by polyDFE for models with and without the effects of beneficial mutations, respectively (bold numbers showed significance < 0.05). The same applies to β_full and β_γ as well. β_full and β_γ were the shape parameters for full DFE and γ DFE model, respectively. β_max corresponds to the maximum value of those estimated by polyDFE for each ranked gene bin. AIC, Akaike information criterion; DFE, distribution of fitness effects.

We calculated the slope of the linear regression (l) of the log-transformed value of the π₀/π₄ ratio on the log-transformed value of π₄, using the “lm” function in R (R Core Team 2018). In pilot runs on 59 species [population data of Chen et al. (2017)], the estimates of l showed extensive variation depending on, among other things, the qualities of genome sequencing, read depth, annotation, and SNP calling. Thus, we selected 11 species for which a high-quality genome sequence and an outgroup were available. Individuals were selected from the same genetic background, i.e., admixture or population structure were carefully removed. At least 20 alleles (i.e., 10 individuals for outcrossing species or 20 for selfing species) were retained from a single ancestral cluster defined in admixture/structure analysis in the original publication. For the two Capsella species, we performed admixture analysis for both species separately. A series of quality controls for l calculation were performed as follows. The longest transcript for each gene model was kept only if it contained both start and stop codons (putative full length), and no premature stop codons. SNPs flanking 5 bp of indels were masked to avoid false-positive calls. A grid of filtering criteria (see details in Supplemental Material, Table S2) was also implemented on each species based on sequence similarity against the Swiss-Prot database (e-value, bit-score, and query coverage) and sequencing quality (sites with low read depth or ambiguous variants). We selected the filtering criteria to maximize the adjusted R² in the log–log regression of π₀/π₄ on π₄. By doing so, we aimed to reduce the error introduced by annotation and quality difference between model and nonmodel organisms. Also, to evaluate the variance introduced by random sampling and grouping of SNPs, we performed 1000-iteration bootstraps to get the bootstrap bias-corrected mean and 95% C.I.s for l calculations.

Estimates of the DFE

The DFE for all nonsynonymous mutations across the genome was first calculated by considering only deleterious mutations. We first reused the DFE parameters estimated in 59 animal and plant species in Chen et al. (2017), which assume that only neutral and slightly deleterious mutations contribute to genetic diversity. In brief, in this previous study, the DFE was modeled using a γ distribution with mean S_d and shape parameter β. Folded SFS were compared between synonymous and nonsynonymous sites, and demography (or any departure from equilibrium) was taken into account by introducing n–1 nuisance parameters for an unfolded SFS of size n, following the method proposed by Eyre-Walker et al. (2006). The possible issues and merits of this approach compared to those based on an explicit (albeit very simplified) demographic model have been discussed previously, and the method introduced by Eyre-Walker et al. (2006) has proved to be relatively efficient (Eyre-Walker and Keightley 2007; Tataru et al. 2017). The calculations were carried out using an in-house Mathematica script implementing the method of Eyre-Walker et al. (2006) provided in supplementary file S2 of Chen et al. (2017).

However, for species with large effective population sizes, like D. melanogaster, ignoring the effects of beneficial mutations could distort the DFE to a great extent and lead to a wrong estimate of β. Therefore, we further estimated the DFE under a full model that takes both deleterious and beneficial mutations into account (Tataru et al. 2017) using unfolded SFS for 11 species. Briefly, the model mixes the γ distribution of deleterious mutations (shape = β and mean = S_d) with an exponential distribution of beneficial mutations (mean = S_b), in proportions of (1−p_b) and p_b, respectively. The unfolded SFS was calculated for the 11 retained species, for which a closely related outgroup with similar sequencing quality was available to polarize the SFS. Ancestral state was assigned as the state of the outgroup if the outgroup was monomorphic for one of the two variants, and the derived allele frequency was calculated from this polarization. Otherwise (in the case of missing data, polymorphic site, or third allele in the outgroup) the site was masked. The percentage of SNPs that could not be polarized and were masked varied between 0 and 29.3%, with a mean of 4.6% and a median value of 0.5% (Table S2).

In addition, since polarization errors could remain, the error rate of the ancestral state assignment (ε_an) was also taken into account in polyDFE. The γ DFE (that only considers deleterious mutations) and the full DFE were estimated for each species. In both cases, a nuisance parameter was also fitted to account for possible misassignment errors in SNP ancestral allele estimation (a step required to obtain the unfolded SFS). Note that, although we used outgroups to polarize SFS, we did not use divergence but only polymorphism to estimate the effects of beneficial mutations. This is at the cost of larger variance in estimates but it avoids the (potentially strong) bias due to ancient variations in N_e that cannot be captured by modeling recent changes in population size (Rousselle et al. 2018). When comparing the estimates of the DFE among several species, the problem arises that the best model is not necessarily the same for all species (the best model can include or not beneficial mutations, and include or not polarization errors). Comparisons cannot be fairly done if all species do not share the same model. Alternatively, estimations under an overparameterized model can lead to large variance and extreme values. To circumvent this problem, we used a model-averaging procedure where each parameter of interest (β, S_b, S_d, and p_b) was estimated as a weighted mean of estimates obtained under four models: the γ DFE and the full DFE models, including polarization errors or not. The weight given to the estimate from model k is $w_k=e^{-1/2\Delta \mathrm{AI}{\mathrm{C}}_k}$, where $\mathrm{\Delta }\mathrm{AI}{\mathrm{C}}_m=\mathrm{AI}{\mathrm{C}}_m-\mathrm{AI}{\mathrm{C}}_{\mathit{min}}$, with AIC being the Akaike information criterion and AIC_min the minimum AIC among the four models (Posada and Buckley 2004). All calculations were performed using the software polyDFE and the associated R script (Tataru et al. 2017). A goodness-of-fit test was carried out by comparing observed SFS to expected SFS under γ DFE or the full DFE model for each SNP category, respectively. P-values were calculated under a χ² distribution with the number of d.f. equal to n (total number of SNP categories) – 2 (synonynmous and nonsynonymous sites).

Expectations under different selection models

Independently of possible indirect effects of selective sweeps, Equation 1 only considers deleterious mutations, in line with the initial view of the nearly neutral theory where beneficial mutations negligibly contribute to polymorphism (Ohta 1973). Giving more weight to beneficial mutations slightly modified the relationship between the slope of the linear regression, l, and the shape parameter, β. For beneficial mutations only, the equivalent of Equation 1 is simply (see Appendix):

$$ln\left({\mathrm{\pi }}_{\mathrm{N}}/{\mathrm{\pi }}_{\mathrm{S}}\right)\approx +{\beta }_{b}ln\left(N_e\right)+constant$$ (2)

where β_b is the shape of the distribution of beneficial mutations, still assuming a γ distribution, so β_b would be 1 in the statistical framework we used. Thus, the π₀/π₄ ratio increases with N_e, so that considering beneficial mutations the global π₀/π₄ decreases more slowly than when only deleterious mutations are taken into account. Thus, with beneficial mutations the slope will always be lower than without. For the majority of species beneficial mutations are rare $\left(p_h\ll 1\right)$ and thus b (thereafter we define b = −l) is approximately equal to β. For those with a relatively high proportion of beneficial mutations, direct positive selection should result in a flattened slope, i.e., a smaller value of b than β. As we mostly observed the reverse pattern, b > β, the observed discrepancy cannot be explained by the direct effect of beneficial mutations.

Trends across the genome and tests for selection

For each of the 20 bins defined above and ranked according to their mean synonymous nucleotide diversity, we calculated β, p_b, and S_b values and a summary statistic of the SFS, Tajima’s D (Tajima 1989). Tajima’s D tests for an excess of rare over intermediate variants compared to the frequencies expected under the standard coalescent, and was calculated from synonymous sites. Demography does affect Tajima’s D and can explain the difference among species; however, a negative Tajima’s D is also expected under recurrent selective sweeps (Jensen et al. 2005; Pavlidis and Alachiotis 2017) and should be more negative in genomic regions more strongly affected by linked positive selection. Background selection can also affect Tajima’s D in the same direction but much more weakly (Charlesworth et al. 1995). Independently of the species mean value, we thus expect a strong positive relationship between recombination and Tajima’s D in species where linked positive selection is prominent.

Forward simulations under selective sweep scenario

The code developed by Castellano et al. (2018), which is based on forward simulations using the software SLiM version 3.2.1 (Haller and Messer 2019), was modified to assess the effect of parameters p_b, S_b, and N on b and Tajima’s D. More specifically, a 20-kb genomic region was simulated with a mutation rate of 1 × 10⁻⁶ to study the behavior of b and Tajima’s D under selective sweep scenarios, with varying parameters of p_b, S_b, and N. First, we simulated equal amounts of neutral and deleterious mutations whose fitness effects were drawn from a γ distribution with a shape parameter 0.4 and a mean S_d of −10. Different percentages of beneficial mutations (p_b= 1%, 0.8%, 0.5%, 0.4%, 0.3%, 0.2%, 0.01%, 0.005%, and 0) were drawn randomly from a distribution with a fixed S_b of 1 to simulate loci experiencing selective sweeps at different frequencies, and we then calculated b [figure 5 of Castellano et al. (2018)] and Tajima’s D. We also investigated the behavior of b and Tajima’s D by varying s_b (1, 0.5, and 0.1), N (100, 500, and 1000), and the recombination rate (Nr = 0, 1e-3, and 1e-2). Simulated values were averaged across 50 samples, which were taken every 5N generations after an initial burn-in period of 10N generations.

Data availability

All calculation files can be found in Supplementary file 1. The VCF files are available upon request, and the data sets analyzed are publicly available and are referenced in Chen et al. (2017). Supplemental material available at figshare: https://doi.org/10.25386/genetics.11536971.

Results

b and β are generally similar, but the variance is large

One of the most important predictions of the nearly neutral theory is that the proportion of effectively neutral mutations is a function of the effective population size (Kimura and Ohta 1971; Ohta 1972, 1973, 1992). In species with large effective population size, selection is efficient and the proportion of effectively neutral mutations is small. Here, we used the ratio of genetic diversity at 0-fold over fourfold degenerate sites (π₀/π₄) in protein-coding regions as a measure of the proportion of effectively neutral mutations, and examined the linearity between log (π₀/π₄) and $\log \left({\widehat{N}}_e\right)$ across the genomes of 59 species used in Chen et al. (2017). The slope [linear regression coefficient between log (π₀/π₄) and $\log \left({\widehat{N}}_e\right)$] was negative for 51 of the 59 species (l < 0), although it was significantly different from zero at P = 0.05 in less than one-half of the species (28/59). The value of l varied from −0.424 (D. melanogaster) to 0.22 (Callithrix jacchus) (Table S1). Since balancing selection can lead to both high π₄ and π₀/π₄, it can generate an increase in π₀/π₄ for high-π_S bins. Thus, we removed the five bins with the highest diversity and recalculated l values for all species. This reduced the l values of 36 species and led to negative l values in 55 species.

We further examined the DFE for mutations across the genome in the same data sets. A γ distribution with two parameters, mean (S_d) and shape (β), was used to describe the distribution of deleterious mutations under purifying selection. Importantly, the contribution of beneficial mutations, even those under weak selection that are potentially behaving neutrally, is ignored in this case. Estimates of the shape parameter, β, varied from 0.01 (C. jacchus) to 0.347 (D. melanogaster), but were only weakly correlated with effective population size (Table S1).

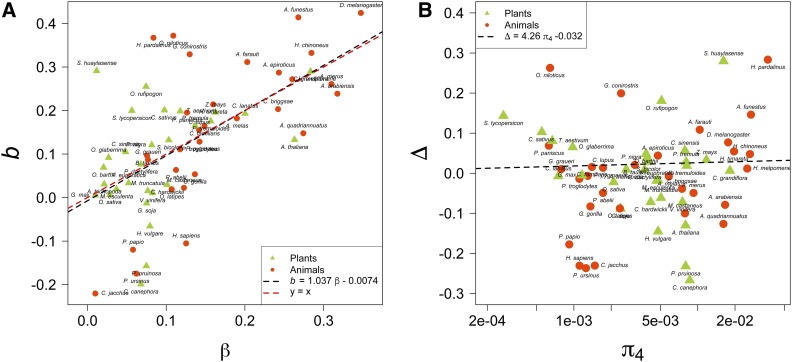
Considering only deleterious mutations and assuming a simple scaling of N_e variation across the genome, the slightly deleterious model predicts that the value of the slope of the linear regression between log (π₀/π₄) and $\log \left({\widehat{N}}_e\right)$, b (recall that b = −l), is equal to β (Welch et al. 2008). The discrepancy between the two might indicate a departure from this model, and Castellano et al. (2018) suggested that in D. melanogaster, where the observed slope was steeper than expected, the departure was caused by linked positive selection across the genome. We observed a general consistency between β and b as estimators of effective neutrality (linear coefficient = 1.04, intercept = 0.007, P-value < 2e-16, and adjusted R² = 0.35; Figure 1A). The difference (Δ = b − β) was small in 40 species and varied from −0.1 to 0.1 (Figure 1B). In 36 species (61%), b values were larger than β and in 23 species (39%) β was larger than b. However, the variation in Δ was not explained by π_S or N_e, as the adjusted R² was only 0.06. Removing the five bins with the highest diversity, the correlation between β and b was still significant (coefficient 0.89 and P-value = 2.14e-6). The median value of Δ increased from 0.0085 to 0.045, but there was still no correlation between Δ and ${\widehat{N}}_e$.

Figure 1.

(A) The correlation between b and the shape parameter of the DFE, β, from the 59 species in Chen et al. (2017). The observed slope of the regression of log (π₀/π₄) over log (π₄), l = −b. (B) The distribution of Δ (= b − β) against genetic diversity at synonymous sites. β values were estimated from DFE models with only deleterious mutations considered (the γ distribution). DFE, distribution of fitness effects.

The effects of quality control and full DFE model

The variation in Δ may come from two sources. First, it can be due to the estimation quality of b and β. Tests have shown that quality control on sequencing and SNP calling can have a dramatic influence on b calculations, and ignoring beneficial mutations in the DFE model could also distort the estimates of β (Tataru et al. 2017). Second, the variation in Δ can be caused by departures from the assumptions underlying the simple version of the nearly neutral theory, for instance, a larger role of direct or linked positive selection than assumed by the theory.

To assess the relative importance of these two sources we selected 11 species with genomic data of high quality and performed a series of stringent quality controls (see details in the Materials and Methods) before reestimating b. This improved the goodness of fit for the log linear regression between π₀/π₄ and π₄ across the genome, and b estimates were significantly different from zero for all 11 species (Figure 2 and Table 1, see also details in Table S2 and Figures S1–S3 for correlation between π₀/π₄ and π₄, and between π₀ and π₄ in linear and log scales). To estimate β, we used closely related species to polarize the SFS, and applied both the γ DFE model and the full DFE model implemented in polyDFE, which considers both deleterious and beneficial mutations. Instead of choosing the best DFE model, an average value weighted by the different models’ AIC scores was calculated for each parameter (Tataru and Bataillon 2019).

Figure 2.

The regression of log (π₀/π₄) over log (π₄) for self-fertilizing A. thaliana (dots) and its outcrossing relative A. lyrata (triangles).

In this case, we observed a better correlation between b and β (Pearson’s correlation ρ = 0.727 and P-value = 0.011) than when we considered the 59 species and used only a γ DFE. In addition, considering beneficial mutations slightly increases β estimates, making them closer to b. However, the linear coefficient between b and β (1.26) is significantly > 1 and the variation of Δ remains large (−0.026 to ∼0.289), suggesting that some additional factors may lie behind the remaining variation.

The roles of effective population size and positive selection

We then tested if the variation in Δ, where Δ = b − β, could simply reflect differences in effective population size (N_e) among species. Estimates of N_e were obtained by rescaling π_S using estimates of the mutation rate (μ) from the literature (see Table S3 for the sources of the μ estimates). When Δ is regressed against $\log \left({\widehat{N}}_e\right)$, $\log \left({\widehat{N}}_e\right)$ explained up to 49% of the variance in Δ (P-value = 0.014). Considering the uncertainty in μ, we also regressed Δ on log (π_S) and obtained similar results (R² = 0.41 and P-value = 0.019; Figure 3).

Figure 3.

The relationship between Δ (= b − β) and effective population size N_e, selective strength S_b, Tajima’s D, and the trend of D across bins ρ_D for 11 selected species. Dotted lines showed the linear regression line. β and S_b values were estimated from full DFE models with both deleterious and beneficial mutations considered (full DFE model with both γ and exponential distributions). DFE, distribution of fitness effects.

Furthermore, we tested whether species with potentially more selective sweeps show higher Δ, as predicted by Castellano et al. (2018). An explicit model of selective sweeps is difficult to fit given the uncertainty about beneficial mutation parameters and would require additional information, especially on the recombination map of the different species. Alternatively, we qualitatively reasoned that, in addition to being more frequent when the effective population is large, the number of selective sweeps should increase with both the proportion (p_b) and the mean strength of beneficial mutations (S_b). Log (S_b) had a significant and positive effect on Δ (P-value = 0.0018; Figure 3) and explained 64.3% of the variance in Δ, but the effect of p_b was not significant (P-value = 0.29). When considered together, the effects of both log (S_b) and log (π₄) (or ${\widehat{N}}_e$) in the joint model explained up to 78% of the variance in Δ (P-value = 0.0068 and 0.059, respectively, Table 2). However, no significant effect of p_b could be detected either in the single regression model (P-value = 0.29) or joint model with other variables (P-value = 0.15). The rate of adaptive evolution relative to the neutral mutation rate ω_a (Galtier 2016) combines the proportion (p_b) and the mean strength of beneficial mutations (S_b) according to ω_a = p_S × S_b / (1 – exp (−S_b)). However, as for p_b, the effect of ω_a on Δ was not significant (P-value = 0.17), although the relationship was positive as expected.

Table 2. Summary table of multiple regression analyses of the effects of π₄, S_b, Tajima’s D, and ρ_D on Δ, the difference between b and β.

Δ∼ π4 + log10(Sb)	Coefficient	SE	t value	P-value
Intercept	0.14	0.031	4.69	0.0016**
π4	7.93	2.96	2.68	0.028*
log10(Sb)	0.015	3.6e-3	4.24	0.0029**
P-value: 0.0008144	Adjusted R2: 0.7888
Δ∼ π4 + D + ρD
Intercept	−0.031	0.035	−0.87	0.41
Tajima’s D	−0.10	0.042	−2.39	0.048*
ρD	0.0015	6.05e-4	2.56	0.038*
π4	15.80	3.39	4.65	0.0040**
P-value: 0.002978	Adjusted R2: 0.708

^***P < 0.001, ** 0.001 < P < 0.01, * 0.01 < P < 0.05.

We also conducted goodness-of-fit tests for both γ DFE and full DFE models by comparing the difference between the observed SFS to that simulated under both DFE models, respectively (Figure S4 and Table S4). For all 11 species, the expected SFS under the full DFE model showed a better or as good fit to the data as the one under the γ DFE model (higher or equal P-values), especially for species like Capsella grandiflora, D. melanogaster, Solanum habrochaites, S. huaylasense, and Populus trichocarpa where either p_b or S_b could not be ignored. Overall, the full DFE model predicted the observed SFS with < 5% error (Figure S4).

Trends across the genome and tests for selection

Variation of DFE parameters across bins could also explain the difference between β and b, since the underlying assumption is that β is constant across bins. Thus, we calculated β for all 20 bins for the 11 species. Seven species had β values increasing weakly with genetic diversity (P-value < 0.05 and mean regression coefficient 0.056), while C. grandiflora and Heliconius timareta had a much faster increase (regression coefficient = 0.2 and 0.15, respectively, Table 3). In five species, the slope was steeper than the maximum β value, similar to what was obtained by Castellano et al. (2018) in Drosophila. However, the slope was shallower than the maximum β value in the six remaining species and in five of them the maximum β value was > 1 (Table 1). We also compared p_b and S_b values across bins. In Arabidopsis thaliana, p_b increased slowly with diversity whereas in C. grandiflora, S. huaylasense, and D. melanogaster p_b decreased significantly (P-value < 0.05). In all 11 species, S_b did not show any significant trend across bins. To more formally test for the significance of these variations, we also divided the genomes into five bins (to get enough power per bin) and tested the invariance of the DFE across bins using likelihood ratio tests as implemented in polyDFE. For all species, a model with independent DFE parameters for each bin is significantly better than a model with shared parameters across bins (see Table S5).

Table 3. Changes of summary statistics and DFE parameters across 20 rank gene groups.

	Tajima’s D		ρβa	ρpba
	Median	ρDa
A. thaliana	−0.38	20.10***	0.033***	9.65e-4**
A. lyrata	−0.60	30.13***	0.057*	7.75e-5
C. rubella	−0.28	15.75*	0.039*	8.26e-4
C. grandiflora	−1.06	23.02**	0.20***	−3.53e-3•
S. habrochaites	0.22	−5.36	0.11	−7.48e-3
S. huaylasense	−0.17	−8.59**	−0.32	−5.54e-2***
S. propinquum	−0.10	60.04***	0.075***	1.82e-3
Z. mays	−0.52	−0.39	0.055***	2.39e-3
P. trichocarpa	−0.43	79.20***	0.079	−2.80e-3
D. melanogaster	−0.73	7.41 **	0.078***	−3.81e-3***
H. timareta	−0.10	6.58**	0.15***	9.87e-4

^***P < 0.001, ** 0.001 < P < 0.01, * 0.01 < P < 0.05, ^• 0.05 < P < 0.1.

^aρ is the slope of the regression of D (β and p_b, respectively) over genetic diversity across ranked groups of genes.

For all 11 selected species, we also calculated Tajima’s D (Tajima 1989), thereafter simply called D, in each bin to test for departure from neutrality across the genome. Mean values of D were slightly negative across bins for most species except S. habrochaites. For 9 of the 11 species, D values increased significantly with genetic diversity (Table 3). Interestingly, we found a negative and strong correlation of Tajima’s D with log (S_b) for all 11 species (Pearson’s correlation ρ = −0.74 and P-value = 0.0086) but not with any other DFE parameters. This is in agreement with the expectation that selective sweeps decrease D. Background selection could also decrease D, albeit to a lower extent. We further tested the trends of positive and negative selection by calculating the proportions of deleterious, or beneficial, mutations over all bins with selective strength <−10 and >10, respectively. However, no significant trends were identified for either type of direct selection.

We also tested whether alternative measures of the possible occurrence of selective sweeps could explain a larger part of the variation in Δ. We used both the mean Tajima’s D and the among-genome regression coefficient of the relationship between D and π_S (ρ_D) as predictors. More negative D and a stronger positive regression coefficient between D and π_S can be viewed as signatures of stronger hitchhiking effects. So, we would expect to see a negative effect of D and a positive effect of ρ_D on the variation in Δ. In combination with π₄ (or ${\widehat{N}}_e$), both D and ρ_D indeed explained a significant part of the variation in Δ (adjusted R² = 0.76, Table 2).

Simulations

Castellano et al. (2018) used forward simulations to assess the extent to which selective sweeps made the slope between log (π₀/π₄) and $\log \left({\widehat{N}}_e\right)$ steeper, and thereby could explain the discrepancy between the slope and the shape parameter of the DFE, β. They tested varying proportions of adaptive mutations (their figure 5). We extended their investigation to test the effect of selective strength (s_b) on b with a fixed β (0.4) and how selective strength (s_b) also affected estimates of Tajima’s D. Without recombination (Nr = 0), Figure 4 shows that when s_b increased from 0.1 to 1, b increased from 0.46 to 0.72 (Δ = 0.06–0.32). As expected, mean Tajima’s D decreased from −0.36 to −0.77 as s_b increased, and ρ_D between D and π₄ increased (see also Table 4). We also increased N from 100 to 500, and to 1000, and fixed the mean selective strength at either S_b = 10 or S_d = −1000. With these parameters, the strength of selection was not affected by N, but the number of sweeps increased with N due to the higher input of (beneficial) mutations. In this case, Δ increased from 0.06 to 0.41 as N increased and Tajima’s D again decreased (Figure 5 and Table 4). With recombination (Nr = 1e-3 and Nr = 1e-2), we noticed similar trends of b, D, and ρ_D when s_b or N are large enough to recover the significance of the linearity between log (π₀/π₄) and log (π₄) (Figure S5 and S6).

Figure 4.

Effect of linked positive selection on the relationship between log (π₀/π₄) and log (N_e) and Tajima’s D. Upper row: the linear regression coefficient (b) between log (π₀/π₄) and log (N_e) increases with increasing positive selective strength (from left to right). The red lines are the regression lines for each case. To facilitate comparisons among figures and illustrate how the slope gets steeper as s_b increases, the regression lines corresponding to s_b = 0.1 and/or s_b = 0.5 values are reported with gray lines. Lower row: the red lines for Tajima’s D panels indicate the mean values.

Table 4. Results of forward simulations showing the effect of linked positive selection on b, Δ, and summary statistics of the site frequency spectrum for different values of the mean selective value of beneficial mutations S_b and the population size N.

	N	Sb	Sd	β	b	Δ	π4	π0/ π4	ρD	D
Nr = 0	100	20	1000	0.4	0.49	0.09	1.39	0.091	874.6	−0.46
	100	50	1000	0.4	0.61	0.21	1.18	0.094	909.9	−0.70
	100	100	1000	0.4	0.72	0.32	1.06	0.111	994.2	−0.77
	100	10	1000	0.4	0.46	0.06	1.52	0.082	739.9	−0.36
	500	10	1000	0.4	0.65	0.25	5.72	0.09	228.6	−0.77
	1000	10	1000	0.4	0.81	0.41	10.35	0.094	132.4	−0.92
Nr = 1e-3	100	20	1000	0.4	0.06	−0.34	1.64	0.076	662.5	−0.18
	100	50	1000	0.4	0.63	0.23	1.48	0.087	738.1	−0.28
	100	100	1000	0.4	0.72	0.32	1.17	0.097	966.8	−0.58
	100	10	1000	0.4	0.09	0.03	1.70	0.075	1011.1	−0.12
	500	10	1000	0.4	0.61	0.21	7.54	0.084	163.9	−0.26
	1000	10	1000	0.4	0.68	0.28	13.67	0.083	99.7	−0.37
Nr = 1e-2	100	20	1000	0.4	0.43	0.03	1.74	0.077	739.3	−0.04
	100	50	1000	0.4	0.63	0.23	1.67	0.081	917.6	−0.12
	100	100	1000	0.4	0.78	0.38	1.61	0.084	898.4	−0.15
	100	10	1000	0.4	0.33	−0.07	1.76	0.080	325.7	−0.01
	500	10	1000	0.4	0.69	0.29	8.55	0.073	165.4	−0.06
	1000	10	1000	0.4	0.99	0.59	16.7	0.072	86.3	−0.12

ρ_D is the correlation between π_S and Tajima’s D.

Figure 5.

The correlation between Tajima’s D and π₄ depending on S_b (left panel) and N (middle panel); correlation between Δ and Tajima’s D (right panel). In all three cases, the results were obtained with forward simulations in Slim assuming no recombination.

Discussion

The aim of the present study was to test quantitatively one of the predictions of the nearly neutral theory of molecular evolution or, more precisely, the slightly deleterious model. More specifically, we used full-genome data sets to test whether the proportion of effectively neutral mutations varies with local variation in N_e across the genome and decreases linearly with increasing N_e, and whether the slope is equal to the shape parameter of the DFE. The negative log linear relationship between π₀/π₄ and N_e observed in previous studies (Gossmann et al. 2011; Murray et al. 2017; Castellano et al. 2018; Vigué and Eyre-Walker 2019) was also observed in the present study, although the slope was not always significantly negative and, when negative, could differ significantly from the shape parameter of the DFE and be much steeper. The latter was especially true in species with large effective population size and the difference was correlated to the estimated mean strength of selection acting on beneficial mutations. In the case of species with large effective population size, neglecting linked positive selection could therefore lead to a significant quantitative discrepancy between predictions and observations. On the other hand, the slightly deleterious model appears to be a good approximation when the effective population size is small. Below, we first consider possible caveats and discuss the implications of the results for the relative importance of purifying and adaptive selection in shaping the genetic diversity of species.

The discrepancy between the slope of the log linear relationship between π_N/π_S and N_e and β could simply be due to difficulties in estimating them precisely. In general, estimates of the DFE shape parameter, β, were rather stable compared to estimates of the slope of the regression of log (π₀/π₄) over log (π₄), b, with the variance of the former being one-half that of the latter independently of quality control, and whether the SFS was folded or unfolded. High variation in b estimates may explain the fact that a significant correlation between π₀/π₄ and π₄ could not be observed for all species, particularly those with low genetic diversity (e.g., great apes). Therefore, stringent quality control for read alignment and SNP calling is necessary, even for D. melanogaster, where an improvement of the fit in l calculation (linear regression adjusted R² = 0.79 to 0.95) leads to a dramatic change in the estimate of Δ (from 0.077 to 0.29). Even if stringent quality control had been implemented, the goodness of fit for the log linear regression leading to the estimation of b would differ significantly from species to species. The fit across the D. melanogaster and A. thaliana genomes was almost perfect (R² > 0.95) while, at the other extreme, the fit was rather poor in S. habrochaites (R² = 0.38). However, even among species for which the fit is almost perfect (R² > 0.95), b could vary rather dramatically: D. melanogaster had a much larger l (0.7) than A. thaliana (0.48), C. rubella (0.43), and Zea mays (teosinte, 0.29), whereas β only changed marginally for these species. However, not all species showed a significant negative linear relationship between π₀/π₄ and _{${\widehat{N}}_e$}, and some even had positive slopes, especially for those of low diversity (e.g., great apes; Figure 2). Therefore, besides purifying selection, the slope is also likely to be affected by additional factors. Factors that affect the likelihood of observing a negative relationship between π₀/π₄ and ${\widehat{N}}_e$, and its relationship with the DFE parameters, were thoroughly discussed by Castellano et al. (2018). Below, we highlight those that seem particularly relevant when considering a group of species with contrasting levels of diversity, as was done here. These factors are the variation in N_e estimates along the genome, which itself reflects the joint distribution along the genome of recombination rate and density of selected sites, the DFE, and the variation along the genome of the rate of adaptive evolution (Castellano et al. 2018).

Lack of joint variation in recombination rate and selected sites seems to be an unlikely cause of an absence of a negative relationship between π₀/π₄ and N_e, as such a relationship is observed in selfing species where this joint variation is expected to be more limited than in outcrossing ones. A possible source of variance in β could be that the single-sided γ distribution does not describe well the real DFE curves, at least not for all species, particularly when the DFE is not unimodal (Tataru et al. 2017). For species like D. melanogaster, for instance, there is mounting evidence of adaptive evolution [reviewed in Eyre-Walker (2006) and Sella et al. (2009)]. Therefore, it is necessary to consider the possible contribution of beneficial mutations. The full DFE model provided a much better fit than the γ DFE that considers only deleterious mutations in D. melanogaster (log likelihood = −187.3 vs. −245.7, respectively). This was also true of some of the outcrossing plants like C. grandiflora and S. huaylasense. In all three species, β estimates increased when estimated with the full DFE instead of the γ DFE, sometimes significantly [from 0.33 to 0.41 in D. melanogaster (Rwanda) and 0.15 to 0.31 in S. huaylasense] and at other times only marginally (0.27 to 0.30 in C. grandiflora). Taking beneficial mutations into account when fitting the shape of the DFE can partly reduce the discrepancy between β estimates and the slope of the regression. However, it is not sufficient, as Δ was positive in 10 of the 11 focal species we studied.

Based on the prediction of the nearly neutral theory with direct positive selection (Equation 2), the proportion of beneficial mutations is the only factor that could alter the relationship between b and β, and should always result in a larger β compared to b. However, this is usually not the case as, on the contrary, values of b larger than β have generally been reported (Chen et al. 2017; James et al. 2017; Castellano et al. 2018). In this paper, we systematically investigated this relationship across the genomes of multiple species. Two-thirds of the 59 species, and 10 out of the subset of 11 species that were selected for the high quality of their genome, had larger b than β values. Hence, direct positive selection is not the main cause of the discrepancy.

Investigation of DFE parameter changes across bins may help to identify changes in natural selection. Increasing β values over bins could be a signal for stronger positive selection in low-diversity regions. Although the maximum β value of some species can be larger than b, β grows slowly for most species and shows hardly any pattern between species. Neither did p_b or S_b. This lack of significant trend in these parameters could simply be due to an increase in variance of their estimates, as only one-twentieth of the total number of polymorphic sites were used for DFE calculations in each bin. It could also again suggest that direct selection is not the main cause of the discrepancy.

One of the main findings of the present study is that a large proportion of variance in the discrepancy can be explained by the estimated strength of positive selection, which can be regarded as an indication for linked selection, such as selective sweeps or, more generally, hitchhiking effects. To test for that, we compared changes in Tajima’s D and its among-genome correlation coefficients over bins. As expected we observed a negative effect of D and a positive effect of ρ_D on Δ, both suggesting the presence of linked selection, with lower diversity at nearby sites and thus increased discrepancy between b and β. This is also in agreement with our simulations and those of Castellano et al. (2018), which illustrate that hitchhiking effects can lower the genetic diversity at nearby neutral or nearly neutral positions. These results can be understood because selective sweep effects cannot simply be captured by a rescaling of N_e. Selective sweeps not only reduce genetic diversity at linked sites but also distort the coalescent genealogy (Fay and Wu 2000; Walsh and Lynch 2018; Campos Parada and Charlesworth 2019), so that we cannot define a single N_e in this context (Weissman and Barton 2012). In particular, the scaling is not expected to be the same for neutral or weakly selected polymorphisms. However, as far as we know, there is no quantitative model predicting the value of the slope as a function of DFE, rates of sweep, and recombination rates, and such models still need to be developed.

Conclusions

There are three major conclusions to the present study. First, the nearly neutral theory in its initial form may not explain all aspects of polymorphisms but, almost 50 years after it was first proposed by Tomoko Ohta (Ohta 1973), it still constitutes an excellent starting point for further theoretical developments (Galtier 2016; Walsh and Lynch 2018). Second, considering linked beneficial selection indeed helps to explain polymorphism data more fully, and this is especially true for species with high genetic diversity. This can explain both patterns of synonymous polymorphism (Corbett-Detig et al. 2015) and how selection reduces nonsynonymous polymorphism [Castellano et al. (2018) and this study]. One could have a progressive increase of the effect of selective sweeps as suggested by Walsh and Lynch (2018, chapter 8) with a shift from genetic drift to genetic draft (Gillespie 1999; 2000; 2001). If so, we could have three domains. For small population sizes, drift would dominate and the nearly neutral theory in its initial form would apply. For intermediate population sizes, beneficial mutations would start to play a more important part, and finally for large population sizes, the effect of selective sweeps would dominate and draft would be the main explanation of the observed pattern of diversity. Third, our study once more emphasizes the central importance of the DFE in evolutionary genomics and we will likely see further developments in this area.

Appendix

In a constant population with population size N_e, π_S = 4N_eµ and π_N is given by (Sawyer and Hartl 1992):

$${\pi }_N=2N_e\mu {\displaystyle {\int }_0^{1}2x\left(1-x\right)H\left(S,x\right)dx}$$ (A1)

where

$$H\left(S,x\right)=\frac{1-e^{-S\left(1-x\right)}}{x\left(1-x\right)\left(1-e^{-S}\right)}$$ (A2)

is the mean time a new semidominant mutation of scaled selection coefficient S = 4N_es spends between x and x + dx (Wright 1938). For constant selection S, by integrating (A1) and dividing by 4N_eµ, we have:

$$\frac{{\pi }_N}{{\pi }_S}=f\left(S\right)=\frac{2}{1-e^{-S}}-\frac{2}{S}$$ (A3)

(A3) is valid for both positive and negative fitness effect. If we consider only beneficial mutations with a γ distribution of effects, with mean S_b and shape β_b: $\phi \left(S_b,\beta ,S\right)=e^{-\frac{S{\beta }_b}{S_b}}{S}^{\beta -1}{\left(\frac{{\beta }_b}{S_b}\right)}^{{\beta }_b}/\mathrm{\Gamma }\left({\beta }_b\right)$, we can use the same approach as Welch et al. (2008) to show that:

$$\frac{{\pi }_N}{{\pi }_S}={\displaystyle \underset{0}{\overset{\mathrm{\infty }}{\int }}f\left(S\right)\phi \left(S_b,{\beta }_b,S\right)dS}=\frac{1}{{\beta }_b-1}{\left(\frac{{\beta }_b}{S_b}\right)}^{{\beta }_b}\left(\xi \left({\beta }_b-1,\frac{{\beta }_b}{S_b}+1\right)+\left({\beta }_b-1\right)\xi \left({\beta }_b,\frac{{\beta }_b}{S_b}\right)-\xi \left({\beta }_b-1,\frac{{\beta }_b}{S_b}\right)\right)$$ (A4)

where $\xi \left(x,y\right)$ is the Hurwith ζ function. (A4) can be approximated under the realistic assumption that $\frac{{\beta }_b}{S_b}\ll 1$ and taking Taylor expansion of (A4) in $\frac{{\beta }_b}{S_b}$ around 0. We thus obtain:

$$\frac{{\pi }_N}{{\pi }_S}\approx {\left(2\pi \right)}^{{\beta }_b}{\left(\frac{S_b}{{\beta }_b}\right)}^{{\beta }_b}$$ (A5)

which leads to Equation 2 in the main text.