A Computational Pipeline to Predict Cardiotoxicity: From the Atom to the Rhythm

Abstract

Rationale

Drug-induced proarrhythmia is so tightly associated with prolongation of the QT interval that QT prolongation is an accepted surrogate marker for arrhythmia. But QT interval is too sensitive a marker and not selective, resulting in many useful drugs eliminated in drug discovery.

Objective

To predict the impact of a drug from the drug chemistry on the cardiac rhythm.

Methods and Results

In a new linkage, we connected atomistic scale information to protein, cell and tissue scales by predicting drug binding affinities and rates from simulation of ion channel and drug structure interactions and then used these values to model drug effects on the hERG channel. Model components were integrated into predictive models at the cell and tissue scales to expose fundamental arrhythmia vulnerability mechanisms and complex interactions underlying emergent behaviors. Human clinical data were used for model framework validation and showed excellent agreement, demonstrating feasibility of a new approach for cardiotoxicity prediction.

Conclusions

We present a multiscale model framework to predict electro-toxicity in the heart from the atom to the rhythm. Novel mechanistic insights emerged at all scales of the system, from the specific nature of proarrhythmic drug interaction with the hERG channel, to the fundamental cellular and tissue level arrhythmia mechanisms. Applications of machine learning indicate necessary and sufficient parameters that predict arrhythmia vulnerability. We expect that the model framework may be expanded to make an impact in drug discovery, drug safety screening for a variety of compounds and targets, and in a variety of regulatory processes.

Graphical Abstract

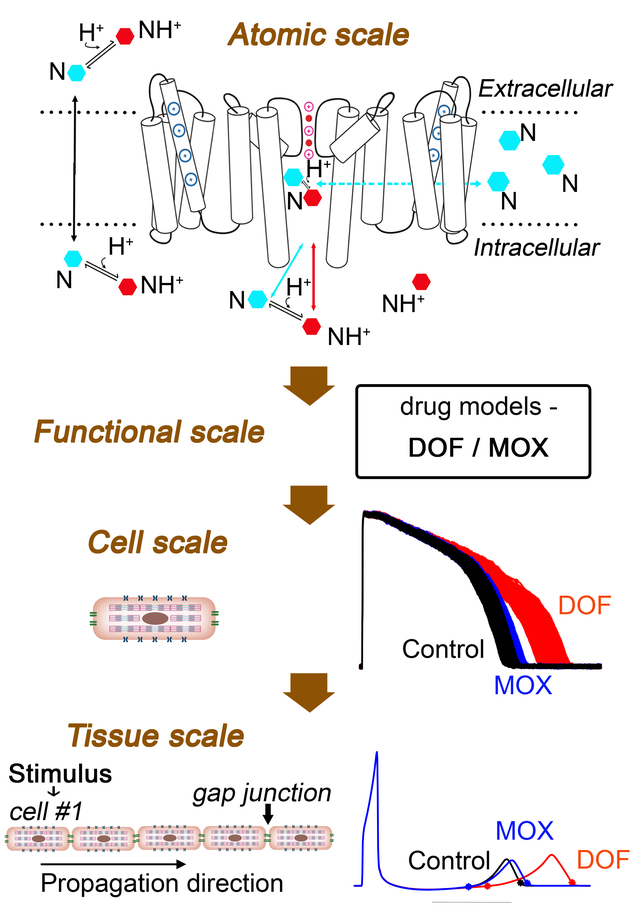
INTRODUCTION

Cardiotoxicity is one of the most common reasons for drug removal from the market, typically manifesting as prolongation of the QT interval on the ECG and potential for fatal ventricular arrhythmias.¹ In the context of drug induced cardiac arrhythmia, the vital hindrance to prevention of electrical rhythm disturbances is a lack of meaningful approaches to distinguish between therapeutic, benign or harmful actions of drugs. An important example is the use of QT interval prolongation as a surrogate marker for proarrhythmia.^2,3,4

Abnormal cardiac electrical activity is most often a side effect from unintended block of the promiscuous drug target hERG, the delayed rectifier K⁺ channel in the heart. hERG block results in prolongation of the QT interval on the ECG, a phase of the cardiac cycle that corresponds to ventricular repolarization. Numerous drugs interact with the promiscuous target hERG, and even seemingly innocuous agents such as grapefruit juice have been shown to prolong QT interval.⁵ In the nearly 25 years since publication of the Survival With Oral d-sotalol (SWORD) trial showed that common antiarrhythmics increased mortality and risk of sudden cardiac death, no failsafe method has emerged to distinguish unsafe hERG blockers from safer drugs.^6–9

There are at least two distinct classes of hERG blockers that prolong QT interval: Drugs that block hERG, prolong QT interval and increase proclivity to potentially deadly torsades de pointes (TdP) arrhythmias. This group includes, for instance, sotalol, dofetilide, ^{10, 11} and cisapride.¹² The second group consists of hERG blockers that prolong QT interval and have lower risk (in the absence of co-morbidities) for ventricular arrhythmias like moxifloxacin, ranolazine, and verapamil. ^13–20 Importantly, FDA guidance does consider drug effects on the QT within a broader context of drug efficacy and utility for non-antiarrhythmic drugs.

The Comprehensive in Vitro Proarrhythmia Assay (CiPA) initiative comprising a team of regulators, academicians and industry scientists proposed a collection of nonclinical assays to move beyond the thorough-QT study and better predict preclinical arrhythmia risk.²¹ This program promotes screening of additional cardiac ion channel targets and assessing net impact on the cellular action potential duration and QT interval via in vitro experiments and in silico functional models. While the consideration of multi-channel block is an improvement, even these newer computational models still generally rely on prolongation of the action potential duration or QT interval as the marker for safety.^22–26 Moreover, there is no mechanistic validation of the accuracy of the model prediction, so a test drug may land in the right category, but for the wrong reason. The in silico CiPA assay cannot distinguish between chemically similar drugs with similar affinity profiles. Moreover, incorporating individual genetic differences into the current model schema is not yet possible.

Although multichannel block is generally safer than hERG block alone, there are a variety of drugs that selectively target hERG and have been shown, in the absence of co-morbidities,^{27, 28} to have lower arrhythmia risk than other hERG blockers. Lower risk hERG blockers include moxifloxacin and the selective-serotonin reuptake inhibitor CONA-437.^{19, 20, 27, 29, 30} To be clear, while numerous studies have indicated a strong safety profile at clinically relevant serum concentrations in healthy individuals^{18, 19}, it has been demonstrated that in the presence of other QT prolonging risk factors, moxifloxacin has been indicated in torsades. ^30–34 Moreover, some recent large scale population studies indicate increased risk, however, they uniformly acknowledge the failure to control for co-existent or concomitant risk factors. ^28,34 In this study, we focus on healthy human tissue, but future studies are planned to include disease states.

We hypothesized that channel conformational state specificity and the associated kinetics of hERG block may promote TdP as indicated by the TRIaD: Triangulation, reverse use dependence, beat-to-beat instability of action potential duration, temporal and spatial action potential duration dispersion.^{10, 35, 36} Here, we use an integrative experimental and computational modeling and machine learning approach that spans scales from the atom to the cardiac rhythm. We predict intrinsic properties of the structure-activity relationship that determine proarrhythmia for the prototype drugs dofetilide and moxifloxacin, hERG blockers with different safety profiles: Dofetilide is a potent hERG blocker, prolongs QT interval and has a high risk for TdP arrhythmias.^{37, 38} Moxifloxacin, on the other hand, is a safer drug in healthy individuals^{19, 27, 30} (but has increased risk with concomitant comorbidities^{27, 28}). Thus, these two drugs chosen as an ideal candidate for our proof-of-the-concept study.

In this study, we take the first necessary steps to answer the question, “Can we predict hERG blocker proarrhythmic risk from the drug chemistry?” We present a novel multiscale approach based on structural and dynamic atomistic models of drug-channel interactions and kinetics intended to predict drug-induced arrhythmia. The method can be also used to distinguish between chemically similar drugs that may appear to have similar effects on the action potential and QT interval, but differ in proarrhythmic risk.

METHODS

The data that support the findings of this study are available from the corresponding author upon reasonable request. Model codes have been made publicly available at Github. Please see the Major Resource Table in the Supplemental Materials.

A detailed description of Materials and Methods is available in the Online Supplemental Materials.

RESULTS

The first step towards predictive cardiac safety pharmacology was development of models of dofetilide and moxifloxacin. Both drugs have weakly basic or acidic functional groups and exist in different ionization states at physiological pH, with correspondingly different polarities, lipophilicities, and lipid membrane permeabilities. For this study, we developed and validated structural models for dofetilide (pK_a 7.0)³⁹ in neutral and cationic ionization states (Figure 1A), and moxifloxacin (pK_a1 6.25, pK_a2 9.29),⁴⁰ in neutral, cationic, and zwitterionic states (Figure 1E), compatible with biomolecular all-atom CHARMM force fields as described in Supplemental Materials.

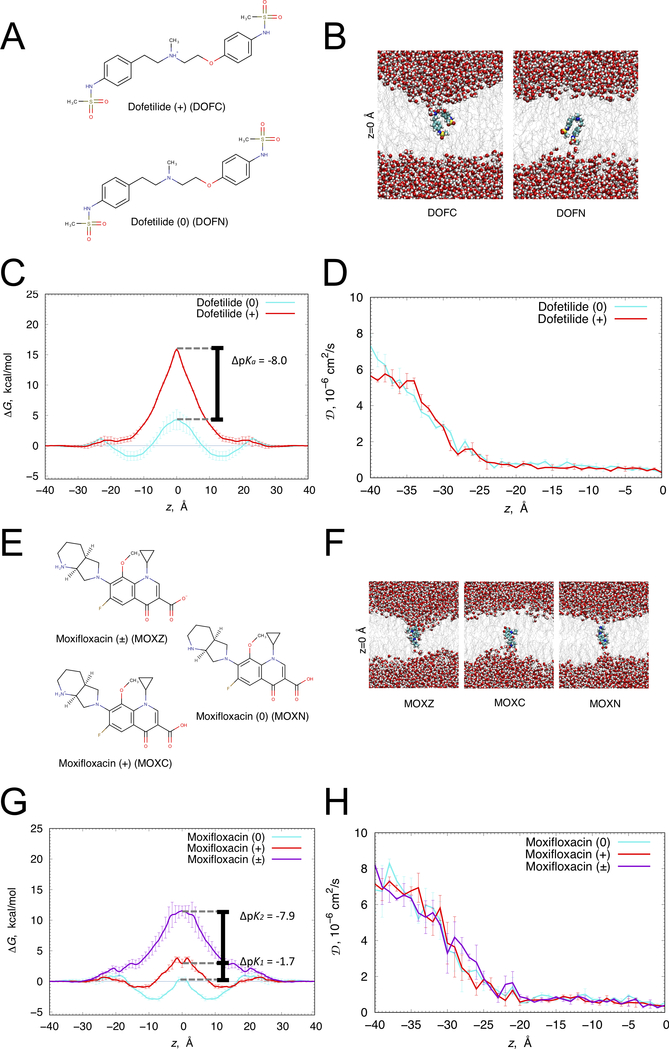
Figure 1. Translocation of dofetilide and moxifloxacin across a hydrated lipid membrane.

(A) Chemical structures of cationic (top) and neutral (bottom) dofetilide. (B) Representative snapshots of dofetilide at the center of POPC bilayer (z = 0) from umbrella sampling molecular dynamics simulations. Dofetilide and water molecule are in space-filling representation (C – cyan, O – red, N – blue, S – yellow, H – white), lipid tails are shown as gray sticks. (C) Free energy (ΔG) and (D) diffusion coefficient (D) profiles of neutral (cyan) and cationic (red) dofetilide crossing POPC membrane. (E) Zwitterionic (top), neutral (right) and cationic (bottom) moxifloxacin chemical structures. (F) Representative snapshots of moxifloxacin at the center of DMPC bilayer (z = 0) from umbrella sampling molecular dynamics simulations. Moxifloxacin and water molecule are in space-filling representation (F – pink, C – cyan, O – red, N – blue, H – white), lipid tails are shown as gray sticks. (G) ΔG and (H) D profiles of zwitterionic (purple), neutral (cyan) and cationic (red) moxifloxacin crossing DMPC membrane. Error bars represent standard errors of mean computed based on profile asymmetries with respect to z = 0.

We validated drug models by performing all-atom umbrella sampling molecular dynamics simulations across a hydrated 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipid bilayer for dofetilide and a 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) lipid bilayer for moxifloxacin, from which we computed one-dimensional free energy profiles, ΔG(z). There are substantial membrane perturbations as cationic dofetilide (Figure 1B) and zwitterionic moxifloxacin (Figure 1F) move towards the membrane center, and correspondingly energetic barriers for their membrane crossing are high (ΔG=15.8±0.1 and ΔG=11.5±0.8 kcal/mol, see Figs. 1C and 1G, respectively). The energetic barriers were substantially lower for neutral dofetilide (ΔG=6.0±1.8 kcal/mol), cationic (ΔG=4.8±0.7 kcal/mol) and neutral (ΔG=3.2±0.3 kcal/mol) moxifloxacin, resulting in the shifts towards those drug ionization states in the membrane center, as shown in Figs. 1C and 1G. This along with their interfacial ΔG troughs suggests their membrane interface accumulation and higher rates of crossing compared to other ionization states.

To estimate membrane lipophilicities and crossing rates, we also computed one-dimensional diffusion coefficient profiles, D(z), across membranes for each drug ionization state, indicating bulk water values (D_W) between ~6 ×10⁻⁶ and ~8 ×10⁻⁶ cm²/s, that attenuate to D_M <0.5 ×10⁻⁶ cm²/s at the membrane center (Figs. 1D and H), consistent with our previous studies.^41–43 We computed the water-membrane distribution coefficients for dofetilide (logD = 0.32±0.15) and moxifloxacin (logD = 0.13±0.11), and estimated the membrane translocation rate of neutral dofetilide as 8.0 ± 1.4 ms⁻¹, and neutral moxifloxacin as 1100 ± 580 ms⁻¹, and cationic moxifloxacin as 43 ± 29 ms⁻¹ using Kramer’s rate equation.⁴² (see Supplemental Materials). For the cationic form of dofetilide and zwitterionic form of moxifloxacin, membrane crossing rates are expected to be several orders of magnitude smaller, and thus not contribute to membrane translocation within the simulated timescales.

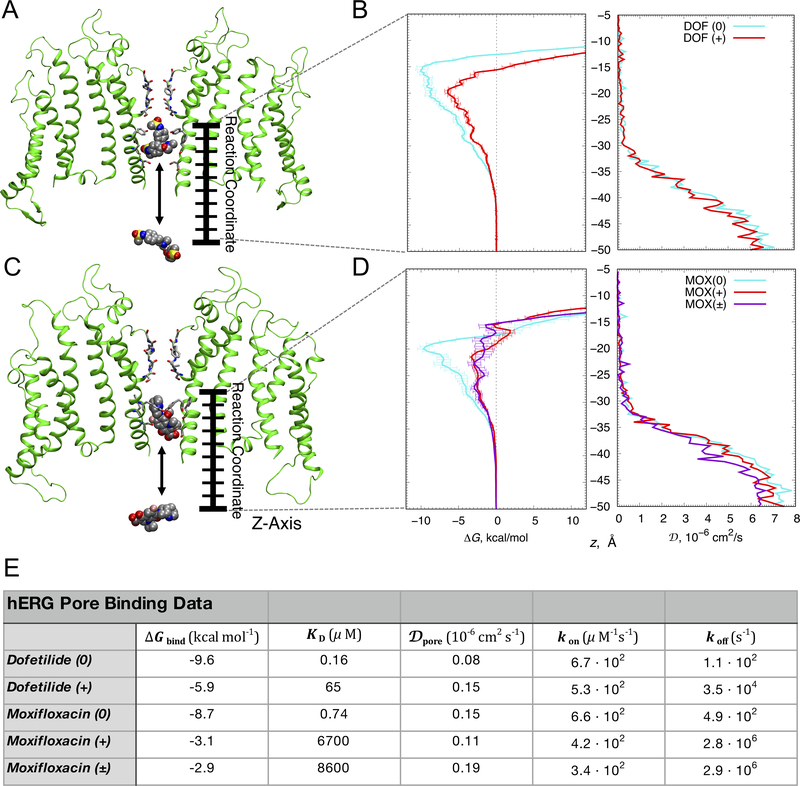
In atomic scale simulations of drug interactions with the hERG open channel model (Figure 2A, 2C), we performed all-atom umbrella sampling simulations to compute one-dimensional free energy, ΔG, and diffusion coefficient, D, profiles (shown in Figure 2B and 2D). From these simulations we computed drug binding free energies (ΔG_bind) and dissociation constants (K_D) for multiple drug ionization states to the open hERG channel. The results reveal stronger binding of neutral dofetilide (Figure 2B), and neutral moxifloxacin (Figure 2D) in the channel pore compared to cationic or zwitterionic counterparts (see ΔG_bind in Figure 2E), and over an order of magnitude decrease in diffusion rates in the confined pore environment, for both drugs in each ionization state (Figure 2B and 2D, right). Accounting for relative fractions of cationic (38%) and neutral (62%) dofetilide forms at pH 7.2, using its pK_a value of 7.0³⁹, the overall K_D is estimated to be ~0.26 μM, which agrees favorably with IC₅₀ values (3.5 μM, 10 μM, 11 μM) from electrophysiology experiments involving non-inactivating mutants of the channel or pulsing conditions disfavoring inactivated state^44–46. Taking into account the dominant forms of moxifloxacin having relative fractions of cationic (10.33%), zwitterionic (83.99%) and neutral (5.68%) forms at pH 7.2.⁴⁰ the overall composite K_D is estimated to be ~13 μM, in agreement with available IC₅₀ and K_D data (29 μM,²⁰ 64.5±10.3 μM,⁴⁷ 129 μM⁴⁸) suggesting that moxifloxacin associates more selectively but less favorably to the open state than dofetilide²⁰. We observed no free energy barriers for drug binding from bulk aqueous solution, suggesting that drug-channel “on” rates k_on will be diffusion limited. We also computed the z-dependent diffusion profiles into the hERG pore for multiple drug forms (Figure 2B and 2D, right). Diffusion coefficients in the intracellular bulk aqueous solution, D_W, were between ~6 ×10⁻⁶ cm²/s and ~8 ×10⁻⁶ cm²/s and attenuated to D_pore < 0.2 ×10⁻⁶ cm²/s for both drugs near their binding sites. Comparing the diffusion coefficient profiles for drugs in the channel pore and membrane interior (see Figure 1D, 1H), diffusion there is an order of magnitude or more slower compared to bulk aqueous solution, due to a more viscous (membrane interior: 20-fold reduction) or constricted space (pore: 40-fold reduction). We computed k_on rates from free energy (ΔG) and diffusion coefficient (D) profiles using the Debye-Smoluchowski equation^{49, 50} (see Supplemental Materials), and they are similar for both drugs in each ionization state (see Figure 2E). Corresponding dissociation rates, k_off, computed as k_on · K_D, are larger for cationic dofetilide and moxifloxacin, and zwitterionic moxifloxacin due to their weaker channel binding affinities (Figure 2E).

Figure 2. Open state hERG block by dofetilide and moxifloxacin.

(A, C) The representative open state hERG structures (two opposite chains shown as green ribbons) used to compute binding free energy (ΔG) and diffusion coefficient (D) profiles for dofetilide (panel A) and moxifloxacin (panel C). Drug molecules inside the hERG ßpore (top) and in bulk solvent (bottom) are in space-filling representation (C – gray, O – red, N – blue, S – yellow, F – pink, H – white), (B, D) ΔG (left) and D (right) profiles for dofetilide (panel B) and moxifloxacin (panel D) interactions, showing dominant binding wells of –10.1 kcal/mol and –6.6 kcal/mol at z = –15.5 Å and z = –20 Å for neutral (cyan) and cationic (red) dofetilide and –9.7 kcal/mol, –3.3 kcal/mol, and –2.9 kcal/mol at z = −20 Å, z = −21.5 Å and z = −22.5 Å, for neutral (cyan), cationic (red) and zwitterionic (purple) moxifloxacin. Error bars for ΔG profiles represent standard errors of mean computed from block averages. D values in the hERG pore (D_pore) of both dofetilide and moxifloxacin were comparable irrespective of drug ionization state as shown in panels B and D, right. (E) Drug binding affinities (ΔG_bind and K_D), diffusion coefficients (D_pore) and drug “on” (k_on) and “off” (k_off) rates computed from the umbrella sampling molecular dynamics simulations.

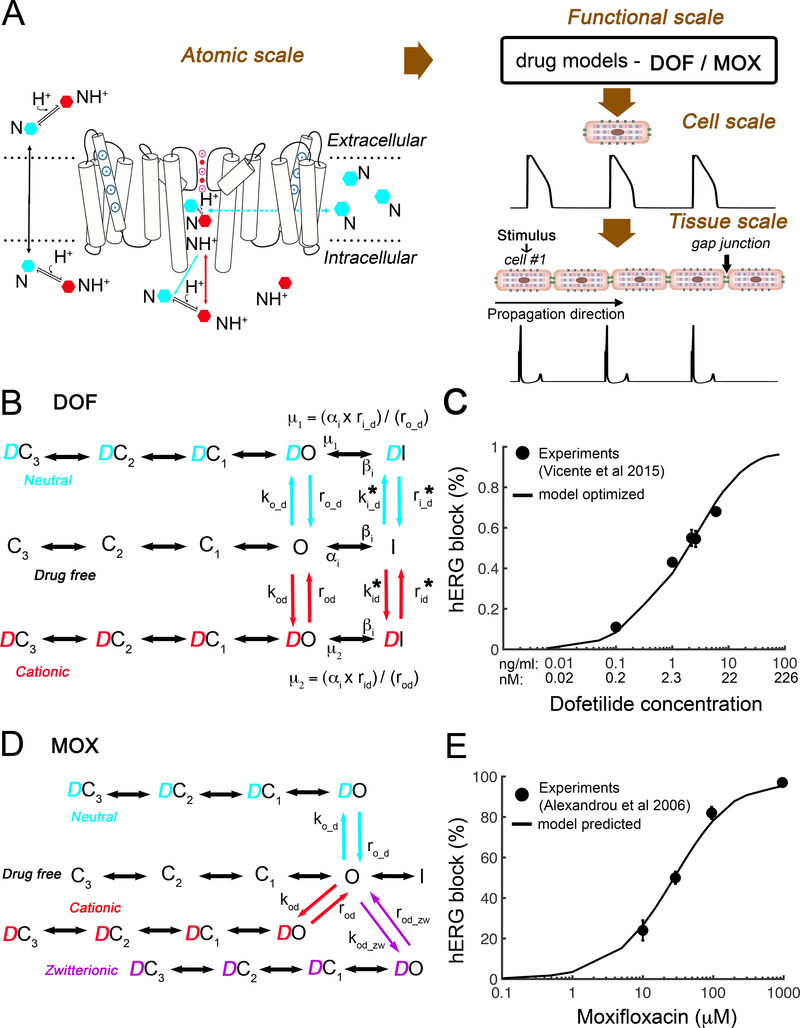
We next used the predicted values obtained from atomic scale simulations (Figure 3A) to seed a multiscale model of drug effects by first populating rate constants in a state dependent hERG function scale model shown schematically in Figure 3B and D for dofetilide and moxifloxacin, respectively. Dofetilide required optimization of one free parameter in the model due to a closed loop in the model (requirement for microscopic reversibility) arising from drug binding to the inactivated state.^{18, 51–55}

Figure 3. Concentration dependent block of hERG by dofetilide and moxifloxacin.

(A) Schematic diagram presents the connection of atomistic scale model of drugs interaction with the hERG channel (left) to the corresponding functional protein scale model (B and D) used in single-cell to tissue level simulations and computed pseudo ECG (bottom). (B) The Markov model represents a map of the hERG channel functional states. Drug free (black), cationic dofetilide bound (red) states, and neutral dofetilide bound (cyan) states are shown. (C) Experimentally measured dose dependent inhibition of hERG by dofetilide (black circles)⁵⁶ and optimized model-based results (black curve). (D) The Markov model of hERG-moxifloxacin system: drug free (black), cationic drug bound (red) states, zwitterionic drug bound (purple), and neutral drug bound (cyan) states are shown. (E) Experimentally measured dose dependent inhibition of hERG by moxifloxacin (black circles)²⁰ and model predicted results (black curve).

Moxifloxacin on the other hand has not been shown to exhibit inactivated state block and so drug binding was not simulated to the inactivated state. Rather, moxifloxacin has been shown to inhibit hERG channels via a rate-independent open state blocking mechanism.^{20, 48} It has also been shown that moxifloxacin does not rely strongly on binding to the S6 aromatic amino acid residues F656.²⁰ The absence of inactivated state block allowed for the model to be parameterized directly from the simulated data with no free parameters and consequently, no optimization was required.

For dofetilide, the “on” rates for open-inactivated state were free parameters and optimized to the experimentally obtained IC₅₀ curve from Vicente et al.⁵⁶ by assuming that dofetilide binds 70-fold stronger to this channel state, i.e. K_DI = (K_Do / 70)⁴⁴ (Online Table III). In both experiment and simulations (Figure 3C), peak I_Kr was recorded at the end of the 3-s activating step to 0 mV with drug concentrations from 0 to 7.5 ng/mL. Percentage of drug block was calculated by (I_control – I_drug)*100/I_control and compared to experimental data,⁵⁶ demonstrating good fit (Figure 3C).

Figure 3D shows three modes of drug bound channel states – neutral (cyan), cationic (red), and zwitterionic (purple) for moxifloxacin. Our predicted (no parameter optimization) percentage of drug block was in remarkable agreement with experiments²⁰ as shown in Figure 3E.

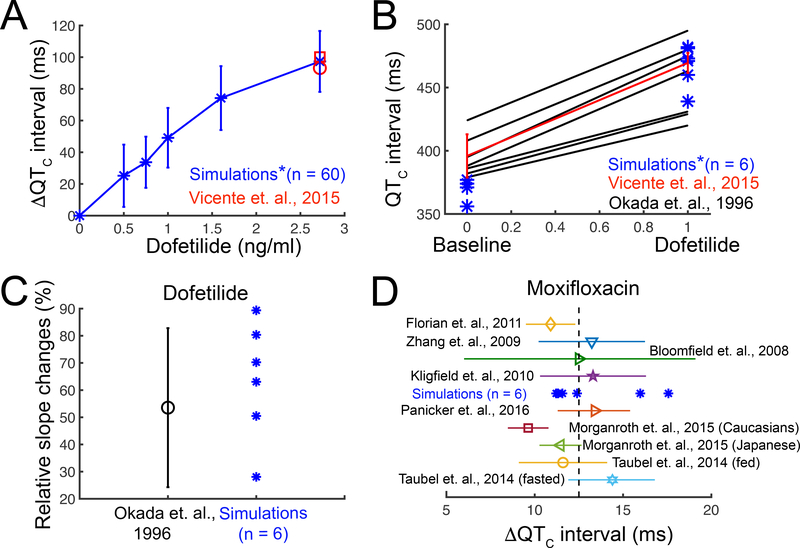
Next, we subjected the model to a validation test using the gold standard data: human clinical data in the form of electrocardiograms in the absence and presence of dofetilide or moxifloxacin. To do so, as shown schematically in Figure 3A, we incorporated the function scale models of drug interaction with the hERG channel (Figure 3B and 3D) into the O’Hara-Rudy human cardiac ventricular myocyte model and then extended this model to construct a one-dimensional strand of O’Hara-Rudy cells.⁵⁷ We applied a simulated stimulus current at one end to initiate a propagating one-dimensional wave at the clinically reported heart rate between 43 and 75 beat per minute (bpm).⁵⁶ Figure 4A shows the computed heart rate corrected pseudo ECG (QT_C interval) for a range of dofetilide concentrations derived from signal averaged spatial and temporal gradients of electrical activity in the computational model. The red symbols are a comparison of human clinical data to model prediction following application of 2.72 ng/mL dofetilide.^{10, 56}

Figure 4. Validation of the drugs computational screening pipeline prototype with human clinical data.

(A) Heart rate corrected pseudo ECG ( ΔQT_C interval) was computed from a 1-dimensional strand of O’Hara-Rudy human cardiac ventricular myocytes for pacing frequencies between 43 – 75 bpm for a range of dofetilide concentrations (blue) compared to clinical data (red). (B) Comparison of human clinical data showing control and dofetilide affected rate corrected QT intervals^{10, 56} (black and red lines) and simulated mean values under the same conditions (blue asterisks). Red line: two subjects received a single dose of 0.5 mg (population’s mean maximum concentration C_max is 2.7±0.3 ng/mL). Blue asterisks (*): concentration 2.72 ng/mL (~6.16 nM) was used in the simulations. Black lines: subjects received 0.5 to 0.75 mg twice a day. (C) The clinically observed and in silico prediction of QT intervals over a wide range of preceding RR intervals after 2.72 ng/mL dofetilide application. Rate dependent changes in the QT interval were tracked as the slope of the linear regression line estimating the QT – $\sqrt{RR}$ relation. (D) Model predicted ΔQT_C intervals with 2.5 mg/L moxifloxacin application (blue asterisks). Color symbols with error bars: clinical data after 400 mg moxifloxacin oral dose (maximum concentration C_max is between 2.3 to 3.7 mg/L).^59–65

Figure 4B shows the comparison of human clinical data from two studies (red and black lines) and model predictions (blue) under drug free conditions and following application of 2.72 ng/mL dofetilide.^{10, 56} Each cell in the simulated tissue was subjected to a physiological noise current in order to introduce physiologically relevant inter-subject variability. The simulated mean values compared to clinically obtained data from humans are in excellent agreement, thereby providing an indication of the validity and predictive value of the computational pipeline to recapitulate the effect of a drug on the human QT interval.

In Figure 4C, we simulated QT intervals over a wide range of preceding RR intervals after 2.72 ng/mL dofetilide application and compared to the clinically observed changes¹⁰ (with noise applied as above). Rate dependent changes in the QT interval were tracked as the slope of the linear regression line estimating the QT – $\sqrt{RR}$ relation. Again, the predicted relationship falls within the range of clinical data, indicating that the model can reproduce rate dependent changes in drug-induced QT interval. Finally, as shown in Figure 4D, our simulated effects of 2.5 mg/L moxifloxacin⁵⁸ on QT intervals are correctly predicted to fall within the range of multiple clinical data from humans.^59–65

We next carried out computational screening in O’Hara-Rudy human computational ventricular myocytes for the effect of dofetilide or moxifloxacin to promote proarrhythmia by tracking key parameters as shown in Figure 5. We tracked each parameter in the absence of drug (control conditions in black) and in the presence of average patient plasma concentration of 2.72 ng/mL dofetilide (red), and 2.5 mg/L moxifloxacin (blue). To explore the effects of species differences we also simulated rabbit ventricular myocytes, which were similar to human (Online Figure I).

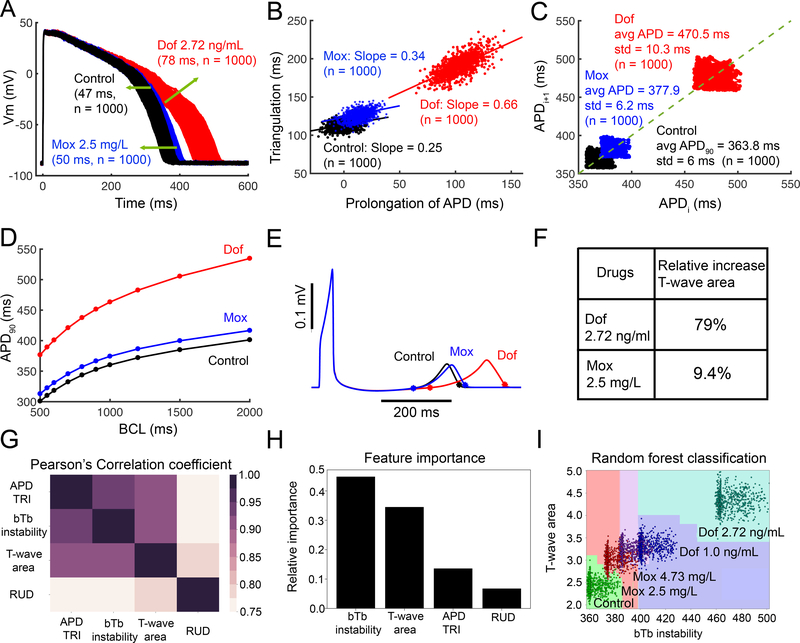
Figure 5. Computational screening for dofetilide and moxifloxacin induced arrhythmia vulnerability.

(A) Predicted temporal APD dispersion of 1000 simulated O’Hara-Rudy human ventricular action potentials generated after incorporating physiological noise to induce beat-to-beat (bTb) variability at 1 Hz in the drug-free control case and following simulated application of dofetilide (2.72 ng/mL), and moxifloxacin (2.5 mg/L). Dispersion of APD was quantified as the difference between the maximum and minimum of 1000 individual cells (Control = 47 ms; Moxifloxacin 2.5 mg/L = 50 ms; Dofetilide 2.72 ng/mL = 78 ms). (B) Action potential triangulation as a function of APD prolongation for individual cells for control (slope = 0.25), Moxifloxacin 2.5 mg/L (slope = 0.34), and Dofetilide 2.72 ng/mL (slope = 0.66) conditions (C) Simulated bTb instability of action potentials to small perturbations before and after application of drugs. Poincaré plots of sequential APD pairs indicating bTb instability are shown. (D) Action potential adaptation curves show APD₉₀ at various pacing frequencies with or without dofetilide or moxifloxacin, demonstrating drug reverse use dependence. (E) Pseudo ECGs after a long pause (5000 ms) are shown for control, moxifloxacin 2.5 mg/L, and dofetilide 2.72 ng/mL conditions. (F) Relative increased T-wave area by 79% with dofetilide 2.72 ng/mL, and 9.4% with moxifloxacin 2.5 mg/L. (G) The Pearson’s correlation coefficients between paired TRIaD parameters. Pearson’s coefficient value indicated by the color gradient, where 1 is highly correlated (black). (H) bTb instability emerged as the most important feature from the TRIaD parameters. (I) Classified regions for control (n = 1000), dofetilide 1 ng/mL (n = 1000), dofetilide 2.72 ng/mL (n = 1000), Moxifloxacin 2.5 mg/L (n = 1000), and Moxifloxacin 4.73 mg/L (n = 1000) using bTb instability and T-wave area.

In Figure 5 the TRIaD was simulated. Temporal APD dispersion was quantified in a cell population of 1000 simulated cardiac myocyte action potentials by incorporating physiological noise.^66–68 Dofetilide within the clinical dosing range promotes temporal APD dispersion (maximum - minimum APD₉₀), while moxifloxacin has a subtle effect (Figure 5A: Control – 47 ms; 2.5 mg/L Moxifloxacin – 50 ms; 2.72 ng/mL Dofetilide – 78 ms). Figure 5B illustrates the effect of dofetilide and moxifloxacin to promote triangulation of the action potential as a function of APD prolongation. In the absence of drug, control cells had a slope of 0.25, while 2.5 mg/L moxifloxacin increased triangulation minimally to 0.34, while 2.72 ng/mL dofetilide increased the slope to 0.66. Figure 5C shows Poincaré plots of sequential APD pairs indicating beat-to-beat (bTb) instability following the application of small electrical perturbations in the absence of drug, with 2.5 mg/L moxifloxacin or with 2.72 ng/mL dofetilide. Instability was assessed by applying small amplitude inward currents randomly between -0.1 to −0.2 pA/pF for 50 ms over the course of the action potential plateau at a basic cycle length of 1000 ms. Dofetilide has a dramatic effect to increase instability, while moxifloxacin has a minor effect. In Figure 5D, reverse use dependence induced by dofetilide or moxifloxacin was evaluated. The curves were generated using APD₉₀ values from human computational ventricular myocytes at steady-state at indicated frequencies. When dofetilide (red) was applied, there was a clear steepening of APD adaptation curve compared to drug-free (black) and moxifloxacin (blue). Panel E shows spatial dispersion of APD quantified in tissue by integrating the area under predicted T-wave following a long pause (5000 ms). (See Supplemental Materials). Panel F shows profound increase in area (79%) under the T-wave when dofetilide is applied compared to moxifloxacin (9.4%).

We next used random forest machine learning to evaluate the importance of arrhythmia vulnerability parameters in the TRIaD to determine the final target classification (control versus drug-affected at different dofetilide and moxifloxacin doses). We used Pearson’s correlation coefficient (see Supplemental Materials) to explore linear dependence of TRIaD parameters in Figure 5G, showing that TRIaD parameters are highly correlated. We then constructed a multiclass random forest classification (see Supplemental Materials) using correlated TRIaD parameters. The classifier indicates importance of each TRIaD parameter to correctly predict the target (drug free, medium or high risk) for two doses each of dofetilide and moxifloxacin. Figure 5H suggested that bTb instability is the most important feature to classify drug-affected cases into risk groups (see Supplemental Materials for details). Figure 5I illustrates the multiclassification for control, dofetilide 1.0 ng/mL, 2.72 ng/mL, moxifloxacin 2.5 mg/L, 4.73 mg/L using bTb instability and T-wave area. Random forest classification accuracy is 98%. This approach can be useful to compare the impact of changes in plasma concentrations and how they would be expected to affect relative risk, so called Anti-hERG activity.⁶⁹

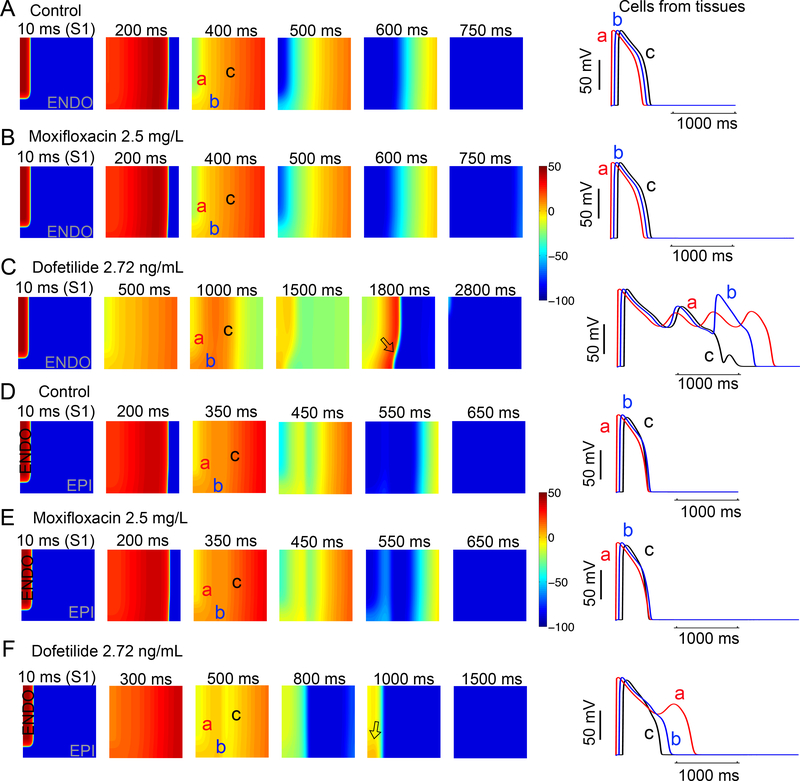
Arrhythmia is fundamentally an emergent spatial phenomenon. Accordingly, two-dimensional homogeneous (Figure 6, Panels A, B and C, endocardial cells) and heterogeneous (Figure 6, Panels D, E and F, endocardial region (cells 1 to 180) and epicardial region (cells 181 to 500)) anisotropic human ventricular in silico tissues (5 cm × 5 cm) with a linear decrease in APD as indicated by experimental data^{70, 71} were simulated. Each simulated tissue contained randomized spatial heterogeneity imposed by the application of randomly applied low amplitude perturbations in the form of small inward currents, 0.1 to −0.45 pA/pF to each cell in the tissue at each time step for the duration of the simulation. In homogeneous tissue simulations in the absence and presence 2.5 mg/L moxifloxacin (Figure 6A and B), the tissue was very electrically stable, and normal cellular and tissue behavior is observed. However, 2.72 ng/ml dofetilide (Figure 6C) resulted in emergence of early afterdepolarizations (EADs) in some cells and not others, resulting in spatial dispersion of repolarization. As shown in D, E and F, the effect persisted when the tissue was heterogeneous (transmural heterogeneity), with considerably reduced dispersion of repolarization (as epicardial cells fire last, but repolarize first), and spatial repolarization gradients were observed only with dofetilide. These simulations suggest that in the presence of low levels of electrical instability, the application of a clinically relevant dose of dofetilide but not moxifloxacin promotes profound spatial dispersion of repolarization.

Figure 6. In silico diagnostic test in tissue reveals arrhythmia triggers with dofetilide and moxifloxacin.

Time snapshots (colored boxes) with voltage gradients are shown for two-dimensional simulated tissue (described in Supplemental Materials). Membrane voltages are indicated by the color gradient. Two-dimensional homogeneous (Panels A, B and C, endocardial cells) and heterogeneous (Panels D, E and F, endocardial region (cells 1 to 180) and epicardial region (cells 181 to 500)) anisotropic human ventricular in silico tissue (5 cm × 5 cm) composed of simulated myocytes. Single APs from sites ‘a’, ‘b’, and ‘c’ in the simulated tissues are shown in the right panels for each case.

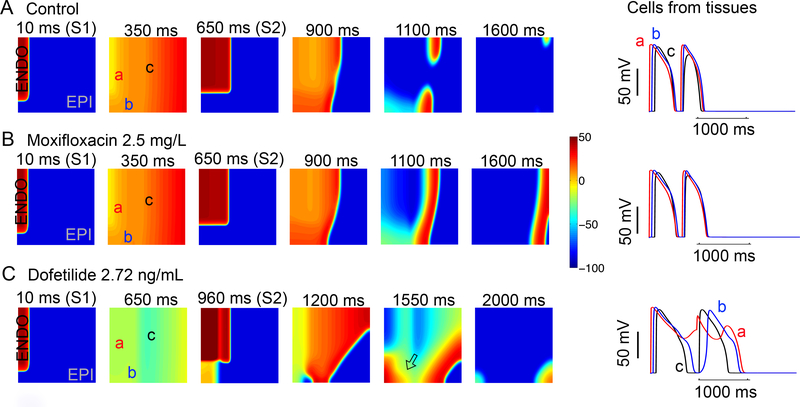
We next set out to test the effect of dofetilide and moxifloxacin in the setting of extrasystolic excitable triggers in heterogeneous tissue (Figure 7). With spatial noise to promote low-level electrical instability (described above), when 2D tissue was simulated using a typical S1-S2 protocol,^{72, 73} 2.72 ng/ml dofetilide application resulted in dispersion of repolarization that was absent with moxifloxacin and drug free tissue. The tissue was paced (S1) (first panel) in a 0.5 cm × 1.1 cm area on the left edge of the endocardial region, and a premature stimulus S2 (third panel) was applied in a 1.8 cm × 1.5 cm area on the top left corner (endocardial region). Time snapshots (panels) with voltage gradients indicated by the color map are shown in Figure 7. These maps were constructed following the last planar wave (S1) (first panel) and throughout termination of the most persistent wave after S2 stimulus (last panel). The corresponding action potentials from three points in space are shown in the right panels. Without drug (Figure 7A) or moxifloxacin application (Figure 7B) there was no persistence of electrical instability. In Figure 7C dofetilide reliably (n = 5 simulations) promoted persistent arrhythmia triggers observed as afterdepolarizations in cellular action potentials (right).

Figure 7. In silico diagnostic test to reveal vulnerability to torsades de points arrhythmias by extrasystoles.

Time snapshots (colored boxes) with voltage gradients are shown for two-dimensional simulated tissue as described below. Membrane voltages are indicated by the color gradient. The corresponding action potentials from three points in space (‘a’, ‘b’, and ‘c’) are shown in the right panels. (A) In the absence of drug (top row), arrhythmia triggers were not inducible. (B) Upon application of moxifloxacin (middle row), arrhythmia triggers were not inducible. (C) In the bottom row the effect of dofetilide is shown: numerous arrhythmia triggers were observed as afterdepolarizations and spatial repolarization gradients in underlying cellular action potentials (right). Single APs from site ‘a’, ‘b’, and ‘c’ in the simulated tissues are shown in the right panels for each case.

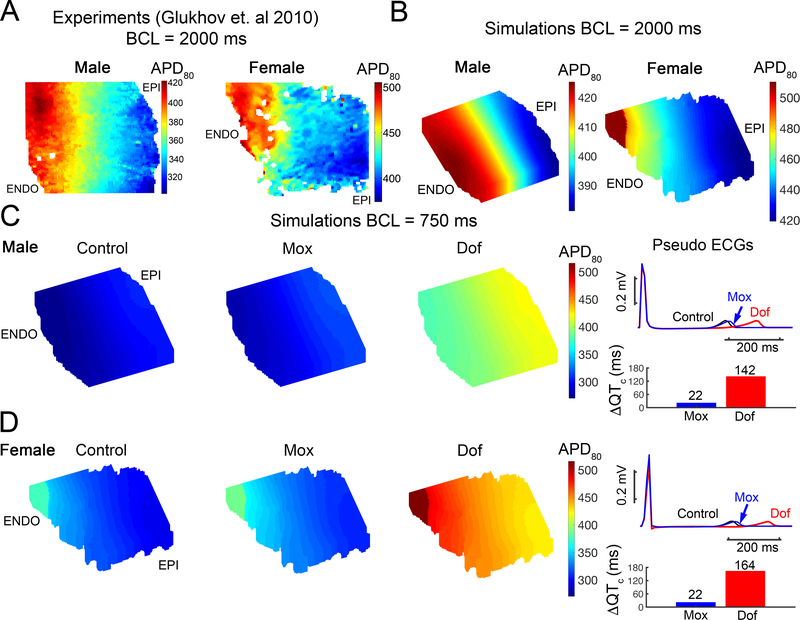
Finally, we developed an in silico left ventricular (LV) 3D wedge reconstruction of the human cardiac tissue based on the experimental data from Glukhov et al. ⁷¹ for the drug free case, with 2.72 ng/mL dofetilide and with 2.5 mg/L moxifloxacin applied. The LV wedges were paced at basic cycle of 750 ms for 20 beats with small amplitude inward currents randomly applied between -0.1 to −0.45 pA/pF to each cell after the ventricular activation. The model simulations show drug-induced QT interval prolongation both in male and female. However, in females, dofetilide caused considerably larger prolongation of the QT interval. This is consistent with clinical and experimental data suggest that male and female subjects respond differently to dofetilide intervention, with females exhibiting increased sensitivity and proclivity to abnormal rhythm ^74–76. A notable prediction from the model was that sex differences did not emerge following application of moxifloxacin under the conditions that we tested. This result is a prediction that can be tested in future experimental and clinical studies.

DISCUSSION

A major factor plaguing drug development is that there is no preclinical drug-screening tool that can accurately predict unintended drug induced cardiac arrhythmias from chemically similar drugs. The current approaches rely on substitute markers such as action potential duration or QT interval prolongation on the ECG. There is an urgent need to identify a new approach that can predict actual proarrhythmia from the drug chemistry rather than relying on surrogate indicators.

In this study we construct a computational pipeline for predictive safety pharmacology. The goal of this study was to develop a framework for detection of unsafe hERG blockers from their drug chemistry. Thus, we have assembled the process and utilized clinical data to demonstrate the utility for a proof-of-concept multiscale computational model to predict cardiac effects of dofetilide, a potent hERG blocker with a high pro-arrhythmia risk and moxifloxacin, which carries low arrhythmia risk in the absence of co-morbidities.^{27, 28}

We began by developing physics-based computer models to account for channel conformational state and drug ionization state specific atomic-scale determinants of dofetilide and moxifloxacin interaction with hERG. This was accomplished through: 1) the development of open-state hERG atomistic structural model based on the published cryo-EM structure and validation via all-atom molecular dynamics simulations of K⁺ conduction through the channel pore; 2) the development of empirical force field models for different ionization forms of dofetilide and moxifloxacin; 3) determination of free energy and diffusion coefficient profiles for drug binding to the channel pore using enhanced sampling all-atom molecular dynamics simulations.

We utilized molecular dynamics simulations to predict association rates and affinities of dofetilide and moxifloxacin to the open state of the hERG K⁺ channel. Interestingly, this approach yielded novel information about the nature of dofetilide interactions with hERG, suggesting that neutral dofetilide and moxifloxacin forms preferentially interact with the open channel state (see Figure 2B and 2D). Our previous function scale dofetilide model⁷⁷ was based on interpretation of experimental data. These data.^44,46,54 were used to estimate drug binding to the inactivated channel state in our model by assuming a 70-fold increase in predicted affinities from molecular dynamics simulations of the open state. Moxifloxacin required no such assumptions, and remarkably, parameters derived from atomistic simulations yielded excellent prediction of dose response (Figure 3E).

Our previous models required higher doses of dofetilide to cause prolongation of the QT interval,⁷⁷ but the model generated from the molecular dynamics generated parameters in this study was able to reproduce dose-dependent prolongation of the QT interval in very close agreement to the clinical data (Figure 4). In the physics-based approach that we used, the channel is restrained to stay in a particular conformation, allowing for an unambiguous calculation of drug-channel affinity for discrete channel conformational states. To ensure convergence of the calculated binding free energies we apply weak conformational restraints on the pore domain backbone atoms to keep the protein receptor structure in the open state. We based this assumption on the large body of prior theoretical work on the accurate computations of binding free energy from the all-atom free energy simulations ^78,79,80. One of the major considerations in accurate evaluation of standard binding free energy for a flexible ligand to a receptor with multiple conformational state is to ensure efficient sampling of all states for the ligand itself to obtain work required for reversible binding/unbinding process from a very well-defined reference state of the receptor (with and without bound ligand). In addition to ensuring accurate calculations of the binding free energy for the ligand to a specific state, the presence of the conformational restraints on the receptor enables direct connections between calculated state-dependent binding affinity (K_D) and structural conformations of the channel implied by the Markov-model of hERG, e.g. open-activated and open-inactivated states. It is important to note that even within the restrained channel regime, atomistic simulation accounts for and includes protein flexibility within a given conformational state allowing adequate sampling of different drug - protein binding modes.

In this study we have attempted to make a novel link between ion channel structure and function. We utilized atomic scale predictions to inform rate constants for constructing computational channel-scale kinetic models for drug interaction with hERG channels. Calculations from drug – channel binding molecular-structure level trajectories allowed for the calculation of free energies and dissociation constants K_D for dofetilide and moxifloxacin interactions with the hERG open state. These simulated data combined with predicted diffusion coefficients from the same atomistic molecular dynamics runs allowed for drug “on” and “off” rates to discrete states to be introduced into the function scale Markov model of hERG. In this work we focused on physics-based models of drug binding to an open conducting state based on available cryo-EM hERG structure ⁸¹ but drug interactions with inactivated and/or closed channel states and drug effect on conformational transitions between those states will be considered in subsequent studies.

Computational models of dofetilide and moxifloxacin interaction with the hERG receptor were integrated into virtual cardiac cell and tissue level models to predict emergent drug effects to promote elements of the TRIaD: Proarrhythmia markers that emerge at cell and tissue scales. The manifestation of the TRIaD parameters can be observed in the tissue level simulations designed to serve as in silico diagnostic indication of arrhythmia vulnerability. In Figs. 6 and 7, the model predictions show the emergence of arrhythmia triggers in the presence of low levels of applied electrical instability and dofetilide, but not moxifloxacin, in the absence and in the presence of extra stimuli as shown in Figure 7C.

Although it has long been clear that the TRIaD linked parameters indicate arrhythmia vulnerability,^{10, 35, 36} it has not been clear which are the minimal and sufficient parameters to predict arrhythmia risk. Thus, we used random forest machine learning algorithm to evaluate the importance of each arrhythmia vulnerability parameter from the TRIaD to determine the final target classification. The Pearson’s correlation coefficient indicated that all TRIaD parameters are highly correlated, thereby containing redundant information. Thus, we employed a multiclass random forest classification machine learning algorithm using the correlated TRIaD parameters to determine the relative importance of each to correctly predict whether a simulated cell belongs to the drug free, or low, medium or high risk category for a given drug and dose. The bTb instability parameter was shown to be most important feature in classifying the drug safety. Other drugs can be compared within this schema with outputs indicating relative risk, which may be useful in the context of FDA guidance as effective drug dose can be modified by physiological parameters that impact magnitude of channel block and pharmacokinetics. An example is the comparison of changes in free plasma concentrations and how they would be expected to affect relative risk, described as Anti-hERG activity.⁶⁹

We investigated the impact of sex as a biological variable in drug induced arrhythmia vulnerability. In Figure 8, we show the impact of dofetilide and moxifloxacin on the male and female electrophysiology. Indeed, the model predictions are consistent with reported clinical data and show increased impact in the female case versus male following dofetilide application.^{74, 75} Interestingly, we did not observe an impact of sex following moxifloxacin application under the conditions tested. This is a novel prediction of the model that can be expanded for a variety of testing conditions and that can be validated in future experimental or clinical studies. It should be noted that the male and female models here best represent the post-menopausal female and senescent male – we have not explicitly considered hormones during various phases of the menstrual cycle as we have done in previous studies.^{82, 83} The male and female models were built from reported differences in male and female human explanted hearts that we utilized to inform the model development.^{82, 84} However, even in senior men and women, substantial differences have been observed following dofetilide administration ^74–76. Future studies are planned to also predict the impact of sex steroid hormones in combination with drug application.

Figure 8. Predicted impact of sex as a biological variable with in silico 3D reconstructed left ventricular (LV) wedge based on Glukhov et al. ⁷¹ paced with before and after drug application.

(A) Experimental data from normal human female (right) and male (left) left ventricle ⁷¹. (B) In silico reconstructed human tissues from these data from normal explanted heart at a pacing cycle length of 2000 ms (male – left and female – right). (C) The LV wedges were paced at basic cycle of 750 ms for 20 beats. The APD₈₀ map was shown for male in the control condition (no drug) (left map in C) and following moxifloxacin (middle map) and dofetilide (right map) applications. Pseudo ECGs (the 20^th beat) shows the effect of drug application on QT interval in the right panel. (D) Shown for female as in (C).

We brought together model simulations at the atomistic level for hERG channel structure, dynamics and channel – drug interactions as well as simulations at the functional levels of the protein, cell and tissue. The power of combining these scales in a predictive framework is that it has allowed a way to derive on and off rates of drugs from atomic scale simulations and to then use these values to inform and build functional level channel models. Function scale drug-channel models were then integrated into cellular and tissue level model to reveal mechanistic links between structure-activity relationships of ion channel – drug systems with higher order emergent electrical phenomena such as cardiac rhythm disturbances.

We anticipate the initial context of use for the technology presented here to be in the preclinical screening environment. Future efforts to automate and improve the efficiency of the process presented here will be required for use in industry, academic or regulatory setting. We must also undertake studies with compounds for which we are blinded to the proarrhythmia impact of the compounds until we have generated independent data that can be compared to in vitro and in vivo tests obtained by the safety pharmacology groups. The information required to do this is simply the chemical signature of the drug. From the drug chemistry, we can develop a model of the drug and the target and utilize simulation to predict rates that can populate parameters in the higher order models. This will constitute a key necessary validation step for the pipeline. Ultimately the added value of an in silico approach to drug screening is faster throughput and reduced cost. The approach can also be extended to other ion channel targets and G-protein coupled receptors as well as compounds that interact with multiple receptor targets and can be expanded to include varied genotypes and risk factors, and to predict individual responses to drug therapy.

There are limitations in the current state of the computational pipeline that should be noted. We did not take into account the pharmacokinetic and pharmacodynamic (PK/PD) profiles of drugs in this analysis, although PK/PD models could be linked to the models described here in a future study. Drug metabolism was not considered but is clearly a critical element that can be influenced by agents as varied as grapefruit to antifungal medication that may directly modify drug metabolic pathways or affect absorption rates. We did not account for multitarget effects of drugs and potential drug interactions, although the model might be expanded in future studies to include these elements. We made predictions in models that represent healthy human cardiac cells and tissue, but most reported incidences of drug-induced arrhythmia occur in the setting of concomitant co-morbidities.

Ultimately, the computational approach we present represents a scalable framework with automation potential to interact with other developing technologies,^85–90,91 and be applied to personalized medicine.⁹² These technologies in conjunction with the multiscale models that we will develop may form a process that can ultimately be used in the regulatory process prior to drug approval, in academia for research, in industry for drug and disease screening, and for clinical medicine.

NOVELTY AND SIGNIFICANCE.

What Is Known?

• Cardiotoxicity in the form of deadly abnormal arrhythmia is one of the most common and dangerous drug risks.

• There is no current drug-screening tool that can distinguish therapies that may promote cardiac arrhythmias from chemically similar safer drugs.

• Current approaches rely on surrogate markers such as action potential duration or QT interval prolongation on the ECG.

What New Information Does This Article Contribute?

• We demonstrate a novel computational pipeline that connects the hugely disparate space and time scales of ion channel structure and function and predicst drug impact from the atom to the rhythm.

• Predictive models at the level of cell and tissue exposes fundamental arrhythmia vulnerability mechanisms and complex interactions underlying emergent behaviors.

• Human clinical data used for model validation showed excellent agreement, demonstrating the feasibility of the approach for cardiotoxicity prediction.

Drugs that share the common property of blocking the hERG potassium channel with consequent prolongation of the cellular action potential and QT interval on the ECG are deemed likely to be unsafe. However, hERG block and QT prolongation alone are not selective indicators for cardiac arrhythmia. In order to move beyond the current screening paradigm, we present a new approach that can predict the impact of a drug on the cardiac rhythm starting from the drug chemistry to distinguish between safe and unsafe hERG blockers. We utilized the cryo-EM structure of the hERG K⁺ channel to develop and validate an atomistic structural model of the open conducting state. We then developed and validated structural atomistic models of dofetilide and moxifloxacin, hERG blockers differing pro-arrhythmia risk profiles. All-atom molecular dynamics simulations were used to probe dofetilide and moxifloxacin interactions with the open hERG channels. We connected atomistic scale information to protein, cell and tissue scales by using predicted drug binding affinities to model drug effects on hERG channel function. Model components were integrated into cell and tissue scale models to expose arrhythmia vulnerability mechanisms and emergent behaviors. Model outputs were validated with human clinical data and showed excellent agreement, demonstrating feasibility.

Nonstandard Abbreviations and Acronyms

AP

action potential

APD

action potential duration

bTb

beat-to-beat

CHARMM

Chemistry at Harvard Macromolecular Mechanics

CiPA

Comprehensive in Vitro Proarrhythmia Assay

DMPC

1,2-dimyristoyl-sn-glycero-3-phosphocholine

DOF

dofetilide

EAD

early afterdepolarizations

ECG

electrocardiogram

MOX

moxifloxacin

POPC

1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine

TdP

torsades de pointes

TQT

Thorough QT Study

TRIaD

Triangulation, reverse use dependence, beat-to-beat instability of action potential duration, temporal and spatial action potential duration dispersion