Integration of Omics Data Sources to Inform Mechanistic Modeling of Immune‐Oncology Therapies: A Tutorial for Clinical Pharmacologists

Abstract

Application of contemporary molecular biology techniques to clinical samples in oncology resulted in the accumulation of unprecedented experimental data. These “omics” data are mined for discovery of therapeutic target combinations and diagnostic biomarkers. It is less appreciated that omics resources could also revolutionize development of the mechanistic models informing clinical pharmacology quantitative decisions about dose amount, timing, and sequence. We discuss the integration of omics data to inform mechanistic models supporting drug development in immuno‐oncology. To illustrate our arguments, we present a minimal clinical model of the Cancer Immunity Cycle (CIC), calibrated for non‐small cell lung carcinoma using tumor microenvironment composition inferred from transcriptomics of clinical samples. We review omics data resources, which can be integrated to parameterize mechanistic models of the CIC. We propose that virtual trial simulations with clinical Quantitative Systems Pharmacology platforms informed by omics data will be making increasing impact in the development of cancer immunotherapies.

Cancer was the second leading cause of death in 2018, remaining one of the major medical challenges attracting substantial investment both in academic research and drug development. Given that cancer originates from molecular changes of DNA in a single cell of an individual patient, oncology has always been at the forefront of the application of molecular and cell biology. The advent of next‐generation sequencing (NGS) has provided experimental capability for determining DNA and RNA sequences of individual tumors in clinical samples obtained from individual patients.1 Remarkably, the full genome and transcriptome sequencing of tens of thousands of single cells from individual tumor biopsies has recently become available as well.2 Intensive effort over the last decade has led to the establishment of data resources of an unprecedented scale and molecular detail. The Cancer Genome Atlas (TCGA)1 alone contains genome and transcriptome sequences of over 20,000 primary cancer and matched normal samples spanning 33 cancer types, amounting to about 1 petabyte of data.

Immunotherapy, where treatments mobilize the patient’s own immune system to fight cancer and provide lasting therapeutic benefit, is currently a hot topic in oncology.3 Although the concept of immuno‐oncology (IO) is not new, recent success stories with immune checkpoint inhibitors have brought it to the forefront of drug discovery and development, and IO is now one of the most competitive and fast‐growing areas of pharmaceutical research and development. Unsurprisingly, this precipitated a lot of recent effort in application of high‐throughput experimental techniques and a corpus of omics data specific to IO is quickly growing. In particular, the “Immune Landscape of Cancer”4 resource integrates multiple omics data (genome, transcriptome and miRNA sequencing, methylation arrays, DNA copy number, and mutation calls) collected and analyzed to characterize immune‐cell composition and gene expression in the tumor microenvironment of 11,080 TCGA samples from 33 cancer types. Figure 1 shows example charts that can be generated through the Shiny App interface accompanying this resource. The DNA sample purity was used to infer the fraction of leukocytes, stroma, and proliferating tumor cells (Figure 1 a); this was followed by deconvolution of transcriptome data to derive fractions of 22 immune cell types (Figure 1 b). These data can be extracted for a particular cancer type (e.g., lung adenocarcinoma), providing unprecedented insight into immune cell infiltration of the tumor microenvironment. Given that IO explores interactions between the immune system and tumor, the datasets describing a baseline state of the immune system in an individual without a tumor are also of great relevance. Figure 1 c shows plots obtained by querying “The Milieu Intérieur”5 resource, which contains results of high‐throughput flow cytometry of 166 immune cell types in peripheral blood and full genome sequencing of 1,000 individuals. These data provide unique insight into baseline numbers of immune system cell types involved in the response to cancer, as a function of age and infection.

Figure 1.

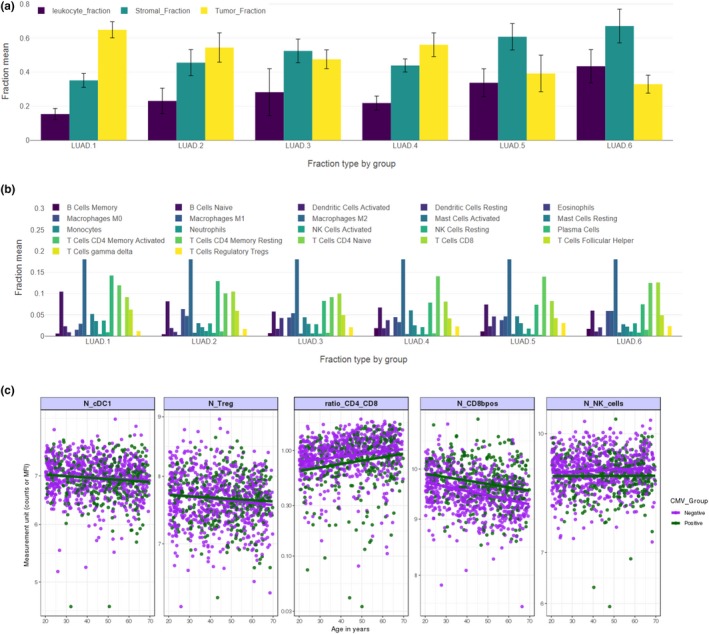
Examples of recent, state‐of‐the‐art molecular and cell biology datasets relevant to immune‐oncology. (a, b) Data on the tumor microenvironment (TME) composition in lung adenocarcinoma (LUAD) extracted from the Immune Landscape of Cancer resource. Distributions are plotted separately for each of the six immune subtypes identified by cluster analysis of all data. a Leukocyte, proliferating tumor, and stroma fractions of the TME, derived from sample purity of full genome sequencing of tumor biopsies. b Fractions of 22 leukocyte types inferred from transcriptome sequencing of tumor biopsies and gene expression signatures. (c) High‐throughput flow cytometry of peripheral blood in healthy volunteers from “The Milieu Intérieur” study, reflecting the state of the immune system as a function of age and infection. All plots were made with Shiny app web interfaces to “Immune Landscape of Cancer” and “The Milieu Intérieur” databases.

The wealth of omics data is currently analyzed by statistical and machine‐learning techniques to discover combinations of therapeutic targets and to formulate complex multivariate diagnostic techniques supporting risk assessment and diagnostics in individual patients. For example, the Immune Landscape of Cancer4 data were subjected to multivariate cluster analysis, which led to stratification of tumor samples into six immune subtypes (Figure 1 a,b). The immune response patterns are hypothesized to impact prognosis and may be used in the future to formulate diagnostic tests assigning individual subjects to the group most likely to respond to a particular combination immunotherapy. Likewise, the gene expression program features—which are unique to these clusters—may lead to the discovery of new combination therapy targets. However, when the identity of pharmacological targets is established, omics data find much lesser utility in target validation and prediction of efficacious doses, timings, and sequences. Quantitative Systems Pharmacology (QSP)6 integrates pharmacokinetic (PK) and pharmacodynamic (PD) models—which are widely used in the pharmaceutical industry to simulate dynamic (longitudinal) responses of clinical biomarkers to different dosing regimens—with mechanistic models of molecular and cellular biology developed over the last 2 decades in the field of systems biology. Thus, QSP provides an ideal quantitative framework for integration of diverse omics data sources and translation of molecular data to clinical outcomes. Moreover, mechanistic models provide insight into the dynamics of the complex network of molecular and cellular interactions between the immune system and cancer, frequently referred to as the Cancer Immunity Cycle (CIC).3 After low‐hanging fruits of checkpoint inhibitors were exploited, validation of new combination targets increasingly requires in‐depth quantitative understanding of the intricate network of feedbacks that lead to counterintuitive, nonlinear dynamic responses to drug doses. This necessitates the use of mathematical models of sufficient scale and detail to inform drug development decisions with virtual trial simulations predicting the effects of dose combinations on clinical outcomes.

Although modeling of the interaction between the immune system and tumors is a longstanding topic in mathematical biology,7, 8, 9 the new interest triggered by the success of IO has led to intensive development of large‐scale QSP platform models to support development of combination therapies.10, 11 However, determination of the parameters of these models and their further calibration for specific compounds, cancers, and patient populations has been an enduring challenge, frequently addressed by the allometric scaling of models developed first for syngeneic mouse tumors. However, the translatability of such preclinical models and their utility for clinical pharmacologists remains controversial. Therefore, here, we argue that the recent availability of clinical omics data now enables direct parameterization of the clinical QSP models in the IO area, and calibration of these models for specific diseases and populations. Mechanistic models then allow “virtual trial” simulations, thus extending the use of molecular data to the prediction of longitudinal responses of clinical biomarkers to different dose amounts. Because many clinical pharmacologists are likely not familiar with this novel approach, we illustrate our arguments through a tutorial using a minimal QSP model of the CIC calibrated with immune landscape data for non‐small cell lung carcinoma (NSCLC) and simulate a virtual trial for anti‐PD1 treatment. We then demonstrate that different types of high‐throughput molecular and cell biology data cover all stages of the cancer immunity cycle, allowing parameterization of large‐scale QSP IO platform models.

A minimal model of cancer immunity cycle

The minimal QSP model of the CIC is shown in Figure 2 and described in detail in the Supplementary Material. Although the model allows realistic simulation of CIC dynamics and an immune checkpoint inhibitor treatment, it has been built for illustration purposes only. We believe that an example showing how specific “omics” data can be integrated with a fully functional mechanistic model and translated to clinical biomarkers will help clinical pharmacologists to appreciate the potential of this novel approach.

Figure 2.

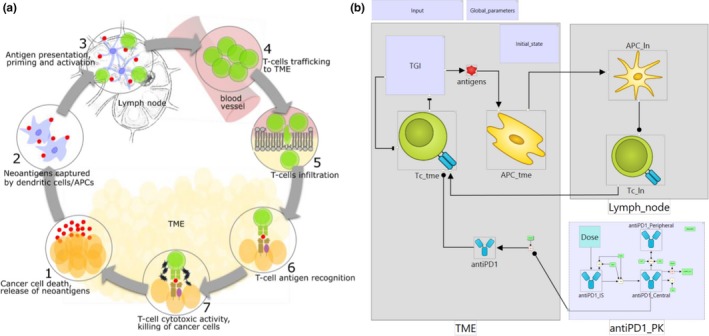
Minimal Cancer Immunity Cycle (CIC) model. (a) Schematic representation of the CIC. (b) Biological process map of the minimal CIC model. TME, lymph_node, tumor microenvironment (TME) and lymph node compartments; TGI, tumor growth inhibition module; antigens, cancer neoantigens; antigen‐presenting cell (APC)_tme, APC_ln, antigen‐presenting cells in the TME and lymph node compartments; Tc_ln, Tc_tme, cytotoxic T‐cells in the lymph node and TME compartments; anti‐PD1_IS, anti‐PD1_Central, anti‐PD1_Peripheral, anti‐PD1, variables of the pharmacokinetic (PK) model representing anti‐PD1 antibody in injection site, central, peripheral, and TME compartments. The map shows modules enclosing model variables, rate laws, and parameters. A detailed map with expanded modules is available in the Supplementary Material.

Briefly, we have built an ordinary differential equation model describing the dynamics of the fundamental CIC stages (Figure 2 a): (i) tumor growth inhibition and neoantigen release, (ii) neoantigens captured by antigen‐presenting cells (APCs) for processing and presentation to T‐cells, (iii) cytotoxic T‐cell priming and activation by APCs, (iv) trafficking of T‐cells to the tumor microenvironment (TME), (v) infiltration of T‐cells into tumors, (vi) recognition of cancer cells by T‐cells, and (vii) killing of cancer cells. This model of basic biology is integrated with a PK and PD model of an anti‐PD1 antibody. The whole model consists of 11 variables, 17 rate laws (interactions), and 49 parameters. Only two compartments are included: TME and lymph node. We do not explicitly model dynamics of immune system cells in peripheral blood. Circulation and migration of leukocytes is implicitly accounted for in rate laws that describe the transition of APCs to the lymph node and infiltration of the TME by T‐cells.

Definitions of model variables and rate laws represent literature knowledge on the cancer immunity cycle. The granularity of variables in the QSP model reflects its context of use. Our aim here is to show how certain types of omics data can be used to inform virtual trial simulations of the dynamic behavior of clinical biomarkers. A full‐scale QSP IO platform allowing discovery and validation of combination targets would require many more variables. The integration of multiple omics datasets in such a platform is discussed below. Our example model was built using our in‐house QSP platform software, which allows visualization of the full model structure in a modular biological process map as well as model code export in MATLAB and R. Figure 2 b shows an overview of the biology; modules are used to hide details of model variables, parameters, rate laws, and algebraic assignments. A map showing the full model structure is available in the Supplementary Material Figure S1 . We also provide executable model code in MATLAB and R, as well as a full list of variable names, rate laws, assignments, compartments, and literature references.

Minimal model calibration using omics data

Having formulated the biological process map of the minimal CIC model and rate laws quantitatively describing the interactions, we proceeded to parameterize the model for a particular disease and therapy of interest. As our example application, we chose NSCLC treatment with pembrolizumab, an anti‐PD1 monoclonal antibody. The aim was to calibrate the minimal CIC model to describe particular patients with NSCLC from the KEYNOTE‐001 clinical trial for which tumor growth was measured during treatment with 10 mg/kg pembrolizumab administered every 3 weeks (10 mg/kg q3w).12 The calibrated QSP model could be used to predict the effects of other dosing regimens and to identify biological processes, which can be pharmacologically targeted to enhance the effect of anti‐PD1 treatment. We note that the purpose of our study is to demonstrate how omics data can be used to calibrate a QSP model, rather than to qualify a model for application in drug development.

Figure 3 shows the constraints on state variables in the minimal CIC model based on data from “Immune Landscape of Cancer” (Figure 1 a,b), high‐throughput flow cytometry of human donor tissues,13, 14, 15 T‐cell repertoire sequencing,16 and the established literature of basic cellular composition of the immune system. State variables describing cell populations in most QSP models in IO—including the minimal model presented here—are expressed as absolute cell numbers rather than relative amounts. Given the sophistication of experimental methods used to obtain relative data, it is surprising that data on reference absolute leukocyte counts in human tissues are still sparse. Here, we used the estimates of absolute numbers of leukocytes in human tissues presented by Trepel in 1974,17 which have also been accepted as a reference in other work in quantitative immunology.18 We combined this information with data reported by Scott et al.19 on the fraction of CD8 events in T‐cells isolated from excised healthy human lymph nodes.

Figure 3.

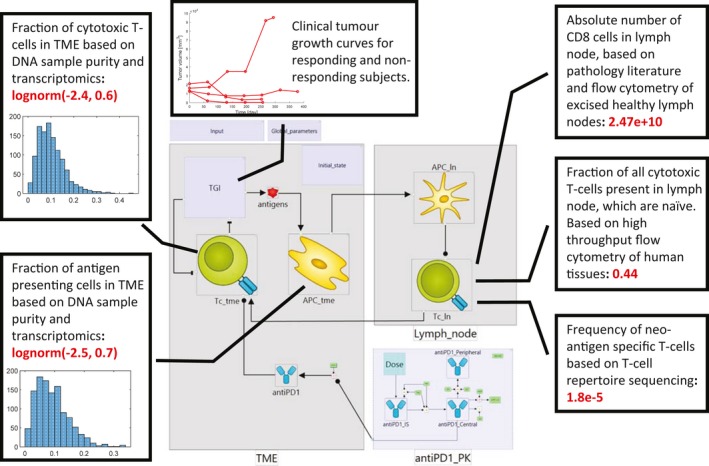
Example integration of omics and clinical biomarker data. Figure shows the constraints on state variables in a minimal Cancer Immunity Cycle model based on omics data. Baseline, log‐normal distributions of the fractions of cytotoxic T‐cells and antigen presenting cells were derived from Immune Landscape of Cancer data. Insets show histograms of cell frequencies inferred from genomes and transcriptomes of individual lung cancer biopsies (N = 1156). The baseline number of neo‐antigen specific T‐cells was calculated based on data from high‐throughput flow cytometry of human tissues, T‐cell repertoire sequencing, and the established literature of basic cellular composition of the immune system. Mechanistic model allows integration of these diverse datasets with longitudinal measurements of clinical biomarkers (tumor growth). APC, antigen‐presenting cell; PK, pharmacokinetic; TGI, tumor growth inhibition; TME, tumor microenvironment.

Finally, we used clinical data for the individual growth trajectories of NSCLC tumors of 4 patients treated with 10 mg/kg pembrolizumab q3w (shown in Figure 3) to calibrate parameters in the model that could not be defined using omics data.12 These parameters correspond to the processes of tumor growth, its killing by cytotoxic T‐cells, and drug action via the PD1 checkpoint. Our model describes, rather than predicts, the behavior of the system for these four tumors subjected to this dosing regimen, and could be used to predict the behavior of other tumors, the effects of other dose regimens applied in the clinical trial (10 mg/kg q2w, 2 mg/kg q3w), as well as sensitivity of dose response to perturbation of individual steps of the CIC, thus informing the discovery of combination targets. However, we emphasize that the model presented here has been built for the purpose of demonstrating data sources that can inform mechanistic modeling of immune‐oncology therapies.

A comprehensive description of the model calibration procedure that uses the latest corpus of omics data is provided in the Supplementary Material.

Virtual trial simulation

In a virtual trial simulation, a mechanistic model is used to predict variability in clinical biomarker responses to treatment resulting from biological variability in the patient population. Following industry‐standard methodology established in the physiologically‐based pharmacokinetic modeling field,20 the parameters and initial states (inputs) of an ordinary differential equation model are randomly generated following distributions derived from literature data. Each configuration of model inputs represents a virtual patient (VP). The virtual trial is a collection of simulation results obtained for a number of VPs. Because a mechanistic model simulates clinical biomarkers quantitatively, simulation results can be analyzed and plotted in the same way as experimental data. Figure 4 shows an example of a virtual trial simulation for a cohort of 489 subjects treated with 19 doses of 10 mg/kg anti‐PD1 pembrolizumab administered every 3 weeks. We chose the number of VPs to be equal to the total number of patients enrolled in the KEYNOTE‐001 clinical trial and the duration of treatment to be representative of a typical length of treatment. A detailed description of the parameters, which were varied to generate the population of VPs is available in the Supplementary Material, which also includes the code used for the simulation.

Figure 4.

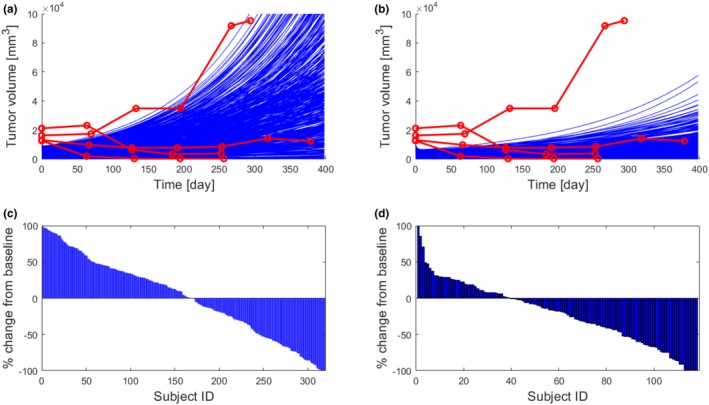
Virtual trial simulation. Four hundred eighty‐nine virtual subjects were generated by randomly varying selected model inputs. (a, b) Comparison of tumor growth curves with clinical data for a untreated subjects and b subjects treated with 19 doses of 10 mg/kg anti‐PD1 pembrolizumab administered every 3 weeks. Simulated data are plotted in blue for all subjects. Red lines and symbols show four treated clinical subjects, and three showing response to therapy. A nonresponding subject was assumed to represent an untreated tumor. (c) Simulated % change of final tumor size from baseline for each simulated subject (sorted in descending order; waterfall plot). Virtual subjects whose tumor doubled in size were removed from the trial (dropout rate 35%). (d) A waterfall plot from the KEYNOTE‐001 clinical study.12

As demonstrated in Figure 4, simulation outputs can be directly compared with clinical biomarker data. The individual time profiles of tumor growth is within the range of longitudinal measurements available for four clinical subjects. Because no data are available for untreated subjects, we can only conclude that tumor growth in treated subjects is much slower than in the case of one clinical subject who did not respond to treatment, and within the range of observations collected for three treatment‐responsive subjects. Simulation results can also be visualized as a clinical waterfall plot, as shown in Figure 4 c, and compared to clinical biomarker measurements, such as the waterfall plot in Figure 4 d (reproduced from the original source) that illustrates the responses of 118 patients in the KEYNOTE‐001 trial that received treatment with pembrolizumab 10 mg/kg q3w. We note that the virtual trial simulation for which results are shown in Figure 4 c could not be set up to reproduce the clinical configuration for which data are shown in Figure 4 d, primarily because the minimal CIC model that we present here does not attempt to simulate clinical subjects dropping out of a study for reasons other than disease progression. We have only applied the criterion that virtual subjects whose tumor volumes double is removed from the trial and, therefore, their response is not recorded in the waterfall plot. Congruence of the clinical trial data and the virtual trial simulation could be further improved by introducing statistical models relating model variables to dropout probability (hazard functions) and calibrating these functions with existing clinical data on other compounds. The inclusion of adverse event modeling would likely lead to increases in dropout rates and waterfall plots more congruent with clinical outcomes. Alternatively, we could calibrate the model against the particular cohort’s waterfall plot data in addition to the four individual tumor trajectories, whereas acknowledging that doing so would restrict the predictive applicability of the model. We believe that our example virtual trial simulation is sufficient to demonstrate that QSP models of the CIC can be informed by multiple omics datasets and that these unique data can be translated to predictions directly comparable with measurements of clinical biomarkers.

The omics data coverage of cancer immunity cycle

A mature QSP platform model, applicable to drug development in IO, requires much more detailed coverage of the biological processes involved in CIC than the minimal example model presented above. This is because the major application of such a platform is in validation of combination targets—prediction of clinical trial results for different combinations of drugs administered at specific doses, timings, and sequences. This requires a large number of variables representing alternative biological processes that can be potentially targeted, as well as variables representing molecular targets of individual compounds. In order to make useful predictions, all these variables need to be connected into one comprehensive system model. Therefore, the QSP platform model of CIC requires a large number of immune system cell types to be explicitly accounted for, such as CD8, CD4, T‐reg T‐cells, dendritic cells, M1 and M2 macrophages, myeloid‐derived suppressor cells, NK cells, and possibly many others. The T‐cells need to be modeled separately as naïve, memory, and effector types. Migration of cells among physiological compartments, such as the TME, lymph, blood, and possibly other tissues, needs to be modeled as well, especially to allow interpretation of biomarkers collected in peripheral blood, which is most experimentally accessible. Expression of targets, such as PD‐1, PD‐L1, and major histocompatibility complex (MHC) receptors, needs to be taken into account and more information about the molecular nature of antigens is needed to account for variability in antigenicity of individual patient tumors. Depending on the molecular nature of new targets that are of interest, this basic platform may need to be extended to include detailed representation of intracellular pathways (e.g., TGF signaling). Mechanistic modeling at this scale and detail seems to be overwhelming and a major limitation is the availability of quantitative experimental data required to parameterize and validate the models. Here, we argue that recently created clinical omics data resources introduce a step change in data availability and thereby enable development of QSP platforms of previously unachievable scale, granularity, and predictive power in IO.

Figure 5 shows different types of omics data that can be used to inform detailed mechanistic modeling of different stages of the CIC. Further references to data resources are provided in Table 1. The Immune Landscape of Cancer4 is arguably the most prominent recently published high‐throughput data resource in IO, which epitomizes the groundbreaking insight delivered by NGS technology. As described above, combination of sample purity analysis of full genome sequences and deconvolution of transcriptome sequencing data to infer the relative contribution of up to 22 distinct gene expression patterns provides quantitative information about TME composition. An example query to the Immune Landscape of Cancer resource, shown in Figure 1 b, demonstrates that quantitative information is available for most of the cell types that are relevant to IO. Perhaps the only major omission are myeloid‐derived suppressor cells, which are a very heterogeneous population of myeloid cells difficult to separate from M2 macrophages and DCs.21 We demonstrate above how this information can be used to parameterize two cellular population variables in an example mechanistic IO model, and a similar procedure could be applied to calibrate a much larger number of cell types in a full scale platform. Moreover, the > 10,000 individual clinical biopsies of 33 tumor types provide a sufficient body of data to allow statistical analysis of the biological variability of TME composition in particular cancers (e.g., lung adenocarcinoma and lung squamous cell). The distributions of cell numbers resulting from this analysis will provide essential input to virtual trial simulations.

Figure 5.

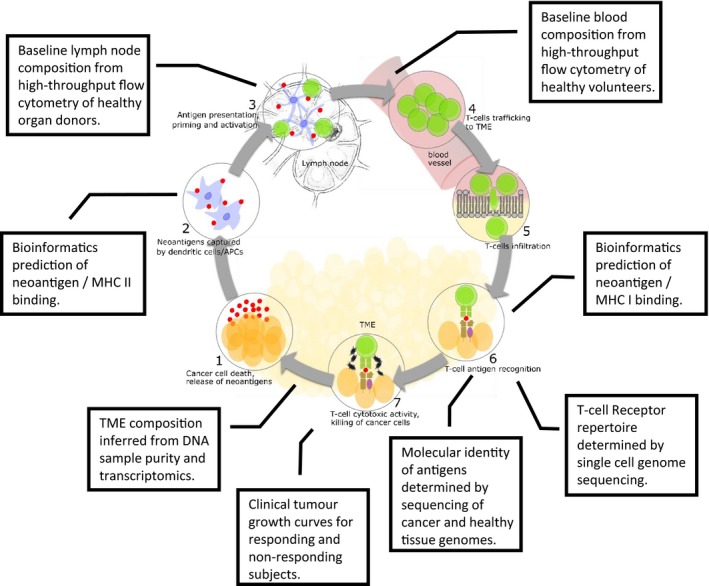
Coverage of Cancer Immunity Cycle (CIC) by clinical omics datasets. The type of datasets obtained from high‐throughput experimental analysis of clinical samples, which can be integrated with observation of tumor growth in responding and nonresponding subjects to parameterize a full‐scale Quantitative Systems Pharmacology platform model of the CIC. MHC, major histocompatibility complex; TME, tumor microenvironment.

Table 1.

High‐throughput, clinical data relevant to mechanistic modeling of CIC

Type of data	Data resource	References
TME composition inferred from DNA sample purity and transcriptomics	https://isb-cgc.shinyapps.io/shiny-iatlas/	4
	https://www.jci.org/articles/view/91190#top	39
	https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6718162/	40
	https://github.com/riazn/bms038_analysis	41
	https://clincancerres.aacrjournals.org/content/23/16/4897.figures-only	42
Bioinformatics prediction of neoantigen/ MHCII binding	Review	43
	NNAlign: http://www.cbs.dtu.dk/services/NNAlign-2.0/	44
	MultiRTA: http://bordnerlab.org/MultiRTA (Dead link)	45
	NetMHCII(2.3) and NetMHCIIpan(3.2): http://www.cbs.dtu.dk/services/NetMHCII-2.3 http://www.cbs.dtu.dk/services/NetMHCIIpan-3.2	46
	SMM‐align: https://doi.org/10.1186/1471-2105-8-238	47
	RANKPEP: http://imed.med.ucm.es/Tools/rankpep.html	48
	OWA‐PSSM: https://doi.org/10.1186/1477-5956-11-S1-S15	49
	ProPred: http://www.imtech.res.in/raghava/propred/	50
	TEPITOPE	51
	TEPITOPEpan: http://datamining-iip.fudan.edu.cn/service/TEPITOPEpan/TEPITOPEpan.html	52
Baseline lymph node composition from high throughput flow cytometry of healthy organ donors	http://dx.doi.org/10.1016/j.immuni.2017.02.019	14
	http://dx.doi.org/10.1016/j.cell.2014.10.026	13
	https://onlinelibrary.wiley.com/doi/full/10.1111/ajt.14434	15
	https://immunology.sciencemag.org/content/suppl/2016/11/29/1.6.eaah6506.DC1	53
	http://dx.doi.org/10.1016/j.immuni.2012.09.020	54
Baseline blood composition from high throughput flow cytometry of healthy volunteers	http://milieu-interieur.cytogwas.pasteur.fr/	5
	http://dx.doi.org/10.1016/j.immuni.2012.09.020	55
	https://immunology.sciencemag.org/content/suppl/2016/11/29/1.6.eaah6506.DC1	53
	https://onlinelibrary.wiley.com/doi/full/10.1111/ajt.14434	15
	http://dx.doi.org/10.1016/j.cell.2014.10.026	13
	http://dx.doi.org/10.1016/j.immuni.2017.02.019	14
Bioinformatics prediction of neoantigen/ MHCI binding	TSNAdb(v1.0): http://biopharm.zju.edu.cn/tsnadb	26
	SMM:	47
	Smmpmbec: https://github.com/ykimbiology/smmpmbec	55
	PickPocket: http://www.cbs.dtu.dk/services/PickPocket/	56
	NetMHC: http://www.cbs.dtu.dk/services/NetMHC-4.0/	57
	NetMHCpan‐4.0: http://www.cbs.dtu.dk/services/NetMHCpan/	28
	NetMHCcons: http://www.cbs.dtu.dk/services/NetMHCcons/	58
	MHCflurry: https://github.com/openvax/mhcflurry	59
	MHCSeqNet: https://github.com/cmbcu/MHCSeqNet	60
	EDGE: https://gritstoneoncology.com/scientific-platform/ (proprietary)	61
T‐cell receptor repertoire determined by single cell genome sequencing	MiXCR: https://github.com/milaboratory/mixcr	62
	MIGEC: https://milaboratory.com/software/migec/	63
	TraCeR:	64
Molecular identity of antigens determined by sequencing of cancer and healthy tissue genomes	https://doi.org/10.1016/j.cell.2017.11.043	65
	https://github.com/ylab-hi/ScanNeo	66
	https://jitc.biomedcentral.com/articles/10.1186/s40425-019-0629-6#availability-of-data-and-materials	67
	https://www.jci.org/articles/view/99538/sd/1	68
	https://github.com/Baltimore-Lab/nat-methods-SABR-trogo	69
	https://doi.org/10.1038/s41590-019-0335-z	70
	https://www.nature.com/articles/s41598-018-36840-z#Sec16	71
	https://journals.plos.org/plosone/article?xml:id=10.1371/journal.pone.0141561#sec024	72

CIC, Cancer Immunity Cycle; TME, tumor microenvironment.

Another fundamental change to mechanistic modeling in IO comes from the knowledge of the molecular nature of cancer neoantigens. Treatment with immune checkpoint blockade agents such anti‐P1, anti‐PD‐L1, or anti‐CTLA4 can result in impressive response rates and durable disease remission; however, it is successful only to a subset of patients. High tumor mutation burden (TMB) is consistently associated with improved response rates of patients treated with checkpoint therapies;22, 23, 24 hence, several ongoing clinical trials are using TMB as a key stratification factor for checkpoint therapies.25 However, not all mutations give rise to immune‐stimulating neoantigens. In other words, although elevated TMB increases the chance of generating immunogenic neoantigens, it may not directly reflect the number of neoantigens that will actually be targeted by T‐cells. Application of NGS to tumor samples has facilitated the generation of bioinformatics tools and databases that predict neoantigen burden in different tumor types, which can directly be used to parametrize antigenicity in mechanistic models. The Tumor‐Specific NeoAntigen database26 provides neoantigens specific to 16 tumor types derived from 7,748 tumor samples from TCGA and The Cancer Immunome Atlas.27 The database provides predicted binding affinities between mutant and wild‐type peptides and HLA class I molecules by NetMHCpan.28 Therefore, a tumor antigenicity parameter that is empirically calibrated against clinical data—for example, by adjusting the rate of T‐cell recruitment or scaling the amount of “effective” antigens produced by dying tumor cells—can now be parametrized by the above mechanistic approach. Remarkably, synthetic peptides designed by translation of altered DNA sequence have been used to create antitumor CAR‐T cells in a landmark example of personalized treatment.29 We note that this strategy has been already applied in QSP platform models of therapeutic protein antigenicity, where well‐established bioinformatics approaches were used to predict T‐cell epitopes and MHCII receptor binding affinities.30, 31, 32, 33 Quantitative assessment of antigenicity can be further informed by high‐throughput ex vivo assays16 used to determine naïve T‐cell precursor frequencies, as demonstrated in our example. Single‐cell sequencing of T‐cell receptors may contribute further insight. Integration of all these data will allow prediction of antigenicity and its biological variability for a particular cancer, informing prospective simulation of a virtual trial before any clinical data for a therapy of interest are available.

A QSP model of the cancer immunity cycle simulates the response of a healthy immune system to a growing tumor. Therefore, information about the baseline state of the immune system and its biological variability in a healthy‐individual population is key for model parameterization. Obviously, the white blood cell count in peripheral blood is one of the most frequently conducted diagnostics and reference ranges based on very large sample sizes are available. However, the resolution of these data is very limited, with all lymphocytes (T‐cells and B‐cells) and monocytes (macrophages and dendritic cells) pooled together. Recent high‐throughput flow cytometry studies provided unprecedented insight into cellular composition of peripheral blood in healthy individuals. In particular, “The Milieu Intérieur” resource contains results of high‐throughput flow cytometry of 166 immune cell types in peripheral blood of 1,000 individuals.5 The sample size is sufficient to compile baseline distributions of cell numbers at different age groups, as well as in individuals subject to infection and healthy individuals (Figure 1 c). Other high‐resolution flow cytometry studies of peripheral blood have also recently become available (Table 1).

Because of immune system cell proliferation, peripheral blood measurements may poorly reflect the state of the healthy immune system in tissues. The lymph node compartment, where recruitment of neoantigen‐specific T‐cells by APCs takes place, is of particular interest. In a series of recent studies, Farber’s group applied high‐throughput flow cytometry to organ donor tissues to quantitatively describe the state of the immune system in healthy individuals.13, 14, 15 These unique data provide insight into relative distributions of multiple T‐cell types and dendritic cells among different tissues, including lymph nodes. Thome et al.13 studied tissues from 56 donors and determined the distribution of CD4 and CD8 T‐cells in peripheral blood, spleen, inguinal lymph node (draining the peripheral skin and muscle), lung‐draining lymph node, lungs, mesenteric lymph node (draining the intestines), small intestine (jejunum and ileum), and colon. Both CD4 and CD8 T‐cells were separated into naïve cells, terminally differentiated effector cells, central memory cells, and effector memory cells. The dataset was sufficiently large to analyze distributions specific to age groups. In another contribution,14 tissues from 78 donors were analyzed to determine the distribution of two dendritic cell subsets in peripheral blood, bone marrow, tracheal lymph node, lung lymph node, pancreatic lymph node, mesenteric lymph node, lungs, jejunum, ileum, colon, and appendix. Crucially, mature and immature dendritic cells were separated. We note that a QSP model relevant to IO is unlikely to require calibration of baseline immune system at this level of tissue resolution. A more likely scenario would entail using data obtained for lymph nodes with the full resolution of cell types. The difference between clinical omics data and classical measurements of clinical biomarkers is that the latter contain observations at the whole system scale, rather than specific biomarkers relevant to a particular clinical question. This, in our view, maximizes the use of precious clinical material for collection of baseline data—largest possible number of biomarkers are recorded in each sample to subsequently allow scientists working on many different projects to query these data and find baseline reference biomarker values relevant to their investigation. For example, the baseline composition of jejunum is unlikely to be relevant for an IO QSP model, but may be relevant for the models of other diseases.

As demonstrated in our example calibration of the minimal CIC model and indicated in Figure 5, we recommend using clinical data on patients’ response to treatment to calibrate parameters describing tumor killing by T‐cells and the influence of the drug target occupancy on checkpoint action. This requirement will not limit prospective QSP platform application in its major context of use, which is discovery and validation of combination targets. For many, if not most, of the targets, which are considered for combinations, clinical data are already available from a study where the target was part of a single drug therapy or a combination. Thus, the model calibrated with the use of publically available clinical data can be used to predict efficacy of novel combinations of drugs doses, timings, and sequences, which were previously not tested in the clinic. This addresses the major challenge of a combinatorial explosion of possible combination therapies, which cannot all be evaluated by clinical trials. Apart of prohibitive costs of a large number of trials, it would not be possible to recruit sufficient number of subjects to test all possible combinations. The virtual trial simulation could inform decisions on which compounds, dose amounts, timings, and sequences are most promising in combination and, thus, should be taken forward to the trial. Moreover, the QSP platform model could also be used to discover identities of potential targets to be combined with the drug for which single‐drug treatment data are available. This could be achieved by sensitivity analysis for highlighting model variables and parameters (potential targets) perturbation of which would increase efficacy of a single‐drug treatment.

Discussion

In this tutorial, we discuss how recent, high‐throughput, molecular and cell biology datasets can be integrated within the framework of mechanistic QSP platform models. We illustrate our discussion by an example calibration of the minimal QSP model of the CIC for NSCLC treatment with pembrolizumab. We argue that integration with mechanistic modeling expands the applicability of these data, which are obtained from unique clinical material, such as clinical tumor biopsies or organ‐donor tissue samples.

First, the mechanistic model connects the wealth of omics data to PKs and PDs and, thus, to the determination of the optimal dose, timing, and sequence of drugs for combination therapy. So far, these data have been analyzed mostly by statistics and machine learning and the words “dose” and “amount” usually do not feature in the analysis protocol. Thus, mechanistic QSP platform models have great potential for fully capitalizing on invaluable data resources to inform decisions on which amount of which substances should be given to whom and with what dosing regimen. Second, mechanistic models use extensive high‐resolution snapshots of the state of tumor biopsies and the healthy immune system to make predictions of systems dynamics and, as a consequence, longitudinal clinical efficacy biomarker information (e.g., tumor size). Given the intricate network of feedbacks involved in the CIC, biomarker responses to drug doses are nonlinear, counterintuitive, subject to complex delays, and sensitive to administration timing and sequence in combination therapy. Mathematical models of the complex immune system and tumor growth dynamics are, therefore, key for making full use of experimental data. Finally, we show that a mechanistic model of the CIC cannot only integrate data collected from tumor biopsies, but also capitalize on the wealth of data collected on the healthy immune system. We show how unique high‐resolution flow cytometry studies of healthy organ‐donor tissues can be used in the context of IO, despite this not being a primary reason why such data were collected. In general, mechanistic models have a unique capability of extrapolating from data collected in different clinical circumstances and, thus, capitalizing on a whole corpus of available knowledge and data for the benefit of a particular drug development project.

Our example QSP model of the CIC, although limited in scope and applicability, already illustrates a type of important prediction for which integration of omics data with mechanistic model is, in our opinion, the method of choice. We present a virtual trial simulation describing the variability of patients’ responses to therapy of a specific human disease: NSCLC. Differences in individual patient outcomes, ranging from long‐term benefit to no response at all, are the major challenges in IO. Because clinical determination of response variability requires a large number of subjects, and the ability to predict variability for a new dosing regimen or combination before a trial is conducted, would make a big impact on drug development. Differences in the TME infiltration in individual patients are a major cause of different clinical outcomes. The Immune Landscape of Cancer for the first time provides a resource allowing determination of the baseline population distribution of leukocyte frequencies in a specific tumor. There is no other resource, which clinical team designing new trial could query for baseline population distributions of 22 leukocyte types in 33 human diseases. Even in the case of just two cell types included in our model, it would be very difficult to identify published datasets, where cytotoxic T‐cells and antigen presenting cells were quantified simultaneously in a large enough number of patients with NSCLC to provide distributions shown in Figure 3. Although this information could be valuable to the team in its own right, the QSP model adds further value by extrapolating from these unique baseline data to the time profiles of clinical biomarkers and, thus, variability of patient responses. Whereas in our example, we used clinical tumor size time profiles from 4 subjects to refine parameters describing cytotoxic T‐cell action, we would still provide extrapolation to much larger population of 489 subjects before they entered the trial. In realistic application of mature QSP platform to assess new combination therapy candidate, clinical data for individual compounds are very likely to be available from previous trials, where the compounds were already tested individually or in other combinations. In this scenario, the QSP model calibrated by omics resources and clinical data from previous trials would be used to predict variability of patients’ responses to new combination therapy before it is tested in the clinic. The virtual trials could be simulated for a large number of possible combinations of compounds, doses, timings, and sequences that would arise in consideration of even a few combination candidate drugs. Predicted outcomes would then inform decision on the selection of best possible combination to be clinically tested. This would be of great value to a clinical pharmacology team as it would otherwise not be possible to test all alternative combination therapies due to the cost as well as limited availability of clinical subjects.

Because the Immune Landscape of Cancer was published only recently, we are not yet able to directly compare the benefits of using the modeling approach proposed here with traditional methods of dose selection. None of the programs currently using QSP models calibrated by these data to inform early stage decisions have been completed yet. However, due to combinatorial explosion of candidate therapies, preventing clinical assessment of all plausible therapeutic options, modeling approaches are necessary to support decisions. Otherwise, there is no other option but to make an educated guess. Modeling approaches currently established in clinical drug development are based nonlinear mixed effects methods, which statistically infer average behavior and random effect from clinical data. This approach is well established for precise interpolation within the range of already recorded clinical data, but there is little scientific rationale that it performs well to extrapolate across biological systems. Extrapolation requires large‐scale mechanistic model capturing interactions between key variables and sufficient data to calibrate the model. The application of QSP as an approach of choice for extrapolation among different species, diseases, populations, and therapies is quickly gaining recognition.34 Here, we demonstrate how the applicability of QSP could be further extended by integration with omics data, which provide unprecedented insight into baseline patient variability. Despite astonishing recent developments of measurement capabilities in the biological sciences, there are still areas where additional research could significantly improve our ability to make quantitative predictions of combination therapy efficacy in IO. Given the effort invested into high‐resolution studies of the cellular composition of the healthy immune system, it is surprising that only relative data are available for tissues and that it is very difficult to find any reference absolute cell numbers. Although we understand that absolute cell count measurement is much more difficult in tissues than in peripheral blood, absolute data would be invaluable for pharmacology. When the drug is dosed it is its absolute amount that is specified, and it is an absolute amount of drug at the site of action, and an absolute amount of its pharmacological target that determine efficacy. Therefore, a rational selection of doses—informed by quantitative modeling rather than a costly and risky trial‐and‐error process—requires absolute quantitative data. In our example study, we have used the number of lymphocytes in tissues estimated by Trepel (1974) as a reference.17 We then multiply this reference absolute number by cell frequencies obtained in high‐resolution studies. Thus, what is required is a contemporary estimation of a reference, total, absolute leukocyte count in tissues, in addition to high‐throughput, high‐resolution measurement of absolute counts of multiple cell types.

A possible weakness of a mechanistic model informed by omics data is that some of the quantities used for model calibration are results of bioinformatics predictions rather than direct measurement. In particular, the tumor microenvironment composition has been calculated by DNA sample purity analysis and deconvolution of bulk expression data to calculate the contribution of 22 gene expression signature patterns.4 The methods, such as CIBERSORT,35 used for deconvolution are validated against immunohistochemistry data and their accuracy is known and acceptable. Moreover, the next generation of these approaches is currently under development, where improvement of predictive power is achieved by availability of new types of data.2 So far, gene expression signature patterns used for deconvolution were obtained from transcriptome data of purified leukocyte fractions. Recently, single‐cell sequencing enabled the definition of these patterns based on analysis of single cells in the tumor microenvironment.36 We agree with the authors of these approaches that using transcriptome data collected for single cells in the tumor microenvironment will increase the accuracy of the deconvolution of bulk transcriptomics data. Moreover, no experimental approach to cell‐type determination is free of assumptions and data analysis. Immunohistochemistry and flow cytometry are subject to gating of fluorescent signals and limited to a small number of surface markers. One may argue that the behavior of an individual differentiated cell is determined by its gene expression state and that analysis of global gene expression programs directly may, in the future, allow better definition of the cell‐type composition of the tumor microenvironment than currently accepted experimental methods.

Another area where we rely on bioinformatics analysis of NGS data is the determination of tumor antigenicity. Although the identity of DNA and protein sequences of neoantigens is directly determined by sequencing, the affinity of these peptides to MHCI and MHCII receptors is predicted by machine‐learning approaches.26, 37 In this way, mechanistic models could integrate not only big data but also an application of machine learning to their analysis. The algorithms used for affinity predictions are mature, validated by comparison with binding data, and commonly applied since the late 1990s.38 Still, we hope that increasing adoption of NGS as a diagnostic technique and determination of neoantigenic peptides will also motivate experimental determination of binding affinities and T‐cell precursor pools in ex vivo and in vitro assays.

Conclusions

In summary, we show how mechanistic models of cancer immunotherapy in humans can be informed by state‐of‐the‐art molecular and cell biology data on clinical tumor biopsies and samples of healthy peripheral blood and tissue, which have recently become available. Mechanistic models expand the applicability of these data beyond target identification and biomarker discovery—they allow quantitative predictions of dose amount sequence and timing. Although there are still gaps in quantitative knowledge, which necessitate incorporation of machine‐learning predictions and model assumptions, we expect that recent publication of landmark omics resources in IO will motivate further effort and that much more data will be available soon. We also hope that increasing adoption of mechanistic modeling to integrate these data will direct experimental work, especially in areas where absolute reference data are needed. We are convinced that, as new omics data accumulate, confidence in virtual trial simulations with clinical QSP models integrating these data will increase, and that these models will be making increasing impact in development of new cancer immunotherapies.

Funding

No funding was received for this work.

Conflict of Interest

As the Editor‐in‐Chief of Clinical Pharmacology & Therapeutics, Piet H. van der Graaf was not involved in the review or decision process for this paper. All other authors declared no competing interests for this work.

Supporting information

Supplementary Information for the Manuscript.

Figure S1.

Model Code.