On the molecular mechanisms regulating animal cell size homeostasis

Abstract

Cell size is fundamental to cell physiology because it sets the scale of intra-cellular geometry, organelles, and biosynthetic processes. In animal cells, size homeostasis is controlled through two phenomenologically distinct mechanisms. First, size-dependent cell cycle progression ensures that smaller cells delay cell cycle progression to accumulate more biomass than larger cells prior to cell division. Second, size-dependent cell growth ensures larger and smaller cells grow slower per unit mass than more optimally sized cells. This decade has seen dramatic progress in single cell technologies establishing the diverse phenomena of cell size control in animal cells. Here, we review this recent progress and suggest pathways forward to determining the underlying molecular mechanisms.

Importance of cell size control in animal cells

Size is one of the most fundamental characteristics of life and has a large impact on animal and cell physiology [1]. Cell size sets the scale of subcellular compartments, cellular biosynthetic capacity, metabolism, mechanical properties, surface-to-volume ratios, and molecular transport [2–8]. Thus, cell size is tightly associated with cell function and metabolism so that different types of cells vary enormously in size [9, 10]. For example, erythrocytes, lymphocytes, and sperm cells are tiny because they have to migrate through tight spaces, while muscle cells are large and elongated to generate and maintain high mechanical force. While cells of different types tend to vary in size, cells within a type are uniform in size, and visible size alterations are often associated with disease states. For example, the coefficient of variation (CV) of the size distribution of red blood cells is used as a common diagnostic parameter in comprehensive blood tests, and many cancers, such as small cell lung cancer, are characterized by altered cell size [11–15].

Over the last century, there have been numerous studies cataloging cell size distributions across the tree of life (for example, see [10, 16, 17]). However, despite all these observations, the underlying molecular mechanisms have remained largely unknown. Here, we will discuss recent developments that shed some light on the century-old problem of how animal cells couple growth to division to regulate their size. We note that this review focuses on animal cells and we only sporadically draw on yeast and bacteria literature to inform our discussion. The extensive literature on micro-organism size control has been reviewed elsewhere [18–21].

Cell size is determined by the balance of cell growth and division

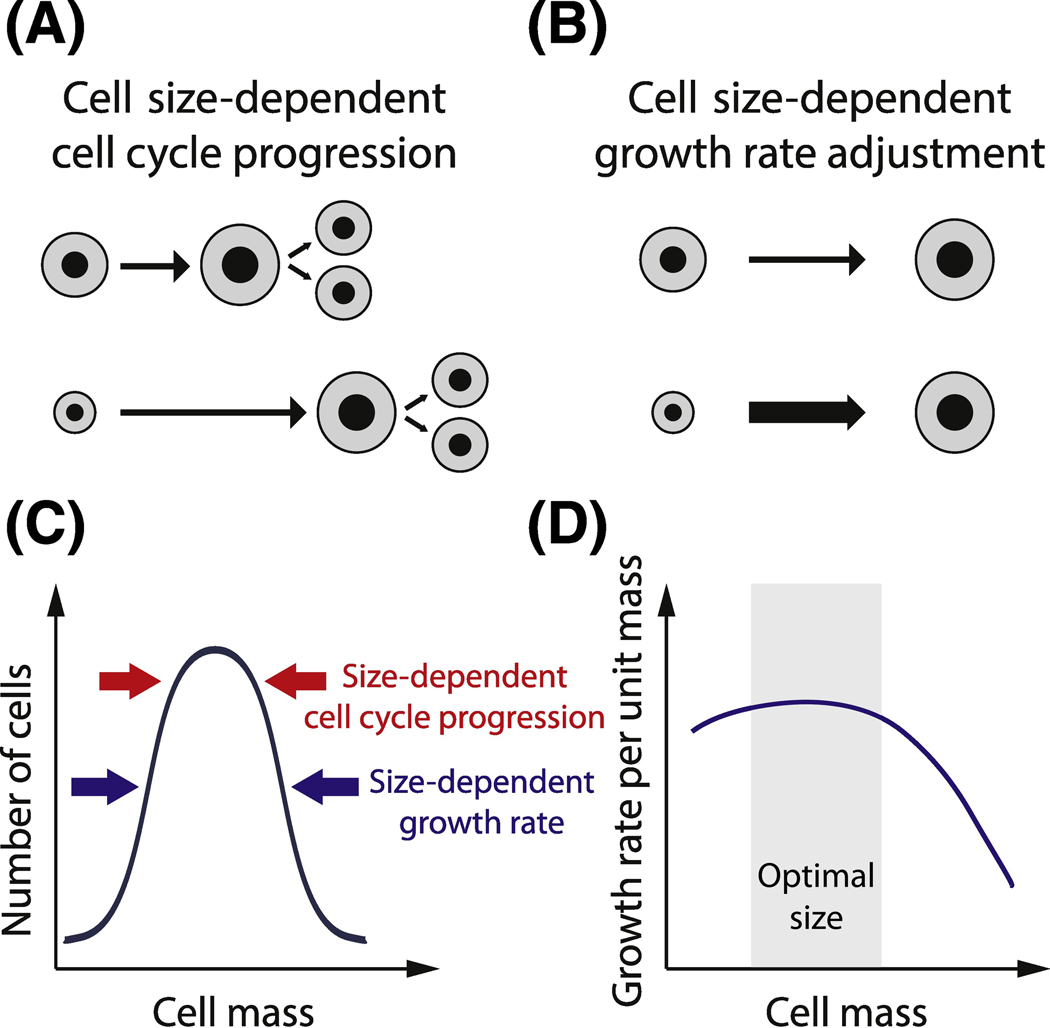
Animal cells maintain size homeostasis through two distinct classes of mechanisms (Figure 1 A–C) [22, 23]. The first mechanism class is size-dependent cell cycle progression so that larger cells transition through the cell cycle to divide earlier than smaller cells. This mechanism promotes size homeostasis because it results in smaller cells spending more time in the cell cycle and therefore growing more than the initially larger cells. The second class of mechanism is size-dependent adjustment of growth rate, in which cells closer to the target size grow more rapidly than smaller or larger cells. Here, growth rate refers to the mass accumulation rate per unit mass. We note that this form of homeostatic cell level size control is distinct from the size “control” phenomena where cells of different cell types or in different environmental conditions modulate their average size.

Figure 1. Balance of cell growth and division determines cell size homeostasis.

A. Cell size-dependent cell cycle progression: smaller cells spend more time in certain phases of the cell cycle and grow more than larger cells. B. Cell size-dependent growth rate adjustment: smaller cells accumulate biomass faster than larger cells. C. Cell size homeostasis is achieved through both cell size-dependent growth rate adjustment and cell size-dependent cell cycle progression. D. Cells closer to the optimal size are more efficient and grow more rapidly than smaller or larger cells.

Through size-dependent growth rate mechanisms, cells closer to a target size outcompete the slower growing cells at the extremes of the size distribution to maintain size homeostasis across the population (Figure 1B,D). In tissue culture, poor growth at larger and smaller sizes was linked to poor mitochondrial function [24], but, in general, we understand little of the molecular mechanisms through which cell size regulates the cell growth rate in animal cells as cell growth rates are only now being measured with recent technical advances (Box 1). We note here that we are considering cell size to determine a cell’s instantaneous growth rate. However, this relationship may well be more complex and depend on the cell’s history of cell cycle progression and previous cell growth that impacts the cells biochemical composition [25–33]. One way forward to untangle this relationship is to combine quantitative measurements of single cell growth over a cell division cycle with genomic approaches such as single-cell RNA sequencing [34]. We look forward to understanding cell growth more quantitatively, and to understand the molecular mechanisms linking cell size and cell cycle phase to the cell’s growth rate. Certainly, becoming too large is not good for cell growth. In yeast cells, the defects of being too large have been carefully described – the cytoplasm is diluted, transcription rates fail to keep pace with growth, and gene regulation is slowed – but, here too the molecular mechanisms through which large size leads to these defects and their interdependence is unclear [35, 36]. The genome has something to do with size-dependent growth breaking down in large cells in yeast because diploids grow to twice the size before exhibiting defects [36]. Thus, size-dependent growth rates arise due to either too much cytoplasm for the genome to support or too little cytoplasm to support the genome. Some theoretical work has been performed to explore how genome, protein synthesis and cell size are coupled [33], however, what cell defects arise at the extremes to slow proliferation remain largely unknown. Moreover, cell size in a multi-cellular context may not be optimized for proliferation so that the optimal size, where cells grow fastest, may be different from the target size of the cell size control mechanism.

Live cell imaging and cell cycle stage reporters

Objective:

Measure correlations between cell size, growth, and cell cycle progression in single cells.

Progress and achievements:

Live cell imaging microscopy with fluorescent cell cycle reporters can be used to monitor cell cycle transitions.

FUCCI (Fluorescent Ubiquitination-based Cell Cycle Indicator) reporter consists of two parts – the red mKO2-hCdt1, expressed in G1 and degraded during G1/S, and the green mAG-hGeminin, expressed in S/G2 and degraded during mitosis [91]. Modifications of this system include additional components for more precise determination of the cell cycle phase [92–94].

Another approach uses the fluorescently labeled PCNA protein, whose amount and intracellular localization pattern can also be used to determine the cell cycle stage of the cell. Endogenously-tagged PCNA can also be used to distinguish G0 from G1 [76].

Limitations and perspectives:

More automated image analysis and efficient storage and sharing of the large imaging datasets is needed.

Accurate live-cell measurements of cell size and growth rate

Objective:

An accurate and high throughput method for measuring cell size dynamics in animal cells is needed. Challenges:

• -simple geometric approach widely used to measure cell size in spherical or ellipsoidal bacterial and yeast cells is not applicable for highly dynamic and irregularly shaped animal cells
• -3D confocal microscopy and volume reconstruction is very sensitive to inaccuracies in cell segmentation, is relatively slow, and can cause phototoxicity in live-cell experiments
• -cell size is interpreted differently by different researchers and could mean cell volume, dry mass of the cell, or total protein content – while often correlated, these quantities are not always equivalent [35, 95, 96].

Progress and achievements:

In the last decade several methods have been developed that give unprecedented accuracy for cell size measurements including:

• -a confined microchannel forcing cells into a cylindrical shape [39]
• -fluorescent dye exclusion from a low-ceiling imaging chamber [23, 27]
• -high-throughput dry mass measurement with quantitative phase microscopy [28, 97]
• -buoyant cell mass measurement with an oscillating microchannel cantilever resonator [95, 98]
• -nuclear size measurement as a proxy for cell size [22, 74]
• -total cellular protein measurement with nuclear-localized constitutively expressed fluorescent protein or total protein dyes [26, 99].

These methods are accurate enough to track cell growth rate through different phases of the cell cycle, or detect the ~10% cell volume swelling during mitosis [35, 95, 96]. Moreover, these single-cell size measurements can be combined with single-cell RNA sequencing to determine molecular features associated with cell size [34].

Limitations and perspectives:

Better software is needed to automatically track and analyze growing and dividing cells. It is unclear how to apply these techniques in vivo.

CRISPR/Cas9-mediated endogenous gene tagging and gene-deletion screens

Objective:

Identification of molecular pathways controlling cell size requires measurements of regulatory protein concentration and localization dynamics during cell growth through the cell cycle.

Progress and achievements:

CRISPR/Cas9 genome editing allows tagging of endogenous genes to measure protein concentration and localization dynamics through the cell cycle. This knock-in technology was used to fluorescently tag cell cycle activators and inhibitors including cyclins, the cyclin-dependent kinase inhibitor p21, and the retinoblastoma protein RB [51, 76, 100, 101]. Simultaneous measurements of cell size, cell cycle phase and these regulatory protein’s dynamics have led to the discovery of the inhibitor-dilution mechanism of cell size control [51]. In addition, high-throughput deletion screens examining cell size should now be possible in animal cells [102].

Limitations and perspectives:

CRISPR/Cas9-mediated knock-in cell line generation is still slow.

While one generally expects size-dependent growth rates to both exist and to support size homeostasis, this mechanism relies on growth being inefficient and slow in a subpopulation of cells at the larger and smaller ends of the cell size distribution. To avoid inefficient growth, cells use active size control mechanisms to accelerate progression through the cell cycle in larger cells [2]. This ensures that smaller cells have more time to grow in the cell cycle than the initially larger cells (Figure 1A). The first evidence of size-dependent cell cycle progression was provided over 50 years ago, when Killander and Zetterberg showed that cell size at cell birth negatively correlates with the time cells spend in the G1 phase of the cell cycle [37, 38]. Recent single-cell studies confirmed this phenomenon of G1 size control but did not provide a clear molecular insight into how cell size is coupled to cell cycle regulation [22, 23, 39].

Size control phenomena

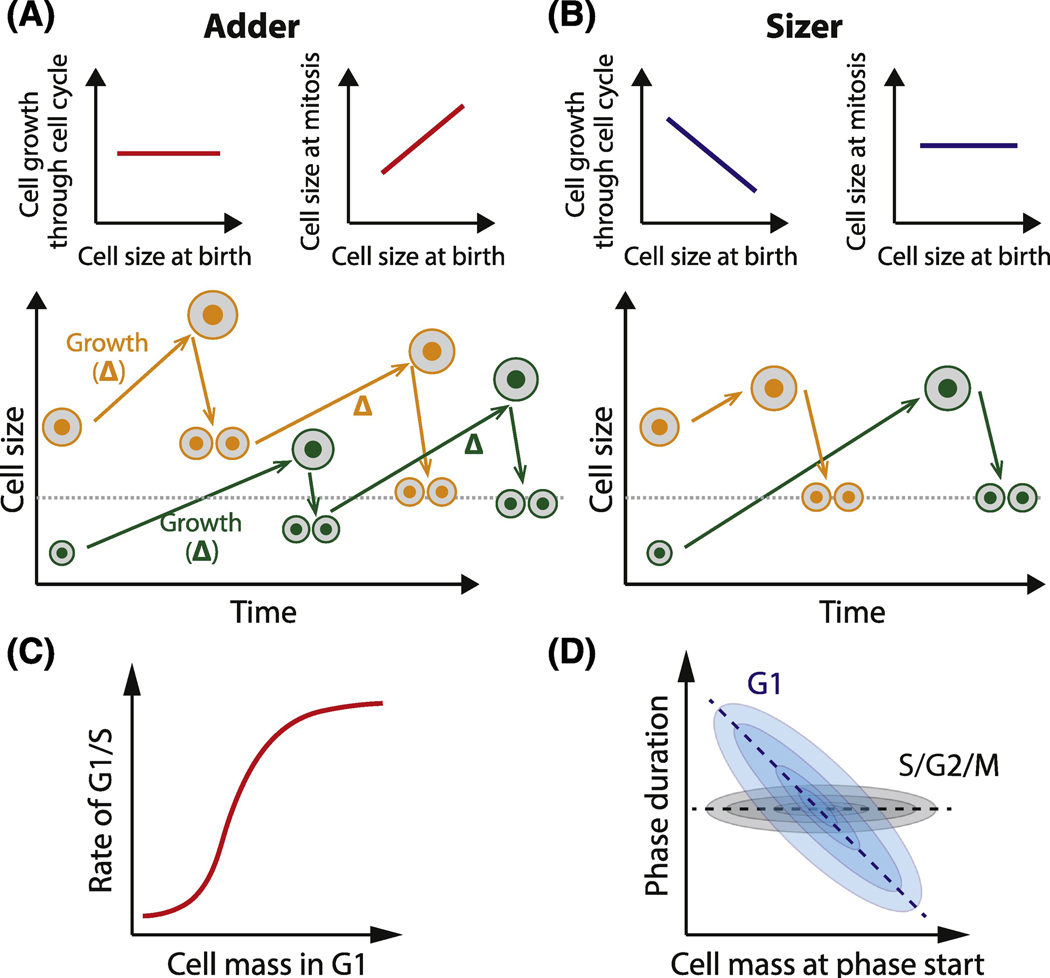
In recent decades, several phenomenological models have been used to describe cell size control. One popular model is called an ‘adder’ (Figure 2A). In an adder, a larger cell will add the same amount of volume or biomass as a smaller cell before dividing so that cells approach the target size over several generations [40]. Importantly, the adder model makes no specific claim on the size-dependence of cell growth and several variants of adder models have been proposed. One long-standing adder variant entails mass accumulating at a constant rate through the cell cycle and a timer triggering division after a fixed time [41]. Subsequently, adders with different growth kinetics have been observed in a wide variety of contexts including bacteria, yeast, and mammalian tissue culture cells [41–44].

Figure 2. Phenomenological models of cell-size-dependent cell cycle progression.

A. Adder model: all cells, small and large, add the same amount of mass through the cell cycle. Consequently, cell size converges to the target value over a few generations. The target value is equal to the increment by which the cells grow through a cell cycle. B. Sizer model: all cells, small and large, divide (or complete a certain phase of the cell cycle) when they reach the same target size. The target cell size is achieved within one generation. C. Stochastic G1/S sizer: larger cells have a higher rate of G1/S progression than smaller cells. This process is probabilistic, as opposed to a deterministic sizer where G1/S passage is determined by a fixed cell size threshold. D. Mammalian cells demonstrate a stochastic G1 sizer and stochastic S/G2/M timer. G1 duration is variable but it is negatively correlated with the cell size at birth, while S/G2/M duration is more size-independent.

An alternative cell size control model is called the ‘sizer’ (Figure 2B). In a sizer, the cell has to be a certain target size to progress through the cell cycle [45]. For example, it was proposed that mammalian cells have to grow to a threshold size to pass the G1/S transition and start DNA replication. While adders require several generations for the cells to correct for birth size deviations, sizers allow cells to hit a target size in a single cell cycle. Sizer-like relationships have been observed in some yeast, as well as in plant and mouse epidermal stem cells in vivo [46–48]. We note that not all observations neatly fit into the adder and sizer models. Intermediate phenomena are frequently observed, and stochastic effects need to be considered [23, 39].

Cell-to-cell variation and stochastic sizers

The simplest versions of the sizer and adder models are deterministic and therefore do not capture the extensive cell-to-cell variability that is frequently observed in single cell studies. In mammalian cells, G1 is the most variable phase of the cell cycle and is the most sensitive to cell size variation. Larger cells progress through G1 more rapidly than smaller cells, but there is not a fixed cell size threshold. Rather, the rate at which cells progress through G1 increases with cell size (Figure 2C). In a stochastic sizer, both larger and smaller cells can pass G1/S at any time, but the probability (or the rate) of progressing through G1/S increases with cell size. For a pure stochastic sizer, this size-dependent rate of cell cycle progression should be independent of the amount of time the cell has spent in the cell cycle, as was found in a linear regression analysis of budding yeast G1/S control [49, 50]. In other words, in a given period of time, it is more likely for a large cell than a small cell to transition through G1/S. While imperfect, stochastic sizers allow smaller cells more time, on average, to grow to the G1/S target size than larger cells. Once a mammalian cell has passed G1/S, the rest of the cell cycle usually takes a fixed size-independent amount of time, albeit with some cell-to-cell variation (Figure 2D) [23, 51]. To capture single cell variation in cell cycle phases, stochastic versions of sizer and adder models have been developed [52–55].

The extent of observed cell-to-cell variation raises a question as to where it comes from [56]. In yeast, which are small, about half the variation was attributed to stochastic fluctuations in molecule numbers, most likely the small numbers of mRNAs of specific G1 regulators [57, 58]. While animal cells are bigger, and have much higher absolute numbers of mRNAs, there are only two copies of each gene in G1 and there has been observed extensive variation in transcriptional activity between two alleles [59]. An additional source of variability in animal cells comes from the fact that multiple intra- and extracellular signals, such as circadian signals, have to be integrated to make an irreversible decision to enter the cell cycle [60–67]. This cell-to-cell variation in the activities of additional pathways may contribute to cell-to-cell variation in cell cycle kinetics [68, 69].

From size control phenomena to molecular mechanism

The frequent observation of adder phenomena suggested there could be a common underlying molecular mechanism [42]. However, studies of budding yeast provide a cautionary tale questioning this assumption. In budding yeast, an adder was observed for the entire cell cycle. However, this adder was not the result of an overarching molecular mechanism working across the entire cell cycle and sensing the amount of added biomass [50]. Rather, the adder arose from a combination of two independent processes: a size-dependent G1 (a stochastic G1 sizer) and a largely size-independent S/G2/M, only slightly modulated by bud size and mother size at the beginning of S/G2/M (resulting in a behavior close to a stochastic S-G2 Timer) [70, 71]. These processes were observed to operate independently. Mutations to genes affecting G1 duration did not affect S/G2 duration, and so the changes in G1 growth were not compensated later in the cell cycle and the adder was broken [50]. Thus, the adder phenomenon is an emergent property resulting from the independent events occurring in different phases of the cell cycle, rather than the consequence of an underlying molecular mechanism measuring the added volume. A careful study of tissue culture cells came to a similar conclusion [23, 37]. Again, the adder was the result of a size-dependent G1 (albeit a weaker size-dependence) and a largely size-independent G2. This resulted in smaller cells growing a bit more in G1 and a bit less in S/G2 so that the total growth through the cell cycle was largely independent of cell size.

Size control in vitro and in vivo

The growth of cells in vitro has revealed a variety of size control phenomena that can be characterized quantitatively by plotting the size of a cell at the time of entry of a cell cycle phase against the size of the cell at the time of exit of that phase. Pure adders have a slope of 1 and pure sizers have a slope of 0. Most tissue culture cells exhibit slopes closer to 1 than 0, but they are not pure adders (see Figure 2B in [23]). In addition, the same cell line can exhibit different behaviors depending on birth size. Rat basophilic leukemia cells and RAW 264.7 macrophages were shown to be sizers when born small, but adders when born large, much like what has been seen for fission yeast [39].

The variation of size control phenomena in vitro raises the question as to what are the best models to study. Clearly, the best in vitro models would recapitulate in vivo physiology. However, until recently there was no similar examination of cell size control in vivo in mammalian cells due to its technical difficulty. Despite the technical difficulty, a recent work measured cell growth and division in vivo by analyzing images of skin regions on the mouse hindpaw over one week [48, 72]. Quantification of the 3D volume growth and cell cycle progression of epidermal stem cells revealed that cell growth is coupled to division through a sizer mechanism operating largely in the G1 phase [48]. That is, regardless of their size at birth, cells transition through G1/S at similar sizes. Thus, while in vitro tissue culture studies mostly identified adder mechanisms, sizer mechanisms are clearly important in vivo and some attention should be given to recapitulating this phenomenon for its molecular study in vitro. Importantly, we note that this is just one example, and other cell types may use different size control mechanisms in vivo. It will be exciting to see how size control is implemented across the diverse animal cell types.

Genetic approaches to discovering cell size regulators identify a p38-dependent mechanism

While phenomenological studies of size control indicate that G1 is an important control point linking growth and division, they do not immediately suggest a molecular mechanism. The genetics of size control mechanisms have been most studied in yeast and some principles have emerged that are likely to become important for mechanistic studies in animal cells. In budding yeast, average cell size can be altered by the mutation of hundreds of genes either through deletion, overexpression, or chemical inhibition [73]. Any mutation affecting cell growth also affected cell size in a predictable, monotonic relationship: the slower the growth rate, the smaller the cell. By screening for mutants that deviated from this average size-growth rate trend, genes that were more specific to size control were identified. While this set of genes included many cell cycle mutations affecting various regulatory steps in the cell division cycle, it did not immediately suggest a size control mechanism. It is therefore clear that a more sophisticated genetic approach is required to crack the size control problem.

One such attempt was a small molecule screen examining the joint effects on cell size and cell cycle phase distributions [74]. Most molecules that slowed growth resulted in smaller, predominantly G1 cells. This was interpreted as being due to a G1/S size control mechanism that extended G1 to allow more time for the slower-growing drugged cells to reach a size threshold. Molecules that disrupted this relationship between size and cell cycle distribution were interpreted as disrupting the size control mechanism. This approach identified a series of p38 stress activated protein kinase pathway inhibitors and suggested that p38 may play an important role in restricting the G1/S transition in small cells. However, follow-up analysis was performed in tissue culture cells that had only weak G1 size control, i.e., there was only a weak inverse correlation between cell size at birth and the duration of G1. While p38 inhibition likely slightly reduced this weak correlation even further, it would be informative to see this analysis performed on a cell line having a stronger correlation between G1 duration and cell size at birth so the effect could be larger. In any case, the p38 pathway is an exciting avenue of research for the mammalian size control field and it will be interesting to see if and how the p38 pathway is differentially activated in small cells.

Examining size-dependent gene expression identifies an RB dilution mechanism

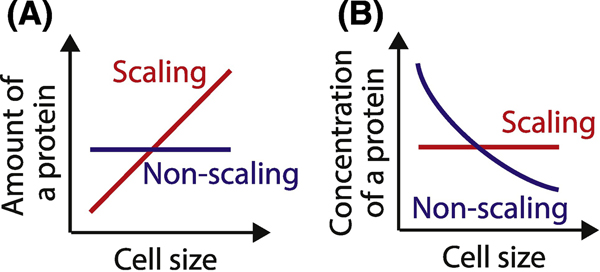
Most cellular components scale proportionally with cell size. This is true both for subcellular organelles, such as the nucleus, and macromolecular complexes, such as the number of ribosomes [3]. The linear scaling of volumes and molecules ensures that the concentrations of most biomolecules remain constant as the cell grows. In addition, the concentration of most mRNA remains constant, as their transcription generally increases in proportion to cell size [33, 68]. Taken together, the linear scaling of proteins and mRNA with cell size likely helps to maintain biochemical reaction rates independent of cell size and thereby promote efficient cell growth over an optimal size range.

That most proteins remain at a constant concentration during cell growth led to the general question as to how a size-dependent signal based on these proteins could emerge. This general question is circumvented in budding yeast by the fact that some proteins were not in fact at constant concentration during cell growth (Figure 3). It was found that cell growth in G1 leads to the dilution of Whi5, which is an inhibitor of the SBF transcription factor that functions like the animal activating E2F factors to drive progression into S phase [46]. In contrast to all the other examined cell cycle regulators including the upstream G1 cyclin Cln3, Whi5 concentration decreases in approximately inverse proportion to cell size so that the rate of entry into the cell cycle through the G1/S transition increases as cells grow larger. This mechanism ensures that smaller cells spend more time in G1 on average and therefore grow more in G1 than larger cells. Importantly, the slower the yeast grow, the smaller they are when they are born and the more important the Whi5 dilution mechanism becomes [58].

Figure 3. Scaling and non-scaling expression of regulatory proteins.

A. The amount of a scaling protein in the cell is proportional to cell size, while the amount of a non-scaling protein does not increase in proportion to cell size. B. Concentration of scaling proteins remains constant across different sizes, while non-scaling proteins are diluted by cell growth.

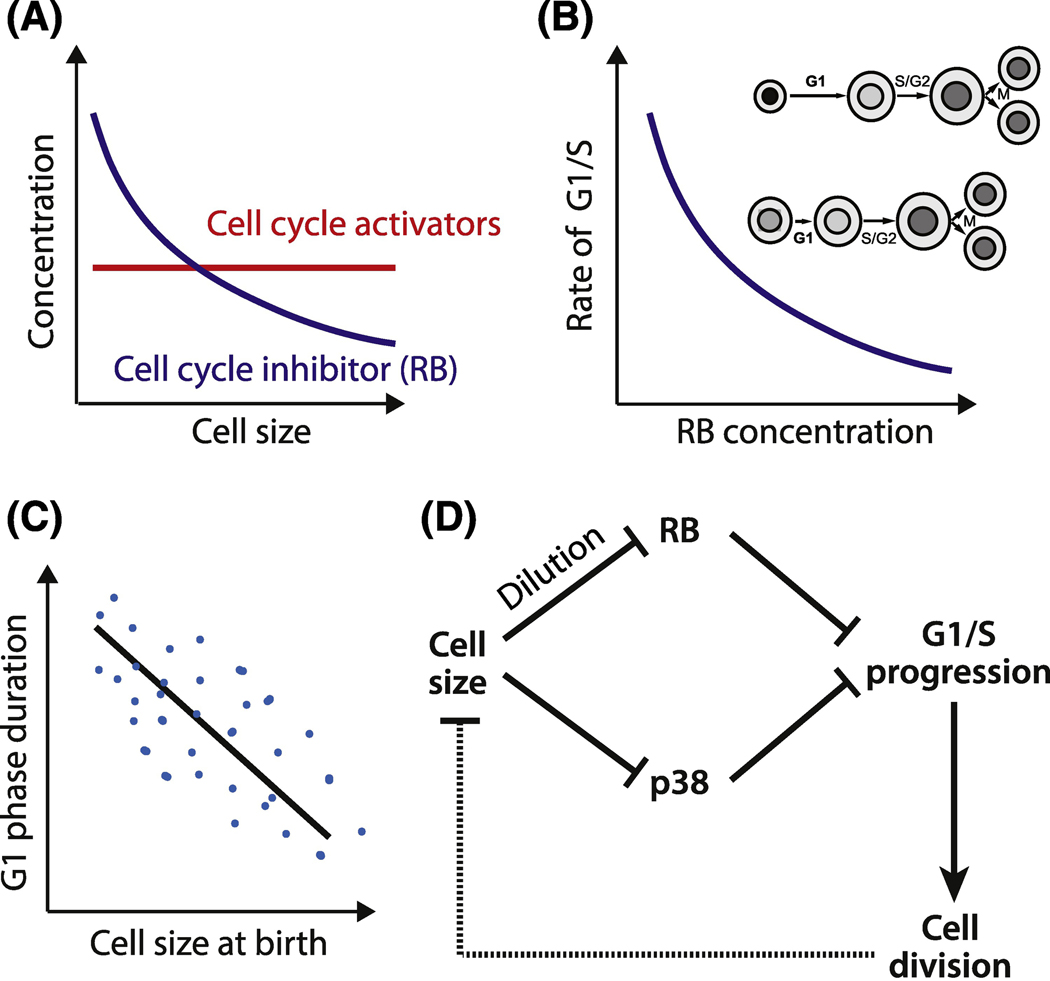
The discovery of the Whi5 dilution mechanism led to the realization that any protein can act as a size sensor if its concentration changes as cells grow and if that size-dependent concentration change drives cell cycle progression. This conceptual advance led to another cell cycle inhibitor dilution model to be proposed to couple cell growth to division in the mammalian cell cycle. The retinoblastoma protein RB, which is the functional ortholog of Whi5, is diluted by cell growth in G1 and this dilution increases the rate of G1/S transition (Figure 4A–C, Key Figure) [51]. Consistent with the RB dilution model, the concentration of the upstream cyclin D was constant, and RB phosphorylation status did not change in early- to mid-G1 [51, 75, 76]. Thus, there was no evidence of increasing upstream kinase concentration or kinase activity as cells grew through G1. Taken together, the discovery of RB and Whi5 dilution solidify inhibitor dilution as an important mechanism linking cell size to cell division. It is also noteworthy that while Whi5 and RB are both cell cycle inhibitors, they share no sequence similarity and have a different evolutionary origin [77]. That both these cell cycle inhibitors serve as size sensors by being diluted by cell growth demonstrates a deep conservation of the systems level logic at the core of cell cycle control.

Figure 4 Key Figure. Molecular mechanisms of mammalian G1/S sizer.

A. Inhibitor dilution model: activators of cell cycle progression scale with cell size so that their concentration does not change, while an inhibitor such as RB does not scale and is diluted by cell growth. B. Dilution of a G1/S cell cycle inhibitor protein RB leads to an increase in the rate cells progress through the G1/S transition. Shades of grey on the inset illustrate changes in the nuclear RB concentration. C. Inhibitor dilution, combined with molecular noise and cell-to-cell variability results is a stochastic sizer: on average, the cells born larger have a shorter G1 phase and grow less than the cells born smaller. D. Two proposed molecular mechanisms for cell-size-dependent G1/S progression: RB dilution by cell growth and size-dependent p38 kinase activation. In RB dilution model, cell growth dilutes the cell cycle inhibitor RB. This leads to the increased G1/S progression rate. In p38 model, small cell size activates the p38 MAP kinase, which inhibits G1/S. Thus, in both mechanisms larger cells pass through G1/S and divide sooner than smaller cells.

Multiple mechanisms, complex control, and heterozygosity

Inhibitor dilution and p38 models are not necessarily purely deterministic as cells do not immediately enter the cell cycle at a precise threshold concentration or activity (Figure 4C,D). Rather, the RB and Whi5 concentrations modulate the rate at which cells traverse the G1/S transition to enter the cell cycle [46, 51]. For example, a two-fold dilution of RB triples the rate a cell crosses G1/S. This mechanism can explain the negative correlation between the birth size of the cell and the duration of time it spends in G1 and also accounts for the observed cell-to-cell variability.

Even though the G1/S transition may be the most size-dependent in its timing, it is not the only cell cycle transition contributing to animal cell size. Most in vitro grown cell lines spend about half their cell cycle in S/G2/M phases and cells grow substantially during this time. This results in complex phenotypes in response to gene dosage changes affecting one particular cell cycle phase. For example, a 50% reduction in RB concentration, as might be expected in a heterozygous mutant, is not predicted to lead to a 50% reduction in cell size. This is because when RB concentration is low, cells will race through G1 so that the majority of cell growth takes place in S/G2. In this case, growth considerations in S/G2 are responsible for determining cell size through an adder type mechanism. In addition, there is negative feedback control on expression of RB family members so that a reduction in RB is expected to lead to an increase in the expression of the related protein p107 [78]. Together, these considerations strongly argue against a simple linear relationship between RB gene dosage and cell size.

An additional complexity in making predictive models for cell size is that multiple mechanisms can operate in parallel or even be interdependent [79, 80]. For example, so far there are no data to suggest that RB dilution or p38 activation are the only mechanism through which cell size is coupled to the cell cycle. RB dilution, p38 activation, and size-dependent cell growth could operate in parallel [22, 23, 74]. In fact, the mechanisms may well be interdependent if, for example, p38 was found to be diluted in G1. This would lead to decreased cell cycle inhibition for larger relative to smaller G1 cells through another mechanism ancillary to p38-activating phosphorylation. Moreover, it is also possible that a size-dependent concentration change directly regulates cell growth rate to promote size homeostasis. It is therefore of paramount importance to examine the scaling of the entire proteome with cell size to determine how protein size-scaling relates both to size-dependent cell growth and cell cycle progression.

Tissue and ploidy control cell growth and division

So far, this review has focused exclusively on cell autonomous modes of cell size regulation. While cell autonomous cell size regulation is clearly applicable to unicellular bacteria and yeast, their applicability to animal cells in vivo is less clear. Besides growth factor signaling and cell autonomous nutritional signals, cells in a tissue also have to sense mechanical signals from their neighbors and down-regulate cell growth in response to crowding to maintain organ size [81–83]. Tissue-level growth pathways have frequently been linked to Hippo signaling, whose modulation in vivo can dramatically affect organ size as seen in the fly retina and mouse liver [84, 85]. However, the presence of tissue-level control mechanisms does not imply that there are no cell autonomous mechanisms. Indeed, evidence for cell autonomous mechanisms were recently seen in mouse epidermal stem cells in vivo, where a sizer was observed [48]. An important open question is how a cell autonomous mechanism like a sizer is integrated with multicellular signals within a tissue. One possibility is that total cell growth within a given tissue is determined by pathways that maintain organ size, while that cellular growth is then partitioned into similar sized cells by cell autonomous size control mechanisms. This model is consistent with the fact that mutations affecting cell cycle control often have little effect on organ size. Rather, cell cycle mutations can affect cell size and number within the organ. More work needs to be done in this area and while we anticipate that cell autonomous size control mechanisms are relevant within tissues, it remains to be seen if, and in which tissues, this is true.

In this review, we have used the words cell size and volume interchangeably. However, there are other geometric features associated with cell size, like distances that could be important for size-sensing mechanisms involving molecular gradients, as have been suggested for fission yeast [86, 87]. While such length-dependent mechanisms may play a role in setting the size of some post-mitotic cells such as neurons, we do not expect them to play a role in the more spherical or irregularly shaped cells that make up the bulk of an animal. This is because distances between two points in a cell is expected to scale as the cube root of the volume so that very large changes in volume are needed to make appreciable distance changes that can be accurately sensed. Moreover, whichever size control mechanism operates in animals must take into account the general scaling of animal cell size with ploidy. This can be seen most dramatically in salamanders, which can survive to adulthood with 1–5 copies of the genome [88]. In these animals, cells are larger in proportion to ploidy, but most organs remain roughly the same size. This observation would be difficult to explain with a gradient-based mechanism. Instead, scaling with ploidy could be implemented in two ways. First, the genome could be used as a ruler to count the number of a tightly chromatin-bound molecule. If this molecule were at constant concentration with respect to the whole cell volume, as most molecules in the cell are, then the density of this molecule on the genome would be a readout of cell size [89, 90]. Second, the number of copies of a gene could directly relate to the number of molecules expressed. This was seen in budding yeast, where the number of Whi5 molecules made was directly proportional to the number of copies of the gene and was independent of cell size or the ploidy of the rest of the genome [46]. If, for example, this was also true for RB, then the ploidy of the animal cell would determine the number of RB molecules made, and thereby determine cell size at the G1/S transition.

Concluding Remarks and Future Perspectives

Cell size homeostasis in proliferating animal cells is achieved through the coupling between cell size, growth rate, and cell cycle progression. Animal cells exhibit a variety of cell line-dependent behaviors (sizers, timers, and adders), and researchers have begun to unravel their molecular mechanisms using new technologies to accurately measure cell size and growth (Box 1). Specifically, RB dilution and p38 based models have been proposed as molecular mechanisms linking growth and division in G1. Cell-size-dependent growth rates showing inefficient growth in cells that were too large and too small have also been revealed. While size-dependent cell growth has been linked to mitochondrial deficiencies in large and small cells, the molecular mechanisms through which cell size regulates cell growth are largely unknown. It is also unknown which, if any, of these mechanisms discovered in vitro operate in vivo, and how such cell autonomous mechanisms are linked to organ level control pathways. An ideal system to explore cell size control in vivo may be mouse epidermal stem cells, where a G1 sizer was recently discovered [48]. This is because the mouse epidermis allows one to combine mouse genetics with recently developed imaging technologies to test proposed mechanisms in vivo. While a lot of progress in understanding animal cell size control has been made in the last decade, more remains to be discovered (see Outstanding Questions). Most crucially, we need to determine how molecular mechanisms found through in vitro studies operate in vivo. Success will bring us closer to the ultimate goal of understanding how cell size control mechanisms are modulated to hit the over million-fold range of cell sizes across diverse animal cell types.