Abstract
Our ability to infer unobservable disease‐dynamic processes such as force of infection (infection hazard for susceptible hosts) has transformed our understanding of disease transmission mechanisms and capacity to predict disease dynamics. Conventional methods for inferring FOI estimate a time‐averaged value and are based on population‐level processes. Because many pathogens exhibit epidemic cycling and FOI is the result of processes acting across the scales of individuals and populations, a flexible framework that extends to epidemic dynamics and links within‐host processes to FOI is needed. Specifically, within‐host antibody kinetics in wildlife hosts can be short‐lived and produce patterns that are repeatable across individuals, suggesting individual‐level antibody concentrations could be used to infer time since infection and hence FOI. Using simulations and case studies (influenza A in lesser snow geese and Yersinia pestis in coyotes), we argue that with careful experimental and surveillance design, the population‐level FOI signal can be recovered from individual‐level antibody kinetics, despite substantial individual‐level variation. In addition to improving inference, the cross‐scale quantitative antibody approach we describe can reveal insights into drivers of individual‐based variation in disease response, and the role of poorly understood processes such as secondary infections, in population‐level dynamics of disease.
Keywords: Antibody, antibody kinetics, disease hazard, force of infection, incidence, individual‐level variation, influenza, serosurveillance, transmission, within‐host
Introduction
Wildlife species are a major source of emerging infectious disease (Jones et al. 2008) yet our understanding of disease dynamics in wildlife host populations is limited (Lloyd‐Smith et al. 2009). Disease dynamics depend on processes within and between individuals (Handel & Rohani 2015). Individual hosts become infected, then infectious. Depending on contact rates and susceptibility of other hosts, infectious hosts transmit pathogens to susceptible hosts. Accordingly, recent work addressing the role of within‐host dynamics on between‐host transmission has revealed the importance of cross‐scale insights for understanding and predicting epidemiological outcomes (Handel & Rohani 2015). Consideration of both scales in the same framework has elucidated how pathogens can circulate persistently under conditions where a single‐scale analysis would predict extinction (Kramer‐Schadt et al. 2009). Multiscale analyses have also improved understanding of phenotypic trade‐offs across scales and how they ultimately determine the evolutionary ecology of pathogens (Alizon & van Baalen 2005; Mideo et al. 2008; Handel et al. 2013); understanding of the spread of drug‐resistant (Handel et al. 2007) and viral immune escape mutations (Pepin et al. 2010; Volkov et al. 2010; Park et al. 2013; Schreiber et al. 2016); and prediction of how individual‐level control methods (e.g. drug regimens) impact epidemic dynamics (Pepin et al. 2013). By incorporating individual‐level heterogeneity into population‐level metrics of disease dynamics, uncertainty from individual‐level processes can be explained to improve prediction and provide a deeper understanding of the role of individual‐level processes in spatio‐temporal patterns of pathogen transmission. We propose a framework for incorporating individual‐level data into inference of disease dynamics using antibody data.
A key quantity describing disease dynamics is the force of infection (FOI), the rate at which susceptible individuals become infected, otherwise described as the infection hazard for susceptible individuals in a population. Thus, FOI is one of the most sought after quantities for understanding and predicting disease dynamics (Caley & Hone 2002; Heisey et al. 2006, 2010; Atkinson & Samuel 2010; Mueller et al. 2012; Henaux et al. 2013; Samuel et al. 2015; Avril et al. 2016), determining disease hazard (Gay 1996b; Rodriguez‐Barraquer et al. 2015), evaluating and planning interventions (Farrington 1992; Caley & Hone 2004), and calculating other key unobservable quantities such as the basic reproductive number (Ferguson et al. 1999; Feng et al. 2014), or the critical vaccination threshold (Whitaker & Farrington 2004). Correspondingly, a long history of estimating FOI from disease surveillance data exists (Hens et al. 2010), although most of this work has been in human disease systems and most methods have not considered individual‐level processes in estimation of FOI.
Another major gap is that conventional methods are designed to estimate a time‐averaged FOI which is relevant to endemic disease dynamics but not appropriate for epidemic patterns. Many pathogens exhibit seasonal and/or interannual variation in disease transmission (Hosseini et al. 2004; Grassly & Fraser 2006; Tamerius et al. 2011; Stoddard et al. 2014), which result in recurrent epidemic peaks. Estimates showing how FOI changes over time (Reiner et al. 2014; Pomeroy et al. 2015) would reveal mechanistic insight into ecological drivers of disease transmission, leading to improved disease prevention and response strategies. We summarise and critically evaluate existing methods for estimating FOI and propose a general cross‐scale framework that transcends many of the limitations of other methods. For wildlife systems, our proposed method overcomes the following limitations of conventional methods: fine‐scaled age data are not required, time‐varying FOI can be inferred from short time series of serosurveillance data, rapidly decaying antibody levels are acceptable and effects of individual‐level processes in disease dynamics can be examined. We demonstrate using simulations that our individual‐level approach can capture population‐level FOI well from cross‐sectional serosurveillance data, even when challenged by substantial individual‐level variation and differences in process behaviour, such as antibody decay rate. We also demonstrate the value of individual‐level inference in advancing disease ecology practice by applying our approach to a case study of influenza A data collected longitudinally in captive mallards (Anas platyrhynchos), and cross‐sectionally in a population of lesser snow geese (Chen caerulescens). Last, we illustrate how our framework can be applied to additional host‐pathogen systems, with complex ecological processes such as variation in route of exposure (e.g. Yersinia pestis in coyotes), and multiple exposures of individuals (e.g. influenza A in mallards). We discuss how these and other epidemiological complexities (listed in Table 1) could be incorporated into our general framework to better understand their contribution to FOI in a variety of host‐pathogen systems.
Table 1.
Epidemiological complexities that present challenges for inference and prospects for addressing them
| Challenge | Experimental data needs | Serosurveillance data needs | Proposed model refinements |
|---|---|---|---|
| 1) Disease‐associated mortality | Time between infection and death for individuals that do not survive; proportion that do not survive | Samples from dead animals (record estimated time of death; test sample for target pathogen) |
Incorporate censoring in within‐host model, g (δ, θ). Use experimental infection data to predict: (1) time between infection and death, (2) time between infection and a particular antibody titre, in a censoring framework. |
| 2) Assay detection and quantitation |
A. Sensitivity (false negative) and specificity (false positive) rates B. Titre variation from assay error |
A. Incorporate assay error through the threshold of detection parameter (y*). B. Incorporate antibody kinetics error (ε term in y = g (δ ϕ, θ)+ ε) |
|
| 3) Biased sampling design | Covariate data including behaviour, social group, spatial location or date (depending on system knowledge) | Incorporate spatial/temporal autocorrelation or other covariate information into probability determining state classification (as susceptible or seropositive). | |
| 4) Endemic dynamics and/or high individual‐level variation | Measure effects of covariates on titre variation (e.g. age, sex, time of year, indicators of stress, pathological signs distinguishing route of exposure, other immune factors, co‐infections, reproductive status, etc. = COVARIATE DATA) |
Relevant COVARIATE DATA, x A. Repeated sampling over time of randomly sampled individuals B. Repeated sampling over time of the same individuals (e.g. Borremans et al. 2016) (Note: B requires substantially more effort than A) |
A. Use model Supporting Information 4 (systematic sampling model); adapt within‐host model, g (δ, θ, x), to include covariate data x such that some variation in kinetics is parsed out by the individual‐level covariate data. B. Incorporate individual‐level correlation, i.e. modify y 2j model to include a covariance matrix describing all times individual j was sampled, y 2j ~ N (g(δj, θ, x j), ∑j, where ∑ accounts for correlation among observations for individual j |
| 5) Anamnestic response | Anamnestic responses for multiple time points and COVARIATE DATA concurrently | COVARIATE DATA distinguishing titres in primary infections from anamnestic responses (see main text) | Similar to (4A): include different within‐host functions, g (δ, θ, x), for different types of responses (primary infection vs. anamnestic response). |
| 6) Multiple strains (cross‐immunity; co‐infection) | Antibody responses to multiple strains in primary and cross‐infections (e.g. primary A and B, B after A, A after B) | Strain‐specific serosurveillance data | Similar to (4A): different within‐host functions, g (δ, θ, x), for each strain and cross‐reaction. |
| 7) Contact structure | Population‐level data describing host contact structure (e.g. average number of individuals making contact) | Modify contact structure function in FOI derivation (currently proportional: newly infected/susceptibles) to reflect the true relationship of the number of susceptibles contacting newly infected hosts. | |
| 8) Complex antibody response (i.e. chronic or acute disease; recurrent antibody production due to latent infections) | Long‐term antibody titres and covariate data quantifying pathological signs, immune factors, external stressors or pathogen loads that distinguish chronic from acute infections, or initial infection from later stages | COVARIATE DATA as determined in experimental infections |
If different stages/types of antibody responses can be informed by covariate data, modify model as in 4A: g (δ, θ, x), to include covariate data x Incorporate appropriate antibody response function by modifying g in g (δ, θ, x) |
Shading indicates effort: low (white), medium (light grey), high (dark grey). Data needs are in addition to current data needs (antibody kinetics in experimental studies and cross‐sectional serosurveillance data).
This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.
Age‐seroprevalence methods
The conventional approach to inferring FOI from serological data is based on ‘age‐seroprevalence methods’. These methods use age‐stratified seroprevalence data (presence or absence of antibody in the host) and assume lifelong immunity such that the cumulative hazard of infection increases with age (Muench 1934, 1959; Farrington 1990; Hens et al. 2010) (Fig. 1a). Age‐seroprevalence methods are inappropriate in wildlife‐host systems where the host is short‐lived (not practical to distinguish ages), where age data are coarse and imprecise (not enough information to fit the age‐seroprevalence curve), or where antibodies decay quickly (no signature of increased seroprevalence with age). Also, age‐seroprevalence methods assume a constant FOI over time (Fig. 1a) and long temporal datasets with large sample sizes are typically required to make inference about time‐varying FOI (Grenfell & Anderson 1985; but see Heisey et al. 2010 for an alternative). A flexible method that relaxes these potentially problematic assumptions (i.e. necessity for age data, reasonably long‐lived hosts, slow antibody decay, serial surveillance sampling, or constant FOI over time) remains to be developed and may improve inference of disease dynamics in wildlife systems that often violate one or more assumptions of conventional methods.
Figure 1.
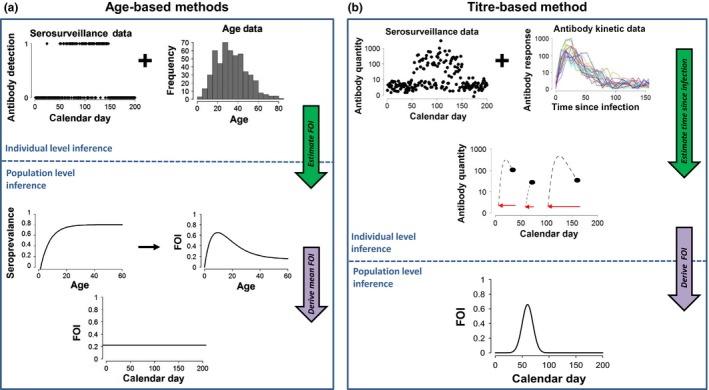
Approaches to estimating disease transmission from serosurveillance data. (a) Age‐based methods: Seroprevalence methods based on antibody detection and age class can estimate FOI as a function of age. (b) Titre‐based methods: Quantitative antibody methods use pathogen‐specific longitudinal antibody kinetic data from laboratory experiments along with quantitative antibody titres from the field‐collected serosurveillance studies, to estimate individual TSI (middle plot, red circles are time of exposure, black are sampling times) for each individual in the serosurveillance sample and derive FOI as a function of time and/or age for the population.
Age‐seroprevalence methods utilise presence/absence data, but the assays used to detect antibodies (e.g. enzyme‐linked immunosorbent assays, ELISA) typically produce quantitative data. Thus, a threshold must be determined to classify the quantitative antibody measurements as seropositive or seronegative, introducing potential misclassification error (de Melker et al. 2006; Bollaerts et al. 2012; Wu et al. 2014; Vink et al. 2015; Borremans et al. 2016; Pothin et al. 2016) that should be treated explicitly (Gay 1996a; Vyse et al. 2006), and neglecting the potentially valuable information that can be gained from considering the quantitative antibody data (Bollaerts et al. 2012; Pothin et al. 2016). As antibody levels decay rapidly over time in many wildlife host‐pathogen systems (especially in non‐mammalian hosts), there is opportunity to learn about temporal disease dynamics in a population by considering antibody levels in individual hosts. Thus, ‘quantitative antibody methods’ circumvent error associated with transforming antibody data to binary values.
Quantitative antibody methods
A new field has emerged that uses quantitative antibody assays to infer incidence (Teunis et al. 2002, 2012; de Melker et al. 2006; Simonsen et al. 2009; Kretzschmar et al. 2010; Borremans et al. 2016; Pothin et al. 2016). By considering the underlying quantitative antibody information, the dependence on age data and long‐term antibody circulation for inference of FOI can be relaxed. In effect, the historical perspective provided by age data can be replaced with antibody response curves because the decay from peak antibody levels becomes a source of information rather than a nuisance. The main concept is that pathogen‐specific antibody kinetics exhibit robust, reproducible patterns, as long as individual‐level heterogeneities in antibody response are accounted for appropriately (Simonsen et al. 2009; Teunis et al. 2012, 2013), and thus can be used to infer the time since infection (TSI) for individuals and population incidence (Teunis et al. 2002, 2012; de Melker et al. 2006; Simonsen et al. 2009; Kretzschmar et al. 2010; Borremans et al. 2016) or FOI (Fig. 1b). Quantitative approaches to inferring incidence lend themselves naturally to estimating time‐varying FOI because historical epidemiological status of sampled individuals can be determined. Quantitative antibody approaches also necessarily consider within‐host immunity dynamics to infer population‐level FOI, which could lead to novel insights into wildlife disease ecology.
To date, quantitative antibody approaches have focused on incidence (rate of new cases) rather than FOI, which considers the number of susceptible individuals and provides a more direct understanding of infection hazard or potential behaviour of an epidemic. Also, these approaches estimate average incidence in the population rather than allowing change in incidence over time (de Melker et al. 2006; Simonsen et al. 2009; Kretzschmar et al. 2010; Teunis et al. 2012; Teunis 2015). A recent advance showed that quantitative longitudinal antibody data (repeat samples from the same individual over time) could be used to estimate time‐varying incidence accurately under complex endemic dynamics (Borremans et al. 2016). However, because it is rare for wildlife surveillance to collect repeat samples from individuals, an approach that works with cross‐sectional serosurveillance data is valuable as well.
We argue that quantitative antibody methods are a promising avenue for studying the mechanisms underlying epidemic patterns. These methods inherently account for individual‐level processes contributing to FOI and reveal time‐varying FOI. Using a hierarchical Bayesian model, variability from multiple epidemiological processes can be accounted for explicitly and described by data, which in turn can improve our mechanistic understanding of heterogeneities driving disease dynamics and improve inference. Also, because age data are not required, quantitative antibody methods have broader application in wildlife populations relative to conventional methods. Similarly, quantitative antibody methods make use of information from waning antibody levels, which can lead to misclassification by conventional methods.
For quantitative antibody methods to reach their full potential in revealing underlying drivers of FOI, incorporating a mechanistic model of within‐host antibody kinetics is valuable, because it allows for explicit description of individual‐level processes with biologically interpretable parameters (Simonsen et al. 2009; Teunis et al. 2012; de Graaf et al. 2014). In what follows, we present a general quantitative antibody framework based on a mechanistic model of antibody kinetics and explicit representation of individual‐level variation, and demonstrate its ability to infer FOI accurately in many circumstances. We show how quantitative antibody data (i.e. concentration of antibody within individuals) from longitudinal studies within hosts (experimental data) can enable estimation of time since infection (TSI) for hosts sampled cross‐sectionally in a population (serosurveillance data). From the individual‐level TSI, we derive the history of epidemiological status (newly infected, susceptible or seropositive) for all hosts sampled in a population, and consequently FOI. The approach we outline addresses many of the challenges faced by current methods: epidemic dynamics, coarse age data, rapidly waning immunity, cross‐sectional serosurveillance data, complex antibody kinetics, and individual‐level variation in antibody responses. We demonstrate how our proposed cross‐scale framework can be used in a variety of host‐pathogen systems to infer epidemic dynamics and understand the role of different ecological processes.
Approach
The premise of our quantitative antibody method (Box 1) is that observed antibody data from both longitudinal antibody‐kinetics experiments in captive animals (y 1), and cross‐sectional serosurveillance in a wild population (y 2), ideally from the same or immunologically similar species, can be combined to provide estimates of the FOI and several other key epidemic quantities. We modelled observed antibody data using a mechanistic function (g) of antibody kinetics that was adapted from (Simonsen et al. 2009; example shape in Fig. 2). The deterministic function g depends on both a vector of parameters that describes antibody kinetics (θ, unknown) and TSI (δ, known for the laboratory experiment data but unknown for the serosurveillance data). The antibody kinetics parameter vector θ includes six parameters (eqn (1)): baseline antibody level prior to exposure (X 1), initial lag between exposure and antibody production (A), antibody production rate (r), period of antibody production in response to infection (B), antibody decay rate (d) and baseline antibody levels following antibody decay (X 2). We assume that both the kinetic and serosurveillance data are measured with error and subject to the same amount of individual‐level variation (). To represent antibody quantities we used signal to noise (S:N) ratios – the output of ELISAs, a commonly used antibody detection assay. We transformed the data by taking the inverse followed by the base 10 logarithm [log10(1/S:N ratio)], prior to analysis. The transformation yielded the characteristic rise and fall of antibody levels (raw S/N ratios fall and then rise) and negative values, which could be modelled with a normal distribution. For an observed antibody quantity y (either y 1 or y 2) collected at time + ε where and
| (1) |
Box 1. General framework for inferring FOI from quantitative antibody data.
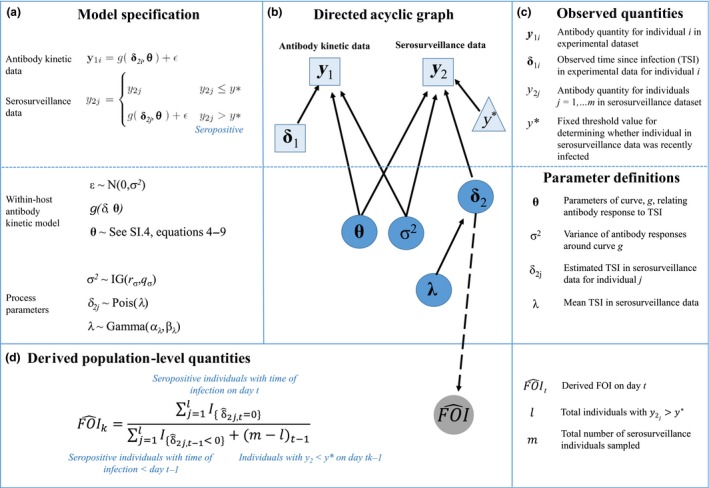
Let y 1i denotes the vector of antibody quantity for individual i = 1,…, n in the antibody kinetic experiment, and let y 2j denote the antibody quantity for individuals j = 1,…, m from the serosurveillance study. In addition, let δ = t−τ be the time since infection (TSI), where τ is the day of infection and t is the sampling day. Furthermore, assume antibody responses for infected individuals are observed with error and are normally distributed around some mean curve, g(δ, θ) (e.g. eqn (1)), with variance . The model specification is given above, where y∗ is a fixed threshold value indicating whether individual j has been recently infected, δ2j is the TSI for individual j, distributed as a Poisson random variable with global mean TSI, λ, for recently infected individuals. The prior for λ was distributed as Gamma with fixed shape and scale parameters of 10 and 1, respectively, while the prior for σ2 was distributed as inverse‐gamma with shape and scale parameters both equal to 2. From each seropositive (y > y*) individual's estimated TSI and sampling day, we get time of infection which we use to determine the number of newly infected individuals (new E) for each calendar day of interest in the past. For each calendar day, we also record the number of susceptible individuals (S) as the number that were seronegative (y ≤ y*) on day t. Then, FOI for day t is derived as: new Et/St‐1.
Assumptions of current model
Individual‐level variation in antibody kinetics is the same for experimental and serosurveillance data.
Individuals sampled as susceptible (y < y*) are classified as susceptible for all previous time steps.
Ratio of newly exposed to susceptible individuals in samples mirrors true population ratios (unbiased random sampling).
No disease‐induced mortality.
Homogenously mixing population: all susceptible individuals have equal probability of contacting infectious individuals. This only applies to deriving FOI, not estimating incidence.
All newly infected hosts become infectious. This only applies to deriving FOI, not estimating incidence.
Figure 2.
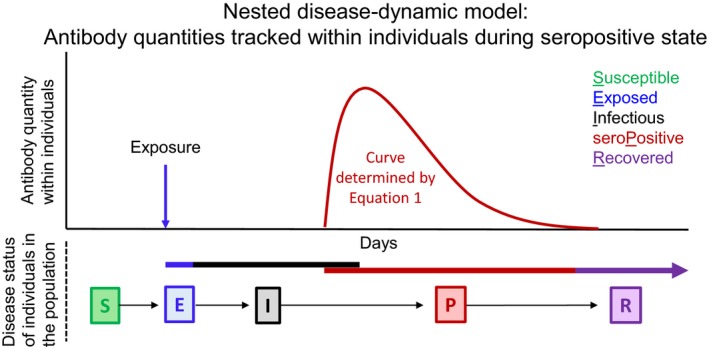
Schematic of simulation model. Top plot shows that antibody quantities over time were tracked within individuals once they became infected (transitioned from S to E). Bottom shows that individuals transitioned between different epidemiological states. Note that seropositivity was possible when individuals were still in the I state, thus there was also an IP state which was not tracked explicitly.
For each serosurveillance sample (y 2j) above the threshold of antibody detection (y*), the measured antibody quantity can be used to estimate TSI for the jth individual (δ2j) through the g function. Using the estimated TSIs for each individual in the serosurveillance data, a disease status history (susceptible, newly exposed or antibody positive) over time can be determined for each individual. Then, we derived incidence as the number of newly infected individuals on day t (i.e. transitions from S to E, Fig. 2) divided by the total sample size on day t. Similarly, we derived FOI for each day t by dividing the number of newly infected individuals on day t (i.e. transitions from S to E, Fig. 2) by the number of susceptible individuals on day t−1 (Box 1). We estimated TSI using Bayesian methods (Supporting Information 1).
To evaluate performance of our quantitative antibody approach, we developed a stochastic population‐level disease transmission model that could produce known trajectories of incidence and FOI while tracking antibody quantities within individuals (Supporting Information 2, Fig. 2). We simulated serosurveillance data (y 2) by sampling the simulated population according to a pattern that matched the sampling of snow goose populations, which involved sampling 200 individuals without replacement (10% of the simulated population) each day for 1 week. We simulated experimental data (y 1) using the antibody kinetic model (enq 1) to generate known antibody trajectories for 30 hypothetical individuals.
Antibody decay rate
Intuitively, one might expect that longer decay rates would increase uncertainty in inference of FOI because individual‐level variation in antibody concentrations is typically highest during the decay phase, leading to more uncertainty in TSI. We tested this hypothesis by simulating antibody kinetic and serosurveillance data based on different mean antibody longevities (time between start of antibody rise and decay to baseline): 100 days (similar to influenza A in mallards – see below), 300 days and 600 days (Fig. 3a, Supporting Information 2 and 3). As expected, uncertainty in inferred quantities (seroprevalence, incidence, FOI) increased as antibody longevity increased (i.e. with decreased antibody decay rate; Fig. 3b–d). With antibody longevities < 600 days, the model captured the magnitude and timing of peak FOI well with low uncertainty (Fig. 3d). With an antibody longevity of 600 days (almost 2 years), the model tended to overestimate FOI but still captured timing of the peak well with a level of uncertainty that gave a clear epidemic signal (Fig. 3d). Under conditions of rapid antibody decay (100 days), the model tended to produce larger misclassification errors (rising vs. decaying phases), generating a second peak that was not present in the true (simulated) dynamics (Fig. 3d, left). Misclassification was less of a problem for slower decay rates, because individuals spend proportionately more time in the decay vs. rising phase.
Figure 3.
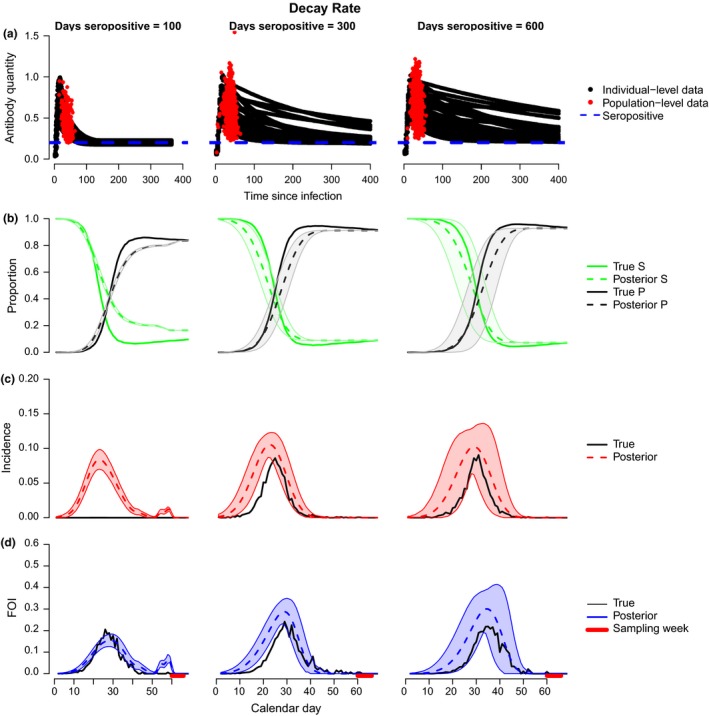
Model performance as a function of antibody decay rate. (a) Black lines show the transformed antibody quantity every 4 days for simulated experimental individuals known to be inoculated at time 0 (y 1i). Red dots show the transformed antibody quantities in all seropositive individuals sampled cross‐sectionally on day t in a simulated population experiencing disease transmission (y 2j). The blue dotted line indicates the threshold for seropositivity (y*). Parameters are given in Supporting Information 3. (b) Posterior estimates for number of individuals in susceptible (green dashed) and seropositive (black dashed) states relative to the true values (solid lines of corresponding colours). (c) Model fits (red) to the true incidence over time in the simulation model (black). (d) Model fits (blue) to the true FOI over time in the simulation model (black). (b–d) Shaded areas show 95% credible intervals for the estimates. The red bar along the bottom indicates the sampling period for b–d.
Timing of sampling relative to epidemic curve
Our simulations used a cross‐sectional sampling design of serosurveillance data where individuals were sampled over a 1‐week period without replacement to match the snow geese data. As this sampling window is narrow, we explored how timing of the sampling pulse relative to the main FOI curve could impact inference. We used antibody kinetic parameters that were estimated by fitting eqn (1) to the experimental mallard data (mean antibody longevity = 100 days, low level of individual variation, only 30 individuals; Fig. 4a). When samples were collected immediately following the main epidemic peak, the model inferred magnitude and timing of the main FOI curve well (Fig. 4d, middle). However, as the time since the epidemic peak increased relative to the time of sampling, the model estimated a later peak FOI relative to the truth and showed increased misclassification of individuals in the rising vs. decaying phase of antibody response (Fig. 4d, right). Similar patterns were observed for incidence (Fig. 4c). In terms of FOI, the mismatch in timing occurred because the model estimated a later onset of susceptible depletion and increased seroprevalence (Fig. 4b). If there is prior information about the timing of the epidemic peak in question, this could be incorporated into the prior distribution for the TSI parameter, thus improving precision.
Figure 4.
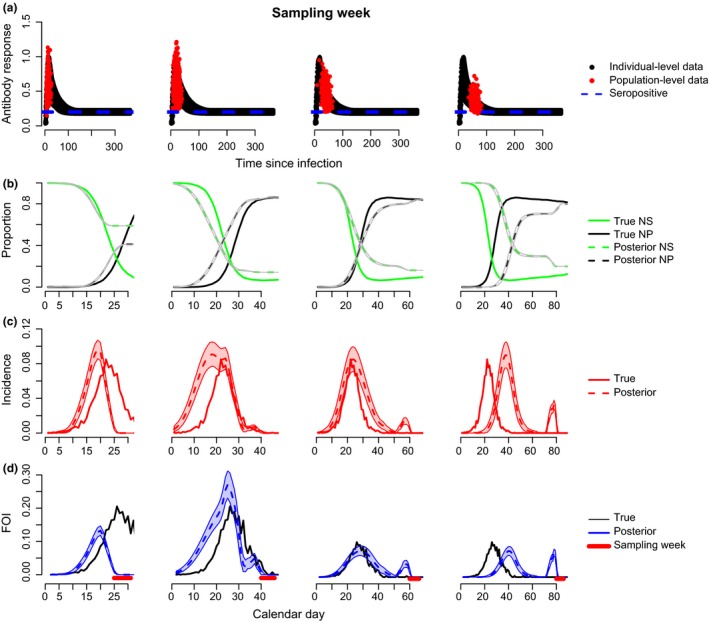
Effects of sampling pulse relative to timing of FOI curve. Same as Fig. 3 but each plot represents a different sampling period for the serosurveillance data. For simulating the two data streams, we used parameters of the within‐host model that were estimated from the experimental mallard data (Supporting Information 3‐Table 1, ‘Fast’).
The timing of sampling relative to the main epidemic curve is important and surveillance sampling design can vary widely across systems, thus, we extended the model to accommodate sampling (cross‐sectionally) more consistently across time (Fig. 5; ‘Systematic Sampling Model’ Supporting Information 4). The main changes to the model included: 1) using a sliding window defining separate sampling periods over which FOI was calculated, and 2) including a temporal smoothing process on mean TSI to account for temporal autocorrelation due to the epidemic curve (Supporting Information 4). The autoregressive process on mean TSI allows the TSI parameter to learn from other samples collected at approximately the same time, which improves our ability to correctly classify antibody quantities into the rising or decaying phase of the antibody response curve, hence improving estimation of TSI. Using the same parameters as Fig. 4, but sampling more consistently across time (20 individuals of 2000 per week for 1 year), resulted in very good inference of true FOI and no secondary peak artefacts (Fig. 5). Thus, increasing the length of the sampling period and number of sampling occasions can provide more reliable inference of the timing of an epidemic curve.
Figure 5.
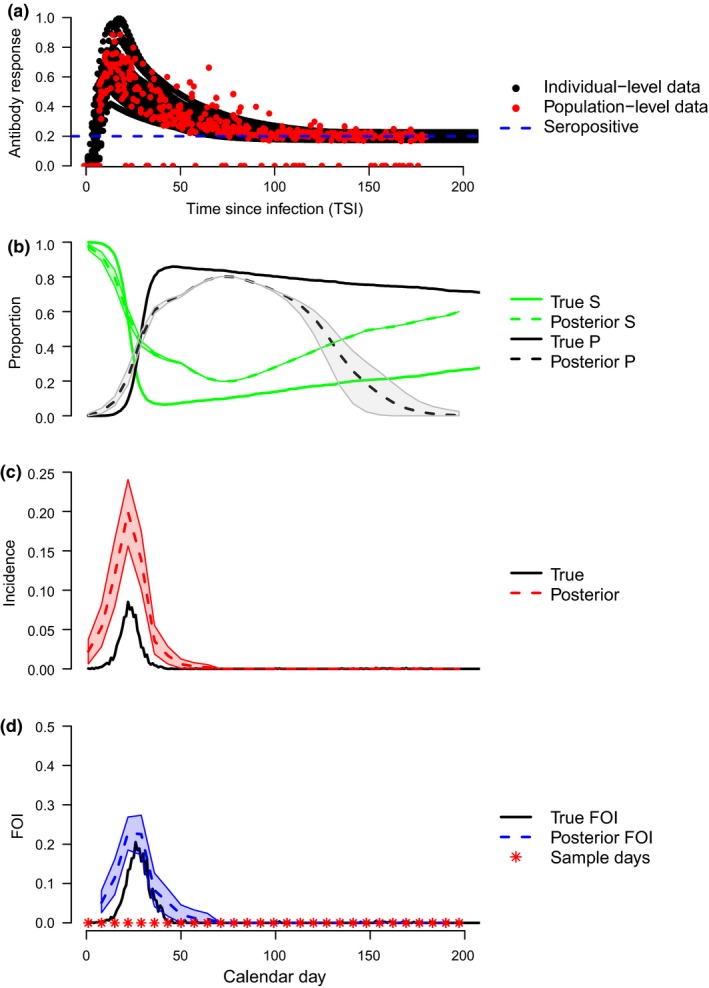
Serial cross‐sectional sampling. Model fit using continuously sampled serosurveillance data and the autoregressive model structure presented in Supporting Information 4. (a–d) plots are as in Fig. 3.
Application to influenza a in snow geese
Understanding the ecology of avian influenza A transmission dynamics in wild bird populations is complicated because serosurveillance data are often temporally constrained to a relatively brief cross‐sectional sampling frame, making it difficult to understand drivers of disease dynamics over time. However, as we have demonstrated, by considering the quantitative antibody information in individuals together with the dynamic nature of immune responses, we can infer transmission dynamics over a longer period in the past, thus providing insights about mechanisms of transmission in populations at particular sites.
We demonstrate the value of this approach using a case study of influenza A in snow geese sampled cross‐sectionally (y2) during the summer of 1995 at Banks Island, Canada (Fig. 7 top left, see Supporting Information 5 for field sampling details). To inform the individual‐level antibody kinetics (y 1), we used experimental antibody kinetic data from six snow geese and 30 mallards (Fig. 6 top right, Supporting Information 5), which had a known time of infection. We compared using mallard and geese data together, or the geese data separately with simulated curves to increase the sample size from 6 to 36 (Fig. 6, top right; Supporting Information 5). We also compared results using two separate distributions of TSI: Poisson as in Box 1, and negative binomial to allow more flexibility in TSI. The two approaches predicted the same timing of peak FOI, but the geese experimental data predicted FOI with lower precision and the mallard/geese experimental data predicted a slower rise to peak FOI under the negative binomial distribution of mean TSI (Fig. 6, bottom). We estimated peak seroprevalence in the snow goose population to be c. 0.65 (Fig. 6). Peak daily incidence was estimated to be c. 0.05–0.18 and peak daily FOI c. 0.09–0.25 (depending on assumptions about the distribution of TSI – Poisson vs. negative binomial, Fig. 6), which is consistent with seroconversion rates estimated with the same dataset (Samuel et al. 2015). The fact that the shape of the epidemic curve differed substantially depending on assumptions about the error structure of the TSI distribution (Poisson vs. negative binomial), suggests future theoretical work may be helpful for refining the general framework we present here. Nonetheless, regardless of the assumption about the error structure underlying the TSI distribution, a similar time of peak FOI was estimated.
Figure 7.
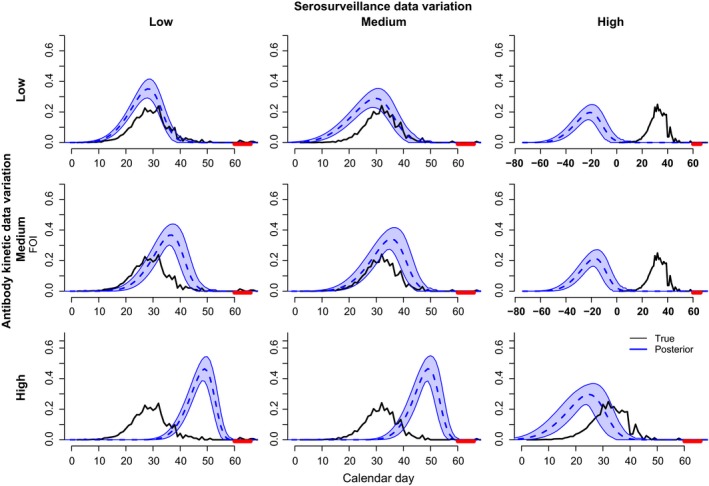
Model performance as a function of individual‐level variation. Levels of individual variation for antibody kinetic (black) and seropositive serosurveillance data (red). Plots are as in Fig. 3d. Three levels of individual variation were examined: low, medium and high. Rows indicate effects of variation in serosurveillance data while holding variation in antibody kinetic data constant. Columns indicate effects of variation in antibody kinetic data while holding variation in serosurveillance data constant. Parameter values are given in Supporting Information 6‐Table 3.
Figure 6.
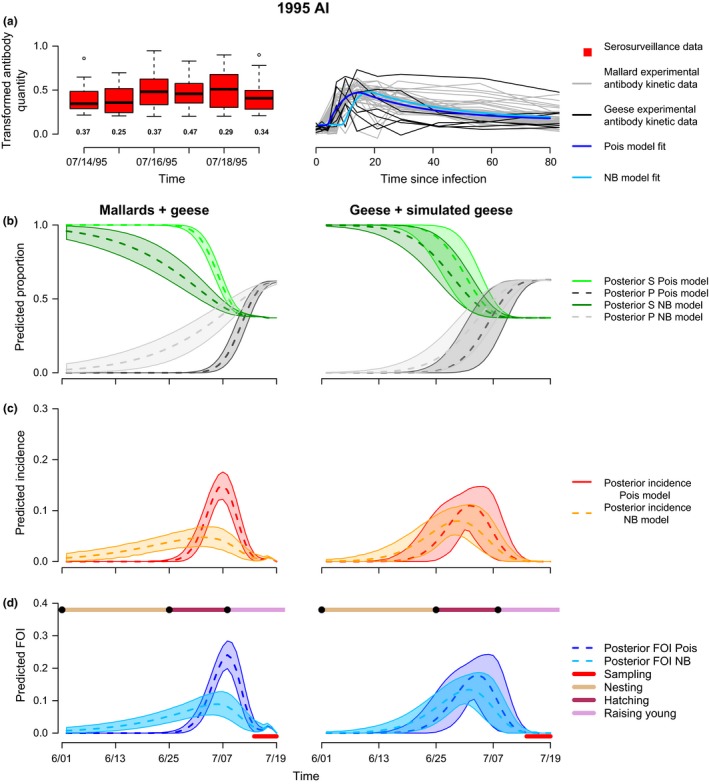
Inference of FOI in snow geese. Transformed antibody quantities for serosurveillance data (y 2j) in snow geese are plotted for each sampling day (top, left). Boxes are the distribution of antibody quantities (median values indicated by line) for seropositive samples while the numbers below the boxes indicated the proportion of samples that were seronegative. Transformed antibody quantities for the 30 experimental mallards (grey lines) and six snow geese (black lines) are plotted over time (top, right) along with the Poisson and negative binomial model fits for the combined mallard/geese data estimated using within‐host function, g. We used two different experimental datasets for model fitting: observed antibody kinetics of 30 mallards and six snow geese (left column plots) and observed antibody kinetics for six snow geese plus 30 simulated antibody kinetic curves generated using parameters of the observed snow geese data fit to eqn (1) (right column plots). Row 2: Model predicted proportions of susceptible (green) and seropositive (black) individuals over time in days. Row 3: Predicted incidence over time. Row 4: Predicted FOI over time. The red bar along the bottom indicates the sampling period. The bar along the top indicates reproductive events in the snow goose life cycle. Two different models were used for fitting: Box 1 model specification (indicated as Pois), and Box 1 model specification with TSI distributed as a negative binomial random variable instead of Poisson (indicated as NB). Shaded areas indicate 95% credible intervals.
The quantitative antibody approach suggests an initial rise in FOI towards the end of the nesting period, with peak FOI occuring at the end of the hatching period. The presence of a rise in FOI to an epidemic peak most new offspring are available is consistent with previous studies showing that avian influenza A viruses overwinter on waterfowl breeding grounds in northern latitudes, leading to viral transmission during the breeding season (Ito et al. 1995; Farnsworth et al. 2012; Hill et al. 2016). Furthermore, snow geese are highly gregarious colony nesting birds, which may promote the transmission and maintenance of density‐dependent pathogens (Samuel et al. 2015) such as influenza A viruses and Pasteurella bacteria (Samuel et al. 1999). Rather than providing a single snapshot of seroprevalence, the quantitative antibody approach infers transmission dynamics throughout the nesting, hatching, and early raising of young phases of the breeding season, demonstrating how quantitative antibody approaches can be applied to advance our understanding of breeding‐season transmission dynamics. Furthermore, if additional data explaining potential sources of individual‐level variation are available, this type of quantitative antibody framework can be used to quantify the relative role of various abiotic and biotic conditions on determining dynamics of FOI.
Individual‐level variation
Individual‐level variation in host antibody responses can be due to intrinsic factors of the pathogen such as genetic variation or immune evasion tactics (Alcami & Koszinowski 2000; Finlay & McFadden 2006); or due to extrinsic factors such as host physiological status, dose (Turmelle et al. 2010), or route of exposure (Baeten et al. 2013). The existence of a multitude of factors affecting individual‐level variation presents potential challenges in extracting FOI from quantitative serosurveillance data (Gilbert et al. 2013). To investigate this potential challenge, we generated antibody kinetic and serosurveillance data under different levels of variation in decay rates (Supporting Information 2, and 6). We compared cases where antibody kinetic data had either low, medium or high individual response variation while holding individual variation in serosurveillance data constant at low, medium or high levels and vice versa to produce all combinations of variation for both data types (Supporting Information 6). In our analysis, plots along the diagonal match the model assumption that individual‐level variation is similar in both data streams while plots outside the diagonal do not match this assumption. In general, the model performed better under equal levels of variation for both data streams (Fig. 7), but this was not consistent (e.g. low variation in antibody kinetic data and medium variation in serosurveillance data performed equally well as matching levels of variation; Fig. 7, top middle). Violation of the equal variation assumption biased results when one of the data streams had high individual‐level variation (Fig. 7, bottom row and right column). In addition, even when the assumption of equal variation was satisfied, high individual‐level variation underestimated the timing of peak FOI, although the magnitude was still captured well (Fig. 7, bottom right). When individual‐level variation in the antibody kinetic data was higher than that in serosurveillance data, the model overestimated the timing and magnitude of peak FOI substantially (Fig. 7 bottom, left and middle). Alternatively, when variation in serosurveillance data was substantially higher than that of antibody kinetic data, the timing of peak FOI was underestimated substantially (Fig. 7, right top and right middle).
Overall, our results show that extreme levels of individual‐level variation can lead to poor performance of the model as formulated; especially if the assumption of equal variation between the data streams is not satisfied. Nonetheless, the model performed very well under medium levels of variation that were similar to those quantified in the mallard data, suggesting it is capable of recovering the epidemic signal under realistic conditions. Also, if the model assumption of equal variation in experimental and serosurveillance data is satisfied, bias from high levels of variation is not as severe. If the model is re‐specified based on improved knowledge of potential differences in individual‐level variation between experimental and serosurveillance data, bias from unbalanced individual‐level variation could be decreased.
Given the flexibility of our approach, there is potential for individual‐level variation to be further informed by data (Table 1; Borremans et al. 2016). Factors such as age, sex (Borremans et al. 2016), environmental conditions, pathological signs, additional immunological factors or reproductive status can be incorporated as covariates predicting a narrower range of responses for individuals with specific characteristics. For example, antinuclear antibodies (ANA) may distinguish inherent differences in immune responsiveness among individuals (Graham et al. 2010). Thus, experimental data of ANA titres (or other general indices of antibody responsiveness, e.g. total IgG concentration) sampled temporally alongside antibody responses, could improve inference in systems with high individual‐level variation when combined with serosurveillance data, where these factors are also collected. By explicit incorporation of factors determining individual‐level variation, inference could be improved and mechanistic knowledge about the role of the additional factors on dynamics of FOI would be revealed, hence improving our understanding of disease ecology.
To demonstrate how data on drivers of individual‐level variation could improve inference, we extended our model to examine how high individual‐level variation from route of exposure of Yersinia pestis (agent of plague) in coyotes affected inference of FOI. We simulated scenarios where two different antibody kinetic responses were possible in individual hosts depending on route of exposure (Supporting Information 7). We adapted the systematic surveillance model (Supporting Information 4) to incorporate a mixture of antibody kinetic models, each with their own parameters (Supporting Information 7). We chose parameters for eqn (1) that mimicked antibody kinetics of Yersinia pestis in coyotes, where the oral route of transmission results is a much stronger response than the intradermal route of infection (Baeten et al. 2013). We assumed that there were covariate data such as pathological signs that may help distinguish the route of exposure (i.e. choice of antibody response distribution) and no misclassification of the response due to oral vs. intradermal infection.
When we used our original model that did not account for multiple distributions of antibody responses, the timing of peak FOI was biased late (Fig. 8, top left). Using the mixture model, we captured the timing of peak FOI accurately, although the curve was slightly lower and wider than predicted (Fig. 8, top right). In general, accounting for the sources of individual‐level variation greatly improved inference and captured the timing and general behaviour of FOI well. Of course, our study provides a simplified version of how drivers of individual‐level variation could be modelled explicitly. If there are more than two different modes of antibody kinetics and measurable predictive factors, then covariate data can be used to predict individual‐level response curves with the appropriate level of uncertainty (Table 1). Note that although the framework we propose can be improved by age data, the age data can be coarse (2–3 age classes), unlike in conventional age‐seroprevalence methods which require fine‐scaled age data.
Figure 8.
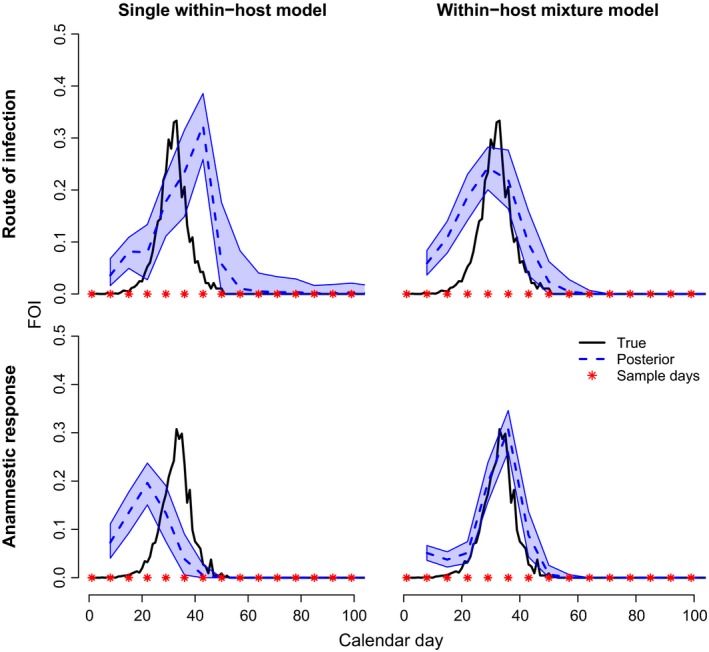
Impacts of variation from route of infection and anamnestic responses. Inferred time‐varying FOI using the systematic sampling model (Supporting Information 4, left columns) adapted to accommodate a mixture of within‐host antibody kinetic distributions (Supporting Information 7). Top: Variation in within‐host kinetics is similar to plague in coyotes inoculated intradermally (low response) or orally (high response) (Baeten et al. 2013; Supporting Information 7‐Table 4, Figure S5). Bottom: Variation in within‐host response is due to primary vs. secondary infections of influenza A (Supporting Information 7‐Table 4, Figure S5; Supporting Information 5‐Figure S2, bottom left).
Anamnestic responses
In many systems, infection history can influence antibody responses because secondary exposures activate memory cells leading to sharp increases in antibody titre (Table 1). Influenza A in mallards highlights this issue – anamnestic responses produce higher antibody titres and achieve peak levels earlier relative to primary infections (Supporting Information 5 and 7). The contribution of anamnestic responses to FOI, or their effect on inference, is not well understood and few studies have attempted to apply a quantitative antibody method while considering anamnestic responses (Pothin et al. 2016). Without explicit consideration, anamnestic responses may be confused with primary infections, adding uncertainty to estimates of TSI and FOI. Currently, FOI for time periods with frequent anamnestic responses may be biased if there is no information for the model to distinguish the two processes.
To explore the idea that our framework could capture FOI in systems with anamnestic responses, we simulated disease transmission under conditions where hosts were allowed to be re‐infected. Re‐infection could occur only after immunity had waned to twice the baseline level, and it generated an anamnestic response which generally arose faster and decayed faster than primary infections (Supporting Information 5 and 7). Hosts with secondary, etc. infections did not become infectious in our example. We fit a similar mixture model as with the Yersinaia pestis example, where there were two separate functions describing antibody responses for primary infections vs. anamnestic responses. We assumed that classification of serosurveillance data into primary infections or anamnestic responses was perfect, and that covariate data such as age, sex or time of year could be used to inform classification of infection history. This type of model could be further developed to estimate the classification group with informed prior distributions. When we used our original model that did not account for multiple distributions of antibody responses, the timing of peak FOI was biased early (Fig. 8, bottom, left). Using the mixture model, we captured the timing of peak FOI accurately (Fig. 8, bottom right), indicating that appropriate data for distinguishing primary infections from anamnestic responses (secondary or more) may allow for accurate inference of FOI. In addition to age, sex and time of the year, data such as IgG:IgM ratios could be collected and used in the inference framework to predict antibody response distributions for individuals based on their covariate data (i.e. moving beyond a two‐component mixture model to multiple distributions of antibody response curves). Modelling anamnestic responses directly will not only improve inference of FOI but will also lead to a better understanding of the contribution of secondary infections in FOI dynamics.
Discussion of additional complexities
Our simulation and case study results demonstrate how quantitative antibody methods can capture the timing, magnitude and width of epidemic curves under multiple sets of conditions, showing that quantitative antibody methods can be used to infer time‐varying FOI for epidemic dynamics in a variety of host‐pathogen systems. However, there are several other epidemiological factors driving variation in serosurveillance data. Each of these factors can increase individual‐level variation in antibody responses and bias or increase uncertainty in FOI. In Table 1 and below, we list many of these complexities and describe how they could be accounted for explicitly by adapting our approach for use in other host‐pathogen systems.
Disease‐associated mortality
In systems with disease‐associated mortality (Table 1), our current model underestimates the number of newly infected individuals (Heisey et al. 2006) because those that die before eliciting an immune response do not provide any antibody information. When disease‐associated mortality is relatively high (e.g. rabies), our method can be adapted to accommodate data from samples of carcasses, which include an estimate of host ‘day of death,’ for improved inference (Table 1). If the distribution of time to death has been measured experimentally, the experimental data can be used similarly in our model to infer TSI based on surveillance data of ‘time of death.’ In cases with less than 100% disease‐associated mortality, the model can be adjusted to accommodate both streams of surveillance data, whereas, if mortality is 100%, the antibody portion of the model can be excluded.
Detection
In most serosurveillance systems, there are at least two important sources of detection‐based uncertainty that should be considered: (1) measurement error when quantifying antibodies, and (2) sampling error when choosing a subset of individuals from the population to sample (Table 1). Imperfect serological assays can be a major source of measurement error, especially in wildlife disease systems (Gilbert et al. 2013) or when there is substantial pathogen diversity and/or cross‐reactivity in a diagnostic system (Mansfield et al. 2011). In these cases, selection of the antigen employed in serological tests is not trivial and impacts quantitative results (Troyer et al. 2005), suggesting it may be useful to consider suites of antigenic markers for estimating TSI to reduce uncertainty. For animal systems, experimental infections conducted in the target host species are extremely valuable for quantifying assay sensitivity and specificity (Bean et al. 2013) and developing epidemiological models that inform disease ecology and surveillance design (e.g. reviewed in Plowright et al. 2016). Previous work has shown that experimental information on assay sensitivity and specificity can be incorporated into models of serosurveillance data, decreasing bias in estimates of prevalence (McClintock et al. 2010). Likewise, the modelling framework we present is amenable for incorporation of this source of error by modelling it explicitly as a factor affecting the threshold of detection (y*) and/or parameters of the antibody kinetic function, depending on the type of error produced by the assay (Table 1).
Epidemiologists studying human diseases have long recognised the importance of accounting for sampling error, often referred to as ‘underreporting’ or variation in reporting rates (CDC 1996). Likewise, mechanistic descriptions of sampling error have been deemed important for inference of wildlife disease parameters such as prevalence (McClintock et al. 2010; Bailey et al. 2014) or FOI (Conn et al. 2012), which were motivated by ecological work accounting for sampling error to provide better inference for unobserved ecological quantities (Williams et al. 2002; Hooten et al. 2007; Royle & Dorazio 2008; Hobbs & Hooten 2015). Recent work also emphasises that, in addition to sample size and independence between sampled individuals, sampling design should consider underlying seasonality in demographic and disease dynamics to obtain the most accurate estimates of disease transmission parameters (Vinh & Boni 2015). In systems with seasonality in disease transmission, it is useful to collect the surveillance data over a time scale that captures cycling and make inference over system‐specific time intervals (i.e. interval no larger than longevity of antibody response) to decipher temporal heterogeneity in the FOI (Simonsen et al. 2009; Vinh & Boni 2015). Provided that surveillance is conducted at intervals that capture epidemic cycling and at least some individuals with antibody titres are found, issues from small sample sizes can be attenuated by aggregating data from several sampling events (Blackwood et al. 2013). In addition, because each sample generates an individual's epidemiological status (susceptible, newly infected, seropositive for each day of interest in the past), more data can be used for calculating FOI at previous time steps as the sampling period increases, which could increase accuracy of the estimates (e.g. temporal quantitative antibody model we present in Supporting Information 4).
Endemic dynamics
We considered the situation where a pathogen invades a completely susceptible population, generating a single epidemic peak. Combined with a brief period of sampling, this led to the assumption that expected TSI has the same mean for all individuals, which is inappropriate when there are multiple epidemic peaks or more complicated dynamics occurring within the time frame of the analysis. In the systematic sampling model (Fig. 5, Supporting Information 4), we relax the equal‐mean assumption by allowing mean TSI to vary over time depending on recent antibody levels, which improves inference for samples collected over longer time periods and is important for adapting this framework for systems with endemic dynamics. One important application of our method could be to better understand transmission dynamics in wildlife species, where disease may be inapparent but where knowledge of FOI could inform spillover hazard to other hosts (e.g. Middle East respiratory syndrome coronavirus in dromedary camels). Using our framework, inference of time‐varying FOI can be made using relatively short‐term cross‐sectional sampling allowing for a more rapid understanding (relative to conventional methods that require long‐term sampling to infer time‐varying FOI) of the link between recent changes in FOI and spillover hazard. In ongoing work, we are investigating the ability of the model to infer FOI beyond a single epidemic curve to further evaluate the breadth of epidemiological behaviour for which this approach is appropriate. Preliminary findings suggest that allowing more flexibility in the distribution of TSI and/or incorporating longitudinal serosurveillance data may be important for modelling endemic dynamics (Table 1; Borremans et al. 2016).
Multiple strains
Several pathogens have complex strain structure and cause multiple infections over longer periods of time. The dynamics of these systems are necessarily driven by induced cross‐immunity responses that can elicit significant antibody responses (Smith et al. 2004; Horton et al. 2010; Mansfield et al. 2011). The importance of multiple strains and cross‐reaction has been recognised in the study of human influenza A for many years as original antigenic sin (Francis 1960), the observation that after a vaccination or natural infection during later life, an individual's antibody boost against their first infection may be as strong or stronger than the boost to the current strain. This concept has been revised as antigenic seniority to indicate that second and subsequent early infections may also be important (Lessler et al. 2012), and incorporated into a life course model of antibody responses to multiple infections in which the number and timing of infections can be inferred (Kucharski et al. 2015). To account for cross‐immunity issues in quantitative antibody methods, it will be important to experimentally measure antibody kinetics for multiple target strains in particular host‐pathogen systems, which is a substantial investment of time and money. However, if such data were available, separate antibody kinetic functions for primary and cross‐reactive antibody kinetics could be incorporated in our framework for improved inference (Table 1), which would also improve understanding of the impacts of particular strains on driving FOI.
Contact structure
In the derivation of FOI, we assume that the host population mixes homogenously, such that all susceptible hosts have equal probability of contact with newly infected hosts. While this may be an appropriate approximation in the case of gregarious goose populations congregating at breeding sites, most populations involve some degree of heterogeneity in host contact structure. In general, heterogeneity decreases population‐level FOI because not all susceptible individuals are in contact with all infectious individuals (as with homogenous mixing). Thus, when applying our framework to populations with heterogeneous contact structure, estimates of FOI could be biased depending on how the population is sampled relative to its contact structure. For example, if only high‐degree nodes are sampled, our model may have low bias because this situation is similar to homogenous mixing. Alternatively, if only low degree nodes are sampled our model would underestimate FOI because we would overestimate the number of susceptible individuals that are available for contact with newly infected hosts. Note that bias from contact structure would not affect estimates of incidence in our model because incidence does not rely on estimates of the number of susceptible individuals. Thus, it is safest to infer incidence rather than FOI in highly structured populations where contact structure is unknown. However, if data on contact structure exist, our calculation of FOI could be adapted to incorporate an appropriate relationship between susceptible and newly infected individuals (currently assumed to be directly proportional: Newly infecteds/susceptibles; Table 1).
Complex antibody responses
In our simulated examples, we adapted a fairly complex function for antibody responses, which included both rising and decaying phases. Our results showed that in some situations, misclassification of these phases could lead to predicting an additional epidemic peak, suggesting that systems with complex antibody dynamics may benefit from incorporating additional data. For example, differentiating between the rising and declining phases of the antibody response (and possibly between primary and anamnestic responses) is possible using data from multiple types of antibodies (e.g. Immunoglobulin (Ig) M and G) because of their different kinetics and timing post‐infection (Simonsen et al. 2009; Teunis et al. 2012). Thus, if data distinguishing phases of antibody responses were collected by surveillance programmes, it may be possible to improve inference by providing more information for the model to distinguishing phases of antibody response.
In general, quantitative antibody methods rely on strong knowledge of the immunology of the focal system for optimal inference. This makes them currently inaccessible for diseases with poorly understood or unpredictable immunological dynamics (see Table 1 for options), but on the positive side, quantitative antibody approaches provide a framework for better understanding the role of complex immunology in wildlife disease dynamics when appropriate experimental studies are conducted. Also, in systems where antibody response is too complex to be explained with a mechanistic function, a non‐parametric, spline‐based model of antibody kinetics (e.g. Borremans et al. 2016) can be used to infer FOI if the research question does not require inference about within‐host processes.
Conclusions
Serosurveillance data are often summarised as seroprevalence, neglecting information that could help reveal the timing and magnitude of epidemic peaks. Conventional methods of estimating FOI are inappropriate in wildlife disease systems where the host is short‐lived (not practical to determine ages), where age data are coarse and imprecise (not enough information to fit the age‐seroprevalence curve), where long serosurveillance time series are infeasible, or where antibodies decay quickly (no signature of increased seroprevalence with age). Recent theoretical advances, extended by the framework presented here, highlight that time‐varying estimates of disease incidence or FOI can be obtained by relaxing these requirements, thus providing an inferential tool for epidemic dynamics and other epidemiological situations where conventional methods (i.e. age‐seroprevalence methods) are inappropriate. In addition to FOI, quantitative antibody methods can estimate other important quantities of interest, such as the proportion of susceptible hosts, proportion of seropositive hosts and incidence. The framework we propose is inherently flexible for incorporating a variety of antibody response curves and sources of individual‐level variation, making it applicable to a number of host‐pathogen systems as well as providing a platform for investigating the role of individual‐level processes in dynamics of FOI.
Our findings indicate that quantitative antibody methods have the potential to be broadly applicable, but additional experimental studies will broaden their scope further and highlight additional data that may improve estimation of key metrics of wildlife disease dynamics. As emphasised above, a key ingredient of quantitative antibody methods is antibody kinetic data. For animal‐host systems, challenge studies with experimental animals can provide detailed antibody kinetic data for identifying the appropriate antibody response functions (Turmelle et al. 2010; Andraud et al. 2012; Baeten et al. 2013; Sun et al. 2015). We found that 30 experimental mallards infected with influenza A captured individual‐level heterogeneity adequately. Depending on the host response, experimental animals need to be monitored regularly for a potentially long duration (3 months or more) to capture the long‐term antibody response profile, which can be expensive and difficult for pathogens that require high level biosecurity. However, a single well‐designed experimental study can be used for inference with many serosurveillance datasets and thus is a worthwhile investment. Such studies are specific to the particular host‐pathogen system being modelled, thus, for quantitative antibody methods to be broadly applicable, experimental datasets need to be available for a range of host‐pathogen systems. An informal survey of the literature revealed that these datasets have been collected in some systems, but the data are rarely presented in a manner that could be used by our model, highlighting a gap for future research. In addition, measuring covariate data alongside antibody responses (Table 1), as well as antibody responses in hosts with different infection histories (i.e. previous infections with the same or different strains/pathogens), will be important for broadening application of quantitative antibody methods.
We predict that using quantitative antibody data to infer FOI will be most successful in situations with epidemic dynamics, where the signal from temporal changes in antibody levels is strongest, but future research to extend these methods to endemic systems would broaden their application to additional wildlife disease systems. Future experimental research to quantify antibody kinetics (empirical) and understand the behaviour of quantitative antibody methods under a range of serosurveillance designs and epidemiological conditions (simulation and field studies), will reveal the full potential of quantitative antibody methods in understanding and predicting disease dynamics.
Statement of authorship
KMP, SLK, BDG, SSS, MBH, JAH, CTW and MGB helped develop the statistical models of antibody kinetics and force of infection inference. KMP developed and implemented the simulation model of disease transmission and wrote the manuscript. SLK developed and implemented the statistical model for estimating force of infection, and prepared all figures. BG developed and implemented the antibody kinetic model. SSS collected the data used for the antibody kinetic model. MDS collected the population‐level serosurveillance data in snow geese and organised the data for analysis. The idea for this work originated as part of a workshop on inferring disease hazard from serology data. All authors attended the workshop (except SLK, ATG and BG) and contributed substantially to the ideas in this work. All authors contributed substantially to editing the manuscript.
Data accessibility
We, the authors, confirm that ‘should the manuscript be accepted, the data supporting the results will be archived in an appropriate public repository such as Dryad or Figshare and the data DOI will be included at the end of the article’.
Supporting information
Acknowledgements
This research emerged from a workshop funded by the Research and Policy in Disease Dynamics (RAPIDD) programme, Fogarty International Center, National Institute of Health and Department of Homeland Security. Thanks to additional workshop participants for contributing talks and ideas during the workshop: Sarah Bevins, Kerri Pedersen, Alan Franklin, Jeff Root, Christine Ellis, Raina Plowright, Angie Luis, David Hayman, Kezia Manlove, Katie Prager, Laurie Baeten, Tom DeLiberto, and Tom Gidlewski. In addition, MGB was funded by RAPIDD. MGB and JOL‐S were also funded by the National Science Foundation (OCE‐1335657). KMP was funded by the United States Department of Agriculture, Animal and Plant Health Inspection Service, Wildlife Services. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government. No warranty, expressed or implied, is made by the USGS or the U.S. Government as to the functionality of the software and related material nor shall the fact of release constitute any such warranty.
References
- Alcami, A. & Koszinowski, U.H. (2000). Viral mechanisms of immune evasion. Immunol. Today, 21, 447–455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alizon, S. & van Baalen, M. (2005). Emergence of a convex trade‐off between transmission and virulence. Am. Nat., 165, E155–E167. [DOI] [PubMed] [Google Scholar]
- Andraud, M. , Lejeune, O. , Musoro, J.Z. , Ogunjimi, B. , Beutels, P. & Hens, N. (2012). Living on three time scales: the dynamics of plasma cell and antibody populations illustrated for hepatitis a virus. PLoS Comput. Biol., 8, e1002418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson, C.T. & Samuel, M.D. (2010). Avian malaria Plasmodium relictum in native Hawaiian forest birds: epizootiology and demographic impacts on ‘apapane Himatione sanguinea. J. Avian Biol., 41, 357–366. [Google Scholar]
- Avril, A. , Grosbois, V. , Latorre‐Margalef, N. , Gaidet, N. , Tolf, C. , Olsen, B. et al (2016). Capturing individual‐level parameters of influenza A virus dynamics in wild ducks using multistate models. J. Appl. Ecol., 53, 1289–1297. [Google Scholar]
- Baeten, L.A. , Pappert, R. , Young, J. , Schriefer, M.E. , Gidlewski, T. , Kohler, D. et al (2013). Immunological and clinical response of coyotes (Canis latrans) to experimental inoculation with Yersinia pestis. J. Wildl. Dis., 49, 932–939. [DOI] [PubMed] [Google Scholar]
- Bailey, L.L. , MacKenzie, D.I. & Nichols, J.D. (2014). Advances and applications of occupancy models. Methods Ecol. Evol., 5, 1269–1279. [Google Scholar]
- Bean, A.G. , Baker, M.L. , Stewart, C.R. , Cowled, C. , Deffrasnes, C. , Wang, L.F. et al (2013). Studying immunity to zoonotic diseases in the natural host ‐ keeping it real. Nat. Rev. Immunol., 13, 851–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackwood, J.C. , Streicker, D.G. , Altizer, S. & Rohani, P. (2013). Resolving the roles of immunity, pathogenesis, and immigration for rabies persistence in vampire bats. Proc. Natl Acad. Sci. USA, 110, 20837–20842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollaerts, K. , Aerts, M. , Shkedy, Z. , Faes, C. , Van der Stede, Y. , Beutels, P. et al (2012). Estimating the population prevalence and force of infection directly from antibody titres. Stat. Mod., 12, 441–462. [Google Scholar]
- Borremans, B. , Hens, N. , Beutels, P. , Leirs, H. & Reijniers, J. (2016). Estimating time of infection using prior serological and individual information can greatly improve incidence estimation of human and wildlife infections. PLoS Comput. Biol., 12, e1004882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caley, P. & Hone, J. (2002). Estimating the force of infection; Mycobacterium bovis infection in feral ferrets Mustela furo in New Zealand. J. Anim. Ecol., 71, 44–54. [Google Scholar]
- Caley, P. & Hone, J. (2004). Disease transmission between and within species, and the implications for disease control. J. Appl. Ecol., 41, 94–104. [Google Scholar]
- CDC (1996). Historical Perspectives Notifiable Disease Surveillance and Notifiable Disease Statistics – United States, June 1946 and June 1996 In: (ed. Systems Operations and Information Br DoSaE, Epidemiology Program Office, Centers for Disease Control and Prevention). U.S. Government Printing Office (GPO) Washington, DC: pp. 530–536. [Google Scholar]
- Conn, P.B. , Cooch, E.G. & Caley, P. (2012). Accounting for detection probability when estimating force‐of‐infection from animal encounter data. J. Ornithol., 152, S511–S520. [Google Scholar]
- Farnsworth, M.L. , Miller, R.S. , Pedersen, K. , Lutman, M.W. , Swafford, S.R. , Riggs, P.D. et al (2012). Environmental and demographic determinants of avian influenza viruses in waterfowl across the contiguous United States. PLoS ONE, 7, e32729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farrington, C.P. (1990). Modeling forces of infection for measles, mumps and rubella. Stat. Med., 9, 953–967. [DOI] [PubMed] [Google Scholar]
- Farrington, C.P. (1992). The measurement and interpretation of age‐specific vaccine efficacy. Int. J. Epidemiol., 21, 1014–1020. [DOI] [PubMed] [Google Scholar]
- Feng, Z.L. , Glasser, J.W. , Hill, A.N. , Franko, M.A. , Carlsson, R.M. , Hallander, H. et al (2014). Modeling rates of infection with transient maternal antibodies and waning active immunity: application to Bordetella pertussis in Sweden. J. Theor. Biol., 356, 123–132. [DOI] [PubMed] [Google Scholar]
- Ferguson, N.M. , Donnelly, C.A. & Anderson, R.M. (1999). Transmission dynamics and epidemiology of dengue: insights from age‐stratified sero‐prevalence surveys. Philos. Trans. R. Soc. Lond. B Biol. Sci., 354, 757–768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finlay, B.B. & McFadden, G. (2006). Anti‐immunology: evasion of the host immune system by bacterial and viral pathogens. Cell, 124, 767–782. [DOI] [PubMed] [Google Scholar]
- Francis, T. Jr (1960). On the doctrine of original antigenic sin. Proc. Am. Philos. Soc., 104, 572–578. [Google Scholar]
- Gay, N. (1996a). Analysis of serological surveys using mixture models: application to a survey of parvovirus B19. Stat. Med., 15, 1567–1573. [DOI] [PubMed] [Google Scholar]
- Gay, N.J. (1996b). A model of long‐term decline in the transmissibility of an infectious disease: implications for the incidence of hepatitis A. Int. J. Epidemiol., 25, 854–861. [DOI] [PubMed] [Google Scholar]
- Gilbert, A.T. , Fooks, A.R. , Hayman, D.T.S. , Horton, D.L. , Muller, T. , Plowright, R. et al (2013). Deciphering serology to understand the ecology of infectious diseases in wildlife. EcoHealth, 10, 298–313. [DOI] [PubMed] [Google Scholar]
- de Graaf, W.F. , Kretzschmar, M.E.E. , Teunis, P.F.M. & Diekmann, O. (2014). A two‐phase within‐host model for immune response and its application to serological profiles of pertussis. Epidemics, 9, 1–7. [DOI] [PubMed] [Google Scholar]
- Graham, A.L. , Hayward, A.D. , Watt, K.A. , Pilkington, J.G. , Pemberton, J.M. & Nussey, D.H. (2010). Fitness correlates of heritable variation in antibody responsiveness in a wild mammal. Science, 330, 662–665. [DOI] [PubMed] [Google Scholar]
- Grassly, N.C. & Fraser, C. (2006). Seasonal infectious disease epidemiology. Proc. Biol. Sci./Royal Soc., 273, 2541–2550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grenfell, B.T. & Anderson, R.M. (1985). The estimation of age‐related rates of infection from case notifications and serological data. J. Hygiene, 95, 419–436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handel, A. & Rohani, P. . (2015). Crossing the scale from within‐host infection dynamics to between‐host transmission fitness: a discussion of current assumptions and knowledge. Philos. Trans. R. Soc. Lond. Series B, Biological sciences, 370, 20140302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handel, A. , Longini, I.M. Jr & Antia, R. (2007). Neuraminidase inhibitor resistance in influenza: assessing the danger of its generation and spread. PLoS Comput. Biol., 3, e240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handel, A. , Brown, J. , Stallknecht, D. & Rohani, P. (2013). A multi‐scale analysis of influenza A virus fitness trade‐offs due to temperature‐dependent virus persistence. PLoS Comput. Biol., 9, e1002989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heisey, D.M. , Joly, D.O. & Messier, F. (2006). The fitting of general force‐of‐infection models to wildlife disease prevalence data. Ecology, 87, 2356–2365. [DOI] [PubMed] [Google Scholar]
- Heisey, D.M. , Osnas, E.E. , Cross, P.C. , Joly, D.O. , Langenberg, J.A. & Miller, M.W. (2010). Linking process to pattern: estimating spatiotemporal dynamics of a wildlife epidemic from cross‐sectional data. Ecol. Monogr., 80, 221–240. [Google Scholar]
- Henaux, V. , Parmley, J. , Soos, C. & Samuel, M.D. (2013). Estimating transmission of avian influenza in wild birds from incomplete epizootic data: implications for surveillance and disease spread. J. Appl. Ecol., 50, 223–231. [Google Scholar]
- Hens, N. , Aerts, M. , Faes, C. , Shkedy, Z. , Lejeune, O. , van Damme, P. et al (2010). Seventy‐five years of estimating the force of infection from current status data. Epidemiol. Infect., 138, 802–812. [DOI] [PubMed] [Google Scholar]
- Hill, N.J. , Ma, E.J. , Meixell, B.W. , Lindberg, M.S. , Boyce, W.M. & Runstadler, J.A. (2016). Transmission of influenza reflects seasonality of wild birds across the annual cycle. Ecol. Lett., 19, 915–925. [DOI] [PubMed] [Google Scholar]
- Hobbs, N.T. & Hooten, M.B. . (2015). Bayesian Models: A Statistical Primer for Ecologists. Princeton University Press. [Google Scholar]
- Hooten, M.B. , Wikle, C.K. , Dorazio, R.M. & Royle, J.A. (2007). Hierarchical spatio‐temporal matrix models for characterizing invasions. Biometrics, 63, 558–567. [DOI] [PubMed] [Google Scholar]
- Horton, D.L. , McElhinney, L.M. , Marston, D.A. , Wood, J.L. , Russell, C.A. , Lewis, N. et al (2010). Quantifying antigenic relationships among the lyssaviruses. J. Virol., 84, 11841–11848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosseini, P.R. , Dhondt, A.A. & Dobson, A. (2004). Seasonality and wildlife disease: how seasonal birth, aggregation and variation in immunity affect the dynamics of Mycoplasma gallisepticum in house finches. Proc. R. Soc. B Biol. Sci., 271, 2569–2577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito, T. , Okazaki, K. , Kawaoka, Y. , Takada, A. , Webster, R.G. & Kida, H. (1995). Perpetuation of influenza A viruses in Alaskan waterfowl reservoirs. Arch. Virol., 140, 1163–1172. [DOI] [PubMed] [Google Scholar]
- Jones, K.E. , Patel, N.G. , Levy, M.A. , Storeygard, A. , Balk, D. , Gittleman, J.L. et al (2008). Global trends in emerging infectious diseases. Nature, 451, 990–U4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer‐Schadt, S. , Fernández, N. , Eisinger, D. , Grimm, V. & Thulke, H. (2009). Individual variations in infectiousness explain long‐term disease persistence in wildlife populations. Oikos, 118, 199–208. [Google Scholar]
- Kretzschmar, M. , Teunis, P.F.M. & Pebody, R.G. (2010). Incidence and reproduction numbers of pertussis: estimates from serological and social contact data in five European countries. PLoS Med., 7, e1000291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucharski, A.J. , Lessler, J. , Read, J.M. , Zhu, H. , Jiang, C.Q. , Guan, Y. et al (2015). Estimating the life course of influenza A(H3N2) antibody responses from cross‐sectional data. PLoS Biol., 13, e1002082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lessler, J. , Riley, S. , Read, J.M. , Wang, S. , Zhu, H. , Smith, G.J.D. et al (2012). Evidence for antigenic seniority in influenza A (H3N2) antibody responses in Southern China. PLoS Pathog., 8, e1002802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd‐Smith, J.O. , George, D. , Pepin, K.M. , Pitzer, V.E. , Pulliam, J.R.C. , Dobson, A.P. et al (2009). Epidemic dynamics at the human‐animal interface. Science, 326, 1362–1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mansfield, K.L. , Horton, D.L. , Johnson, N. , Li, L. , Barrett, A.D. , Smith, D.J. et al (2011). Flavivirus‐induced antibody cross‐reactivity. J. Gen. Virol., 92, 2821–2829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClintock, B.T. , Nichols, J.D. , Bailey, L.L. , MacKenzie, D.I. , Kendall, W.L. & Franklin, A.B. (2010). Seeking a second opinion: uncertainty in disease ecology. Ecol. Lett., 13, 659–674. [DOI] [PubMed] [Google Scholar]
- de Melker, H.E. , Versteegh, F.G.A. , Schellekens, J.F.P. , Teunis, P.F.M. & Kretzschmar, M. (2006). The incidence of Bordetella pertussis infections estimated in the population from a combination of serological surveys. J. Infect., 53, 106–113. [DOI] [PubMed] [Google Scholar]
- Mideo, N. , Alizon, S. & Day, T. (2008). Linking within‐ and between‐host dynamics in the evolutionary epidemiology of infectious diseases. Trends Ecol. Evol., 23, 511–517. [DOI] [PubMed] [Google Scholar]
- Mueller, I. , Schoepflin, S. , Smith, T.A. , Benton, K.L. , Bretscher, M.T. , Lin, E. et al (2012). Force of infection is key to understanding the epidemiology of Plasmodium falciparum malaria in Papua New Guinean children. Proc. Natl Acad. Sci. USA, 109, 10030–10035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muench, H. (1934). Derivation of rates from summation data by the catalytic curve. J. Am. Stat. Assoc., 29, 25–38. [Google Scholar]
- Muench, H. (1959). Catalytic Models in Epidemiology. Harvard University Press, Boston. [Google Scholar]
- Park, M. , Loverdo, C. , Schreiber, S.J. & Lloyd‐Smith, J.O. (2013). Multiple scales of selection influence the evolutionary emergence of novel pathogens. Philos. Trans. R. Soc. Lond. B Biol. Sci., 368, 20120333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepin, K.M. , Volkov, I. , Banavar, J.R. , Wilke, C.O. & Grenfell, B.T. (2010). Phenotypic differences in viral immune escape explained by linking within‐host dynamics to host‐population immunity. J. Theor. Biol., 265, 501–510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepin, K.M. , Riley, S. & Grenfell, B.T. (2013). Effects of influenza antivirals on individual and population immunity over many epidemic waves. Epidemiol. Infect., 141, 366–376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plowright, R.K. , Peel, A.J. , Streicker, D.G. , Gilbert, A.T. , McCallum, H. , Wood, J. et al (2016). Transmission or within‐host dynamics driving pulses of zoonotic viruses in reservoir‐host populations. PLoS Negl. Trop Dis., 10, e0004796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pomeroy, L.W. , Bjornstad, O.N. , Kim, H. , Jumbo, S.D. & Abdoulkadiri, S. & Garabed, R. (2015). Serotype‐specific transmission and waning immunity of endemic foot‐and‐mouth disease virus in cameroon. PLoS ONE, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pothin, E. , Ferguson, N.M. , Drakeley, C.J. & Ghani, A.C. (2016). Estimating malaria transmission intensity from Plasmodium falciparum serological data using antibody density models. Malaria J., 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiner, R.C. , Stoddard, S.T. , Forshey, B.M. , King, A.A. , Ellis, A.M. , Lloyd, A.L. et al (2014). Time‐varying, serotype‐specific force of infection of dengue virus. Proc. Natl Acad. Sci. USA, 111, E2694–E2702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez‐Barraquer, I. , Solomon, S.S. , Kuganantham, P. , Srikrishnan, A.K. , Vasudevan, C.K. , Iqbal, S.H. et al (2015). The Hidden Burden of Dengue and Chikungunya in Chennai, India. PLoS Negl. Trop Dis., 9, 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Royle, J.A. & Dorazio, R.M. (2008). Hierarchical Modeling and Inference in Ecology. Academic Press, San Diego. [Google Scholar]
- Samuel, M.D. , Shadduck, D.J. , Goldberg, D.R. , Baranyuk, V. , Sileo, L. & Price, J.I. (1999). Antibodies against Pasteurella multocida in snow geese in the western Arctic. J. Wildl. Dis., 35, 449. [DOI] [PubMed] [Google Scholar]
- Samuel, M.D. , Hall, J.S. , Brown, J.D. , Goldberg, D.R. , Ip, H. & Baranyuk, V.V. (2015). The dynamics of avian influenza in Lesser Snow Geese: implications for annual and migratory infection patterns. Ecol. Appl., 25, 1851–1859. [DOI] [PubMed] [Google Scholar]
- Schreiber, S.J. , Ke, R. , Loverdo C., Park.M. & Ahsan P., Lloyd.‐Smith.J.L. (2016). Cross‐scale dynamics and the evolutionary emergence of infectious diseases. In Press. DOI: 10.1101/066688. [DOI] [PMC free article] [PubMed]
- Simonsen, J. , Molbak, K. , Falkenhorst, G. , Krogfelt, K.A. , Linneberg, A. & Teunis, P.F.M. (2009). Estimation of incidences of infectious diseases based on antibody measurements. Stat. Med., 28, 1882–1895. [DOI] [PubMed] [Google Scholar]
- Smith, D.J. , Lapedes, A.S. , de Jong, J.C. , Bestebroer, T.M. , Rimmelzwaan, G.F. , Osterhaus, A.D. et al (2004). Mapping the antigenic and genetic evolution of influenza virus. Science, 305, 371–376. [DOI] [PubMed] [Google Scholar]
- Stoddard, S.T. , Wearing, H.J. , Reiner, R.C. , Morrison, A.C. , Astete, H. , Vilcarromero, S. et al (2014). Long‐Term and Seasonal Dynamics of Dengue in Iquitos, Peru. Plos Neglected Tropical Diseases, 8, e3003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun, H.L. , Cunningham, F.L. , Harris, J. , Xu, Y.F. , Long, L.P. , Hanson‐Dorr, K. et al (2015). Dynamics of virus shedding and antibody responses in influenza A virus‐infected feral swine. J. Gen. Virol., 96, 2569–2578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamerius, J. , Nelson, M.I. , Zhou, S.Z. , Viboud, C. , Miller, M.A. & Alonso, W.J. (2011). Global influenza seasonality: reconciling patterns across temperate and tropical regions. Environ. Health Perspect., 119, 439–445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teunis, P. (2015). Estimating Infection Rates from Serological Data. In: R package version 1.0.5. http://ecdc.europa.eu/en/data-tools/seroincidence-calculator-tool/Pages/default.aspx. [DOI] [PubMed] [Google Scholar]
- Teunis, P.F. , van der Heijden, O.G. , de Melker, H.E. , Schellekens, J.F. , Versteegh, F.G. & Kretzschmar, M.E. (2002). Kinetics of the IgG antibody response to pertussis toxin after infection with B. pertussis. Epidemiol. Infect., 129, 479–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teunis, P.F.M. , van Eijkeren, J.C.H. , Ang, C.W. , van Duynhoven, Y. , Simonsen, J.B. , Strid, M.A. et al (2012). Biomarker dynamics: estimating infection rates from serological data. Stat. Med., 31, 2240–2248. [DOI] [PubMed] [Google Scholar]
- Teunis, P.F.M. , Schimmer, B. , Notermans, D.W. , Leenders, A. , Wever, P.C. , Kretzschmar, M.E.E. et al (2013). Time‐course of antibody responses against Coxiella burnetii following acute Q fever. Epidemiol. Infect., 141, 62–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Troyer, J.L. , Pecon‐Slattery, J. , Roelke, M.E. , Johnson, W. , VandeWoude, S. , Vazquez‐Salat, N. et al (2005). Seroprevalence and genomic divergence of circulating strains of feline immunodeficiency virus among Felidae and Hyaenidae species. J. Virol., 79, 8282–8294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turmelle, A.S. , Jackson, F.R. , Green, D. , McCracken, G.F. & Rupprecht, C.E. (2010). Host immunity to repeated rabies virus infection in big brown bats. J. Gen. Virol., 91, 2360–2366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinh, D.N. & Boni, M.F. (2015). Statistical identifiability and sample size calculations for serial seroepidemiology. Epidemics, 12, 30–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vink, M.A. , van de Kassteele, J. , Wallinga, J. , Teunis, P.F.M. & Bogaards, J.A. (2015). Estimating seroprevalence of human papillomavirus type 16 using a mixture model with smoothed age‐dependent mixing proportions. Epidemiology, 26, 8–16. [DOI] [PubMed] [Google Scholar]
- Volkov, I. , Pepin, K.M. , Lloyd‐Smith, J.O. , Banavar, J.R. & Grenfell, B.T. (2010). Synthesizing within‐host and population‐level selective pressures on viral populations: the impact of adaptive immunity on viral immune escape. J. Royal Soc., Inter./Royal Soc., 7, 1311–1318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vyse, A.J. , Gay, N.J. , Hesketh, L.M. , Pebody, R. , Morgan‐Capner, P. & Miller, E. (2006). Interpreting serological surveys using mixture models: the seroepidemiology of measles, mumps and rubella in England and Wales at the beginning of the 21st century. Epidemiol. Infect., 134, 1303–1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitaker, H.J. & Farrington, C.P. (2004). Estimation of infectious disease parameters from serological survey data: the impact of regular epidemics. Stat. Med., 23, 2429–2443. [DOI] [PubMed] [Google Scholar]
- Williams, B.K. , Nichols, J.D. & Conroy, M.J. (2002). Analysis and Management of Animal Populations. Academic Press, San Diego. [Google Scholar]
- Wu, J.T. , Leung, K. , Perera, R.A. , Chu, D.K. , Lee, C.K. , Hung, I.F. Lin, C.K. , Lo, S.V. , Lau, Y.L. , Leung, G.M. , Cowling, B.J. & , Peiris, J.S. (2014). Inferring influenza infection attack rate from seroprevalence data. PLoS Pathog., 10, e1004054. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
We, the authors, confirm that ‘should the manuscript be accepted, the data supporting the results will be archived in an appropriate public repository such as Dryad or Figshare and the data DOI will be included at the end of the article’.


