Abstract
The extent to which interspecific niche differences structure plant communities is highly debated, with extreme viewpoints ranging from fine‐scaled niche partitioning, where every species in the community is specialized to a distinct niche, to neutrality, where species have no niche or fitness differences. However, there exists a default position wherein niches of species in a community are determined by their evolutionary and biogeographic histories, irrespective of other species within the community. According to this viewpoint, a broad range of pair‐wise niche overlaps—from completely overlapping to completely distinct—are expected in any community without the need to invoke interspecific interactions. We develop a method that can test for both habitat associations and niche differences along an arbitrary number of spatial and temporal niche dimensions and apply it to a 24‐yr data set of the eight dominant woody‐plant species (representing 84% and 76% of total community abundance and basal area, respectively) from a 50‐ha permanent plot in a southern Indian tropical dry forest, using edaphic, topographic, and precipitation variables as niche axes. Species separated into two broad groups in niche space—one consisting of three canopy species and the other of a canopy species and four understory species—along axes that corresponded mainly to variation in soil P, Al and a topographic index of wetness. Species within groups tended to have significantly greater niche overlap than expected by chance. Community‐wide niche overlap in spatial and temporal niche axes was never smaller than expected by chance. Species‐habitat associations were neither necessary nor sufficient preconditions for niche differences to be present. Our results suggest that this tropical dry‐forest community consists of several tree species with broadly overlapping niches, and where significant niche differences do exist, they are not readily interpretable as evidence for niche differentiation. We argue, based on a survey of the literature, that many of the observed niche differences in tropical forests are more parsimoniously viewed as autecological differences between species that exist independently of interspecific interactions.
Keywords: autecology, coexistence, habitat association, individualistic concept, Mudumalai Forest Dynamics Plot, niche differentiation, niche specialization, seasonally dry tropical forest
Introduction
The search for order and pattern in the immense complexity of tropical forests led early workers to hypothesize that tree species were associated with microhabitats defined by topography, drainage, soils or light at the local (<1 km2) scale (e.g., Richards 1952, Poore 1968). These ideas have borne out: virtually every study that has looked for evidence of species‐habitat associations in tropical forests has found it (the literature survey in Appendix S1 lists nearly 40 studies from the last two decades alone). Habitat associations are typically inferred from statistically significant differences in densities across discrete habitats or continuous environmental gradients as a first step. Processes underlying this differential success can then be inferred from studies of demography (survival, reproduction, dispersal and growth), traits, and phylogenies (Baraloto et al. 2007, Yamada et al. 2007, Russo et al. 2008, Comita and Engelbrecht 2009, Kraft and Ackerly 2010, Zuidema et al. 2010).
In niche space, habitat associations represent narrowing of habitat niche width (i.e., habitat niche specialization), although the presence or absence of an individual in geographical space is modulated by other spatial processes such as dispersal (Condit et al. 2000) and recruitment (Hurtt and Pacala 1995) limitation, density‐dependent mortality due to host‐specific predation (Bagchi et al. 2011), demographic stochasticity resulting from the uncertainty of biotic neighborhoods (Hubbell and Foster 1986) and other historical accidents.
To what extent does niche specialization result from niche differentiation—i.e., segregation of species along niche axes as predicted by niche theory (Hutchinson 1957)? The two phenomena are often implicitly conflated, but this is unjustified because niche specialization is neither necessary nor sufficient for niche differentiation. It is not necessary because niches could be partitioned amongst sub‐populations of species, and it is not sufficient because multiple species could be specialized to the same niche. Indeed, trees may specialize along niche axes independent of the existence of other tree species: intrinsic tradeoffs in fitness across environments, underlain by costs of adaptation to particular conditions, can force species to specialize (Futuyma and Moreno 1988, Kassen 2002). Species may specialize to different regions in niche space simply as a consequence of their differing evolutionary and biogeographic histories, which, in essence is an individualistic or autecological view of species in communities (Gleason 1926, Strong 1983). In neutrally assembled communities, therefore, species‐pairs can exhibit a gradient of niche overlaps even in the absence of interspecific interactions. Classical niche theory predicts that overlaps in equilibrium communities would be minimized because species occupying identical niches cannot coexist indefinitely (Hardin 1960)—this is one extreme scenario, where every species ends up specialized to a niche distinct from that of all other species in the community. In the other extreme, neutral‐theoretic scenario (Hubbell 2001), species with identical niches and no fitness differences are able to coexist long enough for local and global extinctions to be offset by immigration and speciation, respectively. Testing for the presence of both habitat associations and niche differentiation tells us where a community lies in this spectrum of possibilities. This has rarely been done: the few studies from tropical forests that have tested if observed tree niches differ more than a null model that excludes niche differentiation (Potts et al. 2004, Noguchi et al. 2007, Inman‐Narahari et al. 2013) suggest that niche differentiation is less prevalent in these forests than is suggested by the presence of habitat associations.
Interestingly, the prevalence of habitat associations and niche differentiation appears to vary considerably across studies and forests (Appendix S1). This leads to the question of whether the importance of niche structuring relative to other processes varies across forests and whether this happens in any systematic manner. Comparing data from 14 forests, Brown et al. (2013) found that the variance in the spatial overlap of tree‐species pairs—which they interpreted as importance of spatial niche differentiation—tended to increase with increasing topographic heterogeneity. The idea here is that increasing topographic heterogeneity creates increased spatial niche opportunities. Similarly, it may be hypothesized that the importance of temporal niche differentiation increases with increasing temporal resource heterogeneity—indeed, environmental fluctuations such as seasonality, interannual climatic variation, and disturbance can promote coexistence by creating temporal niche opportunities (Chesson and Huntly 1997, Chesson et al. 2004, Miller and Chesson 2009).
One such ubiquitous gradient in temporal heterogeneity in tropical forests is found along the precipitation seasonality axis. However, studies from seasonally dry tropical forests (SDTFs) are conspicuous by their near absence from the surveyed literature (Appendix S1). Available evidence suggests that tree species distributions are less strongly structured at the local scale by topography or soils, compared to forests in the wetter tropics (Bunyavejchewin et al. 2004, John and Sukumar 2004, Baldeck et al. 2012). SDTFs, which constitute 42% of tropical ecosystems globally, experience—by definition—several months of severe drought (Mooney et al. 1995) which influences the phenology of the forest as a whole (Dirzo et al. 2011). In addition, some SDTFs experience considerable interannual precipitation variability (Murphy and Lugo 1986) and are characterized by pulse disturbance agents such as fire (McShea and Davies 2011) and large herbivorous mammals (Sukumar et al. 2005). It is therefore possible that SDTF tree species stably coexist even if they do not appear to segregate along spatially varying, but temporally fixed, resource gradients, if indeed temporal segregation is more important in these ecosystems than in forests in the wetter, aseasonal tropics.
Our contribution in this study is to test for the existence of tree niche specialization and differentiation with respect to spatial (soils and topography) and temporal (precipitation) environmental gradients in a southern Indian SDTF. We perform three analyses: spatial‐only, in which niche space is defined by spatial variables (soils and topography), temporal‐only, in which niche space is defined by a temporal variable (annual precipitation), and spatiotemporal, in which niche space is defined by both spatial (elevation) and temporal (annual precipitation) variables.
The justification for spatiotemporal analysis is as follows. The stand of a given species at a given point in time is a superimposition of individuals that had recruited at various previous points in time. However, recruitment can shift spatially depending on environmental conditions (e.g., Metz 2012). For instance, we observed that recruitment in most species in a permanent 50‐ha tropical dry forest plot at Mudumalai (Sukumar et al. 2004) during a drought in 2002–2004 was largely restricted to lower elevations, particularly close to stream channels. Conversely, during an above‐average precipitation period of 2006–2008, recruitment occurred more strongly at higher elevations. If niche differentiation is only important at the recruitment (sapling) stage, it is possible that recruits spatially niche‐segregate at every given point in time, but, because recruitment shifts in space over time, no signature of spatial niche segregation is detectable in any given stand, which is an integration of a large number of past recruitment events. On the other hand, niche differences amongst recruits in any given year may be difficult to detect due to small sample sizes, compared to the entire stand. The spatiotemporal analysis of recruits in the elevation‐precipitation niche space provides a means to detect this kind of niche differentiation.
We interpret niche specialization and niche overlap results in light of the known geographical ranges of the constituent tree species at the landscape and regional scales. The method we apply readily extends to an arbitrary number of spatial and temporal niche dimensions.
Methods
Study site
The study was conducted during the period 1988–2012 in a permanent 50‐ha plot (Mudumalai Forest Dynamics Plot) situated in the seasonally dry tropical forest of Mudumalai Wildlife Sanctuary and National Park (henceforth Mudumalai), Tamil Nadu, southern India (11°35′ N 76°32′ E, 910–1,030 m above sea level, 1,000‐m E–W × 500‐m N–S; Sukumar et al. 2004). The plot lies in a transition zone between tropical dry‐deciduous and moist‐deciduous forest types (Champion and Seth 1968) to the east of a local peak (Bellur Betta, 1,083 m). The topography is undulating (elevation range 120 m, slope range 0–30°) and is dissected by a network of ephemeral, monsoonal streams that combine to drain the plot from the southern edge. Weathering‐resistant amphibolites dominate higher elevations while lower elevations are dominated by relatively weathering‐susceptible hornblende‐biotite gneisses; charnockites are distributed throughout in smaller numbers (Pulla et al. 2016). Soils are nutrient rich, nearly neutral, black to reddish‐brown sandy clay loams and sandy clays. Higher elevations in the plot have greater soil moisture, plant‐available Ca, Cu, Mn, Mg, Zn, B, clay and total carbon compared with lower elevations, a pattern that reflects the variation in lithology and topography (Pulla et al. 2016). Other soil properties—Fe, Al, P and K—are either weakly related or unrelated to variation in lithology and topography; a NE–SW trending high‐P patch is notable. All soil properties except pH show spatial autocorrelation up to at least 100 m. Mean annual precipitation at Kargudi, located ~4 km from the plot, during 1988–2015 was 1,260 ± 274 mm (range 763–1,840 mm). Mean monthly maximum and minimum temperatures at Kargudi during 1990–2013 were 27.4°C and 16.4°C, respectively. Precipitation largely occurs during the southwest or summer (June–September) and the northeast or winter (October–November) monsoons; it is <100 mm per month during the 6‐month dry season (November–April). At the landscape scale, dry‐season ground fires occur with an average fire‐return interval of 6 yr in the tropical dry deciduous forest region (Kodandapani et al. 2008) though there are differences in these intervals across a precipitation gradient (Mondal and Sukumar 2016). Logging of select species in the region in which the plot is located extended from at least the early part of the nineteenth century to prior to 1968 (Sukumar et al. 2005). The diameter distribution of the community is left‐skewed, but exhibits large inter‐census variation in the smaller (<20‐cm) size classes, owing mainly to large abundance fluctuations in the understory species; the larger (≥20‐cm) size classes have remained relatively stable across censuses (Sukumar et al. 2005). Most species are spatially aggregated, regardless of abundance, with the intensity of aggregation tending to increase with decreasing spatial scale and with increasing tree diameter (Condit et al. 2000). The canopy cover is 50–75% and canopy height 15–20 m (Sukumar et al. 2004). Characteristic canopy species include Lagerstroemia microcarpa Wt., Terminalia crenulata Roth., Anogeissus latifolia (DC.) Bedd. and Tectona grandis L. f. The understory is characterized by Kydia calycina Roxb., Helicteres isora L., Cassia fistula L., Catunaregam spinosa (Thunb) Tirveng., Phyllanthus emblica L., and the alien invasive species Lantana camara L. and Chromolaena odorata (L.) King & Robinson. The forest floor is dominated by perennial tall grasses, mainly Themeda cymbaria Hac. and Cymbopogon flexuosus (Steudel) Watson.
Data collection
All native woody plant species ≥1 cm in diameter at a height of 1.3 m from the ground (diameter at breast height, dbh) within the plot were identified to species, measured for dbh, tagged, and mapped to the closest 0.5 m during May 1988–May 1989 (Sukumar et al. 1992, 1998) following the Centre for Tropical Forest Science (CTFS) protocols (Condit 1998). Subsequent annual censuses recorded recruitment and mortality in the entire plot for the first 20 yr, following which, owing to a spurt in total number of individuals, annual censuses were restricted to a subsample of 100 40 × 40‐m quadrats, representing roughly one‐third of the plot. Diameter at breast height was measured in the entire plot every fourth year starting 1988. Given the history of logging (prior to about 1968), all logged stumps present in the plot at the time of its establishment were mapped, measured for girth, and identified to species. Soils were sampled during September‐October 2004 for plant‐available nutrients and a digital elevation model of the plot was obtained from satellite imagery as described in Pulla et al. (2016).
Data processing
All further data processing and analyses were performed in R version 3.3 (R Core Team 2016). For spatial analyses, we used plant‐available P, K, Ca, Mg, Mn, Zn, Fe, Cu, B, pH and Al, and the topographic variables elevation, slope, curvature, topographic wetness index (TWI; a relative measure of hydrological conditions of a given site in a landscape that is computed from gridded elevation data) and insolation (annual global radiation, which is computed from gridded elevation data and latitude) as described in Pulla et al. (2016). To reduce the number of variables being considered, we combined Ca, Mg and K into a single measure representing Total Exchangeable Bases (henceforth TEB). Plant‐available N (in nitrate‐ and ammonium‐ N forms) was not used as it appears that stocks were being rapidly modified while sampling progressed from one end of the plot to the other (Pulla et al. 2016). Soil point samples were used to generate nutrient maps using trans‐Gaussian kriging with external drift. Since the number of spatial variables was very large (14) and since several of them were correlated with each other, principal component analysis (PCA) was performed to obtain a smaller set of uncorrelated variables. Topographic and soil variables, and their principal components, are hereafter collectively referred to as spatial environment variables. Each quadrat's spatial environment variable value was calculated as the average of the values of its four vertices. For each census, quadrat values were assigned to all individuals present within the quadrat during that census. Annual precipitation in the year preceding a census was used as the temporal environment variable and assigned to all individuals present in the census.
Analyses
We only used the top four dominant canopy (A. latifolia, L. microcarpa, Tec. grandis and Ter. crenulata) and understory (Cas. fistula, H. isora, K. calycina and Catunaregam spinosa) species in our analyses to ensure that statistical tests had adequate power. These species constituted, on average, 84% of the total community abundance and 76% of total community basal area during 1988–2012. We used the entire stand for the spatial‐only and temporal‐only analyses, while recruitment was analyzed in the spatiotemporal analysis. We performed the spatial‐only analysis on two censuses 20 yr apart (1988 and 2008) and the temporal‐only analysis on all annual censuses during 1988–2012. For the spatiotemporal analysis, we used all annual censuses during 1988–2008, excluding the period following 2008 since only about one‐third of the plot was sampled during 2009–2011.
We define “world space” as the 3‐dimensional (3‐D) space made up of time and the 2‐D Euclidean space representing the 50‐ha plot (Fig. 1). Niche widths and overlaps were calculated in d‐dimensional niche space, where d is the number of niche axes. Thus each point z i = (z 1i, z 2i,…,z di) in niche space represented a unique combination of environment variables present at zero or more locations in world space. For spatial‐only analyses, niche space was defined by the first five principal components of soil and topographic variables (d = 5). For temporal‐only analyses, niche space was defined by annual precipitation (d = 1). For spatiotemporal analyses, niche space was defined by elevation and annual precipitation (d = 2). Finally, to check if all higher‐dimensional niche differences are also detected in lower dimensions, we performed the spatial‐only analysis separately for each of the five principal components (d = 1).
Figure 1.
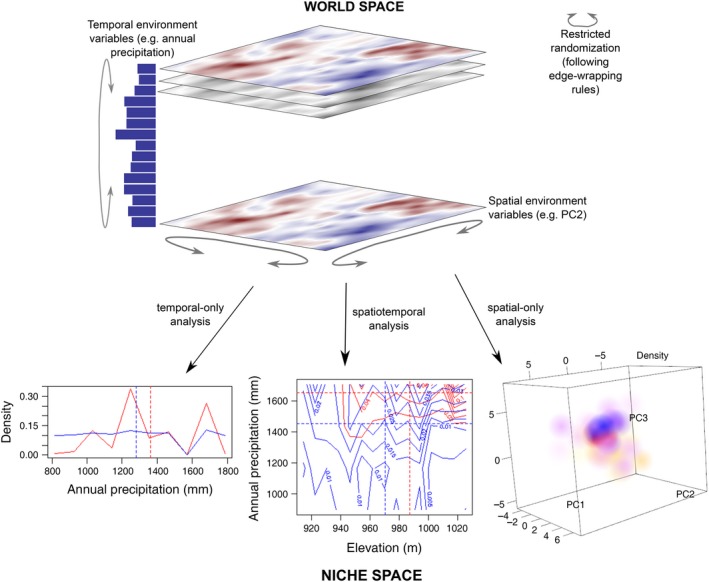
Illustration of the methods used in the paper. The world space consists of spatial and temporal environmental data (soil, topography, annual precipitation) and the locations of individual plants in geographical space and in time. This data is mapped to points in d‐dimensional niche space, where d is the total number of spatial and temporal environmental variables. Points in niche space are then used to estimate the d‐dimensional density. Densities of two species Helicteres isora (red) and Lagerstroemia microcarpa (blue) are shown. The temporal‐only analysis illustrates 1‐D niche space and shows that L. microcarpa abundance remained relatively stable except for a decline in years preceded by annual precipitation of about 1,600 mm whereas H. isora abundance fluctuated considerably with precipitation; these are the marginal distributions, integrated across space. The spatial‐only analysis illustrates 3‐D niche space formed by the first three principal components of soil and topographic variables; high densities of H. isora and L. microcarpa are represented by saturated red and blue spheres and low densities by unsaturated yellow and cyan spheres, respectively. The spatiotemporal analysis illustrates 2‐D niche space (contour plots) formed by elevation and annual precipitation. The joint distributions suggest that H. isora recruitment is high in years that are preceded by high annual precipitation and at intermediate to high elevations, while L. microcarpa recruitment is more even in space and time, although there are two recruitment peaks. Dotted lines show distribution means. The generalized standard deviation of the density a species, then, is a measure of its niche width and the pair‐wise overlap statistic measures niche overlap of a pair of species. Significance of these test statistics is assessed by randomization wherein spatial and/or temporal variable maps are randomly translated and reflected following edge‐wrapping rules as shown by grey arrows. In case of a spatial map, edge‐wrapping results in a torus.
Each individual plant was mapped from world space to a corresponding point in niche space based on environment variable values associated with its position in world space. For a given entity (in our case, a species), this represented its “occurrence” (Broennimann et al. 2012; also referred to in the literature as “utilization”, see (Gotelli and Graves 1996)). Next, for each entity s, the probability density function of occurrence f s(z) was estimated by using a generalized (d‐dimensional) rescaled histogram. In theory, other non‐parametric kernel density estimators can substitute the histogram in this step; indeed, they are sometimes recommended over the histogram for greater accuracy in niche space calculations (e.g., Broennimann et al. 2012). In practice, we found using simulated data that the histogram was as accurate in measuring niche overlap as Gaussian kernel density estimators. In addition, current implementations of the latter were either restricted in dimensionality or were extremely slow to compute in higher dimensions; we therefore used histograms in our analyses. Since not all combinations of environment variable values occur with the same frequency in the plot, the occurrence density was divided by the density f e(z) of the environment variables themselves in order to obtain the “occupancy” density for a given entity (Broennimann et al. 2012; also referred to in the literature as “electivity”, see (Gotelli and Graves 1996); this is the “adjusted” density of Itoh et al. 2010):
where the density is evaluated at k points. g s(z i) was then rescaled to integrate to 1:
Niche width was calculated as the generalized standard deviation of occupancy density g s(z). Generalized standard deviation—the square root of generalized variance (Sengupta 2004)—is a measure of tightness of clustering of multidimensional data that collapses to the standard deviation in the unidimensional case. Niche overlap between entities s and t were calculated using the following pair‐wise overlap statistic (Hurlbert 1978; also referred to in the literature as Schoener's or Czekanowski's index):
which ranges from 0 (no overlap) to 1 (complete overlap). Finally, a community‐level overlap statistic was calculated as the mean of all species pair‐wise overlaps. Community‐level overlap was only calculated for the focal species and not for all species that occurred in the 50‐ha plot, in order to avoid strong influence by the numerous rare species whose pair‐wise overlaps were likely to be estimated inaccurately.
To determine if niche width of a species was smaller than expected by chance (indicating habitat association or niche specialization), the positions of individuals were randomized with respect to the environment without changing the relative positions of individuals. In the spatial analyses, this kind of restricted randomization was needed to account for spatial contagion in both entities and environment variables in our data, which could result in spurious habitat associations if the null distribution was generated by complete randomization of positions of individuals (Harms et al. 2001). Thus, environmental maps were randomly translated and reflected along cardinal directions 2500 times following toroidal edge‐wrapping rules (Lotwick and Silverman 1982, Upton and Fingleton 1985) and the test statistic (i.e., generalized standard deviation) recalculated each time in order to generate its null distribution. A similar procedure was followed to generate the null distribution of the pair‐wise overlap statistic, except that in this case, the geographical distributions of both entities were randomized as described previously. We performed a one‐sided test for generalized standard deviations and a two‐sided test for overlap. The P‐value for a two‐sided test was calculated as:
where t* is the observed value of the test statistic under consideration, t i, i = 1,…,N, are values from the null distribution, A is mean of the null distribution, and I(·)the indicator function (Kulinskaya 2008). We include the observed value in the null distribution to ensure that the P‐value is never 0, which could significantly inflate Type I error rates in our multiple‐testing context (Smyth and Phipson 2010).
Restricted randomization in time, needed to account for temporal contagion in both entities and environment variables, is achieved by translating and reflecting the temporal variables, edge‐wrapping the first and last year. Spatiotemporal analyses involved simultaneous restricted randomizations of spatial as well as temporal variables.
P‐values were adjusted for multiple hypotheses testing using the False Discovery Rate procedure (Benjamini and Hochberg 1995), separately for each analysis (spatial‐only, temporal‐only, and spatiotemporal) and separately for niche specialization and niche overlap tests.
In order to test if niche differences detected in high‐dimensional space were also visible in lower‐dimensional spaces, we re‐performed the aforementioned statistical tests for each principal component of soil and topographic variables individually. P‐values from all PCs were combined and adjusted for multiple hypotheses testing as described earlier.
In order to interpret niche overlap results in light of the known geographical ranges of the species, we used two additional data sets. At the regional scale, we used tree species presence‐absence data from sites across India as per the survey of Champion and Seth (1968). At the landscape scale, we used data from a systematic sampling of all woody plants ≥30‐cm girth at breast height (GBH) across Mudumalai (291 1‐ha plots laid at the intersections of a 1‐km regular grid) carried out by the Tamil Nadu Forest Department during 1983. We excluded the four understory trees and shrubs (Cas. fistula, H. isora, K. calycina, Cat. spinosa) to avoid bias resulting from possible under‐reporting of smaller species in the former data set and the 30‐cm GBH size cutoff used in the latter.
Simulation study
We used a Monte Carlo approach to assess the Type I error rate, power and accuracy of niche specialization and overlap tests. Species distributions in world space were simulated as realizations of spatiotemporal Poisson Cluster Processes (PCPs; Diggle and Gabriel 2010) parameterized on the basis of data from the plot. Homogeneous PCPs were used to simulate species under the null, while inhomogeneous PCPs were used to simulate them under the alternate hypothesis. In both cases, species exhibited spatiotemporal contagion in world space according to PCP parameters (namely, number of cluster centers, number of points per cluster, and the standard deviation of each cluster), regardless of their densities in niche space. The homogeneous PCP case is equivalent to species being distributed uniformly and independently of each other in niche space. In the inhomogeneous PCP case, species were multivariate‐normally distributed in niche space. Variances of this multivariate distribution for each species were drawn randomly and independently from a log‐normal distribution while means were drawn randomly from a normal distribution with a covariance matrix that had negative off‐diagonal elements, which results in overdispersed means and, hence, reduced niche overlaps. The null‐hypothesis rejection rate gives the Type I error rate under the null hypothesis and the power under the alternate hypothesis. The accuracy of each test statistic (pair‐wise overlap, generalized standard deviation) was assessed by comparing the estimated value against the true value used for simulating the data. The simulation study is described in further detail in Appendix S2.
Results
The plot had an average of 23, 912 individuals belonging to 76 species during 1988–2012. A total of 272 logged stumps (mean girth 229 ± 101 cm) belonging to 6 canopy species were present in the plot at the time of its establishment (Appendix S5: Fig. S5). Most of these belonged to the principal timber species Tectona grandis (263); three Lagerstroemia microcarpa and one Terminalia crenulata stump(s) were also present.
The first five principal components (PC1–PC5) explained nearly 82% of the spatial variation in the soil and topographic variables (Table 1). PC1, which explained ~34% of the observed variation, was negatively correlated with elevation, TEB, B, Zn, Cu and Mn. The smaller, negative correlation with TWI is expected since, by construction, TWI tends to be negatively correlated with elevation. PC2 was almost entirely defined by soil variation, being positively correlated with P and Fe, and negatively correlated with Al and Mn. PC3, on the other hand, was largely defined by topographic variation, being positively correlated with slope and negatively correlated with insolation and curvature. PC4 and PC5 were correlated with both soil and topographic variables. Like in the case of elevation and TWI, Al and pH tended to be loaded on opposite ends of PCs, which is expected because the availability of Al is controlled by pH. Fig. 2 shows all environment variables used in analyses.
Table 1.
Principal components analysis of soil and topographic variables. (a) Importance of PCs, (b) PCA loadings
| (a) | |||||
|---|---|---|---|---|---|
| PC1 | PC2 | PC3 | PC4 | PC5 | |
| Standard deviation | 2.18 | 1.56 | 1.27 | 1.19 | 1.10 |
| % variance | 33.9 | 17.4 | 11.5 | 10.1 | 8.6 |
| Cumulative % | 33.9 | 51.3 | 62.8 | 72.9 | 81.5 |
| (b) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Elevation | Slope | Curvature | TWI | Insolation | Mn | Cu | Zn | Fe | B | P | pH | Al | TEB | |
| PC1 | −0.37 | −0.16 | −0.16 | 0.26 | −0.09 | −0.39 | −0.39 | −0.38 | −0.14 | −0.37 | −0.02 | −0.09 | −0.02 | −0.35 |
| PC2 | 0.03 | −0.15 | 0.14 | −0.15 | 0.10 | −0.29 | −0.24 | 0.19 | 0.36 | 0.07 | 0.49 | 0.30 | −0.52 | −0.06 |
| PC3 | −0.21 | 0.57 | −0.28 | 0.08 | −0.64 | 0.01 | −0.03 | −0.02 | 0.05 | 0.08 | 0.22 | 0.14 | −0.09 | 0.20 |
| PC4 | 0.10 | −0.22 | −0.59 | 0.56 | 0.17 | 0.04 | 0.09 | 0.20 | 0.33 | 0.08 | 0.21 | −0.18 | 0.11 | 0.08 |
| PC5 | −0.16 | −0.24 | −0.22 | 0.20 | 0.14 | 0.08 | 0.04 | −0.10 | −0.48 | 0.28 | −0.13 | 0.62 | −0.21 | 0.20 |
TWI, topographic wetness index; TEB, total exchangeable bases; PCA, principal component analysis.
This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.
Figure 2.
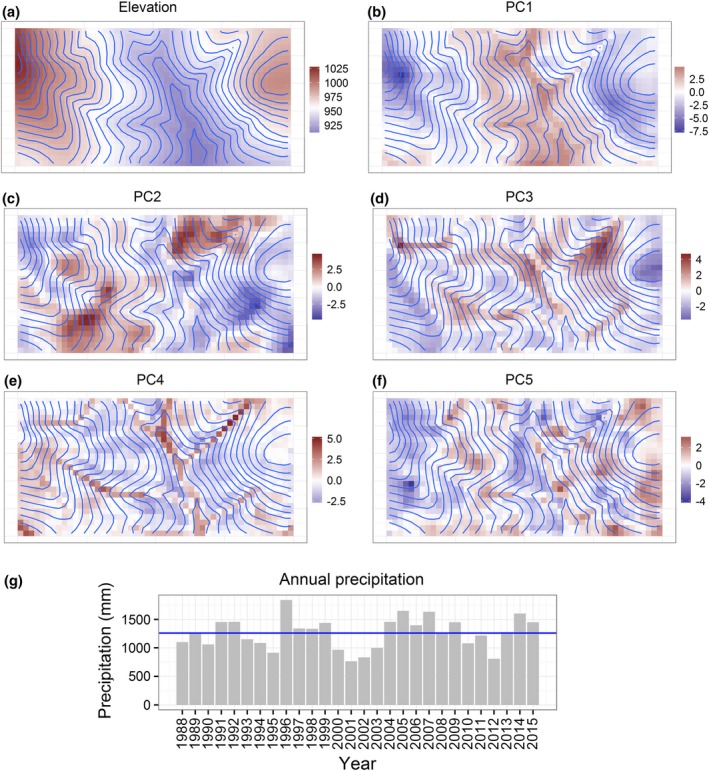
Environment data. Maps (a)–(f) show spatial variables used (elevation in meters above sea level and the first five principal components of soil and topography data). Graph (g) shows temporal variable used (annual precipitation). See Appendix S6 for further maps.
The simulation study showed that—under the assumptions of the simulation data generating process—the Type I error rate of the test (0.06) was close to the nominal level (0.05). In case of the niche overlap test, power increased with (in decreasing order of importance): extreme values of observed niche overlap (effect size), decreasing number of niche dimensions, and increasing number of clusters. In case of the niche specialization test, power increased with (in decreasing order of importance): decreasing niche width (effect size), decreasing number of niche dimensions, increasing number of clusters, and decreasing cluster size (Appendix S2). The observed overlap was a biased estimate of the true overlap—it tended to overestimate small values and underestimate large values—and its variance tended to increase with the number of niche dimensions.
Table 2 shows niche specialization and niche overlap test results (spatial‐only analysis results for the 1988 census are shown in Appendix S4). Across all three analyses, two species—Tec. grandis and Ter. crenulata—had a significantly smaller generalized standard deviation than the 5% simulation quantile in the spatial‐only analysis, construed as an indication of edaphic‐topographic niche specialization, while Anogeissus latifolia had an unadjusted P‐value of 0.052. In the spatial‐only analysis for 1988 (Appendix S4), all three species (Tec. grandis, Ter. crenulata, A. latifolia) were statistically significant in the niche specialization test. Across all three analyses, two species pairs—L. microcarpa–A. latifolia and L. microcarpa–Tec. grandis—had niche overlaps smaller than the 2.5% simulation quantile (i.e., two‐sided test at α = 5%) in the spatial‐only analysis, suggesting significant edaphic‐topographic niche differences (a third species pair, L. microcarpa–Ter. crenulata, had an unadjusted P‐value of 0.064). In the spatial‐only analysis for 1988 (Appendix S4), Kydia calycina–A. latifolia had a significantly small niche overlap in addition to L. microcarpa–A. latifolia and L. microcarpa–Tec. grandis. Conversely, nine species pairs had significantly larger than expected niche overlap: eight in the spatial‐only analysis, one in the temporal‐only analysis, and two in the spatiotemporal analysis (one species pair—A. latifolia–Ter. crenulata—had significantly high overlaps in both spatial‐only and temporal‐only analyses, while another pair—K. calycina– Helicteres isora—had significantly high overlaps in both spatial‐only and spatiotemporal analyses). The spatial‐only analysis for 1988 (Appendix S4), had only one significantly large niche overlap after adjusting P‐values for multiple testing. In all three analyses, community niche overlaps were not significantly smaller than expected by chance. All species spatial maps and abundances are shown in Appendix S5.
Table 2.
Niche specialization, pair‐wise niche overlap and community niche overlap test results for dominant species in the 50‐ha plot. (a) Spatial‐only analysis of all individuals in 2008, (b) temporal‐only analysis of all individuals during 1988–2012, and (c) spatiotemporal analysis of recruits during 1989–2008
| (a) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Niche specialization | Niche overlap (Community overlap = +0.48 *** ) | |||||||
| ANOL | CASF | HELI | KYDC | LAGL | RAND | TECG | ||
| ANOL | 14.4 | |||||||
| CASF | 18.05 | 0.53 | ||||||
| HELI | 14.92 | 0.33 | +0.5 * | |||||
| KYDC | 14.4 | 0.31 | 0.45 | +0.56 ** | ||||
| LAGL | 20.25 | −0.37 * | 0.55 | 0.44 | 0.39 | |||
| RAND | 16.98 | 0.42 | +0.55 * | +0.49 * | +0.45 * | 0.48 | ||
| TECG | −16.55 * | +0.58 * | 0.61 | 0.38 | 0.37 | −0.51 * | 0.48 | |
| TERT | −15.83 * | +0.61 * | 0.62 | 0.37 | 0.35 | 0.5 | 0.48 | +0.66 * |
| (b) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Niche specialization | Niche overlap (Community overlap = 0.79) | |||||||
| ANOL | CASF | HELI | KYDC | LAGL | LAGP | TECG | ||
| ANOL | 332 | |||||||
| CASF | 327.33 | 0.91 | ||||||
| HELI | 265.26 | 0.58 | 0.64 | |||||
| KYDC | 270.92 | 0.68 | 0.71 | +0.8 | ||||
| LAGL | 326.32 | 0.95 | +0.95 | 0.63 | 0.72 | |||
| RAND | 293.98 | 0.7 | 0.77 | +0.83 | 0.79 | 0.75 | ||
| TECG | 327.86 | 0.96 | 0.94 | 0.61 | 0.71 | 0.98 | 0.73 | |
| TERT | 331.5 | +0.99 * | 0.91 | 0.59 | 0.69 | 0.95 | 0.71 | 0.97 |
| (c) | ||||||
|---|---|---|---|---|---|---|
| Niche specialization | Niche overlap (Community overlap = +0.61 *** ) | |||||
| CASF | HELI | KYDC | LAGL | RAND | ||
| CASF | 9861.67 | |||||
| HELI | 4194.23 | 0.49 | ||||
| KYDC | 7646.75 | 0.61 | +0.76 * | |||
| LAGL | 9079.29 | +0.84 * | 0.56 | 0.63 | ||
| RAND | 5268.38 | 0.53 | +0.67 | 0.62 | +0.6 | |
| TECG | 8526.74 | 0.73 | 0.39 | 0.53 | 0.68 | 0.48 |
Species codes: ANOL, Anogeissus latifolia; CASF, Cassia fistula; HELI, Helicteres isora; KYDC, Kydia calycina; LAGL, Lagerstroemia microcarpa; RAND, Catunaregam spinosa; TECG, Tectona grandis; TERT, Terminalia crenulata. Niche space is defined by (1) the first 5 principal components of edaphic and topographic variables, (2) annual precipitation, and (3) elevation and annual precipitation. Tests for niche specialization are one‐tailed and the test statistic is the generalized standard deviation of species occupancy; values smaller than the 5% quantile of randomizations have a ‘−’ prefix. Tests for niche overlap are two‐tailed and the test statistic is the overlap statistic; values smaller (greater) than the 2.5% (97.5%) quantile of randomizations have a ‘−’ (‘+’) prefix.
Statistically significant results after adjustment for multiple‐hypothesis testing (separately for each analysis and separately for niche specialization and niche overlap) are shown in boldface; *P < 0.05, **P < 0.01, ***P < 0.001.
This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.
Results from spatial‐only analysis performed for each principal component separately are shown in Appendix S3. In the test for niche specialization, Tec. grandis, A. latifolia and Cassia fistula had significantly smaller niche standard deviations than expected by chance. Lagerstroemia microcarpa–A. latifolia and L. microcarpa–Tec. grandis, which segregated in 5‐D niche space, also had separate niches along PC4. Four species pairs significantly overlapped only in 5‐D niche space and not along individual niche axes, while one pair significantly overlapped only along individual niche axes.
Table 3 shows species co‐occurrence data at the regional and landscape scales, respectively. At both India and Mudumalai scales, Ter. crenulata, A. latifolia and Tec. grandis tended to co‐occur more often than any of them co‐occurred with L. microcarpa.
Table 3.
Dominant canopy species co‐occurrence across (a) India, based on the forest‐type survey data of Champion and Seth (1968), and (b) Mudumalai, based on the forest survey data of Tamil Nadu Forest Department in 1983
| (a) | ||||
|---|---|---|---|---|
| ANOL | LAGL | TECG | TERT | |
| ANOL | 66 | |||
| LAGL | 4 | 15 | ||
| TECG | 23 | 10 | 36 | |
| TERT | 45 | 12 | 30 | 89 |
| (b) | ||||
|---|---|---|---|---|
| ANOL | LAGL | TECG | TERT | |
| ANOL | 208 | |||
| LAGL | 57 | 104 | ||
| TECG | 168 | 71 | 194 | |
| TERT | 161 | 92 | 171 | 210 |
The total number of sites/plots at which each species occurred is shown on the diagonal. Species codes are as in Table 2.
This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.
Discussion
We considered the niche preferences and geographical distributions of the most dominant woody‐plant species in the Mudumalai 50‐ha permanent plot, located in a southern Indian SDTF, at three scales. At the local scale, the species separated into at least two groups (or guilds) in niche space (Table 2): one consisting of the dominant canopy species Terminalia crenulata, Tectona grandis and Anogeissus latifolia (hereafter, “Group 1”); and the second consisting of the dominant canopy species Lagerstroemia microcarpa and the dominant understory species Helicteres isora, Kydia calycina, Cassia fistula and Catunaregam spinosa (“Group 2”). Species within groups tended to significantly overlap in niche space along both spatial and temporal dimensions. The distinction between Group 1 species and L. microcarpa was evident both in niche and world space (see species maps in Appendix S5), although the pattern of Tec. grandis abundance fluctuations was intermediate to Group 1 and Group 2. Results from the spatial‐only analysis performed on the 1988 census (Appendix S4), while quantitatively different from the 2008‐census results, suggest the same qualitative grouping, with differences in statistical significance at least partly being due to large differences in abundances of focal species in those years. For example, between 1988 and 2008, H. isora and Cat. spinosa populations increased nearly 6‐ and 3‐fold, respectively, while K. calycina declined by 70%. We expect these results to be robust to the effects of past logging because Tec. grandis—the only species to have more than a couple of felled individuals—appears to have been logged more or less evenly wherever it occurred in the plot (Appendix S5: Fig. S5b). Due to slow wood decay rates in this forest (H. S. Dattaraja, H. S. Suresh, R. Sukumar, unpublished data), the census of logged stumps at the time of plot establishment should be reflective of historical logging.
At the landscape and regional scales, we were able to analyze geographic range data only for the canopy species. The three dominant canopy species in Group 1 are widespread in South and Southeast Asia, unlike L. microcarpa, which is endemic to the Western Ghats, and this is reflected in the data from across India (Table 3a) and Mudumalai (Table 3b). Terminalia crenulata and A. latifolia, both belonging to the Combretaceae, frequently co‐occur, with Tec. grandis being an associate in much of peninsular India, being replaced by the highly dominant Shorea robusta above ~25° N and occasionally by species such as Boswellia serrata within peninsular forests (Champion and Seth 1968). Indeed, the similarity of resource niche requirements of Ter. crenulata and A. latifolia appear to extend to recruitment in the 50‐ha plot: although together, they constituted nearly a quarter of all individuals in the plot on average, they recruited (≥1‐cm dbh) only 16 and 14 individuals, respectively, in two decades of monitoring (1988–2008), most of which were during a single year (2008). In fact, the correlation between the total abundances of these two species during 1988–2012 is nearly perfect (Pearson's r = 0.99, Appendix S5; temporal niche overlap = 0.99, Table 2b). Considered together, the data at all three scales suggest that Group 1 species are not only more similar to each other in their tolerances to large‐scale environmental conditions than any of them are to L. microcarpa, but also have similar abiotic requirements at the local scale. Similarity in abiotic requirements for these species could also result from sharing mutualists, such as mycorrhizal fungi, which are associated with those abiotic conditions (e.g., Johnson et al. 1992).
Our results clearly demonstrate that the presence of habitat associations does not necessarily imply niche differences: the Group 1 species Ter. crenulata and Tec. grandis (and A. latifolia at P = 0.054) had significantly narrow niche breadths in 5‐dimensional niche space, but niche overlaps between these species were greater than expected by chance, implying specialization to the same edaphic and topographic conditions. Our results also demonstrate that niche differences may exist between species that do not show niche specialization, as in the case of L. microcarpa, which shows niche differences with Group 1 species but no evidence of specialization in any of the tests. Thus, niche specialization is neither necessary nor sufficient for niche differences to manifest; evidence of habitat association should therefore be examined critically prior to inferring niche differences. Although all observed niche differences in higher‐dimensional space were also visible in lower‐dimensions (individual principal components), this need not be the case. However, the converse is always true: by construction, niche differences in lower‐dimensional space are always visible in higher‐dimensional spaces with the caveat that statistical power to detect the effect may be reduced—one of the consequences of the so‐called “curse of dimensionality” (Keogh and Mueen 2011).
The presence of niche differences between Group 1 species and L. microcarpa is consistent with earlier results showing that recruitment and survival in several common species including L. microcarpa and Tec. grandis tended to get suppressed with increasing conspecific densities, at least during non‐fire years, implying the presence of negative‐density dependence (John et al. 2002, John and Sukumar 2004). Similarly, in a community‐level analysis of several forests including Mudumalai, Wills et al. (2006) found that species that were common at a neighborhood scale (50 × 50‐m or smaller) suffered greater mortality—but also recruited more—than rarer species. Lagerstroemia microcarpa, which is near‐monodominant in some patches (Appendix S5), may suffer greater intraspecific competition than interspecific competition (e.g., Raventós et al. 2010). This negative‐density dependence can act as a stabilizing force (sensu Chesson 2000), although its link to niche (resource, predator or other) differences remains tentative. We had previously reported that higher elevations in the plot tended to have 2–4‐fold greater plant‐available Ca, Cu, Mg, Mn, together with higher soil moisture, total C, B, Zn, and clay content (Pulla et al. 2016). However, this relatively large difference in nutrient stocks did not appear strongly restrict the distributions of the dominant species (Appendix S5), although differences of smaller magnitudes have been reported to significantly restrict tree species distributions in other tropical forests (e.g., Hall et al. 2004). Analyses of individual principal components (Appendix S3) suggest that PC2 and PC4 are particularly important axes for both niche specialization and niche differences. PC2 is most strongly linked to substantial variation in plant‐available P (mean 20.2, SD 27.5 mg/kg) and Al, while PC4 is most strongly linked to curvature and topographic wetness index, both of which capture the stream that ephemerally flows through the plot (Table 1, Fig. 2; see also species maps in Appendix S5). Unlike in the case tropical wet forests, soil Al (mean 137.9, SD 64.1 mg/kg) in this tropical dry forest is too low to be toxic to plants, suggesting that the importance of PC2 to the plant niches is due more to the variation in soil P than Al. We acknowledge the possibility that plant‐soil associations can be due to the influence of plants on soil instead of the other way around (Townsend et al. 2008). However, as we had previously suggested (Pulla et al. 2016), the spatial pattern of Ca, Cu, Mg, and Mn in the plot most likely results from greater stocks of these elements in the amphibolite lithology associated with summit positions; moreover, the variation in soil P far exceeds the variation in leaf P across these tree species.
Anogeissus latifolia, a species abundant in the drier parts of Mudumalai, tended to have higher densities at low P, low Al (and to a lesser extent, low Fe), and low TWI (away from the stream) sites within the plot. The distribution of Tec. grandis, although similarly skewed towards low TWI sites, was more even across the plot, being absent mainly from the highest TWI (stream) sites. The distribution of Ter. crenulata, similar to that of Tec. grandis in tending to be absent near the stream, was more restricted along PC2, like A. latifolia. At the landscape scale, both Tec. grandis and Ter. crenulata are most abundant in the dry‐ and moist‐deciduous forest, although the range of Ter. crenulata extends further into the wetter, semi‐evergreen parts (unpublished data from 1‐ha plots established along the west‐east precipitation gradient in Mudumalai). Amongst the understory species, Cas. fistula, which is widespread both in the Mudumalai landscape and the plot, had its density skewed towards intermediate to high values of PC2 (corresponding to intermediate to high P and low Al). It is notable that all species that had high densities near the stream (L. microcarpa, H. isora, K. calycina, Cat. spinosa, Appendix S5) are, at the landscape scale, more abundant in the wetter parts of Mudumalai (unpublished data from 1‐ha plots); they were not significantly specialized along the environmental axes we considered, but are, apparently, more tolerant of habitat conditions prevalent near stream channels when compared to Group 1 species. Relatively few species characteristics distinguish the two groups (Appendix S5: Table S1). Notably, Group 1 species have dbh distributions that suggest a recruitment bottleneck and are slower growing (Nath et al. 2006) than Group 2 species. The Group 2 shrub H. isora is slower growing than Group 1 species only when individuals >5‐cm dbh are compared (Nath et al. 2006), but this is near the upper dbh limit for the species (Appendix S5: Table S1). It may be suggested based on the available evidence (landscape‐scale distributions, local‐scale habitat associations, and growth rates) that Group 2 species have a more resource‐acquisitive strategy compared to Group 1 species.
It is difficult to generalize these results because our sampling in both space and time covers a fraction of the geographic range and lifespans of these plants. Association of tree species with low‐P soils was also reported by Hall et al. (2004) from a 100‐ha SDTF plot in the Central African Republic, a study that, unlike ours, also found macronutrients and pH to be important to tree spatial distributions. In a 50‐ha SDTF plot in Thailand, Bunyavejchewin et al. (2004) found that 47 of 152 species considered were associated with topographic positions—primarily ridges, hilltops and streams. An analysis of the same plot in a multi‐site analysis (Baldeck et al. 2012) suggested that only 14% of the variation in tree community composition was explained by topographic and soil variables; by contrast, the comparable proportion for 6 wetter lowland tropical forests in the same study was 20–39%. On the other hand, Balvanera et al. (2011), in testing the effect of water‐availability gradients on tree distributions in a Mexican SDTF, have suggested that SDTFs may have a greater degree of habitat‐niche specialization compared to wetter forests. While is clear that both soils and topography exert considerable influence on local‐scale plant distributions in SDTFs, by our reading of the literature (Appendix S1), the variation in the proportion of habitat specialists in a community within either forest type (tropical rainforest, SDTF) exceeds the variation across forest types.
The large within‐group pair‐wise niche overlaps could be interpreted in two ways. First, in the niche‐theoretic view, species within groups differentiate along further niche axes, possibly in higher dimensions. It seems unlikely that the unidentified axes have a 2‐D‐spatial signature because species within groups have largely overlapping distributions within the 50‐ha plot. Most soil and topographic variables in the plot are autocorrelated up to at least 100 m (with the exception of pH, the variation in which is too small—mean 6.7, SD 0.35—to be of consequence), and so cannot provide the fine‐scaled variation necessary for niche differentiation of species whose individuals are highly intermingled. These additional axes might therefore represent predators (sensu Chesson 2000)—including fire, which can be seen as a herbivore (Bond and Keeley 2005), mutualists, light, vertical resource gradients (e.g., water: Chitra‐Tarak et al., in review; Silvertown et al. 2015) or temporal abiotic variables not considered here (e.g., temperature). The niches could also be demographic (competition‐colonization, successional niche). Nevertheless, the near‐identical temporal abundance fluctuations (Appendix S5, Table 2b) of at least one species pair—A. latifolia–Ter. crenulata—makes further niche differentiation of that pair undetectable, and also less likely, based on our data. The second possibility is that species within groups are not further stabilized by niches. If the fitnesses of species within groups are near equal, they would follow neutral dynamics driven by demographic stochasticity, i.e., chance variation in births and deaths, and indefinite coexistence is possible (Hubbell 2001). However, a recent study that included Mudumalai has suggested that, at the scale of a few decades, the magnitude of fluctuations in the populations of tropical forest tree species—particularly the more abundant ones—exceeded what is expected if either temporal niche stabilization or demographic stochasticity dominated (Chisholm et al. 2014).
Our use of the phrase “niche difference” instead of “niche differentiation” is deliberate. Niche differences between Group 1 species and L. microcarpa may be interpreted as resulting from niche differentiation, wherein species with overlapping niches segregate in niche space as a result of competition (character displacement). Alternately, these species may have had non‐overlapping niches in allopatry that were conserved during community assembly. For co‐evolutionary changes resulting in character displacement to occur between two species, they must consistently encounter each other, i.e., co‐occur, at all scales: their geographic ranges must overlap so they may end up in the same communities, and within those communities, individuals of the two species must consistently encounter each other. It has been argued—first verbally (Connell 1980, Goldberg and Werner 1983, Grubb 1986, Hubbell and Foster 1986, Brokaw and Busing 2000) and subsequently using simulation studies (Hubbell 2006)—that the latter is unlikely to occur in species‐rich ecosystems because the likelihood of two species consistently encountering each other is greatly diminished, and is a particularly problematic assumption in the case of sessile organisms such as forest plants, whose biotic neighborhoods are highly unpredictable. Continuing this line of argument, it may be hypothesized that two species whose geographic ranges considerably overlap should be more likely to niche differentiate compared to two species with largely non‐overlapping ranges, since the former are more predictably associated with each other while the latter lack selective pressure to diverge since they rarely encounter each other. In our case, Group 1 species, whose regional and landscape ranges overlap much more with each other than they do with L. microcarpa, should exhibit strong niche differentiation at the local scale, an expectation that is opposite to our findings. Our data therefore suggest the alternative, more parsimonious interpretation that the observed niche differences between Group 1 species and L. microcarpa may have developed independently, instead of through past competitive interactions.
Our study does not directly address coexistence theory because limited paleoecological studies in the region make the assumption of long‐term coexistence of species in this community difficult to justify. Indeed, directional environmental—especially climatic—changes that are known to occur at several time scales could have modified the assemblage at our study site over time (Davis 1986), which makes competitive‐exclusion‐based theories difficult to apply under the resulting non‐equilibrium conditions.
Limitations of the present study
Our study used an incomplete, but large set of variables that captured habitat and resource niches in space and time. The first five principal components we used captured about 82% of the variation in the edaphic and topographic variables. Although most of the important soil nutrients were included, we were unable to include plant‐available soil N because we suspected their spatial pattern reflected changing N stocks while sampling was underway (Pulla et al. 2016). In addition, the presence of strong correlations between spatial variables (e.g., elevation and several cations) precludes identification of individual resources or habitat conditions that control the spatial distributions of species.
A distinct advantage of considering high‐dimensional niche space is the ability to detect niche differences that are not visible in any of the marginal distributions, including interplay between spatial and temporal niches, although we did not detect any in our data. Another advantage of working with multiple niche axes simultaneously is that fewer hypotheses tests need to be conducted (e.g., a single niche‐overlap test in high‐dimensional niche space, as opposed to separate tests along individual niche axes, which would reduce power due to adjustment for multiple testing). Disadvantages of working with high‐dimensional space include the need for larger sample sizes (which implies lower statistical power for a given sample size) and more computational power; in particular, we were unable to use kernel density estimators that could have reduced the sensitivity of our results to the choice of histogram bin widths and breaks (Silverman 1986).
The temporal‐only analysis had relatively less power due to the small sample size (i.e., abundance data for 25 yr); more generally, the study period may not have captured the kind of extreme and unusual events during which species diverge in their responses. Similarly, larger sampling areas are needed to understand the relative frequencies of occurrence of different environmental conditions, and (1) whether or not associations and niche differences are consistent at different locations and (2) whether or not the convergence of more than one species to the same habitats represents adaptation to a frequently occurring condition. Our randomization test also assumes that temporal contagion of entities and environment variables is isotropic; without this assumption, fewer randomizations would be available to assess statistical significance.
Our null hypothesis was that species are distributed uniformly (i.e., no niche specialization) and independently of each other (i.e., no systematic niche differences). Another possible, and arguably more realistic, null expectation would be to retain the second constraint, but relax the first, i.e., species are distributed independently of each other but may or may not specialize in niche space. This null hypothesis would result in a more conservative test yielding fewer significant niche differences.
Prevalence of habitat associations and niche differences in tropical forest plants
While distilling general patterns from the literature survey in Appendix S1 is stymied by differences in sampling design, niche variables considered and statistical analyses performed, a few tentative insights are offered here. There is growing evidence, particularly from large, fully censused plots, which argues that species‐habitat associations at the local scale are the norm in tropical forests around the world. Habitats in these studies were typically defined by topography, soils and light availability. Although topographic variables, being readily available, were used in virtually all studies, inclusion of soil variables tended to further emphasize habitat structuring of communities (Hall et al. 2004, Baldeck et al. 2012). Studies using identical sampling design and statistical tests across multiple sites suggest that the sharper the environment gradient—or the more abrupt a discontinuity—at the local scale, the stronger, apparently, the restriction in species distributions with respect to that gradient or discontinuity (Potts et al. 2004, Davies et al. 2005, John et al. 2007, Brown et al. 2013). Indeed, some of the best examples of habitat‐niche specialization are from highly topographically heterogeneous sites (Gunatilleke et al. 2006, Zhang et al. 2011). Nevertheless, most studies find that species often appear to specialize to the same locations in niche space. Studies that show systematic niche differences across entire plant communities, such as those from lowland wet meadows in the UK or the South African fynbos (Silvertown et al. 1999, Araya et al. 2011), are yet to be replicated in tropical forests. While it is possible that important axes for niche differentiation may have been missed in tropical forest studies, axes relating to resources (water, nutrients, light), substrate and microhabitat conditions have all been considered. Low statistical power may play a part in the inability to detect statistically significant species‐habitat associations or niche differences, especially given the large numbers of rare species in most tropical forest communities, although it is difficult to be sure how prevalent an issue this is since power is rarely quantified. On the other hand, the false‐positive rate in some studies may be higher than the nominal 5%: awareness of violation of statistical test assumptions due to positive spatial autocorrelation was limited in studies prior to the work of Plotkin et al. (2000) and Harms et al. (2001), and P‐values have not always been adjusted for the large numbers of hypotheses tests conducted. An important caveat in our survey is possibility of the presence of both selection bias (e.g., selection of a few “interesting” species from the community rather than on the basis of some objective criteria) and publication bias (under‐reporting of negative results).
Broadly overlapping niches of tree species reported in some studies (Appendix S1) need not automatically invoke undiscovered niches; indeed, they may represent convergent adaptation of several species to a frequently encountered environmental condition (Hubbell and Foster 1986). This is consistent with the idea that niche limits are also imposed by intrinsic tradeoffs (Kassen 2002). Consequently, a substantial amount of the observed niche convergence or divergence in any community may be attributable to chance variation in evolutionary histories of species, independently of the presence of other species in the community (Strong 1983). This autecological perspective is more parsimonious than one involving competitive interactions and is consistent with two recent, global tropical forest studies of large plots that included the Mudumalai 50‐ha plot. Brown et al. (2013) found that species have more restricted distributions with increasing topographic heterogeneity, thereby increasing both positive as well as negative spatial overlaps (Fig. S1 in Brown et al. 2013). If this pattern was caused only by niche differentiation, we would not expect positive spatial overlaps to increase with topographic heterogeneity. If, instead, species became restricted in geographical space primarily due to intrinsic tradeoffs in performance over ever sharper environmental gradients, both positive and negative spatial overlaps would be expected to increase. However, niche differentiation is a possible explanation for the left skew of these distributions, representing a slightly greater proportion of negative, compared to positive, spatial overlaps. Chisholm et al. (2014) reported large abundances fluctuations in tropical forests at the decadal timescale that were greater in magnitude than would be expected if either negative‐density dependence resulting from niche differentiation or species‐neutral demographic stochasticity were dominant. A parsimonious interpretation of this pattern is that species are responding to fluctuations in the environment in an individualistic manner. Thus, the order that many have sought in the complexity of tropical forest communities does exist to the extent that the distributions of several species are restricted to locations in space and time defined by environment gradients. This is not to deny that fine‐scale niche differentiation may exist, but current available evidence from tropical forests does not seem to support it.
Supporting information
Acknowledgments
We are grateful to a large number of staff over the years including C. M. Bharnaiah, Krishnan, Bomman, Maran, Siddan and Kunmari for field assistance, Liza Comita, Richard Condit and Stuart Davies for helpful discussions on earlier analyses, Selvalakshmi for translating species names from Tamil, the Ministry of Environment and Forests (Government of India) for funding the long‐term research, and the Tamil Nadu Forest Department for permissions to work in Mudumalai. Department of Biotechnology (Government of India) provided additional support through its partnership with the Biological Sciences division of the Indian Institute of Science. RS was a J.C. Bose National Fellowship during the tenure of this work. We thank two anonymous referees and editor Kirk Winemiller for valuable comments that helped improve the manuscript.
Corresponding Editor: Kirk O. Winemiller.
Literature Cited
- Araya, Y. N. , Silvertown J., Gowing D. J., McConway K. J., H. Peter Linder , and Midgley G.. 2011. A fundamental, eco‐hydrological basis for niche segregation in plant communities. New Phytologist 189:253–258. [DOI] [PubMed] [Google Scholar]
- Bagchi, R. , et al. 2011. Spatial patterns reveal negative density dependence and habitat associations in tropical trees. Ecology 92:1723–1729. [DOI] [PubMed] [Google Scholar]
- Baldeck, C. A. , et al. 2012. Soil resources and topography shape local tree community structure in tropical forests. Proceedings of the Royal Society of London B: Biological Sciences 280:20122532 http://rspb.royalsocietypublishing.org/content/280/1753/20122532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balvanera, P. , Quijas S., and Perez‐Jimenez A.. 2011. Distribution patterns of tropical dry forest trees along a mesoscale water availability gradient. Biotropica 43:414–422. [Google Scholar]
- Baraloto, C. , Morneau F., Bonal D., Blanc L., and Ferry B.. 2007. Seasonal water stress tolerance and habitat associations within four neotropical tree genera. Ecology 88:478–489. [DOI] [PubMed] [Google Scholar]
- Benjamini, Y. , and Hochberg Y.. 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 57:289–300. [Google Scholar]
- Bond, W. , and Keeley J.. 2005. Fire as a global “herbivore”: the ecology and evolution of flammable ecosystems. Trends in Ecology & Evolution 20:387–394. [DOI] [PubMed] [Google Scholar]
- Broennimann, O. , et al. 2012. Measuring ecological niche overlap from occurrence and spatial environmental data. Global Ecology and Biogeography 21:481–497. [Google Scholar]
- Brokaw, N. , and Busing R. T.. 2000. Niche versus chance and tree diversity in forest gaps. Trends in Ecology & Evolution 15:183–188. [DOI] [PubMed] [Google Scholar]
- Brown, C. , et al. 2013. Multispecies coexistence of trees in tropical forests: spatial signals of topographic niche differentiation increase with environmental heterogeneity. Proceedings of the Royal Society of London B: Biological Sciences 280:20130502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunyavejchewin, S. , Baker P. J., LaFrankie J. V., and Ashton P. S.. 2004. Structure, history, and rarity in a seasonally evergreen forest in western Thailand Pages 145–158 in Losos E. C. and Leigh E. G., Jr., editors. Tropical forest diversity and dynamism: findings from a large‐scale plot network. Chicago University Press, Chicago, Illinois, USA. [Google Scholar]
- Champion, H. G. , and Seth S. K.. 1968. A revised survey of the forest types of India. Govt. of India Press, New Delhi, India. [Google Scholar]
- Chesson, P. 2000. Mechanisms of maintenance of species diversity. Annual Review of Ecology and Systematics 31:343–366. [Google Scholar]
- Chesson, P. , Gebauer R. L. E., Schwinning S., Huntly N., K. Wiegand , Ernest M. S. K., Sher A., Novoplansky A., and Weltzin J. F.. 2004. Resource pulses, species interactions, and diversity maintenance in arid and semi‐arid environments. Oecologia 141:236–253. [DOI] [PubMed] [Google Scholar]
- Chesson, P. , and Huntly N.. 1997. The roles of harsh and fluctuating conditions in the dynamics of ecological communities. American Naturalist 150:519–553. [DOI] [PubMed] [Google Scholar]
- Chisholm, R. A. , et al. 2014. Temporal variability of forest communities: empirical estimates of population change in 4000 tree species. Ecology Letters 17:855–865. [DOI] [PubMed] [Google Scholar]
- Comita, L. S. , and Engelbrecht B. M. J.. 2009. Seasonal and spatial variation in water availability drive habitat associations in a tropical forest. Ecology 90:2755–2765. [DOI] [PubMed] [Google Scholar]
- Condit, R. 1998. Tropical forest census plots: methods and results from Barro Colorado Island, Panama and a comparison with other plots. Springer‐Verlag, Berlin, Germany. [Google Scholar]
- Condit, R. , et al. 2000. Spatial patterns in the distribution of tropical tree species. Science 288:1414–1418. [DOI] [PubMed] [Google Scholar]
- Connell, J. H. 1980. Diversity and the coevolution of competitors, or the ghost of competition past. Oikos 35:131–138. [Google Scholar]
- Davies, S. , Tan S., LaFrankie J., and Potts M.. 2005. Soil‐related floristic variation in a hyperdiverse dipterocarp forest Pages 22–34 in Roubik D. W., Sakai S., and Hamid Karim A. A., editors. Pollination ecology and the rain forest. Springer, New York, New York, USA. [Google Scholar]
- Davis, M. B. 1986. Climatic instability, time, lags, and community disequilibrium Pages 269–284 in Diamond J. and Case T. J., editors. Community ecology. Harper & Row Publishers Inc., New York, New York, USA. [Google Scholar]
- Diggle, P. J. , and Gabriel E.. 2010. Spatio‐temporal point processes Pages 449–461 in Gelfand A. E., Diggle P., Guttorp P., and Fuentes M., editors. Handbook of spatial statistics. CRC Press, Boca Raton, Florida, USA. [Google Scholar]
- Dirzo, R. , Young H. S., Mooney H. A., and Ceballos G.. 2011. Introduction Pages xi–xiii in Dirzo R., Young H. S., and Mooney H. A., editors. Seasonally dry tropical forests: ecology and conservation. Island Press, Washington, D.C., USA. [Google Scholar]
- Futuyma, D. J. , and Moreno G.. 1988. The evolution of ecological specialization. Annual Review of Ecology and Systematics 19:207–233. [Google Scholar]
- Gleason, H. A. 1926. The individualistic concept of the plant association. Bulletin of the Torrey Botanical Club 53:7–26. [Google Scholar]
- Goldberg, D. E. , and Werner P. A.. 1983. Equivalence of competitors in plant communities: a null hypothesis and a field experimental approach. American Journal of Botany 70:1098–1104. [Google Scholar]
- Gotelli, N. J. , and Graves G. R.. 1996. Null models in ecology. Smithsonian Institution Press, Washington, D.C., USA. [Google Scholar]
- Grubb, P. J. 1986. Problems posed by sparse and patchily distributed species in species‐rich plant communities Pages 207–225 in Diamond J. and Case T. J., editors. Community Ecology. Harper & Row Publishers Inc., New York, New York, USA. [Google Scholar]
- Gunatilleke, C. V. S. , Gunatilleke I. A. U. N., Esufali S., Harms K. E., Ashton P. M. S., Burslem D. F. R. P., and Ashton P. S.. 2006. Species–habitat associations in a Sri Lankan dipterocarp forest. Journal of Tropical Ecology 22:371–384. [Google Scholar]
- Hall, J. S. , McKenna J. J., Ashton P. M. S., and Gregoire T. G.. 2004. Habitat characterizations underestimate the role of edaphic factors controlling the distribution of Entandrophragma . Ecology 85:2171–2183. [Google Scholar]
- Hardin, G. 1960. The competitive exclusion principle. Science 131:1292–1297. [DOI] [PubMed] [Google Scholar]
- Harms, K. E. , Condit R., Hubbell S. P., and Foster R. B.. 2001. Habitat associations of trees and shrubs in a 50‐ha neotropical forest plot. Journal of Ecology 89:947–959. [Google Scholar]
- Hubbell, S. P. 2001. The unified neutral theory of biodiversity and biogeography. Princeton University Press, Princeton, New Jersey, USA. [Google Scholar]
- Hubbell, S. P. 2006. Neutral theory and the evolution of ecological equivalence. Ecology 87:1387–1398. [DOI] [PubMed] [Google Scholar]
- Hubbell, S. P. , and Foster R. B.. 1986. Biology, chance, and history and the structure of tropical rain forest tree communities Pages 315–329 in Diamond J. and Case T. J., editors. Community Ecology. Harper & Row Publishers Inc., New York, New York, USA. [Google Scholar]
- Hurlbert, S. H. 1978. The measurement of niche overlap and some relatives. Ecology 59:67–77. [Google Scholar]
- Hurtt, G. C. , and Pacala S. W.. 1995. The consequences of recruitment limitation: reconciling chance, history and competitive differences between plants. Journal of Theoretical Biology 176:1–12. [Google Scholar]
- Hutchinson, G. E. 1957. Concluding Remarks. Cold Spring Harbor Symposia on Quantitative Biology 22:415–427. [Google Scholar]
- Inman‐Narahari, F. , Ostertag R., Cordell S., Giardina C. P., K. Nelson‐Kaula , and Sack L.. 2013. Seedling recruitment factors in low‐diversity Hawaiian wet forest: towards global comparisons among tropical forests. Ecosphere 4:24. [Google Scholar]
- Itoh, A. , Ohkubo T., Nanami S., Tan S., and Yamakura T.. 2010. Comparison of statistical tests for habitat associations in tropical forests: a case study of sympatric dipterocarp trees in a Bornean forest. Forest Ecology and Management 259:323–332. [Google Scholar]
- John, R. , Dattaraja H. S., Suresh H. S., and Sukumar R.. 2002. Density‐dependence in common tree species in a tropical dry forest in Mudumalai, southern India. Journal of Vegetation Science 13:45–56. [Google Scholar]
- John, R. , and Sukumar R.. 2004. Distance‐and density‐related effects in a tropical dry deciduous forest tree community at Mudumalai, southern India Pages 363–383 in Losos E. C. and Jr. Leigh E. G., editors. Tropical forest diversity and dynamism: findings from a large‐scale plot network. Chicago University Press, Chicago, Illinois, USA. [Google Scholar]
- John, R. , et al. 2007. Soil nutrients influence spatial distributions of tropical tree species. Proceedings of the National Academy of Sciences USA 104:864–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, N. C. , Tilman D., and Wedin D.. 1992. Plant and soil controls on mycorrhizal fungal communities. Ecology 73:2034–2042. [Google Scholar]
- Kassen, R. 2002. The experimental evolution of specialists, generalists, and the maintenance of diversity. Journal of Evolutionary Biology 15:173–190. [Google Scholar]
- Keogh, E. , and Mueen A.. 2011. Curse of dimensionality Pages 257–258 in Sammut C. and Webb G. I., editors. Encyclopedia of machine learning. Springer, Boston, Massachusetts, USA. [Google Scholar]
- Kodandapani, N. , Cochrane M. A., and Sukumar R.. 2008. A comparative analysis of spatial, temporal, and ecological characteristics of forest fires in seasonally dry tropical ecosystems in the Western Ghats, India. Forest Ecology and Management 256:607–617. [Google Scholar]
- Kraft, N. J. B. , and Ackerly D. D.. 2010. Functional trait and phylogenetic tests of community assembly across spatial scales in an Amazonian forest. Ecological Monographs 80:401–422. [Google Scholar]
- Kulinskaya, E. 2008. On two‐sided p‐values for non‐symmetric distributions. arXiv:0810.2124 [math.ST].
- Lotwick, H. W. , and Silverman B. W.. 1982. Methods for analysing spatial processes of several types of points. Journal of the Royal Statistical Society. Series B (Methodological) 44:406–413. [Google Scholar]
- McShea, W. , and Davies S.. 2011. Introduction: seasonally dry forests of tropical Asia Pages 59–74 in McShea W., Davies S., and Bhumpakphan N., editors. The ecology and conservation of seasonally dry forests in Asia. Smithsonian Institution Scholarly Press, Washington, D.C., USA. [Google Scholar]
- Metz, M. R. 2012. Does habitat specialization by seedlings contribute to the high diversity of a lowland rain forest? Journal of Ecology 100:1365–2745. [Google Scholar]
- Miller, A. D. , and Chesson P.. 2009. Coexistence in disturbance‐prone communities: How a resistance‐resilience trade‐off generates coexistence via the storage effect. American Naturalist 173:E30–E43. [DOI] [PubMed] [Google Scholar]
- Mondal, N. , and Sukumar R.. 2016. Fires in seasonally dry tropical forest: testing the varying constraints hypothesis across a regional rainfall gradient. PLoS ONE 11:e0159691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mooney, H. A. , Bullock S. H., and Medina E.. 1995. Introduction Pages 1–8 in Bullock S. H., Mooney H. A., and Medina E., editors. Seasonally dry tropical forests. Cambridge University Press, Cambridge, UK. [Google Scholar]
- Murphy, P. G. , and Lugo A. E.. 1986. Ecology of tropical dry forest. Annual Review of Ecology and Systematics 17:67–88. [Google Scholar]
- Nath, C. D. , Dattaraja H. S., Suresh H. S., Joshi N. V., and R. Sukumar . 2006. Patterns of tree growth in relation to environmental variability in the tropical dry deciduous forest at Mudumalai, southern India. Journal of Biosciences 31:651–669. [DOI] [PubMed] [Google Scholar]
- Noguchi, H. , et al. 2007. Habitat divergence in sympatric Fagaceae tree species of a tropical montane forest in northern Thailand. Journal of Tropical Ecology 23:549–558. [Google Scholar]
- Plotkin, J. B. , Potts M., Leslie N., Manokaran N., LaFrankie J. V., and Ashton P. S.. 2000. Species‐area curves, spatial aggregation, and habitat specialization in tropical forests. Journal of Theoretical Biology 207:81–99. [DOI] [PubMed] [Google Scholar]
- Poore, M. E. D. 1968. Studies in Malaysian rain forest: I. The forest on triassic sediments in Jengka Forest Reserve. Journal of Ecology 56:143–196. [Google Scholar]
- Potts, M. D. , Davies S. J., Bossert W. H., Tan S., and Nur Supardi M. N.. 2004. Habitat heterogeneity and niche structure of trees in two tropical rain forests. Oecologia 139:446–453. [DOI] [PubMed] [Google Scholar]
- Pulla, S. , Riotte J., Suresh H. S., Dattaraja H. S., and R. Sukumar . 2016. Controls of soil spatial variability in a dry tropical forest. PLoS ONE 11:e0153212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team . 2016. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria: https://www.R-project.org/ [Google Scholar]
- Raventós, J. , Wiegand T., and Luis M. D.. 2010. Evidence for the spatial segregation hypothesis: a test with nine‐year survivorship data in a Mediterranean shrubland. Ecology 91:2110–2120. [DOI] [PubMed] [Google Scholar]
- Richards, P. W. 1952. The tropical rain forest: an ecological study. Cambridge University Press, Cambridge, UK. [Google Scholar]
- Russo, S. E. , Brown P., Tan S., and Davies S. J.. 2008. Interspecific demographic trade‐offs and soil‐related habitat associations of tree species along resource gradients. Journal of Ecology 96:192–203. [Google Scholar]
- Sengupta, A. 2004. Generalized variance Kotz S., Read C. B., Balakrishnan N., and Vidakovic B., editors. Encyclopedia of statistical sciences. John Wiley & Sons Inc, New York, New York, USA. [Google Scholar]
- Silverman, B. W. 1986. Density estimation for statistics and data analysis. Chapman & Hall, London, UK. [Google Scholar]
- Silvertown, J. , Araya Y., and Gowing D.. 2015. Hydrological niches in terrestrial plant communities: a review. Journal of Ecology 103:93–108. [Google Scholar]
- Silvertown, J. , Dodd M. E., Gowing D. J. G., and Mountford J. O.. 1999. Hydrologically defined niches reveal a basis for species richness in plant communities. Nature 400:61–63. [Google Scholar]
- Smyth, G. K. , and Phipson B.. 2010. Permutation P‐values should never be zero: calculating exact P‐values when permutations are randomly drawn. Statistical Applications in Genetics and Molecular Biology 9. doi: 10.2202/1544-6115 [DOI] [PubMed] [Google Scholar]
- Strong, D. R. 1983. Natural variability and the manifold mechanisms of ecological communities. American Naturalist 122:636–660. [Google Scholar]
- Sukumar, R. , Dattaraja H. S., Suresh H. S., Radhakrishnan J., Vasudeva R., Nirmala S., and Joshi N. V.. 1992. Long‐term monitoring of vegetation in a tropical deciduous forest in Mudumalai, southern India. Current Science 62:608–616. [Google Scholar]
- Sukumar, R. , Suresh H. S., Dattaraja H. S., John R., and Joshi N. V.. 2004. Mudumalai forest dynamics plot, India Pages 551–563 in Losos E. C. and Leigh E. G., Jr., editors. Tropical forest diversity and dynamism: findings from a large‐scale plot network. Chicago University Press, Chicago, Illinois, USA. [Google Scholar]
- Sukumar, R. , Suresh H. S., Dattaraja H. S., and Joshi N. V.. 1998. Dynamics of a tropical deciduous forest: population changes (1988 through 1993) in a 50‐hectare plot at Mudumalai, southern India Pages 495–506 in Dallmeier F. and Comisky J. A., editors. Forest biodiversity research, monitoring and modeling: conceptual background and Old World case studies. Parthenon Publishing Group, New York, New York, USA. [Google Scholar]
- Sukumar, R. , Suresh H. S., Dattaraja H. S., Srinidhi S., and Nath C.. 2005. The dynamics of a tropical dry forest in India: climate, fire, elephants and the evolution of life‐history strategies Pages 510–529 in Burslem D. F. R. P., Pinard M. A., and Hartley S. E., editors. Biotic interactions in the tropics: their role in the maintenance of species diversity. Cambridge University Press, Cambridge, UK. [Google Scholar]
- Townsend, A. R. , Asner G. P., and Cleveland C. C.. 2008. The biogeochemical heterogeneity of tropical forests. Trends in Ecology & Evolution 23:424–431. [DOI] [PubMed] [Google Scholar]
- Upton, G. J. G. , and Fingleton B.. 1985. Spatial data analysis by example: point pattern and quantitative data. John Wiley & Sons, Chichester, UK. [Google Scholar]
- Wills, C. , et al. 2006. Nonrandom processes maintain diversity in tropical forests. Science 311:527–531. [DOI] [PubMed] [Google Scholar]
- Yamada, T. , Zuidema P. A., Itoh A., Yamakura T., Ohkubo T., Kanzaki M., Tan S., and Ashton P. S.. 2007. Strong habitat preference of a tropical rain forest tree does not imply large differences in population dynamics across habitats. Journal of Ecology 95:332–342. [Google Scholar]
- Zhang, L. , Mi X., Shao H., and Ma K.. 2011. Strong plant‐soil associations in a heterogeneous subtropical broad‐leaved forest. Plant and Soil 347:211–220. [Google Scholar]
- Zuidema, P. A. , Yamada T., During H. J., Itoh A., T. Yamakura , Ohkubo T., Kanzaki M., Tan S., and Ashton P. S.. 2010. Recruitment subsidies support tree subpopulations in non‐preferred tropical forest habitats. Journal of Ecology 98:636–644. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials


