SUMMARY:
Standard sample size calculation formulas for stepped wedge cluster randomized trials (SW-CRTs) assume that cluster sizes are equal. When cluster sizes vary substantially, ignoring this variation may lead to an under-powered study. We investigate the relative efficiency of a SW-CRT with varying cluster sizes to equal cluster sizes, and derive variance estimators for the intervention effect that account for this variation under a mixed effects model; a commonly-used approach for analyzing data from cluster randomized trials. When cluster sizes vary, the power of a SW-CRT depends on the order in which clusters receive the intervention, which is determined through randomization. We first derive a variance formula that corresponds to any particular realization of the randomized sequence and propose efficient algorithms to identify upper and lower bounds of the power. We then obtain an “expected” power based on a first-order approximation to the variance formula, where the expectation is taken with respect to all possible randomization sequences. Finally, we provide a variance formula for more general settings where only the cluster size arithmetic mean and coefficient of variation, instead of exact cluster sizes, are known in the design stage. We evaluate our methods through simulations and illustrate that the average power of a SW-CRT decreases as the variation in cluster sizes increases, and the impact is largest when the number of clusters is small.
Keywords: Cluster randomized trials, Cluster size variation, Cross-sectional, Power, Sample size, Stepped wedge
1. Introduction
The popularity of stepped wedge cluster randomized trials (SW-CRTs) has increased in recent years (Hemming et al., 2015). As an alternative to standard cluster randomized trials (CRTs), clusters of individuals are randomized to cross forward from a control to an intervention at certain time points commonly termed as “steps” (Table 1). The design offers great potential to rigorously evaluate cluster-level interventions that can only practically be implemented in a stepwise manner. The focus of this paper is cross-sectional SW-CRTs where the response is evaluated on different individuals between each step. For example, in the Washington state study, communities were randomized to initiate an expedited partner therapy intervention at steps 6–8 months apart, and the response was measured as chlamydia test positivity among cross-sections of women attending sentinel clinics (Golden et al., 2015).
Table 1.
Schematic of a stepped wedge cluster randomized trial (SW-CRT) with one baseline time-point (b = 1), two clusters randomized to initiate the intervention at each step (q = 2), two time-points between each step (t = 2) and four steps (K = 4). 0 represents control and 1 intervention.
| Time | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| Cluster | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 4 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
It is well known standard CRTs require sample size inflation due to positive correlation between outcomes of participants in the same cluster. Letting ρ represent the intra-cluster correlation, a common approach to calculate the number of clusters required is to multiply the number of participants required for an individually randomized trial by a design effect (DE) of the form {1+(n−1)ρ} and then divide by the arithmetic mean cluster size (n). Many articles have reported that cluster size variation reduces statistical power, and the approach needs to be modified (Rutterford et al., 2015). One simple modification replaces n with the cluster size harmonic mean (Hayes and Moulton, 2009). Another modification utilizes the following DE, [1 + {n(1 + κ2) − 1}ρ] where κ is the cluster size coefficient of variation (CV) (Eldridge et al., 2006). Using this latter approach, a further sample size increase of 41% is needed when cluster sizes vary such that the CV is κ = 0.7 for a trial with an arithmetic mean cluster size of n = 100 and an intra-cluster correlation of ρ = 0.05.
Cross-sectional SW-CRTs are frequently analyzed by a linear mixed effects model described in Hussey and Hughes (2007). A DE based on this model that assumes equal cluster sizes has been proposed (Woertman et al., 2013). However, a recent systematic review of 101 SW-CRTs detected that 48% of studies included clusters that were known to vary in size (Kristunas et al., 2017). In some settings, the goal is to recruit all eligible patients from a particular community, which naturally leads to unequal cluster sizes. For example, in the Washington state study numbers of women attending sentinel clinics varied per region. Sometimes it is possible to limit recruitment to the first M consenting participants per cluster (Bashour et al., 2013), but this would result in a prolonged recruitment period for sites with a smaller candidate pool. It would be useful to assess the potential efficiency losses or gains by allowing cluster sizes to vary by recruiting more participants in larger clusters.
The impact of ignoring cluster size variation in sample size calculation for cross-sectional SW-CRTs is unclear. Through simulation studies, Kristunas et al. (2017) reported that a variation in cluster size did not lead to notable power loss for continuous outcomes, but only a small range of parameters were examined. Martin et al. (2019) calculated the power with unequal cluster sizes by numerically inverting the precision matrix, and further noted that the power depended on the order in which the variable size clusters were randomized to initiate the intervention. Matthews (2019) proposes a regression-based approximation to the variance of the treatment effect to allow identification of a near-optimal ordering of treatment initiation to achieve high power without an exhaustive search across all possible randomization sequences. Girling (2018) derived an analytical formula for the relative efficiency (RE) of a SW-CRT with unequal compared to equal cluster sizes under a constrained randomization setting. The derivation relies on several clusters being randomized at each step, such that by stratifying the randomization procedure there is no inequality in the total size of all the clusters randomized to initiate the intervention at each step. To the best of our knowledge, analytical formulas for sample size and power estimation for cross-sectional SW-CRTs in general settings with varying cluster sizes have not been derived.
Under a linear mixed effects model framework, in Section 2 we derive three analytical formulas of variance estimates for power calculations that account for cluster size variation in cross-sectional SW-CRTs. The first assumes cluster sizes and their order of randomization are both known, and allows us to identify upper and lower bounds for the power (Section 2.2 and 2.3). The second provides a closed form expression for the expected variance before randomization when all cluster sizes are known (Section 2.4), and the third approximates this value if only the cluster size arithmetic mean and CV can be estimated in the planning stages of a SW-CRT (Section 2.5). In Section 2.6, we derive the DE for cross-sectional SW-CRTs as compared to individually randomized trials accounting for varying cluster sizes, the expected relative efficiency (RE) of a cross-sectional SW-CRT with unequal compared to equal cluster sizes and a correction factor (CF) to correct sample size calculation. Section 2.7 provides formulas valid under a generalization of the linear mixed effects model. Our simulation results are in Section 3 and illustrative examples on the impact of cluster size variation are in Section 4. We end the paper with a Discussion (Section 5).
2. Methods
2.1. Notation and Model
We consider a cross-sectional design with individuals k = 1, … , ni sampled from cluster i = 1, … , I at every time-point j = 1, … , T. The landmark paper on SW-CRTs by Hussey and Hughes (2007) proposes the following model for response variable Yijk:
where αi is the random effect for cluster i, βj is a fixed effect corresponding to time j (j = 1,…,T − 1 with βT = 0 for identifiability), Xij is an indicator of treatment (1 = intervention, 0 = control) in cluster i at time j, θ is the treatment effect, and eijk is the subject-specific error independent of αi.
2.2. Treatment Effect Variance when Cluster Sizes and Order of Randomization Known
Under the linear mixed effects model, estimates for the fixed effects can be obtained by weighted least squares (WLS). Let Z be the IT × (T + 1) design matrix corresponding to the parameter vector η = (μ, β1, β2, …, β T−1, θ). Then, the WLS estimator is and the treatment effect denoted by is the (T + 1)th element of . The covariance matrix of is (ZTV−1Z)−1, where V is a block diagonal matrix provided in Web Appendix A.
To test the hypothesis H0: θ = 0 versus θ = θA, we can use a Wald test based on where is the estimated treatment effect from WLS. The approximate power for conducting a two-tailed test of size α is:
where 1–β is the statistical power, Φ is the cumulative standard normal distribution function, z1−α/2 is the (1 − α/2)th quantile of the standard normal distribution function, and Var() is the (T + 1), (T + 1) element of the covariance matrix (ZTV−1Z)−1.
A closed form expression for the treatment effect variance given one particular realization of the randomization sequence denoted by P = p was derived (Web Appendix A):
| (1) |
where
and . When the sample size is the same for all clusters this variance simplifies to the variance provided in equation 8 of Hussey and Hughes (2007) (Web Appendix B).
The formula in equation 1 reveals that components of the denominator (ℓ, z, y2, Tw – ℓ2) depend upon the order in which the clusters are randomized to intervention. To gain some insight, we observe will be larger if a large cluster is randomized to initiate the intervention first, i.e. if n1 is large. This is because in SW-CRTs the clusters randomized at the first step receive treatment for the most time periods, so as Xij is the indicator of treatment status, X11 + … + X1T will be greater than or equal to the other summations. If randomization of all clusters has taken place, this variance formula could be utilized to check the power after randomization. If the power is too low, the formula could be used to determine the number of additional measurements needed to increase the power. As it is customary to calculate the power in trial planning stages before randomization, in Section 2.3 and 2.4 we provide a method to identify the upper and lower bound of the treatment effect variance across all possible randomizations, as well as a closed form expression for the expected value of the variance to obtain the study power in an average sense.
2.3. Method to Find Upper and Lower Bounds for the Treatment Effect Variance
To find the upper and lower bounds for the power across all possible randomizations, the maximum and minimum of the denominator D(v1, … ,vI) of the variance of the treatment effect estimator in equation 1 were sought. This requires optimizing D(v1, … , vI) over the order of varying cluster sizes; that is, minimize/maximize: D(v1, … , vI) subject to: (v1, … , vI) is a permutation of (n1, … , nI). The above optimization problem is classified as an assignment problem with a quadratic objective, since D(v1, … , vI) is quadratic in v1, … , vI. In general, an assignment problem with a non-linear objective is not only NP-hard (i.e. cannot be solved in polynomial time), but also does not have a “good” algorithm to find a solution other than cycling through all possible randomization sequences. Fortunately, a reparametrization involving permutation matrices reformulates the problem into a mixed-integer quadratic programming (MIQP) problem, which, while still NP-hard, has excellent algorithms to obtain an exact solution. Specifically, the reparametrization (Web Appendix C) takes the form minimize/maximize: RTMR + DTR
where
R is a vector of length I2 decision variables
M is an I2 × I2 matrix. For s,t,i,j = 1, … , I, the elements are
D is a vector of length I2. For t, j = 1, … I, the elements are
The above form can now be solved by algorithms implemented by solvers such as Gurobi (2019). The decision variable vector R is a vectorization of the permutation matrix which encodes the realization of the randomization sequence that will obtain the highest or lowest possible power. For example, with four clusters of size 10, 15, 45 and 50 and one cluster randomized at each step, an optimal solution R = (0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1) is a vectorization of the matrix
We require the vectorized form R in order to feed the decision variables into a solver. One sequence that optimizes the objective function will be identified and the maximum/minimum power can be obtained by using this optimal sequence to first calculate the treatment effect variance using equation 1 and then to estimate the power of the Wald test using this variance. The randomization sequence achieving highest or lowest power can be non-unique. In the example, a sequence of 50, 10, 15 and 45 would also attain the same maximum power. A search over all possible randomizations could be conducted to identify all sequences of the cluster sizes that have higher power. However, for design purposes, we are most interested in the best and worst case scenarios for the power; identifying all sequences associated with each extreme case is not necessary. We have not restricted the design specified by Xij to devise this algorithm; Web Appendix C describes implementation for additional designs.
2.4. Expected Treatment Effect Variance when Cluster Sizes Known
When all the cluster sizes are known prior to randomization, we derive a closed form expression for a first-order approximation of the expected value of Var(), where the expectation is taken across all possible randomization realizations.
To proceed, we consider only balanced SW-CRT designs where q clusters are randomized at each step, where q is any divisor of the total number of clusters I, and where each cluster contributes samples at one baseline time-point before any cluster begins the intervention and at one time-point after each step. If K = I/q represents the number of steps, then cross-sectional samples from the clusters will be taken at T = K + 1 time-points. As an example, a design with q = 2 results in the following treatment status matrix, where Xij is the indicator of treatment (1=intervention, 0=control) in cluster i at time j:
In the variance formula given in equation 1, three terms in the denominator, (ℓ − z), (y2) and (Tw − ℓ 2) depend on the order clusters are randomly assigned to initiate the intervention. To calculate the three expectations, , and , we derived , the probability cluster i is treated at time-point j, and , the probability cluster i is treated at time-point j and cluster l is treated at time-point m, as follows:
where a ∧ b = min(a, b) and a ∨ b = max(a, b) (Web Appendix D).
Based on these results and a first-order approximation , we obtained the following formula to approximate the expected value of Var():
| (2) |
where
and κ is the cluster size CV. A formula for a more general setting described in Woertman et al. (2013) where each cluster contributes samples at b baseline time-points and at t time-points after each step is provided in Web Appendix D.
2.5. Approximate Expected Treatment Effect Variance with the Arithmetic Mean and Coefficient of Variation (CV) of Cluster Sizes
In the design stage of a SW-CRT, each cluster size may not be known, instead, the investigators may have information on the average and CV of the cluster sizes. We derived the following variance formula to approximate the variance formula provided in equation 8 of Hussey and Hughes (2007) for the same type of design described in Section 2.4 where information on actual cluster sizes ni is replaced by their arithmetic mean and CV:
| (3) |
where
The derivation used the first-order Taylor approximation of the terms f and s1 about the arithmetic mean cluster size (See Web Appendix E for details and for a generalization for b baseline time-points and t time-points after each step).
2.6. Design Effect (DE) and Relative Efficiency (RE) of Designs with Unequal Cluster Sizes, and Correction Factor (CF) for Sample Size Calculation
From the approximation of the treatment effect variance in Section 2.5, we derived a DE for a SW-CRT with unequal cluster sizes relative to an individually randomized trial of total size T · NSW; the overall number of participants sampled in a cross-sectional SW-CRT:
| (4) |
where, a = 2+{(T+1)n−2}ρ,d = {(T+1)/T}{1+(Tn−1)ρ}, , n=NSW/I, ρ is the intra-cluster correlation, n is the arithmetic mean cluster size, and κ is the cluster size CV (Web Appendix F). When κ is zero, DEw,κ reduces to T · DEw, where DEw is a design effect derived in Woertman et al. (2013) for a cross-sectional SW-CRT with equal cluster sizes compared to an individually randomized trial of size NSW (Web Appendix G).
Some insight can be gained by interpreting {1 + (Tn − 1)ρ} in DEw,κ as the inflation due to cluster randomization for a trial with T · NSW individuals. Under equal cluster sizes, {3(T−1)(1−ρ)}/{(T−2)a} is the inflation or reduction in sample size incurred by employing a stepped wedge (SW) design. If ρ = 0 an inflation of {3(T − 1)}/{2(T − 2)} would be needed due to the imbalance of the numbers of participants receiving the intervention compared to control at the early or later stages of a SW design. However, in the vast majority of CRTs the intra-cluster correlation is positive (i.e. ρ > 0), so a SW design is more efficient due to its use of within-cluster comparisons (Rhoda et al., 2011). For example, if ρ = 0.05, n = 30 and T = 5, the relative sample size reduction is {3(T − 1)(1 – ρ)}/{(T − 2)a} = 0.35. This means the variance of the treatment effect is reduced by employing a SW design. Under cluster size variation, the term in the denominator of renders the SW design with unequal cluster sizes less efficient on average compared to a SW design with equal cluster sizes. A key observation is that, for certain orders of randomization, having variable cluster sizes may not result in an efficiency loss, as noted by Martin et al. (2019). This is likely due to the fact that the difference in the number of participants receiving intervention and control at the early or later stages of a SW design may be mitigated if large clusters are randomized to initiate the intervention early and late in the design. The exact randomization order of variable size clusters that provides the most and least efficiency is non-trivial and was the subject of Section 2.3.
Formally, the approximate expected relative efficiency (RE) of a design with unequal cluster sizes compared to equal can be written as (Web Appendix H):
| (5) |
where, the attenuation term, AT = (T − 1)(1 – ρ)/(T[2 + {(T + 1)n − 2}ρ]) is positive and typically small, so the average efficiency loss by having unequal cluster sizes can be approximated as 1 − κ2/I.
A correction factor (CF) for sample size calculation was derived (Web Appendix I):
| (6) |
where
is the total sample size required for an individually randomized trial with an anticipated treatment effect of θA
DEw = [3(T −1)(1 − ρ){1 + (Tn − 1)ρ}]/(T(T − 2)[2 + {(T + 1)n − 2}ρ]) is the Woertman et al. (2013) design effect
CF = nκ2 (1 − AT) is the correction factor for cluster size variation with an attenuation term (AT) defined as AT = (T − 1)(1 − ρ)/(T[2 + {(T + 1)n − 2}ρ])
Before applying the sample size formula knowledge of the following is required: the arithmetic mean cluster size (n), the cluster size CV (κ), and the total number of time-points (T) equal to the number of steps plus one (K +1). The required sample size at each time-point, Nsw, can be calculated by multiplying the unadjusted sample size in an individually randomized trial by the Woertman et al. (2013) DEw, and then adding our CF. The overall sample size in terms of participants each contributing one measurement in a cross-sectional design is T · NSW. The required number of clusters I is ⌈NSW/n⌉ and the number of clusters switching treatment at each step is ⌈I/K⌉, where ⌈·⌉ is the ceiling function. Woertman et al. (2013) suggest distributing the clusters as evenly as possible over the steps.
The correction factor CF slightly underestimates nκ2 and in many cases can be approximated as nκ2. This corresponds to including κ2 additional clusters to account for cluster size variation. The calculation requires the total number of time-points (T) to remain constant, and hence the number of steps (K) to remain the same. Therefore, it is only directly applicable if κ2 is divisible by the number of steps (K) in the proposed design. For example, with a CV of κ ~ 1.4 and a design with two steps (K = 2), you would include two additional clusters, one per step, in the design to account for cluster size variation.
2.7. Generalization to Include a Random Time Effect
The model displayed in Section 2.1 can be generalized as in Hooper et al. (2016) to accommodate a random time effect, as follows:
where nij is the random effect for cluster i at time-point j. Following a similar process, in Web Appendix K, we derived two variance formulas, which mirror those for the Hussey and Hughes (2007) model. The first assumes that the cluster sizes and order of randomization are both known, and allows us to identify upper and lower bounds of the power. The second provides a closed form expression for the expected variance before randomization when all cluster sizes are known. We were not able to derive the third variance formula, a DE, or a CF, using an approximation of the expected value of the variance if only the cluster size arithmetic mean and CV are available. This is because an accurate approximation would require at least a third-order Taylor expansion of some components, and thus requires knowledge of the skewness and potentially higher moments of the cluster size distribution, which would be hard to obtain in trial planning stages.
3. Simulation Study Results
We conducted simulation studies to evaluate the performance of the proposed methods. For each chosen study design with NSW participants contributing data at each time-point, assuming an intra-cluster correlation (ρ) of 0.05, we set the effect size (θA) so that the power calculated based on a fixed cluster size using equation 8 in Hussey and Hughes (2007) would be 80%. Then, the estimated power accounting for cluster size variation was calculated using one of the formulas derived in this paper. Additionally, the power was empirically simulated under cluster size variation using the model in Section 2.1. Web Appendix L provides details of the design parameters and simulation steps.
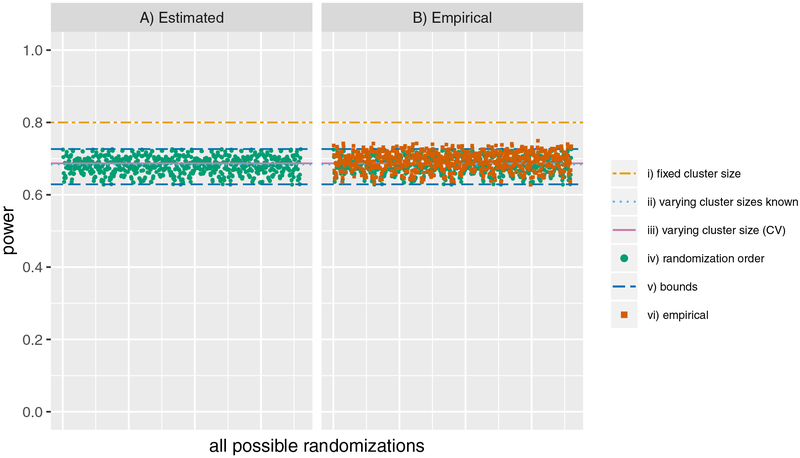
Firstly, the impact of the order of randomization for particular known cluster sizes using the variance formula derived in equation 1 was evaluated. For a design with 6 clusters with one cluster randomized to intervention at each step, we calculated the power for each of the 6! orders of randomization (Figure 1A, green dots). The 6 clusters were of size 4, 11, 18, 21, 22 and 104, resulting in an arithmetic mean cluster size of 30 and a CV of κ = 1.23. Lower and upper bounds for the power were obtained using the algorithm described in Section 2.3 and are displayed in Figure 1A by dashed dark blue lines. The algorithm correctly finds the minimum and maximum power across all possible randomizations of 62.9% and 72.6%, respectively. Performance of the algorithm with a larger number of clusters is described in Web Appendix L. The green dots on Figure 1A displaying the calculated power for each randomization order are almost entirely covered by the orange squares displaying the empirically simulated power on Figure 1B. The lower and upper bounds are very close to the lowest and highest empirically simulated powers of 62.8% and 74.9%, respectively. Furthermore, using equation 2 to estimate the expected treatment effect variance across all randomization sequences when all clusters sizes are known, the study is estimated to have an average power of 68.4% (Figure 1, dotted light blue line). With only knowledge of the cluster size arithmetic mean and CV (equation 3), the average power estimate is 68.7% (Figure 1, solid pink line). Therefore, our method produced power estimates close to the average power. For a particular randomization, the actual power may be higher or lower than this average. In this particular simulation, the average power was 5 to 6% above the minimum simulated power across all randomization sequences, and 6 to 7% below the maximum simulated power. Using the average power estimate was an improvement on assuming a fixed cluster size of the arithmetic mean, which will tend to over-estimate the power by a larger degree; in this case the over-estimation was by at least 5% up to a maximum of 17%. A supplementary figure evaluating clusters of size 4, 11, 18, 21, 62 and 64 is in Web Appendix L.
Figure 1.
Power for all possible randomizations with upper and lower bound indicated for a SW-CRT with 6 clusters of arithmetic mean size (n) 30 and CV (κ) of 1.23. i) fixed cluster size: uses the variance formula in equation 8 of Hussey and Hughes (2007), ii) varying cluster sizes known: uses the variance formula in equation 2, iii) varying cluster size (CV): uses the variance formula in equation 3, iv) randomization order: uses the variance formula in equation 1, v) bounds: uses the method described in Section 2.3, vi) empirical: the empirically simulated power from 3,500 simulations.
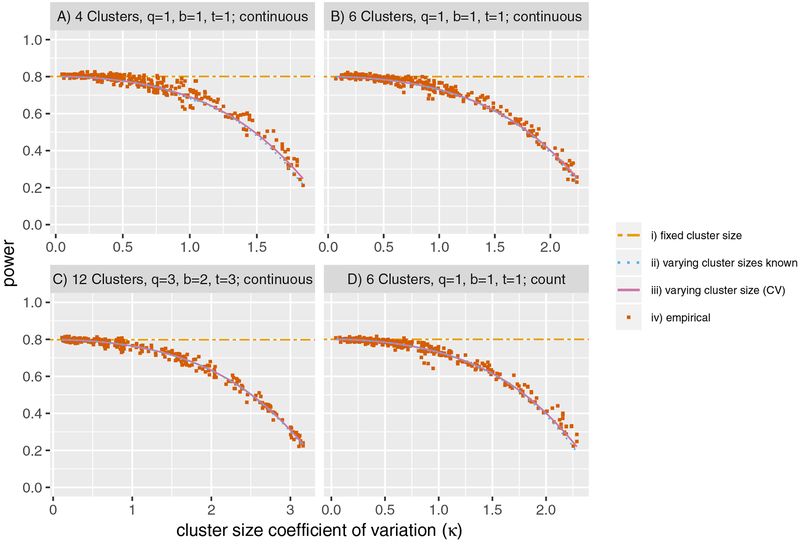
We went on to evaluate the expected variance formulas derived in equations 2 and 3 under four scenarios corresponding to different design parameters. For the four scenarios, as the cluster size CV (κ) increases the power decreases (Figure 2). The expected power when all the clusters sizes are known calculated using the variance formula in equation 2, displayed by the dotted light blue line, is very similar to the approximation using the cluster size arithmetic mean and CV by equation 3 denoted by the solid pink line. By comparing the orange squares showing the empirically simulated power, we can see the expected power is well estimated. Most of the deviation of the orange squares from the dotted light blue and solid pink lines is due to the particular random order clusters received intervention in that simulation, since the Monte Carlo error was estimated to be ⩽ 0.75%. Supplementary figures evaluating the formulas for the generalization defined in Section 2.7 are in Web Appendix L.
Figure 2.
Estimated power as the cluster size coefficient of variation (κ) increases for four simulation scenarios with arithmetic mean cluster size (n) 30. q is the number of clusters randomized at each step, b is the number of time-points each cluster contributes samples at baseline, t is the number of time-points each cluster contributes samples between each step. i) fixed cluster size: uses the variance formula in equation 8 of Hussey and Hughes (2007), ii) varying cluster sizes known: uses the variance formula in equation 2, iii) varying cluster size (CV): uses the variance formula in equation 3, iv) empirical: the empirically simulated power from 3,500 simulations.
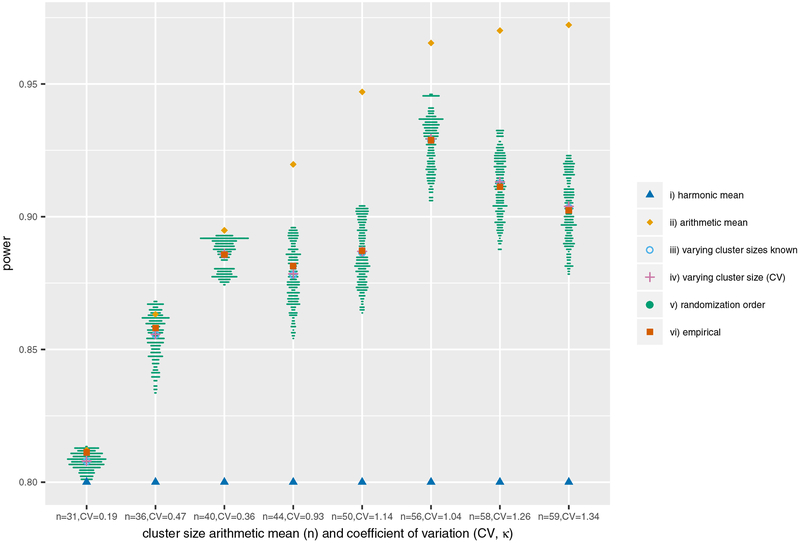
Finally, we evaluated a method that simply plugs-in the harmonic mean of the cluster sizes. We created several example studies of 6 clusters with one cluster randomized to intervention at each step that held the cluster size harmonic mean fixed at 30, but varied the cluster size arithmetic mean and CV. Plugging-in the harmonic mean of 30 in the variance formula given by equation 8 of Hussey and Hughes (2007) with no other adjustment under-estimated the power (Figure 3). Whereas, using the arithmetic mean over-estimated the power. The actual power was somewhere in-between the two estimates, and is displayed for each randomization sequence on Figure 3 (green dots). Our method correctly identified the average power over all the randomization sequences using the arithmetic mean and CV.
Figure 3.
Estimated power at a fixed harmonic mean of 30 for SW-CRTs with 6 clusters. i) harmonic mean: uses the variance formula in equation 8 of Hussey and Hughes (2007) plugging-in a harmonic mean of 30, ii) arithmetic mean: uses the variance formula in equation 8 of Hussey and Hughes (2007) plugging-in the arithmetic mean given on the X-axis, iii) varying cluster sizes known: uses the variance formula in equation 2, iv) varying cluster size (CV): uses the variance formula in equation 3, v) randomization order: uses the variance formula in equation 1, vi) empirical: the mean empirically simulated power from 150 simulations of each randomization order (108,000 simulations in total).
4. Illustrative Examples
4.1. Design of the Washington State Study Accounting for Unequal Cluster Sizes
The Washington state community-level randomized trial of expedited partner therapy aimed to reduce chlamydia test positivity by making free patient-delivered partner therapy and other public health services available (Hussey and Hughes, 2007). The trial was designed to randomly assign 24 local health jurisdictions (LHJs, the clusters) at 4 steps (K = 4) with 6 clusters instituting the intervention (q = 6) at each step. The primary outcome was chlamydia test positivity among cross-sections of women testing in sentinel clinics. Assuming 162 women would test in each LHJ between each step, a 5% chlamydia positivity under control, an intra-cluster correlation ρ of 0.00665, and α = 0.05, the study had approximately 85% power to detect a prevalence difference of 0.015 (i.e. 3.5% chlamydia positivity under intervention, θA = 0.015) using . The results publication revealed that numbers of women tested varied by LHJ (Golden et al., 2015).
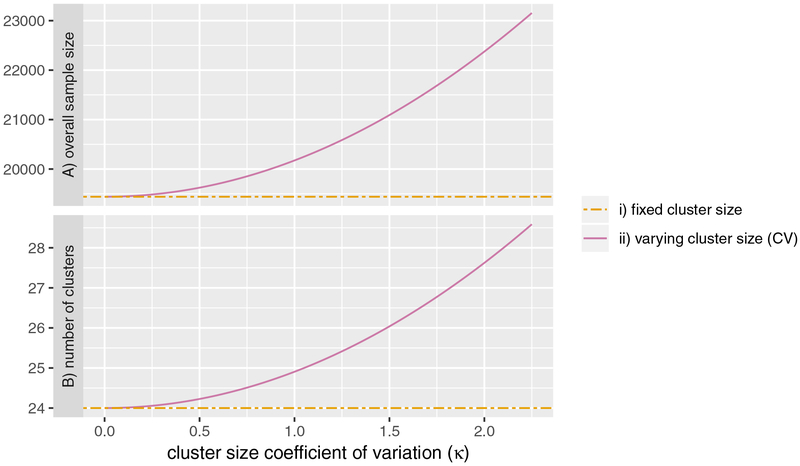
To evaluate the impact of varying cluster sizes on sample size, we estimated the the overall sample size (T · NSW) and number of clusters (I) required to achieve 85% power for a range of cluster size CV (κ) values (Figure 4). If the cluster size CV was high at κ = 2.1, the SW-CRT design with 4 steps would instead require a total of 28 clusters (I = 28) with 7 randomized at each step (q = 7) (Figure 4B). This represents a 17% inflation of overall sample size (T · NSW) from 19,440 to 22,680 (Figure 4A). In this example with 4 steps and CV of κ = 2.1, it is relatively easy to adapt the original design to include four additional clusters by adding one at each step. However, in general, adaptation to incorporate additional clusters may not be as straightforward. For example, if the CV was 1.5, only 2 additional clusters would be required. The design would have to be changed to have a different number of steps or larger mean cluster size, and finding a design that is practical with adequate power may be an iterative process.
Figure 4.
A) Overall sample size (T · Nsw) and B) number of clusters (I) required to achieve 85% power for a SW-CRT with 4 Steps. i) fixed cluster size: estimates the sample size using T · DEw (Woertman et al., 2013), ii) varying cluster size (CV): estimates the sample size using equation 6.
4.2. Relative Efficiency (RE) of the Trial by Bashour et al. (2013) Comparing Unequal to Equal Cluster Sizes
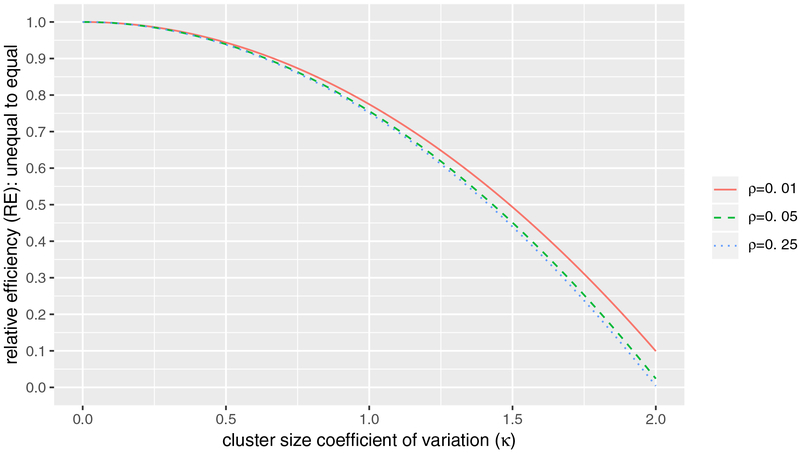
The trial by Bashour et al. (2013) was designed to determine the effect of training residents in interpersonal and communication skills on women’s satisfaction during labour and delivery. Four tertiary care teaching maternity hospitals in Damascus with expected deliveries ranging from 5,000 to 15,000 per year, and number of residents ranging from 7 to 137, were randomized one-per-step (i.e. I = 4, q =1, T = 5). The original study included n = 100 women per hospital per time-point. Given the considerable variation in hospital sizes, we assess the average RE of allowing cluster sizes to vary by recruiting more participants in larger hospitals compared to the design with equal cluster sizes. For intra-cluster correlations (ρ) of 0.01, 0.05 or 0.25, and the cluster size CV (κ) ranging from zero to 2, we calculated the average RE for unequal to equal cluster sizes (Figure 5). If each hospital had recruited 6% of the expected deliveries at each step, a total of 400 women would be recruited at each step, but the cluster sizes would vary such that the CV would be about 0.48. If ρ was 0.05, this would result in an average efficiency loss of about 6%. If each hospital recruited proportional to the number of residents, the CV would be 1.03 and there would be 26% average efficiency loss.
Figure 5.
Average relative efficiency (RE) for 4 clusters with q =1 randomized at each step (T = 5) and arithmetic mean cluster size of n = 100. ρ is the intra-cluster correlation.
5. Discussion
Cluster size variation should be taken into account when designing a SW-CRT. While the effect of unequal cluster sizes on study power appears to be smaller for a cross-sectional SW-CRT than for a parallel CRT, the relationship is more complex. In the presence of unequal cluster sizes, the power of a SW-CRT is heavily dependent upon the order of randomization. It would be useful to consider allocation approaches that may result in efficiency gain (see for example, Matthews (2019)). The variance formula derived in equation 1 is associated with a particular realization of the randomization sequence. As the number of possible randomization sequences increases drastically with the number of clusters and an exhaustive search for the lower and upper bounds for the power would be computationally prohibitive, we devised efficient algorithms for identification of these power bounds. Rapid increase in computing power has made simulations a flexible and attractive alternative to analytical derivations to calculate study power in many settings; here, however, as the time required to conduct such simulations increases considerably with the number of randomization sequences, the availability of analytical formulas with efficient search algorithms makes it more feasible to obtain minimum and maximum power estimates in the study design stage.
In a balanced SW-CRT design where an equal number of clusters are randomized to initiate treatment at each step, we provide formulas to estimate the average power loss associated with cluster size variation. This average power loss is non-negligible, and larger when the number of clusters is small or the cluster size CV is greater than one. Both a formula for the expected treatment effect variance requiring knowledge of the actual cluster sizes, as well as an approximation only requiring the projected cluster size average and CV, are provided. For practitioners, the latter will enable feasible designs to quickly be identified from information available in the early trial planning stages in a way that is considerably more accurate than plugging-in the arithmetic or harmonic mean cluster size. If the number of clusters are sufficiently large and several clusters are randomized to initiate treatment at each step, so that there is no substantial inequality in the total size of all clusters randomized at each step, the power loss will be alleviated (Girling, 2018). However, in settings where total numbers of clusters are not large, this would not be feasible. Indeed, SW-CRT designs benefit from within-cluster comparisons and make CRTs possible in situations where the number of clusters is too small for a parallel design, as the power of a parallel design crucially depends on the number of clusters (Rhoda et al., 2011; Donner and Klar, 1996).
The primary linear mixed effects model used in this paper (Hussey and Hughes, 2007), assumes random cluster effects, fixed time effects, no cluster by time interaction and no treatment by time interaction. This model can be adapted to incorporate more flexible modeling assumptions. In Section 2.7, we generalized the proposed method, when all cluster sizes are known, to allow a random time effect as described in Hooper et al. (2016). Variance formulas that allow random treatment effects were more challenging (Hughes et al., 2015). Furthermore, we have assumed that from each of the i = 1, … , I clusters exactly ni participants will be sampled at each time-point. In practice it is possible that the number of participants sampled at each time-point may vary within a cluster. To what extent this variation affects study power and methods for adjustment requires further investigation.
Hooper et al. (2016) proposed a DE for cohort SW-CRTs with equal cluster sizes, but the effect of cluster size variation has not been determined. For cross-sectional designs, the average RE of unequal compared to equal cluster sizes depends on the intra-cluster correlation, so we expect the within-individual correlation to also play a role in cohort designs. However, since average efficiency loss for cross-sectional SW-CRTs was largely driven by the number of clusters and cluster size CV, it would be interesting to examine if this is also true for cohort designs.
The variance formulas and DE in this paper are derived under a linear model, and therefore are particularly suited to continuous and count outcomes, or to designs evaluating a prevalence difference. Li et al. (2018) proposed a method to determine sample size for binary outcomes on the log-odds scale within the framework of generalized estimating equations. This method assumes equal cluster sizes. In future work we aspire to further investigate power and sample size formulas for binary outcomes accounting for unequal cluster sizes.
Supplementary Material
Acknowledgements
We thank the Editor, Associate Editor, and two reviewers for their helpful comments, which lead to an improved version of the paper. We gratefully acknowledge grants from National Institute of Allergy and Infectious Diseases T32 AI 007358, R37 AI 051164 and R01 AI136947. We thank Xuan Zhang for helpful discussions on devising efficient algorithms for identification of bounds.
Footnotes
Supporting Information
Web Appendices and Figures referenced in Sections 2.2, 2.3, 2.4, 2.5, 2.6, 2.7 and 3 are available with this paper at the Biometrics website on Wiley Online Library. R functions to calculate the variance and resulting power using equation 1, 2 and 3, the sample size using equation 6, and example R code utilizing Gurobi are in Web Appendix J.
References
- Bashour HN, Kanaan M, Kharouf MH, Abdulsalam AA, Tabbaa MA, and Cheikha SA (2013). The effect of training doctors in communication skills on women’s satisfaction with doctor-woman relationship during labour and delivery: a stepped wedge cluster randomised trial in damascus. BMJ Open 3, e002674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donner A and Klar N (1996). Statistical considerations in the design and analysis of community intervention trials. J Clin Epidemiol 49, 435–439. [DOI] [PubMed] [Google Scholar]
- Eldridge SM, Ashby D, and Kerry S (2006). Sample size for cluster randomized trials: effect of coefficient of variation of cluster size and analysis method. Int J Epidemiol 35, 1292–300. [DOI] [PubMed] [Google Scholar]
- Girling AJ (2018). Relative efficiency of unequal cluster sizes in stepped wedge and other trial designs under longitudinal or cross-sectional sampling. Stat Med 37, 4652–4664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golden MR, Kerani RP, Stenger M, Hughes JP, Aubin M, Malinski C, and et al. (2015). Uptake and population-level impact of expedited partner therapy (EPT) on chlamydia trachomatis and neisseria gonorrhoeae: the washington state community-level randomized trial of ept. PLoS Med 12, e1001777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurobi (2019). Gurobi optimizer. http://www.gurobi.com.
- Hayes R and Moulton L (2009). Cluster Randomised Trials. CRC Press. [Google Scholar]
- Hemming K, Haines TP, Chilton PJ, Girling AJ, and Lilford RJ (2015). The stepped wedge cluster randomised trial: rationale, design, analysis, and reporting. BMJ 350, h391. [DOI] [PubMed] [Google Scholar]
- Hooper R, Teerenstra S, de Hoop E, and Eldridge S (2016). Sample size calculation for stepped wedge and other longitudinal cluster randomised trials. Stat Med 35, 4718–4728. [DOI] [PubMed] [Google Scholar]
- Hughes JP, Granston TS, and Heagerty PJ (2015). Current issues in the design and analysis of stepped wedge trials. Contemp Clin Trials 45, 55–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussey MA and Hughes JP (2007). Design and analysis of stepped wedge cluster randomized trials. Contemp Clin Trials 28, 182–91. [DOI] [PubMed] [Google Scholar]
- Kristunas C, Morris T, and Gray L (2017). Unequal cluster sizes in stepped-wedge cluster randomised trials: a systematic review. BMJ Open 7, e017151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kristunas CA, Smith KL, and Gray LJ (2017). An imbalance in cluster sizes does not lead to notable loss of power in cross-sectional, stepped-wedge cluster randomised trials with a continuous outcome. Trials 18, 109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F, Turner EL, and Preisser JS (2018). Sample size determination for GEE analyses of stepped wedge cluster randomized trials. Biometrics 74, 1450–1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin JT, Hemming K, and Girling A (2019). The impact of varying cluster size in cross-sectional stepped-wedge cluster randomised trials. BMC Med Res Methodol 19, 123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews JNS (2019). Highly efficient stepped wedge designs for clusters of unequal size. arXiv:1811.05359v2. [DOI] [PubMed] [Google Scholar]
- Rhoda DA, Murray DM, Andridge RR, Pennell ML, and Hade EM (2011). Studies with staggered starts: multiple baseline designs and group-randomized trials. Am J Public Health 101, 2164–2169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutterford C, Copas A, and Eldridge S (2015). Methods for sample size determination in cluster randomized trials. Int J Epidemiol 44, 1051–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woertman W, de Hoop E, Moerbeek M, Zuidema SU, Gerritsen DL, and Teerenstra S (2013). Stepped wedge designs could reduce the required sample size in cluster randomized trials. J Clin Epidemiol 66, 752–8. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.