Improving Image Resolution of Whole-Heart Coronary MRA Using Convolutional Neural Network

Abstract

Whole-heart coronary magnetic resonance angiography (WHCMRA) permits the noninvasive assessment of coronary artery disease without radiation exposure. However, the image resolution of WHCMRA is limited. Recently, convolutional neural networks (CNNs) have obtained increased interest as a method for improving the resolution of medical images. The purpose of this study is to improve the resolution of WHCMRA images using a CNN. Free-breathing WHCMRA images with 512 × 512 pixels (pixel size = 0.65 mm) were acquired in 80 patients with known or suspected coronary artery disease using a 1.5 T magnetic resonance (MR) system with 32 channel coils. A CNN model was optimized by evaluating CNNs with different structures. The proposed CNN model was trained based on the relationship of signal patterns between low-resolution patches (small regions) and the corresponding high-resolution patches using a training dataset collected from 40 patients. Images with 512 × 512 pixels were restored from 256 × 256 down-sampled WHCMRA images (pixel size = 1.3 mm) with three different approaches: the proposed CNN, bicubic interpolation (BCI), and the previously reported super-resolution CNN (SRCNN). High-resolution WHCMRA images obtained using the proposed CNN model were significantly better than those of BCI and SRCNN in terms of root mean squared error, peak signal to noise ratio, and structure similarity index measure with respect to the original WHCMRA images. The proposed CNN approach can provide high-resolution WHCMRA images with better accuracy than BCI and SRCNN. The high-resolution WHCMRA obtained using the proposed CNN model will be useful for identifying coronary artery disease.

Introduction

Coronary artery stenosis causes ischemic heart disease such as angina pectoris. Ischemic heart disease is the leading cause of death, resulting in approximately eight million deaths around the world [1]. Therefore, it is important to detect coronary artery stenosis at an early stage. A whole-heart coronary magnetic resonance angiography (WHCMRA) permits the noninvasive assessment of coronary artery stenosis without exposing the patient to radiation. Although WHCMRA has several advantages over coronary computed tomography (CT) angiography such as the ability to use non-contrast enhanced imaging and robustness to heavy coronary calcification, low spatial resolution remains a major limitation of WHCMRA.

Learning-based super-resolution (SR) is a post-processing technique to increase image resolution [2–4]. Wu et al. developed a learning-based super resolution technique using kernel partial least squares [2]. Xian et al. also proposed an SR approach that integrates external and internal statistics [3]. Although these studies demonstrate that learning-based SR techniques can achieve high performance, these techniques require a large number of reference images and also take an enormous amount of time to compute.

Deep learning approaches such as convolutional neural networks (CNNs) have achieved superior performance in various fields such as classification, detection, segmentation, and super-resolution in images [5–11]. CNNs can automatically extract multilevel features, specific to the application, from images. The performance of CNNs has been reported to be better than that of conventional methods that use image processing techniques. Dong et al. [12, 13] developed a super-resolution CNN (SRCNN) for improving the image resolution of natural images. The SRCNN is applied in three steps, namely, patch extraction and representation, non-linear mapping, and reconstruction. It learns an end-to-end mapping directly between the low- and high-resolution images. Although Umehara et al. [14] applied SRCNN and demonstrated the effectiveness of this approach in increasing the image resolution of chest radiographs, SRCNN was originally developed for natural images. Therefore, SRCNN might not be suitable for medical images, because there is a large difference in the signal patterns of natural and medical images. It has also been reported that the accuracy of the resolution improvement changes greatly when the structure of SRCNN is changed. Thus, it is important to determine the suitable CNN structure for the target image.

In this study, we optimized the structure of a CNN to improve the image resolution of WHCMRA images and then evaluated their fidelity to the original images. It is desirable to obtain WHCMRA images with a resolution that is higher than 512 × 512 pixels (pixel size = 0.65 mm) in the clinical diagnosis of patients with coronary artery disease. However, owing to the limitations in imaging time that can be tolerated by patients, WHCMRA images with higher spatial resolution cannot be constructed from actual MR image data acquired from human subjects. Thus, 256 × 256 pixel images (pixel size = 1.3 mm) were generated by down-sampling 512 × 512 WHCMRA images (pixel size = 0.65 mm) using nearest-neighbor interpolation. To evaluate the accuracy of the super-resolution images, the 256 × 256 down-sampled images were restored to 512 × 512 pixel images using the CNN, and the fidelity of the restored images was evaluated using the original 512 × 512 WHCMRA images as the gold standard.

Materials and Methods

Materials

The use of the database in this study was approved by the institutional review board at Mie University Hospital. The database was stripped of all patient identifiers.

Free-breathing WHCMRA images 512 × 512 × 150 pixels in size were obtained from 80 patients with known or suspected coronary artery disease using a 1.5 T MR system with 32 channel coils. These images were acquired under the following conditions: a navigator echo for respiratory gating, a narrow ECG-gated acquisition window in the cardiac cycle, T2-prep, and spectral pre-saturation with inversion recovery (SPIR). The voxel size of the WHCMRA images was 0.65 mm × 0.65 mm × 0.8 mm. To train and evaluate a CNN model, we randomly divided the patient data into a training set and a test set. Each set included the data of 40 patients. The CNN was developed and evaluated using MATLAB 2018a on a workstation (CPU: Intel Core i9-7900X processor, RAM: 128 GB, and GPU: NVIDIA GeForce GTX 1080Ti).

Methods

Structure and Optimization of CNN

The number of combinations of hyper-parameters, such as the size of the input layer, the number of convolutional layers, and the kernel size and the number of filters at each convolutional layer, is infinite for a CNN. To build a CNN that is optimized for increasing the resolution of WHCMRA images, we started with a basic CNN model consisting of three convolutional layers followed by a rectified linear unit (ReLU) layer. In the initial model, the first, second, and third convolutional layers had 32 filters with a kernel size of 3 × 3 and a stride of 1, 16 filters with a kernel size of 1 × 1 and a stride of 1, and one filter with a kernel size of 3 × 3 and a stride of 1, respectively.

To optimize the input patch size for the input layers of the CNN model, low-resolution small regions (patches) of 64 × 64, 32 × 32, and 16 × 16 pixels, which were extracted from the low-resolution images, as described in “Training and Testing of the CNN” section, were tested for their ability to increase image resolution (described in “Evaluation of Fidelity” section). Then, the patch size with the best performance was used to optimize the remaining hyper-parameters.

To optimize the three convolutional layer model, three different kernel sizes of 9 × 9, 5 × 5, and 3 × 3 pixels were tested in the first layer while fixing the kernel sizes in the second and third convolutional layers.

We also evaluated CNN models with four and five convolutional layers. A CNN model with four convolutional layers was constructed by adding a new convolutional layer in the penultimate layer of the three convolutional layer model with the best performance. Three different kernel sizes of 9 × 9, 5 × 5, and 3 × 3 pixels were tested in the additional convolutional layer while fixing the kernel sizes in the other convolutional layers. A CNN model with five convolutional layers was constructed by further adding a convolutional layer in the penultimate layer of the best four convolutional layer model. Again, three different kernel sizes (9 × 9, 5 × 5, and 3 × 3 pixels) were tested for the additional convolutional layer.

Training and Testing of the CNN

One of the most common approaches for training a CNN for image super-resolution is to prepare pairs of high-resolution and low-resolution images taken from the same scenes. To double the resolution of WHCMRA images, it would be necessary to prepare pairs of 1024 × 1024 and 512 × 512 WHCMRA images for the same patients. However, 1024 × 1024 WHCMRA images cannot be acquired from patients or healthy volunteers, owing to the extremely long acquisition time and low signal-to-noise ratio. Consequently, in this study, 256 × 256 down-sampled WHCMRA images were restored to 512 × 512 pixels using the CNN to evaluate the accuracy of the resolution improvement. The fidelity of 512 × 512 CNN images with respect to the original 512 × 512 WHCMRA images was evaluated.

To train the CNN model to increase the resolution of 256 × 256 images to 512 × 512 images, the 256 × 256 images (pixel size = 1.3 mm) generated by down-sampling the 512 × 512 WHCMRA images (pixel size = 0.65 mm) were employed as high-resolution images whereas 128 × 128 images (pixel size = 2.6 mm) generated by further down-sampling the 256 × 256 down-sampled WHCMRA images were used as low-resolution images. In other words, the 256 × 256 down-sampled images and 128 × 128 further down-sampled images were used as high-resolution images and low-resolution images, respectively, in the training phase.

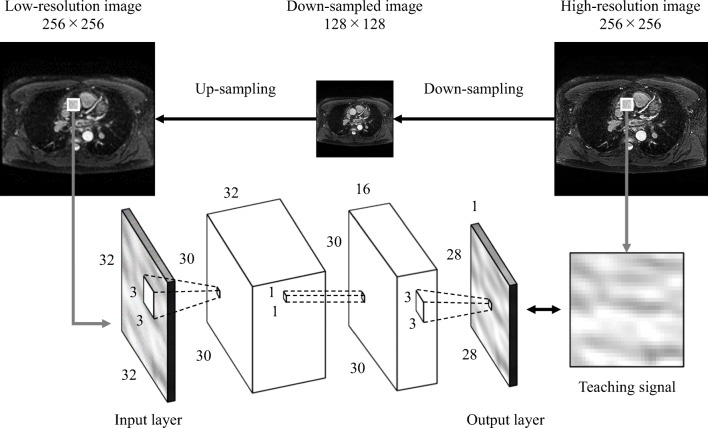
Figure 1 shows the overall training process for the basic CNN model. The 128 × 128 low-resolution images were up-sampled to 256 × 256 low-resolution images using bicubic interpolation (BCI). The 256 × 256 low-resolution images were divided into N × N patches at N/2-pixel intervals whereas the 256 × 256 high-resolution images were divided into N × N patches at positions corresponding to the low-resolution patches. Each low-resolution patch was input to the input layer of the CNN model. The corresponding high-resolution patch was used as the desired output (the teaching signal). The CNN model was trained using the relationship between low-resolution patches and the corresponding high-resolution patches in terms of signal patterns. The weights in the CNN model were updated such that the mean squared errors between the output of the CNN model and the teaching signals were minimized. The learning parameters were as follows: the mini-batch size was 2560, the learning rate was 10⁻⁶, and the maximum number of epochs was 500.

Fig. 1.

Training of the convolutional neural network (CNN) model

To test the CNN model, the trained CNN was given 256 × 256 down-sampled WHCMRA images and 512 × 512 CNN images were output. Note that the 256 × 256 down-sampled images were used as high-resolution images while training the CNN, and 256 × 256 down-sampled images were used as low-resolution images during CNN testing.

Evaluation of Fidelity

The fidelities of the 512 × 512 CNN images generated from the 256 × 256 down-sampled WHCMRA images with respect to the original 512 × 512 WHCMRA images were determined to evaluate the accuracy of the super-resolution images. The fidelities of the images constructed using the CNN were compared with those obtained using SRCNN and BCI. In this study, the root-mean-squared error (RMSE), peak signal-to-noise ratio (PSNR), and structural similarity index measure (SSIM) were employed as evaluation metrics [15, 16].

RMSE is defined as follows:

$$\text{RMSE}=\sqrt{\frac{1}{N}{\sum }_{i=1}^N{\left(I-I\prime \right)}^2}$$ 1

Here, N is the number of pixels in image, I is the original WHCMRA image, and I′ is the constructed image. Values of RMSE closer to 0 indicate a greater fidelity between the super-resolution image and the original image in terms of pixel values.

PSNR is defined by the following equation:

$$\text{PSNR}=20\times {log}_{10}\left(\frac{\mathrm{MA}{\mathrm{X}}_I}{\text{RMSE}}\right)$$ 2

Here, MAX_I is the maximum pixel value in the original WHCMRA image. A higher PSNR indicates a smaller error in the pixel values of the original WHCMRA image and the constructed image.

SSIM [17] is defined as follows:

$$\text{SSIM}=\frac{\left(2{\mu }_x{\mu }_y+C_1\right)\left(2{\sigma }_{\mathit{xy}}+C_2\right)}{\left({\mu }_x^2+{\mu }_y^2+C_1\right)\left({\sigma }_x^2+{{\sigma }_y}^2+C_2\right)}$$ 3

Here, μ_x and μ_y are the mean pixel values of the original WHCMRA image and the constructed image, respectively, and σ_x and σ_y are their respective standard deviations. In addition, σ_xy is the covariance between the original WHCMRA image and the super-resolution image, and C₁ and C₂ are positive constants used to avoid a null denominator. SSIM was used to evaluate the integrated similarity in terms of brightness, contrast, and structure between the two images.

Results

Table 1 compares the fidelities of the CNN images with three different input patch sizes, namely, 16 × 16, 32 × 32, and 64 × 64 pixels. The mean and standard deviation values with respect to RMSE, PSNR, and SSIM for the images obtained using an input patch size of 32 × 32 pixels are 7.07 ± 2.59, 39.41 ± 1.37 dB, and 0.998 ± 0.001, respectively. This indicates a significant improvement over the results obtained using 16 × 16-pixel patches (RMSE 7.27 ± 2.63, P < .001; PSNR 39.03 ± 1.30 dB, P < .001; SSIM 0.997 ± 0.001, P < .001). There are no significant differences in the RMSE, PSNR, and SSIM values of the images obtained using 32 × 32 and 64 × 64 pixel patch sizes (RMSE 7.07 ± 2.59, P = .22; PSNR 39.42 ± 1.38 dB, P = .063; SSIM 0.998 ± 0.001, P = .41). Table 2 compares the fidelities for CNN images obtained with three different kernel sizes of 9 × 9, 5 × 5, and 3 × 3 pixels in the first convolutional layer. Here, the input patch size was set to 32 × 32 pixels. The fidelities for images obtained with a kernel size of 3 × 3 pixels in the first convolutional layer were significantly greater than those obtained using the 9 × 9 and 5 × 5-pixel kernel sizes (P < .001). Tables 3 and 4 compare the fidelities of the images with four and five convolutional layer CNNs using three different kernel sizes in the penultimate convolutional layer while fixing the kernel sizes in the other convolutional layers. The fidelities for images obtained with kernel set (3-1-3) in the three convolutional layers are significantly greater than those obtained using four and five convolutional layers (P < .001). Therefore, the CNN model that was constructed from an input layer with an input patch size of 32 × 32 pixels and kernel sizes of 3 × 3, 1 × 1, and 3 × 3 in the first, second, and third convolutional layers, respectively, was determined to be the optimal CNN model for improving image resolution in WHCMRA images.

Table 1.

Comparison of the fidelities of CNN images with three different input patch sizes

Input patch size	64 × 64	32 × 32	16 × 16
RMSE	7.07 ± 2.59	7.07 ± 2.59	7.27 ± 2.63
PSNR [dB]	39.42 ± 1.38	39.41 ± 1.37	39.03 ± 1.30
SSIM	0.998 ± 0.001	0.998 ± 0.001	0.997 ± 0.001

Table 2.

Comparison of the fidelities of CNN images with three different kernel sizes in the first convolutional layer

Kernel size	9 × 9	5 × 5	3 × 3
RMSE	9.94 ± 3.97	8.13 ± 3.12	7.07 ± 2.59
PSNR [dB]	36.69 ± 1.66	38.33 ± 1.44	39.41 ± 1.37
SSIM	0.995 ± 0.002	0.997 ± 0.001	0.998 ± 0.001

Table 3.

Comparison of the fidelities of CNN images with four convolutional layers by using three different kernel sizes in the penultimate convolutional layer

Kernel set	3-1-9-3	3-1-5-3	3-1-3-3
RMSE	10.62 ± 4.30	9.09 ± 3.57	8.07 ± 3.10
PSNR [dB]	36.13 ± 1.81	37.43 ± 1.55	38.39 ± 1.48
SSIM	0.994 ± 0.002	0.996 ± 0.002	0.997 ± 0.001

Table 4.

Comparison of the fidelities of CNN images with five convolutional layers by using three different kernel sizes in the penultimate convolutional layer

Kernel set	3-1-3-9-3	3-1-3-5-3	3-1-3-3-3
RMSE	11.56 ± 4.59	9.96 ± 3.96	9.05 ± 3.56
PSNR [dB]	35.40 ± 1.76	36.70 ± 1.65	37.49 ± 1.59
SSIM	0.993 ± 0.003	0.995 ± 0.002	0.996 ± 0.002

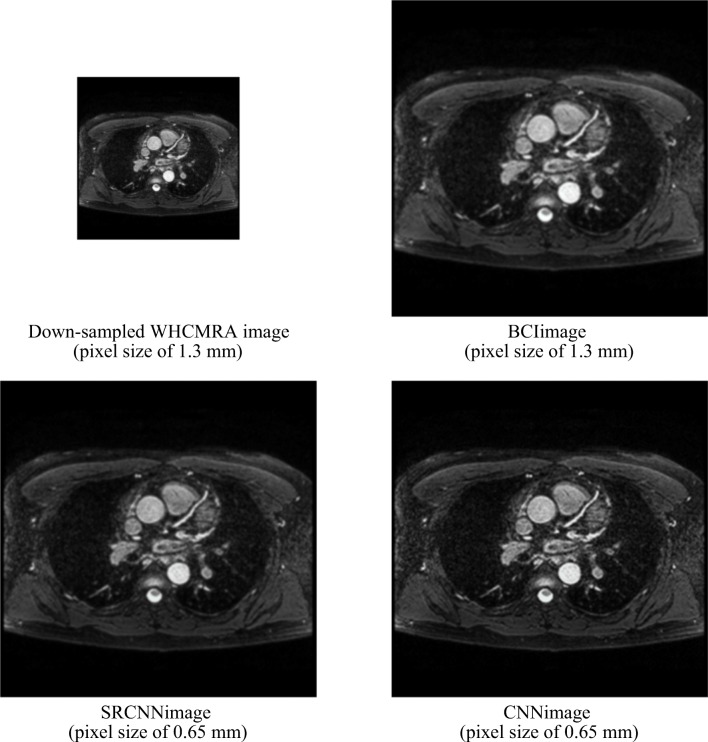
Figure 2 compares the 512 × 512 super-resolution images generated from the 256 × 256 down-sampled WHCMRA images using BCI, SRCNN, and the proposed CNN. The BCI images and the SRCNN images are slightly blurred when compared with the CNN images. Two radiologists compared the 512 × 512 super-resolution images with the original 512 × 512 WHCMRA images and confirmed that no artifacts occur in the super-resolution images. Table 5 compares the fidelities of the images obtained using BCI, SRCNN, and the proposed CNN. The mean RMSE of the CNN images and the original WHCMRA images is 7.07 ± 2.59. This is a significant improvement when compared to the results for the BCI images (11.40 ± 6.46, P < .001) and SRCNN images (13.23 ± 7.73, P < .001). The mean PSNR and SSIM for the CNN images are 39.41 ± 1.37 dB and 0.998 ± 0.001, respectively, which are greater than those of the BCI images (PSNR 36.15 ± 1.32 dB, P < .001; SSIM 0.995 ± 0.004, P < .001) and the SRCNN images (PSNR 35.36 ± 1.71 [dB], P < .001; SSIM 0.993 ± 0.003, P < .001). All indices indicating fidelity demonstrate that our model is significantly better than BCI and SRCNN.

Fig. 2.

Comparison of the images constructed using bicubic interpolation (BCI), super resolution CNN (SRCNN), and the proposed CNN model

Table 5.

Comparison of the fidelities of images constructed using BCI, SRCNN, and the proposed CNN model

	BCI	SRCNN	CNN model
RMSE	11.40 ± 6.46	13.23 ± 7.73	7.07 ± 2.59
PSNR [dB]	36.15 ± 1.32	35.36 ± 1.71	39.41 ± 1.37
SSIM	0.995 ± 0.004	0.993 ± 0.003	0.998 ± 0.001

Discussion

In the current study, we optimized the structure of a CNN to improve the image resolution of WHCMRA images. Using the proposed CNN model, high-resolution WHCMRA images with significantly higher accuracy can be constructed when compared to those obtained using the conventional methods. We also found that the CNN model trained using the relationship between image patterns with pixel sizes of 2.6 mm and 1.3 mm can be used to construct high-resolution images with a pixel size of 0.65 mm from images with a pixel size of 1.3 mm. To the best of our knowledge, this CNN-training approach, which uses images with different resolution relationships for training and testing, has not been employed before.

Table 1 compares the resultant fidelities when the size of the input patch was changed to 16 × 16, 32 × 32, and 64 × 64 pixels. Although the fidelity indices for CNN images with an input patch size of 16 × 16 pixels are significantly lower than those with 32 × 32 pixels and 64 × 64 pixels, there are no significant differences between the results for 32 × 32 pixels and 64 × 64 pixels. However, training the CNN with an input patch size of 64 × 64 pixels took three times as long as training with a patch size of 32 × 32 pixels. Therefore, we believe that an input patch size of 32 × 32 pixels is suitable for this study. The fidelities for the CNN images with kernel size of 3 × 3 pixels in the first convolutional layer were significantly greater than those obtained using the 9 × 9 and 5 × 5-pixel kernel sizes, as shown in Table 2. In SRCNN, for natural images, the kernel size in the first convolutional layer is 9 × 9 pixels. Given that medical images tend to have large local changes in signal patterns, a small kernel size would be suitable for analyzing local information. Therefore, the kernel size in the first convolutional layer was set to 3 × 3 pixels in this study. Recently, deeper CNNs have been developed to improve performance, especially in the field of classification. The fidelities of CNN images with three convolutional layers are significantly better than those obtained using four and five convolutional layers, as shown in Tables 3 and 4. The SRCNN also consists of three convolutional layers. Therefore, we believe that even just three layers may be sufficient for increasing image resolution. This has the advantage of low computational cost.

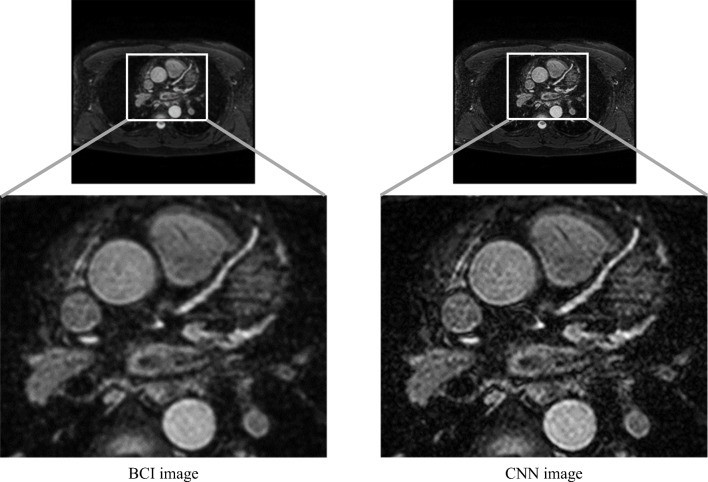
Although the proposed CNN model achieves the highest fidelities when generating 512 × 512 CNN images from 256 × 256 down-sampled WHCMRA images, obtaining WHCMRA images with a resolution higher than 512 × 512 pixels is desirable in clinical practice. Therefore, we attempted to apply the proposed CNN to generate 1024 × 1024 high-resolution images (pixel size = 0.325 mm) from the original 512 × 512 WHCMRA images (pixel size = 0.65 mm). During the training of the proposed CNN model, the 256 × 256 images that were generated by down-sampling 512 × 512 WHCMRA images were used as low-resolution images, whereas the 512 × 512 WHCMRA images were used as high-resolution images. Figure 3 compares the 1024 × 1024 images constructed from the 512 × 512 WHCMRA images using BCI and the proposed CNN model. The proposed CNN model improved the image resolution with less blurring than BCI. Two radiologists confirmed that no obvious artifacts had been generated in the 1024 × 1024 super-resolution images. This result demonstrates the potential for generating high-resolution images by the proposed CNN model in clinical practice. However, it is necessary to clarify the beneficial and detrimental effects of enhancing image resolution using the proposed CNN model. In future study, we plan to comprehensively evaluate the usefulness of enhancing image resolution using this approach in an observer study.

Fig. 3.

Comparison of the constructed images with 1024 × 1024 pixels from WHCMRA images with 512 × 512 pixels using BCI and the proposed CNN model

This study has some limitations. One limitation is that the hyper-parameters such as the number of layers, number of filters, kernel size, learning rate, mini-batch size, and maximum number of epochs in our CNN model may not be the best combination for improving the resolution of WHCMRA images. Although 12 combinations of hyper-parameters were evaluated in this study, the number of combinations of hyper-parameters in a CNN is infinite. Thus, the results in this study might be improved by applying a more optimal combination of hyper-parameters. Another limitation is that WHCMRA images with a resolution larger than 512 × 512 pixels could not be used for training the CNN. Therefore, low- and high-resolution images with resolutions that were different from the testing resolution were used when training the CNN. However, these CNN images could be useful for identifying artery stenosis and for reducing the interpretation time because the fidelities for the images without blurring obtained using the proposed CNN were significantly better than those obtained by the BCI images.

Conclusion

The CNN-based approach developed in this study is able to yield high-resolution WHCMRA images with higher accuracy than those of BCI and SRCNN. The high-resolution WHCMRA images constructed using the proposed CNN model are expected to be useful for identifying artery stenosis and for reducing interpretation time.