Insights into the rheology of cohesive granular media

Significance

An uninterrupted flow of powders is the key to smooth production operations of many industries. However, powders have more difficulty flowing than coarse, granular media like sand because of the interparticle cohesive interactions. What precisely controls the “flowability” of powders remains unclear. Here, we address this issue by performing numerical simulations of the flow of cohesive grains. We show that the cohesiveness during flow is not only controlled by the interparticle adhesion, but also by the stiffness and inelasticity of the grains. For the same adhesion, stiffer and less dissipative grains yield a less cohesive flow, i.e., higher “flowability.” This combined effect can be embedded in a single dimensionless number—a result that enriches our understanding of powder rheology.

Abstract

Characterization and prediction of the “flowability” of powders are of paramount importance in many industries. However, our understanding of the flow of powders like cement or flour is sparse compared to the flow of coarse, granular media like sand. The main difficulty arises because of the presence of adhesive forces between the grains, preventing smooth and continuous flows. Several tests are used in industrial contexts to probe and quantify the “flowability” of powders. However, they remain empirical and would benefit from a detailed study of the physics controlling flow dynamics. Here, we attempt to fill the gap by performing intensive discrete numerical simulations of cohesive grains flowing down an inclined plane. We show that, contrary to what is commonly perceived, the cohesive nature of the flow is not entirely controlled by the interparticle adhesion, but that stiffness and inelasticity of the grains also play a significant role. For the same adhesion, stiffer and less dissipative grains yield a less cohesive flow. This observation is rationalized by introducing the concept of a dynamic, “effective” adhesive force, a single parameter, which combines the effects of adhesion, elasticity, and dissipation. Based on this concept, a rheological description of the flow is proposed for the cohesive grains. Our results elucidate the physics controlling the flow of cohesive granular materials, which may help in designing new approaches to characterize the “flowability” of powders.

Many industrial (wet granulation, food processing, construction, etc.) and geophysical (landslides, mudflow, etc.) processes involve the flows of an assembly of cohesive grains. The cohesion between the grains has different origins. Van der Waals or electrostatic forces are responsible for cohesion in fine grains (1, 2). Liquid capillary (3–5) or solid bridges (6) between the grains give rise to cohesion in large grains. In all cases, the cohesion introduces an additional complexity to granular materials—the flows of cohesive grains are intermittent and less homogeneous (7, 8) in comparison with coarse, cohesionless grains, leading to frequent jamming of industrial units. It is, therefore, necessary to a priori characterize and quantify the capability of flow, so-called “flowability,” of a powder to yield better handling. Different methods are used in industrial contexts for this purpose (1, 9–11). A first method measures the tapped bulk density and the freely settled bulk density of a powder to define the Hausner ratio (or Carr index), which is the ratio of the two. A powder with high Hausner ratio is shown to have poor “flowability.” A second one employs a series of measurements, using the Hosokawa powder tester, comprising angle of repose, aerated bulk density, tapped bulk density, etc., to define a weighted “flowability” index, which ranges from 0 to 100. Very cohesive powders yield “flowability” indices close to zero and the free-flowing ones close to 100. Other methods estimate the macroscopic cohesion from the yield loci of a powder using shear testers (Jenike shear tester or ring shear tester) for various preconsolidation normal stresses, which are useful in understanding the arch formation in silos. All these methods, carried out in the quasistatic limit, are useful for comparing the macroscopic properties of different powders and for characterizing their plastic behavior. However, they do not provide any information about the flow dynamics. Understanding the concept of “flowability” from a physical point of view is still a challenge.

The flow dynamics of rigid, cohesionless grains, interacting solely by contact and friction, is less complex in comparison with cohesive grains, as shown by numerous experimental and numerical studies (12). Flow rules have been evidenced and constitutive laws have been proposed for different flow regimes (13, 14). In the dense flow regime, the rheology of the grains of diameter $d$ and density ${\rho }_p$, sheared at a shear rate $\stackrel{.}{\gamma }$ by imposing a shear stress $\tau$ under a confining normal stress ${\sigma }_{zz}$, is well described by a coefficient of friction $\mu \left(I\right)$ and a volume fraction $\varphi \left(I\right)$, which depend on a single dimensionless parameter, the inertial number $I=\stackrel{.}{\gamma }d/\sqrt{{\sigma }_{zz}/{\rho }_p}$ (15, 16). These constitutive relations are found to be unaffected by the mechanical properties of the grains—for example, stiffness and inelasticity—as long as the grains are sufficiently rigid and inelastic (14, 17–19). This rough description of the rheology has proven to be useful in describing flows in different configurations from inclines to silos (20–23). This rheological framework has been extended to the flows of cohesive grains (24–27) by using discrete numerical simulations. Different force models with different levels of realism have been used in the simulations to account for the cohesive interactions between the grains (28, 29). In the simplest approach used in rheological studies (24, 27), the adhesion is characterized by a minimum pull-off force $N_c$ necessary to detach two grains. The existence of this additional force scale implies that a second dimensionless number, called cohesion number $C=N_c/\left({\sigma }_{zz}{d}^2\right)$, exists besides the inertial number, which compares the adhesive force between the grains with the confining normal stress. The rheology is then described by a coefficient of friction $\mu \left(I,C\right)$ and a volume fraction $\varphi \left(I,C\right)$, which are functions of $I$ and $C$ only (24–27, 30).

In this article, we examine the flow dynamics of cohesive grains down a rough inclined plane using intensive discrete numerical simulations to gain physical insights about the “flowability” of powders. The chosen configuration has inhomogeneous stress distributions and, hence, turns out to be very rich to explore the rheology of cohesive granular materials. We perform a detailed parametric study of the flow to reveal that the flow is significantly affected by the stiffness and the inelasticity of the grains, unlike in the case of cohesionless granular media. We introduce the concept of a dynamic “effective” adhesive force to take into account the effect of the material properties, along with the interparticle adhesion, which is shown to control entirely the flow dynamics. We then define an “effective” cohesion number based on this force, which replaces the cohesion number defined above to form a pair of constitutive relations. The rheology is shown to be well described in this framework.

Results

Simulation of the Flow of Cohesive Grains Down a Rough Inclined Plane.

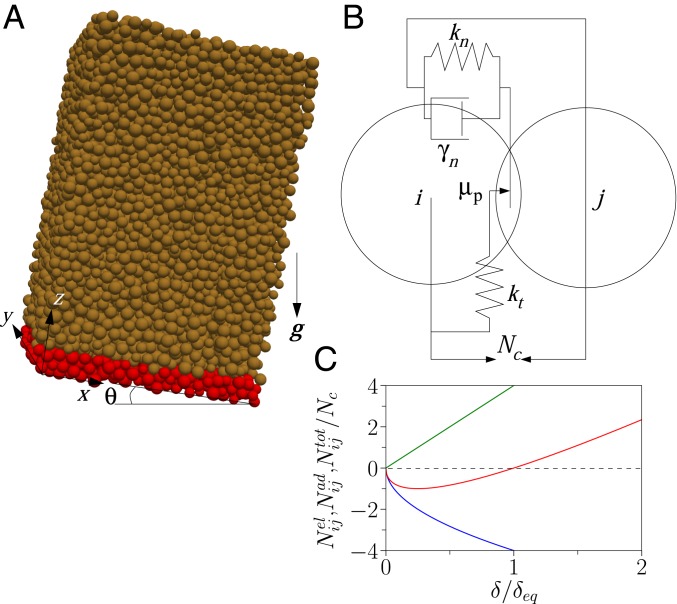
We investigate the flow of frictional, inelastic, cohesive grains down a rough inclined plane (Fig. 1A) using three-dimensional (3D) discrete element method simulations; an in-house code is used, which is validated by comparing the mean velocity and volume fraction profiles of (cohesionless) monodisperse spheres with those in the study of ref. 17. The grains are spherical and have an average size $d$, with a polydispersity of 20% and an average mass $m$. The rough base (shown in red in Fig. 1A) comprises a packed bed of the same grains of height 1.8$d$. The simulation box has length $L_x=20d$, width $L_y=20d$, and height $L_z=40d$. Periodic boundary conditions are applied in the $x$ and $y$ directions. The flow initiates from the collapse of a cubic array of grains under gravity $g$ over the base inclined at a high angle $\theta =45^{○}$ and is continued for a short duration. The flow then attains a steady state after the inclination is lowered and maintained at $\theta \in \left(20^{○},34^{○}\right)$ (the range of angle for a steady flow depends on the interparticle adhesion). The flow is controlled by changing the inclination $\theta$ and four parameters describing the particle properties: the friction coefficient ${\mu }_p$ (kept constant at ${\mu }_p=0.5$ in this study), the stiffness $k_n$, the quality factor $Q$ (a measure of dissipation in an interparticle collision), and the adhesion $N_c$. These parameters are defined below.

Fig. 1.

Simulation of flow of cohesive grains down a rough inclined plane. (A) Snapshot of a simulation, showing the flow of particles (in brown) under gravity $\mathbf{g}$ over a bumpy base (in red) inclined at an angle $\theta$. (B) Depiction of the visco-elastic, frictional, and adhesive interactions between the particles using a spring-dashpot model with a frictional slider and an interparticle adhesion $N_c$. (C) The nonviscous normal contact forces normalized by the interparticle adhesion as a function of the normalized overlap $\delta /{\delta }_{eq}$: elastic part ${\mathit{N}}_{ij}^{el}$ (green), adhesive part ${\mathit{N}}_{ij}^{ad}$ (blue), and the sum of the two ${\mathit{N}}_{ij}^{tot}$= ${\mathit{N}}_{ij}^{el}$+${\mathit{N}}_{ij}^{ad}$ (red). See the main text for ${\delta }_{eq}$.

The interparticle contact forces were computed by using the Hookean spring-dashpot model with a frictional slider (Fig. 1B) and a Johnson–Kendall–Roberts (JKR)-like (31), yet nonhysteretic, adhesive force model (24). The normal contact force (${\mathit{N}}_{ij}$) between particles $i$ and $j$ comprises three forces: 1) elastic force ${\mathit{N}}_{ij}^{el}=-k_n\delta$, where $k_n$ is the normal stiffness and $\delta$ is the normal overlap; 2) viscous force ${\mathit{N}}_{ij}^{vis}=-{\gamma }_n{m}_{eff}{\mathit{c}}_{\mathit{i}\mathit{j}}^{\mathit{n}}$, where ${\mathit{c}}_{\mathit{i}\mathit{j}}^{\mathit{n}}$ is the normal relative velocity, $m_{eff}=m_i{m}_j/\left(m_i+m_j\right)$ is the effective mass, and ${\gamma }_n$ is the normal damping coefficient; and 3) adhesive force ${\mathit{N}}_{ij}^{ad}=\sqrt{4k_n{N}_c\delta }$, which is assumed to be proportional to the area of contact; $N_c$, the minimum pull-off force, is given by the minimum in the plot of the total nonviscous normal force as a function of the normal overlap (red curve) in Fig. 1C. Note that the adhesive interaction model is short-range, meaning that the force vanishes when two grains are not in contact, unlike in wet capillary bridges. The tangential contact force (${\mathit{T}}_{ij}$) comprises only the elastic force ${\mathit{T}}_{ij}^{el}=-k_{t}s$, where $k_t$ ($k_t=2/7k_n$ in this study) is the tangential stiffness, and $s$ is the relative tangential overlap from the beginning of a contact. It is set as ${\mathit{T}}_{ij}={\mu }_p\left({\mathit{N}}_{ij}^{el}+{\mathit{N}}_{ij}^{vis}\right)$, where ${\mu }_p$ is the interparticle friction coefficient, to account for the Coulomb yield criterion. Finally, the total contact force acting on particle $i$ by particle $j$ is ${\mathit{F}}_{ij}$ = ${\mathit{N}}_{ij}\hspace{0.17em}{\mathit{n}}_{ij}$ + ${\mathit{T}}_{ij}\hspace{0.17em}{\mathit{t}}_{ij}$, where ${\mathit{n}}_{ij}$ and ${\mathit{t}}_{ij}$ are normal and tangential unit vectors, respectively. The details of the calculation of viscoelastic forces can be found elsewhere (17). For checking the generality of the results, we also have implemented two other models. One comprises the Hertzian spring-dashpot model and a Derjaguin–Muller–Toporov (DMT)-like adhesive force model (32) (SI Appendix, section SI 1), where the (nonhysteretic) adhesive force is assumed to be independent of the area of contact and is constant. The other one comprises the Hookean spring-dashpot model and a DMT-like, yet hysteretic (SI Appendix, section SI 2), force model, where the grains experience a constant attractive force only during the detachment of a contact, quite similar to a capillary bridge model, but without introducing a finite distance for the detachment.

Using the Hookean-JKR (first) model, the dynamics of two identical ($m_{eff}=m/2$) contacting particles in the absence of any external forces is given by the following equation of a nonlinear damped oscillator:

$$\frac{m}{2}\frac{d^2\delta }{d{t}^2}=-k_n\delta -\frac{m}{2}{\gamma }_n\frac{d\delta }{dt}+\sqrt{4N_c{k}_n\delta }.$$ [1]

In the static limit, the left-hand side and the second term on the right-hand side in Eq. 1 are zero, and the balance between the attractive adhesive force and the repulsive elastic force (Eq. 1) then yields an equilibrium overlap ${\delta }_{eq}=4N_c/k_n$. The quality factor of the oscillator is estimated after linearizing the equation around ${\delta }_{eq}$ as $Q=\sqrt{k_n/m}/{\gamma }_n$; high $Q$ indicates less collisional dissipation. In the cohesionless case, $Q$ is related to the restitution coefficient $e$ as $Q=\sqrt{\left({\pi }^2+{\left(\ln e\right)}^2\right)/\left(8{\left(\ln e\right)}^2\right)}$ (17).

All of the equations are made dimensionless by using $d$ as the length scale, ${\left(d/g\right)}^{1/2}$ as the time scale, and $mg$ as the force scale, and the equations of motion are then solved for each particle by using these interparticle contact forces and gravity. All of the steady-state flow quantities reported below are computed by using the coarse-graining procedure given in SI Appendix, section SI 3.

Not Only the Interparticle Adhesion, but Also the Stiffness and Inelasticity of the Grains Affect the Flow.

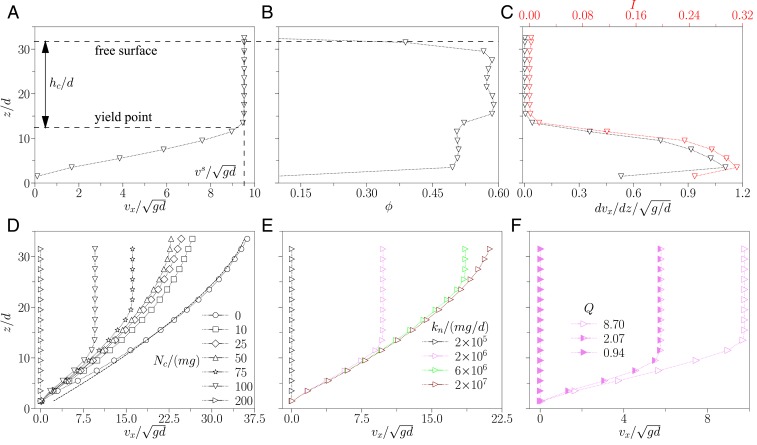
Fig. 2A shows a typical velocity profile for the cohesive grains for an intermediate value of adhesion $N_c/\left(mg\right)=100$ at a given inclination angle $\theta =29^{○}$. Unlike the flow of dry, cohesionless grains down a rough incline, where a Bagnold velocity profile corresponding to shearing throughout the entire pile is noticed (17, 33), a plug appears near the free surface for the cohesive case (25, 34), where the shear rate ($\stackrel{.}{\gamma }=d{v}_x/dz$) is zero (Fig. 2C). The shear rate then gradually increases toward the base (Fig. 2C). The inertial number profile ($I\left(z\right)$) is similar to the shear rate profile (Fig. 2C) and is not uniform over the depth of the pile, unlike in the cohesionless case (17, 33). The volume fraction profile ($\varphi \left(z\right)$) is also not uniform (Fig. 2B) (34) with a highdensity region in the plug, unlike in the cohesionless case (17, 33). The cohesive grains possess a finite yield stress, which is reached at a finite depth in the flowing layer. This, therefore, explains the plug formation near the free surface for the flow of cohesive grains.

Fig. 2.

(A–C) Steady flow profiles: mean velocity ($v_x\left(z\right)$) (A), volume fraction ($\varphi \left(z\right)$) (B), and shear rate ($\stackrel{.}{\gamma }\left(z\right)=d{v}_x/dz\left(z\right)$) and inertial number ($I\left(z\right)$) (C) at $\theta =29^{○}$ for $N_c/\left(mg\right)=100$, $k_n/\left(mg/d\right)=2\times 10^5$, and $Q=8.70$. The free surface velocity ($v^s/{\left(gd\right)}^{1/2}$) and the thickness of plug ($h_c/d$) are denoted in A. (D–F) Effects of different parameters: interparticle adhesion ($N_c$) keeping $k_n/\left(mg/d\right)=2\times 10^5$ and $Q=8.70$ fixed (D), particle stiffness ($k_n$) keeping $N_c/\left(mg\right)=200$ and $Q=8.70$ fixed (E), and quality factor ($Q$) keeping $N_c/\left(mg\right)=200$ and $k_n/\left(mg/d\right)=2\times 10^6$ fixed (F), on the velocity profile at $\theta =29^{○}$. The dashed line in D shows a Bagnold fit.

We now examine the effect of the interparticle adhesion $N_c$ on the velocity profile (Fig. 2D) at a given inclination angle $\theta =29^{○}$. When $N_c$ goes to zero, one recovers the classical Bagnold profile (shown by the fitted dashed line). The Bagnold profile is also observed (fits are not shown for clarity) for small, nonzero values of $N_c$ considered, $N_c/\left(mg\right)=10$, 25, and 50; however, the free-surface velocity decreases in comparison with the cohesionless case with increasing $N_c$. When $N_c/\left(mg\right)$ becomes greater than 50, a plug appears near the free surface, which grows in size with increasing $N_c$ until the flow comes to a halt for $N_c/\left(mg\right)\ge 200$. Such behavior of the velocity profile with increasing $N_c$ has already been reported in some studies (25, 34). More surprising results appear while changing the stiffness of the particles $k_n$ and the dissipation through the quality factor $Q$, as shown in Fig. 2 E and F. The free-surface velocity increases, and the thickness of the plug decreases with increasing the stiffness, keeping other parameters fixed (Fig. 2E). The plug completely disappears for a sufficiently high value of stiffness. A similar observation is made while increasing the quality factor, i.e., decreasing the dissipative nature of contact (Fig. 2F). These observations clearly indicate that the bulk cohesion is not solely controlled by the interparticle adhesion $N_c$ but is dependent on the material properties $k_n$ and $Q$. The sensitivity of the flow to the stiffness and dissipation in the cohesive case contrasts with the flow in the cohesionless case (14, 17–19). This observation has a crucial consequence—the characterization of the degree of bulk cohesion based on the interparticle adhesion using the granular Bond number ($B{o}_g=N_c/mg$) (35, 36) or the cohesion number (24, 25, 28) may not be sufficient. We next attempt to collate the effects of these three independent parameters into a single parameter, the dynamic “effective” adhesion $N_c^{eff}$.

A Scaling for the Dynamic “Effective” Adhesive Force.

We infer from Fig. 2 D–F that decreasing the stiffness or decreasing the quality factor are equivalent to increasing the adhesion. Hence, we seek for an expression of the dynamic “effective” adhesive force as

$$N_c^{eff}=N_c\left[{\left(\frac{N_c}{k_{n}d}\right)}^a\frac{1}{Q^b}\right],$$ [2]

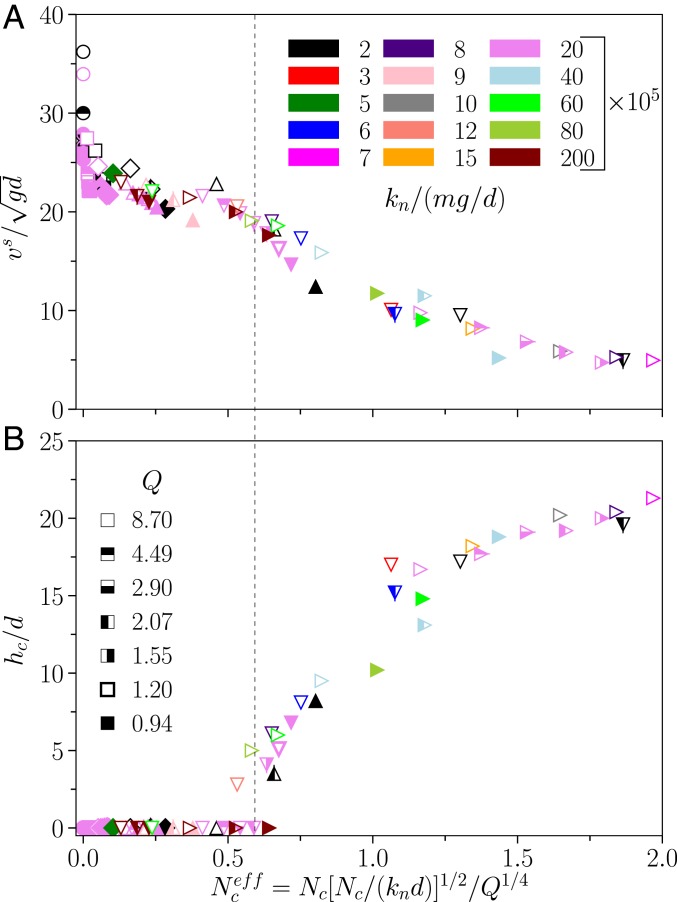
where $a$ and $b$ are unknown constants. The idea behind this scaling is to check if the influence of adhesion, stiffness, and dissipation can be embedded in a single parameter $N_c^{eff}$, acting as an “effective” adhesive force in dynamic conditions. We do the following to test the idea. We systematically carry out simulations by varying $N_c$, $k_n$, and $Q$ (at a fixed inclination $\theta =29^{○}$) and then extract the free-surface velocity $v^s$ and the thickness of the plug $h_c$ from the steady velocity profile in each case. We then plot $v^s$ and $h_c$ separately for all of the simulations as a function of $N_c^{eff}$ computed from Eq. 2 and look for the best collapse of the data in each case by trying out different combinations of $a$ and $b$. For each chosen combination of $a$ and $b$, the two master curves ($v^s\left(N_c^{eff}\right)$ and $h_c\left(N_c^{eff}\right)$) resulting from the data collapses are fitted by power laws (only the data corresponding to velocity profiles with a plug flow are considered), and the quality of the collapses is determined by the determination coefficients $R_{v^s}^2$ and $R_{h_c}^2$ of the fits. The final values of the constants $a=1/2$ and $b=1/4$ are chosen such that they lead to the highest $R_{v^s}^2+R_{h_c}^2$ (SI Appendix, Fig. S3). Finally, two well-defined master curves, $v^s\left(N_c^{eff}\right)$ and $h_c\left(N_c^{eff}\right)$, emerge (Fig. 3), which implies that the flow is indeed controlled by an “effective” adhesive force, which comprises three independent parameters: interparticle adhesion, stiffness, and dissipation. We have checked that two different sets of parameters, corresponding to the same value of $N_c^{eff}$, not only give the same free-surface velocity and plug thickness, but also yield identical velocity, density, and r.m.s. velocity profiles (SI Appendix, Fig. S4). We notice two distinct regions in the figure, separated by a vertical dashed line at $N_c^{eff}/\left(mg\right)\approx 0.6$: 1) a plug-less region on the left, where $v^s$ decreases monotonically with increasing $N_c^{eff}$ and yet $h_c=0$; and 2) a plug-full region where $v^s$ decreases and $h_c$ increases monotonically with increasing $N_c^{eff}$. In order to test the generality of the above result further, we have carried out additional simulations at a given angle ($\theta =29^{○}$) in the same spirit using the Hertzian-DMT model. The sensitivity of the flow to the stiffness and dissipation is recovered, and the velocity profile is again found (SI Appendix, Fig. S5) to be controlled by the dynamic “effective” adhesive force given by a similar equation (SI Appendix, Eq. 4). The origin of the scaling will be discussed in the last section. We also perform some simulations using the hysteretic contact model. We again find the flow dynamics (at a given angle) to be dependent on the stiffness (SI Appendix, Fig. S6), signifying that in this case as well, the contact parameters, along with the interparticle adhesion, determine the bulk cohesion. We examine below if this dynamic “effective” adhesive force is relevant in the description of the rheology.

Fig. 3.

The flow is controlled by the dynamic “effective” adhesive force. Variation of the free surface velocity ($v^s/{\left(gd\right)}^{1/2}$) (A) and the thickness of the plug ($h_c/d$) (B) with the dynamic “effective” adhesive force $N_c^{eff}$ at $\theta =29^{○}$ for different $N_c$ (different symbols; see Fig. 2 for the key), different $k_n$ (different colors), and different $Q$ (different symbol pattern). The dashed line indicates the transition from a plug-less to a plug-full velocity profile.

Flow Cessation Is Controlled by the “Effective” Adhesive Force, but Flow Initiation Is Controlled by the “Actual” Adhesive Force.

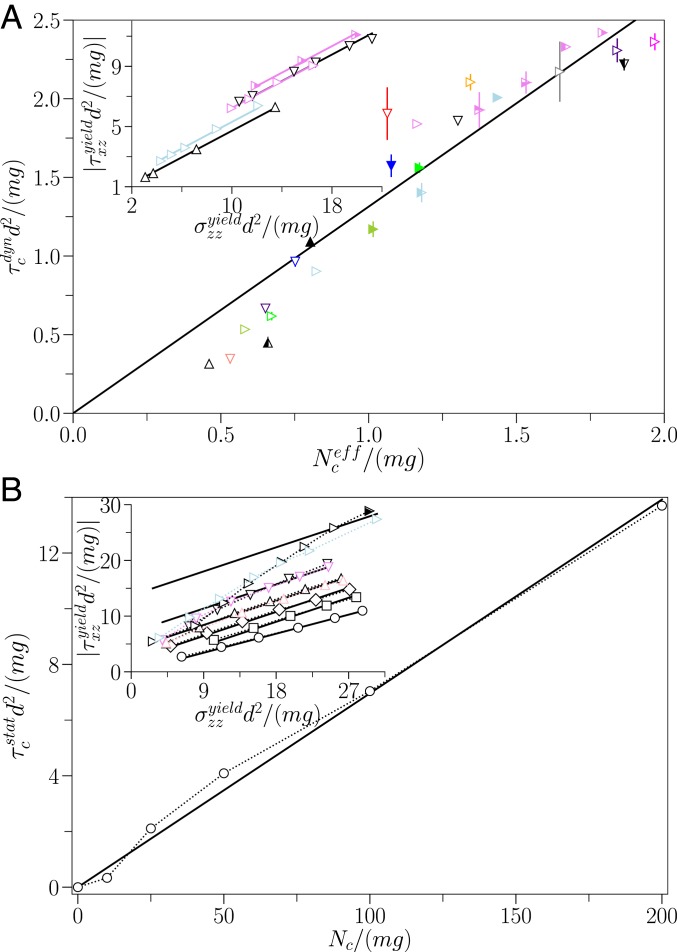
A first step toward exploring the rheology is to study the yield criteria of our model cohesive material, i.e., to study the stress conditions under which the flow stops (dynamic yielding) or starts (static yielding). The yield criteria are usually described by using a cohesive Mohr–Coulomb model stipulating that, on the plane of incipient failure, the shear stress ${\tau }_{xz}^{yield}$ is related to the normal stress ${\sigma }_{zz}^{yield}$ by ${\tau }_{xz}^{yield}={\tau }_c^{stat,dyn}+{\mu }_s^{stat,dyn}{\sigma }_{zz}^{yield}$, where ${\mu }_s^{stat,dyn}$ is the static (respectively [resp.] dynamic) friction coefficient, and ${\tau }_c^{stat,dyn}$ is the static (resp. dynamic) cohesive stress. We first focus on the dynamic yielding by considering the data of the velocity profiles in the previous section. The dynamic yield criterion is satisfied at the intersection of the plug and sheared regions, denoted by “yield point” in Fig. 2A. The location of the “yield point” shifts with changing the inclination angle. Thus, a yield locus for a given set of particle properties ($N_c$, $k_n$, and $Q$) is obtained by noting a series of points (${\tau }_{xz}^{yield}$ and ${\sigma }_{zz}^{yield}$), each corresponding to a “yield point” at a given angle. Fig. 4 A, Inset shows different yield loci (shown by symbols; only a few are shown for clarity) for different sets of particle properties. All of the yield loci are well approximated by straight lines, which are the best fits of the Mohr–Coulomb model. The slope of each straight line gives the dynamic friction coefficient ${\mu }^{dyn}$ and the intercept with the y axis, the dynamic cohesive stress ${\tau }_c^{dyn}$. We have systematically extracted ${\mu }_s^{dyn}$ and ${\tau }_c^{dyn}$ for all of the cases mentioned in Fig. 3. The dynamic friction coefficient ${\mu }_s^{dyn}\approx 0.44$ is found to be constant and to be independent of the particle properties. On the other hand, the dynamic cohesive stress ${\tau }_c^{dyn}$ increases with increasing $N_c$ and decreasing $k_n$ or $Q$. However, they all collapse on a single master curve if plotted against the “effective” adhesion $N_c^{eff}$ (Fig. 4A), showing again that $N_c^{eff}$ is the only variable controlling the dynamic yielding. A linear fit through the data gives

$${\tau }_c^{dyn}\approx 1.31N_c^{eff}/d^2.$$ [3]

We next study the static yielding from the initiation of the flow. We initially bring a steady flow of a given pile thickness $H$ to a halt by gradually lowering the inclination angle. We then gradually increase the inclination by a step of 0.${\mathrm{2}}^{○}$ (a steady state in the kinetic energy profile is ensured after each increment) until the flow starts (indicated by a threshold of kinetic energy $\mathcal{O}\left(10^{-1}\right)$). We finally note the stresses (${\tau }_{xz}^{yield}$ and ${\sigma }_{zz}^{yield}$) at the bottom of the pile, where the yielding happens. The procedure is repeated by varying the initial pile thickness to get a series of points (${\tau }_{xz}^{yield}$ and ${\sigma }_{zz}^{yield}$), which constitutes the yield locus for a given set of particle properties ($N_c$, $k_n$, $Q$). Fig. 4 B, Inset shows different yield loci (shown by symbols) for different sets of particle properties. The striking observation is that two yield loci for two different $k_n$ for a given $N_c$ and $Q$ collapse well on each other. A similar observation is made for two different $Q$ for a given $N_c$ and $k_n$ (only one point is shown). This result implies that the flow initiation is entirely controlled by the interparticle adhesion, which contrasts with the observation made above that the flow cessation is controlled by the dynamic “effective” adhesion. A careful inspection reveals that the static yield loci are not perfectly linear, especially for high values of $N_c$, which have tails comprising data points at low values of the normal stress. However, at sufficiently high values of the normal stress (corresponding to thick piles), one recovers a linear variation of the shear stress with the normal stress, as expected from the Mohr–Coulomb model. Hence, we restrict the fitting of the model (shown by the straight lines) to the linear parts of the yield loci; for a given $N_c$, the combined datasets corresponding to different $k_n$ and $Q$ are considered during fitting. The fitting yields static friction coefficients (estimated by the slopes of the straight lines): ${\mu }_s^{stat}\approx 0.38$ for $N_c=0$ and ${\mu }_s^{stat}\approx 0.48$ for the others. Note that ${\mu }_s^{stat}$ is slightly higher than ${\mu }_s^{dyn}$. We also obtain the static cohesive stress ${\tau }_c^{stat}$ from the intercept of the straight line in each case, which is shown as a function of the interparticle adhesion $N_c$ in Fig. 4B. The variation of ${\tau }_c^{stat}$ with $N_c$ is well approximated by

$${\tau }_c^{stat}\approx 0.07N_c/d^2.$$ [4]

Different studies (4, 37, 38) have predicted theoretically such a linear relation between the static cohesive stress and the adhesion as

$${\tau }_c^{stat}=\frac{3{\mu }_s^{stat}\varphi Z{N}_c}{2\pi d^2},$$ [5]

where $Z$ is the average coordination number (number of contacts per particle). The contact network was assumed to be isotropic in the derivation. Using measured $Z=6$ and $\varphi =0.55$ and extracted ${\mu }_s^{stat}=0.48$, Eq. 5 yields ${\tau }_c^{stat}\approx 0.76N_c/d^2$, with a proportionality constant of 0.76, which is a decade higher in comparison with that (0.07) extracted from the fitting. Anisotropy in the contact network in the present study may lead to this mismatch. A similar mismatch has been reported by Rognon et al. (25) for flows down inclines. The last noteworthy point, which can be inferred from Fig. 4, is that the maximum dynamic cohesive stress ${\tau }_c^{dyn}$ observed is smaller than the static cohesive stress ${\tau }_c^{stat}$ for a given adhesion.

Fig. 4.

Dynamic and static yield criteria. (A, Inset) Yield shear stress (${\tau }_{xz}^{yield}{d}^2/\left(mg\right)$) as a function of yield normal stress (${\sigma }_{zz}^{yield}{d}^2/\left(mg\right)$) for the dynamic yielding in different cases. The keys are the same as in Figs. 2 and 3. The lines are the fits of the Mohr–Coulomb failure equation. In the main plot, the variation of the dynamic macroscopic cohesive stress (${\tau }_c^{dyn}{d}^2/\left(mg\right)$) with the “effective” adhesive force $N_c^{eff}/mg$ for all of the cases. The straight line is the best fit to the data. (B, Inset) Yield shear stress (${\tau }_{xz}^{yield}{d}^2/\left(mg\right)$) as a function of yield normal stress (${\sigma }_{zz}^{yield}{d}^2/\left(mg\right)$) for the static yielding in different cases. The dotted lines are the guides to the eye, and the solid lines are the fits of the Mohr–Coulomb failure equation in the linear part of the data. The main plot shows variation of the static macroscopic cohesive stress (${\tau }_c^{stat}{d}^2/\left(mg\right)$) with the actual adhesive force $N_c/\left(mg\right)$. The dotted line is a guide to the eye, and the straight line is the best fit to the data.

Bulk Rheology Is Described by an “Effective” Cohesion Number.

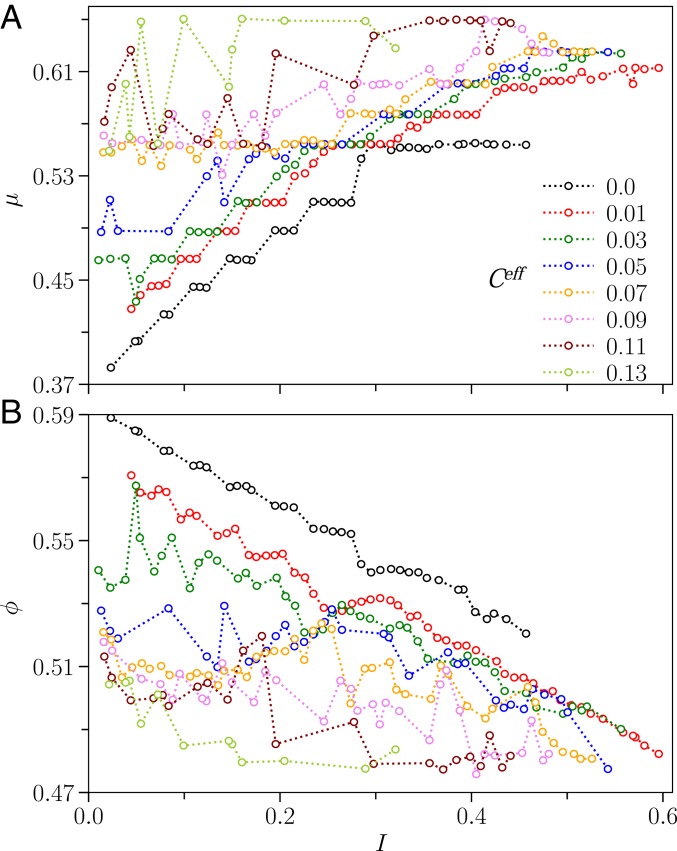
The last step toward exploring the rheology is to go beyond the yield criteria and analyze how the shear stress varies with the shear rate. The inclined plane configuration serves as a rheometer to enable us to measure the local shear rate $\stackrel{.}{\gamma }=d{v}_x/dz$, shear stress ${\tau }_{xz}$, normal stress ${\sigma }_{zz}$, and volume fraction $\varphi$ at every vertical position in the flow. Rognon and coworkers (24–26) proposed the following $\mu \left(I\right)$-rheology framework: $\mu =\mu \left(I,C\right)$ and $\varphi =\varphi \left(I,C\right)$, for describing the rheology of cohesive grains, as mentioned in the introduction. However, the results obtained in the previous sections suggest that the above framework is not sufficient for the complete description of the rheology. The observation that the “effective” adhesion $N_c^{eff}$, not the interparticle adhesion $N_c$, controls the flow dynamics, prompts to define a new cohesion number, the “effective” cohesion number $C^{eff}=N_c^{eff}/\left({\sigma }_{zz}{d}^2\right)$. One can then test if the rheology can be described by using the new framework: $\mu =\mu \left(I,C^{eff}\right)$ and $\varphi =\varphi \left(I,C^{eff}\right)$. We do the following to test the idea. We compute local $\mu ={\tau }_{xz}/{\sigma }_{zz}$, $I$, and $C^{eff}$ for all of the simulations done for different ($k_n$, $Q$, and $N_c$) and at different angles $\theta$. Recent studies (39–41) have emphasized the occurrence of nonlocal effects in inhomogeneous flows, such as the one investigated here. For each simulation, we try to minimize this effect on the analysis by neglecting the data points (for which $I<0.01$) adjacent to the “yield point,” where the effect is significant. We also discard six data points each adjacent to the free surface and the rough base to avoid boundary effects. We consider the rest and combine them for all of the simulations. The combined dataset ($C^{eff}$, $I$, $\mu$, and $\varphi$) is then divided into eight subsets based on the value of $C^{eff}$ (a bin size of 0.02 is chosen). For each subset, $\mu$, $\varphi$, and $I$ are then averaged in small bins of size 0.01 in $I$. Fig. 5 shows the variation of $\mu$ and $\varphi$ with $I$ for the eight different values of $C^{eff}$. The first important observation is that the datasets are reasonably well sorted according to the value of $C^{eff}$, which indicates that the rheology is entirely controlled by two dimensionless numbers, $I$ and $C^{eff}$, validating our model. The $\mu \left(I\right)$ curve (Fig. 5A) shifts upward with increasing $C^{eff}$, showing that $\mu$ increases with increasing $C^{eff}$, particularly for small values of $I$. Substituting ${\tau }_c^{dyn}$ given in Eq. 3 into the Mohr–Coulomb model and using the definition of $\mu$ and $C^{eff}$, we show that $\mu$ increases linearly with increasing $C^{eff}$ in the quasistatic limit ($I\to 0$), following $\mu \left(0,C^{eff}\right)\approx {\mu }_s^{dyn}+1.31C^{eff}$. However, the curves surprisingly seem to merge in the high-$I$ regime, indicating less impact of adhesion on the value of $\mu$. $\mu$ appears to be independent of $I$ for sufficiently high values of $C^{eff}$. The $\varphi \left(I\right)$ curve (Fig. 5B) shifts downward with increasing $C^{eff}$, showing that the volume fraction $\varphi$ decreases with increasing $C^{eff}$. A nonmonotonic behavior of $\varphi \left(I\right)$ appears for intermediate values of $C^{eff}$—the volume fraction first decreases and then increases with increasing inertial number before decreasing again at high values. $\varphi$ also appears to be independent of $I$ for sufficiently high values of $C^{eff}$. Berger et al. (27) observed similar behavior of the effective friction and volume fraction with the inertial and cohesion numbers and proposed an empirical function to capture the rheology (SI Appendix, section SI 8). The same function provides a reasonable fit of our data, as shown in SI Appendix, Fig. S7.

Fig. 5.

Constitutive laws for the flow of cohesive granular media. Variation of the effective friction ($\mu$) (A) and the volume fraction ($\varphi$) (B) with the inertial number ($I$) for different values of the “effective” cohesion number ($C^{eff}$). The assembled data are obtained by varying $\theta \in \left(20^{○},34^{○}\right)$, $N_c/\left(mg\right)\in \left(\mathrm{0,200}\right)$, $k_n/\left(mg/d\right)\in \left(2\times 10^5,2\times 10^7\right)$, and $Q\in \left(0.94,8.70\right)$.

Discussion and Conclusion

In this work, we have examined the flow of cohesive grains down an inclined plane using discrete element method simulations. We use a simplified adhesive interaction law, characterized by a minimum pull-off force $N_c$ necessary to detach two grains, to model the interparticle adhesion. Despite this simple interaction model, a rich flow dynamics appears—the cohesive nature of the flow becomes sensitive to the stiffness $k_n$ and inelasticity of the grains $1/Q$ besides the interparticle adhesion $N_c$, which contrasts with the flow of cohesionless granular media. Although this sensitivity has never been reported for the flows down inclines, a few studies on the fluidization of cohesive powders observed it (42–44). This finding questions the use of granular Bond number or cohesion number (based on the interparticle adhesion) in quantifying the degree of bulk cohesion. We have demonstrated a way to take into account the effects of these parameters, along with the interparticle adhesion into a single parameter called the dynamic “effective” adhesion. This force appears to control the flow dynamics solely and comes out to be $N_c^{eff}=N_c{\left[N_c/\left(k_{n}d\right)\right]}^{1/2}/Q^{1/4}$ for the Hookean-JKR model and $N_c^{eff}=N_c{\left[N_c/\left(k_n{d}^{3/2}\right)\right]}^{1/3}/Q^{3/4}$ for the Hertzian-DMT model; the success of obtaining a single control variable eases the problem from rheological perspectives. One can note from the above equations that increasing $N_c$ and decreasing $k_n$ or $Q$ increases the “effective” adhesion. Interestingly, the scalings obtained in both the cases can be recast by using the equilibrium overlap ${\delta }_{eq}$ in the following form: $N_c^{eff}\propto N_c{\left({\delta }_{eq}/d\right)}^{1/2}/Q^b$, where ${\delta }_{eq}=4N_c/k_n$ for the Hookean-JKR model and ${\delta }_{eq}={\left(N_c/k_n\right)}^{2/3}$ for the Hertzian-DMT model.

We have not succeeded in understanding the scaling. However, the existence of an interplay between the interparticle adhesion and the mechanical properties of the grains can be evidenced, considering the dynamics of a binary collision. When two cohesive grains collide, one can show that they remain glued together if the relative kinetic energy before impact is less than a critical value (SI Appendix, section SI 9) given by $E_c=N_c{\delta }_{eq}G\left(Q\right)$, where $G\left(Q\right)$ is a decreasing function of the quality factor, which depends on the interaction model. This shows that not only the adhesion, but also the mechanical properties of the grains influence a collision: The chance of a rebound is less if $N_c$ is large and also if $k_n$ ($\propto 1/{\delta }_{eq}$) or $Q$ is small. To determine the “effective” adhesive force $N_c^{eff}$, one may estimate the typical kinetic energy involved in a collision in a flow under a shear stress $\tau =N_c^{eff}/d^2$ (45) and compare it to the critical value $E_c$—a work which we aim to do in the near future.

We have shown that the initiation of the flow is controlled by a static cohesive stress proportional to $N_c$, whereas the arrest of the flow, by a dynamic cohesive stress proportional to $N_c^{eff}$. The maximum dynamic cohesive stress observed is smaller than the static cohesive stress for a given interparticle adhesion. This implies that the characterization and quantification of the “flowability” made at the quasistatic limit may not be appropriate for the dynamic limit. Although we have not been able to understand the scaling of dynamic “effective” adhesive force, we have shown that the “effective” cohesion number based on this empirical force and the inertial number yield two constitutive relations: $\mu =\mu \left(I,C^{eff}\right)$ and $\varphi =\varphi \left(I,C^{eff}\right)$, which give a reasonably good description of the rheology. The determination of the exact forms of these two relations is beyond the scope of this work and requires a separate study, possibly using a plane shear flow. In SI Appendix, Fig. S8, we present some preliminary rheological data obtained in a normal stress-imposed shear cell (see SI Appendix, section SI 10 for simulation details). The data of $\mu$ and $\varphi$ for two different sets ($N_c$ and $k_n$) for a given $Q$, yielding the same $C^{eff}$, collapse well on each other and also match reasonably the data from the inclined plane flow (SI Appendix, Fig. S8), showing the generality of the proposed description.

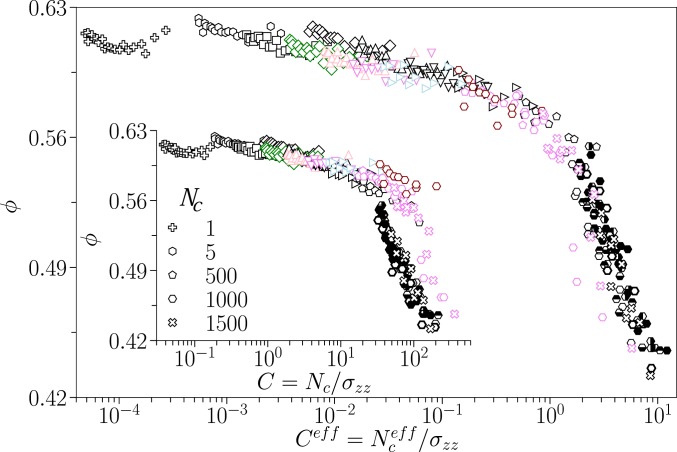
The relevance of the “effective” cohesion number in defining the flow dynamics opens perspectives to analyze the behavior of cohesive granular media in other configurations, and we give one example below. We carry out additional simulations to measure the packing fraction in a pile of cohesive grains for various ($N_c$, $k_n$, and $Q$). The grains are poured randomly under gravity in the same periodic box ($\theta =0$) as used above, and the measurements are taken once all of the grains settle down. Since the packing fraction $\varphi$ and the “effective” cohesion number $C^{eff}=N_c^{eff}/\left({\sigma }_{zz}{d}^2\right)$ vary along the height of the pile, we obtain a series of points ($C^{eff}$ and $\varphi$) from each simulation. Fig. 6 shows the variation of $\varphi$ with $C^{eff}$ for all of the simulations, neglecting the data points adjacent to the rough base and the free surface. We obtain a good collapse of the data, resulting in a master curve. However, this is not valid if the cohesion number $C$ based on the actual adhesion is considered instead (Fig. 6, Inset). More configurations need to be studied to be able to understand to which extent this concept of “effective” cohesion number is valid for the flow of cohesive grains, which might help in developing new approaches for the characterization of powders.

Fig. 6.

A validity check for the “effective” cohesion number. Variation of the volume fraction ($\varphi$) with the “effective” cohesion number ($C^{eff}$) in the case of gravity-driven compaction is shown. See Figs. 2 and 3 for additional legends. (Inset) Variation of the volume fraction ($\varphi$) with the cohesion number ($C$).

Although the concept of “effective” adhesion is based on a simplified model of adhesion, we find that it is generic for other kinds of adhesive interactions; for example, (hysteretic) capillary and electrostatic adhesion. In these cases, the particles experience an attractive force, even without a physical contact over a small separation distance, and this distance plays an equivalent role of the stiffness and influence the “effective” adhesion. The bulk cohesion, in studies (26, 46) using capillary bridge models, was noted to decrease when decreasing this separation distance (named as the “rupture distance,” beyond which a capillary bridge breaks). This outcome can be understood considering the argument of energy proposed above—the work needed to separate two bonded grains, in this case, is proportional to the rupture distance.

One last remark concerns the limit of rigid particles. The scaling reported above suggests that the “effective” adhesion will go to zero in the rigid limit, implying that a direct comparison of our results with those using contact dynamics simulations (27), in which the grains are treated as perfectly rigid, is difficult. We speculate that, in these simulations, the size of the time step could be crucial and could play a role similar to the stiffness in our soft-particle approach.

The main idea conveyed in this article that the “effective” adhesion is not controlled solely by the interparticle adhesion, but also dependent on material properties is a first step toward a better understanding of the flow of cohesive granular media, which may benefit engineering and geophysical communities to understand the long-standing issue of “flowability” of cohesive powders.

All data presented in this article are openly available in the Zenodo repository, https://zenodo.org/record/3699632#.XmJ048tKgaw.