Partially latent class models for case–control studies of childhood pneumonia aetiology

summary

In population studies on the aetiology of disease, one goal is the estimation of the fraction of cases that are attributable to each of several causes. For example, pneumonia is a clinical diagnosis of lung infection that may be caused by viral, bacterial, fungal or other pathogens. The study of pneumonia aetiology is challenging because directly sampling from the lung to identify the aetiologic pathogen is not standard clinical practice in most settings. Instead, measurements from multiple peripheral specimens are made. The paper introduces the statistical methodology designed for estimating the population aetiology distribution and the individual aetiology probabilities in the Pneumonia Etiology Research for Child Health study of 9500 children for seven sites around the world. We formulate the scientific problem in statistical terms as estimating the mixing weights and latent class indicators under a partially latent class model (PLCM) that combines heterogeneous measurements with different error rates obtained from a case–control study. We introduce the PLCM as an extension of the latent class model. We also introduce graphical displays of the population data and inferred latent class frequencies. The methods are tested with simulated data, and then applied to Pneumonia Etiology Research for Child Health data. The paper closes with a brief description of extensions of the PLCM to the regression setting and to the case where conditional independence between the measures is relaxed.

1. Introduction

Identifying the pathogens that are responsible for infectious diseases in a population poses significant statistical challenges. Consider the measurement problem in the Pneumonia Etiology Research for Child Health (PERCH) study, which is a case–control study that has enrolled 9500 children from seven sites around the world. Pneumonia is a clinical syndrome that develops because of an infection of the lung tissue by bacteria, viruses, mycobacteria or fungi (Levine et al., 2012). The appropriate treatment and public health control measures vary by pathogen. Which pathogen is infecting the lung usually cannot be directly observed and must therefore be inferred from multiple peripheral measurements with differing error rates. The primary goals of the PERCH study are to integrate the multiple sources of data

1. to attribute a particular case's lung infection to a pathogen and

2. to estimate the prevalences of the aetiologic pathogens in a population of children that met clinical pneumonia definitions.

The basic statistical framework of the problem is pictured in Fig. 1. The disease status is determined by clinical examination including chest X‐ray (Deloria‐Knoll et al., 2012). The known pneumonia status (case–control) is directly caused by the presence or absence of a pathogen‐caused infection in the lung. For controls, the lung is known to be sterile and has no infection. For a child who has been clinically diagnosed with pneumonia, the pathogen causing the infection in the child's lung is the scientific target of interest. Among the candidate pathogens being tested, we assume that only one is the primary cause. Extensions to multiple pathogens are straightforward. Because, for most cases, it is not possible to sample the lung directly, we do not know with certainty which pathogen infected the lung, so we seek to infer the infection status on the basis of a series of laboratory measurements of specimens from various body fluids and body sources.

Figure 1.

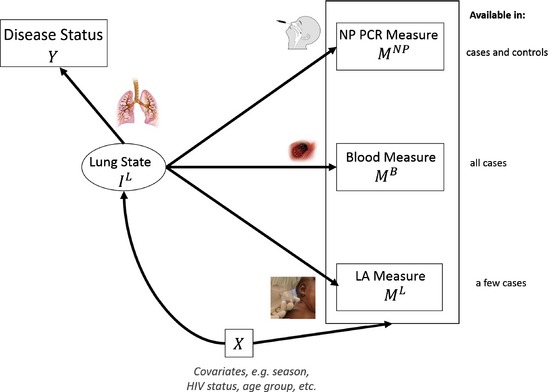
Directed acyclic graph illustrating relationships between lung infection state $I^L$, imperfect laboratory measurements on the presence or absence of each of a list of pathogens at each site $M^{\mathsf{NP}}$, $M^{\mathsf{B}}$ and $M^{\mathsf{L}}$, disease outcome Y and covariates X

The PERCH study was originally designed with three sources of measurements that are relevant to the lung infection: directly from the lung by lung aspirate, from blood culture and from the nasopharyngeal cavity (by swab). Therefore, our model was designed to accommodate all three sources. As the study progressed, less than 1% of cases had direct lung measurements and this sampled group was unrepresentative of all cases. The model, and accompanying software, includes all three sources of measurements for application to other aetiology studies, but the analysis of the motivating PERCH data below uses only blood culture and nasopharyngeal swab data.

The measurement error rates differ by type of measurement. Here, an error rate or epidemiologic error rate is the probability of the pathogen's presence or absence in a specimen test given the presence or absence of infection in the lung. For this application, it is convenient to categorize measures into three subgroups referred to as ‘gold’, ‘silver’ and ‘bronze’ standard measurements. A gold standard (GS) measurement is assumed to have both perfect sensitivity and perfect specificity. Lung aspirate data would have been GS. A silver standard (SS) measurement is assumed to have perfect specificity, but imperfect sensitivity. Culturing bacteria from blood samples (‘B‐cX’) is an example of SS measurements in the PERCH study. Finally, bronze standard (BS) measurements are assumed to have imperfect sensitivity and imperfect specificity. Polymerase chain reaction evaluation of bacteria and viruses from nasopharyngeal samples is an example.

In the PERCH study, both SS and BS measurements are available for all cases. BS, but not SS, measures are available for controls. Our goal was to develop a statistical model that combines GS and SS measurements from cases, with BS data from cases and controls to estimate the distribution of pathogens in the population of pneumonia cases, and the conditional probability that each of the J pathogens is the primary cause of an individual child's pneumonia given her or his set of measurements. Even in applications where GS data are not available, a flexible modelling framework that can accommodate GS data is useful for both the evaluation of statistical information from BS data (Section 3) and the incorporation of GS data if they become available as measurement technology improves.

Latent class models (LCMs) (Goodman, 1974) have been successfully used to integrate multiple diagnostic tests or raters' assessments to estimate a binary latent status for all study subjects (Hui and Walter, 1980; Qu and Hadgu, 1998; Albert et al., 2001; Albert and Dodd, 2008). In the LCM framework, conditional distributions of measurements given latent status are specified. Then the marginal likelihoods of the multivariate measurements are maximized as a function of the disease prevalence, sensitivities and specificities. This framework has also been extended to infer ordinal latent status (Wang et al., 2011).

There are three salient features of the PERCH childhood pneumonia problem that require extension of the typical LCM approach. First, we have partial knowledge of the latent lung state for some subjects as a result of the case–control design. In the standard LCM approach, the study population comprises subjects with completely unknown class membership. In this study, controls are known to have no pathogen infecting the lung. Also, if GS measurements were available from the lung for some cases, their latent variable would be directly observed. As the latent state is known for a non‐trivial subset of the study population, we refer to this model as a partially latent class model (PLCM).

Second, in most LCM applications, the number of observed measurements on a subject is much larger than the number of latent state categories. Here, the number of observations is of the same order as the number of categories that the latent status can assume. For example, if we consider only the PERCH study BS data, we simultaneously observe the presence or absence of each member from a list of possible pathogens for each child. Even with additional control data, the larger number of latent categories of latent status leads to weak model identifiability as is discussed in more detail in Section 2.1

Lastly, measurements with differing error rates (i.e. GS, SS and BS) need to be integrated. Note that the modelling framework that is introduced here is general and can be applied to studies where multiple BS measurements are available, each with a different set of error rates. Understanding the relative value of each level of measurements is important to invest resources into data collection (number of subjects, type of samples) and laboratory assays optimally. An important goal is therefore to estimate the relative information from each type of measurements about the population and individual aetiology distributions.

Albert and Dodd (2008) studied a model where some subjects are selected to verify their latent status (i.e. collect GS measurements) with the probability of verification either depending on the previous test results or being completely at random. They showed that GS data can make model estimates more robust to model misspecifications. We further quantify how much GS data would reduce the variance of model parameter estimates for design purposes. Also, they considered binary latent status and did not have available control data. Another related literature that uses both GS and BS data is on verbal autopsy in the setting where no complete vital registry system has been established in the community (King and Lu, 2008). Quite similar to the goal of inferring pneumonia aetiology from laboratory measurements, the goal of verbal autopsy is to infer the cause of death from a prespecified list by asking close family members questions about the presence or absence of several symptoms. King and Lu (2008) proposed to estimate the cause‐of‐death distribution in a community by using data on dichotomous symptoms and GS data from the hospital where the cause of death and symptoms are both recorded. However, their method involves non‐parametric models and requires a sizable sample of GS data, especially when the number of symptoms is large. In addition, a key difference between verbal autopsy and most infectious disease aetiology studies is that the verbal autopsy studies are by definition case only.

Another approach that has previously been used with case and control data is to perform logistic regression of case status on laboratory measurements and then to calculate point estimates of population attributable risks for each pathogen (Bruzzi et al., 1985; Blackwelder et al., 2012). This method does not account for imperfect laboratory measurements and cannot use GS or SS data if available. Also, the population attributable fraction method assigns zero aetiology for the subset of pathogens that have estimated odds ratios that are smaller than 1, without taking account of the statistical uncertainty for the odds ratio estimates.

In this paper, we define and apply a PLCM to incorporate these three features: known infection status for controls, a large number of latent classes and multiple types of measurement. We use a hierarchical Bayesian formulation to estimate

1. the population aetiology distribution or aetiology fraction (the frequency with which each pathogen ‘causes’ clinical pneumonia in the case population) and

2. the individual aetiology probabilities (the probabilities that a case is ‘caused’ by each of the candidate pathogens, given observed specimen measurements for that individual).

In Section 4, to facilitate communications with scientists, we introduce graphical displays that put data, model assumptions and results together. They enable the scientific investigators to understand better the various sources of evidence from data and their contribution to the final aetiology estimates.

The remainder of this paper proceeds as follows. In Section 2, we formulate the PLCM and the Gibbs sampling algorithms for implementation. In Section 3, we evaluate our method through simulations tailored for the childhood pneumonia aetiology study. Section 4 presents the analysis of PERCH data. Lastly, Section 5 concludes with a discussion of results and limitations and a few natural extensions of the PLCM also motivated by the PERCH data, as well as future directions of research.

The R package implementing the methods proposed in this paper is available from https://github.com/zhenkewu/nplcm.

2. A partially latent class model for multiple indirect measurements

We develop a PLCM to address two characteristics of the motivating pneumonia problem:

1. a partially latent state variable because the pathogen infection status is known for controls but not cases and

2. multiple categories of measurements with different error rates across classes.

As shown in Fig. 1, let $I_i^L$, taking values in {0,1,2,…,J}, represent the true state of child i's lung (i=1,…,N) where 0 represents no infection (control) and $I_i^L=j,j=1,\dots ,J$, represents the jth pathogen from a prespecified cause‐of‐pneumonia list that is assumed to be exhaustive. $I_i^L$ is the scientific target of inference for individual diagnosis. Let ${\mathbf{M}}_i^S$ represent the J×1 vector of binary indicators of the presence or absence of each pathogen in the measurement at site S, where, in our childhood pneumonia aetiology study, S can be nasopharyngeal, blood or lung. Let ${\mathbf{m}}_i^S$ be the actual observed values. In what follows, we replace S with BS, SS or GS, because they correspond to the measurement types nasopharyngeal, blood and lung respectively.

Let $Y_i=y_i\in \{0,1\}$ represent the indicator of whether child i is a healthy control or a clinically diagnosed case. Note that $I_i^L=0$ given $Y_i=0$. To formalize the PLCM, we define three sets of parameters:

1. $\mathit{\pi }={({\mathit{\pi }}_1,\dots ,{\mathit{\pi }}_J)}^{\prime }$, the vector of compositional probabilities for each of J pathogen causes, i.e. $\text{Pr}(I_i^L=j|Y_i=1,\mathit{\pi }),j=1,\dots ,J$;

2. ${\mathit{\psi }}_j^S=\text{Pr}(M_{ij}^S=1|I_i^L=0)$, the false positive rate (FPR) for measurement j (j=1,…,J) at site S (note that the FPRs ${\{{\mathit{\psi }}_j^S\}}_{j=1}^J$ can be estimated from the control data at site S, because $I_i^L=0$ denotes that the ith subject has no infection in the lung, i.e. a control);

3. ${\mathit{\theta }}_j^S=\text{Pr}(M_{ij}^S=1|I_i^L=j)$, the true positive rate (TPR) for measurement j at site S for a person whose lung is infected by pathogen j,j=1,…,J.

We further let ${\mathit{\psi }}^S={({\mathit{\psi }}_1^S,\dots ,{\mathit{\psi }}_J^S)}^{\prime }$ and ${\mathit{\theta }}^S={({\mathit{\theta }}_1^S,\dots ,{\mathit{\theta }}_J^S)}^{\prime }$. Using these definitions, we have FPR ${\mathit{\psi }}_j^{\mathrm{GS}}=0$ and TPR ${\mathit{\theta }}_j^{\mathrm{GS}}=1$ for GS measurements, so $M_{ij}^{\mathrm{GS}}=1$ if and only if $I_i^L=j,j=1,\dots ,J$ (perfect sensitivity and specificity). For SS measurements, the FPR ${\mathit{\psi }}_j^{\mathrm{SS}}=0$ so $M_j^{\mathrm{SS}}=0$ if $I_i^L\ne j$ (perfect specificity).

We formalize the model likelihood for each type of measurement. We first describe the model for BS measurement ${\mathbf{M}}^{\mathrm{BS}}$ for a control or a case. For control i, positive detection of the jth pathogen is a false positive representation of the non‐infected lung. Therefore, we assume that $M_{ij}^{\mathrm{BS}}|{\mathit{\psi }}^{\mathrm{BS}}\sim \text{Bernoulli}({\mathit{\psi }}_j^S),j=1,\dots ,J$, with conditional independence, or equivalently

$$P_i^{0,\mathrm{BS}}=\text{Pr}({\mathbf{M}}_i^{\mathrm{BS}}=\mathbf{m}|{\mathit{\psi }}^{\mathrm{BS}})=\prod _{j=1}^J.5pt{({\mathit{\psi }}_j^{\mathrm{BS}})}^{m_j}{(1-{\mathit{\psi }}_j^{\mathrm{BS}})}^{1-m_j},$$ (1)

where $\mathbf{m}={\mathbf{m}}_i^{\mathrm{BS}}$. For a case infected by pathogen j, the positive detection rate for the jth pathogen in BS assays is ${\mathit{\theta }}_j^{\mathrm{BS}}$. Since we assume a single cause for each case, detection of pathogens other than j will be false positive results with probability equal to the FPR as in the controls: ${\mathit{\psi }}_l^{\mathrm{BS}}$, l≠j. This non‐differential misclassification across the case and control populations is the essential assumption of the latent class approach because it allows us to borrow information from control BS data to distinguish the true cause from background colonization. We further discuss this non‐differential misclassification in the context of the pneumonia aetiology problem in the final section. Then,

$$\begin{array}{cc}\hfill P_i^{1,\mathrm{BS}}=& \text{Pr}({\mathbf{M}}_i^{\mathrm{BS}}=\mathbf{m}|\mathit{\pi },{\mathit{\theta }}^{\mathrm{BS}},{\mathit{\psi }}^{\mathrm{BS}})\hfill \\ & =\sum _{j=1}^J{\mathit{\pi }}_j{({\mathit{\theta }}_j^{\mathrm{BS}})}^{m_j}{(1-{\mathit{\theta }}_j^{\mathrm{BS}})}^{1-m_j}\prod _{l\ne j}{({\mathit{\psi }}_l^{\mathrm{BS}})}^{m_l}{(1-{\mathit{\psi }}_l^{\mathrm{BS}})}^{1-m_l}\hfill \end{array}$$ (2)

is the likelihood contributed by BS measurements from case i, where $\mathbf{m}={\mathbf{m}}_i^{\mathrm{BS}}$.

Similarly, the likelihood contribution from case i's SS measurements that have perfect specificities can be written as

$$P_i^{1,\mathrm{SS}}=\text{Pr}({\mathbf{M}}_i^{\mathrm{SS}}=\mathbf{m}|\mathit{\pi },{\mathit{\theta }}^{\mathrm{SS}})=\sum _{j=1}^{J^{\prime }}{\mathit{\pi }}_j{({\mathit{\theta }}_j^{\mathrm{SS}})}^{m_j}{(1-{\mathit{\theta }}_j^{\mathrm{SS}})}^{1-m_j}{\mathbf{1}}_{\{{\mathrm{\Sigma }}_{l=1}^{J^{\prime }}{m}_l⩽1\}},$$ (3)

where $\mathbf{m}={\mathbf{m}}_i^{\mathrm{SS}}$ and ${\mathbf{1}}_{\{·\}}$ is the indicator function, which equals 1 if the statement in the brackets is true and otherwise is 0. Here $J^{\prime }⩽J$ represents the number of actual SS measurements on each case, and ${\mathit{\theta }}^{\mathrm{SS}}=({\mathit{\theta }}_1^{\mathrm{SS}},\dots ,{\mathit{\theta }}_{J^{\prime }}^{\mathrm{SS}})$. SS measurements test only for a subset of all J pathogens (for example blood culture detects only bacteria) and $J^{\prime }$ is the number of bacteria that are potential causes. Finally, for completeness, GS measurement is assumed to follow a multinomial distribution with likelihood

$$P_i^{1,\mathrm{GS}}=\text{Pr}(M_i^{\mathrm{GS}}=\mathbf{m}|\mathit{\pi })=\prod _{j=1}^J{\mathit{\pi }}_j^{\mathbf{1}\{m_j=1\}}{\mathbf{1}}_{\{{\mathrm{\Sigma }}_j{m}_j=1\}},$$ (4)

where $\mathbf{m}={\mathbf{m}}_i^{\mathrm{GS}}$.

Let ${\mathit{\delta }}_i$ be the binary indicator of a case i having GS measurements; it equals 1 if the case has available GS data and 0 otherwise. Combining likelihood components (1)–(4), the total model likelihood for BS, SS and GS data across independent cases and controls is

$$L(\mathit{\gamma };\mathcal{D})=\prod _{i:Y_i=0}{P}_i^{0,\mathrm{BS}}\prod _{i:Y_i=1,{\mathit{\delta }}_i=1}{P}_i^{1,\mathrm{BS}}{P}_i^{1,\mathrm{SS}}{P}_i^{1,\mathrm{GS}}\prod _{i:Y_i=1,{\mathit{\delta }}_i=0}{P}_i^{1,\mathrm{BS}}{P}_i^{1,\mathrm{SS}},$$ (5)

where $\mathit{\gamma }={({\mathit{\theta }}^{\mathrm{BS}},{\mathit{\psi }}^{\mathrm{BS}},{\mathit{\theta }}^{\mathrm{SS}},\mathit{\pi })}^{\prime }$ stacks all unknown parameters, and data

$$\mathcal{D}={\{{\mathbf{m}}_i^{\mathrm{BS}}\}}_{i:Y_i=0}\cup {\{{\mathbf{m}}_i^{\mathrm{BS}},{\mathbf{m}}_i^{\mathrm{GS}},{\mathbf{m}}_i^{\mathrm{SS}}\}}_{i:Y_i=1,{\mathit{\delta }}_i=1}\cup {\{{\mathbf{m}}_{i^{″}}^{\mathrm{BS}},{\mathbf{m}}_{i^{″}}^{\mathrm{SS}}\}}_{i^{″}:Y_{i^{″}}=1,{\mathit{\delta }}_{i^{″}}=0}$$

collect all the available measurements on study subjects. Our primary statistical goal is to estimate the posterior distribution of the population aetiology distribution π, and to obtain individual etiology ($I_{*}^L$) prediction given a case's measurements.

To enable Bayesian inference, prior distributions on model parameters are specified as follows: $\mathit{\pi }\sim \text{Dirichlet}(a_1,\cdots ,a_J)$, ${\mathit{\psi }}_j^{\mathrm{BS}}\sim \text{beta}(b_{1j},b_{2j})$, ${\mathit{\theta }}_j^{\mathrm{BS}}\sim \text{beta}(c_{1j},c_{2j}),j=1,\dots ,J$, and ${\mathit{\theta }}_j^{\mathrm{SS}}\sim \text{beta}(d_{1j},d_{2j})$, $j=1,\dots ,J^{\prime }$. Hyperparameters for the aetiology prior, $a_1,\dots ,a_J$, are usually 1s to denote equal and non‐informative prior weights for each pathogen if expert prior knowledge is unavailable. The FPR for the jth pathogen, ${\mathit{\psi }}_j^{\mathrm{BS}}$, generally can be well estimated from control data; thus $b_{1j}=b_{2j}=1$ is the default choice. For TPR parameters ${\mathit{\theta }}_j^{\mathrm{BS}}$ and ${\mathit{\theta }}_j^{\mathrm{SS}}$, if prior knowledge on TPRs is available, we choose $(c_{1j},c_{2j})$ so that the 2.5% and 97.5% quantiles of the beta distribution with parameter $(c_{1j},c_{2j})$ match the prior minimum and maximum TPR values elicited from pneumonia experts. Otherwise, we use default value 1s for the beta hyperparameters. Similarly we choose values of $(d_{1j},d_{2j})$ either by prior knowledge or default values of 1. We finally assume prior independence of the parameters as $[\mathit{\gamma }]=[\mathit{\pi }][{\mathit{\psi }}^{\mathrm{BS}}][{\mathit{\theta }}^{\mathrm{BS}}][{\mathit{\theta }}^{\mathrm{SS}}]$, where [A] represents the distribution of random variable or vector A. These priors represent a balance between explicit prior knowledge about measurement error rates and the desire to be as objective as possible for a particular study. As described in the next section, the identifiability constraints on the PLCM require specification of a reasonable subset of parameter values to identify parameters of greatest scientific interest.

2.1. Model identifiability

Potential non‐identifiability of LCM parameters is well known (Goodman, 1974). For example, an LCM with four observed binary indicators and three latent classes is not identifiable despite providing 15 degrees of freedom to estimate 14 parameters (Goodman, 1974). In principle, the Bayesian framework avoids the non‐identifiability problem in LCMs by incorporating prior information about unidentified parameter subspaces (e.g. Garrett and Zeger (2000)). Many researchers point out that the posterior variance for non‐identifiable parameters does not decrease to 0 as the sample size approaches ∞ (e.g. Kadane (1975), Gustafson et al. (2001) and Gustafson (2005)). Even when data are not fully informative about a parameter, an identified set of parameter values that is consistent with the observed data can, nevertheless, be valuable in a complex scientific investigation (Gustafson, 2009) such as the PERCH study.

When GS data are available, the PLCM is identifiable; when they are not, the two sets of parameters π and ${\{{\mathit{\theta }}_j^{\mathrm{BS}}\}}_{j=1}^J$ are not both identified and prior knowledge must be incorporated. Here we restrict attention to the scenario with only BS data for simplicity but similar arguments pertain to the BS plus SS scenario. The problem can be understood from the form of the positive measurement rates for pathogens among cases. In the PLCM likelihood for the BS data (only retaining components in equation (5) with superscripts BS), the positive rate for pathogen j is a convex combination of the TPR and FPR:

$$\text{Pr}(M_{ij}^{\mathrm{BS}}=1|{\mathit{\pi }}_j,{\mathit{\theta }}_j^{\mathrm{BS}},{\mathit{\psi }}_j^{\mathrm{BS}})={\mathit{\pi }}_j{\mathit{\theta }}_j^{\mathrm{BS}}+(1-{\mathit{\pi }}_j){\mathit{\psi }}_j^{\mathrm{BS}},$$ (6)

where the left‐hand side of this equation can be estimated by the observed positive rate of pathogen j among cases. Although the control data provide ${\mathit{\psi }}_j^{\mathrm{BS}}$‐estimates, the two parameters ${\mathit{\pi }}_j$ and ${\mathit{\theta }}_j^{\mathrm{BS}}$ are not both identified. GS data, if available, identify ${\mathit{\pi }}_j$ and resolve the lack of identifiability. Otherwise, we need to incorporate prior scientific information on one of them, usually the TPR (${\mathit{\theta }}_j^{\mathrm{BS}}$). In the PERCH study, prior knowledge about ${\mathit{\theta }}_j^{\mathrm{BS}}$ is obtained from infectious disease and laboratory experts (Murdoch et al., 2012) based on vaccine probe studies (Cutts et al., 2005; Madhi et al., 2005). If the observed case positive rate is much higher than the rate in controls (${\mathit{\psi }}_j^{\mathrm{BS}}$), only large values of the TPR (${\mathit{\theta }}_j^{\mathrm{BS}}$) are supported by the data, making aetiology estimation more precise (Section 2.2).

The full model identification can be generally characterized by inspecting the Jacobian matrix of the transformation F from model parameters γ to the distribution p of the observables, p=F(γ). Let $\mathit{\gamma }={({\mathit{\theta }}^{\mathrm{BS}},{\mathit{\psi }}^{\mathrm{BS}},{\mathit{\pi }}_1,\dots ,{\mathit{\pi }}_{J-1})}^{\prime }$ represent the (3J−1)‐dimensional unconstrained model parameters. The PLCM defines the transformation ${({\mathbf{p}}_1,{\mathbf{p}}_0)}^{\prime }=F(\mathit{\gamma })$, where ${\mathbf{p}}_1$ and ${\mathbf{p}}_0$ are the two contingency probability distributions for the BS measurements in the case and control populations, each with dimension $2^J-1$. It can be shown that the Jacobian matrix has J−1 of its singular values 0, which means that the model parameters γ are not fully identified from the data. The FPRs (${\mathit{\psi }}_j^{\mathrm{BS}},j=1,\dots ,J$) in the PLCM are, however, identifiable parameters that can be estimated from control data. Therefore, the PLCM is termed partially identifiable (Jones et al., 2010).

2.2. Parameter estimation and individual aetiology prediction

The parameters in likelihood (5) include the population aetiology distribution π, TPRs and FPRs for BS measurements, ${\mathit{\psi }}^{\mathrm{BS}}$ and ${\mathit{\theta }}^{\mathrm{BS}}$, and TPRs for SS measurements ${\mathit{\theta }}^{\mathrm{SS}}$. The posterior distribution of these parameters can be estimated by constructing approximating samples from the joint posterior via a Markov chain Monte Carlo (MCMC) Gibbs sampler. The full conditional distributions for the Gibbs sampler are detailed in Appendix A.

We develop a Gibbs sampler with two essential steps:

1. multinomial sampling of lung infection state among cases, $I_i^L|\mathit{\pi },Y_i=1\sim \text{multinomial}(\mathit{\pi })$;

2. the measurement stage given lung infection state,

   $$M_{ij}^{\mathrm{BS}}|I_i^L,{\mathit{\theta }}^{\mathrm{BS}},{\mathit{\psi }}^{\mathrm{BS}}\sim \text{Bernoulli}\{{\mathbf{1}}_{\{I_i^L=j\}}{\mathit{\theta }}_j^{\mathrm{BS}}+(1-{\mathbf{1}}_{\{I_i^L=j\}}){\mathit{\psi }}_j^{\mathrm{BS}}\},j=1,\dots ,J,$$

   conditionally independent.

This is readily implemented by using the freely available software WinBUGS 1.4 (Lunn et al., 2000). In the application below, convergence was monitored by using auto‐correlations, kernel density plots and Brooks–Gelman–Rubin statistics (Brooks and Gelman, 1998) of the MCMC chains. The statistical results below are based on 10 000 iterations of burn‐in followed by 50 000 production samples from each of three parallel chains.

The Bayesian framework naturally allows individual within‐sample classification (infection diagnosis) and out‐of‐sample prediction. This section describes how we calculate the aetiology probabilities for an individual with measurements ${\mathbf{m}}_{*}$. We focus on the more challenging inference scenario when only BS data are available; the general case follows directly.

The within‐sample classification for case i is based on the posterior distribution of latent indicators given the observed data, i.e. $\text{Pr}(I_i^L=j|\mathcal{D}),j=1,\dots ,J$, which can be obtained by averaging along the cause indicator $I_i^L$ chain from MCMC samples. For a case with new BS measurements ${\mathbf{m}}_{*}$, we have

$$\text{Pr}(I_i^L=j|{\mathbf{m}}_{*},\mathcal{D})=\int .3pt\text{Pr}(I_i^L=j|{\mathbf{m}}_{*},\mathit{\gamma }).5pt\text{Pr}(\mathit{\gamma }|{\mathbf{m}}_{*},\mathcal{D}).5pt\mathrm{d}\mathit{\gamma },j=1,\dots ,J,$$ (7)

where the second factor in the integrand can be approximated by the posterior distribution given current data, i.e. $\text{Pr}(\mathit{\gamma }|\mathcal{D})$. For the first term in the integrand, we explicitly obtain the model‐based, one‐sample conditional posterior distribution,

$$\text{Pr}(I_i^L=j|{\mathbf{m}}_{*},\mathit{\gamma })={\mathit{\pi }}_j{l}_j({\mathbf{m}}_{*};\mathit{\gamma })/\sum _m.6pt{\mathit{\pi }}_{{\mathbf{r}}_m}.6pt{l}_m({\mathbf{m}}_{*};\mathit{\gamma }),j=1,\dots ,J,$$

where

$$l_m({\mathbf{m}}_{*};\mathit{\gamma })={({\mathit{\theta }}_j^{\mathrm{BS}})}^{m_{*j}}{(1-{\mathit{\theta }}_j^{\mathrm{BS}})}^{1-m_{*j}}\prod _{l\ne j}{({\mathit{\psi }}_l^{\mathrm{BS}})}^{m_{*l}}{(1-{\mathit{\psi }}_l^{\mathrm{BS}})}^{1-m_{*l}}$$

is the mth mixture component likelihood function evaluated at ${\mathbf{m}}_{*}$. The log‐relative‐probability of $I_i^L=j$ versus $I_i^L=l$ is

$$\begin{array}{cc}& R_{jl}=log\left(\frac{{\mathit{\pi }}_j}{{\mathit{\pi }}_l}\right)+log\{{\left(\frac{{\mathit{\theta }}_j^{\mathrm{BS}}}{{\mathit{\psi }}_j^{\mathrm{BS}}}\right)}^{m_{*j}}{\left(\frac{1-{\mathit{\theta }}_j^{\mathrm{BS}}}{1-{\mathit{\psi }}_j^{\mathrm{BS}}}\right)}^{1-m_{*j}}\}+log\{{\left(\frac{{\mathit{\psi }}_l^{\mathrm{BS}}}{{\mathit{\theta }}_l^{\mathrm{BS}}}\right)}^{m_{*l}}{\left(\frac{1-{\mathit{\psi }}_l^{\mathrm{BS}}}{1-{\mathit{\theta }}_l^{\mathrm{BS}}}\right)}^{1-m_{*l}}\}.\hfill \end{array}$$

The form of $R_{jl}$ informs us about what is required for correct diagnosis of an individual. Suppose that $I_i^L=j$; then, averaging over ${\mathbf{m}}_{*}$, we have $E[R_{jl}]=log({\mathit{\pi }}_j/{\mathit{\pi }}_l)+I({\mathit{\theta }}_j^{\mathrm{BS}};{\mathit{\psi }}_j^{\mathrm{BS}})+I({\mathit{\psi }}_l^{\mathrm{BS}};{\mathit{\theta }}_l^{\mathrm{BS}})$, where $I(v_1;v_2)=v_{1}log(v_1/v_2)+(1-v_1)log\{(1-v_1)/(1-v_2)\}$ is the information divergence (Kullback, 2012) that represents the expected amount of information in $m_{*j}\sim \text{Bernoulli}(v_1)$ for discriminating against $m_{*j}\sim \text{Bernoulli}(v_2)$. If $v_1=v_2$, then $I(v_1;v_2)=0$. The form of $E[R_{jl}]$ shows that there is only additional information from BS data about an individual's aetiology in the person's data when there is a difference between ${\mathit{\theta }}_j^{\mathrm{BS}}$ and ${\mathit{\psi }}_j^{\mathrm{BS}}$, j=1,…,J.

Following equation (7), we average $\text{Pr}(I_i^L=j|{\mathbf{m}}_{*},\mathit{\gamma })$ over MCMC iterations to obtain an individual prediction for the jth pathogen, ${\widehat{p}}_{ij}$, with γ replaced by its simulated values ${\mathit{\gamma }}^{*}$ at each iteration. Repeating for j=1,…,J, we obtain a J probability vector, ${\widehat{\mathbf{p}}}_i={({\widehat{p}}_{i1},\dots ,{\widehat{p}}_{iJ})}^{\prime }$, that sums to 1. This scheme is especially useful when a newly examined case has a BS measurement pattern that is not observed in $\mathcal{D}$, which often occurs when J is large. The final decisions regarding which pathogen to treat can then be based on ${\widehat{\mathbf{p}}}_i$. In particular, the pathogen with largest posterior value might be selected. It is Bayes optimal under mean misclassification loss. Individual aetiology predictions described here generalize the positive or negative predictive value from single to multivariate binary measurements and can aid diagnosis of case subjects under other user‐specified misclassification loss functions.

3. Simulation for three pathogens case with gold standard and bronze standard data

To demonstrate the utility of the PLCM for studies like the PERCH study, we simulate BS data sets with 500 cases and 500 controls for three pathogens A, B and C by using known PLCM specifications. We focus on three states to facilitate viewing of the π‐estimates and individual predictions in the three‐dimensional simplex ${\mathcal{S}}^2$. We use a ternary diagram (Aitchison, 1986) representation where the vector $\mathit{\pi }={({\mathit{\pi }}_{\mathrm{A}},{\mathit{\pi }}_{\mathrm{B}},{\mathit{\pi }}_{\mathrm{C}})}^{\prime }$ is encoded as a point with each component being the perpendicular distance to one of the three sides. The parameters involved are fixed at TPR $\mathit{\theta }={({\mathit{\theta }}_{\mathrm{A}},{\mathit{\theta }}_{\mathrm{B}},{\mathit{\theta }}_{\mathrm{C}})}^{\prime }={(0.9,0.9,0.9)}^{\prime }$, FPR $\mathit{\psi }={({\mathit{\psi }}_{\mathrm{A}},{\mathit{\psi }}_{\mathrm{B}},{\mathit{\psi }}_{\mathrm{C}})}^{\prime }={(0.6,0.02,0.05)}^{\prime }$ and $\mathit{\pi }={({\mathit{\pi }}_{\mathrm{A}},{\mathit{\pi }}_{\mathrm{B}},{\mathit{\pi }}_{\mathrm{C}})}^{\prime }={(0.67,0.26,0.07)}^{\prime }$. We focus on BS and GS data here and have dropped the BS superscript on the parameters for simplicity. We further let the fraction of cases with GS measurements, Δ, be either 1% as in the PERCH study or 10%. Although GS measurements are rare in the PERCH study, we investigate a large range of Δ to understand in general how much statistical information is contained in BS measurements relative to GS measurements.

For any given data set, three distinct subsets of the data can be used: BS only, GS only and BS plus GS, each producing its posterior mean of π, and 95% credible region (Bayesian confidence region), by a transformed Gaussian kernel density estimator for compositional data (Chacón et al., 2011). To study the relative importance of the GS and BS data, the primary quantity of interest in the simulations is the relative sizes of the credible regions for each data mix. Here, we use uniform priors on θ and ψ, and a Dirichlet(1,…,1) prior for π. The results are shown in Fig. 2.

Figure 2.

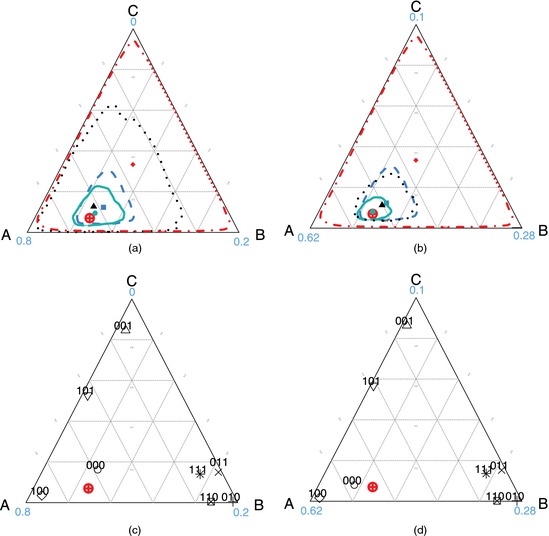
(a), (b) Population and (c), (d) individual aetiology estimates for a single sample with 500 cases and 500 controls with true $\mathit{\pi }={(0\text{.}67,0\text{.}26,0\text{.}07)}^{\prime }$ and either (a), (c) 1% (N=5) or (b), (d) 10% GS data on cases (in (c) and (d), 8 (= 2${}^3$) BS measurement patterns and predictions for individual children are shown with measurement patterns attached; the numbers at the vertices show empirical frequencies of GS measurements): ⊕, true population aetiology distribution π; , , , 95% credible regions for analysis using BS data only, BS plus GS data and GS data only respectively; , , , corresponding posterior mean of π; , 95% highest posterior density region of the uniform prior distribution

First, in Figs 2(a) (1% GS) and 2(b) (10% GS), each region covers the true aetiology π. In data that are not shown here, the nominal 95% credible regions cover slightly more than 95% of 200 simulations. Credible regions narrow in on the truth as we combine BS and GS data, and as the fraction of subjects with GS data, Δ, increases. Also, the posterior mean from the BS plus GS analysis is an optimal balance of information contained in the GS and BS data.

Using the same simulated data sets, Figs 2(c) and 2(d) also show individual aetiology predictions for each of the $8(=2^3)$ possible BS measurements ${(m_{\mathrm{A}},m_{\mathrm{B}},m_{\mathrm{C}})}^{\prime },m_j=0,1$, obtained by the methods from Section 2.2. Consider the example of a newly enrolled case without GS data and with no pathogen observed in her BS data: $\mathbf{m}={(0,0,0)}^{\prime }$. Suppose that she is part of a case population with 10% GS data. In the case that is illustrated in Fig. 2(d), her posterior predictive distribution has highest posterior probability 0.76 on pathogen A reflecting two competing forces: the FPRs that describe background colonization (colonization among the controls) and the population aetiology distribution. Given other parameters, $\mathbf{m}={(0,0,0)}^{\prime }$ gives the smallest likelihood for $I_i^L=A$ because of its high background colonization rate (FPR ${\mathit{\psi }}_{\mathrm{A}}=0.6$). However, before observing ${(0,0,0)}^{\prime }$, ${\mathit{\pi }}_{\mathrm{A}}$ is well estimated to be much larger than ${\mathit{\pi }}_{\mathrm{B}}$ and ${\mathit{\pi }}_{\mathrm{C}}$. Therefore the posterior distribution for this case is heavily weighted towards pathogen A.

Because it is rare to observe pathogen B in a case whose pneumonia is not caused by B, for a case with observation ${(1,1,1)}^{\prime }$, the prediction favours B. Although B is not the most prevalent cause among cases, the presence of B in the BS measurements gives the largest likelihood when $I_i^L$ refers to B. For any measurement pattern with a single positive result, the case is always classified into that category in this example.

Most predictions are stable with increasing GS percentage Δ. Only 000 cases have predictions that move from near the centre to the corner of A. This is mainly because that TPR θ and aetiology fractions π are not as precisely estimated in GS scarce scenarios relative to GS abundant scenarios. Averaging over a wider range of θ and π produces 000 case predictions that are ambiguous, i.e. near the centre. As Δ increases, parameters are well estimated, and precise predictions result.

4. Analysis of Pneumonia Etiology Research for Child Health data

The PERCH study is an on‐going standardized and comprehensive evaluation of aetiologic agents causing severe and very severe pneumonia among hospitalized children aged 1–59 months in seven low and middle income countries (Levine et al., 2012). The study sites include countries with a significant burden of childhood pneumonia and a range of epidemiologic characteristics. The PERCH study is a case–control study that has enrolled over 4000 patients hospitalized for severe or very severe pneumonia and over 5000 controls selected randomly from the community frequency matched on age in each month. More details about the PERCH design are available in Deloria‐Knoll et al. (2012).

To analyse PERCH data with the PLCM model, we have focused on preliminary data from one site with good availability of both SS and BS laboratory results (no missingness). Final analyses of all seven countries will be reported elsewhere on completion of the study. Included in the current analysis are BS data (nasopharyngeal specimens with PCR detection of pathogens) for 432 cases and 479 frequency‐matched controls on 11 species of pathogens (seven viruses and four bacteria, representing a subset of pathogens evaluated; their abbreviations are shown on the right‐hand margin in Fig. 3, and full names in Table 1) and SS data (blood culture results) on the four bacteria for only the cases.

Figure 3.

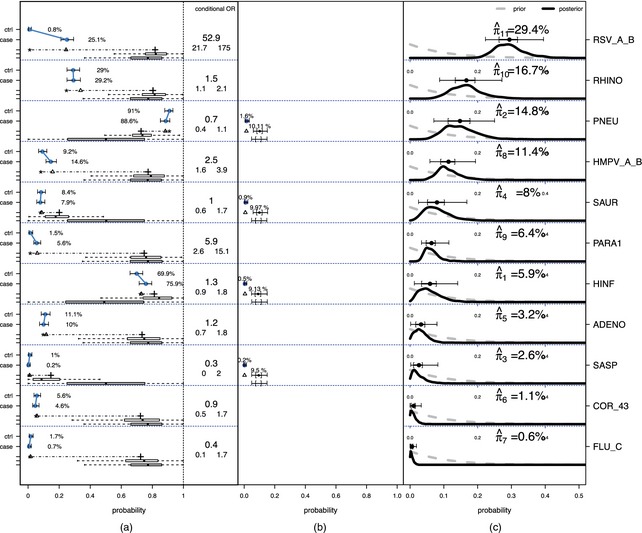
(a) Observed BS rates (with 95% confidence intervals) for cases and controls, (b) SS data and (c) $\widehat{\mathit{\pi }}$ (see the text for further explanation)

Table 1.

Pathogen names and their abbreviations

Bacteria
HINF	Haemophilus influenzae
PNEU	Streptococcus pneumoniae
SASP	Salmonella species
SAUR	Staphylococcus aureus
Viruses
ADENO	Adenovirus
COR_43	Coronavirus OC43
FLU_C	Influenza virus type C
HMPV_A_B	Human metapneumovirus type A or B
PARA1	Parainfluenza type 1 virus
RHINO	Rhinovirus
RSV_A_B	Respiratory syncytial virus type A or B

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

In the PERCH study, prior scientific knowledge of measurement error rates is incorporated in the analysis. On the basis of microbiology studies (Murdoch et al., 2012), the PERCH investigators selected priors for the TPRs of our BS measurements, ${\mathit{\theta }}_j^{\mathrm{BS}}$, in the range of 50–100% for viruses and 0–100% for bacteria. Priors for the SS TPRs were based on observations from vaccine probe studies—randomized clinical trials of pathogen‐specific vaccines where the total number of clinical pneumonia cases prevented by the vaccine is much larger than the few SS laboratory‐confirmed cases prevented. Comparing the total preventable disease burden with the number of blood culture (SS) positive cases prevented provides information about the TPR of the bacterial blood culture measurements, ${\mathit{\theta }}_j^{\mathrm{SS}},j=1,\dots ,4$. Our analysis used the range 5–15% for the SS TPRs of the four bacteria that are consistent with the vaccine probe studies (Cutts et al., 2005; Madhi et al., 2005). We set beta priors that match these ranges (Section 2) and assumed a Dirichlet(1,…,1) prior on aetiology fractions π.

In latent variable models such as the PLCM, key variables are not directly observed. It is therefore essential to picture the model inputs and outputs side by side to understand the analysis better. In this spirit, Figs 3(a) and 3(b) display, for each of the 11 pathogens, a summary of the BS and SS data respectively along with some of the intermediate model results, and the prior and posterior distributions for the aetiology fractions in Fig. 3(c) (the rows are ordered by posterior means). The observed BS rates (with 95% confidence intervals) for cases and controls are shown on the far left with dots. The conditional odds ratio contrasting the case and control rates given the other pathogens is listed with 95% confidence interval in the box to the right of the BS data summary. Below the case and control observed rates is a horizontal line with a triangle. From left to right, the line starts at the estimated FPR $\widehat{\mathit{\psi }}{}_j^{\mathrm{BS}}$ and ends at the estimated TPR $\widehat{\mathit{\theta }}{}_j^{\mathrm{BS}}$, both obtained from the model. Below the TPR are two boxplots summarizing its posterior (top) and prior (bottom) distributions for that pathogen. These boxplots show how the prior assumption influences the TPR estimate as expected given the identifiability constraints that were discussed in Section 2.1. The triangle on the line is the model estimate of the case rate to compare with the observed value above it. As discussed in Section 2.1, the model‐based case rate is a linear combination of the FPR and TPR with mixing fraction equal to the estimated aetiology fraction. Therefore, the location of the triangle, expressed as a fraction of the distance from the FPR to the TPR, is the model‐based point estimate of the aetiologic fraction for each pathogen. The SS data are shown in a similar fashion to the right of the BS data. By definition, the FPR is 0.0% for SS measures and there are no control data. The observed rate for the cases is shown with its 95% confidence interval. The estimated SS TPR $\widehat{\mathit{\theta }}{}_j^{\mathrm{SS}}$ with prior and posterior distributions is shown as for the BS data, except that we plot 95% and 50% credible intervals for the SS TPR above its prior 95% and 50% intervals.

Fig. 3(c) displays the marginal posterior and prior distributions of the aetiologic fraction for each pathogen. We appropriately normalized each density to match the height of the prior and posterior curves. The posterior mean, 50% and 95% credible intervals are shown above the density.

Fig. 3 shows that respiratory syncytial virus, RSV, Streptococcus pneumoniae, PNEU, rhinovirus, RHINO, and human metapneumovirus, HMPV_A_B, occupy the greatest fractions of the aetiology distribution, from 15% to 30% each. That RSV has the largest estimated mean aetiology fraction reflects the large discrepancy between case and control positive rates in the BS data: 25.1% versus 0.8% (marginal odds ratio 38.5 (95% credible interval (18.0,128.7))). RHINO has case and control rates that are close to each other, yet its estimated mean aetiology fraction is 16.7%. This is because the model considers the joint distribution of the pathogens, not the marginal rates. The conditional odds ratio of case status with RHINO given all the other pathogen measures is estimated to be 1.5 (1.1,2.1), in contrast with the marginal odds ratio, which is close to 1 (0.8,1.3).

As discussed in Section 2.1, the data alone cannot precisely estimate both the aetiologic fractions and TPRs without prior knowledge. This is evidenced by comparing the prior and posterior distributions for the TPRs in the BS boxes for some pathogens such as HMPV_A_B and PARA1 (i.e. Fig. 3(a)). The posteriors are similar to their priors, indicating that little else about the TPR is learned from the data. The posteriors for some pathogens making up π (i.e. shown in Fig. 3(c)) are likely to be sensitive to the prior specifications of the TPRs.

We performed sensitivity analyses using multiple sets of priors for the TPRs. At one extreme, we ignored background scientific knowledge and let the priors on the FPR and TPR be uniform for both the BS and the SS data. Ignoring prior knowledge about error rates lowers the aetiology estimates of the bacteria PNEU and Staphylococcus aureus, SAUR. The substantial reduction in the aetiology fraction for PNEU, for example, is a result of the difference in the TPR prior for the SS measurements. In the original analysis (Fig. 3), the informative prior on the SS sensitivity (TPR) places 95% mass between 5% and 15%. Hence the model assumes that almost 90% of the PNEU infections are being missed in the SS sampling. When a uniform prior is substituted, the fraction that is assumed missed is greatly reduced. For RSV, its posterior mean aetiology fraction is stable (29.4−30.0%). The aetiology estimates for other pathogens are fairly stable, with changes in posterior means between −2.3% and 3.4%.

Under the original priors for the TPR, PARA1 has an estimated aetiologic fraction of 6.4%, even though it has conditional odds ratio 5.9 (2.6,15.0). In general, pathogens with larger conditional odds ratios have larger aetiology fraction estimates. But a pathogen also needs a reasonably high observed case positive rate to be allocated a high aetiology fraction. The posterior aetiology fraction estimate of 6.4% for PARA1 results because the prior for the TPR takes values in the range of 50−99%. By equation (6), the TPR weight in the convex combination with the FPR (around 1.5%) must be very small to explain the small observed case rate 5.6%. When a uniform prior is placed on the TPR instead, the PARA1 aetiology fraction increases to 9.4% with a wider 95% credible interval.

We believe that RHINO's aetiologic fraction may be inflated as a result of its negative association with RSV among cases. Under the conditional independence assumption of the PLCM, this dependence can only be explained by multinomial correlation between the latent cause indicators: $I_i^L\equiv \text{RSV}$ versus $I_i^L\equiv \text{RHINO}$, i.e. $-{\mathit{\pi }}_{\mathrm{RSV}}{\mathit{\pi }}_{\mathrm{RHINO}}$. There is strong evidence that RSV is a common cause with a stable estimate ${\widehat{\mathit{\pi }}}_{\mathrm{RSV}}$ around 30%. The strong negative association in the cases' measurements between RHINO and RSV therefore is being explained by a larger aetiologic fraction estimate ${\widehat{\mathit{\pi }}}_{\mathrm{RHINO}}$ relative to other pathogens that have less or no association with RSV among the cases. The conditional independence assumption is leveraging information from the associations between pathogens in estimation of the aetiologic fractions. If true, this issue can be addressed by extending the PLCM to allow for alternative sources of correlation between the measurements, e.g. competition between pathogens within the nasopharyngeal space.

We have checked the model in two ways by comparing the characteristics of the observed measurements' joint distribution with the same characteristic for the distribution of data of the same size generated by the model. By generating the new data characteristics at every iteration of the MCMC chain, we can obtain the posterior predictive distribution by integrating over the posterior distribution of the parameters (Garrett and Zeger, 2000).

Among the cases, the 95% predictive interval includes the observed values in all except two of the BS patterns and even there the fits are reasonable. Among the controls, there is evidence of a lack of fit for the most common BS pattern with only PNEU and HINF (Fig. S1 in the on‐line supplementary materials). Fewer cases with this pattern are observed than predicted under the PLCM. This lack of fit is probably due to associations of pathogen measurements in control subjects. Note that the FPR estimates remain consistent regardless of such correlation as the number of controls increases; however, posterior variances for them may be underestimated.

A second model checking procedure is for the conditional independence assumption. We estimated standardized log‐odds‐ratios for cases and controls (Fig. S2 in on‐line supplementary materials). Each value is the observed log‐odds‐ratio for a pair of BS measurements minus the mean log‐odds‐ratio from the posterior predictive distribution value, under the model's independence assumption, divided by the standard deviation of the same posterior predictive distribution. We find two large deviations among the cases: RSV with RHINO and RSV with HMPV. These are probably caused by strong seasonality in RSV that is out of phase with weaker seasonality in the other two. Otherwise, the number of standardized log‐odds‐ratios that are greater than 2 (eight out of 110) associations is only slightly larger than what is expected under the assumed model (six expected).

An attractive feature of using MCMC sampling to estimate posterior distributions is the ease of estimating posteriors for functions of the latent variables and/or parameters. One interesting question from a clinical perspective is whether viruses or bacteria are the major cause and, among each subgroup, which species predominate. Fig. 4(a) shows the posterior distribution for the rate of viral pneumonia, and the conditional distributions of the two leading viruses and bacteria among viral and bacterial causes in Figs 4(b) and 4(c) respectively. The posterior distribution of the viral aetiologic fraction has mode around 70.0% with 95% credible interval (57.0%,79.2%). As shown in Fig. 4(b), PNEU accounts for most bacterial cases (47.2% (24.9%,71.1%)), and SAUR accounts for 25.5% (8.7%,49.9%). Of all viral cases (Fig. 4(c)), RSV is estimated to cause about 42.9% (32.8%,54.8%), and RHINO about 24.2% (13.7%,37.2%).

Figure 4.

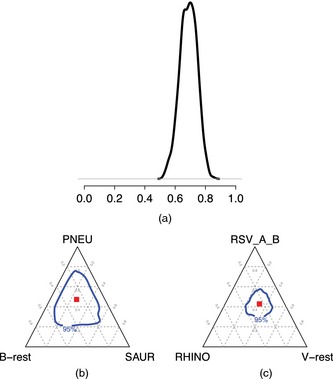
Summary of posterior distribution of pneumonia aetiology estimates (, 95% credible regions within the bacterial or viral groups): (a) posterior distribution of viral aetiology; (b) posterior aetiology distribution for the top two causes given a bacterial infection; (c) posterior aetiology distribution for the top two causes given a viral infection

5. Discussion

In this paper, we estimated the frequency with which pathogens cause disease in a case population by using a PLCM to allow for known states for a subset of subjects and for multiple types of measurement with different error rates. In a case–control study of disease aetiology, measurement error will bias estimates from traditional logistic regression and attributable fraction methods. The PLCM avoids this pitfall and more naturally incorporates multiple sources of data. Here we formulated the model with three levels of measurement error rates.

Without GS data, we show that the PLCM is only partially identified because of the relationship between the estimated TPR and prevalence of the associated pathogen in the population. Therefore, the inferences are sensitive to the assumptions about the TPR. Uncertainty about their values persists in the final inferences from the PLCM regardless of the number of subjects studied.

The current model provides a novel solution to the analytic problems that are raised by the PERCH study. This paper introduces and applies a PLCM to a preliminary set of data from one PERCH study site. Confirmatory laboratory testing, incorporation of additional pathogens and adjustment for potential confounders may change the scientific findings that will be reported in the final complete analysis of the study results when it is completed.

An essential assumption that is relied on in the PLCM is that the probability of detecting one pathogen at a peripheral body site depends on whether that pathogen is infecting the child's lung but is unaffected by the presence of other pathogens in the lung, i.e. the non‐differential misclassification error assumption. We have formulated the model to include GS measures even though they are available for only a small and unrepresentative subset of the PERCH cases. In general, the availability of GS measures makes it possible to test this assumption as has been discussed by Albert and Dodd (2008).

Several extensions have potential to improve the quality of inferences that are drawn and are being developed for the PERCH study. First, because the control subjects have known class, we can model the dependence structure between the BS measurements and use this to avoid aspects of the conditional independence assumption that is central to most LCM methods. The approach is to extend the PLCM to have K subclasses within each of the current disease classes. These subclasses can introduce correlation between the BS measurements given the true disease state. An interesting question concerns the bias–variance trade‐off for different values of K. This idea follows previous work on the parallel factors decomposition of probability distribution for multivariate categorical data (Dunson and Xing, 2009). This extension will enable model‐based checking of the standard PLCM.

Second, in our analyses to date, we have assumed that the pneumonia case definition is error free. Given new biomarkers and availability of chest radiographs that can improve on the clinical diagnosis of pneumonia, one can introduce an additional latent variable to indicate true disease status and use these measurements to assign probabilistically each subject as a case or control. Finally, regression extensions of the PLCM would allow PERCH investigators to study how the aetiology distributions vary with human immunodeficiency virus status, age group and season.

Supporting information

‘Web‐based supplementary materials for “Partially‐latent class models (pLCM) for case‐control studies of childhood pneumonia etiology”’.

Appendix A. Full conditional distributions in Gibbs sampler

In this section, we provide analytic forms of full conditional distributions that are essential for the Gibbs sampling algorithm. We use a data augmentation scheme by introducing latent lung state $I_i^L$ into the sampling chain and we have the following full conditional distributions.

1. $[I_i^L|\text{others}]$: if $M_i^{\mathrm{GS}}$ is available, $\text{Pr}(I_i^L=j|\text{others})\text{equals}1$, if $M_{ij}^{\mathrm{GS}}=1$ and $M_{il}^{\mathrm{GS}}=0$, for l≠j; otherwise it is 0. If $M_i^{\mathrm{GS}}$ is missing, according to whether $M_i^{\mathrm{SS}}$ is available, the full conditional is given by

   $$\begin{array}{cc}\hfill \text{Pr}(I_i^L=j|\text{others})& \propto {({\mathit{\theta }}_j^{\mathrm{BS}})}^{M_{ij}^{\mathrm{BS}}}{(1-{\mathit{\theta }}_j^{\mathrm{BS}})}^{1-M_{ij}^{\mathrm{BS}}}\prod _{l\ne j}{({\mathit{\psi }}_l^{\mathrm{BS}})}^{M_{il}^{\mathrm{BS}}}{(1-{\mathit{\psi }}_l^{\mathrm{BS}})}^{1-M_{il}^{\mathrm{BS}}}\hfill \\ & \times {[{({\mathit{\theta }}_j^{\mathrm{SS}})}^{M_{ij}^{\mathrm{SS}}}{(1-{\mathit{\theta }}_j^{\mathrm{SS}})}^{1-M_{ij}^{\mathrm{SS}}}{\mathbf{1}}_{\{{\mathrm{\Sigma }}_{l\ne j}{M}_{il}^{\mathrm{SS}}=0\}}]}^{{\mathbf{1}}_{\{j\le J^{\prime }\}}}{\mathit{\pi }}_j;\hfill \end{array}$$ (8)

   if SS measurement is not available for case i, we remove terms involving $M_{ij}^{\mathrm{SS}}$.

2. $[{\mathit{\psi }}_j^{\mathrm{BS}}|\text{others}]\sim \text{beta}(N_j+b_{1j},n_1-{\mathrm{\Sigma }}_{i:Y_i=1}.3pt{\mathbf{1}}_{\{I_i^L=j\}}+n_0-N_j+b_{2j})$, where $n_1$ and $n_0$ are the numbers of cases and controls respectively, and $N_j={\mathrm{\Sigma }}_{i:Y_i=1,I_i^L\ne j}{M}_{ij}^{\mathrm{BS}}+{\mathrm{\Sigma }}_{i:Y_i=0}{M}_{ij}^{\mathrm{BS}}$ is the number of positive results at position j for cases with $I_i^L\ne j$ and all controls.

3. $[{\mathit{\theta }}_j^{\mathrm{BS}}|\text{others}]\sim \text{beta}(S_j+c_{1j},{\mathrm{\Sigma }}_{i:Y_i=1}{\mathbf{1}}_{\{I_i^L=j\}}-S_j+c_{2j})$, where $S_j={\mathrm{\Sigma }}_{i:Y_i=1,I_i^L=j}{M}_{ij}^{\mathrm{BS}}$ is the number of positive results for cases with jth pathogen as their causes.

4. $[{\mathit{\theta }}_j^{\mathrm{SS}}|\text{others}]\sim \text{beta}(T_j+d_{1j},{\mathrm{\Sigma }}_{i:Y_i=1,\mathrm{SS}\mathrm{available}}{\mathbf{1}}_{\{I_i^L=j\}}-T_j+d_{2j})$, where

   $$T_j=\sum _{i:Y_i=1,I_i^L=j,\mathrm{SS}\mathrm{available}}{M}_{ij}^{\mathrm{SS}}.$$

   When no SS data are available, this conditional distribution reduces to $\text{beta}(d_{1j},d_{2j})$, the prior.

5. $[\mathit{\pi }|I_i^L,i:Y_i=1]\sim \text{Dirichlet}(a_1+U_1,\dots ,a_J+U_J)$, where $U_j={\mathrm{\Sigma }}_{i:Y_i=1}.4pt{\mathbf{1}}_{\{I_i^L=j\}}$.