Nonparametric tests for transition probabilities in nonhomogeneous Markov processes

Abstract

This paper proposes nonparametric two-sample tests for the direct comparison of the probabilities of a particular transition between states of a continuous time non-homogeneous Markov process with a finite state space. The proposed tests are a linear nonparametric test, an L²-norm-based test and a Kolmogorov–Smirnov-type test. Significance level assessment is based on rigorous procedures, which are justified through the use of modern empirical process theory. Moreover, the L²-norm and the Kolmogorov–Smirnov-type tests are shown to be consistent for every fixed alternative hypothesis. The proposed tests are also extended to more complex situations such as cases with incompletely observed absorbing states and non-Markov processes. Simulation studies show that the test statistics perform well even with small sample sizes. Finally, the proposed tests are applied to data on the treatment of early breast cancer from the European Organization for Research and Treatment of Cancer (EORTC) trial 10854, under an illness-death model.

1. Introduction

Continuous time nonhomogeneous Markov processes with a finite state space are important in many areas of science and particularly in medicine and public health (Tattar and Vaman, 2014; Bakoyannis et al., 2019). Consideration of specific transitions between two states of a multi-state process can provide a deeper and more detailed insight about the treatment effect in clinical trials compared to the analysis of standard survival outcomes, such as event-free survival (Le-Rademacher et al., 2018). Important special cases of a Markov process are the univariate survival model, the competing risks model, and the Markov illness-death model (Andersen et al., 2012).

The stochastic behavior of a Markov process can be described by either the transition intensities, which represent the instantaneous rates of transition between two states, or the transition probabilities. The transition probabilities are also known as survival functions in the framework of the univariate survival model, and as cumulative incidence functions in the competing risks model. It is important to note that, in general, a difference in the transition intensities between two groups does not necessarily imply a difference in the corresponding transition probabilities and vice versa. This phenomenon has been well documented for the special case of the competing risks model (Gray, 1988; Pepe, 1991; Putter et al., 2007; Bakoyannis and Touloumi, 2012). Nonparametric tests for comparing transition intensities between groups in general Markov multi-state processes have been well developed (Andersen et al., 2012). However, the issue of nonparametric comparison of transition probabilities in general Markov multi-state processes has not received much attention. Nevertheless, transition probabilities, unlike transition intensities, directly quantify clinical prognosis (Bakoyannis et al., 2019), which is the target of scientific interest in many applications.

Nonparametric estimation of the transition probabilities of a general Markov process can be performed using the Aalen–Johansen estimator (Aalen and Johansen, 1978). The issue of nonparametric comparison of transition probabilities under the univariate survival model has been extensively studied in the literature. For a review of these methods see Kalbfleisch and Prentice (2011) and Andersen et al. (2012). A number of researchers have proposed nonparametric tests for the comparison of transition probabilities for the special case of the competing risks model (Gray, 1988; Pepe and Mori, 1993; Lin, 1997). Dabrowska and Ho (2000) proposed a graphical procedure based on simultaneous confidence bands to test for differences between transition probabilities in a general Markov process. However, their method imposes proportional hazards assumptions for the transition intensities and, thus, it is not fully nonparametric. Also, this approach does not provide the actual level of statistical significance. Tattar and Vaman (2014) proposed two nonparametric tests for the comparison of the whole transition probability matrices between k groups, by comparing all the possible transition intensities. The first test only compares the transition probability matrices at a specific time point t₀, while the second test is a Kolmogorov–Smirnov-type test based on the supremum norm. However, the tests proposed by Tattar and Vaman (2014) do not provide a direct comparison of the transition probability of a particular transition, which is frequently of scientific interest (Le-Rademacher et al., 2018). A statistically significant result with these tests only indicates a difference in any transition between groups. Recently, Bluhmki et al. (2018) proposed a wild bootstrap approach for the Aalen–Johansen estimator, which can be used to construct a simultaneous confidence band for the difference between the transition probabilities of two independent groups. This approach, which is related to a Kolmogorov–Smirnov-type test, can be used as a graphical two-sample comparison procedure at a predetermined α level. However, this approach does not provide the actual level of statistical significance and, also, a Kolmogorov–Smirnov-type test may not be the most powerful nonparametric test for every alternative hypotheses. Additionally, there is no rigorous justification about the consistency of this graphical hypothesis testing procedure against any fixed alternative hypothesis (Van der Vaart, 2000). Last but not least, the proposed approach is not readily adaptable to more complex situations such as cases with missing data.

This paper addresses the issue of direct nonparametric two-sample comparison of the transition probabilities of a particular transition in a general continuous-time nonhomogeneous Markov process with a finite state space. For this, we propose a linear nonparametric test, an L²-norm-based test and a Kolmogorov–Smirnov-type test. The asymptotic null distributions of the tests are derived. The evaluation of the actual level of statistical significance is based on rigorous procedures justified through the use of modern empirical process theory. Moreover, the L²-norm-based and Kolmogorov–Smirnov-type tests are shown to be consistent against any fixed alternative hypothesis (Van der Vaart, 2000). It has to be noted that the linear nonparametric test can be inconsistent under some alternative hypotheses with crossing transition probability curves. This is because, in such cases, the corresponding test statistic can be equal to zero, since positive and negative differences of the same magnitude cancel out. In less extreme cases with crossing, the linear test is expected to be less powerful compared to the L²-norm-based and Kolmogorov–Smirnov-type tests. We also propose extensions related to interesting practical problems such as cases with missing absorbing states (Bakoyannis et al., 2019) and non-Markov processes (Putter and Spitoni, 2018). The proposed tests exhibit good small sample properties as illustrated in our simulation experiments. Finally, the tests are applied to data on the treatment of early breast cancer from the European Organization for Research and Treatment of Cancer (EORTC) trial 10854.

Compared to the previous work by Bluhmki et al. (2018), which used counting process theory arguments in their derivations, we justify the properties of the proposed tests through the use of modern empirical process theory (Van Der Vaart and Wellner, 1996; Kosorok, 2008). As it will be argued later in the text, the practical advantage of our derivations lies on the fact that our proposed tests can be straightforwardly adapted to more complex settings such as cases with incompletely observed absorbing states (Bakoyannis et al., 2019). This can be done by replacing the influence function of the standard Aalen–Johansen estimator with the influence function of any other well-behaved and asymptotically linear estimator of the transition probabilities in our proposed testing procedures. Such adaptations are not trivial within the framework of the graphical testing procedure proposed by Bluhmki et al. (2018). An important reason for this is that with more complex estimators, certain predictability conditions assumed by counting process and martingale theory techniques are violated. For such situations, empirical process theory provides a powerful alternative tool. Moreover, we provide two additional tests, a linear test and an L²-norm-based test, which may be more powerful compared to a Kolmogorov–Smirnov-type test in certain settings. Additionally, we argue about the consistency of our L²-norm-based and Kolmogorov–Smirnov-type tests against any fixed alternative hypothesis. Finally, our tests provide the actual level of statistical significance which is useful in practical applications.

The structure of this paper is as follows. In Section 2 we introduce some notation about Markov processes, provide the proposed nonparametric tests, and consider extensions to more complex situations that are frequently met in practice. Section 3 presents a simulation study to evaluate the small sample performance of the proposed tests. Section 4 illustrates the use of the proposed tests using data from the EORTC trial 10854. Finally, Section 5 concludes the article with some key remarks. Outlines of the asymptotic theory proofs are provided in the Appendix.

2. Two-sample nonparametric tests

2.1. Nonparametric estimation of transition probabilities

The stochastic behavior of a Markov process {X(t) : t ≥ 0} with a finite state space $\mathcal{I}=\{1,\dots ,q\}$ can be described by the q × q transition probability matrix P₀(s, t) = (P_0,hj(s, t)) whose elements are the transition probabilities

$$\begin{array}{l}{P}_{0,hj}(s,t)=\mathrm{Pr}\left(X\right(t)=j|X\left(s\right)=h,{\mathcal{F}}_{s^{-}})\\ =\mathrm{Pr}\left(X\right(t)=j|X\left(s\right)=h)h,j\in \mathcal{I},0\le s<t\le \tau ,\end{array}$$

where ${\mathcal{F}}_{s^{-}}=\sigma ⟨\left\{N_{\mathit{hj}}\right(u):0\le u<s,h\ne j\}⟩$ is the event history prior to time s, with N_hj (t) being the number of direct transitions from state h to state j, h ≠ j, in [0, t], $\tau =\sup \{t:{\int }_0^t{a}_0,hj(u)du\equiv A_{0}hj(t)<\infty ,h\ne j\}$, and $a_0{,}_{hj}(t)={\lim }_{h\downarrow 0}{P}_{0,hj}(t,t+h)/h,h\ne j$, is the transition intensity at time t. The conditional independence between the probability of X(t) and the prior history ${\mathcal{F}}_{s^{-}}$, conditionally on X(s), is the so-called Markov assumption. Because P_o(s, t) is a stochastic matrix we have that $a_{0,hh}(t)=-{\sum }_{j\ne h}{a}_{0,hj}(t).$

The observed data from a sample of i.i.d. observations of a Markov process are the counting processes {N_ihj (t) : h ≠ j, t ∈ [0, τ]}, i = 1, … , n, which represent the number of direct transitions of the ith observation from the state h to the state j by time t, and the at-risk processes $\left\{Y_{\mathit{ih}}\right(t):h\in \mathcal{I},\in [0,\tau \left]\right\}$ which are the indicator functions of whether the ith observation is at the state $h\in \mathcal{I}$ just before time t ∈ [0, τ]. Based on such a sample, the transition probability matrix of a nonhomogeneous Markov process can be estimated using the nonparametric Aalen–Johansen estimator (Aalen and Johansen, 1978):

$${\widehat{P}}_n(s,t)=\prod _{(s,t]}[I+d{\widehat{A}}_n(u)],s,t\in [0,\tau ],$$

where ∏ is the product integral and Â_n(t) a q×q matrix whose elements are the Nelson–Aalen estimates of the cumulative transition intensities

$${\widehat{A}}_{n,hj}(t)={\int }_0^t\frac{{\sum }_{i=1}^{n}d{N}_{ihj}(u)}{{\sum }_{i=1}^n{Y}_{ih}(u)},h\ne \text{j}.$$

2.2. Linear nonparametric tests

First consider the two-sample problem of comparing the transition probabilities $P_{0,hj}^{(1)}(s,\cdot )$ and $P_{0,hj}^{(2)}(s,\cdot )$, s ∈ [0, τ), of two populations of interest, for a particular transition h → j, with $h,j\in \mathcal{I}$. In many applications the starting point is being set to s = 0, but here we will use an arbitrary s ∈ [0, τ) for the sake of generality. Based on two independent random samples of n₁ and n₂ observations from the two populations, define the pointwise weighted difference

$${\widehat{D}}_{hj}(s,t)={\widehat{W}}_{hj}(t)\left[{\widehat{P}}_{n_1,hj}^{(1)}(s,t)-{\widehat{P}}_{n_2,hj}^{(2)}(s,t)\right],0\le \text{s}\le t\le \tau ,$$

where ${\widehat{W}}_{hj}(t)$ is a weight function and ${\widehat{P}}_{n_1,hj}^{(1)}(s,t)$ and ${\widehat{P}}_{n_2,hj}^{(2)}(s,t)$ are the nonparametric Aalen–Johansen estimates of the transition probabilities of the two populations under comparison. Examples of weight function choices are

$${\widehat{W}}_{hj}(t)=I\left[\prod _{l\in L(h,j)}{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)>0\right],$$

and

$${\widehat{W}}_{hj}(t)=\frac{{\prod }_{l\in L(h,j)}{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)}{{\sum }_{l\in L(h,j)}[{\overline{Y}}_l^{(1)}(t)+{\overline{Y}}_l^{(2)}(t)]},$$

where I(·) is the indicator function, $L(h,j)=\{d\in \mathcal{I}:d$ is a transient state that can be visited during the transition h → j} and, ${\overline{Y}}_h^{(p)}(t)=n_p^{-1}{\sum }_{i=1}^{(p)}{Y}_{ih}^{(p)}(t),p=1,2.$ The latter choice assigns more weight to times with more observations at risk. This is useful for assigning less weight for times with a very small number of observations, such as times close to the end of the study period, where the transition probability estimates can be highly unstable. A natural linear test for the null hypothesis $H_0:P_{0,hj}^{(1)}(s,t)=P_{0,hj}^{(2)}(s,t)$ for a given starting point s ∈ [0, τ) and all t ∈ [s, τ], or, equivalently, $H_0:P_{0,hj}^{(1)}(s,\cdot )=P_{0,hj}^{(2)}(s,\cdot )$ for a given starting point s ∈ [0, τ), is the area under the weighted difference curve

$${\widehat{Z}}_{hj}(s)={\int }_{(s,\tau ]}{\widehat{D}}_{hj}(s,t)dm(t),$$

where m is the Lebesgue measure on the Borel σ-algebra $\mathcal{B}\left(\right[0,\tau \left]\right)$. To establish the asymptotic distributions of the proposed test statistics, we assume the following conditions.

C1. The potential right censoring and left truncation are independent of the counting processes {N_hj(t) : h ≠ j, t ∈ [0, τ]} and noninformative about P₀(s, t).

C2. n₁/(n₁ + n₂) → λ ∈ (0,1) as min(n₁, n₂) → ∞.

C3. The counting processes {N_hj(t) : h ≠ j, t ∈ [0, τ]} satisfy E[N_hj(τ)]² < ∞ for all h ≠ j.

C4. inf_{t∈[0, τ]} E[Y_h(t)] > 0 for all the transient states.

C5. The cumulative transition intensities {A_0,hj(t) : h ≠ j, t ∈ [0, τ]} are continuous functions.

C6. The weight ${\widehat{W}}_{hj}(t)$ converges uniformly, in probability, to a nonnegative uniformly bounded function W_hj(t) on [0, τ].

Remark 1. In some applications condition C4 may not be satisfied for some time points for one or more transient states $h\in \mathcal{I}$. In such cases, provided that the conditions for the uniform consistency of the Aalen–Johansen estimator hold, one can restrict the comparison interval to [τ₁, τ₂] with 0 < τ₁ < τ₂ < τ, such that inf_{t∈[τ1, τ2]} E[Y_h(t)] > 0 for the transient states, and then use nonparametric bootstrap for inference. In such cases the test statistic becomes

$${\widehat{Z}}_{hj}(s)={\int }_{(s,{\tau }_2]}{\widehat{D}}_{hj}(s,t)dm(t),$$

for a fixed s ∈ [τ₁, τ₂).

Before stating the theorem about the asymptotic distribution of test statistic we define the functions

$$M_{ilm}^{(p)}(t)=N_{ilm}^{(p)}(t)-{\int }_{(0,t]}{Y}_{il}^{(p)}(u)d{A}_{0,lm}^{(p)}(u),$$

where $N_{ilm}^{(p)}(t)$ and $Y_{il}^{(p)}(t)$ are the counting and at-risk processes of the ith observation in the pth sample at time t. Also, define $\mathcal{T}$ to be the subset of $\mathcal{I}$ which contains the potential absorbing states. For non-absorbing Markov processes $\mathcal{T}=Ø$.

Theorem 1 provides the asymptotic distribution of ${\widehat{Z}}_{hj}(s)$ under the null hypothesis $H_0:P_{0,hj}^{(1)}(s,\cdot )=P_{0,hj}^{(2)}(s,\cdot )$. In this work, we adopt the convention that 0 · ∞ = 0 as in Athreya and Lahiri (2006).

Theorem 1. Suppose that conditions C1-C6 hold. Then under the null hypothesis $H_0:P_{0,hj}^{(1)}(s,\cdot )=P_{0,hj}^{(2)}(s,\cdot )$ for some (fixed) s ∈ [0, τ),

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{Z}}_{hj}(s)\stackrel{d}{\to }{G}_{hj}(s),$$

where $G_{hj}(s)\sim N(0,{\omega }_{hj}^2(s))$ and

$${\omega }_{hj}^2(s)=(1-\lambda )E{\left[{\int }_{(s,\tau )}{W}_{hj}(t){\gamma }_{1hj}^{(1)}(s,t)dm(t)\right]}^2+\lambda E{\left[{\int }_{(s,\tau )}{W}_{hj}(t){\gamma }_{1hj}^{(2)}(s,t)dm(t)\right]}^2.$$

with

$${\gamma }_{ihj}^{(p)}(s,t)=\sum _{l\notin \mathcal{T}}\sum _{m\in \mathcal{I}}{\int }_s^t\frac{P_{0,hl}^{(p)}(s,u-)P_{0,mj}^{(p)}(u,t)}{E{Y}_{1l}^{(p)}(u)}d{M}_{ilm}^{(p)}(u),0\le s\text{<t}\le \tau ,p=1,2,$$

for i = 1, …, n_p

Remark 2. The functions ${\gamma }_{ihj}^{(p)}(s,t),p=1,2,$ in Theorem 1 are the influence functions of the Aalen–Johansen estimator of $P_{0,hj}^{(p)}(s,t).$

A consistent (in probability) estimator of the variance ${\omega }_{hj}^2(s)$ is

$${\widehat{\omega }}_{hj}^2(s)=\frac{n_2}{(n_1+n_2)n_1}\sum _{i=1}^{n_1}{\left[{\int }_{(s,\tau ]}{\widehat{W}}_{hj}(t){\widehat{\gamma }}_{ihj}^{(1)}(s,t)dm(t)\right]}^2+\frac{n_1}{(n_1+n_2)n_2}\sum _{i=1}^{n_2}{\left[{\int }_{(s,\tau ]}{\widehat{W}}_{hj}(t){\widehat{\gamma }}_{ihj}^{(2)}(s,t)dm(t)\right]}^2,$$

where ${\gamma }_{ihj}^{(p)}(s,t),p=1,2,$ are estimated by replacing the expectations with sample averages and the unknown parameters with their uniform consistent estimates. Now, Theorem 1 and ${\widehat{\omega }}_{hj}(s)$ can be used to construct a Z-test for the null hypothesis as:

$$\frac{{\widehat{Z}}_{hj}(s)}{{\widehat{\omega }}_{hj}(s)/\sqrt{\frac{n_1{n}_2}{n_1+n_2}}}.$$

The actual significance level can then be evaluated under the standard normal distribution as usual.

In some applications it may not be desirable to fix the starting point s. In such cases the scientific interest is on comparing $P_{0,hj}^{(1)}(s,\cdot )$ and $P_{0,hj}^{(2)}(s,\cdot )$ for all s ∈ [0, τ). The null hypothesis in this case is $H_0:P_{0,hj}^{(1)}(\cdot ,\cdot )=P_{0,hj}^{(2)}(\cdot ,\cdot )$ or, more compactly, $H_0:P_{0,hj}^{(1)}=P_{0,hj}^{(2)}.$ The following test statistic can be used for this hypothesis testing problem:

$${\widehat{Z}}_{hj}={\int }_{[0,\tau )}{\widehat{Z}}_{hj}(s)dm(s).$$

Theorem 2 below provides the asymptotic null distribution of the above test statistic.

Theorem 2. Suppose that conditions C1-C6 hold. Then under the null hypothesis

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{Z}}_{hj}\stackrel{d}{\to }{G}_{hj},$$

where $G_{hj}\sim N(0,{\eta }_{hj}^2)$ and

$${\eta }_{hj}^2=(1-\lambda )E{\left\{{\int }_{[0,\tau )}\left[{\int }_{(s,\tau ]}{W}_{hj}(t){\gamma }_{1hj}^{(1)}(s,t)dm(t)\right]dm(s)\right\}}^2+\lambda E{\left\{{\int }_{[0,\tau )}\left[{\int }_{(s,\tau )}{W}_{hj}(t){\gamma }_{1hj}^{(2)}(s,t)dm(t)\right]dm(s)\right\}}^2.$$

A consistent (in probability) estimator of ${\eta }_{\mathit{hj}}^2$ can be obtained by replacing the expectations by sample averages, λ by n₁/(n₁ + n₂), and W_hj(t) and ${\gamma }_{ihj}^{(p)}(s,t)$ by ${\widehat{W}}_{hj}(t)$ and ${\widehat{\gamma }}_{ihj}^{(p)}(s,t)$, respectively.

2.3. L²-norm-based and Kolmogorov–Smirnov-type tests

A linear test is not the optimal choice when the two transition probability curves under comparison cross at one or more time points. In this section, we propose alternative tests for such situations. The first test is a test based on an L² norm

$${\widehat{Q}}_{1hj}(s)={\left\{{{\int }_{(s,\tau ]}\left[{\widehat{D}}_{hj}(s,t)\right]}^{2}dm(t)\right\}}^{1/2},$$

for any (fixed) s ∈ [0, τ), while the second test is a Kolmogorov–Smirnov-type test

$${\widehat{Q}}_{2hj}(s)=\underset{t\in [s,\tau ]}{\sup }|{\widehat{D}}_{hj}(s,t)|.$$

The Kolmogorov–Smirnov-type test is related to the graphical hypothesis testing procedure proposed by Bluhmki et al. (2018). For applications where it is not desirable to fix the starting point s, the following test statistics can be used:

$${\widehat{Q}}_{1hj}={\left\{{\int }_{[0,\tau )}{\widehat{Q}}_{1hj}^2(s)dm(s)\right\}}^{1/2},$$

and

$${\widehat{Q}}_{2hj}=\underset{0\le s<t\le \tau }{\sup }|{\widehat{D}}_{hj}(s,t)|.$$

The asymptotic null distributions of these tests are complicated. However, significance level can be easily calculated numerically by proper simulation realizations from the null distribution of these test statistics. Theorem 3 provides the basis for an approach to properly simulate realizations from the null distributions of ${\widehat{Q}}_{1hj}(s),{\widehat{Q}}_{2hj}(s),{\widehat{Q}}_{1hj}$, and ${\widehat{Q}}_{2hj}$. Before stating Theorem 3 define the estimated functions

$${\widehat{B}}_{hj}(s,t)=\sqrt{1-\lambda }\frac{1}{\sqrt{n_1}}\sum _{i=1}^{n_1}{\widehat{W}}_{hj}(t){\widehat{\gamma }}_{ihj}^{(1)}(s,t){\xi }_i^{(1)}-\sqrt{\lambda }\frac{1}{\sqrt{n_2}}\sum _{i=1}^{n_2}{\widehat{W}}_{hj}(t){\widehat{\gamma }}_{ihj}^{(2)}(s,t){\xi }_i^{(2)},h,j\in \mathcal{I},0\le s<t\le \tau ,$$

where ${\left\{{\xi }_i^{\left(p\right)}\right\}}_{i=1}^{n_p}$, p = 1, 2, are independent draws from N(0, 1).

Theorem 3. Suppose that conditions C1-C6 hold. Then, the following are true:

• (i)
  Under the null hypothesis $H_0:P_{0,hj}^{(1)}(s,·)=P_{0,hj}^{(2)}(s,·)$, for any (fixed) s ∈ [0, τ),

  $$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{D}}_{hj}(s,·)⇝\sqrt{1-\lambda }{\mathbb{G}}_{1hj}(s,.)-\sqrt{\lambda }{\mathbb{G}}_{2hj}(s,.),$$

  and, conditionally on the observed data,

  $${\widehat{B}}_{hj}(s,.)⇝\sqrt{1-\lambda }{\mathbb{G}}_{1hj}(s,.)-\sqrt{\lambda }{\mathbb{G}}_{2hj}(s,.),$$

  where ${\mathbb{G}}_{1hj}(s,.)$ and ${\mathbb{G}}_{2hj}(s,.)$ are two independent tight zero-mean Gaussian processes with covariance functions

  $${\sigma }_{phj}(t_1,t_2;s)=E[W_{hj}(t_1){\gamma }_{1hj}^{(p)}(s,t_1)][W_{hj}(t_2){\gamma }_{1hj}^{(p)}(s_2,t_2)],p=1,2,$$

  for any t₁, t₂ ∈ [s, τ].
• (ii)
  Under the null hypothesis $H_0:P_{0,hj}^{(1)}=P_{0,hj}^{(2)}$

  $$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{D}}_{hj}⇝\sqrt{1-\lambda }{\mathbb{G}}_{1hj}-\sqrt{\lambda }{\mathbb{G}}_{2hj},$$

  and, conditionally on the observed data,

  $${\widehat{B}}_{hj}⇝\sqrt{1-\lambda }{\mathbb{G}}_{1hj}-\sqrt{\lambda }{\mathbb{G}}_{2hj},$$

  where ${\mathbb{G}}_{1hj}$ and ${\mathbb{G}}_{2hj}$ are two independent tight zero-mean Gaussian processes with covariance functions at the points v₁ = (s₁, t₁) and v₂ = (s₂, t₂) equal to

  $${\sigma }_{phj}({\upsilon }_1,{\upsilon }_2)=E[W_{hj}(t_1){\gamma }_{1hj}^{(p)}(s,t_1)][W_{hj}(t_2){\gamma }_{1hj}^{(p)}(s_2,t_2)],p=1,2.$$

Corollary 1. By Theorem 3 and the continuous mapping theorem it follows that under the null hypothesis

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{Q}}_{1hj}(s)\stackrel{d}{\to }{\left\{{\int }_{(s,\tau ]}{\left[\sqrt{1-\lambda }{\mathbb{G}}_{1hj}(s,t)-\sqrt{\lambda }{\mathbb{G}}_{2hj}(s,t)\right]}^{2}dm(t)\right\}}^{1/2},$$

and

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{Q}}_{2hj}(s)\stackrel{d}{\to }\underset{t\in [s,\tau ]}{\sup }|\sqrt{1-\lambda }{\mathbb{G}}_{1hj}(s,t)-\sqrt{\lambda }{\mathbb{G}}_{2hj}(s,t)|,$$

for any fixed s ∈ [0, τ). Similarly, under the null hypothesis

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{Q}}_{1hj}\stackrel{d}{\to }{\left({\int }_{[0,\tau )}\left\{{\int }_{(s,\tau ]}{\left[\sqrt{1-\lambda }{\mathbb{G}}_{1hj}(s,t)-\sqrt{\lambda }{\mathbb{G}}_{2hj}(s,t)\right]}^{2}dm(t)\right\}dm(s)\right)}^{1/2},$$

and

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{Q}}_{2hj}\stackrel{d}{\to }\underset{0\le s<t\le \tau }{\sup }|\sqrt{1-\lambda }{\mathbb{G}}_{1hj}(s,t)-\sqrt{\lambda }{\mathbb{G}}_{2hj}(s,t)|.$$

The asymptotic null distributions of the omnibus tests are quite complicated and, thus, they are of limited use in practical applications. However, Theorem 3 provides justification about a way to numerically calculate p-values through a simple simulation technique. This can be performed as follows. In light of Theorem 3, one can simulate from the asymptotic null asymptotic distributions of the tests ${\widehat{Q}}_{1hj}(s)$ and ${\widehat{Q}}_{2hj}(s)$, for a fixed s ∈ [0, τ], by simulating multiple versions of ${\left\{{\xi }_{ir}^{(1)}\right\}}_{i=1}^{n_1}$ and ${\left\{{\xi }_{ir}^{(2)}\right\}}_{i=1}^{n_2}$ independently from N(0,1) for r = 1, … , R, and then calculating a sample for the corresponding null distributions of ${\widehat{Q}}_{1hj}(s)$ and ${\widehat{Q}}_{2hj}(s)$ as

$${\left\{{{\int }_{(s,\tau ]}\left[{\widehat{B}}_{h,j,r}(s,t)\right]}^{2}dm(t)\right\}}^{1/2},r=1,\dots ,R$$

and ${\sup }_{t\in [s,\tau ]}\left|{\widehat{B}}_{h,j,r}(s,t)\right|$, r = 1, …, R, respectively, where

$${\widehat{B}}_{hj,r}(s,t)=\sqrt{1-\lambda }\frac{1}{\sqrt{n_1}}\sum _{i=1}^{n_1}{\widehat{W}}_{hj}(t){\widehat{\gamma }}_{ihj}^{(1)}(s,t){\xi }_{ir}^{(1)}-\sqrt{\lambda }\frac{1}{\sqrt{n_2}}\sum _{i=1}^{n_2}{\widehat{W}}_{hj}(t){\widehat{\gamma }}_{ihj}^{(2)}(s,t){\xi }_i^{(2)},r=1,\dots ,R.$$

Generating samples from the null distributions of the test statistics ${\widehat{Q}}_{1hj}$ and ${\widehat{Q}}_{2hj}$, given in Corollary 1, can be performed in a similar manner. Now, the significance level for each test can be calculated as the proportion of realizations from the corresponding null distribution that is greater than or equal to the calculated test statistic value from the observed data.

The tests ${\widehat{Q}}_{1hj}(s)$ and ${\widehat{Q}}_{2hj}(s)$, for a given s ∈ [0, τ), are consistent for every fixed alternative hypothesis with $P_{0,hj}^{(1)}(s,\cdot )\ne P_{0,hj}^{(2)}(s,\cdot )$. This follows from Theorem 2, the uniform consistency of the Aalen–Johansen estimator of the transition probabilities (Aalen and Johansen, 1978), condition C6, the continuity of these tests in ${\widehat{D}}_{hj}(s,t)$, and Lemma 14.15 in Van der Vaart (2000). The same conclusion also holds for the test statistics ${\widehat{Q}}_{1hj}$ and ${\widehat{Q}}_{2hj}$.

2.4. Extensions to more complex settings

Many complications that frequently occur in practice make the application of the proposed tests improper. An important example is the problem of incompletely observed absorbing states, where missingness occurs either due to the usual nonresponse or by the study design (Bakoyannis et al., 2019). A special case of this is the issue of missing causes of death in biomedical applications. In such cases, a complete case analysis, which discards cases with a missing cause of death, is well known to lead to biased estimates (Gao and Tsiatis, 2005; Lu and Liang, 2008; Bakoyannis et al., 2019). In general, more complicated cases require extensions of the standard Aalen–Johansen estimator, denoted by ${\tilde{P}}_{n,hj}(s,t)$, to consistently estimate the transition probabilities of interest over an interval [τ₁, τ₂] ⊂ [0, τ]. In such cases, one can replace the standard Aalen–Johansen estimator with another appropriate estimator ${\tilde{P}}_{n,hj}(s,t)$ in the testing procedures. Then, the linear test becomes

$${\tilde{Z}}_{hj}(s)={\int }_{(s,{\tau }_2]}{\tilde{D}}_{hj}(s,t)dm(t),$$

for any (fixed) s ∈ [τ₁, τ₂), where

$${\tilde{D}}_{hj}(s,t)={\widehat{W}}_{hj}(t)\left[{\tilde{P}}_{n_1,hj}^{(1)}(s,t)-{\tilde{P}}_{n_2,hj}^{(2)}(s,t)\right],{\tau }_1\le \text{s}\le t\le {\tau }_2,$$

while the L²-norm based and Kolmogorov–Smirnov-type tests become

$${\tilde{Q}}_{1hj}(s)={\left\{{{\int }_{(s,{\tau }_2]}\left[{\tilde{D}}_{hj}(s,t)\right]}^{2}dm(t)\right\}}^{1/2}$$

and

$${\tilde{Q}}_{2hj}(s)=\underset{t\in [s,{\tau }_2]}{\sup }|{\tilde{D}}_{hj}(s,t)|.$$

The following conditions ensure the validity of the proposed testing procedures for the null hypothesis $H_0:{\tilde{P}}_{n_1,hj}^{(1)}(s,·)={\tilde{P}}_{n_2,hj}^{(2)}(s,·)$ in more complex settings.

D1. The estimator ${\tilde{P}}_{n,hj}(s,\cdot )$ is consistent in the sense

$$\underset{t\in [s,{\tau }_2]}{\sup }|{\tilde{P}}_{n,hj}(s,t)-P_{0,hj}(s,t)|\stackrel{p}{\to }0,$$

for any (fixed) s ∈ [τ₁, τ₂).

D2. The estimator ${\tilde{P}}_{n,hj}(s,·)$ is an asymptotically linear estimator with

$$\sqrt{n}[{\tilde{P}}_{n,hj}(s,t)-P_{0,hj}(s,t)]=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\varphi }_{ihj}(s,t)+o_p(1),$$

with {ϕ_hj(s, t) : t ∈ [s, τ₂]} being a P-Donsker class for any s ∈ [τ₁, τ₂].

D3. The empirical versions of the influence functions ${\widehat{\varphi }}_{ihj}(s,t)$ satisfy

$$\underset{t\in [s,{\tau }_2]}{\sup }\left|n^{-1/2}\sum _{i=1}^n[{\widehat{\varphi }}_{ihj}(s,t)-{\varphi }_{ihj}(s,t)]{\xi }_i\right|\stackrel{p}{\to }0,$$

where ξ_i are independent random draws from N(0, 1).

Remark 3. Condition D2 is sufficient for establishing the weak convergence of the estimator ${\tilde{P}}_{n,hj}(s,·)$ to a tight mean-zero Gaussian process. Condition D3 along with the conditional multiplier central limit theorem (Van Der Vaart and Wellner, 1996; Kosorok, 2008) and condition D2, provide a simulation approach for the construction of simultaneous confidence bands (Kosorok, 2008). Therefore, conditions D1-D3 are expected to have been established in works extending the standard Aalen–Johansen estimator to more complex settings. This is the case, for example, for the nonparametric estimator of the transition probability matrix with incompletely observed absorbing states (Bakoyannis et al., 2019).

Hypothesis testing in more complex settings can be simply performed by replacing the influence functions ${\gamma }_{ihj}^{(p)}(s,t),p=1,2,$ of the standard Aalen–Johansen estimator with the influence functions ${\varphi }_{ihj}^{(p)}(s,t)$ of the estimator ${\tilde{P}}_{n,hj}(s,t)$. The theorems stated below justify the direct use of the proposed tests in more complex situations. Before stating those theorems define the functions

$${\widehat{B}}_{hj}(s,t)=\sqrt{1-\lambda }\frac{1}{\sqrt{n_1}}\sum _{i=1}^{n_1}{\widehat{W}}_{hj}(t){\widehat{\varphi }}_{ihj}^{(1)}(s,t){\xi }_{ir}^{(1)}-\sqrt{\lambda }\frac{1}{\sqrt{n_2}}\sum _{i=1}^{n_2}{\widehat{W}}_{hj}(t){\widehat{\varphi }}_{ihj}^{(2)}(s,t){\xi }_i^{(2)},h,j\in \mathcal{I},{\tau }_1\le s<t\le {\tau }_2,$$

where ${\left\{{\xi }_i^{(p)}\right\}}_{i=1}^{n_p},p=1,2,$ are independent draws from N(0, 1).

Theorem 4. Suppose that conditions C2, C6, D1 and D2 hold. Then under the null hypothesis

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\tilde{Z}}_{hj}(s)\stackrel{d}{\to }{\tilde{G}}_{hj}(s),$$

for any (fixed) s ∈ [τ₁, τ₂), where ${\widehat{G}}_{hj}(s)\sim N(0,{\theta }_{hj}^2(s))$ and

$${\theta }_{hj}^2(s)=(1-\lambda )E{\left[{\int }_{(s,{\tau }_2]}{W}_{hj}(t){\varphi }_{1hj}^{(1)}(s,t)dm(t)\right]}^2+\lambda E{\left[{\int }_{(s,{\tau }_2]}{W}_{hj}(t){\varphi }_{1hj}^{(2)}(s,t)dm(t)\right]}^2.$$

The proof of Theorem 4 involves the same arguments to those used in the proof of Theorem 1 given in the Appendix.

Theorem 5. Assume that conditions C2, C6, and D1-D3 are satisfied. Then, under the null hypothesis and for s ∈ [τ₁, τ₂)

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\tilde{D}}_{hj}(s,·)⇝\sqrt{1-\lambda }{\tilde{\mathbb{G}}}_{1hj}(s,·)-\sqrt{\lambda }{\tilde{\mathbb{G}}}_{2hj}(s,·),$$

and, conditionally on the observed data,

$${\tilde{B}}_{hj}(s,·)⇝\sqrt{1-\lambda }{\tilde{\mathbb{G}}}_{1hj}(s,\cdot )-\sqrt{\lambda }{\tilde{\mathbb{G}}}_{2hj}(s,\cdot ),$$

where ${\tilde{\mathbb{G}}}_{1hj}(s,\cdot )$ and ${\tilde{\mathbb{G}}}_{2hj}(s,\cdot )$ are two independent tight zero-mean Gaussian processes with covariance functions

$${\tilde{\sigma }}_{hjp}(t_1,t_2;s)=E[W_{hs}(t_1){\varphi }_{1hj}^{(p)}(s,t_1)][W_{hj}(t_2){\varphi }_{1hj}^{(p)}(s,t_2)],p=1,2.$$

The proof of Theorem 5 follows from similar arguments to those used in the proof of Theorem 3 given in the Appendix.

2.4.1. Missing absorbing states

In many settings one can observe that a process has arrived at some absorbing state, but the actual absorbing state is unobserved for some study participants, such as in cases with missing causes of death. For such situations, Bakoyannis et al. (2019) proposed a nonparametric maximum pseudolikelihood estimator (NPMPLE) under a missing at random assumption. To review this estimator, let Δ_ij be an indicator variable with Δ_ij = 1 if the ith observation arrived at the absorbing state $j\in \mathcal{I}$, and Δ_ij = 0 otherwise. Also, let R_i be another indicator variable with R_i = 1 indicating that the absorbing state of the ith observation has been successfully observed. Finally, let π_j(O_i, β₀) be the probability that Δ_ij = 1 given the fully observed data O_i, under a parametric model indexed by an unknown Euclidean parameter β₀. In this setting, the cumulative transition intensities can be estimated using the NPMPLE:

$${\tilde{A}}_{n,hj}(t)={\int }_0^t\frac{{\sum }_{i=1}^{n}d{\tilde{N}}_{ihj}(u;{\widehat{\beta }}_n)}{{\sum }_{i=1}^n{Y}_{ih}(u)},h\ne j,j\in \mathcal{T},$$

where

$${\tilde{N}}_{ihj}(t;{\widehat{\beta }}_n)=[R_i{\text{Δ}}_{ij}+(1-R_{ij}){\pi }_j({\mathbf{O}}_i,{\widehat{\beta }}_n)]\sum _{l\in \mathcal{T}}{N}_{ihl}(t),$$

with ${\widehat{\beta }}_n$ being a consistent estimator of β₀. The transition probability matrix can then be estimated as

$${\tilde{P}}_n(s,t)=\prod _{(s,t]}[I+d{\tilde{A}}_n(u)],s,t\in [0,\tau ],$$

where the components of the matrix ${\tilde{\mathbf{A}}}_n(u)$ are ${\tilde{A}}_{n,hj}(u)$. By Theorems 1 and 2 in Bakoyannis et al. (2019) and calculations provided in the proof of Theorem 2 in the same source, the NPMPLE estimator satisfies the conditions D1-D3 above. Therefore, if the conditions in Bakoyannis et al. (2019) and the conditions C2 and C6 above are satisfied, two-sample comparison can be performed by utilizing the NPMPLE of the transition probabilities along with the corresponding influence functions in the proposed tests. This is justified by Theorems 4 and 5 above.

2.4.2. Non-Markov processes

Trivially, the Aalen–Johansen estimator ${\widehat{P}}_{n,hj}(0,·)$ is uniformly consistent for the transition probability P_hj(0, ·) even under a non-Markov process (Datta and Satten, 2001; Titman, 2015). When the interest lies on the marginal Pr(X(t) = j|X(s) = h), i.e. unconditionally on the prior history ${\mathcal{F}}_{s^{-}}$, for some s > 0, under a non-Markov process, then the landmark Aalen–Johansen estimator is consistent for Pr(X(t) = j|X(s) = h) (Putter and Spitoni, 2018) under the conditions of Datta and Satten (2001) and, also, the assumption that Pr(X(s) = h) > 0. The landmark Aalen–Johansen estimator is essentially equivalent to the standard Aalen–Johansen estimator, except for the fact that only observations with X(s) = h are considered. This is achieved by considering the modified counting and at-risk processes ${\tilde{N}}_{ihj}(t)=N_{ihj}(t)I(X(s)=h)$ and ${\tilde{Y}}_{ih}(t)=Y_{ih}(t)I(X(s)=h)$, for t ≥ s. Therefore, the influence functions of the landmark Aalen–Johansen estimator are the same to that of the standard Aalen–Johansen estimator, with the only exception that the former involves the modified ${\tilde{N}}_{ihj}(t)$ and ${\tilde{Y}}_{ih}(t)$ instead of the standard counting and at-risk processes N_ihj(t) and Y_ih(t). Consequently, it is clear that conditions D1–D3 are satisfied if Pr(X(s) = h) > 0 and, also, if the conditions in Datta and Satten (2001) hold. Thus, in light of Theorems 4 and 5, the proposed nonparametric tests can be used with non-Markov processes by utilizing the landmark Aalen–Johansen estimator.

2.4.3. Comparison of state occupation probabilities

The proposed tests can be easily adapted for the comparison of state occupation probabilities $\mathrm{Pr}\left(X\right(t)=j)\equiv P_{0j}\left(t\right)={\sum }_{{h\in \mathcal{T}}^c}{P}_{0,h}\left(0\right)P_{0,hj}(0,t)$, as these are simple linear combinations of the transition probabilities. The state occupation probabilities describe the marginal behavior, i.e. unconditional on the prior history, of the processes and are of interest in many applications, such as in HIV studies focusing on the event history of patients in HIV care (Lee et al., 2018). It is important to note that these probabilities can be consistently estimated based on the Aalen–Johansen estimator of the transition probabilities even in non-Markov processes (Datta and Satten, 2001). An obvious consistent estimator of P_0,h(0) is

$${\widehat{P}}_{n,h}(0)=\frac{1}{n}\sum _{i=1}^{n}I(X_i(0)=h),h\in {\mathcal{T}}^c.$$

By the continuous mapping theorem and the uniform consistency of the Aalen–Johansen estimator, the estimator of the state occupation probabilities ${\widehat{P}}_{n,j}(t)={\sum }_{h\in {\mathcal{T}}^c}{\widehat{P}}_{n,h}(0){\widehat{P}}_{n,hj}(0,t),j\in \mathcal{I},t\in [0,\tau ]$, is uniformly consistent for P_0,j(t). Also, it is not hard to see that, by the asymptotic linearity of the Aalen–Johansen estimator, ${\widehat{P}}_{n,j}(t)$ is an asymptotically linear estimator with

$$\begin{array}{l}\sqrt{n}[{\widehat{P}}_{n,j}(t)-P_{0,j}(t)]=\frac{1}{\sqrt{n}}\sum _{i=1}^n\sum _{h\in {\mathcal{T}}^c}\{P_{0,h}(0){\gamma }_{ihj}(0,t)+P_{0,hj}(0,t)[I(X_i(0)=h)-P_{0,h}(0)]\}+o_p(1)\\ \equiv \frac{1}{\sqrt{n}}\sum _{i=1}^n{\psi }_{ij}(t)+o_p(1).\end{array}$$

The class {ψ_j(t) : t ∈ [0, τ]} formed by the influence functions is P-Donsker. This property is a consequence of the Donsker property of the classes {γ_hj(0, t) : t ∈ [0, τ]} for all $h\in {\mathcal{T}}^c$ and $j\in \mathcal{I}$, as it is argued in the proof of Theorem 1 in the Appendix, the total boundedness of the class of fixed functions {P_0,hj(0, t) : t ∈ [0, τ]} as a result of condition C5, and Corollary 9.32 in Kosorok (2008). Therefore, conditions D1 and D2 are satisfied. Finally, condition D3 is also satisfied by the fact the ψ_ij(t), $j\in \mathcal{I}$, is a linear combination of γ_ihj (0, t), $h\in {\mathcal{T}}^c$, the triangle inequality, and arguments similar to those used in the proof of Theorem 3 in the Appendix. Consequently, Theorems 4 and 5 provide a rigorous justification about the use of the proposed tests for comparing state occupation probabilities based on the aforementioned estimator.

3. Simulation studies

To evaluate the finite sample performance of the proposed test statistics, we conducted a simulation study. We considered a Markov process with 2 transient states {1, 2} and 1 absorbing state {3}, under the illness-death model without recovery (Andersen et al., 2012). This model is illustrated in Figure 1. In this simulation study, we focused on the null hypothesis $H_0:P_{0,12}^{(1)}(0,·)=P_{0,12}^{(2)}(0,·)$. Initially, we independently generated the times from state 1 to states 2 and 3 by assuming the cumulative transition intensities $A_{0,12}^{(p)}(t)={\alpha }_{1p}t$, for p = 1, 2, and $A_{0,13}^{(1)}(t)=A_{0,13}^{(2)}(t)=t/2$. For observations that first arrived at the transient state 2, we generated the time from state 2 to the absorbing state 3, assuming a cumulative transition intensity $A_{0,23}^{(p)}(t)={\alpha }_{2p}t,p=1,2.$ Under this set-up the transition probability of interest was

$$P_{0,12}^{(p)}(s,t)=\frac{{\alpha }_{1p}[e^{{\alpha }_{2p}(s-t)}-e^{({\alpha }_{1p}+0.5)(s-t)}]}{{\alpha }_{1p}-{\alpha }_{2p}+0.5},p=1,2.$$

Different scenarios were considered according to the parameter values α₁ = (α₁₁, α₂₁) and α₂ = (α₁₂, α₂₂). In simulation scenarios 1 to 4 we simulated data under the null hypothesis with α₁ = α₂ ≡ α. This common parameter was set to (1, 0.5), (1.4, 0.75), (1.2, 0.25), and (0.6, 0.25) under scenarios 1, 2, 3, and 4, respectively. In simulation scenarios 5 to 8 we simulated data under the alternative hypothesis. In these cases, the parameter α₁ was set to (0.6, 0.25), (0.6, 0.25), (1, 0.5), and (0.8, 0.25) for scenarios 5, 6, 7, and 8, respectively. The corresponding figures for the parameter α₂ were (0.9, 0.25), (1.2, 0.25), (1.4, 0.75), and (1.4, 0.75). Right censoring times were independently simulated from Exp(0.25). Different sample sizes n_p, p = 1, 2, of the two groups were also considered. 2000 datasets were simulated for each scenario, and the L² distance test and Kolmogorov–Smirnov-type test were calculated using 1000 independent simulations of ${\left\{{\xi }_i^{(1)}\right\}}_{i=1}^{n_1}$ and ${\left\{{\xi }_i^{(2)}\right\}}_{i=1}^{n_2}$ from N(0, 1). Finally, we considered the weight function

$${\widehat{W}}_{12}(t)=\frac{{\prod }_{l=1}^2{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)}{\left\{{\sum }_{l=1}^2[{\overline{Y}}_l^{(1)}(t)+{\overline{Y}}_l^{(2)}(t)]\right\}},$$

in all cases. We also provide simulation results based on the weight function ${\widehat{W}}_{12}(t)=I[{\prod }_{l=1}^2{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)>0]$ in the Supplemental Online Material.

Figure 1:

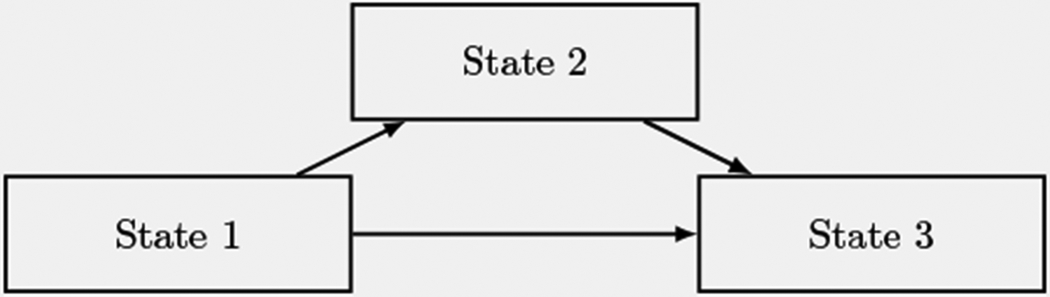
Illness-death model without recovery assumed in the simulation study.

Simulation results regarding the empirical type I error rates are presented in Tables 1 and 2, respectively. Under these scenarios, the empirical type I errors rates for all tests were close to the nominal α levels, even in situations with small sample sizes. Thus, these results provide numerical evidence for the validity of the proposed hypothesis testing procedures under H₀. Simulation results regarding the empirical power levels under alternative hypotheses with non-crossing transition probabilities are presented in Table 3. Under these scenarios, the empirical power levels increased with sample size and, also, with a more pronounced difference between the two groups, as expected. These results provide numerical evidence for the consistency of the proposed tests with non-crossing transition probabilities. The linear test exhibited more power compared to the Kolmogorov–Smirnov-type test in such cases. Simulation results regarding the empirical power levels under alternative hypotheses with crossing transition probabilities are presented in Table 4. These scenarios illustrate numerically that the linear test can exhibit substantially lower power levels compared to the omnibus tests, for alternative hypotheses with crossing transition probability curves. The empirical power of the tests increased with sample size and with a more pronounced difference between the two groups.

Table 1:

Simulation results about empirical type I error rates for the linear test (Linear), the L²-norm-based test (L²), and the Kolmogorov–Smirnov-type test (KS) for testing $H_0:P_{0,12}^{(1)}(0,\cdot )=P_{0,12}^{(2)}(0,\cdot )$, under simulation scenarios 1 and 2.

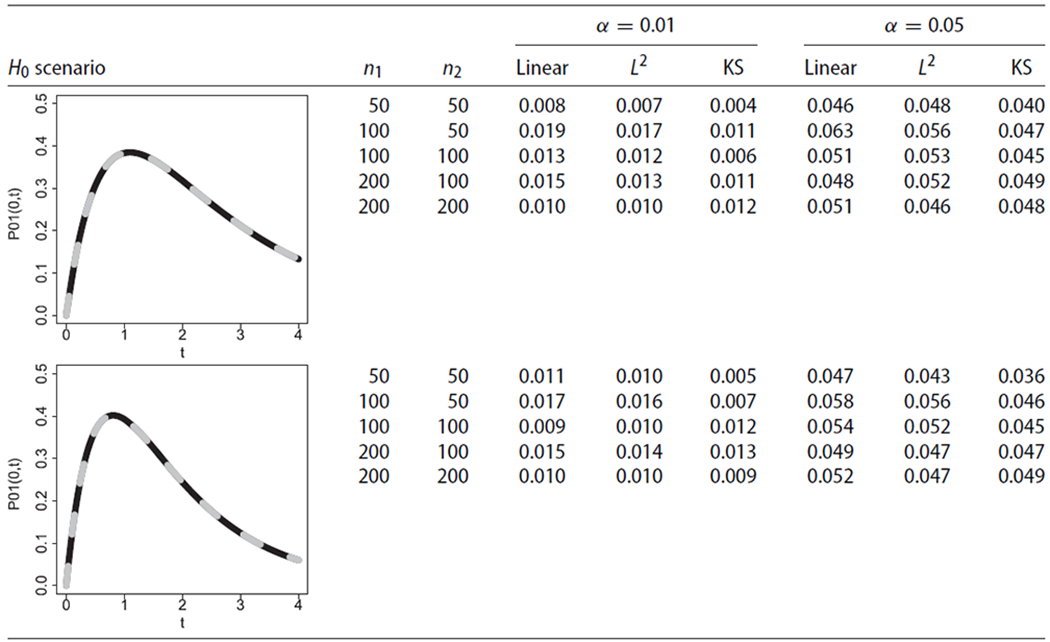Note: The weight function was ${\widehat{W}}_{12}(t)={\prod }_{l=1}^2{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)/\{{\sum }_{l=1}^2[{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)]\}.$

Table 2:

Simulation results about empirical type I error rates for the linear test (Linear), the L²-norm-based test (L²), and the Kolmogorov–Smirnov-type test (KS) for testing $H_0:P_{0,12}^{(1)}(0,\cdot )=P_{0,12}^{(2)}(0,\cdot )$, under simulation scenarios 3 and 4.

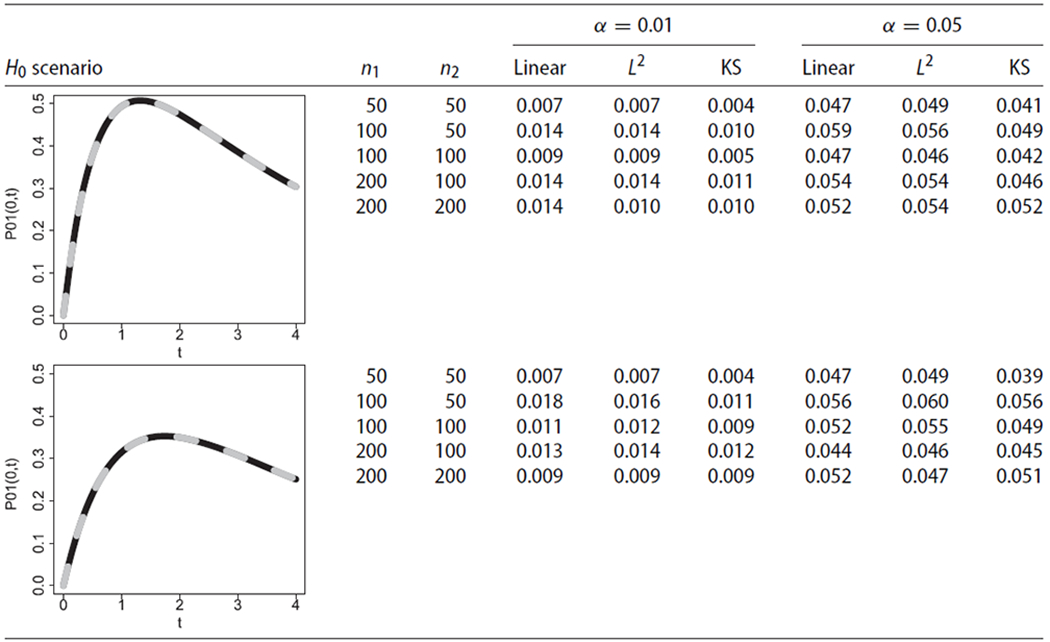Note: The weight function was ${\widehat{W}}_{12}(t)={\prod }_{l=1}^2{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)/\{{\sum }_{l=1}^2[{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)]\}.$

Table 3:

Simulation results about empirical power levels for the linear test (Linear), the L²-norm-based test (L²), and the Kolmogorov–Smirnov-type test (KS) for testing $H_0:P_{0,12}^{(1)}(0,\cdot )=P_{0,12}^{(2)}(0,\cdot )$ under simulation scenarios 5 and 6.

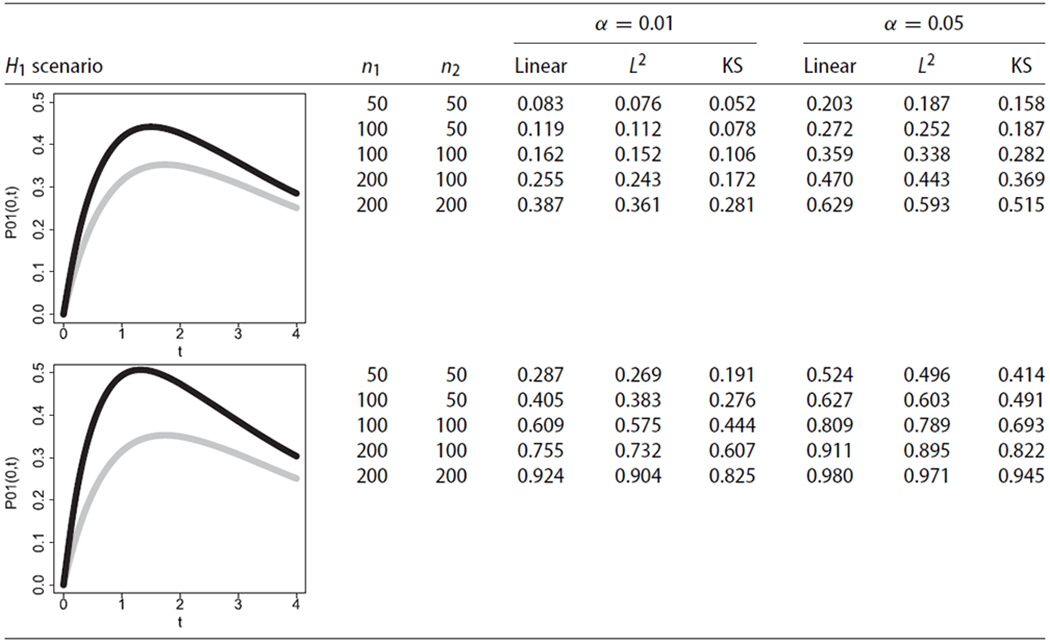Note: The weight function was ${\widehat{W}}_{12}(t)={\prod }_{l=1}^2{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)/\{{\sum }_{l=1}^2[{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)]\}.$

Table 4:

Simulation results about empirical power levels for the linear test (Linear), the L²-norm-based test (L²), and the Kolmogorov–Smirnov-type test (KS) for testing $H_0:P_{0,12}^{(1)}(0,\cdot )=P_{0,12}^{(2)}(0,\cdot )$ under simulation scenarios 7 and 8. The weight function was ${\widehat{W}}_{12}(t)={\prod }_{l=1}^2{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)/\{{\sum }_{l=1}^2[{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)]\}.$

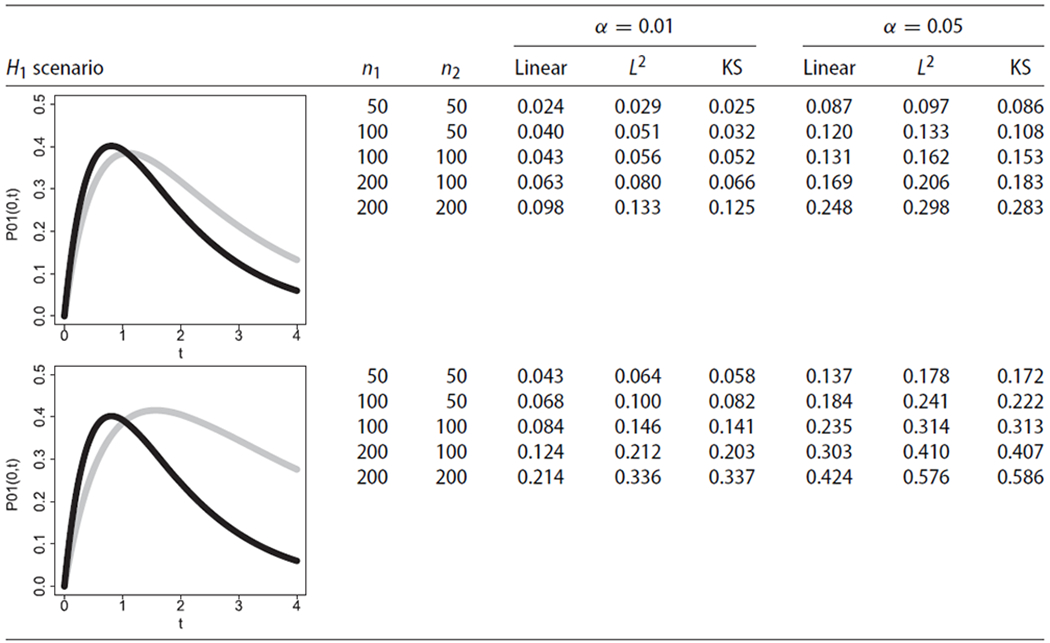Simulation results based on the weight function ${\widehat{W}}_{12}(t)=I[{\prod }_{l=1}^2{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)>0]$ are provided in the Supplemental Online Material. These results are similar to those presented here. However, with the latter weight choice, the Kolmogorov–Smirnov-type test appears to exhibit higher power levels for scenarios with non-crossing transition probability curves. Moreover, the L²-norm-based test appears to be the most powerful test in scenarios with crossing transition probability curves, particularly under a smaller difference between the two groups.

4. Data analysis

In this section we analyze the data on treatment of early breast cancer from the European Organization for Research and Treatment of Cancer (EORTC) trial 10854. This randomized clinical trial was conducted to evaluate whether the combination of surgery with polychemotherapy is beneficial to early breast cancer patients compared to surgery alone. The original analysis of this clinical trial was presented in Van der Hage et al. (2001).

In this trial, 1395 patients where randomly assigned to the surgery group and 1398 to the surgery plus polychemotherapy group. The data set contains information about the time to cancer relapse or death. Therefore, an illness-death model is a natural choice for this data set. It is important to note that the transition probability to relapse, which was not analyzed in the original analysis of this trial, is a non-monotonic function of time as patients can move to the “death” state after relapse. Thus, standard survival and competing risks analysis methods are not applicable for this transition probability. Here, we focus on this probability which can be interpreted as the probability of being alive and in relapse. The estimated transition probabilities of relapse in the two intervention groups are presented in Figure 2. Based on Figure 2, the probability of being alive and in relapse was lower in the group that received polychemotherapy during surgery. To perform hypothesis testing here we considered the weight function ${\widehat{W}}_{12}(t)={\prod }_{l=1}^2{\overline{Y}}_l^{(1)}(t){\overline{Y}}_l^{(2)}(t)/\{{\sum }_{l=1}^2[{\overline{Y}}_l^{(1)}(t)+{\overline{Y}}_l^{(2)}(t)]\}$. For the L²-norm-based and Kolmogorov–Smirnov-type tests we considered 1000 standard normal simulation realizations. The p-value from the linear test was 0.001, while the p-values from the L²-norm-based and Kolmogorov–Smirnov-type tests were both equal to 0.002. These results provide evidence for the superiority of the surgery plus polychemotherapy combination with respect to the transition probability of relapse, in early breast cancer patients.

Figure 2:

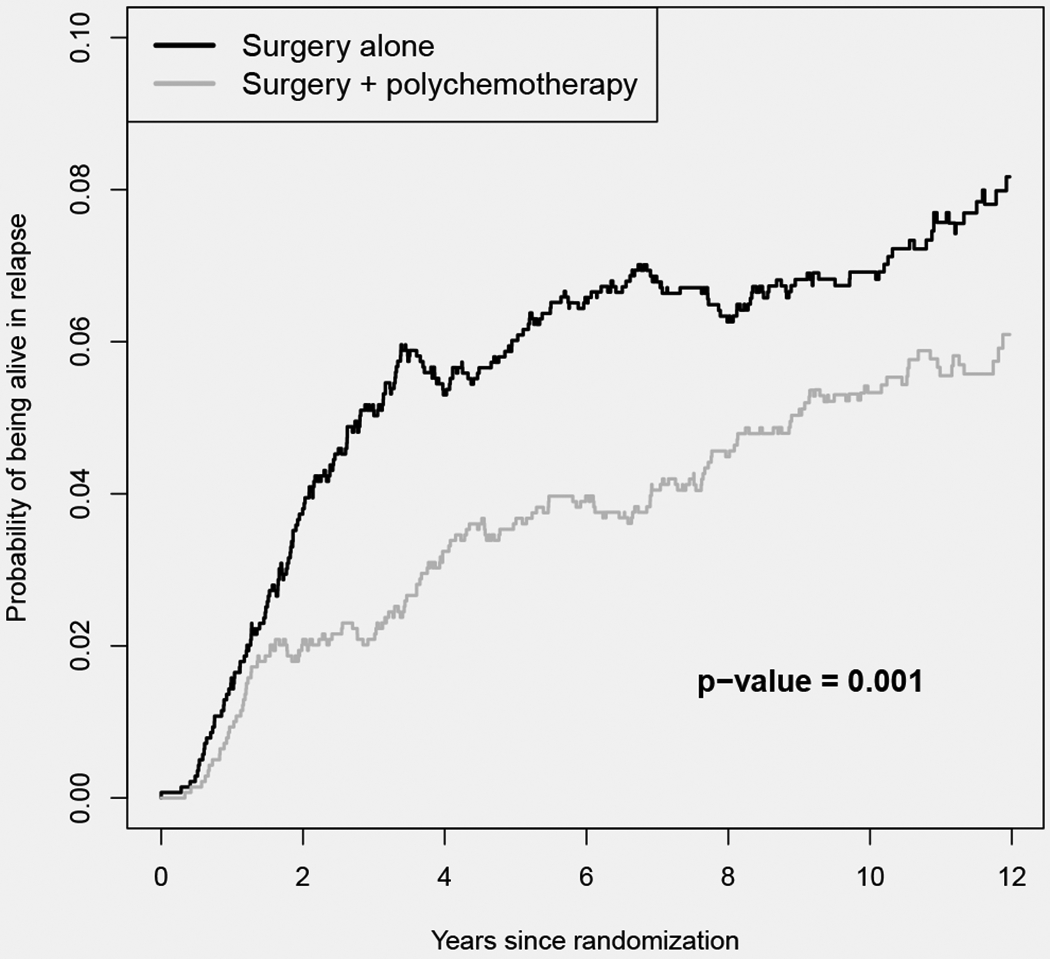
Transition probabilities of being alive in relapse by intervention group in the EORTC Trial 10854.

5. Concluding remarks

This paper addressed the issue of direct nonparametric two-sample comparison of transition probabilities P_0,hj(s, ·), for some (fixed) s ∈ [0, τ), for a particular transition h → j in a continuous time nonhomogeneous Markov process with a finite state space. The proposed tests were a linear nonparametric test, an L²-norm-based test and a Kolmogorov–Smirnov-type test. Rigorous approaches to evaluate the significance level grounded on modern empirical process theory were provided. Moreover, the L²-norm-based and Kolmogorov–Smirnov-type tests were argued to be consistent against any fixed alternative hypothesis. Additionally, we proposed versions of the tests for the null hypothesis $H_0:P_{0,\mathit{hj}}^{(1)}(·,·)=P_{0,\mathit{hj}}^{(2)}(·,·)$, that is for all s ∈ [0, τ) and t ∈ [s, τ]. We also considered extensions of the tests to more complex situations such as cases with missing absorbing states (Bakoyannis et al., 2019) and non-Markov processes (Putter and Spitoni, 2018). The simulation study provided numerical evidence for the validity of the proposed testing procedures, which exhibited good performance even with small sample sizes. Finally, a data analysis of a clinical trial on early breast cancer illustrated the utility of the proposed tests in practice.

The importance of the weight function W_hj(t) in the proposed test statistics lies on the fact that it essentially restricts the comparison time interval to a time interval where the risk set sizes are non-zero for both groups under comparison. Moreover, a weight function can be used to assign less weight to time points with less observations at risk, where the estimated transition probabilities can be unstable.

It has to be noted that the linear nonparametric test can be inconsistent under some alternative hypotheses with crossing transition probability curves. This is because, in such cases, the true area under the weighted difference curve can be equal to zero, since positive and negative differences of the same magnitude cancel out. In less extreme cases with crossing, the linear test is expected to be less powerful compared to the L²-norm-based and Kolmogorov–Smirnov-type tests. This phenomenon was illustrated numerically in our simulation studies.

The issue of nonparametric comparison of transition probabilities in general nonhomogeneous Markov processes has received little attention in the literature. To the best of our knowledge, the only fully nonparametric approach for comparing the transition probabilities for a particular transition in general nonhomogeneous Markov processes is a graphical procedure proposed by Bluhmki et al. (2018). This proposal is based on the construction of a simultaneous confidence band for the difference between the transition probabilities of two groups. This approach relies on the same statistic as our Kolmogorov–Smirnov-type test, that is the supremum of the absolute weighted difference between the Aalen–Johansen estimators of the two groups, and thus it involves the same sampling distribution. Estimation of the 1 − α percentile of the corresponding asymptotic null distribution is achieved through a resampling procedure which is similar to ours. As Bluhmki et al. (2018) state “The confidence band for the difference can also be viewed as a Kolmogorov–Smirnov-type asymptotic level α test”. Thus, evaluating whether a (1 − α)% confidence band for the difference of the two transition probabilities by Bluhmki et al. (2018) does not fully include the line y = 0, is equivalent to assessing whether p-value<α based our Kolmogorov–Smirnov-type test, under the same weight function. However, the graphical approach by Bluhmki et al. (2018) does not provide the exact level of statistical significance and, also, our linear and L²-norm tests can be more powerful compared to the Kolmogorov–Smirnov-type test in certain settings, as shown in the simulation studies. More importantly, the justification of this approach was based on counting process theory arguments and not on modern empirical process theory. A consequence of that is that this approach cannot be directly adapted to more complex settings that are frequently occur in practice, such as cases with missing absorbing states. An important reason for this is that with more complex estimators, certain predictability conditions assumed by counting process and martingale theory techniques are violated. On the contrary, our proposed methods can be trivially adapted to many other complex settings, provided that appropriate estimators, in the sense of conditions D1–D3, of the transition probabilities exist. Such adaptations can be theoretically justified using the Theorems 4 and 5 provided in our manuscript. Such extensions, which are useful in many applications, include the situation with missing absorbing states and the case of nonparametric two-sample comparison of state occupation probabilities, presented in subsections 2.4.1 and 2.4.3, respectively.

An important future task from a practical standpoint is the implementation of the proposed tests in standard statistical software, such as R, for general use. While calculations for the proposed tests of $H_0:P_{0,\mathit{hj}}^{(1)}(s,·)=P_{0,\mathit{hj}}^{(2)}(s,·)$, for some (fixed) s ∈ [0, τ), can be fast, the tests of $H_0:P_{0,\mathit{hj}}^{(1)}(·,·)=P_{0,\mathit{hj}}^{(2)}(·,·)$ are quite computationally intensive, particularly with larger sample sizes. This is because they require calculating the influence functions for all the combinations of times s and t, with s < t, evaluated at the observed transition times. For this case, efficient code implementation along with parallel computing would be useful in practice.

A. Outlines of proofs

Outlines of the proofs of Theorems 1 and 2 are provided below. The proofs of Theorems 3 and 4 follow from similar arguments and, therefore, are omitted. The proofs rely on empirical process theory techniques (Van Der Vaart and Wellner, 1996; Kosorok, 2008). Before providing the proofs it is useful to introduce some notation. First, let $\mathcal{O}$ be the sample space, and O an arbitrary sample point in $\mathcal{O}$. Now, define ${\mathbb{P}}_{n}f=\frac{1}{n}{\sum }_{i=1}^{n}f(O_i),$ for some measurable function $f:\mathcal{O}\mapsto \mathbb{R}$. Also, define $Pf={\int }_{\mathcal{O}}fdP$ to be the expectation of f under the probability measure P on the measurable space $(\mathcal{O},\mathcal{A})$, where $\mathcal{A}$ is a σ-algebra on $\mathcal{O}$. For simplicity, but without loss of generality, we set the starting point s = 0 in the following proofs. It has to be noted that conditions C1 and C3–C5 imply the uniform consistency of the standard Aalen–Johansen estimator. This can be shown using similar arguments to those used in the proof of Theorem 1 in Bakoyannis et al. (2019). In what follows, C will denote a universal constant that may vary from place to place. Before providing the proofs of Theorems 1 and 2, we state and prove two useful lemmas.

Lemma 1. Let h(t) be a fixed and uniformly bounded function on [0, τ] and N(t) be an arbitrary counting process with P[N(τ)]² < ∞. Then, the class of functions

$${\mathcal{F}}_1=\left\{{\int }_s^{t}h(u)dN(u):s\in [0,\tau ],t\in [s,\tau ]\right\}$$

is P-Donsker.

Proof. Let ${\Vert h\Vert }_{Q,2}={(\int |h{|}^{2}dQ)}^{1/2}$ for any probability measure Q. Now, for any probability measure Q and any s₁, s₂ ∈ [0, τ], t₁ ∈ [s₁, τ], and t₂ ∈ [s₂, τ] it follows that

$$\Vert {\int }_{s_1}^{t_1}h(u)dN(u)-{\int }_{s_2}^{t_2}h(u)dN(u){\Vert }_{Q,2}\le \Vert {\int }_{t_1}^{t_2}h(u)dN(u){\Vert }_{Q,2}+\Vert {\int }_{s_1}^{s_2}h(u)dN(u){\Vert }_{Q,2}\le C(\Vert N(t_2)-N(t_1){\Vert }_{Q,2}+\Vert N(s_2)-N(s_1){\Vert }_{Q,2}).$$

By Lemma 22.4 in Kosorok (2008), it follows that the class Φ₁ = {N(t) : t ∈ [0, τ]} has a bounded uniform entropy integral (BUEI) with envelope 2N(τ), and is also pointwise measurable (PM). This implies that, for any s ∈ [0, τ] and t ∈ [s, τ] there exist an s_j ∈ [0, τ], j = 1, …, N(ϵ2‖ N(τ)‖_Q,2, Φ₁, L₂(Q)), and a t_i ∈ [s, τ], i = 1, …, N(ϵ2‖N(τ)‖_Q,2, Φ₁, L₂(Q)), such that ‖N(s) − N(s_j)‖_Q,2 < ϵ2‖N(τ)‖_Q,2 and ‖N(t) − N(t_i)‖_Q,2 < ϵ2‖N(τ)‖_Q,2, for any ϵ > 0 and any finitely discrete probability measure Q. Therefore, for any member of ${\mathcal{F}}_1$, there exist a ${\int }_s^{t_i}h(u)dN(u)$, for i, j = 1, … , N(ϵ, Φ₁, L₂(Q)), such that

$${\Vert {\int }_s^{t}h(u)dN(u)-{\int }_{s_j}^{t_i}h(u)dN(u)\Vert }_{Q,2}\le ϵ4C{\Vert N(\tau )\Vert }_{Q,2},$$

for any ϵ > 0 and any finitely discrete probability measure Q. Consequently, by the minimality of the covering number it follows that for any ϵ > 0 and any finitely discrete probability measure Q, we have that

$$N(ϵ4C{\Vert N(\tau )\Vert }_{Q,2},{\mathcal{F}}_1,L_2(Q))\le {[N(ϵ2{\Vert N(\tau )\Vert }_{Q,2},{\text{Φ}}_1,L_2(Q))]}^2,$$

which yields a BUEI for ${\mathcal{F}}_1$ with envelope 4CN(τ). Using similar arguments to those used in the example of page 142 of Kosorok (2008), it can be shown that the class ${\mathcal{F}}_1$ is also PM. Therefore, by Theorem 2.5.2 in Van Der Vaart and Wellner (1996), the class ${\mathcal{F}}_1$ is P-Donsker. □

Lemma 2. Let h(t) be a fixed and uniformly bounded function, Y(t) be an arbitrary at-risk process, and A(t) a continuous cumulative transition intensity function on [0, τ]. Then, the class of functions

$${\mathcal{F}}_2=\left\{{\int }_s^{t}h(u)Y(u)dA(u):s\in [0,\tau ],t\in [s,\tau ]\right\}$$

is P-Donsker.

Proof. It is not hard to show that for any probability measure Q and any s₁, s₂ ∈ [0, τ], t₁ ∈ [s₁, τ], and t₂ ∈ [s₂, τ] it follows that

$${\Vert {\int }_{s_1}^{t_1}h(u)Y(u)dA(u)-{\int }_{s_2}^{t_2}h(u)Y(u)dA(u)\Vert }_{Q,2}\le C(|A(t_2)-A(t_1)|+|A(s_2)-A(s_1)|).$$

Now, the class of fixed functions Φ₂ = {A(t) : t ∈ [0, τ]} is a compact subset of $\mathbb{R}$ as it consists of continuous functions defined on the compact set [0, τ]. Therefore, this class of fixed functions can be covered by C(1/ϵ) ϵ-balls and, thus, N(ϵ, Φ₂, | · |) ≤ C(1/ϵ). Consequently, for any s ∈ [0, τ] and t ∈ [s, τ] there exist an s_j ∈ [0, τ], j = 1, … , N (ϵ, Φ₂, | · |), and a t_i £ [s, τ], i = 1, … , N(ϵ, Φ₂, | · |), such that |A(s) − A(s_j)| < ϵ and |A(t) − A(t_j)| < ϵ, for any ϵ > 0 and any finitely discrete probability measure Q. Therefore, for any member of ${\mathcal{F}}_2$, there exist a ${\int }_{sj}^{t_i}h(u)dN(u)$, for i, j = 1, … , N(ϵ, Φ₂, | · |), such that

$${\Vert {\int }_s^{t}h(u)Y(u)dA(u)-{\int }_{s_j}^{t_i}h(u)Y(u)dA(u)\Vert }_{Q,2}\le 2Cϵ.$$

for any ϵ > 0 and any finitely discrete probability measure Q. Consequently, by the minimality of the covering number it follows that for any ϵ > 0 and any finitely discrete probability measure Q, we have that

$$N(ϵ2C,{\mathcal{F}}_1,L_2(Q))\le C{\left(\frac{1}{ϵ}\right)}^2,$$

which yields a BUEI for ${\mathcal{F}}_2$. Finally, similar arguments to those used in the proof of Lemma 1 lead to the conclusion that the class ${\mathcal{F}}_2$ is P-Donsker. □

A.1. Proof of Theorem 1

Theorem 1 relies on the asymptotic linearity of the estimators ${\widehat{P}}_{n_p,hj}^{(p)},p=1,2$. This can be established by first utilizing the asymptotic linearity of the Nelson–Aalen estimators of the cumulative transition intensities and then by applying the functional delta method (Van der Vaart, 2000). The steps to achieve this utilize conditions C1 and C3–C5 and arguments similar to those used in the proof of Theorem 2 of Bakoyannis et al. (2019). After this analysis it can be shown that

$$\sqrt{n_p}[{\widehat{P}}_{n_p,hj}^{(p)}(s,t)-P_{0,hj}^{(p)}(s,t)]=\sqrt{n_p}{\mathbb{P}}_{n_p}{\gamma }_{hj}^{(p)}(s,t)+o_p(1),p=1,2,h,j\in \mathcal{I},$$

for 0 ≤ s ≤ t ≤ τ, where

$$\begin{array}{l}{\gamma }_{ihj}^{(p)}(s,t)=\sum _{l\notin \mathcal{T}}\sum _{m\in \mathcal{I}}{\int }_s^t\frac{P_{0,hl}^{(p)}(s,u-)P_{0,mj}^{(p)}(u,t)}{P{Y}_{1l}^{(p)}(u)}d{M}_{ilm}^{(p)}(u)\\ =\sum _{l\notin \mathcal{T}}\sum _{m\in \mathcal{I}}\left[{\int }_s^t\frac{P_{0,hl}^{(p)}(s,u-)P_{0,mj}^{(p)}(u,t)}{P{Y}_l^{(p)}(u)}d{N}_{ilm}^{(p)}(u)-{\int }_s^t\frac{P_{0,hl}^{(p)}(s,u-)P_{0,mj}^{(p)}(u,t)}{P{Y}_l^{(p)}(u)}{Y}_{il}^{(p)}{\text{(u)A}}_{0,lm}^{(p)}\right],p=1,2.\end{array}$$ (1)

The first integral in the brackets in the right side of (1) forms a P-Donsker class of functions indexed by s ∈ [0, τ] and t ∈ [s, τ], as a consequence of Lemma 1 and conditions C3 and C4. The second integral in the bracket in (1) also forms a P-Donsker class indexed by s ∈ [0, τ] and t ∈ [s, τ], by Lemma 2 and conditions C4 and C5. Therefore, the class

$${\mathcal{F}}_3=\{{\gamma }_{hj}^{(p)}(s,t):s\in [0,\tau ],t\in [s,\tau ],p=1,2\}$$

is P-Donsker by Corollary 9.32 in Kosorok (2008), as it is formed by the union of the classes $\{{\gamma }_{hj}^{(1)}(s,t):s\in [0,\tau ],t\in [s,\tau ]\}$ and $\{{\gamma }_{hj}^{(2)}(s,t):s\in [0,\tau ],t\in [s,\tau ]\}$ which consist of finite sums of functions that belong to P-Donsker classes. This implies that the Aalen–Johansen estimator converges weakly to a tight zero mean Gaussian process. Next, by condition C6 and the weak convergence of the Aalen–Johansen estimator it follows that

$$\underset{t\in [s,\tau ]}{\sup }\left|\left[{\widehat{W}}_{hj}\left(t\right)-W_{hj}\left(t\right)\right]\sqrt{\frac{n_1{n}_2}{n_1+n_2}}\left[{\widehat{P}}_{n_1,hj}^{\left(1\right)}\left(s,t\right)-{\widehat{P}}_{n_2,hj}^{\left(2\right)}\left(s,t\right)\right]\right|=o_p\left(1\right)O_p(1)=o_p(1),$$

for any (fixed) s ∈ [0, τ). Now, it is not hard to see that under the null hypothesis and by condition C2, the asymptotic linearity of the transition probability estimators, and the continuous mapping theorem:

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{Z}}_{hj}(s)=\sqrt{1-\lambda }\sqrt{n_1}{\mathbb{P}}_{n_1}{\int }_{(s,\tau ]}{W}_{hj}(t){\gamma }_{hj}^{(1)}(s,t)dm(t)-\sqrt{\lambda }\sqrt{n_1}{\mathbb{P}}_{n_2}{\int }_{(s,\tau ]}{W}_{hj}(t){\gamma }_{hj}^{(2)}(s,t)dm(t)+o_p(1).$$ (2)

for any (fixed) s ∈ [0, τ). By the Donsker property of the class ${\mathcal{F}}_3$ and Lemma 15.10 in Kosorok (2008), it follows that the classes {${\int }_s^t{W}_{hj}(u){\gamma }_{hj}^{(p)}(s,u)dm(u):i\in [s,\tau ]$}, p = 1, 2, are P-Donsker for any fixed s ∈ [0, τ). This implies that for t = τ,

$$\sqrt{n_p}{\mathbb{P}}_{n_p}{\int }_{(s,\tau ]}{W}_{hj}(u){\gamma }_{hj}^{(p)}(s,u)dm(u),p=1,2,$$

is asymptotically normally distributed with variance

$$P{\left[{\int }_{(s,\tau ]}{W}_{hj}(t){\gamma }_{hj}^{(p)}(s,t)dm(t)\right]}^2,p=1,2.$$

Finally, the statement of Theorem 1 follows from the independence between the two terms in the right side of (2), as a consequence of the fact that the two samples are independent.

A.2. Proof of Theorem 2

First, the estimators ${\widehat{P}}_{hj}^{(p)}(s,t),p=1,2$, are consistent uniformly in s ∈ [0, τ] and t ∈ [s, τ] by a continuity result for the Duhamel equation (Andersen et al., 2012) and the continuous mapping theorem (Kosorok, 2008). Next, by condition C6 and the weak convergence of the Aalen–Johansen estimator, as a consequence of its asymptotic linearity and the Donsker property of the class ${\mathcal{F}}_3$, it follows that

$$\underset{0\le s\le t\le \tau }{\sup }\left|\left[{\widehat{W}}_{hj}\left(t\right)-W_{hj}\left(t\right)\right]\sqrt{\frac{n_1{n}_2}{(n_1+n_2)}}\left[{\widehat{P}}_{n_1,h_j}^{\left(1\right)}\left(s,t\right)-{\widehat{P}}_{n_2,hj}^{\left(2\right)}\left(s,t\right)\right]\right|=o_p\left(1\right)O_p(1)=o_p(1).$$

Similarly to the proof of Theorem 2, under the null hypothesis and due to the asymptotic linearity of the transition probability estimators, and the continuous mapping theorem, it follows that

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{Z}}_{hj}=\sqrt{1-\lambda }\sqrt{n_1}{\mathbb{P}}_{n_1}{\int }_{[0,\tau )}\left[{\int }_{s,\tau }{W}_{hj}(t){\gamma }_{hj}^{(1)}(s,t)dm(t)\right]dm(s)-\sqrt{\lambda }\sqrt{n_2}{\mathbb{P}}_{n_2}{\int }_{[0,\tau )}\left[{\int }_{(s,\tau ]}{W}_{hj}(t){\gamma }_{hj}^{(2)}(s,t)dm(t)\right]dm(s)+o_p(1).$$ (3)

By the Donsker property of the class ${\mathcal{F}}_3$ and Lemma 15.10 in Kosorok (2008), it follows that the classes {${\int }_{[s,\tau )}\left[{\int }_{(u,\tau ]}{W}_{hj}(t){\gamma }_{hj}^{(p)}(u,t)dm(t)\right]dm(u):s\in [0,\tau ]$}, p = 1, 2, are P-Donsker. Thus, for s = 0,

$$\sqrt{n_p}{\mathbb{P}}_{n_p}{\int }_{[0,\tau )}\left[{\int }_{(u,\tau ]}{W}_{hj}(t){\gamma }_{hj}^{(p)}(u,t)dm(t)\right]dm(u),p=1,2,$$

is asymptotically normally distributed with variance

$$P{\left\{{\int }_{\left[0,\tau \right)}\left[{\int }_{\left(s,\tau \right]}{W}_{hj}\left(t\right){\gamma }_{hj}^{\left(p\right)}\left(s,t\right)dm\left(t\right)\right]dm\left(s\right)\right\}}^2,p=1,2.$$

Now, the statement of Theorem 2 follows from (3) and the independence of the two samples.

A.3. Proof of Theorem 3

As it was argued in the proof of Theorem 1

$$\underset{t\in \left[s,\tau \right]}{\sup }\left|\left[{\widehat{W}}_{hj}\left(t\right)-W_{hj}\left(t\right)\right]\sqrt{\frac{n_1{n}_2}{n_1+n_2}}\left[{\widehat{P}}_{n1,hj}^{\left(1\right)}\left(s,t\right)-{\widehat{P}}_{n2,hj}^{\left(2\right)}\left(s,t\right)\right]\right|=o_p\left(1\right),$$

for any (fixed) s ∈ [0, τ]. Due to the asymptotic linearity of the transition probability estimators ${\widehat{P}}_{n_p,hj}^{(p)}(s,t)$, for p = 1, 2, as argued in the proof of Theorem 1, along with condition C2, it follows that

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{D}}_{hj}\left(s,t\right)=\sqrt{1-\lambda }\sqrt{n_1}{\mathbb{P}}_{n_1}{W}_{hj}\left(t\right){\gamma }_{ihj}^{\left(1\right)}\left(s,t\right)-\sqrt{\lambda }\sqrt{n_2}{\mathbb{P}}_{n2}{W}_{hj}\left(t\right){\gamma }_{ihj}^{\left(2\right)}\left(s,t\right)+o_p\left(1\right).$$

Now, by the Donsker property of the class ${\mathcal{F}}_3$ and condition C6, it follows that $\{W_{hj}(t){\gamma }_{hj}^{(p)}(s,t):p=1,2,t\in [s,\tau ]\},$ is a P-Donsker class for any (fixed) s ∈ [0, τ). Therefore, by the independence between the two samples, it follows that

$$\sqrt{\frac{n_1{n}_2}{n_1+n_2}}{\widehat{D}}_{hj}\left(s,\cdot \right)⇝\sqrt{1-\lambda }{\mathbb{G}}_{1hj}\left(s,.\right)-\sqrt{\lambda }{\mathbb{G}}_{2hj}\left(s,\cdot \right),$$

where ${\mathbb{G}}_{1hj}(s,\cdot )$ and ${\mathbb{G}}_{2hj}(s,\cdot )$ are two independent tight zero-mean Gaussian processes with covariance functions

$${\sigma }_{phj}(t_1,t_2;s)=P[W_{hs}(t_1){\gamma }_{hj}^{(p)}(s,t_1)][W_{hj}(t_2){\gamma }_{hj}^{(p)}(s,t_2)],p=1,2.$$

Now, define

$${\overline{B}}_{hj}(s,t)=\sqrt{1-\lambda }\sqrt{n_1}{\mathbb{P}}_{n_1}{W}_{hj}(t){\gamma }_{ihj}^{(1)}(s,t){\xi }_{ir}^{(1)}-\sqrt{\lambda }\sqrt{n_2}{\mathbb{P}}_{n_2}{W}_{hj}(t){\gamma }_{hj}^{(2)}(s,t){\xi }^{(2)},$$

where ξ^(p), p = 1, 2, are independent random draws from N(0,1). By the Donsker property of the class $\{W_{hj}(t){\gamma }_{hj}^{(p)}(s,t):p=1,2,t\in [s,\tau ]\},$ for $h,j\in \mathcal{I}$ and any (fixed) s ∈ [0, τ), and the conditional multiplier central limit theorem (Van Der Vaart and Wellner, 1996) it follows that

$$\sqrt{n_p}{\mathbb{P}}_{n_p}{W}_{hj}(\cdot ){\gamma }_{hj}^{(p)}(s,\cdot ){\xi }^{(p)}⇝{\mathbb{G}}_{phj}(s,\cdot ),$$

conditionally on the observed data. Therefore

$${\overline{B}}_{hj}(s,\cdot )⇝\sqrt{1-\lambda }{\mathbb{G}}_{1hj}(s,\cdot )-\sqrt{\lambda }{\mathbb{G}}_{2hj}(s,\cdot ),$$

for any (fixed) s ∈ [0, τ), conditionally on the observed data. Now it remains to argue that ${\sup }_{t\in [s,\tau ]}|{\widehat{B}}_{hj}(t)-{\overline{B}}_{hj}(t)|=o_p(1),$ for any fixed s ∈ [0, τ), unconditionally on the observed data. By the triangle inequality it follows that

$$\underset{t\in \left[s,\tau \right]}{\sup }\left|{\widehat{B}}_{hj}\left(s,t\right)-{\overline{B}}_{hj}\left(s,t\right)\right|\le \sqrt{1-\lambda }\underset{t\in \left[s,\tau \right]}{\sup }\left|\sqrt{n_1}{\mathbb{P}}_{n1}\left[{\widehat{W}}_{hj}\left(t\right){\widehat{\gamma }}_{hj}^{\left(1\right)}\left(s,t\right)-W_{hj}\left(t\right){\gamma }_{hj}^{\left(1\right)}\left(0,t\right)\right]{\xi }^{\left(1\right)}\right|+\sqrt{\lambda }\underset{t\in \left[s,\tau \right]}{\sup }\left|\sqrt{n_2}{\mathbb{P}}_{n2}\left[{\widehat{W}}_{hj}\left(t\right){\widehat{\gamma }}_{hj}^{\left(2\right)}\left(s,t\right)-W_{hj}\left(t\right){\gamma }_{hj}^{\left(2\right)}\left(s,t\right)\right]{\xi }^{\left(2\right)}\right|,$$

for any (fixed) s ∈ [0, τ). By similar calculations to those in the proof of Theorem 2 in Bakoyannis et al. (2019) and conditions C1-C6 it follows that both normed terms in right side the above inequality are o_p(1). This concludes the proof of part (i) of Theorem 3.

The first statement of part (ii) of Theorem 3 follows from condition C6, the fact that under the null hypothesis

$$\underset{0\le s\le t\le \tau }{\sup }\left|\left[{\widehat{W}}_{hj}\left(t\right)-W_{hj}\left(t\right)\right]\sqrt{\frac{n_1{n}_2}{n_1+n_2}}\left[{\widehat{P}}_{n_1,h_j}^{\left(1\right)}\left(s,t\right)-{\widehat{P}}_{n_2,h_j}^{\left(2\right)}\left(s,t\right)\right]\right|=o_p\left(1\right),$$

as it was argued in the proof of Theorem 2, and the Donsker property of the class ${\mathcal{F}}_3$. The second statement of part (ii) of Theorem 3 follows from the uniform consistency of the estimators ${\widehat{P}}_{hj}^{(p)}(s,t)$, p = 1, 2 in s ∈ [0, τ] and t ∈ [s, τ] as it was argued in the proof of Theorem 2, and arguments similar to those used for the proof of part (i) of Theorem 3.