The Poisson Ratio of the Cellular Actin Cortex Is Frequency Dependent

Abstract

Cell shape changes are vital for many physiological processes such as cell proliferation, cell migration, and morphogenesis. They emerge from an orchestrated interplay of active cellular force generation and passive cellular force response, both crucially influenced by the actin cytoskeleton. To model cellular force response and deformation, cell mechanical models commonly describe the actin cytoskeleton as a contractile isotropic incompressible material. However, in particular at slow frequencies, there is no compelling reason to assume incompressibility because the water content of the cytoskeleton may change. Here, we challenge the assumption of incompressibility by comparing computer simulations of an isotropic actin cortex with tunable Poisson ratio to measured cellular force response. Comparing simulation results and experimental data, we determine the Poisson ratio of the cortex in a frequency-dependent manner. We find that the Poisson ratio of the cortex decreases in the measured frequency regime analogous to trends reported for the Poisson ratio of glassy materials. Our results therefore indicate that actin cortex compression or dilation is possible in response to acting forces at sufficiently fast timescales. This finding has important implications for the parameterization in active gel theories that describe actin cytoskeletal dynamics.

Significance

Cell shape changes are vital for many physiological processes such as cell migration and morphogenesis. They emerge from an interplay of active cellular force generation and cell mechanical properties, both crucially influenced by the actin cytoskeleton. Cell mechanical models commonly make the simplifying assumption that the actin cytoskeleton is an incompressible material with the Poisson ratio 0.5. Here, we present a new technique for the measurement of the actin cytoskeletal Poisson ratio. Comparing results from computer simulations and experimental data, we determine the Poisson ratio of the actin cytoskeleton, taking into account the timescale-dependent nature of its mechanics. Our findings refute the prevalent assumption that the cytoskeleton can in general be modeled as an incompressible material with the Poisson ratio 0.5.

Introduction

The actin cytoskeleton, a cross-linked meshwork of actin polymers, is a key structural element that crucially influences mechanical properties of cells (1). In fact, for rounded mitotic cells, the mitotic actin cortex—a thin actin cytoskeleton layer attached to the plasma membrane—could be shown to be the dominant mechanical structure in whole-cell deformations (2). In the past, cell mechanical models have been developed to rationalize cell deformation in different biological systems (3,4). Such models require being parameterized by cell mechanical parameters. The mechanics of a simple isotropic elastic material is fully characterized by two mechanical parameters, e.g., its shear modulus G and its Poisson ratio ν. The Poisson ratio rates the magnitude of the Poisson effect, which is the expansion of the material in directions perpendicular to the direction of a compression; ν = 0.5 corresponds to an infinite bulk modulus of the material and thus incompressibility.

Commonly, cell mechanical models describe the actin cytoskeleton as a contractile isotropic incompressible material (5). Incompressibility of the actin cytoskeleton is motivated by the incompressibility of water and the high water content in the actin cytoskeleton (6). This assumption is justified for high-frequency deformations because in this case, substantial water movement past the elastic scaffold of the polymerized actin meshwork would give rise to strong friction and is thus energetically suppressed (see Supporting Materials and Methods, Section 1). The anticipated high-frequency incompressibility was confirmed experimentally in in vitro reconstituted actin meshworks in a frequency range of 500–10,000 Hz (7). However, in particular at slow frequencies, there is no compelling reason to assume incompressibility because the water content of the cytoskeleton may change via water fluxes past the cytoskeletal scaffold, leading to a bulk compression or dilation. Furthermore, the actin cytoskeleton is subject to dynamic turnover (1) and exhibits viscoelastic material properties (2, 3, 4,8). Therefore, it is expected that the cortical Poisson ratio is frequency dependent, as has been reported for other viscoelastic materials such as acrylic glass. There, the Poisson ratio was shown to increase from 0.32 to 0.5 for increasing timescales (9,10).

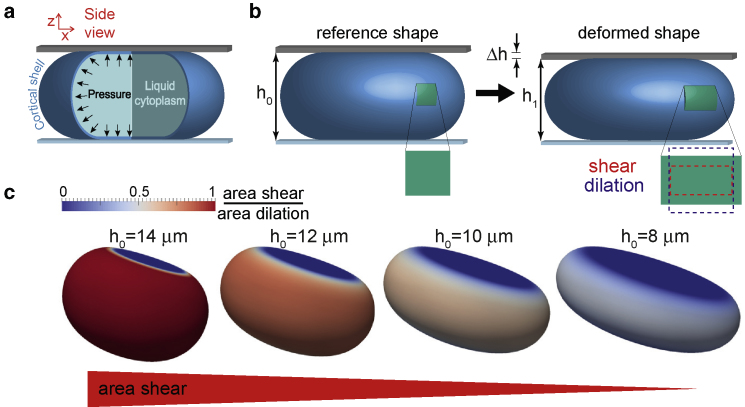
Here, we critically examine the assumption of actin cortex incompressibility by measuring the Poisson ratio of the actin cortex independent of the frequency of time-periodic deformations. To this end, we compare the measured force response of the actin cortex in HeLa cells in mitotic arrest to the simulated force response of elastic model cortices with known Poisson ratios (Fig. 1).

Figure 1.

Elastic uniaxial compression of a cortical shell. (a) Cell-mechanical model is shown. (b) Left panel: a square-shaped surface element (green) in the elastic reference shape of the shell. Right panel: after a small amount of uniaxial compression through reduction of shell height, the surface element is deformed (deformation is exaggerated here for illustration purposes). (c) The elastic deformation of model cells exhibits a decreasing ratio of area shear/area dilation at decreasing reference cell heights (simulation parameters as in Fig. 2). To see this figure in color, go online.

Because our goal is to measure the Poisson ratio of the actin cortex within live cells, we are not in a position to mechanically probe a work piece of cortical material in an arbitrary shape (such as a cylindrical work piece, which would allow the most direct measurement of the Poisson ratio (11)); the actin cortex in mitotic cells presents itself in the form of a thin cortical shell with a thickness of ∼200 nm (12). Detection of shape changes of this cortical shell upon mechanical perturbation is hampered by the resolution of optical imaging (∼200 nm) and the time dependence of viscoelastic cortex mechanics. In our approach, we circumvent these pitfalls by establishing that the contribution of cortical area dilation and area shear depend in a particular way on the elastic reference shape of the cortex. With this insight, we developed a scheme to extract two independent mechanical parameters of the actin cortex in mitotic HeLa cells—the area bulk modulus K_B and the area shear modulus K_S. We then infer the frequency-dependent Poisson ratio of the cortex from the relation ν = (K_B − K_S)/(K_B + K_S).

Materials and Methods

Cell culture

We cultured HeLa Kyoto cells expressing a green-fluorescent histone construct (H2B-GFP) and red-fluorescent membrane label (mCherry-CAAX) in Dulbecco’s modified Eagle’s medium (PN:31966-021; Life Technologies, Carlsbad, CA) supplemented with 10% (vol/vol) fetal bovine serum, 100 μg/mL penicillin, 100 μg/mL streptomycin, and 0.5 μg/mL geneticin (all Invitrogen; Carlsbad, CA) at 37°C with 5% CO₂. 1 day before the measurement, 10,000 cells were seeded into a silicon cultivation chamber (0.56 cm², from ibidi 12 well chamber; Martinsried, Germany) that was placed in a 35 mm cell culture dish (FluoroDish FD35-100, glass bottom; World Precision Instruments, Sarasota, FL) such that a confluency of ∼30% is reached at the day of measurement. For atomic force microscopy (AFM) experiments, medium was changed to Dulbecco’s modified Eagle’s medium (PN:12800-017; Invitrogen) with 4 mM NaHCO₃ buffered with 20 mM HEPES/NaOH (pH 7.2). Mitotic arrest of cells was achieved by addition of S-trityl-l-cysteine (Sigma-Aldrich, St. Louis, MO) 2–8 h before the experiment at a concentration of 2 μM. This allowed conservation of cell mechanical properties during measurement times of up to 30 min for one cell (13). Cells in mitotic arrest were identified by their shape and/or H2B-GFP. Diameters of uncompressed, roundish mitotic cells typically ranged from 19–23 μm.

AFM

The experimental setup consisted of an atomic force microscope (Nanowizard I; JPK Instruments, Bruker, Billerica, MA) mounted on a Zeiss Axiovert 200M optical wide-field microscope (Carl Zeiss, Oberkochen, Germany). For imaging, we used a 20× objective (Plan Apochromat, NA= 0.80; Carl Zeiss) and a CCD camera (DMK 23U445 from The Imaging Source, Bremen, Germany). During measurements, cell culture dishes were kept in a petri dish heater (JPK Instruments) at 37°C. On every measurement day, the spring constant of the cantilever was calibrated using the thermal noise analysis (built-in software; JPK Instruments). Cantilevers were tipless, 200–350 μm long, 35 μm wide, and 2 μm thick (NSC12/tipless/noAl or CSC37/tipless/noAl; Mikromasch, Wetzlar, Germany), with nominal force constants between 0.3 and 0.8 N/m. Cantilevers were modified with wedges to correct for the 10° cantilever tilt consisting of ultraviolet curing adhesive (63; Norland, Cranbury, NJ) (14). During measurements, measured force, piezo height, and time were outputted at a time resolution of $100$Hz.

Cell compression protocol

Before cell compression, the atomic force microscope cantilever was lowered to the dish bottom near the cell until it came into contact with the surface and then retracted to ∼15 μm above the surface. Thereafter, the free cantilever was moved over the cell. At this stage, a brightfield picture of the equatorial plane of the confined cell is recorded to estimate the area of the equatorial cross section and, in turn, to estimate cell volume as described in (2). The cantilever was then gradually lowered in steps of 0.5 or 1 μm at a set speed of 0.2 μm/s interrupted by waiting times of 50–150 s. During this waiting time, we performed sinusoidal oscillations around the mean cantilever height at different frequencies (f = 0.02, 0.1, 1, and 10 Hz), with a piezo height amplitude of 0.25 μm. The cycle of compression and subsequent oscillations around a constant mean height was repeated until the cell started to bleb, which was typically at a height of 10 μm. For frequencies f = 0.1–10 Hz, height oscillations were performed for ≥5 periods. For frequency f = 0.02 Hz, height oscillation were performed for ≥2 periods. For a first subset of cells (N ≈ 50), mechanical probing was performed jointly at frequencies f = 0.1, 1, 10 Hz; for a second subset of cells (N ≈ 10), all frequencies (f = 0.02, 0.1, 1, 10 Hz) were measured on one cell; and for a third subset of cells (N ≈ 25), only the slow frequency of f = 0.02 Hz was measured to limit the overall measurement time on one cell. During the entire experiment, the force acting on the cantilever was continuously recorded. The height of the confined cell was computed as the difference between the height that the cantilever was raised from the dish surface and lowered onto the cell plus the height of spikes at the rim of the wedge (due to imperfections in the manufacturing process (14)) and the force-induced deflection of the cantilever. We estimate a total error of cell height of ∼0.5 μm due to unevenness of the cantilever wedge and due to the vertical movement of the cantilever to a position above the cell.

Data analysis

Geometrical parameters of each analyzed cell (such as contact area A_c with the wedge, mean curvature H of the free cell surface, and cell surface area A) are for each cell, estimated as previously described in (2). Briefly, we estimated cell volume by the formula V = $-\left(\pi /24\right)h\left(h^2\left(3\pi -10\right)-6h\left(\pi -4\right)R_{eq}-24R_{eq}^2\right)$, which can be derived by approximating the profile of the free cell contour by a semicircle. Here, R_eq is the equatorial radius of the confined cell at confinement height h. Further, we estimated radii of principle curvatures at the equator of the cell surface as h/2 and R_eq. The area of contact between cells and cantilever was estimated as A_c = π$r_c^2$ with the contact radius r_c determined by the approximative formula r_c = $\left(R_{eq}-\left(h/2\right)\right)+\left(2/3\right)\left(\sqrt{\left(2R_{eq}^3-h{R}_{eq}^2\right)}/\sqrt{\left(h+2R_{eq}\right)}-\left(R_{eq}-\left(h/2\right)\right)\right)$ described in (15).

In turn, these parameters are used to calculate the effective cortical tension γ_eff according to Eq. 2.

Because we impose only small deformation oscillations on the cell, we may use an analysis scheme in the framework of linear viscoelasticity, as shown in our previous work (2; Supplementary Material). Oscillation amplitudes of effective cortical tension ${\hat{\gamma }}_{eff}$ and cell surface area $\hat{A}$ were determined by performing a linear fit using the fit function a cos(2πt/T) + b sin(2πt/T) + c t, where T is the oscillation period of the imposed cantilever oscillations. The oscillation amplitude was then calculated as a² + b². The strain amplitude ${\hat{\epsilon }}_A$ was calculated as $\hat{A}/\langle A\rangle$.

For data analysis, only cells that had a roughly constant average cortical tension during the measurement (not more than 10% deviation) were considered. This was true for ∼70% of the cells. Major variations in the cortical tension could mostly be attributed to visible blebbing events.

For the calculation of cortical Poisson ratios, we demanded that oscillatory measurements of cells had to be in a range of normalized height $\tilde{h}$ between 0.5 and 0.75 to match the parameters of the simulations. Only cells with at least four different heights sampled in this range were considered for analysis, in which the highest normalized height had to be larger than 0.68. Furthermore, we demanded that the r-squared value of the exponential fit of the obtained effective elastic modulus according to Eq. 5 had to be larger than 0.5. This constraint was released for Poisson ratio estimates larger than 0.7 because this indicates an almost constant value of effective modulus in dependence of cell height. For the case of a constant functional dependence, the fit cannot be better than the approximation of the data by the mean, leading to an r-squared value that approaches zero.

Results

Theory of cortical shell deformation

Throughout this manuscript, we model the actin cortex of mitotic cells as a thin shell (Fig. 1 a). In the following section, we discuss the mechanics of thin shells and its dependence on the Poisson ratio of cortical shell material. We numerically determine the mechanical response of idealized model cells using established continuum mechanical concepts (11). The obtained insight is used to develop an analysis scheme that allows to extract the Poisson ratio of actin cortices from experimental data.

Our model cells are constituted by an isotropic contractile elastic thin shell mimicking the actin cortex, enclosing an incompressible liquid interior representing the cytoplasm (12). Cortical shells are thus assumed to enclose a constant volume V independent of elastic stresses because the associated hydrostatic pressures in the cell are negligible as compared to the osmotic pressure associated to the osmolarity of the medium (16). We assume a model shell thickness t_c of 200 nm, as measured before for the actin cortex of mitotic HeLa cells (12), and a model cell volume of V = 4300 μm³, which was approximately the average volume of mitotic HeLa cells in our experiments.

According to elasticity theory, the shell’s elastic behavior is characterized by three elastic moduli: 1) the area bulk modulus K_B, characterizing the resistance to area dilation or compression; 2) the area shear modulus K_S, characterizing the resistance to shear deformation of a surface patch of the shell; and 3) the bending modulus B, characterizing the resistance to shell bending. In the case of an isotropic material, only two of the three moduli are independent, and we have K_B = t_cG(1 + ν)/(1 − ν), K_S = t_cG, and B = $t_c^3$G/(12(1 − ν)), where G is the shear modulus of the shell (11,17).

Analogous to our experimental setup, we consider model cells that are confined between two parallel plates in an elastic reference configuration of height h₀; see Fig. 1, a and b. There, we anticipate a constant isotropic contractile in-plane stress σ_a in the cortical shell that captures active actomyosin contractility of the actin cortex, which gives rise to a constant active cortical tension γ_a = t_cσ_a. This active tension is balanced by the internal hydrostatic pressure of the liquid interior. In the absence of elastic stresses, the contractile tension γ_a drives the model cell into the shape of an axisymmetric nonadherent droplet that is characterized by a constant mean curvature H in the regions of unsupported shell surface (15). We use these confined droplet shapes as the elastic reference configuration because the actin cortex has been previously characterized to be viscoelastic, with complete stress relaxations after ≤1 min (2). Therefore, mechanically confining cells to a height h leads to a new droplet-shaped reference shape of height h after a short waiting time. In this elastic reference state, a model cell exerts a constant force because of active tension

$$F_a\left(h\right)=2{\gamma }_{a}H\left(h\right)A_c\left(h\right)$$ (1)

on the confining plates, where A_c(h) is the circular contact area between the cell and the plate and H is the mean curvature, both at height h of the cell (2,15).

This force exerted on the confining plates is the central quantity of our investigations because we can measure it in our experiments and compute it in our finite element simulations (18). To probe the force response of a model cell, steps of uniaxial compression are imposed that lower the cell height from a starting height h₀ to h₁ = h₀ − Δh. In turn, the shell material is deformed, and elastic stresses are induced (Fig. 1, a and b). Together with an increase of the shell’s plate contact, this contributes to an increase of the force exerted on the confining plates. The new force for the decreased plate distance h₁ is denoted as F_tot(h₀, Δh) = F_a(h₁) + ΔF(h₀, Δh), where ΔF(h₀, Δh) captures the elastic contribution of the force increase and F_a(h₁) captures the force contribution from active tension at new height h₁. For our study, we consider small compression steps in which ΔF(h₀, Δh) is well approximated as a linear function of Δh. Furthermore, we verified in numerical simulations that the force response of the liquid interior adds ≤1% to the effective modulus for cytoplasmic viscosities of up to $1$Pa ⋅ s, oscillation frequencies ≤10 Hz (see Supporting Materials and Methods, Section 2), and normalized cell height lower than 80%. Therefore, we henceforth neglect viscous flows in the cytoplasm, simulating only the elastic deformation of a shell and an internal pressure.

In analogy to Eq. 1, we can relate the overall force of the cortex after elastic deformation to an effective cortical tension (2)

$${\gamma }_{eff}\left(h_0,\Delta h\right)=\frac{F_{tot}\left(h_0,\Delta h\right)}{2H\left(h_1\right)A_c\left(h_1\right)},$$ (2)

where γ_eff = γ_a + Δγ_eff, with Δγ_eff = ΔF(h₀, Δh)/(2H(h₁)A_c(h₁)). Here, γ_a captures the constant active contribution to cortical tension, whereas Δγ_eff denotes the passive deformation-induced tension change.

We define an effective elastic modulus of uniaxial shell compression as

$$K\left(h\right)=\frac{\Delta {\gamma }_{eff}}{{\epsilon }_A},$$ (3)

where h = (h₀ + h₁)/2 and ε_A is the surface area strain

$${\epsilon }_A=\Delta A\left(h_0,\Delta h\right)/A\left(h_0\right),$$ (4)

with ΔA the increase in overall surface area of the model cell through deformation and A(h₀) the original surface area at height h₀ in the absence of elastic stresses (2).

We determined values of K(h) of shells of known mechanical properties via simulations of thin-shell continuum mechanics (Fig. 2 b; (19)).

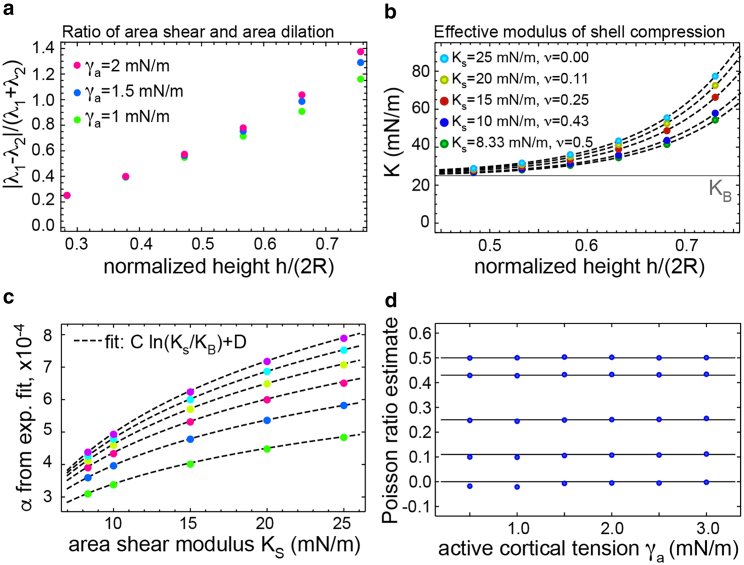
Figure 2.

Uniaxial compression of elastic model cells with varying reference height. (a) Ratio of area shear/area dilation at the shell equator is quantified as |λ₁ − λ₂|/(λ₁ + λ₂), where λ₁ and λ₂ are the equatorial eigenvalues of the in-plane shear tensor. (b) Effective elastic modulus K is shown as a function of mean shell height h = h₀ − Δh/2 for cortical tension γ_a = 1.5 mN/m (dashed lines: fitted by Eq. 5). The numerical uncertainty of K was estimated to be ≤0.4%. (c) Fit coefficient α is shown as a function of K_S for varying cortical tensions γ_a (bottom to top: 0.5–3 mN/m in increments of 0.5 mN/m, dashed lines: fitted by Eq. 6). The choice of cortical tension reflects the range of experimental values. (d) Reconstructed Poisson ratios (blue dots) from effective elastic moduli are as shown in (b). Black lines indicate actual Poisson ratio values of underlying simulations. Elastic parameters were chosen to be K_B = 25 mN/m and K_S = 8.3, 10, 15, 20, or 25 mN/m, corresponding to Poisson ratios of ν = 0.5, 0.43, 0.25, 0.11, and 0. Values of K_B were motivated by measurement results reported by (2). The cell volume was 4300 μm³, and Δh = 0.5 μm. To see this figure in color, go online.

Finite element simulations were carried out to extract the effective elastic modulus K(h) for 540 combinations of cell heights, area shear moduli, bending stiffnesses, and surface tensions (see Supporting Materials and Methods, Sections 3 and 4). For convenience, we introduce now the normalized cell height $\tilde{h}$ = h/(2R) with $R={\left(\left(3/4\pi \right)V\right)}^{1/3}$. We find that at low values of normalized reference cell height $\tilde{h}$, the effective modulus K approaches the area bulk modulus K_B because of the dominance of area dilation over area shear during shell deformation (Fig. 2, a and b). For larger normalized heights $\tilde{h}$, the effective modulus K increases because of an increasing contribution of area shear during model cell deformation (Fig. 2 b). We can capture this increase phenomenologically by an exponential rise

$$K\left(\tilde{h}\right)\approx K_B\left(1+\alpha \text{exp}\left(\tilde{h}/\lambda \right)\right),$$ (5)

where λ ≈ 0.09 (dashed lines in Fig. 2 b; see Supporting Materials and Methods, Section 3). The amplitude of the exponential increase α depends on the normalized shear modulus ${\tilde{K}}_S$ = K_S /K_B as well as the normalized surface tension ${\tilde{\gamma }}_a$ = γ_a /K_B. In the experimentally relevant range 0.45 < $\tilde{h}$ < 0.75, we capture this dependence again by a phenomenological law

$$\alpha \left({\tilde{K}}_S,{\tilde{\gamma }}_a\right)\approx C\left({\tilde{\gamma }}_a\right)\text{log}\left[{\tilde{K}}_S\right]+D\left({\tilde{\gamma }}_a\right),$$ (6)

where C$\left({\tilde{\gamma }}_a\right)$ and D$\left({\tilde{\gamma }}_a\right)$ are polynomials of the third degree in ${\tilde{\gamma }}_a$ (dashed lines in Fig. 2 c; Supporting Materials and Methods, Section 3).

The characterizing Eqs. 5 and 6 provide now an analysis scheme to extract the Poisson ratio from measured effective moduli K$\left(\tilde{h}\right)$ for known γ_a (Fig. 3 a): fitting an exponential increase to K$\left(\tilde{h}\right)$ yields fit parameters α and K_B (compare Eq. 5). Inverting the function (6) at α numerically, an estimate of ${\tilde{K}}_S$ is obtained that, in turn, allows us to determine the Poisson ratio by ν = $\left(1-{\tilde{K}}_S\right)/\left(1+{\tilde{K}}_S\right)$. As a test of self-consistency, we verified that the application of this analysis scheme closely reproduces the chosen values of the Poisson ratio for model cells (Fig. 2 d). Thus, the exponential increase of the effective elastic modulus K as a function of $\tilde{h}$ stores the information about the Poisson ratio of the shell.

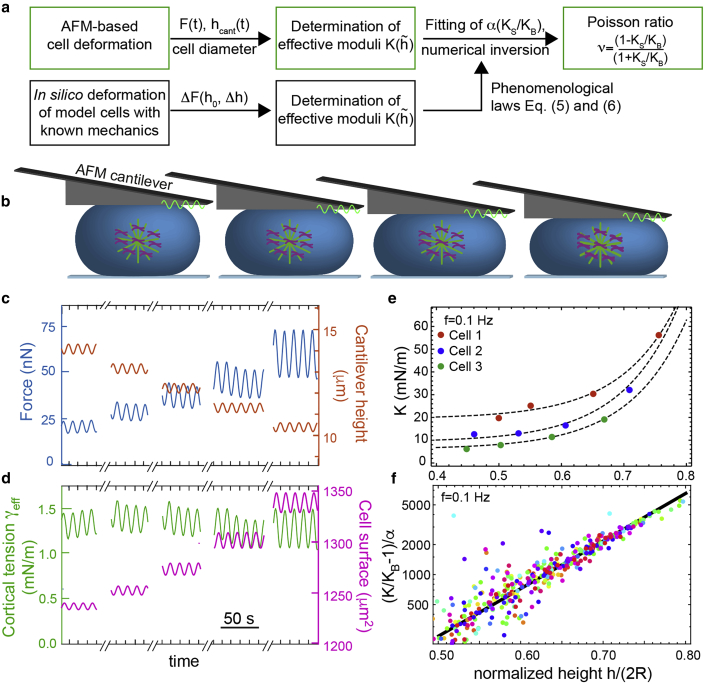
Figure 3.

AFM-based deformation of HeLa cells. (a) A scheme of data analysis workflow is given. (b) Cells in mitotic arrest were confined through a wedged cantilever (schematic: green, microtubules; violet, chromosomes). Oscillatory cell height modulations are applied at decreasing mean cell heights. (c) Exemplary force and cantilever height output at f = 0.1 Hz is shown. (d) Values of cortical tension and cell surface area associated with (c) were calculated from force and cantilever height as described before in (2). (e) Exemplary effective elastic moduli of cell cortices versus normalized cell heights is shown. Dashed lines show a fit according to Eq. 5 with fit parameters K_B and α. Uncertainties of estimated moduli because of sinusoidal fitting of output tension data are estimated to be ≤5%. (f) Normalized effective elastic moduli (K/K_B −1)/α of all cells measured at f = 0.1 Hz is shown. The phenomenological dependence predicted by Eq. 5 is captured by the solid black line. Different colors represent different cells. To see this figure in color, go online.

Experimental results

We now want to use our theoretical insight to determine the Poisson ratio of the actin cortex in live cells. As a cellular model system, we use HeLa cells in mitotic arrest because they are void of a nucleus and exhibit a large cell surface tension that ensures droplet-shaped cells in confinement (15). Furthermore, for mitotic cells, we could show in a previous study that the actin cortex is the dominant mechanical structure and that the influence of cell adhesion is negligible in our measurement setup (2,15).

We mechanically deform these cells in an oscillatory manner around different heights of confinement via the wedged cantilever of an atomic force microscope (Fig. 3 b; (2,15)). During these measurements, we record the force exerted by the atomic force microscope cantilever and the respective cantilever height h_cant (Fig. 3 c). We then calculate the associated time-periodic effective cortical tension γ_eff(t) and area strain ε_A(t) according to Eqs. 2 and 4 with h₁(t) = h_cant(t), h = <h_cant(t)>, and Δh(t) = h₁(t) − h (Fig. 3 d). We determine the volume of the measured cell V from imaging and calculate an associated cell radius R (see Materials and Methods). In analogy to Eq. 3, we infer an effective modulus of the actin cortex of measured cells K = $\left({\hat{\gamma }}_{eff}/{\hat{\epsilon }}_A\right)$, where ${\hat{\gamma }}_{eff}$ and ${\hat{\epsilon }}_A$ are the amplitudes of the time-periodic signal of γ_eff and ε_A = ΔA/$\langle A\rangle$, respectively (Fig. 3 d; (2)). Our measurement and analysis procedure is repeated at different cell heights to obtain K as a function of normalized cell confinement height $\tilde{h}$ (Fig. 3, e and f).

Cell mechanical measurements are performed at frequencies 0.02, 0.1, 1, and 10 Hz. Using the correspondence principle, we apply our insight on the mechanical response of elastic model cells to our measurements of viscoelastic live cells (20): we fit the measured height dependence of the cortical modulus K by Eq. 5 and obtain the fit parameter α and K_B (Fig. 3 f). In general, we find a good agreement between measured values and the exponential increase predicted by our elastic shell calculations with a median r-squared value of 0.94 for f = 0.1–10 Hz and 0.84 for f = 0.02 Hz. The good agreement between data points and the fitting function provided by numerical simulation illustrates the suitability of our cell mechanical description.

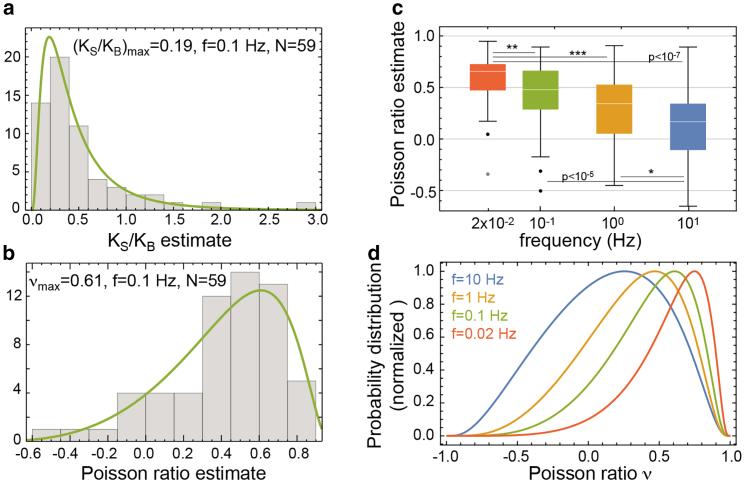
Furthermore, we estimate the cortical tension as the time-average γ_a ≈ <γ_eff>. Inverting Eq. 6, we obtain an estimate for ${\tilde{K}}_S$ = K_S/K_B and thus the Poisson ratio ν (Fig. 4, a–c; Fig. S3, a and b). We find that the obtained Poisson ratio estimate depends on the frequency of time-periodic cell deformations, with lower Poisson ratios for fast cell deformations. Median values of the Poisson ratio vary between values of 0.17 and 0.48 for decreasing frequencies between 10 and 0.1 Hz (Fig. 4, c and d). For the slowest frequency 0.02 Hz, at which cortex turnover is expected to influence cell mechanics, we estimate a median Poisson ratio of 0.66 (Fig. 4, c and d).

Figure 4.

Poisson ratio estimates of the actin cortex in mitotic HeLa cells. (a) A histogram of estimated K_S/K_B at f = 0.1 Hz (green line represents lognormal distribution of maximal likelihood) is given. (b) A histogram of corresponding Poisson ratios is given (green line: distribution induced by lognormal distribution in a). (c) Box plots of estimated Poisson ratios at different frequencies are given. From left to right, median values: 0.66, 0.48, 0.34, 0.17; IQR: 0.26, 0.38, 0.48, 0.45. Stars indicate significant differences between distributions according to p-values of a Mann-Whitney test (^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001). (d) Fitted distributions of estimated Poisson ratios for cell deformations at frequencies F = 0.02, 0.1, 1, and 10 Hz are shown. To see this figure in color, go online.

Our results show a substantial scatter of Poisson ratio estimates at a given frequency (Fig. 4 c). To examine the origin of this statistical spread, we quantify the influence of experimental uncertainties. To this end, we assess the error of our cell volume estimate to be 7.5% and of cell height to be 0.5 μm. In turn, we calculate the resulting variation of Poisson ratios for elastic model cells with a known Poisson ratio by introducing corresponding artificial errors in cell volume and cell height (see Fig. S3 c). In this way, we find resulting interquartile ranges (IQRs) between 0.24 and 0.39, which are close to IQR values found for experimental spreads. Therefore, we conclude that statistical scatter in our experimental data stems a substantial amount from measurement errors and not exclusively from cell-cell variations.

Among cell-cell variations, we expect variations in cortical thickness and thus in the contribution of bending stiffness to cell deformations as a major source for variations in Poisson ratio estimates (see Supporting Materials and Methods, Section 6). In summary, despite large statistical scatter, we observe a robust, significant trend of increasing Poisson ratio values of the mitotic actin cytoskeleton with decreasing frequency (Fig. 4, c and d) in which Poisson ratio distributions are significantly different from each other at different frequencies (two-sided Mann-Whitney test: p-values ≤ 0.02 for neighboring frequencies, ≤10⁻⁴ for all other frequency pairs).

Discussion

Here, we report a new measurement method to determine the Poisson ratio of the actin cortex in biological cells that is based on the time-periodic deformation of initially round mitotic cells through the wedged cantilever of an atomic force microscope. The key idea behind this technique is that mechanical deformation at different reference shapes probes the cortical shell at varying contributions of area dilation and area shear (Figs. 1, b and c and 2 a).

For our measurements at the largest frequency (f = 10 Hz), we expect that cortex turnover plays a negligible role for the mechanical properties of the cortex (1). There, we find a median Poisson ratio of 0.17. This value is considerably lower than the incompressible case of ν = 0.5 and reasonably close to theoretical predictions of 0.25 for foamed elastic materials or polymer gels (21,22).

Furthermore, we find a clear trend for the Poisson ratio to increase with timescale; median values of the Poisson ratio increase from 0.17 to 0.66 in a timescale range of τ ≈ 0.016–8 s, associated with a frequency range of f = 0.02–10 Hz by τ = 1/(2πf) (Fig. 4, c and d). A plausible explanation for this trend is that turnover of actin and, in particular, actin cross-linkers (taking place on timescales of ∼0.2–20 s (1)) leads to a significant decrease of the shear modulus at increasing timescales. For cross-linker turnover, this effect has been demonstrated by Broedersz et al. (23). On the other hand, turnover supposedly gives rise to a minor change of the bulk modulus of the cortex because the actin polymer density is preserved. Correspondingly, the Poisson ratio would decrease with timescale and increase with frequency (for an elastic isotropic material with shear modulus G and bulk modulus $\mathcal{K}$, the Poisson ratio is given by ν = (3$\mathcal{K}$/G − 2)/(6$\mathcal{K}$/G + 2). If $\mathcal{K}$/G increases, ν increases and approaches 0.5 for large $\mathcal{K}$/G). Indeed, a similar effect was reported as a hallmark for the glass transition of synthetic polymer materials (9). There, an increase of Poisson ratio as a function of timescale was reported when moving from glassy to rubbery rheological behavior. Correspondingly, this transition is accompanied by a strong decrease of the shear modulus because of jamming release but a minor decrease of the bulk modulus with timescale (9,10,24).

It is noteworthy that for a thin shell of an isotropic material, the associated two-dimensional Poisson ratio ν_2d coincides with the three-dimensional Poisson ratio ν. In this case, ν_2d may adopt values in the range [−1, 0.5] (see Supporting Materials and Methods, Section 7). However, if the assumption of material isotropy is relaxed, ν_2d may adopt values that may reach up to 1. For the slowest frequency probed in our measurements, the Poisson ratio estimate exceeds 0.5. This might hint at a violation of cortical isotropy at slower frequencies. Cortical turnover is critically influenced by the cortex interface with the plasma membrane (1,25), which might account for the emergence of anisotropy at large timescales.

Poisson ratios of cellular material have been previously estimated: Mahaffy et al. developed a method to estimate the Poisson ratio of adherent cells through slow atomic force microscope indentation at a gradually increasing indentation depth into a thin cytoskeletal layer above a substrate (26). Poisson ratio estimates from this method are between 0.4 and 0.5 (26, 27, 28). Trickey et al. (29) measured the Poisson ratio of chondrocytes through a whole-cell perturbation via micropipette aspiration and subsequent shape relaxation, thereby estimating values of 0.38. However, both methods (26,29) ignored the possible timescale dependence of the Poisson ratio. This fact makes it hard to compare these earlier findings to our data. We do, however, anticipate that our measurement results do not contradict with those previous measurements because of our comparable results in the frequency range 0.1–1 Hz.

For in vitro reconstituted branched actin meshworks, Bussonnier et al. clearly showed the compressibility of branched actin meshworks on a timescale of a few seconds (Poisson ratio between 0.1 and 0.2) (30). By contrast, entangled actin meshworks without cross-linking were shown to be close to incompressible (31). This discrepancy indicates that not only the timescale but also the presence of actin cross-linkers plays a crucial role for the Poisson ratio of actin meshworks.

To the best of our knowledge, we present here for the first time measurements of the Poisson ratio of the actin cortex in live cells independent of frequency, showing a clear frequency-dependent trend. In particular, our measurements indicate a nonmonotonic dependence of cortical Poisson ratio on timescale: for very short timescales, poroelastic effects and incompressibility of water will give rise to a decrease of Poisson ratio with timescale (see Supporting Materials and Methods, Section 1). At larger timescales, at which turnover of cortical constituents starts to kick in, there is an increase of the Poisson ratio with timescale. In summary, we give evidence that the actin cortex may not in general be treated as an incompressible material. Therefore, compression or dilation of the actin cytoskeleton is possible in response to acting forces at sufficiently fast timescales. In particular, local compression of actin cytoskeleton may be caused by motor-induced cytoskeletal contractility, which would, in turn, increase myosin motor concentration locally. This may contribute to a self-amplifying effect that could induce instability and pattern formation in the material (17,32, 33, 34). Our results therefore make a contribution to the parameterization of active gel theory and mechanical modeling of the dynamics of the actin cytoskeleton (35,36).

Author Contributions

S.A. and E.F.-F. designed the research. M.M. and S.A. developed the numerical method. M.M. performed simulations. K.H. and E.F.-F. performed the experiments. M.M., K.H. and E.F.-F. performed data analysis. M.M., S.A., and E.F.-F. wrote the manuscript.

Editor: Ana-Suncana Smith.

Supporting Citations

References (37, 38, 39, 40, 41, 42, 43) appear in the Supporting Material.