From summary statistics to gene trees: Methods for inferring positive selection

Abstract

Methods to detect signals of natural selection from genomic data have traditionally emphasized the use of simple summary statistics. Here, we review a new generation of methods that consider combinations of conventional summary statistics and/or richer features derived from inferred gene trees and ancestral recombination graphs (ARGs). We also review recent advances in methods for population genetic simulation and ARG reconstruction. Finally, we describe opportunities for future work on a variety of related topics including the genetics of speciation, estimation of selection coefficients, and inference of selection on polygenic traits. Together, these emerging methods offer promising new directions in the study of natural selection.

Natural Selection and DNA Sequencing

Together, mutation and selection act on natural populations to carry out the largest mutagenesis screen the world has ever known, evaluating the relative fitnesses of alternative genotypes on a massive scale. In response to differences in fitness together with genetic drift, newly arising genetic variants change in frequency over time, leaving distinctive patterns of variation in the genomes characterized by modern genome sequencing efforts [1-4]. The ability to accurately detect and quantify the influence of selection from genome sequence data enables a wide variety of insights, ranging from understanding historical events to characterizing the phenotypic relevance of observed or potential genetic variants. These insights, in turn, are relevant in diverse areas ranging from biomedicine to agriculture and ecology. The development of tools that can accurately measure natural selection has thus emerged as a primary goal of modern population genomics.

This review covers recent methodological developments in the detection of natural selection from DNA sequence data. We begin by briefly reviewing classical methods for detecting selection based on population genetic summary statistics, and then discuss strategies that consider combinations of summary statistics using machine learning or Approximate Bayesian Computation (ABC). We then proceed to the main focus of the review, which is the use of explicit gene trees and/or ancestral recombination graphs (ARGs) (see Glossary), as inferred from sequence data, for detecting selection. Because they are central to this research area, we also briefly review simulation methods for population genetic data and emerging methods for genome-scale ARG or gene-tree inference. We end with a broad discussion of new directions in this general area, with applications ranging from the study of the genetics of speciation to inference of selection on polygenic traits and the detection of ancient introgression. We note that, throughout this review, we address both negative (purifying) and positive directional selection (adaptation), but we primarily focus on positive selection, for which the emerging ARG and gene-tree-based methods have been most widely used. ARG-based methods could also potentially be useful in analyzing features such as background and balancing [5] selection, but we leave these topics for future work.

Reasons to detect and measure selection

Positive and negative directional selection are both informative about basic biological processes [6-11], applied topics in medicine [12-16], plant and animal breeding [17-19], and ecology [20-22]. However, they create somewhat different patterns of genetic variation, which has led to the development of different methods for detection.

Positive selection, or adaptation, is the process by which alleles that increase organismal fitness increase in frequency in a population. By detecting signatures of this process, investigators have improved their understanding of the genetic basis for important phenotypic traits, in both human and non-human contexts (Box 1).

Box 1: Positive selection in adaptation and speciation.

Adaptation in human populations

A classic example of local adaptation is a family of mutations in the hemoglobin-β cluster, which confer resistance to malaria and are at high frequencies in many Asian and African populations [12,13]. Another well-known example is mutations within and near the LCT gene, leading to lactase persistence in adults in European and certain African populations [6-8]. Other prominent examples of adaptation in humans include short stature in Western Central African hunter-gatherer populations [9-11], the hypoxic response at high altitude in Tibetan populations based on Denisovan-like introgression at the EPAS1 gene [23-25], and several genes involved in skin pigmentation (such as SLC24A5 and SLC45A2), hair follicle development (EDAR and EDA2R), and immunity (LARGE and DMD) [26].

Non-human examples of adaptation

One particularly interesting system has been dogs, where hundreds of different breeds have been placed under strong artificial selection for diverse traits. Scans for positive selection in dogs have implicated genes underlying a variety of traits ranging from body size and athleticism to anxiety disorders [27,28]. Other studies have uncovered the role of adaptive introgression in the evolution of novel traits in many other organisms such as mimetic butterfly wing patterns [29] and resistance to rodenticides in mice [22]. Studies of adaptation at the level of microscopic organisms also have immense practical relevance. By studying the genetics of antibiotic/antiviral resistant populations, investigators can better understand the mechanisms by which these pathogens evade therapies and develop countermeasures [30-33]. Similar principles are being applied to study clonal adaptation in cancer, providing another way to identify mutations that enable proliferation, metastasis, and resistance to various therapies [34,35].

Positive selection can contribute to speciation

Characterizing the locations, strength, and direction of selection across the genome is critical in understanding the genetic basis of speciation. Many investigators have argued that selection contributes to genetic heterogeneity that leads to reproductive isolation, which then permits speciation to occur [36-38]. For example, Cruickshank and Hahn (2014) discussed a model (divergence-after-speciation) that explains heterogeneous genetic differentiation through local adaptation acting at a few key loci while the rest of the genome of the diverged species remains similar due to shared ancestral polymorphism and incomplete lineage sorting [38]. A classical example of speciation associated with local adaptation is Darwin’s finches [39]. Additional examples include ongoing speciation in Tibetan frogs [40], and an adaptive radiation in butterflies [21].

In contrast to advantageous mutations, variants with a negative effect on organismal fitness will tend to be driven to low frequencies or purged from a population entirely, a process called negative selection. A number of recently developed methods that use this signature of negative selection have shown reasonable power to differentiate between benign and pathogenic variants in humans [30-34] with implications for precision medicine [14-16,41-44]. For a more thorough review of these methods, see Eilbeck et al., [47]. These methods also show promise for practical applications beyond humans. For example, it has been shown that domestication increases the mutation load in plants [17-19]. Applying computational methods to identify deleterious alleles followed by selective crossing or gene editing to remove them has the potential to both speed up and reduce the cost of improving crop yield [46]. Recently, measures of negative selection have also been applied to study the long-term implications of small founder populations and inbreeding in ways that may have implications for conservation biology [20]. In an intractably large space of genetic variation, consistent improvements in methodology and data quality for negative selection inference will enable improved experimental and therapeutic designs.

Advances in population genomic simulations

The process of simulating sequence data under a stochastic population genetic model is fundamental to modern population genomics. Many methods for inferring selection make direct use of simulations, as discussed below. However, even methods that do not use simulations for inference are typically benchmarked against simulated data as there is generally no other ground truth against which to evaluate performance. In this section, we briefly discuss two main types of simulations, coalescent and forward simulations, their capabilities and their current limitations.

Coalescent simulators start from individuals in the present generation and work backwards until all samples reach a common ancestor. Coalescent theory, initially developed by Kingman in 1982 (see also Hudson [47] and Tajima [48]), describes this “backward” process in terms of the probabilities of pairs of lineages coalescing (finding common ancestry) in a randomly mixing population [49]. In the absence of selection, coalescent theory provides an elegant and efficient means for simulating genealogical histories because it allows only the lineages leading to the observed samples to be considered; the many more numerous lineages that have gone extinct or are unsampled are naturally ignored when the data generation process is described backwards rather than forwards in time. Importantly, extensions to recombination, mutation, structured populations, and changes in population size can be accommodated efficiently in this framework. Forward simulators, by contrast, start with an ancestral population and track it forward in time. As forward simulations make none of the assumptions of the coalescent, this strategy has the advantage of being immensely flexible, allowing for any combination of selected alleles. Currently there are several available state-of-the-art simulators for population genetics, but major technical challenges remain in performing simulations at scale (Box 2).

Box 2: Modern simulators and remaining challenges.

Coalescent simulators

An early and widely used coalescent simulator was ms [50]. With the need for genome-scale simulations, researchers have developed more efficient coalescent simulators. At present, the state-of-the-art in this area is represented by msprime [51], which dramatically improves both computational and storage efficiency through the use of tree sequence recording [52]. Tree sequences leverage the high similarity of adjacent local genealogies to compactly encode a series of trees as lists of individual edges defined over specific genomic intervals. Thus, edges that are shared between adjacent trees are only recorded once, rather than requiring a separate entry per tree, resulting in massive reduction in disk usage and processing time. Since the naive coalescent assumes that all genotypes have equal fitness, neither ms nor msprime is able to accommodate selection. Despite this limitation, neutral simulations remain useful in providing null distributions that can be compared with the observed data to detect deviations suggestive of selection or other unmodeled phenomena. Recently, coalescent simulators, such as discoal [53] and msms [54], have implemented limited ability to handle selection in the coalescent setting by conditioning on the frequency of a designated selected allele. However, these methods depend on a number of restrictive assumptions that are not appropriate in all settings.

Forward simulators

At present, the most full-featured and robust forward simulator is SLiM [55,56]. SLiM supports simulating complex demographic and selection scenarios under different mating and reproductive strategies and recently has been extended to support spatially structured populations [57]. SLiM also now supports tree sequences, which results in large performance gains that make forward simulations of whole genomes possible [58]. SLiM also considerably improves performance by a combination of forward and backward simulation termed “recapitation”; first a forward simulation is performed, then msprime is used to generate full coalescent histories for the subset of members of the initial population that have one or more descendants in the modern population. Finally, neutral mutations are overlaid on the simulated coalescent histories to efficiently generate neutral variation in the initial population for the forward simulation. In this way, the time scale of a forward simulation can be substantially extended at minimal computational cost. Even with these performance innovations, however, forward simulations are still much more computationally expensive than coalescent simulations.

Large-scale forward simulation

Despite algorithmic advances and improvements in computing power, simulating large populations can be challenging, especially using forward simulations. Because many important parameters are products of the population size and per-individual rates, the additional computational cost of forward simulations can be mitigated by scaling down the effective population size and rescaling the mutation rate, recombination rate, selection coefficients, and number of generations accordingly. However, if population sizes are made too small, stochastic effects will dominate in the simulation process. Thus, rescaling simulations should be undertaken with care, and validated against tractable, non-scaled scenarios. Despite these limitations, simulating more complex and realistic population scenarios at scale is becoming increasingly viable.

Summary statistics for inferring selection

A wide variety of summary statistics have been developed to detect signals of positive and negative selection from DNA sequence data. For example, a widely used classical statistic for detecting ongoing or recurrent selection on phylogenetic time scales is the ratio dN/dS [59-61], which is estimated as the rate of divergence at functional sites (typically, non-synonymous sites in protein-coding genes) relative to that at neutrally evolving sites (typically, synonymous sites). This ratio may exceed or fall below one in protein sequences under positive or negative selection, respectively. Other approaches, such as the McDonald-Kreitman (MK) test, have been introduced to detect adaptation on shorter time scales, by contrasting patterns of polymorphism within species and divergence between species [62,63]. The basic idea behind both of these approaches is to contrast patterns of variation that likely have fitness effects (e.g., alleles that change the amino acid sequence) and those that likely do not have fitness effects (e.g., alleles that do not change the amino acid sequence). Because mutation rates are expected to be similar for both types of sites, differences in these patterns are indicative of selection. Similarly, the Hudson-Kreitman-Aguadé (HKA) test was developed to facilitate the detection of recurrent and recent selection by contrasting divergence and polymorphism data [64,65]. Other summary statistics measure reduced diversity from linked selection at putatively neutral sites (see B statistic [66]), identify an excess of SNPs with extreme population differentiation (e.g. high Fst [67] values), and identify accelerated regions [68,69].

An alternative way to study positive selection—our main focus for the remainder of the article—is by exploiting the hitchhiking effect, which alters the spatial haplotype structure and the site frequency spectrum (SFS) in the local region of a positively selected allele. Box 3 provides a high-level overview of traditional summary statistics based on haplotype structure or the SFS.

Box 3: Haplotype- and SFS-based summary statistics.

Various summary statistics based on functionals of the site frequency spectrum can be used to indicate possible positive selection, such as Tajima’s D [70], Θ_w[71], and Θ_H[72]. These summary statistics are fast and easy to compute, and do not require phasing of genotypes into haplotypes. They are generally effective in detecting selection on intermediate to long evolutionary timescales. At the same time, they have several disadvantages: they can confound selection with non-equilibrium model conditions such as changes in population size; they do not directly translate into estimates of selection coefficients; and they generally require direct characterization of a null distribution for the summary statistic to obtain a measure of statistical significance. SFS-based summary statistics also do not directly account for haplotype structure, which can be a powerful indicator of selection.

To address this haplotype-structure limitation, researchers have introduced haplotype-based summary statistics such as H₁, H₁₂, and $\frac{H_2}{H_1}$ [73,74]. H₁ measures the frequency of the most abundant haplotype, which assumes high values in a hard sweep owing to local reductions in heterozygosity. Similarly, H₂ measures the frequency of the second most common haplotype. H₂ is expected to be larger in soft sweeps compared with hard sweeps due to the existence of multiple haplotype backgrounds. Extensions to these statistics can be used to summarize both soft and hard sweeps or to differentiate between them. For example, H₁₂ measures the combined frequencies of the first and second most abundant haplotypes and has good power in the general detection of both soft and hard sweeps [73]. Alternatively, the ratio $\frac{H_2}{H_1}$ tends to be higher for soft sweeps than hard sweeps and has been used to distinguish the two [73]. These statistics all require phasing of genotypes into haplotypes, and can be sensitive to phasing errors. Additionally, as with SFS-based statistics, these summary statistics are designed for detecting selection on intermediate-to-long evolutionary time scales and do not directly translate into selection coefficients.

Another haplotype-based test statistic is the integrated haplotype score (iHS) [75], a statistic based on the extent of decay of linkage disequilibrium surrounding a core site subjected to strong positive selection. This test statistic captures the property that, when a beneficial allele has risen to high frequency due to positive selection, it tends to have high levels of haplotype homozygosity extending much further than what is expected under a neutral model. The iHS statistic is suited to detect selective sweeps where the selected allele has reached intermediate frequency.

Composite Likelihood

Statistical methods based on composite likelihood functions provide an advantage over traditional summary statistics by enabling consideration of the spatial distribution and marginal allele frequencies at linked sites [76,77]. For example, Kim and Nielsen introduced a composite likelihood ratio (CLR) test, with a test statistic called ω, that captures an excess of linkage disequilibrium at a locus of interest, a strong indicator of a selective sweep [77]. This method compares the likelihoods of a sweep model and a neutral model at a locus of interest. Many extensions and improvements to this composite likelihood approach have been introduced in methods such as SweepFinder [78], SweepFinder2 [79], SweeD (Sweep Detector) [80], and OmegaPlus [81] (for a recent survey of these methods, see [82]). These methods are computationally efficient compared with more advanced statistical methods (such as Approximate Bayesian Computation and likelihood-based approaches) and supervised machine learning, but appear to have limited sensitivity when selection is weak. The power of these tests tends to decrease as the time since the fixation of the beneficial mutation increases [77]. Importantly, statistical methods based on composite likelihood (such as the approach of Kim and Nielsen) provide a rigorous parametric model to test for selection.

Approximate Bayesian Methods

Another widely used statistical approach is Approximate Bayesian Computation (ABC), which bypasses direct computation of the likelihood function through the use of simulations. In particular, ABC works by simulating data sets according to a prior distribution of model parameters, or in more advanced applications, from a proposal distribution in a Markov chain Monte Carlo (MCMC) setting [83,84]. These simulated data sets are reduced to a compact set of summary statistics designed to capture the important properties of the data relative to the questions of interest. Simulated data sets are then accepted or rejected, by a rejection sampling scheme, essentially based on how similar their summary statistics are to those of the observed data set. Because this approach can be highly inefficient if most simulated data sets are rejected, investigators have developed a variety of different weighting schemes to increase the acceptance rate. In the end, ABC provides an approximate posterior distribution over the model parameters conditioned on a chosen set of summary statistics. The approach offers several advantages over traditional summary-statistic and composite-likelihood approaches in the inference of selection: (i) it provides an approximate posterior distribution, (ii) it can be used to jointly infer a selection coefficient and time of selection onset, (iii) it can accommodate dependencies between linked sites, and (iv) it can be generalized to detect sweeps starting from either standing genetic variants or de novo mutations [85]. The main disadvantage of ABC is that it tends to become prohibitively computationally expensive as the number of parameters and summary statistics increases, due to the large size of the parameter space and the inevitable inefficiency of the rejection-sampling scheme. As a result, ABC is difficult to apply to complex questions and highly parameterized models, although regression-based ABC approaches offer some improvements in this area [86]. It is also often non-trivial to identify a priori an appropriate subset of summary statistics to use in ABC. Notably, tools such as ABCtoolbox [87] help to make ABC more accessible to the user, by facilitating steps such as sampling from a prior distribution, summary statistics calculations, estimation of the posterior distribution, and model selection and validation.

Machine learning

Supervised machine learning methods have recently been introduced as an alternative way to detect positive selection, particularly hard and soft selective sweeps [88-90]. These machine-learning methods are well-known for their flexibility and power in a general classification setting, even with complex data sets that potentially require non-linear classification rules. By combining rich feature vectors and large numbers of labeled examples (typically simulated neutral or sweep regions), machine-learning models have demonstrated state-of-the-art performance as well as reasonable robustness to demographic model misspecification in the detection of selective sweeps [88,90]. Methods such as S/HIC [89], diploS/HIC [88], SFselect [91], and evolBoosting [92] aggregate summary statistics as informative sequence features for prediction (e.g., Tajima’s D, Θ_w, etc.), then train classifiers based on patterns of variation in the feature set to discriminate among hard sweeps, soft sweeps, and neutral regions. Additionally, these classifiers have been used to detect partial sweeps [93] and balancing selection [90]. These machine-learning analyses provide new insights into how selection has shaped the genomes of humans and other organisms, and shed light on the driving forces behind the enormous phenotypic diversity in the natural world. A recent review [94] has surveyed supervised machine learning methods and their use in population genetics.

One of the main disadvantages of using supervised machine learning in this setting is the need for a large number of simulated examples to train a classifier. Additionally, the training procedure requires subjective decisions about which sorts of examples to simulate and will naturally be biased towards the assumed scenarios for simulation [95]. Hence, it is essential to test the model on data simulated from alternative scenarios. Generally, studies that employ ML-based methods should conduct a careful and thorough robustness analysis to show that their model is not too sensitive to changes in the assumed demographic model, or in other parameters such as mutation or recombination rates, selection coefficients, and times of selection onset. Furthermore, it is particularly crucial in this setting to make use of independent and complementary methods to confirm the predicted sweeps.

Both supervised machine learning and ABC are similar in that the inference is based on simulations. They both require a large number of simulations to obtain accurate estimates, especially as the dimensionality of the observed data increases. The nature of the output is black-box in the sense that there is no clear way to tell which features or statistics are the most informative. Hybrid models combining machine learning and ABC have been developed to perform dimensionality reduction or selection of informative summary statistics. For example, Blum and Francois performed dimensionality reduction via a neural network, followed by improving parameter estimation using importance sampling [86]. Finally, ABC and supervised machine learning are effective (depending on the sample size) in detecting selection across different evolutionary timescales.

Beyond summary statistics: ARGs and gene trees

The ancestral recombination graph (ARG) is a data structure that summarizes the coalescence and recombination events that have occurred in the evolutionary history of a collection of DNA sequences (Figure 1). In addition to representing the explicit evolutionary history across a set of DNA sequences, the ARG is useful in addressing a wide variety of biological questions, including: (i) estimation of the recombination rate, (ii) estimation of demographic model [96], including divergence times, effective population sizes, and gene flow, (iii) estimation of allele ages, based on mapping of mutation events to branches of the ARG, and (iv) characterization of the influence of selection on each allele, based on departures from the patterns of coalescence and recombination expected under neutrality [5,97-99].

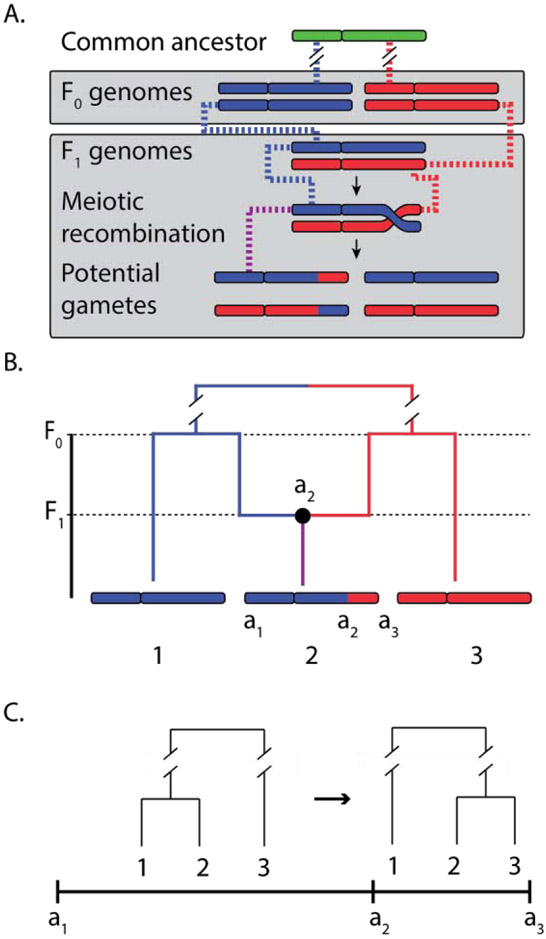
Figure 1: The Ancestral Recombination Graph (ARG).

Recombination gives rise to local gene trees which are embedded in an ARG. (A) An illustration of how meiotic recombination leads to differing genealogies between two genetic loci. The chromosomes are colored by lineage (e.g., blue for maternal, red for paternal). The F1 offspring have one chromosome from each lineage from which mosaic chromosomes can be created via recombination during meiosis. For one of these chromosomes, the physical generating process is indicated by dashed lines, with the color representing the lineage. A theoretical ancestor is also assumed for the red and blue lineages for simplicity. (B) The generative process for three whole sampled chromosomes is represented as an ARG. The recombination event on chromosome 2 is represented as a single lineage splitting one generation back at the a₂ locus. The left interval (a₁,a₂] then coalesces with chromosome 1 and the right interval (a₂,a₃] coalesces with chromosome 2 in the F₀ generation. (C) It can be useful to extract local gene trees from the ARG to interpret the evolutionary histories at an individual locus. In this case there are two loci with different histories. To extract a local tree for a given locus, one can start at the tips of tree, then for each recombination event, follow the lineage that corresponds to the chosen locus. For example, given a locus in the interval (a₁,a₂], one would follow the left lineage at the recombination node, producing the left tree in panel (C). Given a locus in the interval (a₂,a₃], one would follow the right lineage and obtain the right tree.

Our focus here is on this fourth application, the use of the ARG in detecting selection (Figure 2), but we begin by summarizing several recently developed methods for the general problem of ARG inference. These methods differ in terms of their algorithmic complexity, scalability, and accuracy. We focus on a representative set of state-of-the-art methods. After briefly describing the algorithmic details of each method, we discuss the use of ARGs and gene trees for inferring selection, then conclude by discussing future directions that involve using the ARG.

Figure 2: The effect of selection on local genealogies at and near the focal site and proximal trees.

(A) A subset of a full ARG for simulated data based on the discoal simulator [53], expressed as a sequence of local genealogies with one tree for each non-recombining locus. The central locus shows the tree that encapsulates the allele under positive selection, resulting in a burst of coalescence events beneath the emergence of that allele. Flanking loci are considered linked gene trees and are dragged along, resulting in shorter coalescence times for those lineages than at more distal loci (neutral gene trees). (B) A number of traditional summary-statistics collected across five contiguous windows. These summary statistics were used by S/HIC [89], then aggregated as informative sequence features for prediction of soft and hard sweeps. Each summary statistic is normalized by the sum of its values across all windows. The hitchhiking effect provides a key signature of positive selection in modern sequence datasets, causing aberrations or changes in the spatial pattern of genetic diversity across windows of regions.

ARGweaver

ARGweaver [5,96] is currently the only available method that samples from the posterior distribution of ARGs given DNA sequence data and is efficient enough to apply on a genome-wide scale (but see also the earlier ARG-sampling methods LAMARC [100] and ACG [101]). The ARG representation in ARGweaver—like those in several other methods considered here—is interchangeable with a sequence of local trees and the recombination events that transform each local tree to the next. This representation is slightly simplified from earlier ARGs [102-104], in that it excludes edges not ancestral to the present-day sample, but the simplified representation follows naturally from the assumption in ARGweaver of the Sequentially Markov Coalescent (SMC) [105] as the generating process for ARGs. By using discrete time points and enumerating tree topologies, ARGweaver approximates the continuous state space of the SMC by a finite set, which permits the use of standard dynamic programming algorithms for hidden Markov models (HMMs) in ARG inference. The main innovation of ARGweaver is to use a Markov Chain Monte Carlo (MCMC) algorithm to sample only a portion of the ARG at a time, in such a manner that the sequence of sampled ARGs is guaranteed to eventually converge to the desired posterior distribution. ARGweaver enables the recovery of the distribution of the local genealogies (topology and branch lengths), recombination breakpoints, recombination rates, time to most recent common ancestry (TMRCA) and other derived statistics, as well as the recovery of allele ages. It can additionally accommodate unphased data, missing genotypes, and ancient DNA samples. The main disadvantage of ARGweaver is its computational cost, particularly as the number of individuals increases. The method can currently only be applied to a few dozen individuals at a time.

RENT+

The key idea of RENT [106] and its extension RENT+ [107] is to construct a sequence of local gene trees based on SNPs near each focal site using a parsimony-based approach that minimizes the number of recombination events. The motivation behind the approach is that SNPs that occur near one another are likely to share similar tree topologies. The algorithm constructs a tree topology (guide tree) for each SNP, then generates a single refined tree for a maximal set of consecutive SNP trees such that the refined tree is compatible with the local SNP trees. Notably, it has been shown that ARGs inferred by parsimony, as in RENT+, often severely underestimate the true number of recombination events in the history of the sample [108]. An additional limitation of RENT+ is that it generates a single point-estimate of the ARG, rather than a distribution, and therefore provides no direct information about gene tree uncertainty. Owing to its heuristic rules and approximations, RENT+ is considerably faster and more scalable than ARGweaver but it appears to be somewhat less accurate [107]. One advantage of RENT+ is that, unlike ARGweaver, it is not sensitive to a variety of user-defined parameters such as the mutation rate, recombination rate, and number of sampling iterations.

tsinfer

tsinfer [109] is an ultra-fast, heuristic ARG inference method that scales to hundreds of thousands of complete genomes. The method requires an input of bi-allelic sample haplotypes, phased data, and ancestral/derived states. It proceeds by reconstructing ancestral genome fragments for each site, and then inferring the relationships among these fragments according to an ancestral copying process. After explaining all haplotypes in this manner, the method outputs a tree sequence. Notably, tsinfer does not explicitly infer an ARG but rather a sequence of local gene trees, described by their topologies only. tsinfer was shown to be substantially faster and more scalable than ARGweaver and RENT+, with comparable topological accuracy to ARGweaver [109]. Importantly, however, these comparisons were based on tree topologies only and ignore the absence of branch-lengths in tsinfer’s reconstructed ARG. Additionally, like RENT+, tsinfer infers a single point estimate of an ARG rather than allowing for gene-tree uncertainty.

RELATE

RELATE [110] generates genome-wide genealogies for up to 10 000 sequences and subsequently estimates branch lengths, allele ages, and population size trajectories. The first step of RELATE estimates a local genealogy at each variable site in the genome. For each SNP, a distance matrix is computed using a modified Li-and-Stephens algorithm [111], then the algorithm reconstructs one haplotype as a mosaic of the other sample haplotypes and stores position-specific probabilities of the copying process from each of the other samples in a distance matrix. The local coalescent tree is constructed via hierarchical clustering from the distance matrix. The second step of RELATE estimates the time of particular coalescent events across the local genealogical histories. The mutations are superimposed on their corresponding branches in the local gene trees, then the branch lengths are estimated using an MCMC algorithm based on the coalescent. Using the inferred genome-wide genealogies, RELATE can simultaneously estimate the population size trajectory over time in a stepwise manner. Furthermore, the estimated local genealogical histories can be used for other downstream analyses such as identifying signals of introgression and positive selection. Speidel et al. showed that RELATE was faster than both ARGweaver and RENT+ [110]. To evaluate accuracy, they compared RELATE against ARGweaver and RENT+ using the TMRCA metric across different model conditions and found that RELATE performed best. Like RENT+ and tsinfer, RELATE produces a point estimate of the genealogy, with no allowance for gene tree uncertainty, a well-known problem in gene-tree reconciliation coalescent-based methods [112-115].

It is worth noting that RELATE and tsinfer have one major similarity in that they both use approaches based on Li-and-Stephens algorithm [111] to estimate ancestral relatedness. In principle, RELATE and tsinfer could be combined into a hybrid model where tsinfer is run as a preprocessing step to group individuals by their relatedness due to its scalability in handling sample sizes up to millions of samples, then RELATE is used for branch-length inference and refining topologies.

ARGs and gene trees to infer selection

The coalescent [49] provides an elegant framework for studying patterns of genetic variation. As noted above, the coalescent process traces lineages backwards in time until they have all converged on their most recent common ancestor (MRCA). A major attraction of the coalescent is its modularity in terms of separating the genealogical history from the neutral mutation process. This property allows the coalescent tree to be generated first, then the neutral mutations to be superimposed on the tree. The basic coalescent model accounts for genetic drift assuming no recombination. However, extensions have been introduced to account for myriad other factors such as recombination [47,102] and complex demography [116-120].

When selection is present, however, the coalescent model becomes far more difficult to characterize because the coalescence and mutation processes are no longer independent. The ambitious endeavor of extending the coalescent to the setting of both mutation and selection at a non-recombining locus was undertaken by Krone and Neuhauser [121,122]. Their solution involved embedding the gene tree in another graph known as the ancestral selection graph, which distinguished between alleles having different selection coefficients. Using this graph, they were able to integrate out the population allele frequency and the genealogy. One drawback of this approach is that the size of the graph tends to grow with the selection coefficient, making the simulation of strong selection difficult. The original work by Krone and Neuhauser did not allow for direct inference of model parameters from data, but subsequent efforts have attempted inference based on this framework [123].

An alternative way to accommodate selection in the coalescent is by explicitly considering the frequency trajectory of the allele under selection as characterized using diffusion theory [124]. For example, Kaplan et al. derived the distribution of the coalescent tree conditioned on the frequency trajectory of the selected allele [125]. This generative framework can be extended to inference from data by treating both the allele frequency trajectory and the coalescent tree conditional on that trajectory as “hidden” or “latent” variables. Following this approach, Coop and Griffiths introduced a method to approximate the full likelihood of the selection coefficient by integrating over both of these hidden layers in the setting of a single non-recombining locus [126]. They estimated the likelihood using an importance sampling scheme to marginalize out the allele frequency trajectory and the conditional genealogy for a particular selection parameter.

Recently, Stern et al. introduced a clever method, called CLUES, that extends the approach of Coop and Griffiths to allow for recombination [127]. CLUES infers both the selection coefficient and historical allele frequency trajectory for a specific allele and nucleotide site of interest. This likelihood-based method uses ARGweaver to efficiently sample coalescent trees from the posterior distribution of ARGs at the locus of interest. It then uses a hidden Markov model to marginalize out the allele frequency trajectory conditioned on these trees. Because the ARGs sampled by ARGweaver reflect the assumption of selective neutrality, CLUES treats them as “proposals” only and uses an importance sampling scheme to estimate the selection coefficient. Stern et al. estimated the selection coefficients at various pigmentation-associated variants and found evidence of adaptation, consistent with previous work.

In principle, ARGs could also aid in making inferences of polygenic selection across a set of loci associated with a trait based on genome-wide association study (GWAS) summary statistics. Along these lines, Edge and Coop reconstructed changes to polygenic scores over time using local genes trees at GWAS loci [128]. They used various estimators for allele frequency change in a population based on the branch lengths of coalescent trees, and studied human polygenic scores over time using preestimated effect sizes for height and inferred coalescent trees for the trait-associated loci. At least one research group is exploring extensions of this approach that makes use of the full ARG.

The Singleton Density Score (SDS) is another method that indirectly makes use of features of gene trees in the inference of selection. The SDS provides information about selection on very recent time scales by measuring changes in the branch lengths at the tips of the genealogy [129]. The intuition behind the score is that, in the presence of adaptation, the tip branches carrying causal alleles for the trait in question will on average be shorter than those carrying non-causal alleles. Because mutations that occur on tip branches will appear in the data as singletons (present in one sample only), the causal alleles will therefore tend to have a lower “singleton density”. An extension of SDS that explicitly uses the terminal branch lengths from inferred local gene trees has also been developed [110,128]. The application of SDS to human data showed that the measure permits powerful inferences about recent selection starting from standing genetic variation. In particular, the SDS was used to study adaptation in the setting of polygenic selection on complex traits.

While these new methods for detecting polygenic selection can be quite powerful, it is worth bearing in mind that they can also be confounded by latent population structure, just as methods based on summary statistics can. For example, several groups have recently reported evidence of positive selection for height in European populations [130-134], but these findings failed to replicate in the UK Biobank, potentially due to its reduced population stratification [135,136]. Even within the UK Biobank, population stratification could remain an issue for some analysis [137]. In general, care must be taken to avoid subtle biases from population structure in tests for polygenic selection, and where possible researchers should try to replicate results in independent populations.

Concluding Remarks and Future Directions

The full ARG inference may shed new light on natural selection. As in the identification of selective sweeps, most methods for inferring selection coefficients or times of selection onset make use of individual or combined traditional summary statistics. Recently, deep learning has achieved tremendous success unmatched by other machine learning techniques in a variety of challenging problems, including image recognition, machine translation, and game play [138]. Deep learning is not only very powerful but also highly flexible, which allows the design of novel model architectures motivated by biological knowledge. One particular architecture that provides a natural way to handle the temporal and sequential nature of biological datasets is recurrent neural networks (RNNs) [139,140]. A natural approach to infer sweeps could involve the use of RNNs. Recently, Adrion et. al. developed ReLERNN, a deep learning method that uses a RNN, to accurately estimate the genome-wide recombination landscape from genotype alignments [141]. Instead of using sequences across genomes for inferring the recombination landscape, one could use the local genealogies derived from inferred ARGs as input to an RNN for inferring selection. Importantly, RNNs are capable of handling data summaries that are exceptionally complex and high-dimensional. By analogy to speech recognition, these individual gene trees can be thought of as high-dimensional “words” and sequences of contiguous gene trees can be thought of as “sentences”. The RNN provides a natural framework for temporal features derived from the ARG, such as the number of lineages remaining at each of a set of pre-identified time points. We anticipate that this approach will provide new insight into how selection has shaped the human genome and the genomes of other species.

Another possibility is to make use of machine-learning methods in inferring the Distribution of Fitness Effects (DFE) for loci associated with a polygenic trait based on GWAS summary statistics. Such a method could potentially use properties of the ARG (e.g., the cross-coalescence time between sampled individuals or the number of lineages remaining at distinct time points of the gene trees) at GWAS-associated loci as features. One possible approach would involve the following steps: (i) Simulate regions based on a predefined demographic model with a variety of assumed DFEs and infer the ARG for each simulated region, (ii) Train a deep neural network to estimate the DFE based on features extracted from the simulated ARGs, (iii) Extract regions of the human (or another) genome corresponding to a trait of interest based on GWAS summary statistics and infer the ARG for each region, and (iv) Apply the deep neural network to these ARGs to estimate a DFE for the real data.

Full ARG inference is also potentially useful in studying the genetic basis of the separation of populations into distinct species. For example, the inferred ARGs could be examined for signs of recent selective sweeps, local to one or a few species. These apparent sweeps should exhibit reduced time to most recent common ancestry (TMRCA) within species in the inferred ARGs. In addition, they are expected to show reduced values of another ARG-derived statistic, the relative TMRCA half-life (RTH) [5], which takes on low values when a recent “burst” of coalescence due to a sweep follows earlier coalescence events that are more widely spaced, as expected under neutral drift. Much work studying the genetics of speciation involves identifying loci having unusually high levels of population differentiation, as measured by Fst. ARG-based measures provide an alternative and complementary way to infer selective sweeps where such observations would not be possible using only simple summary statistics such as Fst, π or Tajima’s D.

Recent advances to the ARGweaver algorithm, implemented in ARGweaver-D [96], allow it to consider a full demographic model, including a tree of populations with divergence times, ancestral effective population sizes, and “bands” in which inter-population gene flow is allowed. Like ARGweaver, ARGweaver-D probabilistically samples ARGs from the posterior distribution, but in this case this distribution is conditioned on the user-specified demographic model. This extension to ARGweaver permits the accurate identification of ancient introgression and improved estimates of TMRCAs, allele ages, and other quantities of interest.

The ARGweaver-D algorithm is also naturally suited for a different type of analysis, where a new “query” sequence is provided, and the core sampling algorithm in ARGweaver is used to “thread” that sequence into a pre-computed ARG for a database of reference genomes such as those from the Simons Genome Diversity Project [2]. This approach would have many potential applications, including local ancestry inference for admixed query sequences (i.e., identifying which segments derive from which source populations), identification of Neanderthal- or Denisovan-derived sequences, estimation of the ages of variants present in each query genome, or estimation of time to most recent common ancestry with the database samples. In effect, it would allow the accumulation of evolutionary information from a large, diverse set of genomes to be “projected” onto a user-provided query sequence.

In this review, we have discussed both motivations and methods for measuring natural selection. We have also reviewed some of the critical supporting infrastructure for these analyses, including simulators for population genetic data and methods for gene tree and ARG inference. Finally, we have discussed potential studies that show inferred gene trees and ARGs are rich sources of information that aid in addressing a wide range of problems in population genetics. Looking forward (see Outstanding Questions), we anticipate that continuing advances in ARG inference will provide an increasingly flexible and powerful alternative to summary-statistic-based methods for inferring natural selection from DNA sequences.

Outstanding Questions.

• The most scalable ARG-based method can only infer gene tree topologies. How can we extend these approaches to infer branch lengths along with topologies?

• How can we better leverage existing ARG-based summary statistics and design new ones to infer signatures of selection?

• How can we use more advanced machine-learning models (such as convolutional or recurrent neural networks) to exploit the sequential and temporal nature of gene trees in making predictions about selection?

• Supervised machine learning methods have been widely applied to detect selective sweeps. Can we leverage such approaches to study complex traits that undergo polygenic selection?

• How can we best make use of ARGs that consider full demographic models, including a tree of populations with divergence times, ancestral effective population sizes, and “bands” in which inter-population gene flow is permitted?

• How can we develop more scalable strategies for inferring approximate posterior distribution of ARGs?

Highlights.

• Gene trees and ARGs represent powerful and rich data structures for the detection of signatures of natural selection from DNA sequences.

• Methodological advances in inferring genome-wide genealogies provide an alternative and complementary way to infer natural selection by making use of the full data set rather than traditional summary statistics.

• In this review, we discuss the biological importance of studying selection and advances in selection simulators. Furthermore, we review traditional summary statistics and methods that aggregate multiple statistics, including Approximate Bayesian Computation (ABC) and supervised machine-learning methods.

• We also discuss future directions in inferring sequences of gene trees and scalable ARGs, and their use in studying selection.

Glossary

Ancestral recombination graph (ARG)

a data structure that specifies the genealogical relationships among a sample of chromosomes while accounting for recombination events in the history of the sample.

Balancing selection

a selective process that favors genetic diversity, and therefore tends to maintain genetic variation at a locus for longer than expected by genetic drift alone.

Classifier

a model that assigns samples to discrete categories.

Composite likelihood function

(also known as a pseudo-likelihood function), an inference function generated by combining a collection of individual component likelihood functions, often by assuming independence where it is not strictly warranted.

Complex trait

or polygenic trait, a trait that does not follow Mendelian inheritance patterns and thus is likely affected by a large number of loci.

Deep neural network

an artificial neural network with more than two layers used to process data with complex mathematical functions.

Distribution of fitness effects (DFE)

genome-wide distribution of selection coefficients for a set of variants.

Effect size

a measure of the effect a particular variant has on the value of a phenotype.

Fst

a relative measure of divergence that compares total-population variation relative to within-subpopulation variation.

GWAS summary statistics

summary of a GWAS describing the marginal association of each individual allele with a trait of interest, typically including a p-value, effect size estimate, and standard-error.

Haplotype

group of alleles on a single contiguous DNA sequence that are inherited from a single parent.

Hard sweep

increase in frequency of a newly arising beneficial mutation, together with its haplotype background. In the case of a “complete” hard sweep scenario, the beneficial mutation reaches fixation.

Hitchhiking

the process by which alleles in linkage disequilibrium to a beneficial allele in a site under positive selection increase their allele frequencies.

Linkage disequilibrium

a statistically nonrandom association of alleles at two or more loci.

Partial sweep

increase in frequency of a beneficial mutation together with its haplotype background, without the beneficial mutation reaching fixation.

Polygenic score

a numeric score that measures the expected influence of a collection of assayed genotypes on a trait.

Polygenic selection

selection on a complex trait that is determined by the alleles at multiple loci across the genome. As a result, polygenic selection simultaneously alters allele frequencies at many genomic loci.

Recurrent neural network (RNN)

a class of artificial neural networks used to evaluate temporal and sequence data.

Relative TMRCA half-life (RTH)

the time at which half of the samples in a population of interest reach a common ancestor, as a fraction of the time to the most recent common ancestor of all the samples in the population.

Sequentially Markov Coalescent (SMC)

an approximation of the coalescent that assumes that the distribution of the genealogies at position i depends only on the genealogy at position i - 1 and not on the previous genealogies.

Site frequency spectrum (SFS)

distribution of allele frequencies within a population.

Soft sweep

increase in frequency of a standing genetic variant, together with the associated haplotype backgrounds, when that variant becomes beneficial, for example, due to a change in the environment. In the case of a “complete” soft sweep, the beneficial mutation reaches fixation.

Supervised machine learning

a technique that learns a model from labeled training samples, and then uses the learned model to assign a discrete category or a continuous value to an unlabeled sample (test sample).

Tajima’s D

summary statistic that compares the average number of pairwise differences with the number of segregating sites.

Time to most recent common ancestry (TMRCA)

most recent time at which a given set of lineages trace to a common ancestor.