Abstract
Eutectic systems offer a wide range of new (green) designer solvents for diverse applications. However, due to the large pool of possible compounds, selecting compounds that form eutectic systems is not straightforward. In this study, a simple approach for preselecting possible candidates from a pool of substances sharing the same chemical functionality was presented. First, the melting entropy of single compounds was correlated with their molecular structure to calculate their melting enthalpy. Subsequently, the eutectic temperature of the screened binary systems was qualitatively predicted, and the systems were ordered according to the depth of the eutectic temperature. The approach was demonstrated for six hydrophobic eutectic systems composed of L-menthol and monocarboxylic acids with linear and cyclic structures. It was found that the melting entropy of compounds sharing the same functionality could be well correlated with their molecular structures. As a result, when the two acids had a similar melting temperature, the melting enthalpy of a rigid acid was found to be lower than that of a flexible acid. It was demonstrated that compounds with more rigid molecular structures could form deeper eutectics. The proposed approach could decrease the experimental efforts required to design deep eutectic solvents, particularly when the melting enthalpy of pure components is not available.
Keywords: eutectic mixtures, deep eutectic solvents, solid–liquid equilibria, hydrophobic DESs, melting properties
1. Introduction
Eutectic systems are mixtures of two or more compounds that exhibit partial immiscibility or negligible mutual solubility in the solid phase [1]. Deep eutectic solvents (DESs) are eutectic mixtures characterized by a large depression of the melting temperature of the mixture at the eutectic point relative to the melting temperature of the pure components [2,3]. DESs are analogous to ionic liquids (ILs) in terms of being designer solvents and possessing low vapor pressure. However, DESs are usually less toxic, easier to prepare, and less expensive than ILs. These advantages have led to the recent increase in applications of DESs, for example, as solvents in diverse separation methods [4,5,6,7,8], media for chemical [9,10,11,12,13,14], electrochemical [15,16,17,18,19], and biological reactions [20,21], in polymer chemistry [22,23,24], and for increasing the solubility of active pharmaceutical ingredients [25,26,27,28].
Although their preparation may be easier than that of ILs, DESs are more difficult to design. The ratio of the ions in ILs is defined by the electroneutrality of the solution. In contrast, the ratio of DES components is not fixed and can be of any value. One of the first pieces of information required when designing DESs for a specific application is the eutectic temperature and eutectic composition of the system. Thus far, the design of DESs has been performed primarily using a trial and error approach. In most published works, preselected components are mixed at several fixed molar ratios, such as 1:1 or 1:2, and mixtures that remain liquid at room temperature are selected for further testing [29,30]. To determine the system composition and melting temperature at the eutectic point, the solid–liquid equilibria (SLE) of the eutectic systems should be known. The SLE also provides information about the melting temperature of the system at any specific composition.
The experimental determination of SLE phase diagrams of eutectic systems is non-trivial and is often accompanied by difficulties and limitations. For example, the hygroscopic nature of some DES components [31], the high viscosity and paste-like consistency of some DESs close to their melting temperature [32], the decomposition of DES constituents before melting, and the chemical reaction between DES constituents after storage [33]. Owing to the previously mentioned difficulties, predictive methods are required. Abranches et al. [34] proposed Conductor like Screening Model for Real Solvents (COSMO-RS) to predict the SLE of eutectic mixtures. Wolbert et al. [35] used UNIFAC (Do) to model the activity coefficient of constituents in binary eutectic mixtures.
The SLE of simple eutectic systems, whose components show negligible mutual solubility in the solid phase, is commonly calculated in the literature using the following simplified equation:
| (1) |
where and are the mole fraction and activity coefficient of the component in the liquid solution, respectively; and are the melting enthalpy and melting temperature of the pure component , respectively; T is the liquidus temperature (i.e., melting temperature of the mixture at the mole fraction ); and R is the universal gas constant. As seen in Equation (1), SLE calculations require information about the pure components melting properties, namely, the melting enthalpy and temperature , as well as information about the behavior of the components in the liquid phase (i.e., activity coefficients).
Strong intermolecular interactions between unlike molecules in the liquid phase—low activity coefficient values of components—and/or low melting enthalpy values of pure components lead to a deep depression of the melting temperature of the mixture at the eutectic point [35,36,37,38]. The melting enthalpy of components is not always easily measured because of polymorphism, kinetic limitations, and/or thermal instability. As a result, the melting enthalpy of many components is unavailable. The aim of this work was to demonstrate the correlation between the molecular structure and melting enthalpy of a component to simplify the selection of components, especially when no experimental data on melting enthalpy is available.
At the melting point of a pure component, the solid and liquid phases are in equilibrium. The melting temperature of a pure component is the ratio between the melting enthalpy and the melting entropy :
| (2) |
Melting enthalpy is the energy required to melt solid crystals [39] and depends on the type of interactions between molecules in the lattice structure [39,40]. Melting entropy is the increase in the disorder and randomness upon melting [41] and depends on the molecular symmetry and conformational degrees of freedom of the molecule [41,42,43,44]. Despite several attempts to correlate the melting properties of a component with its molecular structure, there is no generic model that can predict the melting properties of pure components [45].
The melting temperature of pure components is difficult to predict [43]; however, unlike the melting enthalpy, experimental data on the melting temperature are, in many cases, available. However, depending on the method of determination as well as the purity of the components, the reported values may deviate by several degrees Celsius from the actual melting temperature. However, as seen from Equation (1), an uncertainty of several degrees Celsius in the melting temperature of pure components would have a small effect on the SLE of the mixture. According to Bondi [46], the melting entropy of compounds can be better related to the molecular structure than the melting enthalpy. The melting entropy calculated from the molecular structure with the available melting temperature can be used to estimate the melting enthalpy of the components with Equation (2). Using this information, the eutectic temperature can be approximately calculated using Equation (1) under the assumption of ideal behavior).
The objective of this study was to test a simple approach that could be used to select potential eutectic system constituents based on their melting enthalpies. It is assumed that mixtures of components with a lower melting enthalpy would result in eutectic mixtures with a larger melting temperature depression, as previously demonstrated [35,36,37,38]. This approach aims to reduce the experimental efforts required to measure pure components’ melting enthalpy, as well as the SLE of eutectic mixtures. To evaluate the proposed approach, binary eutectic mixtures of L-menthol with six different monocarboxylic acids were considered in this work. The goal was to predict the eutectic temperature of each system relative to other systems. Although the eutectic temperatures were calculated with the unitary activity coefficient, it was not claimed that the components should behave ideally. The proposed approach was based on the assumption that any component in its binary solutions with other components sharing the same type and number of functional groups behaves similarly (i.e., in any binary mixture with monocarboxylic acids, L-menthol behaves in a similar manner). The latter assumption has been validated for many eutectic systems, for example, in [Ch]Cl/sugar [32], [Ch]Cl/dicarboxylic acids [47], [Ch]Cl/fatty acids or alcohols [48], and thymol/fatty acids [49].
2. Results and Discussion
2.1. Melting Properties of Pure Components
The melting entropy of acids was calculated using the model proposed by Jain et al. [44] (Equations (4)–(6)). The model parameters and calculated melting entropies are presented in Table 1. Linear acids possessed higher melting entropy than cyclic acids. This was a result of the higher flexibility of a linear chain compared to a ring structure. The lowest predicted melting entropy was for cyclohexanecarboxylic acid with a flexibility number Φ equal to zero. The model predicted the same melting entropy for 3-phenylpropionic acid and 3-cyclohexylpropionic acid. This was because the model did not differentiate between phenyl and aliphatic ring and predicted the same flexibility number Φ for both components. Due to the asymmetry of the carboxylic acid group, the symmetry number σ of all acids tested in this work was one.
Table 1.
Symmetry number σ, flexibility number Φ, and calculated melting entropy Δsm of components using the model proposed by Jain et al. [44].
| Compound | σ | SP3 | SP2 | Ring | τ | Φ | Δsm (J mol–1 K–1) |
|---|---|---|---|---|---|---|---|
| 3-cyclohexylpropionic acid | 1 | 2 | 1 | 1 | 2 | 5.93 | 64.80 |
| caprylic acid | 1 | 6 | 1 | 0 | 5.5 | 133.58 | 90.69 |
| cyclohexanecarboxylic acid | 1 | 0 | 1 | 1 | 0 | 1 | 50 |
| capric acid | 1 | 8 | 1 | 0 | 7.5 | 792.03 | 105.49 |
| 3-phenylpropionic acid | 1 | 2 | 1 | 1 | 2 | 5.93 | 64.80 |
| lauric acid | 1 | 10 | 1 | 0 | 9.5 | 4696.13 | 120.29 |
Table 2 presents the melting properties that were experimentally determined in this study using DSC. The obtained values were in good agreement with those reported in the literature. To the best of our knowledge, the melting properties of cyclohexylpropionic acid have not been measured before. As seen in Table 2, the melting enthalpy of l-menthol had a low value, thus making l-menthol a good candidate for designing deep eutectic systems. In general, linear acids have higher melting enthalpies than cyclic acids. The melting enthalpy of linear acids increases by increasing the chain length; for example, lauric acid > capric acid > caprylic acid. The lowest melting enthalpy was observed for cyclohexanecarboxylic acid, which is the component with the most rigid molecular structure.
Table 2.
Comparison of melting enthalpies Δhm and temperatures Tm measured in this study and reported in the literature.
| Compound | Tm (K) | Δhm (kJ mol–1) | ||
|---|---|---|---|---|
| This Work * | Lit. | This Work * | Lit. | |
| l-menthol | 314.6 ± 0.1 | 315.68 [49] | 13.74 ± 0.5 | 12.89 [49] |
| 3-cyclohexylpropionic acid | 291.3 ± 0.1 | – | 16.96 ± 0.5 | – |
| caprylic acid | 288.0 ± 0.7 | 288.20 [49] | 21.43 ± 0.3 | 19.80 [49] |
| cyclohexanecarboxylic acid | 299.4 ± 1.1 | 301.9 [50] | 10.69 ± 0.2 | 9.20 [50] |
| capric acid | 303.9 ± 0.1 | 304.75 [51] | 28.39 ± 0.7 | 27.50 [51] |
| 3-phenylpropionic acid | 321.6 ± 0.1 | 321.2 [52] | 15.11 ± 0.1 | 15.68 [52] |
| lauric acid | 316.6 ± 0.1 | 317.48 [51] | 35.81 ± 0.4 | 37.83 [51] |
* Uncertainties are considered as the standard deviation of three measurements.
Table 3 presents a comparison between the melting entropies predicted by the model by Jain et al. [44] (Equations (4)–(6)) and the experimental melting entropies calculated with Equation (2) using the experimentally determined melting enthalpy and melting temperatures of acids. As seen in Table 3, the predicted melting entropy of all acids was overestimated.
Table 3.
Comparison of predicted Δsm predicted and experimental Δsm experimental melting entropy of monocarboxylic acids.
| Compound | Δsm predicted | Δsm experimental |
|---|---|---|
| 3-cyclohexylpropionic acid | 64.80 | 58.22 |
| caprylic acid | 90.69 | 74.41 |
| cyclohexanecarboxylic acid | 50 | 35.72 |
| capric acid | 105.49 | 93.44 |
| 3-phenylpropionic acid | 64.80 | 46.97 |
| lauric acid | 120.29 | 113.12 |
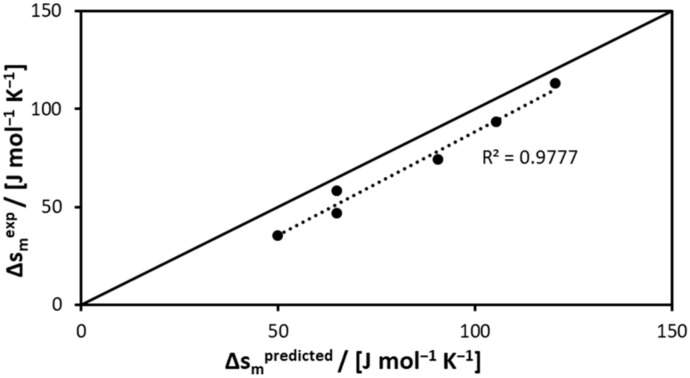
Figure 1 depicts the predicted melting entropy values in comparison to the experimental values. The linear correlation between the predicted melting entropies indicated that the model proposed by Jain et al. [44] could provide a reasonably good estimation of the melting entropy of compounds sharing the same chemical functionality.
Figure 1.
Experimental melting entropies measured in this study in comparison with predicted melting entropies.
2.2. Solid–Liquid Equilibria
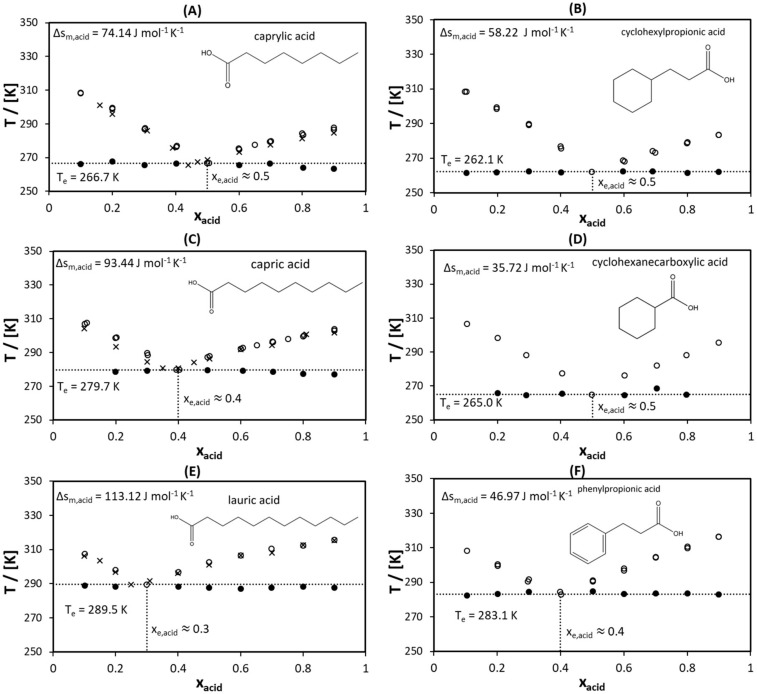
To validate the proposed approach, the SLE of the six eutectic systems was measured using DSC. Figure 2 presents the measured SLE data for l-menthol with six different monocarboxylic acids. To simplify the comparison between systems, the systems containing acids of similar melting temperatures are presented next to each other (Figure 2A–F). The approximated melting temperature of acids in each pair increased from Figure 2A,B (≈ 15 °C) to Figure 2E,F (≈ 45 °C). Martins et al. [49] measured the SLE of binary eutectic mixtures of L-menthol with caprylic acid, capric acid, and lauric acid. As seen from Figure 2A,C,E, the determined eutectic temperatures were in good agreement with the results reported by Martins et al. [49]. The slightly higher liquidus temperatures measured in this study might be due to the greater heating rate; in this study, a heating rate of 5 K min–1 was used, while in Martins et al. [49], 1 K min–1 was used.
Figure 2.
Solid–liquid phase diagrams of binary eutectic mixtures consisting of l-menthol and (A) caprylic acid, (B) cyclohexylpropionic acid, (C) capric acid, (D) cyclohexanecarboxylic acid, (E) lauric acid, and (F) phenylpropionic acid. The melting properties presented are experimentally determined values. Legend: ◦ liquidus temperature measured in this study, • the experimental eutectic temperature measured in this study, × Martins et al. [49].
As demonstrated in previous studies [35,36,37,38], the lower the melting enthalpy of the pure components, the higher the depression at the eutectic point. This could be confirmed by comparing the eutectic temperatures of eutectic systems formed between l-menthol and acids presented in Figure 2. The molecules with cyclic structures (Figure 2B,D,F) had lower flexibility than molecules with linear structures (Figure 2A,C,E). Therefore, the cyclic compounds possessed lower melting entropies. Because the melting temperatures of each pair of acids were similar (caprylic acid and cyclohexylpropionic acid ≈ 15 °C, capric acid and cyclohexanecarboxylic acid 30 °C, and lauric acid and phenylpropionic acid ≈ 45 °C), the melting enthalpy of cyclic compounds was lower than that of linear ones. As a result, the eutectic temperature of a system formed by a cyclic acid was lower than that of a system formed by a linear acid when both acids had the same melting temperature.
As seen in Figure 2, as the difference in the melting entropy of acids increased, the difference in the eutectic temperature increased. For example, the melting entropy of capric acid was almost three times higher than that of cyclohexanecarboxylic acid (see Figure 2C,D). This resulted in a eutectic temperature for l-menthol/cyclohexanecarboxylic acid (Figure 2C), which was approximately 15 K lower than that of l-menthol/capric acid (Figure 2D). For l-menthol/caprylic acid (Figure 2A) and l-menthol/3-cyclohexylpropionic acid (Figure 2B), the difference between their eutectic temperatures was only 4.5 K. This might be the result of a small difference between the melting entropies of caprylic acid and 3-cyclohexylpropionic acid (see Figure 2A,B). In a previous study [38], it was demonstrated that the eutectic composition was shifted toward the component that had a lower melting enthalpy. Comparing the eutectic composition between the systems revealed that the lower the melting enthalpy compared to that of l-menthol (13.74 kJ mol−1), the higher the mole fraction of the acid at the eutectic point.
It could be concluded that a lower melting enthalpy of pure components led to a larger melting temperature depression at the eutectic point of all l-menthol/monocarboxylic acid systems studied in this work. The melting enthalpy of components could be correlated with the molecular structure of acids possessing the same melting temperature. Therefore, the eutectic systems formed between l-menthol and cyclic acids exhibited a deeper eutectic point than that of systems formed with linear acids. Because the depression at the eutectic point was related to the difference in the melting entropy of the pure components, the relative depression at the eutectic point between the systems could also be predicted. Thus, the approach of selecting components by assessing the flexibility of their molecular structures could be used to design deeper eutectic systems.
3. Materials and Methods
3.1. Prediction of Melting Entropy
The melting entropy of the pure components was calculated as the sum of the rotational , conformational , and expansional entropies as follows [41]:
| (3) |
where W is a constant. In this study, the model proposed by Jain et al. [44] was used to predict the melting entropy of the pure components. The melting entropy in J mol–1 K–1 was calculated as follows [44]:
| (4) |
| (5) |
| (6) |
where is the symmetry number, is the flexibility number, and is the universal gas constant. Readers are directed to the original paper [44] for more information about the determination of the symmetry number of the components. The flexibility number was calculated as follows [44]:
| (7) |
| (8) |
where SP3 is the number of non-ring SP3 atoms (CH2, CH, C, NH, N, O, S), SP2 is the number of SP2 atoms (=CH,=C,=N, C=O), and Ring is the number of independent single, fused, or conjugated ring systems. If is less than zero, the flexibility number is set to 1.
In the search for components with low melting enthalpy values, components with low melting entropy were sought. According to Equations (4)–(6), components with symmetrical (large symmetry number σ) and/or more rigid molecular structures (small flexibility number Φ) should possess lower melting entropy. According to Equations (7) and (8), components with ring systems and double bonds should have a lower flexibility number Φ than single bond chains.
3.2. Eutectic Mixture Constituents
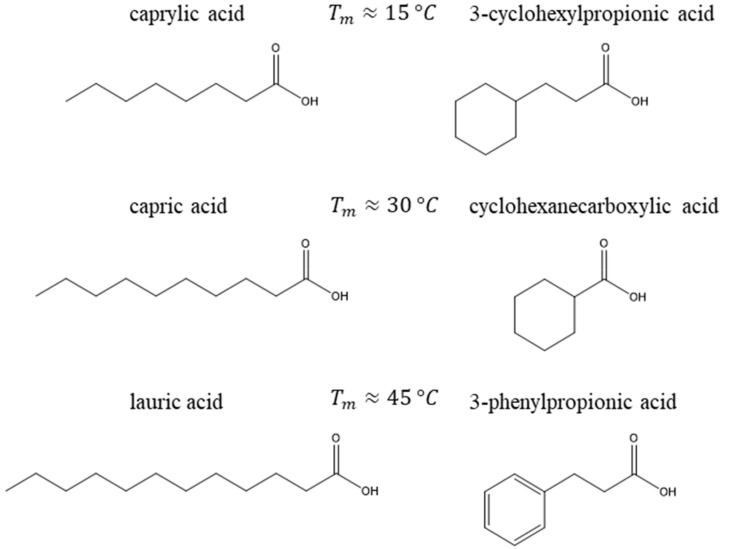
Binary eutectic mixtures of l-menthol with six different monocarboxylic acids were considered. The acids were sorted into three pairs according to the melting temperatures reported by the suppliers. The acids of each pair had close melting temperatures. The acids pairs were as follows:
-
(i)
Caprylic acid and 3-cyclohexylpropionic acid with a melting temperature of approximately 15 °C,
-
(ii)
Capric acid and cyclohexanecarboxylic acid with a melting temperature of approximately 30 °C,
-
(iii)
Lauric acid and 3-phenylpropionic acid with a melting temperature of approximately 45 °C.
In each pair, the acid with a more rigid molecular structure was expected to have lower melting entropy, and according to Equation (2), lower melting enthalpy. Therefore, the eutectic systems formed between l-menthol and rigid acids were expected to have a deeper eutectic temperature as a result of their lower melting enthalpy. Figure 3 illustrates the differences in the molecular structures of the acids, paired based on the melting temperatures obtained from the suppliers.
Figure 3.
Molecular structures of monocarboxylic acids considered in this study. The melting temperatures are approximate values reported by the suppliers used to select each pair of acids.
3.3. Eutectic Mixture Preparation
Table 4 lists the chemicals used in this study, along with their purity, as declared by the suppliers. All chemicals were used as received without further purification. The binary eutectic mixtures were prepared by weighing the pure components in a glass vessel. The mixture was heated to 45 °C while stirring with a magnetic stirrer until a homogenous liquid was obtained.
Table 4.
Chemicals used in this study.
| Name | CAS Number | Supplier | Purity * |
|---|---|---|---|
| l-menthol | 2216–51–5 | Sigma Aldrich Chemie GmbH | ≥ 99 % |
| 3-cyclohexylpropionic acid | 701–97–3 | ThermoFisher (Kandel) GmbH | > 98 % |
| caprylic acid | 124–07–2 | Merck KGaA | 99 % |
| cyclohexanecarboxylic acid | 98–89–5 | ThermoFisher (Kandel) GmbH | 98 % |
| capric acid | 334–48–5 | Alfa Aesar GmbH | 99 % |
| 3-phenylpropionic acid | 501–52–0 | Alfa Aesar GmbH | 99 % |
| lauric acid | 143–07–7 | Merck KGaA | 99 % |
* As declared by the supplier.
The liquid samples were weighed in aluminum DSC crucibles using a syringe and then sealed by cold welding. Depending on the density of the eutectic mixture, the mass of the samples in the crucibles ranged between 4 and 6 mg.
3.4. Differential Scanning Calorimetry
SLE data and the pure components’ melting properties were measured using DSC (NETZSCH DSC 200 F3). Temperature and sensitivity calibrations were performed prior to the measurements using five calibration standards with a purity of over 99.999%. The calibration standards included adamantane, bismuth, indium, zinc, and tin. The uncertainties after the temperature and sensitivity calibration were < 0.1 K and < 3%, respectively.
The DSC measurements were performed in an inert nitrogen environment. First, a cooling cycle with a rate of 10 K min−1 to a final temperature of −80 °C was performed. Then, the sample was heated at a heating rate of 5 K min–1 up to approximately 10 K above the sample liquidus temperature. The eutectic temperature, as well as the pure components’ melting temperature, were determined as the onset temperature of the respective thermal event. The liquidus temperatures were determined as the peak temperature, and the melting enthalpy of the pure components was determined as the peak area of the respective thermal event. The DSC curves of the samples obtained during the heating cycle are shown in Figures S2–S4 in Supplementary Materials.
4. Conclusions
In this study, a simple approach was proposed to select constituents for eutectic systems. This approach could be used to select constituents from a pool of substances sharing the same functionality and melting temperature based on their melting enthalpy. If the melting enthalpy is not available, it can be estimated from the melting entropy, which is correlated with the molecular structure, using the simple non-group contribution model proposed by Jain et al. [44].
The proposed approach was used to predict the relative depression of the melting temperature at the eutectic point of l-menthol/monocarboxylic acid systems. It was demonstrated that components with more rigid molecular structures possessed lower melting entropy. For linear and cyclic acids with similar melting temperatures, the cyclic acids possessed lower melting enthalpy due to their lower melting entropy. As a result, deeper eutectic systems could be formed by cyclic acids than by linear acids sharing the same melting temperature. Furthermore, the larger the difference in the melting entropy between the acids in each pair, the higher the relative depression at the eutectic point between the two eutectic systems.
From this study, it could be concluded that in the search for new DES systems, constituents with more rigid and symmetrical structures should be pursued. This could narrow the pool of possible components to be screened for a specific application based on eutectic temperature (i.e., when eutectic mixtures that are liquid at room temperature are investigated). It should be mentioned, however, that for quantitative predictions, experimental melting properties should be used along with activity coefficient modeling, using, for example, excess Gibbs energy models (gE) or equation of states.
Acknowledgments
The authors would like to thank Lea Kefalianakis for helping in performing a part of the DSC experiments as a part of her B. Sc. thesis.
Supplementary Materials
The following are available online. Figure S1. Solid-liquid phase diagrams of binary eutectic systems consisting of l-menthol and (A) cyclohexylpropionic acid (B) caprylic acid (C) cyclohexanecarboxylic acid (D) capric acid (E) phenylpropionic acid (F) lauric acid. Dashed lines are ideal liquidus lines of components modeled using the Schöder-van-Laar equation and using experimental melting properties. Figure S2. DSC curves of l-menthol/3-cyclohexylpropionic acid and l-menthol/caprylic acid systems. Figure S3. DSC curves of l-menthol/cyclohexanecarboxylic acid and l-menthol/capric acid systems. Figure S4. DSC curves of l-menthol/3-phenylpropionic acid and l-menthol/lauric acid systems.
Author Contributions
Designing and performing experiments, analyzing the results, and preparing the manuscript A.A.; revising and discussing the manuscript, L.M.; supervising, revising, and discussing the manuscript, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the German Research Foundation (DFG) and the Technical University of Munich (TUM) in the framework of the Open Access Publishing Program.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Sample Availability: Samples of the compounds are no longer available from the authors.
References
- 1.Gamsjäger H., Lorimer J. W., Scharlin P., Shaw David G. Glossary of terms related to solubility (IUPAC Recommendations 2008) Pure Appl. Chem. 2008;80:233. [Google Scholar]
- 2.Abbott A.P., Boothby D., Capper G., Davies D.L., Rasheed R.K. Deep Eutectic Solvents Formed between Choline Chloride and Carboxylic Acids: Versatile Alternatives to Ionic Liquids. J. Am. Chem. Soc. 2004;126:9142–9147. doi: 10.1021/ja048266j. [DOI] [PubMed] [Google Scholar]
- 3.Abbott A.P., Capper G., Davies D.L., Rasheed R.K., Tambyrajah V. Novel solvent properties of choline chloride/urea mixtures. Chem. Commun. 2003:70–71. doi: 10.1039/b210714g. [DOI] [PubMed] [Google Scholar]
- 4.Abbott A.P., Cullis P.M., Gibson M.J., Harris R.C., Raven E. Extraction of glycerol from biodiesel into a eutectic based ionic liquid. Green Chem. 2007;9:868–872. doi: 10.1039/b702833d. [DOI] [Google Scholar]
- 5.Abbott A.P., Harris R.C., Ryder K.S., D’Agostino C., Gladden L.F., Mantle M.D. Glycerol eutectics as sustainable solvent systems. Green Chem. 2011;13:82–90. doi: 10.1039/C0GC00395F. [DOI] [Google Scholar]
- 6.Bezold F., Minceva M. A water-free solvent system containing an L-menthol-based deep eutectic solvent for centrifugal partition chromatography applications. J. Chromatogr. A. 2019;1587:166–171. doi: 10.1016/j.chroma.2018.11.083. [DOI] [PubMed] [Google Scholar]
- 7.Gouveia A.S.L., Oliveira F.S., Kurnia K.A., Marrucho I.M. Deep Eutectic Solvents as Azeotrope Breakers: Liquid–Liquid Extraction and COSMO-RS Prediction. ACS Sustain. Chem. Eng. 2016 doi: 10.1021/acssuschemeng.6b01542. [DOI] [Google Scholar]
- 8.Roehrer S., Bezold F., Garcia E.M., Minceva M. Deep eutectic solvents in countercurrent and centrifugal partition chromatography. J. Chromatogr. A. 2016;1434:102–110. doi: 10.1016/j.chroma.2016.01.024. [DOI] [PubMed] [Google Scholar]
- 9.Alonso D.A., Baeza A., Chinchilla R., Guillena G., Pastor I.M., Ramón D.J. Deep Eutectic Solvents: The Organic Reaction Medium of the Century. Eur. J. Org. Chem. 2016;2016:612–632. doi: 10.1002/ejoc.201501197. [DOI] [Google Scholar]
- 10.Hayyan A., Ali Hashim M., Mjalli F.S., Hayyan M., AlNashef I.M. A novel phosphonium-based deep eutectic catalyst for biodiesel production from industrial low grade crude palm oil. Chem. Eng. Sci. 2013;92 doi: 10.1016/j.ces.2012.12.024. [DOI] [Google Scholar]
- 11.Hayyan A., Hashim M.A., Hayyan M., Mjalli F.S., AlNashef I.M. A new processing route for cleaner production of biodiesel fuel using a choline chloride based deep eutectic solvent. J. Clean. Prod. 2014;65 doi: 10.1016/j.jclepro.2013.08.031. [DOI] [Google Scholar]
- 12.Khandelwal S., Tailor Y.K., Kumar M. Deep eutectic solvents (DESs) as eco-friendly and sustainable solvent/catalyst systems in organic transformations. J. Mol. Liq. 2016;215:345–386. doi: 10.1016/j.molliq.2015.12.015. [DOI] [Google Scholar]
- 13.Wagle D.V., Zhao H., Baker G.A. Deep eutectic solvents: Sustainable media for nanoscale and functional materials. Acc. Chem. Res. 2014;47 doi: 10.1021/ar5000488. [DOI] [PubMed] [Google Scholar]
- 14.Liu P., Hao J.-W., Mo L.-P., Zhang Z.-H. Recent advances in the application of deep eutectic solvents as sustainable media as well as catalysts in organic reactions. RSC Advances. 2015;5:48675–48704. doi: 10.1039/C5RA05746A. [DOI] [Google Scholar]
- 15.Abbott A.P., Griffith J., Nandhra S., O’Connor C., Postlethwaite S., Ryder K.S., Smith E.L. Sustained electroless deposition of metallic silver from a choline chloride-based ionic liquid. Surf. Coat. Technol. 2008;202:2033–2039. doi: 10.1016/j.surfcoat.2007.08.055. [DOI] [Google Scholar]
- 16.Boisset A., Menne S., Jacquemin J., Balducci A., Anouti M. Deep eutectic solvents based on N-methylacetamide and a lithium salt as suitable electrolytes for lithium-ion batteries. PCCP. 2013;15:20054–20063. doi: 10.1039/c3cp53406e. [DOI] [PubMed] [Google Scholar]
- 17.Chen Z., McLean B., Ludwig M., Stefanovic R., Warr G.G., Webber G.B., Page A.J., Atkin R. Nanostructure of Deep Eutectic Solvents at Graphite Electrode Interfaces as a Function of Potential. J. Phys. Chem. C. 2016;120:2225–2233. doi: 10.1021/acs.jpcc.5b10624. [DOI] [Google Scholar]
- 18.Gómez E., Cojocaru P., Magagnin L., Valles E. Electrodeposition of Co, Sm and SmCo from a Deep Eutectic Solvent. J. Electroanal. Chem. 2011;658:18–24. doi: 10.1016/j.jelechem.2011.04.015. [DOI] [Google Scholar]
- 19.Zaidi W., Boisset A., Jacquemin J., Timperman L., Anouti M. Deep Eutectic Solvents Based on N-Methylacetamide and a Lithium Salt as Electrolytes at Elevated Temperature for Activated Carbon-Based Supercapacitors. J. Phys. Chem. C. 2014;118:4033–4042. doi: 10.1021/jp412552v. [DOI] [Google Scholar]
- 20.Pätzold M., Siebenhaller S., Kara S., Liese A., Syldatk C., Holtmann D. Deep Eutectic Solvents as Efficient Solvents in Biocatalysis. Trends Biotechnol. 2019;37:943–959. doi: 10.1016/j.tibtech.2019.03.007. [DOI] [PubMed] [Google Scholar]
- 21.Oh Y., Park S., Yoo E., Jo S., Hong J., Kim H.J., Kim K.J., Oh K.K., Lee S.H. Dihydrogen-bonding deep eutectic solvents as reaction media for lipase-catalyzed transesterification. Biochem. Eng. J. 2019;142:34–40. doi: 10.1016/j.bej.2018.11.010. [DOI] [Google Scholar]
- 22.Jablonský M., Škulcová A., Šima J. Use of Deep Eutectic Solvents in Polymer Chemistry–A Review. Molecules. 2019;24:3978. doi: 10.3390/molecules24213978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Roda A., Matias A.A., Paiva A., Duarte A.R.C. Polymer Science and Engineering Using Deep Eutectic Solvents. Polymers. 2019;11:912. doi: 10.3390/polym11050912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gómez A.V., Biswas A., Tadini C.C., Furtado R.F., Alves C.R., Cheng H.N. Use of natural deep eutectic solvents for polymerization and polymer reactions. J. Braz. Chem. Soc. 2019;30:717–726. doi: 10.21577/0103-5053.20190001. [DOI] [Google Scholar]
- 25.Abbott A.P., Ahmed E.I., Prasad K., Qader I.B., Ryder K.S. Liquid pharmaceuticals formulation by eutectic formation. Fluid Phase Equilib. 2017;448:2–8. doi: 10.1016/j.fluid.2017.05.009. [DOI] [Google Scholar]
- 26.Aroso I.M., Craveiro R., Rocha Â., Dionísio M., Barreiros S., Reis R.L., Paiva A., Duarte A.R.C. Design of controlled release systems for THEDES—Therapeutic deep eutectic solvents, using supercritical fluid technology. Int. J. Pharm. 2015;492:73–79. doi: 10.1016/j.ijpharm.2015.06.038. [DOI] [PubMed] [Google Scholar]
- 27.Aroso I.M., Silva J.C., Mano F., Ferreira A.S., Dionísio M., Sá-Nogueira I., Barreiros S., Reis R.L., Paiva A., Duarte A.R.C. Dissolution enhancement of active pharmaceutical ingredients by therapeutic deep eutectic systems. Eur. J. Pharm. Sci. 2016;98:57–66. doi: 10.1016/j.ejpb.2015.11.002. [DOI] [PubMed] [Google Scholar]
- 28.Jeong K.M., Ko J., Zhao J., Jin Y., Yoo D.E., Han S.Y., Lee J. Multi-functioning deep eutectic solvents as extraction and storage media for bioactive natural products that are readily applicable to cosmetic products. J. Clean. Prod. 2017;151:87–95. doi: 10.1016/j.jclepro.2017.03.038. [DOI] [Google Scholar]
- 29.Van Osch D.J.G.P., Dietz C.H.J.T., van Spronsen J., Kroon M.C., Gallucci F., van Sint Annaland M., Tuinier R. A Search for Natural Hydrophobic Deep Eutectic Solvents Based on Natural Components. ACS Sustain. Chem. Eng. 2019;7:2933–2942. doi: 10.1021/acssuschemeng.8b03520. [DOI] [Google Scholar]
- 30.Francisco M., van den Bruinhorst A., Kroon M.C. New natural and renewable low transition temperature mixtures (LTTMs): Screening as solvents for lignocellulosic biomass processing. Green Chem. 2012;14:2153–2157. doi: 10.1039/c2gc35660k. [DOI] [Google Scholar]
- 31.Van den Bruinhorst A., Kollau L.J.B.M., Kroon M.C., Meuldijk J., Tuinier R., Esteves A.C.C. A centrifuge method to determine the solid–liquid phase behavior of eutectic mixtures. J. Chem. Phys. 2018;149:224505. doi: 10.1063/1.5051515. [DOI] [PubMed] [Google Scholar]
- 32.Silva L.P., Fernandez L., Conceição J.H.F., Martins M.A.R., Sosa A., Ortega J., Pinho S.P., Coutinho J.A.P. Design and Characterization of Sugar-Based Deep Eutectic Solvents Using Conductor-like Screening Model for Real Solvents. ACS Sustain. Chem. Eng. 2018 doi: 10.1021/acssuschemeng.8b02042. [DOI] [Google Scholar]
- 33.Rodriguez Rodriguez N., van den Bruinhorst A., Kollau L.J.B.M., Kroon M.C., Binnemans K. Degradation of Deep-Eutectic Solvents Based on Choline Chloride and Carboxylic Acids. ACS Sustain. Chem. Eng. 2019;7:11521–11528. doi: 10.1021/acssuschemeng.9b01378. [DOI] [Google Scholar]
- 34.Abranches D.O., Larriba M., Silva L.P., Melle-Franco M., Palomar J.F., Pinho S.P., Coutinho J.A.P. Using COSMO-RS to design choline chloride pharmaceutical eutectic solvents. Fluid Phase Equilib. 2019;497:71–78. doi: 10.1016/j.fluid.2019.06.005. [DOI] [Google Scholar]
- 35.Wolbert F., Brandenbusch C., Sadowski G. Selecting Excipients Forming Therapeutic Deep Eutectic Systems-A Mechanistic Approach. Mol. Pharm. 2019;16:3091–3099. doi: 10.1021/acs.molpharmaceut.9b00336. [DOI] [PubMed] [Google Scholar]
- 36.Kollau L.J.B.M., Vis M., van den Bruinhorst A., Esteves A.C.C., Tuinier R. Quantification of the liquid window of deep eutectic solvents. Chem. Commun. 2018;54:13351–13354. doi: 10.1039/C8CC05815F. [DOI] [PubMed] [Google Scholar]
- 37.Martins M.A.R., Pinho S.P., Coutinho J.A.P. Insights into the Nature of Eutectic and Deep Eutectic Mixtures. J. Solut. Chem. 2018 doi: 10.1007/s10953-018-0793-1. [DOI] [Google Scholar]
- 38.Alhadid A., Mokrushina L., Minceva M. Modeling of Solid-Liquid Equilibria in Deep Eutectic Solvents: A Parameter Study. Molecules. 2019;24 doi: 10.3390/molecules24122334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Williams D.H., O’Brien D.P., Bardsley B. Enthalpy/Entropy Compensation as a Competition between Dynamics and Bonding: The Relevance to Melting of Crystals and Biological Aggregates. J. Am. Chem. Soc. 2001;123:737–738. doi: 10.1021/ja0029230. [DOI] [PubMed] [Google Scholar]
- 40.Jain A., Yalkowsky S.H. Estimation of Melting Points of Organic Compounds-II. J. Pharm. Sci. 2006;95:2562–2618. doi: 10.1002/jps.20634. [DOI] [PubMed] [Google Scholar]
- 41.Yalkowsky S.H. Carnelley’s Rule and the Prediction of Melting Point. J. Pharm. Sci. 2014;103:2629–2634. doi: 10.1002/jps.24034. [DOI] [PubMed] [Google Scholar]
- 42.Dearden J.C. The QSAR prediction of melting point, a property of environmental relevance. Sci. Total Environ. 1991;109:59–68. doi: 10.1016/0048-9697(91)90170-J. [DOI] [PubMed] [Google Scholar]
- 43.Brown R.J.C., Brown R.F.C. Melting Point and Molecular Symmetry. J. Chem. Educ. 2000;77:724. doi: 10.1021/ed077p724. [DOI] [Google Scholar]
- 44.Jain A., Yang G., Yalkowsky S.H. Estimation of Total Entropy of Melting of Organic Compounds. Ind. Eng. Chem. Res. 2004;43:4376–4379. doi: 10.1021/ie0497745. [DOI] [Google Scholar]
- 45.Preiss U.P., Beichel W., Erle A.M., Paulechka Y.U., Krossing I. Is universal, simple melting point prediction possible? Chemphyschem. 2011;12:2959–2972. doi: 10.1002/cphc.201100522. [DOI] [PubMed] [Google Scholar]
- 46.Bondi A. Physical Properties of Molecular Crystals, Liquids, and Glasses. John Wiley and Sons; New York, NY, USA: 1968. [Google Scholar]
- 47.Crespo E.A., Silva L.P., Martins M.A.R., Bülow M., Ferreira O., Sadowski G., Held C., Pinho S.P., Coutinho J.A.P. The Role of Polyfunctionality in the Formation of [Ch]Cl-Carboxylic Acid-Based Deep Eutectic Solvents. Ind. Eng. Chem. Res. 2018;57:11195–11209. doi: 10.1021/acs.iecr.8b01249. [DOI] [Google Scholar]
- 48.Crespo E.A., Silva L.P., Martins M.A.R., Fernandez L., Ortega J., Ferreira O., Sadowski G., Held C., Pinho S.P., Coutinho J.A.P. Characterization and Modeling of the Liquid Phase of Deep Eutectic Solvents Based on Fatty Acids/Alcohols and Choline Chloride. Ind. Eng. Chem. Res. 2017;56:12192–12202. doi: 10.1021/acs.iecr.7b02382. [DOI] [Google Scholar]
- 49.Martins M.A.R., Crespo E.A., Pontes P.V.A., Silva L.P., Bülow M., Maximo G.J., Batista E.A.C., Held C., Pinho S.P., Coutinho J.A.P. Tunable Hydrophobic Eutectic Solvents Based on Terpenes and Monocarboxylic Acids. ACS Sustain. Chem. Eng. 2018;6:8836–8846. doi: 10.1021/acssuschemeng.8b01203. [DOI] [Google Scholar]
- 50.Domańska U., Morawski P., Piekarska M. Solubility of perfumery and fragrance raw materials based on cyclohexane in 1-octanol under ambient and high pressures up to 900MPa. J. Chem. Thermodyn. 2008;40:710–717. doi: 10.1016/j.jct.2007.10.004. [DOI] [Google Scholar]
- 51.Pontes P.V.A., Crespo E.A., Martins M.A.R., Silva L.P., Neves C.M.S.S., Maximo G.J., Hubinger M.D., Batista E.A.C., Pinho S.P., Coutinho J.A.P., et al. Measurement and PC-SAFT modeling of solid-liquid equilibrium of deep eutectic solvents of quaternary ammonium chlorides and carboxylic acids. Fluid Phase Equilib. 2017;448:69–80. doi: 10.1016/j.fluid.2017.04.007. [DOI] [Google Scholar]
- 52.Monte M.J.S., Hillesheim D.M. Thermodynamic study on the sublimation of 3-phenylpropionic acid and of three methoxy-substituted 3-phenylpropionic acids. J. Chem. Thermodyn. 2001;33:837–847. doi: 10.1006/jcht.2000.0767. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.