Designing complex architectured materials with generative adversarial networks

Complex architectured materials are designed with generative adversarial networks to approach Hashin-Shtrikman upper bounds.

Abstract

Architectured materials on length scales from nanometers to meters are desirable for diverse applications. Recent advances in additive manufacturing have made mass production of complex architectured materials technologically and economically feasible. Existing architecture design approaches such as bioinspiration, Edisonian, and optimization, however, generally rely on experienced designers’ prior knowledge, limiting broad applications of architectured materials. Particularly challenging is designing architectured materials with extreme properties, such as the Hashin-Shtrikman upper bounds on isotropic elasticity in an experience-free manner without prior knowledge. Here, we present an experience-free and systematic approach for the design of complex architectured materials with generative adversarial networks. The networks are trained using simulation data from millions of randomly generated architectures categorized based on different crystallographic symmetries. We demonstrate modeling and experimental results of more than 400 two-dimensional architectures that approach the Hashin-Shtrikman upper bounds on isotropic elastic stiffness with porosities from 0.05 to 0.75.

INTRODUCTION

Consisting of periodic arrays of truss, plate, and/or shell elements, architectured materials are ubiquitous in biological systems (1), structural engineering (2), and materials science (3) (Fig. 1). Architectured materials have also found broad and important applications, such as light-weight structures (4, 5), thermal insulation (5), battery electrodes (6), optic and acoustic metamaterials (7, 8), and energy damping (9, 10). In addition, recent advances in additive manufacturing technologies such as three-dimensional (3D) printing have further made mass production of architectured materials with very complex structures feasible both technologically and economically.

Fig. 1. Schematics of procedures to design complex architectured materials.

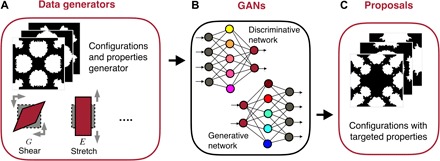
(A) Data generators to generate datasets of configurations and properties of architectured materials. (B) GANs trained by the datasets. (C) New designs of architectured materials with the targeted properties proposed by the GANs.

Despite the important applications and great potential of architectured materials, designing them is challenging. Existing designs of architectured materials generally follow approaches such as bioinspiration, Edisonian, theoretical analysis, and topology optimization. In the bioinspired approach, various naturally occurring biological structures such as honeycomb, trabecular bone, plant parenchyma, and sponge have been used as templates and inspirations for designing architectured materials for applications such as light-weight structural components (11), energy absorption (12), heat exchange (13), catalyst supports (14), filtration (15), and biomaterials (16). However, bioinspired designs usually do not guarantee optimal performances. In addition, many desired properties and functions of architectured materials cannot find counterparts in the biological system either. In the Edisonian approach, trial and errors in both experiments and simulations have been used to design Auxetic materials (17, 18), acoustic materials (19), phase-transformation materials (20), and kirigami shells for soft robots (21). The trial-and-error nature makes this approach not very efficient, and the resultant designs usually do not guarantee optimal performances either. Topology optimization uses gradient-based methods to reach architecture designs that give locally minimized/maximized properties. This strategy has been widely used in designing architectured materials with negative/zero thermal expansion (22, 23), multiscale porosity–induced high rigidity (24), and negative Poisson ratio (25). Despite its success and promise, topology optimization may suffer from the limitation of initial-guess dependence. The initial guess of the material topology can have an influence on the final design; different initial guesses may lead to different structures and properties (24, 26). Several theoretical analyses (27) of composites have helped understand the designs from the abovementioned approaches (28).

Furthermore, these traditional approaches usually require substantial prior knowledge of experienced designers and provide limited numbers of designs. The challenge in designing architectured materials becomes particularly daunting when targeting at extreme properties such as designing configurations that reach the Hashin-Shtrikman (HS) upper bounds of isotropic elasticity and strain energy storage. For instance, so far, only a few classes of configurations that reach the HS upper bounds on isotropic elasticity in 2D via the topology optimization, such as coated spheres assemblages, rank-n laminates, Vigdergauz structures, and Sigmund structures (Fig. 2) (29).

Fig. 2. Four example classes of 2D structures designed with the topology optimization that reach the HS upper bounds of isotropic elasticity and strain energy storage.

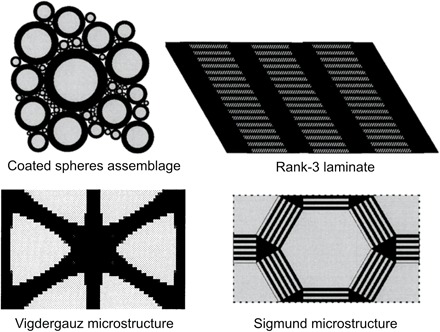
Adopted from (29).

Here, we present an experience-free and systematic approach for the design of complex architectured materials by harnessing machine-learning algorithms to analyze massive simulation data of randomly generated architectures categorized into different crystallographic symmetries. We first generate a set of data, composed of millions of configurations and their calculated properties, to represent the design space (Fig. 1A). We further categorize the dataset according to the crystallographic symmetries of the configurations. The data from selected crystallographic symmetries are then used to train the generative adversarial networks (GANs; Fig. 1B). In the GAN-based design, the discriminative network will map out the relationship between configurations and properties through learning the provided dataset. Meanwhile, armed with this knowledge on the relationship, the GANs are capable of promptly generating new configurations that approximately achieve the extreme properties (Fig. 1C). We demonstrate the capability of the proposed experience-free design with modeling and experimental results of more than 400 2D architectures that approach the HS upper bounds with porosities ranging from 0.05 to 0.75. This new design approach will not only facilitate the design of architectured materials (and structures in general) to achieve other extreme (or desired) properties but also shed light on a systematic method for various inverse designs. While neural networks have been used for structural optimization (30–32) and machine learning for the design of previously unknown composites (33, 34) and materials (35–37), the current work presents the design of complex architectured materials with GANs.

RESULTS

Definitions

As illustrated in Fig. 3A, architectured materials consist of periodic arrays of units. A unit is composed of several identical elements, which undergo possible operations including reflect, rotate, and/or glide by following a specific crystallographic symmetry. Each element is discretized into a number of pixels that give a certain resolution of the element. A pixel can be in either solid or void phase, which is corresponding to the solid or void part in the architectured material, respectively. The porosity of an element (and the corresponding architectured material) is defined as the number of void pixels divided by the total number of pixels in the element. For example, Fig. 3A illustrates a 2D architectured material with p4 symmetry and the corresponding units, elements, and pixels.

Fig. 3. Illustrations of the pixel-wise architectured materials.

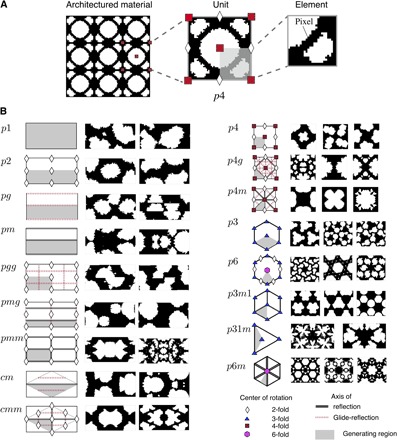
(A) Definition of units, elements, and pixels in an architectured material. (B) Topology generation in 2D space by harnessing 17 groups of crystallographic symmetries. The porosity of architectures in (A) and (B) is set to be 0.5.

There are 17 and 230 crystallographic symmetry groups in 2D and 3D spaces, respectively. For simplicity of conveying the key ideas of our method, we will focus on designs in 2D space in the current study. In Fig. 3B, we illustrate examples of units that follow the 17 symmetry groups in 2D. These symmetry groups have been characterized by mirror lines, fixed points, and/or glide lines to represent the reflect, rotate, and/or glide operations, respectively.

Topology generation

To generate the topology of an architectured material, we first generate the topology of its constituent element (e.g., gray part in Fig. 3B), map the element to a unit following a symmetry group, and then periodically translate the unit to form the architectured material. For a systematic design approach, the topology of the element needs to satisfy the following criteria: (i) the topology should be randomly generated to represent the whole design space; (ii) the number of the void pixels in an element should follow the assigned porosity; and (iii) the solid phase in the unit needs to be path-connected (38). Here, we develop an algorithm to generate the required configurations of elements. Briefly, we begin with an element composed of all solid pixels and then randomly disperse voids with random size and shape to the element. Meanwhile, we guarantee that the remaining solid pixels are path-connected and that the total area of the voids follows the assigned porosity for the element. The details of our algorithm of random topology generation are given in section S1.

Elastic constant calculation

Once the topology of an architectured material is generated (e.g., Fig. 3B), the finite element simulation is implemented to calculate the corresponding properties. For units with rectangular shape, the simulation domains are the units by themselves with periodic boundary conditions. For units with triangular and hexagonal shape, we map them into equivalent rectangular domains for simulation (39). In the calculation, we apply trial strain fields on the rectangular domain to obtain the reaction forces and the storage elastic energy. From the obtained reaction forces and the storage elastic energy, the equivalent constitutive behaviors of periodically patterned structures can be derived. Within the scope of linear elasticity, the equivalent constitutive behaviors of periodically patterned structures can be calculated using the homogenization method (40). By considering the first-order terms in the asymptotic expansion of the displacement field, it can be shown that the effective elastic tensor of the architectured materials ${\tilde{C}}_{\mathit{\text{ijkl}}}$can be expressed in the following form with the Einstein index summation notation (23, 24, 41)

$${\tilde{C}}_{\mathit{\text{ijkl}}}=\frac{1}{S}{\int }_S{C}_{\mathit{\text{pqrs}}}({\mathrm{ϵ}}_{\mathit{pq}}^{0(\mathit{ij})}-{\mathrm{ϵ}}_{\mathit{pq}}^{*(\mathit{ij})})({\mathrm{ϵ}}_{\mathit{rs}}^{0(\mathit{kl})}-{\mathrm{ϵ}}_{\mathit{rs}}^{*(\mathit{kl})})\mathit{dS}$$

where C_pqrs is the elastic tensor of the solid phase, ${\mathrm{ϵ}}_{\mathit{pq}}^{0(\mathit{ij})}$ is the applied unit test strain, ${\mathrm{ϵ}}_{\mathit{pq}}^{*(\mathit{ij})}$ is the fluctuation strain corresponding to the unit test strain, and S is the area of the rectangular domain. Physically, the fluctuation strain is used to satisfy the periodic boundary condition for the rectangular domain, which is the periodic solution of

$${\int }_S{C}_{\mathit{\text{ijpq}}}{\mathrm{ϵ}}_{\mathit{pq}}^{*(\mathit{\text{kl}})}\frac{\mathrm{\partial }{v}_i}{\mathrm{\partial }{y}_j}\mathit{dS}={\int }_S{C}_{\mathit{\text{ijpq}}}{\mathrm{ϵ}}_{\mathit{pq}}^{0(\mathit{\text{kl}})}\frac{\mathrm{\partial }{v}_i}{\mathrm{\partial }{y}_j}\mathit{dS}$$

where v is a periodic admissible displacement field (23). After ${\tilde{C}}_{\mathit{\text{ijkl}}}$ is obtained, we can calculate the effective elastic properties (such as Young’s modulus, shear modulus, and Poisson’s ratio) of the architectured material along any direction. This method (41) has been broadly adopted in literature.

Isotropy calculation

In many applications, it is desirable to achieve designs with isotropic properties. To guarantee the isotropy, the elastic constants, such as Young’s modulus$\tilde{E}$, should be independent of the orientations of the architectured materials. However, in reality, the perfect isotropy is difficult to achieve in architectured materials. To measure the isotropy of architectured materials, we follow the method given in (42, 43). We denote the maximum and minimum Young’s modulus in all possible directions of an architectured material with ${\tilde{E}}_{\text{max}}$ and ${\tilde{E}}_{\text{min}}$, respectively (see Fig. 4A for an example). The degree of isotropy can be defined as $\mathrm{\Omega }=\mathrm{\Delta }\tilde{E}/{\tilde{E}}_{\text{mean}}$, where $\mathrm{\Delta }\tilde{E}=\frac{{\tilde{E}}_{\text{max}}-{\tilde{E}}_{\text{min}}}{2}$and ${\tilde{E}}_{\text{mean}}=\frac{{\tilde{E}}_{\text{max}}+{\tilde{E}}_{\text{min}}}{2}$. We call the architectured material nearly isotropic if Ω ≤ 5%. This isotropic criterion is comparable with or stricter than those used in the literature (42, 43).

Fig. 4. Architectured materials (ϕ = 0.5) that approximate the HS bounds.

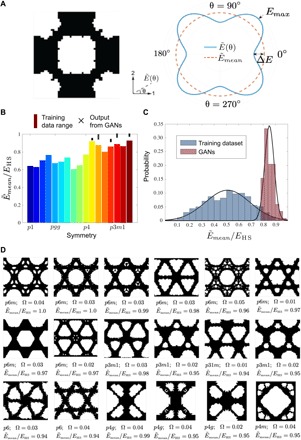
(A) An example architecture and its Young’s Moduli in different directions. (B) Ranges of normalized Young’s Moduli ${\tilde{E}}_{\text{mean}}/E_{\text{HS}}$ (Ω ≤ 5%) of randomly generated architectures in 17 crystallographic symmetries. (C) The distributions of ${\tilde{E}}_{\text{mean}}/E_{\text{HS}}$ for the training dataset and for the GAN outputs (p6m, Ω ≤ 5%) (D) Examples of GAN-generated architectured materials with ${\tilde{E}}_{\text{mean}}(\mathrm{\Omega }\le 5\%)$achieving more than 94% of E_HS. The normalized Young’s moduli of three highest ${\tilde{E}}_{\text{mean}}$ (Ω ≤ 5%) generated by GANs in high-potential symmetries are marked as “×” in (B).

Database generation

After topology generation and properties calculation, we can construct 17 datasets corresponding to the 17 symmetry groups in 2D (note that 230 datasets can be generated corresponding to the 230 symmetry groups in 3D in the future). In each dataset, a data point is a combination of three items: pixel matrix for the element of an architectured material (fig. S3 and table S1), effective mean Young’s modulus ${\tilde{E}}_{\text{mean}}$ of the architectured material, and isotropy Ω of the architectured material. The size of the dataset for each symmetry group is around one million configurations.

Machine learning algorithms

The datasets generated in previous sections will be used to train the GANs. GAN is a recently developed machine learning framework proposed to creatively generate complex outputs, such as fake faces, speeches, and videos (44). The adversarial structure can be composed of two competing deep neuron networks, a generative network and a discriminative network. In the GAN-based strategy, we use the discriminative network to map out the relationship between the pixel matrices of elements and their corresponding probability to be the high elastic modulus configurations from zero to a hundred percent. Meanwhile, armed with this knowledge on the relationship, the generative network is capable to fast generate thousands of new configurations to achieve desired properties such as the HS upper bound for isotropic Young’s modulus. We train a GAN for each symmetry group separately. The machine learning calculations are performed using TensorFlow (45), a system for large-scale machine learning. For our cases, stochastic training is implemented to train our machine learning models. We split 80% of all data points in each symmetry group (~0.8 million) as the training set and keep the remaining 20% data (~0.2 million) as the testing set. All training details are discussed in section S2.

Achieving HS upper bounds

Next, we demonstrate the capability of the proposed approach to design architectured materials that approximately achieve the HS upper bounds of isotropic Young’s moduli. We first focus on designing architectures to achieve the HS upper bound at porosity ϕ = 0.5. Figure 4B shows the ranges of normalized mean Young’s moduli ${\tilde{E}}_{\text{mean}}/E_{\text{HS}}$ of nearly isotropic materials [Ω ≤ 5% (42, 43)] generated in 17 crystallographic symmetries, where E_HS = E(1 − ϕ)/(1 + 2ϕ) is the theoretical HS upper Young’s modulus in 2D (46). It is noticeable that certain symmetries, i.e., p4, p4g, p3, p6, p3m1, p31m, and p6m, tend to give higher Young’s moduli in the training datasets; and thus, these symmetries have higher potential to achieve the HS upper bound. For simplicity, we call these symmetries, i.e., p4, p4g, p3, p6, p3m1, p31m, and p6m, as high-potential symmetries. Next, we use the datasets of the high-potential symmetries to train our GAN models. In Fig. 4D, we display 18 GAN-generated configurations with ϕ = 0.5 and Ω ≤ 5%, whose ${\tilde{E}}_{\text{mean}}$ achieve more than 94% of E_HS. Evidently, the maximum ${\tilde{E}}_{\text{mean}}$ of architectures generated by the GAN in each symmetry group is higher than the range of the corresponding training dataset (Fig. 4B). This is consistent with the distributions of ${\tilde{E}}_{\text{mean}}/E_{\text{HS}}$ for the training dataset and for the GAN outputs (Fig. 4C and fig. S16). This comparison shows that GANs can effectively extrapolate from the training data to provide multiple better designs than the randomly generated ones in each symmetry group. Notably, this design approach does not require any prior knowledge, bioinspiration, or trial-and-error iteration on the possible geometry of the architectured materials.

This experience-free design approach is widely applicable to other porosities. In Fig. 5A, we present a selected set of nearly isotropic configurations [Ω ≤ 5% (42, 43)], whose ${\tilde{E}}_{\text{mean}}$achieve more than 94% of E_HS with porosities from 0.05 to 0.75. In figs. S5 to S15, we further provide more than 360 additional nearly isotropic configurations that achieve more than 90% of E_HS for a wide range of porosities. The proximity of these configurations’ Young’s moduli to the HS upper bounds is comparable with or superior to that of previous designs in the literature (42, 43). While previous designs only gave a few configurations, the new capability of generating many desired configurations (e.g., more than 400) are impactful, due to two reasons. First, the proposed approach addresses a challenging inverse problem with multiple solutions in a systematic and experience-free manner. The proposed approach may also be useful for other inverse-design problems, such as designing architectured materials achieving the Suquet bound in plasticity (42). Second, if more constraints such as manufacturability were imposed in practical applications, the multiple designs generated with the proposed approach would provide designers more choices for further selection.

Fig. 5. Architectured materials (ϕ = 0.05 − 0.75) that approximate the HS bounds.

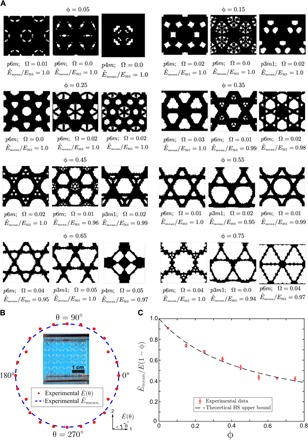
(A) Examples of architectures with multiple porosities with ${\tilde{E}}_{\text{mean}}(\mathrm{\Omega }\le 5\%)$achieving more than 94% of E_HS. (B) Photo of a laser-cut sample for an architecture and the measured Young’s moduli of the sample along various directions. (C) Comparison of ${\tilde{E}}_{\text{mean}}$of experimental samples and the theoretical HS upper bounds. The experimental samples are fabricated on the basis of three architectures generated by GANs with the highest ${\tilde{E}}_{\text{mean}}$ (Ω ≤ 5%).

We further demonstrate our design approach with experiments by fabricating GAN-generated architectured materials and measuring their Young’s moduli. Considering the requirement of isotropy of the solid phase, we choose to use laser-cut samples instead of 3D-printed ones. We measure the Young’s moduli of a number of proposed configurations with porosity from 0.05 to 0.75. For each porosity, three nearly isotropic architectures (Ω ≤ 5%) with the highest ${\tilde{E}}_{\text{mean}}$ generated by GANs have been selected to fabricate into testing samples. For the convenience of fabrication, the boundaries between void phase and solid phase in the units are mapped to smooth curves with spline interpolation. Each unit is repeated three times in each direction to represent the periodic architectured material. Before performing experiments, finite element simulations are adopted to validate that the 3 × 3 units are sufficient to represent the periodic architectured materials and give the effective Young’s moduli (see section S4 for details). Also, note that the 2D HS upper bound is defined under plane strain condition. To mimic the plane strain condition, we adopt the constrained uniaxial tension tests in the measurements (see section S4 for details). In Fig. 5B, we compare the Young’s moduli of a sample measured along various directions with the mean value of the measured Young’s moduli. The very mild deviations of the Young’s moduli from the mean value validate the near isotropy of the architectured material.

In Fig. 5C, we summarize the experimentally measured effective mean Young’s moduli of various samples with porosities from 0.05 to 0.75. For each porosity, the samples are based on three nearly isotropic architectures (Ω ≤ 5%) generated by GANs with the highest ${\tilde{E}}_{\text{mean}}$. We further compare the experimental results with the theoretical HS upper bounds at various porosities. The measured effective mean Young’s moduli of GAN-generated nearly isotropic (Ω ≤ 5%) configurations can achieve more than 94% of the theoretical HS bound with porosities from 0.05 to 0.75.

DISCUSSION

Here, we have proposed an experience-free and systematic approach for the design of complex architectured materials with GANs. The networks are trained using simulation data of millions of randomly generated architectured materials categorized into different crystallographic symmetries. We demonstrate the capability of the proposed approach with modeling and experimental results of more than 400 2D architectures that approximately achieve the HS upper bounds of stiffness with porosities ranging from 0.05 to 0.75. While the proposed approach may take longer time to calculate the training datasets than the topology optimization, it represents an experience-free and systematic method that requires no prior knowledge and can be readily adopted in broad applications. In addition, the architectures generated in the current method can also serve as initial guess for the further topology optimization if needed. This work not only provides a new method that harnesses simulation data and machine learning to potentially design future acoustic metamaterials (7, 8), auxetic materials (17, 18), and soft robotics (21) in an experience-free and systematic manner but also opens new avenues to addressing various inverse design problems in materials and structures.

MATERIALS AND METHODS

Structure of database

The database is composed of 17 separated datasets. Each dataset corresponds to a particular symmetry and include 0.8 million data points for training and 0.2 million data points for testing. Each data point contains the normalized Young’s modulus ${\tilde{E}}_{\text{mean}}/E_{\mathit{HS}}$, the isotropy Ω, and the configuration of the corresponding architectured material. The configuration is stored in the form of a vector composed of 0 and 1, corresponding to void and solid pixels, respectively, in the element of the architectured material.

Structure of the GAN

The GAN consists of a generator and a discriminator. The generator is composed of five layers of neural networks. The first layer is a fully connected layer composed of 1024 neurons to receive the data from the database. The second layer is also a fully connected layer composed of 1600 neurons. The third and fourth layers are convolutional layers composed of 64 and 32 neurons, respectively. The last layer is a deconvolutional layer associated with a tanh activation function to produce configurations with bounded pixel values.

The discriminator is composed of three layers of neural networks. The first and second layers are convolutional layers composed of 64 and 128 neurons, respectively. Their convolutional window size is set to be 4 × 4. The first convolutional layer is associated with batch normalization operations and leaky rectified linear unit activations, and the second convolutional layer has a sigmoid activation function to produce probabilities between 0 and 1. The second layer has been flattened, and the output of the second layer is sent to the third layer, which is a fully connected layer composed of 1024 neurons.

The total loss is composed of the adversarial loss and the style transfer loss. The adversarial loss is for the minimum-maximum training process of GAN, and the style transfer loss enables the porosity of the generated configuration to approach the target porosity. The weight of the style transfer loss is set to be 0.03 to prevent the style transfer loss from diminishing to zero or overwhelming the GAN adversarial loss. The Adam optimizer is applied in training by setting the learning rate as 0.0001. The batch size for training is set to be 32.

Fabrication of architectured materials

The pixel-wise architectures generated by GANs were first imported into the sketch module of SOLIDWORKS to smooth the solid-void boundaries by the cubic spline interpolation. Thereafter, each architecture was uploaded to the laser cutter (Epilog Mini/Helix; Epilog Laser), which cut an acrylic plate multiple times with minimal laser energy. The resultant testing sample has overall dimensions of 50 mm by 50 mm by 2.25 mm. A constrained uniaxial tensile test was carried out on the sample to obtain the stress-strain curve.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/17/eaaz4169/DC1