Significance
There is a great need for simple and reliable methods to detect DNA of interest in the presence of other DNA, e.g., to detect bacterial infections in the presence of nonpathogenic bacteria. We propose that the sensitivity and selectivity of existing DNA screening methods can be enhanced by multivalent targeting of the whole bacterial genome. Unlike existing methods, our approach exploits superselectivity. We propose designing oligonucleotide probes that bind weakly but selectively to nucleotide sequences that occur with high frequency in the genome of the target bacterial pathogen. We have developed a numerical scheme to identify such target sequences and we have tested our approach in large-scale, coarse-grained simulations of the multivalent binding of entire bacterial genomes.
Keywords: DNA-based detection, multivalent binding, superselectivity, computer simulations, polymer physics
Abstract
Rapid methods for diagnosis of bacterial infections are urgently needed to reduce inappropriate use of antibiotics, which contributes to antimicrobial resistance. In many rapid diagnostic methods, DNA oligonucleotide probes, attached to a surface, bind to specific nucleotide sequences in the DNA of a target pathogen. Typically, each probe binds to a single target sequence; i.e., target–probe binding is monovalent. Here we show using computer simulations that the detection sensitivity and specificity can be improved by designing probes that bind multivalently to the entire length of the pathogen genomic DNA, such that a given probe binds to multiple sites along the target DNA. Our results suggest that multivalent targeting of long pieces of genomic DNA can allow highly sensitive and selective binding of the target DNA, even if competing DNA in the sample also contains binding sites for the same probe sequences. Our results are robust to mild fragmentation of the bacterial genome. Our conclusions may also be relevant for DNA detection in other fields, such as disease diagnostics more broadly, environmental management, and food safety.
Rapid diagnostic methods for bacterial infections are urgently needed to combat the threat of antimicrobial resistance (AMR) (1). Due to the scarcity of simple practical methods to diagnose bacterial infections at the point of care, antibiotics are often prescribed inappropriately, e.g., for conditions that are not caused by bacteria (2–4). Since AMR prevalence correlates with antibiotic usage (5), improving point-of-care diagnosis for bacterial infections is central in the battle against AMR (1, 6). Diagnostic methods need to be not only sensitive, such that target pathogens are detected at low abundance, but also specific, such that false positive results are not triggered by other, nonpathogenic bacteria that may be present in a sample. Here we show computationally that the sensitivity and specificity of detection of a target bacterial pathogen can be improved significantly by leveraging the length of bacterial genomic DNA to achieve multivalent binding of the target DNA to a surface coated in oligonucleotide probes. Although we focus here on bacterial infections, DNA detection also has a plethora of other applications. These include diagnosis of nonbacterial infections such as malaria (7) or viral infections; tracing of rare species in the natural environment (8); and testing for pathogens, allergens, or authenticity in food products (9–11).
Current DNA-based detection methods typically use oligonucleotide probes that are complementary to particular sequences within the target DNA, such that each probe has a single binding site on the target DNA (Fig. 1 A, Inset, blue). Usually, specific short fragments of target DNA are amplified from the sample by PCR, fluorescently labeled, and exposed to a surface that has been spotted with an array of oligonucleotide probes. Probe-binding sequences that are present in the sample are then detected as fluorescent dots (12). Related methods include attaching the oligonucleotide probes to gold nanoparticles, which aggregate upon binding to the target DNA (13, 14). Current DNA-based methods are extremely promising, with the potential for rapid and affordable detection, but questions remain about whether they can achieve sufficient sensitivity and specificity to compete with standard culture-based methods for diagnosis of bacterial infections (15).
Fig. 1.
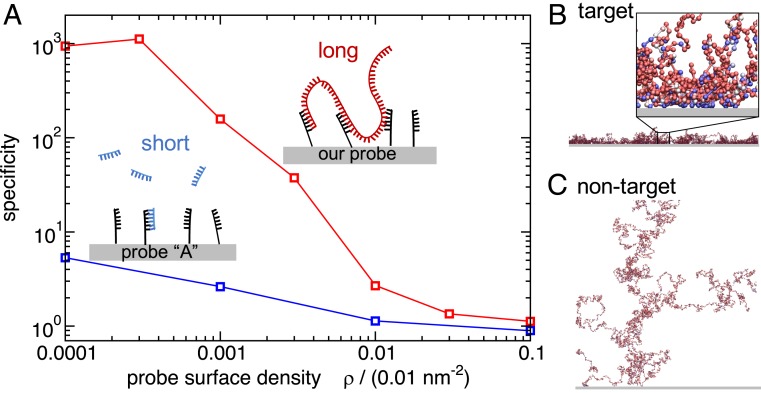
Simulating multivalent detection of bacterial DNA. (A) Simulation results for the specificity of binding of target vs. nontarget DNA to surfaces coated with probes targeting E. coli. Specificity is defined as the ratio of DNA–surface contacts for the target E. coli versus nontarget DNA from the bacterium B. subtilis. The blue curve shows results for a published 40-nt probe, “probe A” (18) that targets the 16S ribosomal gene of E. coli, binding to DNA fragmented into 400-nt segments. The red curve shows results for our top-scoring multivalent 20-nt probe binding to unfragmented genomic DNA (for the same total amount of DNA as in the blue curve). (B and C) Snapshots from our simulations for genomic DNA of E. coli (B) and B. subtilis (C) binding to the surface coated in multivalent probes. The genomic DNA is modeled as a chain of 400-nt “blobs.” Each ball represents a single blob and its color indicates the interaction strength between the blob and the surface: weak interaction, red; strong interaction, blue. The blow-up in B, Inset shows that blue blobs with a stronger surface-binding interaction are predominantly found close to the surface. The density of probes on the surface was set to . The lateral size of the snapshots is m, while the Inset to B is of size 300 nm.
The genomic DNA of bacterial pathogens is typically several million base pairs long. Here we propose that the length of bacterial genomic DNA can be leveraged to improve probe design in DNA-based detection. We propose designing oligonucleotide probes such that a single probe can bind to multiple sites along the entire genome of the target bacterial pathogen. PCR would not be required for such an approach; rather, the entire complement of DNA in a sample could be amplified via whole-genome amplification methods [e.g., multiple-displacement amplification, which does not require temperature cycling (16, 17)]. Using computer simulations, we show that multivalent binding of target genomic DNA to a probe-coated surface should greatly enhance the sensitivity and specificity of DNA-based detection of bacterial pathogens.
Our approach builds on the concept of superselectivity: the fact that the strength of a multivalent-binding interaction can depend critically on the number of binding sites on the target (19–26) (see also a discussion of the theory in Materials and Methods). Based on this concept, we design oligonucleotide probe sequences that can hybridize with multiple regions along the length of the genomic DNA of a target pathogen. This leads to multivalent binding of the target genomic DNA to the probe-coated surface. Due to superselectivity, this multivalent binding should be more selective for the target DNA compared to probes that are designed to hybridize to just a single site on a short DNA target fragment (19–21, 25, 26).
A key challenge is to identify which probe sequences to use to optimize the multivalent binding. Selecting the correct probe sequences is highly nontrivial and this is where computational probe design and testing come into play.
Below we present a computational approach to multivalent probe design. Crucially we optimize the multiplicity, rather than the strength, of probe–target binding. To test the performance of our multivalent probes, we perform computer simulations of genome–surface binding. We use a model that takes into account the polymer physics of genomic DNA interacting with a probe-coated surface as well as the sequence specificity of the target–probe binding. In Fig. 1, we summarize our main result. Here, we ran simulations for a surface coated in probes designed to detect Escherichia coli DNA, in the presence of two different single-stranded genomes: the target E. coli and nontarget Bacillus subtilis (a different bacterial species). We measured the number of probe–target contacts, , for each of the two genomes and defined detection specificity as the ratio of these numbers for the target vs. nontarget: . The blue curve in Fig. 1A shows the specificity for a surface coated in a published probe targeting a specific E. coli gene [the 40-nt probe A (18)] and with the genomic DNA fragmented into segments of length 400 nt to model typical fragments amplified by PCR. As the density of probes on the surface decreases, the specificity of detection of the target DNA gradually increases. However, there is a trade-off, because for very low probe densities (), the number of probe–target contacts decreases rapidly (SI Appendix, Fig. S9 and Fig. 2), resulting in a reduction of the measurable signal. The red curve in Fig. 1A shows the result for our proposed improved method. Here, we optimized 20-nt probes to bind multivalently to many positions in the E. coli genome and simulated the binding of the nonfragmented genome to the probe-coated surface. Our results show that, in this multivalent-binding approach, the specificity of detection of the target DNA is greatly enhanced (E. coli DNA binds two orders of magnitude more than B. subtilis DNA).
Fig. 2.
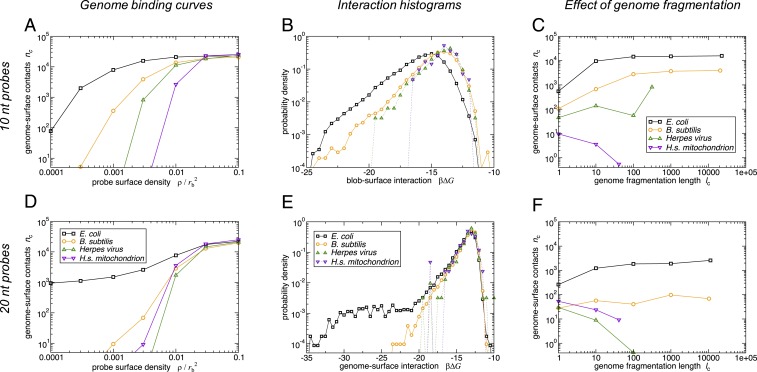
Adsorption of four different genomes: E. coli, B. subtilis, herpes virus, and human mitochondrion, to a probe-coated surface designed to target E. coli. In A and D, B and E, and C and F, respectively, we show the number of genome–surface contacts for the full genome as function of the probe density , the interaction free-energy histograms for the full genome at the probe density , and the as a function of the fragmentation length (measured in blobs) at the probe density . A–C present results for short probes (10 nt) and D–F those for longer probes (20 nt). In all cases, the surface is coated with the highest-scoring oligonucleotide probe targeting the E. coli genome, together with its reverse complement. We use a blob size of 400 nt, C, a periodic box of size , and a blob–surface contact is defined as a blob being located within 2 = 20 nm of the surface.
Simulation snapshots (Fig. 1B for E. coli genomic DNA and Fig. 1C for B. subtilis) from our multivalent-binding simulations also illustrate this finding. In these simulations, we use an approach common in polymer physics, where a long polymer is represented as a connected chain of “blobs.” Thus, genomic DNA is represented as a chain of 400-nt blobs, each of which has a sequence-specific interaction with the surface (see Materials and Methods for details of our simulation model). In Fig. 1 B and C, each ball represents one blob and its color indicates the interaction strength of the blob with the surface probes. It is evident that E. coli genomic DNA forms many distinct contacts with the surface and that these contacts are mediated by the blobs that have a strong binding affinity to the surface. In contrast, B. subtilis genomic DNA shows much less binding and, correspondingly, the genome is not confined to the surface. In these snapshots, the specificity achieved by the multivalent-binding approach is .
Depending on the diagnostic requirements, our approach can be used either to detect a known target genome in the presence of other, unknown, nontarget DNA or, with a modified approach to probe design, to detect a target genome in the presence of a known, but very similar, nontarget genome.
Computational Approach to Probe Design and Testing
Designing Oligonucleotide Probes for Multivalent Binding to Bacterial Genomic DNA.
To achieve multivalent probe–target binding, we aim to design oligonucleotide probes (of length ) with as many regions of complementarity with the target bacterial genome as possible (i.e., to maximize the multiplicity of genome–surface binding). To choose the probe sequences, we designed an “in-house” bioinformatics algorithm that considers all sequences of length that occur within the pathogen genome and assigns to each sequence a “multiplicity score” . The multiplicity score measures the number of binding sites for that probe on the target genome. While there are many possible ways to measure multiplicity of binding, we use the score function , where denotes the number of continuous regions of complementarity of length between sequence and the pathogen genome. The numbers could be obtained using, e.g., the BLAST+ (27) software package or via our in-house implementation, as described in Materials and Methods.
The sequences with the highest score have the longest overlaps with, and multiple repeats in, the target genome, and thus our algorithm works similarly to existing methods that search for motifs, such as MobyDick (28). However, the aim of our score function is not to find motifs within the target genome but instead to find the probe sequence with the highest multiplicity of binding to the target. The simple form of the score function is crucial to ensure we are able to search over the many candidate probes for a given genome (the number of candidate probes is equal to the genome length in nucleotides, typically ).
Having assigned score values to all possible oligonucleotide probe sequences of length , one can design a probe surface by functionalizing it either with the top-scoring probe sequence or with a mixture of high-scoring probe sequences. Unless specified otherwise, we optimized the probe sequences for binding to the entire genome of our model pathogen, E. coli (wild-type strain bl21-de3 [ASM956v1]). We considered two cases: (“short probes”) and (“longer probes”).
Coarse-Grained Polymer Model for Genomic DNA.
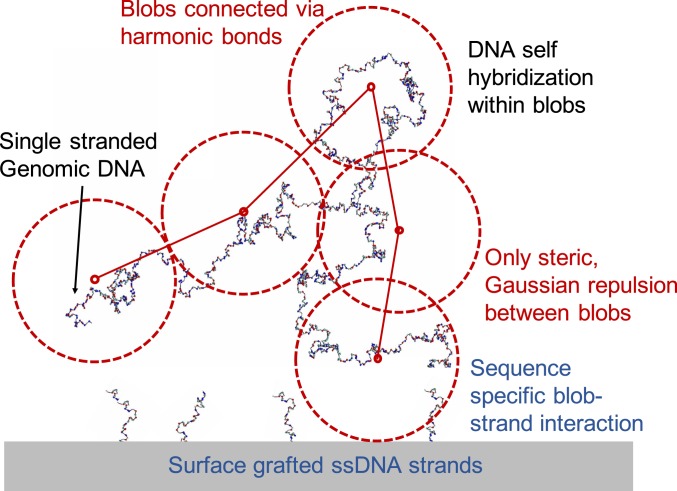
To assess the performance of our multivalent probe design, we developed a computer simulation model that allows us to predict the binding of single-stranded pathogen genomic DNA to a surface which is grafted with short, single-stranded, oligonucleotide DNA probes (see Fig. 4 in Materials and Methods). These simulations are challenging, because our model needs to include the entire genome of to nt, while also taking account of the sequence specificity of the DNA-binding interactions. Established models that can include sequence-specific interactions (e.g., refs. 29–31) would not be computationally feasible for the long genomic DNA.
Fig. 4.
Illustration of our model. Single-stranded genomic DNA is represented as a chain of blobs, connected by harmonic springs. Each blob represents -nt bases. The interactions among the blobs, and between each blob and the probe DNA-coated surface, are sequence specific and are calculated from the SantaLucia interaction free energies (34, 35) (see SI Appendix for a full description). The oxDNA model is used to represent the configuration of the single-stranded DNA chain (40).
To overcome this problem, we implemented a coarse-grained approach to the polymeric structure of the genomic DNA, invoking an experimentally validated polymer model (24). The model builds on an important insight provided by polymer theory: At a coarse-grained level, a polymer that is in a good solvent (under semidilute conditions) or interacting with a surface can be modeled as a chain of blobs, each representing many monomers, that interact via soft, repulsive potentials (32, 33). Therefore, we model the single-stranded genomic DNA as a chain of blobs, each of which represents 400 nt, implying a blob size of nm (Materials and Methods and SI Appendix). Such coarse-grained interactions are sequence specific since each blob is unique in its interaction with the probe-coated surface. This interaction is calculated based on a nearest-neighbor model of DNA hybridization free energy, using the SantaLucia empirical parameters (34, 35) (Materials and Methods and SI Appendix). A similar coarse-grained model has been experimentally validated and shown to predict accurate structure formation and melting transitions in multicomponent DNA brick assembly (36). We have verified that changing the number of nucleotides per blob (and scaling the blob size accordingly) does not affect our results (SI Appendix).
The probe-coated surface is represented in a mean-field way via a uniform attractive potential; i.e., individual probes are not resolved.
Simulating the Binding of Genomic DNA to a Probe-Coated Surface.
To investigate the binding of bacterial genomic DNA to probe-coated surfaces, we performed Langevin dynamics simulations of our coarse-grained model using the LAMMPS open-source simulation package (37). In all simulations, both the forward and reverse strands of the genomic DNA were present in the system as single-stranded DNA; consequently, we assumed the surface to be coated by a mixture of the forward and reverse-complement strands of the top-scoring oligonucleotide probe sequence. In our simulations, we varied the density of probes on the surface, in the range where there is negligible probability of probe self-hybridization.
To investigate the selectivity with which the surface targets E. coli genomic DNA as opposed to other, nontarget DNA, we performed simulations with four different genomes: the target E. coli (which was used to optimize the probes) and three different nontarget DNAs: B. subtilis (strain QB928), human mitochondrial DNA (NCBI reference sequence NC_012920.1), and the herpes virus 3 genome (strain 03-500, DQ479957). Each single-stranded genome was modeled as a chain of blobs with the blob–probe interactions being determined for each blob during the coarse-graining procedure.
Results
Binding Regimes.
To quantify the surface–genomic DNA binding, we measured the average number of blob–surface contacts (defined as blobs located within 2 nm of the surface), over a set of simulations with different densities of the surface-grafted oligonucleotide probes. Our results are presented in Fig. 2 A and D. For E. coli genomic DNA, we observe a rapid increase in binding above a probe density of , showing that the binding is sensitive. Nontarget genomes also bind to the probe surface, but only for significantly higher probe densities; in other words, the binding of E. coli genomic DNA is also highly selective.
The origin of the observed selectivity for target vs. nontarget genomic DNA can be understood by plotting the distribution of blob–surface binding free energies (Fig. 2 B and E; see Materials and Methods for the definition). For the target E. coli genomic DNA (black lines in Fig. 2 B and E), we observe a broad distribution of binding free energies, with some blobs binding strongly (more negative ) and many binding weakly. The nontarget genomes (colored lines in Fig. 2 B and E) contain some blobs that bind strongly to the surface, but the frequency of such strongly binding blobs is lower ( i.e., these curves are shifted to the right compared to the E. coli data). Thus, selectivity of the surface for E. coli genomic DNA is achieved not by designing oligonucleotide probes that bind exclusively to the target genome, but rather by designing probes that have a greater number of binding sites on the target genome than on a nontarget genome. This is the key feature of superselective binding (22–24).
An important parameter in our model is the length of the oligonucleotide probes. A longer probe is expected to have fewer perfectly complementary matches along the genomic DNA sequence, but where it binds, its interaction is expected to be stronger. Fig. 2E shows that indeed, for the longer probes, the predicted distribution of probe–blob binding free energies for the coarse-grained model of E. coli genomic DNA (black data) has a low-abundance “tail” of strong interactions (strongly negative ). Comparing Fig. 2B with Fig. 2E, the strongest interaction for long probes whereas for the short probes it is . But this increased binding strength comes at a price: If we count the absolute number of blobs that interact more strongly than , there are about twofold fewer for the longer than for the shorter probes. For the other three genomes considered (orange, green, and purple data in Fig. 2E), the strong interactions are not present, while the weak interactions remain.
The emerging picture suggests that there may exist a long-probe regime that is qualitatively different from the superselective-binding short-probe regime—and that our 20-nt “longer” probes show some features of this long-probe regime. In the long-probe regime, surface–genome binding is still selective (Fig. 2D). However, this selectivity arises because the few strong interactions that mediate binding of the E. coli genome are absent for the nontargeted genomes. This is quite different from the superselective short-probe regime, where the surface–genome binding interactions are equivalent in strength between the genomes, but are simply more numerous for the E. coli genome. While the superselective short probes give better sensitivity for intermediate probe density (Fig. 2A vs. Fig. 2D, black lines), we shall see later on (Distinguishing between Similar Genomes) that we need to resort to longer probes to distinguish between very similar genomes such as different strains of the same bacterial species (Fig. 3).
Fig. 3.
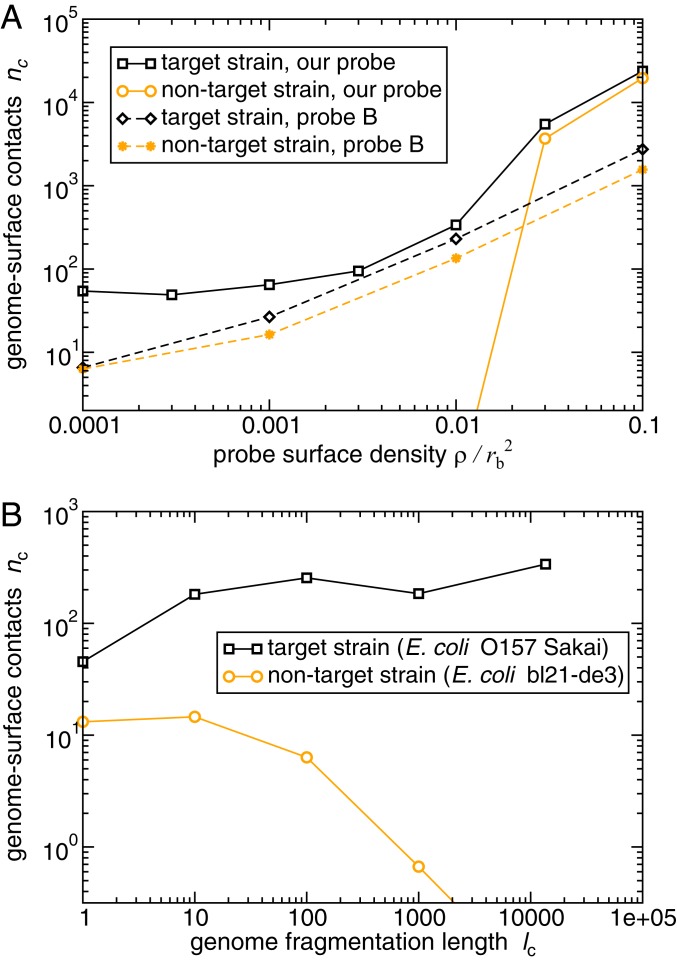
Distinguishing between similar genomes: the target strain E. coli O157 Sakai and the nontarget strain E. coli bl21-de3 (wild type). (A) Results of our Langevin dynamics simulations for the average degree of binding (number of blob–surface contacts ), for the target and nontarget genomic DNA. The solid lines show results for the top-scoring 20-nt probe, which is designed to maximize the difference function . The dashed lines show results for the published 70-nt “probe B” (38), which targets the rfbE gene specific to E. coli O157. For the published probe, the genomic DNA has been fragmented into 400-nt pieces to mimic standard DNA microarray conditions while for our 20-nt probe we assume unfragmented genomic DNA. (B) The effect of genome fragmentation at surface probe density , for our top-scoring 20-nt probe. As in our other simulations, , and a genome–surface contact was defined as a DNA blob being located within 2 nm of the surface.
Effects of Genome Fragmentation.
In our approach, in the short-probe regime, the efficacy of binding relies on the length of the target genomic DNA: More sensitive and more selective binding is achieved for a long genomic DNA target because it contains many binding sites for the probe-coated surface. Therefore, we expect that cutting the target DNA into fragments will compromise the sensitivity and selectivity of binding. To test this, we performed simulations where we cut the genomic DNA chain into fragments of length blobs (or nt). Fig. 2 C and F shows that fragmentation has a drastic effect: Upon reducing the fragment length, both the number of genome–probe contacts and the selectivity of binding drop significantly. Consistent with the above discussion, the effect is weaker when we use longer probes (compare Fig. 2F with 2C).
The difference in the degree of binding between target and nontarget is compromised as the degree of fragmentation increases ( blobs). Thus, leveraging the length of the target genomic DNA is central to achieving sensitive and selective detection in this approach. However, although these results show that extensive fragmentation is bad for binding, they also indicate that the sensitivity and specificity of binding are barely affected by “mild” fragmentation (values of greater than 10 blobs or genome fragment lengths above 4,000 nt). This is of practical interest because sample preparation methods could introduce a small number of breaks in the genomic DNA; our results show that our approach is robust to such mild fragmentation.
Interestingly, we note that for the target E. coli genome, and for B. subtilis, the extent of binding (sensitivity) decreases as the genome is fragmented (decreasing in Fig. 2 C and F), while for human mitochondrial DNA (and for herpes virus in the long-probe regime) net binding increases with fragmentation. For herpes virus, the effect is nonmonotonic at this probe density. These contrasting trends arise from a balance between energetic and entropic effects. Longer DNA fragments can bind to multiple oligonucleotide probes simultaneously, increasing the adsorption, but there is also an entropic cost of confining a long polymer close to the surface. Shorter DNA fragments are less likely to bind to multiple probes, but their binding also involves a smaller entropic cost. The herpes virus genome, which is relatively short (16,500 nt), contains only a few probe-binding sites even when unfragmented, so for this genome the reduction in entropic penalty upon fragmentation outweighs the loss of binding multiplicity.
Distinguishing between Similar Genomes.
It is often important to detect target DNA in the presence of closely related nontarget DNA. For example, the O157 Sakai strain of E. coli, which causes food poisoning, differs from the harmless laboratory strain bl21-de3 in only a few regions of the genome (SI Appendix). Closely related genomes can be distinguished using a modified version of our approach, in which oligonucleotide probes are selected based on the difference in binding score between the target and nontarget genomes, . The resulting probes bind to the regions of the target genome that are most different from those of the nontarget genome.
The performance of this approach is illustrated in Fig. 3A (solid lines), where we simulate the binding of target O157 Sakai genomic DNA and nontarget wild-type E. coli DNA (bl21-de3) to a surface coated in 20-nt probes designed to discriminate O157 Sakai from the wild-type strain. Comparing the predicted binding of O157 Sakai (orange points, solid line) to the nontarget strain (black points, solid line), we see that this surface is highly selective for the target O157 Sakai strain when the probe density is low. At high probe density, the nontarget strain binds appreciably to the surface, which in turn reduces the selectivity. We note that the use of 20-nt, as opposed to 10-nt, probe strands is required here to obtain sufficient discrimination between the two genomes. However, fragmenting the genome has a strong effect on the selectivity, suggesting that multivalent-binding effects are still at play (Fig. 3B).
It is instructive to compare the performance of our multivalency approach for discriminating between similar genomes with the results of equivalent simulations for an existing probe from the literature. The 70-nt “probe B” targets the rfbE gene, which is specific to the O157 Sakai strain (38). We simulated the binding of target E. coli O157 Sakai DNA (fragmented into 400-nt pieces), compared to nontarget wild-type E. coli DNA, to a surface coated in the monovalently binding probe B (see SI Appendix for details). Fig. 3A (dashed lines) shows that binding is predicted to be less extensive (especially at low probe density) and less selective (compare orange and black dashed lines) for the 70-nt probe B than for the 20-nt probe designed using our multivalent-binding approach (binding unfragmented genomic DNA). A different published probe [the 27-nt “probe C” (39) that also targets the rfbE gene] behaves similarly to the 70-nt probe B (see SI Appendix for details).
The superior performance of our approach compared to that of existing probes is due to multivalent binding to the genomic DNA. To maximize performance, the method requires both long pieces of target DNA (Fig. 3B) and the design of probes that target multiple sites on the target genome (see SI Appendix, Fig. S10, comparing the probe performance for equal degrees of fragmentation).
Discussion
DNA-based detection methods have wide relevance, including in disease diagnostics, environmental management, and the food industry (7–11). For detection of infections, DNA-based methods are attractive because they can target specific pathogen species or specific genes (such as those encoding virulence or antibiotic resistance). In such methods, oligonucleotide probes are typically designed to bind to a single region within the pathogen DNA. Here, we have investigated a “whole-genome binding” approach in which the oligonucleotide probes are instead designed to have the maximal number of regions of complementarity with the target genome. Using computer simulations, we show that multivalent binding can lead to highly sensitive and specific binding of the target DNA. Our approach exploits the concept of “superselectivity,” in which the target genome is selectively detected even though other, nontarget genomes may also have regions of complementarity with the probe sequences. Our method depends on the target DNA being long; when the genome is fragmented into short pieces, binding becomes less sensitive and less selective. However, mild fragmentation barely affects the performance of our multivalent-targeting approach.
The success of our approach depends on the oligonucleotide probes being relatively short; if the probes are long, they will typically have fewer (although stronger) binding sites on the target bacterial genome. We have shown that, with a modified probe selection criterion, our approach can be used to distinguish between genomes that are very similar: e.g., the O157 Sakai strain of E. coli versus a wild-type strain. However, distinguishing very similar genomes requires that the oligonucleotide probes are selected to maximize the difference in binding score between target and nontarget genomes. We note that distinguishing between very similar genomes could be relevant, in some cases, for distinguishing between antibiotic-resistant and -sensitive strains, thus facilitating the prediction of the antibiotic susceptibility profile of bacterial pathogens.
We tested our approach using simulations of a coarse-grained model in which the genomic DNA is modeled as a series of blobs, each of which represents hundreds of nucleotides of DNA, but in which sequence-specific interactions between a particular blob and the probe-coated surface are included via a mean-field approach based on the nearest-neighbor SantaLucia hybridization free energy (34, 35). This allows us to simulate the relatively long bacterial genome, while retaining sequence-specific interactions with the oligonucleotide-coated surface. In our simulations, a number of approximations have been made. In particular, we assume that different blobs along the genome chain interact only via steric repulsion; in other words, we neglect the possibility that blob–blob binding leads to the formation of long loops within the single-stranded DNA genome. However, recent results using a more detailed simulation model show that the macroscopic properties of ssDNA (e.g., the radius of gyration) are not significantly affected by such self-hybridization, at least for temperatures above C (40). Our simulations include both complementary strands of the genomic DNA, but do not take into account the interactions between the two strands. Nevertheless, our simulation model allows us to bridge the gap between the large-scale genomic DNA and the microscale sequence-specific hybridization interactions. Our calculations would not have been possible with higher-resolution, more computationally expensive DNA models that account for detailed base-pairing interactions (29–31). We also note that it is essential to include both the sequence specificity and the correct polymer physics; models that include only sequence specificity (34, 35), or only the polymer physics (41), cannot be used to predict the performance of the multivalent-binding strategy. Here we have chosen to vary the probe density on the surface as a control parameter—this is convenient for our simulations as the polymer–surface interaction parameters do not change with probe density. However, experimentally, it may be more convenient to vary temperature or salt concentration. Since temperature and salt concentration have equivalent effects to those of probe density on genome–surface binding (SI Appendix, Fig. S7), we expect this to lead to equivalent results.
We note that our coarse-grained model may not capture the kinetics of interaction of the genome with the surface correctly. Kinetic effects are expected to be important as longer DNA strands are likely to take a longer time than shorter ones to attach themselves to the probe-coated surface, even though this problem may be mitigated by the presence of multiple probe-binding sites along the genome. Another kinetic effect is related to the length of the oligonucleotide probes: Longer probes hybridize more slowly (42). Clearly, experiments (or further simulations) will be needed to quantify the kinetic effects.
Here we have used the bacterium E. coli as our model target. To apply this approach to other targets, one would need to design appropriate probes, following the probe design procedure set out here. The large-scale coarse-grained simulations of target–surface binding are, however, not necessary; the simulations that we present here are meant as a validation of the approach and should not be necessary for every new genome that is to be targeted. Of course, the need for sensitive and selective detection of specific DNA sequences extends well beyond bacterial infections. Examples include disease detection more broadly in humans, animals, and plants; detection of rare species in the environment (whether they are at risk or are invaders); and detection of pathogens, allergens, or fraudulent substitutions in the food industry (7–11). Our conclusions may therefore be of broad relevance.
We stress that this paper proposes a strategy rather than providing a recipe for an experimental approach to DNA detection. However, our approach can be tested using standard methods available in molecular biology and DNA microarray laboratories. The crucial quantity to measure in an experiment would be the number of bound probes. In principle, the use of fluorescent dyes that bind to double-stranded DNA should provide a fairly direct method to measure the number of probe–genome bonds. We also envisage that genomic DNA amplification, if needed at all, could be done using whole-genome amplification, which does not necessarily require thermal cycling (16, 17). Of course, the target DNA in the experiments should be free and should have been largely dehybridized, without massive fragmentation; protocols exist to achieve this.
Materials and Methods
Design of Oligonucleotide Probes.
Our in-house algorithm chooses oligonucleotide probes based on a score function that measures the number of regions of complementarity (continuous sequences, i.e., those without bubbles) between the probe sequence and the target DNA (considering both the forward and reverse strands of the pathogen genome). We first choose the length , in nucleotide bases, of the desired probes. For short probes, , our algorithm generates and evaluates all possible test-probe sequences (e.g., there exist different sequences of length 10 nt). If , the algorithm instead considers all distinct sequences of length that occur within the target pathogen genome.
A test-probe sequence of length is compared to all length subsequences in the genome and its reverse complement, and the numbers of exact matches of length between and the are tallied. For example, if , AAAAA, and ATAAA, then and . Probe sequence is then assigned a score , evaluated according to
| [1] |
This score function sums the numbers of matches over all subsequence lengths . Matches of length are weighted by a factor to account for the fact that longer matches are less likely to happen by chance (the probability of finding a match of length in a random target DNA sequence is ).
The score function, Eq. 1, can be thought of as an estimate of the interaction free energy between the probe and the target. Briefly, the factor of can be seen as a Boltzmann factor , where the “energy” is per matching nucleotide. The term in the square brackets in Eq. 1 would then correspond to a partition function. The 10- and 20-nt top scoring sequences targeting E. coli bl21-de3 are CGCCAGCGCC and AGGCGTTCACGCCGCATCCG.
In some cases, it is important to be able to detect the target genome in the presence of other genomic DNA that is closely related to it. For example, one might need to distinguish between strains of the same bacterial species, such as the O157 Sakai strain of E. coli, which causes food poisoning, in the presence of harmless strains (represented here by the wild-type laboratory strain bl21-de3). In this case, it is likely that the top-scoring oligonucleotide probe sequences for both target genomes will be very similar, making it hard to achieve selective binding.
To differentiate between similar genomes (here denoted and ) we propose a modified method of probe selection. Rather than simply scoring probe sequences according to their number of regions of complementarity with the target genome, we propose instead to rank them by the difference in their score for genomes and :
| [2] |
The 20-nt sequence maximizing the difference between O157 and bl21-de3 strains of E. coli is GGAGACTAAACTCCCTGAGA.
Coarse-Grained Model for Genomic DNA.
We model the single-stranded genomic DNA as a chain of blobs, each of which represents nt (Fig. 4). Following coarse-grained polymer theory (32), neighboring blobs are connected via harmonic potentials of the standard form
| [3] |
where is the thermal energy and the center–center distance. Repulsive interactions between distant parts of the genome polymer are included via a soft Gaussian potential acting between any pair of blobs
| [4] |
The origin of the dimensionless constants in these equations is detailed in ref. 32. We also need to model the interaction between the genomic DNA and the surface, which is assumed to be uniformly coated with oligonucleotide probes (which are taken to be well mixed if more than one probe type is present). Blobs interact with the surface via the potential
| [5] |
where is the distance between the blob center and the surface. This interaction is specific to a given blob. The first term in Eq. 5 represents the entropic repulsion between the DNA polymer and the surface and is taken from coarse-grained polymer theory (22, 24). The second term describes the attractive interaction between a given blob and the surface, due to DNA base pairing between the genomic DNA and the DNA that is grafted to the surface. This model has been experimentally verified in a study of multivalent binding of hyaluronan HA–-CD to receptor-coated surfaces (24, 43). The model provided an accurate description of polymer–surface interactions including multivalent-binding effects; superselective response; and the dependence of binding on receptor interaction strength, valency, and concentration. In ref. 24 the binding strength was uniform for all blobs, while here the prefactor is specific to each blob and captures sequence-specific information about the genomic DNA in that blob.
To obtain the sequence-specific prefactor for the interaction of a given blob with the surface, we need to know the free energy of hybridization between the blob DNA and the oligonucleotide probes on the surface. Here, we make use of the large body of work on nearest-neighbor (NN) models for DNA hybridization (34, 35, 44, 45). These models approximate the binding free energy between two DNA sequences as sums over base pairs, in which the contribution for a given base pair depends on its identity and that of its immediate neighbors (e.g., CG/GC; SI Appendix). SantaLucia has provided a parameterization of these free-energy contributions for all possible pairs of base pairs (34, 35); we use this to compute the free energy of interaction between a given 400-nt blob and a given surface-grafted oligonucleotide probe. Briefly, the binding free energy between blob sequence and probe sequence is given by , where is the SantaLucia binding free energy between the blob and probe, and and are the self-binding free energies due to DNA base-pairing interactions within the blob and within the probe, respectively.
To obtain the binding free energy between the blob and the surface, we also need to take into account the surface density of the probes. If all of the probes are identical in sequence (i.e., only probes of sequence are present), is given by
| [6] |
The detailed form of Eq. 6 arises because , as defined by SantaLucia, includes a contribution from the state where no base pairs are formed (SI Appendix).
If a mixture of probe sequences is present on the surface, Eq. 6 can be generalized to , where is the occurrence probability of probe within the mixture of probes on the surface (SI Appendix). In deriving this equation, we assume that the same mixture of probes is to be found at every position on the surface; i.e., we ignore any heterogeneity in the spatial distribution of probes on the surface.
Finally, we need to map the free energy of blob–surface binding (Eq. 6) to the interaction potential prefactor (Eq. 5). This is done by matching the partition functions for microscopic and coarse-grained representations of the system (SI Appendix), which turns out to be linear,
| [7] |
where is the blob radius, mol/L is the concentration of pure water, and is Avogadro’s number.
Theory of Superselective Binding.
We consider two distinct cases for probe–target binding: monovalent (a probe and target can form a single bond only) and multivalent. In the monovalent case, for a low density of probes on the surface, we expect the fraction of probe strands that bind to the target DNA to be proportional to the target DNA concentration and to the binding constant : . The binding constant in turn is related to the probe–target hybridization free energy by , where and M is a standard reference concentration. Therefore, for a given target concentration, the number of target–probe bonds can be enhanced by increasing the density of probes on the surface (as in Fig. 5, blue curve) or, equivalently, by increasing the strength of probe–target hybridization, , i.e., by designing probes that bind more strongly to the target DNA.
Fig. 5.
Theoretical prediction (Eq. 8) for specificity as a function of the probe density. Specificity is defined as a ratio between the number of bound probes to “target” DNA () and to “nontarget” DNA (). The blue (“short target”) curves are in the monovalent-binding regime ( in ref. 8), while the red curves describe binding of “long targets” in the multivalent-binding regime (). Here we have assumed that that target size scales with target length (or multiplicity) as with the self-avoiding walk scaling exponent and that the target concentration is .
In contrast, for multivalent probe–target binding, probes are designed to have multiple regions of hybridization with the target DNA. Therefore each piece of target DNA can bind simultaneously to two or more of the (identical) probe molecules on the surface (as in the case of the long target; red curve in Fig. 5). As was shown in refs. 23, 24, and 46 (also SI Appendix), the fraction of probes that are bound to the target is still proportional to the target DNA concentration, but now depends nonlinearly on the binding constant:
| [8] |
Here, is the number of regions of hybridization of the probe with the target ( i.e., the multiplicity of binding), is the surface density of oligomer probes, and measures the physical size of the target (in this case, the radius of gyration of the target DNA molecule). Eq. 8 shows that in the multivalent case, probe–target binding depends not only on the probe density and hybridization free energy , but also on the multiplicity of binding . For large , the target binding becomes switch-like, increasing sharply over a narrow range of values of probe density, or equivalently (Fig. 5, red curve). This implies that target binding can be highly specific: Even if nontarget DNA within the sample can also hybridize with the probe sequence, it will typically bind to far fewer probe sequences because it has a smaller binding free energy, or fewer hybridization sites for the probe sequences, or both.
Langevin Dynamics Simulations.
We used the LAMMPS open-source simulation package (37) to perform Langevin dynamics simulations (see SI Appendix for implementation details). In our simulations, the blob radius was used as the unit of length. The time step used was and the temperature was set to in Lennard-Jones units. Langevin damping was used, with the damping time parameter chosen to be high, to speed up the diffusion, with being the Lennard-Jones unit of time with the mass of each blob and the Boltzmann constant, and real temperature used was C. In all simulations both the forward and reverse-complement genomes are modeled and the surface is assumed to be coated with a mixture of the chosen oligonucleotide probe and its reverse complement. Simulations of bacterial genomes included a single genome and its reverse complement while the simulation of shorter viral (42 copies) and mitochondrial (320 copies) DNA included multiple copies of the genome such that the nucleotide concentration matched that in the simulations of E. coli genomic DNA.
All simulation scripts, input files, SantaLucia calculation script, and data analysis routines pertinent to this work are freely available in ref. 47.
Supplementary Material
Acknowledgments
This work was supported by the Royal Society of London under Global Challenges Research Fund Challenge Grant CH160103, by the European Research Council under Consolidator Grant 682237 EVOSTRUC, and by an international collaboration grant from the K. C. Wong Educational Foundation. C.A.B. was funded by the European Research Council under Consolidator Grant 648050 THREEDCELLPHYSICS. T.C. was supported by Slovenian Research Agency: Javna agencija za raziskovalno dejavnost Republike Slovenije Grant Z1-9170, National Natural Science Foundation of China (NSFC) Grant 11850410443, and National Science Foundation Grant DMR-1610796. J.D.F. was funded by NSFC Grant 21850410459 and J.D. acknowledges support from NSFC Grant 11874398 and from the European Union’s Horizon 2020 Program through Grants ETN 674979-NANOTRANS and FET-OPEN 766972-NANOPHLOW. U.B. acknowledges the financial support by the Slovenian Ministry of Science under Program Grant AB FREE.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data deposition: All simulation scripts, input files, SantaLucia calculation script, and data analysis routines pertinent to this work are freely available in GitHub (https://github.com/tc387/Genome-targeting).
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1918274117/-/DCSupplemental.
References
- 1.O’Neill J., Rapid diagnostics: Stopping unnecessary use of antibiotics: The review on antimicrobial resistance. https://amr-review.org/sites/default/files/Paper-Rapid-Diagnostics-Stopping-Unnecessary-Prescription-Low-Res.pdf. Accessed 19 March 2020.
- 2.Shapiro D. J., Hicks L. A., Pavia A. T., Hersh A. L., Antibiotic prescribing for adults in ambulatory care in the USA, 2007-09. J. Antimicrob. Chemother. 69, 234–240 (2014). [DOI] [PubMed] [Google Scholar]
- 3.Smieszek T., et al. , Potential for reducing inappropriate antibiotic prescribing in English primary care. J. Antimicrob. Chemother. 73, ii36–ii43 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Caliendo A. M., et al. , Better tests, better care: Improved diagnosis for infectious diseases. Clin. Infect. Dis. 57, S139–S170 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Albrich W. C., Monnet D. L., Harbarth S., Antibiotic selection pressure and resistance in Streptococcus pneumoniae and Streptococcus pyogenes. Emerg. Infect. Dis. 10, 514–517 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.World Health Organization, Global action plan for antimicrobial resistance. https://apps.who.int/iris/bitstream/handle/10665/193736/9789241509763_eng.pdf?sequence=1. Accessed 19 March 2020.
- 7.Reboud J., et al. , Paper-based microfluidics for DNA diagnostics of malaria in low resource underserved rural communities. Proc. Natl. Acad. Sci. U.S.A. 116, 4834–4842 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Thomsen P. F., Willerslev E., Environmental DNA–An emerging tool in conservation for monitoring past and present biodiversity. Biol. Conserv. 183, 4–18 (2015). [Google Scholar]
- 9.McKillip J. L., Drake M., Real-time nucleic acid–based detection methods for pathogenic bacteria in food. J. Food Protect. 67, 823–832 (2004). [DOI] [PubMed] [Google Scholar]
- 10.Senyuva H. Z. Jones I. B. Sykes M., Baumgartner S., A critical review of the specifications and performance of antibody and DNA-based methods for detection and quantification of allergens in foods. Food Addit. Contam. 36, 507–547 (2019). [DOI] [PubMed] [Google Scholar]
- 11.Rasmussen R. S., Morrissey M. T., DNA-based methods for the identification of commercial fish and seafood species. Compr. Rev. Food Sci. Food Saf. 7, 280–295 (2008). [DOI] [PubMed] [Google Scholar]
- 12.Schena M., DNA Microarrays: A Practical Approach (Oxford University Press, New York, NY, 1999). [Google Scholar]
- 13.Mocan T., et al. , Development of nanoparticle-based optical sensors for pathogenic bacterial detection. J. Nanobiotechnol. 15, 25 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Larguinho M., Baptista P. V., Gold and silver nanoparticles for clinical diagnostics–From genomics to proteomics. J. Proteomics 75, 2811–2823 (2012). [DOI] [PubMed] [Google Scholar]
- 15.Pulido M. R., García-Quintanilla M., Martín-Peña R., Cisneros J. M., McConnell M. J., Progress on the development of rapid diagnostic methods for antimicrobial susceptibility testing. J. Antimicrob. Chemother. 68, 2710–2717 (2013). [DOI] [PubMed] [Google Scholar]
- 16.Lizardi P. M., Mutation detection and single-molecule counting using isothermal rolling-circle amplification. Nature Genet. 19, 225–232 (1998). [DOI] [PubMed] [Google Scholar]
- 17.Dean F. B., Nelson J. R., Giesler T. L., Lasken R. S., Rapid amplification of plasmid and phage DNA using phi29 DNA polymerase and multiply-primed rolling circle amplification. Genome Res. 11, 1095–1099 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wiesinger-Mayr H., Identification of human pathogens isolated from blood using microarray hybridisation and signal pattern recognition. BMC Microbiol. 7, 78 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kitov P. I., Bundle D. R., On the nature of the multivalency effect: A thermodynamic model. J. Am. Chem. Soc. 125, 16271–16284 (2003). [DOI] [PubMed] [Google Scholar]
- 20.Huskens J., A model for describing the thermodynamics of multivalent host-guest interactions at interfaces. J. Am. Chem. Soc. 126, 6784–6797 (2004). [DOI] [PubMed] [Google Scholar]
- 21.Diestler D. J., Knapp E. W., Statistical thermodynamics of the stability of multivalent ligand-receptor binding. Phys. Rev. Lett. 100, 178101 (2008). [DOI] [PubMed] [Google Scholar]
- 22.Martinez-Veracoechea F. J., Frenkel D., Designing super selectivity in multivalent nano-particle binding. Proc. Natl. Acad. Sci. U.S.A. 108, 10963–10968 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dubacheva G. V., Superselective targeting using multivalent polymers. J. Am. Chem. Soc. 136, 1722–1725 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dubacheva G. V., Curk T., Auzély-Velty R., Frenkel D., Richter R. P., Designing multivalent probes for tunable superselective targeting. Proc. Natl. Acad. Sci. U.S.A. 112, 5579–5584 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tito N. B., Frenkel D., Optimizing the selectivity of surface-adsorbing multivalent polymers. Macromolecules 47, 7496–7509 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tito N. B., Angioletti-Uberti S., Frenkel D., Communication: Simple approach for calculating the binding free energy of a multivalent particle. J. Chem. Phys., 144, 161101 (2016). [DOI] [PubMed] [Google Scholar]
- 27.Camacho C., BLAST+: Architecture and applications. BMC Bioinf. 10, 421 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bussemaker H. J., Li H., Siggia E. D., Building a dictionary for genomes: Identification of presumptive regulatory sites by statistical analysis. Proc. Natl. Acad. Sci. U.S.A. 97, 10096–10100 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ouldridge T. E., Louis A. A., Doye J. P. K., Structural, mechanical and thermodynamic properties of a coarse-grained DNA model. J. Chem. Phys. 134, 085101 (2011). [DOI] [PubMed] [Google Scholar]
- 30.Šulc P., Sequence-dependent thermodynamics of a coarse-grained DNA model. J. Chem. Phys. 137, 135101 (2012). [DOI] [PubMed] [Google Scholar]
- 31.Snodin B. E. K., Introducing improved structural properties and salt dependence into a coarse-grained model of DNA. J. Chem. Phys. 142, 234901 (2015). [DOI] [PubMed] [Google Scholar]
- 32.Pierleoni C., Capone B., Hansen J.-P., A soft effective segment representation of semidilute polymer solutions. J. Chem. Phys. 127, 171102 (2007). [DOI] [PubMed] [Google Scholar]
- 33.Louis A. A., Bolhuis P. G., Hansen J. P., Meijer E. J., Can polymer coils be modeled as “soft colloids”? Phys. Rev. Lett. 85, 2522–2525 (2000). [DOI] [PubMed] [Google Scholar]
- 34.SantaLucia J., A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. U.S.A. 95, 1460–1465 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.SantaLucia J. Jr, Hicks D., The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 33, 415–440 (2004). [DOI] [PubMed] [Google Scholar]
- 36.Sajfutdinow M., Jacobs W. M., Reinhardt A., Schneider C. Smith D. M., Direct observation and rational design of nucleation behavior in addressable self-assembly. Proc. Natl. Acad. Sci. U.S.A. 115, E5877–E5886 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Plimpton S., Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1–19 (1995). [Google Scholar]
- 38.Vora G. J., Meador C. E., Stenger D. A., Andreadis J. D., Nucleic acid amplification strategies for DNA microarray-based pathogen detection. Appl. Environ. Microbiol. 70, 3047–3054 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Jin H.-Y., Tao K.-H., Li Y.-X., Li F.-Q., Li S.-Q., Microarray analysis of Escherichia coli O157:H7. World J. Gastroenterol. 11, 5811–5815 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Henrich O., Gutiérrez Fosado Y. A., Curk T., Ouldridge T. E., Coarse-grained simulation of DNA using LAMMPS. Eur. Phys. J. E 41, 57 (2018). [DOI] [PubMed] [Google Scholar]
- 41.Marenduzzo D., et al. , DNA-DNA interactions in bacteriophage capsids are responsible for the observed DNA knotting. Proc. Natl. Acad. Sci. U.S.A. 106, 22269–22274 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Okahata Y., et al. , Kinetic measurements of DNA hybridisation on an oligonucleotide-immobilized 27-MHz quartz crystal microbalance. Anal. Chem. 70, 1288–1296 (1998). [DOI] [PubMed] [Google Scholar]
- 43.Dubacheva G. V., Curk T., Frenkel D., Richter R. P., Multivalent recognition at fluid surfaces: The interplay of receptor clustering and superselectivity. J. Am. Chem. Soc. 141, 2577–2588 (2019). [DOI] [PubMed] [Google Scholar]
- 44.Crothers D. M., Zimm B. H., Theory of melting transition of synthetic polynucleotides–Evaluation of stacking free energy. J. Mol. Biol. 9, 1–9 (1964). [DOI] [PubMed] [Google Scholar]
- 45.DeVoe H., Tinoco I., Stability of helical polynucleotides: Base contributions. J. Mol. Biol. 4, 500–517 (1962). [DOI] [PubMed] [Google Scholar]
- 46.Curk T., Dobnikar J., Frenkel D., Rational design of molecularly imprinted polymers. Soft Matter 12, 35–44 (2016). [DOI] [PubMed] [Google Scholar]
- 47.Curk T., Simulation scripts and data for the Genome targeting project published in Curk et al, PNAS (2020). GitHub. https://github.com/tc387/Genome-targeting. Deposited 18 March 2020.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.