Minimization-Aware Recursive K*: A Novel, Provable Algorithm that Accelerates Ensemble-Based Protein Design and Provably Approximates the Energy Landscape

Abstract

Protein design algorithms that model continuous sidechain flexibility and conformational ensembles better approximate the in vitro and in vivo behavior of proteins. The previous state of the art, iMinDEE-A*-K*, computes provable ɛ-approximations to partition functions of protein states (e.g., bound vs. unbound) by computing provable, admissible pairwise-minimized energy lower bounds on protein conformations, and using the A* enumeration algorithm to return a gap-free list of lowest-energy conformations. iMinDEE-A*-K* runs in time sublinear in the number of conformations, but can be trapped in loosely-bounded, low-energy conformational wells containing many conformations with highly similar energies. That is, iMinDEE-A*-K* is unable to exploit the correlation between protein conformation and energy: similar conformations often have similar energy. We introduce two new concepts that exploit this correlation: Minimization-Aware Enumeration and Recursive K*. We combine these two insights into a novel algorithm, Minimization-Aware Recursive K* (MARK*), which tightens bounds not on single conformations, but instead on distinct regions of the conformation space. We compare the performance of iMinDEE-A*-K* versus MARK* by running the Branch and Bound over K* (BBK*) algorithm, which provably returns sequences in order of decreasing K* score, using either iMinDEE-A*-K* or MARK* to approximate partition functions. We show on 200 design problems that MARK* not only enumerates and minimizes vastly fewer conformations than the previous state of the art, but also runs up to 2 orders of magnitude faster. Finally, we show that MARK* not only efficiently approximates the partition function, but also provably approximates the energy landscape. To our knowledge, MARK* is the first algorithm to do so. We use MARK* to analyze the change in energy landscape of the bound and unbound states of an HIV-1 capsid protein C-terminal domain in complex with a camelid V_HH, and measure the change in conformational entropy induced by binding. Thus, MARK* both accelerates existing designs and offers new capabilities not possible with previous algorithms.

1. Introduction

The objectives of computational structure-based protein design algorithms are (1) to accurately calculate properties of a protein or protein complex (e.g., stability, binding affinity, etc.) and (2) to efficiently search for optimal sequences given an objective function defined on these properties. These algorithms search over a space defined by a user-specified input model (i.e., a structural model, allowed sidechain and backbone flexibility, allowed mutations, energy function, etc.). Designs for ensemble-average, macromolecular properties such as binding affinity and stability are more biophysically accurate when modeling thermodynamic, conformational ensembles (Gilson et al., 1997; Lilien et al., 2005; Georgiev et al., 2008a,b; Chen et al., 2009; Sciretti et al., 2009; Roberts et al., 2012; Tzeng and Kalodimos, 2012; Silver et al., 2013). However, accurately modeling these ensembles can be challenging: the space of possible conformations available in vitro and in vivo to a protein can be massive, and furthermore grows exponentially with the number of residues.

Various simplifications to the input model and the search methodology have been used to reduce the complexity of this problem, of which we discuss three: (1) discretized, rigid sidechain and backbone flexibility; (2) design to a single, static global minimum energy conformation (GMEC); and (3) non-provable search over possible conformations and sequences.

(1) Although amino acid sidechains are continuously flexible, sidechains are often modeled as discrete, frequently observed low-energy states called rotational isomers, or rotamers (Lovell et al., 2000). Furthermore, protein backbone flexibility is frequently modeled as fixed, or restricted to a small set of discrete alternate conformations (Leaver-Fay et al., 2011; Traoré et al., 2013; Simoncini et al., 2015; Viricel et al., 2016). Designs made with these simplifications do not model small, commonly observed sidechain and backbone movements, much less larger structural rearrangements. Even under these simplifications, calculating the partition function for a protein remains #P-hard (Valiant, 1979; Nisonoff, 2015; Viricel et al., 2016). Moreover, the conformation space grows exponentially with the number of residues.

(2) As a result, many design algorithms optimize the energy of a single static GMEC structure (Dahiyat and Mayo, 1997; Leach and Lemon, 1998; Chazelle et al., 2004; Georgiev et al., 2006; Traoré et al., 2013; Hallen et al., 2015, 2017). GMEC-based algorithms do not model conformational entropy, which can contribute significantly to protein structure and function (Frederick et al., 2007; Fleishman et al., 2011), and as a result can overlook thermodynamically favorable sequences (Roberts et al., 2012).

(3) Finally, some algorithms attempt to estimate the partition function by stochastically sampling the conformation space for low-energy microstates (Lee and Subbiah, 1991; Kuhlman and Baker, 2000; Leaver-Fay et al., 2011). These algorithms provide no guarantees on the quality of the lowest energy conformation returned, much less on the quality of the approximation of the overall partition function. Indeed, Simoncini et al. (2015) demonstrated that as the size of the search space increases, the probability that stochastic methods find even the GMEC falls rapidly to zero. Furthermore, because these methods are nondeterministic, it is profoundly difficult to deconvolve methodological error (i.e., undersampling) from input model error (Donald, 2011; Gainza et al., 2016).

Algorithms distributed in the osprey (Hallen et al., 2018) package efficiently solve protein design problems without the mentioned simplifications, provably returning the optimal sequences and conformations without sacrificing accuracy. osprey models not only continuous sidechain flexibility (Georgiev et al., 2008b; Gainza et al., 2012; Hallen et al., 2015, 2017), but also discrete and continuous backbone flexibility (Georgiev and Donald, 2007; Georgiev et al., 2008a; Hallen et al., 2013; Hallen and Donald, 2017).

Additionally, the branch and bound over K* (BBK*) algorithm (Ojewole et al., 2018) provably returns protein sequences in order of decreasing binding affinity and runs in time sublinear in the number of sequences. These algorithms have been used to prospectively predict drug resistance (Frey et al., 2010; Reeve et al., 2015; Ojewole et al., 2017) and design enzymes (Lilien et al., 2005; Stevens et al., 2006; Georgiev and Donald, 2007; Georgiev et al., 2008b; Chen et al., 2009), new drugs (Gorczynski et al., 2007), peptide inhibitors of protein–protein interactions (Roberts et al., 2012), epitope-specific antibody probes (Georgiev et al., 2012), and broadly neutralizing antibodies (Georgiev et al., 2014; Rudicell et al., 2014). These designs have been experimentally validated in vitro, some in vivo, and one designed anti-HIV broadly neutralizing antibody, VRC07-523LS, is currently in nine clinical trials (ClinicalTrials.gov, 2018).

The K* algorithm in osprey estimates binding affinity with the K* score (Lilien et al., 2005), a ratio of ɛ-approximate Boltzmann-weighted partition functions for bound and unbound states. These partition functions are computed by combining an admissible lower bound on conformational energy with the A* search algorithm to quickly and provably enumerate a gap-free list of the lowest energy conformations (Hart et al., 1968; Leach and Lemon, 1998; Roberts et al., 2015). We will refer to algorithms that compute K* scores using A* as A*-K* algorithms.

Although significantly more efficient than exhaustive enumeration, A*-K* algorithms are guaranteed to return the GMEC first and, therefore, focus on efficiently finding low-energy conformations. However, a GMEC-first enumeration strategy may not efficiently approximate the full partition function. Modeling continuous flexibility further compounds the difficulties of partition function approximation. Previous A*-K* algorithms (Georgiev et al., 2008b; Gainza et al., 2012) that incorporate continuous flexibility, such as iMinDEE-A*-K* (Gainza et al., 2012), enumerate conformations in order of energy lower bounds on the minimized energy. However, when these bounds are loose, iMinDEE-A*-K* must perform many computationally expensive full minimizations (wherein all mutable and flexible residues minimize simultaneously) to provably approximate the partition function. In the worst case, A*-K* algorithms must minimize a combinatorial number of conformations that are loosely bounded at the same residues.

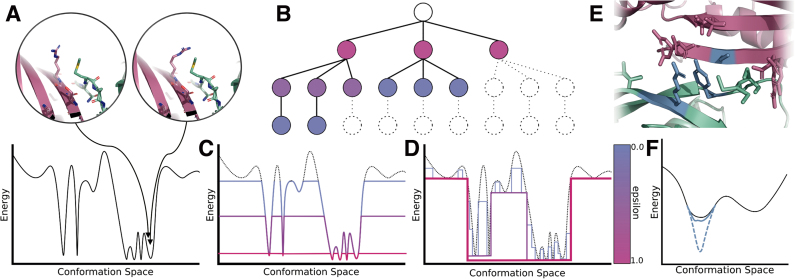
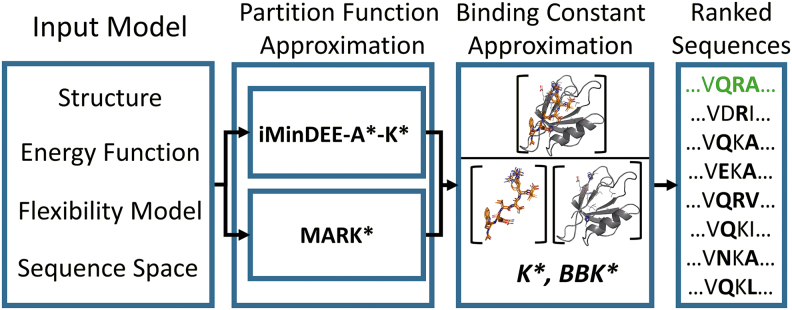
To overcome the limitations of A*-K*, we present a novel algorithm that combines two new concepts: Recursive K* (RK*) and Minimization-Aware Enumeration (MAE). RK* prioritizes low-entropy regions of the energy landscape, instead of prioritizing low-energy conformations (Fig. 2D vs. 2C), and MAE tightens bounds on a combinatorial number of conformationally similar, loosely bounded conformations (Fig. 2E). This combination, Minimization-Aware Recursive K* (MARK*), achieves significant efficiency and runtime improvements for large protein design problems that confound previous A*-K* algorithms, as well as algorithms that call A*-K* algorithms as a subroutine, such as BBK* (Ojewole et al., 2018; Fig. 1). Where BBK* would previously call iMinDEE-A*-K* to tightly approximate the partition function of a sequence, MARK* can be directly substituted. As such, we were able to combine the multisequence search capabilities of BBK* with the novel algorithmic improvements of MARK* to not only efficiently approximate partition functions, but also efficiently search over sequences by K* score (detailed explanation is available in Section B.5 of the Supplementary Information in Jou et al., 2019). Because MARK* replaces iMinDEE-A*-K*, we ran BBK* with iMinDEE-A*-K* as a control, and compared it with the performance of BBK* with MARK* on 200 protein design problems. We found that MARK* accelerates BBK* by up to 2 orders of magnitude, efficiently completing designs an order of magnitude larger than was possible using BBK* with iMinDEE-A*-K*.

FIG. 2.

RK* and MAE exploit positive correlation between conformation and energy to efficiently bound the partition function. (A) Structurally similar conformations within the same energy well often have similar energies, shown as two points in the black energy landscape. (B) When the conformation space is represented as a conformation tree, some conformations (white leaf nodes) may be tightly bounded by computing bounds on their parent nodes (colored internal nodes). (C) Previous provable partition function approximation algorithms tightly bounded all conformations within some energy window of the GMEC. To decrease the error bound ɛ (colored by the scale beside D), these algorithms incrementally increased the energy window, computing exact energies for more and more conformations (colored curves). (D) RK* instead exploits the correspondence between conformation and energy to more efficiently bound similar conformations with bounds on regions of the energy landscape. As the error bound ɛ decreases and the approximation becomes more accurate (colored step curves), RK* iteratively tightens bounds on loosely bounded (and often low-entropy) regions of the landscape, rather than tightly bounding low-energy conformations. (E) Loosely-bounded pairwise-minimized bounds can affect a combinatorial number of conformations, shown as an ensemble of conformations that share the same sidechain assignments at the blue residues. Although the blue residues have favorable pairwise-minimized lower bounds, when all three are minimized in concert, their post-minimized energy is higher. (F) By computing a tighter bound on the three blue residues, MAE tightens the bounds on the combinatorial number of conformations containing the sidechain assignments at the blue residues. Thus, a loosely bounded energy well (black curve vs. dotted blue curve) may be bounded more tightly (solid blue curve) without minimizing all conformations in the well.

FIG. 1.

Provably computing the best binding sequences with respect to the input model. When designing for macromolecular, ensemble-average properties such as binding affinity K_a, provable algorithms such as K* (Lilien et al., 2005; Georgiev et al., 2008b; Roberts et al., 2012) and BBK* (Ojewole et al., 2018) take as input an input structure, energy function, allowed backbone and sidechain flexibility, and allowed mutations that define the sequence space. Both algorithms used the previous state of the art, iMinDEE-A*-K*, to provably approximate partition functions (with respect to the input model) and combined these partition function approximations into a K* score (Lilien et al., 2005), which approximates K_a. By approximating K_a, designers can rank candidate sequences in order of binding affinity, and identify the best binding sequence (green) with respect to the input model. In this design protocol, MARK* replaces iMinDEE-A*-K* as a provable partition function approximation module.

Finally, we show that MARK* not only outperforms the previous state of the art in speed, but also offers new design capabilities. Because MARK* tightly bounds low-entropy regions of the conformation space instead of low-energy conformations, it computes a provable approximation of the energy landscape, which bounds the energy of every conformation in the conformation space. MARK* is, to our knowledge, the first provable algorithm to do so. In contrast, previous algorithms (provably or nonprovably) return only low-energy conformations, and do not tightly and provably approximate the energy landscape. This energy landscape approximation provides additional insight into the higher energy regions between tightly-bounded low-energy conformational wells (Fig. 2D). Using MARK* to compute the partition function and energy landscape for the design problem of an HIV-related protein–protein interface, we demonstrate the ability of MARK* to reveal components of binding thermodynamics. That is, we show that MARK* not only approximates the partition function more efficiently, but also computes an entire energy landscape that enables insight into thermodynamics.

By presenting this algorithm, our article makes the following contributions:

• 1.A novel algorithm that more quickly and efficiently predicts binding affinity using partition functions over molecular ensembles.
• 2.Proofs of correctness and admissibility of the bounds used in the branch and bound strategy by MARK*, as well as the optimality of MARK* for a given energy bounding function.
• 3.200 designs showing that BBK* with MARK* returned the five best sequences up to 2 orders of magnitude faster, minimized 685-fold fewer conformations, and completed designs up to an order of magnitude larger than was possible using BBK* with iMinDEE-A*-K*.
• 4.An application of MARK* to compute a provable approximation of the energy landscape for an HIV-related protein–protein interface, revealing components of binding thermodynamics.
• 5.An implementation of MARK* in our laboratory's open-source protein design software, osprey (Hallen et al., 2018).

2. Background

To accurately model macroscopic properties such as binding affinity, design algorithms must approximate the Boltzmann-weighted partition function over bound and unbound states. For a protein design with n residues, let the sequence s be a set of n ordered pairs (i, a), each containing the residue index i and an amino acid a. For a sequence s, we can define the conformation space Q(s) to be the set of conformations defined by s. In addition, we denote the maximum number of rotamers (at any one residue) to be q. Let E_X(c) be the minimized energy of a conformation c in state X (e.g., bound or unbound). Under this formulation, the partition function Z_X (s) for a protein with sequence s in state X can be defined as

$$Z_{{}_X}\left(s\right)={\sum }_{c\in Q\left(s\right)}exp\left(-E_{{}_X}\left(c\right)∕RT\right).$$ (1)

Notably, the set of all conformations Q(s) grows exponentially with the number of residues n and, therefore, the exact value of the partition function becomes intractable to compute as n increases. As a result, many protein design algorithms instead approximate Z_X with stochastic (Hastings, 1970; Lee, 1993; Nosé 2006; Lou et al., 2017b) or provable (Lilien et al., 2005; Georgiev et al., 2008b; Roberts et al., 2012; Silver et al., 2013; Viricel et al., 2016; Lou et al., 2017a; Ojewole et al., 2017) methods. Provable algorithms have mathematical guarantees on their computed approximation of Z_X, and thus obviate any need for deconvolution of error in the output.

One class of provable algorithms computes an ɛ-approximation of the partition function by using the A* search algorithm to enumerate a gap-free list of conformations in order of increasing energy (Lilien et al., 2005; Georgiev et al., 2008b; Gainza et al., 2012; Roberts et al., 2012; Ojewole et al., 2018). By enumerating a gap-free list of low-energy conformations, A*-K* algorithms compute both upper and lower bounds on the overall partition function, and return a partition function approximation that is guaranteed to be within a ($1-\epsilon$) factor of the true partition function. When incorporating continuous flexibility, A*-K*-based enumeration proceeds in order of a provable lower bound $E^{\ominus }$ on the full-minimized energy of a conformation. By minimizing the enumerated conformations, A*-K* algorithms tighten the upper and lower bounds on the partition function.

In practice, A*-K* algorithms have been shown to run in time sublinear in the number of conformations (Lilien et al., 2005). However, in their focus on returning the lowest energy conformations, these algorithms can tightly bound the energy of a large number of low-energy conformations while still achieving only a loose energy lower bound on the unenumerated conformations, and thus the overall partition function upper bound. In the worst case, A*-K* algorithms must enumerate a large number of conformations to compute an ɛ-approximate partition function. This issue is especially common when a design problem contains many low-energy conformations with similar energies. Furthermore, when the energy lower bounds are loose, the difference between the partition function upper and lower bounds can remain large, even after enumerating and minimizing a large number of conformations. As a result, A*-K* algorithms can be trapped in loosely bounded low-energy wells, enumerating and minimizing a combinatorial number of low-energy conformations without efficiently tightening the partition function bounds. To overcome the limitations of A*-K*-based methods, we introduce two concepts: MAE and RK*, both of which exploit the correlation between protein structure and energy to efficiently bound a combinatorial number of conformations

3. Algorithm

3.1. Recursive K*: enumerating in order of Z-uncertainty

It may at first seem counter-intuitive to tightly bound the partition function of a protein conformation space without computing the energies of any one conformation. Indeed, previous provable algorithms have efficiently approximated the partition function by computing a gap-free list of the lowest energy conformations (Lilien et al., 2005; Georgiev et al., 2008b; Roberts et al., 2012; Ojewole et al., 2018). The key insight is that structurally similar conformations are often energetically similar: although a set of low-energy conformations may constitute the vast majority of the partition function, these conformations may in fact be both structurally and energetically similar (Fig. 2A). Therefore, computing one upper and one lower bound on a set of similar conformations can efficiently bound the partition function contribution of the entire set. More formally, when the energy upper and lower bounds on a set C of structurally similar conformations are very close, the statistical weight of the set may be tightly approximated by simply scaling the upper and lower bounds by |C|. The following definitions of these new bounds are sufficient for the theorems provided in the main article—the precise definitions involve some subtleties, which are deferred to Section A of the Supplementary Information in Jou et al. (2019). For a set of conformations C that all share the partial conformation c′, we can define partition function upper and lower bounds as follows:

$$U\left(c\prime \right)=exp\left(-E^{\ominus }\left(c\prime \right)∕RT\right)\tau \left(c\prime \right),$$ (2)

$$L\left(c\prime \right)=exp\left(-E^{\oplus }\left(c\prime \right)∕RT\right)\tau \left(c\prime \right),$$ (3)

where $E^{\ominus }$ and $E^{\oplus }$ are lower and upper energy bounds on the best and worst energies of any conformation in C, respectively, and $\tau \left(c\prime \right)=\left|C\right|$.

Fundamentally, computing K* scores for a sequence can be formulated as computing energy upper and lower bounds on the conformation spaces (one for each state, e.g., bound and unbound) to reduce the difference between partition function upper and lower bounds. We refer to this difference as Z-uncertainty. To directly explore the conformation space in order of Z-uncertainty, RK* calculates the Z-uncertainty of a full or partial conformation c by computing the difference between the upper and lower bounds on its partition function contribution:

$$\gamma \left(c\right)=U\left(c\right)-L\left(c\right).$$ (4)

In effect, RK* divides the conformation space into smaller subspaces along the allowed rotamers at a residue, and bounds regions of the conformation space rather than tightly bounding the next best unenumerated conformation. By using γ(c) to explore the conformation space in order of Z-uncertainty, RK* approximates the partition function by branching and bounding the most loosely bounded regions first, rather than enumerating the next-lowest energy conformation A*-K* does.

We now give a theorem that shows γ(c) never underestimates the Z-uncertainty.

Theorem 1. Given a set C of all conformations containing a partial conformation c′, $\gamma \left(c\prime \right)\ge \gamma \left(c\right)$ for all $c\in C$.

We can further show that, when the energy lower and upper bounds on all conformations are tight (e.g., when using a pairwise-decomposable energy function for a rigid-rotamer, rigid-backbone design), the number of nodes expanded by RK* is optimal.

Theorem 2. Let T be a conformation tree where each conformation in the conformation space corresponds to a leaf node in T. For any given upper bounding function $U\left(c\prime \right)$ and lower bounding function $L\left(c\prime \right)$ over T, RK* expands the minimum number of nodes required to compute a provable ɛ-approximation of the partition function Z using those bounding functions.

For details on these bounds and the full proofs of Theorems 1 and 2, see Section A of the Supplementary Information in Jou et al. (2019).

Figure 2C and D illustrate this strategy, showing how RK* can use lower bounds on partial conformations (shown as colored step curves) to efficiently and incrementally bound regions of the energy landscape (black curve). For clarity, the figure omits upper bounds, but the same strategy can be applied. MARK* computes one upper bound and one lower bound on a combinatorial number of energetically similar conformations that contain the same partial conformation c′, whereas in the worst case A*-K* must enumerate all $q^{n-\left|c\prime \right|}$ conformations, where |c′| is the number of residues whose sidechain conformations are assigned by c′.

3.2. Minimization-Aware Enumeration: tightening loose bounds during enumeration

MAE exploits the conformational similarity between loosely-bounded conformations to tighten loosely-bounded pairwise-minimized lower bounds as they are encountered during conformation enumeration. Upon encountering a loosely-bounded pair, a tighter bound is computed by minimizing the pair in the presence of a third witness residue (Fig. 2E). For a pairwise-decomposable energy function, a loosely-bounded residue pair is only overly optimistic when the presence of the other flexible residues changes the postminimization conformation and energy of that pair. As has been shown previously, these higher-order interactions are often represented with high accuracy by simply modeling three-residue interactions as well, as is done by the local unpruned tuple expansion (LUTE; Hallen et al., 2017) algorithm. Indeed, the HOT/PartCR (Roberts and Donald, 2015) algorithm has identified both overly flexible residues whose pairwise-minimized conformation varies widely depending on the conformation of nearby residues, and higher-order clashing tuples whose pairwise-minimized conformation is clash free, but cannot be achieved when all residues in the tuple are minimized together. Although these algorithms both successfully tighten pairwise-minimized lower bounds, both are effectively preprocessing algorithms. HOT/PartCR changes the conformation space each iteration, repeatedly restarting A* search, whereas LUTE is run before A*-K* enumeration.

In effect, both HOT/PartCR and LUTE must be run to satisfactory energy bound tightness before any approximation of the partition function can be computed. MAE instead computes LUTE-like energy corrections when a conformation with a loose lower bound is encountered, and applies all computed corrections to unexplored regions of the conformation space. Notably, MAE combines LUTE-like corrections with HOT/PartCR-like lowest lower bound-first tightening, thus correcting only loosely bounded conformations that also share rotamer assignments with other conformations with low lower bounds. Unlike either algorithm, MAE can then incorporate these corrections into its partition function computation without restarting A* search: that is, it corrects the energy of a combinatorial number of conformations online. Thus, MAE provides an efficient way to tighten conformational lower bounds during partition function approximation, further reducing computational cost.

3.3. Minimization-Aware Recursive K*

In combination, the improvements of MAE and RK* are further enhanced. RK* not only prioritizes low-entropy regions of the conformation space, it is able to also weigh the potential benefits of full minimization versus branching and bounding. MAE converts the tighter bounds on each full minimization into tighter bounds on a region of the conformation space (i.e., a combinatorial number of conformations). Thus, MARK* chooses the most effective of both possible bound-tightening strategies: recursively bounding one region of the conformation space or minimizing another. In doing so, MARK* distinguishes itself from the GMEC-first, A*-K*-based previous state of the art: rather than enumerating or minimizing one conformation at a time, it bounds and minimizes regions of the conformation space. For a full description of the algorithm, see Section A of the Supplementary Information in Jou et al. (2019).

4. Computational Experiments

We implemented MARK* in our laboratory's open source osprey (Hallen et al., 2018) protein design package and compared our algorithm with the previous state of the art, iMinDEE-A*-K*. To do so, we first measured performance of the BBK* (Ojewole et al., 2018) algorithm with either iMinDEE-A*-K* (A*-BBK*) or MARK* (MARK*-BBK*) as its partition function approximation subroutine. Using A*-BBK* and MARK*-BBK*, we computed the five best binding sequences for 200 different protein design problems from 38 different protein–ligand complexes used in Ojewole et al. (2018). This was a head-to-head comparison: for both A*-BBK* and MARK*-BBK*, we measured performance using the BBK* implementation from Hallen et al. (2018). The size of the resulting design problems ranged from 18 to 400 sequences, and the number of conformations over all sequences (which is the total size of a design problem searched by BBK*) ranged from 1.62 × 10³ to 3.26 × 10¹⁷ conformations.

In all cases, we modeled continuous sidechain flexibility using continuous rotamers (Gainza et al., 2012; Roberts and Donald, 2015). As in Georgiev et al. (2008b), Gainza et al. (2012), and Ojewole et al. (2018), rotamers from the Penultimate Rotamer Library (Lovell et al., 2000) were allowed to minimize to any conformation ±9° of their modal χ-angles (18° of dihedral angle flexibility). Next, to investigate the comparative advantage of RK* over A*-K*, we performed additional computational experiments designed to deconvolve the challenge of minimizing conformations from the challenge of exploring the conformation space. We computed the wildtype K* scores for 344 rigid rotamers, rigid backbone design problems, created from 38 protein structures used in Ojewole et al. (2018). For each rigid design problem we selected up to 29 residues at a protein–protein interface to be flexible. The size of the resulting design problems ranged from 3.46 × 10³ to 6.76 × 10²⁵ conformations.

For all design problems, each algorithm computed ɛ-approximate bounds to an accuracy of ɛ < 0.683 (as was derived in Ojewole et al., 2018) or was terminated after 7 days for the continuous design problems and 6 days for the rigid design problems. All continuous designs were run on 40–48 core Intel Xeon nodes with up to 200 GB of memory, and rigid designs were run on the same machines with 60 GB of memory. A detailed description of the 544 total protein design problems, the 38 protein–ligand systems they are based on, and our continuous and rigid sidechain flexibility experimental protocols is given in Section B of the Supplementary Information in Jou et al. (2019).

5. Results

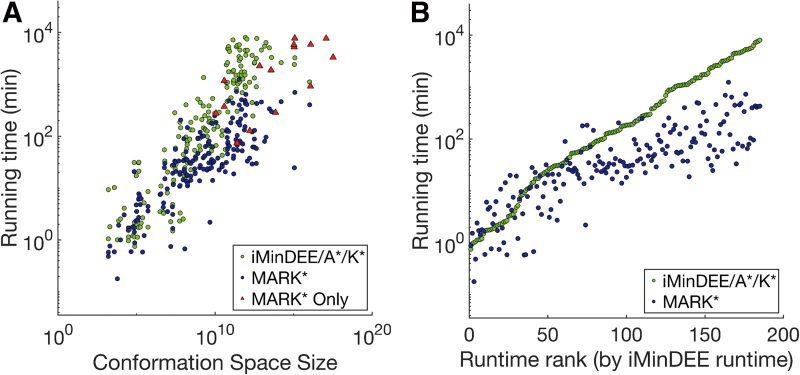
We first compared overall runtime and demonstrated that, for large designs, MARK*-BBK* completed designs faster than A*-BBK* (Fig. 3A). Notably, MARK*-BBK* completes designs that were previously too large or memory intensive for the previous state of the art. Out of 200 total designs, iMinDEE-A*-K* computed an ɛ-approximation to the partition function within 7 days for only 185. For 10 design problems, iMinDEE-A*-K* ran for more than 7 days and was terminated, and for 5 other cases iMinDEE-A*-K* ran out of 200 GB of memory. In particular, iMinDEE-A*-K* was unable to complete any of the largest designs that contained more than 10¹⁷ conformations. In contrast, MARK* provably returned the 5 best sequences for all 200 in under 6 days, including the 15 for which iMinDEE-A*-K* could not (Fig. 3A). The largest design, a 17-residue design of a llama antibody in complex with the C. botulinum neurotoxin serotype A catalytic domain (PDB id: 3k3q), contained 3.26 × 10¹⁷ conformations, which is an order of magnitude larger than the largest design completed by iMinDEE-A*-K*. Whereas iMinDEE-A*-K* ran out of memory after 5 days, MARK* returned the five best binding sequences in 55 hours.

FIG. 3.

Speed: MARK* is up to 135 times faster than iMinDEE-A*-K*, and its speedups increase as iMinDEE-A*-K* takes longer. (A, B) Times to return the five best sequences for MARK* (blue, red) and iMinDEE-A*-K* (green) are shown. (A) Times for all 200 continuous design problems are shown, plotted against conformation space size. MARK* completes 15 challenging design problems (size larger than 10¹⁰ conformations, red triangles) that iMinDEE-A*-K* cannot. (B) Runtimes for the 185 designs completed by iMinDEE-A*-K*, sorted along the x-axis by iMinDEE-A*-K* runtime (ranks for designs given in Table 1 of the Supplementary Information in Jou et al., 2019), are shown. For all designs that required longer than 146 minutes, MARK* required less time (up to 135 times faster).

Furthermore, the advantage of MARK* over iMinDEE-A*-K* grew as designs became more complex. As shown in Figure 3A, although the performance of iMinDEE-A*-K* varied as conformation space size increased, the design problems for which iMinDEE-A*-K* performed slowly are the very designs where MARK* demonstrated the largest improvements (Fig. 3B). For design problems for which iMinDEE-A*-K* required longer than 146 minutes, MARK* required less time (completing up to 2 orders of magnitude faster) to calculate an ɛ-approximation to the K* score for the best five sequences. In one design at the binding interface between an HIV-1 capsid protein C-terminal domain in complex with a camelid V_HH (PDB id: 2xxm), the conformation space was 1.14 × 10¹² conformations, and iMinDEE-A*-K* computed provable, ɛ-approximate K* scores for the five best sequences in 4.5 × 10³ minutes. In contrast, MARK* completed in 33 minutes, 135 times faster than iMinDEE-A*-K*.

To further elucidate the improvements of MARK*, we measure the effects of RK* and MAE separately. Although, for reasons of accuracy, we recommend always using continuous flexibility, we show that the speed improvements for rigid rotamer, rigid backbone wildtype K* score computation are even more dramatic. Results from these simplified design problems suggest that design with continuous flexibility considerably increases the challenge of the design problem. In particular, MARK*, with its RK* bounding strategy, is able to efficiently bound the conformation space when the conformational energy upper and lower bounds are tight, but cannot avoid minimizing conformations with loose energy bounds.

5.1. RK* is orders of magnitude more efficient and faster than A*-K*

For the 344 rigid rotamer, wildtype-only design problems, we compared overall runtime and the number of conformations enumerated, shown in Figure 4. Notably, RK* computed the K* score for all 344 design problems, whereas A*-K* was only able to do so for 321. Of the 30 largest design problems (conformation space size of 4.5 × 10²² or more conformations), A*-K* completed only 8. In fact, A*-K* was unable to compute any K* scores for design problems containing more than 10²⁵ conformations, showing that RK* is able to complete designs larger than was possible with the previous state of the art.

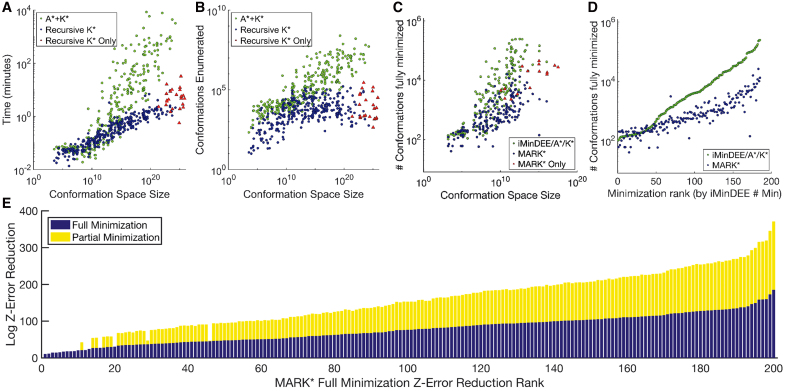
FIG. 4.

RK* and MAE both significantly improve efficiency over iMinDEE-A*-K*. (A, B) Times and conformations enumerated by MARK* (blue, red) and iMinDEE-A*-K* (green) plotted against conformation space size. When computing wildtype K* scores with rigid backbones and rigid rotamers, MARK* not only computes ɛ-approximate scores up to 3 orders of magnitude faster and 5 orders of magnitude more efficiently, it also completes design problems larger than was possible with iMinDEE-A*-K* (red triangles). (C, D) Number of conformations minimized by MARK* (blue, red) and iMinDEE-A*-K* (green) is shown, plotted against conformation space size (C) or full minimizations computed by iMinDEE-A*-K* (D, ranks for designs given in Table 1 of the Supplementary Information in Jou et al., 2019). MARK* completes 15 challenging design problems (size larger than 10¹⁰ conformations, red triangles) that iMinDEE-A*-K* cannot. MARK* minimizes up to 685-fold fewer conformations than iMinDEE-A*-K*, and is more efficient on the problems for which iMinDEE-A*-K* minimizes the most conformations. (E) Log Z-uncertainty reduction achieved by full minimization (blue) and corrections from partial minimizations (yellow) are shown as stacked bar charts. x-Axis shows design problems, sorted by Z-uncertainty reduction attributable to full minimization (ranks for designs given in Table 1 of the Supplementary Information in Jou et al., 2019). As the number of full minimizations increases, MAE efficiency increases, reducing Z-uncertainty by up to 3 orders of magnitude more than full minimization does.

For the largest design problem, a 24-residue design of the Llama V_HH-02 binder of ORF49 (PDB id: 4hem), the conformation space was 6.76 × 10²⁵ conformations, and A*-K* timed out after 6 days, whereas RK* finished in merely 4.7 minutes. Furthermore, RK* finishes up to 3 orders of magnitude faster than A*-K*. In the case of the 24-residue design of an HIV-1 capsid protein bound to a camelid V_HH (PDB id: 2xxm), A*-K* enumerated more than 162 million conformations, taking 5.4 days, whereas RK* enumerated merely 11,699 conformations in under 75 seconds, finishing 6230 times faster than the previous state of the art. RK* also enumerated far fewer conformations than A*-K*. In the case of a 29-residue design of the TRF2 TRFH domain bound to an Apollo peptide (PDB id: 3bua), A*-K* took 2.2 days to enumerate over 52 million conformations. In contrast, RK* enumerated merely 576 conformations in 2.2 minutes, and was over 90,800 times more efficient.

5.2. MAE is more efficient and effective than full minimization alone

Using MAE, MARK* tightens bounds on a potentially exponential number (up to $O\left(q^{n-3}\right)$) of conformations by performing a merely polynomial number (up to $O\left(\left(\begin{array}{c}n\\ 3\end{array}\right)q^3\right)$) of minimizations. In contrast, iMinDEE-A*-K* must, in the worst case, minimize the same (potentially exponential) number of loosely bounded conformations. In our experiments, the energy bounds were often very loose. The median energy difference between pairwise-minimized lower bounds and full-minimized energy was 4.9 kcal/mol, leading to overestimation of statistical weight by orders of magnitude for many conformations. To measure the efficiency of MAE, first we compared the number of full conformations minimized by MARK* and by iMinDEE-A*-K*. Then, to analyze the benefits of the partial minimizations performed by MAE, we measured the reduction of Z-uncertainty (Z-uncertainty reduction) from full minimizations and MAE corrections for each of the 200 continuous design problems.

Figure 4 illustrates the improvement in efficiency of MARK* over iMinDEE-A*-K*: MARK* minimizes up to 685-fold fewer full conformations. As shown in Figure 4D, MARK* minimizes fewer conformations than iMinDEE-A*-K* for all designs in which iMinDEE-A*-K* minimizes more than 1344 conformations. In addition, the bound-correcting effect of MAE increases as the conformation space grows larger and more complex. For one design of a Scribble PDZ34 domain complexed with its target peptide (PDB id: 4wyu), total Z-uncertainty reduction from full minimizations was 4.12 × 10⁹⁷, and total Z-uncertainty reduction from partial minimizations was 8.36 × 10¹⁰⁰. Thus, for every full minimization computed by MARK*, MAE achieved Z-uncertainty reduction equivalent to 2030 additional minimizations. The trend shown in Figure 4E emphasizes the increasing number of loosely bounded conformations as the conformation space grows, showing that for every conformation MARK* minimizes, it also tightens the bound on a combinatorial number of conformations.

6. Discussion

6.1. MARK* reveals components of binding thermodynamics

Previously, provable algorithms have been applied to analyze the landscape of low-energy sequences, and this analysis revealed insights into the energy function, flexibility model, and computational challenges of protein design (Simoncini et al., 2018). MARK* is able to not only bound the low-energy conformations, but also provably approximate the entire energy landscape. To test the ability of MARK* to approximate the energy landscape, we ran MARK* on a 10-residue design problem at the protein–protein interface an HIV-1 capsid protein C-terminal domain bound to a camelid V_HH and compared the partition functions of the wildtype sequence for both proteins in the bound (PDB id: 2xxm), unbound camelid V_HH (PDB id: 2xxc), and unbound HIV-1 capsid protein C-terminal domain (PDB id: 3ds2) states with continuous sidechain flexibility, in a manner similar as was done in Qi et al. (2018; Fig. 5). For these three states, we modeled bound and unbound backbones using the three separate bound and unbound structures described above. We computed a provable ɛ-approximation of $\epsilon <0.01$ for the partition functions of the bound and unbound states for both proteins, and computed the corresponding energy landscapes, where the energies of all conformations within 5 kcal/mol of the GMEC were computed exactly. Next, for each protein we computed bounds on its binding-competent ensemble, which is the ensemble consisting of all conformations that exist in the bound state, modeled with the energies of the unbound state.

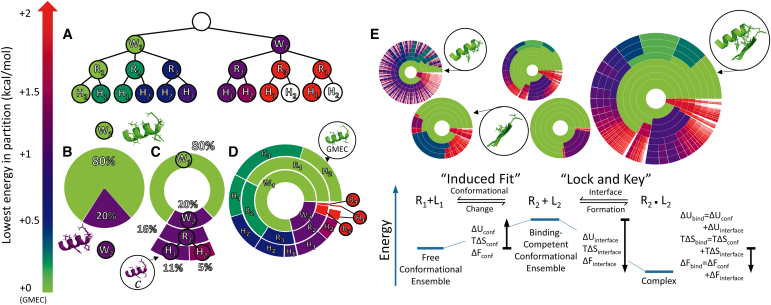
FIG. 5.

MARK* reveals components of binding thermodynamics. Upper bounds on the Boltzmann-weighted partition function for a 10-residue design at the protein–protein interface an HIV-1 capsid protein and a camelid V_HH domain are shown as colored ring charts (explained in panels A–D). For context, secondary structure near the design problem is shown when identifying conformations (colored proteins), but the full protein is not shown. (A) The conformation space can be represented as a tree, where leaf nodes correspond to full conformations, and each node c in the tree is colored by the smallest energy difference min ${min}_{c^{\ast }\in C}E\left(c^{\ast }\right)-{min}_{c\prime \in C\prime }E\left(c\prime \right)$ between the GMEC c* and the lowest energy conformation c′ contained in the subtree beneath c. (B–D) The partition function can be projected onto the tree, in the form of concentric ring charts. Each node of the tree in (A) corresponds to an arc in (D). Arc angle for each node is proportional to the partition function contribution of all nodes in a subtree (80% vs. 20% for rotamer W₁ vs. rotamer W₂). Notably, high-energy conformations are shown as white gaps in (D). (E) For HIV-1 capsid protein bound to camelid V_HH domain, the binding reaction is broken down into two parts: change in conformational ensembles of HIV-1 capsid protein and camelid V_HH from R₁ and L₁ (conformational ensembles when not bound) to R₂ and L₂ (conformational ensembles when bound), and the formation of the protein–protein interface. The order of events is arbitrary and the overall binding mechanism can be deconstructed without regard to mechanism. The left ring charts (R₁ + L₁) show the distribution of the free conformational ensembles for HIV-1 capsid protein and camelid V_HH. The middle charts (R₂ + L₂) show the change in conformational distribution, where nonbinding low-energy states have reduced statistical weight, and the right ring chart (R₂·L₂) represents the bound conformational ensemble, where the internal energy of the bound complex increases due to binding. When energetic contributions from the conformational change and interface formation reactions are added, they give the thermodynamics of the overall coupled binding reaction. As described in the text (Section 6.1), bounds on ΔU_conf, ΔS_conf, ΔU_interface, and ΔS_interface can all be estimated from the energy landscape approximation returned by MARK*.

As has been observed in Reeve et al. (2015) and Hallen et al., (2018), the correlation between K* scores and K_a is not yet quantitative, although it is good enough for ranking. In particular, for current K* computations, only a subset of biologically available structural flexibility is allowed and waters are not explicitly modeled, both of which lead to underestimated entropy. In addition, most physical effective energy functions are based on small-molecule energetics, which can overestimate van der Waals terms and thereby overestimate internal energy. Despite these input model limitations, in Hallen et al. (2018) and Reeve et al. (2015) significant changes in energy corresponded to large changes in K* score, and correlated well with experimental measurements. Therefore, in our comparisons, we expect K* scores to (1) correctly predict if one state is more favorable than another and (2) compute free energy terms that are comparable within an order of magnitude. For our analysis, scaling entropy up by a factor of 2 and internal energy down by a factor of 8 resulted in energies within the range of typical experimental measurements for 10 residues at a protein–protein interface. We report all computed energies after scaling.

Using the results from MARK*, we computed the ensemble-weighted internal energy and entropy for both binding partners in their bound and unbound states. At the computed temperature of ∼298 K, HIV-1 capsid protein undergoes a change in its conformational distribution upon binding. This entails a decrease in entropy, lowering $T\Delta S$ by 3.06 kcal/mol. $T\Delta S$ decreases by 1.74 kcal/mol for camelid V_HH as well. To compensate, the complex internal energy decreases upon binding. Whereas the unbound protein and the ligand have a combined ensemble-weighted internal energy of −8.69 kcal/mol, the internal energy of the complex is −14.0 kcal/mol, which is 5.31 kcal/mol lower than the combined internal energy of unbound HIV capsid protein and camelid V_HH. The change in Helmholtz free energy $\Delta F$ is, therefore, −0.51 kcal/mol. Importantly, the internal energy of the binding-competent HIV-1 capsid protein ensemble is only 0.044 kcal/mol less than the internal energy of its free ensemble, which agrees with the unfavorable overall increase in Helmholtz free energy of 3.01 kcal/mol between the free ensemble and the binding-competent ensemble. Similarly, the internal energy of the binding-competent camelid V_HH ensemble is 0.939 kcal/mol higher than the energy of the free ensemble, for a total increase in Helmholtz free energy of 2.68 kcal/mol. As these data show, both binding partners incur an energy penalty when assuming the binding-competent ensemble, which is overcome by favorable interactions gained upon binding.

Thus, MARK* reveals the loss of entropy, and its commensurate increase in internal energy upon binding. Figure 5 shows the change in the conformational ensemble between the free and binding-competent ensemble, followed by internal energy change upon binding. As shown in Figure 5, there are many low-energy states in the free ensemble of camelid V_HH, shown as numerous blue and purple arcs, and by the comparatively small green arc for the GMEC of the free ensemble. In contrast, both the binding-competent ensemble and the bound ensemble show significantly fewer low-energy states, and in both ensembles the GMEC comprises a much larger fraction of the corresponding partition function. Accordingly, our novel ring charts for the energy landscapes of the free, binding-competent, and bound states show visually how the bound and unbound states differ, emphasizing the novel capabilities of MARK*, and the significance of modeling more than just the lowest energy conformations when designing for affinity.

7. Conclusion

We presented a novel algorithm that not only efficiently bounds the partition function, but also computes a provably good approximation of the energy landscape, which bounds the energy of every conformation in the conformation space. MARK* is, to our knowledge, the first algorithm to do so. Previously, designers were limited to optimizing for the lowest-energy conformations for a limited number of predefined states, and could only approximate aggregate values such as internal energy or K_a. With MARK*, we showed that designers can directly compute changes to the entire energy landscape, such as conformational rearrangement upon binding. MARK* was also used in a recent analysis (Holt et al., 2019) of energy landscapes for inhibitors of cystic fibrosis (CF) transmembrane conductance regulator trafficking. Therein, MARK* not only enabled approximation of binding thermodynamics for protein–peptide interactions that are important in CF, but also revealed important structural and dynamic features of inhibitor binding. With this capability, MARK* empowers designers to evaluate sequences not by low-energy conformations, but instead by energy landscape. Thus, MARK* enables not only faster design, but also a new potential strategy to design for conformational dynamics (Reardon et al., 2014; Davey et al., 2017). We believe that MARK* will accelerate existing designs, enhance future designs, and enable a novel, dynamics-based strategy for computational structure-based protein design.

Author Disclosure Statement

The authors declare the following competing financial interest(s): B.R.D. and J.D.J. are founders of Gavilán Biodesign, Inc. All other authors declare no conflicts of interest.

Funding Information

We thank the NIH (R01-GM078031 and R01-GM118543 to BRD) for funding.