Modeling avian full annual cycle distribution and population trends with citizen science data

Abstract

Information on species’ distributions, abundances, and how they change over time is central to the study of the ecology and conservation of animal populations. This information is challenging to obtain at landscape scales across range‐wide extents for two main reasons. First, landscape‐scale processes that affect populations vary throughout the year and across species’ ranges, requiring high‐resolution, year‐round data across broad, sometimes hemispheric, spatial extents. Second, while citizen science projects can collect data at these resolutions and extents, using these data requires appropriate analysis to address known sources of bias. Here, we present an analytical framework to address these challenges and generate year‐round, range‐wide distributional information using citizen science data. To illustrate this approach, we apply the framework to Wood Thrush (Hylocichla mustelina), a long‐distance Neotropical migrant and species of conservation concern, using data from the citizen science project eBird. We estimate occurrence and abundance across a range of spatial scales throughout the annual cycle. Additionally, we generate intra‐annual estimates of the range, intra‐annual estimates of the associations between species and characteristics of the landscape, and interannual trends in abundance for breeding and non‐breeding seasons. The range‐wide population trajectories for Wood Thrush show a close correspondence between breeding and non‐breeding seasons with steep declines between 2010 and 2013 followed by shallower rates of decline from 2013 to 2016. The breeding season range‐wide population trajectory based on the independently collected and analyzed North American Breeding Bird Survey data also shows this pattern. The information provided here fills important knowledge gaps for Wood Thrush, especially during the less studied migration and non‐breeding periods. More generally, the modeling framework presented here can be used to accurately capture landscape scale intra‐ and interannual distributional dynamics for broadly distributed, highly mobile species.

Introduction

Information on the factors that shape species’ distribution and abundance constitute the foundation for much of our ecological knowledge on animal populations. To date, the study of these factors has been largely restricted to either (1) broad extent, coarse‐resolution spatial information collected during a single time of the year (Marra et al. 2015; e.g., distributions during the breeding season), or (2) small extent, fine‐resolution spatial information collected at a limited number of locations (e.g., local extinction and colonization dynamics). However, organisms are influenced by processes acting simultaneously across a range of spatial and temporal scales throughout the year (Levin 1992, Chave 2013). Thus, to understand the full range of processes affecting species, we need information on distribution and abundance both at fine spatial and temporal resolutions and across the entire spatial extent experienced by species throughout the year (Heffernan et al. 2014, Sandel 2015).

Similarly, information on interannual changes in species’ distributions and abundance constitute the foundation for conservation monitoring and management. To date, the assessment and study of population trends has largely been restricted to the analysis of highly structured monitoring surveys. For most taxonomic groups, structured surveys with the spatial coverage necessary to study trends range wide and throughout the year do not exist (Hortal et al. 2015, Chandler et al. 2017). For birds, one of the best‐surveyed taxonomical groups, there are a few broad extent monitoring programs that are able to generate continental‐scale trends in abundance and distributions (North America, Sauer and Link 2011; Europe, European Bird Census Council 2016). Even these surveys are restricted to only one stage of the annual life cycle, and these do not go far beyond existing political boundaries to cover the entire distributional range of many species of interest. Moreover, most of these surveys lack the landscape‐scale resolution (~1–25 km²) necessary to understand the effects of habitat composition and configuration useful for conservation planning (Tscharntke et al. 2012).

Recent efforts to estimate species’ distributions (Kéry et al. 2010), abundance (Johnston et al. 2015), and trends (Horns et al. 2018, Baker et al. 2019, and Meehan et al. 2019) across broad spatial extents have turned to the use of less structured survey data collected by citizen scientists. Citizen science projects have been very successful at collecting species observation data with high spatial and temporal resolution across broad extents throughout the year (Dickinson et al. 2010). However, the data gathered by these projects contain several biases due to the opportunistic approach of data collection (Hochachka et al. 2012, Bird et al. 2014, Kelling et al. 2019). There has been considerable work over the past decade developing methods to minimize the effects of these biases, including biases due to heterogeneous and imperfect observation processes (Kéry and Royle 2015, Johnston et al. 2018) and biases in the distribution of survey effort across space and time (Robinson et al. 2017, Johnston et al. 2019). There has also been work developing methods to tackle the challenges associated with estimating distributions and abundance across very large spatial extents throughout the year, including the variation in data density across broad spatial and temporal extents (Fink et al. 2013) and the spatial and temporal variation in a species’ response to landscape conditions (Fink et al. 2010, Finley 2011).

Here we build on previous work (Fink et al. 2014, Johnston et al. 2015) to develop an analytical framework designed to estimate species’ distributions, abundance, and trends at landscape‐scale spatial resolutions across continental extents and weekly temporal resolution across the full annual cycle while accounting for many of the biases inherent in citizen science data. This task required the consideration of three analytical challenges in addition to the ones outlined above. First, to capture species’ complete distributions the framework needs to be able to accurately estimate whether locations are occupied or unoccupied with high spatial resolution (2.8 and 25.2 km²) along range boundaries. This is challenging because occurrence rates are, by definition, very low in these areas. To meet this challenge, we began by extending the work of Robinson et al. (2017) to develop a novel spatiotemporal case‐control sampling procedure to increase the amount of occurrence information in these data poor areas. Then we utilized the ensemble model structure of Fink et al. 2014 to test whether individual locations were occupied or unoccupied by the species. The second challenge is to account for the strong interannual increases in eBird data volume, 20–30% per yr since 2005, when estimating trends in abundance. To do this, we balanced the per year sample size, after spatiotemporal case‐control sampling, for the training data used to estimate trends. The third challenge centers on using spatial covariates to estimate interannual trends in abundance with landscape‐scale (25.2 km²) spatial resolution from irregularly and sparsely distributed citizen science data. To address this challenge, we implemented a two‐step approach based on the ensemble model of Fink et al. (2014). The first step used a hypothesis test to exploit variability across the ensemble and identify locations where the direction of the trend was consistently estimated. Then we averaged across the ensemble to remove the intra‐ensemble variation while estimating the magnitude of the trends. To assess the performance of the trend estimation procedure, we also performed a simulation study across a wide range of spatially explicit trend scenarios coupled with a realistic data observation process and quantified false detection (type I error) and power (type II error) rates.

As a case study, we analyzed data from the global citizen science project eBird (Sullivan et al. 2014) for the long‐distance migratory songbird, Wood Thrush (Hylocichla mustelina) that breeds in eastern North America and winters largely in Mesoamerica. The Wood Thrush is a species of conservation concern, having suffered population‐wide declines over the past several decades (Sauer et al. 2017). Although recent studies (Rushing et al. 2017) have begun to address potential drivers of these declines, definitive answers are limited by the lack of comprehensive information on patterns of distribution, abundance, and trends. Due to the migratory nature of this species, full annual cycle information on distribution and abundance is critical for providing a unifying framework to integrate data on population movement and connectivity. Although we present a case study focused on a bird species, the growing need and support for citizen science programs on other taxonomical groups, e.g., sharks (Vianna et al. 2014), lichen (Casanovas et al. 2014), bats (Newson et al. 2015), and butterflies (Dennis et al. 2017), will make various aspects of this framework useful in future efforts to map and monitor species populations.

Materials

Observational data

We obtained bird observation data from the global bird monitoring project, eBird (Sullivan et al. 2014), specifically the 2016 eBird Reference Dataset (ERD2016; Fink et al. 2017). We used a subset of data in which the time, date, and location of each survey were reported and observers recorded the number of individuals of all bird species detected and identified during the survey period, resulting in a “complete checklist” of species on the survey (Sullivan et al. 2009). The checklists were restricted to those collected with the “stationary,” “traveling,” or “area search” protocols from 1 January 2004 to 31 December 2016 within the spatial extent between 180° to 30° W longitude and north of 0° latitude. Area surveys were restricted to those covering <56 km² and traveling surveys were restricted to those of ≤15 km. The resultant data set consisted of 11.7 million checklists, of which a random 10% were withheld for model validation (Appendix S1: Fig S1).

Predictor data

We incorporated three classes of predictors in the models: (1) five observation‐effort predictors to account for variation in detection rates, (2) three predictors to account for variation at different temporal scales, and (3) 79 environmental descriptors from remote‐sensing data to capture associations of birds with a variety of landscapes, elevation, and topography across the continent (Box 1). The effort predictors were (1) the duration spent searching for birds, (2) whether the observer was stationary or traveling, (3) the distance traveled during the search, (4) the number of people in the search party, and (5) the checklist calibration index, a standardized measure indexing differences in behavior among observers (Kelling et al. 2015, Johnston et al. 2018). To model variation in availability for detection, e.g., variation in behavior such as participation in the dawn chorus (Diefenbach et al. 2007), we used the observation time of the day. To capture intra‐ and interannual variation, we included the day of the year (1–366) and the year on which the search was conducted.

Box 1. Land and water cover class predictors.

Land cover	Water cover
Evergreen needleleaf forest Evergreen broadleaf forest Deciduous needleleaf forest Deciduous broadleaf forest Mixed forest Closed shrublands Open shrublands Woody savannas Savannas Grasslands Croplands Urban and built‐up Barren	Shallow ocean Ocean coastlines and lake shores Shallow inland water Deep inland water Moderate or continental ocean Deep ocean

All 19 cover classes were summarized within a 2.8 × 2.8 km (784 ha) landscape centered on each checklist location. We computed four statistics to describe the composition and configuration of each class across the landscape. Landscape composition was described as the proportion of each class in the neighborhood (PLAND). To describe the spatial configuration of each class, we computed three further statistics: LPI, an index of the largest contiguous patch; PD, an index of the patch density; and ED, an index of the edge density. Together these four metrics for each of 19 land cover categories produced 76 predictors.

The environmental descriptors included variables describing elevation, topography, and land cover. To account for the effects of elevation and topography, each checklist location was associated with elevation, eastness, and northness. These latter two topographic variables combine slope and aspect to provide a continuous measure describing geographic orientation in combination with slope at 1‐km² resolution (Amatulli et al. 2018). Each checklist was also linked to a series of covariates derived from the NASA MODIS land cover data (Friedl et al. 2010). We selected this data product for its moderately high spatial resolution, annual temporal resolution, and global coverage. We used the University of Maryland (UMD) land cover classifications (Hansen et al. 2000) and derived water cover classes from the MODIS Land Cover Type QA Science Dataset resulting in a class label for each 500‐m pixel into one of 19 classes (Box 1). To capture interannual changes in land cover, we linked checklists to the MODIS data by year from 2004 to 2013. The checklist data after 2013 were matched to the 2013 data, as MODIS data from after 2013 were unavailable at the time of analysis.

To describe the composition and configuration of the local landscapes searched by participants, we summarized all cover classes within a 2.8 × 2.8 km (784 ha) neighborhood centered on the checklist location. In each neighborhood, we computed the composition as the proportion of each class in the neighborhood (PLAND). To describe the spatial configuration of each class, we computed three further statistics using FRAGSTATS (McGarigal et al. 2012, VanDerWal et al. 2014): LPI, an index of the largest contiguous patch; PD, an index of the patch density; and ED, an index of the edge density. Together these four metrics for each of 19 land cover categories produced 76 predictors.

Analysis overview

To meet the analytical challenges of modeling eBird data, we adopted an ensemble modeling strategy based on the Adaptive Spatio‐Temporal Exploratory Model (AdaSTEM; Fink et al. 2013). AdaSTEM is a framework for analyzing large‐scale patterns with an ensemble of local regression models. For each of 100 ensemble runs, the data are independently subsampled and the study extent is partitioned using a randomly located and oriented grid. Each grid cell is a spatiotemporal block (or stixel) and an independent regression model, called a base model, is fit within each stixel.

Ensemble estimates are made by averaging across the corresponding base model estimates. Combining estimates across the ensemble controls for variability between models (Efron 2014), providing a simple way to control for overfitting while naturally adapting to non‐stationary relationships between species and their environments (Fink et al. 2010). To make ensemble predictions at a particular location and time, predictions are made from the 100 base models, each from a single ensemble partition, and each fit to an independent subsample of local data in space and time. Because data are subsampled for each base model, point‐level uncertainty estimates can be produced by examining variation in the suite of base model predictions across the ensemble. All analysis was conducted in R, version 3.4.2 (R Development Core Team 2017) and deployed using Apache Spark 2.1 (Zaharia et al. 2016).

In the following sections, we describe the AdaSTEM ensemble design, the spatiotemporal sampling procedure, and the base models trained within each stixel. Then we describe how we used the ensemble to estimate four population parameters: (1) landscape‐scale estimates of occurrence and abundance, (2) landscape‐scale estimates of the area of occurrence, (3) regional‐scale habitat use, and (4) landscape‐scale trends in abundance. Definitions of all four population parameters are presented in the sections below.

AdaSTEM ensemble design

Stixel size controls a bias–variance trade‐off (Fink et al. 2013) and must strike a balance between stixels that are large enough to achieve sufficient sample sizes to fit good base models (i.e., limiting variance of estimates), and small enough to assume stationarity (controlling bias). Under the AdaSTEM framework, we set all stixels’ temporal width to 30.5 d. The spatial dimensions were adaptively sized to generate smaller stixels in regions with higher data density, using QuadTrees (Samet 1984), a recursive partitioning algorithm. This partitioning process was constrained not to split stixels smaller than 5° longitude × 5° latitude, and was forced to split stixels larger than 25° longitude × 25° latitude. The AdaSTEM ensemble consisted of 100 randomly located and oriented grids of overlapping spatiotemporal stixels generated in this way. See Appendix S1:Fig. S2 to see two realizations of the AdaSTEM spatial partition and see Appendix S1 for additional information about the specification of the ensemble design.

Spatiotemporal sampling

Within each stixel, a spatial case‐control sampling strategy was used to address the challenges of highly imbalanced data and site selection bias. Imbalanced data arise when there are a very small number of species detections and a very large number of non‐detections. This is a modeling concern because binary regression methods (like the first component of the zero‐inflated boosted regression tree base model, described in Base models), become overwhelmed by the non‐detections and perform poorly (King and Zeng 2001, Robinson et al. 2017). Case‐control sampling treats detection and non‐detection cases separately, resampling each case to improve spatial and temporal balance in the data and model performance (Breslow 1996, Fithian and Hastie 2014). See Appendix S2 for additional information about the spatiotemporal sampling procedure.

For estimating interannual trends, we also balanced the per year sample size, after spatiotemporal case‐control sampling, to control for potential bias associated with the strong interannual increases in eBird data volume, 20–30% per yr since 2005. Years with fewer data than the average were over‐sampled (i.e., randomly sampled with replacement) and years with more data than the average were under‐sampled (i.e., randomly sampled without replacement). This sampling strategy resulted in training data sets with the same total sample size and equal per year sample sizes for each stixel.

Base models

Within each stixel, relationships between the species response and the predictor variables were assumed to be stationary. To estimate occurrence and abundance from the large predictor set while accounting for high numbers of zero counts, we used a two‐step zero‐inflated boosted regression tree (ZI‐BRT) model (Johnston et al. 2015, Ridgeway 2017). In the first step, a Bernoulli response BRT was trained to predict the probability of occurrence and in the second step a Poisson response BRT was trained to predict expected counts conditional on occurrence. To facilitate the estimation of the binary occurrence state from the predicted occurrence probabilities, we also recorded the threshold that maximized the Kappa statistic (Cohen 1960). All predictors were included in both BRTs. The inclusion of the five observation‐effort predictors allowed the models to account for several important sources of variation in detectability. Similarly, including the day of the year and the year predictors allowed the models to make daily resolution estimates for specified years. See Appendix S3 for additional information about base model boosted regression tree parameters.

A base model for a stixel was trained only when there were at least 50 checklists (prior to oversampling) from the spatially balanced case‐control sampling procedure and at least 10 species detections (prior to oversampling). To guard against the effects of replicate surveys at popular birding locations, only one detection per day is considered from each location. Stixels that did not meet these minimum sample size requirements were dropped without replacement from the ensemble, leading to fewer overlapping base model estimates, and higher variance among ensemble average estimates in regions with low data density or low species detection rates.

To estimate interannual trends in abundance, we trained a second ZI‐BRT base model, identical to the one above except for two important modifications. First, to increase species’ encounter rates and strengthen trend signals we aggregated the training data across a 25.2 × 25.2 km grid, separately for each year. The aggregation summed the counts of species seen, the durations spent searching for birds, the distances traveled during the search, the numbers of people in the search party, and the checklist calibration values (weighted by search duration) across all checklists within each grid cell. All other covariates were averaged across all checklists within each grid cell. Second, to control for the interannual increases in eBird data volume, we sampled the aggregated training data to have the same number of surveys each year. See Spatiotemporal sampling and Appendix S2 in Supporting Information for more information about the sampling procedure, and the rationale for using a different procedure from that used for modeling distribution and relative abundance.

Estimating occurrence and abundance

Within each stixel, we used the binomial BRT submodel to predict the expected occurrence rate. To estimate the expected abundance we computed the product of the predicted occurrence and the predicted abundance conditional on occurrence. To control for variation in detection rates, the search effort predictors (search duration, protocol, search length, number of observers, and checklist calibration index) were held constant for the predictions. Additionally, to maximize the species’ availability for detection within each stixel, we calculated the expected values for the time of day value that maximized the species’ probability of being reporting, based on the partial dependence estimate for time of day (see Regional habitat associations for information on partial dependence estimates.)

The resulting quantity used to estimate occurrence was defined as the probability that an expert eBird participant (top 1% of checklist calibration indices) would detect the species on a search at the optimal time of day for detection while traveling 1 km on the given day at the given location. Abundance was estimated as the expected count of individuals of the species on the same standardized checklist. Although this approach accounts for variation in detection rates, it does not directly estimate the absolute detection probability. For this reason, our estimates of occurrence can only be considered as a relative measure of species occupancy. Similarly, the expected count of individuals of the species on the same standardized checklist is a measure of relative abundance, an index of the total count of the individuals of the species present in the search area. Note that this measure of abundance is equivalent in many respects to the relative abundance estimates used to estimate trends with the North American Breeding Bird Survey (BBS; Sauer and Link 2011, Sauer et al. 2017) and with the North American Christmas Bird Count (Meehan et al. 2019). To match the common terminology in the literature, we will also refer to this as an estimate of relative abundance.

The ensemble estimates of occurrence and relative abundance were calculated by averaging across all the base model estimates for a given location and date. We generated two sets of ensemble estimates for relative abundance, one designed for high‐resolution, year‐round, population mapping and one designed as the basis of the seasonal trend estimates. For the high‐resolution, year‐round, population mapping, we estimated occurrence and relative abundance for a single day at the center of each week for all 52 weeks of 2016 for each 2.8 × 2.8 km grid cell across the study area. For the seasonal trend estimates, we generated weekly estimates of relative abundance for each week within the specified seasons, separately for each year 2007–2016, within each 25.2 × 25.2 km grid cell across the study area.

Uncertainty was estimated as the lower 10th and upper 90th percentiles based on the variation in the base model estimates. Ensemble average estimates were not made in areas of low data density, where base model minimum sample size requirements were not met. See Appendix S4 for information about subsampling procedures used to estimate uncertainty of the occurrence and abundance estimates.

Estimating area of occurrence

To estimate the area of occurrence (AOO) we evaluated whether grid cells should be considered occupied vs. unoccupied, what we refer to as the binary un/occupied state, for each week and prediction location using both the 2.8‐ and 25.2‐km spatial grids, described in Estimating occurrence and abundance. The resulting set of AOO values provides landscape‐scale information about the distributional range of a species and can be used to generate range boundaries throughout the year.

At the base model level, each location was considered to be occupied if the predicted occurrence probability was above the Kappa‐maximized threshold for that base model. Aggregating across the ensemble, a location was considered to be occupied if at least one out of seven base models predicted it was occupied. This is equivalent to an expert observer detecting the species at least once during seven consecutive days of standardized surveys, taking account of the variation across base models. See Appendix S5 in Supporting Information for further information about the methods used to estimate AOO.

Estimating trends

To estimate the average annual rate of change in a species’ relative abundance with landscape‐scale spatial resolution (25.2 km × 25.2 km) we use a two‐step approach that exploits the ensemble structure of AdaSTEM. In the first step, a hypothesis‐testing approach uses the variation across the ensemble to filter out regions where the estimated direction of the trend was inconsistent. We call this step the signal filter. Then we averaged across the ensemble to remove the intra‐ensemble variation while generating trend estimates.

The signal filter began by generating the base model estimates of the slope of the log‐linear regression of relative abundance on year and then testing across the ensemble to determine if the slopes were increasing or decreasing. The ensemble averaged estimate of the trend was computed as the percent per year change in population size. This trend was estimated as the slope from the log‐linear regression of the ensemble average estimates of relative abundance, as described in Estimating occurrence and abundance.

Finally, we estimated the range‐wide trend for the breeding and non‐breading seasons computed as the abundance‐weighted average of the 25.2‐km estimates across the species’ range for each season. We compared the breeding season estimate to the independently estimated range‐wide breeding season trend based on the North American Breeding Bird Survey data (Sauer et al. 2017; data available online).¹ See Appendix S6 in Supporting Information for further information about the methods used to estimate local trends.

Estimating regional habitat associations

For each base model, we quantified the strength and direction of association for each cover class predictor. Predictor importance (PI) statistics measured the strength of the overall contribution of individual predictors as the change in predictive performance between the model that includes all predictors and the same model with permuted values of the given predictor (Breiman 2001). PI statistics capture both positive and negative effects arising from both additive and interacting model components. Partial dependence (PD) statistics described the functional form of the additive association for each individual cover class predictor by averaging out the effects of all other predictors (Hastie et al. 2009). To measure the direction of association, we estimated the slope of each PD estimate using simple linear regression.

To examine how species’ habitat use varied among regions and seasons, we computed two seasonal trajectories: one describing the strength of the cover class associations based on the PI statistics and one describing the direction of the cover class associations based on the slope of the PD estimates. Given the region and the set of predictors to compare, we standardized the PI statistics to sum to 1 across the predictor set for each base model within the specified region. Then, loess smoothers (Cleveland et al. 1992) estimated the trajectories of the strength of the cover class associations measured as the relative predictor importance throughout the year for each predictor. Similarly, a loess smoother was used to estimate the direction of the cover class associations measured as the proportion of increasing PD estimates, based on the slope of the estimates, throughout the year for each predictor. We considered predictors with proportions of increasing cover class associations >70% across base models to have consistent positive associations with species abundance. Similarly, we considered predictors with proportions of increasing cover class associations <30% to have consistent negative associations. Predictors with inconsistent directions, those between 30% and 70%, were excluded from summaries.

To quantify changes in habitat use throughout the annual cycle, we made weekly estimates of the association between Wood Thrush occurrence and the amount of each habitat class in the local landscape. For each week, we summarized the associations across the population core area, the 5° longitude × 5° latitude area located at the abundance‐weighted population center for that week. For each cover class, values were combined for both PLAND and LPI predictors to describe the relative strength and direction of the association. Larger absolute values indicate stronger associations. Classes with inconsistent direction of association were removed, resulting in total weekly relative importance that sums to <1.

Model validation

To assess the quality of the ensemble estimates of AOO, occurrence, and abundance, we validated the model predictions at 2.8 km × 2.8 km × 1 week resolution using independent validation data. Evaluations were performed separately for each week of the year to control for seasonal variation in occurrence and abundance of the species’ population.

To help control for the uneven spatial distribution of the validation data within each week, we used a Monte Carlo design of 25 spatially balanced samples to evaluate all predictive performance statistics (Fink et al. 2010, Roberts et al. 2017).

To quantify the predictive performance for the AOO we used the area under the curve (AUC) and Kappa (Cohen 1960) statistics to describe the models’ ability to classify occupied vs. unoccupied sites (Freeman and Moisen 2008). To quantify the quality of the occurrence estimate as a rate within areas estimated by the AOO to be occupied, we also used AUC and Kappa statistics. AUC measures a model's ability to discriminate between positive and negative observations (Fielding and Bell 1997) as the probability that the model will rank a randomly chosen positive observation higher than a randomly chosen negative one. The AUC statistic ranges from 0 to 1.0. Larger values indicate better discrimination, with 1.0 indicating perfect discrimination and 0.5 or below indicating no better than random discrimination. Cohen's Kappa statistic (Cohen 1960) was designed to measure classification performance accounting for the background prevalence. The Kappa statistics ranges from −1.0 to 1.0. Larger values indicating better classification performance, with 1.0 indicating perfect classification and 0 or below indicating no better than random discrimination. Guidelines for interpreting the magnitude of the Kappa statistic have appeared in the literature (Landis and Koch 1977, McHugh 2012) though they are subjective and tend to be geared toward specific application domains. Cohen's original article suggested that values 0.01–0.20 be interpreted as slight agreement, 0.21–0.40 as fair, 0.41–0.60 as moderate, 0.61–0.80 as substantial, and 0.81–1.00 as almost perfect agreement. When interpreting AUC and Kappa, it is useful to keep in mind that imperfect detection of species among the validation data will produce misclassifications even when estimates of AOO and occurrence rates are perfect. Thus, the maximum attainable AUC and Kappa statistics are always <1.0. Additionally, both AUC (Lobo et al. 2008) and Kappa (Sim and Wright 2005) are known to increase with decreasing prevalence rates among the validation data. For these reasons, AUC and Kappa are best used as relative measures of predictive performance useful for comparing outputs from different analyses.

To quantify the quality of the abundance estimates we computed Spearman's rank correlation (SRC) and the percent Poisson deviance explained (P‐DE). SRC measures how well the abundance estimates rank the observed abundances. The SRC ranges from −1.0 to 1.0 with values above zero indicating a positive association between estimated and observed abundances with a value of 1.0 indicating perfect ranking. The P‐DE measures the correspondence between the magnitude of the estimated counts and observed counts relative to an estimate of the sample mean. The P‐DE ranges between −100% and 100% with positive values indicating that the abundance estimates explain more variation in the observed counts than using a constant estimate equal to the sample mean. In practice, imperfect detection will decrease the maximum attainable values of the SRC and P‐DE statistics. Finally, because the sample mean for the P‐DE statistic is computed based on the validation data, P‐DE values will be conservative measures of predictive performance.

Trend simulations

To validate the methods used to estimate the trends, we conducted a simulation analysis to assess performance across a wide range of trend scenarios coupled with a realistic data observation process. Qualitatively, we wanted to understand how performance varies with the strength of the trend and if this analytical approach can detect spatial patterns among the landscape‐scale trend estimates.

By comparing estimated trends to the simulated truth, we quantified false detection (type I error) and power (type II error) rates at the 25.2 km × 25.2 km resolution when identifying locations with increasing and decreasing trends. To test how power varied with trend strength, simulations were constructed with increasing and decreasing trends across a range of magnitudes. To test if the method could detect spatial patterns in local trends both spatially constant and spatially varying trends were constructed. Spatially varying trends were constructed so that trend direction and magnitude varied as a function of local population density, giving rise to different trend directions at the core and edges of population distributions. Flat population trends were also included in the design to assess false‐positive rates. Altogether, the study consisted of 22 combinations of spatial pattern and magnitude.

For each simulation, we evaluated the power and error rate of the signal filter along with the correspondence between the magnitude of known and estimated trends. The proportion of false detections was calculated as the number of cells within the 25‐km grid for which trends were erroneously detected as a proportion of the total number of cells where trends were detected. The power was calculated as the number of cells within the 25‐km grid for which a trend was correctly identified as a proportion of the total number of cells known to have non‐zero trends across the entire range. To understand how power varied as a function of the local trend strength, power was also evaluated across all grid cells with known trends with a minimum magnitude, ranging from 0 to 15% per year. Where the signal filter detected local trends, the coefficient of determination (R ²) was computed to describe the proportion of variation in the known magnitudes explained by the estimates.

Two simulation studies were conducted for the Wood Thrush over the 2007–2016 study period, one for the breeding season (30 May–3 July) across the species’ range in the northeastern North America and the second for the non‐breeding season (1 December–28 February) across the species’ range in Mesoamerica. The information generated from the simulation study provides insight about the robustness of the trend analysis. See Appendix S7 for further information about the trend simulation study design.

Results

Weekly area of occurrence, occurrence, and relative abundance

Using the Wood Thrush as exemplar analysis, we generated estimates of AOO, occurrence and relative abundance at a spatiotemporal resolution of 2.8 km × 2.8 km × 1 week (Fig. 1). Across the study extent, the AOO estimates show seasonal changes in the range size and shape while the abundance estimates capture regional and seasonal variation in population structure within the species’ range. The breeding season range fills in the eastern deciduous forests east of the Great Plains with highest population concentrations in the Appalachian Mountains (Fig. 1A). During autumn migration, the population concentrates in the southern part of the Appalachian Mountains (Fig. 1B) before crossing the Gulf of Mexico into Central America. The non‐breeding distribution (Fig. 1C) is concentrated in the Yucatán Peninsula, with lower concentrations extending north into Veracruz and south to Costa Rica and Panama. During the spring migration (Fig. 1D), Wood Thrush crosses the Gulf of Mexico, concentrating on the Gulf Coast and again in the southern part of the Appalachian Mountains.

Figure 1.

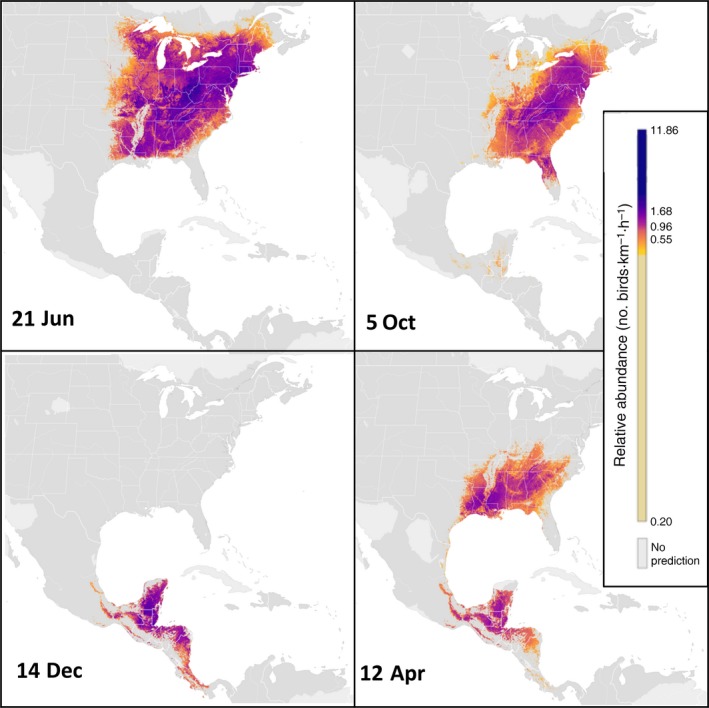
Wood Thrush estimates of area of occurrence (AOO) and relative abundance at 2.8 × 2.8 km resolution during (A) breeding (20 June), (B) autumn migration (3 October), (C) non‐breeding (12 December), and (D) spring migration (28 March) seasons. Positive abundance is only shown in areas estimated to be occupied and the AOO is depicted as the boundary between pixels with and without color. Darker colors indicate areas occupied with higher abundance. Relative abundance was measured as the expected count of the species on a standardized 1‐km survey conducted at the optimal time of day for detection. Note that detectability varies seasonally, complicating comparisons of population size between seasons.

Overall, all of the predictive performance statistics for AOO, occurrence, and relative abundance were above baseline levels indicating the model's ability to explain spatial variation in these 2.8‐km landscape‐scale quantities throughout the annual cycle at a weekly resolution. Variation in all the predictive performance statistics was highest during the non‐breeding season for all metrics, reflecting the challenges of estimating AOO, occurrence, and relative abundance during the spring and autumn migrations when the Wood Thrush population is moving, as well as the lower data densities in Mesoamerica.

To assess the accuracy of estimates at 2.8 km, we calculated range‐wide validation estimates based on spatially balanced samples of independent eBird observations for each week of the year. AOO weekly median AUC scores were between 0.73 and 0.91 with mean 0.82 (Fig. 2A) and AOO weekly median Kappa scores were between 0.26 and 0.62 with mean 0.40 (Fig. 2B) Because these statistics were calculated across full study extent, they can be used to assess and compare the quality of the weekly range boundaries at a 2.8‐km spatial resolution. Occurrence weekly median AUC scores were between 0.57 and 0.91 with mean 0.72 (Fig. 2C) and occurrence weekly median Kappa scores were between 0 and 0.61 with mean 0.28 (Fig. 2D). Because the assessment of the occurrence estimates is limited to those areas estimated to be occupied, the validation data used for the occurrence estimates are better balanced than validation data used for the AOO estimates. This difference results in AUC and Kappa statistics that tend to be lower for the occurrence estimates compared to the AOO estimates. These weekly occurrence AUC scores are much higher than those reported in Fink et al. (2010) as part of the continent‐scale eBird analyses of Tree Swallow and the Northern Cardinal, two easily detected and identified species. This improvement in AUC statistics reflects increases in eBird data volume and improvements in predictor data and modeling methodology.

Figure 2.

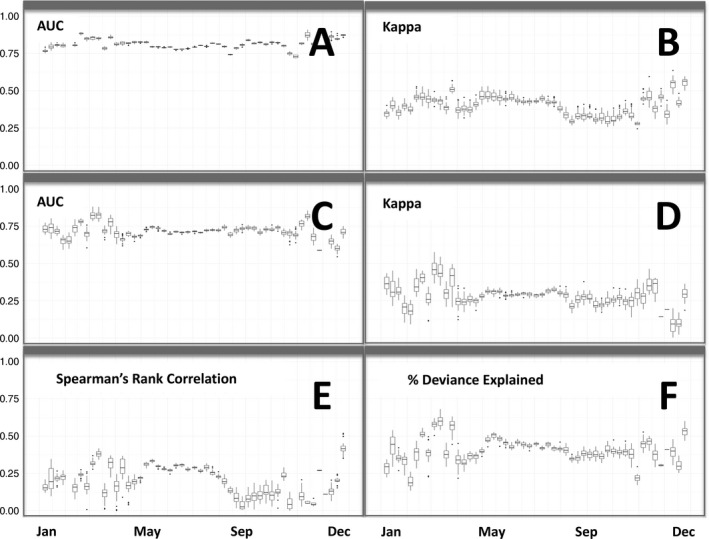
Box plots of range‐wide weekly predictive performance for area of occurrence, occurrence, and relative abundance estimates across 25 Monte Carlo samples of spatially balanced validation data. (A) AUC and (B) Kappa scores for area of occurrence estimates. (C) AUC and (D) Kappa scores for occurrence estimates. (E) Spearman's rank correlation and (F) percent of deviance explained scores for relative abundance estimates.

Relative abundance weekly median P‐DE scores were between 0 and 0.52 with mean 0.19 (Fig. 2E) and relative abundance weekly median SRC scores were between 0.16 and 0.70 with mean 0.41 (Fig. 2F). The positive weekly median P‐DE scores indicate that the model reliably captures landscape‐scale spatial structure in weekly abundance patterns. The weekly SRC statistics are lower than the monthly SRC statistics reported as part of the state‐wide eBird analysis of shorebirds (Johnston et al. 2015). This is likely due to the fact that Wood Thrush are not typically encountered in large flocks, resulting in lower average counts, and, consequently, a more challenging ranking task.

Seasonal habitat use

The breeding season is characterized by the strong positive association with deciduous broadleaf forest and the non‐breeding season is characterized by the strong positive association with broadleaf evergreen forest (Fig. 3). During spring and autumn migrations, the population is associated with a wider variety of cover classes, and a more even distribution of associations, both positive and negative. This includes a notable positive association with the urban developed class.

Figure 3.

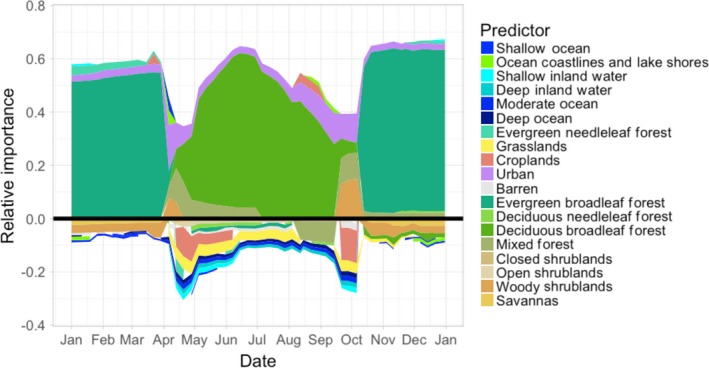
The weekly relative importance for the amount of each land and water cover class for the core Wood Thrush population. Positive importance indicates class use and negative importance indicates class non‐use. The strength of the association with each class is proportional to the width of the class color. Classes with inconsistent direction of association were removed, resulting in total weekly relative importance that sums to <1.

Breeding season trends

The largest population changes have occurred across the core of the population, the large area of high abundance in Eastern Kentucky, West Virginia, and southern Ohio (Fig. 4A). Declines of 1–3.5% per yr were estimated in most locations across this region. However, declines have not occurred range‐wide. Population increases occurred in regions of low abundance in the southeastern part of the range and in a small region in Wisconsin. Appendix S6: Fig. S1 shows trend maps of the location‐wise upper 2.5% and lower 97.5% confidence limits from the subsampling analysis. These maps show declines with similar spatial patterns and magnitudes to those in Fig. 4A.

Figure 4.

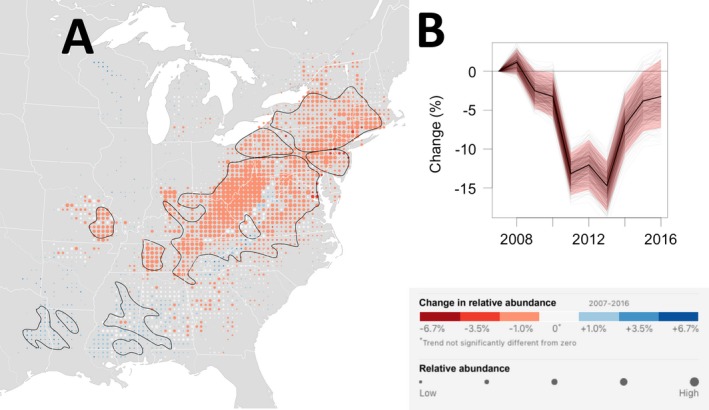
Wood Thrush breeding trend map and range‐wide population trajectory. (A) The breeding season (30 May–3 July) average annual percent change in relative abundance from 2007 to 2016. Increases in population size are shown in blue and decreases are shown in red. Darker colors indicate stronger trends. Each dot on the map represents a 25 × 25 km area. To help visualize the relative change in population size at each location, the size of each dot has been scaled according to the average abundance at that location during the 10‐yr study period. Within the regions delineated by the black contour line, the expected false discovery rate (type I error) is up to 5% when identifying locations with increasing and decreasing trends. Outside the black contours, the direction of population change is less certain. The breeding season power analysis suggests that regions within the black contours contain 60% of all locations across the breeding range with non‐zero trends and contain 80% of all trends with trend magnitudes of 6.7% per yr or more (approximately equivalent to halving or doubling of the population across 10 yr). (B) The trajectory shows the range‐wide change in population size standardized as the percent change since 2007. The dark black line is the conditional mean estimate, the red polygon are the 95% confidence limits, and the light gray trajectories show the 500 replicate estimates.

The range‐wide, abundance‐weighted trend estimate for the breeding season was −1.48% per yr, with a 95% confidence interval between −1.89% and −1.01% per yr. The range‐wide population trajectory, standardized as the percent change since 2007 (Fig. 4B), shows the steepest declines in population size (−10% to −15%) between 2010 and 2013 followed by shallower rates of decline in the population size from 2013 to 2016. The BBS range‐wide trend estimate for Wood Thrush from 2007 to 2016 has a posterior mean of −1.26% per yr with 95% credible interval between −1.7259 and −0.7980. Fig. 5 shows the range‐wide population trajectories, standardized as the percent change since 2007, for the eBird and BBS estimates.

Figure 5.

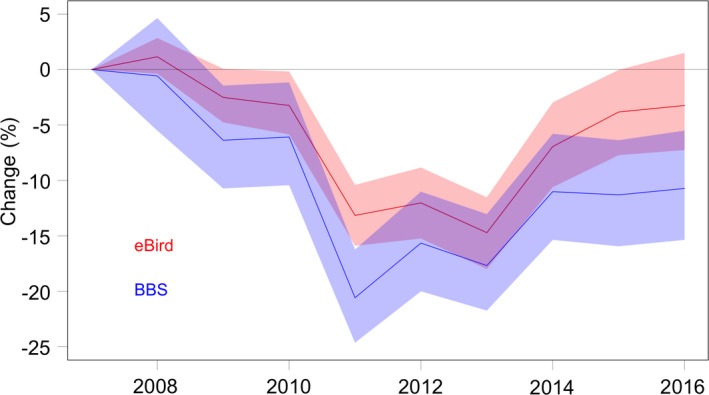
Wood Thrush range‐wide breeding season population trajectories for eBird and BBS. The trajectories show the estimated range‐wide changes in population size standardized as the percent change since 2007. The dark lines indicate the conditional mean estimates and the polygons are corresponding 95% confidence intervals. The eBird estimate is shown in red and the BBS estimate in blue.

The simulation study for the breeding season Wood Thrush trends provides information about likely false detection (type I error) and power (type II error) rates when identifying locations with increasing and decreasing trends. The black contour lines in Fig. 4A delineate those regions across which the expected false discovery rate is at most 5%. These regions include most of the high‐abundance areas within the breeding range. The breeding season power analysis (Appendix S7: Fig. S5A) suggests that regions within the black contours contain ~60% of all locations across the entire breeding range with non‐zero trends, >67% of trends ≥|1% per yr|, >75% of trends ≥|3.5% per yr|, and 80% of trends ≥|6.7% per yr|. Based on the results of this power analysis, we can infer the likely number of locations with trends of a given magnitude outside the black contour. The breeding season simulation study also suggests that a variety of spatially varying trend patterns can be reliably estimated (Appendix S7: Figs. S1 and S2). Overall, these simulation results suggest that there is sufficient data density to estimate trends across a range of magnitudes with low false discovery rates (FDR; type I errors) and fairly high power (i.e., low type II errors) across much of the breeding range at a 25.2‐km spatial resolution.

Nonbreeding season trends

There were declines of 1–3.5% per yr across most of the non‐breeding range with the steepest declines in areas of high abundance in the northeastern part of the Yucatan peninsula, in the northernmost part of Guatemala and Belize, and in a low abundance area in the southern portion of the range extending though eastern Nicaragua (Fig. 6A). Trend maps of the location‐wise upper and lower 95% confidence limits (Appendix S6: Fig. S2) generally show similar spatial patterns with consistent declines surrounding the high‐abundance population areas centered near the shared boundaries of Mexico, Guatemala, and Belize.

Figure 6.

Wood Thrush non‐breeding trend map and range‐wide population trajectory. (A) The non‐breeding season (1 December–28 February) average annual percentage change in relative abundance from 2007 to 2016. Increases in population size are shown in blue and decreases are shown in red. Darker colors indicate stronger trends. Each dot on the map represents a 25 × 25 km area. To help visualize the relative change in population size at each location, the size of each dot has been scaled according to the average abundance at that location during the 10‐yr study period. Within the regions delineated by the black contour line, the expected false discovery rate (type I error) is up to 5% when identifying locations with increasing and decreasing trends. Outside the black contours, the direction of population change is less certain. The breeding season power analysis suggests that regions within the black contours contain 40% of all locations across the breeding range with non‐zero trends and contain 70% of all trends with trend magnitudes of 6.7% per yr or more (approximately equivalent to halving or doubling of the population across 10 yr). (B) The trajectory shows the range‐wide change in population size standardized as the percent change since 2007. The dark black line is the conditional mean estimate, the red polygon are the 95% confidence limits, and the light gray trajectories show the 500 replicate estimates.

The estimated non‐breeding season trend is −2.16% per yr, with a 95% confidence interval between −2.98% and −1.28% per yr, a little steeper than the breeding season range‐wide estimate. The range‐wide population trajectory (Fig. 6B) shows the steepest declines in population size between 2010 and 2013 followed by lower rates of decline in the population size from 2013 to 2016, qualitatively similar to the range‐wide trajectory for the breeding season (Fig. 4B). However, the rate of change between 2010 to 2013, almost 30%, is steeper than the corresponding drop for the breeding season estimate.

The 5% FDR regions delineated by the black contour lines in Fig. 6A surround the high‐abundance region centered near the shared boundaries of Mexico, Guatemala, and Belize. The non‐breeding‐season power analysis (Appendix S7: Fig S5B) found that regions within the black contour contain ~40% of all locations across the non‐breeding range with non‐zero trends, >41% of trends ≥|1% per yr|, 50% of trends ≥|3.5% per yr|, and 70% of trends ≥|6.7% per yr|. These simulation results suggest that there is sufficient data density to estimate stronger trends across a range of magnitudes with low FDR and moderate power. However, it should be noted that higher power can be achieved by accepting higher false detection rates, a trade‐off often considered to be prudent in conservation monitoring applications. The estimated and simulated non‐breeding trend maps presented in Appendix S7: Figs. S3, S4 suggests that spatially varying trend patterns can be reliably estimated.

Discussion

Our results show that the use of semi‐structured (Kelling et al. 2019) citizen science data with analyses designed to deal with the biases in these data can accurately estimate complex patterns of species’ distribution, abundance, and trends at landscape spatial scales across continental extents, and at weekly temporal scales across the full annual cycle. The resolution, extent, and completeness of the information that can be generated with this approach have the potential to increase our understanding of the processes that affect species populations and improve monitoring and conservation planning across a range of spatial and temporal scales (Runge et al. 2015).

The comprehensive Wood Thrush analysis presented here fills important knowledge gaps on population‐level information during the less studied migration and non‐breeding periods (Evans et al. 2011). For example, the spatiotemporally explicit habitat association estimates provide a previously unavailable source of quantitative information about Wood Thrush habitat use throughout the annual cycle. The general patterns of habitat use shown in Fig. 3 are consistent with the qualitative patterns described in Evans et al. (2011); however, the current results provide more specific details about where and when transitions in habitat associations occur. Moreover, because these estimates are based on a single source of both observational and environmental data, they provide a basis for direct comparisons across regions and seasons. The seasonal patterns of habitat use shown in Fig. 3 are also consistent with those documented by Zuckerberg et al. (2016) for eastern North America, including the increased diversity of habitats used during migrations and the strong positive association with deciduous forest during the breeding season. In particular, the positive association with the urban developed class has also been found to be common among Neotropical migrants during their migrations across eastern North America (La Sorte et al. 2017) and is at least is partially explained by an attraction to artificial night light during migration (Van Doren et al. 2017).

The spatially and seasonally explicit trend estimates also provide new information about interannual changes in Wood Thrush population size. The spatial resolution of the trend estimates presented here is relatively high compared to other studies with similarly broad spatial extents (Sauer et al. 2017, Baker et al. 2019, Meehan et al. 2019, Rushing et al. 2019). Both breeding and non‐breeding trend maps show significant spatial variation in the pattern of declines, with the steepest declines within the 5% FDR regions (Figs. 4A, 6A; Appendix S6: Figs. S1, S2). The high spatial resolution of these estimates is valuable for informing state wildlife action plans and other regional conservation initiatives, instead of relying on trends from coarser regions, e.g., Bled et al. (2013). Trend estimates with high spatial resolution are also valuable because of the increased power to detect correlations with other spatial processes potentially affecting populations.

The range‐wide breeding season population trajectory shows a close correspondence with the range‐wide breeding season population trajectory estimated from the independently collected and analyzed BBS data (Fig. 5). Both estimates show a similarly steep decline between 2010 and 2013 followed by shallower rates of decline in the population size from 2013 to 2016. Interestingly, the previously unavailable non‐breeding season population trend estimate shows the same qualitative pattern (Fig 6B). The strong correspondence between the independently estimated eBird breeding (Fig. 4B) and non‐breeding (Fig. 6B) population trajectories provides compelling evidence that the same population is sampled in each season. Understanding this provides a basis for cross‐season comparisons and simplifies integration with other seasonal sources of information. The range‐wide annual rate of decline is slightly stronger for the non‐breeding season (−2.2%) compared to the breeding season (−1.5%), with 95% confidence intervals (−3.0%, −1.3%) and (−1.9%, −1.0%), respectively. The non‐breeding population trajectory also shows stronger rates of decline during the 2010–2013 dip, with non‐breeding rates as high as −30% (Fig. 6B) and breeding rates nearly −20% (Fig. 4B). These differences could be due to differences in mortality during migration, since demographic work points to relatively high survival for the non‐breeding period (Rushing et al. 2017).

This spatial trend information, in conjunction with the spatiotemporally explicit habitat association estimates, could also help tease apart current contrasting results on the drivers of population declines for Wood Thrush. Taylor and Stutchbury (2016) concluded that WOTH declines are most likely driven by habitat loss during the non‐breeding season, while Rushing et al. (2017) concluded that declining trends are likely driven by habitat loss during the breeding season. However, both studies relied on much coarser spatial information from the breeding season trends. Therefore, the ability to generate spatially explicit estimates of trends and habitat associations at different times of the year provides essential additional contextual information to understand where and when in the annual cycle populations are most limited, and point toward possible causes of these limitations. Based on the strong positive associations with deciduous and evergreen broadleaf forests during the majority of the year, coupled with significantly declining trends in both breeding and non‐breeding seasons, forest loss may be important driver of Wood Thrush declines. For Wood Thrush, these results highlight the need to formally evaluate how spatial information on regional threats (e.g., deforestation, fire, drought), during all stages of the life cycle (e.g., breeding, migratory, non‐breeding), correlate with seasonal trends and influence population declines (Kramer et al. 2018).

We designed the analytical framework presented here for pattern discovery and description of broadly distributed and migratory species across the full annual cycle. However, several of the analytical approaches described here can be used for other applications. The AdaSTEM framework can be modified to estimate distributions and abundance for species with smaller ranges, by modifying the ensemble to have a single spatial region, or for resident species, by modifying the ensemble to have a single full‐year temporal season. Similarly, the AdaSTEM framework can be geared toward the analysis of rare species by using alternative base models, modifying the spatiotemporal case‐control sampling, and increasing the number of base models in the ensemble. In general, the selection of the class of base models should be made to match the objectives of the analysis. For example, confirmatory analysis can be performed by selecting base models that support hypothetico‐deductive analysis (Mentch and Hooker 2016, Wood 2017) or causal analysis can be performed by selecting models designed for this purpose (Wager and Athey 2018). The ZI‐BRT base models are generally well suited for pattern discovery; however, because they only account for variation in detection rates and do not directly estimate the absolute detection probability, strong changes in detectability (e.g., across seasons or species) can make it harder to compare predictions. Practical solutions to this problem include standardizing the relative abundance estimates by the total relative abundance to generate a measure of the proportion of the total population or using the AOO estimates of the binary un/occupied state, which is less sensitive to changes in detectability (La Sorte et al. 2017). Finally, several of the approaches used here to control for biases in citizen science data can be applied more generally. Johnston et al. (2019) discuss how information describing participant search effort along with complete checklists can be used to account for the bias of imperfect detection and how spatiotemporal sampling can be used to balance the data used to train distribution and abundance models.

Deploying the AdaSTEM framework at scales sufficient to cover the full annual cycle for broadly distributed species with landscape‐scale resolution is computationally intensive, requiring thousands of CPU‐hours and terabytes of storage on high performance and cloud computing systems. To ensure that this computational cost is not an impediment to those wishing to analyze other bird species with eBird data, we have analyzed a taxonomically diverse set of North American breeding species. Visualizations, summaries, and the data products (i.e., AOO, occurrence, and relative abundance estimates) from these analyses are available online.² We have also made the ebirdst R package available to facilitate the access and analysis of these data products (available online).³

More broadly, this study helps demonstrate the reliability of using citizen science data to estimate trends in relative abundance, a task usually left to monitoring programs that employ more stringent sampling protocols that can be challenging to deploy, manage, and maintain across such broad spatial and temporal extents. The analysis presented here also demonstrates how citizen science data can be used to generate accurate species‐level information for broad‐scale biodiversity monitoring like those outlined by the Group on Earth Observations Biodiversity Observation Network (Kissling et al. 2017, Jetz et al. 2019). However, we are not suggesting that citizen science data can or should supplant data collected using more formal sampling protocols. On the contrary, data collected from formal sampling protocols and citizen science projects tend to be complementary. Data collected using formal sampling protocols are often, by design, higher resolution, and repeatedly sample the same locations to effectively detect changes in population size during specific time periods and locations. Citizen science data, on the other hand, provide information outside of the scope of any one individual sampling design, providing a basis for inference in additional habitat types, regions, and seasons. The framework presented here can be used as a unified data backbone to integrate other data sources, e.g., monitoring, migratory connectivity, isotope, etc., and to identify the most critical and threatened places that are vital for preserving North America's avifauna.

Supporting information

 

 

 

 

 

 

 

Fink, D. , Auer T., Johnston A., Ruiz‐Gutierrez V., Hochachka W. M., and Kelling S.. 2020. Modeling avian full annual cycle distribution and population trends with citizen science data. Ecological Applications 30(3):02056 10.1002/eap.2056

Data Availability

The data used to conduct this study are freely available on the eBird website https://ebird.org/science/download-ebird-data-products. The data version used in this study was the eBird Reference Dataset from 2016, using checklists within the Western Hemisphere from 1 January 2004 to 31 December 2016. Further details of checklists used for the analysis are in the Supporting Information.