Development of a Relative Risk Model for Drinking Water Regulation and Design Recommendations for a Peri Urban Region of Argentina.

Abstract

Argentina is a developing Latin American nation that has an aim of achieving the United Nations Millennium Development Goals for potable water supplies. Their current regulations however, limit the continued development of improved potable water quality and infrastructure from a microbiological viewpoint. This is since the current regulations are focused solely to pathogenic Eschericia coli (E. coli), Pseudomonas aeruginosa (P. aeruginosa) and fecal indicators. Regions of lower socioeconomic status such as peri-urban areas are particularly at risk due to lessened financial and political ability to influence their environmental quality and infrastructure needs. Therefore, a combined microbiological sampling, analysis and quantitative microbial risk assessment (QMRA) modelling effort were engaged for a peri-urban area of Salta Argentina. Drinking water samples from home taps were analyzed and a QMRA model was developed, results of which were compared against a general 1:10,000 risk level for lack of a current Argentinian standard. This QMRA model was able to demonstrate that the current regulations were being achieved for E. coli but were less than acceptable for P. aeruginosa in some instances. Appropriate health protections are far from acceptable for Giardia for almost all water sources. Untreated water sources were sampled and analyzed then QMRA modeled as well, since a significant number of the community (~9%) still use them for potable water supplies. For untreated water E. coli risks were near 1:10,000, however, P. aeruginosa and Giardia risks failed to be acceptable in almost all instances. The QMRA model and microbiological analyses demonstrate the need for improved regulatory efforts for the peri-urban area along with improved investment in their water infrastructure.

1.0. Introduction:

1.1. Motivation and Purpose of Study:

The essential nature of water means that a consistent source of high quality water is vital to the survival and thriving of a community. Therefore, poor microbiological water quality poses a serious and immediate problem for human health. Some communities do not have access to either appropriate sanitation or potable water facilities, thus complicating the already poor water quality conditions. This lack of infrastructure is known to allow these communities to be exposed to pathogenically contaminated water (Razzolini et al, 2011). Additionally even if some water infrastructure is equipped, a significant fraction of waterborne disease burden can still be attributed to the way water resources are managed (Prüss-Ustün et al., 2014; Wolf et al., 2014).

The last report of the Joint Monitoring Programme for Water Supply and Sanitation (JMP; WHO/UNICEF, 2014a) indicate that 116 countries have already met the Millennium Development Goal (MDG) related to water between 1990 and 2012. This achievement resulted in 2.3 billion people gaining access to improved drinking water. While this is an important achievement, it is important to note that the MDG indicators do not take water quality measurements into account. Therefore it is increasingly recognized that water from improved sources does not guarantee increased water quality or safety. Bain et al. (2014) provides evidence of the presence of fecal contamination in sources considered improved in Low- and Middle-Income countries and suggest that, by equating improved with safe, the number of people with access to a microbiologically and chemically safe water have been greatly overstated. In this context, JMP indicated that one of the objectives for 2030 is to halve the proportion of the population without access at home to safe drinking water and progressively eliminate inequalities to its access (WHO/UNICEF, 2014b).

Water standards in Argentina are governed by the Argentine Food Code (Código Alimentario Argentino) (CAA, 2014). While this is a good step in developing safe drinking water standards and regulations, there are some potentially hazardous omissions in the development of these regulations. Namely microbiological quality of water is ascertained using indicator organisms, coliform bacteria, Escherichia coli (E. coli) and Pseudomonas aeruginosa (P. aeruginosa). Considering that potable water engineering design most typically follows pertinent regulations, there exists the potential for known pathogens other than those regulated to cause waterborne disease burden. Therefore, this study was designed to compare the relative differences in pathogenic hazard and controls through the lens of quantitative microbial risk assessment (QMRA).

QMRA is a powerful tool to project an estimated likelihood of deleterious health effects from exposure to pathogenic hazards. Even if high risks can be surmised the quantification of these risks gives weight of evidence to decisions and designs to address these risks. The QMRA paradigm has progressively been relied upon in regulatory and engineering design fields (Gale, 1996; Haas et al., 1999; Weir et al., 2011). The QMRA developed utilizes the Monte Carlo method to develop confidence intervals for the risk values, and account for variable uncertainty in the model.

1.2. Study Area and Description:

Argentina is a developing country of Latin America and the Caribbean region with 91–100% of the population using improved sources of drinking water and is among the countries that met the MDG for water (WHO/UNICEF, 2014a). Nevertheless, there is evidence of improved water sources with presence of waterborne pathogens (Abramovich et al., 1996; Basualdo et al., 2000; Lurá et al., 2000; Costamagna et al., 2005; Basualdo et al., 2007; Gamboa et al., 2011; Vidaurre et al., 2010). In Salta, a province in the northwest region of Argentina, more than half of the total population of infants is affected by diarrhea annually by infectious pathogens. Seasonal trends can be observed as well with bacteria predominating in spring and summer, viruses particularly in the winter and parasites being endemic year round in some areas (Rajal et al., 2009). Public health monitoring is limited by poor epidemiological records, exacerbated by the lack of diarrhea cases having the etiological agent assayed (only in 4% studied in 2013; Ministerio de Salud, 2014). This lack of records also means that monitoring for water quality or treatment faults through epidemiological evidence (monitoring for the clusters of similar symptoms) cannot be reliably performed. The determination of etiological agent is also important for increased weight of evidence to target specific pathogens in future regulations or changes to current regulations. Therefore a QMRA model developed to describe the potential water quality impacts for a set of treatment options will be valuable to start addressing some of these knowledge gaps.

The indicators and pathogens for microbiological drinking water control under current regulations in the CAA 2014 are limited to coliform bacteria, E.coli and P. aeruginosa. With these bacteria as the only design criteria for a treatment plant obviously the efficiency of pathogenic protozoa and virus removal in water treatment systems is being overlooked. This leads to the treatment systems allowing for waterborne disease outbreaks, sometimes without corresponding evidence of microbiological contamination of drinking water (CEPIS/OPS, 2004; Hrudey and Hrudey, 2004).

Seghezzo et al. (2013) outlined the commitment of the water utility of Salta to improving water treatment efficiency with the implementation of an initial Water Safety Plan (WSP). Important results showed there is need for improvement namely: 1.) define health based targets, 2.) assess whether the treatment is appropriate to achieve health based targets, and 3.) define required sample sizes and frequency. These improvements to the WSP can be addressed by utilizing a QMRA approach (Medema and Ashbolt, 2006). Both methodologies, WSP and QMRA, are useful to evaluate and improve the microbial safety of drinking water and are recommended by the third and fourth editions of the Guidelines for Water Quality (WHO, 2008; WHO, 2011). Importantly by using a WSP and QMRA together more weight of evidence can be used for regulatory reform, water treatment process selection and system maintenance prioritization. Actual adaptations to the scope of the WSP are outside the bounds of this work but are currently underway.

Since QMRA is computationally intensive there is occasional reluctance to engage in such a significant quantitative effort. Additionally as Argentina has no history of developing or using QMRA models in the drinking water industry there is the possibility for trepidation and need of regulator education. In this work we outline the development of a QMRA model and outline the general decisions and recommendations that can be made from the results. This model will also serve to help educate Argentine utilities and regulatory agencies on the applicability and use of QMRA models, particularly in drinking water.

The QMRA is developed using data from an intensive drinking water sampling and assay research (here in termed drinking water assessment). The drinking water assessment was developed for a peri-urban area near Salta, Argentina. This area has two water treatment plants that have been designed and developed based on the current regulations. Therefore to compare the risks under current regulations and for an additional known hazard three pathogens were chosen for assay and QMRA modelling: enteropathogenic E.coli, P.aeruginosa and Giardia subspecies. Viruses were not sampled for due to costs of analysis as well as parasites being prioritized since they are a known source water hazard.

There are at least four types of E.coli pathogenic to humans: enterotoxigenic (ETEC), enterohemorrhagic (EHEC), enteropathogenic (EPEC), and enteroinvasive (EIEC). The organisms are excreted in the feces of warm-blooded animals (including humans) and transmitted by direct contact or via contaminated food and water. Ingestion of E.coli results in a wide range of possible outcomes, from asymptomatic infection to death particularly due to EHEC most typically via haemolytic uremic syndrome (HUS) (Rubino et al., 2011). Further details about the other strains are well outlined in Percival et al. (2004). E.coli is sensitive to chlorine and other oxidant disinfectants, therefore it is known that adequate chlorination effectively reduces infection and illness risks (Hunter, 2003). However, if the chlorination process is not designed, optimized or maintained properly then health risks will increase if this is the primary or sole means of microbial control.

P. aeruginosa is part of a large group of free-living bacteria that are ubiquitous in the environment, often found in natural waters such us lakes or rivers but not often found in drinking water (Mena and Gerba, 2009). Occasional occurrence in drinking water is typically indicative of water quality deterioration, if present in drinking water, the population is potentially exposed to a pathogen capable of ocular infections, especially the immunocompromised communities (Percival et al., 2004). P. aeruginosa does not exhibit resistance to common drinking and waste water disinfectants such as chlorine or chloramines, however, P. aeruginosa has a reputation for being resistant to some medical disinfection (Mena and Gerba, 2009).

Giardia is an anaerobic flagellated protozoa capable of encystation, and known pathogenic hazard in warm blooded animals, including man (Erlandsen et al, 1984) Clinical features could be from asymptomatic carriage to diarrhea, abdominal pain and rapid weight loss (Thompson, 2000). Because of their cyst formation Giardia particularly known for its resistance to common disinfection controls such as chlorine and chloramines (Rose et al., 1991). Therefore, if the presence of Giardia is known, typically traditional water treatment design would require additional disinfection options such as ozone or ultraviolet disinfection. In addition to these design considerations, typically there would also be a monitoring strategy to ensure that treatment for Giardia and other protozoa such as Cryptosporidium were effective.

Knowledge of public health risks associated with the consumption of water is important for decision-making, to evaluate risk mitigation measures, and in the best case, to modify and implement new water quality standards. Even though Argentina produces a weekly report of nationwide diarrhea cases, only 4% of those cases undergo laboratory analysis for etiologic agent (Ministerio de Salud, 2014), therefore, there are no official data regarding outbreaks related to any gastrointestinal pathogen. To formulate national public health goals, these goals need to be based on data from within the country and not extrapolated from other nations (WHO, 2011). The main objective of this research is to use data generated from a drinking water assessment for a peri-urban area (population of ~ 4,575) of the city of Salta in Northwestern Argentina to develop a QMRA model to assess the public health risks associated with water consumption.

2.0. Methods and Materials:

The study was developed in Vaqueros, a peri-urban locality of Salta in Northwest Argentina (24°41’17“ S 65°24’40” W; 1318 meters above sea level). Climate is best defined as subtropical (Serrano), warm, humid and with a dry season (Bianchi and Yánez, 1992). Mean ambient temperature in January (the warmest month) is 20.2°C and in July (the coldest month) is 8.7°C. The area has highly variable rainfall with a well-defined rainy season from December to April, in generally January is the wettest month, with an average of 258 mm between the years 2007–2011 (INTA, 2014). During the months of July and August, there is typically no registered rain during these driest months.

Of the 4575 inhabitants of the study area 13.2% live with unsatisfied basic needsin access to adequate sanitation and drinking water infrastructure (INDEC, 2010). Despite the rapid growth in the last decade and expansion of the area, adequate sanitation and drinking water systems have not followed this growth. The population has a variety of potable source water supplies. A part of the population is supplied through the water provided by the water company “Aguas del Norte” (AdN), which uses two surface water treatment plants and a deep well. The remainder of the population use water from shallow wells and surface irrigation channels without any treatment. For sanitation, there are no sewer connections, which leads to the exclusive use of cesspools and septic tanks in every household. This lack of adequate sanitation can lead to additional exposures and source water contamination. The socioeconomic characteristics, inadequate sanitation infrastructure, the diversity of water sources and poor water quality in this location constitute a surmisable risk. A QMRA model for this area will add to weight of evidence for a reexamination of current regulations and support infrastructure improvements.

2.1. Sampling and Microbial Analysis

Samples were taken from tap water within households, and when it was not possible, from water used by the family for drinking (either the surface irrigation channel or inside shallow wells). Due to the diversity of sources of water (three managed by AdN and one without any treatment) sampling was divided into 4 groups:1.) New Plant, samples correspond to tap water in houses supplied from a new potable treatment plant in Vaqueros managed by AdN (constructed in 1989, serving 982 households or 67% of the area’s total population). The New Plant operates using flocculation, sedimentation, rapid sand filtration and chlorination (AdN, personal communication, 18th June 2013). 2.) Old Plant, samples correspond to tap water in houses supplied from an old treatment plant constructed in 1972 in Vaqueros also managed by AdN, supplying 227 households (15,5% of total area’s population), using the same process train as the New Plant. 3.) Neighborhood borehole samples correspond to tap water supplied by a deep borehole installed and managed by AdN, with only chlorination as treatment, supplying 130 households (8.9% of total area’s population). 4.) Without treatment. In this case samples are taken either directly from the surface of the irrigation channel or from inside the shallow wells in households (in both cases the water is used as drinking water). In Vaqueros 35 households use water from irrigation channels and 93 households have shallows wells in their homes (8.7% of total area’s population) (INDEC, 2010).

Three sites of each group were selected for the sampling over a total of eight months, four months in dry season (August, September, October and November 2010) and four during the rainy season (January, February, March and April 2011). A total of 96 water samples were collected and analyzed for E. coli and P. aeruginosa. In the case of Giardia, where several serial dilutions and 3–5 replicates of each sample were necessary for the quantification, at least one site of each group was selected for quantification.

E.coli was assayed with most probable number (MPN) method using multiple tube fermentation with Lauryl tryptose broth with MUG (Fluorocult Merck), as described in 9221 F method (APHA, 2005). According to this protocol for treated water, a series of 5 tubes with 10 mL of samples and medium double concentration each. For untreated water, three series of 5 tubes with 10mL of medium double concentration and 10 mL, 1 mL and 0.1 mL seeded in each series respectively. If after 24 h of incubation at 35 ± 0.5 ° C tubes were blue fluorescent under UV light, and after covering the medium with 5 mm of Kovacs reagent, formed a red cherry ring, the tubes were considered a positive result. Using 9213 F method (APHA, 2005) the multi-tube MPN method was also used for P.aeruginosa, with Asparagine broth for the presumptive test and Acetamide broth as confirmed test, using the same number of tubes as for E. coli.

Sampling and analysis of Giardia was performed according to CEPIS (1993), US EPA (1995) and APHA (2005) with several modifications. Samples were filtered in situ by cartridge filtration. The filtering apparatus included a 25-cm (10”) long 1 μm porosity, yarn-wound polypropylene cartridge in a filter housing with flow meter. For samples from tap water (groups 1, 2and 3) the filtration apparatus was connected directly in the tap and 1000L of water was filtered. Samples from the irrigation channel were pumped through the filter using a bilge pump and a 12V battery. Samples from shallow wells were collected directly from a tap connected to a pump, both installed for this purpose. For group 4 samples 100L of water were filtered. After the filtration the filter was aseptically removed, packed in sterile plastic bags and transported into a cooler containing ice pack to the laboratory for further processing. The filters were removed from the cartridge, filter fibers were cut with a pre-sterilized knife and the central plastic cores of the filters were removed. Fibers were hand-washed three times in 3 portions of 1 L of 0.2% Tween 80 solution (for very dirty fibers more than 3L of eluted solution was necessary). The 3-L solution that resulted from the elution procedure was further concentrated by centrifugation at 2500 rpm × 10 min. Supernatants were discarded and the volume of the packed pellet was recorded. After the supernatant was aspirated, the pellet was re-suspended in an equal volume of 10% formalin. Due to the large amount of debris in the samples, the quantification was performed using the NMP applied to microscopy, making 3 to 5 replicates of dilutions of the pellets and calculating equivalent volumes to obtain the final MPN/L value.

Numeric results of the MPN analyses presented censored data (less than and greater than values), therefore, statistical analysis was performed where half of the detection limit was used for the less than values (Petterson et al., 2006; Smeets, 2011). In the case of E. coli and P. aeruginosa, where MPN results included values greater than a maximum detection limit, the calculations of the means and median values of the MNP concentrations were calculated using the Kaplan Meier method (Kaplan and Meier, 1958).

2.2. Modelling Methods.

A complete description of the QMRA framework can be found in Haas et al (1999). In brief the development of a QMRA model is broken into four distinct but inter communicated phases. 1.) Hazard identification; understanding of the microbiology of the target pathogen(s), as well as understanding the population for which the model is being developed. 2.) Exposure assessment develop (or utilize an existing) model that describes how a concentration (estimated or known) is introduced to the human host. 3.) Dose response; the yardstick of risk, the underlying probability of illness or infection is modeled by optimizing physiologically plausible models to available data. 4.) Risk characterization and management; Combine the other phases typically into an uncertainty modelling method (i.e. Monte Carlo or bootstrap).

This QMRA was aided in that the target pathogens were clearly outlined by the current regulations, E. coli and P. aeruginosa. Giardia was selected as an additional pathogens since it is desired to determine the utility of including Giardia into the regulations or treatment plant design based on public health risks. The QMRA model was constructed using the Monte Carlo method. The Monte Carlo method is an iterative Bayesian technique. Being Bayesian it requires; known, optimized or assumed probability distributions to describe uncertain variables. All models and inferences from them were performed in 64bit R (v2.15.3 http://www.r-project.org/).

The MPN values were loaded into R from the csv files made from the original spreadsheet. The resulting data from the microbial assays presented a challenge in that there were a substantial number of censored results (greater than or less than a detection limit, DL). Therefore for these censored values a probability distribution could not be optimized, however, they were used to inform assumed distributions. As with the statistical methods in the QMRA model, one-half of the DL was used for values less-than the DL (Haas et al., 1999; Petterson et al., 2006; Weir et al., 2011).

As any logarithm has the effect of shrinking large differences and expanding small ones in data, only those data with a wide spread between data points had the natural logarithm taken for probability distribution optimization. Table 1 shows the results of the optimization, and only those models with the best fit, determined by the Akaike information criterion (AIC) and weighted AIC (AICw) are shown, the models tested were; beta, binomial, Cauchy, truncated Cauchy, χ², Exponential, gamma, geometric, hypergeometric, logistic, log normal, normal, negative binomial, Poisson, triangular, uniform and Weibull. The truncated Cauchy and triangular distributions are not embedded in R, these distributions therefore needed to be programmed into R for this work, as with previous research (Razzolini et al., 2011; Weir et al., 2011). As will be discussed in the exposure modelling description, the percentage of face that is a person’s eyes is important for the exposure to P. aeruginosa.

Table 1.

Optimized probability distributions and associated AIC (AICw). Distribution optimization to drinking water concentration was limited to values not dominated by censored results.

Water Type / Model Parameter	Pathogen	Optimized Probability Distribution / AIC / AICw	Parameter(s)
New Plant*	Giardia**	Exponential / 35.517 / 0.442	Rate = 0.422
Old Plant*	Giardia**	Exponential / 19.991 / 0.378	Rate = 0.883
Irrigation Channel*	E. coli***	Weibull / 21.482 / 0.420	Scale = 1178581.3178 Shape = 1073.651
	Giardia**	Exponential / 33.379 / 0.336	Rate = 0.564
	P. aeruginosa***	Truncated Cauchy / 25.60 / 0.348	Location = 1134.666 Scale = 1.960
Shallow Well*	E. coli***	Truncated Cauchy / 24.174 / 0.309	Location = 479.390 Scale = 1.479
	Giardia**	Log Normal / 15.633 / 0.432	LogMean = −1.611 LogSD = 1.873
	P. aeruginosa***	Exponential / 34.438 / 0.304	Rate = 1.346
Percentage of Face that are Eyes****	NA	Logistic / −5.261 / 0.331	Location = 2.113 Scale = 0.0994

^{* -}Drinking water samples corresponding to the referenced sample locations

^{** -}Units of cysts/L

^{*** -}Units of CFU/100L

^{**** -}Optimized to data obtained from (van Graan, 1969), unitless

For those data and the dose response parameters, for which a probability distribution could not be optimized, an assumed distribution was chosen. Typically there are a very limited set of options for assumed distributions; binomial, Poisson, triangular or uniform distributions being the most common and available. Another option is using a distribution optimized to data from another study similar to or in the study area. Since Vaqueros has not had an intensive sampling and assay project there were no previously optimized probability distributions to choose from. Additionally as a large proportion of the population uses untreated water, maximum use of data specific to these households was preferred. Since these data were not Boolean the binomial was disregarded, the data could not be assumed random, and therefore, the Poisson was not an option. The random triangular distribution (equation 1) was chosen for an assumed distribution for the remaining data as well as the dose response parameters, where T(C) is the randomly generated value (concentration or dose response parameter); x is the random variable (generated in R), M is the theoretical maximum, m in the theoretical minimum and L is the likeliest (median) value. The triangular was chosen as it can address a maximum and minimum and median or likeliest value, something the uniform distribution cannot perform (table 2). Those values greater than an upper bound DL would be used as a reference point for the upper bound of the assumed distributions (Weir et al., 2011).

Table 2.

Assumed distributions for the QMRA model, for the pathogens where the data was not suitable for optimization of a probability distribution.

Water Type / QMRA Uncertain Variable	Pathogen	Assumed Distribution	Parameters
New Plant*	E. coli***	Triangular	Minimum = 0 Likeliest = 1.1 Maximum = 2.2
	P. aeruginosa***	Triangular	Minimum = 0 Likeliest = 1.1 Maximum = 16
Old Plant*	E. coli***	Triangular	Minimum = 0 Likeliest = 1.1 Maximum = 16
	P. aeruginosa***	Triangular	Minimum = 0 Likeliest = 1.1 Maximum = 16
Neighbourhood Boreholes*	E. coli***	Triangular	Minimum = 0 Likeliest = 1.1 Maximum = 9.2
	Giardia**	Triangular	Minimum = 0 Likeliest = 0.0275 Maximum = 0.055
	P. aeruginosa***	Triangular	Minimum = 0 Likeliest = 1.1 Maximum = 16
Ingestion Volume (L)	NA	Triangular	Minimum = 0 Likeliest = 1 Maximum = 2
α	E. coli†	Triangular	Minimum = 0.119 Likeliest = 0.178 Maximum = 0.321
N50	E. coli****	Triangular	Minimum = 3.25 (107) Likeliest = 8.60 (107) Maximum = 2.63 (108)
k	Giardia†	Triangular	Minimum = 0.0126 Likeliest = 0.0199 Maximum = 0.0292
k	P. aeruginosa†	Triangular	Minimum = 0.0000784 Likeliest = 0.000105 Maximum = 0.000148

^{* -}Drinking water samples corresponding to the referenced sample locations

^{** -}Units of cysts/L

^{*** -}Units of CFU/100 L

^{**** -}Units of CFU

^{† -}Unitless

$$T\left(C\right)=\{\begin{array}{ll}\frac{2\left(x-m\right)}{\left(L-m\right)\left(M-m\right)}\hfill & form\le x\le M\hfill \\ \frac{2\left(L-x\right)}{\left(L-m\right)\left(L-M\right)}\hfill & forM\le x\le L\hfill \end{array}$$ (1)

The dose response parameters were chosen from an extensive literature search, starting with a database of dose response parameters housed in the peer reviewed QMRA information hub (http://www.qmrawiki.canr.msu.edu). This information hub has been constructed partially by Dr. Weir and the dose response parameters are from peer-reviewed publications. Giardia’s dose response parameter (Table 2) was originally developed and used in a drinking water scenario by Rose et al (1991). Giardia illness is best described using an exponential model (equation 2). The dose response parameters for the beta Poisson (equation 3) model were chosen for enteropathogenic E.coli from Haas et al (1999). This model and associated parameters were chosen as it is a coupled model using data for enterotoxigenic, enteroaggregative and enteropathogenic E. coli in human volunteers. The use of this dose response model assumes that the E. coli sampled are of a lower virulence EPEC, therefore, risking potential overestimation of risks, assuming all E. coli assayed is pathogenic. The dose response parameter for P. aeruginosa was also drawn from the peer reviewed QMRA information hub. This pathogen is also best described using the exponential model (equation 2), with k parameter and upper and lower bounds shown in Table 2.

$$P\left(r\right)=1-e^{-k\cdot \mathit{\text{dose}}}$$ (2)

$$P\left(r\right)=1-{\left[1+\frac{\mathit{\text{dose}}\cdot 2^{1/\alpha }-1}{N_{50}}\right]}^{-\alpha }$$ (3)

For E. coli and Giardia the dose was calculated by first obtaining the concentration randomly, sampled from the respective distribution for each pathogen and multiplying this by the distribution for ingestion volume. Since P. aeruginosa is not typically considered an ingestion hazard, although has proven to be a potential hazard for potable water (Mena and Gerba, 2009), the exposure calculation is more involved.

P. aeruginosa is typically associated with ocular infections from external exposures, also the dose response is for a resulting eye illness, therefore, a means of modelling eye exposure was developed. First we assume a nominal amount of water used for washing the face and head, 1/2 L of water. Then using data on percentages of average adult face size (van Graan, 1969) shown in table 3, a volume of water being in contact with the face was calculated. This method of calculation is limited in the base assumption of 1/2 liter of water for washing head and face, however, no such data exists to go beyond this assumption. This method is also limited to adults due to the data for percentage of body that is a person’s face, however, is improved over using a dose response for eye exposure in an ingestion related exposure. The logistic distribution was the best fitting probability distribution for the percentage of a human face is eyes (table 1). Optimization was accomplished using the same methods as previously described.

Table 3.

Data used to determine eye exposure volume, data obtained from (van Graan, 1969).

Subject No.	Percentage of Head that is Eyes
74	2.0
1	2.2
75	1.9
76	2.2
77	1.8
20	2.2
19	2.1
22	2.2
23	2.6
21	2.1
78	2.2
79	2.0
80	1.8
81	2.2
82	2.2
83	2.1

Annual risks were calculated using equation 4 (Razzolini et al., 2011). In equation 4 an annual risk (P_a) is estimated using the daily probability of illness (P(r)) from the respective dose response models, where n = 365 for annual risk estimations.

$$P_a=1-{\left[1-P\left(r\right)\right]}^n$$ (4)

At iteration 1 of the Monte Carlo simulation the estimated dose is entered into the respective dose response model for the pathogen, resulting in a static risk estimate. The Monte Carlo simulation is then iterated 10,000 times to generate a distribution of computational data. Therefore for each iteration, there is one concentration randomly sampled for each pathogen, one ingestion volume randomly sampled, and one dose response parameter (or set of dose response parameters for the beta Poisson), resulting in one ingested dose then one risk value is estimated for each pathogen, then the model iterates once more. This computational data also allows for a means of comparing different water sources with greater statistical rigor, allowing more strength to inferences than comparing single relative risk values. Essentially the iterative nature of the Monte Carlo technique allows the risk modeler to use statistical test based on computational data to evaluate and characterize the data better.

As a check a simple point estimate was conducted where for the detection limit (DL) both C = 0.5*DL and C = DL were both used to generate initial point estimates. This allows for a relative comparison to determine the level of justification that may exist to use the Monte Carlo method. This also then allows for a relative comparison between the two methods of using DL values in the QMRA.

2.3. Model Code Verification:

The R codes used were verified independent from this project. The codes for the triangular and truncated Cauchy distribution were previously independently verified by having an R programming expert separate from the project review and test the code. Any errors were evaluated and addressed; the same and another blinded reviewer then reevaluated the code. The same process was used for the Monte Carlo code; in this case this review was enacted again separate from the review in the previous work. All R source codes passed this independent quality assurance check.

3.0. Results:

3.1. Microbial Sampling and Assay Results.

Table 4 shows a summary of microbiological assay results, with raw data plotted in Figure 1. The maximum values show that the values of E. coli and/or P. aeruginosa exceed the limit established by the CAA at some point of sampling in all sampling sites. This occurred in all the samples of untreated water, except in only one sample from shallow well. In treated waters, positive samples were found only in the rainy season, while in the dry season all samples were negatives for E. coli and P. aeruginosa. The new plant presented positive samples for P. aeruginosa only in the sampling of April (>16, 9.2 and 9.2 MPN/100mL) but not positive for E. coli; the old plant was positive for E. coli in February (2.2 MPN/100mL) and in April (>16 MPN/100mL); and samples of the neighbourhood borehole was positive once for E. coli in April (9.2 MPN/100mL) and in February (9.2 MPN/100mL), while for P. aeruginosa was positive only in April (5.1, 9.2, 16 MPN/100mL). Thus demonstrating that in rainy season the purification process is not prepared for increases in flows and turbidity, which is evidenced by registered microbiological results.

Table 4.

Microbiological assay results.

				Median	95% Confidence Interval for Median		Mean	95% Confidence Interval for Mean
Water Type	Pathogen	Minimum	Maximum	Estimate	Lower Bound	Upper Bound	Estimate	Lower Bound	Upper Bound
Neighbourhood Boreholes*	E. coli***	<2.2	9.2	1.1	.	.	1.5	0.8	2.1
	Giardia**	<0.017	<0.088	0.026	0.023	0.029	0.028	0.021	0.036
	P. aeruginosa***	<2.2	>16	1.1	.	.	3.5	1.4	5.6
Irrigation Channel*	E. coli***	240	>1600	1600	967	2233	1204	949	1460
	Giardia**	1.2	98	24.0	0.0	62.5	36.3	9.9	62.6
	P. aeruginosa***	4	>1600	540	0	1180	878	547	1208
New Treatment Plant*	E. coli***	<2.2	<2.2	1.1	.	.	1.1	1.1	1.1
	Giardia**	0.059	4.8	3.3	0	10.3	2.4	1.1	3.6
	P. aeruginosa***	<2.2	>16	1.1	.	.	2.4	1.0	3.8
Old Treatment Plant*	E. coli***	<2.2	>16	1.1	.	.	1.8	0.6	3.0
	Giardia**	0.11	2.8	0.74	0.52	0.96	1.13	0.53	1.74
	P. aeruginosa***	<2.2	>16	1.1	.	.	3.3	1.3	5.4
Shallow Wells*	E. coli	<3	>1600	350	0	781	537	200	874
	Giardia	<0.01	7.5	0.11	0.00	0.38	1.12	0.00	2.91
	P. aeruginosa	<2.2	>1600	5	0	16	424	0	934

^{* -}Drinking water samples corresponding to the referenced sample locations

^{** -}Units of cysts/L

^{*** -}Units of MPN/100L

Figure 1.

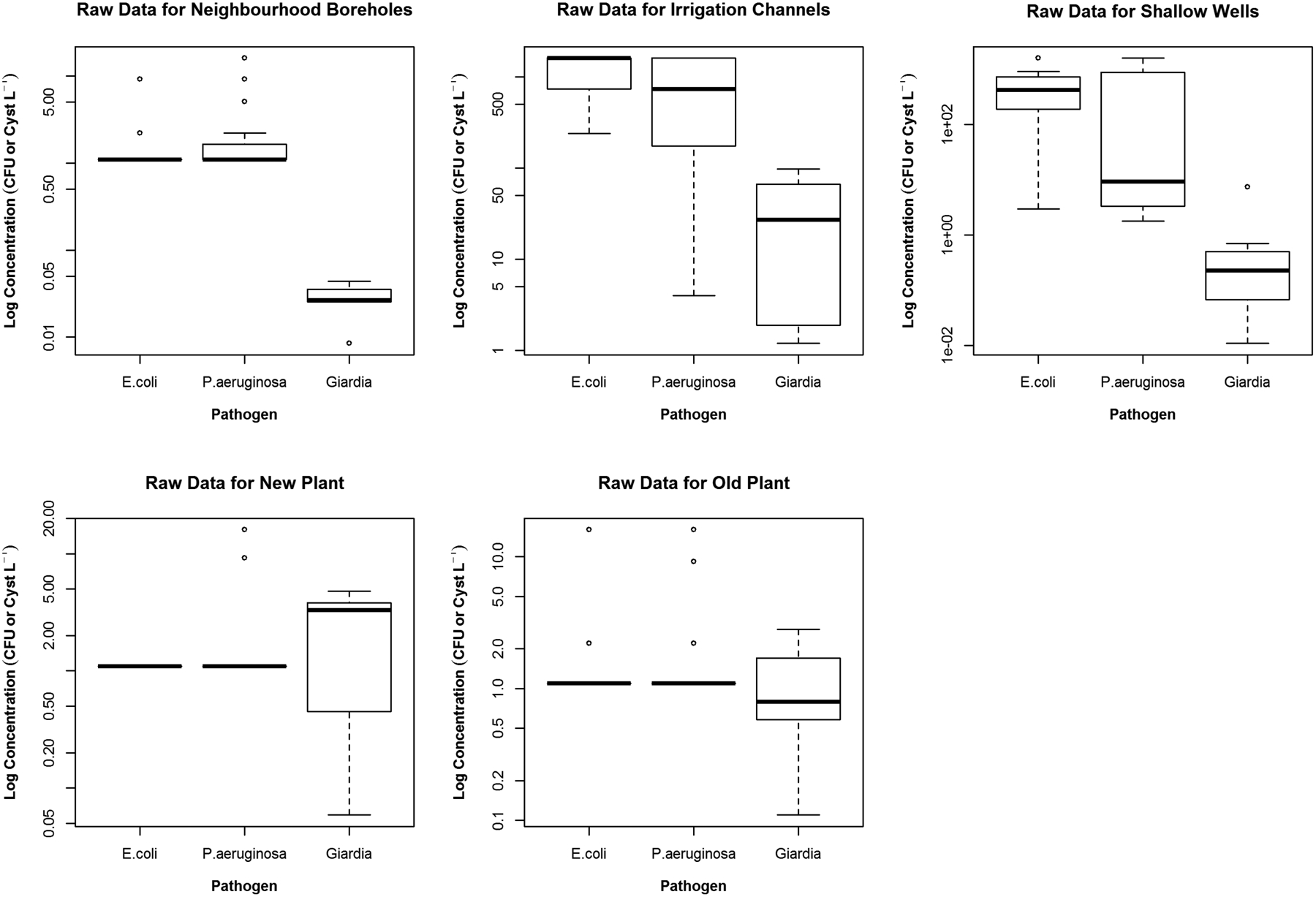
Boxplots depicting the raw data used in the analysis. Note how similar the new and old potable treatment plants are for E. coli and P. aeruginoisa other than some outliers. The untreated water sources, Irrigation Channel and Shallow Wells demonstrate a higher concentration than the other sources, however, with very different value between them, as the Shallow Wells have a slight benefit from subsurface filtration.

ANOVA analysis indicated for both, E. coli and P. aeruginosa values, that samples from treated water were statistically significant in their difference from the untreated water samples (p<0.0001). Giardia, not yet regulated in CAA, was present in all samples except in neighbourhood boreholes, possibly due to it being a deep well with limited natural subsurface filtration. This subsurface filtration effects, is occasionally overestimated for groundwater systems, as culturable enteric viruses (DeBonde et al., 1998) and Giardia (Saad and Schmidt, 1999) have been found in groundwater samples. Giardia was found in all samples of the new and old plants, even if in the cases where E. coli and P. aeruginosa were not detected. This increased prevalence may also be an artifact of the increased sample volume required by the method. In addition, concentrations of Giardia could not be correlated with the concentration of either bacteria. ANOVA analysis for Giardia indicates that while not as strong as for E. coli and P. aeruginosa the treated samples are significantly different of untreated samples (p≅0.0086).

3.2. Risk Modelling Results.

Some level of uncertainty modeling is typically recommended for modern QMRA models such as recently outlined (US EPA 2014). However as a check to determine the level of justification for developing this more complex model a set of point estimates were calculated. As can be seen in table 5 it will be very useful to determine the median and percentile risk values especially for the P. aeruginosa and Giardia risks which are very high in these point estimates. Additionally as discussed earlier table 5 shows the consistent over estimation of the risks when using DL=DL as compared to the 0.5*DL method. Therefore from these point estimates we can see the need for the slightly more complex Monte Carlo method, as well as using the 0.5*DL estimate for the DL range.

Table 5.

Point risk estimates for the three pathogens at each of the water sample types.

	Population Annual Risk Values – Point Estimates
Water Source	Pathogen	0.5*DL	DL
Neighbourhood Boreholes	E. coli Giardia P. aeruginosa	2.28×10−08 5.17×10−04 4.97×10−05	4.55×10−08 1.06×10−03 9.93×10−05
Irrigation Channel	E. coli Giardia P. aeruginosa	3.31×10−05 3.79×10−01 2.41×10−02	3.31×10−05 3.79×10−01 2.41×10−02
New Treatment Plant	E. coli Giardia P. aeruginosa	2.28×10−08 6.35×10−02 4.97×10−05	4.55×10−08 6.35×10−02 9.93×10−05
Old Treatment Plant	E. coli Giardia P. aeruginosa	2.28×10−08 1.46×10−02 4.97×10−05	2.28×10−08 4.28×10−02 9.93×10−05
Shallow Wells	E. coli Giardia P. aeruginosa	7.24×10−06 1.09×10−03 2.23×10−04	7.28×10−06 2.18×10−03 2.75×10−04

The concept of acceptable risk is not a simple one, and is best if an understanding of the current disease burden within the population being modeled (WHO 2008). Since this level of epidemiological data is unavailable for this population, the US EPA (2006) acceptable risk level of 1:10,000 will be used as a baseline acceptable risk level. There is significant discussion in the appropriateness of this acceptable risk level. However, as it is used globally in determining acceptable risk levels in drinking water and recently reinforced for use in modelling illness as well (US EPA 2014)EPA ref, 1:10,000 remains a good target, especially as this research is targeted to assess the need for risk-based regulatory targets in Argentina.

An interesting result is that the new plant, compared with the old plant, has no statistically significant reduction in risk from any of the pathogens modeled when tested through an ANOVA. E. coli was the most similar with an ANOVA p-value of 0.649, P. aeruginosa was the next most similar with p-value = 0.0971 and Giardia having a p-value of 0.015. While this is not unexpected as the processes are not changed, this does inform that the treatment processes of the old plant are likely well maintained and operated, resulting in no statistical difference between the new and old treatment plant. Additionally this may indicate that new equipment and processes may not always infer a higher degree of safety to the consumers.

While it is not a statistically significant result, treated neighbourhood boreholes risk results were very close to being significantly similar to the old plant for P. aeruginosa (ANOVA p-value = 0.00115). All other permutations of water samples for each pathogen were significantly different from each other (p-value < 0.0001)

As can be seen in Figure 2, the untreated irrigation channel water is of the highest risk water source among the water not delivered from the treatment plants. In the case of the untreated irrigation channel water, P. aeruginosa develops the greatest risk of the targeted pathogens. Closely following the irrigation channel are the shallow wells the risks from which are most dominated by Giardia. For all of these water sources Giardia risks are consistently higher than the 1:10,000 acceptable risk level developed by the US EPA. Overall Giardia risks are elevated for all drinking water sources, with P. aeruginosa having a noticeably increased risk for the irrigation channel water, most likely due to the source type: untreated, open for additional contamination and potential for P. aeruginosa growth.

Figure 2.

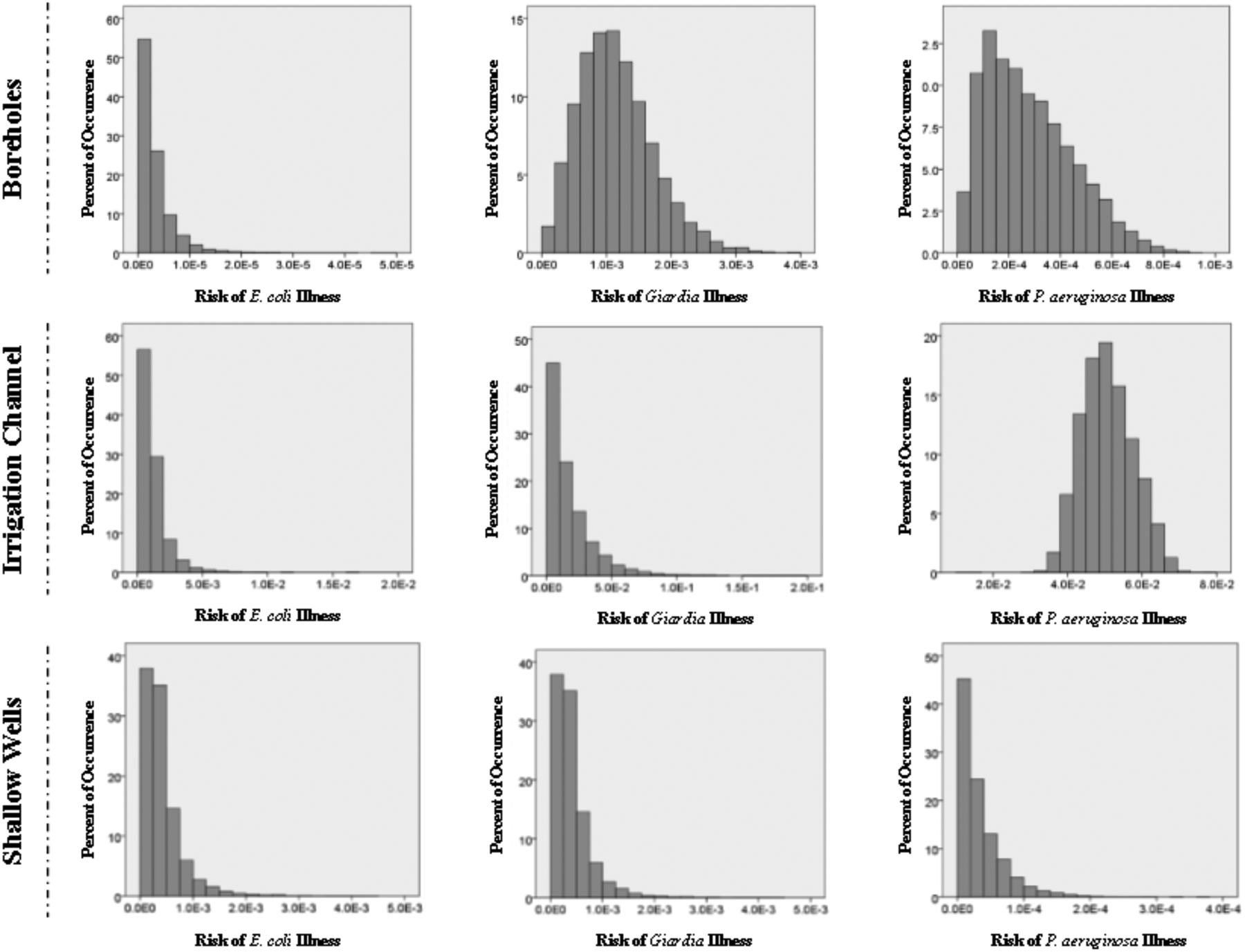
Annual risk estimates for water sources other than the two potable treatment plants. Histograms depict the percent of risk occurrence over 10,000 Monte Carlo iterations. It is important to note that Neighborhood B oreholes have very limited, disinfection only treatment and the Irrigation Channel and Shallow Wells have no treatment at all.

Figure 3 shows the estimated risk levels for the new and old treatment plants. The results of an ANOVA demonstrated the difference in risk reduction is negligible between the new and old treatment plants (p = 0.0089). In the case of these two treatment plants Giardia is driving the overall risk from direct ingestion of the produced water. After that is P. aeruginosa illness risks showing a wider distribution of risk estimates than E. coli or Giardia, which are skewed to the lower risk regions. It is evident that these treatment plants are realistically only achieving appropriate health risk protection for pathogenic E. coli, certainly not for Giardia and highly unlikely for P. aeruginosa. Since these plants are using standard flocculation and rapid filtration they likely would see improved treatment efficacy for Giardia and P. aeruginosa by including an additional disinfection process such as ozone or UV. An additional consideration would be for improving or adding an additional filtration process, a QMRA developed for the exact system configuration AdN operates will greatly assist in making these decisions. However likely a more cost-effective option would be to install slow sand filtration as it is effective up to 5 log₁₀ reductions for protozoa and 3 log₁₀ reduction for bacteria (Hijnen et al. 2004; Smeets, 2011; Weir et al., 2011). A summary of risk values for each group and pathogen set can be seen in Table 6.

Figure 3.

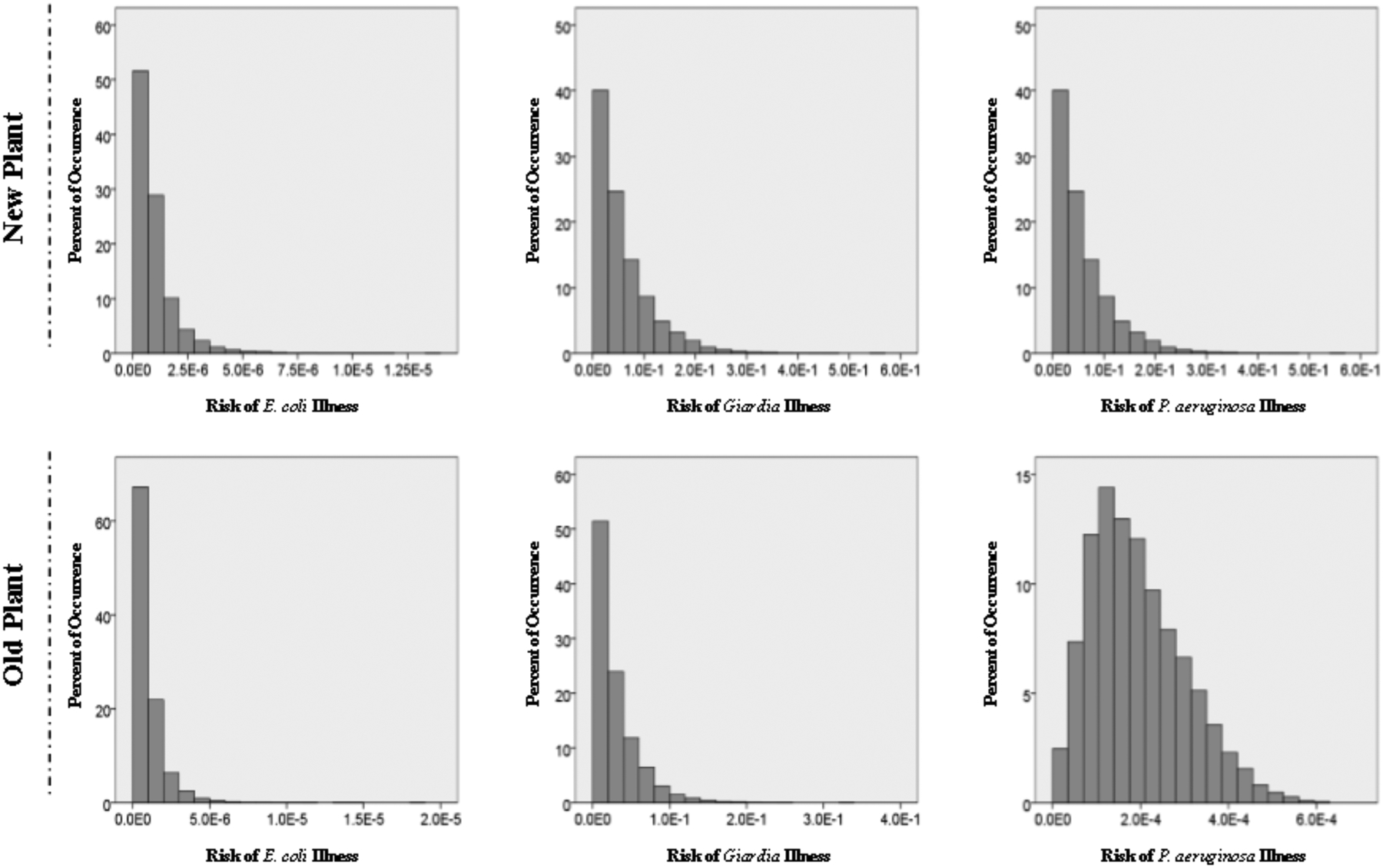
Annual risk estimates for the two potable treatment plants. Histograms depicting the percent of risk occurrences from 10,000 Monte Carlo iterations.

Table 6.

Population annual risk values, those risk estimates in bold-italics are greater than the EPA acceptable risk level of 1:10,000.

		Population Annual Risk Values*
Water Source	Pathogen	Minimum	Maximum	Median	Lower 95th Percentile	Upper 95th Percentile
Neighbourhood Boreholes	E. coli	1.50×10−8	4.90×10−5	2.23×10−6	4.54×10−7	1.02×10−5
	Giardia	1.57×10−6	3.96×10−3	1.07×10−3	3.25×10−4	2.21×10−3
	P. aeruginosa	1.11×10−4	3.88×10−2	7.35×10−3	1.70×10−3	1.90×10−2
Irrigation Channel	E. coli	1.32×10−4	1.23×10−2	8.86×10−4	3.03×10−4	3.22×10−3
	Giardia	9.68×10−7	2.10×10−1	1.20×10−2	8.02×10−4	5.41×10−2
	P. aeruginosa	2.93×10−1	9.57×10−1	7.86×10−1	6.50×10−1	9.00×10−1
New Treatment Plant	E. coli	3.10×10−9	1.27×10−5	6.82×10−7	1.53×10−7	2.89×10−6
	Giardia	6.62×10−6	5.84×10−1	4.04×10−2	2.87×10−3	1.76×10−1
	P. aeruginosa	1.68×10−5	2.01×10−2	4.76×10−3	1.25×10−3	1.12×10−2
Old Treatment Plant	E. coli	6.54×10−9	1.67×10−5	6.87×10−7	1.53×10−7	2.87×10−6
	Giardia	5.72×10−7	2.44×10−1	1.92×10−2	1.39×10−3	8.83×10−2
	P. aeruginosa	1.12×10−4	2.21×10−2	4.74×10−3	1.29×10−3	1.10×10−2
Shallow Wells	E. coli	2.80×10−5	5.08×10−3	3.10×10−4	1.07×10−4	1.12×10−3
	Giardia	8.32×10−6	9.98×10−1	5.01×10−3	2.31×10−4	1.12×10−1
	P. aeruginosa	1.17×10−8	1.36×10−2	7.03×10−4	5.15×10−5	3.24×10−3

A differential sensitivity analysis was performed using the differential method. As can be seen from the results of the sensitivity analysis (figure 4), the pathogen concentration was the most sensitive variable in the QMRA model. Following closely after the concentration is the ingestion rate. Considering E. coli had the widest range in dose response parameter size it is not unsurprising that the sensitivity to the dose response parameter value was higher than the ingestion rate for E. coli. To improve the uncertainty from the pathogen concentration, more sampling is required. This will expand the current data set and allow for improved probability distribution optimization. There is a possibility that additional sampling may not address this issue, however, improved pathogen characterization can still be recommended for a broader hazard and risk characterization. Performing surveys within this peri-urban area to determine local ingestion rate patterns would allow for decreasing the impact ingestion rate has on model uncertainty, however, pathogen concentration should be the highest priority.

Figure 4.

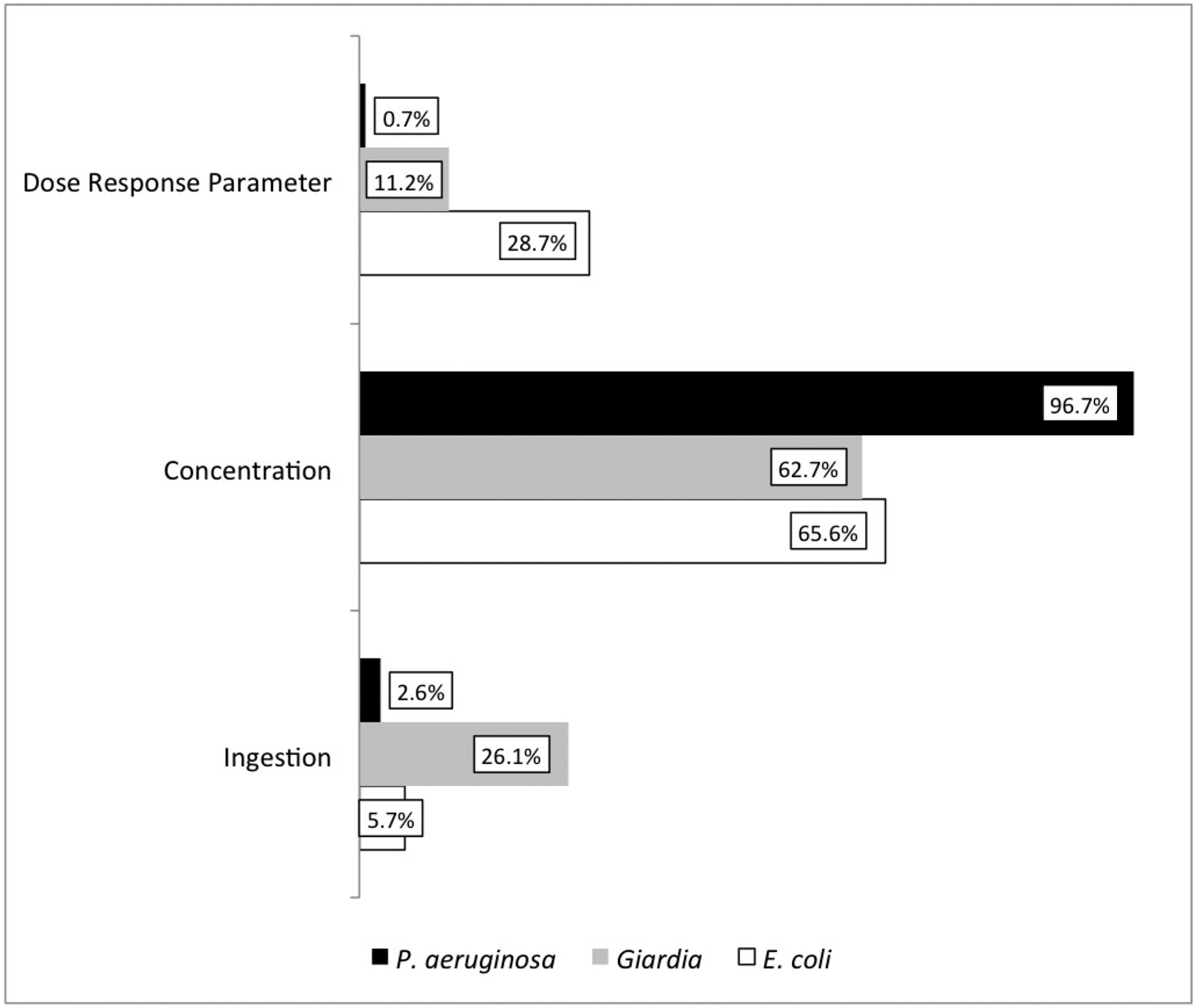
Sensitivity analysis plot for QMRA model using differential method, showing that the pathogen concentration was the most significant variable to the model uncertainty.

The results of the QMRA model demonstrating biased control for E. coli risk is not surprising considering that the treatment systems (old and new) are comprised of; coagulation, clarification, rapid sand filtration and chlorine based disinfection. This type of system is quite capable of treating simpler microorganisms such as E. coli but is more challenged by more robust ones such as Giardia. While filtration can be effective for Giardia it is dependent on proper maintenance the current Cryptosporidium risks are unknown, therefore, a final barrier of non-oxidant disinfection would present a greater level of protection. Given the costs, however, those costs of the additional processes may be better spent to connect more of the population to the treated water.

4. Discussion

Both the microbiological analysis and risk model results demonstrate that the water considered safe from the treatment process still contains a significant level of gastrointestinal pathogens, even those with current regulations (E. coli and P. aeruginosa). Also the presence of Giardia in all samples demonstrates that despite the assumption in the regulations, the absence of bacteria does not result in the absence of further pathogenic hazards including protozoa. Therefore, the entirety of this population in the peri-urban area is likely consistently exposed to gastrointestinal pathogens including a serious health threat such as Giardia. The irrigation channel is one of the water sources for both the new and old treatment plants, therefore, considering significant differences between treated and untreated water (p < 0.0001) we can infer that while still suboptimal the treatment system is capable of health protections. Unfortunately the effects of the distribution system cannot be ascertained from this research. As it likely has an effect on the resulting water quality should be investigated in future research.

The treatment systems while not optimal, is still an improvement compared to households using untreated water. Therefore it should be highlighted that each sub-population’s risks is determined by their drinking water source, giving evidence towards the need for infrastructure improvement. The worst case scenario has also been demonstrated as being for those people using untreated water, therefore, recommending their water source being upgraded as soon as possible.

It is unfortunate that his model cannot be compared to pathogen incidence and outbreak data for this community or Argentina. This is due to the very limited testing or reporting requirements when people present to hospital or general practitioners for gastrointestinal symptoms. Therefore the only tracking that is possible is levels of diarrhea and nothing pathogen(s) specific, thus complicating the targeting of future regulations. Additionally attempting to compare agent specific risks not including common viral agents would be erroneous. An additional recommendation on the regulatory side would be to investigate or implement discretionary or mandatory testing for etiological agent related to severe diarrhea, although this may be cost prohibitive. However, disease burden from key pathogens such as E. coli, Giardia, or Cryptosporidium may warrant this additional centralized cost.

The QMRA model shows the need for Argentina to consider advancements to their current drinking water regulations. The current method with targets for E. coli, P. aeruginosa and indicator concentrations are not providing adequate public health protections for their citizens. The produced water from both the new and old treatment plants provide risk levels well above the 1:10,000 that has been used globally in drinking water assessments. Giardia can be and evidently is an issue for this peri-urban area of Salta Argentina, however, future research should also focus on the relative burden of both Cryptosporidium and Giardia to the community risks. This means that regulations not directly addressing this pathogen or parasites in general represents a significant failing in their potential health protections. It is strongly recommended from these results that similar research is performed for Cryptosporidium and virus targets (initially targeting rotavirus and norovirus). These pathogens pose known health risks from potable water systems and could possibly be a hazard for this community as well. This preliminary research presents weight of evidence to investigate the need to expand current regulations to include more than the current set of pathogens. The current and proposed follow on research would illuminate the real underlying risks to this specific community as well as this type of community, and enlighten how to address these risks.

The efforts in the development of a water safety plan (WSP) are notable and commendable, however, semi-quantitative approaches in WSP often are not sufficient to support decisions. The QMRA is primarily a tool to be used in any risk management framework and can then provide objective and quantitative support for decision making in management thereby bolstering their WSP with a QMRA (WHO, 2014). By including a QMRA into the WSP, projections can be made regarding longevity of processes or infrastructure for the water treatment systems. The QMRA informed WSP can also then be used to target investments into water treatment infrastructure for this area and further into the future. The current QMRA in this research would be a first step to incorporating QMRA into the WSP, however, the risk model needs to be bolstered with additional data.

With the failing of drinking water regulations so follows the failing of engineering design in a regulatory driven environment. The designing firm could have alleviated some of these risks in the new or old plant, by looking to minimizing risks from known pathogens rather than only following requisite regulations. This is compounded by the peri-urban area having low socioeconomic capabilities, meaning their personal protective options are severely limited. Overall we also see how a less than optimal regulatory decisions and engineering design can work in tandem to harm a population, the opposite of what we aim for.

5. Conclusions:

The sampling protocol and microbial analyses represented a realistic spread of annual water conditions for Vaqueros Argentina. This peri-urban area of Salta demonstrates a lack of potable water resources. This population is not properly serviced and the regulations intended to support or improve their health are failing especially in the light of protozoa risks. The QMRA model presented in this research provides weight of evidence to support inclusion of pathogenic protozoa into the current regulations. The input of viruses into the regulations could not be investigated as they were not included in the microbial analyses, something that should be targeted for future research.

The microbial analysis and QMRA model also demonstrate that the current treatment system those few citizens have access to, is not sufficient even for the limited regulations present. Overall there is significant work that needs to be accomplished to improve access to safe drinking water for Vaqueros. In Argentina water utilities are only obliged to meet CAA regulations, which has been a sustainable solution for Argentina’s utilities despite the quality standards being based on a limited number of indicator organisms and bacterial pathogens. Therefore it is necessary to demonstrate in a more objective manner, that health risks to which the population is exposed due to lack of control of other pathogens is high, and it is essential to take steps to ensure public health. CAA has several shortcomings compared with other laws, especially those in developed countries like the USA, Australia and the Netherlands, and even with many Latin American laws. CAA only refers to indicator organisms and a small set of pathogenic bacteria, leaves process selection to local companies to choose and implement to comply with the standards. In many cases such as in Vaqueros this is insufficient even to control indicators. Objective evidence to start changing this legislation begins with this QMRA that with careful research can be extrapolated to other systems of Salta and Argentina.

Highlights:

• Argentine drinking water regulations need to account for pathogenic protozoa

• Indicator dominated drinking water regulations limit drinking water protection.

• Design for peri-urban regions require combined WSP, QMRA and engineering analysis