Abstract
A scientifically sound integrated assessment modeling (IAM) system capable of providing optimized cost-benefit analysis is essential in effective air quality management and control strategy development. Yet scenario optimization for large-scale applications is limited by the computational expense of optimization over many control factors. In this study, a multi-pollutant cost-benefit optimization system based on a genetic algorithm (GA) in machine learning has been developed to provide cost-effective air quality control strategies for large-scale applications (e.g., solution spaces of ~1035). The method is demonstrated by providing optimal cost-benefit control pathways to attain air quality goals for fine particulate matter (PM2.5) and ozone (O3) over the Pearl River Delta (PRD) region of China. The GA is found to be > 99% more efficient than the commonly used grid searching method while providing the same combination of optimized multi-pollutant control strategies. The GA method can therefore address air quality management problems that are intractable using the grid searching method. The annual attainment goals for PM2.5 (< 35 μg m−3) and O3 (< 80 ppb) can be achieved simultaneously over the PRD region and surrounding areas by reducing NOx (22%), volatile organic compounds (VOCs, 12%), and primary PM (30%) emissions. However, to attain stricter PM2.5 goals, SO2 reductions (> 9%) are needed as well. The estimated benefit-to-cost ratio of the optimal control strategy reached 17.7 in our application, demonstrating the value of multi-pollutant control for cost-effective air quality management in the PRD region.
Keywords: Air pollution control strategies, Cost-benefit analysis, Multi-pollutant optimization, Genetic algorithm, Ozone, PM2.5
Graphical Abstract
1. Introduction
Tropospheric ozone (O3) and fine particulate matter (PM2.5) impose adverse effects upon human health and ecosystems. To alleviate these impacts, the China State Council has implemented substantial air quality control policies to reduce their precursor emissions. Since the Air Pollution Prevention and Control Action Plan was promulgated in 2013, the Pearl River Delta (PRD) region has taken the lead in effectively attaining the national annual averaged PM2.5 standard of 35 μg m−3 in 2015 (Li et al., 2019a). However, O3 concentrations in the PRD region have exhibited an increasing trend since 2015, and the number of days with elevated O3 pollution in PRD greatly exceeds the number of days with elevated levels of other pollutants combined. Therefore, the current air quality control strategy for PRD emphasizes the need for coordinated control of both PM2.5 and O3 pollution.
Integrated assessment modeling (IAM) for cost-benefit analysis (CBA) is considered an effective tool to guide the design of control strategies (Amann et al., 2011; Daily et al., 2009; Harmsen et al., 2015; Wegner and Pascual, 2011; Xing et al., 2017a). For instance, the Greenhouse Gas-Air Pollution Interactions and Synergies (GAINS) model, which was developed by the International Institute for Applied Systems Analysis (IIASA) (Amann et al., 2011), has been widely used to assess the benefits and costs of air quality improvement (Amann et al., 2011b; Amann et al., 2008; Cheewaphongphan et al., 2017; Li et al., 2019b). GAINS uses reduced-form source-receptor relationships derived from a sample of sensitivity simulations using the European Monitoring and Evaluation Programme (EMEP) (Simpson et al., 2012). Nevertheless, secondary organic aerosols and nonlinear atmospheric chemistry associated with the joint control of pollutant precursors are not addressed well by the GAINS model (Amann et al., 2011). As a new policy-oriented IAM, the Air Benefit and Cost and Attainment Assessment System (ABaCAS) can provide a streamlined cost-benefit analysis for the development of effective multi-pollutant control strategies (Xing et al., 2017a). ABaCAS incorporates an advanced response surface model (RSM) that can quantify the nonlinear interactions of O3 and PM2.5 to their precursor emission reductions quickly with minimal computation. The RSM used in ABaCAS was developed by applying advanced statistical interpolation techniques to meta-simulation scenarios performed with a comprehensive photochemical air quality model (Wang et al., 2011; Xing et al., 2011; Zhao et al., 2015a; Zhao et al., 2015b). An advantage of ABaCAS is that the nonlinear interactions among different precursor emissions can be simulated relatively well. However, the previous ABaCAS system did not contain a cost-benefit optimization module, and thus did not facilitate assessments of cost-effective pollution control strategies.
A series of research efforts have been undertaken to improve the development of cost-effective control strategies for PM2.5 (Amann et al., 2001; Carnevale et al., 2012; Harley et al., 1989) and O3 (Carnevale et al., 2012; Carnevale et al., 2007; Cohan et al., 2006; Fu et al., 2006; Guariso et al., 2004). In particular, the LEast-COst control strategy optimizer (LE-CO) module was recently developed and applied in ABaCAS to identify optimized cost-benefit control strategies for air quality in the Beijing-Tianjin-Hebei (BTH) region of China (Xing et al., 2019). In LE-CO, the polynomial function RSM (pf-RSM) significantly improves the computational efficiency of estimating the air quality response to emission changes compared to the previous RSM (Xing et al., 2018). However, the high computational expense of the grid searching (GS) optimization method limits the applicability of LE-CO to cases with ≤ 5 precursors and ≤ 5 regions.
Machine learning (ML) methods are suitable for addressing complex problems that involve massive combinatorial spaces or nonlinear processes, which conventional procedures either cannot solve or can tackle only at great computational cost (Butler et al., 2018). The genetic algorithm (GA), a well-known ML algorithm inspired by natural selection processes in biology (Goldber and Holland, 1988), is a robust and effective technology for solving multi-objective optimization problems (Filipic et al., 1999; Sirikum and Techanitisawad, 2006; Song et al., 2019). The GA has been widely used in environmental management and engineering (Collins et al., 2010; Hong et al., 2018; Rogers et al., 1995; Seyedpour et al., 2019; Von Arx et al., 1998) and has been successfully applied in designing ozone control strategies (Loughlin et al., 2000; Reis et al., 2005). In this study, the GA was implemented into LE-CO to address multi-pollutant optimization problems with large solution spaces (~1035). The Environmental Benefits Mapping and Analysis Program-Community Edition (BenMAP-CE, version 1.4) (Fann et al., 2018; Sacks et al., 2018) was then used within ABaCAS to estimate the health benefits of the optimized control strategies. This innovative system, named ABaCAS-Optimized Edition, or ABaCAS-OE, was applied to generate the optimized control strategies to meet specific air quality goals for PM2.5 and O3 in PRD, and the performance of ABaCAS-OE was evaluated for the PRD case study. The ABaCAS-OE is available for download upon request (http://www.abacas-dss.com/abacas/Default.aspx).
2. Materials and Methods
2.1. Overview of the ABaCAS-OE System
The ABaCAS-OE system was designed to generate the cost-benefit optimal control strategies for PM2.5 and O3 air quality attainment. An overview of ABaCAS-OE is displayed in Fig. 1. First, annual PM2.5 and O3 goals were set to 35 μg m−3 and 80 ppb, respectively, for cities in the PRD region in 2020, the target year of the 13th Five-Year Plan in China. Air quality is required to meet these Class II National Ambient Air Quality Standard levels according to the 13th Five-Year Plan of Environmental Protection in PRD. For cases where the goals cannot be achieved through full control of all anthropogenic emissions in Domain 3, the goals are relaxed in the ABaCAS-OE system (Fig. 2). Second, the LE-CO module including the GA (hereafter GA-LECO) is used to select the optimal combination of emission controls to meet the air quality goals with the least cost based on the International Control Cost Estimate Tool (ICET). Third, the optimized control strategies are input into BenMAP-CE to estimate the monetized health benefits resulting from the PM2.5 and O3 reductions based on concentration-response (C-R) functions from epidemiology studies. Finally, a sorted list of control strategies that meet the air quality goals at relatively low cost is reported.
Fig. 1.
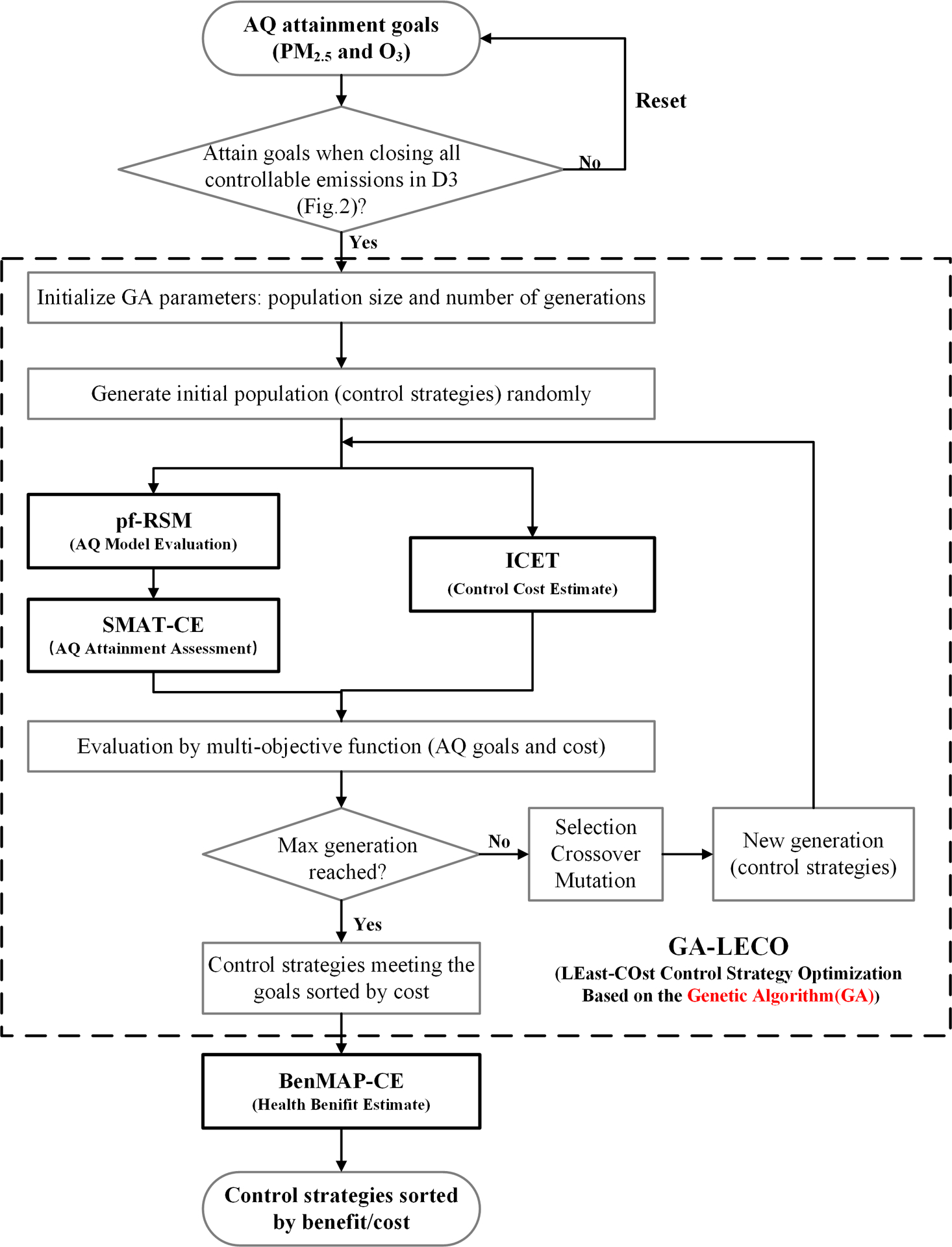
Overview of the Air Benefit and Control and Attainment Assessment System-Optimized Edition (ABaCAS-OE). AQ, air quality; SMAT-CE, Software for Model Attainment Test-Community Edition; GA-LECO, LEast-COst control strategy optimization based on the genetic algorithm (GA); pf-RSM, Response Surface Model with polynomial functions; ICET, International Control Cost Estimate Tool; BenMAP-CE, Environmental Benefits Mapping and Analysis Program-Community Edition.
Fig. 2.
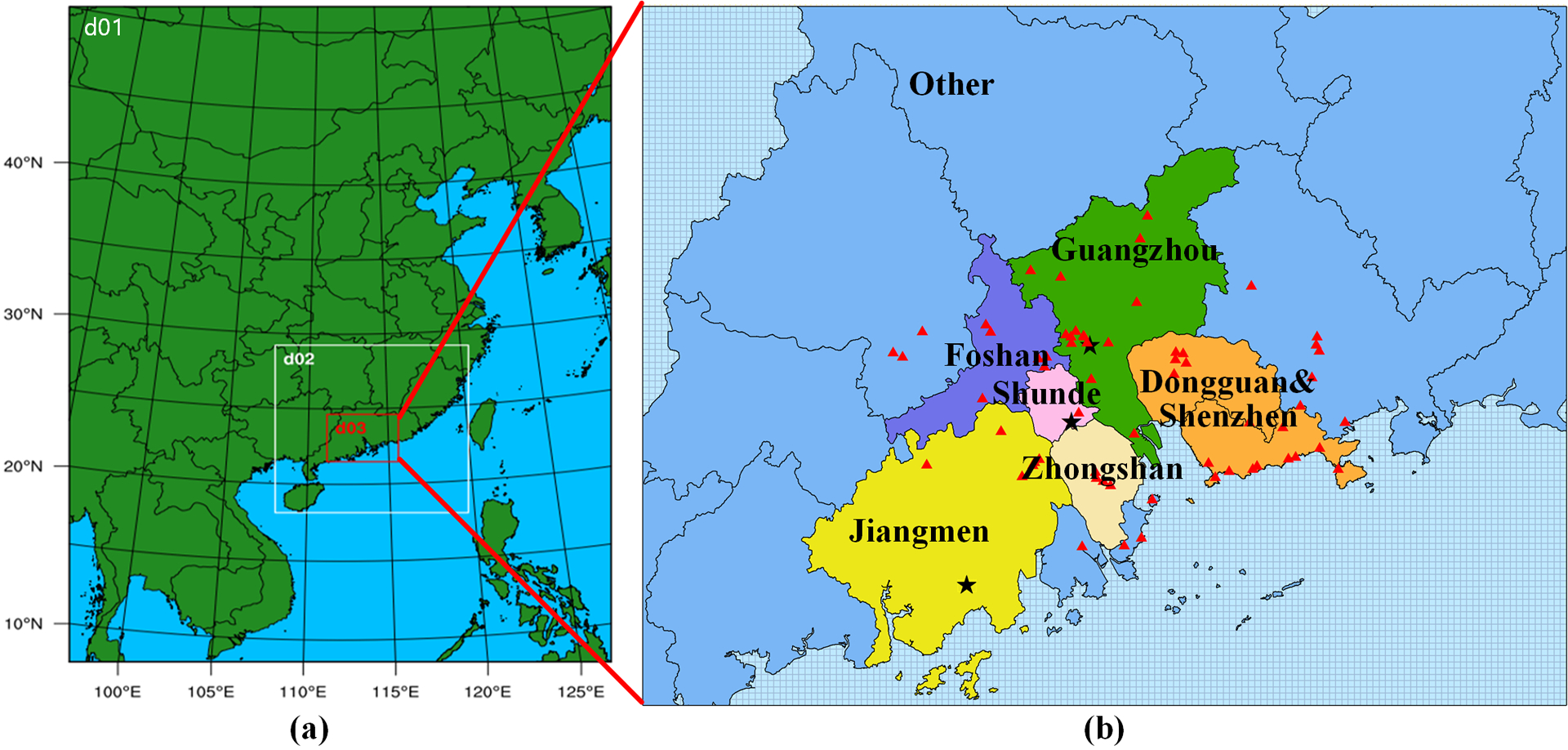
(a) WRF-CMAQ simulation domains: 27 km (d01), 9 km (d02), and 3 km (d03); (b) regions defined in the pf-RSM with air quality monitor site locations. The triangular points represent the monitors in the PRD, the pentacle points represent the selected monitors for evaluation of the model performance.
In the functional module of GA-LECO, the GA parameters, including population size and the number of generations, are set first. The “population size” refers to the number of control strategies that are considered in a given generation, and the “number of generations” refers to the number of cycles applied in the GA to generate a set of optimized control strategies. As discussed in detail in Section 3.2, the population size and the number of generations were set to 400 and 180, respectively, in this study. After setting these parameters, the initial population of control strategies was randomly generated to begin the operation process of GA-LECO. Third, the performance of each strategy was evaluated by a multi-objective function accounting for total control costs and air quality concentrations associated with the strategies. The ICET cost module was applied to estimate the control cost associated with each control scenario based on the marginal cost curves of pollutant controls (Sun et al., 2014). The pf-RSM air quality module was run to provide the estimated response of PM2.5 and O3 concentrations to emission changes (Wang et al., 2011; Xing et al., 2011; Xing et al., 2017b; Zhao et al., 2017). Fourth, the Software for Model Attainment Test-Community Edition (SMAT-CE), an air quality attainment assessment module that combines the simulated results from the pf-RSM and monitor data using an improved Voronoi Neighbor Averaging (eVNA) algorithm, was applied to improve the accuracy of predicted pollutant concentrations (Ding et al., 2016; Wang et al., 2015; Xing et al., 2017a). During the GA search process, steps of evaluating control strategies, selection, crossover, and mutation generated a new generation of control strategies such that the cost of the strategies generally decreased by generation. Finally, the algorithm terminated when the maximum number of generations was reached, and a cost-sorted list of optimized control strategies was output. Further description of the GA is provided in Section 2.2.
2.2. Optimization Method
As one of the most popular ML algorithms, the GA was developed in the 1970s by Holland (1975). It is a random search optimization algorithm that simulates biological evolution theory and searches for the optimum of an objective function (Song et al., 2019). Unlike other search techniques, the GA simultaneously processes a population of solutions and requires no specific knowledge about the problem space to successfully search for good solutions. Also, the GA exhibits a high degree of robustness in finding ideal solutions to difficult optimization problems (Goldberg, 1989; Holland, 1975). These characteristics have led to the increasing use of the GA in ML (Filipic et al., 1999; Giordana and Neri, 1996; Massoudieh et al., 2008; Mousavi et al., 2014; Seyedpour et al., 2019). The evolutionary strategy of GA in this study is shown in the dotted rectangle in Fig. 1. Here, the GA is initiated through random a generation of a specified number of control strategies, and then each control strategy is evaluated by the multi-objective function. Subsequently, optimal control strategies are combined to create offspring by the selection, crossover, and mutation, and the scheme is repeated over many generations until the maximum number of generations is reached (Stramer et al., 2010).
The GA evolution cycle is based on three fundamental operators: (1) Selection: This operator selects effective control strategies with low fitness values to participate in crossover to transfer the beneficial control factors to offspring. In this study, the rank selection method is applied by directly comparing the fitness values without contrasting looping statements (Song et al., 2019). (2) Crossover: This operator generates high-quality “child” control strategies by swapping the control factor values of the two-parent control strategies identified by the selection operator. The crossover probability is usually very high, in the range of [0.7, 1], because crossover occurs sparsely if the probability is too small and is inefficient for evolution (Elhoseny et al., 2018; Yang, 2014). (3) Mutation: This operator introduces random variation in the reduction rate of control factors after crossover. The mutation operator maintains the diversity of the population and avoids entrapment of the GA in local optima. Mutation rates of less than 5% are typically applied in the current literature, but exceptional cases have considered much higher rates. In this system, the crossover probability and mutation rate were set to 1 and 0.05, respectively, to maximize the retention of elite individuals to enhance the population characteristics.
In our work, the objective function was optimized for air quality goals of PM2.5 and O3 and control costs, all of which depended on the emission reduction levels of control factors. The search sample space was defined as emission reduction levels from 0 to 90%, with reduction levels stepped by 10%, resulting in 1035 possible control strategies based on the combination of different reduction rates for the control factors. The control factors consisted of five pollutants in seven regions over PRD. The pollutants were NOx, SO2, NH3, volatile organic compounds (VOCs; i.e., VOC and intermediate VOC), and primary PM (including primary organic aerosol (POA) and other primary PM), and the regions were Shunde (SD), Foshan (FS), Guangzhou (GZ), Jiangmen (JM), Zhongshan (ZS), Dongguan and Shenzhen (DG&SZ), and other regions (OTH). NH3 emission control can be an efficient strategy to reduce PM2.5, but the costs of controlling NH3 in PRD are much higher than those of primary PM and SO2. Moreover, the air quality standard of PM2.5 in PRD can be achieved by controlling primary PM and SO2 emissions alone, and so the emission reduction ratio for NH3 was set to 0 for all control strategies designed in this study. The objective function is defined as follows:
Minimize
| (1) |
Subject to
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where F is the fitness of the control scenario (to be minimized); Cost is the cost of the control scenario; Costmax is the cost of the control scenario when reduction ratios of all control factors reach maximum; ΔConcsp is the concentration delta between the control concentration and goal concentration for pollutant sp (i.e., PM2.5 and O3); ΔConcsp,max is the concentration delta between the baseline concentration and goal concentration for pollutant sp; is the cost for pollutant p (i.e., NOx, SO2, NH3, VOCs, and primary PM) at region r (i.e., SD, FS, GZ, JM, ZS, DG&SZ, and OTH); is the control concentration for pollutant sp at region r; Concsp,goal is the air quality goal of pollutant sp; and is the baseline concentration for pollutant sp at region r. The cost for pollutant p over all control technologies is calculated with (8):
| (8) |
| (9) |
| (10) |
where is the cost of technology i for pollutant p at region r; UCp,i is the unit cost of technology i for pollutant p; is the emission reduction by the technology i for pollutant p at region r; is the baseline emissions of pollutant p at region r in sector s where control technology i is applied; and is the emission reduction ratio of pollutant p at region r, which is the optimized variable based on the GA.
In this study, the data of was derived from the collaborative research team of Tsinghua University and South China University of Technology. The parameters of UCp,i were based on Zhang et al. (2020). The cost estimated refers to the cost related to control technology application, while the social cost (e.g., subsidy to carry out the control policy) was not considered in ICET (Xing et al., 2019). The average control concentration of sp over monitors in a region is calculated with (11):
| (11) |
where is the observed concentration for pollutant sp at monitoring site j of region r; is the function of modeled control concentration of pollutant sp at monitoring site j to based on the pf-RSM; is the modeled baseline concentration of pollutant sp at monitoring site j based on the pf-RSM; and n is the number of monitoring sites in region r. In this study, the PM2.5 and O3 monitoring data over PRD were obtained from the Chinese Guangdong Environment Information Issuing Platform (http://www.gdep.gov.cn/). The response of O3 and PM2.5 concentrations to individual emissions changes (ΔConc) is calculated with the pf-RSM as follows:
| (12) |
where ΔConc is the response of O3 and PM2.5 concentrations to individual emissions changes; EP1 and EP2 are the emission change rates of two precursors (P1 and P2 can denote any two of NOx, VOCs, NH3, SO2, or POA) emissions associated with the baseline; a and a′ are the highest degrees of precursors; Ai, , Bi, C are the coefficients of terms; the superscript i, j are the degrees of the polynomials for the precursors; ai,1 and ai,2 are the polynomial degrees of precursors P1 and P2, respectively; the superscript b is the total number of interaction terms between P1 and P2 (i.e., ai,1 multiplied by ai,2); and EPM is the emission change ratio of primary PM relative to the baseline.
The selection of terms to represent pollutant response in the pf-RSM are based on Xing et al. (2018), and the coefficients Ai, , Bi, C were fit to daily concentrations of O3 and PM2.5 as well as the precursor concentrations of NOx, VOCs, NH3, SO2, and POA in seven regions of PRD. The terms in Eq.(12) for O3 and PM2.5 in single-region RSMs are summarized in Table S1. The single-region RSMs were combined using the pf-RSM technique accounting for multi-region interactions from three components: 1) local formation of PM2.5 and O3 related to their precursor emissions changes at receptor regions; 2) regional transport of pollutants from source regions to receptor regions; 3) inter-regional chemical interactions among multiple regions (Xing et al., 2017b). The simulation periods were January, April, July, and October, representing the average concentration in each season in 2015. Annual average PM2.5 was represented by the average concentration of these four months (Wang et al., 2018; Yin et al., 2017b). O3 is a seasonal pollutant with a higher concentration in summer and autumn. Therefore, the annual average O3 was represented by a two-month (July and October) average of monthly 90th percentile of maximum daily 8-hr averaged O3 (Monthly 90th per MDA8 O3) concentration (equation provided in Section S1). The SMAT-CE was used to adjust the simulation results with the monitor data to reduce the model bias. Four-month average PM2.5 concentrations were projected to the annual mean concentrations of PM2.5 in this study, as follows. First, the ratio of the twelve-month average to the four-month average of monitor data in 2015 was calculated. Next, the resulting ratio was multiplied by the four-month average of the monitor-adjusted modeling results under different control scenarios to represent the annual mean concentrations (equation provided in Section S2). Similarly, for O3, the average of the Monthly 90th per MDA8 O3 in July and October under different control scenarios was multiplied by the ratio of the annual 90th percentile of maximum daily 8-hr averaged O3 concentration (Annual 90th per MDA8 O3) to the two-month average of Monthly 90th per MDA8 O3.
2.3. Health Benefits Evaluation
The health impact function was used to quantify air pollution-related health impacts in BenMAP-CE.
| (13) |
where Δy is the change in the health or environmental effect; y0 is the incidence rate in the base year; Pop is the exposed population; β is the unitless C-R function coefficient derived from the relative risk (RR) reported in epidemiologic studies; and Δx is the estimated change in pollutant concentration exposure.
The population data for exposure in 2015 were extracted from Landscan (https://landscan.ornl.gov/), which is a community standard for global population distribution data. The mortality rates in 2015 were gained from the GBD results tool (http://ghdx.healthdata.org/gbd-results-tool) (Ding et al., 2019). Health benefits for five leading causes of PM2.5-related premature mortality (lung cancer, stroke, chronic obstructive pulmonary disease, lower respiratory infection, and ischemic heart disease) and four leading causes of O3-related premature mortality (coronary heart disease, stroke, cardiovascular disease, and hypertension) were estimated. C-R function coefficients used to estimate O3-related health impacts were based on Yin et al. (2017a), and those for estimating PM2.5-related health impacts were based on Cohen et al. (2017). The economic benefits associated with the health impact estimates were quantified using the willingness to pay (WTP) method. The unit value of avoided premature deaths was 1.68 million Chinese Yuan (CNY) based on Xie (2011).
2.4. Case Study Domain
The Weather Research and Forecasting (WRF, version 3.9.1) (NCAR, 2017) model was used to simulate meteorological conditions in 2015 to drive simulations with the Community Multiscale Air Quality (CMAQ, version 5.2) (U.S.EPA, 2017) model under various emission control strategies. Three nested simulation domains were used as illustrated in Fig. 2a. The vertical resolution for all domains was based on twenty layers from the surface to the tropopause. Domain 1 (d01) covers most of China and some other parts of Asia with 27 km × 27 km horizontal resolution, Domain 2 (d02) covers southeastern China with 12 km × 12 km resolution, and Domain 3 (d03) covers all of PRD with 3 km × 3 km resolution and was the focus of this study. The innermost domain was divided into seven major regions: SD, FS, GZ, ZS, JM, DG&SZ, and OTH. Air quality monitoring data from the national network were used in representing local air quality in each city (Fig. 2b). The initial and boundary conditions for Domain 1 were based on the default profile, and those for Domain 2 and Domain 3 were extracted from simulation results on Domain 1 and Domain 2, respectively. The emission inventories for Domain 1 and Domain 2 were provided by Tsinghua University (Ma et al., 2017), and the high-resolution emission inventory for Domain 3 was developed by the collaborative research team of Tsinghua University and South China University of Technology. The boundary conditions used for simulations over Domain 3 were estimated from simulations over Domain 2 to represent the impacts of inflow from regions outside of PRD. The same boundary conditions were used in multiple simulation scenarios to build pf-RSM.
3. Results and Discussion
3.1. Validation of WRF-CMAQ and pf-RSM Performance
The performance of the WRF model was evaluated using the meteorological observation data at the Sugang and Ronggui monitoring sites centrally located in the domain of this study as in our previous paper (Li et al., 2019a). Table S2 provides model performance statistics for temperature, wind speed, and relative humidity for January, April, July, and October in 2015. The Pearson correlation coefficient (R) for wind speed is about 0.5 or greater at the sites, but the wind speed is biased high (NMB: 101.02%) in January at Sugang. For temperature and relative humidity, the R is greater than 0.7, and the NMB ranges from −4.73% to 1.22% and 2.99% to 15.83%, respectively. These values are within typical performance ranges in meteorological modeling studies (Wang et al., 2016). The CMAQ model performance was evaluated by comparing model predictions with observations from three representative sites in the PRD air-quality-monitoring network. The sites are located in GZ, SD, and JM and represent urban (Guangdong Business College), industrial (Sugang), and rural (Duanfen) locations, respectively (Table S3). The R is higher for O3 than for PM2.5, which ranges from 0.71 to 0.79. Generally, the NMBs for PM2.5 and O3 predictions meet the recommended value for acceptable performance (NMB±30% for PM2.5, ±15% for O3) (Emery et al., 2017), and range from −29.42 to 28.48% and −15.85 to 13%, respectively.
The accuracy of the pf-RSM prediction system was tested by out-of-sample validation, i.e., comparing the PM2.5 and O3 concentrations calculated by the pf-RSM with the corresponding CMAQ simulations for ten out-of-sample control strategies. The predictive performance of the pf-RSM was evaluated using five statistical indices; namely, the mean normalized error (MeanNE), maximal normalized error (MaxNE), mean fractional error (MeanFE), maximal fractional error (MaxFE), and R, are defined as follows:
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
where Mi and Oi are the pf-RSM-predicted and CMAQ-simulated value of the i th data in the series of grid cells, and and are the average pf-RSM-predicted and CMAQ-simulated value over the series.
The MeanNEs for PM2.5 and O3 are 0.88% and 1.58%, respectively, as shown in Table S4. The MeanFE and MaxFE in PM2.5 are 0.85% and 1.59%, respectively. The MeanFE and MaxFE in O3 are 1.51% and 3.23%, respectively. The R values are greater than 0.96. The MeanNE and MaxNE are less than 2% and 4% for both PM2.5 and O3, which meet the criteria of the MeanNE within 2% and MaxNE within 10% defined in our previous paper (Xing et al., 2018). The pf-RSM-predicted PM2.5 and O3 concentrations match with CMAQ model simulations fairly well, with normalized errors within 1.53% and 3.48% for PM2.5 and O3, respectively.
3.2. GA Parameter Setting
Parameter setting is a key step in designing the optimization algorithm. The GA parameters greatly influence the speed of convergence and the success of the optimization. The influence of the population size and number of generations was thoroughly investigated in this study. Other GA parameters were selected based on recent literature. The rank selection method was used to select parents for the next generation. The crossover with a probability of 1 was applied to the parents to produce the offspring. Random mutation with a probability of 0.05 was used to maintain the diversity of individuals. Using this configuration, the effect of the population size was investigated by varying the population size from 50 to 550 with the number of generations fixed at a large value (300). Since the GA is a stochastic algorithm, results differed in each run; hence, each experiment was repeated ten times and the average value of costs and run time was calculated. The GA-LECO runs were done on the same workstations with Intel (R) Xeon (R) CPU, 2.60 GHz, 32-core processor, and 128 GB RAM. The population size that provided the most cost-effective control was then used in additional trials to select the number of generations.
Fig. 3 shows the range of control costs and computational time required for each of the combinations of the population size (Fig. 3a) and the number of generations (Fig. 3b). GA performance initially improves with increasing population size and number of generations until reaching a level where results are insensitive to further increase. As population size increases, performance improves (i.e., costs and the mean and standard deviation for repeated tests decrease), but more computational time is needed. The least control-cost solution using GA is similar to that for the GS method when the population size is greater than 400, and so the population size of 400 is considered as the optimal parameter in this study. As shown in Fig. 3b, the algorithm approximately converges when the number of generations is 180, yielding an extremely efficient optimization result. Hence, the maximum number of generations is set to 180. Based on this parameter analysis and the goal of obtaining high accuracy of the GA in our application, the population size and number of generations of the GA are set to 400 and 180, respectively, in this study. The performance of the GA generally depends on the choice of population size and the number of generations, and these choices require tradeoffs between accuracy and runtime for a given application.
Fig. 3.
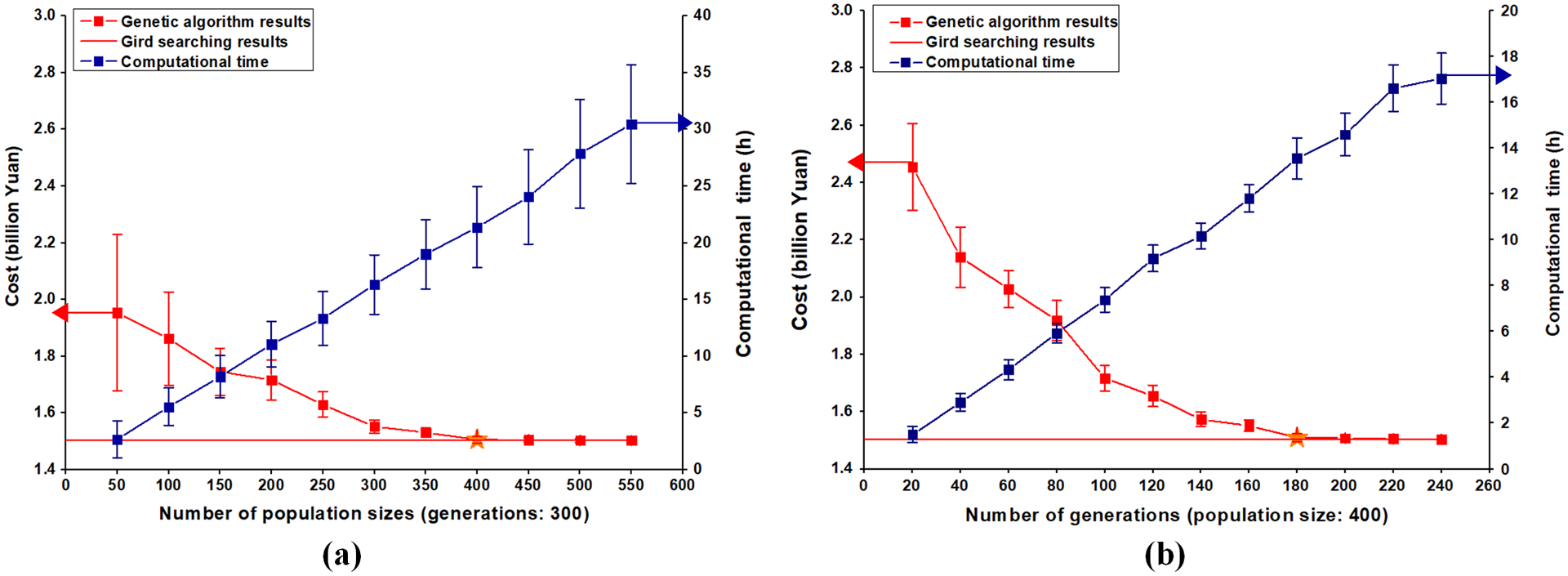
Effect of the population size and number of generations on the performance of the proposed model, (a) average cost and computational time of different population size with 300 generations in ten runs and (b) cost of different number of generations with 400 population size in ten runs, respectively, and the pentagrams were chosen to search the result. The programs were run on the same workstations with Intel (R) Xeon (R) CPU, 2.60 GHz, 32-core processor, and 128 GB RAM.
3.3. Performance Comparison for GA and GS
To explore the performance of the GA, a series of computational experiments with different numbers of control factors were conducted to search for the least-cost control scenarios that satisfied targets using the GA and GS methods (Fig. 4). Not all cities could attain the targets using a small number of variable control factors (a limitation of the GS method), and so the goals were set for the whole PRD region in these experiments. The annual attainment goals of PM2.5 and O3 were selected to be 33 μg m−3 and 80 ppb respectively, which correspond to the 13th Five-Year Plan. Each experiment was conducted using ten runs with a uniform sample space, and then the average computational time was calculated for the runs. The number of variable control factors in the performance comparison experiments for GA and GS ranged from 3 to 28 as summarized in Table 1. Different numbers of emission source types were considered for NOx, VOCs, primary PM, SO2 and NH3. For instance, in the case three control factors, one type of NOx emission source, one type of VOCs emission source, and one type of primary PM emission source were considered, and the reduction ratios of other control factors were set to zero. Since simulations with the GS method were limited by computational resources, the number of control factors stopped at 12 in runs with the GS method.
Fig. 4.
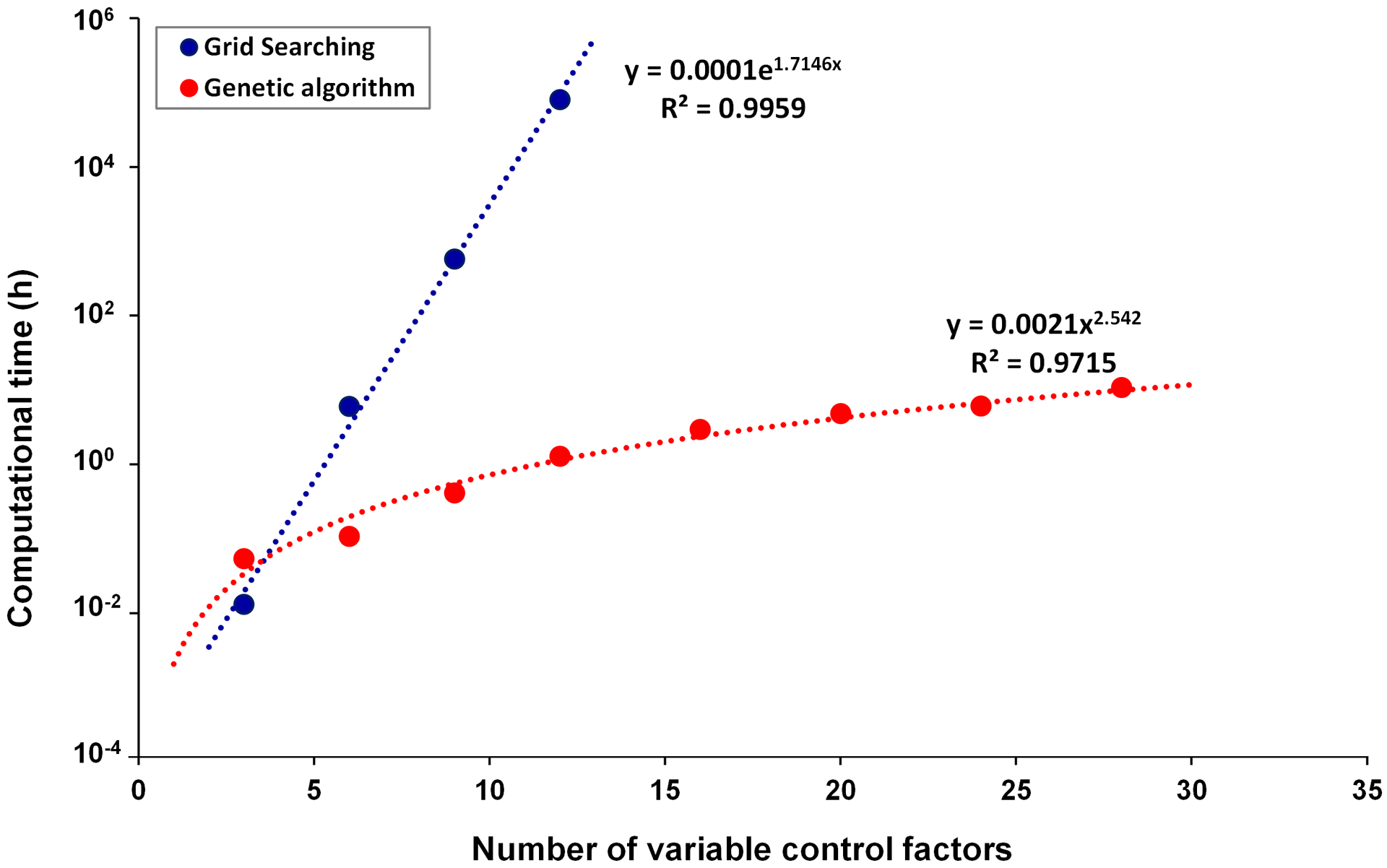
The comparison of genetic algorithm and grid searching method in the computational time with the different number of variable control factors to search the same least-cost control strategies satisfying the targets.
Table 1.
The number of variable control factors in the performance comparison for GA and GS.
| Number of variable control factors | ENOx | EVOCs | Eprimary PM | ESO2 | ENH3 |
|---|---|---|---|---|---|
| 3 | 1 | 1 | 1 | 0 | 0 |
| 6 | 2 | 2 | 2 | 0 | 0 |
| 9 | 3 | 3 | 3 | 0 | 0 |
| 12 | 4 | 4 | 4 | 0 | 0 |
| 16 | 4 | 4 | 4 | 4 | 0 |
| 20 | 5 | 5 | 5 | 5 | 0 |
| 24 | 6 | 6 | 6 | 6 | 0 |
| 28 | 7 | 7 | 7 | 7 | 0 |
ENOx, EVOCs, Eprimary PM, ESO2 and ENH3 is the number of the emission source of NOx, VOCs, primary PM, SO2, and NH3, respectively.
As shown in Fig. 4, as the number of control factors increases, the more computational time is needed due to the increased search space. The same objective function was used to evaluate the control strategies by GA and GS. According to the values of the objective function, the proposed GA method yields the same optimal control strategies as the GS method with a much shorter runtime. The runtime of the proposed GA increases linearly with the numbers of the variables, whereas the runtime of the GS method increases exponentially. The computational time of the GA is 99.99% less than that of the GS method when the number of control factors reaches 9. Therefore the computational efficiency of the GA method facilitates large-scale optimization of multi-pollutant control strategies.
3.4. Case Study
3.4.1. Optimized Control Strategies to Attain Air Quality Goals
The formation of O3 and PM2.5 is strongly coupled because of the interactions of their common precursors (Liao et al., 2008). To explore the effectiveness of coordinated emission controls for O3 and PM2.5 pollution over the PRD region, two types of control combinations were designed to achieve goals for PRD cities at minimum cost (Fig. 5). The air quality targets for the two cases are as follows: (1) PM2.5 goal only (Fig. 5a), and (2) PM2.5 and O3 goals together (Fig. 5b). The PM2.5 goals were ranged from 35 μg m−3 to 25 μg m−3 to examine moderate to strengthened control, while the O3 goal was 80 ppb in all cases. In Fig. 5a (PM2.5 goal only), the PM2.5 goal of 35 μg m−3 is achieved by controlling primary PM emissions alone. The control on primary PM emissions is the dominant selection, because primary PM emission reductions are very efficient in reducing ambient PM2.5 concentrations and control costs for primary PM emissions are much lower than for other pollutants (see Fig. S1). For PM2.5 targets less than 30 μg m−3, SO2 and NOx emissions are also partially controlled to meet the strengthened goals. In Fig. 5b (PM2.5 and O3 goals together), the O3 goal is attained through reducing VOCs by about 12% and NOx by about 23%, which also helps attain the PM2.5 goal. The control ratios on primary PM are lower than in Fig. 5a because they are partly substituted with controls on NOx and VOCs. The NOx and VOCs controls also significantly increase costs, because the control costs of NOx and VOCs are considerably higher than those of primary PM and SO2.
Fig. 5.
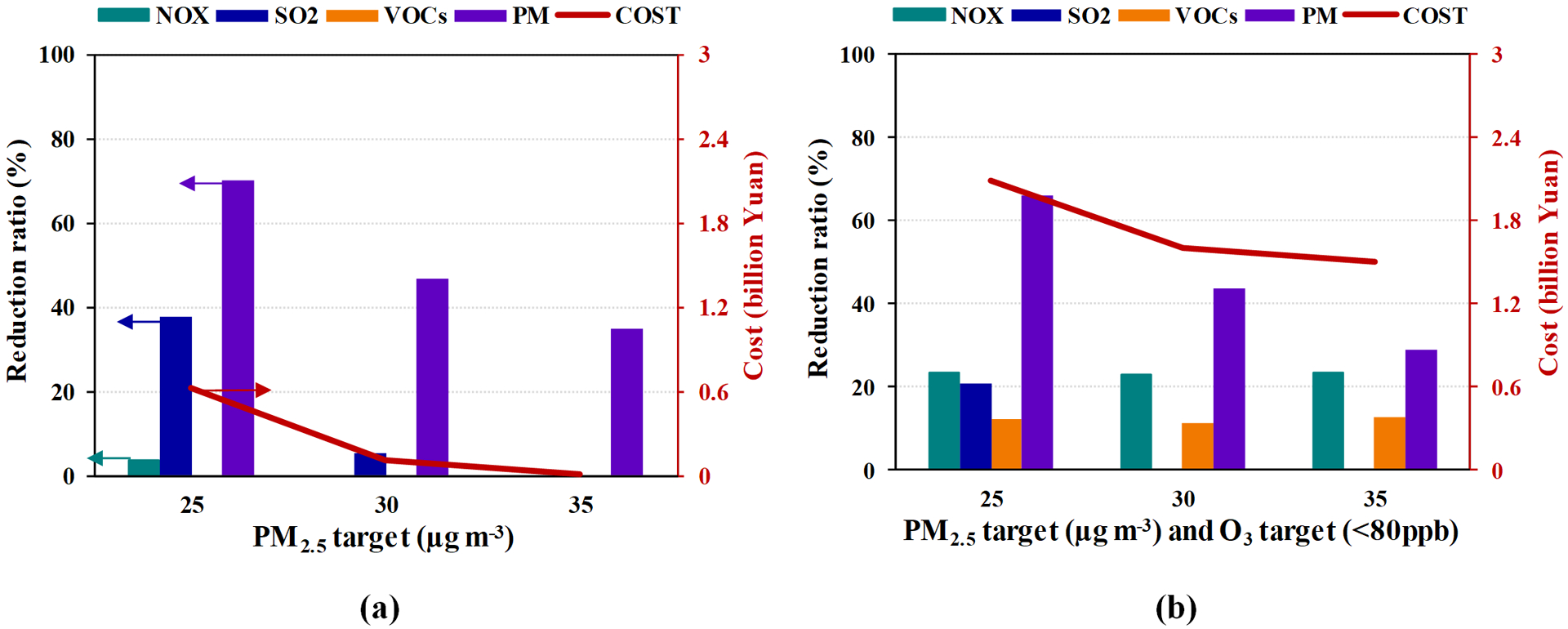
Selected the least-cost control strategies to achieve certain PM2.5 and O3 goals for cities in the PRD region (a: only PM2.5 target; b: both PM2.5 and O3 (< 80 ppb) targets).
Multiple pollutant emissions contribute to the ambient concentrations of O3 and PM2.5, and so various combinations of pollutant controls can achieve air quality targets with the consideration of costs. The top ten scenarios derived from the optimal parameter are listed in Table 2. All the scenarios can meet the air quality targets (PM2.5 < 35 μg m−3 and O3 < 80 ppb) for cities in the PRD region. The overall reductions in NOx (22%) and VOCs (12%) are similar in Scenario 1 and 10, but the reduction in O3 concentrations is greater in Scenario 10. Scenario 1 applies more aggressive controls on VOCs in JM and NOx in GZ than Scenario 10, but weaker controls on VOCs in SD and NOx in FS (see Table S5). Besides, more strengthened controls of SO2 and primary PM result in higher PM2.5 reductions in Scenario 1. The control costs of NOx and VOCs are considerably higher than that of the primary PM and SO2, and higher health benefits obtained from PM2.5 reductions lead to a higher benefit-to-cost ratio in Scenario 1. The higher benefit-to-cost ratio in FS for Scenario 2 than Scenario 3 can be attributed to the larger primary PM control ratio and smaller NOx and VOCs control ratios; however, more reduction in O3 concentrations is obtained in FS for Scenario 2. This indicates that O3 concentration may not be monotonically declining along with the increase of the control ratios of NOx and VOCs due to the nonlinearities in the air quality response. The ten scenarios in Table 1 suggest that there are multiple options to attain certain air quality goals. Decision-makers can choose control scenarios by comprehensively considering the control ratio of each pollutant, control cost, and the benefit-to-cost ratio in each region to make sound policy.
Table 2.
Potential candidates to meet the PM2.5 and O3 target achievementa of the cities in PRD
| Scenario | NOx | SO2 | VOCs | Primary PM | Cost (billion yuan) | Economic benefit (billion yuan) | Benefit-to-cost ratio |
|---|---|---|---|---|---|---|---|
| 1 | 22% | 0% | 12% | 30% | 1.51 | 26.70 | 17.7 |
| 2 | 21% | 16% | 12% | 33% | 1.78 | 28.97 | 16.0 |
| 3 | 23% | 18% | 12% | 29% | 1.66 | 25.89 | 15.5 |
| 4 | 20% | 19% | 12% | 29% | 1.70 | 26.17 | 15.5 |
| 5 | 23% | 9% | 12% | 29% | 1.66 | 25.52 | 15.5 |
| 6 | 23% | 9% | 12% | 29% | 1.66 | 25.41 | 15.5 |
| 7 | 23% | 0% | 12% | 29% | 1.64 | 24.89 | 15.0 |
| 8 | 23% | 17% | 12% | 29% | 1.72 | 25.85 | 15.0 |
| 9 | 22% | 9% | 13% | 25% | 1.92 | 20.81 | 11.0 |
| 10 | 22% | 0% | 12% | 25% | 1.90 | 20.28 | 10.5 |
based on ABaCAS-OE; PM2.5-target: annual averaged concentration less than 35 μg m−3; O3-target: annual averaged concentration less than 80 ppb.
3.4.2. Attainment Assessment and Benefit-Cost Evaluation
Achieving the PM2.5 and O3 targets for all cities requires joint controls in multiple regions across the PRD. The cost-benefit optimal control scenario 1 (Table 2) that meets the PM2.5 (< 35 μg m−3) and O3 (< 80 ppb) targets in 2020 was selected as one example in Fig.6. The emission reduction ratios vary distinctly across the PRD for all pollutants in this case (e.g., NOx reductions ranged from 10% to 50%, VOCs from 10% to 20%, and primary PM from 20% to 40%). GZ and FS have a lower potential to reduce NOx emissions than the other regions due to the strict controls applied to NOx emission sources since 2015. Overall, the emission reduction ratios for VOCs are lower than those of PM2.5 and NOx.
Fig. 6.
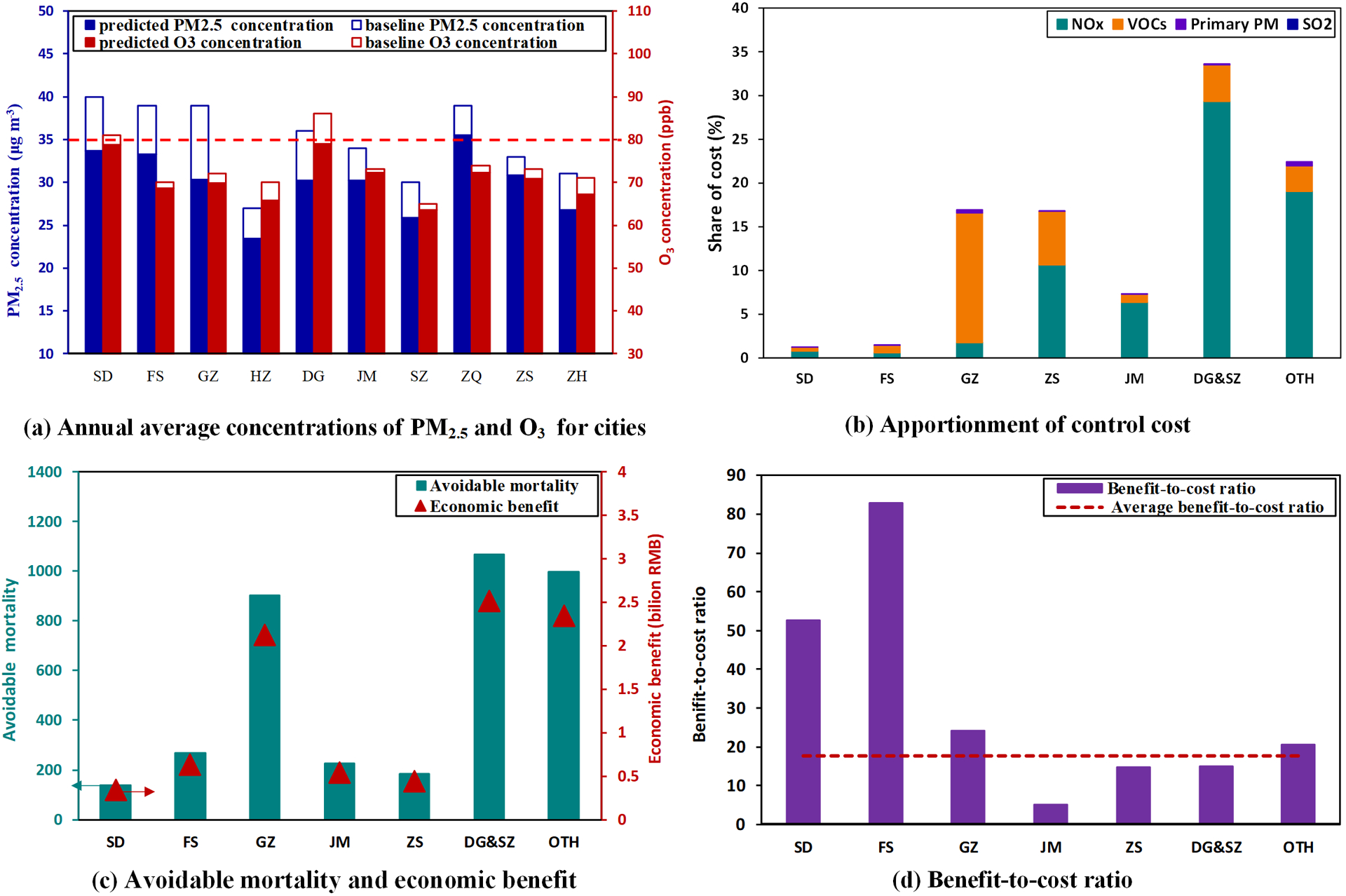
The optimal cost-benefit control strategies to attain PM2.5 (< 35 μg m−3) and O3 (< 80 ppb) goals for cities over PRD in the 2020 scenario based on ABaCAS-OE. SD - Shunde, FS - Foshan, GZ - Guangzhou, HZ - Huizhou, DG - Dongguan, JM - Jiangmen, SZ - Shenzhen, ZQ - Zhaoqing, ZS - Zhongshan, ZH - Zhuha.
The predicted annual average concentrations of PM2.5 and O3 for cities over PRD are shown in Fig.6a. The coordinated control of PM2.5 and O3 requires a regional joint prevention and control strategy because of the regional characteristics of PM2.5 and O3 pollution. Compared with 2015, the average annual decrease in PM2.5 and O3 required for cities in 2020 range from 7% to 18% and from 1% to 8%, respectively, so that all cities can reach the targets. Under this scenario, NOx, SO2, VOCs, NH3, and primary PM emissions in the study region are expected to be reduced by 22%, 0%, 12%, 0%, and 30%, respectively, relative to the year of 2015.
The cost of the control strategy was estimated based on the marginal cost curves of the PRD region in the ICET model (Zhang et al., 2020). As illustrated in Fig.6b, NOx and VOCs control account for the dominant share of the total cost. Although the emission reduction ratios for primary PM are greater than for VOCs and NOx, the cost of primary PM controls is lower because of the high cost of VOCs and NOx emission controls. Control costs are higher in the DG&SZ region, because DG experiences the most serious O3 pollution and requires more NOx emission reduction. The cost estimated in this study (1.51 billion CNY) is acceptable based on comparison with estimates from the special fund for air pollution control (1.27 billion CNY) from 2016 to 2019 reported by the Department of Ecology and Environment of Guangdong Province (http://gdee.gd.gov.cn/).
The number of avoided premature deaths attributable to pollution reductions in each sub-region is expected to range from 139 to 1045, with a total of over 3700 deaths per year in the PRD region (Fig.6c). As a result of the PM2.5 concentration reductions, the avoided premature deaths and economic benefits are estimated to be about 7468 and 17.52 billion CNY, respectively (Table S6). In response to the O3 concentration reductions, 110 avoided premature deaths and 0.06 billion CNY economic benefits are estimated. The estimated PM2.5-attributable mortality reductions and economic benefits are higher than for O3, because of the stronger association of PM2.5 with mortality compared with O3. PM2.5-attributable premature deaths are predicted to decline by 10% compared to the base year (2015), and the average PM2.5 concentration in PRD is estimated to be about 30 μg m−3 under this scenario. Maji et al. (2018) indicated that reducing the PM2.5 concentrations in the PRD to 25 μg m−3 in 2020 would reduce the number of premature deaths by 17.4% compared with 2015. Hence, the avoided premature deaths estimated in this study are consistent with the literature. Additionally, using the statistical life value for monetization as our previous study (Ding et al., 2016; Li et al., 2019a), the reductions in PM2.5 and O3 concentrations are estimated to yield economic benefits of over 8.90 billion CNY which was acceptable.
Fig.6d shows the benefit-to-cost ratios for the seven sub-regions and the average benefit-to-cost ratio for the PRD region. Assuming that the disease burden declines linearly from 2015 to 2020, the economic benefits obtained within the five years are calculated to be 26.70 billion CNY. In this scenario, the benefit-to-cost ratio is estimated as 17.7, which corresponds to a 1,770% monetary gain from the investment in air quality controls. The cost-benefit analysis provides key information to air quality managers and should be considered to relate air pollution controls to economic benefits for society.
4. Conclusions
In this study, an innovative integrated assessment system ABaCAS-OE was developed to provide the optimized cost-benefit control strategies to attain the air quality goals for PM2.5 and O3 in the PRD region. GA-based optimization is also conducted and compared to the GS method for estimating the performance of the system. The results demonstrate that the GA method is > 99% more efficient than the GS method while generating the same optimal multi-pollutant control strategies. In other words, the system has the ability to design optimal PM2.5 and O3 control strategies for large-scale applications. The annual attainment goals for PM2.5 (< 35 μg m−3) and O3 (< 80 ppb) can be achieved over the PRD region and surrounding areas by only controlling NOx, VOCs, and primary PM emissions; however, to achieve more strengthened goals, SO2 reductions need be considered as well. The suggested control strategies can bring considerable health benefits, with the benefit-to-cost ratio reaching 17.7. The ABaCAS-OE system is expected to greatly help policymakers to design control strategies that comprehensively consider air quality targets, costs, and health benefits to fully support effective decision-making for air pollution prevention and control in China.
Several uncertainties influenced the results of the optimized control strategies in this study. (1) For cost estimation, using the provincial marginal cost curves to conduct the cost assessment causes uncertainties due to the lack of local information about control cost and efficiency. Future investigation into the detailed costs is necessary to obtain an accurate estimation of urban control costs. (2) For health impact evaluations, uncertainties exist in the epidemiological literature and the incidence and population data. However, uncertainties in the incidence and population data were difficult to quantify. For estimation of economic loss due to premature mortality, only the WTP method was used to evaluate economic benefits, and the unit value for monetization was based on studies in other regions, due to the limited information available for the PRD region.
Supplementary Material
Acknowledgements and Disclaimer
This work was supported by the National Key Research and Development Program of China (No. 2016YFC0207606 and 2016YFC0207605), U.S. EPA Emission, Air quality, and Meteorological Modeling Support (No. EP-D-12-044), the National Natural Science Foundation of China (21625701), the Fundamental Research Funds for the Central Universities (No. D2160320, D6180330, and D2170150), and the Natural Science Foundation of Guangdong Province, China (No. 2017A030310279). The views expressed in this manuscript are those of the authors alone and do not necessarily reflect the views and policies of the U.S. Environmental Protection Agency.
References
- Amann M, Bertok I, Borken-Kleefeld J, Cofala J, Heyes C, Hoglund-Isaksson L, Klimont Z, Nguyen B, Posch M, Rafaj P, Sandler R, Schopp W, Wagner F, Winiwarter W, 2011. Cost-effective control of air quality and greenhouse gases in Europe: Modeling and policy applications. Environ. Modell. Softw 26, 1489–1501. 10.1016/j.envsoft.2011.07.012. [DOI] [Google Scholar]
- Amann M, Bertok I, Borken-Kleefeld J, Cofala J, Heyes C, Hoglund-Isaksson L, Klimont Z, Rafaj P, Schopp W, Wagner F, 2011b. Cost-effective emission reductions to improve air quality in Europe in 2020: analysis of policy options for the EU for the revision of the Gothenburg Protocol.
- Amann M, Johansson M, Lukewille A, Schopp W, Apsimon H, Warren R, Gonzales T, Tarrason L, Tsyro S, 2001. An integrated assessment model for fine particulate matter in Europe. Water Air Soil Pollut. 130, 223–228. 10.1023/a:1013855000652. [DOI] [Google Scholar]
- Amann M, Kejun J, Jiming HAO, Wang S, Xing Z, Xiang DY, Hong L, Xing J, Zhang C, Bertok I, Borken-Kleefeld J, 2008. GAINS Asia. Scenarios for cost-effective control of air pollution and greenhouse gases in China
- Butler KT, Davies DW, Cartwright H, Isayev O, Walsh A, 2018. Machine learning for molecular and materials science. Nature. 559, 547–555. 10.1038/s41586-018-0337-2. [DOI] [PubMed] [Google Scholar]
- Carnevale C, Finzi G, Pisoni E, Volta M, Guariso G, Gianfreda R, Maffeis G, Thunis P, White L, Triacchini G, 2012. An integrated assessment tool to define effective air quality policies at regional scale. Environ. Modell. Softw 38, 306–315. 10.1016/j.envsoft.2012.07.004. [DOI] [Google Scholar]
- Carnevale C, Pisoni E, Volta M, 2007. Selecting effective ozone exposure control policies solving a two-objective problem. Ecol. Model 204, 93–103. 10.1016/j.ecolmodel.2006.12.036. [DOI] [Google Scholar]
- Cheewaphongphan P, Junpen A, Garivait S, Chatani S, 2017. Emission Inventory of On-Road Transport in Bangkok Metropolitan Region (BMR) Development during 2007 to 2015 Using the GAINS Model. Atmos. 8, 34 10.3390/atmos8090167. [DOI] [Google Scholar]
- Cohan DS, Tian D, Hu YT, Russell AG, 2006. Control strategy optimization for attainment and exposure mitigation: Case study for ozone in Macon, Georgia. Environ. Manage 38, 451–462. 10.1007/s00267-005-0226-y. [DOI] [PubMed] [Google Scholar]
- Cohen AJ, Brauer M, Burnett R, Anderson HR, Frostad J, Estep K, Balakrishnan K, Brunekreef B, Dandona L, Dandona R, Feigin V, Freedman G, Hubbell B, Jobling A, Kan H, Knibbs L, Liu Y, Martin R, Morawska L, Pope CA, Shin H, Straif K, Shaddick G, Thomas M, van Dingenen R, van Donkelaar A, Vos T, Murray CJL, Forouzanfar MH, 2017. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: an analysis of data from the Global Burden of Diseases Study 2015. Lancet (London, England). 389, 1907–1918. 10.1016/S0140-6736(17)30505-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins AL, Zhang Y, Walling DE, Grenfell SE, Smith P, 2010. Tracing sediment loss from eroding farm tracks using a geochemical fingerprinting procedure combining local and genetic algorithm optimisation. Sci. Total Environ 408, 5461–5471. 10.1016/j.scitotenv.2010.07.066. [DOI] [PubMed] [Google Scholar]
- Daily GC, Polasky S, Goldstein J, Kareiva PM, Mooney HA, Pejchar L, Ricketts TH, Salzman J, Shallenberger R, 2009. Ecosystem services in decision making: time to deliver. Front. Ecol. Environ 7, 21–28. 10.1890/080025. [DOI] [Google Scholar]
- Ding D, Xing J, Wang SX, Liu KY, Hao JM, 2019. Estimated Contributions of Emissions Controls, Meteorological Factors, Population Growth, and Changes in Baseline Mortality to Reductions in Ambient PM2.5 and PM2.5-Related Mortality in China, 2013–2017. Environ. Health Perspect 127, 12 10.1289/ehp4157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding DA, Zhu Y, Jang C, Lin CJ, Wang SX, Fu J, Gao J, Deng S, Xie JP, Qiu XZ, 2016. Evaluation of health benefit using BenMAP-CE with an integrated scheme of model and monitor data during Guangzhou Asian Games. J. Environ. Sci 42, 9–18. 10.1016/j.jes.2015.06.003. [DOI] [PubMed] [Google Scholar]
- Elhoseny M, Tharwat A, Hassanien AE, 2018. Bezier Curve Based Path Planning in a Dynamic Field using Modified Genetic Algorithm. J. Comput. Sci 25, 339–350. 10.1016/j.jocs.2017.08.004. [DOI] [Google Scholar]
- Emery C, Liu Z, Russell AG, Odman MT, Yarwood G, Kumar N, 2017. Recommendations on statistics and benchmarks to assess photochemical model performance. J. Air Waste Manage. Assoc 67, 582–598. 10.1080/10962247.2016.1265027. [DOI] [PubMed] [Google Scholar]
- Fann N, Baker KR, Chan EAW, Eyth A, Macpherson A, Miller E, Snyder J, 2018. Assessing Human Health PM2.5 and Ozone Impacts from US Oil and Natural Gas Sector Emissions in 2025. Environ. Sci. Technol 52, 8095–8103. 10.1021/acs.est.8b02050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filipic B, Urbancic T, Krizman V, 1999. A combined machine learning and genetic algorithm approach to controller design. Eng. Appl. Artif. Intell 12, 401–409. 10.1016/s0952-1976(99)00019-6. [DOI] [Google Scholar]
- Fu JS, Brill ED, Ranjithan SR, 2006. Conjunctive use of models to design cost-effective ozone control strategies. J. Air Waste Manage. Assoc 56, 800–809. 10.1080/10473289.2006.10464492. [DOI] [PubMed] [Google Scholar]
- Giordana A, Neri F, 1996. Genetic algorithms in machine learning. AI Commun. 9, 21–26. [Google Scholar]
- Goldber DE, Holland JH, 1988. Genetic algorithms and machine learning. Mach. Learn 3, 95–99. 10.1023/a:1022602019183. [DOI] [Google Scholar]
- Goldberg D, 1989. Genetic Algorithm in Search, Optimization, and Machine Learning. Addison-Wesley, Reading, Massachusetts: xiii. [Google Scholar]
- Guariso G, Pirovano G, Volta M, 2004. Multi-objective analysis of ground-level ozone concentration control. J. Environ. Manage 71, 25–33. 10.1016/j.jenvman.2003.12.015. [DOI] [PubMed] [Google Scholar]
- Harley R, Hunts S, Cass G, 1989. Strategies for the Control of Particulate Air Quality: Least-Cost Solutions Based on Receptor-Oriented Models. Environ. Sci. Technol 23 10.1021/es00066a013. [DOI] [Google Scholar]
- Harmsen M, van Vuuren DP, van den Berg M, Hof AF, Hope C, Krey V, Lamarque JF, Marcucci A, Shindell DT, Schaeffer M, 2015. How well do integrated assessment models represent non-CO2 radiative forcing? Clim. Change 133, 565–582. 10.1007/s10584-015-1485-0. [DOI] [Google Scholar]
- Holland JH, 1975. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. University of Michigan Press, USA: 49, 1880–1902. 10.1007/s10489-018-1370-4. [DOI] [Google Scholar]
- Hong HY, Panahi M, Shirzadi A, Ma TW, Liu JZ, Zhu AX, Chen W, Kougias I, Kazakis N, 2018. Flood susceptibility assessment in Hengfeng area coupling adaptive neuro-fuzzy inference system with genetic algorithm and differential evolution. Sci. Total Environ 621, 1124–1141. 10.1016/j.scitotenv.2017.10.114. [DOI] [PubMed] [Google Scholar]
- Li JB, Zhu Y, Kelly JT, Jang CJ, Wang SX, Hanna A, Xing J, Lin CJ, Long SC, Yu L, 2019a. Health benefit assessment of PM2.5 reduction in Pearl River Delta region of China using a model-monitor data fusion approach. J. Environ. Manage 233, 489–498. 10.1016/j.jenvman.2018.12.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li N, Chen WY, Rafaj P, Kiesewetter G, Schopp W, Wang H, Zhang HJ, Krey V, Riahi K, 2019b. Air Quality Improvement Co-benefits of Low-Carbon Pathways toward Well Below the 2 degrees C Climate Target in China. Environ. Sci. Technol 53, 5576–5584. 10.1021/acs.est.8b06948. [DOI] [PubMed] [Google Scholar]
- Liao KJ, Tagaris E, Napelenok SL, Manomaiphiboon K, Woo JH, Amar P, He S, Russell AG, 2008. Current and future linked responses of ozone and PM(2.5) to emission controls. Environ. Sci. Technol 42, 4670–4675. 10.1021/es7028685. [DOI] [PubMed] [Google Scholar]
- Loughlin DH, Ranjithan SR, Baugh JW, Brill ED, 2000. Application of genetic algorithms for the design of ozone control strategies. J. Air Waste Manage. Assoc 50, 1050–1063. 10.1080/10473289.2000.10464133. [DOI] [PubMed] [Google Scholar]
- Ma QA, Cai SY, Wang SX, Zhao B, Martin RV, Brauer M, Cohen A, Jiang JK, Zhou W, Hao JM, Frostad J, Forouzanfar MH, Burnett RT, 2017. Impacts of coal burning on ambient PM2.5 pollution in China. Atmos. Chem. Phys 17, 4477–4491. 10.5194/acp-17-4477-2017. [DOI] [Google Scholar]
- Maji KJ, Dikshit AK, Arora M, Deshpande A, 2018. Estimating premature mortality attributable to PM2.5 exposure and benefit of air pollution control policies in China for 2020. Sci. Total Environ 612, 683–693. 10.1016/j.scitotenv.2017.08.254. [DOI] [PubMed] [Google Scholar]
- Massoudieh A, Abrishamchi A, Kayhanian M, 2008. Mathematical modeling of first flush in highway storm runoff using genetic algorithm. Sci. Total Environ 398, 107–121. 10.1016/j.scitotenv.2008.02.050. [DOI] [PubMed] [Google Scholar]
- Mousavi SM, Husseinzadeh D, Alikhani S, 2014. Optimal Modeling of Urban Ambient Air Ozone Concentration Based on Its Precursors’ Concentrations and Temperature, Employing Genetic Programming and Genetic Algorithm. J. Environ. Sci. Eng 56, 199–208. [PubMed] [Google Scholar]
- NCAR, 2017. ARW Version 3.9.1 Modeling System User’s Guide https://www.mmm.ucar.edu/wrf.
- Reis S, Nitter S, Friedrich R, 2005. Innovative approaches in integrated assessment modelling of European air pollution control strategies - Implications of dealing with multi-pollutant multi-effect problems. Environ. Modell. Softw 20, 1524–1531. 10.1016/j.envsoft.2004.07.019. [DOI] [Google Scholar]
- Rogers LL, Dowla FU, Johnson VM, 1995. Optimal field-scale groundwater remediation using neural networks and the genetic algorithm. Environ. Sci. Technol 29, 1145–1155. 10.1021/es00005a003. [DOI] [PubMed] [Google Scholar]
- Sacks JD, Lloyd JM, Zhu Y, Anderton J, Jang CJ, Hubbell B, Fann N, 2018. The Environmental Benefits Mapping and Analysis Program - Community Edition (BenMAP-CE): A tool to estimate the health and economic benefits of reducing air pollution. Environ. Modell. Softw 104, 118–129. 10.1016/j.envsoft.2018.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seyedpour SM, Kirmizakis P, Brennan P, Doherty R, Ricken T, 2019. Optimal remediation design and simulation of groundwater flow coupled to contaminant transport using genetic algorithm and radial point collocation method (RPCM). Sci. Total Environ 669, 389–399. 10.1016/j.scitotenv.2019.01.409. [DOI] [PubMed] [Google Scholar]
- Simpson D, Benedictow A, Berge H, Bergstrom R, Emberson LD, Fagerli H, Flechard CR, Hayman GD, Gauss M, Jonson JE, Jenkin ME, Nyiri A, Richter C, Semeena VS, Tsyro S, Tuovinen JP, Valdebenito A, Wind P, 2012. The EMEP MSC-W chemical transport model - technical description. Atmos. Chem. Phys 12, 7825–7865. 10.5194/acp-12-7825-2012. [DOI] [Google Scholar]
- Sirikum J, Techanitisawad A, 2006. Power generation expansion planning with emission control: a nonlinear model and a GA-based heuristic approach. Int. J. Energy Res 30, 81–99. 10.1002/er.1125. [DOI] [Google Scholar]
- Song YY, Wang FL, Chen XX, 2019. An improved genetic algorithm for numerical function optimization. Appl. Intell 49, 1880–1902. 10.1007/s10489-018-1370-4. [DOI] [Google Scholar]
- Stramer Y, Brenner A, Cohen SB, Oron G, 2010. Selection of a Multi-Stage System for Biosolids Management Applying Genetic Algorithm. Environ. Sci. Technol 44, 5503–5508. 10.1021/es902981t. [DOI] [PubMed] [Google Scholar]
- Sun J, Schreifels J, Wang J, Fu JS, Wang SX, 2014. Cost estimate of multi-pollutant abatement from the power sector in the Yangtze River Delta region of China. Energy Policy. 69, 478–488. 10.1016/j.enpol.2014.02.007. [DOI] [Google Scholar]
- U.S.EPA, 2017. CMAQv5.2 Operational Guidance Document U.S. Environmental Protection Agency, Washington, DC: https://www.epa.gov/cmaq. [Google Scholar]
- Von Arx KB, Manock JJ, Huffman SW, Messina M, 1998. Using limited concentration data for the determination of rate constants with the genetic algorithm. Environ. Sci. Technol 32, 3207–3212. 10.1021/es970947+. [DOI] [Google Scholar]
- Wang H, Zhu Y, Jang C, Lin CJ, Wang SX, Fu JS, Gao J, Deng S, Xie JP, Ding D, Qiu XZ, Long SC, 2015. Design and demonstration of a next-generation air quality attainment assessment system for PM2.5 and O-3. J. Environ. Sci 29, 178–188. 10.1016/j.jes.2014.08.023. [DOI] [PubMed] [Google Scholar]
- Wang LQ, Li PF, Yu SC, Mehmood K, Li Z, Chang SC, Liu WP, Rosenfeld D, Flagan RC, Seinfeld JH, 2018. Predicted impact of thermal power generation emission control measures in the Beijing-Tianjin-Hebei region on air pollution over Beijing, China. Sci. Rep 8, 10 10.1038/s41598-018-19481-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang N, Lyu XP, Deng XJ, Guo H, Deng T, Li Y, Yin CQ, Li F, Wang SQ, 2016. Assessment of regional air quality resulting from emission control in the Pearl River Delta region, southern China. Sci. Total Environ 573, 1554–1565. 10.1016/j.scitotenv.2016.09.013. [DOI] [PubMed] [Google Scholar]
- Wang SX, Xing J, Jang CR, Zhu Y, Fu JS, Hao JM, 2011. Impact Assessment of Ammonia Emissions on Inorganic Aerosols in East China Using Response Surface Modeling Technique. Environ. Sci. Technol 45, 9293–9300. 10.1021/es2022347. [DOI] [PubMed] [Google Scholar]
- Wegner G, Pascual U, 2011. Cost-benefit analysis in the context of ecosystem services for human well-being: A multidisciplinary critique. Glob. Environ. Change-Human Policy Dimens 21, 492–504. 10.1016/j.gloenvcha.2010.12.008. [DOI] [Google Scholar]
- Xie X, 2011. Health Value: Environmental Benefit Assessment Method and Urban Air Pollution Control Strategy. Peking Univercity; (PhD thesis, in Chinese). [Google Scholar]
- Xing J, Ding D, Wang SX, Zhao B, Jang C, Wu WJ, Zhang FF, Zhu Y, Hao JM, 2018. Quantification of the enhanced effectiveness of NOx control from simultaneous reductions of VOC and NH3 for reducing air pollution in the Beijing-Tianjin-Hebei region, China. Atmos. Chem. Phys 18, 7799–7814. 10.5194/acp-18-7799-2018. [DOI] [Google Scholar]
- Xing J, Wang S, Jang C, Zhu Y, Zhao B, Dian D, Wang J, Zhao L, Xie H, Hao J, 2017a. ABaCAS: An Overview of the Air Pollution Control Cost-Benefit and Attainment Assessment System and Its Application in China. Mag. Environ. Manag.- Air Waste Manag. Assoc (April) [Google Scholar]
- Xing J, Wang SX, Jang C, Zhu Y, Hao JM, 2011. Nonlinear response of ozone to precursor emission changes in China: a modeling study using response surface methodology. Atmos. Chem. Phys 11, 5027–5044. 10.5194/acp-11-5027-2011. [DOI] [Google Scholar]
- Xing J, Wang SX, Zhao B, Wu WJ, Ding DA, Jang C, Zhu Y, Chang X, Wang JD, Zhang FF, Hao JM, 2017b. Quantifying Nonlinear Multiregional Contributions to Ozone and Fine Particles Using an Updated Response Surface Modeling Technique. Environ. Sci. Technol 51, 11788–11798. 10.1021/acs.est.7b01975. [DOI] [PubMed] [Google Scholar]
- Xing J, Zhang FF, Zhou Y, Wang SX, Ding D, Jang C, Zhu Y, Hao JM, 2019. Least-cost control strategy optimization for air quality attainment of Beijing-Tianjin-Hebei region in China. J. Environ. Manage 245, 95–104. 10.1016/j.jenvman.2019.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X-S, 2014. Nature-inspired optimization algorithms, Elsevier. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin P, Chen RJ, Wang LJ, Meng X, Liu C, Niu Y, Lin ZJ, Liu YN, Liu JM, Qi JL, You JL, Zhou MG, Kan HD, 2017a. Ambient Ozone Pollution and Daily Mortality: A Nationwide Study in 272 Chinese Cities. Environ. Health Perspect 125, 7 10.1289/ehp1849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin XH, Huang ZJ, Zheng JY, Yuan ZB, Zhu WB, Huang XB, Chen DH, 2017b. Source contributions to PM2.5 in Guangdong province, China by numerical modeling: Results and implications. AtmRe. 186, 63–71. 10.1016/j.atmosres.2016.11.007. [DOI] [Google Scholar]
- Zhang F, Xing J, Zhou Y, Wang S, Zhao B, Zheng H, Zhao X, Chang H, Jang C, Zhu Y, Hao J, 2020. Estimation of abatement potentials and costs of air pollution emissions in China. J. Environ. Manage 260, 110069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao B, Wang SX, Donahue NM, Chuang WN, Hildebrandt Ruiz L, Ng NL, Wang YJ, Hao JM, 2015a. Evaluation of One-Dimensional and Two-Dimensional Volatility Basis Sets in Simulating the Aging of Secondary Organic Aerosol with Smog-Chamber Experiments. Environ. Sci. Technol 49, 2245–2254. 10.1021/es5048914. [DOI] [PubMed] [Google Scholar]
- Zhao B, Wang SX, Xing J, Fu K, Fu JS, Jang C, Zhu Y, Dong XY, Gao Y, Wu WJ, Wang JD, Hao JM, 2015b. Assessing the nonlinear response of fine particles to precursor emissions: development and application of an extended response surface modeling technique v1.0. Geosci. Model Dev 8, 115–128. 10.5194/gmd-8-115-2015. [DOI] [Google Scholar]
- Zhao B, Wu WJ, Wang SX, Xing J, Chang X, Liou KN, Jiang JH, Gu Y, Jang C, Fu JS, Zhu Y, Wang JD, Lin Y, Hao JM, 2017. A modeling study of the nonlinear response of fine particles to air pollutant emissions in the Beijing-Tianjin-Hebei region. Atmos. Chem. Phys 17, 12031–12050. 10.5194/acp-17-12031-2017. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


