Abstract
In the past decades, substantial effort has been devoted to the development of computational models of the cardiovascular system. Some of these models simulate blood pressure regulation in humans and include components of the circulatory, renal, and neurohormonal systems. Although such human models are intended to have clinical value in that they can be used to assess the effects and reveal mechanisms of hypertensive therapeutic treatments, rodent models would be more useful in assisting the interpretation of animal experiments. Also, despite well-known sexual dimorphism in blood pressure regulation, almost all published models are gender neutral. Given these observations, the goal of this project is to develop the first computational models of blood pressure regulation for male and female rats. The resulting sex-specific models represent the interplay among cardiovascular function, renal hemodynamics, and kidney function in the rat; they also include the actions of the renal sympathetic nerve activity and the renin-angiotensin-aldosterone system as well as physiological sex differences. We explore mechanisms responsible for blood pressure and renal autoregulation and notable sexual dimorphism. Model simulations suggest that fluid and sodium handling in the kidney of female rats, which differs significantly from males, may contribute to their observed lower salt sensitivity as compared with males. Additionally, model simulations highlight sodium handling in the kidney and renal sympathetic nerve activity sensitivity as key players in the increased resistance of females to angiotensin II-induced hypertension as compared with males.
Keywords: hemodynamics, renal autoregulation, renin-angiotensin system, sex differences
INTRODUCTION
Hypertension is a global health problem that is estimated to be the greatest risk factor for mortality among all cases of cardiovascular disease, despite various treatment efforts (4). Part of the insufficient success in treatment is that hypertension is a complex disease with multiple underlying pathophysiological mechanisms, some of which are not fully understood. Compounding the issue is that males and females typically receive the same antihypertensive therapy, despite differences in success rates between the sexes (18, 27).
Blood pressure is regulated through multiple organs and systems, including the kidney, nervous system, and endocrine system. As first proposed by Guyton et al. (19), the kidney plays a critical role in blood pressure regulation by means of the pressure-natriuresis mechanism, whereby an increase in blood pressure leads to an increase in sodium excretion. This leads to a decrease in water retention, which reduces blood volume (19). Pressure-natriuresis occurs by adjusting sodium transport in the kidney, which is mediated predominantly by the renin-angiotensin system (RAS; Ref. 10). Another key regulator of blood pressure is the renal sympathetic nervous system, which acts to modify the resistance of the renal vasculature, renin secretion, and sodium reabsorption in the nephron (12). Aberrance in one or more of these regulators can lead to hypertension. There is uncertainty regarding the mechanisms responsible for blood pressure regulation, so it is important to note that alternative hypotheses exist (46). One such hypothesis is proposed by Osborn (48) in which the regulation of blood pressure is achieved through neurogenic mechanisms independent of the kidney. In this paradigm of blood pressure regulation, the sympathetic nervous system acts to reduce peripheral vascular resistance in response to elevated arterial pressure, thereby reducing blood pressure without affecting blood volume.
Fewer hypertensive women achieve blood pressure control compared with men, even though compliance and treatment rates are higher in women (18), spotlighting the importance of understanding the sexual dimorphism in blood pressure regulation. Sex differences in blood pressure regulation and hypertension are found in humans (18, 27) as well as in many mammalian and avian species (54, 58, 66a). There is a plethora of data regarding sex differences in the RAS and kidney function (17, 23, 42, 49, 52, 57, 58, 64, 67, 70). Indeed, sex is a critical component in understanding blood pressure regulation and developing antihypertensive therapy.
In this work, we utilize computational models to study sex-specific blood pressure regulation in the rat. The seminal computational model for blood pressure regulation was developed by Guyton et al. (20) and is based on the kidney’s control of blood pressure through fluid balance. Alternatively, Averina et al. (2) have developed a computational model for blood pressure regulation, whereby the central nervous system regulates blood pressure by controlling arterial resistances. Models formulated from these different hypotheses for blood pressure regulation can produce certain similar experimental observations, such as the pressure-natriuresis phenomenon. However, the mechanisms by which this is achieved are different. Therefore, when utilizing a computational model to study blood pressure regulation, it is important to consider not just the observable behavior of the model, but also the underlying hypothesis on which the model is formulated. In this work, we focus on the model developed by Guyton et al. (20). It has been expanded by a number of researchers (e.g., Refs. 22, 30, 41, 66). The first and only sex-specific computational model for blood pressure regulation was developed by Leete and Layton (41). All of these computational models are for humans. In the present study, we formulated sex-specific computational models for rats, based on Ref. 41. We applied the models to identify the factors that contribute to females’ enhanced resistance to salt- and angiotensin II (ANG II)-induced hypertension.
METHODS
The models are based on published sex-specific computational models of blood pressure regulation in men and women (41). These models describe, using a large system of coupled nonlinear algebraic differential equations, the interactions among the cardiovascular system, the renal system, the renal sympathetic nervous system, and the RAS and how these systems regulate blood pressure and kidney function and respond to various perturbations. (For a list of all of the model equations, see the online data supplement; all supplemental material is available at https://doi.org/10.5281/zenodo.3651698.) For instance, the model represents the adjustment of renal blood flow (RBF), via renal autoregulatory mechanisms (32, 59, 60), according to hormonal and nervous inputs; and model renal blood flow determines, in part, urinary output and Na+ excretion, which impacts blood volume and blood pressure (41).
In this work, we extend Ref. 41 and develop the first sex-specific computational model of long-term blood pressure regulation in the rat. A schematic diagram of the model is given in Fig. 1. Changes and improvements from the previous model include a reparametrization for a rodent model, representation of segmented water reabsorption in the nephron, incorporation of up-to-date physiological sex differences, and refinement of autoregulatory mechanisms. We also thoroughly calibrate and validate the model by integrating data from typical experimental protocols in rats.
Fig. 1.
Schematic model of blood pressure regulation. Pink nodes denote variables that describe cardiovascular function; green nodes, renal hemodynamics; orange nodes, renal Na+ and fluid handling; blue nodes, the renin-angiotensin system. Red outlines denote sex-specific components. ACE, angiotensin-converting enzyme; ADH, antidiuretic hormone; AGT, angiotensinogen; ALD, aldosterone; ANG I, angiotensin I; ANG II, angiotensin II; ANP, atrial natriuretic peptide; AT1R-bound ANG II, angiotensin II type 1 receptor-bound angiotensin II; AT2R-bound ANG II, angiotensin II type 2 receptor-bound angiotensin II; CD, collecting duct; DT, distal tubule; MAP, mean arterial pressure; MD, macula densa; PRA, plasma renin activity; PRC, plasma renin concentration; PT, proximal tubule; RSNA, renal sympathetic nerve activity; W, water.
Reparametrization for the rat.
Although human models are intended to have clinical value in that they can be used to assess the effects and reveal the mechanisms of hypertensive therapeutic treatments, rodent models are more useful in assisting the interpretation of animal experiments. We reparametrize the human model (41) for the rat by accounting for differences in size, renal hemodynamics, and RAS hormone concentrations. Unless otherwise stated, all variables are the same as the human values reported in Refs. 30 and 41. Our rat model is based on mature rats, the females of which are premenopausal. In all of the experimental papers that we refer to for data, the rats are ~10 wk old. The species used are either Munich-Wistar or Sprague-Dawley (9, 23, 47, 57).
We create the virtual rat based on the 2- to 4-mo-old Munich-Wistar rat used by Munger and Baylis (47). We account for size difference by a proportional rescaling of all volumes. The size disparity between males and females is more pronounced in rats than in humans (1a). Therefore, the scaling is between both species and sexes. The male and female rats weigh 238 and 194 g, respectively (47), from which we determine their blood volumes to be 15.1 and 12.5 mL, respectively, by using the body weight-to-blood volume relationship in Ref. 39. In a comparison of the models of the two species and two sexes, the male rat has ~0.30% of the volume of the male human, and the female rat has ~80% of the volume of the male rat. We obtain male and female rat renal hemodynamic data from Ref. 47 and use these to reparametrize equations involving RBF, glomerular filtration rate (GFR), and renal vascular resistance. With the knowledge of the renal vascular resistance, we calculate the afferent and efferent arteriolar resistances by assuming that the afferent arteriolar resistance-to-efferent arteriolar resistance ratio is the same as in Ref. 30, which is 0.61. Based on these data, the resistance of the male rat vasculature is taken to be ~95 times higher than that of man, and the resistance of the female rat vasculature is ~1.6 times higher than that of male rat. We also scale for differences in excretion, where both male and female rats are assumed to excrete ~3.0 and ~1.9% of urine and sodium, respectively, of human. The human-to-rat scaling is then given by:
| (1) |
where the scaling factors, SFα, are determined by the ratio of the male and female rat values reported in Ref. 47 and the human values reported in Ref. 30. For details, see the appendix. Finally, male and female rat RAS steady-state values and parameters are obtained from Ref. 40.
Since normotensive humans and rats have similar blood pressure ranges, we assume that all pressures in the model are the same between humans and rats. In the relationship:
| (2) |
the species difference lies in the flow and resistance. Thus we determine the blood flow by assuming the same blood pressure in humans and rats and scaling all vascular resistances in the model as aforementioned. For instance, venous return is given in terms of the mean filling pressure, Pmf, right atrial pressure, Pra, and resistance to venous return, Rvr, by:
| (3) |
and the cardiac output is equal to the venous return at steady state:
| (4) |
Pmf and Pra are known from the human values reported in Ref. 30, and Rvr is scaled based on the resistance scaling factor determined from the ratio of the rat to human renal vascular resistance values reported in Refs. 47 and 30, respectively. Cardiac output is then determined from Eqs. 3 and 4. For full details, see the online data supplement.
Renal sodium and fluid transport.
A key component of blood pressure regulation occurs through the adjustment of sodium reabsorption in different segments of the nephron, which drives fluid balance. The model includes a coarse-grained representation of the nephron, separating it into three lumped segments: the proximal segment (pt), consisting of the proximal tubule and loop of Henle; the distal segment (dt), consisting of the distal convoluted tubule and the connecting tubule; and the collecting duct segment (cd). Such a representation is as fine-grained as necessary to study the mechanisms considered in this work.
The model predicts sodium or water reabsorption by assuming that for a given segment α, sodium/water reabsorption is determined by the product of the inflow, , and sodium/water reabsorption as a fraction of segmental delivery, :
| (5) |
Novel to this work, sodium/water reabsorption as a fraction of segmental delivery, , is chosen separately for male and female, based on observed differences in transporter and channel abundance (discussed below). Fractional sodium reabsorption, , in the segments is regulated by the amount of sodium delivered, aldosterone concentration, ANG II type 1 receptor (AT1R)-bound ANG II concentration, atrial natriuretic peptide concentration, and renal sympathetic nervous activity (RSNA; Refs. 22, 30). Fractional water reabsorption, , in each segment is affected by the osmotic gradient in that segment. The collecting duct segmental water transport is additionally regulated by the antidiuretic hormone concentration (30). For details of the equations and the individual regulation by these factors on particular segments, see the appendix.
Sex differences.
Our model accounts for the following sex differences in blood pressure regulation: 1) the vasodilation of the renal afferent and efferent arterioles by AT2R-bound ANG II in the RAS (which is assumed to occur only in females; Refs. 61, 64, 70); 2) sex differences in the RAS (17, 23, 70); 3) the less excitable and more easily repressed female RSNA (24); and 4) sex differences in renal sodium and fluid handling, based on recent findings and analysis of sexual dimorphism in renal transporter abundance patterns (26, 42, 67).
The afferent arterial resistance is given by:
| (6) |
where is the baseline afferent arterial resistance and βrsna, Σtgf, Σmyo, ΨAT1R-AA, and ΨAT2R-AA denote the effects of RSNA, tubuloglomerular feedback (TGF), myogenic response, AT1R-bound ANG II, and AT2R-bound ANG II, respectively. The efferent arterial resistance is given by:
| (7) |
where is the baseline efferent arterial resistance and ΨAT1R-EA and ΨAT2R-EA denote the effects of AT1R-bound ANG II and AT2R-bound ANG II, respectively. ΨAT1R-AA and ΨAT1R-EA are formulated to be increasing functions of AT1R-bound ANG II concentration to represent the vasoconstrictive effects of AT1R-bound ANG II (22). AT2R-bound ANG II is reported to be either absent or present at low levels in the adult male rat kidney (61, 64, 70). Therefore, we incorporate the vasodilatory effect of AT2R-bound ANG II only in the female model (41):
| (8) |
whereas in the male model, these terms are set to 1. TGF and myogenic response are described below.
Sex-specific parameters for the RAS reaction cascade are calculated from male and female rat RAS hormone baseline levels from literature, as in Ref. 40.
RSNA is inhibited by mean arterial pressure (MAP) and right atrial pressure (14) and is modeled as the product of a normalized baseline value, Nrsna, and the effects of MAP, αMAP, and right atrial pressure, αRAP, as follows:
| (9) |
where αMAP and αRAP are empirical relationships (30). To account for the difference in male and female RSNA sensitivity, we set rsna to (41):
| (10) |
Given that at baseline rsna is 1, this formula accounts for the less excitable and more easily repressed RSNA of the female (24). For rsna >1, female RSNA level increases more slowly compared with that of the male. For rsna <1, RSNA level decreases more sharply.
Male and female rats have different GFR and filtered sodium load but excrete similar amounts of sodium and urine (63). This may be attributable, in part, to sexual dimorphism in renal transporter pattern and segmental water and sodium transport. In particular, Na/H exchanger 3 (NHE3) activity is significantly lower in females, and the female proximal tubule is significantly smaller. Thus the proximal tubule in females absorbs a substantially lower fractional amount of water and sodium than in males (42, 67). Male sodium and fluid transport parameters are taken from Refs. 30 and 34, respectively. Fractional sodium and water reabsorption values in the female are taken to satisfy the physiological constraints reported in Refs. 42 and 67 and calibrated based on the findings in Ref. 23. For details, see the appendix. The model assumes that the proximal, distal, and collecting duct segments reabsorb 80, 50, and 93%, respectively, of the sodium delivered to that segment in male; the corresponding segmental fractional reabsorption rates are taken to be 50, 50, and 96%, respectively, in female. Analogously, segmental fractional water reabsorption is taken to be 86, 60, and 78%, respectively, in male, and 50, 60, and 91%, respectively, in female.
Renal autoregulation calibration.
In addition to the RAS (10) and RSNA (31), afferent arteriolar vasotone is also regulated by TGF and the myogenic response (Eq. 6). TGF, which responds to a change in the luminal sodium chloride concentration in the macula densa, Φmd-sod (28), is given by (30):
| (11) |
Myogenic response adjusts afferent arteriole vasotone based on changes in local blood pressure and is effective for a wide range of blood pressure (28, 45). However, the myogenic response is either absent or not fully validated in previous iterations of this model (20, 22, 30, 41). With the use of data from pressure-natriuresis experiments in which kidney function is measured in response to manipulating renal perfusion pressure (23), we calibrate actions of the myogenic response for maintenance of GFR over a range of blood pressure:
| (12) |
where Pgh denotes glomerular hydrostatic pressure and is determined by MAP, Pma, RBF, Φrb, and renal vascular resistance, Rr:
| (13) |
| (14) |
| (15) |
RESULTS
Baseline results.
Under baseline parametrization, the model produces steady-state results for key cardiovascular and renal variables that fall within physiological ranges. Results are given in Table 1, where experimental data are cited to show that simulated values are within physiological ranges. (For a complete list of values for all model variables and parameters, see the online data supplement.) We note that as expected, males and females have similar blood pressure and plasma sodium concentration values. On the other hand, their vascular resistance and volume values are significantly different, which is a consequence of the difference in size and weight, respectively. Additionally, males and females have different RBF and GFR values but similar excretion values (further discussed below).
Table 1.
Predicted baseline values of key cardiovascular and renal variables in male and female
| Variable/Parameter | Description | Units | Baseline Value M | Baseline Value F | Reference |
|---|---|---|---|---|---|
| Pma | Mean arterial pressure | mmHg | 103 | 103 | 47 |
| Φco | Cardiac output | mL/min | 54.6 | 34.8 | 5 |
| Φrb | Renal blood flow | mL/min | 13.1 | 8.35 | 47 |
| Φgfilt | Glomerular filtration rate | mL/min | 2.44 | 1.67 | 47 |
| Rr | Renal vascular resistance | mmHg/(mL/min) | 7.87 | 12.3 | 47 |
| Φu-sod | Urine sodium flow | μeq/min | 2.44 | 2.44 | 6 |
| Φu | Urine flow | mL/min | 0.0300 | 0.0300 | 6 |
| Wb | Body weight | g | 238 | 194 | 47 |
| Vb | Blood volume | mL | 15 | 12 | 39 |
| Csod | Plasma Na+ concentration | μeq/mL | 143 | 147 | 15 |
F, female; M, male.
Pressure-natriuresis.
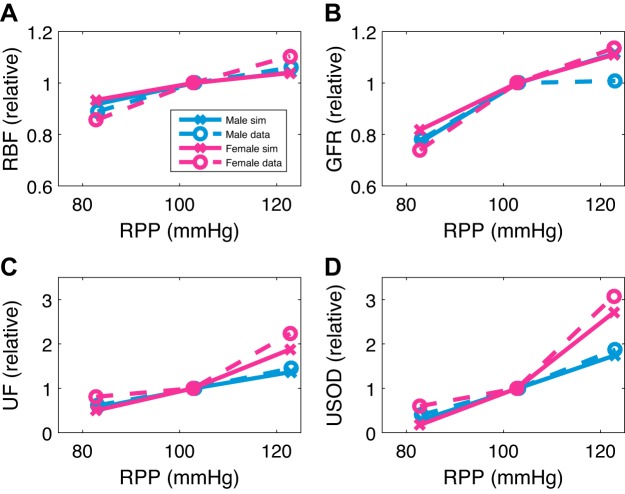
We simulate the pressure-natriuresis experiment from Hilliard et al. (23), in which the left kidney is exposed and denervated and clamps are placed around the arteries to control renal perfusion pressure (RPP). RPP is then either decreased or increased by 20 mmHg from baseline, after which urine flow, sodium excretion, RBF, and GFR are measured. Unilateral denervation alters the excretion of individual kidneys but leaves MAP, GFR, and total excretion unchanged (13, 51). Thus, to replicate the experimental protocol, we conduct model simulations in which effects of RSNA are eliminated, i.e., rsna is set to 1, to simulate the left denervated kidney. To simulate the control of RPP, the pressure that induces RBF and leads to glomerular hydrostatic pressure is controlled, i.e., Pma in Eqs. 13 and 14 is replaced with a user input. Simulations results are summarized in Fig. 2.
Fig. 2.
Pressure-natriuresis. Predicted renal blood flow (RBF; A), glomerular filtration rate (GFR; B), urine flow (UF; C), and urinary Na+ excretion (USOD; D) when renal perfusion pressure (RPP) is perturbed from its baseline value in both directions by 20 mmHg are shown. Predicted renal responses in male and female are plotted as relative change from baseline values. Dashed lines are experimental data from Ref. 23, and solid lines are simulated data (sim) from our model.
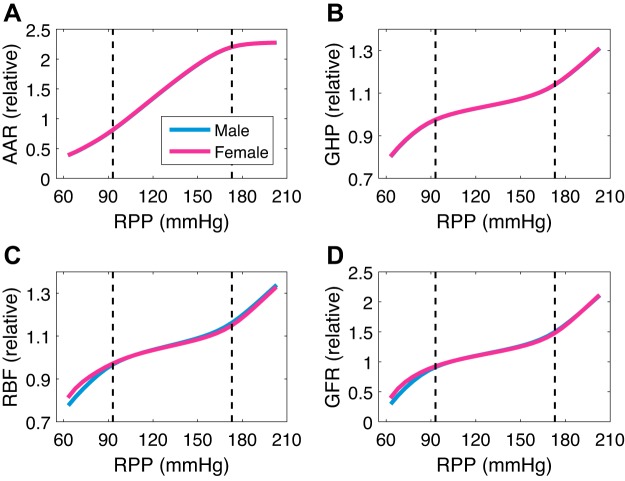
Our baseline values for the physiological quantities of interest in this simulation are similar to the ones reported by Hilliard et al. (23) yet different since they are parametrized from rats from different references. For male experimental and simulated values, we have, respectively, 10.7 and 13.1 mL/min RBF, 3.12 and 2.44 mL/min GFR, 0.0228 and 0.0300 mL/min urine excretion, and 2.16 and 2.44 μmol/min urine sodium excretion. For female experimental and simulated values, we have, respectively, 7.38 and 8.35 mL/min RBF, 2.14 and 1.67 mL/min GFR, 0.0236 and 0.0300 mL/min urine excretion, and 3.06 and 2.44 μmol/min urine sodium excretion. Increasing RPP from 100 to 120 mmHg results in a sharp increase in urine flow and sodium excretion (1.37- and 1.75-fold, respectively, for the male and 1.88- and 2.71-fold, respectively, for the female). This is the pressure-natriuresis/diuresis mechanism response to increased blood pressure (Fig. 2, C and D). However, the corresponding changes in RBF and GFR are relatively minor (~5 and ~10%, respectively, for both the male and female). In contrast, lowering RPP from 100 to 80 mmHg results in a sharper decline in GFR (~20% for both the male and female; Fig. 2, A and B), which is consistent with the findings in Ref. 23. We extend this simulation for the entire physiological range of RPP (Fig. 3). We see that afferent arteriolar resistance changes sharply (by ~20% per 10 mmHg; Fig. 3A) to regulate GFR to change slightly (by ~5% per 10 mmHg for both the male and female) within the autoregulatory range of approximately 90–170 mmHg. Outside of the autoregulatory range, GFR changes sharply, reaching as low as 30 and 40% of its baseline value in males and females, respectively, for an RPP of 60 mmHg, and as high as 210% of its baseline value in both males and females for an RPP of 200 mmHg (Fig. 3D). When the TGF, the myogenic response, or both are assumed absent (by setting Σtgf, Σmyo, or both to 1), the predicted GFR is markedly less effectively autoregulated (slope of ~9, ~27, and ~36% per 10 mmHg, respectively; see Supplemental Fig. S1).
Fig. 3.
Renal autoregulation. Following the same experimental protocol as in Ref. 23, renal perfusion pressure (RPP) is perturbed from its baseline value of 103 mmHg within a wide range. Predicted afferent arteriolar resistance (AAR; A), glomerular hydrostatic pressure (GHP; B), renal blood flow (RBF; C), and glomerular filtration rate (GFR; D) are plotted as relative change from baseline value. Dashed vertical lines are at the end points of the autoregulatory range of approximately 90–170 mmHg.
Sodium sensitivity of blood pressure.
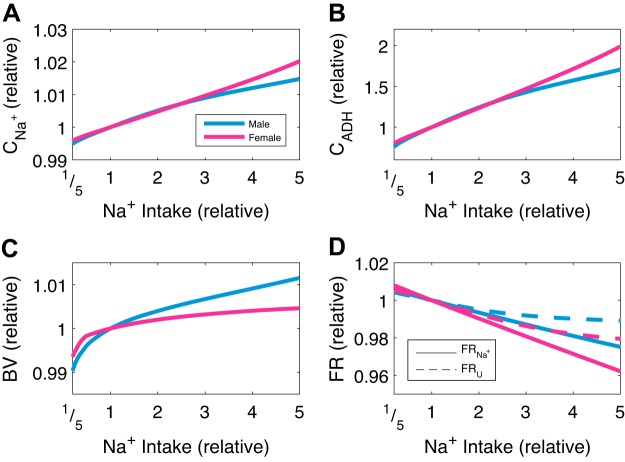
One way that the pressure-natriuresis phenomenon is observed experimentally in conscious animals is by varying sodium intake and measuring blood pressure at steady state (9, 21). We simulate this scenario shown in Fig. 4, where relative change in sodium intake is plotted against predicted MAP at steady state. Note that the steady-state sodium excretion is equal to the intake. Consistent with experimental findings (9), the model predicts that a slight increase in MAP leads to a sharp increase in sodium excretion. The mechanisms that explain this behavior are plotted in Fig. 5. Increasing sodium intake increases sodium concentration (Fig. 5A), which increases antidiuretic hormone concentration (Fig. 5B). This then induces thirst (results not shown), which increases blood volume (Fig. 5C) and thus MAP. Pressure-driven natriuresis and diuresis prevent MAP from sharply increasing by decreasing the total fractional sodium and water reabsorption (Fig. 5D). In the steady state, the slightly elevated MAP is marked by a slight increase in both cardiac output and total peripheral resistance (see Supplemental Fig. S2). A leftward shift can be noted in the pressure-natriuresis curve in females, whereby females excrete more sodium for a given perturbation in MAP (Fig. 4), which is consistent with findings in Refs. 25 and 53.
Fig. 4.
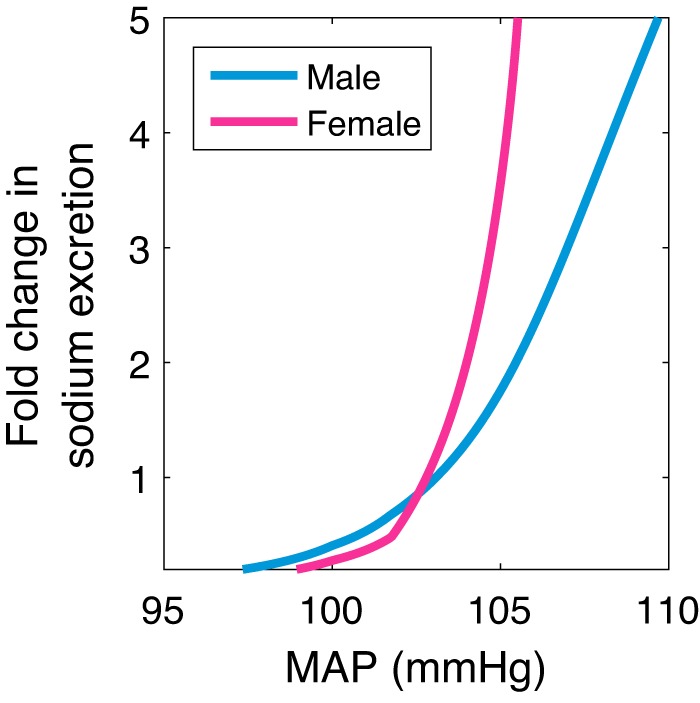
Sodium sensitivity of blood pressure. Relative change in sodium excretion with respect to the baseline value is plotted against mean arterial pressure (MAP). The female model exhibits a leftward shift in the pressure-natriuresis curve relative to male.
Fig. 5.
Mechanisms involved in sodium sensitivity. Predicted sodium concentration (CNa+; A), antidiuretic hormone concentration (CADH; B), blood volume (BV; C), and total fractional sodium/water reabsorption (FR; D) when sodium intake is varied from 1/5- to 5-fold are shown. Predicted responses in male and female are plotted as relative change from baseline values. U, urine.
What explains the leftward shift in pressure-natriuresis relationship in females? The more efficient natriuresis/diuresis in females than males can be observed in Fig. 5D, where the decrease in total fractional sodium/water reabsorption versus sodium intake has a greater slope. We hypothesize that this sex difference can be attributed to the greater amount of sodium transport in the distal and collecting duct nephron segments in females. Recall that an increase in MAP inhibits the RSNA and thereby the RAS, lowering fractional sodium reabsorption along the distal and collecting duct segments. Furthermore, recall that these segments are responsible for a larger fraction of sodium transport in female relative to male. Thus a smaller change in MAP is needed in females to excrete the same increased amount of sodium, i.e., a leftward shift and a greater slope in pressure-natriuresis curve in females relative to males. To understand the underlying mechanisms, we revert the sex differences in the model simulation (see above) by setting individual female model parameters to male values. Indeed, model simulations confirm this hypothesis: only the reversion of renal transport parameters leads to the female behaving like the male, i.e., the pressure-natriuresis curve no longer being left-shifted for the female (results not shown).
ANG II infusion.
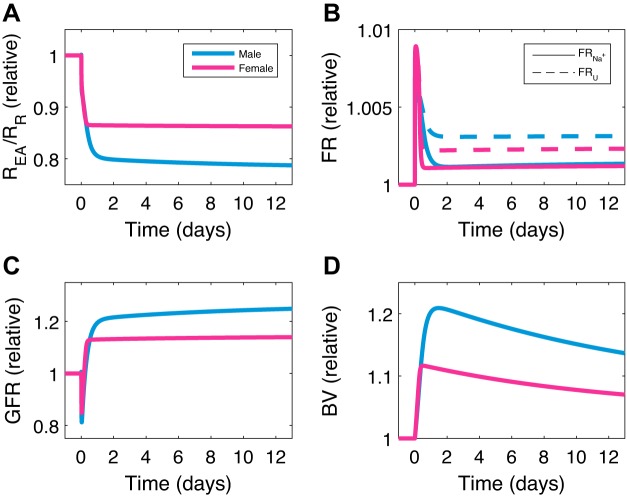
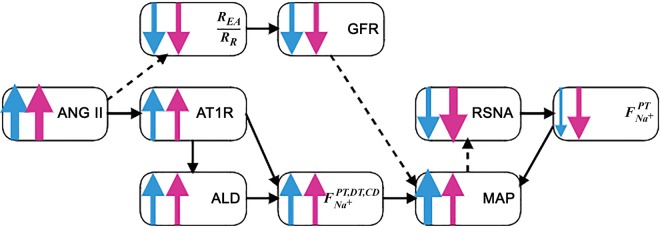
In the next set of simulations, we investigate the role of the RAS in blood pressure regulation by predicting the response of MAP to an infusion of ANG II. Model predictions are shown for males and females in Fig. 6, together with experimental data from Sampson et al. (57). ANG II is infused at a high dose of 400 ng·kg−1·min−1 in male and female rats, which we simulate by adding kII = 2,022 fmol·min−1·mL−1 (male) or kII = 2,060 fmol·min−1·mL−1 (female) to the right-hand side of the equation for ANG II concentration (see Supplemental Eq. S66). Model results agree well with the data. ANG II infusion induces a large increase in MAP, with the increase being larger in males than females. The mechanisms that explain this behavior are plotted in Fig. 7. Infusing ANG II dilates the afferent arteriole more than the efferent arteriole (results not shown), thereby decreasing the efferent arteriolar-to-renal vascular resistance ratio (Fig. 7A), which decreases GFR (Fig. 7C). Infusing ANG II also increases the total fractional sodium and water reabsorption (Fig. 7B). Together, both of these actions increase blood volume (Fig. 7D) and thus MAP. After ~1 day, increase in MAP is then mitigated by a decrease in total fractional sodium and water reabsorption (Fig. 7B). The large increase in MAP is marked by a large increase in cardiac output and a slight decrease in total peripheral resistance. After ~1 day, cardiac output and total peripheral resistance gradually decrease and increase, respectively (see Supplemental Fig. S3). A flowchart representing these mechanisms is given in Fig. 8.
Fig. 6.
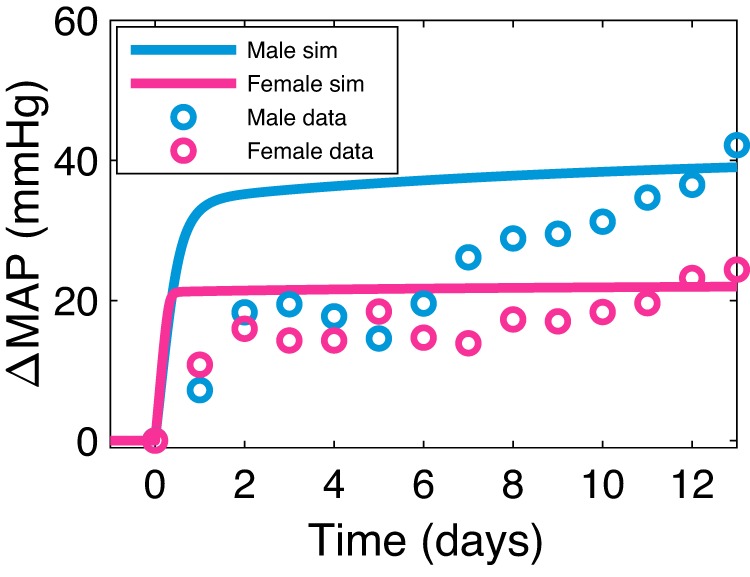
Simulated response of mean arterial pressure (MAP) to angiotensin II (ANG II) infusion. ANG II is infused at 400 ng·kg−1·min−1 at time 0. The symbols are experimental data from Ref. 41, and the lines are simulated data (sim) from our model. Consistent with experimental data, model predicts that ANG II infusion elicits a greater MAP increase in male relative to female.
Fig. 7.
Mechanisms involved in angiotensin II (ANG II) infusion. Predicted efferent arteriolar-to-renal vascular resistance ratio (REA/RR; A), total fractional sodium/water reabsorption (FR; B), glomerular filtration rate (GFR; C), and blood volume (BV; D) when ANG II is infused at time 0 are shown. Predicted responses in male and female are plotted as relative change from baseline values. U, urine.
Fig. 8.
Flowchart of mean arterial pressure (MAP) response to angiotensin II (ANG II) infusion. ALD, aldosterone; AT1R, ANG II type 1 receptor; CD, collecting duct; DT, distal tubule; F, fraction; GFR, glomerular filtration rate; PT, proximal tubule; REA/RR, efferent arteriolar-to-renal vascular resistance ratio; RSNA, renal sympathetic nerve activity.
What explains the lower sensitivity of females than males to ANG II-induced hypertension? After ~1 day, the more efficient natriuresis/diuresis in females than males can be observed in Fig. 7D, where the females reabsorb relatively less sodium/water than males. To understand the underlying mechanisms, we revert the sex differences in the model simulation (see above) by setting individual female model parameters to male values. Reversion of none of the individual sex differences leads to the female behaving like the male. Similarly, all pairwise reversions of sex differences retain the female-male disparity, except for one. The one exception is using the same fractional sodium reabsorption in the nephron segments for females as males, coupled with the same RSNA sensitivity. In this scenario, simulations yield similar increase in MAP due to ANG II infusion between the two sexes (results not shown). This is due to the following. The female now reabsorbs a larger fractional amount of sodium in the proximal segment, which is regulated, in part, by RSNA. The increase in blood pressure causes a decrease in RSNA. Previously, since the female RSNA is more easily repressed, it would decrease more than the male. Now, RSNA decreases by about the same amount in both male and female. Recall that a decrease in RSNA decreases the fractional amount of sodium reabsorbed in the proximal segment (see Supplemental Eq. S43). That natriuretic effect is now blunted in the female. Taken together, a larger baseline fractional sodium reabsorption in the proximal segment, along with a blunted RSNA sensitivity to MAP increase, would cause the female to reabsorb a greater fractional amount of sodium in the proximal segment, thus leading to the increased sensitivity of MAP to ANG II infusion (Fig. 8).
Sensitivity analysis.
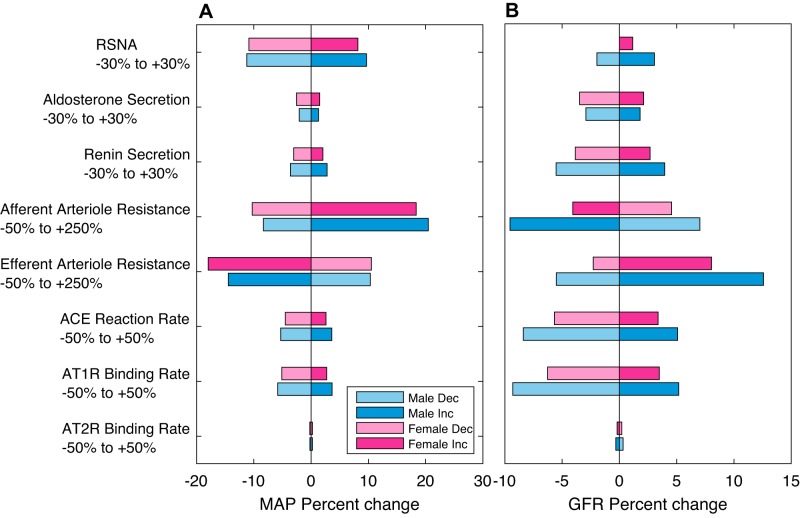
We conduct a local sensitivity analysis by perturbing a single parameter at a time within its physiological range and determining the relative change in key model outputs at steady state. Results are summarized in Fig. 9. MAP is highly sensitive to RSNA and afferent and efferent arteriolar resistance. RSNA exerts substantial impacts on MAP because it acts in a multifaceted way: it controls afferent arteriolar resistance, activation of the RAS, and sodium reabsorption in the proximal segment. Afferent and efferent arteriolar resistance greatly impact MAP because of their impact on GFR. GFR is highly sensitive to afferent and efferent arteriolar resistance, as expected. The rates of angiotensin-converting enzyme reaction and ANG II binding to AT1R also have significant impact on GFR because these affect AT1R-bound ANG II concentration, which, in turn, affects renal vascular resistance.
Fig. 9.
Sensitivity analysis. Percentage change in mean arterial pressure (MAP; A) and glomerular filtration rate (GFR; B) due to various single perturbations in physiological parameters. Blue bars, responses predicted in male; red bars, female. Darker and lighter bars correspond to increases (Inc) and decreases (Dec) in model parameters, respectively. ACE, angiotensin-converting enzyme; AT1R, angiotensin II type 1 receptor; RSNA, renal sympathetic nerve activity.
The model assumes that the RSNA of the female is less excitable than male. Thus, in response to a stimulation of RSNA (30% increase), the female MAP exhibits an 8.2% increase, which is less than the 9.7% increase in the male MAP. For vasoconstriction of the afferent arteriole (250% increase), the female MAP and GFR exhibit an 18.4% increase and 4.1% decrease, respectively, which is less than the 20.5% increase and 9.6% decrease of the male MAP and GFR, respectively. RSNA acts to mitigate the increase in MAP by decreasing the afferent arteriolar resistance. Since the female RSNA is more easily repressed than that of the male, this effect is greater (see Supplemental Fig. S4A). In response to vasoconstriction of the efferent arteriole (250% increase), the female and male MAP decrease by 18.0 and 14.5%, respectively, whereas the female and male GFR increase by 8.0 and 12.6%, respectively. The lower female GFR, compared with that of male, can be attributed, in large part, to the lower MAP. Despite the lower GFR, the female is excreting more urine than the male (see Supplemental Fig. S4B; a result of the differences between the sexes in sodium and fluid handling in the kidney; see above), which leads to the female MAP being lower than that of the male. MAP, and thus GFR, is largely insensitive to changes in aldosterone secretion, although it can be noted that females are more sensitive to aldosterone secretion than males. This is because aldosterone acts on the distal and collecting duct segments, which transport a larger fraction of the filtered sodium load in females than in males.
DISCUSSION
Given the multiple systems involved, studying whole body blood pressure regulation is well suited for a systems biology approach. Computational modeling is a useful tool in quantifying the interactions of these different systems. Computational modeling of the circulatory system for blood pressure regulation was pioneered by Guyton et al. (20) in their seminal work in 1972 and has since undergone a series of extensions and revisions (22, 30, 66), with the latest iteration by Leete and Layton (41) being the only sex-specific one. The models include components for cardiovascular function, renal hemodynamics, and renal function while accounting for the effects of RSNA and the RAS. All of these models are for blood pressure regulation in humans. Updating the latest iteration of the model by Leete and Layton (41) with novel contributions of model components for fluid balance, physiological sex differences, and autoregulatory mechanisms, we have developed the first sex-specific computational model for blood pressure regulation in the rat.
Sex differences.
Despite well-known sexual dimorphism in hypertension (49, 70), the only sex-specific computational model for blood pressure regulation is that of Leete and Layton (1, 41). Female sex hormones are attributed for causing sex differences in blood pressure regulation (49). Although our model does not account for sex hormones explicitly, by incorporating known physiological sex differences, the mechanistic effects of sex hormones are accounted for implicitly. On incorporation of physiological sex differences, our model captures observed sex differences in blood pressure regulation (Figs. 4 and 6). It is important to note that we did not calibrate the sex differences based on these data. Rather, we incorporated the known physiological sex differences in blood pressure regulation, and the experimental outcomes are a consequence of this. Thus these physiological sex differences provide insight into why males and females behave differently in hypertensive studies.
An observed sex dissimilarity in pressure-natriuresis is that females excrete more sodium for a given increase in MAP (23). Our model simulations suggest that the left shift of the female pressure-natriuresis curve can be attributable, in large part, to sodium handling in the kidney. Female rats have a smaller filtered sodium load than males but excrete a similar amount of sodium, which reflects the dimorphism in renal transporter activities between the two sexes (67). Because of the lower NHE3 activity and a smaller transport area in females, their proximal convoluted tubules reabsorb a smaller fractional amount of filtered sodium than that of males (42, 67). This is compensated by downstream segments. The female distal tubular segments exhibit a higher abundance of sodium chloride cotransporter (NCC) and epithelial Na+ channel (52, 67) and are thus capable of enhanced fractional sodium reabsorption. Calibration of model parameters suggests that the female collecting duct segments also reabsorb a larger fractional amount of the sodium load. Distal tubular and collecting duct segments are responsible for fine-tuning of sodium transport. With distal and collecting duct sodium reabsorption mediated by aldosterone, female kidneys are more effective at inducing natriuresis to regulate increases in blood pressure.
Another observed sex dissimilarity is that the arterial pressure response to ANG II infusion is attenuated in females as compared with males (57, 64). Interestingly, our model simulations suggest that this dimorphism cannot be explained with a single sex difference, implying greater complexity in the etiology of sexual dimorphism in blood pressure regulation. Our model simulations suggest that the higher sensitivity of males is due to the combined effects of the differences between the sexes in renal sodium handling and RSNA sensitivity. RSNA is a significant regulator of blood pressure (12), and sex differences in this regulator can lead to major observable sex differences (24). As noted previously, a larger fraction of the filtered sodium and fluid load is reabsorbed by the distal tubular and collecting duct segments in the female nephron. Sodium and fluid transport along those nephron segments are mediated by the RAS. Aberrant regulation of the RAS can lead to hypertension. ANG II is the major biologically active hormone generated by this system (10, 62). Thus knowing the underlying physiological cause of sex differences in response to variations in ANG II levels can help to guide antihypertensive drugs that target the RAS to be tailored individually to males and females.
The present models are developed for the rat. We identify sexually dimorphic mechanisms, namely differences in RSNA sensitivity and sodium/fluid transport in the kidney, that may explain sexually dimorphic observances in blood pressure regulation. To what extent do the mechanistic sexual dimorphisms in blood pressure regulation in rats apply to humans? Cardiovascular responses to stress in humans are generally sex dependent, where men typically have a greater response to stress than women. Thus the ability of females to more tightly control the sympathetic nervous system may serve as a mechanism whereby women are protected against hypertension (24). Our study identifies the load shift in sodium/fluid transport from the proximal segment to the distal and collecting segments in female kidneys to be the functional cause of the observed advantage of female rats in blood pressure regulation, as compared with males. Lower fractional sodium reabsorption in the proximal convoluted tubules is due, in part, to the size disparity between male and female rats (42). This disparity is much smaller in humans. Higher fractional sodium reabsorption in the distal tubular segments is due, in part, to the higher expression and phosphorylation of NCC in females, which is present in both rats and humans (52). Indeed, like female rats, women also face the challenge of circulating volume adaptation during pregnancy and lactation, and the potential for increasing reabsorption along the proximal nephron coupled to the more abundant transporters in the distal nephron may facilitate that adaptation. Taken together, this suggests that the aforementioned sex difference in load distribution of sodium/fluid transport in rat kidneys is likely present in human kidneys, albeit less pronounced, and thus may also be the cause of women’s advantage in blood pressure regulation over men. However, as sex differences in renal transporter activity, and kidney function in general, may not be the same between species, caution is needed in translating these rat results to humans (55, 67). A sex-specific computational model for blood pressure regulation in humans would be appropriate to analyze these mechanisms (41).
Model utility.
Although the aforementioned human models for blood pressure regulation may have clinical value, our rodent model would be more useful in the interpretation of sexual dimorphism in blood pressure regulation in rodent experiments. Just as experimental outcomes in rats are not guaranteed to occur in the same way in humans, computational models for humans are not directly transferable to rats. Therefore, species-specific models have greater predictive power. Moreover, our model has the versatility to simulate both dynamic and steady-state scenarios for intact circulation while also being amenable to performing in silico experiments on rats that are conscious, anesthetized, denervated, et cetera. Thus the model’s utility covers a wide range of typical rodent experimental protocols for long-term blood pressure regulation.
Our model is sex specific, so it can be used to investigate the etiology of sexual dimorphism in blood pressure regulation in rats. As done in this work, the sex-specific model can be used for hypothesis testing to map observable sexual dimorphism to underlying sexual physiological differences. Additionally, sensitivity analysis reveals different sensitivities between males and females to physiological perturbations. Since the “one-size-fits-all” approach to achieve blood pressure regulation in both males and females is not optimal (70), the ultimate benefit of having a sex-specific model is to then guide antihypertensive treatment tailored to each sex.
Model limitations and future extensions.
Although we have incorporated several sex differences in the model, this account is not complete. Several sex differences still exist that we have not accounted for. For instance, nitric oxide contributes to blood control by regulating vascular tone and tubular sodium reabsorption. Renal levels of endothelial nitric oxide synthase mRNA are higher in female rats, whereas male blood pressure and renal vasculature in rats is more responsive to nitric oxide synthase inhibitor (50, 56). In the present study, we have analyzed some sexually dimorphic mechanisms that are sufficient to explain certain sexually dimorphic observances in blood pressure regulation. Future studies to develop a more comprehensive computational model including other sex differences are necessary to fully understand the sex disparity in blood pressure regulation.
We note that in the experimental data reported from Ref. 57, the female MAP response to ANG II differs from that of the male not only quantitatively, but also qualitatively. In addition to being lower, the female MAP levels off more quickly, whereas the male MAP gradually increases. This phenomenon may not be an anomaly as a similar trend is seen in other rodent experiments (68, 69). It is possible that ANG II-induced hypertension has sexually distinct mechanisms that lead to temporal variations (65). We observe the quantitative, but not the qualitative, difference between the sexes in our model simulation of ANG II infusion, thus suggesting that additional sexually distinct mechanisms need to be incorporated in our model.
Our model accounts for the systemic RAS only and assumes direct interactions with the kidney; that is, intrarenal RAS is not represented explicitly. To better approximate the effect of the RAS on kidney function, one may use a compartmental approach that differentiates between systemic and intrarenal RAS concentrations and takes into account transfer exchange between the two compartments, as done in Ref. 44. Intrarenal ANG II level is known to be elevated in diabetic nephropathy (8). With the compartmental approach incorporated, the resulting blood pressure regulation model would be well suited to simulate the effect of diabetic nephropathy on cardiovascular function.
The kidney component of our model is a single lumped kidney that acts as the net function of both kidneys. A worthwhile extension of the model would be to model the left and right kidneys individually as in Ref. 29. This would allow simulations of scenarios such as uninephrectomy as well as more accurate simulations of scenarios in which either kidney reacts differently, such as unilateral denervation (13, 51).
Our model accounts for tubular sodium and fluid handling in the nephron through three lumped segments: proximal, distal, and collecting duct. A possible extension of the model would be to fully account for each of the functionally distinct nephron segments. For instance, the model proximal segment includes the proximal convoluted tubule and the thick ascending limb, even though the sodium and fluid handling in these segments is markedly different. The model already has the framework to incorporate this extension as it would require further dividing the three lumped segments into their constituents. The benefit of this more fine-grained representation would be for a more detailed description of nephron function, allowing for a more accurate account of the different functions of each segment and for modeling the exact segment where regulators of kidney function act. Moreover, the actions of the transporters and channels along the nephron cell membranes that regulate sodium and fluid balance are represented implicitly in our model. Another possible extension of the model would be to explicitly model these transporters and channels as done in epithelial transport models (16, 33–38, 42). The benefit of coupling individual nephron with whole kidney dynamics would be in simulating the administration of drugs that target these transporters. The exact action of the drug could be simulated instead of inferred.
Although we present our model in the context of hypertension in males and nonpregnant, premenopausal females, the model can be applicable to studying blood pressure regulation in pregnant or menopausal females. Blood pressure regulation in pregnant females requires special treatment due to differences in hemodynamics and the RAS (3, 7). However, special treatment is also needed for menopausal females since with the onset of menopause, females lose much of their cardiovascular advantage due to increased salt sensitivity (49). As we have translated physiological sex and species differences into mathematical model components, the nonpregnant, premenopausal female model can be used as a basis to formulate a pregnant or menopausal female model. Moreover, although blood pressure regulation in females varies with respect to the menstrual cycle, such model formulation is beyond the scope of this paper and thus not considered. Incorporation of such mechanisms may require modeling time-varying, periodic parameters that vary with respect to the menstrual cycle. In addition to hypertension, the model can be applied to simulate prerenal acute kidney injury.
GRANTS
This research was supported by the Canada 150 Research Chairs Program and by the National Institutes of Health via the National Institute of Diabetes and Digestive and Kidney Diseases Grant R01-DK-106102.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
A.T.L. conceived and designed research; S.A. performed experiments; S.A. and A.T.L. analyzed data; S.A. and A.T.L. interpreted results of experiments; S.A. prepared figures; S.A. and A.T.L. drafted manuscript; S.A. and A.T.L. edited and revised manuscript; S.A. and A.T.L. approved final version of manuscript.
APPENDIX
Renal sodium and fluid transport.
Novel to this work, we calculate water transport for each model segment. The water reabsorption in the proximal segment, which includes the proximal convoluted tubule, S3 segment, and the loop of Henle, is given by the product of the GFR, Φgfilt, and the fractional water reabsorption in the proximal segment, ηpt-wreab:
| (A1) |
The flow of ultrafiltrate in the macula densa is the difference between the GFR, Φgfilt, and how much water is reabsorbed in the proximal segment, Φpt-wreab:
| (A2) |
Equations for fluid reabsorption and flow in the distal segment (distal convoluted tubule and the connecting tubule) and the collecting duct segment are formed similarly, ending with urine flow, Φu:
| (A3) |
| (A4) |
| (A5) |
| (A6) |
We also include the effect of the osmotic gradient, whereby changes in fractional sodium reabsorption (sodreab) in a particular segment affect fractional water reabsorption in that segment. The fractional water reabsorption terms for each segment are given by:
| (A7) |
| (A8) |
| (A9) |
where the effects of the osmotic gradient in each segment are given by:
| (A10) |
The effect of the osmotic gradient acts as a scaling factor to modify the fractional water reabsorption in a segment when the fractional sodium reabsorption in that segment differs from its baseline. The effect is assumed to be the same in all segments and is formulated as follows. The scaling factor is 1, i.e., no change in fractional water reabsorption, when fractional sodium reabsorption is at the baseline value. The scaling factor is greater/less than 1 when fractional sodium reabsorption is above/below the baseline value. The hyperbolic tangent function is chosen so that the scaling factor is symmetric around 1 and levels off for sufficiently high or low values. The fitting constants for the maximum value and the slope of the function are calibrated to match the urine excretion in the renal perfusion pressure experiment in Ref. 23. This calibration is done sequentially, whereby for a given perturbation in renal perfusion pressure, once simulated GFR and urine sodium excretion match the experimental data, the effect of the osmotic gradient is then calibrated so that urine excretion matches as well. The effect of antidiuretic hormone concentration on fractional water reabsorption in the collecting duct, μadh, is given by Karaaslan et al. (30).
Sodium transport is modeled analogously to fluid transport (11, 30). The filtered sodium (filsod) load is the product of the GFR, Φgfilt, and the sodium concentration, Csod:
| (A11) |
Equations for sodium reabsorption and flow in the segments are formed similarly as with fluid, ending with urine sodium flow, Φu-sod:
| (A12) |
| (A13) |
| (A14) |
| (A15) |
| (A16) |
| (A17) |
The fractional sodium reabsorption terms are given by:
| (A18) |
| (A19) |
| (A20) |
γfilsod, γAT1R, and γrsna are the effects of the amount of sodium delivered, AT1R-bound ANG II concentration, and RSNA, respectively, on sodium reabsorption in the proximal segment and are given by Karaaslan et al. (30). ψal And λal are the effects of aldosterone concentration on the distal and collecting duct segments, respectively, and are given in terms of the aldosterone concentration, Cal, by:
| (A21) |
| (A22) |
λal is given by Hallow et al. (22). ψal is formulated from the terms given by both Hallow et al. (22) and Karaaslan et al. (30) for low and high aldosterone concentration, respectively. λdt And λanp are the effects of the amount of sodium delivered and the atrial natriuretic peptide concentration, respectively, on sodium reabsorption in the collecting duct segment and are given by Karaaslan et al. (30).
Baseline parameters for fractional sodium and water reabsorption in the male proximal, distal, and collecting duct segments (, α = pt, dt, cd, and β = sod, w, respectively) are reported in Refs. 30 and 34. To determine these parameters in the female, we calibrate them based on the renal perfusion experiment in Hilliard et al. (23). Specifically, the calibration is done sequentially: first GFR, then sodium excretion, and then finally urine flow. For a perturbed RPP, first the myogenic response (Eq. 12) is calibrated so that the predicted and experimental GFR values match. Under a perturbed RPP, given that the GFR values match, we postulate that a discrepancy between the predicted and experimental sodium excretion values must be due to uncalibrated renal sodium transport parameters. Therefore, based on known sexual differences (42, 67), the female sodium transport parameters are calibrated so that the predicted and experimental sodium excretion values match. Finally, the female water transport parameters are then calibrated similarly so that the predicted and experimental urine flow values match.
Human-to-rat scaling.
Here, we summarize how we calculate the human-to-rat scaling factors. For full details, see the online data supplement.
GFR in male and female rats is reported in Ref. 47, whereas plasma sodium concentration is taken to be the same as the human value in Ref. 30. From these two, the filtered sodium load is determined from Eq. A11. Urine sodium flow in rats is determined from the filtered sodium load and the sodium transport parameters reported in Ref. 30. The urine sodium flow scaling factor is then given by:
| (A23) |
Similarly, urine flow in rats is determined from the GFR reported in Ref. 47 and the water transport parameters reported in Ref. 34. The urine flow scaling factor is then given by:
| (A24) |
The body weights of male and female rats are reported in Ref. 47, from which we determine their blood volumes from the relationship given in Ref. 39. Human blood volume is reported in Ref. 30. The volume scaling factor is then given by:
| (A25) |
Renal plasma flow in male and female rats is reported in Ref. 47, from which we determine RBF. We assume the same MAP in rats as the human value reported in Ref. 30. Renal vascular resistance in rats is then determined from Eq. 14. Human renal vascular resistance is reported in Ref. 30. The resistance scaling factor is then given by:
| (A26) |
REFERENCES
- 1.Ahmed S, Hu R, Leete J, Layton AT. Understanding sex differences in long-term blood pressure regulation: insights from experimental studies and computational modeling. Am J Physiol Heart Circ Physiol 316: H1113–H1123, 2019. doi: 10.1152/ajpheart.00035.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 1a.Animal Resources Centre Animal Resources Centre > Rodent Reference Information > Rat and Mice Weights (Online) http://www.arc.wa.gov.au/?page_id=125.
- 2.Averina VA, Othmer HG, Fink GD, Osborn JW. A new conceptual paradigm for the haemodynamics of salt-sensitive hypertension: a mathematical modelling approach. J Physiol 590: 5975–5992, 2012. doi: 10.1113/jphysiol.2012.228619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Baylis C. The mechanism of the increase in glomerular filtration rate in the twelve-day pregnant rat. J Physiol 305: 405–414, 1980. doi: 10.1113/jphysiol.1980.sp013372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Benjamin EJ, Muntner P, Alonso A, Bittencourt MS, Callaway CW, Carson AP, Chamberlain AM, Chang AR, Cheng S, Das SR, Delling FN, Djousse L, Elkind MSV, Ferguson JF, Fornage M, Jordan LC, Khan SS, Kissela BM, Knutson KL, Kwan TW, Lackland DT, Lewis TT, Lichtman JH, Longenecker CT, Loop MS, Lutsey PL, Martin SS, Matsushita K, Moran AE, Mussolino ME, O’Flaherty M, Pandey A, Perak AM, Rosamond WD, Roth GA, Sampson UKA, Satou GM, Schroeder EB, Shah SH, Spartano NL, Stokes A, Tirschwell DL, Tsao CW, Turakhia MP, VanWagner LB, Wilkins JT, Wong SS, Virani SS; American Heart Association Council on Epidemiology and Prevention Statistics Committee and Stroke Statistics Subcommittee . Heart Disease and Stroke Statistics–2019 update: a report from the American Heart Association. Circulation 139: e56–e528, 2019. doi: 10.1161/CIR.0000000000000659. [DOI] [PubMed] [Google Scholar]
- 5.Beznak M. Cardiac output in rats during the development of cardiac hypertrophy. Circ Res 6: 207–212, 1958. doi: 10.1161/01.RES.6.2.207. [DOI] [PubMed] [Google Scholar]
- 6.Bogzil AH, Eardley R, Ashton N. Relaxin-induced changes in renal sodium excretion in the anesthetized male rat. Am J Physiol Regul Integr Comp Physiol 288: R322–R328, 2005. doi: 10.1152/ajpregu.00509.2004. [DOI] [PubMed] [Google Scholar]
- 7.Brosnihan KB, Neves LA, Anton L, Joyner J, Valdes G, Merrill DC. Enhanced expression of Ang-(1-7) during pregnancy. Braz J Med Biol Res 37: 1255–1262, 2004. doi: 10.1590/S0100-879X2004000800017. [DOI] [PubMed] [Google Scholar]
- 8.Carey RM, Siragy HM. The intrarenal renin-angiotensin system and diabetic nephropathy. Trends Endocrinol Metab 14: 274–281, 2003. doi: 10.1016/S1043-2760(03)00111-5. [DOI] [PubMed] [Google Scholar]
- 9.Carlström M, Sällström J, Skøtt O, Larsson E, Persson AE. Uninephrectomy in young age or chronic salt loading causes salt-sensitive hypertension in adult rats. Hypertension 49: 1342–1350, 2007. doi: 10.1161/HYPERTENSIONAHA.107.087213. [DOI] [PubMed] [Google Scholar]
- 10.Chappell MC. Nonclassical renin-angiotensin system and renal function. Compr Physiol 2: 2733–2752, 2012. doi: 10.1002/cphy.c120002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Coleman TG, Hall JE. A mathematical model of renal hemodynamics and excretory function. Structuring Biological Systems: A Computer Modelling Approach, edited by Iyengar SS. Boca Raton, FL: CRC Press, 1992, p. 89–124. [Google Scholar]
- 12.DiBona GF. Neural control of renal function: cardiovascular implications. Hypertension 13: 539–548, 1989. doi: 10.1161/01.HYP.13.6.539. [DOI] [PubMed] [Google Scholar]
- 13.DiBona GF, Rios LL. Renal nerves in compensatory renal response to contralateral renal denervation. Am J Physiol Renal Physiol 238: F26–F30, 1980. doi: 10.1152/ajprenal.1980.238.1.F26. [DOI] [PubMed] [Google Scholar]
- 14.DiBona GF, Sawin LL. Reflex regulation of renal nerve activity in cardiac failure. Am J Physiol Regul Integr Comp Physiol 266: R27–R39, 1994. doi: 10.1152/ajpregu.1994.266.1.R27. [DOI] [PubMed] [Google Scholar]
- 15.Dosekun FO, Mendel D. The effect of alterations of plasma sodium on the sodium and potassium content of muscle in the rat. J Physiol 140: 190–200, 1958. doi: 10.1113/jphysiol.1958.sp005926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Edwards A, Castrop H, Laghmani K, Vallon V, Layton AT. Effects of NKCC2 isoform regulation on NaCl transport in thick ascending limb and macula densa: a modeling study. Am J Physiol Renal Physiol 307: F137–F146, 2014. doi: 10.1152/ajprenal.00158.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fischer M, Baessler A, Schunkert H. Renin angiotensin system and gender differences in the cardiovascular system. Cardiovasc Res 53: 672–677, 2002. doi: 10.1016/S0008-6363(01)00479-5. [DOI] [PubMed] [Google Scholar]
- 18.Gu Q, Burt VL, Paulose-Ram R, Dillon CF. Gender differences in hypertension treatment, drug utilization patterns, and blood pressure control among US adults with hypertension: data from the National Health and Nutrition Examination Survey 1999–2004. Am J Hypertens 21: 789–798, 2008. doi: 10.1038/ajh.2008.185. [DOI] [PubMed] [Google Scholar]
- 19.Guyton AC, Coleman TG, Cowley AV Jr, Scheel KW, Manning RD Jr, Norman RA Jr. Arterial pressure regulation. Overriding dominance of the kidneys in long-term regulation and in hypertension. Am J Med 52: 584–594, 1972. doi: 10.1016/0002-9343(72)90050-2. [DOI] [PubMed] [Google Scholar]
- 20.Guyton AC, Coleman TG, Granger HJ. Circulation: overall regulation. Annu Rev Physiol 34: 13–44, 1972. doi: 10.1146/annurev.ph.34.030172.000305. [DOI] [PubMed] [Google Scholar]
- 21.Hall JE, Guyton AC, Smith MJ Jr, Coleman TG. Blood pressure and renal function during chronic changes in sodium intake: role of angiotensin. Am J Physiol Renal Physiol 239: F271–F280, 1980. doi: 10.1152/ajprenal.1980.239.3.F271. [DOI] [PubMed] [Google Scholar]
- 22.Hallow KM, Lo A, Beh J, Rodrigo M, Ermakov S, Friedman S, de Leon H, Sarkar A, Xiong Y, Sarangapani R, Schmidt H, Webb R, Kondic AG. A model-based approach to investigating the pathophysiological mechanisms of hypertension and response to antihypertensive therapies: extending the Guyton model. Am J Physiol Regul Integr Comp Physiol 306: R647–R662, 2014. doi: 10.1152/ajpregu.00039.2013. [DOI] [PubMed] [Google Scholar]
- 23.Hilliard LM, Nematbakhsh M, Kett MM, Teichman E, Sampson AK, Widdop RE, Evans RG, Denton KM. Gender differences in pressure-natriuresis and renal autoregulation: role of the angiotensin type 2 receptor. Hypertension 57: 275–282, 2011. doi: 10.1161/HYPERTENSIONAHA.110.166827. [DOI] [PubMed] [Google Scholar]
- 24.Hinojosa-Laborde C, Chapa I, Lange D, Haywood JR. Gender differences in sympathetic nervous system regulation. Clin Exp Pharmacol Physiol 26: 122–126, 1999. doi: 10.1046/j.1440-1681.1999.02995.x. [DOI] [PubMed] [Google Scholar]
- 25.Hinojosa-Laborde C, Lange DL, Haywood JR. Role of female sex hormones in the development and reversal of dahl hypertension. Hypertension 35: 484–489, 2000. doi: 10.1161/01.HYP.35.1.484. [DOI] [PubMed] [Google Scholar]
- 26.Hu R, McDonough AA, Layton AT. Functional implications of the sex differences in transporter abundance along the rat nephron: modeling and analysis. Am J Physiol Renal Physiol 317: F1462–F1474, 2019. doi: 10.1152/ajprenal.00352.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.James PA, Oparil S, Carter BL, Cushman WC, Dennison-Himmelfarb C, Handler J, Lackland DT, LeFevre ML, MacKenzie TD, Ogedegbe O, Smith SC Jr, Svetkey LP, Taler SJ, Townsend RR, Wright JT Jr, Narva AS, Ortiz E. 2014 Evidence-based guideline for the management of high blood pressure in adults: report from the panel members appointed to the Eighth Joint National Committee (JNC 8). JAMA 311: 507–520, 2014. doi: 10.1001/jama.2013.284427. [DOI] [PubMed] [Google Scholar]
- 28.Just A. Mechanisms of renal blood flow autoregulation: dynamics and contributions. Am J Physiol Regul Integr Comp Physiol 292: R1–R17, 2007. doi: 10.1152/ajpregu.00332.2006. [DOI] [PubMed] [Google Scholar]
- 29.Karaaslan F, Denizhan Y, Hester R. A mathematical model of long-term renal sympathetic nerve activity inhibition during an increase in sodium intake. Am J Physiol Regul Integr Comp Physiol 306: R234–R247, 2014. doi: 10.1152/ajpregu.00302.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Karaaslan F, Denizhan Y, Kayserilioglu A, Gulcur HO. Long-term mathematical model involving renal sympathetic nerve activity, arterial pressure, and sodium excretion. Ann Biomed Eng 33: 1607–1630, 2005. doi: 10.1007/s10439-005-5976-4. [DOI] [PubMed] [Google Scholar]
- 31.Kopp UC. Neural control of renin secretion rate. In: Neural Control of Renal Function. San Rafael, CA: Morgan & Claypool Life Sciences, 2011. [PubMed] [Google Scholar]
- 32.Layton AT. Feedback-mediated dynamics in a model of a compliant thick ascending limb. Math Biosci 228: 185–194, 2010. doi: 10.1016/j.mbs.2010.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Layton AT, Edwards A, Vallon V. Adaptive changes in GFR, tubular morphology, and transport in subtotal nephrectomized kidneys: modeling and analysis. Am J Physiol Renal Physiol 313: F199–F209, 2017. doi: 10.1152/ajprenal.00018.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Layton AT, Laghmani K, Vallon V, Edwards A. Solute transport and oxygen consumption along the nephrons: effects of Na+ transport inhibitors. Am J Physiol Renal Physiol 311: F1217–F1229, 2016. doi: 10.1152/ajprenal.00294.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Layton AT, Vallon V. SGLT2 inhibition in a kidney with reduced nephron number: modeling and analysis of solute transport and metabolism. Am J Physiol Renal Physiol 314: F969–F984, 2018. doi: 10.1152/ajprenal.00551.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Layton AT, Vallon V, Edwards A. Modeling oxygen consumption in the proximal tubule: effects of NHE and SGLT2 inhibition. Am J Physiol Renal Physiol 308: F1343–F1357, 2015. doi: 10.1152/ajprenal.00007.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Layton AT, Vallon V, Edwards A. Predicted consequences of diabetes and SGLT inhibition on transport and oxygen consumption along a rat nephron. Am J Physiol Renal Physiol 310: F1269–F1283, 2016. doi: 10.1152/ajprenal.00543.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Layton AT, Vallon V, Edwards A. A computational model for simulating solute transport and oxygen consumption along the nephrons. Am J Physiol Renal Physiol 311: F1378–F1390, 2016. doi: 10.1152/ajprenal.00293.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lee HB, Blaufox MD. Blood volume in the rat. J Nucl Med 26: 72–76, 1985. [PubMed] [Google Scholar]
- 40.Leete J, Gurley S, Layton A. Modeling sex differences in the renin angiotensin system and the efficacy of antihypertensive therapies. Comput Chem Eng 112: 253–264, 2018. doi: 10.1016/j.compchemeng.2018.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Leete J, Layton AT. Sex-specific long-term blood pressure regulation: modeling and analysis. Comput Biol Med 104: 139–148, 2019. doi: 10.1016/j.compbiomed.2018.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Li Q, McDonough AA, Layton HE, Layton AT. Functional implications of sexual dimorphism of transporter patterns along the rat proximal tubule: modeling and analysis. Am J Physiol Renal Physiol 315: F692–F700, 2018. doi: 10.1152/ajprenal.00171.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lo A, Beh J, De Leon H, Hallow MK, Ramakrishna R, Rodrigo M, Sarkar A, Sarangapani R, Georgieva A. Using a systems biology approach to explore hypotheses underlying clinical diversity of the renin angiotensin system and the response to antihypertensive therapies. Clinical Trial Simulations, edited by Kimko HHC, Peck CC. New York: Springer, 2011, p. 457–482. [Google Scholar]
- 45.Loutzenhiser R, Griffin K, Williamson G, Bidani A. Renal autoregulation: new perspectives regarding the protective and regulatory roles of the underlying mechanisms. Am J Physiol Regul Integr Comp Physiol 290: R1153–R1167, 2006. doi: 10.1152/ajpregu.00402.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Malpas S. Editorial comment: Montani versus Osborn exchange of views. Exp Physiol 94: 381–382, 2009. doi: 10.1113/expphysiol.2008.043273. [DOI] [PubMed] [Google Scholar]
- 47.Munger K, Baylis C. Sex differences in renal hemodynamics in rats. Am J Physiol Renal Physiol 254: F223–F231, 1988. doi: 10.1152/ajprenal.1988.254.2.F223. [DOI] [PubMed] [Google Scholar]
- 48.Osborn JW. Hypothesis: set-points and long-term control of arterial pressure. A theoretical argument for a long-term arterial pressure control system in the brain rather than the kidney. Clin Exp Pharmacol Physiol 32: 384–393, 2005. doi: 10.1111/j.1440-1681.2005.04200.x. [DOI] [PubMed] [Google Scholar]
- 49.Pechère-Bertschi A, Burnier M. Female sex hormones, salt, and blood pressure regulation. Am J Hypertens 17: 994–1001, 2004. doi: 10.1016/j.amjhyper.2004.08.009. [DOI] [PubMed] [Google Scholar]
- 50.Reckelhoff JF, Hennington BS, Moore AG, Blanchard EJ, Cameron J. Gender differences in the renal nitric oxide (NO) system: dissociation between expression of endothelial NO synthase and renal hemodynamic response to NO synthase inhibition. Am J Hypertens 11: 97–104, 1998. doi: 10.1016/S0895-7061(97)00360-9. [DOI] [PubMed] [Google Scholar]
- 51.Rogenes PR, Gottschalk CW. Renal function in conscious rats with chronic unilateral renal denervation. Am J Physiol Renal Physiol 242: F140–F148, 1982. doi: 10.1152/ajprenal.1982.242.2.F140. [DOI] [PubMed] [Google Scholar]
- 52.Rojas-Vega L, Reyes-Castro LA, Ramírez V, Bautista-Pérez R, Rafael C, Castañeda-Bueno M, Meade P, de Los Heros P, Arroyo-Garza I, Bernard V, Binart N, Bobadilla NA, Hadchouel J, Zambrano E, Gamba G. Ovarian hormones and prolactin increase renal NaCl cotransporter phosphorylation. Am J Physiol Renal Physiol 308: F799–F808, 2015. doi: 10.1152/ajprenal.00447.2014. [DOI] [PubMed] [Google Scholar]
- 53.Rowland NE, Fregly MJ. Role of gonadal hormones in hypertension in the Dahl salt-sensitive rat. Clin Exp Hypertens A 14: 367–375, 1992. doi: 10.3109/10641969209036195. [DOI] [PubMed] [Google Scholar]
- 54.Ruiz-Feria CA, Zhang D, Nishimura H. Age- and sex-dependent changes in pulse pressure in fowl aorta. Comp Biochem Physiol A Mol Integr Physiol 137: 311–320, 2004. doi: 10.1016/j.cbpb.2003.10.006. [DOI] [PubMed] [Google Scholar]
- 55.Sabolić I, Asif AR, Budach WE, Wanke C, Bahn A, Burckhardt G. Gender differences in kidney function. Pflugers Arch 455: 397–429, 2007. doi: 10.1007/s00424-007-0308-1. [DOI] [PubMed] [Google Scholar]
- 56.Sáinz J, Osuna A, Wangensteen R, de Dios Luna J, Rodríguez-Gómez I, Duarte J, Moreno JM, Vargas F. Role of sex, gonadectomy and sex hormones in the development of nitric oxide inhibition-induced hypertension. Exp Physiol 89: 155–162, 2004. doi: 10.1113/expphysiol.2003.002652. [DOI] [PubMed] [Google Scholar]
- 57.Sampson AK, Moritz KM, Jones ES, Flower RL, Widdop RE, Denton KM. Enhanced angiotensin II type 2 receptor mechanisms mediate decreases in arterial pressure attributable to chronic low-dose angiotensin II in female rats. Hypertension 52: 666–671, 2008. doi: 10.1161/HYPERTENSIONAHA.108.114058. [DOI] [PubMed] [Google Scholar]
- 58.Sandberg K, Ji H. Sex differences in primary hypertension. Biol Sex Differ 3: 7, 2012. doi: 10.1186/2042-6410-3-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Sgouralis I, Layton AT. Autoregulation and conduction of vasomotor responses in a mathematical model of the rat afferent arteriole. Am J Physiol Renal Physiol 303: F229–F239, 2012. doi: 10.1152/ajprenal.00589.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Sgouralis I, Layton AT. Theoretical assessment of renal autoregulatory mechanisms. Am J Physiol Renal Physiol 306: F1357–F1371, 2014. doi: 10.1152/ajprenal.00649.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Silva-Antonialli MM, Tostes RCA, Fernandes L, Fior-Chadi DR, Akamine EH, Carvalho MHC, Fortes ZB, Nigro D. A lower ratio of AT1/AT2 receptors of angiotensin II is found in female than in male spontaneously hypertensive rats. Cardiovasc Res 62: 587–593, 2004. doi: 10.1016/j.cardiores.2004.01.020. [DOI] [PubMed] [Google Scholar]
- 62.Sparks MA, Crowley SD, Gurley SB, Mirotsou M, Coffman TM. Classical renin-angiotensin system in kidney physiology. Compr Physiol 4: 1201–1228, 2014. doi: 10.1002/cphy.c130040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Stakišaitis D, Dudėnienė G, Jankūnas RJ, Graželienė G, Didžiapetrienė J, Pundzienė B. Cisplatin increases urinary sodium excretion in rats: gender-related differences. Medicina (Kaunas) 46: 45–50, 2010. doi: 10.3390/medicina46010008. [DOI] [PubMed] [Google Scholar]
- 64.Sullivan JC. Sex and the renin-angiotensin system: inequality between the sexes in response to RAS stimulation and inhibition. Am J Physiol Regul Integr Comp Physiol 294: R1220–R1226, 2008. doi: 10.1152/ajpregu.00864.2007. [DOI] [PubMed] [Google Scholar]
- 65.Sullivan JC. Sex differences in angiotensin II hypertension. Sodium and Water Homeostasis: Comparative, Evolutionary and Genetic Models, edited by Hyndman KA, Pannabecker TL. New York: Springer, 2015, p. 91–117. [Google Scholar]
- 66.Uttamsingh RJ, Leaning MS, Bushman JA, Carson ER, Finkelstein L. Mathematical model of the human renal system. Med Biol Eng Comput 23: 525–535, 1985. doi: 10.1007/BF02455306. [DOI] [PubMed] [Google Scholar]
- 66a.Van Liere EJ, Stickney JC, Marsh DF. Sex differences in blood pressure of dogs. Science 109: 489, 1949. doi: 10.1126/science.109.2837.489. [DOI] [PubMed] [Google Scholar]
- 67.Veiras LC, Girardi ACC, Curry J, Pei L, Ralph DL, Tran A, Castelo-Branco RC, Pastor-Soler N, Arranz CT, Yu ASL, McDonough AA. Sexual dimorphic pattern of renal transporters and electrolyte homeostasis. J Am Soc Nephrol 28: 3504–3517, 2017. doi: 10.1681/ASN.2017030295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Xue B, Pamidimukkala J, Hay M. Sex differences in the development of angiotensin II-induced hypertension in conscious mice. Am J Physiol Heart Circ Physiol 288: H2177–H2184, 2005. doi: 10.1152/ajpheart.00969.2004. [DOI] [PubMed] [Google Scholar]
- 69.Xue B, Zhang Z, Beltz TG, Guo F, Hay M, Johnson AK. Estrogen regulation of the brain renin-angiotensin system in protection against angiotensin II-induced sensitization of hypertension. Am J Physiol Heart Circ Physiol 307: H191–H198, 2014. doi: 10.1152/ajpheart.01012.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Zimmerman MA, Sullivan JC. Hypertension: what’s sex got to do with it? Physiology (Bethesda) 28: 234–244, 2013. doi: 10.1152/physiol.00013.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]