A Well-balanced Force Field ff03CMAP for Folded and Disordered Proteins

Abstract

Molecular dynamics simulation as an important complement of experiment is widely used to study protein structures and functions. However, previous studies indicate that current force fields cannot, simultaneously, provide accurate descriptions of folded proteins and intrinsically disordered proteins (IDPs). Therefore, a CMAP optimized force field based on the Amber ff03 force field (termed ff03CMAP herein) was developed for balanced sampling of folded proteins and IDPs. Extensive validations of short peptides, folded proteins, disordered proteins, and fast-folding proteins show that simulated chemical shifts, J-coupling constants, order parameters, and residual dipolar couplings with the ff03CMAP force field are in very good agreement with NMR measurements and are more accurate than other ff03-series force fields. The influence of solvent models was also investigated. It was found that the combination of ff03CMAP/TIP4P-Ew is suitable for folded proteins and that of ff03CMAP/TIP4PD is better for disordered proteins. These findings confirm that the newly developed force field ff03CMAP can improve the balance of conformer sampling between folded proteins and IDPs.

Introduction

Proteins can exist in three states, folded, molten globule, and random coil.^[1] Folded proteins are easier to study because they are ordered and stable. But disordered proteins also need exploring. In eukaryotes, more than 30 percent of proteins contain disordered regions with more than 50 consecutive residues.^[1] Proteins with disordered regions or overall intrinsically disordered proteins (IDPs) have been proved to have important biological functions, such as molecular recognition, molecular assembly, protein modification, and so on.^[2] Furthermore, IDPs are associated with many human diseases, such as Alzheimer’s disease, Parkinson’s disease, Huntington’s disease, cancer, and cardiovascular disease, to name a few.^[3–4] IDPs are more flexible and unstable with little secondary structures than structured or ordered proteins. “Intrinsically disordered” implies a sequence-dependent nature in IDPs that trend to be lack of ordered structures.^[5] Many experimental methods have been utilized to study IDPs, such as electron paramagnetic resonance (EPR), X-ray diffraction, Nuclear Magnetic Resonance (NMR), and small-angle X-ray scattering (SAXS).^[6–8]

Because of their important biological functions, IDPs have become common topics in molecular dynamics studies in recent years. Due to limited accuracy in standard protein force fields, a set of special-purpose force fields have been developed for simulating IDPs, such as ff99IDPs, ff14IDPs, ff14IDPSFF, ff03ws, RSFF2, a99SB-disp, CHARMM36IDPSFF and so on.^[9–15] In addition, the D. E. Shaw group also modified the dispersion interaction of TIP4P water model (TIP4P-D) to improve the quality of IDPs simulations.^[16] However, it remains elusive to reach a good balance between ordered and disordered states with either standard or special-purpose force fields.

ff03 is a new-generation Amber force field that has become widely used in biomolecular simulation studies.^[17] Based on ff03, the Best group modified backbone dihedral potentials in the context of the TIP4P/2005 water model. Their efforts lead to three ff03 variants: ff03*, ff03w, and ff03ws.^{[12, 18–19]} These modifications were shown to partially improve the performance of conformer sampling of IDPs and folded proteins. The effect of solvent model was found to be important in the sampling of IDPs in their studies.^{[12, 18–19]} TIP3P is the most commonly used water model in earlier force fields.^[20] Improvement of water models has always been concurrent with protein force field developments. Besides TIP4P-D, TIP4P-Ew and TIP4P/2005 are also two commonly used four-site water models and should be investigated in any force field improvement efforts.^[21–22] These four-site water models have been found to reproduce well the hydrophobic effect and water density in a wide temperature range.

In this development, we systematically analyzed the original ff03 force field, its published variants, and explored a new variant based on the CMAP method, ff03CMAP. The combinations of force fields and corresponding solvent models are ff03 with TIP3P, ff03* with TIP3P, ff03w with TIP4P/2005, ff03ws with TIP4P/2005 as in the published efforts. Based on our analyses, we recommend the combinations of ff03CMAP with TIP4P-Ew and TIP4P-D, respectively, suitable for folded proteins and IDPs.^{[12, 17–19]} In order to evaluate the performance of these force fields, 16 proteins were simulated to probe the quality of various force field/water model combinations in reproducing experimental measurables. The tested short peptides and proteins are shown in Figure 1.

Figure 1.

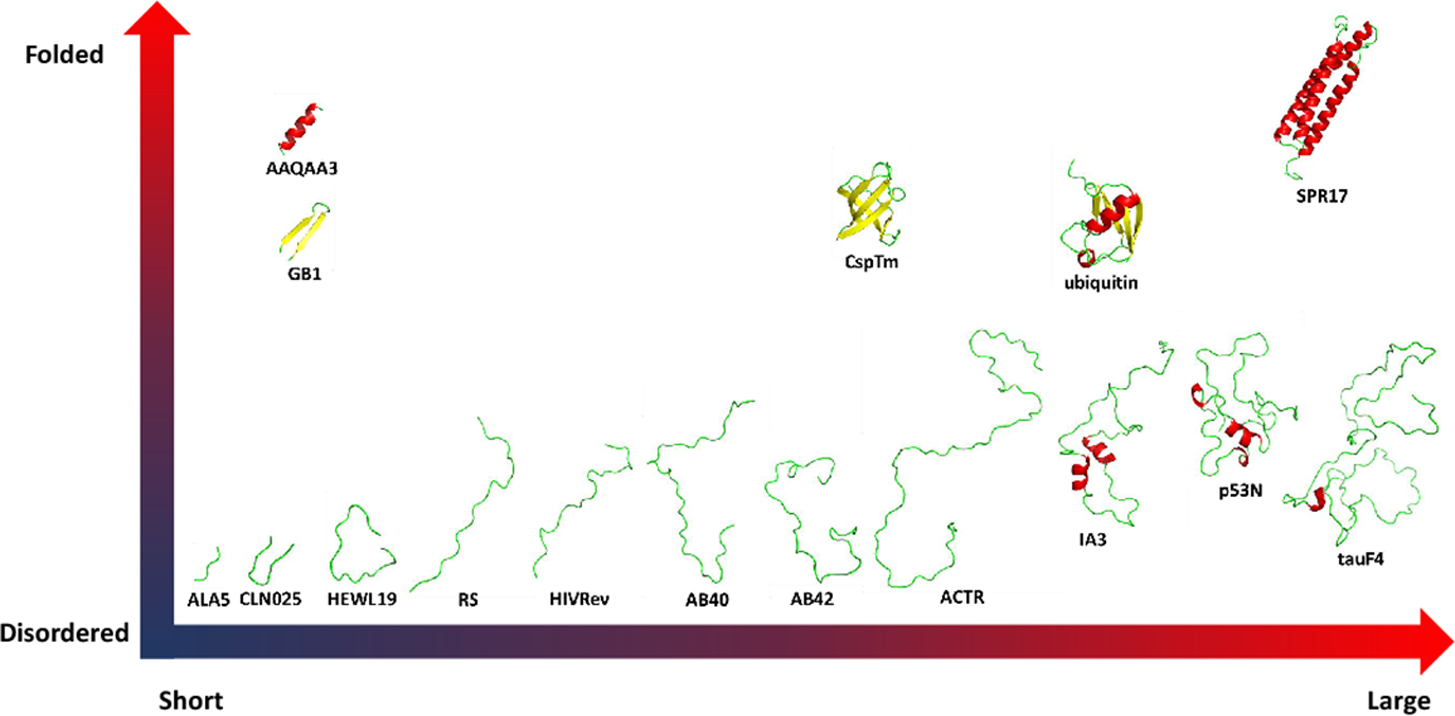
Test system from short peptides to proteins. Three representative folded proteins such as cold-shock protein from the hyperthermophilic bacterium Thermotoga maritima (CspTm, all-β),^[23] ubiquitin of human (α/β)^[24] and chicken brain alpha spectrin repeat 17 (SPR17, all-α).^[25] 9 typical disordered protein including 19 length peptide of hen egg-white lysozyme (HEWL19),^[26] phosphorylated SRSF1 (RS),^[27] HIV-1 Rev ARM peptide (HIVRev),^[28] 40 length amyloid-beta-peptides (AB40),^[29] 42 length amyloid-beta-peptides (AB42),^[29] activation domain of the nuclear hormone receptor coactivator (ACTR),^[30] an aspartic proteinase inhibitor for Saccharomyces cerevisiae (IA3),^[31] p53 N-terminal transactivation domain (p53N)^[32] and tau protein fragment (TauF4).^[33] 3 fast-folding proteins including 15-residue helix-forming peptide Ac-(AAQAA)₃-NH₂ (AAQAA3),^[34] β-hairpin B1 domain of protein G (GB1)^[35–36] and Chignolin, a 10 residue folded peptide designed by segment statistics (CLN025).^[37]

Material and Methods

Molecular Dynamics Simulations.

Initial structures were built by the LEaP module in the AMBER 14 suite if not available,^[38] which was also used to conduct MD simulations.^[39] All systems were neutralized and solvated in boxes of different water models.^[20] All bonds involving hydrogen atom were constrained with the SHAKE algorithm.^[43] Particle Mesh Ewald (PME) algorithm was used to calculate long-range electrostatic interactions.^[41] Initial structures were relaxed with 10000 steps of minimization, then subject to heating up for 20ps, and equilibration for 10ps in the NPT ensemble with PMEMD. The CUDA version of PMEMD was used to accelerate the simulations.^[42] The simulation temperature and ion strength were set according to their respective experimental conditions. The number of replica-exchange molecular dynamics (REMD) replicas and temperatures were set by an online temperature predictor for parallel tempering simulations.^[40] All simulation conditions are shown in Table S1.

Insert a table for all tested force field water combinations.

Benchmark of PDB Coil Structures.

Coil database was built and extracted from PDB. The DSSP program was utilized to classify the secondary structures and extract main chain dihedrals from these structures.^[44–45] 2,611,450 amino acids without secondary structure were collected. The counts of amino acids in the coiled database are shown in Figure S1. The Ramachandran plots for the database were used as the benchmark for the optimization of dihedral distribution.

CMAP Method.

Grid-based energy correction maps (CMAP) is a useful method for automatically correcting dihedral distribution for the additive force field, which is based on the backbone dihedral distribution and has been used to develop IDP-specific force fields.^{[10, 46]} CMAP was first published to modify the CHARMM force field and was transferred into Amber software.^{[9–11, 47–50]} We minimized the main-chain dihedral distribution differences between the MD simulation and the benchmark for each of the 20 amino acids. A 576-(24 × 24) grid was used to cover the phi/psi map. The tetrapeptide models (Nme-Ala-X-Ala-Ace, where X represents one of 20 naturally amino acids, Nme for aminomethyl, and Ace for acetyl) were utilized in the CMAP optimization via MD simulations in the TIP4PEw water model. Ten cycles of CMAP optimization were conducted to minimize the distribution differences between the MD simulation and the benchmark. In each cycle, the solvated tetrapeptides were simulated for 200 nanoseconds. After the CMAP optimization, we added an additional structural factor which is the partial dihedral energy distribution of ‘S’ fragments predicted by DSSP in the PDB coil database to avoid overestimation of disordered state when using the new force field. Root-mean-square deviations of population (RMSp) is calculated to compare the difference between the MD simulation and the benchmark with equation (1).

$$\mathit{\text{RMSp}}=\sqrt{\frac{{\sum }_{i=1}^{576}{\left(P_i^{DB}-P_i^{MD}\right)}^2}{576}}$$ (1)

where $P_i^{DB}$ is the population of the i-th grid in database benchmark and $P_i^{MD}$ is the population of the i-th grid in the MD simulation.

Quantification in the Evaluation for Force Fields.

To quantitatively compare different ff03 variants for folded proteins and disordered proteins with experimental measurements, we utilized the normalized force-field score.^[14] For folded proteins, equation (2) was used to calculate averaged normalized RMSD from each class of experimental data as

$$\mathit{\text{Folded}}\mathit{\text{Protein}}F{F}_{\mathit{\text{Score}}}=\frac{1}{N}{\sum }_{i=1}^N\frac{F{F}_{\mathit{\text{rmsd}}}}{rms{d}_{\mathit{\text{Norm}}}}$$ (2)

where N is the number of classes of experimental measurements, FF_rmsd is the RMSD of the i-th class for simulated and experimental values, and rmsd_Norm is the lowest RMSD of i-th class in all force fields. According to this metric, FF_Score is always greater than or equal to 1, and 1 is the best score theoretically which means this force field perfectly reproduced the experimental data. For disordered protein, we divided the experimental measurements into two groups because there are fewer experimental measurements than the folded proteins, for which there are chemical shifts and other NMR measurements. If experimental data for both chemical shifts and NMR measurements are available, FF_Score is calculated with equation (3).

$$\mathit{\text{Disordered}}\mathit{\text{Protein}}F{F}_{\mathit{\text{Score}}}=\frac{C{S}_{\mathit{\text{Score}}}+NM{R}_{\mathit{\text{Score}}}}{2}$$ (3)

and if there is only chemical shift, the FF_Score is calculated with equation (4).

$$\mathit{\text{Disordered}}\mathit{\text{Protein}}F{F}_{\mathit{\text{Score}}}=C{S}_{\mathit{\text{Score}}}$$ (4)

Where CS_Score and NMR_Score are calculated as same as the score of class in folded protein FF_Score.

Calculation of Experimental Observables.

Backbone chemical shifts were calculated by SHIFTX2 for Cα, Cβ, C, N, Hα and HN atom types.^[51] Backbone scalar coupling constants were calculated using published Karplus relations for ³J_HNHα, ³J_HαC, ³J_HNC, ³J_CC, ³J_HNCα, ³J_HNCβ, ²J_CαN, ¹J_CαN, ¹J_HαCα, and ¹J_CαCβ^[52–60] and side-chain scalar coupling constants with Karplus relations for ³J_CCγ and ³J_NCγ.^[61] Backbone RDCs were calculated using PALES with a local alignment window of 15 residues.^[62–63] Backbone amide and side-chain methyl axis S² order parameters were calculated with the direct method described in Trbovic et al.^[64] Small angle X-ray scattering (SAXS) curves were calculated using the FoXS package.^[65] Cα RMSD and radius of gyrations (Rg) were calculated using CPPTRAJ in AmberTools.^[38] Conformational clustering was performed with the kClust program in the MMTSB tool.^[66] MDTraj, a python package, was also used for miscillenous calculations.^[67] The PyMOL molecular visualization system was used to show 3D structures for all proteins.^[68] All experimental measurements are listed in Table S2.

Biphasic exponential decay model was used to analyze the IDPs sampling convergence for force fields. The equations (5) and (6) were used to calculate the fitting half-time.^[71]

$$\Delta C\alpha \mathit{\text{Chemical}}\mathit{\text{Shift}}\left(N_t\right)=A_1{e}^{-\left(\frac{x}{{\tau }_1}\right)}+A_2{e}^{-\left(\frac{x}{{\tau }_2}\right)}+N_0$$ (5)

$$t_{1/2}=\tau ln\left(2\right)$$ (6)

where N₀ is the plateau of an observable, t_1/2 is the half-life time, A and τ are constants. In this model, the decay consists of two stages for fast stage and slow stage. The slower τ₂ value was utilized to calculate the slow stage half-life and evaluate the convergence rate of IDPs simulation.

Results and Discussion

CMAP Optimization.

Ten cycles of CMAP optimization were performed for each amino acid. In the first cycle (CMAP0), the initial φ/ψ distribution was obtained from the standard ff03 force field, where the lowest RMSp is 0.234% among 20 amino acids. In contrast, after 10 cycles of optimization, the lowest RMSp is less than 0.064%, as shown in Figure S2. Comparison of the distributions of CMAP0 and the benchmark database, we found that there is almost no left-handed helix distribution except MET, GLY and LEU. In addition, an obviously energy barrier exists between the β-sheet region and the α-helix region, so it would be difficult to sample both types of structures. After optimization, these limitations no longer present. The parameters for the best RMSp for each amino acid were selected as the final CMAP values. These parameters and structural factors were integrated with standard ff03 force field to generate the new force field ff03CMAP.

Evaluation of ff03-series Force Fields.

We assessed the performance of ff03-series force fields in reproducing experimental data. The same conditions were used in all MD simulation among all tested force fields. The FF scores for short peptides, IDPs, and fold proteins are shown in Figure 2 and specific values are listed in supplementary Table S3. Figure 2 suggests that combination ff03CMAP/TIP4PD agrees the best with experiment for short peptides and IDPs. In addition, combination ff03CMAP/TIP4PEw leads to the best agreement with experiment for folded proteins. In summary, use of ff03CMAP can yield more accurate sampling the conformers for short peptide, IDPs and folded proteins.

Figure 2.

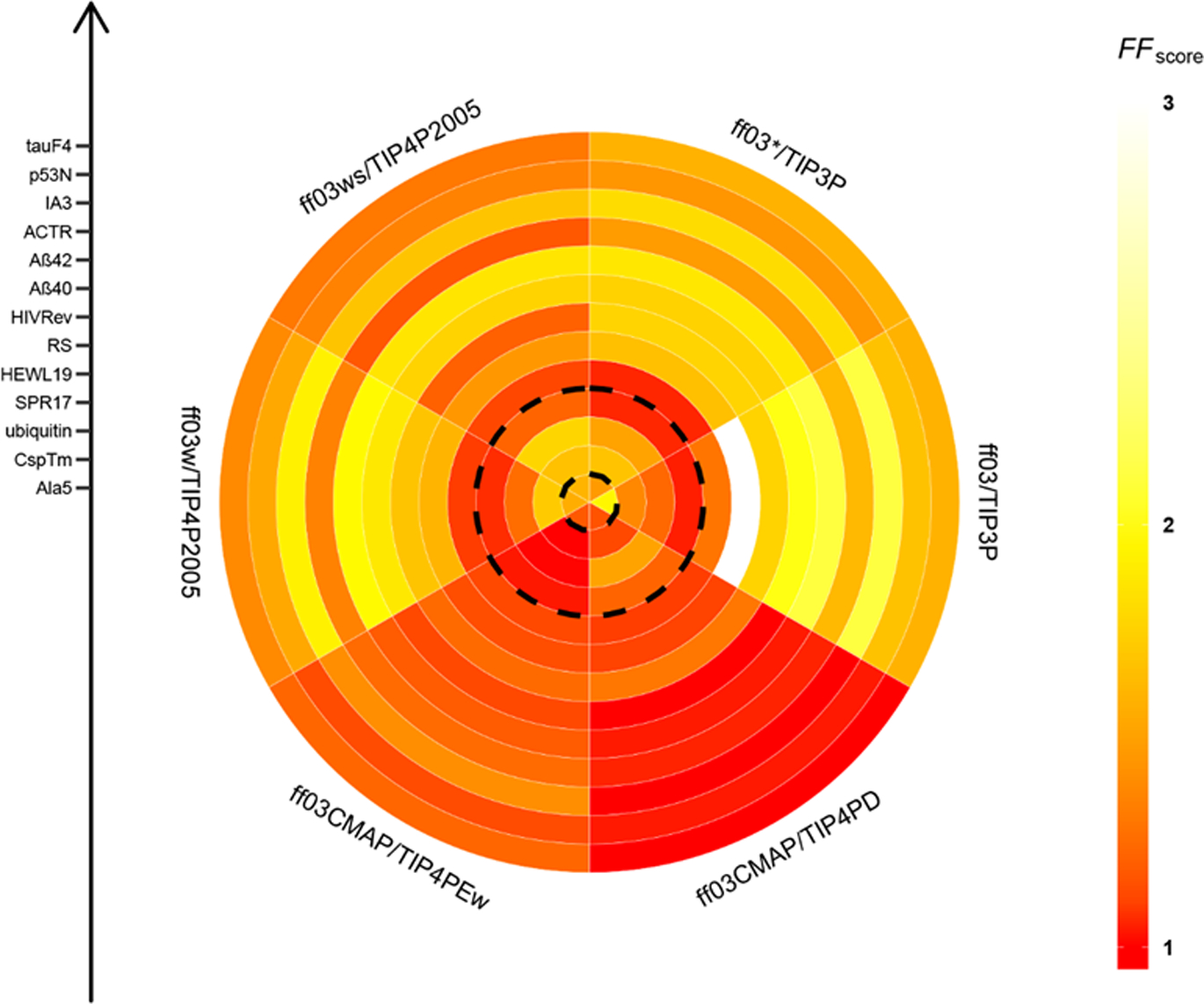
FF scores for short peptide, disordered proteins, and folded proteins. The plot is divided into six sectors which represent six ff03-series force fields. From inner circle to outer circle, there are 13 simulated system for 1 short peptide, 9 disordered proteins, and 3 folded proteins sorted by the residue length in each category.

Short Peptide Ala₅.

Table 1 shows the RMSD’s of secondary chemical shifts, J-coupling constants and force field score for Ala₅. There are 6 types of secondary chemical shifts and 7 types of J-coupling constants. For the CS score, the performance of ff03CMAP/TIP4PEw are much better than all other force fields. However, the performance of ff03*/TIP3P is the best for the NMR score. If we combine CS and NMR scores (i.e. overall FF score), ff03-drived force fields are significantly improved over the origin ff03 and the ff03CMAP/TIP4PEw is the best. The detail RMSD’s of secondary chemical shifts and J-coupling constants are shown in Figures S3–S4.

Table 1.

RMSD’s of secondary chemical shifts, J-coupling constants and force field scores of ff03-series force fields for Ala5.^a

	ff03	ff03*	ff03w	ff03ws	ff03CMAP/ TIP4PEw	ff03CMAP/TIP4PD
Cα	0.321	0.182	0.192	0.173	0.162	0.183
Cβ	0.372	0.474	0.499	0.514	0.192	0.204
C	0.297	0.453	0.471	0.490	0.346	0.348
N	1.633	1.022	1.112	1.177	0.417	0.415
Hα	0.045	0.057	0.055	0.057	0.024	0.021
HN	0.352	0.375	0.381	0.384	0.346	0.348
3JHNHα	0.443	0.292	0.281	0.297	0.319	0.259
3JHNCα	0.104	0.047	0.046	0.047	0.047	0.042
3JHNCβ	0.374	0.234	0.264	0.275	0.359	0.296
3JHαC	0.120	0.131	0.135	0.137	0.124	0.154
3JHNC	0.224	0.133	0.168	0.179	0.188	0.160
1JCαN	0.265	0.092	0.141	0.136	0.166	0.179
2JCαN	0.435	0.217	0.222	0.217	0.222	0.228
CSscore	1.995	1.888	1.950	1.997	1.049	1.061
NMRscore	1.905	1.047	1.178	1.202	1.307	1.250
FFscore	1.950	1.468	1.564	1.599	1.178	1.155

^aChemical shifts are in ppm, J-coupling constants are in Hz and the scores are unitless.

Folded Proteins.

In order to evaluate the stability of folded proteins when modeled with ff03CMAP, three representative folded proteins were simulated: CspTm (all-β), ubiquitin (α/β) and SPR17 (all-α). The initial structures are extracted from PDB and the simulation time is 1 μs for each system.

Table 2 shows the FF scores of the three tested proteins for all ff03-series force fields. It is obviously that the FF score for combination ff03CMAP/TIP4P-Ew is the best among all tested force fields and the value close to 1. This suggests that ff03CMAP/TIP4PEw indeed can be used to simulate folded proteins. And we also found that the original ff03 force field performs better performance than other revised ff03 force fields. It is no surprise that the performance of ff03CMAP/TIP4PD is a little worse than that of ff03CMAP/TIP4PEw because TIP4P-D water model would destabilize the folded states of proteins as reported.^[16] The details of the FF score composition for the three proteins are shown in Tables S4–S6.

Table 2.

FF scores of three folded proteins for six ff03-series force fields

Protein	ff03	ff03*	ff03w	ff03ws	ff03CMAP/TIP4PEw	ff03CMAP/TIP4PD
CspTm	1.376a	1.674	1.718	1.663	1.000	1.123
Ubiquitin	1.231	1.506	1.249	1.769	1.003	1.509
SPR17	1.026	1.041	1.052	1.219	1.019	1.220

To quantify the fluctuation in simulations, Cα RMSD’s of the folded proteins are shown in Figure 3 [Can you only compute the RMSDs of the secondary structures/i.e. stable portions of the proteins?]. For CspTm and ubiquitin, the RMSDs in the ff03CMAP/TIP4PEw simulations are small and stable, which is consistent with the FF score. However, the RMSD’s for SPR17 rise over 4Å after 700ns in the ff03CMAP/TIP4PEw simulation. The RMSDs of ff03ws for all three folded proteins fluctuate quite significantly, implying less stable folded states for the tested proteins.

Figure 3.

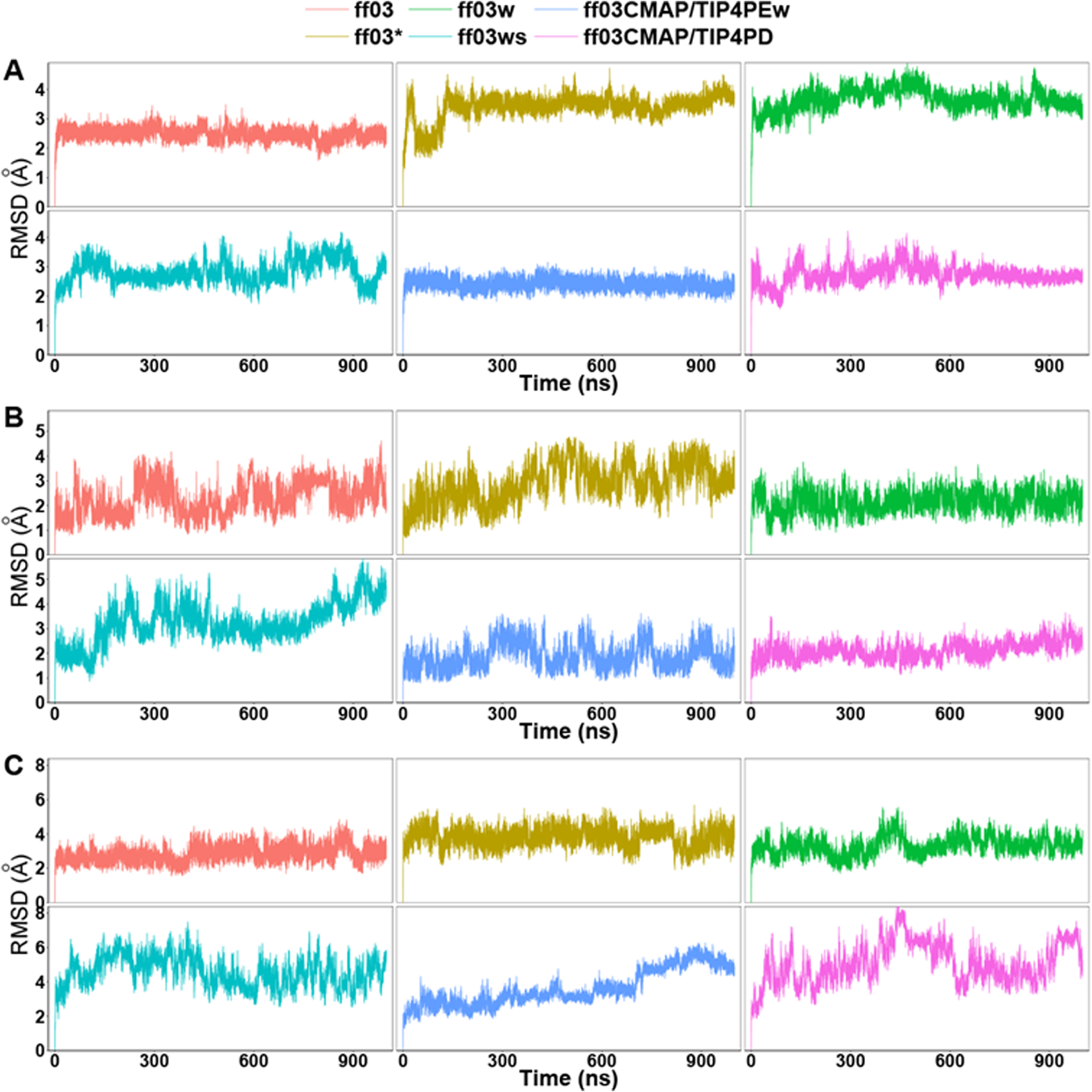
Cα RMSD of six ff03-series force fields. A: CspTm. B: ubiquitin. C: SPR17.[See my comments]

More detailed analyses were conducted for ubiquitin to compare the performances of these force fields. Secondary chemical shifts and backbone scalar coupling constants of ubiquitin (Figures S6–S7) suggest that ff03CMAP/TIP4PEw simulation agree the best with experimental data. The same can be said for the side-chain scalar coupling constants as shown in Tables S16–S17. RDCs of backbone N-HN, Cα-Hα, Cα-C, C-N and C-HN were also calculated shown in Figure S8. Similar to chemical shifts and scalar coupling constants, the performance of ff03CMAP/TIP4PEw simulation also agrees among the best, along with the ff03 simulation, while the ff03ws simulation agrees the worse. The order parameters for backbone amide and side-chain methyl groups are shown in Figure 4 and Table S18, respectively. The order parameters in the ff03CMAP/TIP4PEw simulation are also in good agreement with experimental data. The figure further indicates that the order parameters of the loop regions in the ff03CMAP/TIP4PD simulation are much lower than those from other force fields. [What is the point of the following statement?]Only ff03CMAP/TIP4PEw exhibited similar behavior to experiment for side-chain order parameters (Table S18?).

Figure 4.

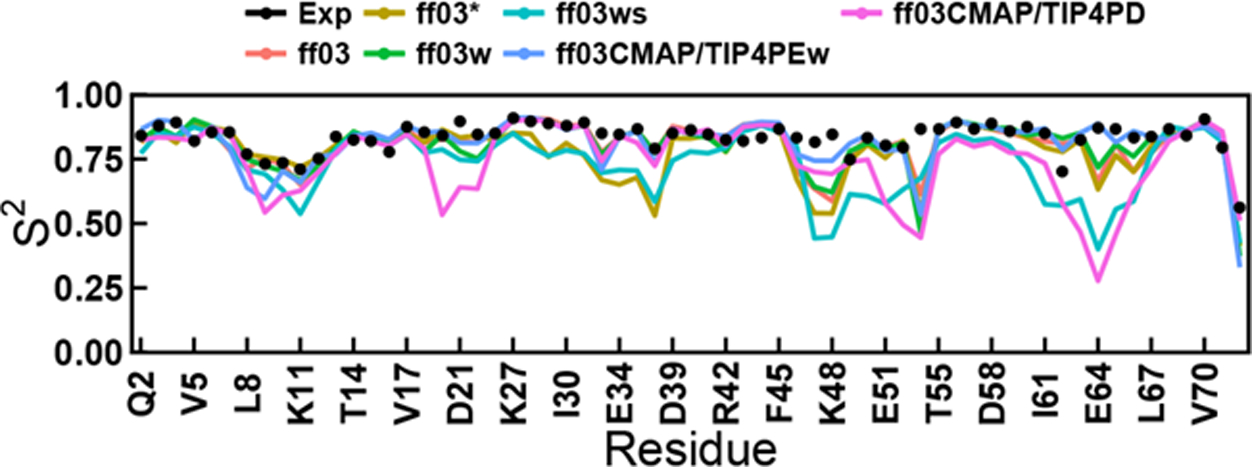
Backbone amide order parameters of six ff03-series force fields for ubiquitin. The RMSDs between simulation and experiment for ff03, ff03*, ff03w, ff03ws, ff03CMAP/TIP4PEw and ff03CMAP/TIP4PD are 0.074, 0.104, 0.081, 0.149, 0.069 and 0.154.

The RMSDs of secondary chemical shift, J-coupling, order parameters, and RDCs are gathered in Table 3. The summary indicates that ff03CMAP/TIP4PEw performs excellently in in reproducing all available experimental measurements and its FF score is very close to 1. While the FF score of ff03CMAP/TIP4PD is more than 1.5, which suggests TIP4P-D water model unsuitable for the simulation of folded proteins.

Table 3.

RMSDs of secondary chemical shifts, J-coupling constants, RDCs, S² parameters and FF scores of ubiquitin for six ff03-series force fields.^a

	ff03	ff03*	ff03w	ff03ws	ff03CMAP/TIP4PEw	ff03CMAP/TIP4PD
Cα	0.481	0.716	0.507	0.723	0.485	0.575
Cβ	0.816	0.885	0.825	1.069	0.770	0.860
C	0.607	0.702	0.611	0.789	0.609	0.650
N	2.050	2.450	2.188	2.625	2.142	2.573
HA	0.145	0.185	0.141	0.234	0.106	0.165
HN	0.329	0.349	0.326	0.407	0.298	0.293
3JHNHα	1.341	1.487	1.484	1.597	1.196	1.319
3JHαC	0.684	0.725	0.623	0.986	0.410	0.609
3JHNCβ	0.643	0.734	0.671	0.701	0.633	0.612
3JHNC	0.681	0.734	0.701	0.852	0.564	0.662
1JCαN	0.465	0.567	0.494	0.588	0.415	0.469
1JHαCα	2.669	2.717	2.628	3.030	2.225	2.476
1JCαCβ	0.984	1.056	0.977	1.229	0.856	0.966
2JCαN	0.464	0.555	0.437	0.682	0.361	0.477
2JCCγ	0.650	0.973	0.717	0.936	0.419	0.775
3JNCγ	0.490	0.592	0.501	0.557	0.428	0.496
S2NH	0.074	0.104	0.081	0.149	0.069	0.154
S2axis	0.279	0.260	0.247	0.289	0.174	0.279
RDC	0.174	0.249	0.187	0.325	0.166	0.222
CSscore	1.092	1.321	1.107	1.512	1.012	1.200
Backbone 3J	1.225	1.359	1.228	1.562	1.004	1.182
Sidechain 3J	1.348	1.853	1.440	1.768	1.000	1.504
Backbone S2	1.070	1.510	1.175	2.156	1.000	2.226
Sidechain S2	1.603	1.493	1.418	1.657	1.000	1.603
Backbone RDC	1.048	1.500	1.127	1.958	1.000	1.337
FFscore	1.231	1.506	1.249	1.769	1.003	1.509

^aChemical shifts are in ppm, J-coupling constants and RDC are in Hz, and the scores and S² parameters are unitless.

In order to further evaluate the stability of ff03CMAP for folded proteins, the dominant conformers of ubiquitin from six ff03-series force fields are retrieved and shown in Figure 5. It was found that top 3 clusters in the ff03 simulation occupy 100.00% of the snapshots. All the conformers include high percentage of helical structures. Top 5 clusters in the ff03* simulation also occupy 100.00% of the snapshots with partially non-helical structures. In the ff03w simulation, only 2 clusters were found, and the conformers are highly structured. In the ff03ws simulation, top 8 clusters only occupy 78.70% of the snapshots. In the ff03CMAP/TIP4PEw simulation there is only one cluster and 4 clusters in the ff03CMAP/TIP4PD simulation. Additional conformation clustering was also conducted for the CspTm and SPR17 simulations (supplementary Figures S24–S25). These conformer clusters indicate that ff03CMAP/TIP4PEw, ff03, and ff03w may be the better ff03 choices for folded proteins MD simulation.

Figure 5.

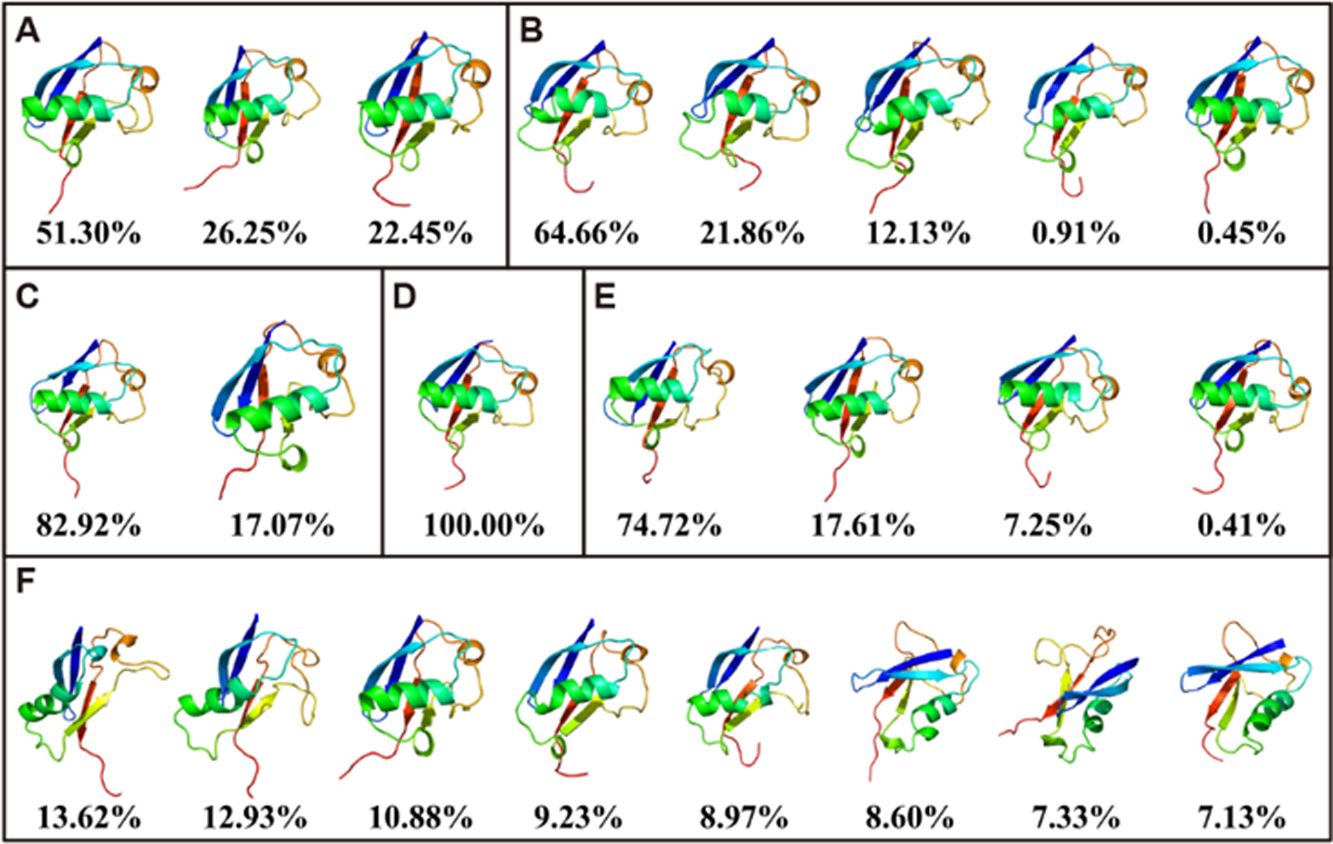
Conformation clustering of simulation for ubiquitin. The figure shows the top 8 clusters at most with dominant conformations and percentage for ff03 (A), ff03* (B), ff03w (C), ff03CMAP/TIP4PEw (D), ff03CMAP/TIP4PD (E), and ff03ws (F).

Intrinsically Disordered Proteins.

We tested 9 typical disordered proteins with 19 to 124 residues. The FF scores of the six ff03-series force fields are listed in Table 4. Except for HEWL19 and HIVRev, the FF scores of ff03CMAP/TIP4P-D simulations are the lowest, and most of them are very close to 1, indicating very good agreement with experiment. Although the FF scores of ff03CMAP/TIP4PD for HEWL19 and HIVRev are not the best, the differences with the best performing force fields are not significant. This suggests that ff03CMAP/TIP4P-D can reproduce well conformers of tested IDPs. The details of the FF score composition for each tested system are shown in Tables S7–S15.

Table 4.

FF scores of six ff03-series force field for 9 disordered proteins

Protein	ff03	ff03*	ff03w	ff03ws	ff03CMAP/TIP4PEw	ff03CMAP/TIP4PD
HEWL19	1.290a	1.039	1.089	1.117	1.125	1.092
RS	4.453	1.657	1.600	1.454	1.140	1.105
HIVRev	1.761	1.763	1.677	1.208	1.244	1.295
AB40	2.016	1.756	1.872	1.758	1.124	1.001
AB42	2.106	1.866	1.972	1.858	1.184	1.021
ACTR	1.618	1.474	1.354	1.172	1.245	1.033
IA3	2.111	1.810	1.923	1.677	1.404	1.000
p53N	1.668	1.441	1.537	1.351	1.133	1.019
tauF4	1.587	1.590	1.384	1.301	1.226	1.000

It is interesting to note that all ff03 revisions improve over the original ff03 in IDP simulations, as they are all designed to reproduce the properties of IDPs. As expected, the CMAP method can provide accurate descriptions of IDPs as in previous developments.^{[9–11, 15, 72]} In addition, the TIP4P-D water model is demonstrated again to be suitable for IDP simulations.^[16] In order to understand the influence of solvent models, three IDPs were simulated with ff03/TIP4P-D (Tables S10, S12–S13). The results show that TIP4P-D water model indeed partly improves the performance of tested IDPs conformers. However, the results are still much worse than those of ff03CMAP/TIP4P-D, suggesting that the CMAP improvement in ff03CMAP/TIP4P-D simulations plays a key role in reproducing the IDPs conformers.

To further illustrate the property of ff03CMAP force fields, we calculated the average RMSDs for different experimental measurements of IDPs (Table 5). We found that the performance of ff03CMAP/TIP4PD is the best for all experimental observables, and ff03CMAP/TIP4PEw also performs reasonably well. It is noticeable that ff03CMAP significantly improved the quality of simulated Cα and N secondary chemical shifts and ³J_HNHα scalar coupling constant, which have are closely related to backbone dihedrals. It is clear that the CMAP method can be used to correct the dihedral distributions and the TIP4P-D water model further refines the interactions between protein and water, leading to excellent observed performance in the ff03CMAP/TIP4PEw simulations for IDPs.

Table 5.

Average of RMSDs for experimental observables of IDPs^a

Exp. Type	ff03	ff03*	ff03w	ff03ws	ff03CMAP/TIP4PEw	ff03CMAP/TIP4PD
Cα	1.332	0.986	1.001	0.849	0.641	0.535
Cβ	0.545	0.607	0.559	0.566	0.461	0.405
C	0.853	0.745	0.649	0.613	0.553	0.544
N	2.545	2.153	2.275	1.958	1.575	1.208
Hα	0.146	0.132	0.137	0.126	0.118	0.114
HN	0.334	0.311	0.320	0.297	0.262	0.237
3JHNHα	1.322	0.996	1.026	0.920	0.475	0.462
RDC	0.928	0.788	0.764	0.737	0.764	0.722

^aThe experimental measurements are calculated in 4 different IDP systems at least. Chemical shifts are in ppm, J-coupling constants and RDCs are in Hz.

For IDP simulations, underestimation of Rg is a common limitation for generic protein force fields.^{[14, 16]} We calculated Rg distributions for all tested IDPs (Figure S23). The force field with four-site water models [Which one, be specific] can sample a wider range of Rg distributions and larger Rg mean values, especially for ff03CMAP/TIP4P-D and ff03ws. Conformers are more compact in force fields in the TIP3P water model such as ff03 and ff03*. We compared the experimental Rg and simulated Rg of three IDPs. The analysis indicates that ff03CMAP force field and ff03ws overestimate the Rg of Aβ40 and RS. The average RMSDs[What is this RMSD? For a single Rg value?] of ff03CMAP/TIP4PEw are also very small and close to experimental value. For ACTR, only the Rg in the ff03CMAP/TIP4PD simulation is located within the experimental range and other force fields significantly underestimate it.

Besides the above overall assessments, we next use a classical example of IDPs, RS, in the following discussion to illustrate the performance of these force fields. To evaluate the backbone and side-chain sampling for RS, we compared secondary chemical shifts and scalar coupling constants. Figure 6 shows the secondary chemical shifts and backbone scalar coupling constants for six ff03-series force fields. Tables S19–S20 list detailed data used in analysis. The chemical shifts and scalar coupling constants calculated from all revised ff03 force fields are much closer to experimental data than those from the original ff03 force field, and the RMSDs between simulated and experimental values from ff03CMAP/TIP4P-Ew and ff03CMAP/TIP4P-D combinations are smaller than those from other ff03-series force fields (Table 4). We also calculated the backbone N-HN, Cα-Hα and Cα-C RDCs with a local alignment window of 15 residues (Figure 7), whose performance is similar to that of chemical shifts and coupling constants, with both ff03CMAP/TIP4PEw and ff03CMAP/TIP4PD giving lower RDC(Q, what does Q mean? Why lower value is better) with smaller standard deviations (why smaller sd is better?) than other tested force fields.

Figure 6.

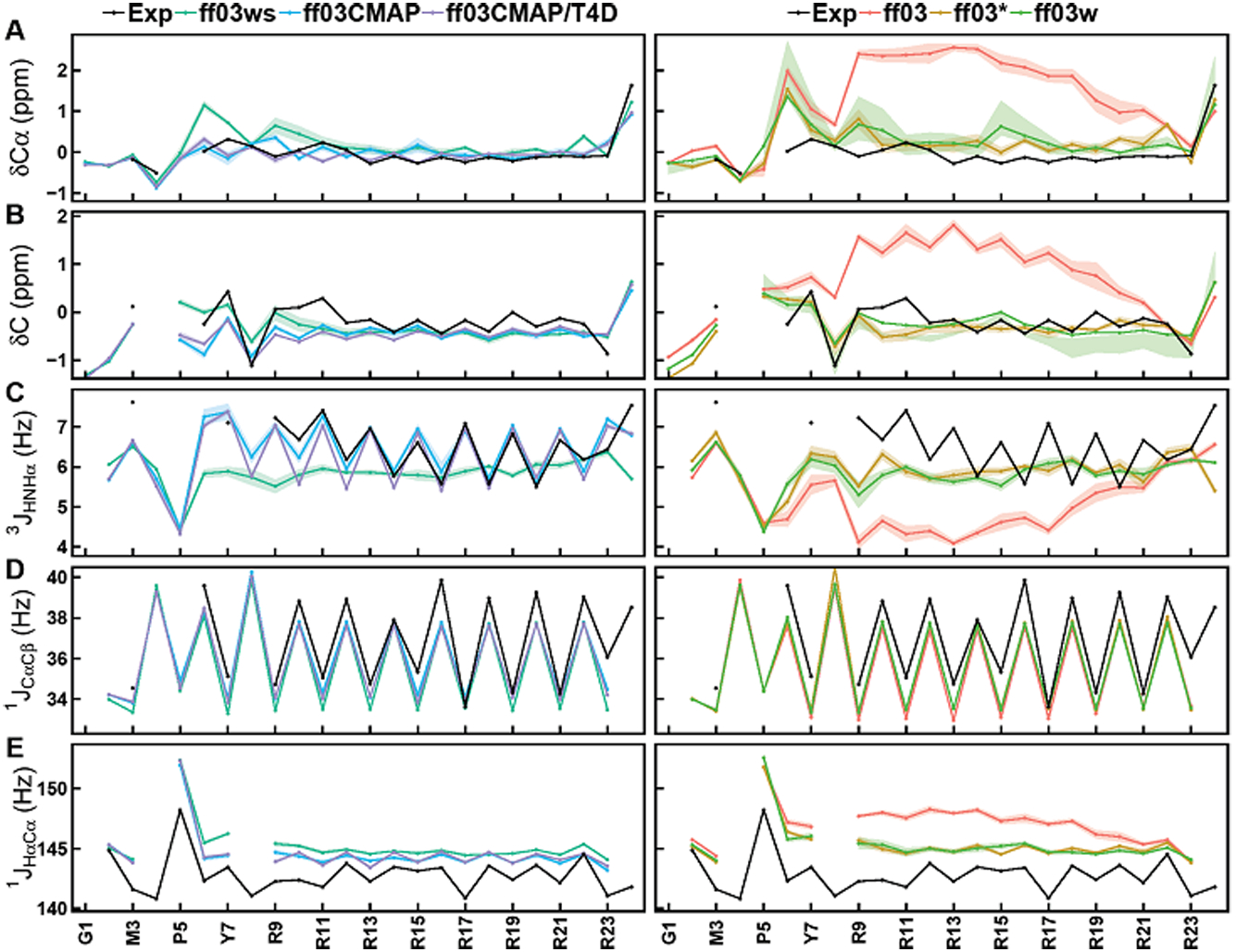
Secondary chemical shifts and backbone scalar coupling constants of simulation and experimental data for RS. Simulated and experimental secondary chemical shifts for (A) Cα and (B) C, backbone scalar coupling constants for (C) ³J_HNHα, (D) ¹J_CαCβ and (E) ¹J_HαCα. Simulated values are shown for ff03 (red), ff03* (brown), ff03w (light green), ff03ws (cyan), ff03CMAP (blue), and ff03CMAP/T4D (violet). Experimental values are displayed as black lines. The shadow means the stand error of mean.

Figure 7.

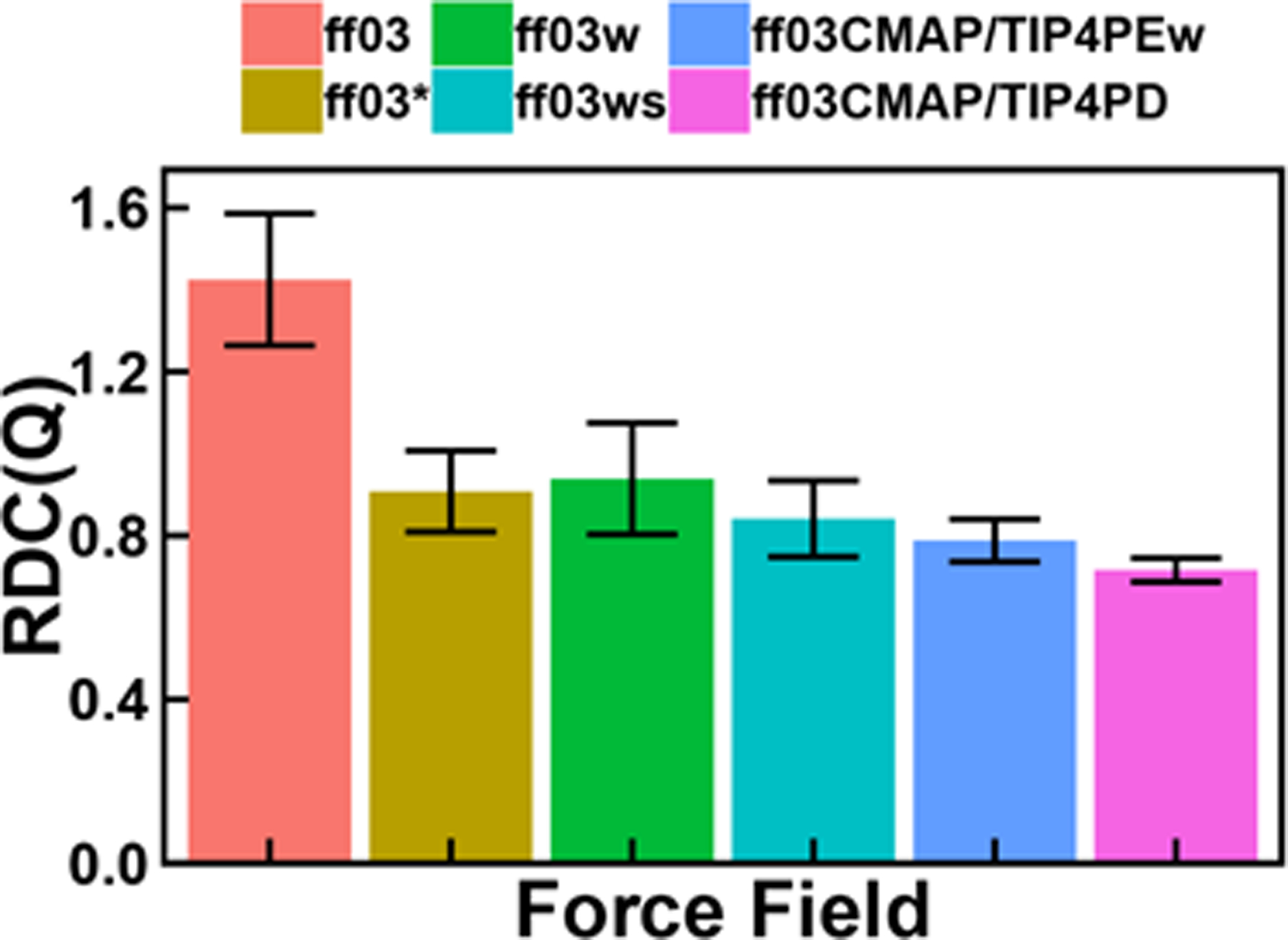
Backbone RDCs of simulation with six ff03-series force fields for RS. Error bar means the standard deviations of calculation.

Next FF scores were used to compare the performance of all force fields (listed in Table 6) in RS simulations. The RMSDs of the original ff03 force field are the largest and FF score is larger than 4. ff03CMAP/TIP4PD combination gives the best agreement with all experimental measurements and the FF scores are around 1.1.

Table 6.

RMSD of secondary chemical shifts, J-coupling constants, RDC and FF score of RS for six ff03-series force fields.^a

	ff03	ff03*	ff03w	ff03ws	ff03CMAP/TIP4PEw	ff03CMAP/TIP4PD
Cα	1.813	0.502	0.484	0.385	0.239	0.193
C	1.199	0.333	0.296	0.307	0.354	0.373
3JHNHα	1.777	0.987	0.974	0.981	0.407	0.491
1JCαCβ	1.625	1.407	1.420	1.438	1.084	1.195
1JHαCα	4.190	2.462	2.511	2.395	1.774	1.824
3JCCγ	0.302	0.314	0.271	0.278	0.330	0.311
3JNCγ	0.386	0.254	0.272	0.233	0.230	0.217
RDC	1.425	0.908	0.939	0.841	0.788	0.716
CSscore	6.720	1.862	1.753	1.514	1.217	1.128
NMRscore	2.186	1.451	1.448	1.394	1.063	1.081
FFscore	4.453	1.657	1.600	1.454	1.140	1.105

^aChemical shifts are in ppm, J-coupling constants and RDCs are in Hz.

Finally we computed the ensemble-averaged SAXS curves for RS and fitted with the experimental curve (Figure 8). The χ² value was used to evaluate the quality of the fitted result to the given experimental SAXS profile as shown in the literature.^[73] Our analysis shows that the χ² of ff03CMAP/TIP4PEw is the smallest among 6 tested ff03-series force fields. This suggests that ff03CMAP/TIP4PEw can reproduce the SAXS property for RS, while the ff03CMAP/TIP4PD combination leads to conformers that are too expansive.

Figure 8.

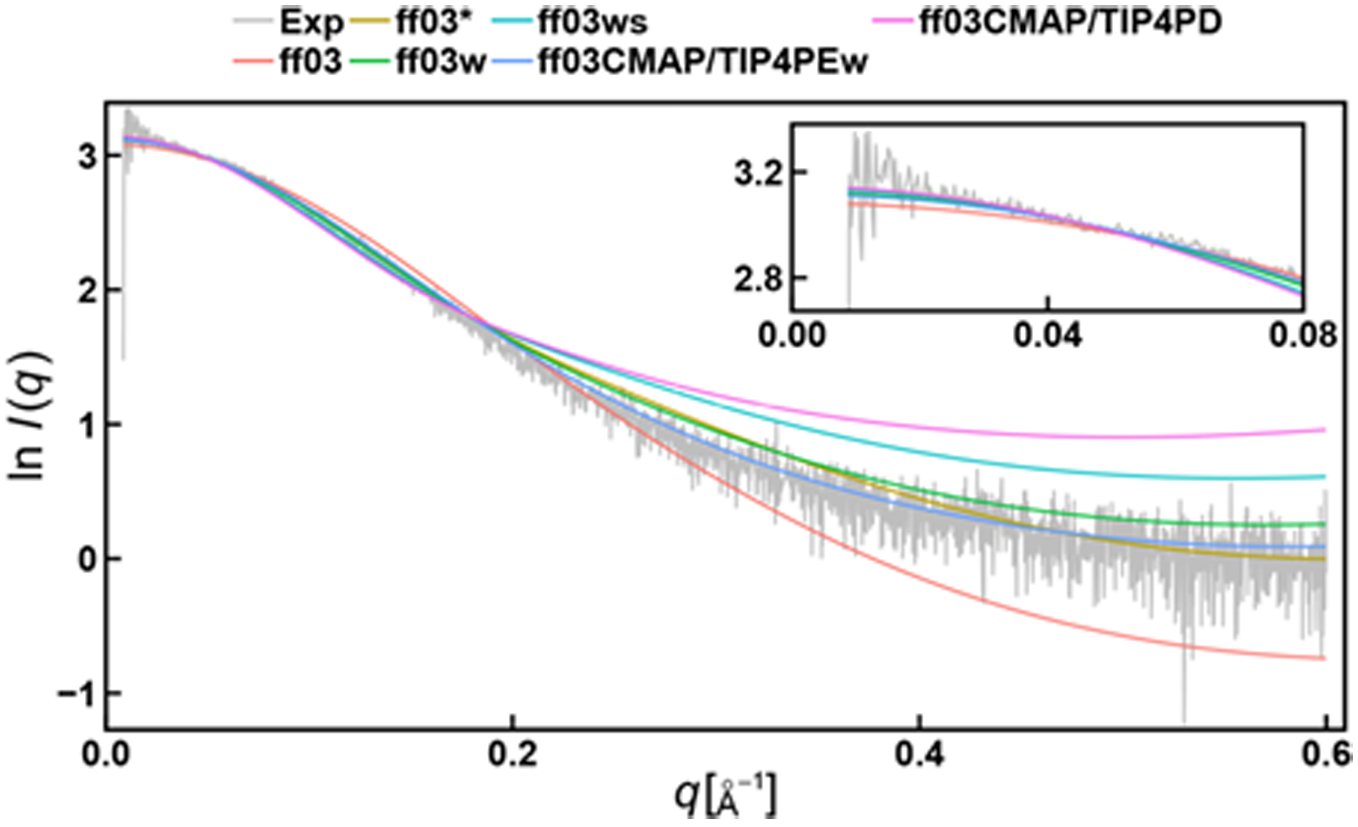
SAXS profiles of simulation and experimental data for RS. Experimental values are displayed as grey drawing. The χ² of ff03, ff03*, ff03w, ff03ws, ff03CMAP/TIP4PEw and ff03CMAP/TIP4PD are 5.118, 2.217, 2.418, 10.708, 1.319 and 23.658.

To further illustrate the conformer sampling efficiency, kClust was used to cluster conformers according to φ angle and Cα RMSD. Representative conformers and their occupations are shown in Figures S26–S34. The results indicate that both ff03CMAP and ff03ws can sample more flexible and diverse disordered conformers, while the representative conformers in the ff03 simulation contain several short helixes with tight packing. Convergence of conformer sampling is another important issue for IDP simulations. We used biphasic decay model to evaluate the convergence time scales for IDP simulations. It is interesting to note that ff03CMAP simulations have smaller decay half times, which suggests ff03CMAP simulations converge earlier than other ff03-series simulations.

Ab Initio Folding of Fast-Folding Proteins.

We performed REMD for 3 typical fast-folding proteins, such as 16-residue two β-sheets GB1, small β-hairpin-forming protein CLN025, and helical 15-mer AAQAA3.^{[34, 36–37]} The melting curves in the ff03CMAP/TIP4PEw simulations are shown in Figure 9. The melting curves show that GB1 and CLN025 can be ab initio folded when modeled with ff03CMAP/TIP4PEw. However, a few folded structures were observed in the REMD simulation of AAQAA3. To study whether the ab initio folding of helical structures can be improved by modifying CMAP parameters, we updated a new set of CMAP parameters by only decreasing the parameters in α_h region with the revised force field termed as ff03CMAP2. Our REMD simulation shows that ff03CMAP2/TIP4PEw performs significantly better in helix folding. In the meantime, ff03CMAP2/TIP4PEw can maintain almost same melting curves for sheet and hairpin fast-folding proteins. [You should say whether the IDP performance can still be maintained.]

Figure 9.

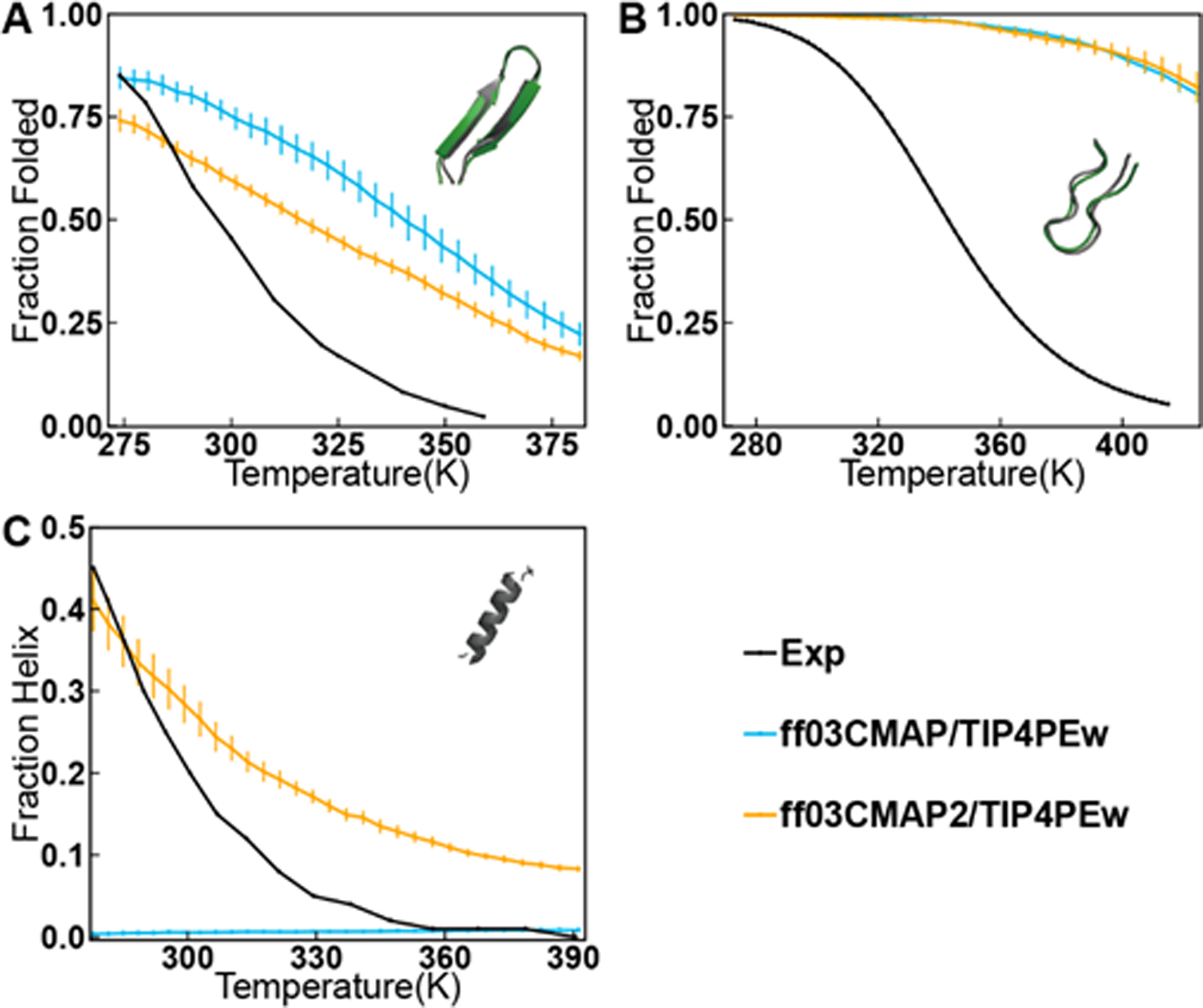
Melting curves for ff03CMAP/TIP4PEw and ff03CMAP2/TIP4PEw with experimental values. (A) Temperature-dependent folded population of GB1. (B) Temperature-dependent folded population of CLN025. (C) Temperature-dependent helix formation of AAQAA3 (The definition of helicity calculation is mention in SI). Simulated values are shown for ff03CMAP/TIP4PEw are in blue lines, ff03CMAP2/TIP4PEw are in orange line, and experimental melting curves are shown in black lines. All simulations initiated from fully unfolded structures and 100 ns (for CLN025 and AAQAA3) and 300 ns (for GB1) for equilibration. Folded structures obtained from REMD simulations (gray) starting from completely unfolded state are compared with the native structure from the PDB database (green), and the RMSD between folded structure and native structure is 0.728Å for GB1 and 0.993Å for CLN025.

Conclusion

The backbone dihedral term for all 20 amino acids was optimized to improve the performance of the current force field. TIP4P-Ew and TIP4P-D are combined with newly developed force field ff03CMAP to simulate different type proteins. Extensive tests of typical short peptide, folded proteins, disordered proteins, and fast-folding proteins show that the simulated chemical shifts, J-coupling, order parameters, and RDC with the ff03CMAP force fields are in quantitative agreement with those from NMR experiment and are more accurate than other ff03-series force fields. The influences of solvent models were also investigated. The results indicate that ff03CMAP/TIP4PEw for folded proteins and ff03CMAP combined with TIP4P-D was suitable for disordered proteins (ff03CMAP/TIP4PEw also shows good performance in IDPs). Therefore, these findings confirm that the newly developed force field ff03CMAP can improve the balance and efficiency of conformer sampling between intrinsically folded proteins and disordered proteins. Although ff03CMAP force field has the limitation of folding helix structures, this can be improved by adjusting CMAP parameters which is the ff03CMAP2.