Abstract
Understanding the individual and joint contribution of multiple protein levels toward a phenotype requires precise and tunable multigene expression control. Here we introduce a pair of mammalian synthetic gene circuits that linearly and orthogonally control the expression of two reporter genes in mammalian cells with low variability in response to chemical inducers introduced into the growth medium. These gene expression systems can be used to simultaneously probe the individual and joint effects of two gene product concentrations on a cellular phenotype in basic research or biomedical applications.
Keywords: tunable, orthogonal control, low variability, 2-dimensional, gene expression control, mammalian synthetic gene circuits, synthetic biology
Modern biology has illuminated the complexity of molecular processes that determine cellular phenotype.1−6 For example, while mutations within the coding sequence of a gene can alter some phenotype, similar phenotypic effects can also arise without any mutations, solely from changes in the levels of the mRNA and protein encoded by the gene. The origins and consequences of gene expression changes are at least as complex and as difficult to unravel as those of coding sequence changes. Disrupting regulatory sequences or epigenetic controllers of any gene can have effects that propagate through the gene regulatory network7 causing emergent phenomena such as cell death, phenotype switching,8 and carcinogenesis.9 Moreover, gene expression levels can be tighly constrained within narrow ranges, or they can differ substantially from cell to cell in genetically identical populations, giving rise to complex expression patterns with phenotypic consequences.10−12
Genetic studies have predominantly focused on identifying and characterizing phenotypes associated with gene expression through knockout, knockdown, and overexpression, but the nuanced effects of gene expression levels on phenotype remain poorly understood. For example, simultaneous changes in the levels of two proteins can result in synergistic, nonadditive effects conceptually similar to mutational epistasis.13 As a first step toward understanding such effects, multigene expression control could reveal how specific protein levels jointly induce or suppress a phenotype. Such multigene expression-control methods should be precise, reliable, robust, and ubiquitously applicable across different cell types. They should enable engineering applications that investigate the cell as a black box, generating transfer functions of cellular outcomes given a set of gene expression inputs, and may be critical for cell fate reprogramming in biomedical applications.8,14,15
Synthetic biology is primed to provide such gene expression control methods.16−18 Synthetic gene circuits are comprised of non-native DNA and can manipulate the expression of genes in response to a multitude of cues, including external chemicals or intracellular signaling events, with possible applications in cellular control, perturbation, reprogramming, and outcome reporting.19 For example, the gene expression linearizer circuit24,25 offers precise protein level tuning compared to widely used induction systems like Tet-On,20 which can have a steep dose–response region with uncharacterized variability, making it difficult to titrate inducer dosage to achieve desired levels of gene expression. The linearizer gene circuit architecture utilizes negative feedback to beget uniform protein levels proportional to external inducer dose for any single gene. However, whether linearizer gene circuits can independently and precisely control the expression of two genes in mammalian cell lines has been unexplored.
Multigene expression control was previously accomplished in yeast through the use of human hormone-inducible regulators.21 However, without negative autoregulation such gene circuits might generate nonlinear and noisy gene expression responses. Nonlinearity and cell–cell variability can complicate cellular control or mapping of gene expression to cellular phenotype. Lastly, those gene circuits, while functional in yeast, cannot readily translate to mammalian cells due to the use of estradiol and progesterone hormone inducers, which are biologically active in mammalian cells and prone to elicit off-target cellular responses. Multigene expression control has been implemented in mammalian cells as well, but without negative feedback, and with unknown variability.22 Currently, independent and precise control of multigene expression in mammalian cells is lacking.
Here we introduce a chemically inducible system of dual orthogonal linearizers to enable studies of individual and joint contributions of multiple gene expression levels toward an observable phenotype or behavior in mammalian cells. Together, orthogonal linearizer gene circuits provide a system that can simultaneously overexpress a pair of genes to desirable levels independently and precisely in the same cell. This enables exploring the phenotypic landscape of multigene expression, to reveal epistasis-like effects unexpected from separately controlling single protein levels, or to implement multigene control toward the induction of a specific phenotype or cell reprogramming.
Results
Developing an Orthogonal Linearizer Using the PhlF Repressor Protein
Gene expression linearizers are gene circuits that can linearly and precisely increase the expression of a target gene according to inducer dose in eukaryotic cells.23 This linear, low-noise dependence of average gene expression on induction is due to negative autoregulation and identical promoters controlling gene expression. The TetR-mLin linearizer gene circuit used the Tet repressor protein (TetR) binding to two tetO2 operator sequences (2xtetO2) in two identical promoter regions to repress its own expression as well as that of a reporter gene.23,24 Increasing concentrations of Doxycycline (Dox) relieve repression by TetR, causing the average expression of both TetR and the target eGFP protein to increase linearly, with low variability across the effective Dox concentrations. This TetR-mLin gene circuit can control a gene of interest (GOI) downstream from another copy of the TetR-regulated promoter or under the same promoter, using a 2A sequence25 to produce a tetR-GOI multicistronic transcript.26
To precisely and independently control the expression of multiple genes simultaneously, we aimed to construct a second inducible linearizer gene circuit that could function in tandem with the existing TetR-mLin gene circuit. Previously, we have shown that TetR-based linearizer gene circuits function robustly in yeast and various mammalian cell lines if TetR self-represses and its promoter is identical with that of the target gene. Whether this holds for a different repressor protein has not been tested. In order to replicate the same linearizer gene circuit architecture, we chose the candidate repressor protein PhlF, a TetR homologue22,27 originally derived from Pseudomonas fluorescens.28 Like TetR, the PhlF transcriptional repressor protein contains both a ligand and a DNA binding domain. The addition of the inducer chemical 2,4-diacetylphloroglucinol (DAPG)29 allosterically prevents PhlF binding to a 30 bp operator sequence (phlFO site).
We designed two variants of the PhlF-mediated negative feedback gene circuit (PhlF-mLin). These variants bore either a single PhlF operator site upstream of the initiator element (PhlFs-mLin) or two operator sites flanking the initiator (PhlFd-mLin) in the strong CMV promoter driving PhlF expression (Figure 1). We linked PhlF repressor protein expression to the mCherry fluorescent reporter protein through a porcine teschovirus-1 2A (P2A) self-cleaving peptide. This minimal design allowed us to control both PhlF and mCherry expression through a common promoter as required by linearizer design, while minimizing sequence length to aid in genomic integration. As previously described,23 these designs featured a nuclear localization sequence (NLS) to increase nuclear repressor concentration, Kozak sequence (KS) to optimize translation rate, and the Woodchuck post-transcriptional regulatory element (WPRE) to increase expression. Our goals were to generate a linear, low-noise gene expression response to inducer dose with (i) low basal expression in the OFF state; (ii) a high range of DAPG doses wherein the gene circuit responds linearly; (iii) appreciable fold induction between induced and uninduced states; and (iv) low gene expression noise measured as the coefficient of variation (CV).
Figure 1.

Schematic of orthogonal linearizer gene circuits: TetR-mLin (top) and PhlF-mLin (bottom). At the core of each gene circuit a self-repressing protein (TetR and PhlF). The repressor protein inhibits its own expression as well as that of the corresponding reporter protein (eGFP and mCherry, respectively). A different chemical inducer (Dox and DAPG, respectively) alleviates each repression. We created two variants (inset) of the PhlF-mLin circuit: one with a single phlFO operator site upstream of the initiator element, and another with two operator sites flanking the initiator.
To test these criteria in the novel PhlF linearizer gene circuit prototypes, we integrated both genomically into HEK 293 cell lines and assessed clonal DAPG dose responses through flow cytometry. In order to insert these and subsequent gene circuits into the same genomic locus in single copy robustly and reliably, we used Flp-In-293 cells bearing a Flp-recombinase compatible FRT site in a well-expressed30 genomic locus. To minimize any heritable variability that could confound our assessment, we sorted polyclonal populations into single cell clones prior to downstream experimentation. DAPG did not affect the growth rate of the cells. We measured the dose response of the cell lines bearing the PhlF-mLin gene circuits across a broad range of DAPG concentrations (0 to 25 μM DAPG). For each cell line bearing a circuit variant, we seeded samples at different inducer concentrations, and allowed gene expression to stabilize over ∼2 days (confirming that the histograms did not change in time). We then measured the steady-state mean and coefficient of variation (CV) of fluorescence intensity at each of the inducer doses. Both variants showed linearity of mean fluorescence with increasing DAPG concentrations prior to saturation (Figure 2a, 2d) and consistently low noise as measured by CV across all doses (Figure 2c, 2f). Single cell fluorescence distributions were uniformly narrow and unimodal across doses (Figure 2b, 2e) and between experimental replicates (Figure S5–S6). Both variants had comparable basal expression in the absence of DAPG (Table 1) and had linear dose–responses of mean fluorescence as measured by L1-norm and R2 regression (Figure S8). The PhlFd-mLin gene circuit had a higher maximum fold induction, exhibited more pronounced linearity across a broader range of inducer doses, and had lower gene expression noise as measured by average CV (Table 1, Figure 2b,c and 2e,f, Figure S8) than the PhlFs-mLin variant. Overall, these results demonstrate that the existing linearizer gene circuit design applies to a repressor different from TetR, enabling similar functional characteristics.
Figure 2.
Steady-state dose responses of individual PhlF-mLin (top) and TetR-mLin (bottom) gene circuits. (a) Mean mCherry fluorescence intensity calculated across 3 independent replicates for each DAPG inducer concentration. Flow cytometry measurements of single operator variant phlFs-mLin cells cultured under different DAPG doses were taken after the histograms did not change anymore (i.e., at steady state). Error bars represent standard deviation. The black dashed line is a linear fit across the corresponding DAPG inducer concentration range. (b) Representative steady-state fluorescence distributions of phlFs-mLin at selected doses. (c) Average CV of phlFs-mLin mCherry fluorescence versus DAPG inducer concentrations. Error bars represent standard deviation calculated across 3 independent replicates per inducer dose. (d) Mean mCherry fluorescence calculated across 3 independent replicates for each DAPG inducer concentration. Error bars represent standard deviation. The black dashed line is a linear fit across the corresponding DAPG dose range. (e) Representative fluorescence distributions of phlFd-mLin at selected doses. Flow cytometry results of the double operator variant phlFd-mLin cells cultured under different DAPG doses. (f) Average CV of phlFd-mLin mCherry fluorescence versus DAPG inducer concentration. Error bars represent standard deviation calculated across 3 independent replicates per inducer dose. (g) Mean eGFP fluorescence intensity calculated across 3 independent replicates per Dox inducer concentration. Flow cytometry measurements of TetR-mLin cells cultured under different Dox doses were taken after the histograms did not change anymore (i.e., at steady state). Error bars represent standard deviation over 3 replicates. The black dashed line is a linear fit across the corresponding Dox inducer concentration range. (h) Representative fluorescence distributions of TetR-mLin at selected Dox concentrations. (i) Average CV of TetR-mLin eGFP fluorescence intensity versus Dox inducer concentrations. Error bars represent standard deviation calculated across 3 independent replicates per inducer concentration.
Table 1. Evaluation Metrics of Clonal Cell Lines Bearing Variant Linearizer Gene Circuits.
| gene circuit | maximum fold induction | range of linearity | slope of linear regime | average CV | basal expression |
|---|---|---|---|---|---|
| PhlFs-mLinearizer | 11.0 | 0 to 4 μM DAPG | 5410 A.U. per μM DAPG | 0.49 | 2773 ± 206 A.U. |
| PhlFd-mLinearizer | 12.0 | 0 to 5 μM DAPG | 6870 A.U. per μM DAPG | 0.38 | 3805 ± 364 SD A.U. |
| TetR-mLinearizer | 43.8 | 0 to 10 ng/mL Doxycycline | 683 A.U. per ng/mL Doxycycline | 0.47 | 212 ± 17.3 A.U. |
To compare these novel phlF-based gene circuits against previously established TetR-based linearizer gene circuits, we inserted a TetR-mLin construct into the HEK 293 Flp-In cell line as described above and conducted a flow cytometry dose response across a validated range of Doxycycline concentrations.23 We likewise quantified fluorescence mean and CV dose–responses (Figure 2g–i and Figure S7). As expected, eGFP fluorescence mean increased linearly with inducer concentrations (Figure 2g), with low noise (Figure 2i, S7). We observed a somewhat greater range of linearity and fold induction (Table 1, Figure S8) than previously reported in other cell lines with random integration of the TetR-mLin gene circuit.23 Interestingly, the dose–responses of both PhlF-mLin gene circuits had lower slopes than TetR-mLin, requiring larger inducer doses to approach saturation. To investigate why this occurs, we conducted computational modeling as previously described,23,24 which suggested that slower diffusion of DAPG compared to Doxycycline across the cell membrane could be causing this slope difference (Figure S8).
Investigating Clonal Heterogeneity
To investigate whether gene expression control by the linearizer gene circuits depends on the clones bearing the gene circuit, we tested fluorescent reporter expression of uninduced and induced isogenic clones (Figure S11) across the two PhlF promoter variants (n = 7 clonal cell lines). We found heterogeneity in dose–response across clones, possibly reflecting genetic and epigenetic clone–clone differences in global gene expression control. The double operator site PhlFd variant, on average, produced clones with lower basal expression (p < 0.001, Figure S11a) than the single operator PhlFs variant. Both double operator site linearizers (TetR-mLin and PhlFd-mLin) exhibited stronger correlations between uninduced and induced expression levels than those of the single operator PhlFs-mLin (Figure S11b), suggesting that additional operator sites strengthen the correlation between basal expression and saturation levels (Figure S11c).
To further understand the variability in dose response between clones, we performed flow cytometry measurements of higher dose resolution for 3 clones per PhlF-mLin variant (Figure S12). We found that both variants exhibited similar dose–responses (Figure S12b). However, the PhlFd-mLin gene circuit had markedly lower CV and therefore gene expression noise (Figure S12a). Across these clones, the PhlFd-mLin gene circuit’s dose–response tended to be linear over a greater range of inducer doses (0 to 8.4 μM DAPG) than the PhlFs-mLin circuit (0 to 5.7 μM DAPG, Figure S12c).
Assessing Orthogonality through Inducer Response
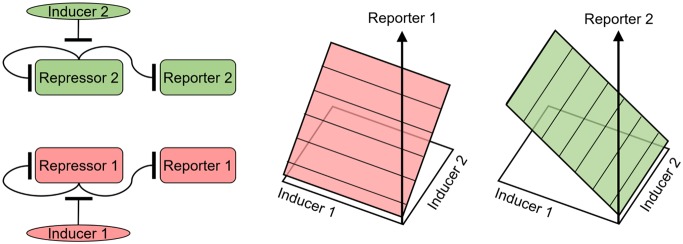
To orthogonally control the expression of two genes simultaneously, linearizer gene circuits constructed with different repressor proteins should not be cross-inducible. That is, the presence of DAPG in the growth medium of cells integrated with TetR-mLin should not elicit eGFP fluorescence response, and the presence of Dox should not cause mCherry fluorescence changes in cells genetically modified with the phlF-mLin circuit. For orthogonal control in the space spanned by the two inducer concentrations, visually we expect the PhlF-mLin and TetR-mLin gene circuits to generate planar bivariate dose response surfaces, each dose–response plane being parallel to one inducer axis and orthogonal to the vertical coordinate plane containing the other inducer axis. In other words, we expect smooth, planar dose response surfaces of mean fluorescence, each invariant either versus Dox or versus DAPG concentrations in the growth medium (Figure 3a). Such linear bivariate mappings from inducers onto two noninteracting protein levels, wherein the total reporter level depends additively on the inducer concentrations, are a special case for more complex mappings.31−33 Deviations of a phenotype from such additivity would indicate interacting gene expression inputs in future applications.
Figure 3.
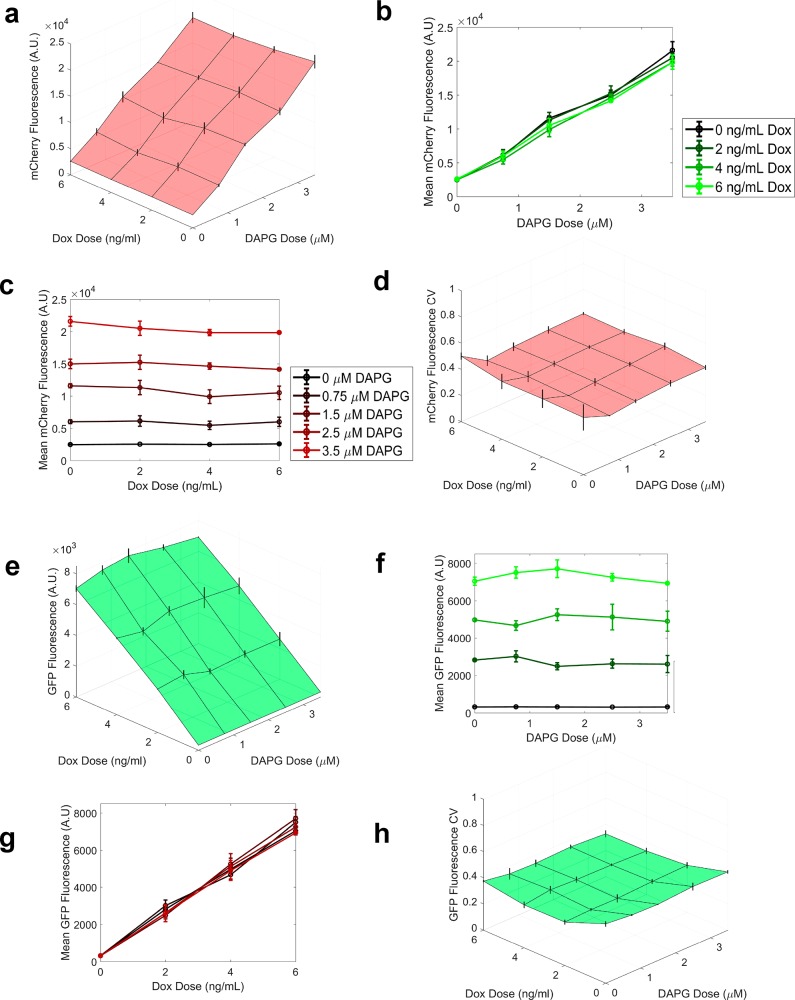
Bivariate dose–responses of gene expression for cell lines bearing single phlF-mLin and tetR-mLin gene circuits. (a) Schematic representation of expected bivariate dose–response surfaces (planes) for the PhlF-mLin (left) and TetR-mLin (right) gene circuits under pairwise induction by Dox and DAPG. (b) Fluorescence images of polyclonal HEK 293 Flp-In cells harboring stably integrated phlFs-mLin gene circuit cultured in media without inducer chemicals, Dox-only media, and media containing Dox and DAPG. Overlaid eGFP and mCherry channels show mCherry expression only in the presence of DAPG. Scale bars represent 500 μm. (c) Fluorescence images of polyclonal HEK 293 Flp-In cells harboring stably integrated TetR-mLin gene circuit cultured in media without inducer chemicals, DAPG-only media, and media containing Dox and DAPG. Overlaid eGFP and mCherry channels show eGFP expression only in the presence of Dox. Scale bar: 500 μm. (d) Bivariate dose response (plane) of clonal HEK 293 Flp-In cells harboring the stably integrated phlFd variant of the PhlF-mLin gene circuit. Surface representation of mean mCherry fluorescence expression across pairwise DAPG and Dox induction doses. Error bars represent standard deviation calculated from 3 independent replicates per inducer dose-pair. (e) 2-Dimensional slices through the mCherry fluorescence plane showing mean fluorescence across DAPG inducer concentrations for different Dox concentrations (red colors). (f) 2-Dimensional slices through the mCherry fluorescence plane showing mean fluorescence across Dox inducer concentrations for different Dox concentrations (green colors). No significant differences between Dox groups were detected by one-way ANOVA (p > 0.05). (g) Bivariate dose response of clonal HEK 293 Flp-In cells harboring stably integrated TetR-mLin gene circuit. Surface (plane) representation of mean eGFP fluorescence expression averaged from 3 replicates across pairwise DAPG and Doxycycline induction doses. Error bars represent standard deviation calculated from 3 independent replicates per dose-pair. (h) 2-Dimensional slices through the eGFP fluorescence planes showing mean fluorescence across DAPG inducer concentrations for different Dox concentrations (red colors). No significant differences between DAPG groups were detected by one-way ANOVA (p > 0.05). (i) 2-Dimensional slices through the eGFP fluorescence plane showing mean fluorescence across Dox inducer concentrations for different Dox concentrations (green colors).
To assess the ability of the PhlF-mLin gene circuits to reliably and precisely actuate gene expression irrespective of the induction state of the TetR-mLin gene circuit, we cultured both linearizer cell lines in the presence of either Dox or DAPG. TetR-mLin cells exhibited a marked increase in eGFP fluorescence in the presence of Doxycycline but behaved as their uninduced cohort in the presence of DAPG. Likewise, PhlF-mLin cells increased mCherry fluorescence when cultured in media containing DAPG, but did not respond to Dox induction. (Figure 3b,c) To confirm and quantify these findings with greater sensitivity, we conducted 2-dimensional dose response measurements across 4 Dox doses and 7 DAPG doses within the linear range of each gene circuit on stably selected clonal TetR-mLin and PhlF-mLin cell lines. Indeed, we observed that each gene circuit still functioned as expected, producing bivariate dose–response planes with no visible cross-talk effects from the presence of the other inducer chemical. (Figure 3d,e) We found no significant differences between Dox induction groups (p > 0.05) in phlF-mLin cells under cross-induction as evidenced by one-way analysis of variance (Table S2). Likewise, we found no significant differences in TetR-mLin cells across DAPG induction (Table S3). The mean CV of each gene circuit remained low and did not change appreciably across the dose pairs, resulting in flat, uniform planes. (Figure S9) Taken together, these findings suggest that these gene circuits are not cross-inducible (are orthogonal) and thus can be used in tandem.
Multiplexing Orthogonal Linearizer Gene Circuits
To determine whether the TetR and PhlF linearizer gene circuits could operate orthogonally in the same cell, we integrated a plasmid bearing the TetR-mLin gene circuit into the genome of cell lines with a stably integrated PhlF-mLin gene circuit. The plasmid bore constitutively expressed zeocin resistance (zeoR) protein which allowed us to select for successful integration events with zeocin. Cells surviving selection were single cell sorted, expanded, and assessed for orthogonality using a 2-dimensional dose response as outlined above. The fluorescent reporters chosen in this study were spectrally resolvable, with no visible cross-talk between channels. The bivariate steady-state dose–responses to two inducer concentrations were linearly increasing planes of protein expression, with no cross-induction effects in single cells bearing multiplexed linearizers (Figure 4, S10). The expression of mCherry as measured by mean fluorescence increased linearly with DAPG concentration. Also, mCherry fluorescence for cellular populations induced with increasing concentrations of Dox were invariant to Dox dose (p > 0.05, Table S4), generating horizontal lines parallel to one another and to the Dox inducer axis for increasing DAPG concentrations (Figure 4c). Similarly, eGFP protein expression as a function of Dox induction behaved linearly with no significant response to DAPG levels in the medium (Figure 4f, p > 0.05, Table S4). Noise remained consistently low and did not vary across paired inducer concentrations for either gene circuit. These results demonstrate that TetR-mLin and PhlF-mLin gene circuits may be used for precise, independent, and orthogonal multigene expression control, raising the potential for testing phenotypic responses to multiple protein levels in mammalian cells.
Figure 4.
Assessing experimental orthogonality of multiplexed linearizer circuits. (a) Bivariate dose response of mean mCherry fluorescence intensity in HEK 293 Flp-In cells harboring both stably integrated phlF-mLin and TetR-mLin gene circuits within the same clonal cell line versus pairwise DAPG and Dox inducer concentrations. Error bars represent standard deviation calculated from 3 independent replicates per inducer dose-pair. (b) 2-Dimensional slices through the mCherry fluorescence plane showing mean fluorescence across DAPG inducer concentrations for different Dox concentrations (red colors). (c) 2-Dimensional slices through the mCherry fluorescence plane showing mean fluorescence across Dox inducer concentrations for different Dox concentrations (green colors). No significant differences were found in mCherry fluorescence between groups of Dox concentrations (ANOVA, p > 0.05) (d) Bivariate dose–response of average mCherry CV across pairwise DAPG and Dox induction doses. (e) Bivariate dose–response (plane) of mean eGFP fluorescence expression averaged from 3 replicates across pairwise DAPG and Doxycycline inducer concentrations. Error bars represent standard deviation calculated from 3 independent replicates per dose-pair. (f) 2-Dimensional slices through the eGFP fluorescence plane showing mean fluorescence across DAPG inducer concentrations for different Dox concentrations (red colors). No significant differences were found in eGFP fluorescence between groups of DAPG concentrations (ANOVA, p >.05). (g) 2-Dimensional slices through the eGFP fluorescence plane showing mean fluorescence across Dox inducer concentrations for different Dox concentrations (green colors). (h) Bivariate dose–response of average eGFP CV across pairwise DAPG and Dox inducer concentrations.
Discussion
Current heterologous expression systems are limited in their ability to precisely induce gene expression responses in mammalian cell lines. Linearizer gene circuits23,24,26 can tune the protein levels of a GOI placed under the control of a synthetic promoter. However, cell states and phenotypes are often controlled by multiple genes. Likewise, to understand how genes relate and interact with one another to produce cell-level responses, we need to control the expression of multiple genes. We previously have built a TetR-based linearizer gene circuit capable of precisely controlling gene expression in various cell types.23,24,26 Ideally, many such linearizers operating independently and orthogonally to one another could achieve precise multidimensional gene expression control and multivariate phenotype mapping. Toward this goal, we constructed additional linearizer circuits utilizing a different repressor (PhlF) and its operator sequences, which had no operational cross-talk with TetR. We outlined the design, construction and validation of the PhlF-based linearizer gene circuit. We further demonstrated the orthogonality of this gene circuit to the TetR-based linearizer gene circuit and showed the ability of the combined dual-linearizer system to control the expression of two individual GOIs precisely when genomically integrated into Flp-In-293 cells. Such a toolset would beget novel methods of perturbational investigation of nonadditive gene expression effects34 and would enable biomedical applications in cellular reprogramming14,35 and beyond.
Further modification and optimization of the PhlF-mLin gene circuit orthogonal to TetR-mLin may be possible through the consideration of other repressors of the phl gene cluster36 as well as other inducers in the form of DAPG analogues.36,37 One such potential repressor is the phlH gene. This gene-product has recently been identified to bind a 35-bp sequence motif in the promoter of phlG to negatively inhibit DAPG biosynthesis in Pseudomonas. This mechanism is a similar motif to repression through PhlF. The phlH repressor protein interacts strongly with DAPG, but has other binding partners, including MAPG, which may be used as inducers.36 Other variants of the TetR-orthogonal PhlF repressor-based gene circuit may result in different dose response functions. Moreover, other repressors38 could be employed to build additional gene circuits orthogonal to both TetR-mLin and PhlF-mLin.
This work focuses on building a technological framework that is broadly applicable, bearing the potential to promote basic biology or biomedical research. These two orthogonal linearizer gene circuits permit precise, linear control of key genes, allowing the investigation of the phenotypic landscape34 through linearly tunable expression of driver genes. Depending on the desired experimental design, the endogenous GOIs may be deleted in the cell line prior to reintroduction under linearizer control. Considering the length of the phlFO operator, the orthogonality to the TetR-mLin system, and the apparent lack of DAPG toxicity, this new system should be broadly applicable for controlling specific protein levels in eukaryotic cells, with minimal side effects.
Gene regulatory networks governing phenotypic outcome are often complex.1,8,15 They consist of many feedback processes, interacting with one another in nontrivial ways. Therefore, studying how network modifications alter gene expression and thereby phenotype is difficult. This work serves to broaden the range of investigational methods of gene pair relationships.31,34 Multiplexed linearizer gene circuits can be used for basic biological research of selective and precise perturbation of genes interacting with one another in complex networks.1,8,15 They can reveal unexpected interactions between the expression levels of two genes, which is analogous to studies of epistasis between two or more coding sequence changes.13,39 Likewise, these gene circuits can be used for cellular reprogramming8,14,35,40 or measurements of titrated gene expression contributions toward a disease state.34
Methods
Plasmid Construction
For the construction of the PhlF-linearizer, DNA bearing a portion of the CMV promoter and either 1× and 2× PhlF operator sites and corresponding restriction sites were synthesized by GenScript and restriction cloned into the tetR-linearizer plasmid. The PhlF and the mCherry genes were cloned in through overlap PCR and restriction digest.
Cell Culture and Transfection
Plasmids were integrated into HEK 293 Flp-In cells (Invitrogen, R750–07) through Flp-recombination using the pOG44 vector (Invitrogen, V600520) in a 9:1 ratio or pCAG-FlpO (Addgene, 63798) in a 1:1 ratio. Two μg total DNA was introduced into 1–2 × 106 cells per well using the Lipofectamine 3000 transfection kit (Life Technologies, L3000008), used as per manufacturer’s instructions. Approximately 90% transfection efficiency was confirmed with positive control transfection of constitutive eGFP (pmaxGFP, Lonza). A negative control was transfected with only the linearizer plasmid to test for random integration. Cells were selected 3 days post transfection with 50 μg/mL Hygromycin B (Invitrogen, 10687–010). Selection dose was chosen via standard kill curve. All control wells did not survive selection.
Surviving cells were single cell sorted into a 96 well plate and grown out for 2 weeks before being passaged to flasks. Clones were selected through flow cytometry with two inducer doses representing ON/OFF to verify single cell population with a uniform fluorescence response. Due to a small subpopulation silencing the inset, we maintained selection pressure in between flow cytometry experiments.
For random integration of the TetR-mLin gene circuit into a stably expressing cell line bearing a PhlF-mLin gene circuit, we randomly integrated the plasmid pDN-D2irTNG4kwh into a clonal HEK 293 PhlF-mLin cell line. Two μg total DNA was introduced into 1–2 × 106 cells per well using the Lipofectamine 3000 transfection kit (Life Technologies, L3000008), used as per manufacturer’s instructions. Approximately 90% transfection efficiency was confirmed with positive control transfection of constitutive eGFP (pmaxGFP, Lonza). A negative control was transfected with only the linearizer plasmid to test for random integration. Cells were selected 3 days post transfection with 700 μg/mL Zeocin (Thermo Fisher Scientific, R25001). Selection dose was chosen via standard kill curve. The control well did not survive selection.
Dose Response and Flow Cytometry
Clonal populations were outgrown and plated onto 96-well plates at a seeding density of 5–10 × 103 cells per well. Cells were dosed with media containing appropriate doses of Doxycycline, DAPG, or both, with 3 dose replicates per experiment. After a 48 h induction period, cells were trypsinized with 0.25% Trypsin-EDTA (Life Technologies, 25200056), resuspended in calcium and magnesium free 1× DPBS (Life Technologies, 14190250), and underwent flow cytometry on a BD LSR Fortessa. We obtained 3–10 000 FSC/SSC gated events per sample in the FITC (530/30 nm) and PE-Cy5 (695/40 nm) channels. Each dose level consisted of 3 replicate samples.
Fluorescence Microscopy
For fluorescence microscopy, cells were passaged onto 6-well plates and induced for 48 h prior to imaging. Images were acquired on a Nikon TiE inverted fluorescence microscope equipped with a Nikon DSQi2 Digital Camera using CFI Plan Fluor 10×/0.30/16.00 objective and ET Sputter Coat Ex470/40 Dm495 Bar525/50 FITC/GFP filter for EGFP and a ET Sputter Coat Ex560/40 Dm585 Bar630/75 TX Red filter for mCherry. Composite images with scale bars were assembled in Nikon NIS Elements.
Data Analysis
FCS files were gated and analyzed using custom MATLAB scripts. Cells were adaptively gated with a density-threshold fit of log-transformed SSC and FSC values per sample to exclude debris and cell clumps. To normalize out autofluorescence from the data, we measured fluorescence of the HEK Flp-In parental cell line and subtracted the mean fluorescence of the appropriate channel from each sample flow event.
L1-norm analysis, linear regression fits and R2 were computed for a moving dose window starting from uninduced (0 μM DAPG or 0 ng/mL Dox) to maximal induction dose used experimentally per gene circuit.
Statistical tests including two-sample t tests and one-way ANOVA for assessing differences between clones and between cross-induced groups, respectively, were conducted in Matlab.
Acknowledgments
We would like to thank Chris A. Voigt for sharing the PhlF construct and all Balázsi lab members for useful comments and suggestions. This work was supported by the National Institutes of Health, NIGMS MIRA Program (R35 GM122561), and by the Laufer Center for Physical and Quantitative Biology.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acssynbio.9b00534.
Supporting Methods (descriptions for vectors and data analysis), Supporting Tables S1–S5 (primer sequences and ANOVA results), Supporting Figures S1–S12 (plasmid maps, additional dose–response data and clone-specific data) (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Albert R. (2005) Scale-free networks in cell biology. J. Cell Sci. 118 (21), 4947–4957. 10.1242/jcs.02714. [DOI] [PubMed] [Google Scholar]
- Felix M. A.; Barkoulas M. (2015) Pervasive robustness in biological systems. Nat. Rev. Genet. 16 (8), 483–96. 10.1038/nrg3949. [DOI] [PubMed] [Google Scholar]
- Nijhout H. F.; Sadre-Marandi F.; Best J.; Reed M. C. (2017) Systems Biology of Phenotypic Robustness and Plasticity. Integr. Comp. Biol. 57 (2), 171–184. 10.1093/icb/icx076. [DOI] [PubMed] [Google Scholar]
- Albergante L.; Blow J. J.; Newman T. J. (2014) Buffered Qualitative Stability explains the robustness and evolvability of transcriptional networks. eLife 3, e02863. 10.7554/eLife.02863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai Z.; Dai X.; Xiang Q.; Feng J. (2009) Robustness of transcriptional regulatory program influences gene expression variability. BMC Genomics 10, 573. 10.1186/1471-2164-10-573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macneil L. T.; Walhout A. J. (2011) Gene regulatory networks and the role of robustness and stochasticity in the control of gene expression. Genome Res. 21 (5), 645–57. 10.1101/gr.097378.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeong H.; Mason S. P.; Barabasi A. L.; Oltvai Z. N. (2001) Lethality and centrality in protein networks. Nature 411 (6833), 41–2. 10.1038/35075138. [DOI] [PubMed] [Google Scholar]
- Gomez Tejeda Zanudo J.; Guinn M. T.; Farquhar K.; Szenk M.; Steinway S. N.; Balazsi G.; Albert R. (2019) Towards control of cellular decision-making networks in the epithelial-to-mesenchymal transition. Phys. Biol. 16 (3), 031002. 10.1088/1478-3975/aaffa1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brock A.; Huang S. (2017) Precision Oncology: Between Vaguely Right and Precisely Wrong. Cancer Res. 77 (23), 6473–6479. 10.1158/0008-5472.CAN-17-0448. [DOI] [PubMed] [Google Scholar]
- Raj A.; van Oudenaarden A. (2008) Nature, nurture, or chance: stochastic gene expression and its consequences. Cell 135 (2), 216–26. 10.1016/j.cell.2008.09.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balazsi G.; van Oudenaarden A.; Collins J. J. (2011) Cellular decision making and biological noise: from microbes to mammals. Cell 144 (6), 910–25. 10.1016/j.cell.2011.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldar A.; Elowitz M. B. (2010) Functional roles for noise in genetic circuits. Nature 467 (7312), 167–73. 10.1038/nature09326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Visser J. A.; Cooper T. F.; Elena S. F. (2011) The causes of epistasis. Proc. R. Soc. London, Ser. B 278 (1725), 3617–24. 10.1098/rspb.2011.1537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Vecchio D.; Abdallah H.; Qian Y.; Collins J. J. (2017) A Blueprint for a Synthetic Genetic Feedback Controller to Reprogram Cell Fate. Cell Syst 4 (1), 109–120. 10.1016/j.cels.2016.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanudo J. G. T.; Yang G.; Albert R. (2017) Structure-based control of complex networks with nonlinear dynamics. Proc. Natl. Acad. Sci. U. S. A. 114 (28), 7234–7239. 10.1073/pnas.1617387114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slomovic S.; Pardee K.; Collins J. J. (2015) Synthetic biology devices for in vitro and in vivo diagnostics. Proc. Natl. Acad. Sci. U. S. A. 112 (47), 14429–14435. 10.1073/pnas.1508521112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bashor C. J.; Collins J. J. (2018) Understanding Biological Regulation Through Synthetic Biology. Annu. Rev. Biophys. 47, 399–423. 10.1146/annurev-biophys-070816-033903. [DOI] [PubMed] [Google Scholar]
- Becskei A.; Serrano L. (2000) Engineering stability in gene networks by autoregulation. Nature 405 (6786), 590–3. 10.1038/35014651. [DOI] [PubMed] [Google Scholar]
- Guinn M. T.; Balazsi G. (2019) Noise-reducing optogenetic negative-feedback gene circuits in human cells. Nucleic Acids Res. 47 (14), 7703–7714. 10.1093/nar/gkz556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das A. T.; Tenenbaum L.; Berkhout B. (2016) Tet-On Systems For Doxycycline-inducible Gene Expression. Curr. Gene Ther. 16 (3), 156–167. 10.2174/1566523216666160524144041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aranda-Diaz A.; Mace K.; Zuleta I.; Harrigan P.; El-Samad H. (2017) Robust Synthetic Circuits for Two-Dimensional Control of Gene Expression in Yeast. ACS Synth. Biol. 6 (3), 545–554. 10.1021/acssynbio.6b00251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanton B. C.; Siciliano V.; Ghodasara A.; Wroblewska L.; Clancy K.; Trefzer A. C.; Chesnut J. D.; Weiss R.; Voigt C. A. (2014) Systematic Transfer of Prokaryotic Sensors and Circuits to Mammalian Cells. ACS Synth. Biol. 3 (12), 880–891. 10.1021/sb5002856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevozhay D.; Zal T.; Balazsi G. (2013) Transferring a synthetic gene circuit from yeast to mammalian cells. Nat. Commun. 4, 1451. 10.1038/ncomms2471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevozhay D.; Adams R. M.; Murphy K. F.; Josic K.; Balazsi G. (2009) Negative autoregulation linearizes the dose-response and suppresses the heterogeneity of gene expression. Proc. Natl. Acad. Sci. U. S. A. 106 (13), 5123–8. 10.1073/pnas.0809901106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J. H.; Lee S. R.; Li L. H.; Park H. J.; Park J. H.; Lee K. Y.; Kim M. K.; Shin B. A.; Choi S. Y. (2011) High cleavage efficiency of a 2A peptide derived from porcine teschovirus-1 in human cell lines, zebrafish and mice. PLoS One 6 (4), e18556. 10.1371/journal.pone.0018556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farquhar K. S.; Charlebois D. A.; Szenk M.; Cohen J.; Nevozhay D.; Balázsi G. (2019) Role of network-mediated stochasticity in mammalian drug resistance. Nat. Commun. 10 (1), 2766. 10.1038/s41467-019-10330-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramos J. L.; Martinez-Bueno M.; Molina-Henares A. J.; Teran W.; Watanabe K.; Zhang X.; Gallegos M. T.; Brennan R.; Tobes R. (2005) The TetR family of transcriptional repressors. Microbiol. Mol. Biol. Rev. 69 (2), 326–56. 10.1128/MMBR.69.2.326-356.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bangera M. G.; Thomashow L. S. (1999) Identification and characterization of a gene cluster for synthesis of the polyketide antibiotic 2,4-diacetylphloroglucinol from Pseudomonas fluorescens Q2–87. J. Bacteriol. 181 (10), 3155–63. 10.1128/JB.181.10.3155-3163.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnider-Keel U.; Seematter A.; Maurhofer M.; Blumer C.; Duffy B.; Gigot-Bonnefoy C.; Reimmann C.; Notz R.; Defago G.; Haas D.; Keel C. (2000) Autoinduction of 2,4-diacetylphloroglucinol biosynthesis in the biocontrol agent Pseudomonas fluorescens CHA0 and repression by the bacterial metabolites salicylate and pyoluteorin. J. Bacteriol. 182 (5), 1215–25. 10.1128/JB.182.5.1215-1225.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y. C.; Boone M.; Meuris L.; Lemmens I.; Van Roy N.; Soete A.; Reumers J.; Moisse M.; Plaisance S.; Drmanac R.; Chen J.; Speleman F.; Lambrechts D.; Van de Peer Y.; Tavernier J.; Callewaert N. (2014) Genome dynamics of the human embryonic kidney 293 lineage in response to cell biology manipulations. Nat. Commun. 5, 4767. 10.1038/ncomms5767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setty Y.; Mayo A. E.; Surette M. G.; Alon U. (2003) Detailed map of a cis-regulatory input function. Proc. Natl. Acad. Sci. U. S. A. 100 (13), 7702–7. 10.1073/pnas.1230759100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson J. C.; Voigt C. A.; Arkin A. P. (2007) Environmental signal integration by a modular AND gate. Mol. Syst. Biol. 3, 133. 10.1038/msb4100173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips K. N.; Widmann S.; Lai H. Y.; Nguyen J.; Ray J. C. J.; Balazsi G.; Cooper T. F. (2019) Diversity in lac Operon Regulation among Diverse Escherichia coli Isolates Depends on the Broader Genetic Background but Is Not Explained by Genetic Relatedness. mBio 10.1128/mBio.02232-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magen A.; Das Sahu A.; Lee J. S.; Sharmin M.; Lugo A.; Gutkind J. S.; Schaffer A. A.; Ruppin E.; Hannenhalli S. (2019) Beyond Synthetic Lethality: Charting the Landscape of Pairwise Gene Expression States Associated with Survival in Cancer. Cell Rep. 28 (4), 938–948. 10.1016/j.celrep.2019.06.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang A. H.; Li H.; Collins J. J.; Mehta P. (2014) Epigenetic landscapes explain partially reprogrammed cells and identify key reprogramming genes. PLoS Comput. Biol. 10 (8), e1003734. 10.1371/journal.pcbi.1003734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan X.; Yang R.; Zhao R. X.; Han J. T.; Jia W. J.; Li D. Y.; Wang Y.; Zhang N.; Wu Y.; Zhang L. Q.; He Y. X. (2017) Transcriptional Regulator PhlH Modulates 2,4-Diacetylphloroglucinol Biosynthesis in Response to the Biosynthetic Intermediate and End Product. Appl. Environ. Microbiol. 10.1128/AEM.01419-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong L.; Tan H.; Chen F.; Li T.; Zhu J.; Jian Q.; Yuan D.; Xu L.; Hu W.; Jiang Y.; Duan X. (2016) Novel synthesized 2, 4-DAPG analogues: antifungal activity, mechanism and toxicology. Sci. Rep. 6, 32266. 10.1038/srep32266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanton B. C.; Nielsen A. A.; Tamsir A.; Clancy K.; Peterson T.; Voigt C. A. (2014) Genomic mining of prokaryotic repressors for orthogonal logic gates. Nat. Chem. Biol. 10 (2), 99–105. 10.1038/nchembio.1411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams R. M.; Kinney J. B.; Walczak A. M.; Mora T. (2019) Epistasis in a Fitness Landscape Defined by Antibody-Antigen Binding Free Energy. Cell Syst 8 (1), 86–93. 10.1016/j.cels.2018.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buganim Y.; Faddah D. A.; Cheng A. W.; Itskovich E.; Markoulaki S.; Ganz K.; Klemm S. L.; van Oudenaarden A.; Jaenisch R. (2012) Single-cell expression analyses during cellular reprogramming reveal an early stochastic and a late hierarchic phase. Cell 150 (6), 1209–22. 10.1016/j.cell.2012.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.