Abstract
Positive selection causes beneficial alleles to rise to high frequency, resulting in a selective sweep of the diversity surrounding the selected sites. Accordingly, the signature of a selective sweep in an ancestral population may still remain in its descendants. Identifying signatures of selection in the ancestor that are shared among its descendants is important to contextualize the timing of a sweep, but few methods exist for this purpose. We introduce the statistic SS-H12, which can identify genomic regions under shared positive selection across populations and is based on the theory of the expected haplotype homozygosity statistic H12, which detects recent hard and soft sweeps from the presence of high-frequency haplotypes. SS-H12 is distinct from comparable statistics because it requires a minimum of only two populations, and properly identifies and differentiates between independent convergent sweeps and true ancestral sweeps, with high power and robustness to a variety of demographic models. Furthermore, we can apply SS-H12 in conjunction with the ratio of statistics we term and to further classify identified shared sweeps as hard or soft. Finally, we identified both previously reported and novel shared sweep candidates from human whole-genome sequences. Previously reported candidates include the well-characterized ancestral sweeps at LCT and SLC24A5 in Indo-Europeans, as well as GPHN worldwide. Novel candidates include an ancestral sweep at RGS18 in sub-Saharan Africans involved in regulating the platelet response and implicated in sudden cardiac death, and a convergent sweep at C2CD5 between European and East Asian populations that may explain their different insulin responses.
Keywords: expected haplotype homozygosity, multilocus genotype, ancestral sweep, convergent sweep
ALLELES under positive selection increase in frequency in a population toward fixation, causing nearby linked neutral variants to also rise to high frequency. This process results in selective sweeps of the diversity surrounding selected sites, and these sweeps can be hard or soft (Hermisson and Pennings 2005, 2017; Pennings and Hermisson 2006a,b). Under hard sweeps, beneficial alleles exist on a single haplotype at the time of selection, which rises to high frequency with the selected variants. In contrast, soft sweeps occur when beneficial alleles are present on multiple haplotypes, each of which increases in frequency with the selected variants. Thus, individuals carrying the selected alleles do not all share a common haplotypic background. The signature of a selective sweep, hard or soft, is characterized by elevated linkage disequilibrium (LD) on either side of the beneficial mutation, and elevated expected haplotype homozygosity (Maynard Smith and Haigh 1974; Sabeti et al. 2002; Schweinsberg and Durrett 2005). Thus, the signature of a selective sweep decays with distance from the selected site as mutation and recombination erode tracts of sequence identity produced by the sweep, returning expected haplotype homozygosity and LD to their neutral levels (Messer and Petrov 2013).
Various approaches exist to detect signatures of selective sweeps in single populations, but few methods can identify sweep regions shared across populations, and these methods rely primarily on allele frequency data as input. Existing methods to identify shared sweeps (Bonhomme et al. 2010; Fariello et al. 2013; Racimo 2016; Cheng et al. 2017; Librado et al. 2017; Peyrégne et al. 2017; Johnson and Voight 2018) leverage the observation that study populations sharing similar patterns of genetic diversity at a putative site under selection descend from a common ancestor in which the sweep occurred. Such approaches therefore infer a sweep ancestral to the study populations from what may be coincidental (i.e., independent) signals. Moreover, many of these methods require data from at least one reference population in addition to the study populations, and, of these, most may be misled by sweeps in their set of reference populations. These constraints may therefore impede the application of these methods to study systems that do not fit these model assumptions or data requirements.
Identifying sweeps common to multiple populations provides an important layer of context that specifies the branch of a genealogy on which a sweep is likely to have occurred. In this way, the timing and types of pressures that contributed to particular signals among sampled populations can become clearer. For example, identifying sweeps that are shared ancestrally among all populations within a species highlights the selective events that contributed to their most important modern phenotypes. On a smaller scale, methods to identify shared sweeps can be leveraged to distinguish signatures of local adaptation in particular populations (Librado and Orlando 2018). In contrast, single-population tests would provide little information about the timing and therefore relative importance of detected sweeps. More generally, tests tailored to the detection of sweeps within samples drawn from multiple populations are likely to have higher power to detect such events than are tests that do not account for sample complexity (Bonhomme et al. 2010; Fariello et al. 2013), underscoring the usefulness of multi-population approaches.
Accordingly, the breadth of questions that can be addressed using shared sweep approaches covers a variety of topics and organisms. Among the most fundamental examples of local adaptation seen ancestrally in related populations are those related to diet and metabolism, which can reflect important responses to changes in nutritional availability. An example of such adaptation is the shift toward eating rice in East Asian populations (Cheng et al. 2017). Supplementing this idea, characterizing the attributes of shared sweeps in related populations can uncover the number of adaptive events underlying an observed phenotype, such as the number of times selection for reduced insulin sensitivity among cave-dwelling populations of the fish Astyanax mexicanus has occurred (Riddle et al. 2018), or whether convergent resistance to industrial pollutants seen in populations of the flower Mimulus guttatus derives from ancestral standing variation (Lee and Coop 2017). Increasingly, the availability of ancient genomes is allowing for the construction of time transect datasets (Lindo et al. 2016; Librado et al. 2017) that can be used not only to lend support to hypotheses generated from modern data, but also to infer the point in time at which a shared sweep may have emerged. Such sweeps may have important implications for understanding domestication events (Librado et al. 2017; Pendleton et al. 2018), the emergence of particular cultural traits, such as human fishing and farming practices (Chaplin and Jablonski 2013; Snir et al. 2015; Marciniak and Perry 2017), and the complex relationships between modern populations such as those of South Asia described in Metspalu et al. (2011).
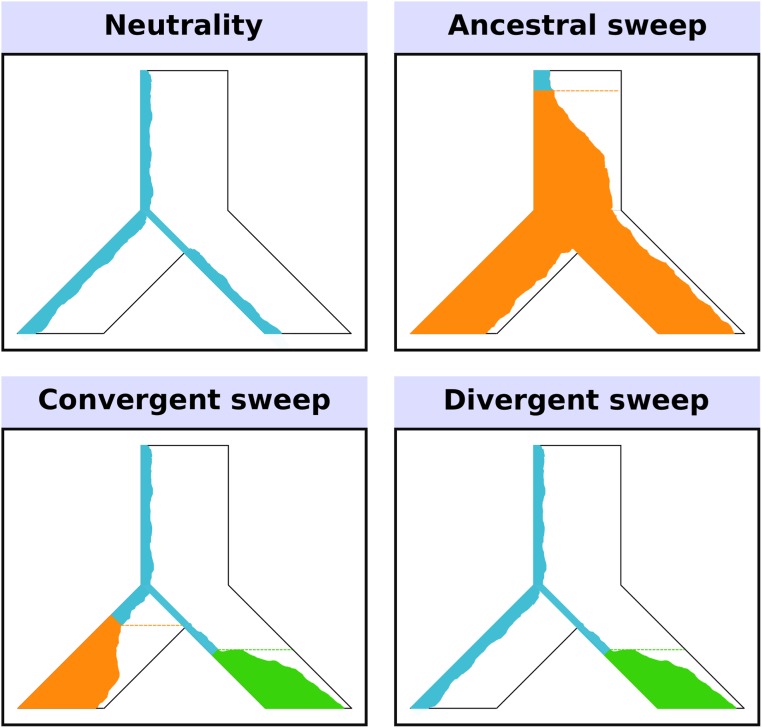
To address the constraints of current methods, we developed SS-H12, an expected haplotype homozygosity-based statistic that detects shared selective sweeps from a minimum of two sampled populations (see Materials and Methods). Beyond simply detecting shared sweeps, SS-H12 uses haplotype data to classify sweep candidates as either ancestral (shared through common ancestry) or convergent (occurring independently; Figure 1). SS-H12 is based on the theory of H12 (Garud and Rosenberg 2015; Garud et al. 2015)—a summary statistic that measures expected homozygosity in haplotype data from a single population. H12 has high power to detect recent hard and soft selective sweeps due to its unique formulation. For a genomic window containing I distinct haplotypes, H12 is defined as
| (1) |
where is the frequency of the ith most frequent haplotype, and . The two largest haplotype frequencies are pooled into a single value to reflect the presence of at least two high-frequency haplotypes under a soft sweep. Meanwhile, the squares of the remaining haplotype frequencies are summed to reflect the probability of drawing two copies of the third through Ith most frequent haplotypes at random from the population. Thus, H12 yields similar values for hard and soft sweeps. The framework of the single-population statistic also distinguishes hard and soft sweeps using the ratio H2/H1 (Garud and Rosenberg 2015; Garud et al. 2015), where is the expected haplotype homozygosity, and where is the expected haplotype homozygosity omitting the most frequent haplotype. H2/H1 is small under hard sweeps because the second through Ith frequencies are small, as the beneficial alleles exist only on a single haplotypic background. Accordingly, H2/H1 is larger for soft sweeps (Garud et al. 2015), and can therefore be used to classify sweeps as hard or soft, conditioning on an elevated value of H12.
Figure 1.
Model of a two-population phylogeny for which SS-H12 detects recent shared sweeps. Here, an ancestral population splits in the past into two modern lineages, which are sampled. Each panel displays the frequency trajectory of a haplotype across the populations. Under neutrality, there is high haplotypic diversity such that many haplotypes, including the reference haplotype (blue), exist at low frequency. In the ancestral sweep, the reference haplotype becomes selectively advantageous (turning orange) and rises to high frequency prior to the split, such that both modern lineages carry the same selected haplotype at high frequency. The convergent sweep scenario involves different selected haplotypes independently rising to high frequency in each lineage after their split. Under a divergent sweep, only one sampled lineage experiences selection.
Using simulated genetic data, we show that SS-H12 has high power to detect recent shared sweeps in population pairs, displaying a similar range of detection to H12. Additionally, we demonstrate that SS-H12 correctly differentiates between recent ancestral and convergent sweeps, generally without confusing the two. Furthermore, we extended the application of SS-H12 to an arbitrary number of populations K (see Materials and Methods), finding once again that our approach classifies sweeps correctly and with high power. Moreover, the SS-H12 approach retains the ability to distinguish between hard and soft shared sweeps by inferring the number of distinct sweeping haplotypes (see Materials and Methods). Finally, our analysis of whole-genome sequences from global human populations recovered previously identified sweep candidates at the LCT and SLC24A5 genes in Indo-European populations, corroborated recently characterized sweeps that emerged from genomic scans with the single-population approach (Harris et al. 2018), such as RGS18 in African and P4HA1 in Indo-European populations, and uncovered novel shared sweep candidates, such as the convergent sweeps C2CD5 between Eurasian populations and PAWR between European and sub-Saharan African populations.
Materials and Methods
Constructing SS-H12
Here, we formulate SS-H12 using the principles of H12 applied to a sample consisting of multiple populations. SS-H12 provides information about the location of a shared sweep on the phylogenetic tree relating the sampled populations. SS-H12 is computed from multiple statistics that quantify the diversity of haplotypes within each population, as well as within the pool of the populations, therefore making use of the haplotype frequency spectrum and measures of shared haplotype identity to draw inferences. Consider a pooled sample consisting of haplotypes from populations, in which a fraction γ of the haplotypes derives from population 1 and a fraction derives from population 2. For the pooled sample, we define the total-sample expected haplotype homozygosity statistic within a genomic window containing I distinct haplotypes as
| (2) |
where , , is the frequency of the ith most frequent haplotype in the pooled population, and where and are the frequencies of this haplotype in populations 1 and 2, respectively. That is, , , and refer to the same haplotype, indexed according to its frequency in the pooled sample. The value of is therefore large at the genomic regions of shared sweeps because the overall haplotypic diversity at such loci is small, reflecting the reduced haplotypic diversity of component populations.
Next, we seek to define a statistic that classifies the putative shared sweep as ancestral or convergent between the pair of populations. To do this, we define a statistic , which measures the sum of the squared difference in the frequency of each haplotype between both populations. takes on values between 0, for population pairs with identical haplotype frequencies, and 2, for populations that are each fixed for a different haplotype. The former case is consistent with an ancestral sweep scenario, whereas the latter is consistent with a convergent sweep—though we caution that genetic drift can also produce extreme values of , which is unlikely to be problematic provided test populations are closely enough related.
From the summary statistics (based on the haplotype frequency spectrum) and (quantifying shared haplotype identity), we now define SS-H12, which measures the extent to which an elevated is due to shared ancestry. First, we specify a statistic that quantifies the shared sweep, . The value of lies between −1 for convergent sweeps, and 1 for ancestral sweeps, with a typically negative value near 0 in the absence of a sweep. is therefore easy to interpret because convergent sweeps on nonidentical haplotypes cannot generate positive values, and ancestral sweep signals that have not eroded due to the effects of recombination and mutation cannot generate negative values. Because a sufficiently strong and complete sweep in one population (divergent sweep; Figure 1) may also generate negative values of with elevated magnitudes distinct from neutrality, we introduce a correction factor that yields SS-H12 by dividing the minimum value of H12 between a pair of populations by the maximum value. This modification allows SS-H12 to overlook spurious signals driven by strong selection in a single population by reducing their prominence relative to true shared sweep signals. Applying this correction factor yields SS-H12, which is computed as
| (3) |
where and are the H12 values for populations 1 and 2, respectively. The correction factor has a value close to 1 for shared sweeps of either type, but a small value for divergent sweeps. Thus, the corrected SS-H12 is sensitive only to shared sweeps, while maintaining a small magnitude value under neutrality. We note that the performance of SS-H12 is dependent upon the size of the sample, requiring sufficient captured haplotypic diversity to distinguish sweeps from the neutral background, similarly to H12 and other haplotype-based methods. Therefore, while our analyses concern large simulated and empirical sample sizes around per population, we expect that per population will provide enough resolution to detect sweeps given a similar, broadly mammalian demographic history (Harris et al. 2018).
We now extend SS-H12 to diploid unphased multilocus genotype (MLG) data as SS-G123. Results for SS-G123 experiments appear in the subsection Detection and classification of shared sweeps from unphased data. The ability to analyze MLGs is important because haplotype data are often unavailable for nonmodel organisms. To generate MLGs from our original unphased data, we manually merged an individual’s two haplotypes into a single MLG. In this way, we were able to directly assess the effects of phasing on our inferences. MLGs are character strings, as are haplotypes, but, in contrast to a haplotype, each character within the MLG may take one of three values representing a homozygous reference, homozygous alternate, or heterozygous genotype. The definition of SS-G123 is analogous to that of SS-H12:
| (4) |
where G123 is the MLG equivalent of H12 (Harris et al. 2018) computed as (for J distinct MLGs and ). and are G123 computed in populations 1 and 2, respectively, , , and ; note that . Finally, we note that both the haplotype- and MLG-based approaches are compatible with an arbitrary number of sampled populations K, and demonstrate this in Part 1 of the Supplemental Note.
General simulation parameters
We first tested the power of SS-H12 (phased haplotypes) and SS-G123 (unphased MLGs) to detect shared selective sweeps on simulated multilocus sequence data. We generated all data as haplotypes using the forward-time simulator SLiM 2 (version 2.6; Haller and Messer 2017), which follows a Wright-Fisher model (Hartl and Clark 2007) and can reproduce complex demographic and selective scenarios. For the first set of experiments (“power simulations” of Table 1), we simulated population pairs following human-inspired parameters (Takahata et al. 1995; Nachman and Crowell 2000; Payseur and Nachman 2000; Narasimhan et al. 2017; Terhorst et al. 2017). To account for the variation in recombination rates across natural genomes, we drew recombination rates r at random from an exponential distribution with maximum truncated at (Schrider and Kern 2017; Mughal and DeGiorgio 2019). We created the joint demographic history for simulated two-population models from empirical whole genome polymorphism data (1000 Genomes Project Consortium et al. 2015) using smc++ (version 1.13.1; Terhorst et al. 2017). The populations in our models were the CEU—Utah residents with northern and western European ancestry—paired with either the GIH, Gujarati Indians from Houston, or the YRI, Yoruba individuals from Ibadan in Southern Nigeria (Table 1). We additionally examined the performance of our approach to detect shared sweeps in a generalized mammalian model (Table 2, first row) for samples drawn from populations to determine the effect of sampling more than two populations. We describe this in detail in Part 1 of the Supplemental Note.
Table 1. Summary of parameters for experiments involving simulated human models.
| Experiment | Sample sizes | Mutation rate (μ) [θ] | Recombination rate (r) [ρ] | Sequence length; window size | Split time (τ, generations) [coalescent units] | Selection coefficient (s) [σ] and time (t, generations) [coalescent units] | Figures |
|---|---|---|---|---|---|---|---|
| Power simulations | 99 (CEU), 103 (GIH), 108 (YRI) | [ (no SSA), (with SSA)] | , drawn at random from exponential distribution [ (no SSA), (with SSA)] | 100; 20 (CEU-YRI), 40 (CEU-GIH) | CEU-GIH: 1100 [0.055]; CEU-YRI: 3740 [0.0935] | [ (no SSA), (with SSA)], [ (no SSA), (with SSA)]; [] (CEU-GIH), (CEU-YRI) [] | 2, 3; S2–S8; S11–S18; S34–S43 |
| Background selection | Same as above | Same as above | Same as above, but reduced to across central gene | Same as above | Same as above | , occurring from the start of the simulation on central gene | S23 |
| Hard/soft classification | Same as above; also 91 (GBR), 99 (KHV), 104 (JPT), 99 (LWK) | Same as above | [ (no SSA), (with SSA)], drawn as above | 20 (with SSA), 40 (no SSA); sequence treated as a single window | Same as above; also, 300 (CEU-GBR), 1560 (CEU-JPT), 3740 (GIH-YRI), 1580 (JPT-GIH), 660 (JPT-KHV), 3740 (JPT-YRI), 2800 (LWK-YRI) | uniformly at random from log-scale; t dependent on population pair, ancestral sweeps finish 40 generations before τ, convergent sweeps start 40 generations after τ | 5; S24–S29 |
| p-value assignment | Same as above | Same as above | Same as hard/soft classification | Same as hard/soft classification | Same as hard/soft classification | No selection | Tables S1, S3, and S4–S21 |
| False discovery rate | Same as above | Same as above | Same as hard/soft classification | Same as hard/soft classification | Same as hard/soft classification | Same as hard/soft classification for sweeps, and same as p-value simulations for neutral | Table S2 |
We provide diploid sample sizes, per-site per-generation mutation and recombination rates, and sequence length in kilobases. Additionally, we indicate the population-scaled values for mutation and recombination rates in brackets upon their first appearance, scaling by where for population pairs not containing sub-Saharan African (SSA) populations, and otherwise (; ; ). The relationship between generations and coalescent units is generations per coalescent unit.
Table 2. Summary of parameters for experiments involving the generalized mammalian model.
| Experiment | Sample sizes | Mutation (μ) [θ] and recombination (r) [ρ] rates | Sequence length; window size | Split time (τ, generations) [coalescent units] | Selection coefficient (s) [σ] and time (t, generations) [coalescent units] | Other parameters | Figures |
|---|---|---|---|---|---|---|---|
| Generalized mammalian model, including star tree and nonsimultaneous sweeps () | 100 per population | [], (uniform across replicates) [] | 100; 40 | ,500,750, [, 0.025, 0.0375, ]; for and star tree (), and sequential starting from otherwise | []; [] | Population splits separated by 250 generations for scenarios; trees are asymmetric | S1; S4; S9 and Supplemental note SN1–SN3; SN5; SN6, SN7 |
| Admixture, distant donor () | Same as above | Same as above | Same as above | [] between sampled sisters | s same as above; [] for ancestral sweeps, and [] for convergent and divergent sweeps | Distant donor split from sampled populations generations [] ago; admixture occurred 200 generations [0.01 coalescent units] ago; admixture proportion | 4; S19 |
| Admixture, intersister () | Same as above | Same as above | Same as above | Same as above | Same as above | Adaptive mutation originates in donor population and may be adaptive or not in its target sister; timing and proportion of admixture same as above | Supplemental note SN4 |
| Uneven sample sizes () | Pooled sample size is 200 diploids; smaller sample size is | Same as above | Same as above | Same as above | s and t same as generalized mammalian model | Protocol identical to unmodified generalized mammalian model | S20–S22 |
We provide diploid sample sizes, per-site per-generation mutation and recombination rates, and sequence length in kilobases. Additionally, we indicate the population-scaled values for mutation and recombination rates in brackets upon their first appearance, scaling by where (; ; ). The relationship between generations and coalescent units is generations per coalescent unit.
Our smc++ protocol was as follows: we first extracted polymorphism data separately for a subset of individuals from each study population from the source VCF file using the function vcf2smc, selecting two individuals uniformly at random to be distinguished individuals within their sample. Distinguished individuals are used to compute the conditional site frequency spectrum during each round of model optimization (Terhorst et al. 2017). During the conversion step, we also masked out regions with missing data using the accessibility masks provided by 1000 Genomes Project Consortium et al. (2015). Following this, we generated each model with the estimate function, choosing a thinning parameter of . Using model estimates for the component populations jointly with polymorphism data extracted for samples containing individuals from both populations ( for each for a total of 54), we generated models for population pairs.
Simulations generated under all aforementioned schemes lasted for an unscaled duration of generations. This consisted of a burn-in period of generations to produce equilibrium levels of variation in which the ancestor to the sampled modern populations was maintained at size diploids (Messer 2013), and another generations during which population size was allowed to change (in the case of two-population experiments). We note that population split events occurred within the latter generations of the simulation. As is standard for forward-time simulations (Yuan et al. 2012; Ruths and Nakhleh 2013), we scaled all parameters by a factor to reduce simulation runtime, dividing the population size and duration of the simulation by , and multiplying the mutation and recombination rates, as well as the selection coefficient (s), where applicable, by . Thus, scaled simulations maintained the same expected levels of genetic variation as would unscaled simulations.
Selection experiment procedures
Across our simulation scenarios, we examined three classes of sweeps, consisting of ancestral, convergent, and divergent. For ancestral sweeps, we introduced a selected allele to one or more randomly drawn haplotypes in the ancestor of all sampled populations (i.e., more anciently than any population split), which ensured that the same selective event was shared in the histories of the populations. This meant ancestral sweeps were constrained to occur at selection time t more ancient than the root time τ of the set of sampled populations. For convergent sweeps, we simultaneously introduced the selected mutation independently in each extant population at the time of selection, after the split had occurred. Finally, divergent sweeps comprised scenarios in which the sweep event occurred in fewer than all sampled populations, such that at least one did not experience a sweep, but at least one did experience a sweep. Accordingly, convergent and divergent sweeps were defined as those for which t was more recent than the root time τ of the set of sampled populations. Across all simulations, we conditioned on the maintenance of at least one copy of the selected allele in any affected population after its introduction.
To generate distributions of SS-H12 and SS-G123 for power analysis, we scanned 100 kb of sequence data from simulated individuals using a sliding window approach, as in Harris et al. (2018). Although sweep footprints are likely to extend much farther than 100 kb (Gillespie 2004; Hermisson and Pennings 2017), we chose our sequence length in order to focus on haplotype frequency distortions surrounding the epicenter of the sweep, which necessarily contains the genomic window of maximum signal on which we base inferences. Moreover, the use of a larger simulated region is likely to downwardly bias the ratio of true positives to false positives by providing a greater possibility of generating SS-H12 values of large magnitude by chance under neutrality. We demonstrate this effect in Supplemental Material, Figure S2 by simulating 1 Mb sequences following the same protocol as for the 100 kb sequences, and see little overlap in their distributions. Trends in power would nonetheless remain similar, but, with this in mind, and considering that SS-H12 does not make use of polymorphism data lying outside of the analysis window, we determined that our choice of a 100 kb simulated region was appropriate for our present purposes.
We computed statistics in 20 (CEU-YRI) or 40 kb (CEU-GIH and generalized mammalian models) windows, advancing the window by increments of 1 kb across the simulated chromosome for a total of 61 (CEU-GIH, generalized) or 81 (CEU-YRI) windows. For each replicate, we retained the value of SS-H12 or SS-G123 from the window of maximum absolute value as the score. We selected window sizes sufficiently large to overcome the effect of short-range LD in the sample, which may produce a signature of expected haplotype homozygosity resembling a sweep (Garud et al. 2015). We measured the decay of LD for SNPs in neutral replicates separated by 1–100 kb at 1-kb intervals using mean and found that LD falls below half its original value, on average, at our chosen window sizes. In practice, it is important to choose window sizes that satisfy such a constraint to control against false positives. Our choice of window sizes here also matched those for empirical scans. For all parameter sets, we generated sweep replicates and neutral replicates with identical numbers of sampled populations, sample sizes, and split times.
Overall, our chosen experimental protocols across performance evaluation experiments comprised a broad spectrum of sweeps (Table 1 and Table 2). We varied selection strength and start time, as well as population split time, which we expect has covered relevant models for hypothesized selective sweeps in recent human history (Przeworski 2002; Sabeti et al. 2007; Beleza et al. 2012; Jones et al. 2013; Clemente et al. 2014; Fagny et al. 2014). Our primary goal was to evaluate the ability of SS-H12 and SS-G123 to identify hard selective sweeps from a de novo mutation and soft sweeps from selection on standing genetic variation, for both strong and moderate strengths of selection. These settings were equivalent to those from the experimental approach of Harris et al. (2018) for single-population statistics, and correspond to scenarios for which those statistics have power under the specific mutation rate, recombination rate, effective size, and simulated sequence length we tested here. For all selection scenarios, we placed the beneficial allele at the center of the simulated chromosome, and introduced it only once, constraining the selection start time, but not the selection end time. For hard and soft sweeps, we allowed the selected allele to rise in frequency toward fixation, but with no guarantee of reaching fixation. Indeed, most simulations did not reach fixation under our parameters for sweeps more recent than generations before sampling, while most simulations have fixed by the time of sampling for all parameter sets. To specify soft sweep scenarios, we conditioned on the selected allele being present in the population on or 8 distinct (scaled) haplotypes at the start of selection, without defining the number of selected haplotypes remaining in the population at the time of sampling, as long as the selected allele was not lost.
Classifying sweeps as hard or soft
The SS-H12 approach can distinguish shared sweeps as hard or soft, conditioning on the value of the expected homozygosity ratio statistic, This ratio derives from H2/H1 of Garud et al. (2015) and is computed similarly, but using pooled population frequencies. We define and , with defined as in Equation 2. Likewise, for MLGs, we have the ratio , with and (see explanation of Equation 4). As with the single-population statistic, the and ratios are larger for soft sweeps and smaller for hard sweeps, following the same logic (see Introduction). A larger sample size is necessarily required to properly classify sweeps as hard or soft because hard and soft sweeps resemble each other to a greater degree than sweeps and neutrality. As with the single-population approach (Harris et al. 2018), we expect that a minimum of haplotypes per population is sufficient to resolve harder sweeps from softer sweeps under demographic histories comparable to that of humans.
As in Harris et al. (2018), we employed an approximate Bayesian computation (ABC) approach to demonstrate the ability of SS-H12 (SS-G123), in conjunction with the statistic, to classify shared sweeps as hard or soft from the inferred number of sweeping haplotypes ν (Table 1, “hard/soft classification”). Hard sweeps derive from a single sweeping haplotype, while soft sweeps consist of at least two sweeping haplotypes. Whereas the single-population approach (Garud and Rosenberg 2015; Garud et al. 2015; Harris et al. 2018) identified hard and soft sweeps from their occupancy of paired values, we presently use paired and values to classify shared sweeps. We defined a grid corresponding to paired or values with each axis bounded by [0.005–0.995] at increments of 0.01, and assigned the most probable value of ν to each test point in the grid.
We define the most probable ν for a test point as the most frequently observed value of ν from the posterior distribution of sweep replicates within a Euclidean distance of 0.1 from the test point. For each replicate, we drew uniformly at random, as well as uniformly at random from a log-scale. Across ancestral and convergent sweep scenarios for sampled sister populations, we generated replicates for the CEU-GIH and CEU-YRI models. Thus, an understanding of the demographic history of study populations is required to classify sweeps as hard or soft (this is also true when evaluating the significance of candidate results; see Empirical analysis procedures). As previously, ancestral sweeps were more ancient than τ, while convergent sweeps were more recent. We drew sweep times t uniformly at random from ranges as described in Table 1. Simulated haplotypes were of length 40 kb (CEU-GIH) or 20 kb (CEU-YRI), corresponding to the window size for method performance evaluations, because, in practice, a value of ν would be assigned to a candidate sweep based on its most prominent associated signal. All other parameters were identical to previous experiments using these demographic models (Table 1).
Testing performance across diverse scenarios
We additionally observed the effects of potentially common scenarios that deviate from the basic model defined in previous sections to determine whether these deviations could mislead SS-H12. First, we examined the effect of admixture from a distantly related donor on one of the two sampled populations under the simplified demographic model (Table 2, “admixture, distant donor”). Second, we simulated a scenario in which a pair of sister populations experiences a sweep, followed by unidirectional admixture from one sister to the other, once again under the simplified model (Table 2, “admixture, intersister”). Next, we provided greater depth to previous experiments by varying the relative sample sizes of the simulated populations (Table 2, “uneven sample sizes”), and varying the time at which convergent sweeps occurred in either population, keeping one fixed and changing the other (otherwise identical to generalized mammalian model). To provide context on the effect of tree topology, we also simulated a scenario as a star tree, in which all populations split from the common ancestor simultaneously at time τ (otherwise identical to generalized mammalian model). Finally, we generated samples under long-term background selection (Table 1, “background selection”), which is known to yield similar patterns of diversity to sweeps (Charlesworth et al. 1993, 1995; Seger et al. 2010; Cutter and Payseur 2013; Nicolaisen and Desai 2013; Huber et al. 2016), following the CEU-GIH and CEU-YRI models.
For the distant-donor admixture experiments, we simulated single pulses of admixture at fractions between 0.05 and 0.4, at intervals of 0.05, from a diverged unsampled donor (, one coalescent unit), generations prior to sampling. Admixture follows a strong sweep (; ), which occurred at either (ancestral) or (convergent and divergent). We simulated three different scenarios of admixture into the sampled target population from the donor population, where the target and its sister were separated by generations. The scenarios consisted of admixture from a highly diverse donor population (, tenfold larger than the sampled population), which may obscure a sweep signature in the sampled target, and from a low-diversity donor population (, the size of the sampled population), which may produce a sweep-like signature in the target, in addition to an intermediately diverse donor population (, equal to the size of the sampled population). For divergent sweeps here, the population experiencing the sweep was the target. In the intersister admixture experiment, a pair of equally sized sister populations ( diploids) splits generations ago. Parameters are identical to the previous experiment (Table 2), except that admixture occurs between the sister populations. We modeled two divergent admixture scenarios, one in which the selected allele was adaptive in only the original population, and one where it was identically adaptive in both.
In further experiments under the simplified model, we sought to determine the manner in which changes to our basic model assumptions changed the performance of SS-H12. First, we reduced the sample size of one of the populations from diploids to , , or , while increasing the size of the other population () to maintain , keeping all other parameters identical to previous experiments. This distorted γ in the computation of (Equation 2), yielding a new , , or , respectively, up from originally. Second, for convergent sweeps and equal sample sizes , we modeled unequal sweep start times, with , the time of selection in population 1, fixed at 800 generations prior to sampling, paired with a variable . This provided a more realistic scenario than identical start times, which should not be expected a priori. Third, we tested the susceptibility of SS-H12 to detecting and classifying sweeps on populations under a star tree model . Here, all sister populations are equally related, having radiated simultaneously from their common ancestor. With this model, we assessed the extent to which the tree topology may influence shared sweep inference.
Our background selection simulations followed the same protocol as in previous work (Cheng et al. 2017). At the start of the simulation, we introduced a centrally located 11-kb gene composed of untranslated regions (UTRs; 5′ UTR of length 200 nt, 3′ UTR of length 800 nt) flanking a total of 10 exons of length 100 nt separated by introns of length 1 kb. Strongly deleterious () mutations arose throughout the course of the simulation across all three genomic elements under a gamma distribution of fitness effects with shape parameter 0.2 at rates of 50, 75, and 10% for UTRs, exons, and introns, respectively. The sizes of the genic elements follow human mean values (Mignone et al. 2002; Sakharkar et al. 2004). To enhance the effect of background selection on the simulated chromosome, we also reduced the recombination rate within the simulated gene by two orders of magnitude to per site per generation.
Empirical analysis procedures
We applied SS-H12 and SS-G123 to human empirical data from the 1000 Genomes Project Consortium et al. (2015). We scanned all autosomes for signatures of shared sweeps in nine population pairs using 40-kb windows advancing by increments of 4 kb for samples of non-African populations, and 20-kb windows advancing by 2 kb for any samples containing individuals from any African population. We based these window sizes on the interval over which LD, measured as , decayed beyond less than half its original value relative to pairs of loci separated by 1 kb. As in Harris et al. (2018), we filtered our output data by removing analysis windows containing <40 SNPs, equal to the expected number of SNPs under the extreme case in which a selected allele has swept across all haplotypes except for one, leaving two lineages (Watterson 1975). Following Huber et al. (2016), we also divided all chromosomes into nonoverlapping bins of length 100 kb and assigned to each bin a mean CRG100 score (Derrien et al. 2012), which measures site mappability and alignability. We removed windows within bins whose mean CRG100 score was <0.9, with no distinction between genic and nongenic regions. Thus, our overall filtering strategy was identical to that of Harris et al. (2018). We then intersected remaining candidate selection peaks with the coordinates for protein- and RNA-coding genes from their hg19 coordinates.
For each genomic analysis window of each population pair analysis, we assigned a p-value. To do this, we first generated neutral replicate simulations in ms (Hudson 2002) under appropriate two-population demographic histories inferred from smc++, using our aforementioned protocol and parameters described in Table 1. We initially computed a window’s p-value as the proportion of neutral replicate values exceeding the associated with that window. Because some comparisons yielded windows with , meaning that no neutral replicate exceeded their value, we first performed a linear regression of and through the origin, and predicted the p-value of each window according to the inferred relationship. We demonstrate the linear relationship between and by significant and strong Pearson correlation (Table S1). However, we found by QQ-plot that the distribution of empirical p-values was inflated relative to the theoretical expectation of uniform distribution (Klammer et al. 2009). To determine our inflation factor λ, which measures the extent to which empirical p-values are inflated relative to the theoretical, we used a linear regression approach (Yang et al. 2011). Here, we performed a linear regression, through the origin, of the quantile function evaluated for our uncorrected p-values, as a function of quantiles derived from a vector of uniform probabilities. We adjusted our uncorrected quantiles, dividing by λ, and used their probabilities as our calibrated p-values (Figure S3). Our Bonferroni-corrected, genome-wide significance cutoff for a population pair at the threshold was , adjusting for an assumed 1 million independent test sites in the human genome (Altshuler et al. 2008).
Additionally, we determined whether the maximum associated (the score), and therefore p-value, of a gene was related to the recombination rate of the genomic region in which it resided. We determined this by computing the Spearman correlation between the maximum SS-H12 of a gene, and the recombination rate (centimorgan/megabase) within the genomic analysis window of maximum signal associated with that gene (International HapMap Consortium et al. 2007). Furthermore, we observed the effect of model misspecification on critical SS-H12 values. To do this, we compared the distribution of SS-H12 simulated under the nine appropriate smc++-inferred nonequilibrium demographic models, and the distribution under models with equal to the correct models, but with constant sizes of diploids per population throughout the simulation. We computed mean (Wright 1943, 1951) across 1000 neutral replicates of size 20 or 40 kb under the smc++-derived models, and used these values to solve the equation (Slatkin 1991), where τ is the split time in generations between population pairs in each misspecified model.
We assigned the most probable ν for each sweep candidate following the same protocol as previously (Table 1, “hard/soft classification”), generating replicates of sweep scenarios in SLiM 2 under smc++-inferred demographic histories for ancestral and convergent sweeps. Once again, for ancestral sweep scenarios and for convergent sweep scenarios, where τ is defined by the specific demographic history of the sample. The CEU-GIH and CEU-YRI replicates used here were identical to those in the prior classification experiments (Classifying sweeps as hard or soft). Sequence length for each replicate was identical to analysis window length for equivalent empirical data (20 or 40 kb), because in practice we assign ν to windows of this size. For both p-value and most probable ν assignment, we used an alternative per-site per-generation recombination rate of (Terhorst et al. 2017), finding that this more closely matched the distribution of values in the empirical data. Using these simulations in combination with neutral simulations of the matching length, we determined the 1% false discovery rate (FDR) cutoffs for . To do this, we drew a random sample of selection simulations to construct a total sample of replicates, half neutral and half sweep. The 1% FDR cutoff was the value for which 1% of the replicates exceeding that value were neutral, and 99% were sweeps. We repeated this process times to get a distribution of cutoffs based on our simulations.
Data availability
To make the results of our work maximally accessible, we have uploaded all relevant scripts, as well as all outputs from analyses, into a Dryad repository (https://datadryad.org/stash/share/tqLw6lJN0uqtyfvj46INlHHGg0nAbFKmsxiFVJ0a0SM). Our upload is divided into directories labeled to match the broad directions of our research in this manuscript: simulations using the smc++-derived CEU-GIH and CEU-YRI models, simulations using the simplified mammalian model for sampled populations, admixture model simulations, background selection simulations, misspecified model simulations, simulations to infer ν, simulations to assign p-values, and scans of the 1000 Genomes data. Outside of the latter two batteries of simulations, we provide all of the raw SLiM-simulated outputs in addition to analyses on those simulations. For simulations to infer ν and p-value simulations, we retain only the summary statistics from windows of maximum signal for each replicate because each scenario featured at least replicates. Our summary files condense those simulations into single, more manageable, documents for reader reference. In addition to simulations and scripts, we have also included the builds of ms and SLiM used for simulations, and our SS-X12 software package. We affirm that the results of all analyses deriving from our data, using the scripts, replicates, and summary files within our Dryad repository, are present within this manuscript’s figures and tables. Supplemental materials, consisting of Tables S1–S21, Figures S1–S46, and Supplemental Note Figures SN1–SN7, are available online through FigShare. Supplemental material available at figshare: https://doi.org/10.25386/genetics.11953632.
Results
We evaluated the ability of SS-H12 to differentiate among the simulated scenarios of shared selective sweeps, sweeps unique to only one sampled population, and neutrality, using the signature of expected haplotype homozygosity in samples consisting of individuals from two or more populations. Although our formulation of SS-H12 does not explicitly constrain the definition of a population, we define a population as a discrete group of individuals that mate more often with each other than they do with individuals from other discrete groups, and the models we considered here represent extreme examples in which there is no gene flow between populations after their split.
We performed simulations using SLiM 2 (Haller and Messer 2017) under human-inspired parameters (Takahata et al. 1995; Nachman and Crowell 2000; Payseur and Nachman 2000; Narasimhan et al. 2017; Terhorst et al. 2017) for diploid populations of fluctuating size (N) under nonequilibrium models, as well as constant-size models, subject to changing selection start times (t) and strengths (s), across differing split times (τ) between sampled populations. Additionally, we evaluated the robustness of SS-H12 to a variety of potentially confounding deviations from the basic simulation parameters (such as equal sample sizes, no admixture, and asymmetric tree topology). We then used an ABC approach in the same manner as Harris et al. (2018) to demonstrate our ability to distinguish between shared hard and soft sweeps in samples from multiple populations. Finally, we show that SS-H12 recovers previously hypothesized signatures of shared sweeps in human whole-genome sequences (1000 Genomes Project Consortium et al. 2015), while also uncovering novel candidates. We supplement results from SS-H12 analyses with results using SS-G123 in Detection and classification of shared sweeps from unphased data. See Materials and Methods, as well as Table 1 and Table 2, for further explanation of experiments. We include a summary of the major results in Table 3.
Table 3. Summary of SS-H12 signals and their interpretation across various scenarios.
| Scenario | Sign of SS-H12 | Magnitude of SS-H12 | Comments | Reference |
|---|---|---|---|---|
| Neutrality | Typically negative | Small | Magnitude becomes positive in bottleneck scenarios where the number of shared haplotypes between populations is higher by chance. | Figure 2, Figure 3, and Figure S5–S8, see first boxplot of left column in each figure. |
| Ancestral sweep | Positive | Large | Magnitude is generally smaller than for convergent sweeps because ancestral sweeps are older; rare negative values may arise for weaker sweep strengths. | Figure 2, Figure 3, and Figure S5–S8 for power curves and boxplots, Figures S11–S14 for sign of SS-H12, center column of each figure. |
| Convergent sweep | Predominantly negative | Large | Largest magnitude of SS-H12 across tested scenarios; positive values may arise in the rare event that two independent sweeps on the same haplotype occur between sampled populations. | Figure 2, Figure 3, and Figure S5–S8, Figure S11–S14, left column of each figure; Supplemental note Figure SN5. |
| Divergent sweep | Typically negative | Small | Trends in magnitude of SS-H12 match those of neutrality without exception; large magnitudes are impossible for divergent sweeps due to the correction factor (Equation 3). | Figure 2, Figure 3, and Figure S5–S8, Figures S11–S14, right column of each figure. |
| Relative sample sizes | Negative or positive | Small or large | The performance of SS-H12 does not depend on the relative sizes of each sample, with values of (Equation 2) behaving as with . | Figures S20–S22. |
| Background selection | Typically negative | Small | Background selection has no discernible effect on the distribution of SS-H12 relative to neutrality. | Figure S23 |
| Admixture | Predominantly negative (see comments) | Small or large | Sufficient admixture from a diverse enough donor population will erode the signal of a sweep, yielding negative values of small magnitude; admixture with a low-diversity donor does not affect magnitude or signal of convergent sweeps, but will cause ancestral sweeps to spuriously resemble convergent sweeps. Admixture between closely related sampled sister populations yields positive values. | Figure 4 and Figure S19 for distant-donor scenario; Supplemental note Figure SN4 for intersister scenario. |
| Number of sampled populations (K) | Negative or positive | Small or large | The number of populations included in the sample does not affect inference with SS-H12, across tested asymmetric and star phylogenies. | Figures S9 and Supplemental note Figures Sn1-SN3 (asymmetric); Figures SN6 and SN7 (star). |
| Unphased data | Negative or positive | Small or large | Applied to unphased multilocus genotypes (MLGs) as SS-G123, our approach has similar power and yields comparable inferences to SS-H12. Classification ability decays more rapidly because MLGs are more diverse than haplotypes | Figures S34–S41. |
Detection of ancestral and convergent sweeps with SS-H12
We conducted experiments to examine the ability of SS-H12 to not only identify shared sweep events among two or more sampled populations , but categorize them as shared due to common ancestry, or due to convergent evolution. Across all scenarios, we scanned 100 kb simulated chromosomes using a 20 or 40 kb sliding window with a step size of 1 kb, which was sufficient to analyze sweeps in single populations (Harris et al. 2018). These windows provide an interval over which neutral pairwise LD, measured with , decays below half of the value for loci 1 kb apart (Figure S4), and so we do not expect elevated values of SS-H12 due to background LD. For each sweep scenario, we studied power at 1 and 5% false positive rates (FPRs) for detecting shared selective sweeps (Figure 2, Figure 3, Figures S5–S9, and Figure SN1–SN3) as a function of time at which beneficial alleles arose, under scenarios of ancestral, convergent, and divergent sweeps.
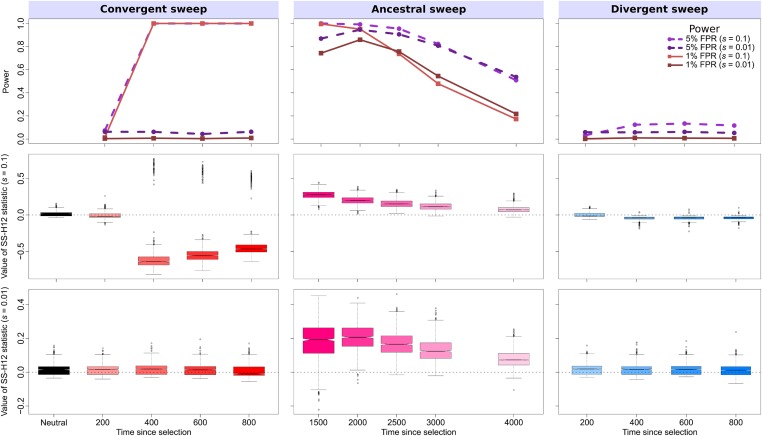
Figure 2.
Properties of SS-H12 for simulated strong (; ) and moderate (; ) hard sweep scenarios under the CEU-GIH model ( generations, or 0.055 coalescent units, before sampling). (Top row) Power at 1% (red lines) and 5% (purple lines) false positive rates (FPRs) to detect recent ancestral, convergent, and divergent hard sweeps (see Figure 1) as a function of time at which positive selection of the favored allele initiated (t), with FPR based on the distribution of maximum across simulated neutral replicates. (Middle row) Box plots summarizing the distribution of SS-H12 values from windows of maximum across strong sweep replicates, corresponding to each time point in the power curves, with dashed lines in each panel representing . (Bottom row) Box plots summarizing the distribution of SS-H12 values across moderate sweep replicates. For convergent and divergent sweeps, , while for ancestral sweeps, . All replicate samples for the CEU-GIH model contain 99 simulated CEU individuals and 103 simulated GIH individuals, as in the 1000 Genomes Project dataset (1000 Genomes Project Consortium et al. 2015), and we performed 1000 replicates for each scenario. CEU: Utah Residents with Northern and Western European Ancestry. GIH: Gujarati Indians from Houston, Texas.
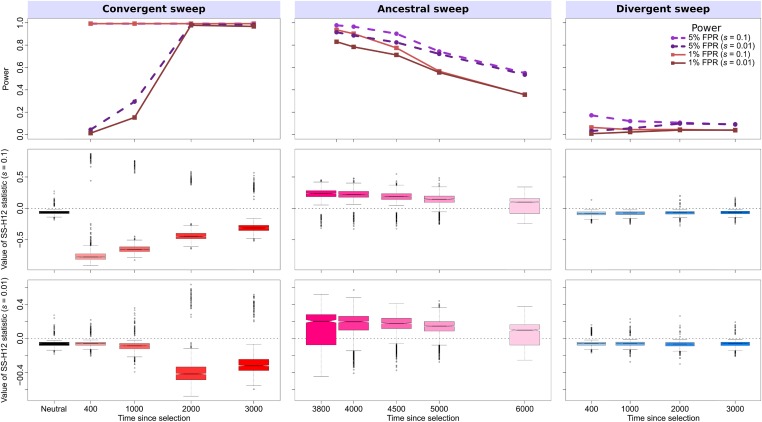
Figure 3.
Properties of SS-H12 for simulated strong (; ) and moderate (; ) hard sweep scenarios under the CEU-YRI model ( generations, or 0.0935 coalescent units, before sampling). (Top row) Power at 1% (red lines) and 5% (purple lines) false positive rates (FPRs) to detect recent ancestral, convergent, and divergent hard sweeps (see Figure 1) as a function of time at which positive selection of the favored allele initiated (t), with FPR based on the distribution of maximum across simulated neutral replicates. (Middle row) Box plots summarizing the distribution of SS-H12 values from windows of maximum across strong sweep replicates, corresponding to each time point in the power curves, with dashed lines in each panel representing . (Bottom row) Box plots summarizing the distribution of SS-H12 values across moderate sweep replicates. For convergent and divergent sweeps, , while for ancestral sweeps, . All replicate samples for the CEU-YRI model contain 99 simulated CEU individuals and 108 simulated YRI individuals, as in the 1000 Genomes Project dataset (1000 Genomes Project Consortium et al. 2015), and we performed 1000 replicates for each scenario. YRI: Yoruba people from Ibadan, Nigeria.
First, we simulated scenarios in which an ancestral population split into descendant populations using a realistic nonequilibrium model based on the history of the human CEU (European descent) and GIH (South Asian descent) populations, which we inferred from variant calls (1000 Genomes Project Consortium et al. 2015) with smc++ (Terhorst et al. 2017) (Figure S10). We began with scenarios of strong hard ( sweeping haplotype) sweeps, starting between 200 and 4000 generations prior to sampling, and applied an analysis window of size 40 kb (Figure 2). Our CEU-GIH model features a split time of generations prior to sampling, which matches prior estimates of the split time between Eurasian human populations (Gravel et al. 2011; Gronau et al. 2011; Schiffels and Durbin 2014). This series of experiments illustrates the range of sweep start times over which SS-H12 can detect prominent selective sweeps. SS-H12 has high power for recent strong shared sweeps starting between 400 and 2500 generations prior to sampling, with power dropping rapidly for shared sweeps older than 2500 generations (Figure 2).
As expected, the distribution of SS-H12 for detectable convergent sweeps centered on negative values (Figure 2, left column), whereas the SS-H12 distributions of ancestral sweeps centered on positive values (Figure 2, center column). The vast majority of such replicates had the correct sign, underscoring the consistency with which SS-H12 correctly classifies shared sweeps (Figure S11, top). However, in the rare event that identical haplotypes convergently experience an identical sweep, a positive value of SS-H12 emerges at the locus under selection, with larger values expected for more recent sweeps. Conversely, detectable ancestral sweeps are highly unlikely to yield negative SS-H12 values in closely related populations, as SS-H12 is acutely sensitive to the presence of shared haplotypes in the sample even as the signal decays. We also found that the power of SS-H12 to detect convergent sweeps was uniformly greater than for ancestral sweeps because convergent sweeps are more recent events, with the selected haplotype not yet eroding due to the effect of mutation and recombination, as with older ancestral sweeps. Additionally, because we compute power from the distribution of maximum values for each sweep scenario, this means that the magnitude of SS-H12 for replicates of shared sweeps must exceed the magnitude under neutrality for the sweep to be detected, which, for any combination of t and s, is more likely for convergent than ancestral sweeps.
To further characterize the performance of SS-H12 for hard sweeps, we repeated experiments on simulated samples from populations both for more anciently diverged populations (larger τ), and for weaker sweeps (smaller s). SS-H12 maintains excellent power to distinguish strong shared sweeps from neutrality for a model based on the more ancient split between CEU and the sub-Saharan African YRI population (Figure 3; 20-kb window), while keeping . We inferred for this model using smc++ (Terhorst et al. 2017) (Figure S10), and this estimate fits existing estimates of split times between African and non-African human populations (Gravel et al. 2011; Gronau et al. 2011; Schiffels and Durbin 2014). Notably, the signal of ancestral sweeps remains elevated across many of the tested CEU-YRI sweep scenarios. Power stayed >0.6 for sweeps more recent than generations before sampling, representing a range of sweep sensitivity ∼1500 generations wider than that of the CEU-GIH model. This is because it is easier to detect selective sweeps in more diverse genomic backgrounds (Harris et al. 2018), such as that of the YRI population. Despite this, we observed a greater proportion of ancestral sweeps with spuriously negative values of SS-H12 in the CEU-YRI model than in the CEU-GIH model because over 3740 generations, the two simulated populations had sufficient time to accumulate unique mutations and recombination events that differentiated their common high-frequency haplotypes (Figure S12, top).
Reducing the selection coefficient to for both models had the effect of shifting the range of t over which SS-H12 had power to detect shared sweeps. Because weakly selected haplotypes rise to high frequency more slowly than strongly selected haplotypes, there is a greater delay between the selection start time and the time at which a shared sweep can be detected for smaller values of s. Thus, SS-H12 reaches a maximum power to detect moderate shared sweeps for older values of t, additionally maintaining this power for less time than for strong sweeps under both models (top rows of Figure 2 and Figure 3). The misclassification rate for shared sweeps is also greater for weaker sweeps, especially for convergent sweeps in the CEU-GIH model and ancestral sweeps in the CEU-YRI model (Figures S13 and S14, top).
Because the single-population statistic H12 has power to detect both hard and soft sweeps, we next performed analogous experiments for simulated soft sweep scenarios. Maintaining values of t, τ, and s identical to those for hard sweep experiments, we simulated soft sweeps as selection on standing genetic variation for and distinct sweeping haplotypes (Figures S5–S8). We found that trends in the power of SS-H12 to detect shared soft sweeps remained consistent with those for hard sweeps. However, the power of SS-H12 for detecting soft sweeps, as well as classification ability (Figures S11–S14, middle and bottom rows), were attenuated overall relative to hard sweeps, proportionally to the number of sweeping haplotypes, with a larger drop in power for older sweeps and little to no effect on power for more recent sweeps. Our observations therefore align with results for the single-population H12 statistic (Garud et al. 2015; Harris et al. 2018). Thus, the ability to detect a sweep derives from the combination of s, t, and ν, with stronger recent sweeps on fewer haplotypes being easiest to detect, and detectable over larger timespans.
We contrast our results for shared sweeps across population pairs with those for divergent sweeps, which we present in parallel (right columns of Figure 2, Figure 3, and Figure S5–S8). Across identical values of t as for each convergent sweep experiment, we found that divergent sweeps, in which only one of the two simulated sampled populations experiences a sweep , are not visible to SS-H12 for any combination of simulation parameters. To understand the properties of divergent sweeps relative to shared sweeps, we compared the distributions of their SS-H12 values at peaks identified from the maximum values of for each replicate. We observed that the distributions of the divergent sweeps remain broadly unchanged from one another under all parameter combinations, and closely resemble the distribution generated under neutrality, as all are centered on negative values with small magnitude, and have small variance. Thus, the use of a correction factor that incorporates the values of H12 from each component population in the sample (see Equation 3) provides an appropriate approach for preventing sweeps that are not shared from appearing as outlying signals. In the absence of correction, the shared sweep statistic (properly termed ), incorrectly treats the reduced haplotype diversity around the site under selection in one population as the locus of a convergent sweep, owing to the large disparities in haplotype frequencies between the sampled populations (right columns of Figures S15 and S16). We additionally explore the properties of SS-H12 on a simplified demographic history with constant population size, and up to sampled populations (Figure S1), intended as a more general mammalian model, in Part 1 of the Supplemental Note.
In addition to detecting shared sweeps under a variety of scenarios with high power, we also found that detecting sweeps with SS-H12 provides more power than performing multiple independent analyses across populations with the single-population statistic H12 (Garud et al. 2015). To demonstrate this, we reanalyzed our simulated CEU-GIH and CEU-YRI replicates (Figure 2 and Figure 3), assessing the ability of H12 to simultaneously detect an outlying sweep signal in both populations. That is, we measured the power of H12 at the 0.5% FPR [Bonferroni-corrected for multiple testing (Neyman and Pearson 1928), providing the entire experiment with a 1% FPR cutoff] to detect an outlying sweep in the CEU sample and in either the GIH (Figure S17) or YRI (Figure S18) samples. For the most recent convergent hard sweeps, joint analysis with H12 has equivalent power to SS-H12 analysis, but the power of H12 never matches that of SS-H12 for ancestral hard sweeps, and for the majority of tested soft sweeps ( and ), regardless of timing. These trends persisted even for SS-H12 computed from half-sized samples (thus, matching the sample sizes of individual H12 analyses), indicating that avoiding multiple testing with SS-H12 analysis is likely to yield a greater return on sampling effort, especially as the number of sampled populations, K, increases.
Performance of SS-H12 across diverse scenarios
Admixture:
Because SS-H12 relies on a signal of elevated expected haplotype homozygosity, it may be confounded by nonadaptive processes that alter levels of population-genetic diversity. For this reason, we examined the effect of admixture on the power of SS-H12 in the context of ancestral, convergent, and divergent strong () sweeps between population pairs. Parameters were derived from the simplified mammalian model (Table 2). For the first set of experiments (termed distant-donor), one sampled population (the target) receives gene flow from a diverged, unsampled donor outgroup population (Figure 4 and Figure S19). Admixture occurred as a single unidirectional pulse 200 generations before sampling, and in the case of the divergent sweep, occurred specifically in the population experiencing the sweep. The donor split from the common ancestor of the two sampled populations (the target and its unadmixed sister) generations before sampling—within a coalescent unit of the sampled populations, similar to the relationship between Neanderthals and modern humans (Harris and Nielsen 2016; Juric et al. 2016)—and had an effective size either one-tenth, identical to, or tenfold the size of the target. Although the donor does not experience selection, extensive gene flow from a donor with low genetic diversity may resemble a sweep. Correspondingly, gene flow from a highly diverse donor may obscure sweeps. The second admixture scenario we examined featured only the two sister populations separated by generations, wherein one admixed into the other 200 generations prior to sampling, as previously (intersister admixture; see Supplemental Note, Part 2).
Figure 4.
Effect of admixture from a diverged, unsampled donor lineage on distributions of SS-H12 values at peaks of maximum , in samples consisting of individuals from populations following the simplified mammalian model (; 0.05 coalescent units), under simulated recent ancestral, convergent, and divergent sweeps. For ancestral sweeps, selection occurred 1400 generations (0.07 coalescent units) before sampling. For convergent and divergent sweeps, selection occurred 600 generations (0.03 coalescent units) before sampling. The effective size of the donor population varies from (an order of magnitude less than that of the sampled populations), to (an order of magnitude more), with admixture at 200 generations (0.01 coalescent units) before sampling at rates 0.2 to 0.4, modeled as a single pulse. The donor diverged from the sampled populations generations (one coalescent unit) before sampling. In divergent sweep scenarios, admixture occurred specifically into the population experiencing a sweep. All sample sizes are of diploid individuals, with 1000 replicates performed for each scenario. For comparison, we include unadmixed results in each panel.
As expected, gene flow from a distant donor into the target population distorted the SS-H12 distribution of the two-population sample relative to no admixture (Figure 4), and this distortion was proportional to the level of admixture from the donor, as well as the donor population’s size. Ancestral sweeps were the most likely to be misclassified following admixture from a donor of small effective size (; Figure 4, top row), increasingly resembling convergent sweeps as the rate of gene flow increased (though ultimately with little change in power to detect the shared sweep; Figure S19, top row). The confounding effect of admixture on ancestral sweep inference emerges because low-diversity gene flow into one population yields a differing signal of elevated expected haplotype homozygosity in each population, spuriously resembling a convergent sweep. In contrast, the distributions of SS-H12 values and the power of SS-H12 for convergent and divergent sweeps remained broadly unchanged relative to no admixture under low-diversity admixture scenarios (Figure 4 and Figure S19, top rows). Because two populations subject to convergent or divergent sweeps are already extensively differentiated, further differentiation due to admixture does not impact the accuracy of sweep timing classification using SS-H12.
For intermediate donor effective size (; Figure 4 and Figure S19, middle rows), the magnitudes of both the ancestral and convergent sweep signals attenuate toward neutral levels, and the power of SS-H12 wanes as the admixture proportion increases. This is because the genetic diversity in the target population increases to levels resembling neutrality, overall yielding a pattern spuriously resembling a divergent sweep that SS-H12 cannot distinguish from neutrality. Accordingly, the magnitude and power of SS-H12 under a divergent sweep scenario following admixture scarcely change under the scenario. As the effective size of the donor population grows large (; Figure 4 and Figure S19, bottom rows), SS-H12 becomes more robust to the effect of admixture for shared sweeps, accurately identifying ancestral and convergent sweeps with high power at greater admixture proportions relative to the scenario. However, the power of SS-H12 spuriously rises to 1.0 for divergent sweeps under the admixture scenario. Both the increased robustness to admixture for the ancestral and convergent sweeps, as well as the elevated power for divergent sweeps, result from a reduction in the magnitude of SS-H12 under neutrality for the admixture scenario relative to , which does not occur for the sweep scenarios. That is, remains similar across the and admixture scenarios for sweeps, while for the neutral background is smaller, meaning that any sweep, even a divergent sweep, is more prominent for larger donor population sizes.
Different sample sizes:
Next, we performed experiments to understand the effect of deviating from basic parameters of the simplified unadmixed mammalian model, changing one parameter at a time. First, we generated replicates for populations containing an overall sample size of diploids representing the sum of component sample sizes and , modifying these such that more individuals were sampled from one subpopulation than the other. This therefore changed the value of for the computation of (see Equation 2). We simulated values of (), 0.8 (), or 0.9 () in contrast to the standard (; as seen in Figure S9). Regardless of γ, we found that trends in power for shared sweeps (, ) were consistent with one another, and that the distribution of SS-H12 values yielded the expected sign—negative for convergent sweeps and positive for ancestral sweeps—suggesting that sample composition should not generally affect these inferences (Figure S20–S22). We also observed a slight, spurious increase in power for divergent sweeps (occurring in population 1) that was most prominent for , but visible at for all three scenarios. This effect emerged as a result of two factors. First, strong sweeps have not established by , meaning that the sampled sister populations are not yet extensively differentiated at this point, and have somewhat closer H12 values to one another than for older sweeps. Second, smaller sample sizes for either subpopulation translate to reduced haplotypic diversity in the sample overall, resulting in elevated magnitudes of SS-H12. Thus, while extreme distortions in γ and smaller sample sizes may yield more prominent divergent sweeps, their signature remains minor, rendering them highly unlikely to yield outlying signals relative to shared sweeps. We subsequently tested power and classification ability for convergent sweeps initiating at different timepoints on the simplified mammalian tree, as well as for a deviation to the bifurcating tree assumption by simulating a star phylogeny with subpopulations (see Supplemental Note, Part 3).
Background selection:
Finally, we observed the effect of long-term background selection on the neutral distribution of SS-H12 values (Figure S23). Background selection may yield signatures of genetic diversity resembling selective sweeps (Charlesworth et al. 1993, 1995; Seger et al. 2010; Cutter and Payseur 2013; Nicolaisen and Desai 2013; Huber et al. 2016), though previous work suggests that background selection does not drive particular haplotypes to high frequency (Enard et al. 2014; Harris et al. 2018). Our two background selection scenarios for samples from populations, with (CEU-GIH model) and 3740 (CEU-YRI model) generations, were performed as described in the Materials and Methods, following the protocol of Cheng et al. (2017). Briefly, we simulated a 100-kb sequence featuring a centrally located 11-kb gene consisting of exons, introns, and untranslated regions, across which deleterious variants arose randomly throughout the entire simulation period. In agreement with our expectations, we found that background selection is unlikely to confound inferences from SS-H12, yielding only marginally larger values of |SS-H12| than does neutrality (Figure S23). Accordingly, SS-H12 does not classify background selection appreciably differently from neutrality.
Classifying shared sweeps as hard or soft from the number of sweeping haplotypes
Because the primary innovation of the single-population approach is its ability to classify sweeps as hard or soft from paired (H12, H2/H1) values, we evaluated the corresponding properties of our current approach for samples consisting of populations (Figure 5). Here, we color a space of paired values, each bounded by , according to the inferred most probable number of sweeping haplotypes ν for each point in the space. Similarly to the approach of Harris et al. (2018), we inferred the most probable ν using an ABC approach in which we determined the posterior distribution of ν from replicates of sweep scenarios with and , both drawn uniformly at random for each replicate (the latter drawn from a log-scale), and where simulations are neutral replicates. A test point in space was assigned a value of ν based on the most frequently occurring ν among simulations whose coordinates were within a Euclidean distance of 0.1 from that test point (see Materials and Methods). We were able to classify recent shared sweeps as hard or soft, but found our current approach to have somewhat different properties to the single-population approach.
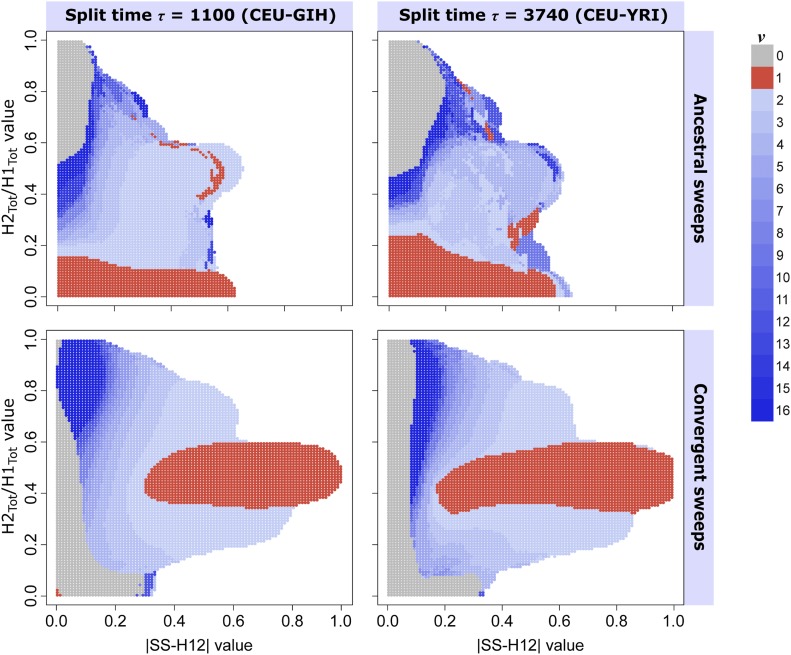
Figure 5.
Ability of paired values to infer the most probable number of sweeping haplotypes ν in a shared sweep. Most probable ν for each test point was assigned from the posterior distribution of sweep replicates with , drawn uniformly at random. (Top row) Ancestral sweeps for the CEU-GIH model (, coalescent units, left) and the CEU-YRI model (, coalescent units, right), with ( coalescent units, left) and ( coalescent units, right). (Bottom row) Convergent sweeps for the CEU-GIH model (left) and the CEU-YRI model (right), with ( coalescent units, left) and ( coalescent units, right). Colored in red are points whose paired values are more likely to result from hard sweeps, those colored in shades of blue are points more likely to be generated from soft sweeps, and gray indicates a greater probability of neutrality. Regions in white are those for which no observations of sweep replicates within a Euclidean distance of 0.1 exist.
For ancestral sweep scenarios and generations (, CEU-GIH model), the pattern of paired values generally followed that of single-population analyses (Harris et al. 2018) (Figure 5, top-left). For a given value of , smaller values of were generally more probable for ancestral sweeps from smaller ν, and inferred ν increased with . This fit our expectations because, as the number of ancestrally sweeping haplotypes in the pooled population increases, the value of H2 increases relative to H1. Additionally, ancestral sweeps from larger ν (softer sweeps) are unlikely to generate large values of or small values of , and the most elevated values of were rarely associated with more than four sweeping haplotypes. Accordingly, harder and softer ancestral sweeps yielded distinct probability densities of and from one another (Figure S24, left column).
We note, however, the presence of paired values inferred to derive from for some intermediate values of , as well as the presence of points with inferred at smaller This may indicate that, among ancestral sweep replicates for the CEU-GIH model, weaker hard sweep signals may occasionally be difficult to resolve from stronger soft sweep signals, as both should yield intermediate levels of haplotypic diversity. The difficulty in resolving this region of the plot also derives from the low number of nearby observations (within a Euclidean distance of 0.1) from which to make inferences, despite the higher than average support for these observations (Figure S26, top row). Additionally, the next-most likely ν for most points tended to be an immediately adjacent value (for example, if , then the next most likely ν is either 3 or 5; Figure S27, top row). Under simulated CEU-YRI ancestral sweep scenarios (, ; Figure 5, top right), we observed a broadly similar pattern of inferred ν. However, the increased age of sweeps relative to the CEU-GIH model resulted in more erratic inferences across intermediate paired with intermediate , smaller mean and larger mean across all classes (Figure S25, left column), and somewhat less support for inferences throughout the plot (Figures S28 and S29, top row). Our approach still maintains a clear tendency to infer sweeps with smaller as hard, thereby preserving its basic classification ability.
The convergent sweep experiments yielded distinctly different occupancies and distributions of possible paired values relative to ancestral sweeps, and provided greater resolution and inferred support among the tested values of ν, showing little irregularity in the assignment of ν (bottom rows of Figure 5, and Figures S26–S29). In addition, trends in the occupancy of hard and soft sweeps were generally concordant between replicates for both the CEU-GIH (, ) and CEU-YRI (, ) models, though was larger on average for CEU-GIH (Figures S24 and S25, right columns). For these experiments, we simulated simultaneous independent sweeps, either both soft or both hard, allowing each population to follow a unique but comparable trajectory. Thus, there were always at least two sweeping haplotypes in the pooled population. Accordingly, convergent hard sweeps, unlike ancestral hard sweeps, are associated primarily with large values of and intermediate values of . Furthermore, strong convergent sweeps of any sort could not generate small values unless |SS-H12| was also small. Even so, convergent sweeps from larger ν occupy a distinct set of paired values that is shifted either toward smaller , larger , or both, demonstrating that the accurate and consistent inference of ν is possible for convergent sweeps. Unlike for ancestral sweeps or single-population analyses, we observed that the smallest values of paired with the smallest values of were associated with neutrality, representing scenarios in which similar highly diverse haplotype frequency spectra arose in both populations by the time of sampling.
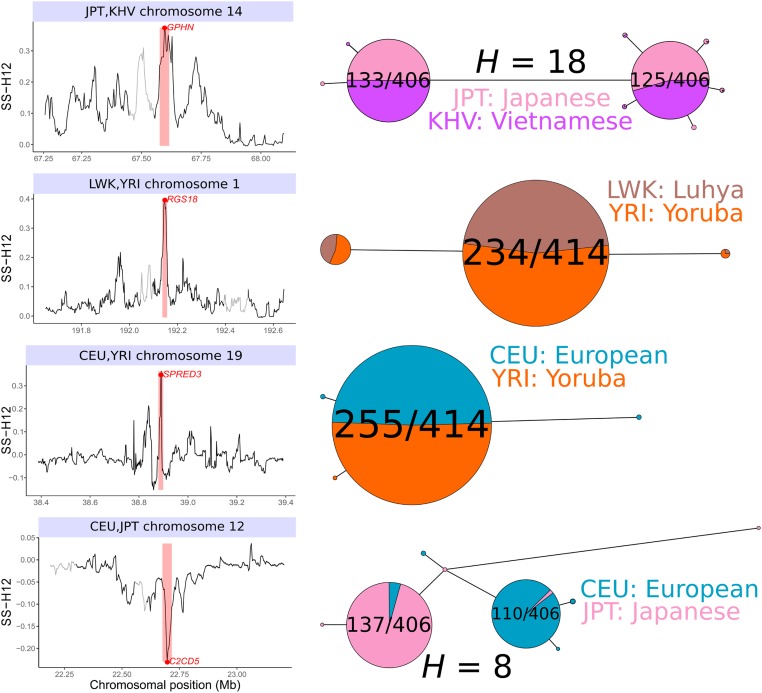
Application of SS-H12 to human genetic data
We applied SS-H12 to whole-genome sequencing data from global human populations in phase 3 of the 1000 Genomes Project (1000 Genomes Project Consortium et al. 2015), which is ideal as input because it contains large sample sizes and no missing genotypes at polymorphic sites. We searched for shared sweep signals within the RNA- and protein-coding genes of geographically proximate and distant human population pairs, performing various comparisons of unadmixed European, South Asian, East Asian, and Sub-Saharan African populations (Tables S4–S12). We scanned with sliding analysis windows of 40 kb with a step size of 4 kb for samples with non-African populations, or 20 kb with step size 2 kb otherwise, to overcome the effect of short-term LD (Figure S30). For the top 40 outlying candidate shared sweeps among population pairs, we assigned p-values from a neutral distribution of replicates following human demographic models inferred from smc++ (see Materials and Methods). Our Bonferroni-corrected genome-wide significance threshold (Neyman and Pearson 1928) for single comparisons was (Altshuler et al. (2008); we did not assess significance across multiple global-scale tests). We additionally inferred the maximum posterior estimates on for each top candidate from a distribution of simulated convergent or ancestral sweep replicates, depending on our classification of the candidate from the sign of SS-H12, following the same smc++-derived models. We categorized sweeps from as hard, and sweeps from as soft. By using both neutral and sweep simulations, we were also able to assign 1% FDR cutoffs for each population pair comparison (Table S2).
Overview of genome-wide trends:
Across all comparisons, we found that ancestral hard sweeps comprised the majority of prominent candidates at RNA- and protein-coding genes, regardless of population pair. Many of these candidate ancestral sweeps were detected with H12 in single populations (Harris et al. 2018), including novel sweeps at RGS18 in the sub-Saharan African pair of YRI and LWK (Luhya people from Webuye, Kenya; ; previously identified in YRI; Figure 6, second row) and at P4HA1 between the European CEU and South Asian GIH populations (; previously identified in GIH, though as a soft sweep; Figure S32, middle row). We also observed a dearth of large-magnitude negative values in Tables S4–S12, with prominent convergent sweep candidates only occurring between the most diverged population pairs. These consisted of C2CD5 between CEU and the East Asian JPT population (Japanese in Tokyo; ), PAWR between Indo-European populations CEU and GIH with the sub-Saharan African YRI population (small and almost-significant for the CEU-YRI comparison, , for both comparisons; Tables S7 and S9), and MPHOSPH9 and EXOC6B between JPT and YRI (both with ). Regardless of genome-wide significance threshold, our 1% FDR cutoffs for indicate that the outlying values we identified in our scans were much more likely for sweeps than for neutrality, especially for more distantly related populations, which are unlikely to produce high-magnitude SS-H12 values in the absence of a sweep (Table S2). Supporting this pattern, we observed that the proportion of genic windows >1% FDR cutoff was uniformly higher than the proportion of nongenic windows exceeding the cutoff (Table S2).
Figure 6.
Top outlying shared sweep candidates at RNA- and protein-coding genes in global human populations. The signal peak, including chromosomal position, magnitude, and highlighted window of maximum SS-H12 (left column), as well as the pegas haplotype network for the window (Paradis 2010) are displayed for each candidate. The East Asian JPT and KHV populations experience an ancestral soft sweep at GPHN (top row). The sub-Saharan African populations LWK and YRI share an ancestral hard sweep at RGS18 (second row). The European CEU population experiences a shared sweep with YRI at SPRED3 (third row). The European CEU and East Asian JPT have a convergent sweep at C2CD5, with a different, single high-frequency haplotype present in each population (bottom row). Haplotype networks are truncated to retain only haplotypes with an observed count . The number of haplotypes belonging to the sweeping class (es) is indicated as a fraction, and the Hamming distance (H) between sweeping haplotypes is indicated where applicable. New population abbreviations: Japanese people from Tokyo (JPT); Kinh people of Ho Chi Minh City, Vietnam (KHV); Luhya people from Webuye, Kenya (LWK).
Our observations also reflect the broader pattern that negative SS-H12 values are rare between closely related populations. Indeed, the majority of SS-H12 values at protein-coding genes between populations from the same geographic region are positive, and this distribution shifts toward negative values for more differentiated population pairs, consisting primarily of intermediate-magnitude negative values between the YRI and non-African populations (Figure S31). Our present results are also consistent with the H12-based observations of Harris et al. (2018) in single populations, in that we found a greater proportion of hard sweeps than soft sweeps among outlying sweep candidates in humans, though both were present between all population pairs. We additionally found that the maximum associated with a gene had a significantly negative Spearman correlation with its recombination rate regardless of population comparison, consistent with previous observations (O’Reilly et al. 2008) and highlighting a secondary pattern potentially responsible for observed genome-wide SS-H12 values (Table S3).
The top shared sweep candidates comprised genes that have been described in greater detail in the literature (Bersaglieri et al. 2004; Sabeti et al. 2007; Gerbault et al. 2009; Liu et al. 2013), including LCT and the surrounding cluster of genes on chromosome 2 including MCM6, DARS, and R3HDM1 in the European CEU-GBR (GBR: English and Scottish) pair ( for all; Table S4), reflecting selection for the lactase persistence phenotype. We also recovered the sweep on the light skin pigmentation phenotype in Indo-Europeans (Sabeti et al. 2007; Coop et al. 2009; Basu Mallick et al. 2013; Liu et al. 2013) for comparisons between the CEU population with GBR (Table S4; almost-significant with and ) and GIH (Table S5; , ). Although the selected allele for this sweep is thought to lie within the SLC24A5 gene encoding a solute carrier (Lamason et al. 2005), the CRG100 filter that we applied to our data removed SLC24A5, but preserved the adjacent SLC12A1, which we use as a proxy for the expected signal. Finally, we find KIAA0825 as a top candidate across comparisons between the CEU and GIH (Table S5; ), YRI and CEU (Table S7; , ), YRI and LWK (Table S8, ), JPT and YRI (Table S10; , ), and GIH and YRI (Table S9; , ) populations. Although the function of KIAA0825 has not yet been characterized, it is a previously reported sweep candidate ancestral to the split of African and non-African human populations (Racimo 2016).
Specific sweep candidates of interest:
Across all population comparisons, the top shared sweep candidates at RNA- and protein-coding genes comprised both hard and soft sweeps, yielding a wide range of values. This emphasizes the multitude of sweep histories that have shaped shared variation among human populations. In Figure 6, we highlight four distinct results that capture the diversity of sweeps we encountered in our analysis, each generating wide, well-defined SS-H12 peaks. We first examine GPHN, which we found as an outlying candidate shared soft sweep in the East Asian JPT and KHV (Kinh of Ho Chi Minh City in Vietnam) populations (; Table S12). GPHN encodes the scaffold protein gephyrin, which has been the subject of extensive study due to its central role in regulating the function of neurons, among the many other diverse functions of its splice variants (Ramming et al. 2000; Lencz et al. 2007; Tyagarajan and Fritschy 2014). GPHN has received attention as the candidate of a recent selective sweep ancestral to the human out-of-Africa migration event (Voight et al. 2006; Williamson et al. 2007; Park 2012), which has resulted in the maintenance of two high-frequency haplotypes worldwide (Climer et al. 2015). Although not meeting the genome-wide significance threshold, we see that a large signal peak is centered over GPHN, and the underlying haplotype structure shows two high-frequency haplotypes at similar frequency in the pooled population and in the individual populations (Figure 6, top row).
Next, we recovered RGS18 as a top novel outlying ancestral sweep candidate in the sub-Saharan African LWK and YRI populations. RGS18 occurs as a significant sweep in the YRI population (Harris et al. 2018) and correspondingly displays a single shared high-frequency haplotype between the LWK and YRI populations (Figure 6, second row), matching our assignment of this locus as a hard sweep . RGS18 has been implicated in the development of hypertrophic cardiomyopathy, a leading cause of sudden cardiac death in American athletes of African descent (Maron et al. 2003; Chang et al. 2007). Between the CEU and YRI populations, we found another novel shared sweep at SPRED3 (Figure 6, third row; significant , ), which encodes a protein that suppresses cell signaling in response to growth factors (Kato et al. 2003). Although elevated levels of observed homozygosity at this gene have previously been reported in European and sub-Saharan African populations separately (Granka et al. 2012; Ayub et al. 2013), these observations have not previously been tied to one another. Once again, we see the pattern of an ancestral shared sweep wherein a single haplotype predominates within both populations, but with even noticeably less background variation than what we observed in the aforementioned LWK-YRI comparison.
Finally, we present the novel convergent hard sweep candidate that we uncovered at C2CD5 (also known as CDP138) between the CEU and JPT populations. As expected of a convergent sweep, the SS-H12 peak here is large in magnitude but negative, corresponding to the presence of a different high-frequency haplotype in each population, each of which is also at high frequency in the pooled population. Notably, both haplotypes exist in both populations (Figure 6, bottom row). The protein product of C2CD5 is involved in insulin-stimulated glucose transport (Xie et al. 2011; Zhou et al. 2018), and the insulin response is known to differ between European and East Asian populations (Kodama et al. 2013). Therefore, our discovery of C2CD5 is in agreement with the results of Kodama et al. (2013), and illustrates the importance of differentiating ancestral and convergent sweeps in understanding the adaptive histories of diverse populations.
We also highlight our discovery of PAWR (Figure S33, top) as another outlying novel convergent hard sweep candidate with complementary clinical support, for comparisons between GIH and CEU with YRI. The protein product of PAWR is involved in promoting cancer cell apoptosis, and is implicated in the development of prostate cancer (Yang et al. 2013). Because mutations within and adjacent to PAWR have been specifically implicated in the development of prostate cancer among individuals of African descent (Bonilla et al. 2011), our identification of a candidate convergent sweep at PAWR is consistent with the observation of elevated prostate cancer rates for populations with African ancestry (Kheirandish and Chinegwundoh 2011; Shenoy et al. 2016).
To further validate our identified sweep candidates, we also constructed signal plots and pegas (Paradis 2010) haplotype networks for each highlighted gene outside of Figure 6, grouping these into inferred ancestral (Figure S32) and convergent sweeps (Figure S33). Prominent ancestral sweeps—SPIDR (, CEU-JPT), SLC12A1 (, CEU-GIH), P4HA1, KIAA0825 (, GIH-YRI), and LCT—were characterized by the presence of one or two high-frequency haplotypes in the population pool, divided between either component population in approximately equal proportions. The nonsweeping minor haplotypes also present in the sample generally differed from the sweeping haplotypes at one to two sites, and frequently only observed once (mostly omitted, as we removed haplotypes with less than six copies from the network). Minor haplotypes observed at higher frequencies were often shared between both populations (SLC12A1, LCT, and RGS18) and may also be representative of persistent ancestral polymorphism (Figure S32).
Notably, the sweeping haplotypes observed in convergent sweeps were not always exclusive to either population, and separated by a range of Hamming distances (which we denote H). Whereas the independently sweeping haplotypes within PAWR in CEU-YRI () belonged to either the CEU or YRI populations (Figure S33, top), both sweeping haplotypes of C2CD5 () were visible in both CEU and JPT, suggesting that they were segregating ancestrally to their independent selection following the CEU-JPT split and may be more closely related (Figure 6, bottom). Additionally, we found the selected haplotype of JPT present at low frequency in YRI at EXOC6B (; Figure S33, middle), and similarly the selected haplotype of YRI present in JPT at MPHOSPH9 (; Figure S33, bottom). Even so, we note that for convergently selected loci, each population’s haplotypes tended to cluster together in the network, reflecting the genetic differentiation of the populations.
Detection and classification of shared sweeps from unphased data
Here, we briefly describe the results from our application of the unphased MLG approach, SS-G123. We explored the properties of SS-G123 in equivalent scenarios to our SS-H12 tests by manually merging diploid study individuals’ two haplotypes into MLGs. The ability to identify and classify shared sweeps from unphased data are consequential because nonmodel organisms may not have phased data from which to make inferences. Nonetheless, previous work (Harris et al. 2018) has indicated that distortions in the MLG frequency spectrum can convey the signature of a recent selective sweep.
Overall, SS-G123 performed comparably to SS-H12 at detecting sweeps across identical CEU-GIH and CEU-YRI scenarios (Figures S34–S43), with only slight reductions in power at both the 1 and 5% FPRs for MLGs relative to haplotypes. Reductions in power generally occurred for older sweep times, as MLGs are more diverse than haplotypes (Harris et al. 2018), and so the signal of a sweep erodes more rapidly for MLG data as mutation and recombination events accumulate. Under both the CEU-GIH and CEU-YRI models, we found that the magnitude of SS-G123 was, due to the greater baseline diversity of MLGs, generally smaller than the magnitude of SS-H12, matching trends from results with the single-population statistics H12 and G123 (Harris et al. 2018).
However, SS-G123 values were also shifted toward the negative for all scenarios, including ancestral sweeps, indicating that the unphased approach may not be as adept at classifying shared sweeps as ancestral after identifying them, except for strongly outlying candidates (Figures S11–S14). Thus, we expect that the detection of shared selective sweeps will be possible across the wide variety of organisms for which unphased whole-genome sequence data are available, but urge caution in blindly classifying negative signals as convergent. Classification notwithstanding, the comparable power between SS-H12 and SS-G123 underscores the importance of the latter as a tool (Figures S37, S38, S42, and S43). Crucially, we also found that our empirical analysis of the 1000 Genomes Project dataset (1000 Genomes Project Consortium et al. 2015) in which we paired individuals’ haplotypes into their MLGs yielded congruent results to the phased approach in practice, with similar inclusion and classification of candidates between data types (Tables S13–S21).
The primary difference that we encountered between haplotype and MLG empirical analyses was in the inferred softness of candidate sweeps. We found that, as in the single-population analyses of Harris et al. (2018), a greater proportion of top candidate sweeps in the MLG data were classified as soft than in haplotype data, including both candidates classified as hard sweeps in the haplotype data, and candidates absent from the top 40 haplotype candidates. The explanation for both of these discrepancies, which were minor in scope, lies once again in the greater diversity of MLGs relative to haplotypes. A genomic region with one high-frequency haplotype and one or more intermediate-frequency haplotypes may yield a paired value that most resembles a hard sweep under the ABC approach using haplotypes, but yield an MLG frequency spectrum featuring multiple intermediate-frequency MLGs that may be inferred as a soft sweep. Meanwhile, the greater background diversity of MLG data may allow for the more subtle signatures of soft sweeps to be more readily detectable than in haplotype data. Overall, the rarity of discrepancies between SS-H12 and SS-G123 top candidate lists corroborates the high level of concordance between the power of the two statistics that we found in simulated data.
Discussion
Characterizing the selective sweeps shared between geographically close and disparate populations can provide insights into the adaptive histories of these populations that may be unavailable or obscure when analyzing single populations separately. To this end, we extended the H12 framework of Garud et al. (2015) to identify genomic loci affected by selection in samples composed of individuals from two or more populations. Our approach, SS-H12, has high power to detect recent shared selective sweeps from phased haplotypes, and is sensitive to both hard and soft sweeps. SS-H12 can also distinguish hard and soft sweeps from one another in conjunction with the statistic , thus retaining the most important feature of the single-population approach. Furthermore, SS-H12 has the unique ability to distinguish between sweeps that are shared due to common ancestry (ancestral sweeps), and shared due to independent selective events (convergent sweeps). Analysis with the SS-H12 framework therefore provides a thorough characterization of selection candidates, both previously described and novel, unlike that of comparable methods. In addition, we extended analyses to unphased MLG data as SS-G123, maintaining excellent power in the absence of phased haplotypes, expanding the range of study systems from which we may draw selective sweep inferences.
Power and classification
Because SS-H12 and SS-G123 derive fundamentally from measures of expected homozygosity, they are tailored to detect recent shared selective sweeps. Stronger sweeps are detectable over a wider range of selection start times (t) than weaker sweeps due to their greater distortion of the haplotype frequency spectrum resulting in larger sweep footprints (Gillespie 2004; Garud et al. 2015; Hermisson and Pennings 2017) and larger values of the sweep statistics. However, because stronger sweeps reach fixation sooner than do weaker sweeps, their signals begin to erode sooner, especially for sweeps from larger ν (compare, for example, the center columns of Figure 2, Figure S5, and Figure S6 for ancestral sweeps). Accordingly, there is an inverse relationship between the strength of detectable shared sweeps (s), and the selection start times for which we can detect a sweep. The interaction between t and s is also important for classifying the timing of shared sweeps. Barring rare convergent sweeps on the same haplotype between sister populations, we found that simulated convergent sweeps were reliably identified from the sign of SS-H12 or SS-G123 under scenarios in which they have power to detect shared sweeps (see boxplots of Figure 2, Figure 3, and Figures S5–S8, and classification curves of Figures S11–S14).
For weaker ancestral sweeps, in contrast, negative values of elevated magnitude could emerge if the time of selection t was close to the split time τ for the CEU-GIH model (bottom row of Figure 2, Figure S5, and Figure S6), or for the CEU-YRI model in general (bottom row of Figure 3, Figure S7, and Figure S8), especially for SS-G123 (boxplots of Figures S34–S36 and S39–S41). In the CEU-GIH case, it is likely that the beneficial allele, and its haplotypic background(s), have not risen to high frequency before the ancestral population splits into the modern sampled populations. In the CEU-YRI case, enough time has passed since τ by the time of sampling that extensive population differentiation exists. Thus, in both cases, copies of the beneficial haplotype present in each of the two descendant populations may follow distinct trajectories. Using a smaller analysis window may therefore increase power to detect sweeps with less prominent footprints, but at the risk of misinterpreting elevated signal due to short-range LD as a sweep.
More generally, the strengths and limitations of our methods to identify shared sweeps as ancestral or convergent depend upon the underlying genealogy of the analysis region. In our analyses, we may expect a particular combination of t and s to be readily detectable and classifiable across any demographic history, such as a strong sweep () initiating generations before sampling. Under the CEU-GIH model, this would be an ancestral sweep, while it would be convergent for the CEU-YRI model. Similarly, because we had no power in our simulation experiments to detect weaker () sweeps younger than generations old, we could not detect convergent sweeps in the CEU-GIH model unless their selection coefficient is large. Furthermore, the background haplotypic diversity inherent to different populations’ demographic histories may be highly variable, affecting signal duration and intensity. This meant we could detect ancestral sweeps up to 2000 generations more ancient under the CEU-YRI model than under the CEU-GIH model. In these ways, genealogy constrains which sweeps are identifiable under a particular parameter set. In practice, most outlying shared sweep candidates in humans were ancestral (Tables S4–S21), despite the high power of our approach to detect simulated convergent sweeps. Indeed, convergent sweeps may simply be uncommon because beneficial mutations are rare (Orr 2010). Thus, it should be especially rare for beneficial mutations to independently establish at the same locus across multiple populations, for all but the most strongly selected mutations (Haldane 1927; Kimura 1962; Wilson et al. 2014).
While powerful for detecting shared sweeps, an equally important property of our statistics is that they ignore divergent sweeps, assigning only values of small magnitude in such cases. The ability to eliminate unshared sweeps as potentially outlying signals is important because a sweep in a subset of sampled populations still produces distorted haplotype frequencies between them. This can result in values of (or ) that may spuriously resemble convergent sweeps, yielding values of the uncorrected H12 statistic that are distinct from neutrality (Figures S15 and S16, right column). By applying a correction factor to H12 (Equation 3), we dampened the signals of divergent sweeps for samples drawn from any number of populations K (right columns of Figure 2, Figure 3, Figure S9, and Figure SN1–SN3). As such, the distributions of SS-H12 and SS-G123 generated under divergent sweeps often appears visually no different from neutrality, leaving no possibility of misidentifying divergent sweeps as shared sweeps.
Our ability to detect recent shared sweeps remained consistent across samples composed of populations, which we demonstrate with haplotype results from the generalized mammalian model in the Supplemental Note (Figure S9 and Figure SN1–SN3). Power curves across experiments were nearly identical to one another, regardless of K, and regardless of whether we employed the conservative or grouped approach (see Materials and Methods) for samples. However, we were frequently unable to classify convergent sweeps shared across populations correctly, often assigning when the time of the sweep is more ancient than the most recent population split time but younger than the root of the population tree, due to the presence of internal ancestral sweeps (Figures SN1-SN3, left columns). True ancestral sweeps, in contrast, were unambiguous because in these cases, all populations share identical sweeping haplotypes (Figures SN1–SN3, center columns). Finally, divergent sweeps never produced outlying values of SS-H12, but we observed spuriously elevated power for sweeps shared ancestrally among more populations (Figures SN1–SN3, right columns). To avoid misinterpreting shared sweep signals deriving from sampled populations, we recommend performing follow-up analyses on identified signal peaks to determine the specific populations involved in the sweep.
Similarly to the single-population approach (Garud et al. 2015; Harris et al. 2018), SS-H12 and SS-G123 have power to detect shared soft sweeps, and can assign these as ancestral or convergent. We found that softer sweeps were more difficult to detect than harder sweeps, proportional to ν. Sweeps from larger ν produce smaller haplotype frequency spectrum distortions than do hard sweeps, but trends in the distributions of SS-H12 (Figure 2, Figure 3, and Figure S5–S8) and SS-G123 (Figures S34–S41) were nonetheless consistent between hard and soft sweeps. Our results also indicate that all haplotypes need not be shared between sampled populations in order to yield outlying signals. This is because simulated population split events represented a random sampling of ancestral haplotypes without guaranteeing identical haplotype frequency spectra between descendant sister populations or their ancestor. As an example, we consider a simple hypothetical scenario in which ancestrally sweeping haplotypes are distributed unevenly between two descendant sister populations (Figure S44, bottom-left). A shared haplotype exists at frequency 0.55 in Population 1 (P1), and at 0.45 in Population 2 (P2). Meanwhile, P1 has two exclusive haplotypes at frequencies 0.25 and 0.2, while P2 has exclusive haplotypes at frequencies 0.3 and 0.25; corresponding to ∼50% exclusive haplotypes per population. In this (albeit extreme) scenario, , a positive value lying outside the distributions of neutrality for our all of our models.
Beyond detecting recent shared sweeps with high power, accuracy, and specificity, ours is the only one among comparable methods that can classify shared sweeps as hard or soft from the inferred number of sweeping haplotypes (ν). Using an ABC approach to assign the most likely number of sweeping haplotypes in a genomic window, we found that the classification of recent ancestral sweeps broadly followed that of sweeps in single populations, with smaller corresponding to harder sweeps, and the largest ν associated with the largest (Figure 5, top). Resolving the most probable ν can be challenging depending on the age of the sweep, and so we find that boundaries between ν classes are somewhat irregular within the posterior distribution, especially for the CEU-YRI model. In contrast, convergent sweeps are easily classified as hard or soft due to their necessarily stronger signal relative to ancestral sweeps (Figure 5, bottom). The classification profile of convergent sweeps is distinctly different from that of ancestral sweeps because the strongest hard sweeps will yield two high-frequency haplotypes in the population, corresponding to intermediate values, with soft sweeps generating at either extreme. Thus, we can adeptly classify shared sweeps as hard or soft using the SS-H12 framework across any parameter combination for which we have power (Figure 2, Figure 3 and Figures S5–S8).
Confounding factors and model deviations
SS-H12 displayed an extensive robustness to confounding admixture across scenarios in which a distantly related donor targeted one of the sampled populations (Figure 4 and Figure S19). As this covers a variety of potential cases, and is a fairly common occurrence (Chun et al. 2010; Patterson et al. 2012; Pool et al. 2012; Nedić et al. 2014), we believe SS-H12 may be confidently applied to a wider set of complex demographic scenarios. In contrast, SS-H12 could not properly classify the timing of a sweep passed from one sampled population to its sampled sister through admixture (Supplemental Note Figure SN4). This scenario may be avoided by restricting sampling to only populations that have been separated geographically by a barrier to migration for an appreciable amount of time, making admixture unlikely. Distant-donor admixture most impacted the ability of SS-H12 to detect and classify ancestral sweeps, whereas convergent sweeps remained broadly unobscured and distinct from neutrality except in extreme scenarios (admixture above 30%; Figure 4 and Figure S19, left columns). Admixture here introduces new haplotypes into the target, resulting in differing haplotype frequency spectra between the pair. Lower donor genetic diversity thus expectedly yields a spurious convergent sweep-like pattern, while admixture from a more diverse donor recreates a divergent sweep-like pattern (Figure 4 and Figure S19, middle columns). Overall, the effect of distant-donor admixture is likely to be a reduction in the prominence of SS-H12, which may impact estimates of sweep age and intensity (Malaspinas et al. 2012; Mathieson and McVean 2013; Smith et al. 2018), but without yielding false positive signals (Figure S19, left and center columns).
As with unadmixed samples, SS-H12 for divergent sweeps showed little departure in prominence from neutrality following admixture from a diverged donor (Figure 4, right column). However, we observed a spurious, though not impactful, rise in power when a diverse () donor admixes into the sweeping population at a rate of 10% or more (Figure S19, bottom-right). While our statistics are insulated against picking up these divergent sweeps as outliers due to their small magnitude, we caution that the opposite scenario—admixture from a donor of small size into the nonsweeping population—may resemble a convergent sweep as H12 in the target population, and between populations, rises. SS-H12 does not ignore divergent sweeps in intersister admixture, which results in extensive haplotype sharing that, at any level, yielding positive values of SS-H12 (Supplemental Note Figure SN4). Because the basis for our shared sweep classifications is a quantification of haplotype frequency overlap, intersister admixture is the main confounding scenario for SS-H12. It is therefore prudent to test for evidence of admixture between sampled sister populations before searching for shared sweeps, and also to obtain ecological and paleontological evidence to support the origin of an adaptive haplotype (Seeley 1986; Remigereau et al. 2011; Wogelius et al. 2011; Gallego Romero et al. 2012). Ultimately, admixture was the only confounding factor we tested that could affect SS-H12 values, and only a narrow range of scenarios is likely to do so.
The other major model violation we examined, background selection, accordingly posed a much smaller risk of affecting SS-H12. Background selection results in a loss of polymorphism as deleterious alleles and alleles at nearby linked sites are removed from the population, resulting in an ablation of genetic diversity reminiscent of selective sweeps (Charlesworth et al. 1993, 1995; Seger et al. 2010; Cutter and Payseur 2013; Nicolaisen and Desai 2013; Huber et al. 2016). However, background selection is expected only to reduce levels of neutral polymorphism without driving particular haplotypes to high frequency (Enard et al. 2014). Indeed, our results indicate that background selection could scarcely distort the distribution of SS-H12 values relative to neutrality (Figure S23), because it affects neither H12 (Harris et al. 2018) nor the haplotype frequency spectrum (Harris and DeGiorgio 2019 preprint). Thus, we do not expect that a detailed understanding of background selection in a study system will be required to detect shared sweeps.
Our experiments across common deviations to the basic parameters of the simplified mammalian model—equal sample sizes, simultaneous sweeps, and bifurcating population splits—highlight the variety of scenarios to which we can apply SS-H12 and SS-G123. Our statistics are agnostic to these deviations because none should affect haplotype sharing between populations. Modifying the relative sample sizes for each subpopulation had the effect of changing γ (Equation 2), but this scarcely affects patterns of haplotypic diversity, and therefore power and classification (Figures S20–S22), relative to equal sample sizes (Figure S9). The relative timing of convergent sweeps also did not change their differentiating effect between populations, and so once again we found that power here (Supplemental Note Figure SN5) fit with that of simultaneous convergent sweeps (Figure S9). We can also consider a more complex scenario in which the rate of adaptation in each population differs, as with a nonuniform environment. If the study populations are sampled before the beneficial mutation establishes in each, then we may overlook a true shared sweep as divergent because a subset of populations will show a sweep signature, and a subset will not. This is a limitation of any shared sweep method, however. Finally, we found that the power of SS-H12 to detect and classify sweeps for a star tree with descendants (Supplemental Note Figures SN6 and SN7) matched that under an asymmetric topology (Figure SN2), while more accurately classifying sweeps as ancestral or convergent. SS-H12 can only be misled by nonadaptive changes to the haplotype frequency distribution that affect the level of haplotype sharing between populations, yielding a wide robustness to many common scenarios.
While in our experiments we analyzed only ideal dense polymorphism data with no missing sites, we briefly pause to consider the performance of SS-H12 outside of these conditions. This is especially relevant for SNP array data, which features a lower density of polymorphisms relative to sequencing data. For the single-population statistics, Harris et al. (2018) recommended constructing analysis windows using a SNP-delimited (rather than nucleotide-delimited) approach, wherein windows are defined by the number of SNPs contained within rather than their physical size. Constructing windows in this way ensures the inclusion of sufficient haplotypic variation for inference, and may also confer robustness to demographic processes that reduce diversity locally, such as population bottlenecks (Harris et al. 2018). In the case of missing data, insights from the single-population approach (Harris et al. 2018) suggest that removing sites with >5% missing data (for data missing at random) yields acceptable power. Sites with an extensive number of low-confidence genotypes should also be removed, because such errors can lead to the spurious detection of new haplotypes, which increases background diversity and reduces the magnitude of SS-H12, potentially causing sweeps to be overlooked. Taken together, we suggest that it may be beneficial to employ SNP- rather than nucleotide-delimited windows on datasets with extensive missing data, regardless of whether sites are missing due to sparse sampling or from genotype or sequencing errors.
Discovery and characterization of shared sweeps in humans
The high power, robustness, and flexibility of SS-H12 allowed us to discover outlying sweep candidates in humans that both corroborated previous investigations, and uncovered novel shared sweep candidates. Most importantly, our approach provided inferences about the timing and softness of shared sweeps, yielding enhanced levels of detail about candidates that were until now not directly available. As SS-H12 is the only method that distinguishes between recent ancestral and convergent shared sweeps, our investigation was uniquely able to identify loci at which independent convergent sweeps, though rare, may have played a role in shaping modern patterns of genetic diversity. Among these was EXOC6B (Figure S33, middle row), which produces a protein component of the exocyst (Evers et al. 2014) and has been previously highlighted as a characteristic site of selection in East Asian populations (Baye et al. 2009; 1000 Genomes Project Consortium et al. 2011; Pybus et al. 2014). The shared hard sweep at EXOC6B appeared as convergent between the East Asian JPT and sub-Saharan African YRI populations (Table S10), but as ancestral between all other population pairs—pairs of non-African populations—in which it appeared (Tables S5, S6, S11, and S12). Thus, we believe that a sweep at EXOC6B occurred globally in both African and non-African populations alike, and was not limited to a single region or event.
More broadly, our investigation into sweeps shared between disparate populations also updates existing notions about when during human history particular selective events may have occurred. For example, a sweep at NNT, involved in the glucocorticoid response, has been previously reported in sub-Saharan Africa (Voight et al. 2006; Fagny et al. 2014). As expected, we recovered NNT as an ancestral hard sweep in the comparison between LWK and YRI (Table S8), but additionally in all comparisons between YRI and non-African populations (Tables S7, S9, and S10; genome-wide significant for all but the JPT-YRI pair). Selection at NNT preceded the out-of-Africa event and was not exclusive to sub-Saharan African populations. Another unexpected top outlier was SPIDR (Figure S32, first row), involved in double-stranded DNA break repair (Wan et al. 2013; Smirin-Yosef et al. 2017), and inferred to be a shared candidate among Eurasian populations (Racimo 2016). SPIDR previously appeared as an outlying H12 signal in the East Asian CHB (Han Chinese individuals from Beijing) population (Harris et al. 2018), but, in our present analysis, was shared ancestrally not only between the East Asian KHV and JPT populations (Table S12), but also between JPT and the European CEU (Table S6; ), and the sub-Saharan African LWK and YRI (Table S8) populations. Once again, we see a strong sweep candidate shared among a wider range of populations than previously expected, illustrating the role of shared sweep analysis in amending our understanding of the scope of sweeps in humans worldwide.
In addition to recovering expected and expanded sweep signatures, we also found top outlying ancestral sweep candidates not especially prominent within single populations, emphasizing that localizing an ancestral sweep depends not only on elevated expected homozygosity generating the signal, but highly on the presence of shared haplotypes between populations. Foremost among such candidates was CASC4, a candidate ancestral hard sweep in all comparisons with YRI (Tables S7–S10; genome-wide significant for CEU and GIH with YRI). Because a sweep ancestral to the out-of-Africa event at this cancer-associated gene (Ly et al. 2014; Anczuków et al. 2015) had been previously hypothesized (Racimo 2016), we expected to see it. However, CASC4 does not have a prominent H12 value outside of sub-Saharan African populations, and within YRI is a lower-end outlier (Harris et al. 2018). Despite this, CASC4 is within the top 12 outlying candidates across all comparisons with YRI, and appears as the eighth-most outlying gene in for CEU-JPT (Table S6; ), even though it is not an outlier in either population individually. Similarly, we found PHKB, involved in glycogen storage (Hendrickx and Willems 1996; Burwinkel et al. 1997; Burwinkel and Kilimann 1998), as an ancestral hard sweep of CEU-YRI (Table S7; ) that was not prominent in either population alone, though once again previously inferred to be a sweep candidate to Eurasians (Racimo 2016). We also identified MRAP2, which encodes a melanocortin receptor accessory protein implicated in glucocorticoid deficiency (Chan et al. 2009; Asai et al. 2013), similarly to NNT, as an ancestral hard sweep between the CEU and JPT populations (Table S6; , ), and is not prominent in either CEU or JPT. Thus, our empirical results fit well with the expectation deriving from our power comparison between multiple tests of H12 and a single SS-H12 test (Figures S17 and S18), but we caution that we did not establish global significance between regions for our candidate genes, and are unlikely to have sufficient power to do so after correcting for all comparisons.
An important trend from our empirical analysis was the significantly negative correlation between recombination rate across protein- and RNA-coding genes, and assigned . Outlying sweep candidates were uniformly associated with regions of low recombination, yielding significant correlations for each population pair comparison according to Spearman’s ρ. The most apparent implication for this observation is that we are more likely to observe sweep signals in regions of low recombination because it is within such regions that sweep footprints persist for the longest time. Consequently, the haplotypic signature of a selective sweep should be difficult to elucidate for regions of high recombination, where sweeping haplotypes would rapidly homogenize into the background diversity, leaving only a transient footprint. It may be possible to guard against misinterpreting regions of elevated LD as sweeps, or overlooking sweeps in regions with high recombination, by adjusting the size of the analysis window when computing SS-H12. Following this approach, it would be helpful to use a smaller analysis window where recombination rates are large in order to identify subtle haplotype frequency distortions, and larger windows where recombination rates are low and haplotypic diversity is already expected to be small. Although we did not pursue this strategy, we instead assigned p-values and inferred ν using simulations drawn from a spectrum of recombination rates, which we expect conferred a high degree of robustness to our conclusions.
The assignment of p-values additionally depended upon our inferred population model. Because a reconstruction of the demographic history was required for us to assign p-values, we evaluated the effect of misspecifying the model on significance cutoffs (Figures S45 and S46). To do this, we simulated neutral replicates either under our more accurate “true” smc++-derived histories with population size changes, or under “wrong” histories with identical mean to the true models but with constant population sizes (Figure S46). Model misspecification could potentially impact inferences of significant SS-H12 signals, and this effect depended on the relatedness between sampled populations (Figure S45). For more closely related population pairs (CEU-GBR and JPT-KHV, mean on the order of ), the wrong constant-size model yielded smaller values, corresponding to a less stringent threshold. For more diverged pairs of subpopulations (YRI with CEU, GIH, or JPT, mean on the order of ), an inverse effect occurs, such that the misspecified model becomes too conservative and significant signals may be overlooked. Accordingly, intermediately related populations (CEU-GIH and LWK-YRI, mean on the order of ) may be insulated from the effect of model misspecification. Thus, the selection of a model with parameters derived from the study data are paramount to the proper interpretation of genomic SS-H12 signals within those data.
We conclude our discussion of the empirical analysis by underscoring its practical implications for the analysis of unphased data. Across our simulation experiments, we found that SS-G123 demonstrated power to detect shared sweeps that was wholly concordant with the power of SS-H12 on phased haplotypes (Figures S37, S38, S42, and S43). The area in which SS-G123 appeared to be lacking was in its ability to properly classify the timing of a shared sweep. That is, outside of recent sweeps, SS-G123 was highly susceptible to assigning negative values to ancestral sweeps, thereby misclassifying them as convergent [compare purple (SS-G123) and red (SS-H12) lines within the central columns of Figures S11–S14]. The reason for this disparity in classification lies with the data type itself. Unphased MLGs have a much greater diversity than haplotypes under most scenarios if we assume random mating (Harris et al. 2018). For this reason, the homogeneity among MLGs following a sweep returns to background levels more rapidly than that of haplotypes, leading to across scenarios for which Contrary to these expectations, however, we found that detection and classification with SS-G123 matched that of SS-H12 for a wide majority of candidates across our empirical scans. Ultimately, this indicates that the sweep candidates most likely to pass the significance threshold, likely to be important for adaptation, are those for which phasing does not affect inferences, which underscores the importance of a tool with the ability to make those inferences.
Conclusions
The SS-H12 and SS-G123 frameworks are an important advancement in our ability to contextualize and classify shared sweep events using multilocus sequence data. Whereas prior methods have identified shared sweeps and can do so with high power, some without the need for MLGs or phased haplotypes, the ability to distinguish both hard and soft shared sweeps from neutrality, as well as differentiate ancestral and convergent sweeps, is invaluable for understanding the manner in which an adaptive event has proceeded. Discerning whether a selective sweep has occurred multiple times or only once can provide novel and updated insights into the relatedness of study populations, and the selective pressures that they endured. Moreover, the sensitivity of our approach to both hard and soft sweeps, and our ability to separate one from the other, add an additional layer of clarity that is otherwise missing from previous analyses, and is especially relevant because uncertainty persists as to the relative contributions of hard and soft sweeps in human history (Jensen 2014; Schrider and Kern 2017; Mughal and DeGiorgio 2019). We expect inferences deriving from shared sweep analyses to assist in formulating and guiding more informed questions about discovered candidates across diverse organisms for which sequence data—phased and unphased—exist. As part of this, SS-H12 and SS-G123 may be incorporated into machine learning algorithms that leverage the spatial signature of sweep statistics to construct powerful sweep detection protocols (e.g., Schrider and Kern 2017; Mughal and DeGiorgio 2019). After establishing the timing and softness of a shared sweep, appropriate follow-up analyses can include inferring the age of a sweep (Smith et al. 2018), identifying the favored allele or alleles (Akbari et al. 2018), or identifying other populations connected to the shared sweep. We believe that our approach will serve to enhance investigations into a diverse variety of study systems, and facilitate the emergence of new perspectives and paradigms.
To this end, we provide open-source software (titled SS-X12) to perform scanning window analyses on haplotype input data using SS-H12 or MLG input data using SS-G123, as well as results from our empirical scans and other analyses, within our Dryad repository. SS-X12 provides flexible user control, allowing the input of samples drawn from arbitrary populations K, and the output of a variety of expected homozygosity summary statistics.
Acknowledgments
We thank three anonymous reviewers and editor Nicholas Barton for their helpful comments that improved this manuscript. This work was funded by National Institutes of Health grant R35-GM128590, by National Science Foundation grants DEB-1753489, DEB-1949268, and BCS-2001063, and by the Alfred P. Sloan Foundation. Portions of this research were conducted with Advanced CyberInfrastructure computational resources provided by the Institute for CyberScience at Pennsylvania State University.
Footnotes
Supplemental material available at figshare: https://doi.org/10.25386/genetics.11953632.
Communicating editor: N. Barton
Literature Cited
- 1000 Genomes Project Consortium; Abecasis G. R., Altshuler D., Auton A., Brooks L. D., Durbin R. M. et al. , 2011. A map of human genome variation from population-scale sequencing. Nature 467: 1061–1073. 10.1038/nature09534 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 1000 Genomes Project Consortium;Auton A., Brooks L. D., Durbin R. M., Garrison E. P., Kang H. M. et al. , 2015. A global reference for human genetic variation. Nature 526: 68–74. 10.1038/nature15393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akbari A., Vitti J. J., Iranmehr A., Bakhtiari M., Sabeti P. C. et al. , 2018. Identifying the favored mutation in a positive selective sweep. Nat. Methods 15: 279–282. 10.1038/nmeth.4606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altshuler D., Daly M. J., and Lander E. S., 2008. Genetic mapping in human disease. Science 322: 881–888. 10.1126/science.1156409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anczuków O., Akerman M., Cléry A., Wu J., Shen C. et al. , 2015. SRSF1-regulated alternative splicing in breast cancer. Mol. Cell 60: 105–117. 10.1016/j.molcel.2015.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asai M., Ramachandrappa S., Joachim M., Shen Y., Zhang R. et al. , 2013. Loss of function of the melanocortin 2 receptor accessory protein 2 is associated with mammalian obesity. Science 341: 275–278. 10.1126/science.1233000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayub Q., Yngvadottir B., Chen Y., Xue Y., Hu M. et al. , 2013. FOXP2 targets show evidence of positive selection in European populations. Am. J. Hum. Genet. 92: 696–706. 10.1016/j.ajhg.2013.03.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basu Mallick C., Iliescu F. M., Möls M., Hill S., Tamang R. et al. , 2013. The light skin allele of SLC24A5 in South Asians and Europeans shares identity by descent. PLoS Genet. 9: e1003912 10.1371/journal.pgen.1003912 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baye T. M., Wilke R. A., and Olivier M., 2009. Genomic and geographic distribution of private SNPs and pathways in human populations. Per. Med. 6: 623–641. 10.2217/pme.09.54 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beleza S., Santos A. M., McEvoy B., Alves I., Martinho C. et al. , 2012. The timing of pigmentation lightening in Europeans. Mol. Biol. Evol. 30: 24–35. 10.1093/molbev/mss207 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bersaglieri T., Sabeti P. C., Patterson N., Vanderploeg T., Schaffner S. F. et al. , 2004. Genetic signatures of strong recent positive selection at the lactase gene. Am. J. Hum. Genet. 74: 1111–1120. 10.1086/421051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonhomme M., Chevalet C., Servin B., Boitard S., Abdallah J. et al. , 2010. Detecting selection in population trees: the lewontin and krakauer test extended. Genetics 186: 241–262. 10.1534/genetics.110.117275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonilla C., Hooker S., Mason T., Bock C. H., and Kittles R. A., 2011. Prostate cancer susceptibility loci identified on chromosome 12 in African Americans. PLoS One 6: e16044 10.1371/journal.pone.0016044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burwinkel B., and Kilimann M. W., 1998. Unequal homologous recombination between LINE-1 elements as a mutational mechanism in human genetic disease. J. Mol. Biol. 277: 513–517. 10.1006/jmbi.1998.1641 [DOI] [PubMed] [Google Scholar]
- Burwinkel B., Maichele A. J., Aegenaes Ø., Bakker H. D., Lerner A. et al. , 1997. Autosomal glycogenosis of liver and muscle due to phosphorylase kinase deficiency is caused by mutations in the phosphorylase kinase beta subunit (PHKB). Hum. Mol. Genet. 6: 1109–1115. 10.1093/hmg/6.7.1109 [DOI] [PubMed] [Google Scholar]
- Chan L. F., Webb T. R., Chung T., Meimaridou E., Cooray S. N. et al. , 2009. MRAP and MRAP2 are bidirectional regulators of the melanocortin receptor family. Proc. Natl. Acad. Sci. USA 106: 6146–6151. 10.1073/pnas.0809918106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang Y. C., Liu X., Kim J. D. O., Ikeda M. A., Layton M. R. et al. , 2007. Multiple genes for essential-hypertension susceptibility on chromosome 1q. Am. J. Hum. Genet. 80: 253–264. 10.1086/510918 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaplin G., and Jablonski N. G., 2013. The human environment and the vitamin D compromise: Scotland as a case study in human biocultural adaptation and disease susceptibility. Hum. Biol. 85: 529–552. 10.3378/027.085.0402 [DOI] [PubMed] [Google Scholar]
- Charlesworth B., Morgan M. T., and Charlesworth D., 1993. The effect of deleterious mutations on neutral molecular variation. Genetics 134: 1289–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B., Charlesworth D., and Morgan M. T., 1995. The pattern of neutral molecular variation under the background selection model. Genetics 141: 1619–1632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng X., Xu C., and DeGiorgio M., 2017. Fast and robust detection of ancestral selective sweeps. Mol. Ecol. 26: 6871–6891. 10.1111/mec.14416 [DOI] [PubMed] [Google Scholar]
- Chun Y. J., Fumanal B., Laitung B., and Bretagnolle F., 2010. Gene flow and population admixture as the primary post-invasion processes in common ragweed (Ambrosia artemisiifolia) populations in France. New Phytol. 185: 1100–1107. 10.1111/j.1469-8137.2009.03129.x [DOI] [PubMed] [Google Scholar]
- Clemente F. J., Cardona A., Inchley C. E., Peter B. M., Jacobs G. et al. , 2014. A selective sweep on a deleterious mutation in CPT1A in Arctic populations. Am. J. Hum. Genet. 95: 584–589. 10.1016/j.ajhg.2014.09.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Climer S., Templeton A. R., and Zhang W., 2015. Human gephyrin is encompassed within giant functional noncoding yin–yang sequences. Nat. Commun. 6: 6534 10.1038/ncomms7534 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coop G., Pickrell J. K., Novembre J., Kudaravalli S., Li J. et al. , 2009. The role of geography in human adaptation. PLoS Genet. 5: e1000500 10.1371/journal.pgen.1000500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutter A. D., and Payseur B. A., 2013. Genomic signatures of selection at linked sites: unifying the disparity among species. Nat. Rev. Genet. 14: 262–274. 10.1038/nrg3425 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derrien T., Estellé J., Sola S. M., Knowles D. G., Rainieri E. et al. , 2012. Fast computation and applications of genome mappability. PLoS One 7: e30377 10.1371/journal.pone.0030377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enard D., Messer P. W., and Petrov D. A., 2014. Genome-wide signals of positive selection in human evolution. Genome Res. 24: 885–895. 10.1101/gr.164822.113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evers C., Maas B., Koch K. A., Jauch A., Janssen J. W. G. et al. , 2014. Mosaic deletion of EXOC6B: further evidence for an important role of the exocyst complex in the pathogenesis of intellectual disability. Am. J. Med. Genet. A. 164: 3088–3094. 10.1002/ajmg.a.36770 [DOI] [PubMed] [Google Scholar]
- Fagny M., Patin E., Enard D., Barreiro L. B., Quintana-Murci L. et al. , 2014. Exploring the occurrence of classic selective sweeps in humans using whole-genome sequencing data sets. Mol. Biol. Evol. 31: 1850–1868. 10.1093/molbev/msu118 [DOI] [PubMed] [Google Scholar]
- Fariello M. I., Boitard S., Naya H., SanCristobal M., and Servin B., 2013. Detecting signatures of selection through haplotype differentiation among hierarchically structured populations. Genetics 193: 929–941. 10.1534/genetics.112.147231 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallego Romero I., Basu Mallick C., Liebert A., Crivellaro F., Chaubey G. et al. , 2012. Herders of Indian and European cattle share their predominant allele for lactase persistence. Mol. Biol. Evol. 29: 249–260. 10.1093/molbev/msr190 [DOI] [PubMed] [Google Scholar]
- Garud N. R., and Rosenberg N. A., 2015. Enhancing the mathematical properties of new haplotype homozygosity statistics for the detection of selective sweeps. Theor. Popul. Biol. 102: 94–101. 10.1016/j.tpb.2015.04.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garud N. R., Messer P. W., Buzbas E. O., and Petrov D. A., 2015. Recent selective sweeps in North American Drosophila melanogaster show signatures of soft sweeps. PLoS Genet. 11: e1005004 10.1371/journal.pgen.1005004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerbault P., Moret C., Currat M., and Sanchez-Mazas A., 2009. Impact of selection and demography on the diffusion of lactase persistence. PLoS One 4: e6369 10.1371/journal.pone.0006369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie J. H., 2004. Population Genetics: A Concise Guide, Ed. 2 The Johns Hopkins University Press, Baltimore. [Google Scholar]
- Granka J. M., Henn B. M., Gignoux C. R., Kidd J. M., Bustamante C. D. et al. , 2012. Limited evidence for classic selective sweeps in African populations. Genetics 192: 1049–1064. 10.1534/genetics.112.144071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gravel S., Henn B. M., Gutenkunst R. N., Indap A. R., Marth G. T. et al. , 2011. Demographic history and rare allele sharing among human populations. Proc. Natl. Acad. Sci. USA 108: 11983–11988. 10.1073/pnas.1019276108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gronau I., Hubisz M. J., Gulko B., Danko C. G., and Siepel A., 2011. Bayesian inference of ancient human demography from individual genome sequences. Nat. Genet. 43: 1031–1034. 10.1038/ng.937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haldane J. B. S., 1927. A mathematical theory of natural and artificial selection. V. selection and mutation. Math. Proc. Camb. Philos. Soc. 23: 838–844. 10.1017/S0305004100015644 [DOI] [Google Scholar]
- Haller B. C., and Messer P. W., 2017. SLiM 2: flexible, interactive forward genetic simulations. Mol. Biol. Evol. 34: 230–240. 10.1093/molbev/msw211 [DOI] [PubMed] [Google Scholar]
- Harris A. M., and DeGiorgio M., 2019. A likelihood approach for uncovering selective sweep signatures from haplotype data. bioRxiv. (Preprint posted June 21, 2019). 10.1101/678722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris A. M., Garud N. R., and DeGiorgio M., 2018. Detection and classification of hard and soft sweeps from unphased genotypes by multilocus genotype identity. Genetics 210: 1429–1452. 10.1534/genetics.118.301502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris K., and Nielsen R., 2016. The genetic cost of Neanderthal introgression. Genetics 203: 881–891. 10.1534/genetics.116.186890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartl D. L., and Clark A. G., 2007. Principles of Population Genetics, Ed. 4 Sinauer Associates, Inc., Sunderland, MA. [Google Scholar]
- Hendrickx J., and Willems P. J., 1996. Genetic deficiencies of the glycogen phosphorylase system. Hum. Genet. 97: 551–556. 10.1007/BF02281858 [DOI] [PubMed] [Google Scholar]
- Hermisson J., and Pennings P. S., 2005. Soft sweeps: molecular population genetics of adaptation from standing genetic variation. Genetics 169: 2335–2352. 10.1534/genetics.104.036947 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermisson J., and Pennings P. S., 2017. Soft sweeps and beyond: understanding the patterns and probabilities of selection footprints under rapid adaptation. Methods Ecol. Evol. 8: 700–716. 10.1111/2041-210X.12808 [DOI] [Google Scholar]
- Huber C. D., DeGiorgio M., Hellmann I., and Nielsen R., 2016. Detecting recent selective sweeps while controlling for mutation rate and background selection. Mol. Ecol. 25: 142–156. 10.1111/mec.13351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson R. R., 2002. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18: 337–338. 10.1093/bioinformatics/18.2.337 [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium; Frazer K. A., Ballinger D. G., Cox D. R., Hinds D. A., Stuve L. L. et al. , 2007. A second generation human haplotype map of over 3.1 million SNPs. Nature 449: 851–861. 10.1038/nature06258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen J. D., 2014. On the unfounded enthusiasm for soft selective sweeps. Nat. Commun. 5: 5281 10.1038/ncomms6281 [DOI] [PubMed] [Google Scholar]
- Johnson K. E., and Voight B. F., 2018. Patterns of shared signatures of recent positive selection across human populations. Nat. Ecol. Evol. 2: 713–720. 10.1038/s41559-018-0478-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones B. L., Raga T. O., Liebert A., Zmarz P., Bekele E. et al. , 2013. Diversity of lactase persistence alleles in Ethiopia: signature of a soft selective sweep. Am. J. Hum. Genet. 93: 538–544. 10.1016/j.ajhg.2013.07.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juric I., Aeschbacher S., and Coop G., 2016. The strength of selection against Neanderthal introgression. PLoS Genet. 12: e1006340 10.1371/journal.pgen.1006340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato R., Nonami A., Taketomi T., Wakioka T., Kuroiwa A. et al. , 2003. Molecular cloning of mammalian Spred-3 which suppresses tyrosine kinase-mediated Erk activation. Biochem. Biophys. Res. Commun. 302: 767–772. 10.1016/S0006-291X(03)00259-6 [DOI] [PubMed] [Google Scholar]
- Kheirandish P., and Chinegwundoh F., 2011. Ethnic differences in prostate cancer. Br. J. Cancer 105: 481–485. 10.1038/bjc.2011.273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M., 1962. On the probability of fixation of mutant genes in a population. Genetics 47: 713–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klammer A. A., Park C. Y., and Noble W. S., 2009. Statistical calibration of the SEQUEST XCorr function. J. Proteome Res. 8: 2106–2113. 10.1021/pr8011107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kodama K., Tojjar D., Yamada S., Toda K., Patel C. J. et al. , 2013. Ethnic differences in the relationship between insulin sensitivity and insulin response. Diabetes Care 36: 1789–1796. 10.2337/dc12-1235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamason R. L., Mohideen M. P. K., Mest J. R., Wong A. C., Norton H. L. et al. , 2005. SLC24A5, a putative cation exchanger, affects pigmentation in Zebrafish and humans. Science 310: 1782–1786. 10.1126/science.1116238 [DOI] [PubMed] [Google Scholar]
- Lee K. M., and Coop G., 2017. Distinguishing among modes of convergent adaptation using population genomic data. Genetics 207: 1591–1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lencz T., Lambert C., DeRosse P., Burdick K. E., Morgan T. V. et al. , 2007. Runs of homozygosity reveal highly penetrant recessive loci in schizophrenia. Proc. Natl. Acad. Sci. USA 104: 19942–19947. 10.1073/pnas.0710021104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Librado P., and Orlando L., 2018. Detecting signatures of positive selection along defined branches of a population tree using LSD. Mol. Biol. Evol. 35: 1520–1535. 10.1093/molbev/msy053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Librado P., Gamba C., Gaunitz C., Sarkissian C. D., Pruvost M. et al. , 2017. Ancient genomic changes associated with domestication of the horse. Science 356: 442–445. 10.1126/science.aam5298 [DOI] [PubMed] [Google Scholar]
- Lindo J., Huerta-Sánchez E., Nakagome S., Rasmussen M., Petzelt B. et al. , 2016. A time transect of exomes from a Native American population before and after European contact. Nat. Commun. 7: 13175 10.1038/ncomms13175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X., Ong R. T., Pillai E. N., Elzein A. M., Small K. S. et al. , 2013. Detecting and characterizing genomic signatures of positive selection in global populations. Am. J. Hum. Genet. 92: 866–881. 10.1016/j.ajhg.2013.04.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ly T., Ahmad Y., Shlien A., Soroka D., Mills A. et al. , 2014. A proteomic chronology of gene expression through the cell cycle in human myeloid leukemia cells. eLife 3: e01630 10.7554/eLife.01630 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malaspinas A., Malaspinas O., Evans S. N., and Slatkin M., 2012. Estimating allele age and selection coefficient from time-serial data. Genetics 192: 599–607. 10.1534/genetics.112.140939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marciniak S., and Perry G. H., 2017. Harnessing ancient genomes to study the history of human adaptation. Nat. Rev. Genet. 18: 659–674. 10.1038/nrg.2017.65 [DOI] [PubMed] [Google Scholar]
- Maron B. J., Carney K. P., Lever H. M., Lewis J. F., Barac I. et al. , 2003. Relationship of race to sudden cardiac death in competitive athletes with hypertrophic cardiomyopathy. J. Am. Coll. Cardiol. 41: 974–980. 10.1016/S0735-1097(02)02976-5 [DOI] [PubMed] [Google Scholar]
- Mathieson I., and McVean G., 2013. Estimating selection coefficients in spatially structured populations from time series data of allele frequencies. Genetics 193: 973–984. 10.1534/genetics.112.147611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard Smith J., and Haigh J., 1974. The hitch-hiking effect of a favourable gene. Genet. Res. 23: 23–35. 10.1017/S0016672300014634 [DOI] [PubMed] [Google Scholar]
- Messer P. W., 2013. SLiM: simulating evolution with selection and linkage. Genetics 194: 1037–1039. 10.1534/genetics.113.152181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Messer P. W., and Petrov D. A., 2013. Population genomics of rapid adaptation by soft selective sweeps. Trends Ecol. Evol. 28: 659–669. 10.1016/j.tree.2013.08.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metspalu M., Romero I. G., Yunusbayev B., Chaubey G., Mallick C. B. et al. , 2011. Shared and unique components of human population structure and genome-wide signals of positive selection in South Asia. Am. J. Hum. Genet. 89: 731–744. 10.1016/j.ajhg.2011.11.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mignone F., Gissi C., Liuni S., and Pesole G., 2002. Untranslated regions of mRNAs. Genome Biol. 3: REVIEWS0004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mughal M. R., and DeGiorgio M., 2019. Localizing and classifying adaptive targets with trend filtered regression. Mol. Biol. Evol. 36: 252–270. 10.1093/molbev/msy205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nachman M. W., and Crowell S. L., 2000. Estimate of the mutation rate per nucleotide in humans. Genetics 156: 297–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narasimhan V. M., Rahbari R., Scally A., Wuster A., Mason D. et al. , 2017. Estimating the human mutation rate from autozygous segments reveals population differences in human mutational processes. Nat. Commun. 8: 303 10.1038/s41467-017-00323-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nedić N., Francis R. M., Stanisavljević L., Pihler I., Kezić N. et al. , 2014. Detecting population admixture in honey bees of Serbia. J. Apic. Res. 53: 303–313. 10.3896/IBRA.1.53.2.12 [DOI] [Google Scholar]
- Neyman J., and Pearson E. S., 1928. On the use and interpretation of certain test criteria for purposes of statistical inference: part I. Biometrika 20A: 175–240. [Google Scholar]
- Nicolaisen L. E., and Desai M. M., 2013. Distortions in genealogies due to purifying selection and recombination. Genetics 195: 221–230. 10.1534/genetics.113.152983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Reilly P. F., Birney E., and Balding D. J., 2008. Confounding between recombination and selection, and the Ped/Pop method for detecting selection. Genome Res. 18: 1304–1313. 10.1101/gr.067181.107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr H. A., 2010. The population genetics of beneficial mutations. Philos. Trans. R. Soc. Lond. B Biol. Sci. 365: 1195–1201. 10.1098/rstb.2009.0282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paradis E., 2010. pegas: an R package for population genetics with an integrated–modular approach. Bioinformatics 26: 419–420. 10.1093/bioinformatics/btp696 [DOI] [PubMed] [Google Scholar]
- Park L., 2012. Linkage disequilibrium decay and past population history in the human genome. PLoS One 7: e46603 10.1371/journal.pone.0046603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N., Moorjani P., Luo Y., Mallick S., Rohland N. et al. , 2012. Ancient admixture in human history. Genetics 192: 1065–1093. 10.1534/genetics.112.145037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payseur B. A., and Nachman M. W., 2000. Microsatellite variation and recombination rate in the human genome. Genetics 156: 1285–1298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pendleton A. L., Shen F., Taravella A. M., Emery S., Veeramah K. R. et al. , 2018. Comparison of village dog and wolf genomes highlights the role of the neural crest in dog domestication. BMC Biol. 16: 64 10.1186/s12915-018-0535-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pennings P. S., and Hermisson J., 2006a Soft sweeps II: molecular population genetics of adaptation from recurrent mutation or migration. Mol. Biol. Evol. 23: 1076–1084. 10.1093/molbev/msj117 [DOI] [PubMed] [Google Scholar]
- Pennings P. S., and Hermisson J., 2006b Soft sweeps III: the signature of positive selection from recurrent mutation. PLoS Genet. 2: e186 10.1371/journal.pgen.0020186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peyrégne S., Boyle M. J., Dannemann M., and Prüfer K., 2017. Detecting ancient positive selection in humans using extended lineage sorting. Genome Res. 27: 1563–1572. 10.1101/gr.219493.116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pool J. E., Corbett-Detig R. B., Sugino R. P., Stevens K. A., Cardeno C. M. et al. , 2012. Population genomics of Sub-Saharan Drosophila melanogaster: African diversity and non-African admixture. PLoS Genet. 8: e1003080 10.1371/journal.pgen.1003080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Przeworski M., 2002. The signature of positive selection at randomly chosen loci. Genetics 160: 1179–1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pybus M., Dall’Olio G. M., Luisi P., Uzkudun M., Carreño-Torres A. et al. , 2014. 1000 Genomes Selection Browser 1.0: a genome browser dedicated to signatures of natural selection in modern humans. Nucleic Acids Res. 42: D903–D909. 10.1093/nar/gkt1188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Racimo F., 2016. Testing for ancient selection using cross-population allele frequency differentiation. Genetics 202: 733–750. 10.1534/genetics.115.178095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramming M., Kins S., Werner N., Hermann A., Betz H. et al. , 2000. Diversity and phylogeny of gephyrin: tissue-specific splice variants, gene structure, and sequence similarities to molybdenum cofactor-synthesizing and cytoskeleton-associated proteins. Proc. Natl. Acad. Sci. USA 97: 10266–10271. 10.1073/pnas.97.18.10266 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remigereau M., Lakis G., Rekimah S., Leveugle M., Fontaine M. C. et al. , 2011. Cereal domestication and evolution of branching: evidence for soft selection in the Tb1 orthologue of pearl millet (Pennisetum glaucum [L.] R. Br.). PLoS One 6: e22404 10.1371/journal.pone.0022404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riddle M. R., Aspiras A. C., Gaudenz K., Peuß R., Sung J. Y. et al. , 2018. Insulin resistance in cavefish as an adaptation to a nutrient-limited environment. Nature 555: 647–651. 10.1038/nature26136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruths T., and Nakhleh L., 2013. Boosting forward-time population genetic simulators through genotype compression. BMC Bioinformatics 14: 192 10.1186/1471-2105-14-192 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabeti P. C., Reich D. E., Higgins J. M., Levine H. Z. P., Richter D. J. et al. , 2002. Detecting recent positive selection in the human genome from haplotype structure. Nature 419: 832–837. 10.1038/nature01140 [DOI] [PubMed] [Google Scholar]
- Sabeti P. C., Varilly P., Fry B., Lohmueller J., Hostetter E. et al. , 2007. Genome-wide detection and characterization of positive selection in human populations. Nature 449: 913–918. 10.1038/nature06250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakharkar M. K., Chow V. T. K., and Kangueane P., 2004. Distributions of exons and introns in the human genome. In Silico Biol. 4: 387–393. [PubMed] [Google Scholar]
- Schiffels S., and Durbin R., 2014. Inferring human population size and separation history from multiple genome sequences. Nat. Genet. 46: 919–925. 10.1038/ng.3015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrider D. R., and Kern A. D., 2017. Soft sweeps are the dominant mode of adaptation in the human genome. Mol. Biol. Evol. 34: 1863–1877. 10.1093/molbev/msx154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schweinsberg J., and Durrett R., 2005. Random partitions approximating the coalescence of lineages during a selective sweep. Ann. Appl. Probab. 15: 1591–1651. 10.1214/105051605000000430 [DOI] [Google Scholar]
- Seeley R. H., 1986. Intense natural selection caused a rapid morphological transition in a living marine snail. Proc. Natl. Acad. Sci. USA 83: 6897–6901. 10.1073/pnas.83.18.6897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seger J., Smith W. A., Perry J. J., Hunn J., Kaliszewska Z. A. et al. , 2010. Gene genealogies strongly distorted by weakly interfering mutations in constant environments. Genetics 184: 529–545. 10.1534/genetics.109.103556 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shenoy D., Packianathan S., Chen A. M., and Vijayakumar S., 2016. Do African-American men need separate prostate cancer screening guidelines? BMC Urol. 16: 19 10.1186/s12894-016-0137-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M., 1991. Inbreeding coefficients and coalescence times. Genet. Res. 58: 167–175. 10.1017/S0016672300029827 [DOI] [PubMed] [Google Scholar]
- Smirin-Yosef P., Zuckerman-Levin N., Tzur S., Granot Y., Cohen L. et al. , 2017. A biallelic mutation in the homologous recombination repair gene SPIDR is associated with human gonadal dysgenesis. J. Clin. Endocrinol. Metab. 102: 681–688. [DOI] [PubMed] [Google Scholar]
- Smith J., Coop G., Stephens M., and Novembre J., 2018. Estimating time to the common ancestor for a beneficial allele. Mol. Biol. Evol. 35: 1003–1017 (erratum: Mol. Biol. Evol. 35: 1821). 10.1093/molbev/msy006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snir A., Nadel D., Groman-Yaroslavski I., Melamed Y., Sternberg M. et al. , 2015. The origin of cultivation and proto-weeds, long before neolithic farming. PLoS One 10: e0131422 10.1371/journal.pone.0131422 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahata N., Satta Y., and Klein J., 1995. Divergence time and population size in the lineage leading to modern humans. Theor. Popul. Biol. 48: 198–221. 10.1006/tpbi.1995.1026 [DOI] [PubMed] [Google Scholar]
- Terhorst J., Kamm J. A., and Song Y. S., 2017. Robust and scalable inference of population history from hundreds of unphased whole genomes. Nat. Genet. 49: 303–309. 10.1038/ng.3748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyagarajan S. K., and Fritschy J., 2014. Gephyrin: a master regulator of neuronal function? Nat. Rev. Neurol. 15: 141–156. 10.1038/nrn3670 [DOI] [PubMed] [Google Scholar]
- Voight B. F., Kudaravalli S., Wen X., and Pritchard J. K., 2006. A map of recent positive selection in the human genome. PLoS Biol. 4: e72 (erratum: PLoS Biol. 4: e154); [corrigenda: PLoS Biol. 5: e147 (2007)]. 10.1371/journal.pbio.0040072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan L., Han J., Liu T., Dong S., Xie F. et al. , 2013. Scaffolding protein SPIDR/KIAA0146 connects the Bloom syndrome helicase with homologous recombination repair. Proc. Natl. Acad. Sci. USA 110: 10646–10651. 10.1073/pnas.1220921110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watterson G. A., 1975. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 7: 256–276. 10.1016/0040-5809(75)90020-9 [DOI] [PubMed] [Google Scholar]
- Williamson S. H., Hubisz M. J., Clark A. G., Payseur B. A., Bustamante C. D. et al. , 2007. Localizing recent adaptive evolution in the human genome. PLoS Genet. 3: e90 10.1371/journal.pgen.0030090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson B. A., Petrov D. A., and Messer P. W., 2014. Soft selective sweeps in complex demographic scenarios. Genetics 198: 669–684. 10.1534/genetics.114.165571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wogelius R. A., Manning P. L., Barden H. E., Edwards N. P., Webb S. M. et al. , 2011. Trace metals as biomarkers for eumelanin pigment in the fossil record. Science 333: 1622–1626. 10.1126/science.1205748 [DOI] [PubMed] [Google Scholar]
- Wright S., 1943. Isolation by distance. Genetics 28: 114–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S., 1951. The genetical structure of populations. Ann. Eugen. 15: 323–354. 10.1111/j.1469-1809.1949.tb02451.x [DOI] [PubMed] [Google Scholar]
- Xie X., Gong Z., Mansuy-Aubert V., Zhou Q. L., Tatulian S. A. et al. , 2011. C2 domain-containing phosphoprotein CDP138 regulates GLUT4 insertion into the plasma membrane. Cell Metab. 14: 378–389. 10.1016/j.cmet.2011.06.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Weedon M. N., Purcell S., Lettre G., Estrada K. et al. , 2011. Genomic inflation factors under polygenic inheritance. Eur. J. Hum. Genet. 19: 807–812. 10.1038/ejhg.2011.39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang K., Shen J., Xie Y., Lin Y., Qin J. et al. , 2013. Promoter-targeted double-stranded small RNAs activate PAWR gene expression in human cancer cells. Int. J. Biochem. Cell Biol. 45: 1338–1346. 10.1016/j.biocel.2013.03.022 [DOI] [PubMed] [Google Scholar]
- Yuan X., Miller D. J., Zhang J., Herrington D., and Wang Y., 2012. An overview of population genetic data simulation. J. Comput. Biol. 19: 42–54. 10.1089/cmb.2010.0188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Q. L., Song Y., Huang C., Huang J., Gong Z. et al. , 2018. Membrane trafficking protein CDP138 regulates fat browning and insulin sensitivity through controlling catecholamine release. Mol. Cell. Biol. 38: pii: e00153-17. 10.1128/MCB.00153-17 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
To make the results of our work maximally accessible, we have uploaded all relevant scripts, as well as all outputs from analyses, into a Dryad repository (https://datadryad.org/stash/share/tqLw6lJN0uqtyfvj46INlHHGg0nAbFKmsxiFVJ0a0SM). Our upload is divided into directories labeled to match the broad directions of our research in this manuscript: simulations using the smc++-derived CEU-GIH and CEU-YRI models, simulations using the simplified mammalian model for sampled populations, admixture model simulations, background selection simulations, misspecified model simulations, simulations to infer ν, simulations to assign p-values, and scans of the 1000 Genomes data. Outside of the latter two batteries of simulations, we provide all of the raw SLiM-simulated outputs in addition to analyses on those simulations. For simulations to infer ν and p-value simulations, we retain only the summary statistics from windows of maximum signal for each replicate because each scenario featured at least replicates. Our summary files condense those simulations into single, more manageable, documents for reader reference. In addition to simulations and scripts, we have also included the builds of ms and SLiM used for simulations, and our SS-X12 software package. We affirm that the results of all analyses deriving from our data, using the scripts, replicates, and summary files within our Dryad repository, are present within this manuscript’s figures and tables. Supplemental materials, consisting of Tables S1–S21, Figures S1–S46, and Supplemental Note Figures SN1–SN7, are available online through FigShare. Supplemental material available at figshare: https://doi.org/10.25386/genetics.11953632.