Supervised machine learning for diagnostic classification from large-scale neuroimaging datasets

Abstract

There are growing concerns about the generalizability of machine learning classifiers in neuroimaging. In order to evaluate this aspect across relatively large heterogeneous populations, we investigated four disorders: Autism spectrum disorder (N=988), Attention deficit hyperactivity disorder (N=930), Posttraumatic stress disorder (N=87) and Alzheimer’s disease (N=132). We applied 18 different machine learning classifiers (based on diverse principles) wherein the training/validation and the hold-out test data belonged to samples with the same diagnosis but differing in either the age range or the acquisition site. Our results indicate that overfitting can be a huge problem in heterogeneous datasets, especially with fewer samples, leading to inflated measures of accuracy that fail to generalize well to the general clinical population. Further, different classifiers tended to perform well on different datasets. In order to address this, we propose a consensus-classifier by combining the predictive power of all 18 classifiers. The consensus-classifier was less sensitive to unmatched training/validation and holdout test data. Finally, we combined feature importance scores obtained from all classifiers to infer the discriminative ability of connectivity features. The functional connectivity patterns thus identified were robust to the classification algorithm used, age and acquisition site differences, and had diagnostic predictive ability in addition to univariate statistically significant group differences between the groups. A MATLAB toolbox called Machine Learning in NeuroImaging (MALINI), which implements all the 18 different classifiers along with the consensus classifier is available from Lanka et al. (Lanka, et al., 2019) The toolbox can also be found at the following URL: https://github.com/pradlanka/malini.

1. Introduction

The identification of many neurological disorders is based on subjective diagnostic criteria. The development of objective diagnostic tools is a work in progress in the promising field of neuroimaging. Univariate between-group differences in neuroimaging between healthy controls and clinical populations are not yet sufficiently predictive of disease states at the individual level. For automated disorder/disease diagnosis, a machine learning classifier is trained to model the relationship between features extracted from brain imaging data and the labels of individuals in the training dataset (the labels are typically determined via clinical assessment by a licensed clinician), and the model is then used to predict the diagnostic label of a new and unseen subject drawn from a test dataset. However, there are many challenges to this paradigm which include: (i) Lack of availability of large clinical imaging datasets, (ii) Challenges in generalizing results across study populations, (iii) Difficulty in identifying reliable image-based biomarkers which are robust to progress and maturation of the disorder, and (iv) Variability in classifier performance. Many of these issues are interrelated. In fact, the ultimate goal for machine learning based diagnostic classification is to achieve high classification accuracy, in unseen data with varying characteristics (Kelly, Biswal, Craddock, Castellanos, & Milham, 2012). So, to be useful in clinical settings, machine learning classifiers should be generalizable to the wider population. This can be achieved using larger samples that are aggregated by including data from several imaging sites (Huf, et al., 2014). To summarize, the utility of machine learning classifiers as clinical diagnostic tools, depends on them achieving high accuracies in unseen observations in samples representative of the disease populations, using reliable and valid ways to estimate classification performance, that are representative of how such diagnostic tools will be deployed in real-word scenarios.

The main reason for the failure of identification of precise neuroimaging-based biomarkers for various disorders, despite high accuracies reported in many neuroimaging studies, is that many of these studies use small, biologically homogenous samples, and therefore, generalizing their results to larger heterogeneous clinical populations is difficult (Huf, et al., 2014; Nielsen, et al., 2013; Arbabshirani, Plis, Sui, & Calhoun, 2017; Schnack & Kahn, 2016). In fact, results by Arbabshirani et al. (2017) as well as Schnack & Kahn (2016) indicate that the classification accuracy decreases even with increased sample size in multi-site data as compared to smaller single-site data sets. Single study analyses in which the training and the test data are from the same acquisition site give higher classification accuracies than when they are from distinct imaging sites (Nielsen, et al., 2013). A classifier that works well on a particular dataset might fail to discriminate the classes with good accuracy on a different dataset sharing the same clinical diagnosis (Huf, et al., 2014). These prior findings indicate that a classifier may achieve high accuracy in a given data set even with cross-validation, but the accuracy may drop significantly when the classifier is used on a more general p copulation which was not used in cross-validation, as was observed with autism (Chen, et al., 2015). Generalizability of the classifiers cannot be assessed using only a few samples from a single site, but can be shown by including data from various imaging sites. Classifiers which perform well on small training sets generalize poorly, and hidden correlations in the training and validation sets might lead to overoptimistic performance of the classifier (Foster, Koprowski, & Skufca, 2014). This is also borne out by the observation that the overall performance accuracy decreases with sample size (Schnack & Kahn, 2016; Arbabshirani, Plis, Sui, & Calhoun, 2017). Hence, investigators should be extremely cautious in interpreting over-optimistic classification performance results from small datasets.

Classification across heterogeneous populations with considerable variation in demographic and phenotypic profiles, although desirable for generalizability, is extremely challenging, particularly when neuroimaging data is pooled from multiple acquisition sites (Demirci, et al., 2008). Variance introduced in the data due to scanner hardware, imaging protocols, operator characteristics, demographics of the regions and other factors that are acquisition site specific, can affect the classification performance (Schnack & Kahn, 2016). Thus, the neuroimaging-based biomarkers identified must be reliable across imaging sites and age ranges to be useful clinically.

Given the difficulties in disorder/disease classification with multisite studies, the appropriate selection of reliable and sensitive features associated with the underlying disorder/disease is the primary motivating factor in our choice of resting-state functional connectivity (RSFC). RSFC measures the spontaneous low-frequency fluctuations between remote regions in the brain in baseline functional magnetic resonance imaging (fMRI) data, and is typically estimated using the Pearson’s correlation coefficient. This approach has been used extensively to characterize the functional architecture of the brain in both healthy and clinical populations. The reliability and validity of RSFC measures across subjects and scanning sites is of prime importance in order to be useful in disorder/disease classification for improving screening and diagnostic accuracy. RSFC has been shown to have moderate to high reliability and reproducibility across healthy (Chou, Panych, Dickey, Petrella, & Chen, 2012; Shehzad, et al., 2009; Choe, et al., 2015; Guo, et al., 2012; Wang, et al., 2011; Anderson, Ferguson, Lopez-Larson, & Yurgelun-Todd, 2011; Birn, et al., 2013; Braun, et al., 2012; Meindl, et al., 2009), clinical (Pinter, et al., 2016; Somandepalli, et al., 2015), pediatric (Somandepalli, et al., 2015), and elderly (Marchitelli, et al., 2016; Orban, et al., 2015) populations. It has also been shown to have long-term test-retest reliability (Fiecas, et al., 2013; Liang, et al., 2012; Shah, Cramer, Ferguson, Birn, & Anderson, 2016). RSFC is altered in clinical populations such as attention deficit hyperactivity disorder (ADHD), depression, autism, schizophrenia, post-traumatic stress disorder (PTSD) and Alzheimer’s disease (AD). Hence there is growing optimism in the field that modulations in RSFC can help us understand the pathogenesis behind several neurological and psychiatric disorders due to its sensitivity to changes in development, aging, and disease progression. These factors, combined with the ability to standardize protocols, have paved the way for data aggregation across multiple sites, leading to increased statistical power and the generalizability of the findings, and have catapulted RSFC into increasing prominence for diagnostic classification. Given the relatively lower prevalence of certain disorders along with the costs and time associated with aggregating large datasets, the efficiency of data pooling from multiple sites is critical. RSFC protocols are simple to run with little overhead, and hence, it has been implemented in different imaging protocols employing various clinical populations. Also, resting-state fMRI (Rs-fMRI) does not require subjects in uncooperative clinical populations to comply with task instructions, and this has given rise to considerable interest in the use of Rs-fMRI in patients with brain disorders (Horwitz & Rowe, 2011).

With the advent of big data initiatives such as autism brain imaging database (ABIDE), where a large amount of data is collected from multiple sites, there is renewed optimism for reliable and validated disorder/disease classification (Huf, et al., 2014). Generalizability of classifier performance can be increased, by avoiding overfitting, when we have large training data sizes. Another consequence of such big data initiatives and exploratory data analyses is that reliable and repeatable studies for testing novel hypotheses about the identification of relevant clinical biomarkers has taken ground (Kang, Caffo, & Liu, 2016). In the current study we used RSFC measures for diagnostic classification using 18 different classifiers in 4 clinical populations: (i) Autism brain imaging data exchange (ABIDE) for autism spectrum disorder (ASD), (ii) ADHD-200 dataset for attention deficit hyperactivity disorder (ADHD), (iii) PTSD data which were acquired at the Auburn MRI research center for post-concussion syndrome (PCS) and posttraumatic stress disorder (PTSD) and, (iv) Alzheimer’s disease neuroimaging initiative (ADNI) for mild cognitive impairment (MCI) and Alzheimer’s disease (AD). These disorders and datasets were chosen due to the the following factors. Three of the datatsets including ABIDE, ADHD-200, and ADNI are open datasets easily accessable to researchers. Consequently, there are a lot of papers on diagnostic classification using these three datasets. In addition, ABIDE and ADHD-200 datasets have more than 900 subjects which are relatively large datasets, especially in neuroimaging. Finally, the PTSD dataset was acquired in-house at a single acquisition site and each subject was scanned twice. This allowed us to contrast multi-site data sets with single site datasets. These properties of the datasets allowed us to be able to test the generalizability of classifiers under various conditions: (a) Using various disorders whose etiologies are likely different, (b) Using both smaller and larger size of datasets, (c) Using data obtained from both multiple sites as well as single-site, and finally, (d) Using both homogeneous and heterogeneous samples from the population. It should however be noted that several of these factors we plan to study in this paper may be interdependent, and it may not be possible to cleanly attribute the observed effects in classification accuracy into their constituent factors in some cases.

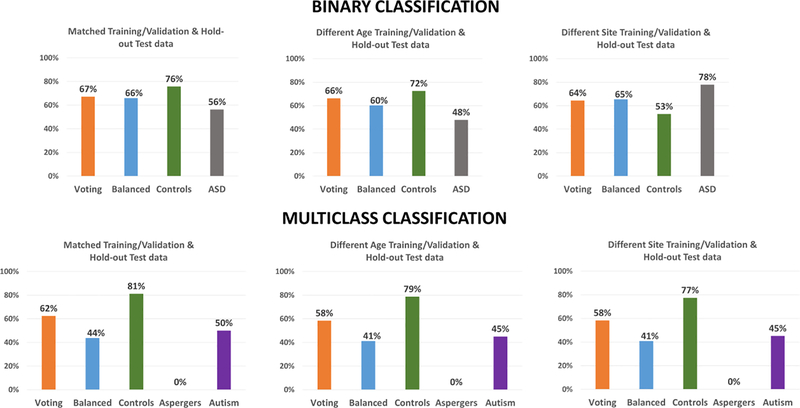
There are four primary goals of this paper. The first goal is to understand the generalizability of machine learning classifiers in the presence of disorder/disease and population heterogeneity, variability in disorder/disease across age, and variations in data caused by multisite acquisitions. We report an optimistic estimate of cross-validation accuracy and an unbiased estimate of performance on a completely independent and blind hold-out test dataset. The entire datasets were split into training/validation, and hold-out test data (with both splits containing both controls and clinical populations) and the cross-validation accuracy was estimated using the training/validation data by splitting it further into training data and validation data. The hold-out test datasets were constructed under three different scenarios: (i) subjects with different, non-overlapping age range compared to training/validation data, (ii) subjects drawn from different imaging sites compared to training/validation data and, (iii) training/validation and hold-out test data matched on all demographics including age as well as acquisition site. We hypothesized that testing our classifiers on homogenous populations could give us optimistic estimates of classifier performance, which might not generalize well to the real-world classification scenarios encountered in the clinic. Therefore, by comparing a holdout test data with the same disorder/disease diagnosis and matched in age and acquisition site as well as unmatched to the training/validation data, would give us a better idea of generalizability and robustness of the classifiers under more challenging classification scenarios.

The second goal is to understand how overfitting can occur in the context of machine learning applied to neuroimaging-based diagnostic classification, whether in feature selection or performance estimation. We demonstrate how smaller datasets might give unreliable estimates of classifier performance which could lead to improper model selection further leading to poor generalization across the larger population. Using ABIDE (N=988) and ADNI (N=132) datasets as examples of large and comparatively smaller datasets, we explore how large variation in the estimate of classification performance in relatively smaller datasets could affect the selection of optimal models and thereby prevent generalization.

The third goal of our paper was to combine multiple classifiers to build a consensus classifier which could transcend the inductive biases of any individual classifier and thus be robust and less sensitive to its assumptions about the underlying mapping between connectivity features and the diagnosed labels. Thus, using multiple classifiers along with consensus classifier could eliminate the possibility that accuracy differences observed between training/validation and hold-out test datasets in unmatched scenarios as an artifact of any single classifier. Using multiple classifiers helps us understand the predictive power of the features and could also help identify which classifiers or class of classifiers give consistently better performance compared to others. Since, a comparison of performance of so many classifiers, has not been done before in the context of neuroimaging, we think such a comparison could be of use to others by helping them choose the appropriate classifier for similar endeavors.

The final goal of this study is to understand how specific functional connectivity patterns encode disorder/disease states and might possess predictive ability (as opposed to conventionally reported statistical separation) to distinguish between health and disease in novel individual subjects. Unlike in some other applications where the final classification performance is more important than identifying discriminative features, in neuroimaging, the goal of identifying discriminative features is equally, if not more important than the classification performance, as it can gives us valuable insight into dysfunctional connectivity patterns in the diseased populations. We set out to identify these connectivity patterns which were not only statistically separated, but also were important for classification irrespective of age mismatch, acquisition site mismatch or the type of classifier used. These connectivity patterns must, therefore, be relatively robust to the age and acquisition site variations, and their predictive ability must not be limited to a single classifier or a particular group of classifiers. In order to accomplish this, we propose feature ranking from multiple classifiers and data splits to construct a single score for the predictive ability of the connectivity features which can potentially be useful in clinical settings.

To achieve our goals, we applied 18 machine learning classifiers based on different principles including probabilistic/Bayesian classifiers, tree-based methods, kernel based methods, a few architectures of neural networks and nearest neighbor classifiers to RSFC metrics derived from ABIDE, ADNI, ADHD-200 and PCS/PTSD datasets described above. Seven of the 18 classifiers were implemented in a feature reduction framework called Recursive cluster elimination (RCE) (Deshpande, et al., 2010). We also built a consensus classifier which leverages the classifying power of all these classifiers to give reliable and robust predictions on the hold-out test dataset. Though many of the issues raised are well known, there is a disconnect between the fact that the issues raised are well known in literature, and yet, in practice, research reports with inflated cross-validation accuracies continue to be published in neuroimaging. Therefore, we want to directly address these issues and provide an open source software such that best practices are adopted.

2. Materials and methods

2.1. Data

2.1.1. Autism spectrum disorder (ASD)

ASD in a heterogeneous neurodevelopmental disorder in children characterized by impaired social communication, repeated behaviors, and restricted interests. With a relatively high prevalence of 1 in 68 children, it is one of the most common developmental disorders in children (CDC, 2014). According to DSM-V, ASD encompasses several disorders previously considered distinct including autism and Asperge’s syndrome (American Psychiatric Association, 2013). Asperge’s syndrome is considered to be a milder form of ASD, with patients in the higher functioning end of the spectrum. Autism is associated with large scale network disruptions of brain networks (Maximo, Cadena, & Kana, 2014; Gotts, et al., 2012; Di Martino, et al., 2014), thus making these clinical groups excellent candidates for diagnostic classification using RSFC.

Resting state fMRI data from 988 individuals from the autism brain imaging data exchange (ABIDE) database (Di Martino, et al., 2014) was used for this study. The imaging data were acquired from 15 different acquisition sites and consists of 556 healthy controls, 339 subjects diagnosed with autism, and 93 with Asperge’s syndrome. The distribution of the data used in this study with the acquisition site can be found in Table 1. Each subject’s information was fully anonymized and was approved by the local Institutional Review Boards of the respective data acquisition sites. More details about the data including scanning parameters can be obtained from http://fcon_1000.proiects.nitrc.org/indi/abide/index.html.

Table 1.

The site distribution for the autism brain imaging data exchange (ABIDE) dataset used in our study

Imaging Site	Controls	Asperger’s	Autism	Total
CALTECH	19	0	13	33
CMU	13	0	14	27
KKI	33	11	11	55
LEUVEN	35	0	29	64
MAX-MUN	33	22	2	57
NYU	105	21	53	179
OLIN	36	0	0	36
PITT	27	0	30	57
SBL	15	7	2	24
SDSU	22	7	3	32
TRINITY	25	7	10	42
UCLA	45	0	54	99
UM	77	10	55	142
USM	43	0	57	100
YALE	28	8	6	42
Total Subjects	556	93	339	988

Note. CALTECH, California Institute of Technology; CMU, Carnegie Mellon University; NYU, NYU Langone Medical Center; KKI, Kennedy Krieger Institute; MAX-MUN, University of Ludwig Maximilians University Munich; PITT, Pittsburgh School of Medicine; SDSU, San Diego State University; OLIN, Olin Institute of Living at Hartford Hospital; UCLA, University of California, Los Angeles; LEUVEN, University of Leuven; TRINITY, Trinity Centre for Health Sciences; USM, University of Utah School of Medicine; YALE, Yale Child Study Center; UM, University of Michigan; SBL, Social Brain Lab

2.1.2. Attention deficit hyperactivity disorder (ADHD)

ADHD is one of the most common neurodevelopmental disorders in children with a childhood prevalence ratio as high as 11%, with significant increases in diagnoses every year (Visser, et al., 2014). ADHD diagnoses can be categorized into three subtypes based on the symptoms exhibited, including ADHD-I (inattention) for persistent inattention, ADHD-H (hyperactive/impulsive) for hyperactivity-impulsivity and ADHD–C (combined) for a combination of both symptoms. There has been a massive increase in research efforts for automated detection of ADHD due to the ADHD-200 competition in 2011 (Consortium, 2012). Although there are standardized approaches to diagnose subtypes of ADHD, there is evidence of multiple etiologies that, while they present as similar clinically, will have unique neurologic underpinnings (Curatolo, D’Agati, & Moavero, 2010).

Nine hundred and thirty subjects were selected from the ADHD-200 dataset, which was used for the ADHD-200 challenge (Consortium, 2012). The sample consists of 573 healthy controls, 208 subjects with ADHD-C, 13 subjects with subtype ADHD-H, and 136 subjects with ADHD-I. Imaging data for a few subjects were not included, as they did not pass the quality control thresholds. The subjects were scanned at seven different acquisition sites as shown in Table 2. The acquisition parameters and other information about the scans be obtained from http://fcon_1000.proiects.nitrc.org/indi/adhd200/

Table 2.

The site distribution for the attention deficit hyperactivity disorder-200 (ADHD-200) data across the seven imaging sites used in our study

Imaging Site	Controls	ADHD -C	ADHD -H	ADHD-I	Total
Peking University	143	38	1	63	245
Kennedy Krieger Institute	69	19	1	5	94
NeuroIMAGE Sample	37	29	6	1	73
New York University Child Study Center	110	95	2	50	257
Oregon Health & Science University	70	27	3	13	113
University of Pittsburgh	94	0	0	4	98
Washington University	50	0	0	0	50
Total Subjects	573	208	13	136	930

Note. We did not include the data from Brown University in our study since their diagnostic labels were not released; ADHD-C, attention deficit hyperactivity disorder-combined; ADHD-H, attention deficit hyperactivity disorder-hyperactive/impulsive; ADHD-I, attention deficit hyperactivity disorder-inattentive

2.1.3. Post-traumatic stress disorder (PTSD) & post-concussion syndrome (PCS)

PTSD is a debilitating condition which develops in individuals exposed to a traumatic or a life-threatening situation. The estimated lifetime prevalence of PTSD among adult Americans is 6.8% (Kessler, et al., 2005). PCS consists of a set of symptoms that occur after a concussion from a head injury. PTSD is highly prevalent in individuals who sustain a traumatic brain injury, especially combat veterans. Such subjects display overlapping symptoms of both PCS and PTSD. Head injuries and traumatic experiences in the battlefield could be the main reasons for an unusually high prevalence rate of PTSD in combat veterans with a prevalence of 12.1% in Gulf war veteran population (Kang, Natelson, Mahan, Lee, & Murphy, 2003) and 13.8% in military veterans deployed in Afghanistan and Iraq during Operation Enduring Freedom and Operation Iraqi Freedom (Tanielian, Jaycox, & eds, 2008). Unfortunately, despite the serious nature of the problem, the current methods for diagnosis of the disorders rely on subjective reporting and clinician-administered interviews. An objective assessment of these disorders using image-based biomarkers could improve diagnostic accuracy and assessment of PTSD and PCS. One limitation of this data set is that PTSD has subtypes defined by symptom clusters, and severity of symptoms can evolve temporally (e.g., months and years post-trauma). As such, there is likely to be significant heterogeneity in neurologic underpinnings within any given sample of patients with PTSD.

While the three other datasets used in this study are publicly available, PTSD/PCS dataset was acquired in-house. Eighty-seven active duty male US Army soldiers were recruited to participate in this study from Fort Benning, GA and Fort Rucker, AL, USA. In the recruited subjects, 28 were combat controls, 17 were diagnosed with only PTSD, while 42 were diagnosed with both PCS and PTSD. All subject groups were matched for age, race, education and deployment history. The subjects were diagnosed as having PTSD if they had no history of mild traumatic brain Injury (mTBI), or symptoms of PCS in the past five years, with scores > 38 on the PTSD Checlist-5 (PCL5), and <26 on Neurobehavioral Symptom Inventory (NSI). Subjects with medically documented mTBI, post-concussive symptoms, and scores ≥ 38 on PCL5 and ≥ 26 on NSI were grouped as PCS & PTSD. The procedure and the protocols in this study were approved by the Auburn University Institutional Review Board (IRB) and the Headquarters U.S. Army Medical Research and Material Command, IRB (HQ USAMRMC IRB).

The participants were scanned in a Siemens 3T MAGNETOM Verio Scanner (Siemens, Erlangen, Germany) with a 32-channel head coil at Auburn University MRI Research Center. The participants were instructed to keep their eyes open and fixated on a small white cross on a screen with a dark background. A T2* weighted multiband echo-planar imaging (EPI) sequence was used to acquire two runs of resting state data in each subject with the following sequence parameters: TR=600ms, TE=30ms, FA=55°, multiband factor=2, voxel size= 3×3×5 mm³ and 1000 time points. Brain coverage was limited to the cerebral cortex, subcortical structures, midbrain and pons, with the cerebellum excluded.

2.1.4. Mild cognitive impairment (MCI) & Alzheimer’s disease (AD)

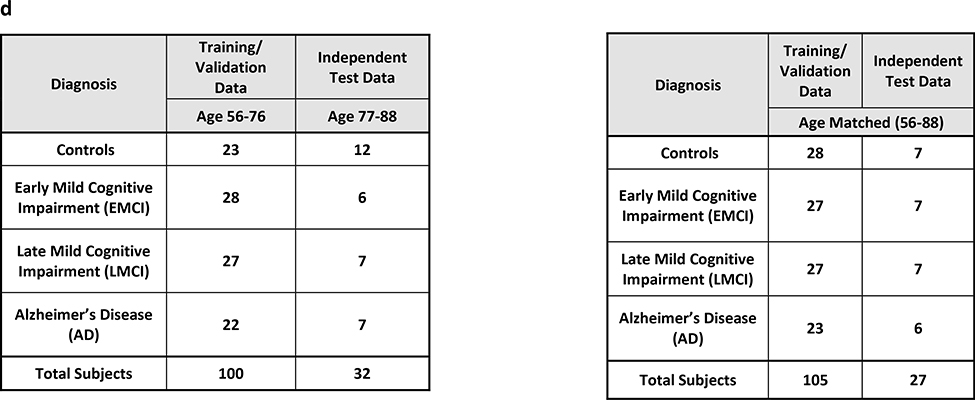
MCI can be defined as greater than the normal cognitive decline for a given age, but it does not significantly affect the activities of daily life (Gauthier, et al., 2006). It has a prevalence ranging from 3% to 19 % in adults older than 65 years. AD on the other hand, does significantly affect daily activities of the person. It is the most common neurodegenerative disorder in adults aged 65 and older. It is characterized by cognitive decline, intellectual deficits, memory impairment and difficulty in social interactions. As a large percentage of MCI patients slowly progress to Alzheimer’s disease, the boundaries separating healthy aging from early/late MCI and AD are not very precise leading to diagnostic uncertainty in the disease status (Albert, et al., 2011). Therefore, classifying MCI from AD and healthy older controls is extremely crucial and is particularly challenging. Resting-state functional brain imaging data of 132 subjects were obtained from the Alzheimer’s disease neuroimaging initiative (ADNI) database. The sample consists of subjects in various stages of cognitive impairment and dementia, including 34 subjects with early mild cognitive impairment (EMCI), 34 with late mild cognitive impairment (LMCI), 29 with AD and finally 35 matched healthy controls. More information about the data used for this study along with the image acquisition parameters can be obtained from http://adni.loni.usc.edu/.

2.2. Processing of the Rs-fMRI data

Standard preprocessing pipeline for Rs-fMRI data was implemented using Data Processing Assistant for Resting-State fMRI Toolbox (DPARSF) (Yan & Zang, 2010). The preprocessing pipeline consisted of removal of first five volumes, slice timing correction, volume realignment to account for head motion, co-registration of the T1-weighed anatomical image to the mean functional image, nuisance variable regression which included linear detrending, mean global signal, white matter and cerebrospinal fluid signals and 6 motion parameters. After nuisance variable regression, the data were normalized to the MNI template. The blood-oxygen-level-dependent (BOLD) time series from every voxel in the brain was deconvolved by estimating the voxel-specific hemodynamic response function (HRF) using a blind deconvolution procedure to obtain the latent neural signals (Wu, et al., 2013). The data were then temporally filtered with a band pass filter of bandwidth 0.01–0.1 Hz. Mean time series were extracted from 200 functionally homogeneous brain regions as defined by the CC200 template (Craddock, James, Holtzheimer, Hu, & Mayberg, 2012). After extracting the timeseries, functional connectivity (FC) between the 200 regions was calculated as the Pearson’s correlation coefficient between all region pairs giving us a total of 19,900 FC values. These were then used as features for the classification procedure. For ADHD and PTSD datasets, we did not have whole brain coverage. Therefore, we obtained time series from just 190 regions and 125 regions, respectively. The number of FC paths were accordingly lower for these datasets.

2.3. Data splits for training/validation and hold-out test data

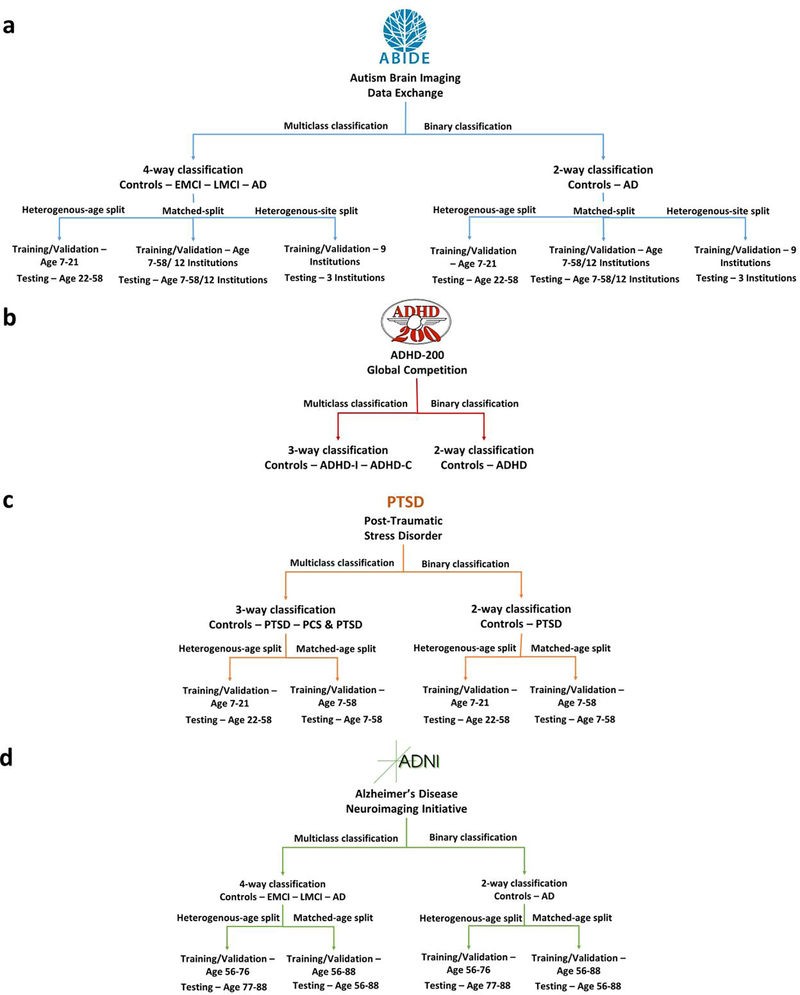
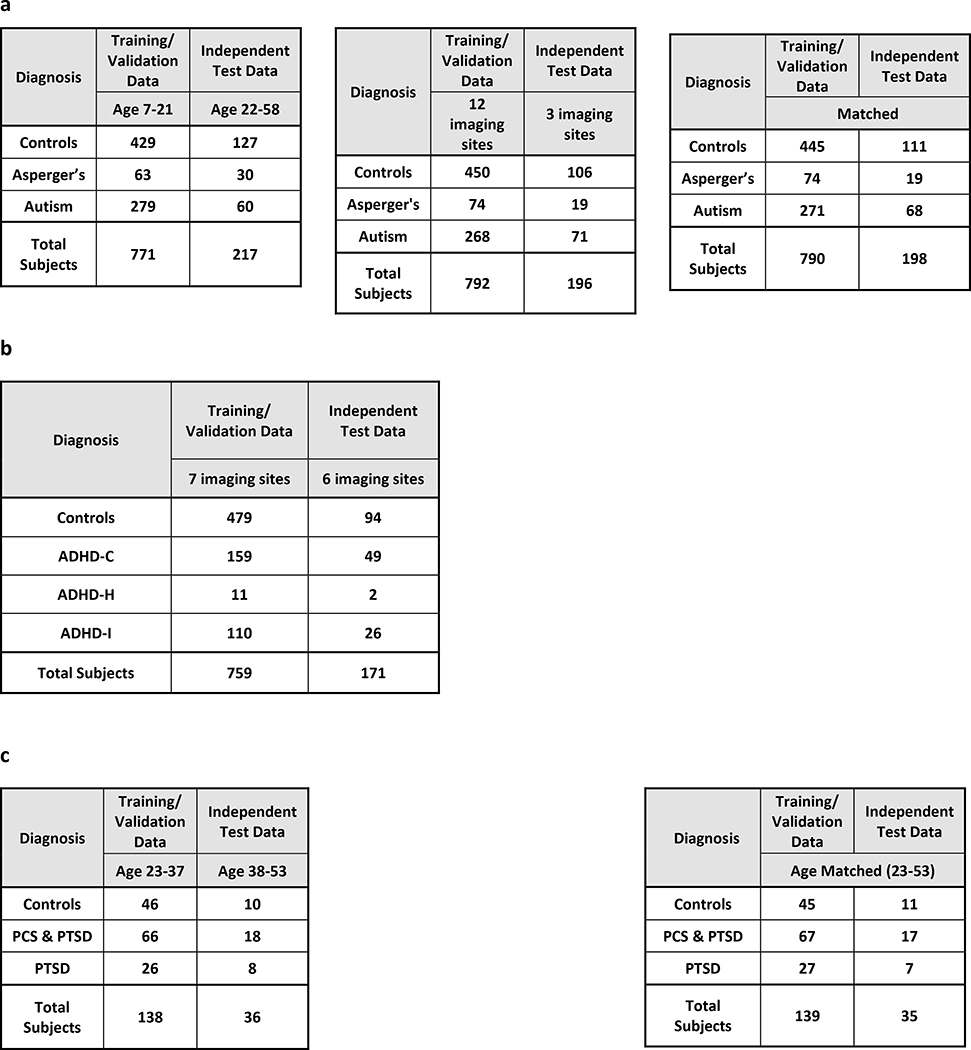
In order to test the generalizabllity of the classifier models, we split all Imaging data into two components. Approximately, 80% of the data was used for training/validation, and the remaining 20% was used as a hold-out test data set (We aimed for an 80–20 split between the training/validation and the hold-out test data. Since we are splitting based on the age and the acquisition site, the ratio is not exact). The training/validation data as a percentage of the total data ranged from 75.8% to 80.2% for various splits for various datasets. More information can be obtained from Table 3. The training/validation datasets were split even further for cross-validation in order to estimate the classifier models as we explain later. However, the hold-out test datasets were not used in cross-validation; instead, they were used only once with the classifier models obtained from cross-validation to obtain truly unbiased test accuracy on completely unseen data. In a few splits, the training/validation and test data came from homogeneous populations, i.e. they were matched for age and acquisition site. In some other splits, the training/validation and hold-out test data were not matched, i.e. they had different age range or acquisition site. With matched data, it is important to note that training/validation and the hold-out test data were matched in age, race, education and gender. In the unmatched splits, age/acquisition site was unmatched, while race, gender, education and acquisition site/age, respectively, were matched. This was done to ensure that only the factor of interest, either age or acquisition site, differed between training/validation and test data in the unmatched splits. All these splits on the four datasets are summarized in Fig. 1 and will be elaborated below. The age-splits in some cases may seem unreasonable as there is a wide difference in age-ranges between the training/validation and the hold-out test datasets considering brain plasticity and maturation as we age. But the primary purpose on such splits was that we wanted to see, whether the patterns learned by the classifier about the underlying disorder generalize to an independent sample with a different age group sharing the same diagnosis. In essence, we wanted to see which classifier could perform reliably well even under such “worst-case” extreme age-mismatch scenarios.

Table 3.

The data distributions for training/validation and hold-out test data for the age and imaging site splits for a autism brain imaging data exchange (ABIDE) dataset, b attention deficit hyperactivity disorder-200 (ADHD-200) dataset, c post-traumatic stress disorder (PTSD) dataset, and d Alzheimer’s disease neuroimaging initiative (ADNI) dataset

Note. ADHD-C, attention deficit hyperactivity disorder-combined; ADHD-H, attention deficit hyperactivity disorder-hyperactive/impulsive; ADHD-I, attention deficit hyperactivity disorder-inattentive; PCS, post-concussion syndrome

Fig. 1.

The age and imaging site split for the training/validation and the test data both for binary and multiclass classification scenarios. a For the ABIDE dataset, we had age- and site-matched splits as well as unmatched splits for both 2-way and 4-way classifications. In the first split, subjects from an age range of 23–37 years were used in training/validation data and the subjects from the age range 38–53 years formed the hold-out test data. Second, we performed an imaging site split wherein the data from the 12 imaging sites (PITT, OLIN, SDSU, TRINITY, UM, USM, CMU, LEUVEN, NYU, MAXMUN, CALTECH, SBL) were used for the training/validation data while the rest of the 3 imaging sites (Yale, KKI, UCLA) were used as a hold-out test dataset. In the third split, training/validation and hold-out test data were matched for age and acquisition site. b For ADHD we directly used the training/validation and hold-out test data provided by the ADHD-200 Consortium for binary and multiclass classification. c For binary and 3-way classification of the PTSD dataset, we followed an age split in which the training/validation data contained subjects from an age range of 23–37 years while the hold-out test data contained subjects from the age range 38–53 years. This was then compared with a matched training/validation data and hold-out test data with subjects in the age range of 23–53 years. d For both 2-way and 4-way classification of ADNI dataset, we split the entire data by age wherein the training/validation data contained subjects from an age range of 56–76 years while the hold-out test data contained subjects from the age range 77–88 years. This scenario was compared with a matched training/validation data and hold-out test data with subjects in the age range of 56–88 years

ABIDE

We split the ABIDE data into two heterogeneous sets for training/validation and testing, with differences in age group and imagining site: (i) The first heterogeneous split had the training/validation data from age range 7 −21 years while the holdout test data had both ASD and healthy controls in the age range 22–58 years. (ii) For the second split, the training validation data came from 12 imaging sites which participated in the study. The hold-out test data was drawn from the remaining three institutions. (iii) We also had a matched split with data for training/validation and testing drawn from the same age range and institutions. Since the ABIDE data has healthy controls and two subgroups of ASD in autism and Asperge’s syndrome, we performed both binary and multiclass classification with each of the three splits, giving us a total of six splits. The distribution of the subjects in each split is shown in Table 3a.

ADHD-200

The ADHD-200 global competition was structured in a way that training/validation data with diagnostic labels were first provided to the public and many groups around the world submitted their predictions on unlabeled hold-out test data dataset. The organizers of the competition assessed the performance of the classification tools on the hold-out test data set based on the predicted diagnostic labels submitted by the groups. Following the completion of the competition, the labels for hold out test dataset was also publicly released. Therefore, we used the training/validation and hold-out test datasets originally provided by the organizers of the competition and no further splits were performed on the data by age or by acquisition site, as was done for other datasets used in this study. This also helps us stay true to the spirit of the ADHD-200 Global Competition to some extent. We performed binary classification between Controls and ADHD (data from all ^{3 ADHD} subgroups were combined) as well as a three-way classification between controls, ADHD-C, and ADHD-I. ADHD-H was left out in multiclass classification because only 11 subjects with ADHD-H were present in the data. The data distributions for the training/validation and hold i-out test data is shown in Table 3b.

PTSD

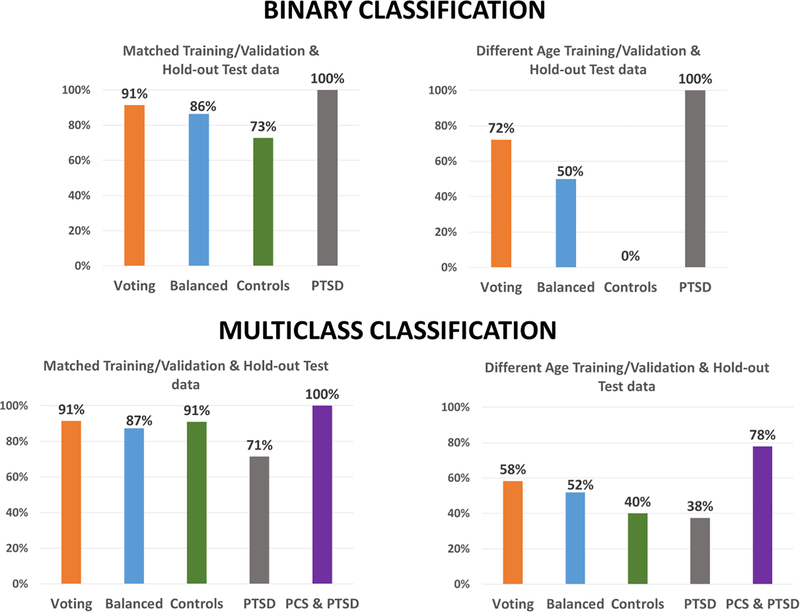
Since the imaging data for PTSD was collected solely at our research site (Auburn University MRI Research Center), we could not test the effects of the performance accuracy due to site variability. We performed binary (Controls vs. PTSD) as well as 3-way classification with Controls vs. PTSD vs. PCS & PTSD. Subjects in the age range from 23–37 years were used in training/validate data and ages 38–53 were used in the hold-out test data for the heterogeneous split. Age matched training/validation and test data were also used. These two splits were used for each of the two classification scenarios (binary and 3-way), giving us a total of four splits. It is noteworthy that we had two runs from each of the 87 subjects in this dataset and we considered each run as a separate subject. Therefore, effectively, we had 174 subjects in this dataset. The data distributions of splits are shown in Table 3c.

ADNI

ADNI data contains subjects at various stages of cognitive impairment. Therefore, we tested a 4way classification between healthy adults, EMCI, LMCI and AD. We also performed binary classification using just healthy adults and AD subjects at the extreme ends of the spectrum. We tested the effect of age heterogeneity on the classification performance with subjects from the age range 56–76 years chosen for training/validation data and 77–88 years selected for hold-out test data. We also had a homogeneous split with training /validation and hold-out test data chosen randomly from the entire dataset with the age range of 56–88 years. The data distributions of each of the classes in these splits are shown in Table 3d.

We made no effort to balance the classes with unbalanced sample sizes in the four data sets because: (i) We wanted to identify classifiers which are robust to differences in class occurrences in the training data and, (ii) The number of healthy subjects are usually far greater than the number of subjects with disorders in neuroimaging databases which are assembled retrospectively. While concerted efforts to acquire large and homogenized balanced datasets are currently underway (Miller, et al., 2016), it will be many years before they become publicly available.

2.4. Classification procedure

The number of features obtained by resting state functional connectivity metrics are usually orders of magnitude greater than the number of subjects/samples available. Due to the “curse of dimensionality,” when using high dimensional data, overfitting is a huge concern because the underlying distribution may be under-sampled (Mwangi, Tian, & Soares, 2014; Demirci, et al., 2008; Guyon & Elisseeff, 2003). Having an excess number of features compared to the number of data samples might lead to overfitting and give us poor generalization on the test data (Pereira, Mitchell, & Botvinick, 2009; Mwangi, Tian, & Soares, 2014). The most useful strategies to deal with this issue include collecting more data, adding domain knowledge about the problem to the model or reduce the number of features, while ideally preserving class-discriminative information. Therefore, feature selection is a necessary step either before classification or as a part of the classification procedure, given the sample size of current neuroimaging databases. Most existing feature selection methods can be grouped into filter and wrapper methods.

Filter methods are independent of the classification strategy. A simple univariate score such as a T-score can be used to rank the features and the top ranked features can be utilized for classification (Craddock, Holtzheimer, Hu, & Mayberg, 2009). Although computationally quick, this univariate approach does not take into consideration the relationships between different features and the classifier performance when retaining features.

A wrapper method selects subsets of features which give good classification performance and contain class-discriminative information. Hence the classification procedure is embedded with feature selection in the wrapper method framework. A combination of wrapper and filter methods have been shown to perform well with minimum resources (Deshpande, et al., 2010; Deshpande, Wang, Rangaprakash, & Wilamowski, 2015; Deshpande, Libero, Sreenivasan, Deshpande, & Kana, 2013). Therefore, we have adopted this strategy in the current study. As our filter method, we used a two-sample t-test/ANOVA and selected the features whose means were significantly different between the groups (p<0.05, FDR corrected), after controlling for confounding factors such race, gender, and education for the age unmatched splits. However, for the age-matched splits, age was also controlled for along with race, gender, and education. When selecting significant features in the age-unmatched splits, age was not included because including it in the model would have removed age-related variance from the data.

Rs-fMRI data was then divided into training/validation data and hold-out test data with approximately 80% of the data used for training and validation, and the remaining 20% of the data was used as a separate hold-out test dataset as was mentioned in the previous section on the data splits. In many cases, the training/validation data and hold-out test data differed in a few factors as mentioned previously such as age and acquisition site. As mentioned above, an initial “feature-filtering” was performed wherein only the connectivity paths that were significantly different between the groups (p<0.05, FDR corrected) in the training/validation data were retained (after controlling for head motion, age, race, and education) thereby reducing the number of features from 19,100 to around 1000. No statistical tests were performed on the independent hold-out test data to avoid introducing bias. Therefore, the features with p<0.05 (FDR corrected) in the training/validation dataset were also removed from the hold-out test dataset. Please note that the hold-out test dataset was not used in feature or model selection, and thus, can be expected to give an unbiased estimate of the generalization accuracy. This is contrary to the cross-validation accuracy estimate because using t-test filtering in reducing features on the entire training/validation data will lead to optimistic accuracy estimates given that the training data and the validation data are not completely separated. Even if a t-test was not performed on the validation data during cross-validation, cross-validation accuracy, by definition, is the average accuracy obtained from different splits. Therefore, it does not provide a conservative estimate of the classifier’s performance in a clinical diagnostic classification scenario. To further reduce the number of features while retaining discriminative information, some of the classifiers were embedded in the recursive cluster elimination (RCE) framework (Deshpande, et al., 2010) for feature section (Fig. S1). As we describe later, some of the classifiers had some form of feature selection embedded within them, and hence, such methods were implemented without the RCE framework (Fig. S2).

2.4.1. Recursive cluster elimination (RCE) framework

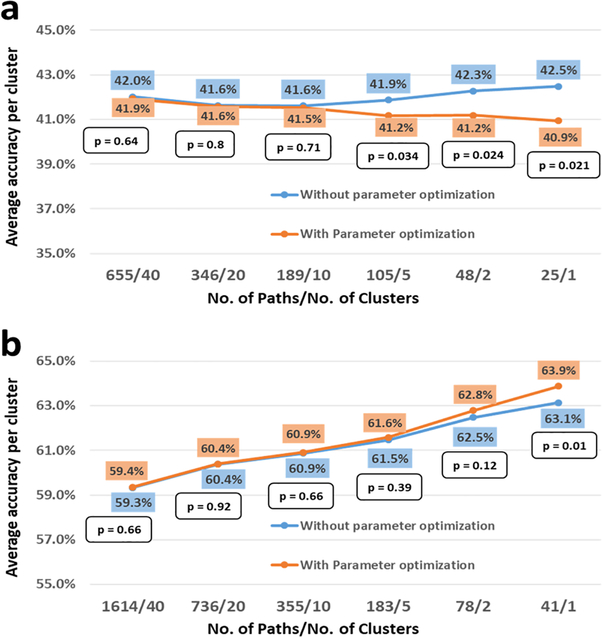
RCE is a heuristic method for identifying a subset of features that have class-discriminative information. RCE is a wrapper method that combines K-means feature clustering with a machine learning classifier to score the discriminative ability of clusters of features, helps retain only features with good discriminative power, and remove the ones without any discriminative power (Deshpande, et al., 2010; Yousef, Jung, Showe, & Showe, 2007). RCE exploits the fact that features (functional connectivity paths in our case) are often correlated with each other, and hence, their discriminative abilities can be ascertained together by clustering the feature space. This provides an order of magnitude increase in speed compared to eliminating each feature individually (Yousef, Jung, Showe, & Showe, 2007). We implemented classifiers in a nested cross-validation (CV) procedure, with the inner CV loop performing feature selection via RCE, and the outer CV loop was used for performance estimation (Fig. S1). We first started with all features after t-test filtering, and clustered these features using the k-means algorithm. The correlation coefficient was used as the distance metric while clustering. Each cluster of features was then used to train a machine learning classifier, and a score was assigned to the cluster based on the performance of the cluster on the validation data. The clusters were ranked according to their classification performance, the clusters with lowest scores were eliminated, and the features in the remaining clusters were merged. This process was iteratively repeated until any further removal of clusters decreased the classification accuracy. This ensured that the best set of feature clusters were identified. This optimal set of feature clusters for each k-fold and partitioning of data of the CV loop, and the final decision surface (or hyper-plane in higher dimension), which gave the best CV performance were saved and used for calculating the accuracy from hold-out test data. For each repetition, a different model, with distinct hyperparameters and features were selected. These models were then used to assess the CV accuracy in the outer k-fold. This ensured that separation was maintained between feature selection by RCE and performance estimation.

Using FC features from training/validation data, classification accuracy was calculated using repeated 6-fold CV. The classifier models obtained from the differences in the partitioning of the training data (repeats × folds) were saved. Test accuracy was calculated on the independent hold-out test data using the saved classifier models by a voting procedure. Each classifier would vote towards a decision on test subjects (accuracy was the percentage of correct votes). This is the voting test accuracy reported. The w/o voting accuracy refers to the mean accuracy and standard deviation for the test data obtained by each of the individual 600 classifier models obtained in each iteration during the cross-validation. To examine the validity of the classifier models, as well as the classification procedure, we first tested them using simulated data by systematically changing the separation between the groups and plotting the classification accuracy. More information on the performance of the classifier on simulated data can be found in the section-2 of Supplementary Information.

2.4.2. Classifier Models

We used a number of classifier models to address the issues in performance estimation and generalizability so that our results are not specific to any particular classifier or type of classifiers. The classifiers we implemented can be broadly divided into the following categories (i) Probabilistic/Bayesian methods: Gaussian naïve Bayes (GNB), linear discriminant analysis (LDA), quadratic discriminant Analysis (QDA), sparse logistic regression (SLR), ridge logistic regression (RLR), (ii) Kernel methods: linear and radial basis function (RBF)-kernel support vector machines (SVM), relevance vector machine (RVM), (iii) Artificial neural networks: MLP-Net (multilayer perceptron neural net), FC-Net (fully connected neural net), ELM (extreme learning machine), LVQNET (linear vector quantization net), (iv) Instance-based learning: k-nearest neighbors (KNN), (v) Decision tree based ensemble methods: bagged trees, boosted trees, boosted stumps, random forest, rotation forest. A brief introduction to the machine learning classifiers used in this paper, can be found in section-1 of Supplementary Information. For classifiers with hyper-parameters in them that needed to be optimized, we performed a grid search to estimate an optimum value. Therefore, it may be possible to further optimize these parameters using more advanced methods. However, a concern with fine-tuning the parameters and testing a large number of models in cases with limited data is that it might lead to overfitting (Rao, Fung, & Rosales, 2008). All the classifiers were implemented in MATLAB environment (Natick, MA). Also note that in this paper, the terms parameters and weights are used interchangeably and refer to values optimized during the learning process whereas the term hyperparameter refers to values that are set before the learning process begins. A toolbox implementing these classifiers to classify subjects into either controls or clinical groups can be obtained from Lanka et al. (Lanka, et al., 2019). The toolbox can also be found at the following URL: https://github.com/pradlanka/malini.

We implemented linear- &RBF-kernel SVM, GNB, LDA, QDA, KNN and ELM in the RCE framework. Many other classifiers we used, such as SLR, RLR, RVM, FC-NN and MLP-NN have built in regularization to control model complexity. Ensemble methods such as bagged trees, random forests, boosted stumps, boosted trees, and rotation forests are not as sensitive to classification problems with a large number of features. Therefore, we did not implement classifiers with built-in regularization as well as ensemble methods in the RCE-framework. KNN was implemented both within and outside the RCE-framework.

2.5. Classification performance metrics

Since many of the datasets which are used in this study are unbalanced in class labels (i.e. each class contains an unequal number of instances), it is important to investigate individual class accuracies. In such cases where one class has more observations in the dataset than the other class, the classifier reports a high accuracy even if the classifier just assigns the majority class label to all instances in the test dataset (Demirci, et al., 2008). In these cases, the overall/unbalanced accuracy is not indicative of the actual performance of the classifier. Therefore, in addition to presenting the overall/unbalanced accuracy, we also report individual class accuracies as well as the balanced accuracy. The individual class accuracies report the ratio of correctly classified instances of a particular class to the total number of instances of the class in the data. The mean of individual class accuracies obtained from both the training/validation data and the hold-out test dataset represents the balanced CV accuracy and the balanced hold-out test accuracy, respectively.

For all the classification scenarios aforementioned, we report the following: (i) The CV accuracy and its standard deviation (in parenthesis), (ii) CV class accuracies of the individual groups, (iii) the balanced CV accuracy obtained by the mean of individual CV class accuracies, (iv) hold-out test accuracy by voting (unbalanced hold-out test accuracy), (v) mean hold-out test accuracy, which is obtained by using mean of the test accuracies calculated from individual classifier models and its standard deviation (in parenthesis), (vi) individual class accuracies of the groups obtained from the hold-out test data, and (vii) the balanced hold-out test accuracy as an average of individual class hold-out test accuracies. A schematic illustrating the derivation of the classification performance metrics from a confusion matrix is shown in Fig. S3.

The evaluation of the classification performance and the diagnostic utility of the classifier must be made taking into consideration all the above performance metrics as well as the classification scenario. It should be noted that in datasets in which some classes have very few instances, classifiers can find it extremely difficult to learn those patterns. The balanced accuracy might also suffer because some disorders such as Asperge’s have a tiny number of samples compared to other groups in the ABIDE dataset, thereby making any reliable classification extremely difficult and giving a low balanced accuracy. The holdout accuracy is a pessimistic estimator of the generalization accuracy because only a portion of the data was given to the classifier for training and the holdout test dataset in our study was chosen to be from a slightly different population than training data. As we demonstrate in this study, the high accuracies commonly reported for leave-one-out cross-validation (LOOCV) and k-fold CV in neuroimaging studies (Anderson, et al., 2011; Deshpande, Wang, Rangaprakash, & Wilamowski, 2015) are misleading, especially when there is significant heterogeneity in the population. It should be noted that though classification accuracy is the most reported classifier performance metric, there are others, such as area under the curve (AUC), sensitivity, specificity, precision or positive predictive value (PPV) etc. But in this manuscript, we limit ourselves to balanced classification accuracy for assessing classification performance since it can be easily interpreted in binary and multiclass classification scenarios. Ideally, one has to evaluate the performance of a classifier using multiple metrics presented above, to assess its performance under both optimistic and pessimistic scenarios, depending on the classification objectives. However, interpreting some of the other measures in the multiclass scenario may not be straightforward.

2.6. Calculation of feature importance scores (FIS)

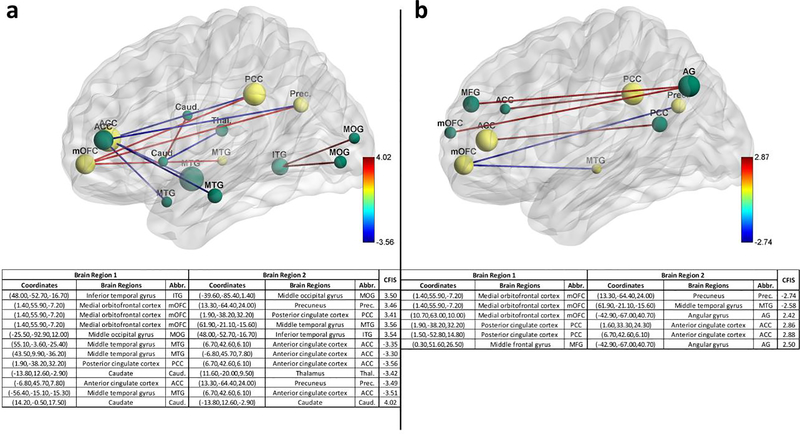
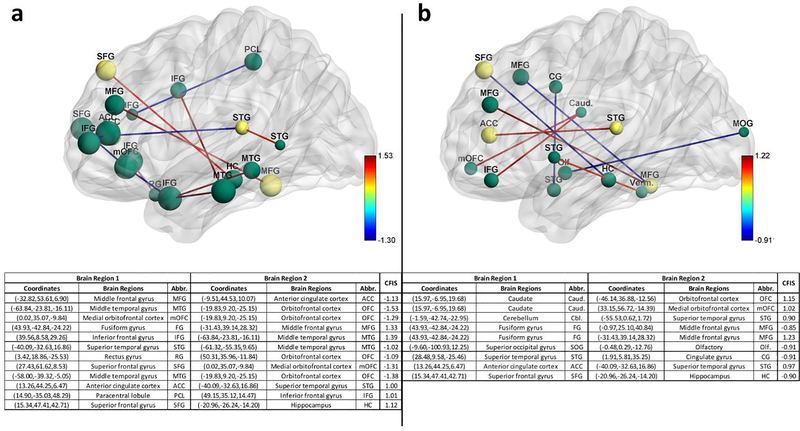
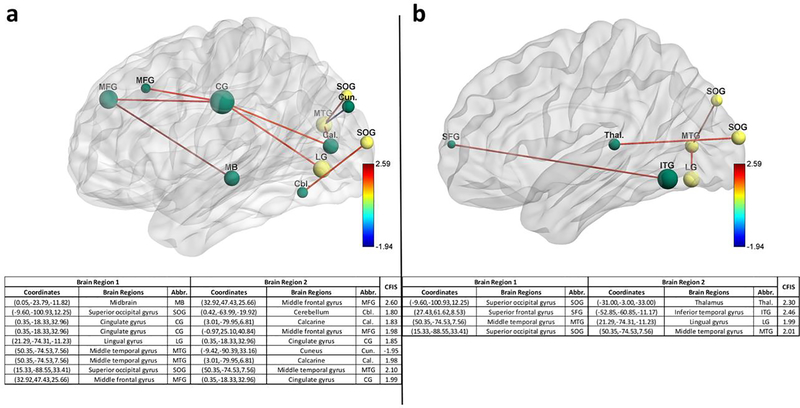
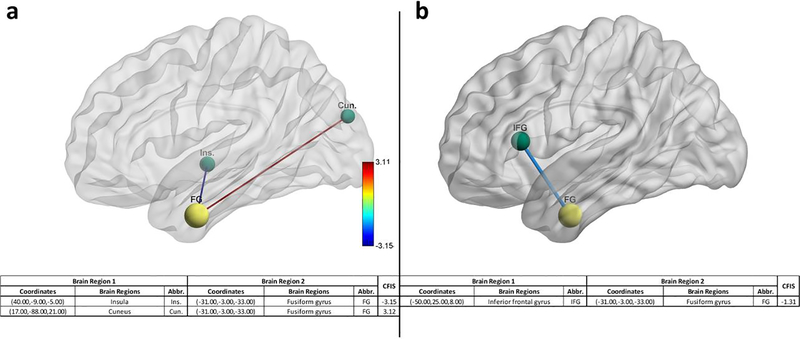
RCE procedure provides us with a feature ranking that indicates the importance of a particular feature in discriminating between the classes. For every step of the RCE loop, we kept the count of the features retained and used the count to assign higher feature importance scores (FIS) to features that were retained by the classification procedure while assigning lower scores to features eliminated early in the feature elimination process. We repeated this for every partitioning of data in the outer k-fold, thereby obtaining the FIS for every classifier implemented in the RCE-framework. We combined the feature importance score of all the classifiers implemented in the RCE-Framework, weighted by their balanced cross-validation accuracy, to obtain a combined score of feature importance (CFIS) for the classification problem. Multiple splits of the entire data into training/validation and hold-out test data gave a slightly different ranking to most classifiers across different splits. We plotted the CFIS of the features commonly found in all the data splits as a scatter plot. We repeated this procedure separately for multiclass and binary classification problems for every dataset. To obtain features which are generalizable across age groups and data acquisition sites, we identified a subset of features in each split, which have high feature importance scores (top 100), implying that they play a significant role in class discriminative ability as well as have significantly different means between the groups (p<0.05, corrected for multiple comparisons using permutation test (Edgington, 1980) by modeling the null distribution of maximum t-scores of features by permuting the class labels of the data). The features or connectivity paths thus identified were then visualized in BrainNet Viewer (Xia, Wang, & He, 2013). Similarly, we also ranked brain regions based on the sum of the CFIS of connectivity paths associated with them. A list of the top 20 brain regions was obtained for every neurological disorder considered in this study.

2.7. Consensus classifier

We have employed 18 different classifiers in this study. Many of them are based on entirely different principles, yet they all attempt to achieve the same result of determining the decision boundary which separates the groups. When multiple classifiers are used in neuroimaging, it is customary to report and emphasize on the one which gave highest classification accuracy (Brown, et al., 2012; Sato, Hoexter, Fujita, & Luis, 2012). This might give an optimistic estimate of the accuracy, and the result might not be repeatable even for data from the same population. Alternatively, we developed an ensemble classifier wherein the performance of all 18 classifiers were combined to provide a consensus estimate, which is referred to as a consensus classifier.

For every classifier, during CV, we resampled the data 600 times (6-fold × 100 repetitions), to get 600 different classifier models for each resampling. We used these 600 models for each classifier to predict the class of the observations in the validation data, giving us a total of 600 predictions for every observation in the hold-out test data. We then calculated individual class probabilities for the hold-out test data by estimating the relative frequency of the 600 target class predictions for the hold-out test data. In this way, the relative frequency of the target class was estimated for each test observation. Then the final class probabilities of the consensus classifiers were calculated by weighing the predicted class frequencies of each classifier with its balanced CV accuracy. The test observation was assigned to the class with the highest probability. This way multiple classifiers can be averaged to provide a consensus classifier which greatly improves the reliability and robustness of inferences made from them and makes the performance estimates more stable. A schematic depicting the predictions of the consensus classifier on the hold-out test data is shown in Fig. S4.

3. Results

This section is organized as follows. We present classification results for all disorders grouped based on the cross-validation scheme. Accordingly, results from the matched split is first presented, followed by heterogeneous age splits for ABIDE, PTSD and ADNI datasets and the heterogenous site split for ABIDE. Since we followed the split provided by the ADHD consortium, corresponding results are presented separate. Next, results from statistical tests on the difference between classification accuracies obtained across different classifiers and cross-validation schemes are presented. This is followed by results from the consensus classifier, a visualization of the effect of age and site variability, as well as reliability of feature selection and parameter optimization. Finally, we present important connectivity features discriminating each of the disorders as identified by supervised machine learning.

3.1. Matched-split

ABIDE

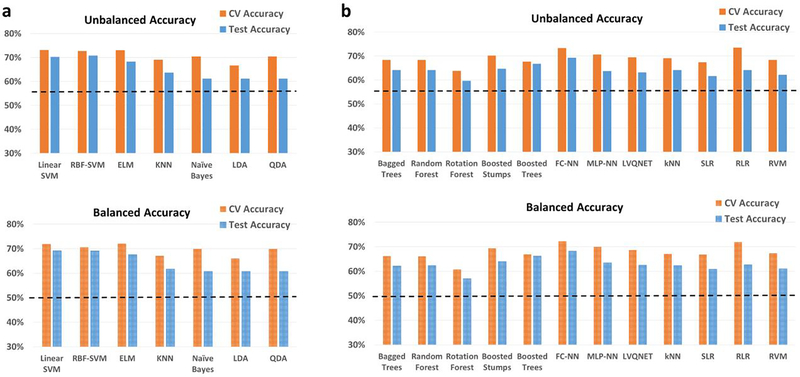
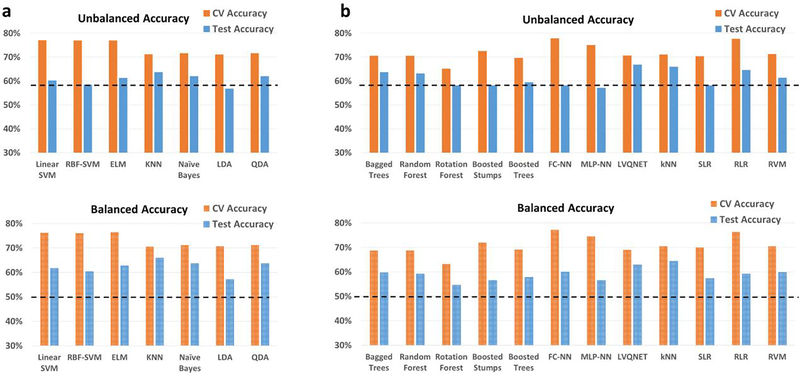
In the matched-split scenario, wherein the training/validation and the holdout test data are matched for age and imaging site, the binary classification results for the binary classification scenario between controls and ASD is shown in Fig. 2. Similarly, in the matched-split scenario, the clasification results for the 3-way multiclass classification scenaio between healthy controls, autism and Asperge’s syndrome are shown in Fig. S5 for the 18 classifiers. The corresponding tables for the binary and multiclass classification scenarios for the matched-split scenario detailing individual class accuracies is shown in Table S1 and Table S2 respectively. For the binary classification scenario, the best hold-out test accuracy at 70.7% obtained with RBF-SVM within the RCE framework while the best-balanced hold-out test accuracy was 69.2% obtained with linear-SVM implemented within the RCE framework. For the 3-way classification, the best hold-out test accuracy was 65.7% achieved with boosted trees while the best balanced hold-out test accuracy was 48.5% obtained with QDA implemented within RCE framework. In multiclass classification scenario, no classifier was able to reliably classify Asperge’s syndrome, which was the reason for lower balanced accuracy, even in this homogeneous matched-split scenario.

Fig. 2.

Unbalanced and balanced accuracy estimates for various classifiers a within the Recursive cluster elimination (RCE) framework, b outside RCE framework for autism brain imaging data exchange (ABIDE) data when the training/validation data and the hold-out test data are matched in imaging sites as well as age group for the binary classification problem between healthy controls and subjects with autism spectrum disorder (ASD). The training/validation and the hold-out test data are from all 15 imaging sites and age range of 7–58 years. The balanced accuracy was obtained by averaging the individual class accuracies. The orange bars indicate the cross-validation (CV) accuracy while the blue bars indicate the accuracy for the hold-out test data obtained by the voting procedure. The dotted line indicates the accuracy obtained when the classifier assigns the majority class to all subjects in the test data. For unbalanced accuracy, this happens to be 56% since healthy controls formed 56% of the total size of the hold-out test data. For balanced accuracy, this is exactly 50%. We chose the majority classifier as the benchmark since the accuracy obtained must be greater than that if it learns anything from the training data. The discrepancy between the biased estimates of the CV accuracy and the unbiased estimates of the hold-out accuracy is noteworthy. The best hold-out test accuracy was 70.7% obtained with RBF-support vector machine (SVM) within the RCE framework, while the best balanced hold-out test accuracy was 69.2% obtained with linear SVM implemented within the RCE framework. ELM, extreme learning machine; KNN, k-nearest neighbors; LDA, linear discriminant analysis; QDA, quadratic discriminant analysis; FC-NN, fully connected neural network; MLP-NN, multilayer perceptron neural network; LVQNET, learning vector quantization neural network; SLR, sparse logistic regression; RLR, regularized logistic regression; RVM, relevance vector machine

PTSD

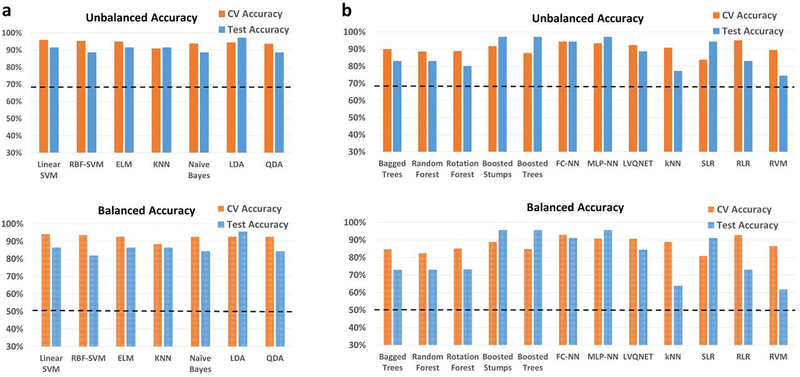
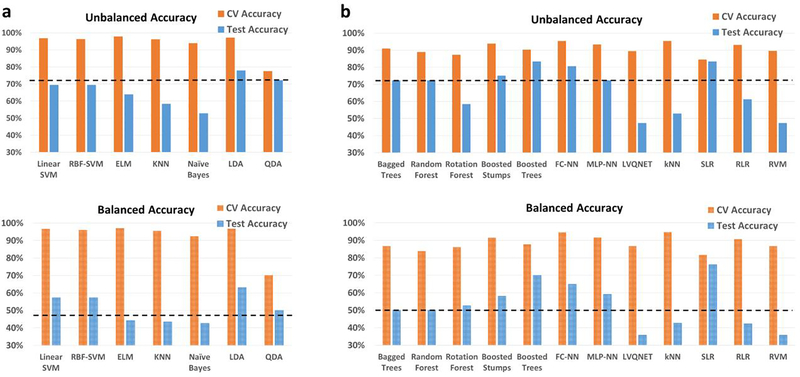
In the matched-age split, the binary classification results with healthy soldiers and PTSD, along with the 3-way multiclass classification between healthy soldiers, PTSD without PCS, and PTSD with PCS are shown in Fig. 3 and Fig. S6, respectively. Similarly, individual class accuracies for both scenarios are shown in Table S3 and Table S4. The best hold-out test accuracy for the binary case was 97.1%, whereas the best balanced hold-out test accuracy obtained was 95.5%, using boosted stumps, MLP-NN and LDA implemented within the RCE framework. For the 3-way classification, the best hold-out test accuracy was 94.3% with boosted stumps, and LDA implemented within RCE framework, while the best balanced hold-out test accuracy obtained was 93.3% with LDA implemented within RCE framework.

Fig. 3.

Unbalanced and balanced accuracy estimates for various classifiers a within recursive cluster elimination (RCE) framework, b outside RCE framework for post-traumatic stress disorder (PTSD) data when the training/validation data and the hold-out test data are from same age groups in the range for the multiclass classification between healthy controls and subjects with PTSD. The training/validation data and the hold-out test data are matched in age with subjects from age range of 23–53 years. The balanced accuracy was obtained by averaging the individual class accuracies. The orange bars indicate the cross-validation (CV) accuracy while the blue bars indicate the accuracy for the hold-out test data obtained by the voting procedure. The dotted line indicates the accuracy obtained when the classifier assigns the majority class to all subjects in the test data. For unbalanced accuracy, this happens to be 68.6% since subjects with PTSD formed 68.6% of the total size of the hold-out test data. For balanced accuracy, this is exactly 50%. We chose the majority classifier as the benchmark since the accuracy obtained must be greater than that if it learns anything from the training data. The discrepancy between the biased estimates of the CV accuracy and the unbiased estimates of the hold-out accuracy is noteworthy. The best hold-out test accuracy was 97.1%, whereas the best balanced hold-out test accuracy obtained was 95.5%, obtained by boosted stumps, boosted trees, multilayer perceptron neural network; (MLP-NN) and linear discriminant analysis (LDA) implemented within the RCE framework. ELM, extreme learning machine; KNN, k-nearest neighbors; QDA, quadratic discriminant analysis; SVM, support vector machine; FC-NN, fully connected neural network; LVQNET, learning vector quantization neural network; SLR, sparse logistic regression; RLR, regularized logistic regression; RVM, relevance vector machine

ADNI

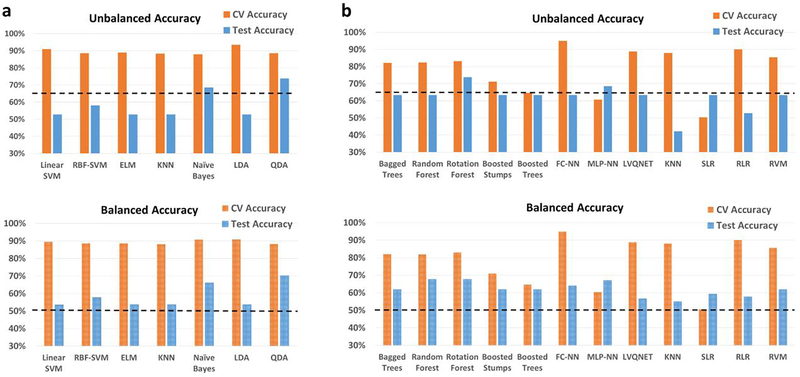
In the homogenous matched-age split, the classification performance for the binary classification scenario between healthy adults and adults diagnosed with Alzheimer’s disease is shown in Fig. 4, with the detailed information about individual class accuracies shown in Table S5. Similarly, results for the multiclass classification scenario (Controls, EMCI, LMCI and AD) are shown in Fig. S7, and Table S6. The best hold-out test accuracy was 84.6% while the best balanced hold-out test accuracy obtained was 85.7%, by both boosted trees and stumps. For the 4-way classification across the spectrum, the best hold-out test accuracy was 51.8% while the best balanced hold-out test accuracy was 53%, obtained with RLR.

Fig. 4.

Unbalanced and balanced accuracy estimates for various classifiers a within recursive cluster elimination (RCE) framework, b outside RCE framework for Alzheimer’s disease neuroimaging initiative (ADNI) data when the training/validation data and the hold-out test data are from the same age groups in the range for the binary classification between healthy controls and subjects with Alzheimer’s disease. The training/validation data and the hold-out test data are matched in age with subjects from age range of 56–88 years. The balanced accuracy was obtained by averaging the individual class accuracies. The orange bars indicate the cross-validation (CV) accuracy while the blue bars indicate the accuracy for the hold-out test data obtained by the voting procedure. The dotted line indicates the accuracy obtained when the classifier assigns the majority class to all subjects in the test data. For unbalanced accuracy, this happens to be 53.8% since healthy controls formed 53.8% of the total size of the hold-out test data. For balanced accuracy, this is exactly 50%. We chose the majority classifier as the benchmark since the accuracy obtained must be greater than that if it learns anything from the training data. The discrepancy between the biased estimates of the CV accuracy and the unbiased estimates of the hold-out accuracy is noteworthy. The best hold-out test accuracy was 84.6% while the best balanced hold-out test accuracy obtained was 85.7%, with boosted trees and stumps. ELM, extreme learning machine; KNN, k-nearest neighbors; LDA, linear discriminant analysis; quadratic discriminant analysis; SVM, support vector machine; FC-NN, fully connected neural network; MLP-NN, multilayer perceptron neural network; LVQNET, learning vector quantization neural network; SLR, sparse logistic regression; RLR, regularized logistic regression; RVM, relevance vector machine

3.2. Heterogeneous-age split

ABIDE

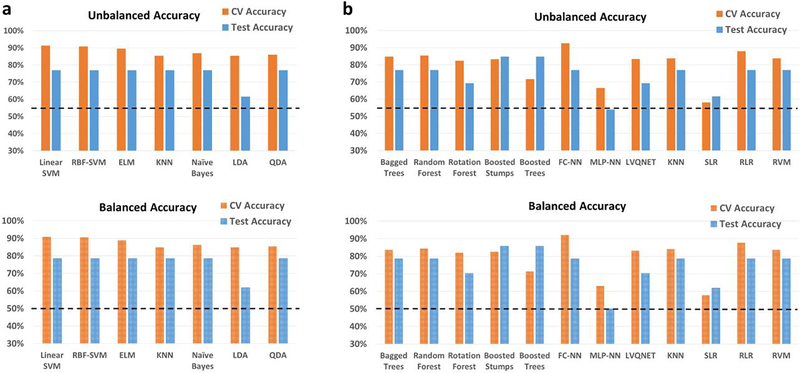
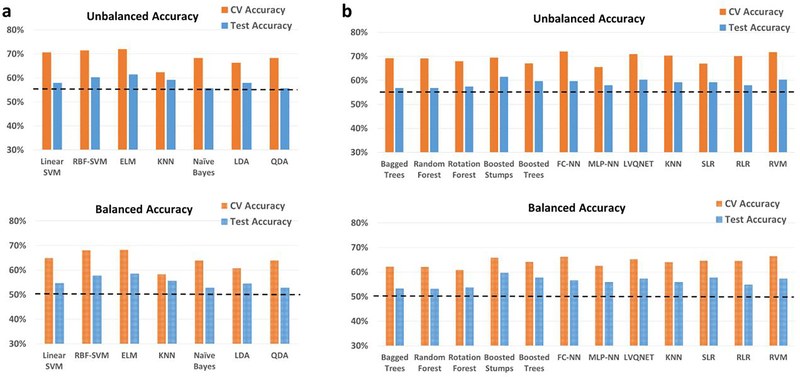
For the heterogeneous-age split, where the training/validation data and the hold-out test data belong to different age ranges, the classification results for the binary classification scenario between healthy controls and subjects with ASD using the ABIDE dataset is shown in Fig. 5. Similarly, the 3-way multiclass classification scenario between the controls, Asperge’s and autism using the ABIDE dataset is shown in Fig. S8. The tables for the binary and multi-class classification showing the detailed individual class accuracies can be found in Table S7 and Table S8, respectively. In the binary classification scenario for the split in which the training/validation and the hold-out test data belong to different age ranges, the best hold-out test accuracy was 66.8% obtained with LVQNET, while the best-balanced hold-out test accuracy was 64.4% obtained with KNN implemented outside the RCE framework. In the multiclass classification for the same split, the best hold-out test accuracy was 61.3% while the best balanced hold-out test accuracy obtained was 46.5%, obtained with LVQNET.

Fig. 5.

Unbalanced and balanced accuracy estimates for various classifiers a within recursive cluster elimination (RCE) framework, b outside RCE framework for autism brain imaging data exchange (ABIDE) data when the training/validation data and the hold-out test data are from different age groups for the binary classification between healthy controls and subjects with autism spectrum disorder. The training/validation data is from an age range of 7–21 years while the data from the age range of 22–58 years was used as a hold-out test data. The balanced accuracy was obtained by averaging the individual class accuracies. The orange bars indicate the cross-validation (CV) accuracy while the blue bars indicate the accuracy for the hold-out test data obtained by the voting procedure. The dotted line indicates the accuracy obtained when the classifier assigns the majority class to all subjects in the test data. For unbalanced accuracy, this happens to be 58.5% since healthy controls formed 58.5% of the total size of the hold-out test data. For balanced accuracy, this is exactly 50%. We chose the majority classifier as the benchmark since the accuracy obtained must be greater than that if it learns anything from the training data. The discrepancy between the biased estimates of the CV accuracy and the unbiased estimates of the hold-out accuracy is noteworthy. The best hold-out test accuracy was 66.8% obtained with learning vector quantization neural network (LVQNET) while the best balanced hold-out test accuracy was 64.4% obtained with k-nearest neighbors (KNN) implemented outside the RCE framework. ELM, extreme learning machine; LDA, linear discriminant analysis; QDA, quadratic discriminant analysis; SVM, support vector machine; FC-NN, fully connected neural network; MLP-NN, multilayer perceptron neural network; SLR, sparse logistic regression; RLR, regularized logistic regression; RVM, relevance vector machine

PTSD

The classification results in the heterogeneous-age split for the binary classification scenario between healthy soldiers and soldiers diagnosed with PTSD is shown in Fig. 6. In the multiclass classification scenario between healthy controls, soldiers diagnosed with just PTSD and soldiers diagnosed with PTSD and PCS is shown in Fig. S9. The corresponding tables for binary and multiclass scenarios can be found in Table S9 and Table S10. In the binary classification scenario for the split in which the training/validation and the hold-out test data belonged to different age ranges, the best hold-out test accuracy was 83.3% obtained by SLR and boosted trees, while the best balanced hold-out test accuracy obtained was 76.2% with SLR. In the multiclass classification for the same split, the best hold-out test accuracy was 80.6% while the best balanced hold-out test accuracy obtained was 73.3%, obtained with boosted stumps.

Fig. 6.

Unbalanced and balanced accuracy estimates for various classifiers a within recursive cluster elimination (RCE) framework, b outside RCE framework for post-traumatic stress disorder (PTSD) data when the training/validation data and the hold-out test data are from different age groups in the range for the multiclass classification between healthy controls and subjects with PTSD. The training/validation data is from an age range of 23–37 years while the data from the age range of 38–53 years was used as a hold-out test data. The balanced accuracy was obtained by averaging the individual class accuracies. The orange bars indicate the cross-validation (CV) accuracy while the blue bars indicate the accuracy for the hold-out test data obtained by the voting procedure. The dotted line indicates the accuracy obtained when the classifier assigns the majority class to all subjects in the test data. For unbalanced accuracy, this happens to be 72.2% since subjects with PTSD formed 72.2% of the total size of the hold-out test data. For balanced accuracy, this is exactly 50%. We chose the majority classifier as the benchmark since the accuracy obtained must be greater than that if it learns anything from the training data. The discrepancy between the biased estimates of the CV accuracy and the unbiased estimates of the hold-out accuracy is noteworthy. The best hold-out test accuracy was 83.3% obtained by sparse logistic regression (SLR) and boosted trees, while the best balanced hold-out test accuracy obtained was 76.2% with SLR. ELM, extreme learning machine; KNN, k-nearest neighbors; LDA, linear discriminant analysis; QDA, quadratic discriminant analysis; SVM, support vector machine; FC-NN, fully connected neural network; MLP-NN, multilayer perceptron neural network; LVQNET, learning vector quantization neural network; RLR, regularized logistic regression; RVM, relevance vector machine

ADNI

In the heterogenous-age split, the classification performance for the binary classification scenario between healthy adults and adults diagnosed with Alzheimer’s disease is shown in Fig. 7, with the detailed information about individual class accuracies shown in Table S11. Similarly, for results for results for the multiclass classification scenario (Controls, EMCI, LMCI and AD) are shown in Fig. S10, and Table S12. In the binary classification scenario between Controls and AD, the best hold-out test accuracy was 73.7% obtained with random forest, and QDA implemented within RCE framework, while the best balanced hold-out test accuracy obtained was 70.2% with QDA implemented within RCE framework. In the multiclass classification for the same split, the best hold-out test accuracy was 46.9% while the best balanced hold-out test accuracy was 47.9%, obtained with boosted trees.

Fig. 7.

Unbalanced and balanced accuracy estimates for various classifiers a within recursive cluster elimination (RCE) framework, b outside RCE framework for Alzheimer’s disease neuroimaging initiative (ADNI) data when the training/validation data and the hold-out test data are from different age groups in the range for the binary classification between healthy controls and subjects with Alzheimer’s disease. The training/validation data is from an age range of 56–76 years while the data from the age range of 77–88 years was used as a hold-out test data. The balanced accuracy was obtained by averaging the individual class accuracies. The orange bars indicate the cross-validation (CV) accuracy while the blue bars indicate the accuracy for the hold-out test data obtained by the voting procedure. The dotted line indicates the accuracy obtained when the classifier assigns the majority class to all subjects in the test data. For unbalanced accuracy, this happens to be 63.2% since healthy controls formed 63.2% of the total size of the hold-out test data. For balanced accuracy, this is exactly 50%. We chose the majority classifier as the benchmark since the accuracy obtained must be greater than that if it learns anything from the training data. The discrepancy between the biased estimates of the CV accuracy and the unbiased estimates of the hold-out accuracy is noteworthy. The best hold-out test accuracy was 73.7% obtained by Random forest, and quadratic discriminant analysis (QDA) implemented within RCE framework, while the best balanced hold-out test accuracy obtained was 70.2% with QDA implemented within RCE framework. ELM, extreme learning machine; KNN, k-nearest neighbors; LDA, linear discriminant analysis; SVM, support vector machine; FC-NN, fully connected neural network; MLP-NN, multilayer perceptron neural network; LVQNET, learning vector quantization neural network; SLR, sparse logistic regression; RLR, regularized logistic regression; RVM, relevance vector machine

3.3. Heterogeneous-site split

ABIDE

For the heterogeneous-site split, when the training/validation data is from 12 imaging sites, and the hold-out test data is from the remaining three imaging sites, the classification performance for binary and 3-way multiclass classification scenario is shown in Fig. 8 and Fig. S11, respectively. Similarly, detailed information about individual class accuracies for binary and multiclass classification scenarios are shown in Table S13 and Table S14, respectively. For the heterogeneous site split on the ABIDE data, the best accuracy on the hold-out test data was 65.8% obtained with bagged trees as well as Linear SVM implemented within SVM framework, while the best balanced hold-out test accuracy was 66.8% obtained with linear SVM implemented within the RCE framework. In the multiclass scenario between healthy controls, subjects with Asperge’s syndrome and autism, the best hold-out test accuracy was 66% obtained with RLR while the best balanced hold-out test accuracy was 66.8% obtained with ELM implemented within the RCE framework.

Fig. 8.

Unbalanced and balanced accuracy estimates for various classifiers a within recursive cluster elimination (RCE) framework, b outside RCE framework for autism brain imaging data exchange (ABIDE) data when the training/validation data and the hold-out test data are from different acquisition sites for the binary classification between healthy controls and subjects with autism spectrum disorder. The training/validation data are from 12 institutions while the data for the remaining three institutions was used as a hold-out test data. The balanced accuracy was obtained by averaging the individual class accuracies. The orange bars indicate the cross-validation (CV) accuracy while the blue bars indicate the accuracy for the hold-out test data obtained by the voting procedure. The dotted line indicates the accuracy obtained when the classifier assigns the majority class to all subjects in the test data. For unbalanced accuracy, this happens to be 54% since healthy controls formed 54% of the total size of the hold-out test data. For balanced accuracy, this is exactly 50%. We chose the majority classifier as the benchmark since the accuracy obtained must be greater than that if it learns anything from the training data. The discrepancy between the biased estimates of the CV accuracy and the unbiased estimates of the hold-out accuracy is noteworthy. The best hold-out test accuracy was 65.8% obtained with Bagged trees and Linear support vector machine (SVM) implemented within the RCE framework, while the best balanced hold-out test accuracy was 66.8% obtained with Linear SVM implemented within the RCE framework. ELM, extreme learning machine; KNN, k-nearest neighbors; LDA, linear discriminant analysis; QDA, quadratic discriminant analysis; FC-NN, fully connected neural network; MLP-NN, multilayer perceptron neural network; LVQNET, learning vector quantization neural network; SLR, sparse logistic regression; RLR, regularized logistic regression; RVM, relevance vector machine

3.4. ADHD-200 split

For the ADHD-200 dataset, as mentioned earlier, the split of the data into training/validation and hold-out test data was given by the competition organizers themselves. The classification results for the binary classification scenario between healthy controls and subjects with ADHD are shown in Fig. 9. Table S15 provides corresponding detailed individual class accuracies. Results for the 3-way classification scenario between healthy controls and subjects with ADHD-I and ADHD-C are provided in Fig. S12 with detailed accuracy performance presented in Table S16. The results indicate the apparent difficulty in classifying controls from ADHD as reported by several papers which used the same data with reported performances similar to our own results (Consortium, 2012). For binary classification, best hold-out test accuracy was 61.4%, obtained by boosted stumps and ELM implemented within RCE framework, while the best balanced hold-out test accuracy obtained was 59.6%, obtained with boosted stumps. Similarly, for the multiclass classification, the best hold-out test accuracy was 58% using boosted trees while the best balanced hold-out test accuracy obtained was 38.7% using RBF-SVM implemented within RCE framework. These results indicate the difficulty of multiclass classification with ADHD-200 data compared to a binary classification.

Fig. 9.

Unbalanced and balanced accuracy estimates for various classifiers a within recursive cluster elimination (RCE) framework, b outside RCE framework for the attention deficit hyperactivity disorder-200 (ADHD-200) data between healthy controls and subjects with ADHD. The training/validation data and the hold-out test data are from 7 imaging sites as released by ADHD-200 consortium. The balanced accuracy was obtained by averaging the individual class accuracies. The orange bars indicate the cross-validation (CV) accuracy while the blue bars indicate the accuracy for the hold-out test data obtained by the voting procedure. The dotted line indicates the accuracy obtained when the classifier assigns the majority class to all subjects in the test data. For unbalanced accuracy, this happens to be 55.6% since healthy controls formed 55.6% of the total size of the hold-out test data. For balanced accuracy, this is exactly 50%. We chose the majority classifier as the benchmark since the accuracy obtained must be greater than that if it learns anything from the training data. The best hold-out test accuracy was 61.4%, obtained by boosted stumps and extreme learning machine (ELM) implemented within RCE framework, while the best balanced hold-out test accuracy obtained was 59.6%, obtained with boosted stumps. KNN, k-nearest neighbors; LDA, linear discriminant analysis; QDA, quadratic discriminant analysis; SVM, support vector machine; FC-NN, fully connected neural network; MLP-NN, multilayer perceptron neural network; LVQNET, learning vector quantization neural network; SLR, sparse logistic regression; RLR, regularized logistic regression; RVM, relevance vector machine

3.5. Significance of the classification accuracy

We performed a 2-way ANOVA of classification accuracy, with type of validation (i.e. cross validation using training/validation dataset or independent validation using hold-out test data) as one factor and the different classifiers as another factor for ABIDE, ADHD-200, PTSD and ADNI datasets. This was done for both binary and multiclass classification scenarios. The corresponding results are shown in Table S17. Both main and interaction effects were significant in all cases.

3.6. Performance metrics from the consensus classifier

The hold-out test accuracies obtained from the consensus classifier (when all the classifiers are combined) for each of the four datasets are shown in Table 4. We list voting hold-out test accuracy, balanced hold-out test accuracy and individual class accuracies obtained by the consensus classifier. It is clear from the results of the various splits that the classifier which has the best hold-out test accuracy in one split may not perform as well on the other splits. Similarly, the classifiers which have high cross-validation accuracy does not always have a high hold-out test accuracy. Though the performance of the consensus classifier is less than the performance of the best classifier for the split, it consistently gives excellent performance across all splits by leveraging the predictive power of individual classifiers.

Table 4.

Accuracy obtained by the consensus classifier for the various splits with a autism brain imaging data exchange (ABIDE) dataset, b attention deficit hyperactivity disorder-200 (ADHD-200) dataset, c post-traumatic stress disorder (PTSD) dataset, and d Alzheimer’s disease neuroimaging initiative (ADNI) dataset

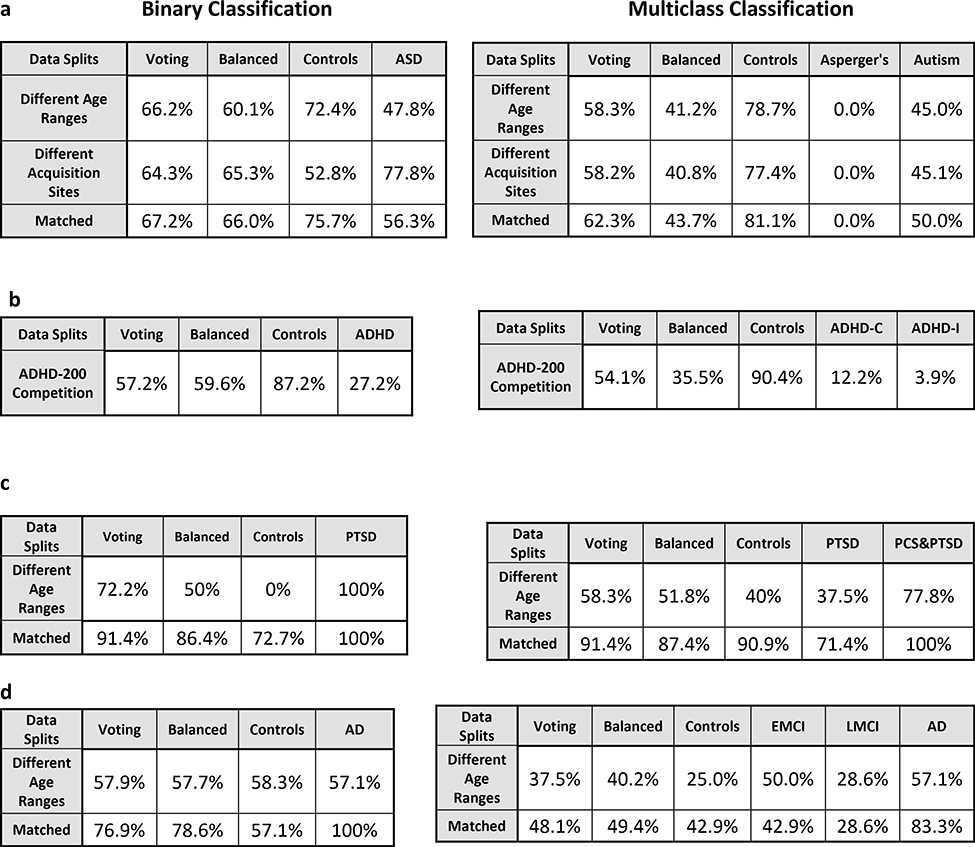Note. ADHD-C, attention deficit hyperactivity disorder-combined; ADHD-H, attention deficit hyperactivity disorder-hyperactive/impulsive; ADHD-I, attention deficit hyperactivity disorder-inattentive; PCS, post-concussion syndrome; EMCI, early mild cognitive impairment; LMCI, late mild cognitive impairment; AD, Alzheimer’s disease

3.7. Effect of age and site variability

To better understand the effects of age and site variability on the accuracy obtained from the hold-out test data, we used the consensus classifier to compare and contrast. This way we can draw generalized inferences about the predictive capability of the classifiers without reference to any specific classifier. We compared the overall accuracies and the individual class accuracies when the training/validation data and the hold-out test data were matched as well as a case in which there was age or site differences between the two, i.e., the homogenous and heterogenous split scenarios. The corresponding consensus accuracies for ABIDE, PSTD and ADNI datasets are shown in Figs. 10, 11 and 12, respectively. As expected, the accuracies on the hold-out test data was higher in the homogenous-matched data than in the heterogenous-unmatched cases. The difference in consensus accuracies due to age was particularly sharp in small datasets such as PTSD and ADNI. These figures illustrate that smaller datasets with high homogeneity overestimate the actual predictive capability of the classifiers and could give optimistic accuracy results that do not generalize well to the larger population.

Fig. 10.

The figure shows the differences in overall accuracy as well as individual class accuracies in the autism brain imaging data exchange (ABIDE) dataset which can be attributed to age and site variability. These consensus accuracies were obtained by combining the predictions of all the 19 classifiers in a probabilistic way to vote on the hold-out test dataset. As expected, the split wherein the training and hold-out test data were matched for age and acquisition site had the best performance, though it was more pronounced in the multiclass classification scenario. In fact, a three-way classification between healthy controls, subjects with Asperge’s syndrome and autism reduced the overall accuracy due to the relatively fewer subjects with Asperge’s syndrome in the dataset. Overall the classifiers were reasonably successful in classifying the test observations. ASD, autism spectrum disorder

Fig. 11.

The figure shows the differences in overall accuracy as well as individual class accuracies in the posttraumatic stress disorder (PTSD) dataset which can be attributed to age range differences in training/validation and hold-out test data. These consensus accuracies were obtained by combining the predictions of all the 19 classifiers in a probabilistic way to vote on the hold-out test dataset. As expected, the split wherein the training and hold-out test data were matched for age had the best performance. The accuracy in the split where the age range was different for training/validation and hold-out test data was terrible with all observations being classified as PTSD in the binary classification scenario. This shows that smaller datasets with homogeneity overestimate the actual predictive capability of the classifiers and do not generalize well to the overall population. PCS, post-concussion syndrome

Fig. 12.

The figure shows the differences in overall accuracy as well as individual class accuracies in the Alzheimer’s disease neuroimaging initiative (ADNI) dataset which can be attributed to age range differences in training/validation and hold-out test data. These consensus accuracies were obtained by combining the predictions of all the 19 classifiers in a probabilistic way to vote on the hold-out test dataset. Similar to the other two datasets, the split where the training and hold-out test data were matched on age had the best performance, though it was more pronounced in the binary classification scenario. The binary classification performed way better than multiclass classification as expected due to the difficulty in modeling the four classes with relatively small sample size. Like results with posttraumatic stress disorder dataset, smaller datasets with homogeneity overestimate the actual predictive capability of the classifiers and do not generalize well to the overall population. EMCI, early mild cognitive impairment; LMCI, late mild cognitive impairment; AD, Alzheimer’s disease

3.8. Reliability of feature selection and parameter optimization

To investigate the wide discrepancies between cross-validation and hold-out test accuracies in smaller datasets, we compared the average accuracy per cluster plots as a function of features for every recursive cluster elimination step in the RCE framework. This was done for both ADNI and ABIDE datasets, which we used as examples of a small and a large dataset respectively. The figure for the Linear SVM classifier comparing both the datasets is shown in Fig. 13. The results from a 2-way ANOVA with recursive cluster elimination steps as one factor and type of validation (i.e. cross validation using training/validation dataset or independent validation using hold-out test data) as another factor is presented in Table S18. It can be seen that both the main effects as well as their interaction were significant. As non-discriminative features are eliminated in the RCE-framework, training accuracy increases. For the ADNI dataset, unlike with the ABIDE dataset, removal of features did not translate to improvement in accuracy in the validation dataset. Similarly, model selection via parameter optimization for SVM within the RCE-framework does not particularly seem to improve the accuracy significantly for the ADNI dataset beyond that obtained by using a default value for the tuning parameter C equal to 0.1 as shown in Fig. 14. The results from a 2-way ANOVA with recursive cluster elimination steps and with/without parameter optimization as factors is presented in Table S19. Both the main effects as well as their interaction were significant for ABIDE. For ADNI, the main effect of RCE steps was not significant while the main effect of parameter optimization as well as the interaction effect were significant. In fact, the accuracy was significantly less by using model selection than just using the default parameter. Whereas, for ABIDE dataset, hyperparameter optimization by grid search improved the accuracy compared to using the default parameter. The significance of the differences in accuracy with and without parameter optimization in ABIDE data becomes more appreciable as recursive cluster elimination progresses. The reason for the unreliability in feature selection and parameter optimization can be attributed to the lack of enough data to choose the optimal models due to large variance in accuracy estimates, a problem, unfortunately, more pronounced in high dimensional datasets with smaller sample sizes.

Fig. 13.

Changes in classification accuracy with feature elimination during training compared to validation. Results are shown in smaller datasets such as a Alzheimer’s disease neuroimaging initiative (ADNI) as well as in larger datasets such as b Autism brain imaging data exchange (ABIDE). The recursive cluster elimination (RCE) framework seemed to improve the accuracy as unnecessary features were eliminated in the training data. In ADNI dataset, unlike with the ABIDE dataset, removal of features did not translate to improvement in accuracy in the validation dataset. This demonstrates the unreliability of feature selection in smaller datasets. The results from a 2-way ANOVA of classification accuracies, with RCE-steps and training/validation or hold-out test data as factors, can be found in Table S18

Fig. 14.

Changes in classification accuracy with feature elimination, both with and without model selection/hyperparameter optimization. Results are shown in smaller datasets such as a Alzheimer’s disease neuroimaging initiative (ADNI) as well as with large datasets such as b Autism brain imaging data exchange (ABIDE). For the ADNI dataset, parameter optimization did not lead to an increase in the accuracy than the default parameters. In fact, it is less than what is observed without parameter optimization. Whereas, for the ABIDE dataset hyperparameter optimization by grid search improved the accuracy compared to using the default parameters as identifying the optimum hyperparameters is more reliable. This figure raises important questions about the unreliability of model selection/hyperparameter optimization in smaller datasets. The results from a 2-way ANOVA of classification accuracies, with recursive cluster elimination (RCE)-steps and with or without parameter optimization as factors, can be found in Table S19

3.9. Identification of important features discriminating the disorders

ASD

The combined feature importance scores (CFIS) were calculated for all classifiers implemented within the RCE framework on the ABIDE dataset. These CFIS for various splits are plotted in a scatter plot and a linear regression line was fit as shown in Fig. S13. The figure indicates that, though there is significant (p<10⁻¹⁰) agreement (as obtained from the linear regression line) in the FIS across the splits, age range and scanner variability do contribute to the increase in variance in these score estimates. Using the FIS, we identified the top connectivity paths whose means were significantly different between the groups (p<0.05, FDR corrected) as well as have high FIS. These paths are visualized in Fig. 15. Along with these connectivity paths, we also identified the top 20 regions associated with altered and discriminative connectivity paths as shown in the Table S20.

Fig. 15.

The figure illustrates the connectivity paths which have significantly different means between the groups (p<0.05, corrected for multiple comparisons using permutation test) as well as are among the top hundred most discriminative paths in autism brain imaging data exchange (ABIDE) dataset for a binary classification between controls and autism spectrum disorder. b 3-way classification between healthy controls, Asperge’s syndrome and autism. The size of the nodes indicates the relative importance of the region (Table S20). Common nodes between binary and multiclass classification are indicated in yellow while other nodes are indicated in green. The sign of the paths indicates overconnectivity (positive) or under-connectivity (negative) in healthy controls compared to clinical populations. Consequently, red represents a higher connectivity between controls compared to the clinical populations and blue represents a lower connectivity. The numerical values in the color bar denote the combined feature importance score (CFIS) of the path obtained from classification. A higher absolute number indicates more discriminative ability for the functional connectivity path. The table below the figure tabulates the brain regions involved in the paths visualized above along with the abbreviations of the two regions and the CFIS for the connectivity paths

ADHD

Since we did not perform multiple splits on the ADHD-200 dataset, we did not plot the FIS for the splits as a scatter plot, as was done with other datasets in this study. After calculating the CFIS for all classifiers implemented within the RCE framework, we used the CFIS to identify the top connectivity paths whose means were significantly different between the groups (p<0.05, FDR corrected) as well as have high CFIS, as we have done with the ABIDE dataset. These paths are shown in Fig. 16 and the top 20 regions in the brain whose connectivity paths were altered in the disorder are shown in Table S21.

Fig. 16.

The figure illustrates the connectivity paths which have significantly different means between the groups (p<0.05, corrected for multiple comparisons using permutation test) as well as are among the top hundred most discriminative paths in attention deficit hyperactivity disorder (ADHD) for a binary classification between controls and ADHD. b 3-way classification between healthy controls, ADHD-inattentive and ADHD-combined. The size of the nodes indicates the relative importance of the region (Table S21). Common nodes between binary and multiclass classification are indicated by yellow while other nodes are indicated by green. The sign of the paths indicates over-connectivity (positive) or under-connectivity (negative) in healthy controls compared to clinical populations. So, red represents a higher connectivity between controls compared to the clinical populations and blue represents a lower connectivity. The numerical values in the color bar denote the combined feature importance score (CFIS) of the path obtained from classification. A higher absolute number indicates more discriminative ability for the functional connectivity path. The table below the figure tabulates the brain regions involved in the paths visualized above along with the abbreviations of the two regions and the CFIS for the connectivity paths

PTSD

The CFIS for the two splits performed on the PTSD dataset are plotted in a scatter plot as shown in Fig. S14 for the binary and multiclass scenarios. The plot illustrates variability and the negative slope particularly in the multiclass classification case which can be attributed to the age ranges in each split. This means that the CFIS for multiclass classification which are higher in one split were lower in the other. Therefore, age has an impact in altering the feature importance. For binary classification, however, the slope was still positive. Using the CFIS, we identified the top connectivity paths (shown in Fig. 17) whose means were significantly different between the groups (p<0.05, FDR corrected) as well as have high combined feature importance scores. The top 20 regions in the brain whose connectivity paths were altered in the disorder are listed in the Table S22, obtained during binary and multiclass classification scenarios.

Fig. 17.

The figure illustrates the connectivity paths which have significantly different means between the groups (p<0.05, corrected for multiple comparisons using permutation test) as well as are among the top hundred most discriminative paths for post-concussion syndrome (PCS) and post-traumatic stress disorder (PTSD) for a binary classification between combat controls and PTSD. b 3-way classification between healthy combat controls, PTSD, and both PCS and PTSD. The size of the nodes indicates the relative importance of the region (Table S22). Common nodes between binary and multiclass classification are indicated by yellow while other nodes are indicated by green. The sign of the paths indicates over-connectivity (positive) or under-connectivity (negative) in healthy controls compared to clinical populations. So, red represents a higher connectivity between controls compared to the clinical populations and blue represents a lower connectivity. The numerical values in the color bar denote the combined feature importance score (CFIS) of the path obtained from classification. A higher absolute number indicates more discriminative ability for the functional connectivity path. The table below the figure tabulates the brain regions involved in the paths visualized above along with the abbreviations of the two regions and the CFIS for the connectivity paths

ADNI

For the ADNI dataset, the CFIS for the two splits were plotted in a scatter plot as shown in Fig. S15 for the binary and multiclass cases. The CFIS have higher variability and a smaller slope in binary compared to the multiclass classification scenario. The top connectivity paths whose means were significantly different between the groups (p<0.05, FDR corrected) as well as have high CFIS are shown in Fig. 18, while the top 20 regions in the brain whose connectivity paths were altered in the disease, identified during the binary and multiclass classification scenarios, are shown in Table S23.

Fig. 18.

The figure illustrates the connectivity paths which have significantly different means between the groups (p<0.05, corrected for multiple comparisons using permutation test) as well as are among the top hundred most discriminative paths in ADNI data for a binary classification between controls and Alzheimer’s disease (AD). b 4-way classification between healthy controls, early mild cognitive impairment, late mild cognitive impairment, and AD. The size of the nodes indicates the relative importance of the region (Table S23). Common nodes between binary and multiclass classification are indicated by yellow while other nodes are indicated by green. The sign of the paths indicates over-connectivity (positive) or under-connectivity (negative) in healthy controls compared to clinical populations. So, red represents a higher connectivity between controls compared to the clinical populations and blue represents a lower connectivity. The numerical values in the color bar denote the combined feature importance score (CFIS) of the path obtained from classification. A higher absolute number indicates more discriminative ability for the functional connectivity path. The table below the figure tabulates the brain regions involved in the paths visualized above along with the abbreviations of the two regions and the CFIS for the connectivity paths

4. Discussion

The findings demonstrate that cross-validation accuracy can provide overoptimistic estimates of classifier performances in homogeneous datasets. Further, we show how the hold-out test performance can actually be much lower than the cross-validation performance. This is an important conclusion given that cross-validation is a generally accepted standard in neuroimaging-based classification, and yet is something that is completely unacceptable in other fields including industry, where the use-case scenario dictates the classification methodology (for a more detailed discussion on how cross-validation is viewed outside the neuroimaging literature, please refer to section-3 of the supplementary information). Our results suggest that neuroimaging must adopt industry-standards while employing machine learning for diagnostic classification, wherein the classification performance is always assessed using a completely independent hold-out test data.

Second, we sought to understand how overfitting can occur in the context of machine learning applied to neuroimaging-based diagnostic classification. We implemented 18 classifiers covering a spectrum of popular machine learning classifiers based on diverse principles. Our results show that during both feature selection and performance estimation, smaller datasets might give unreliable estimates of classifier performance due to inadequate sampling, which could lead to improper model selection leading to poor generalization across the larger population. To address issues with classifier variance and improve predictive ability, we also proposed a consensus classifier, which was the third goal of our study. The consensus classifier is an ensemble classifier which exploits the predictive abilities of individual classifiers to build a single classifier so that inferences drawn are not driven by overfitting due to the inductive biases of any individual classifier.

Finally, we wanted to identify functional connectivity features that are insensitive to different sources of variability identified above, as well as have a good statistical separation between groups and good predictive ability. In fact, the proposed combined feature importance scores we assigned to connectivity features were aggregated from multiple classifiers implemented in the RCE framework. Connectivity features thus identified are likely to be robust and genuine markers of underlying brain network disruptions caused by the disorders rather than an artifact of other extraneous factors. We make our data and code in form of a toolbox publicly available for replication of our results and to encourage better practices in research. A MATLAB toolbox called Machine Learning in NeuroImaging (MALINI), which implements all the 18 different classifiers along with the consensus classifier is available from Lanka et al. (Lanka, et al., 2019). The toolbox can also be found at the following URL: https://github.com/pradlanka/malini. To the best of our knowledge, this is the most comprehensive exploration of state-of-the-art machine learning algorithms for neuroimaging based diagnostic classification and could be used for disorder/disease classification based on connectivity metrics.

The discussion section is organized as follows. We start with a discussion of the methodological aspects associated with our study, which is then followed by a discussion of specific insights we obtained using each of the four clinical datasets. We first discuss the strengths of our study with regard to the use of a data-driven feature selection strategy. We then examine in detail the issues encountered during classification. Specifically, we discuss how data heterogeneity in age and acquisition site can affect the classifier performance by summarizing our observations in heterogeneous splits. As our results indicate, data heterogeneity can reduce classification accuracy, and the effect is much more pronounced in relatively smaller datasets such as PTSD and ADNI. We also expand on how model selection and performance estimation can be unreliable in these small datasets. We then discuss some issues in the acquisition and processing of data that can effect classification accuracy and speculate on how multimodal imaging might improve classification performance. We end this section by discussing the classification results, connectivity paths and the regions associated with the four disorders we examined – ASD, ADHD, PCS & PTSD and MCI & AD, in order – with special emphasis on disrupted functional connectivity networks we identified.

4.1. Use of a data-driven approach for feature selection

We used a data-driven model in this study where we made no prior assumptions about the brain regions or connectivity paths involved in the underlying disorders. Prior assumptions about the effects of the disorders on the brain regions have been used before to reduce the number of features to a more reasonable number (Uddin, et al., 2013; Zhou, et al., 2010; Koch, et al., 2012). However, in this paper, we used a data-driven approach to reduce the number of features and improve the classification accuracy of the classifiers for three reasons: (i) The feature selection methods we used, can potentially provide insights into the neurophysiological aspects of the disorder and help validate current hypotheses about the underlying connectivity disruptions in these disorders (Castellanos, Di Martino, Craddock, Mehta, & Milham, 2013). (ii) There is a growing body of evidence that neurological disorders target large-scale distributed brain networks. Hence by limiting ourselves to a few regions in the brain, we might not even consider features with potentially useful information that might contribute to our understanding of the underlying neuropathology of the disorder. (iii) There is a lack of specificity of brain networks in identification of disorders. For example, default mode network (DMN) dysregulation is implicated in several disorders. Therefore, using a data-driven feature selection algorithm can help us characterize networks which are likely to be specific to individual disorders.

4.2. Effect of the data heterogeneity on the classification performance

Our results, taken together with previous reports, indicate that generalizing a classifier across different age groups and acquisition sites is difficult. We observed differences in accuracies when the model trained on data acquired at particular sites or age ranges were tested on data from a different age range or acquisition site (Table 4, Figs. 10–12). In many studies, matching for age, sex, motion, scanning protocol, acquisition site, and IQ may not be feasible between the training/validation and the hold-out test data as well as between the controls and the clinical group. This is truer for datasets which are pooled from many acquisition sites retrospectively, given the prohibitive costs involved in acquiring such large data homogeneously and prospectively [(although large retrospective studies have gotten underway recently. E.g. UK biobank study (Miller, et al., 2016)]. It is also possible that clinical populations in a particular age range might exhibit over-connectivity compared to age-matched Controls while subjects with the same clinical diagnosis from a different age range may exhibit under-connectivity compared to age-matched Controls, as in ASD, due to brain plasticity and other compensatory mechanisms.

Data from different scanning sites are associated with variability in scanning equipment, scanning parameters, demographic, genetic, and other experimental factors (Demirci, et al., 2008). The datasets we encounter might not sample the entire population distribution. CV accuracy and hold-out test accuracy in our results suffer due to two primary factors. The first factor is the difficulty in generalizing the classifier to variations in the clinical populations. The second factor is the bias introduced by feature selection on the training/validation data. Because of this bias, choosing the optimum model from a large number of models with limited validation data is difficult, as the data samples we collect might not adequately sample the population distribution space and the performance estimates of the models may be unreliable. Hence, the selected hyperplane may deviate from the optimum separating hyperplane in the population.

With low disorder/disease prevalence and the high heterogeneity in clinical populations, identifying reliable biomarkers with high sensitivity to the disorder/disease as well as good generalization in the population can only be achieved with the help of large collaborative multisite neuroimaging efforts even if they are put together retrospectively (Arbabshirani, Plis, Sui, & Calhoun, 2017; Castellanos & Aoki, 2016). Examples of such efforts include ADNI for Alzheimer’s disease (Mueller, et al., 2005), ABIDE for autism (Di Martino, et al., 2014), ADHD-200 for ADHD (Consortium, 2012), 1000 functional connectomes project for healthy subjects (Biswal, et al., 2010), and International Neuroimaging Data-sharing Initiative (INDI) (Mennes, Biswal, Castellanos, & Milham, 2013). The classification performances tested on such large datasets help in reproducibility and generalizability of classification results. Three of the four datasets we used – ADNI, ABIDE and ADHD-200 – are from collaborative multisite acquisitions. Hence, even if our accuracy appears to be lower compared to that reported by single-site studies with relatively smaller sample sizes, we expect our classification accuracy, and consequently the disorder/disease encoding neuroimaging features, to generalize well to the larger clinical population. Another factor limiting the utility of automated diagnostic tools is low disorder prevalence in the general population. For developing diagnostic classification tools for the general population, low prevalence of the disorder could lead to large false positives despite high specificity, thereby limiting its usefulness.

Since we are using supervising machine learning, the performance of our algorithms is constrained by the ability of current clinical diagnostic instruments to accurately represent the neurobiology of the underlying disorders. Therefore, the diagnostic label associated with spectrum disorders such as autism spectrum disorder might not be entirely informative given the potential of multiple etiologies, and thus, finding biomarkers and attaining reliable predictors is difficult (Arbabshirani, Plis, Sui, & Calhoun, 2017). Many disorders are highly heterogeneous, and clinical variability within many disorders is yet to be thoroughly established. Also, some disorders have a range of symptom/disability severity that may be influenced by age, such as cognitive impairments in Alzheimer’s disease. Another issue which is gaining attention is dual-diagnosis and high comorbidity of some disorders, which can contribute to the difficulty in classifying the actual disorder state of the subject using predictive learning models.

The above factors can make classification of sub-classes within spectrum disorders extremely difficult. All classifiers we tested struggled with the multiclass classification for almost all datasets compared to binary classification when using the hold-out test dataset. In a three-way classification between healthy controls, Asperge’s syndrome, and autism, most classifiers failed to discriminate even a single subject with Asperge’s syndrome accurately in the hold-out test data (Tables S2, S8, S14). The 3-way classification between healthy controls, ADHD-I, and ADHD-C, (Table S16) resulted in decreased accuracy compared to binary classification between healthy controls and ADHD (Table S15). As discussed previously, the presence of multiple diagnoses, over-diagnosis and/or misdiagnosis hinders supervised classification. One way to overcome this issue will be to use unsupervised classification to drive subject labeling (Zhao, Rangaprakash, Dutt, & Deshpande, 2016; Gamberger, Ženko, Mitelpunkt, Shachar, & Lavrač, 2016). In the case of ADNI dataset the high accuracy obtained from the four-way classification using cross-validation did not generalize well to the holdout test dataset (Figs. S7, S10). The primary factor contributing to the low accuracies in multiclass scenarios is the lack of large training data available for disorder/disease subtypes, which is particularly the case for the ADNI dataset and the Asperge’s sample in the ABIDE dataset.

4.3. Issues with performance estimation and feature selection for small datasets

Cross-validation accuracy is an unreliable estimate of the true generalization accuracy in small datasets (i.e., few hundreds of samples) (Isaksson, Wallman, Göransson, & Gustafsson, 2008; Rao, Fung, & Rosales, 2008; Varoquaux, 2018; Varoquaux, et al., 2017). When we use cross-validation to select a large number of models, we risk overfitting and choosing the less optimal model, due to large error bars and random effects. In machine learning literature, it is widely accepted that cross-validation performance is an ineffective measure of the true generalization performance due to the large variance associated with its estimates (Cawley & Talbot, 2010; Varoquaux, 2018; Varoquaux, et al., 2017). Yet, this fact is not widely appreciated in the neuroimaging community (Castellanos, Di Martino, Craddock, Mehta, & Milham, 2013; Varoquaux, 2018). Also, in smaller datasets, the hyperparameter values selected by minimizing the validation error might be tailored to the sample used for training and validation. This leads to overfitting in model selection, and hence, provides a biased estimate of classification performance in such small samples (Cawley & Talbot, 2010). As we have shown in Fig. 14, model selection by parameter optimization does not improve the performance in ADNI data in contrast to ABIDE data. In fact, model selection by parameter optimization in ADNI data performs significantly worse compared to the case without parameter optimization. In ABIDE data, the optimal model can be selected based on cross-validation, as the cross-validation estimate is more reliable due to the size of the dataset. Similar to performance estimation, this fact also rings true in wrapper methods for feature selection or model selection when we use cross-validation with small datasets with higher dimensional features, as is the case for typical neuroimaging datasets. It is noteworthy that datasets with hundreds of subjects are considered large in neuroimaging (which may be true for detecting activation and even for characterizing resting state networks). However, they are small, given the dimensionality of the data, and the goals we are trying to achieve with machine-learning based supervised diagnostic classification. This problem unfortunately is only exacerbated by multiple nested CV loops required for feature selection, parameter optimization and performance estimation, steps that might be essential for obtained unbiased estimation of classification performance in diagnostic classification scenarios. This results in increased computational time and the fraction of training data available in the CV folds for the inner loops decreases accordingly, by having multiple cross-validation loops, which may not be ideal for smaller datasets.

Given the problems associated with the “curse of dimensionality,” reducing the number of features is important (Mwangi, Tian, & Soares, 2014; Brown & Hamarneh, 2016). Although useful for reducing features to more manageable numbers, t-test filtering might not be the best initial feature selection method as T-scores of features can, in principle, vary drastically across different folds of training data; and consequently, have poor predictive power (Venkataraman, Kubicki, Westin, & Golland, 2010; Arbabshirani, Plis, Sui, & Calhoun, 2017). In t-test filtering, we are using statistical separation as a proxy for discriminative power, which may not be true in some instances, especially if groups of features, when combined, provide discriminative ability in comparison to when used alone. Therefore, a filtering strategy by univariate tests might remove features with discriminative ability, especially since those features are not selected based on a metric which directly assesses their discriminative power (Venkataraman, Kubicki, Westin, & Golland, 2010). Our results indicate such dangers posed by the use of filter methods such as t-test filtering, as shown by the substantial variance in the selected feature importance scores and potential overfitting in small datasets such as PSTD (Fig. S14) and ADNI (Fig. S15). Therefore, instead of feature selection by t-test filtering, quick and reliable methods such as GINI index might be superior as they can provide a better estimate of feature importance (Venkataraman, Kubicki, Westin, & Golland, 2010).

In our study, many classifiers implemented within the RCE framework resulted in better performance compared to the classifiers not implemented within RCE. The performance of the classifiers improved as the sample size increased. However, wrapper methods such as RCE also have limitations. Specifically, the inner cross-validation we use in RCE for model selection does not reliably select the true model of the mapping between inputs and outputs in smaller datasets such as ADNI (Fig. 13). This results in non-significant changes in accuracy per cluster in the validation data when such features are removed from the training data. In fact, models are prone to overfitting when a large number of models are tested against small samples of data (Rao, Fung, & Rosales, 2008), which holds true when RCE and/or parameter optimization is used in small datasets. Along with its feature reduction capabilities, RCE framework (and wrapper methods in general) has significant downsides as well, such as the difficulty in optimizing its tunable parameters. For obtaining the best results from RCE framework, we have to consider the dimensionality of each cluster, the computation time, number of clusters/models that we choose from, and the number of features which needed to be eliminated at each step of the algorithm.

In our study, many features which had significant group differences were not useful in classification, and some features with good classification scores did not necessarily show significant group differences as these are univariate, whereas classification methods are multivariate. Therefore, we investigated features which were significantly different between the groups as well as had high discriminative/predictive ability (high feature importance scores or FIS). Since different classifiers are sensitive to different patterns of features (Brown & Hamarneh, 2016), the FIS obtained for the same features from different classifiers can, in principle be, different. Therefore, we combined the FIS obtained from multiple classifiers for a given feature to provide a single combined feature importance score (CFIS). CFIS is our novel contribution, and has not been done in previous studies to the best of our knowledge.

Finally, it is important that features are not selected using the entire dataset as it could lead to overoptimistic results, which could generalize poorly to unseen data. Unfortunately, this practice is quite common in neuroimaging, and it could lead to the leakage of information from training data to test data. This is sometimes referred to as “double dipping” (Kriegeskorte, Simmons, Bellgowan, & Baker, 2009) and could result in extremely optimistic accuracies in smaller datasets with large number of features (Foster, Koprowski, & Skufca, 2014). In our results, some of the difference in CV accuracy and the test accuracy, even in the case where the training/validation data and the hold-out test data are matched for age and imaging site, can be attributed to the t-test filtering performed on just the training/validation data. It should also be noted that if the features selected by the t-test indeed do have predictive power and are mostly reproducible, especially for larger datasets, then feature selection by t-test filtering should have a minimal impact on the classification accuracy.

Dividing the data into training/validation and hold-out test data and performing feature selection only using the training/validation data, may not be feasible in smaller datasets which are typical in neuroimaging. It is likely that the use of classifiers, with built-in feature selection such as SLR or feature ranking such as random forest, might be the way forward with feature reduction in noisy and relatively small datasets. It is also important to remember that the hold-out test accuracy is a conservative estimate of the actual predictive performance, and hence, is a better indicator of the performance on unseen data - especially in disorders with high heterogeneity and/or features which are not highly reproducible.

4.4. Issues with the use of machine learning classifiers

The choice of the classifier and the features extracted are extremely crucial in providing insights about the neurobiological origins of various disorders and diseases. There is no universally best learning algorithm that gives excellent performance for all datasets and features. So, it is extremely difficult to know beforehand which classifier might give the best performance. High prediction accuracy and interpretability of the classifier model are somewhat conflicting goals in neuroimaging (Kelly, Biswal, Craddock, Castellanos, & Milham, 2012). Using complex classifiers with RBF kernels or neural networks might give excellent performance, but utility in translating the models to understanding the disrupted neural circuits in neurological disorders and diseases is limited given the “black box” nature of such classifiers. Also, non-linear methods might not give optimal performance compared to linear methods when available training data is limited in order to model the complex relationships between the features and the disease status of the subject. In fact, the relative success of linear classifiers in neuroimaging is not due to the absence of complex relationships between features and subjects’ diagnostic status, but rather the unavailability of large datasets required to model such relationships (Pereira, Mitchell, & Botvinick, 2009). In our study, we get the best of both the worlds in our use of machine learning classifiers in that we achieve high prediction accuracy as well as interpretability for our results. Due to the use of multiple classifiers within the RCE framework, we were able to leverage the strengths of multiple types of machine learning classifiers, not only to improve the stability and robustness of the classification performance, but also to provide us with scores for feature importance (CFIS). CFIS were then used to identify the connectivity paths and regions encoding the states for the various disorders studied. This greatly aids in interpretability of our results and provides us with valuable information about connectivity dysregulation in the clinical populations.

To facilitate comparison of the performance of classifiers across different datasets and splits, we tabulated the balanced CV accuracy and the balanced hold-out accuracy for all the 18 different classifiers (KNN was implemented twice, within and outside the RCE framework), in Tables S24, S25 and S26 for ABIDE, PTSD and ADNI respectively, for the binary classification scenarios. Compared to other classifiers, generally the difference between cross-validation and the hold-out test accuracy was generally small for boosted trees and stumps, indicating that it may not be overfitting the data compared to other classifiers. This may be because boosting is generally considered relatively robust to overfitting (Vezhnevets & Barinova, 2007; Grove & Schuurmans, 1998). Another observation from our results pertains to models with built-in regularization. Models with regularization to control model complexity performed consistently across all datasets. In fact, sparse models such as RVM, SLR, RLR, and regularized neural networks gave consistently good performance across most datasets and the multiple splits we performed on each dataset. Therefore, we believe that quality and the quantity of the data available should guide the best feature extraction methods as well as the choice of the classifier for each study.

In some cases, the classifiers which performed best on the cross-validation dataset did not perform as well on the hold-out test data. It is possible that by reporting only the results of the classifier having the best performance, we are prone to using optimistic estimates of classification performance which might not even generalize well to subjects from the same population (Brown, et al., 2012). It is one of the reasons as to why we combined predictions from multiple classifiers to build an ensemble classifier, which we call the consensus classifier, rather than reporting and emphasizing accuracy obtained by the best classifier. Also, combining multiple predictions from different classifiers can usually improve the overall classification performance as different types of classifiers rarely make the same kinds of mistakes on unseen data.

4.5. Issues with disorder/disease classification using RSFC metrics

Some issues we have not considered in this study might influence reported classification performance. The confounding effects of head motion and the correction strategies applied to ameliorate head motion artifacts, inclusion/exclusion of global signal regression in the preprocessing pipeline, spatial variation in the Hemodynamic response function across brain regions and subjects, as well as the duration of the scans can affect the reliability and reproducibility of RSFC metrics. All of these aspects might ultimately affect classification performance. However, there is no general consensus in neuroimaging community on how to address these issues.

Scan duration is of particular importance in clinical populations when motion corrupted volumes are removed from the data (censoring). It is crucial to have the necessary amount of data to reliably estimate RSFC metrics. Also, proper motion correction might improve the accuracy in classifying healthy controls from clinical subjects (Fair, et al., 2013). The easiest way to potentially increase the accuracy of classification is to have longer scans times to make the features derived from RSFC more reliable (Anderson, Ferguson, Lopez-Larson, & Yurgelun-Todd, 2011; Birn, et al., 2013).

4.6. Multimodal imaging

RSFC measures may not necessarily contain discriminative information for all mental disorders. With the rise of multimodal imaging, using multiple imaging metrics as features can capture different aspects of neuropathology. Structural connectivity measures obtained from DTI, morphological features from anatomical images, network theoretic measures derived from graph theory such as local connectivity, global efficiency, clustering coefficient, network modularity, characteristic path length (etc.), RSFC derived measures such as amplitude of low-frequency fluctuations/fraction of amplitude of low-frequency fluctuations, regional homogeneity, degree centrality, seed-based connectivity, causal directional relationships between brain regions (effective connectivity) (Deshpande, LaConte, James, Peltier, & Hu, 2009) or use dynamic measures of synchronization between brain regions (dynamic functional and effective connectivity) (Wang, Katwal, Rogers, Gore, & Deshpande, 2017), task-based activation, as well as measures derived from magnetic resonance spectroscopy, could potentially be used as features to train classifiers. Multimodal measures have been used for classification in autism with good results (Price, Wee, Gao, & Shen, 2014; Libero, DeRamus, Lahti, Deshpande, & Kana, 2015). In fact, to build a better model, along with multimodal imaging, we can move beyond imaging metrics and incorporate prior information about the disease/disorder prevalence and its distribution in the population based on demographic and phenotype data into the classification algorithm. The results reported by several research groups who participated in the ADHD-200 global competition (Consortium, 2012) suggest that better accuracies can be achieved by combining neuroimaging data with the phenotypic data, rather than by using neuroimaging-based data alone.

4.7. ASD

In the binary classification of controls versus ASD, we achieved accuracy as high as 67.2% (balanced accuracy of 66%) on the separate hold-out test dataset (Table 4) for the homogenous-matched case scenario. However, when the training/validation and the hold-out datasets are from different age ranges, the accuracy was reduced to 66.2% (balanced accuracy of 60.1%). In fact, the impact of age on the classification performance in the ABIDE data has been previously documented by Vigneshwaran et al. (2015). They report higher accuracies on the hold-out test dataset when adult males and adolescent males (age<18) were considered separately in classification, than when all male subjects were considered (Vigneshwaran, Mahanand, Suresh, & Sundararajan, 2015). This study also reports higher hold-out test accuracy for adult males compared to adolescents, indicating the difficulty in classifying ASD in adolescents compared to young adults using RSFC metrics. The results of this study contradict an earlier study which obtained better classification performance for adolescents (89% with LOOCV, 91% with replication dataset) compared to young adults (79% with LOOCV, 71% with replication dataset) with 80 subjects for training/validation and 21 subjects in the replication dataset (Anderson, et al., 2011). Age dependence is to be expected since ASD is a developmental disorder with atypical developmental trajectories including compensatory mechanisms in adulthood (Gentile, Atiq, & Gillig, 2006; Maximo, Cadena, & Kana, 2014). Previous studies have reported increased resting state functional connectivity in ASD subjects under the age of : 12 years, while studies involving adolescents and adults have reported reduced functional connectivity compared to healthy controls (Uddin, Supekar, & Menon, 2013). Also, behavioral measures have been shown to outperform fMRI-based measures for supervised classification of autism (Plitt, Barnes, & Martin, 2015). Previous studies report accuracies in the mid to high 70s for single site studies with 40–80 subjects (Anderson, et al., 2011; Uddin, et al., 2013). The classification accuracy drops as the size of the dataset increases, with 79% LOOCV accuracy reported with 240 subjects (Chen, et al., 2016) and dropping to as low as 60% LOOCV accuracy with 964 subjects (Nielsen, et al., 2013) in multisite studies using the ABIDE dataset. Motion does seem to play a signficant role in reducing classification performance as several studies using low-motion subjects achived much higher accuracies. Using 252 low-motion, age and motion matched cohorts from ABIDE, Chen et al (2015) achieved accuracies an of 91% (1- out of bag error (OOB)) with Random forests (Chen, et al., 2015), and using 640 subjects with age<20, Iidaka (2015) achieved cross-validation accuracy of 90% with probabilistic neural network (Iidaka, 2015). It is noteworthy that these high accuracies have been obtained using cross-validation. Differences between the training/validation and the hold-out test data in several factors such as imaging site, head motion, age, sex, IQ, and imaging protocol can cause an overestimation of classification accuracy in cross-validation and may not be representative of the population, or the clinical diagnosis scenario. In fact, compared to 91% accuracy reported by using OOB error for random forests, considerably lower accuracies of 62% was obtained from hold-out test data in the same study (Chen, et al., 2015).

ASD involves disruptions of interacting large-scale brain networks distributed across the brain (Gotts, et al., 2012). We observed both under-connectivity and over-connectivity in subjects with ASD compared to the controls (Fig. 15) as reported in previous studies (Uddin, et al., 2013; Maximo, Cadena, & Kana, 2014). In fact, several of the regions (Table S20) and connectivity paths (Fig. 15) obtained in this study were also shown to be implicated in autism (Cheng, Rolls, Gu, Zhang, & Feng, 2015). Many regions associated with the default mode network such as posterior cingulate cortex (PCC), precuneus, medial prefrontal cortex (MPFC), and angular gyrus were found to be disrupted in subjects with ASD as several previous studies have indicated (Assaf, et al., 2010; Di Martino, et al., 2014; Monk, et al., 2009; Washington, et al., 2014). The MPFC and anterior cingulate cortex (ACC) are involved in social processing (Mundy, 2003), and hence, are likely to be altered in subjects with ASD. Using ABIDE dataset, Iidaka (2015) found that the superior frontal gyrus (SFG), ACC & PCC as well as the thalamus were most disrupted in autism (Iidaka, 2015). Connectivity between the fusiform gyrus (FG) and middle occipital gyrus (MOG) (Di Martino, et al., 2014) was reported to be lower in children with autism compared to controls, which might explain the difficulty in facial information processing for subjects with autism. Other regions involved in autism include caudate and thalamus. Middle temporal gyrus (MTG) is implicated in speech processing, Theory of Mind, and memory encoding and has also been shown to be affected by ASD (Cheng, Rolls, Gu, Zhang, & Feng, 2015; Salmond, et al., 2005). The features we identified not only had predictive power, but also had statistically significant univariate group differences across all the 3 splits accounting for variations in age and acquisition site. Therefore, it is likely that these features are robust to age changes and variations in acquisition sites. This factor is especially crucial given the atypical developmental trajectories in ASD. Therefore, unlike results reported by other studies which may have considered narrow age ranges, the connectivity paths we identified are reliable across age variations, though further study is necessary to confirm our findings about the age invariance of disorder encoding paths and regions involved in ASD.

4.8. ADHD

For ADHD, we report accuracies of 57.2% and 54.1% for binary and multiclass classification, respectively (Table 4). Although we did not perform the classification strictly according to the ADHD-200 competition guidelines (Consortium, 2012), it is still crucial to examine the results obtained from the competition because it elicited a response from several research institutions on a common dataset. The winning team for the competition from Johns Hopkins University reported classification results on the hold-out test dataset release by the competition with a specificity of 94% and a sensitivity of 21% using a weighted combination of several algorithms (Eloyan, et al., 2012). Most teams reported hold-out test accuracies in the range of 37.4–60.5%, which are similar to those obtained by us. In fact, using just phenotypic data allowed a team from University of Alberta to achieve a higher accuracy (62.5%) than using neuroimaging-based metrics (Brown, et al., 2012). Combining phenotypic data with imaging data helped several groups to achieve higher accuracies than using imaging data alone (Sidhu, Asgarian, Greiner, & Brown, 2012; Colby, et al., 2012). Using ADHD-200 data, Colby et al. reported using site-specific classifiers and suggested that the top features varied across sites, and classifiers trained with data across imaging sites performed worse than classifiers trained using data from the same imaging site (Colby, et al., 2012). Similar to our results, none of their classifiers performed well for the 3-way classification between controls, ADHD-I, and ADHD-C. Though these accuracies were above chance levels, they still highlight the challenges encountered in neuroimaging-based metrics from multisite acquisitions (Consortium, 2012). By combining structural, functional and demographic information, an accuracy of 55% with 33% sensitivity and 80% specificity was achieved (Colby, et al., 2012). Many studies reported higher accuracies classifying the subtypes of ADHD i.e. ADHD-I from ADHD-C than the between controls and ADHD (Deshpande, Wang, Rangaprakash, & Wilamowski, 2015; Colby, et al., 2012; Eloyan, et al., 2012). This result is surprising given that we expect children with ADHD subtypes to be more similar to each other than with healthy controls. It is not clear at this stage whether it is due to the base rate (true positives and false positives) of the ADHD diagnostic instruments (i.e., misdiagnosis), or the complex etiologies of ADHD and related neurological underpinnings, or an artifact of the peculiarities of the ADHD-200 data. Some studies achieved higher performance of 80–85% using LOOCV and regional homogeneity features in a relatively small sample (20–46 subjects) of age-matched populations (Zhu, et al., 2008; Wang, Jiao, Tang, Wang, & Lu, 2013). Using the entire dataset and artificial neural nets based on deep learning architectures, LOOCV accuracies of 80% have been reported in classifying controls from ADHD-I and controls from ADHD-C, and 95% in classifying the ADHD subtypes (Deshpande, Wang, Rangaprakash, & Wilamowski, 2015). Since the ADHD-200 competition closely resembles real world classification scenarios, the challenges in classification encountered in this dataset, will apply to future studies utilizing multisite acquisitions.

From our results as well as from those reported previously, it is apparent that ADHD is characterized by large-scale disruptions in connectivity in the frontal and the temporal lobes. We did not find a lot of overlap between the connectivity paths for the two-way and the multiclass classification though roughly the same brain regions appear to be involved in both classification schemes (Fig. 16, Table S21). In fact, one of the top regions associated with changes in functional connectivity is the dorsal region of the anterior cingulate cortex (d-ACC). It is one of the most critical nodes involved in ADHD, playing a key role in attention (Casey, et al., 1997; Bush, et al., 1999). ACC and insula are part of the salience network and have been previously implicated in ADHD (Lopez-Larson, King, Terry, McGlade, & Yurgelun-Todd, 2012). This result is not surprising as these regions are involved in attention and control (Menon & Uddin, 2010). Dorsolateral prefrontal cortex (DLPFC), anterior prefrontal cortex (aPFC) and caudate are part of the executive control network and these regions along with the supplementary motor area (SMA) are involved in attentional control (Castellanos & Proal, 2012; Elton, Alcauter, & Gao, 2014). Along with these networks, DMN also plays a crucial role in ADHD (Konrad & Eickhoff, 2010; Tomasi & Volkow, 2012; Elton, Alcauter, & Gao, 2014; Castellanos & Aoki, 2016; Mostert, et al., 2016). Several studies have demonstrated the role of the frontal cortex, caudate, basal ganglia, insula, and cingulate gyrus in ADHD (Aylward, et al., 1996; Garrett, et al., 2008; Rubia, et al., 1999; Qiu, et al., 2011; Dickstein, Bannon, Xavier Castellanos, & Milham, 2006; Tian, et al., 2006; Cortese, et al., 2012). The connections between the nodes in the frontal cortex and basal ganglia form a part of the frontal–striatal network which is involved in response inhibition (Aron & Poldrack, 2006; Cubillo, et al., 2010; Makris, Biederman, Monuteaux, & Seidman, 2009) with inferior frontal gyrus (IFG) playing an especially important role in salience processing and initiation of the response inhibition signal. Though several networks such as salience network, executive control network and default mode network are implicated in ADHD, only a subset of connections between the regions seemed to have predictive power as well as statistical separation as our results indicate (Fig. 16). In accordance with our results connectivity between IFG, ACC, SFG, and temporal regions have been reported to be altered in ADHD (Rooij, et al., 2016). There is also growing evidence of temporal lobe as a key area for ADHD (Kobel, et al., 2010; Carmona, et al., 2005; Sowel, et al., 2003), though further studies might be needed to support our findings. Our results are in general conformity with prior results discussed above.

4.9. PCS & PTSD

We achieved excellent performance in classifying subjects with PTSD from controls in age-matched (Figs. 3, S6) training/validation and hold-out test data than in the unmatched scenario (Figs. 6, S9, Table 4). This result underscores the issues with overfitting the data. Unfortunately, there are not many studies which used RSFC or RSFC- derived metrics for classification of PTSD. However, the few studies which looked at the classification of PTSD using RSFC indicate that by integrating multiple features, higher accuracies can be achieved. Using features derived from both RSFC and amplitude of low-frequency fluctuations (ALFF), Liu et al. obtained cross-validation accuracies of 92.5%, an increase of 17.5% in the cross-validation accuracy compared to using just ALFF in a sample containing 40 subjects (Liu, et al., 2015). Using gray matter volume from structural MRI, as well as ALFF and regional homogeneity from Rs-fMRI, an LOOCV accuracy of 90% was obtained in classifying controls from PTSD using a multi-kernel SVM classifier in a sample containing 37 trauma exposed subjects (Zhang, et al., 2016).

Some of the most important regions associated with PTSD classification which we obtained (shown in Fig. 17, Table S22), such as right superior frontal gyrus, cingulate gyrus, right middle temporal gyrus, calcarine fissure and lingual gyrus, have been reported to have alterations in PTSD before (Yin, et al., 2012; Zhang, et al., 2016; Liu, et al., 2015). Several of our top classification paths involved regions such as middle occipital gyrus (MOG), angular gyrus, cuneus, middle temporal gyrus (MTG), (Christova, James, Engdahl, Lewis, & Georgopoulos, 2015), cingulate gyrus (CG), calcarine fissure, and occipital cortex (Liu, et al., 2015). Many functional connectivity paths in the visual areas were observed in our study, and is in agreement with previous reports of such alterations in PTSD (Zhu, et al., 2014; Bremner, et al., 1999; Bremner, et al., 2004; Liu, et al., 2015; Chao, Lenoci, & Neylan, 2012). These alterations may be associated with visual imagery in PTSD (Clark & Mackay, 2015). Increased activity in the superior frontal gyrus and middle temporal gyrus might be linked to anxiety and have been shown to be affected in subjects with PTSD (Kroes, Rugg, Whalley, & Brewin, 2011). Regions identified in our study such as middle cingulate cortex, thalamus are some of the regions reported to be affected by PTSD along with some other regions not identified as important such as hippocampus, putamen, amygdala, insula, orbitofrontal cortex (OFC) and ACC (Zhong, et al., 2015; Lanius, et al., 2005; Shin, et al., 2004; Zhu, et al., 2014; Dunkley, et al., 2014; Lei, et al., 2015; Li, et al., 2016).

4.10. MCI and AD

In previous classification studies of MCI and AD, integration of imaging modalities such as diffusion tensor imaging (DTI) and Rs-fMRI achieved a much higher cross-validation accuracy of 96.3% than Rs-fMRI alone, which achieved only 70.37%, in cross-validation accuracy in a dataset of 27 subjects (Wee C.-Y., et al., 2012). Even when classifying healthy controls from patients with AD, a relatively lower cross-validation accuracy of 74% for Rs-fMRI was achieved using a dataset containing 43 subjects (Dyrba, Grothe, Kirste, & Teipel, 2015). Employing the same dataset by integrating multiple imaging modalities such as DTI, Rs-fMRI and gray matter volume, a much higher cross-validation accuracy of 85% was reported (Dyrba, Grothe, Kirste, & Teipel, 2015). This result is similar to our results in the age-matched split in which we achieved a hold-out test accuracy of 76.9% and a balanced hold-out test accuracy of 78.6% (Table 4). In an age-matched sample of 40 subjects, using graph theory-based metrics derived from Rs-fMRI data, Khazaee et al. achieved an LOOCV accuracy of 100% in classifying patients with Alzheimer’s disease using Linear-SVM (Khazaee, Ebrahimzadeh, & Babajani-Feremi, 2015). In a sample containing 27 subjects with AD, 50 with MCI and 30 controls, using Bayesian Gaussian process logistic regression (GP-LR) model, Challis et al. (2015) achieved an accuracy of 75% in separating healthy controls from MCI and 97% in separating MCI from AD on a hold-out test data (Challis, et al., 2015). Using network-based measures several studies obtained a LOOCV accuracy in the range of 86% to 92% in separating in controls from MCI (Jie, et al., 2014; Jie, Zhang, Wee, & Shen, 2014; Wee C., Yap, Zhang, Wang, & Shen, 2012) on a dataset with 12 subjects with MCI and 25 healthy controls. Similar to our results, a study using structural MRI, Positron emission tomography (PET) and cerebrospinal fluid data from ADNI, does indicate the relative ease in separating healthy controls from Alzheimer’s than from MCI and healthy controls (Zhang, Wang, Zhou, Yuan, & Shen, 2011).

Our results (Fig. 18) indicate that the connectivity paths between fusiform gyrus and insula, cuneus and inferior frontal gyrus seem to be most important in the binary and multiclass classification of early and late MCI and Alzheimer’s disease. Since the data size was small for this dataset, very few paths crossed significance for both age-unmatched and the age-matched split. Since the features we observe are a subset of features which satisfy 3 criteria: (i) Robust to effects of age (ii) High predictive ability (iii) statistically significant group difference, very few features are reported for this dataset. So fusiform gyrus is associated with visual cognition and plays a key role in MCI and AD (Cai, et al., 2015). Insula, on the other hand, is associated with perception, cognition, emotion and self-awareness (Craig, 2009; Karnath, Baier, & Nägele, 2005; Devue, et al., 2007) and has been implicated in Alzheimer’s disease as well (Foundas, Leonard, Mahoney, Agee, & Heilman, 1997; Karas, et al., 2004; Rombouts, et al., 2000). We found several brain regions in the temporal lobe (Table S23) to be affected in Alzheimer’s disease, including the hippocampus, temporal pole, parahippocampal gyrus. These regions are involved in memory related processes (Rombouts, et al., 2000) and have been implicated in AD before (Allen, et al., 2007; Wang, et al., 2006; Bai, et al., 2009; Celone, et al., 2006; Galton, et al., 2001). Along with regions in the temporal gyrus, other regions with discriminative ability in MCI as reported in other studies include insula, precuneus and inferior frontal gyrus (Farràs-Permanyer, Guàrdia-Olmos, & Peró-Cebollero, 2015; Wee C., Yap, Zhang, Wang, & Shen, 2012). Given that the regions involved in functional connectivity paths are in general conformity with the existing results, it is likely that the few connectivity paths we identified might have large discriminative ability and is robust to variations in age.

In summary, the findings from our results indicate that cross-validation accuracy, although ubiquitously used in neuroimaging, is a biased measure of true classifier performance and hold-out test data must be used to assess the ability of the classifier to generalize to the population. Also, extraneous variables such as age and site acquisition variability might have a significant impact on classification accuracy, particularly in smaller samples. Our results also underline the difficulty in achieving a high accuracy and good generalization performance especially in heterogeneous clinical populations. With better understanding of the progression of the disorders and continued research in the sensitivity of neuroimaging derived metrics to the underlying pathology, neuroimaging-based machine learning tools could conceivably be used to aid the clinician in diagnosis in the future. But several challenges involved with classification of various disorders and diseases, as mentioned previously in the paper must be addressed before we get there.