Abstract
The nuclear environment is highly crowded by biological macromolecules, including chromatin and mobile proteins, which alter the kinetics and efficiency of transcriptional machinery. These alterations have been described, both theoretically and experimentally, for steady-state crowding densities; however, temporal changes in crowding density (“dynamic crowding”) have yet to be integrated with gene expression. Dynamic crowding is pertinent to nuclear biology because processes such as chromatin translocation and protein diffusion lend to highly mobile biological crowders. Therefore, to capture such dynamic crowding and investigate its influence on transcription, we employ a three-pronged, systems-molecular approach. A system of chemical reactions represents the transcription pathway, the rates of which are determined by molecular-scale simulations; Brownian dynamics and Monte Carlo simulations quantify protein diffusion and DNA-protein binding affinity, dependent on macromolecular density. Altogether, this approach shows that transcription depends critically on dynamic crowding as the gene expression resultant from dynamic crowding can be profoundly different than that of steady-state crowding. In fact, expression levels can display both amplification and suppression and are notably different for genes or gene populations with different chemical and structural properties. These properties can be exploited to impose circadian expression, which is asymmetric and varies in strength, or to explain expression in cells under biomechanical stress. Therefore, this work demonstrates that dynamic crowding nontrivially alters transcription kinetics and presents dynamic crowding within the bulk nuclear nanoenvironment as a novel regulatory framework for gene expression.
Significance
Crowding is a consequence of the confined nature of cells. Within the cell, both biological macromolecules and chromatin, termed crowders, importantly influence reactions, including the transcription of genes with which they do not specifically interact. However, as far as we know, crowding has only been considered at steady state; therefore, it is unclear how crowding kinetics influence transcription. We developed a model of transcription that accounts for time-dependent crowding (“dynamic crowding”). We show that dynamic crowding, in addition to average crowding effects, can cause differential expression to a given gene, regulate circadian expression, and alter the expression of cells under stress. This demonstrates an additional mechanism through which crowding may, to a great extent, regulate transcription in vivo.
Introduction
Living cells contain a significant fraction of macromolecules, which not only participate directly in their target reactions, but also exclude volume from, and thereby influence, adjacent reactions. These macromolecules are termed “crowders” and comprise the physical cellular environment. In the cytoplasm, this physical environment is created by macromolecules such as the cytoskeleton and organelles, which occupy 15–25% of the volume (1). In the nucleus, this fraction is even higher. The ∼98% of chromatin that is noncoding, as well as mobile proteins, occupy 20–40% of the nuclear volume (1, 2, 3, 4, 5). In fact, this noncoding chromatin, including the three-dimensional (3D) chromatin packing structure, comprises a significant fraction of the nucleus. Consequently, crowding from adjacent noncoding DNA segments, though not directly involved in transcription reactions, could still greatly impact their kinetics and equilibria. By occupying space and excluding volume from the cellular interior, crowders sterically hinder the diffusion of protein machinery (6, 7, 8, 9) and promote binding through attractive depletion interactions of entropic origin (5,10, 11, 12, 13). In these ways, crowding affects the accessibility, availability, and thermodynamic activity of protein machinery, which shifts chemical equilibria and influences reaction rates.
Pioneering work in biological crowding was first presented by Minton in 1981, in which statistical mechanical models were used to represent the effects of crowding volume exclusion on reactions and macromolecular stability (8). Since then, numerous in vitro models have confirmed both the existence and potency of the volume exclusion theory of biological crowding. Of important consequence to gene transcription, these studies have established that crowding can alter the equilibria and efficiency of protein folding (12,14, 15, 16, 17, 18), enzyme activity (11,16,19, 20, 21, 22), and DNA condensation (23). Some studies have even demonstrated that differential crowding can induce transcriptional bursting (24) and alter DNA replication (25). However, though these studies indicate that crowding would significantly alter eukaryotic transcription, these and other studies investigate crowding in the cytoplasm (12,21, 22, 23) or artificial crowding environments (12,14,15,17, 18, 19, 20,24,25). These same effects in the nucleus have yet to be studied in depth.
Notably, there has been some similar experimental observations of nuclear crowding. Studies have noted reduced diffusion and binding of nuclear proteins to heterochromatin (26), chromatin condensation (27), and RNA synthesis shut off (28) under high nuclear crowding conditions. In addition, molecular dynamics simulations probed atomistic details of crowder motion or nuclear body formation (29,30), Monte Carlo (MC) simulations determined probable conformations of proteins or chromatin under crowded conditions (31, 32, 33), and mathematical models investigated the effect of crowding on network reactions (34,35). However, current understanding of the effect of macromolecular crowding on transcription and other biological phenomena is still incomplete; current studies do not account for one crucial aspect of physiologic crowding: kinetics.
Crowding kinetics are present on many scales because of the movement of almost every nuclear constituent. Globally, crowding density can be altered because of changes in cell volume (5,36,37) or nuclear shape, which has been shown to fluctuate on the order of seconds (38). Within this fluctuating volume, proper nuclear function necessitates constant movement. Transcription and replication require proteins to diffuse through the nuclear space to sample the genome (39, 40, 41), whereas chromatin reorganizes to facilitate access to genes of interest and, in doing so, compacts adjacent nucleosomal regions (42,43). In fact, a recently burgeoning amount of experimental evidence has demonstrated that chromatin is highly dynamic. Topologically associated domains, largely mediated by DNA loops, consistently form and dissolve (44), whereas chromatin coherently migrates throughout the nuclear space (45,46). On a larger scale, there is a wealth of evidence that demonstrates that dynamic crowding impacts cell function and cell fate. To name a few, changes in macromolecular density as a consequence of altered cell volume has been shown to alter stem cell differentiation (47). Additionally, one of the hallmarks of cancer and its progression is a change in nuclear volume and density (48). However, despite the abundance of evidence that proper cell function, as well as many disease states, alters crowding continuously in time, kinetic crowding has not been conceptually considered in the nucleus or otherwise. Instead, experimental studies report the average (in time or space) gene expression based on average crowding levels. Likewise, theoretical studies of crowding are conducted under equilibrium conditions and at steady state, meaning for fixed crowder density. Theoretical models predict that even small changes in the local crowding density will influence reaction rates (34). Therefore, these dynamics within the nuclear environment, 3D chromatin packing structure and otherwise, will additionally alter local crowding densities and, in turn, influence expression. Consequently, within the dynamic nucleus, we expect that fluctuations in crowding will additionally affect both the steric and thermodynamic properties of the local environment and thereby further regulate transcription.
Therefore, we will investigate the functional effects of the dynamic, crowded nucleus. Building upon our previous model, which studies gene expression under steady-state crowding, we will construct a three-pronged, time-evolving model of transcription to fully capture the dynamic crowding environment. Notably, to our knowledge, this is the first study to investigate non-steady-state crowding regarding gene expression. To do so, molecular-level detail will be provided by two simulation methodologies. As a function of crowding, BD simulations will provide the diffusion constants of proteins, and MC simulations will provide the change in free energy due to protein-DNA association or dissociation. In addition, network-level detail will be provided by a series of chemical reactions that represents the transcription pathway. The rates of the transcription reactions will be determined by the interplay of the theoretically determined diffusion constants and free energy changes, which are sensitive to crowding. We will conduct this investigation at physiologically relevant crowding levels and kinetic conditions, specifically for cells under normal growth conditions, genes that display circadian expression, and cells undergoing extravasation. Notably, we investigate the average effect of dynamic crowding on individual genes as well as for groups of genes and entire gene populations. Because crowding is a general, physical effect that likely affects many genes simultaneously, dynamic crowding could have a nontrivial effect on the long-term behavior and fate of a cell (49). Therefore, altogether, we probe a range of genetic and kinetic changes within crowded environments and determine the effect of these changes on gene expression.
Methods
Three-pronged, systems-molecular approach
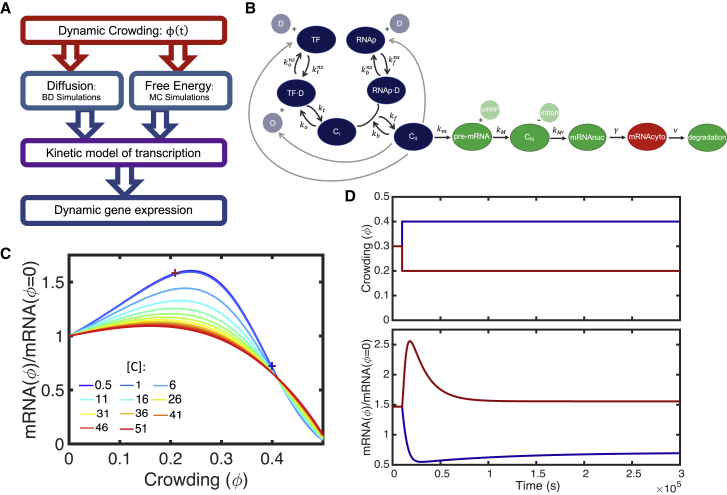
Although crowding interactions occur on the molecular-level, gene expression and regulation require network-level interactions. Therefore, we leverage three computational approaches simultaneously to bridge the gap between molecular crowding interactions and network gene expression (Fig. 1 A). All three approaches are detailed in the following sections, but in short, we explicitly consider molecular-level crowding interactions with Brownian dynamics (BD) simulations of diffusion and MC simulations of binding. These simulations were originally developed by Matsuda et al. (34) to describe crowding effects under steady-state conditions. Novel to our approach is that dynamic crowding is the driver of the changes in diffusion and free energy. The BD and MC simulations determine the degree to which changing crowding affects the physical properties and efficiencies of molecular species and integrate to affect every step of the transcription pathway. Notably, we consider transcription as 1) a continuous process in time and 2) insensitive to other regulatory elements, such as signaling. We do so to elucidate, and not obscure, the effect of dynamic crowding on gene expression. Although other regulatory elements undoubtedly affect gene expression, we aim to uncover the specific contribution of dynamic crowding, relative to what is expected from steady-state crowding predictions. Therefore, we report gene expression relative to steady-state predictions.
Figure 1.
Transitioning from a steady-state crowding model to a dynamic crowding model. The workflow developed for the steady-state model is largely continued for the dynamic crowding model (blue, (A)). However, now the primary input for both the simulations, and therefore the kinetic model, is dynamic crowding (red, (A)). Additionally, the kinetic model was modified so that all nuclear reaction rates are dependent (purple, (A)). The kinetic model describes the physical steps of transcription, including the search and binding of transcriptional proteins to gene promotors (blue, (B)), transcription of processing of pre-mRNA (green, (B)), and transportation of mRNA to the cytoplasm (red, (B)). When solved at steady state (without dynamic crowding), gene expression is nonmonotonic, with less sensitivity to crowding as gene concentration ([C]) increases (C). Steady-state gene expression (crosses, C) can be recovered by solving the dynamical model to steady state (D). To see this figure in color, go online.
Representation of dynamic crowding
Central to our approach is the robust and accurate representation of dynamic crowding. This is nontrivial because direct experimental measurements of dynamic crowding is currently lacking. However, indirect experimental observations suggest a highly dynamic crowding environment. Continuous motion has been demonstrated within the nuclei of cells at homeostasis due, for example, to protein exchange between nuclear bodies and the nucleoplasm (39), local and large chromatin translocations (50), and alterations in chromatin structure (44). Additionally, nuclear size has been shown both to fluctuate and to be altered in disease (48). With no apparent loss of mass, altering nuclear size would therefore affect the volume fraction of crowders within.
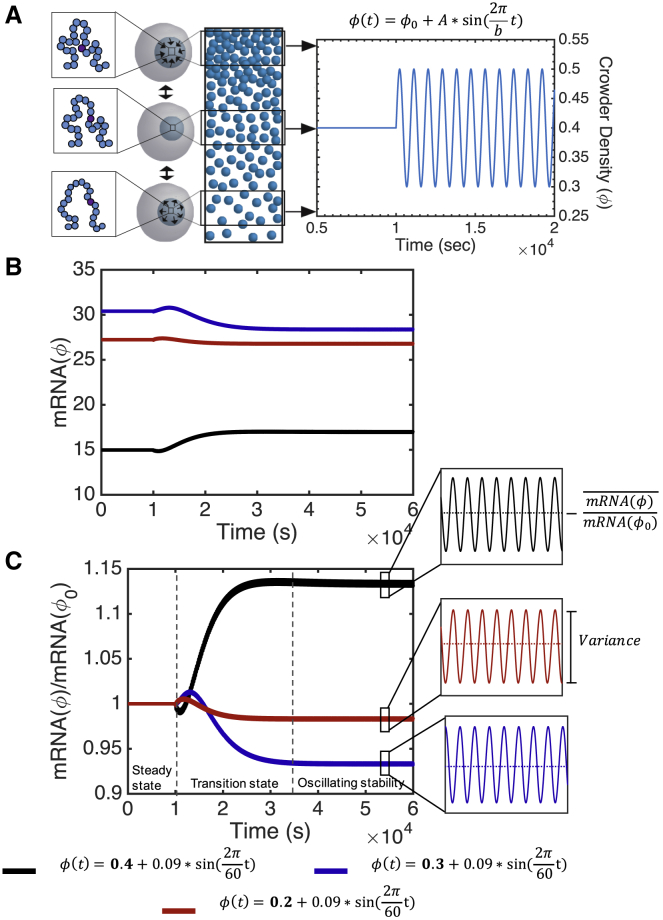
These and other observations allow us to determine parameters that are relevant for nuclear crowding. First, we consider a range of genes with different copy numbers and concentrations of transcriptional proteins that are specifically suited for that gene (Concentration of genes [C] = concentration of gene promotors [O] = concentration of transcription factors [TF] = concentration of RNA polymerases [RNAp]). We consider both individual genes with a range of copy number variants as well as population average expression of groups of genes. Therefore, we consider genes with [C] less than 1 nM as well as groups of genes with [C] of up to 51 nM. The estimation of these gene concentrations can be found in the Supporting Materials and Methods. Next, as chromatin is the most abundant crowder in the nucleus, the volume fraction of crowding must be within the range of chromatin volume concentrations (CVCs) observed in vitro (51). ChromEMT observes that CVCs in vitro are within the range of 0–0.6 (51). We consider within the range of 0–0.5 as there is a glass-like transition at 0.5 (52), and our past modeling has revealed that steady-state gene expression halts above 0.5 (34). Additionally, the amplitudes of that we consider preserve the probabilities of these CVCs. Finally, we consider dynamic crowding on the timescale of coordinated chromatin or nuclear matrix movement (seconds) (38,46) and DNA looping dynamics (minutes) (44).
Within the confines of the above parameters, we consider that is able to change in time. To decouple the effects of an overall change in the average crowding density and dynamic crowding itself, we represent homeostasis as an oscillating function. Note that the timescale of crowding movement is much smaller than the timescale of gene expression relaxation; therefore, all oscillatory functions give the same results. We consider a sinusoidal fluctuation in , as follows:
| (1) |
where b is the period of one cycle in seconds, and A is the amplitude of the fluctuation or the variation in crowding (Fig. 2 A). is the initial crowding volume fraction used to determine the initial conditions of the model.
Figure 2.
We approximate homeostasis by nonequilibrium, oscillatory dynamic crowding (A). After a transition state, oscillatory dynamic crowding causes suppression of genes that have a high expression at steady state, amplification of genes that have a low expression at steady state, and relatively unchanged expression of genes with midrange expression (here, [C] = 1 nM) (B). Both the steady-state and dynamic expression of each of these genes depends on the initial condition of the dynamic crowding profile. When normalized by expression at this initial condition, these genes display different sensitivities to dynamic crowding at oscillating stability (C). To see this figure in color, go online.
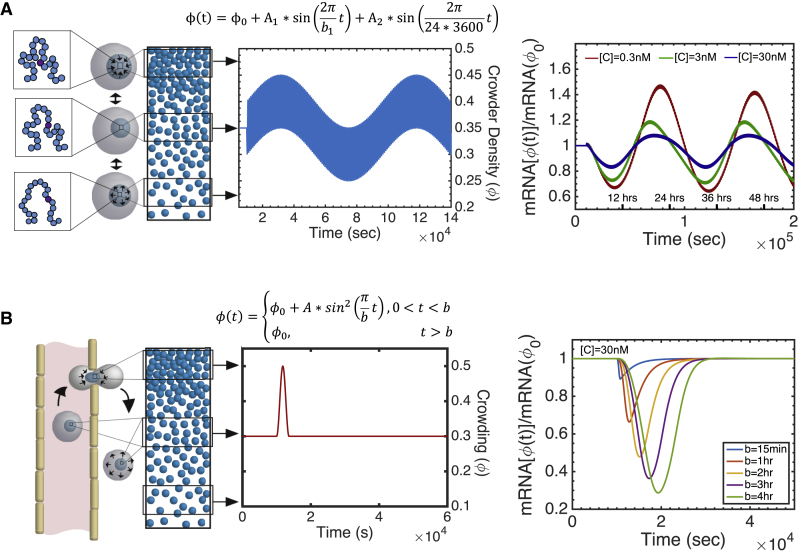
The majority of our analysis is conducted on this oscillating crowding for cells at homeostasis. However, we also consider two additional applications of dynamic crowding for gene regulation and disease. First, we consider that motion due to active cellular processes exists in conjunction with a slow, underlying secondary frequency. In this case, transcription would be influenced both by the above dynamic crowding, and additionally, by another sinusoidal component that could, for example, impose a circadian rhythm (Fig. 3 A), as follows:
| (2) |
Figure 3.
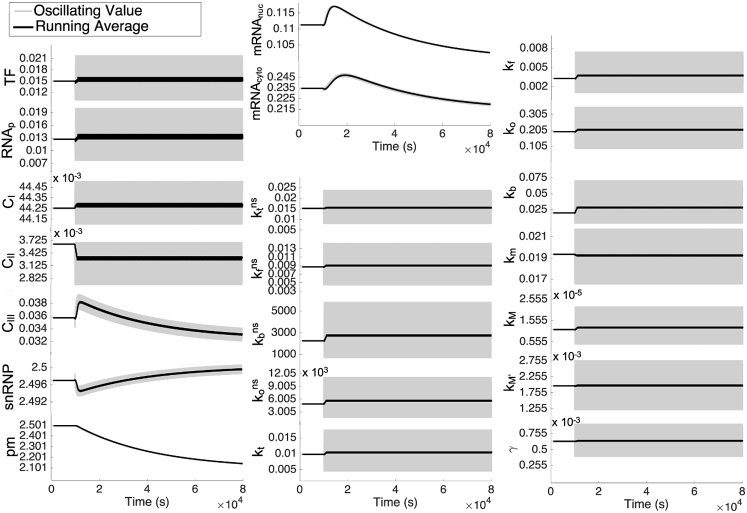
Once dynamic crowding begins ([C] = 1 nM, = 0.3, A = 0.09, b = 300 s), the species involved in the reversible reactions (TF, RNAp, C1, and C2) reach equilibrium almost immediately. This dynamic crowding shifts the reversible reactions toward the reactants; therefore, once all species reach oscillating stability, expression will be downregulated on average. Until that point, pre-mRNA monotonically decreases. This initially decreases the free snRNP as more snRNP is driven to bind to C3. C3 and snRNP are anticorrelated throughout the entire time course. With an increase in C3, mRNA is created more quickly, which in turn increases mRNA in the cytoplasm. All of these species relax slowly; therefore, the irreversible reactions are responsible for the long transition time between steady-state crowding and oscillating stability. The slow relaxation is due to the slow reaction rate coefficients of irreversible reactions, kM, kM′, and γ. All reaction rate coefficients have different average values than would be expected for Running average is defined as the average over every 100 s.
Finally, we consider that cells can experience acute changes in crowding, which are imposed through biomechanical stresses that may not necessarily exist during normal cell function. We consider transient changes, such as those applied during the extravasation of tumor or immune cells through the endothelial vascular layer (Fig. 3 B), by the following:
| (3) |
Although there are undoubtedly many additional ways in which dynamic crowding may manifest in the nucleus, we present these examples to show that 1) dynamic crowding does in fact effect expression and 2) that different types of dynamic crowding affect expression in different ways.
Kinetic model of transcription
We represent gene transcription as a series of chemical reactions adapted from Matsuda et al. (34). This model was developed to describe gene expression under steady-state conditions (i.e., fixed crowder concentrations). Under steady-state conditions, this transcription model matched with independently obtained computational data and with experiments of transcription in cell-free systems of varied synthetic crowding densities (53). Now, we extend the model by incorporating the effect of time-dependent crowding kinetics, as outlined above.
We represent gene expression by a series of chemical reactions that describe the transcription and exportation of messenger RNA (mRNA) to the cytoplasm (Fig. 1 B). As represented in Eqs. 4, 5, 6, 7, 8, 9, 10, 11, and 12, transcription factors (TF) and RNA polymerases (RNAp) engage in 3D searching for specific promotors by nonspecifically associating and dissociating with DNA (D) to form complexes TF·D and RNAp·D, respectively (Eqs. 4 and 5). In addition to 3D searching, TF·D one-dimensionally diffuses along DNA and binds to a promotor (O), forming complex CI (Eq. 6). Likewise, RNAp·D one-dimensionally diffuses to CI, forming a second complex, CII (Eq. 7). Once CII is formed, transcription commences, and subsequent products are created irreversibly. Pre-mRNA is formed (Eq. 8), which reacts with a small nuclear ribonucleic particle (snRNP) to form a complex (CIII) and splice out an intron (Eq. 9). CIII then forms mRNA (Eq. 10), which travels to the cytoplasm (Eq. 11) and degrades (Eq. 12). We define gene expression as cytoplasmic mRNA concentration. In our model, cytoplasmic mRNA is degraded as we are interested in gene expression, not protein formation (34). The original transcription scheme considered by Matsuda et al. (34) only considered crowding effects in the reversible reactions (Eqs. 4, 5, 6, and 7) as they state that the other reactions do not influence the final, steady-state mRNA level, just the time necessary to reach steady state. However, because we now consider the time dependence of the whole reaction scheme, we introduce crowding effects into the nuclear irreversible reactions, as follows (Eqs. 8, 9, 10, and 11):
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
This transcription scheme is solved in conjunction with three conservation equations, as follows:
| (13) |
| (14) |
| (15) |
Simulation methodologies
The dependence of the transcription pathway on dynamic crowding is enacted through the reaction rate coefficients, which depend on the volume fraction of crowders, . A representative example of one of the reaction rate coefficients is the rate of nonspecific association of TF with DNA, the forward reaction rate of Eq. 1, as follows:
| (16) |
All nuclear reaction rates are affected by at least one, and up to three, crowding-dependent variables. These variables are determined by simulations and are as follows: 1) increased crowding slows diffusion, which we quantify with BD simulations of protein diffusion (Fig. S1). The BD simulations determine the size-dependent diffusion constant of protein species. These diffusion constants are solved with respect to , relative to diffusion in an uncrowded medium. The reaction rate above is affected by the diffusion constant of the TF, . 2) Crowding creates a kinetic barrier that must be overcome for association or dissociation. We quantify this kinetic barrier with MC simulations of protein-DNA interactions (Figs. S2–S4), yielding the crowder-mediated potential of mean force between the two reactants. For this example, the rate of TF nonspecific association with DNA is affected by the nonequilibrium, entropic barrier of association between TF and DNA, βFbarrier,TF. This same barrier must be overcome for dissociation, for example, for the reverse reaction of Eq. 1. 3) Crowding changes the equilibrium free energy of binding, which can be quantified by the potential of mean force determined earlier (Figs. S2–S4). However, unlike βFbarrier,TF, this contribution, βFcrowd,TF, is the change in free energy at equilibrium due to the volume fraction of crowders. Both the BD and MC simulations depend on the geometries of the molecules involved as does the initial reaction rates at 0. The initial reaction rate of the above reaction, , describes the chemical affinity between TF and DNA (34).
Note that the simulations of diffusion and free energy are performed under steady-state conditions; the diffusion constant and change in free energy are determined for each independently. However, although this may suggest that the results of these simulations are not applicable to the dynamic system—which is not at equilibrium—an intrinsic assumption of the dynamic model is that there is a separation of timescales that allows diffusion and free energy to reach pseudoequilibrium at each time step. Based on our simulations, the time needed to reach a stable diffusion constant in the BD simulations is on the timescale of tens of nanoseconds. However, we only consider changes in crowding density that are much slower, on the order of seconds to hours (b = 30–3600 s). Furthermore, we find that a dynamic crowding imposed by a step function can reproduce the same results as the steady-state model (Fig. 1 D). Therefore, diffusion and free energy have sufficient time to reach pseudoequilibrium at each time step, and the results of the steady-state simulations are applicable to the dynamic system.
The derivation of each of the crowding-dependent reaction rate coefficients for Eqs. 4, 5, 6, and 7, as well as the results of their accompanying BD and MC simulations, were previously published (34). However, because we now introduce crowding effects into the irreversible reactions (Eqs. 8, 9, 10, 11, and 12), we have to compute the -dependent diffusion constant and free energy of these previously unconsidered reactants (e.g., snRNP, CIII). The results of the BD and MC simulations for these reactions, as well as further explanation of the simulation methodology, and a derivation of each of the crowding-dependent reaction rate coefficients are outlined in the Supporting Materials and Methods.
The initial conditions for the dynamic crowding model
We now have a full description of each of the crowding-dependent reactions necessary to calculate transcription. Before solving these reactions with time dependence, we solve the reaction scheme at steady state to determine the initial conditions of the dynamical model (Fig. 1 C). Initially, gene expression changes when increasing the volume fraction of crowders primarily by increasing the binding affinities of the transcriptional proteins as a bound complex has lower excluded volume than free reactants. However, after reaching a maximum around physiological nuclear crowding levels (54), the change in gene expression is dominated by the slowing of diffusion, and both the reaction rates and expression levels decrease. Above 0.5, steady-state gene expression halts and is equal to 0 because the diffusion constant approaches 0.
We consider both the response in the crowding of individual genes ([C] ≈ 5 nM and below) as well as population-averaged expression for groups of genes (5 nM ≤ [C] ≤ 26 nM) and for the entire population of genes (26 nM < [C] ≤ 51 nM). The [C] of populations of genes depends on both the copy number of the gene(s) and the volume of the nucleus, both of which vary substantially both between genes and between cells (55). Therefore, we consider a wide range of gene concentrations (see Supporting Materials and Methods for the derivation of gene concentration). Note that [C] = [O] = [TF] = [RNAp], as changing gene concentration also changes the number of promotors and transcriptional proteins specifically suited for that gene’s transcription. Increasing [C] causes the expression to be less sensitive to crowding (Fig. 1 C). This is in part because high [C] has more overall expression than low [C]; therefore, relative changes in expression are less pronounced as [C] increases (Fig. S5).
The steady-state expression level of mRNA in the cytoplasm at each , as well as the concentration of all components at each , are input as the initial conditions of the dynamical model. All intrinsic chemical reaction rates and crowding volume fractions are within physiologically appropriate ranges. The first 10,000 s of each calculation is steady state , after which dynamic crowding is imposed by Eqs. 1, 2, or 3. See the Supporting Materials and Methods for justification of the reaction rates.
Results and Discussion
Transitioning from steady state to dynamic crowding
Before determining the effects of dynamic crowding, we test that the dynamic crowding model can reproduce the results of the steady-state model. By imposing a step function for , we allow the dynamical model to start at steady state (first 10,000 s) and then reach a new steady state at a fixed crowder level. In doing so, we obtain the same value of gene expression with the dynamical model as determined by the steady-state model (Fig. 1, C and D, crosses). Therefore, we can conclude that the dynamical model is accurate and can be used with more complicated changes in dynamic crowding.
The time course of dynamic crowding-induced gene expression
An oscillating crowding profile, imposed by Eq. 1 (Fig. 2 A), causes gene expression to follow one of three time courses. Each time course begins at steady state because of the fixed crowder level for the first 10,000 s (Fig. 2 C). However, once dynamic crowding is imposed, expression enters a several-hour-long transition state. The transition state is characterized by a nonmonotonic change in expression. In Fig. 2 C, this lasts for several hours, though the exact time is dependent on the parameters of dynamic crowding. Finally, expression reaches a stable average value about which it oscillates on the timescale of dynamic crowding. This we refer to as “oscillating stability” (Fig. 2 C, insets). For example, all conditions in Fig. 2 C reach oscillating stability after 6 h. The qualitative expression level during the transition state and at oscillating stability depends on the initial, steady-state expression level. To illustrate the three time courses followed by dynamic crowding, we examine a gene for which [C] = 1 nM with a 9% change in crowding over 1 min. For three different initial crowding levels, 0.2, 0.3, or 0.4, either 1) expression begins high, is temporarily amplified during the transition state, and then becomes suppressed compared to its initial, steady-state level (Fig. 2 B, blue); 2) begins in the midrange of steady-state expression and remains approximately neutral throughout the entire time course (Fig. 2 B, red); or 3) begins with low expression, is temporarily suppressed during the transition state, and is ultimately amplified compared to the initial, steady-state level (Fig. 2 B, black).
The transition state between steady-state crowding and oscillating stability is due to the slow relaxation of the species involved in the irreversible reactions (Eqs. 8, 9, 10, 11, and 12). Many classic studies in systems biology have shown that transcriptional protein search and binding is on a much faster timescale than transcription as a whole (56). In our model, TF, RNAp, and their associated complexes equilibrate almost immediately to dynamic crowding (Fig. 3). Whether dynamic crowding on average shifts these reactions toward the reactants or toward the products determines whether expression on average will be shifted toward amplification or suppression at oscillating stability. However, until oscillating stability is reached, the species involved in the irreversible reactions relax slowly, causing a transition state that is not necessarily correlated qualitatively with oscillating stability. Therefore, we find that expression at early time points after dynamic crowding is dominated by the slow mRNA processing reactions, whereas expression at oscillating stability is dominated by protein search and binding.
Although the step function of corresponded both qualitatively and quantitatively with the steady-state model, an oscillating, dynamic does not correspond with the steady-state model . Instead, the qualitative change in expression can be estimated by the concavity of the steady-state solution. 0.2 and 0.3 are within the concave down regions of the steady-state solution, whereas 0.4 is within the concave up region of the steady-state solution. These parameters are simply examples that illustrate that dynamic expression is not fully captured by calculating the expression with the average of the dynamic profile. As, to our knowledge, expression has only ever been quantified in comparison to average we further examine this dichotomy, both theoretically and parametrically below.
Expression at oscillating stability is not dependent on all reaction rates
Under steady-state conditions, there is an analytical relationship between [mRNAcyto] and the other products and reaction rates (Fig. S6). This analytical relationship reveals that steady-state [mRNAcyto] does not depend on the concentrations of the intermediate, irreversibly produced products and their reaction rates, kM, kM′, and γ. However, because the dynamic system is not at steady state, dynamic [mRNAcyto] depends on all products and reaction rates. Interestingly, although oscillating stability is not the same as steady state and has no analytical relationship between [mRNAcyto] and the other products and reaction rates, oscillating stability is also insensitive to kM, kM′, and γ (for example, Fig. S6). Instead, these reaction rates determine the amount of short-term expression during the transition state. Short-term expression can additionally be affected marginally by the other reaction rates of the transcription pathway; however, short-term expression is primarily and critically dependent on kM, kM′, and γ. In contrast, the other reaction rates determine long-term expression during oscillating stability (for example, Fig. S6). Importantly, for all of these reaction rates, —the average reaction rate resultant from dynamic crowding—is not always the same as —the reaction rate of the average crowding density (Fig. 3). It is the parameters of dynamic crowding that determine whether or not and will be sufficiently similar to produce the same expression level. Therefore, we now perform a parametric study to determine when may be sufficient to predict .
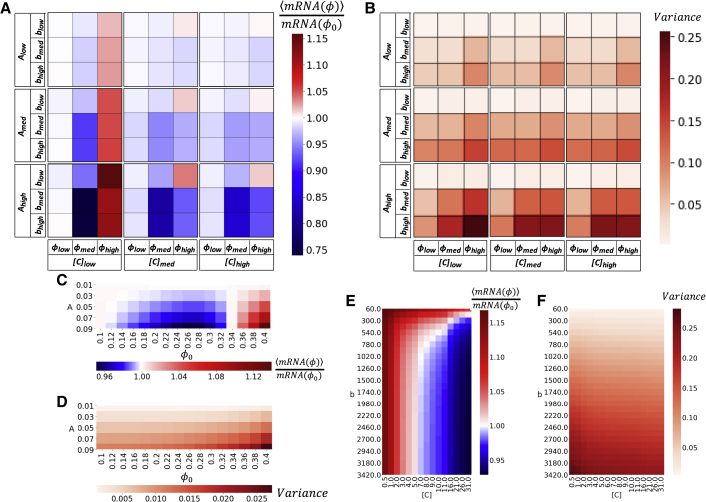
All parameters of dynamic crowding and gene property affect expression at oscillating stability
It is perhaps most useful to examine the expression as it relates to observable genetic and structural properties. Therefore, we systematically vary the parameters of the system and find that gene expression is both qualitatively and quantitatively dependent upon four parameters. As with the steady-state solution, dynamic expression at oscillating stability is highly dependent upon [C] and . However, [C] and alone are not sufficient to determine dynamic expression levels as it is the combination of these parameters, together with the amplitude of dynamic crowding (A) and the period of dynamic crowding (b), that determines dynamic expression levels at oscillating stability. Notably, A and b are temporal variables that are impossible to account for with steady-state investigation. Therefore, it is necessary to investigate transcription temporally to accurately predict the expression of genes that exist in a dynamic, nonequilibrium environment, which, to our knowledge, has not been done.
For each combination of the above parameters, we examine both the average expression level at oscillating stability as well as the variance about that average expression level. It is important to note that the majority of conditions have a variance less than 5% (Fig. 4, B, D, and F). In these cases, once oscillating stability is reached, the time at which [mRNA] is measured is trivial. However, variance can be significantly increased by slowing the b or increasing the A. It is notable that it is the purely temporal variables that most significantly impact variance. This can have great weight experimentally because in the cases of dynamic crowding, which changes slowly (bhigh) and/or with a large amplitude, [mRNA] can vary by up to 25%, depending on the time that it is measured. In these cases, the estimation of gene expression based on a single point in time is quite difficult.
Figure 4.
Once expression reaches an oscillating stability, both the average expression (A, C, and E) and the variance of oscillation (B, D, and F) vary with respect to the concentration of genes ([C]), the average crowding level , the period of oscillation (b), and the amplitude of oscillation (A). The combination of these parameters determine the gene expression level. The majority of conditions have a variance less than 5%; however, variance is increased by increasing A or b (B, D, and F). Increasing A also universally amplifies the impact of dynamic crowding on the average expression (A, B, and E). As predicted by steady state, expression behaves nonmonotonically with for the same [C] and b ([C] = 1 nM and b = 300 s in C and D). The majority of dynamic crowding parameters cause at least slight downregulation (A). This is not the case for 1) low and low A, which cause dynamic expression to remain approximately neutral; 2) highly crowded environments with rapid dynamic crowding, which amplify expression (A, top right corners); or 3) highly crowded environments that contain low [C], which is universally amplified by dynamic crowding (E, [C] = 1 nM, A = 0.09). To see this figure in color, go online.
Two trends that are predicted by the steady-state solution are also true for dynamic crowding. First, for the same [C] and b ([C] = 1 nM and b = 300 s in Fig. 4 C), expression behaves nonmonotonically with . However, the transition between downregulation and upregulation does not occur at the same as maximum steady-state expression. Second, as the majority of each of the steady-state solutions are concave down, the majority of dynamic crowding leads to at least slight downregulation (Fig. 4 A). This is not the case for both low and low A, which cause dynamic expression to remain approximately neutral or within 5% of the steady-state prediction. This is also not the case for highly crowded environments with rapid dynamic crowding. These conditions, regardless of [C] or A, amplify expression (Fig. 4 A, top right corners). Although amplification is more difficult to achieve, highly crowded environments with low [C] universally amplify expression (Fig. 4 E). Moreover, there is a smooth transition between [C], which universally results in upregulation to [C], which can be either amplified or suppressed, depending on the b (Fig. 4 E, note the scale of the x axis is nonlinear to more clearly show this transition). The reverse is true as well. One dynamic crowding environment smoothly transitions from amplifying genes at low concentrations to suppressing genes at high concentrations for both midrange and slow periods. Because low [C] corresponds with single genes and high [C] corresponds with groups of genes, this means that the same dynamic environment may amplify single genes while suppressing the expression of a group of genes as a whole. Therefore, gene expression is nonadditive and may be more complex than suggested analytically.
It is important to note that altering A and b has no effect on ; however, both significantly alter dynamic expression. Expression can be sensitive to even small fluctuations in crowding; therefore, dynamic crowding cannot be ignored. Likewise, there is no single frequency of dynamic crowding that causes all concentrations of genes to remain neutral (Fig. 4 E). Therefore, these purely temporal variables demonstrate that, independent from the average crowding effects, dynamic crowding itself can differentially regulate expression.
Applications of dynamic crowding for gene regulation and disease
Circadian gene regulation
All prior analysis is based on the assumption that dynamic crowding manifests itself as fluctuations about an average crowding level. Now, we consider that, in addition to these fluctuations, there exists a slow secondary frequency. Without discounting the existence of an oscillatory dynamic crowding due to the processes of normal cell function, a secondary frequency could correspond with, for example, a circadian rhythm. A secondary frequency with a period of 24 h could contribute to the regulation of circadian genes, of which there are between 642 and 3186 in every human tissue (57). Circadian crowding could be imposed by transcriptional or structural regulators, such as TF like MYOD1, genes like Bmal1, light signaling, or histone acetylation. All of these regulators have been linked to circadian regulation (58, 59, 60, 61) and could, in addition to their specific targets and effects, regulate expression through a secondary mechanism—imposing a 24-h crowding cycle.
We consider a 24-h circadian cycle underlying physiologic dynamic crowding by the following: . Here, dynamic crowding is only altered by 10% over the full 24-h cycle (Fig. 5 A). Even so, genes are differentially expressed every 12 h. The timescale of differential expression does not depend on average crowding density, but rather, only on the b, which is the same for all genes undergoing circadian regulation. In addition, as would be predicted from the oscillating dynamic crowding above, genes with lower concentrations exhibit a greater sensitivity to circadian dynamic crowding. Whereas genes with higher concentrations do fluctuate with a circadian rhythm, genes with lower concentrations experience both more amplification and more suppression throughout the 24-h cycle (Fig. 5 A). In vivo, this would suggest that housekeeping genes may be more consistently expressed, whereas more rare genes may operate more circadianly. This is an attractive application as dynamic crowding could concurrently regulate the hundreds to thousands of circadian genes that exist in the human genome, without necessitating specific regulatory factors.
Figure 5.
Dynamic crowding can be used to model processes of gene regulation and disease. The addition of a 24-h secondary frequency to the fluctuations studied at homeostasis displays circadian regulation () (A). The 24-h secondary frequency causes the expression to switch from amplification to suppression every 12 h, sensitive to gene concentration. Alternatively, transient forces, such as those experienced during extravasation, have a qualitatively different gene expression profile than that of continuous, sinusoidal dynamical crowding (B). The force of extravasation (A = 0.2, causes universal downregulation of gene expression for all gene concentrations and lengths of extravasation. To see this figure in color, go online.
Extravasation
Finally, the dynamical model can investigate how gene expression is sensitive to dynamic crowding, not only under normal growth conditions but also when cells undergo acute mechanical stress. Here, we consider the effect of compression during extravasation of cells from the blood stream to a distal tissue. This phenomenon is a critical event during tumor metastasis and is a common function of immune cells (62). Cells that undergo extravasation begin in the bloodstream, presumably with consistent volume (and therefore crowding volume fraction) as cells under normal growth conditions. As they pass through the endothelial membrane, both the total and nuclear volume decrease, and therefore nuclear crowding volume fraction increases. The crowding density returns to initial levels as cells exit the endothelial membrane and populate a distal tissue. Therefore, we model extravasation as a single cycle of compression to reflect nuclear compression during passage through the endothelial cell boundary and nuclear relaxation after passage is complete (Fig. 5 B). After extravasation, we consider the return of cells to constant crowding, not dynamic crowding, as we are only interested in the effect of the compression on gene expression.
We represent extravasation with Eq. 3 and compare different durations of compression. Experimentally, extravasation has been shown to last between 15 min and 4 h and decrease nuclear volume up to 50% (63,64). Within this range of extravasation times, the force of compression universally decreases gene expression, with longer compressions causing greater downregulation. Notably, unlike the sinusoidal compressions investigated above, this trend is consistent across all gene concentrations and initial conditions (Fig. S7). In fact, for each duration of compression, all genes, regardless of concentration, display similar changes in mRNA production (Fig. S7). As the duration of compression increases, the percentage of change in mRNA production increases, leveling off after several hours. Importantly, there is never a complete loss of mRNA production; therefore, transcription does not completely halt during these slow, sustained compressions.
Interestingly, the peak-to-peak distance between maximum compression and maximum effect on expression is also similar for all three genes (Fig. S7). As the duration of compression increases, peak-to-peak distance increases until reaching a plateau. However, the time it takes for expression to recover to within 99% of initial expression is nonmonotonic. Short compressions have disproportionately long recovery times (Fig. S7) and is dependent upon gene concentration. Notably, these properties may explain why cells that undergo similar obstacles have different outcomes. For example, tumor cells that extravasate over several hours become more aggressive postmetastasis. However, leukocytes, which are more suited to undergo this phenomenon, extravasate in under an hour (65) and therefore may not experience as drastic a change in expression as tumor cells. Conversely, the alterations in expression that do result from extravasation may result in differential expression in genes that are primed to be altered by dynamic crowding and aid in the transition from monocyte to macrophage at a distal tissue. Therefore, the stress imposed on a cell by events such as extravasation can be translated into alterations in local crowding densities. Although regulation through dynamic crowding might be imposed by the cell during proper function, these results indicate that this mechanism can be co-opted in disease or stress to significantly impact expression.
Conclusions
The model presented here predicts that transcription is dependent both on crowding and on time. With this model, we determine that transcription is altered as a result of a time-evolving, crowded nanoenvironment and cannot be explained simply by the average volume fraction of dynamic crowding. As the nucleus is an organelle that exists at nonequilibrium, it could be questioned whether the volume fraction of crowding density is ever truly at steady state. Therefore, dynamic crowding becomes even more pertinent to study in regards to nuclear function. As would be expected for regulation, not all genes are significantly altered because of dynamic crowding. However, other genes are primed to respond rapidly to changes in dynamic crowding. Therefore, we present temporal fluctuations in the crowded environment as a novel regulatory phenomenon.
Through this potent, nonspecific regulation, we can capture experimentally observed expression patterns of cells under normal growth conditions, circadian genes, and cells under biomechanical stress. Notably, this regulation could be imposed by the 3D chromatin packing structure. The idea that 3D packing affects expression is not new. Noncoding chromatin has long been hypothesized to be involved in gene selection and regulation (66). In fact, the 3D interactions between noncoding and coding chromatin that have recently been demonstrated to effect gene expression (67). The kinetics that we model on the order of minutes correspond with such events as chromatin translocation (50), chromatin remodeling (68), or loop formation (44). We further propose that each of these processes additionally exposes the underlying genome to a nanoenvironment with optimal crowding kinetics for gene regulation, including those that do not alter the average crowding density. As dynamic crowding has yet to be measured in conjunction with experimental data, this could aid in explaining the transcriptional variability and noise that is observed in live cells. Here, we emphasize that time-dependent crowding is so far conceptually unconsidered and requires experimental attention to verify the wealth of experimental evidence that lends toward the idea that dynamic crowding would be an influential part of both normal gene regulation and disease dysregulation.
Our model additionally indicates that genes will have different responses to dynamic crowding in different locations throughout the nucleus. Consider that throughout the nucleus, crowding density is heterogeneous but that each density is altered homogeneously in response to changes in cell volume. Genes in less crowded areas of the nucleus would therefore not respond dramatically to changes in cell volume, whereas genes in more crowded areas of the nucleus would be significantly altered. Moreover, the same gene can either respond negligibly or dramatically to dynamic crowding just by relocating to an area with a different average crowding density. Although it may seem more pertinent to study the dramatic changes in expression, it is also interesting to note the lack of response of genes to some dynamic crowding environments, which is still an important hallmark of regulation.
Likewise, we alter the gene copy number and compare the expression of single genes with the expression of groups and the population of genes. This is important for two reasons: 1) we find that if the entire nucleus is affected by changing volume, as discussed above, the entire population of genes will be suppressed on average, though individual genes may be amplified. This is echoed in our studies of extravasation in which amplification is never achieved, even for the conditions in which oscillating crowding causes significant amplification. Therefore, it is much easier for the cell to silence genes than it is to increase their expression. 2) Copy number variation is extremely important in the progression of human disease. Among others, altered copy numbers of particular genes have been linked to many cancers (69) and a variety of childhood psychological disorders (70). For these diseases, the altered change in expression due to the interplay of gene concentration with the dynamic crowding environment could be influential in disease phenotype. To that end, it is important that we recognize that the total number of transcripts of a particular gene may not be indicative of disease prognosis. We report expression relative to steady-state predictions, not only to compare with steady state but also because the percentage of change in expression is much more likely to predict a change in phenotype than the total amount of expression.
The phenomena studied herein are just the first of many that could be probed by changing the assumptions and complexity of the dynamical model. For example, we do not consider transcriptional bursting, which indicates that expression is not a continuous process, but occurs in short bursts followed by a latency period (71). Likewise, we presently do not explore the effect of gene networks because it would obscure the biophysical effect of dynamic crowding studied here.
The dynamical model presented here has the potential to study many different physiological phenomena. The power of our approach is that the large amount of molecular detail, which allows us to study these phenomena, are coupled to crowding, a general, biophysical effect that underlies much of biology. Whereas crowding is often viewed as an environmental complexity, crowding in fact underlies nuclear kinetics, aids in gene selection, allows the cell to reduce its inventory of components, and influences structure and function in vivo. A recently burgeoning understanding of nuclear and chromatin mobility (50) reveals that there are large changes in the physical nuclear environment. As these processes consume ATP, the nucleus as a whole may not be at equilibrium and must be considered as a dynamic environment. Therefore, there is a significant need for models, such as the one presented here, that incorporate a time-dependent, crowded nuclear environment.
Author Contributions
A.R.S. performed the research and wrote the manuscript. R.J.N., K.H., L.M.A., V.B., and I.S. assisted in critical analysis of the results and commented on the manuscript. H.M. provided the original framework for the project. I.S. designed the project.
Acknowledgments
We thank Gregory Putzel and Sung Hyun Park for assistance with simulations.
L.M.A. acknowledges support from the National Institutes of Health (grant T32GM008152). I.S. and A.R.S. acknowledge support from the National Cancer Institute (grant U01CA202177). L.M.A., I.S., K.H., and V.B. acknowledge support from the National Science Foundation (grant EFMA-1830961). V.B., I.S., and L.M.A. acknowledge support from the National Institutes of Health (grant R01CA228272). This research was supported in part through the computational resources and staff contributions provided for the Quest high performance computing facility at Northwestern University, which is jointly supported by the Office of the Provost, the Office for Research, and Northwestern University Information Technology.
Editor: Andrew Spakowitz.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.11.007.
Supporting Citations
References (72, 73, 74, 75, 76) appear in the Supporting Material.
Supporting Material
References
- 1.Buldyrev S.V., Goldberger A.L., Stanley H.E. Long-range correlation properties of coding and noncoding DNA sequences: GenBank analysis. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1995;51:5084–5091. doi: 10.1103/physreve.51.5084. [DOI] [PubMed] [Google Scholar]
- 2.Richter K., Nessling M., Lichter P. Experimental evidence for the influence of molecular crowding on nuclear architecture. J. Cell Sci. 2007;120:1673–1680. doi: 10.1242/jcs.03440. [DOI] [PubMed] [Google Scholar]
- 3.Richter K., Nessling M., Lichter P. Macromolecular crowding and its potential impact on nuclear function. Biochim. Biophys. Acta. 2008;1783:2100–2107. doi: 10.1016/j.bbamcr.2008.07.017. [DOI] [PubMed] [Google Scholar]
- 4.Handwerger K.E., Cordero J.A., Gall J.G. Cajal bodies, nucleoli, and speckles in the Xenopus oocyte nucleus have a low-density, sponge-like structure. Mol. Biol. Cell. 2005;16:202–211. doi: 10.1091/mbc.E04-08-0742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Al-Habori M. Macromolecular crowding and its role as intracellular signalling of cell volume regulation. Int. J. Biochem. Cell Biol. 2001;33:844–864. doi: 10.1016/s1357-2725(01)00058-9. [DOI] [PubMed] [Google Scholar]
- 6.Luby-Phelps K., Castle P.E., Lanni F. Hindered diffusion of inert tracer particles in the cytoplasm of mouse 3T3 cells. Proc. Natl. Acad. Sci. USA. 1987;84:4910–4913. doi: 10.1073/pnas.84.14.4910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Putzel G.G., Tagliazucchi M., Szleifer I. Nonmonotonic diffusion of particles among larger attractive crowding spheres. Phys. Rev. Lett. 2014;113:138302. doi: 10.1103/PhysRevLett.113.138302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Minton A.P. Excluded volume as a determinant of macromolecular structure and reactivity. Pept Sci. 1981;20:2093–2120. [Google Scholar]
- 9.Zhou H.X., Rivas G., Minton A.P. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hancock R. A role for macromolecular crowding effects in the assembly and function of compartments in the nucleus. J. Struct. Biol. 2004;146:281–290. doi: 10.1016/j.jsb.2003.12.008. [DOI] [PubMed] [Google Scholar]
- 11.Minton A.P. The effect of volume occupancy upon the thermodynamic activity of proteins: some biochemical consequences. Mol. Cell. Biochem. 1983;55:119–140. doi: 10.1007/BF00673707. [DOI] [PubMed] [Google Scholar]
- 12.Zimmerman S.B., Minton A.P. Macromolecular crowding: biochemical, biophysical, and physiological consequences. Annu. Rev. Biophys. Biomol. Struct. 1993;22:27–65. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 13.Minton A.P. Molecular crowding: analysis of effects of high concentrations of inert cosolutes on biochemical equilibria and rates in terms of volume exclusion. Methods Enzymol. 1998;295:127–149. doi: 10.1016/s0076-6879(98)95038-8. [DOI] [PubMed] [Google Scholar]
- 14.Sarkar M., Smith A.E., Pielak G.J. Impact of reconstituted cytosol on protein stability. Proc. Natl. Acad. Sci. USA. 2013;110:19342–19347. doi: 10.1073/pnas.1312678110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.van den Berg B., Ellis R.J., Dobson C.M. Effects of macromolecular crowding on protein folding and aggregation. EMBO J. 1999;18:6927–6933. doi: 10.1093/emboj/18.24.6927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zimmerman S.B., Trach S.O. Macromolecular crowding extends the range of conditions under which DNA polymerase is functional. Biochim. Biophys. Acta. 1988;949:297–304. doi: 10.1016/0167-4781(88)90155-8. [DOI] [PubMed] [Google Scholar]
- 17.Lindner R., Ralston G. Effects of dextran on the self-association of human spectrin. Biophys. Chem. 1995;57:15–25. doi: 10.1016/0301-4622(95)00063-4. [DOI] [PubMed] [Google Scholar]
- 18.Rivas G., Fernandez J.A., Minton A.P. Direct observation of the self-association of dilute proteins in the presence of inert macromolecules at high concentration via tracer sedimentation equilibrium: theory, experiment, and biological significance. Biochemistry. 1999;38:9379–9388. doi: 10.1021/bi990355z. [DOI] [PubMed] [Google Scholar]
- 19.Jarvis T.C., Ring D.M., von Hippel P.H. “Macromolecular crowding”: thermodynamic consequences for protein-protein interactions within the T4 DNA replication complex. J. Biol. Chem. 1990;265:15160–15167. [PubMed] [Google Scholar]
- 20.Shearwin K.E., Winzor D.J. Thermodynamic nonideality in macromolecular solutions. Evaluation of parameters for the prediction of covolume effects. Eur. J. Biochem. 1990;190:523–529. doi: 10.1111/j.1432-1033.1990.tb15605.x. [DOI] [PubMed] [Google Scholar]
- 21.Agius L. Substrate modulation of aldolase B binding in hepatocytes. Biochem. J. 1996;315:651–658. doi: 10.1042/bj3150651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Knull H., Minton A.P. Structure within eukaryotic cytoplasm and its relationship to glycolytic metabolism. Cell Biochem. Funct. 1996;14:237–248. doi: 10.1002/cbf.698. [DOI] [PubMed] [Google Scholar]
- 23.Murphy L.D., Zimmerman S.B. Macromolecular crowding effects on the interaction of DNA with Escherichia coli DNA-binding proteins: a model for bacterial nucleoid stabilization. Biochim. Biophys. Acta. 1994;1219:277–284. doi: 10.1016/0167-4781(94)90049-3. [DOI] [PubMed] [Google Scholar]
- 24.Norred S.E., Caveney P.M., Simpson M.L. Macromolecular crowding induces spatial correlations that control gene expression bursting patterns. ACS Synth. Biol. 2018;7:1251–1258. doi: 10.1021/acssynbio.8b00139. [DOI] [PubMed] [Google Scholar]
- 25.Akabayov B., Akabayov S.R., Richardson C.C. Impact of macromolecular crowding on DNA replication. Nat. Commun. 2013;4:1615. doi: 10.1038/ncomms2620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bancaud A., Huet S., Ellenberg J. Molecular crowding affects diffusion and binding of nuclear proteins in heterochromatin and reveals the fractal organization of chromatin. EMBO J. 2009;28:3785–3798. doi: 10.1038/emboj.2009.340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Robbins E., Pederson T., Klein P. Comparison of mitotic phenomena and effects induced by hypertonic solutions in HeLa cells. J. Cell Biol. 1970;44:400–416. doi: 10.1083/jcb.44.2.400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pederson T., Robbins E. RNA synthesis in HeLa cells. Pattern in hypertonic medium and its similarity to synthesis during G2-prophase. J. Cell Biol. 1970;47:734–744. doi: 10.1083/jcb.47.3.734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cho E.J., Kim J.S. Crowding effects on the formation and maintenance of nuclear bodies: insights from molecular-dynamics simulations of simple spherical model particles. Biophys. J. 2012;103:424–433. doi: 10.1016/j.bpj.2012.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Smith S., Cianci C., Grima R. Macromolecular crowding directs the motion of small molecules inside cells. J. R. Soc. Interface. 2017;14:20170047. doi: 10.1098/rsif.2017.0047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kim J.S., Yethiraj A. Crowding effects on protein association: effect of interactions between crowding agents. J. Phys. Chem. B. 2011;115:347–353. doi: 10.1021/jp107123y. [DOI] [PubMed] [Google Scholar]
- 32.Cook P.R., Marenduzzo D. Entropic organization of interphase chromosomes. J. Cell Biol. 2009;186:825–834. doi: 10.1083/jcb.200903083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Barbieri M., Fraser J., Nicodemi M. A polymer model explains the complexity of large-scale chromatin folding. Nucleus. 2013;4:267–273. doi: 10.4161/nucl.25432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Matsuda H., Putzel G.G., Szleifer I. Macromolecular crowding as a regulator of gene transcription. Biophys. J. 2014;106:1801–1810. doi: 10.1016/j.bpj.2014.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Golkaram M., Hellander S., Petzold L.R. Macromolecular crowding regulates the gene expression profile by limiting diffusion. PLoS Comput. Biol. 2016;12:e1005122. doi: 10.1371/journal.pcbi.1005122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Parry-Billings M., Bevan S.J., Newsholme E.A. Effects of changes in cell volume on the rates of glutamine and alanine release from rat skeletal muscle in vitro. Biochem. J. 1991;276:559–561. doi: 10.1042/bj2760559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pedersen S.F., Hoffmann E.K. Possible interrelationship between changes in F-actin and myosin II, protein phosphorylation, and cell volume regulation in Ehrlich ascites tumor cells. Exp. Cell Res. 2002;277:57–73. doi: 10.1006/excr.2002.5529. [DOI] [PubMed] [Google Scholar]
- 38.Chu F.Y., Haley S.C., Zidovska A. On the origin of shape fluctuations of the cell nucleus. Proc. Natl. Acad. Sci. USA. 2017;114:10338–10343. doi: 10.1073/pnas.1702226114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Phair R.D., Misteli T. High mobility of proteins in the mammalian cell nucleus. Nature. 2000;404:604–609. doi: 10.1038/35007077. [DOI] [PubMed] [Google Scholar]
- 40.Misteli T. Physiological importance of RNA and protein mobility in the cell nucleus. Histochem. Cell Biol. 2008;129:5–11. doi: 10.1007/s00418-007-0355-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Schuldt A. The dynamic nucleus. Nat. Rev. Mol. Cell Biol. 2010;11:678–679. doi: 10.1038/nrm2983. [DOI] [PubMed] [Google Scholar]
- 42.Bickmore W.A. The spatial organization of the human genome. Annu. Rev. Genomics Hum. Genet. 2013;14:67–84. doi: 10.1146/annurev-genom-091212-153515. [DOI] [PubMed] [Google Scholar]
- 43.Almassalha L.M., Tiwari A., Backman V. The global relationship between chromatin physical topology, fractal structure, and gene expression. Sci. Rep. 2017;7:41061. doi: 10.1038/srep41061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hansen A.S., Cattoglio C., Tjian R. Recent evidence that TADs and chromatin loops are dynamic structures. Nucleus. 2018;9:20–32. doi: 10.1080/19491034.2017.1389365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zidovska A., Weitz D.A., Mitchison T.J. Micron-scale coherence in interphase chromatin dynamics. Proc. Natl. Acad. Sci. USA. 2013;110:15555–15560. doi: 10.1073/pnas.1220313110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Saintillan D., Shelley M.J., Zidovska A. Extensile motor activity drives coherent motions in a model of interphase chromatin. Proc. Natl. Acad. Sci. USA. 2018;115:11442–11447. doi: 10.1073/pnas.1807073115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Guo M., Pegoraro A.F., Weitz D.A. Cell volume change through water efflux impacts cell stiffness and stem cell fate. Proc. Natl. Acad. Sci. USA. 2017;114:E8618–E8627. doi: 10.1073/pnas.1705179114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jevtić P., Edens L.J., Levy D.L. Sizing and shaping the nucleus: mechanisms and significance. Curr. Opin. Cell Biol. 2014;28:16–27. doi: 10.1016/j.ceb.2014.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Almassalha L.M., Bauer G.M., Backman V. Macrogenomic engineering via modulation of the scaling of chromatin packing density. Nat. Biomed. Eng. 2017;1:902–913. doi: 10.1038/s41551-017-0153-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gasser S.M. Visualizing chromatin dynamics in interphase nuclei. Science. 2002;296:1412–1416. doi: 10.1126/science.1067703. [DOI] [PubMed] [Google Scholar]
- 51.Ou H.D., Phan S., O’Shea C.C. ChromEMT: visualizing 3D chromatin structure and compaction in interphase and mitotic cells. Science. 2017;357:eaag0025. doi: 10.1126/science.aag0025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kang H., Yoon Y.G., Hyeon C. Confinement-induced glassy dynamics in a model for chromosome organization. Phys. Rev. Lett. 2015;115:198102. doi: 10.1103/PhysRevLett.115.198102. [DOI] [PubMed] [Google Scholar]
- 53.Tan C., Saurabh S., Leduc P. Molecular crowding shapes gene expression in synthetic cellular nanosystems. Nat. Nanotechnol. 2013;8:602–608. doi: 10.1038/nnano.2013.132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Richter K., Nessling M., Lichter P. Macromolecular crowding and its potential impact on nuclear function. Biochim. Biophys. Acta. 2008;1783:2100–2107. doi: 10.1016/j.bbamcr.2008.07.017. [DOI] [PubMed] [Google Scholar]
- 55.Girirajan S., Campbell C.D., Eichler E.E. Human copy number variation and complex genetic disease. Annu. Rev. Genet. 2011;45:203–226. doi: 10.1146/annurev-genet-102209-163544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gunawardena J. Time-scale separation--Michaelis and Menten’s old idea, still bearing fruit. FEBS J. 2014;281:473–488. doi: 10.1111/febs.12532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Zhang R., Lahens N.F., Hogenesch J.B. A circadian gene expression atlas in mammals: implications for biology and medicine. Proc. Natl. Acad. Sci. USA. 2014;111:16219–16224. doi: 10.1073/pnas.1408886111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hirayama J., Sahar S., Sassone-Corsi P. CLOCK-mediated acetylation of BMAL1 controls circadian function. Nature. 2007;450:1086–1090. doi: 10.1038/nature06394. [DOI] [PubMed] [Google Scholar]
- 59.Grimaldi B., Nakahata Y., Sassone-Corsi P. Chromatin remodeling and circadian control: master regulator CLOCK is an enzyme. Cold Spring Harb. Symp. Quant. Biol. 2007;72:105–112. doi: 10.1101/sqb.2007.72.049. [DOI] [PubMed] [Google Scholar]
- 60.Barneche F., Malapeira J., Mas P. The impact of chromatin dynamics on plant light responses and circadian clock function. J. Exp. Bot. 2014;65:2895–2913. doi: 10.1093/jxb/eru011. [DOI] [PubMed] [Google Scholar]
- 61.Purnell B.A. Circadian muscle mastery. Science. 2019;363:1188–1189. [Google Scholar]
- 62.Denais C.M., Gilbert R.M., Lammerding J. Nuclear envelope rupture and repair during cancer cell migration. Science. 2016;352:353–358. doi: 10.1126/science.aad7297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Stoletov K., Kato H., Klemke R. Visualizing extravasation dynamics of metastatic tumor cells. J. Cell Sci. 2010;123:2332–2341. doi: 10.1242/jcs.069443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Irianto J., Pfeifer C.R., Discher D.E. Nuclear constriction segregates mobile nuclear proteins away from chromatin. Mol. Biol. Cell. 2016;27:4011–4020. doi: 10.1091/mbc.E16-06-0428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Hyun Y.M., Sumagin R., Kim M. Uropod elongation is a common final step in leukocyte extravasation through inflamed vessels. J. Exp. Med. 2012;209:1349–1362. doi: 10.1084/jem.20111426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Chuang C.H., Belmont A.S. Moving chromatin within the interphase nucleus-controlled transitions? Semin. Cell Dev. Biol. 2007;18:698–706. doi: 10.1016/j.semcdb.2007.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Delaneau O., Zazhytska M., Dermitzakis E.T. Chromatin three-dimensional interactions mediate genetic effects on gene expression. Science. 2019;364:eaat8266. doi: 10.1126/science.aat8266. [DOI] [PubMed] [Google Scholar]
- 68.Hihara S., Pack C.G., Maeshima K. Local nucleosome dynamics facilitate chromatin accessibility in living mammalian cells. Cell Rep. 2012;2:1645–1656. doi: 10.1016/j.celrep.2012.11.008. [DOI] [PubMed] [Google Scholar]
- 69.Shlien A., Malkin D. Copy number variations and cancer. Genome Med. 2009;1:62. doi: 10.1186/gm62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Thapar A., Cooper M. Copy number variation: what is it and what has it told us about child psychiatric disorders? J. Am. Acad. Child Adolesc. Psychiatry. 2013;52:772–774. doi: 10.1016/j.jaac.2013.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Lenstra T.L., Rodriguez J., Larson D.R. Transcription dynamics in living cells. Annu. Rev. Biophys. 2016;45:25–47. doi: 10.1146/annurev-biophys-062215-010838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Maeshima K., Kaizu K., Takahashi K. The physical size of transcription factors is key to transcriptional regulation in chromatin domains. J. Phys. Condens. Matter. 2015;27:064116. doi: 10.1088/0953-8984/27/6/064116. [DOI] [PubMed] [Google Scholar]
- 73.Stark H., Dube P., Kastner B. Arrangement of RNA and proteins in the spliceosomal U1 small nuclear ribonucleoprotein particle. Nature. 2001;409:539–542. doi: 10.1038/35054102. [DOI] [PubMed] [Google Scholar]
- 74.Milo R., Jorgensen P., Springer M. BioNumbers--the database of key numbers in molecular and cell biology. Nucleic Acids Res. 2010;38:D750–D753. doi: 10.1093/nar/gkp889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Berg O.G., Winter R.B., von Hippel P.H. Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory. Biochemistry. 1981;20:6929–6948. doi: 10.1021/bi00527a028. [DOI] [PubMed] [Google Scholar]
- 76.Willyard C. New human gene tally reignites debate. Nature. 2018;558:354–355. doi: 10.1038/d41586-018-05462-w. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.