Microrheology for Hi-C Data Reveals the Spectrum of the Dynamic 3D Genome Organization

Abstract

The one-dimensional information of genomic DNA is hierarchically packed inside the eukaryotic cell nucleus and organized in a three-dimensional (3D) space. Genome-wide chromosome conformation capture (Hi-C) methods have uncovered the 3D genome organization and revealed multiscale chromatin domains of compartments and topologically associating domains (TADs). Moreover, single-nucleosome live-cell imaging experiments have revealed the dynamic organization of chromatin domains caused by stochastic thermal fluctuations. However, the mechanism underlying the dynamic regulation of such hierarchical and structural chromatin units within the microscale thermal medium remains unclear. Microrheology is a way to measure dynamic viscoelastic properties coupling between thermal microenvironment and mechanical response. Here, we propose a new, to our knowledge, microrheology for Hi-C data to analyze the dynamic compliance property as a measure of rigidness and flexibility of genomic regions along with the time evolution. Our method allows the conversion of an Hi-C matrix into the spectrum of the dynamic rheological property along the genomic coordinate of a single chromosome. To demonstrate the power of the technique, we analyzed Hi-C data during the neural differentiation of mouse embryonic stem cells. We found that TAD boundaries behave as more rigid nodes than the intra-TAD regions. The spectrum clearly shows the dynamic viscoelasticity of chromatin domain formation at different timescales. Furthermore, we characterized the appearance of synchronous and liquid-like intercompartment interactions in differentiated cells. Together, our microrheology data derived from Hi-C data provide physical insights into the dynamics of the 3D genome organization.

Significance

Genomic DNA is hierarchically packed inside the eukaryotic cell nucleus, and the genome organization in three-dimensions (3D) contributes to proper genome function at multiple scales. Although thermal fluctuations inevitably drive movements of the genome molecules in the microscale cell environment, there is no method, as of yet, to quantify such dynamic three-dimensional genome organization of hierarchical and structural chromatin units. Here, we describe a method to calculate rheological properties as measures of flexibility and liquid-like behavior of the genome. We show that boundaries of known megabase-scale chromatin domains are more rigid than sequences inside these domains. Our method allows the conversion of static and population-averaged genome-wide chromosome conformation capture data to information that can reveal the dynamic and hierarchical properties of the three-dimensional genome organization.

Introduction

In eukaryotes, the one-dimensional information of genomic DNA is spatiotemporally organized inside the cell nucleus, which is only a few microns in size (1,2). Dynamic orchestration of genomic regulatory elements in three-dimensional (3D) space contributes to proper expression of genes. Genome-wide chromosome conformation capture (Hi-C) and related methods have revealed that chromatin hierarchically forms various sized genomic domains such as topologically associating domains (TADs) at the submegabase scale and A/B compartments at the megabase scale as functional and cooperative units (2, 3, 4, 5). These hierarchical folding patterns depend on cell types and states during cell differentiation (6, 7, 8). Although Hi-C experiments require fixed cells and Hi-C data make sense in population average, the tracking of single nucleosomes by single-molecule and superresolution live-cell imaging experiments has revealed the dynamic organization of chromatin domains in single cells (9, 10, 11, 12). The dynamic property is just like a “polymer melt” state and reveals liquid-like behavior (13,14). However, the relation of the liquid-like behavior of chromatin to its hierarchical 3D genome organization remains poorly understood.

Thermal fluctuations are dominant in a microscale medium as well as within the cell environment and cause random and stochastic motion of tiny particles, such as Brownian motion. The stochastic dynamics of the Brownian particle can be described by the generalized Langevin equation, which is formulated from micromechanics with the aid of projection methods (15, 16, 17). The formalism of microrheology was developed based on the generalized Langevin equation (18); the generalized Stokes-Einstein relation (GSER) allows the calculation of linear viscoelastic quantities from the mean-squared displacement (MSD) of tracer particles in a complex fluid. Microrheology to measure elastic or viscous properties as mechanical responses in a microscale complex fluid has been verified for over two decades (18,19). Besides, bio-microrheology, the study of deformation and flow of biological materials at small length scales, has revealed the nature of the dynamic coupling between cell microenvironment and mechanical response (20, 21, 22).

Recently, the quantitative significance of Hi-C contact matrix data was elucidated mathematically by several independent groups (23, 24, 25). We developed a polymer modeling and a simulation method called polymer dynamics deciphered from Hi-C data (PHi-C) to decipher Hi-C data into polymer dynamics (25). In the mathematical formalism, we found a one-to-one correspondence between a Hi-C contact matrix and an interaction matrix of the polymer model. Once an optimal interaction matrix of the polymer model to an input Hi-C matrix data is obtained, the method allows the calculation of not only dynamic information such as the MSD of a modeled genomic region but also conformations of the polymer model. Therefore, integrating PHi-C with the GSER can provide a new microrheology for Hi-C data to characterize the viscoelastic properties of the modeled chromosome dynamics.

Here, we demonstrate that our microrheology converts an Hi-C matrix into the spectrum of the complex compliance J^∗(ω) as a measure of the flexibility of a modeled genomic region. Because ω represents a frequency of oscillatory shear stress in the rheology formalism (26), the inverse t = ω⁻¹ corresponds to a time, and J^∗(ω) should include dynamic information along the time. Thus, the converted spectrum of the complex compliance describes how an individual genomic region as a part of the modeled polymer flexibly deforms at a specific timescale. We show that rigid boundaries in a profile of the complex compliance along a genomic coordinate at a timescale statistically characterize TAD boundaries. Moreover, by applying Hi-C data during cell differentiation, we find the appearance of synchronous and liquid-like intercompartment interactions in differentiated cells. Together, our microrheology enables us to interpret static and population-averaged Hi-C data as a dynamic and hierarchical rheology spectrum regarding the dynamic 3D genome organization.

Materials and Methods

Theory of microrheology to convert Hi-C data into complex compliance

First, for an N × N-sized Hi-C matrix of a single chromosome with an appropriate bin resolution, we modeled the chromosome fiber as a polymer system {R₀, R₁, …, R_{N − 1}}, where R_i represents the position vector of the i-th monomer. Besides, we proposed a model for deciphering Hi-C data into polymer dynamics in which the attractive or repulsive interaction between two monomers was assumed as a linear force proportional to the displacement between the two monomers (25). We refer to this model as the polymer network model. Then, the physical interactions of all pairs can be described as an N × N matrix $\mathrm{K}$ = (K_ij). The dynamics of the polymer system is described by the Langevin equation, $\gamma \left(d{\mathit{R}}_i\left(t\right)/dt\right)={\sum }_{j=0}^{N-1}{K}_{ij}\left[{\mathit{R}}_j\left(t\right)-{\mathit{R}}_i\left(t\right)\right]+{\mathit{g}}_i\left(t\right)$, where γ is the friction coefficient of the monomers. The thermal random force g_i(t) satisfies zero average, $\langle g_{i,\alpha }\left(t\right)\rangle$ = 0, and the fluctuation-dissipation relation, $\langle g_{i,\alpha }\left(t\right)g_{j,\beta }\left(s\right)\rangle$ = 2γk_BTδ_αβδ_ijδ(t − s), where k_B is the Boltzmann constant, T is the temperature of the environment, $\langle \cdot \rangle$ stands for the averaging at thermal equilibrium, and the suffixes α and β represent the spatial coordinates x, y, and z. Because the equation is linear, we can analytically solve the equation under thermal equilibrium. Therefore, once the interaction matrix $\mathrm{K}$ is given, we can calculate and simulate the dynamics and conformations of the polymer model in thermal equilibrium. The positive values of the matrix $\mathrm{K}$ stand for elastic forces between two monomers, and the model formally resembles the Gaussian network model (27, 28, 29). Mathematically, although a negative value of the matrix $\mathrm{K}$ can make the polymer system unstable, the positive semidefiniteness of the Laplacian matrix of $\mathrm{K}$ is a necessary and sufficient condition for the stability of the polymer network model (25). As long as the Laplacian matrix of $\mathrm{K}$ is positive semidefinite, the eigenvalues of the Laplacian matrix are nonnegative, and the stability of the polymer system is ensured (25). Therefore, the negative values are acceptable as repulsive forces in the polymer network model. This assumption is a unique point of our modeling, and different from the recently developed similar polymer modeling (23,24).

PHi-C (https://github.com/soyashinkai/PHi-C) is a simulation tool to decipher Hi-C data based on the mathematical formalism of the polymer network model, in which a normalized contact matrix $\mathrm{C}$ = (C_ij) is connected in a one-to-one correspondence with the normalized interaction matrix $\overline{\mathrm{K}}=\frac{{\sigma }^2}{3k_{\text{B}}T}\left(K_{ij}\right)$ (25). Here, σ represents the contact distance. The PHi-C optimization procedure allows for extracting an optimal normalized interaction matrix $\overline{\mathrm{K}}$ from an input-normalized contact matrix $\mathrm{C}$ (Fig. 1). Therefore, we can interpret an input population-averaged Hi-C contact matrix for a single chromosome as interaction parameters of the polymer network model in thermal equilibrium. In practice, as long as the Laplacian matrix of the matrix $\overline{\mathrm{K}}$ is positive semidefinite, PHi-C simulation to calculate polymer dynamics and conformations returns physically stable results.

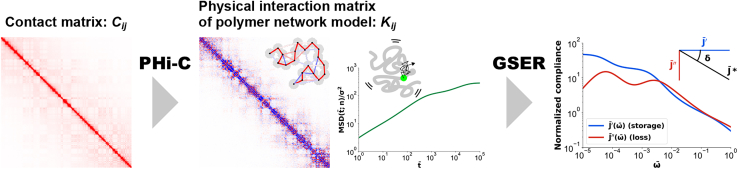
Figure 1.

Microrheology pipeline for Hi-C data using PHi-C and GSER. A normalized contact matrix C_ij as input data is deciphered into a normalized physical interaction matrix of the polymer network model ${\overline{K}}_{ij}$ through the PHi-C optimization. The red and blue colors in the bins of ${\overline{K}}_{ij}$ represent the intensity of the attractive and repulsive interactions, respectively. The MSD of the n-th monomer in the polymer model is analytically calculated from the interaction matrix ${\overline{K}}_{ij}$. Finally, the GSER allows us to obtain the normalized complex compliance ${\overline{J}}^{\ast }\left(\overline{\omega }\right)=\overline{J}\text{'}\left(\overline{\omega }\right)-i\overline{J}\text{'}\text{'}\left(\overline{\omega }\right)$. The ratio $\overline{J}\text{'}\text{'}/\overline{J}\text{'}$ corresponds to the loss tangent, tanδ, where δ is the phase angle. To see this figure in color, go online.

In theory, the physical interaction matrix $\mathrm{K}$ includes all information with respect to not only dynamics, but also conformations in thermal equilibrium. The matrix $\mathrm{K}$ can be converted into the Laplacian matrix $\mathrm{L}=\mathrm{D}-\mathrm{K}$ to characterize the properties of the network, where the degree matrix is defined by $\mathrm{D}$ = diag(D₀, D₁, …, D_N−1) and D_i = ${\sum }_{j=0}^{N-1}{K}_{ij}$. Because the Laplacian matrix $\mathrm{L}$ is symmetric, $\mathrm{L}$ is diagonalizable. Furthermore, the N eigenvalues satisfy 0 = λ₀ < λ₁ ≤ λ₂ ≤ … ≤ λ_{N − 1} as long as $\mathrm{L}$ is positive semidefinite and there is an orthogonal matrix $\mathrm{Q}$ such that ${\mathrm{Q}}^{\mathrm{T}}\mathrm{L}\mathrm{Q}$ = diag(λ₀, λ₁, …, λ_{N − 1}). Then, the MSD of the n-th monomer within the modeled single chromosome can be written as

$$\text{MSD}\left(t;n\right)=6k_{\text{B}}T\sum _{p=1}^{N-1}{Q}_{np}^2{\lambda }_p^{-1}\left(1-e^{-{\lambda }_p/\gamma \cdot t}\right),$$ (1)

where t represents actual time (25), and the movement of the center-of-mass is eliminated to take into account the dynamic fluctuations within a single chromosome.

The GSER connects the MSD to the complex shear modulus in the Laplace domain (18) with the inertia being neglected, $\tilde{G}\left(s\right)=\left(k_{\text{B}}T/\pi a\right)\left(1/s\langle \Delta {\tilde{\mathit{r}}}^2\left(s\right)\rangle \right)$, and the complex compliance is defined as the inverse of the complex shear modulus (26),

$$\tilde{J}\left(s\right)\equiv \frac{1}{\tilde{G}\left(s\right)}=\frac{\pi a}{k_{\text{B}}T}s\langle \Delta {\tilde{\mathit{r}}}^2\left(s\right)\rangle .$$ (2)

Here, we employed the MSD of a modeled genomic monomer derived by PHi-C to consider the dynamic viscoelastic properties of the genome itself within a single chromosome. Calculating the Laplace transformation of Eq. 1, the complex compliance of the n-th monomer within a single chromosome was expressed by using the eigenvalues ${\left\{{\lambda }_p\right\}}_{p=1}^{N-1}$ and the orthogonal matrix $\mathrm{Q}$ as

$$\tilde{J}\left(s;n\right)=6\pi a\sum _{p=1}^{N-1}\frac{Q_{np}^2}{\gamma s+{\lambda }_p}.$$ (3)

The matrix one-to-one correspondence between $\mathrm{C}$ and $\overline{\mathrm{K}}$ is formally closed as dimensionless quantities in PHi-C, where the two physical quantities σ and γ are unknown factors. Therefore, our theory cannot directly deal with the above complex compliance with the physical unit Pa⁻¹. We should give normalized expressions. In PHi-C, the eigenvalues of the normalized Laplacian matrix $\overline{\mathrm{L}}=\left({\sigma }^2/3k_{\text{B}}T\right)\mathrm{L}$ were normalized as $\overline{{\lambda }_p}=\left({\sigma }^2/3k_{\text{B}}T\right){\lambda }_p$. Moreover, using the normalized inverse time $\overline{s}=\left(\gamma {\sigma }^2/k_{\text{B}}T\right)s$, we could rewrite Eq. 3 as

$$\tilde{J}\left(\overline{s};n\right)=\frac{6\pi a{\sigma }^2}{k_{\text{B}}T}\sum _{p=1}^{N-1}\frac{Q_{np}^2}{\overline{s}+3{\overline{\lambda }}_p}.$$ (4)

In general, the complex compliance was defined by the Fourier-Laplace transformation, replacing $\overline{s}=i\overline{\omega }$: $J^{\ast }\left(\overline{\omega }\right)=\tilde{J}\left(i\overline{\omega }\right)=J\text{'}\left(\overline{\omega }\right)-iJ\text{'}\text{'}\left(\overline{\omega }\right)$, where $\overline{\omega }$, J′, and J″ are the normalized frequency, the storage, and the loss compliances, respectively. Thus, the normalized complex compliance was derived from the result of PHi-C with no reference to physical parameters,

$${\overline{J}}^{\ast }\left(\overline{\omega };n\right)\equiv J^{\ast }\left(\overline{\omega };n\right)\frac{k_{\text{B}}T}{6\pi a{\sigma }^2}=\sum _{p=1}^{N-1}\frac{Q_{np}^2}{i\overline{\omega }+3{\overline{\lambda }}_p},$$ (5)

and the normalized storage and loss compliances can be written as

$$\overline{J}\text{'}\left(\overline{\omega };n\right)=\sum _{p=1}^{N-1}\frac{3Q_{np}^2{\overline{\lambda }}_p}{{\overline{\omega }}^2+9{\overline{\lambda }}_p^2}\text{and}\overline{J}\text{'}\text{'}\left(\overline{\omega };n\right)=\sum _{p=1}^{N-1}\frac{Q_{np}^2\overline{\omega }}{{\overline{\omega }}^2+9{\overline{\lambda }}_p^2},$$ (6)

respectively. The ratio of $\overline{J}\text{'}\text{'}$/$\overline{J}\text{'}$ is called the loss tangent,

$$\text{tan}\delta \left(\overline{\omega };n\right)=\overline{J}\text{'}\text{'}\left(\overline{\omega };n\right)/\overline{J}\text{'}\left(\overline{\omega };n\right),$$ (7)

where δ represents the phase angle between stress and strain (26). A flow of our microrheology procedure based on both PHi-C and the GSER is summarized in Fig. 1.

Hi-C data of mouse embryonic stem cells

We used Hi-C data of mouse embryonic stem (ES) cells during neural differentiation by Bonev et al. (8) (Gene Expression Omnibus, GEO: GSE96107) on the Hi-C data archive of Juicebox (30). Using Juicer Tools (30), we extracted the Hi-C matrix data with Knight-Ruiz (KR) normalization and at a 250-kb resolution from “.hic” files and calculated the eigenvector. The extracted Hi-C matrix data were analyzed through the PHi-C pipeline (25).

Analysis of the distance between TAD boundaries and the genomic positions of the troughs

The analysis was performed as previously described with small modifications (31,32). We used TAD boundary data, defined by Bonev et al. (2), on chromosomes 6 and 17 of ES cells during neural differentiation. To generate the control trough list, the genomic positions of the troughs at each frequency ($\overline{\omega }$ = 10⁻¹, 10⁻², and 10⁻³) were randomly permutated at 250-kb genomic bin resolution on a chromosome excluding the centromeric region (0–3 Mb). Then, cumulative probabilities of the overlap between the lists of TAD boundaries and the troughs (original or randomly permutated) at a given frequency were computed based on their nearest distance.

PHi-C simulation to calculate polymer dynamics and conformations

We carried out PHi-C simulations to calculate polymer dynamics of the polymer network model. First, we obtained an optimal normalized interaction matrix $\overline{\mathrm{K}}$ by the PHi-C optimization procedure. Then, $\overline{\mathrm{K}}$ is converted into the normalized Laplacian matrix $\overline{\mathrm{L}}$. Using the eigendecomposition of the matrix $\overline{\mathrm{L}}$, the normalized eigenvalues ${\left\{{\overline{\lambda }}_p\right\}}_{p=0}^{N-1}$ and the orthogonal matrix $\mathrm{Q}$ are obtained. For a normalized polymer conformation vector ${\overline{\mathit{R}}}_{\alpha }={\left(\left(R_{0,\alpha }/\sigma \right),\left(R_{1,\alpha }/\sigma \right),\cdots ,\left(R_{N-1,\alpha }/\sigma \right)\right)}^{\mathrm{T}}$, where R_i,α stands for the α (= x, y, z) coordinate of the i-th monomer, the converted vector ${\overline{\mathit{X}}}_{\alpha }={\mathrm{Q}}^{\mathrm{T}}{\overline{\mathit{R}}}_{\alpha }$ satisfies the variance relationship $\langle {\overline{X}}_{p,\alpha }^2\rangle =1/\left(3{\overline{\lambda }}_p\right)$ for p = 1, 2, …, N − 1. Therefore, an initial conformation of the converted vector in thermal equilibrium is given: ${{\overline{X}}_{0,\alpha }|}_{t=0}=0$, so that the center-of-mass is the origin, and ${{\overline{X}}_{p,\alpha }|}_{t=0}$ is a random variable obeying the normal distribution with mean 0 and variance $1/\left(3{\overline{\lambda }}_p\right)$ for p = 1, 2, …, N − 1. Then, the initial normalized conformation in thermal equilibrium is calculated as ${{\overline{\mathit{R}}}_{\alpha }|}_{t=0}={\mathrm{Q}{\overline{\mathit{X}}}_{\alpha }|}_{t=0}$. Finally, to calculate the polymer dynamics, we numerically integrated the stochastic differential equation by using Heun’s method (17): the integral algorithm assures the second-order convergence in the parameter E and is defined by first predicting ${{\bar{\mathit{R}}}_{\alpha }|}_{\stackrel{\sim }{t}}{={\bar{\mathit{R}}}_{\alpha }|}_t{-3ϵ\bar{\mathrm{L}}{\bar{\mathit{R}}}_{\alpha }|}_t+\sqrt{2ϵ}{\mathit{\xi }}_{\alpha }$ and then correcting ${{\bar{\mathit{R}}}_{\alpha }|}_{t+ϵ}={{\bar{\mathit{R}}}_{\alpha }|}_t-3ϵ\bar{\mathrm{L}}\left({{\bar{\mathit{R}}}_{\alpha }|}_t+{{\bar{\mathit{R}}}_{\alpha }|}_{\stackrel{\sim }{t}}\right)/2+\sqrt{2ϵ}{\mathit{\xi }}_{\alpha },$ where the vector ${\mathit{\xi }}_{\alpha }={\left({\xi }_{0,\alpha },{\xi }_{1,\alpha },\cdots ,{\xi }_{N-1,\alpha }\right)}^{\mathrm{T}}$ consists of random variables ${\left\{{\xi }_{i,\alpha }\right\}}_{i=0}^{N-1}$ obeying the normal distribution with mean 0 and variance 1. The parameter $ϵ=\left(k_{\text{B}}T\Delta t/\gamma {\sigma }^2\right)$ is nondimensional and represents a normalized step time, and it determines the accuracy of the stochastic differential equation integration. Δt stands for the step time of the integration in actual time. We also eliminated the dynamics of the center of mass to keep the position at the origin.

To estimate the physical size of polymer conformations in thermal equilibrium, we sampled a normalized polymer conformation ${\left\{{\overline{\mathit{R}}}_i=\left({\overline{R}}_{i,x},{\overline{R}}_{i,y},{\overline{R}}_{i,z}\right)\right\}}_{i=0}^{N-1}$ by the same method as the above to obtain the initial normalized conformation. Then, we calculated the radius of gyration by $\overline{R_{\text{g}}}=\sqrt{\left(1/N\right){\sum }_{i=0}^{N-1}{\overline{\mathit{R}}}_i^2}$.

To visualize and analyze the simulated polymer dynamics and conformations, we used VMD (33).

Results

Spectrum of complex compliance during mouse neural differentiation

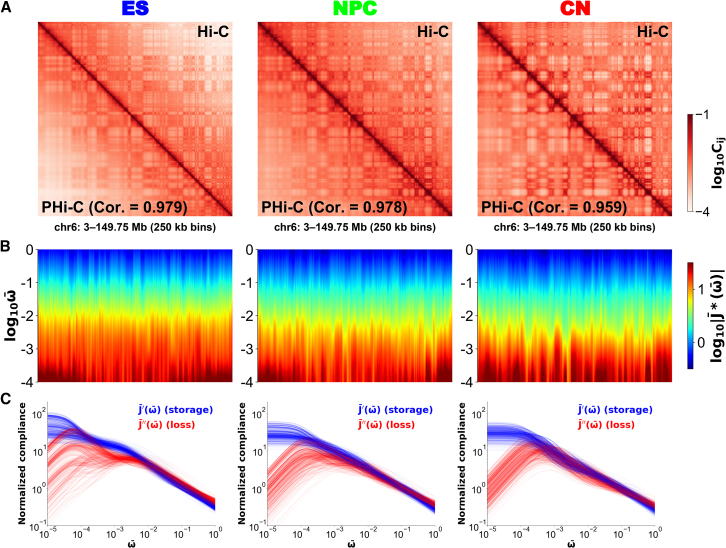
Because we had previously analyzed Hi-C data of chromosomes 6 and 17 in mouse ES cells by the PHi-C method (25), we focused on these two chromosomes as a demonstration of our microrheology method. In addition, to uncover changes in rheological properties of the 3D genome organization during cell differentiation, we needed to analyze deep-coverage Hi-C data of mouse ES cells, neural progenitor cells (NPCs), and cortical neurons (CNs) (8). First, we performed the PHi-C optimization procedure for the 3- to 149.75-Mb genomic region of chromosome 6 to obtain an optimal normalized interaction matrix $\overline{\mathrm{K}}$ of the polymer network model. The optimized contact matrices for ES cells, NPCs, and CN cells showed very high Pearson’s correlations (0.979, 0.978, and 0.959, respectively) between the Hi-C matrix and the optimized contact matrix (Fig. 2 A). The same analysis for the 3- to 95-Mb genomic region of chromosome 17 also showed a good agreement between the Hi-C matrix and the optimized contact matrix with very high Pearson’s correlations (0.978, 0.983, and 0.969, respectively) (Fig. S1 A). Also, based on the optimal normalized interaction matrix, our PHi-C simulation allows for calculating and visualizing chromosome conformations for each differentiation stage (Fig. S2).

Figure 2.

(A) Contact matrices for chromosome 6 during neural differentiation of mouse embryonic stem (ES) cells (left), neural progenitor cells (NPCs) (middle), and cortical neuron (CN) cells (right) at 250-kb resolution. The upper right and lower left elements in each matrix correspond to the normalized Hi-C contact probabilities and the optimized ones by PHi-C, respectively. (B) The spectra of the normalized complex compliance $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ for chromosome 6 in mouse ES cells (left), NPCs (middle), and CN cells (right) are shown. Along the genomic coordinate and the logarithmic frequency ${\text{log}}_{10}\overline{\omega }$, a spectrum of ${\text{log}}_{10}\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ is depicted as a heat map. (C) Frequency-dependent normalized storage (blue) and loss (red) compliances, $\overline{J}\text{'}\left(\overline{\omega };n\right)$ and $\overline{J}\text{'}\text{'}\left(\overline{\omega };n\right)$, for all genomic regions n (= 0, 1, …, 586) on chromosome 6 in mouse ES cells (left), NPCs (middle), and CN cells (right) are shown. To see this figure in color, go online.

Using Eqs. 5 and 6, we calculated the normalized complex compliance ${\overline{J}}^{\ast }\left(\overline{\omega };n\right)=\overline{J}\text{'}\left(\overline{\omega };n\right)-i\overline{J}\text{'}\text{'}\left(\overline{\omega };n\right)$ as a measure of flexibility for an oscillatory stress with the normalized frequency $\overline{\omega }$. Also, the parameter n represents a genomic region (3 + 0.25 × n)–(3 + 0.25 × (n + 1)) Mb. Thus, we obtained a two-dimensional spectrum of $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ along the genomic coordinate (Figs. 2 B and S1 B). In general, at a fixed frequency ω, rheological quantities express the viscoelastic response to the periodic perturbation with ω, and these quantities include the dynamic information on the viscoelastic mobility at the timescale t = ω⁻¹. The values of $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ gradually increase along with time evolution from the short timescale $\overline{\omega }$ = 10⁰ to the long timescale $\overline{\omega }$ = 10⁻⁴. The vertical stripe patterns in the spectrum are variable along the chromosome, suggesting different viscoelastic responses depending on the genomic regions of the chromosome. Furthermore, according to changes in the Hi-C patterns during mouse neural differentiation, the spectra of $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ also showed different patterns.

To visualize the frequency-dependent viscoelastic response, we plotted the normalized storage and loss compliances, $\overline{J}\text{'}\left(\overline{\omega }\right)$ and $\overline{J}\text{'}\text{'}\left(\overline{\omega }\right)$, for all genomic regions (Figs. 2 C and S1 C). The blue bundle of the storage compliances shows a step-like pattern with slopes on the double logarithmic plot, suggesting dynamic and hierarchical viscoelastic responses in the 3D genome organization. Furthermore, the red curves of the loss compliances show convex upward shapes, indicating that the viscous dynamics of a genomic position n within a chromosome relaxes at the time corresponding to the inverse of the normalized frequency $\overline{\omega }$ at the peak.

Taken together, our microrheology method allows the conversion of a hierarchical Hi-C pattern to a dynamic and hierarchical rheological spectrum.

TAD boundaries are more rigid as nodes than intra-TAD sequences

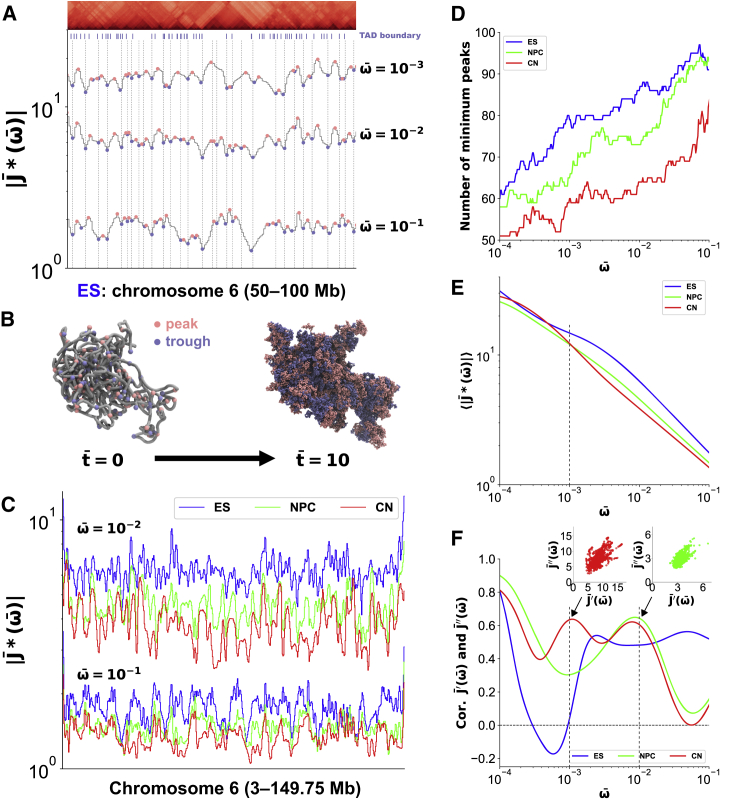
To understand what the values of the complex compliance ${\overline{J}}^{\ast }$ reveal along the genomic coordinate, we plotted $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ at $\overline{\omega }$ = 10⁻¹, 10⁻², and 10⁻³ focusing on the 50- to 100-Mb region of the chromosome 6 in ES cells (Fig. 3 A). According to variously sized triangles corresponding to chromatin domains such as TADs and compartments on the Hi-C contact pattern, the shapes of $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ displayed peaks and troughs marked with pink and blue dots, respectively. Our statistical analysis revealed that the troughs in the $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ profile were located near the reported TAD boundaries at each frequency $\overline{\omega }$ = 10⁻¹, 10⁻², and 10⁻³ for chromosomes 6 and 17 of mouse ES cells, NPCs, and CN cells (Fig. S3; Table S1), suggesting that TAD boundaries are characterized as more rigid nodes than the intra-TAD sequences according to the timescale $\overline{t}={\overline{\omega }}^{-1}$. Therefore, the vertical stripe patterns in the spectrum in Fig. 2 B show the variation of peaks and troughs, depending on the frequency.

Figure 3.

Complex compliance characterizes chromatin domain boundaries and internal regions during mouse neural differentiation. (A) $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ at $\overline{\omega }$ = 10⁻¹, 10⁻², and 10⁻³ and a cropped Hi-C contact matrix for the 50- to 100-Mb region on chromosome 6 in mouse ES cells with a TAD boundary profile (8) are shown. Pink and blue dots correspond to peaks and troughs for each curve, respectively. The vertical dashed lines represent the genomic position at the troughs of $\left|{\overline{J}}^{\ast }\left(\overline{\omega }={10}^{-2}\right)\right|$. (B) A snapshot of an initial polymer conformation (left) in PHi-C simulations for chromosome 6 in mouse ES cells is shown, where pink and blue dots represent the genomic positions at the peaks and troughs of $\left|{\overline{J}}^{\ast }\left(\overline{\omega }={10}^{-1}\right)\right|$. Also shown is a cumulative plot (right) of the 3D positions of the peaks and troughs in the simulation within time $\overline{t}$ = 10. (C) $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ at $\overline{\omega }$ = 10⁻¹ and 10⁻² for chromosome 6 in mouse ES cells, NPCs, and CN cells is shown. (D) The frequency dependence of the number of minimal peaks as the troughs on $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ for chromosome 6 in mouse ES cells, NPCs, and CN cells is shown. (E) The frequency-dependent average values of $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ along chromosome 6 in mouse ES cells, NPCs, and CN cells are shown. (F) The frequency-dependent Pearson’s correlation between the normalized storage and loss compliances, $\overline{J}\text{'}\left(\overline{\omega }\right)$ and $\overline{J}\text{'}\text{'}\left(\overline{\omega }\right)$, on chromosome 6 in mouse ES cells, NPCs, and CN cells is shown. The scatter plots at $\overline{\omega }$ = 10⁻² and $\overline{\omega }$ = 10⁻³ for NPCs and CNs are displayed, respectively. To see this figure in color, go online.

Next, we tried to visualize the role of the trough positions in the 3D genome organization. Our PHi-C simulation allows for polymer dynamics consistent with the optimized Hi-C matrix. Fig. 3 B shows a snapshot of an initial polymer conformation for chromosome 6 in mouse ES cells, where pink and blue dots represent the genomic positions corresponding to the peaks and troughs of $\left|{\overline{J}}^{\ast }\left(\overline{\omega }={10}^{-1}\right)\right|$, respectively. Video S1 shows the dynamic fluctuation of the polymer model within time $\overline{t}$ = 10. It seems that, at every time step, the conformation is irregularly folded, and we cannot find distinct chromatin domains. Then, we piled up the pink and blue dots in the dynamics (Fig. 3 B; Video S2). We can see that these two color regions are separated and that the blue-labeled trough regions look functional as dynamic boundaries to interfere with interdomain interactions between the pink-labeled intradomain regions.

Video S9. Spinning Green- and Red-Labeled 3D Compartments and Labeled Cumulative Dots

Spinning green- and red-labeled 3D compartments (upper) with positive and negative eigenvectors, respectively, for chromosome 6 in mouse CN cells and the labeled cumulative dots (lower) in the PHi-C simulation for time intervals $\overline{t}$ = 10 (left), 100 (middle), and 1000 (right).

Video S1. A PHi-C Simulation for Chromosome 6 in Mouse ES Cells within Time $\overline{t}$= 10

This video is in reference to Fig. 3 B. Here 10⁴ steps of numerical integration were carried out with the normalized step time ϵ = 0.001. Pink and blue dots represent the genomic positions at the peaks and troughs of $\left|\overline{J}\ast \left(\overline{\omega }={10}^{-1}\right)\right|$in Fig. 3A.

Dynamic and hierarchical changes of chromosome rigidness during cell differentiation

The peaks and troughs in the shape of $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ were also observed for chromosome 6 in ES cells, NPCs, and CN cells (Fig. 3 C). The number of troughs decreased from the short timescale (high ω) to the long timescale (low ω) (Figs. 3 D and S4 A). This indicated that dynamic and hierarchical compartmentalization with domain fusions occur in the 3D genome organization according to the time evolution. For example, intra-TAD dynamics is dominant until $\overline{t}$ = 10¹, then inter-TAD communications and fusions of TADs arise up to $\overline{t}$ = 10² in intracompartments, and intercompartment interactions occur over $\overline{t}$ = 10³. Besides, the numbers of troughs for ES cells, NPCs, and CNs were ordered, revealing that the number of chromatin domains as chromosome structural units decreases depending on an individual frequency, and the rearrangement occurs during cell differentiation. Furthermore, the average values of $\left|{\overline{J}}^{\ast }\left(\overline{\omega }\right)\right|$ were also ordered until the time $\overline{t}$ = 10³ (Figs. 3 E and S4 B), suggesting that the physical property of chromosomes averagely becomes rigid and less flexible during cell differentiation.

The complex compliance ${\overline{J}}^{\ast }\left(\overline{\omega }\right)$ is divided into the storage and loss components (Eq. 6), which are not independent of each other in rheological relations (26). We plotted these two compliances within chromosome 6 in ES cells, NPCs, and CN cells at different frequencies (Video S3), relating to the Cole-Cole plot in dielectrics (34). At a fixed frequency $\overline{\omega }$, the scattering pattern should reflect a cooperative rheological response within a chromosome. Therefore, we calculated the correlation between these two compliances on the scatter plots for different frequencies (Fig. 3 F). For ES cells, broad positive correlations were detected in the frequency region $\overline{\omega }$ = 10⁻³–10⁻¹. A high positive correlation indicates that the elastic and viscous responses described by $\overline{J}\text{'}\left(\overline{\omega }\right)$ and $\overline{J}\text{'}\text{'}\left(\overline{\omega }\right)$ synchronize within a chromosome to the periodic stress with a frequency $\overline{\omega }$. Therefore, a positive peak of the correlation indicates a characteristic time $\overline{t}={\overline{\omega }}^{-1}$ of the synchronous response. For NPCs and CNs, a broad region showing high correlations was not observed. Instead, some peaks were observed around $\overline{\omega }$ = 10⁻² for NPCs and $\overline{\omega }$ = 10⁻² and 10⁻³ for CNs. Note here that the peaks around $\overline{\omega }$ = 10⁻⁴ are excepted because the response to the extremely slow fluctuation corresponds to a whole movement of the chromosome. Because we could confirm that the checkerboard pattern corresponding to the A/B compartment organization in Fig. 2 A gradually becomes dense during cell differentiation, the correlations for ES cells, NPCs, and CNs at $\overline{\omega }$ = 10⁻³ are ordered, suggesting that the timescale $\overline{t}$ = 10³ must be related to intercompartment organization. For chromosome 17, we observed similar features of the correlations (Fig. S4 C).

Video S2. Spinning 3D Structure of Cumulative Dots of the Peaks and Troughs in the Simulation within Time $\overline{t}$ = 10

This video is in reference to Fig. 3 B and Video S1.

Synchronous and liquid-like intercompartment interactions appear in differentiated cells

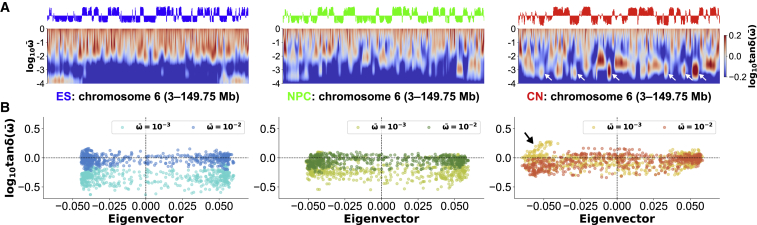
As shown in Eq. 7, the loss tangent is defined as the ratio of the normalized loss compliance $\overline{J}\text{'}\text{'}$ to the normalized storage compliance $\overline{J}\text{'}$. Therefore, positive and negative values of the logarithmic loss tangent indicate liquid-like viscosity and solid-like elasticity, with higher and lower energy dissipation, respectively. Here, we asked whether there is a difference in the liquid-like and solid-like properties between the A and B compartment organization or not. We depicted spectra of the loss tangent $\text{tan}\delta \left(\overline{\omega };n\right)$ (see Eq. 7) with the eigenvector to characterize the compartment organization (3) during differentiation in Fig. 4 A.

Figure 4.

(A) Eigenvectors and spectra of the loss tangent $\text{tan}\delta \left(\overline{\omega }\right)$ for chromosome 6 in mouse ES cells (left), NPCs (middle), and CN cells (right) at a 250-kb resolution. Along the genomic coordinate and the logarithmic frequency ${\text{log}}_{10}\overline{\omega }$, a spectrum of ${\text{log}}_{10}\text{tan}\delta \left(\overline{\omega }\right)$ is depicted as a heat map. The white arrows for CNs indicate definite “island” regions around $\overline{\omega }$ = 10⁻³ with negative eigenvectors. (B) The scatter plots between the logarithmic loss tangent and the eigenvalue for $\overline{\omega }$ = 10⁻² and $\overline{\omega }$ = 10⁻³ are shown. For CNs, the black arrow indicates the appearance of the “islands” in (A). To see this figure in color, go online.

For chromosome 6 in ES cells, the spectrum showed that viscous behavior with higher energy dissipation is dominant in the frequency $\overline{\omega }$ = 10⁰–10⁻², and the shape at a fixed frequency has peaks and troughs. However, the positive and negative values of the logarithmic loss tangent for $\overline{\omega }$ = 10⁻² did not correlate with the eigenvalues (Fig. 4 B; left), implying that there is little difference in the liquid-like and solid-like properties between the A and B compartments. In addition, the scatter plot for $\overline{\omega }$ = 10⁻³ dropped horizontally compared with that for $\overline{\omega }$ = 10⁻². For NPCs, we confirmed a different pattern in the spectrum, although the scatter plots for $\overline{\omega }$ = 10⁻² and 10⁻³ showed an overall decrease similar to that for ES cells (Fig. 4, A and B; middle).

In contrast, the spectrum for CNs revealed a characteristic pattern of isolated regions like “islands” with positive values (Fig. 4 A; right). Interestingly, some islands appeared around the frequency $\overline{\omega }$ = 10⁻³ belonging to the genomic regions with negative eigenvalues, indicating the synchronous and liquid-like intercompartment response to the periodic force with the frequency. The synchronous appearance was also confirmed in the scatter plots for $\overline{\omega }$ = 10⁻² and 10⁻³ (Fig. 4 B; right), where the solid-like elastic property ($\text{tan}\delta <1$) for $\overline{\omega }$ = 10⁻² turns into the liquid-like viscous property (tanδ > 1) for $\overline{\omega }$ = 10⁻¹. For chromosome 17, we observed similar features on the loss tangent spectra (Fig. S5).

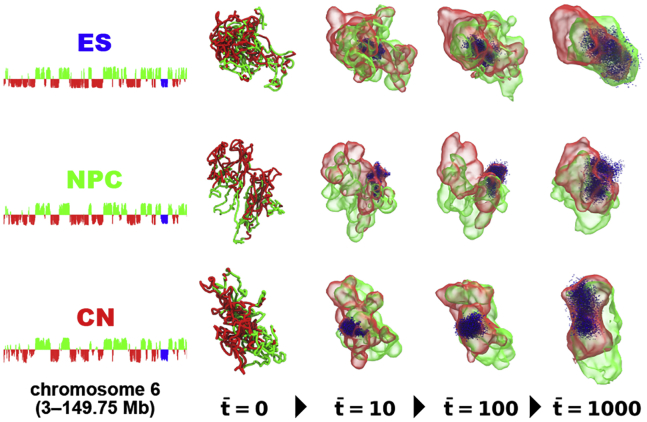
Although it would be hard to visualize and express the dynamic rheology response in three dimensions, we tried to visualize the dynamic changes of 3D formation of the A/B compartments along with the time evolution in Fig. 5 and in Videos S4, S5, S6, S7, S8, and S9. We depicted the time evolution of green- and red-labeled 3D compartments with positive and negative eigenvectors, respectively, in PHi-C simulations for mouse ES cells, NPCs, and CN cells within time intervals t = 10, 100, and 1000. The blue dots represent cumulative dots of a compartment region (128.5–134 Mb for ES cells, 128.5–134 Mb for NPCs, and 128.5–134.5 Mb for CNs) with negative eigenvectors in the simulations. We can see a complicatedly separated 3D formation of the compartments for the short timescale (t = 10). For the long timescale (t = 1000), the separated compartments polarize with an overlap. Within the red-labeled 3D compartment region, the blue-labeled genomic region, which belongs to one of the “islands” in the case of CNs, dynamically moves around.

Figure 5.

Time evolution of green- and red-labeled 3D compartments with positive and negative eigenvectors, respectively, in PHi-C simulations for chromosome 6 in mouse ES cells (top), NPCs (middle), and CN cells (bottom) within time intervals $\overline{t}$ = 10, 100, and 1000. The blue dots represent cumulative dots of a compartment region (128.5–134 Mb for ES cells, 128.5–134 Mb for NPCs, 128.5–134.5 Mb for CNs) with negative eigenvectors in simulation. Fig. S6 explains how to make isosurface plotting of 3D compartments from a PHi-C simulation. To see this figure in color, go online.

Video S3. Time Evolution of the Cole-Cole Plots between the Normalized Storage and Loss Compliances

Normalized storage and loss compliances $\overline{J}\text{'}\left(\overline{\omega }\right)$, and $\overline{J}\text{'}\text{'}\left(\overline{\omega }\right)$, from $\overline{\omega }=$10⁻¹ to 10⁻³ within chromosome 6 in mouse ES (left, blue), NPC (middle, green), and CN (right, red) cells.

Video S4. A PHi-C Simulation for Chromosome 6 in Mouse ES Cells within Time $\overline{t}$ = 10

This video is in reference to the dynamics in Video S1, which were identical to the dynamics shown here. According to an eigenvector profile of a Hi-C matrix, compartment regions with positive and negative eigenvectors are labeled by green and red colors, respectively.

Video S5. Spinning Green- and Red-Labeled 3D Compartments and Labeled Cumulative Dots

Spinning green- and red-labeled 3D compartments (upper) with positive and negative eigenvectors, respectively, for chromosome 6 in mouse ES cells and the labeled cumulative dots (lower) in the PHi-C simulation for time intervals $\overline{t}$ = 10 (left), 100 (middle), and 1000 (right).

Video S6. A PHi-C Simulation for Chromosome 6 in Mouse NPCs within Time $\overline{t}$ = 10

Here 10⁴ steps of numerical integration were carried out with the normalized step time ϵ = 0.001. According to an eigenvector profile of a Hi-C matrix, compartment regions with positive and negative eigenvectors are labeled by green and red colors, respectively.

Video S7. Spinning Green- and Red-Labeled 3D Compartments and Labeled Cumulative Dots

Spinning green- and red-labeled 3D compartments (upper) with positive and negative eigenvectors, respectively, for chromosome 6 in mouse NPC cells and the labeled cumulative dots (lower) in the PHi-C simulation for time intervals $\overline{t}$ = 10 (left), 100 (middle), and 1000 (right).

Video S8. A PHi-C Simulation for Chromosome 6 in Mouse CN Cells within Time $\overline{t}$ = 10

Here 10⁴ steps of numerical integration were carried out with the normalized step time ϵ = 0.001. According to an eigenvector profile of a Hi-C matrix, compartment regions with positive and negative eigenvectors are labeled by green and red colors, respectively.

Discussion

In this study, we revealed the rheological information of the dynamic 3D genome organization as a spectrum by integrating the theoretical MSD by PHi-C and the GSER. On the spectrum, the differences in the compliance along the genomic coordinate at a particular timescale revealed the distinct characteristics of the boundaries and insides of chromatin domains; especially, TAD boundaries were found to be more rigid than the intra-TAD regions. During cell differentiation, we quantitatively estimated increasing rigidity of the chromosome, with dynamic organization of chromatin domains with time evolution.

Particularly, our microrheology method allows for interpreting static and population-averaged Hi-C matrix data as a dynamic and hierarchical 3D genome picture. Definite boundaries with higher rigidness at a particular timescale $\overline{t}={\overline{\omega }}^{-1}$ characterize an individual triangle region corresponding to a chromatin domain such as a TAD or a compartment on an Hi-C pattern. In other words, the appearance of a chromatin domain as a functional unit of the 3D genome organization correlates to a specific timescale with the dynamics. In addition, organization of an interdomain interaction is relatively slow, and synchronous and liquid-like intercompartment interactions were notable in the mouse neural-differentiated cells. Therefore, the spectrum revealed by our microrheology method explicitly shows the hierarchical four-dimensional genome organization beyond schematic and static 3D genome pictures on paper.

Large-scale numerical simulations for modeling the interphase cell nucleus environment have revealed viscoelastic properties based on the GSER (35). As microrheology experiments have tracked the motion of tracer particles, the authors simulated the viscoelastic response of dispersed Brownian particles in polymer solutions and found a caged effect at short times with large particles. In the current study, our microrheology method did not focus on the tracer particles but rather on modeled chromosome dynamics itself by calculating the theoretical MSD and using the GSER. Thus, we could characterize the rheological properties of a chromosome along the genome coordinate. Moreover, we used the complex compliance J^∗(ω) as a measure of flexibility, but we can convert it into the complex modulus G^∗(ω) and the dynamic viscosity η^∗(ω) by the relationship G^∗(ω) = iωη^∗(ω) = 1/J^∗(ω) (26).

Although the PHi-C optimization procedure can return a high correlation value between an input Hi-C and the optimized contact matrices, the correlation value depends on not only the quality and matrix normalization of the Hi-C data but also the computational time of the PHi-C optimization. In addition, it is crucial to bridge our theoretical prediction and the real dynamics of genomic loci in living cells. In our theoretical framework, two physical parameters, the contact distance σ (m) and the friction coefficient γ (kg/s), are unknown. These values must be determined by comparison with experimental MSD data of genomic loci. Although the theoretical MSD result was not comprehensively verified by experiments, the MSD curves theoretically derived by PHi-C for Nanog and Oct4 loci of ES cells were partially consistent with the genomic movements in a live-cell imaging experiment (25,36). Under a high correlation value by the PHi-C optimization and assuming that a chromosome modeled by the polymer network model is in thermal equilibrium, our microrheology method is reliable and competent.

In this study, we focused on the rheological properties of a specific chromosome during cell differentiation, but we could not elucidate a relationship between the physical properties of chromatin and gene expression, i.e., how physical rigidness or flexibility of a specific genomic region including some loci might relate to the gene expression levels. Our findings on TAD boundaries as more rigid nodes would suggest they might be the molecular mechanism regulating the physical rigidness of the boundaries.

In summary, the microrheological spectrum generated from Hi-C data describes the dynamic changes in rigidness and flexibility between individual genomic regions as well as during cell differentiation. To fully understand chromatin domain formation and interdomain interactions, we need to understand chromatin dynamics at different timescales. Our microrheology method opens the possibility of interpreting Hi-C data as information that can reveal the dynamic and hierarchical properties of the 3D genome organization.

Author Contributions

S.S., T.S., and S.O. designed the research. S.O. supervised the study. S.S. carried out analytical calculations and PHi-C analysis, as well as analyzing the data. H.M. and I.H. performed TAD boundary analysis. S.S. wrote the article.

Editor: Toshio Tsukiyama.