Abstract
The three-dimensional (3D) organization of chromatin, on the length scale of a few genes, is crucial in determining the functional state—accessibility and amount of gene expression—of the chromatin. Recent advances in chromosome conformation capture experiments provide partial information on the chromatin organization in a cell population, namely the contact count between any segment pairs, but not on the interaction strength that leads to these contact counts. However, given the contact matrix, determining the complete 3D organization of the whole chromatin polymer is an inverse problem. In this work, a novel inverse Brownian dynamics method based on a coarse-grained bead-spring chain model has been proposed to compute the optimal interaction strengths between different segments of chromatin such that the experimentally measured contact count probability constraints are satisfied. Applying this method to the α-globin gene locus in two different cell types, we predict the 3D organizations corresponding to active and repressed states of chromatin at the locus. We show that the average distance between any two segments of the region has a broad distribution and cannot be computed as a simple inverse relation based on the contact probability alone. The results presented for multiple normalization methods suggest that all measurable quantities may crucially depend on the nature of normalization. We argue that by experimentally measuring predicted quantities, one may infer the appropriate form of normalization.
Significance
Chromosome conformation capture experiments such as 5C and Hi-C provide information on the contact counts between different segments of chromatin, but not the interaction strengths that lead to these counts. Here, a methodology is proposed by which this inverse problem can be solved, namely, given the contact probabilities between all segment pairs, what is the pairwise interaction strength that leads to this value? With the knowledge of pairwise interactions determined in this manner, it is then possible to evaluate the three-dimensional organization of chromatin and to determine the true relationship between contact probabilities and spatial distances.
Introduction
Even though all the cells in multicellular organisms have the same DNA sequence, they function differently based on the cell type. For example, the phenotype of a skin cell is significantly different from that of a neuronal cell (1,2). One of the important factors for this variation is hypothesized to be the three-dimensional (3D) organization of DNA inside the cell nucleus and its variability from cell type to cell type (3, 4, 5, 6). Although findings of the recent chromosome configuration capture experiments (3C, 4C, 5C, Hi-C) (7, 8, 9, 10) lend credence to this hypothesis, the outcomes of these experiments are frozen snapshots of a sparse set of points along DNA that do not give a complete understanding of the 3D organization of the genome. In this work, a methodology based on a coarse-grained polymer model for DNA is proposed that enables the unraveling of its spatiotemporal organization, which is consistent with experimentally observed contact maps.
The complex folding of meter-long DNA into micrometer-sized chromosome, with topologically associated domains and contact domains, has been revealed at a few kb resolution by state-of-the-art Hi-C experiments (11, 12, 13, 14, 15, 16). More insight into the role played by the 3D organization of the genome in the functioning of a cell on the length scale of genes is provided by 3C and 5C experiments (17). Essentially, all these chromatin conformation capture experiments lead to information on the count of contacts between any pair of segments along the DNA chain backbone, represented in the form of contact (“heat”) maps.
Several attempts have been made to understand the 3D organization of the genome using a variety of techniques developed previously to understand the statics and dynamics of polymers (18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31). Early models focused on understanding the nonequilibrium nature of chromatin organization and the polymer physics behind large-scale packaging (26, 27, 28). Subsequent studies that focus on reconstructing the 3D structure from the contact maps are predominantly based on assuming that there is a direct correlation between the magnitude of the contact count and the spatial distance between the relevant pairs (32, 33, 34, 35, 36, 37, 38). These investigations have led to important insights about the 3D consequences of differences present in the contact maps, such as the spatial organization of ON and OFF states of certain genes. However, all these efforts have certain limitations. As mentioned above, nearly all the computational studies convert contact counts obtained from Hi-C experiments into spatial distances using a predecided formula. That means, given a contact count matrix, such methods do not predict the distances between different chromatin segments; rather they take the distance values as inputs, based on certain assumptions. They then use conventional Monte Carlo (or equivalent) methods to find steady-state configurations of the chromatin, given a distance map between different DNA segment pairs. In other words, the existing models consider this as a “forward” problem of computing equilibrium configurations of chromatin as a consequence of assuming certain spatial distance between bead pairs. However, the problem of computing 3D configurations of a chromatin polymer, given a contact map, is not a “forward” problem, but rather an “inverse” problem (39). The question is, given a contact map, what are the optimal interactions between different segments of chromatin such that the experimentally seen contact map emerges? To the best of our knowledge, no study exists that solves chromatin configurations of genes considering it as an inverse problem. Another shortcoming is that the experimentally obtained contact counts are not converted to “absolute” contact probabilities. Some of the existing methods remove various systematic biases and convert the contact counts to relative contact probabilities. Some of these techniques are iterative correction and eigenvector decomposition (ICE) (40), sequential component normalization (41), Knight-Ruiz (42), chromoR (43), multiHiCcompare (44), and HiCNorm (45). In this work, we examine the existing ICE normalization method and compare it with a method processed here based on a simple process of converting contact counts to contact probabilities though a parameter representing the ensemble size. We show that the structural properties of the gene loci depend on the precise values of contact probabilities. It should also be noted that all prior efforts are based on Monte Carlo methods, and hence, they cannot predict the dynamics of chromatin—they only obtain information on static configurations of the genome.
In summary, although current models have made important progress in constructing 3D structure from the contact maps, they suffer from one or more of the following shortcomings:
-
1)
an a priori assumption regarding the probability of contact between pairs of segments and their spatial distances;
-
2)
the introduction of harmonic springs between interacting pairs that implies an attractive force between these pairs that does not decay with distance, but rather increases;
-
3)
the use of simulation methods that are limited to providing information on static configurations;
-
4)
considering the problem of computing 3D configurations as a “forward” problem, with no attempt to determine the interaction strengths between segment pairs that lead to 3D structures that are consistent with observed contact maps;
-
5)
the failure to obtain an accurate representation of dynamic behavior by failing to include hydrodynamic interactions (46) between segment pairs.
In this work, a methodology is introduced that addresses all these shortcomings. Chromatin on the length scale of a gene is represented by a coarse-grained bead-spring chain polymer model with a potential of interaction between pairs of beads that can be tuned to accommodate varying strengths of interaction. A Brownian dynamics simulation algorithm, which includes hydrodynamic interactions and an iterative scheme based on inverse Monte Carlo, is developed that enables the generation of 3D configurations that are consistent with the contact maps. This methodology is then applied to obtain the static 3D configurations from 5C contact maps of the α-globin gene locus, both in the ON and OFF states of the gene. Further, because hydrodynamic interactions are taken into account, the approach has the potential to examine the dynamic transitions between the ON and OFF states. In our work, however, because the focus is on reproducing heatmaps and generating 3D configurations (which are both static properties), dynamic properties have not been considered.
The outline of the study is as follows. The key governing equations of the model and the simulation algorithm are summarized in Polymer Model. In IBD, the inverse Brownian dynamics (IBD) method is introduced in a general context. The validation of the proposed approach with the help of a prototype is presented in Validation of the IBD Method with a Prototype. The coarse-graining procedure used here is described in The Coarse-Graining Procedure. Resolution of the issue of determining the contact probabilities from contact counts is proposed in Conversion of Contact Counts to Contact Probabilities: The Normalization Problem. Results for the static 3D configurations of α-globin locus are discussed in 3D Configuration of the α-Globin Gene Locus, and the relationship between spatial distances and contact probabilities is highlighted in 3D Spatial Distances and Contact Probabilities. The principal conclusions of this work are summarized in Conclusions.
Methods
Chromosome conformation capture experiments such as 5C and Hi-C provide information about the contact counts between different segments of chromatin, but not the interaction strengths that lead to these counts. Here, we propose a methodology by which this inverse problem can be solved, namely, given the contact probabilities between all segment pairs, what is the pairwise interaction strength that leads to this value? Additionally, the fact that experiments only give contact counts and not probabilities needs to be dealt with. In Polymer Model, we first provide the principal governing equations and the details of the interactions. In IBD, we describe the IBD algorithm by which the interaction strengths εμν can be estimated given the set of contact probabilities pμν.
Polymer model
To compute the 3D organization of the genome, the chromatin is coarse grained into a bead-spring chain of N beads connected by N − 1 springs. The chain configuration is specified by the set of position vectors of the beads rμ (μ = 1, 2, …, N). For simulation purposes, all distances are made dimensionless by using the characteristic length scale l0 = arising from the ratio of thermal energy—where kB is the Boltzmann constant and T is the temperature—and the spring constant ks. Throughout this manuscript, the asterisk superscript is used to indicate dimensionless quantities ( = rμ/l0). The adjacent beads in the polymer chain are bonded via a Fraenkel spring, with a nondimensional spring potential between bead μ and (μ + 1), given by
| (1) |
where is the nondimensional distance between beads μ and μ + 1 and is the dimensionless natural length of the Fraenkel spring. To mimic protein-mediated interactions between different parts of the chromatin polymer, it is necessary to introduce a potential energy function. Typically, this is achieved with a Lennard-Jones (LJ) potential or with harmonic spring interactions (39). However, in this study, the following nondimensional Soddemann-Duenweg-Kremer (SDK) (47) potential is introduced between any two nonadjacent beads μ and ν,
| (2) |
Here, is the nondimensional distance between beads μ and ν, εμν is an independent parameter to control the bead-bead attractive interaction strength between beads μ and ν, and 21/6σ∗ represents the minima of the potential where = εμν. The SDK potential has the following advantages compared to the LJ potential: 1) the repulsive part of the SDK potential ( ≤ 21/6σ∗) representing steric hindrance remains unaffected by the choice of the parameter εμν, and 2) protein-mediated interactions in chromatin are like effective “bonds” formed and broken with a finite range of interaction. Unlike the LJ potential, the SDK potential has a finite attractive range—the SDK potential energy smoothly reaches zero at the cutoff radius, , whose value is set by the choice of two parameters α and β. The parameters α and β are determined by applying the two boundary conditions, namely, = 0 at and = −εμν at = 21/6σ∗. The appropriate choice of the cutoff radius has been investigated extensively in a recent study (48), and it has been shown that a value of = 1.82σ∗ leads to an accurate prediction of the static properties of a polymer chain in poor, theta, and good solvents. The same value is adopted in this study.
Given a set of values εμν and an initial configuration of the bead-spring chain, the time evolution of the configurations of the polymer chain is evaluated using Brownian dynamics simulations (49), which is a numerical method for solving the following Euler finite difference representation of the stochastic differential equation for the bead position vectors,
| (3) |
Here, t∗ = t/λ0 is the dimensionless time, with λ0 = ζ/4ks being the characteristic timescale, in which ζ = 6πηa is the Stokes friction coefficient of a spherical bead, η is the solvent viscosity, and a is the bead radius. and are the nondimensional spring and interaction forces computed from the respective potential energy functions provided in Eqs. 1 and 2. ΔWν is a nondimensional Wiener process with mean zero and variance Δt∗, and Bμν is a nondimensional tensor whose presence leads to multiplicative noise (49). Its evaluation requires the decomposition of the diffusion tensor Dμν defined as Dμν = δμνδ + Ωμν, where δμν is the Kronecker delta, δ is the unit tensor, and Ωμν = Ω is the hydrodynamic interaction tensor. Defining the matrices and as block matrices consisting of N × N blocks each having dimensions of 3 × 3, with the (μ, ν)-th block of containing the components of the diffusion tensor Dμν and the corresponding block of being equal to Bμν, the decomposition rule for obtaining can be expressed as . The hydrodynamic tensor Ω is assumed to be given by the Rotne-Prager-Yamakawa tensor
| (4) |
with
and
Here, the hydrodynamic interaction parameter h∗ is the dimensionless bead radius in the bead-spring chain model and is defined by h∗ = a/.
Because we are interested in the 3D organization of chromatin, we use a number of different static properties to describe the shape of the equilibrium chain. The radius of gyration of the chain Rg , where is defined by
| (5) |
with , , and being the eigenvalues of the gyration tensor G (arranged in ascending order), with
| (6) |
Note that G, , , and are calculated for each trajectory in the simulation before the ensemble averages are evaluated. The asymmetry in equilibrium chain shape has been studied previously in terms of various functions defined in terms of the eigenvalues of the gyration tensor (50, 51, 52, 53, 54, 55, 56). Apart from , , and themselves, we have examined the following shape functions: the asphericity (B), the acylindricity (C), the degree of prolateness (S), and the shape anisotropy (k2), as defined in Table 1.
Table 1.
Definitions of Shape Functions in Terms of Eigenvalues of the Gyration Tensor G
| Shape Function | Definition |
|---|---|
| Asphericity (55,65) | B = (7) |
| Acylindricity (55,65) | C = (8) |
| Degree of prolateness (52,56,65) | S = (9) |
| Relative shape anisotropy (52,55,56,65) | κ2 = 1 − 3 (10) |
Note that I1 = and I2 = are invariants of G.
The stochastic differential equation (Eq. 3) can be solved with a semi-implicit predictor-corrector algorithm developed in Prabhakar and Prakash (57) once all the parameters are specified. However, the strength of interaction εμν between any two beads μ and ν is unknown a priori. Because they control the static conformations of a chain, their values will be different depending on whether the gene is in an “ON” or “OFF” state. Ultimately, the contact probability between any two segments on the gene is determined by the values of εμν for all pairs on the gene. The parameters that need to be specified for us to carry out the simulations are 1) the hydrodynamic interaction parameter h∗, 2) the natural length of Fraenkel spring , 3) the SDK potential parameter σ∗, 4) the characteristic length scale l0, and 5) the characteristic timescale λ0. We are not probing the dynamic properties of chromatin (46) in this work, so we chose h∗ = 0. The natural physical length scale in the problem is the diameter of the bead. We assume that chromatin of size 10 kb determines the length scale in our model l0, and we coarse grain 10 kb chromatin to one bead. The other two length parameters are determined as σ∗ = 1 and = 1 such that two neighboring beads are typically at a distance of the order of l0. All our length results are presented in units of l0. The timescale in our problem is given by λ0 = ζ/4ks. The timestep Δt∗ = Δt/λ0 is chosen to be 10−3. This will decide the time intervals in our simulation. However, because we are only presenting steady-state quantities in this work, all the results are independent of time.
In our model, the distance between the neighboring beads fluctuates about r0 with the value of order l0, which is the equilibrium length of the spring. For the parameters chosen in this work, r0 ± l0 can be greater than σ. This allows the chain to cross itself to explore the whole phase space faster. However, this is a result of our choice of parameters values, and we can also choose to have a parameter that makes strand passage more difficult.
In the section below, we first describe the IBD algorithm by which the interaction strengths εμν can be estimated given the set of contact probabilities pμν. The issue of converting experimental contact counts to contact probabilities is addressed in Conversion of Contact Counts to Contact Probabilities: The Normalization Problem.
Inverse Brownian dynamics
In this investigation, a well-established standard method is utilized to optimize the parameters of a model Hamiltonian such that it reproduces, as closely as possible, the values of some externally given quantities (e.g., from experiment or from other simulations). In the literature, the method is typically referred to as “inverse Monte Carlo” (58, 59, 60). It is, however, completely independent of the underlying sampling scheme, as long as the latter produces thermal averages in the canonical ensemble. We prefer to highlight the underlying Brownian dynamics sampling of this study and hence refer to it here as the IBD method. The method is best explained in general terms. It is assumed that the system is described by a phase-space variable Γ and a model Hamiltonian (Γ). Another assumption is that the simulation produces the canonical average of some observable, given by a phase-space function A(Γ):
| (11) |
Here, β = 1/(kBT). On the other hand, we have a given “target” value At (e.g., from experiment), which will typically differ from our simulation result. We are now interested in the dependence of the Hamiltonian on some coupling parameter J, and we wish to adjust J to bring as close to At as possible within the limitations of the Hamiltonian as such in general and its dependence on J in particular. To do this, it is desirable to obtain information on 1) in which direction J should modified and 2) by what amount (at least by order of magnitude). If the change of the coupling constant, ΔJ, is small, we can write down a Taylor expansion around the value J = J0 at which we performed the simulation:
| (12) |
where the “generalized susceptibility” χ is an abbreviation for the thermodynamic derivative
| (13) |
The crucial point is now that χ can be directly sampled in the simulation by making use of a standard fluctuation relation. Indeed, taking the derivative of Eq. 11 with respect to J, one finds directly
| (14) |
where B denotes another phase-space function, which is just the observable conjugate to J:
| (15) |
In deriving Eq. 14, it is assumed that the phase-space function A(Γ)does not depend on J, i.e., ∂A(Γ)/∂J = 0. This is the case for most typical applications and certainly for this investigation.
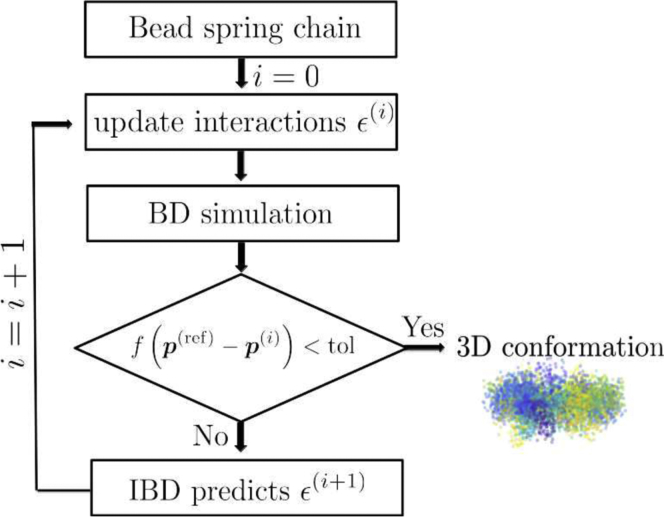
The simplest way to do IBD, therefore, consists of 1) neglecting all nonlinear terms in Eq. 12, 2) setting its left-hand side equal to At, 3) solving for ΔJ, and 4) taking J0 + ΔJ as a new and improved coupling parameter. The entire process is then repeated with the updated coupling parameter. In other words, Brownian dynamics simulations are carried out again, and the difference between the updated simulation value and the reference value of the observable is compared with the prescribed tolerance and checked to see whether convergence has been achieved. If not, the coupling parameters are updated once more until convergence has been achieved. The schematic representation of the IBD algorithm described here is displayed as a flowchart in Fig. 1. To avoid overshoots, it is often advisable to not update J by the full increment ΔJ that results from solving the linear equation, but rather, only by ΔJ = λΔJ, where λ is a damping factor with 0 < λ < 1. The iteration is terminated as soon as − At does not decrease any more, within some tolerance. One also has to stop as soon as χ becomes zero within the statistical resolution of the simulation (this is, however, not a typical situation).
Figure 1.
Flowchart for the inverse Brownian dynamics (IBD) method. Here, p(ref) represents the reference contact probability matrix, and p(i) represents the contact probability matrix from simulations at iteration i. The interaction strength between beads μ and ν is given by εμν. To see this figure in color, go online.
The method may be straightforwardly generalized to the case of several observables Am and several coupling parameters Jn, where the number of observables and the number of couplings may be different. The Taylor expansion then reads
| (16) |
where the matrix of susceptibilities is evaluated as a cross-correlation matrix:
| (17) |
with
| (18) |
Typically, the matrix χmn will not be invertible (in general, it is not even square). Therefore, one should treat the linear system of equations via a singular-value decomposition (SVD) and find ΔJ via the pseudoinverse (PI). In practice, this means that one updates the couplings only in those directions and by those amounts when one has a clear indication from the data that one should do so, whereas all other components remain untouched. For details on the concepts of SVD and PI, the reader may refer to Press et al. (61) and Fill and Fishkind (62).
In this instance, the averages are the contact probabilities as produced by the simulations, whereas the target values are the corresponding experimental values (discussed in greater detail below). The corresponding phase-space functions can be written as indicator functions, which are one in case of a contact and zero otherwise. The coupling parameters that we wish to adjust are the well depths of the SDK attractive interactions, which we allow to be different for each monomer pair. The IBD algorithm discussed here in general terms is described in more detail in Supporting Materials and Methods, Section S1 and applied to the specific problem considered here, along with a discussion of the appropriate SVD and PI.
Results and Discussion
Validation of the IBD method with a prototype
To validate the IBD method, a prototype of a chromatin-like polymer chain with artificially set interaction strengths (εμν) was constructed. The data from this simulated chain were used to test the IBD algorithm as described below. The IBD algorithm was validated for chains of length 10, 25, and 45 beads. Here, we discuss the 45-bead chain case as a prototype. A few bead pairs (μν) were connected arbitrarily with a prescribed value of the well-depth of the SDK potential. The nonzero reference interaction strengths for the connected bead pairs are shown in Table 2; the remaining pairs were considered to have no attractive interaction ( = 0). The bead-spring chain was simulated until it reached equilibrium, which was quantified by computing Rg as a function of time. A stationary state was observed to be reached after eight Rouse relaxation times (63). However, equilibration was continued for a further 15 Rouse relaxation times. After equilibration, an ensemble of 105 polymer configurations was collected from 100 independent trajectories, from each of which 103 samples were taken at intervals of 103 dimensionless time steps, which correspond to roughly two to three Rouse relaxation times. From this ensemble, the contact probability for each bead pair in the chain was computed. Here, is an indicator function that is equal to 1 or 0 depending upon whether the μth and νth beads are within the cutoff distance of SDK potential or not . The reference contact probabilities determined in this manner are shown in Fig. 2 b. In this instance, although has been constructed by simulating the bead-spring chain for the given values of , in general it refers to the experimental contact probabilities.
Table 2.
Interaction Strengths εμν and Contact Probabilities pμν for Selected Bead Pairs (μ, ν) in a Bead-Spring Chain with 45 Beads
| Initial State: SAW Polymer | |||||||
|---|---|---|---|---|---|---|---|
| Bead Pair |
Interaction Strength, εμν |
Contact Probability, pμν |
|||||
| Reference | Recovered | % Error | Initial | Reference | Recovered | % Error | |
| 3-13 | 7.00 | 6.70 | 4.29 | 0.0033 | 0.44 | 0.46 | 4.55 |
| 13-23 | 7.00 | 7.28 | 4.00 | 0.0036 | 0.51 | 0.49 | 3.92 |
| 23-33 | 7.00 | 7.08 | 1.14 | 0.0057 | 0.39 | 0.37 | 5.13 |
| 33-43 | 7.00 | 7.35 | 5.00 | 0.0041 | 0.62 | 0.59 | 4.84 |
| 8-18 | 7.00 | 6.94 | 0.86 | 0.0056 | 0.47 | 0.47 | 0.00 |
| 18-28 | 7.00 | 6.89 | 1.57 | 0.0052 | 0.31 | 0.32 | 3.23 |
| 28-38 | 7.00 | 7.16 | 2.29 | 0.0071 | 0.55 | 0.53 | 3.64 |
| 3-43 | 7.00 | 7.18 | 2.57 | 0.0002 | 0.22 | 0.22 | 0.00 |
| Initial State: Collapsed Polymer | |||||||
|---|---|---|---|---|---|---|---|
| Bead Pair |
Interaction Strength, εμν |
Contact Probability, pμν |
|||||
| Reference | Recovered | % Error | Initial | Reference | Recovered | % Error | |
| 3-13 | 7.00 | 6.67 | 4.71 | 0.139 | 0.44 | 0.44 | 0.00 |
| 13-23 | 7.00 | 6.99 | 0.14 | 0.141 | 0.51 | 0.52 | 1.96 |
| 23-33 | 7.00 | 6.75 | 3.57 | 0.133 | 0.39 | 0.38 | 2.56 |
| 33-43 | 7.00 | 7.19 | 2.71 | 0.136 | 0.62 | 0.59 | 4.84 |
| 8-18 | 7.00 | 7.22 | 3.14 | 0.132 | 0.47 | 0.45 | 4.26 |
| 18-28 | 7.00 | 6.77 | 3.29 | 0.135 | 0.31 | 0.3 | 3.23 |
| 28-38 | 7.00 | 6.89 | 1.57 | 0.133 | 0.55 | 0.55 | 0.00 |
| 3-43 | 7.00 | 7.11 | 1.57 | 0.067 | 0.22 | 0.22 | 0.00 |
Values of these variables recovered using IBD are compared with those of the reference polymer chain, along with the percentage error between the reference and recovered values. Initial εμν-values for all bead pairs were chosen to be 0 for the SAW polymer, whereas εμν = 1 for all bead pairs in the collapsed polymer.
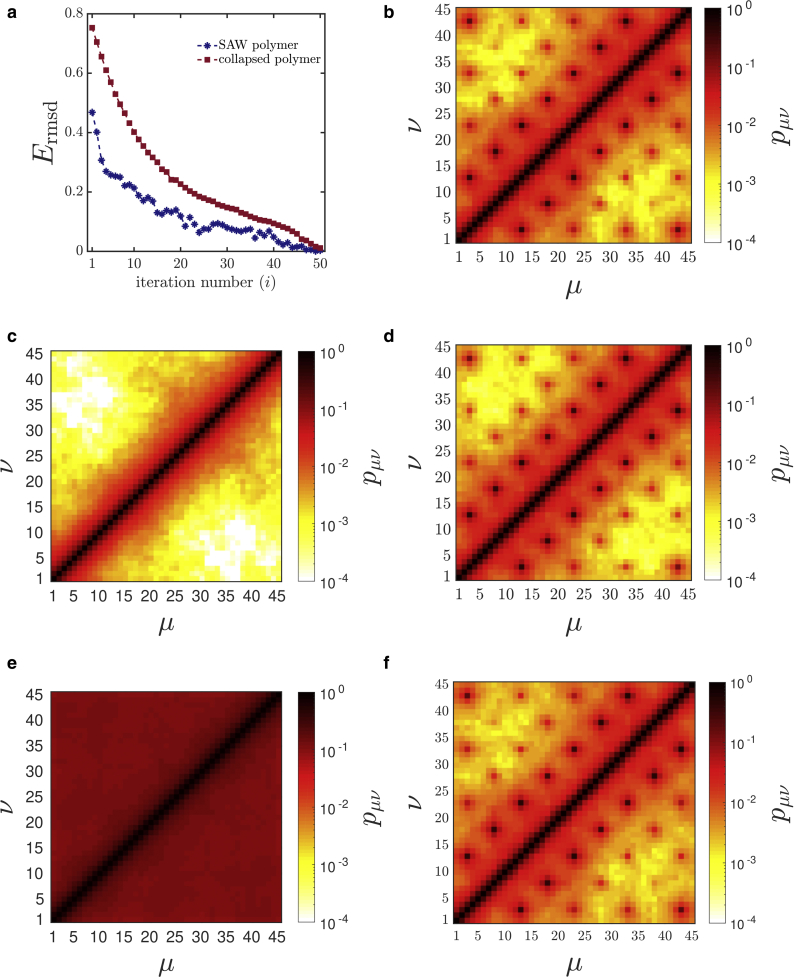
Figure 2.
Validation of the IBD method with a prototype bead-spring chain with 45 beads. (a) Root mean-square deviation Ermsd (Eq. 19) as a function of iteration number showing convergence of the IBD method is given. (b) A reference contact probability matrix is shown. Two different initial states have been considered for testing IBD convergence: (c) initial contact probability for the self-avoiding walk (SAW) in which no bead pairs have attractive interaction and (d) recovered contact probability matrix through IBD starting from the SAW state. Similarly, (e) initial contact probability for the collapsed state in which all bead pairs have attractive interaction, ε = 1, and (f) recovered contact probability matrix through IBD starting with the collapsed state are shown. The abscissa and ordinate represent the bead number along the polymer chain. The color represents the contact probability between the beads μ and ν (see color bar). To see this figure in color, go online.
The IBD method was then applied to recover the reference contact probabilities , starting with an initial guess of a self-avoiding walk in which = 0, i.e., all the interaction strengths are set equal to zero. The contact probability for the initial state of self-avoiding walk is shown in Fig. 2 c. As illustrated in Fig. 1, at each iteration step i, Brownian dynamics was performed for the given , and an ensemble of 105 conformations were collected. To quantify the difference between contact probabilities computed from simulation at iteration i and reference contact probabilities , the root mean-squared deviation (rmsd) was calculated as
| (19) |
at each iteration. The error criteria has been used previously in Meluzzi and Arya (39) and is adopted here. At each iteration i, if the value is greater than the preset tolerance limit (tol), the interaction strength parameters for the next iteration were calculated as given in Eq. S11. To avoid the overshoot in interaction strength , the range of was constrained to [0, 10]. For the investigated polymer chain with 45 beads, the IBD algorithm converges ( < tol) in ∼50 iterations, and was recovered. The error Ermsd for each iteration is shown in Fig. 2 a, and the recovered contact probability matrix is shown in Fig. 2 d. The recovered contact probability values along with the optimized interaction strengths εμν are shown in Table 2. The error in the recovered contact probabilities and interaction strengths is less than 5%, proving the reliability of the IBD method. The largest contact probabilities are for those bead pairs for which values of the interaction strength were chosen a priori, as given in Table 2. However, the existence of these interactions leads to the existence of contact probabilities pμν between all bead pairs μ and ν. The IBD algorithm was applied to not just the specified bead pairs but to recover all contact probabilities pμν for all possible pairs. The errors are given in Table 2 only for the specified values because they are the largest. To check the robustness of the IBD algorithm, the same reference contact probability of the prototype was recovered from an entirely different initial configuration of a collapsed chain in which = 1 for all the bead pairs μ and ν. The initial contact probability matrix of the collapsed chain is shown in Fig. 2 e, and the recovered contact probability matrix starting from the collapsed chain is shown in Fig. 2 f. The recovered contact probability values along with the optimized interaction strengths εμν for a few bead pairs are shown in Table 2. Thus, even starting from a very different configuration, the IBD algorithm converges to the target contact probability matrix, establishing the power of the method. For the sake of completeness, the difference between the reference and recovered contact probability matrices is presented in Supporting Materials and Methods, Section S2, along with a discussion of the pathways by which the polymer chain converges from different initial configurations (swollen or collapsed) to the final reference state. Having validated the IBD algorithm, the next section applies this technique to experimentally obtained contact probabilities of a chromatin on the length scale of a gene.
The coarse-graining procedure
To study the 3D organization of a gene region, the α-globin gene locus (ENCODE region ENm008) is chosen for which Baù et al. (36) have experimentally determined the contact counts using the 5C technique. This is a 500-kb-long region on human chromosome 16 containing the α-globin gene and a few other genes such as LUC7L. Because 5C data do not interrogate the contact counts between all feasible 10 kb segment pairs, many elements in the heat map have no information. This is in contrast with typical Hi-C experiments, in which information on all possible contact pairs is obtained. In principle, this method can be applied to Hi-C data; however, in this instance, we chose the 5C data because they have sufficiently good resolution.
For simulation purpose, the α-globin locus is coarse grained to a bead-spring chain of 50 beads. That is, the experimental 5C data (contact count matrix of size 70 × 70) for the EMn008 region was converted to a contact count matrix of size 50 × 50. The coarse-graining procedure is as follows: 500 kb of the gene locus was divided into 50 beads, each comprising 10 kb equal-sized fragments. The midpoint of each restriction fragment was located and was assigned to the corresponding bead in the coarse-grained polymer. There are cases where two or more restriction fragments (each of size less than 10 kb) get mapped to the same bead. For example, consider restriction fragments r1 and r2 being mapped on to a single coarse-grained bead μ and fragments r3 and r4 being mapped on to another bead ν. The contact counts of the coarse-grained bead pair Cμν can then be computed in at least three different ways, namely independent, dependent, and average coarse-graining procedures, as described below.
-
•
Independent coarse graining: Take the sum of all contact counts for the four restriction fragment combinations (Cμν = )—i.e., assume that all contacts occur independently of each other; in other words, not more than one of the contact pairs occurs in the same cell.
-
•
Dependent coarse graining: Take the maximal contact count among all four restriction fragment combinations (Cμν = max). This assumes that whenever the pairs having small contact counts are in contact, the pair with the largest contact count is also in contact. These are the two extreme cases, and the reality could be somewhere in between.
-
•
Average coarse graining: The third option is then to choose some such intermediate value. Here, we use the approximation that the coarse-grained contact count is equal to the average of the two extreme contact counts mentioned earlier, namely Cμν = .
Conversion of contact counts to contact probabilities: The normalization problem
The contact counts obtained from the chromosome conformation capture experiments are not normalized. That is, the contact count values can vary from experiment to experiment, and the total number of contacts is not quantified. These data cannot be compared across cell lines or across different experimental sets. Although several normalization techniques exist, the ICE method is one of the more widely used techniques, in which through an iterative process, biases are removed, and equal “visibility” is provided to each bin or segment of the polymer. The resulting contact count matrix is a normalized matrix in which = 1. Although the existing normalization techniques help in removing biases, they still only give relative contact probabilities and not the absolute values. To accurately predict the distance between any two segments in chromatin, it is essential to know their absolute contact probabilities. Because the total number of genome equivalent (number of cells) cannot be estimated in a chromosome conformation capture experiment, the calculation of absolute contact probability from the contact count is highly challenging. A simple technique to normalize these counts is described here. The contact count matrix can be normalized by imposing the following constraint, namely that the sum of times any segment pairs (μ, ν) are in contact and the number of times they are not in contact must be equal to the total number of samples Ns. This is true for all bead pairs, i.e., = Ns for all μν. Because only is known, two limiting values of Ns are estimated using the following scenarios. In one scenario, it is assumed that for the segment pairs (μ, ν) that have the largest contact count in the matrix, μ and ν are always in contact in all cells. In other words, = 0; in this case, Ns is simply equal to the largest element of the contact count matrix. Because this is the smallest value of Ns possible, it is denoted by = Nmin. The other scenario estimates the sample size from the row μ for which the sum over all contact counts is the largest, i.e., Ns = maximum of . This assumes that μ is always in contact with only one other segment in a cell and there is no situation when it is not in contact with any segment. This case is denoted as Nmax. However, in a real system, there might be situations in which segment μ is not in contact with any of the remaining segments. In such a case, Ns could be greater than Nmax. We have investigated this question in the context of simulations, in which we know the exact ensemble size and can normalize the contact count matrix with the exact ensemble size, i.e., Ns. From this analysis, it was observed that there are very few samples in which the bead μ is not in contact with any of the remaining beads. It supports our hypothesis that Nmax could be considered to be the upper limit in estimating the ensemble size Ns. Because the precise value of Ns is not known in experiments, Ns is varied as a parameter from Nmin to Nmax. To systematically vary Ns, for convenience, a parameter Nf is defined,
| (20) |
in the range of [0, 1]. Clearly, Nf = 0 implies Ns = Nmin, which is the lower bound for Ns, and Nf = 1 implies Ns = Nmax, which is the upper bound. The contact probabilities at various Nf-values are calculated as pμν = (/Ns) where Ns = Nmin + Nf(Nmax − Nmin).
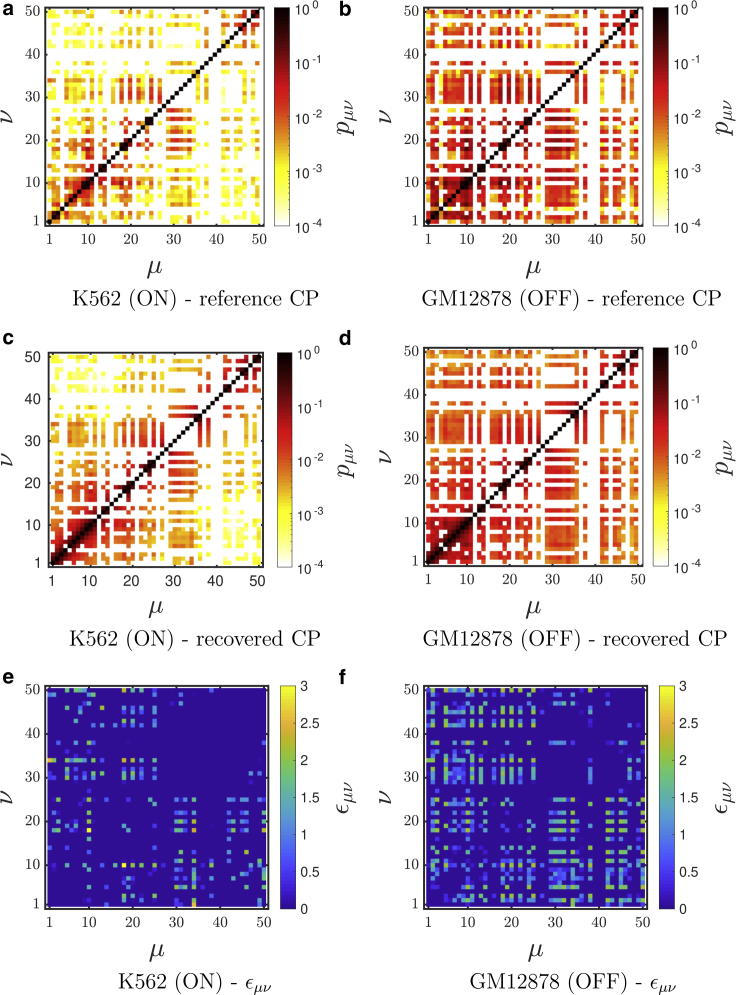
For several values of Nf, the contact count matrices are normalized, and IBD is carried out to obtain the optimal interaction strengths between the bead pairs. Fig. 3, a and b show the normalized contact probabilities at Nf = 0 for cell lines K562 (ON state) and GM12878 (OFF state), respectively (reference contact probabilities), when they are coarse grained to 50 segments of length 10 kb each as per the procedure described above, and the corresponding recovered contact probability matrices for both the cell lines from simulation are shown in Fig. 3, c and d. The corresponding optimized interaction energies (εμν) are plotted in Fig. 3, e and f. The values range approximately from 0 to 3kBT. Given that typical contact probability numbers are very small, the optimized energies are just above thermal energy and are comparable to interaction energies of certain proteins. Exact values of the interaction parameters have been given in Tables S1 and S2 for the GM12878 and K562 cell lines, respectively.
Figure 3.
Comparison of the reference normalized contact probabilities (CPs) (a and b) with the recovered CPs (c and d), obtained with the IBD method for K562 and GM12878, respectively, at Nf = 0. The value of interaction strength parameter εμν is shown for the (e) K562 (ON state) and (f) GM12878 (OFF state) cell lines, respectively, at the converged state. To see this figure in color, go online.
To compare the normalization method introduced in this work with the normalization procedure that is commonly used, namely the ICE technique, we have also carried out the IBD procedure on an ICE-normalized matrix. More details of the ICE method that has been used here are given in the Supporting Materials and Methods, Section S3. The ICE-normalized contact matrix and the corresponding recovered matrix through IBD for both the cell line K562 and GM12878 are shown in Fig. S3. Clearly, the IBD method also recovers the contact probability matrix obtained with the ICE normalization. As will be discussed in further detail below, the normalization method has a significant effect on all the structural properties that have been evaluated in the current work.
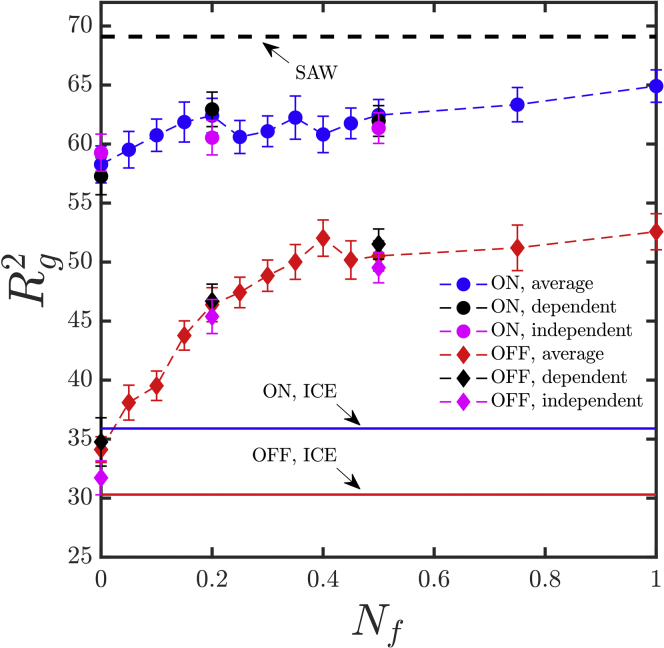
The spatial extent of the chromatin polymer, as quantified by the square radius of gyration , for different values of Nf is presented in Fig. 4. In the case of the cell line in which the gene is ON (K562), the increase in for small values of Nf is relatively less prominent and becomes nearly independent of Nf as Nf approaches one. It is clear that contact probabilities decrease with increasing Nf because Ns increases with Nf. It is consequently expected that with sufficiently large Nf, should approach the value for a self-avoiding walk. We have simulated a self-avoiding walk using the SDK potential with εμν = 0; this represents a purely repulsive potential, and the result is shown as a black dashed line in Fig. 4. In the cell line in which the gene is OFF (GM12878), the value of increases relatively rapidly for small values of Nf and reaches a nearly constant value for Nf 0.4. However, the limiting value is significantly smaller than that of a self-avoiding walk. This suggests that some significant interactions are still present among the bead pairs, even for Nf approaching 1. The influence of the different coarse-graining procedures was examined, and it was found that the value of from all three coarse-graining procedures agreed with each other within error bars (as seen from the data at Nf = 0, 0.2, and 0.5 for both cell lines). This suggests that at least as far as is concerned, the choice of coarse-graining method is not vitally important.
Figure 4.
Spatial extension of the polymer chain quantified by the radius of gyration, , computed at various values of the normalization parameter Nf (see Eq. 20 for definition), for both K562 (ON state) and GM12878 (OFF state) cell lines. All three coarse-graining techniques, i.e., dependent, independent, and average, have been used. The black dashed line represents the value of for a chain executing SAW statistics. Blue and red lines indicate the Rg for ICE-normalized ON and OFF state, respectively. Error bars represent a statistical uncertainty of one standard error of the mean. To see this figure in color, go online.
However, the IBD results for ICE-normalized reference contact probability predicts a very different value for Rg of the ON state (blue line) and OFF state (red line). As can been seen, the for ON state using ICE normalization is close to the obtained here for OFF state at Nf = 0. Interestingly this similarity is observed for many of the properties considered here, as will be discussed in more detail below.
3D configuration of the α-globin gene locus
Shape functions
Because chromatin folded in three dimensions can have spatial organization that is beyond simple spherically symmetric packing, various nonglobular 3D shape properties (as described in Polymer Model) have been analyzed here.
Eigenvalues of the radius of gyration tensor for polymer chains are usually reported in terms of ratios, either between individual eigenvalues or with the mean-square radius of gyration. For a chain with a spherically symmetric shape about the center of mass, we expect = 1/3 for i = 1, 2, 3 and = 1 for all combinations i and j. For chain shapes with tetrahedral or greater symmetry, the asphericity B = 0, otherwise B > 0. For chain shapes with cylindrical symmetry, the acylindricity C = 0, otherwise C > 0. With regard to the degree of prolateness, its sign determines whether chain shapes are preponderantly oblate (S ∈ [−0.2, 0]) or prolate (S ∈ [0, 2]). The relative anisotropy (k2), on the other hand, lies between 0 (for spheres) and 1 (for rods).
All these properties are investigated for Nf = 0 and 1 and for the ICE normalization and compared in the ON and OFF states, as displayed in Table 3. It is clear that although the chain is highly nonspherical in both states, it appears to be slightly more spherical in the OFF than in the ON state. The biggest difference is observed at Nf = 0 between ON and OFF states. As we approach Nf = 1, the difference between the ON and OFF states is not so significant. With ICE, there is not much difference between the two states. As previously observed with the radius of gyration, ICE values are very close to the OFF state at Nf = 0.
Table 3.
Various Shape Properties Based on the Eigenvalues of Gyration Tensor G Are Defined Here for Nf = 0, Nf = 1, and ICE-Normalized Contact Matrix for K562 and GM12878 Cell Lines
| Shape properties |
K562 (ON state) |
GM12878 (OFF state) |
||||
|---|---|---|---|---|---|---|
| Nf = 0 | Nf = 1 | ICE | Nf = 0 | Nf = 1 | ICE | |
| 0.058 | 0.057 | 0.078 | 0.081 | 0.066 | 0.083 | |
| 0.164 | 0.175 | 0.189 | 0.201 | 0.177 | 0.195 | |
| 0.778 | 0.768 | 0.732 | 0.718 | 0.757 | 0.722 | |
| 2.828 | 3.054 | 2.417 | 2.479 | 2.703 | 2.357 | |
| 13.412 | 13.422 | 9.356 | 8.874 | 11.563 | 8.727 | |
| B/ | 0.667 | 0.652 | 0.599 | 0.578 | 0.636 | 0.583 |
| C/ | 0.106 | 0.118 | 0.111 | 0.120 | 0.112 | 0.112 |
| S | 0.913 | 0.816 | 0.988 | 0.772 | 0.926 | 0.867 |
| κ2 | 0.545 | 0.513 | 0.537 | 0.452 | 0.525 | 0.497 |
Density profiles
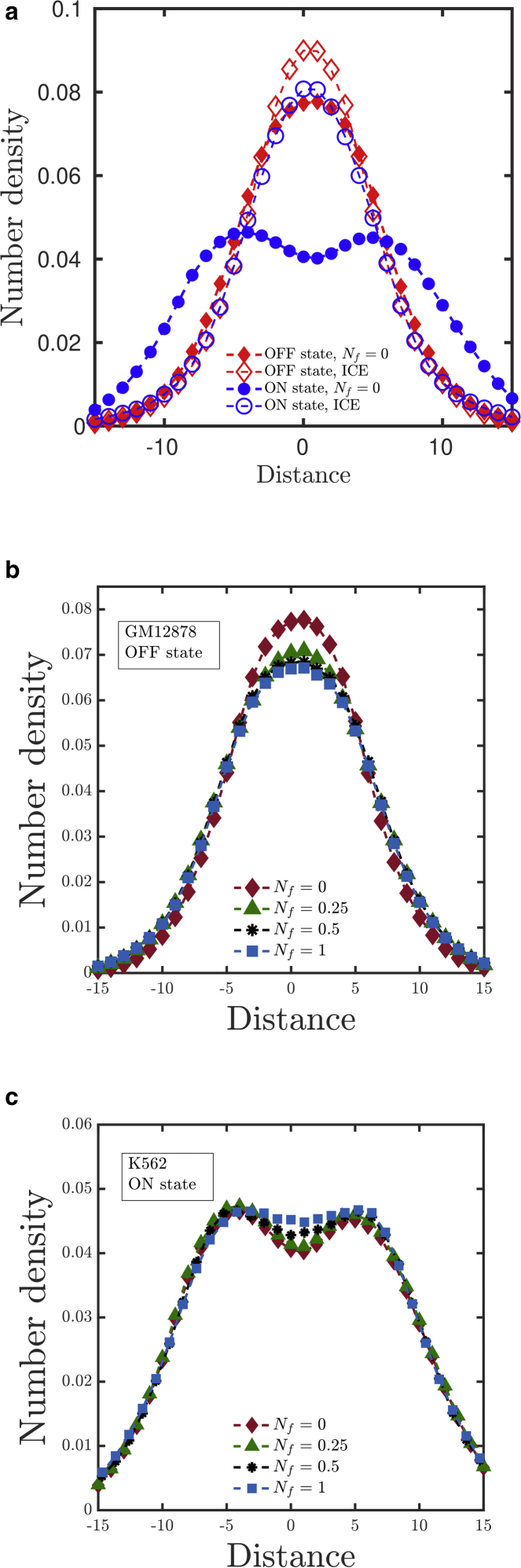
To get a different prospective on the 3D organization of the gene, the density distribution about the center of mass was considered. To do this, all polymer configurations were aligned along the major axis of the radius of gyration tensor G, each bead position was binned, and the number density of beads along the major axis was computed. As displayed in Fig. 5 a, in GM12878 (OFF state) cells, the number density shows a single peak at the center of mass position, suggesting a symmetric organization around the center of mass along the major axis. In the case of K562 (ON state) cells, the number density is seen to have a double peak, implying a bimodal distribution of polymer beads around the center of mass along the major axis (Fig. 5 a), as suggested by earlier 3D models for the α-globin gene (36,38). With an increase in Nf, a slight decrease in the number density at the core of the α-globin gene in the OFF state is observed (Fig. 5 b), and a decrease in extent of bimodality is observed in the ON state (Fig. 5 c). However, the differences for different Nf-values are less prominent at the peripheral regions of the globule. Data comparing the density profiles for the three coarse-graining techniques (dependent, independent, and average) are provided in the Supporting Materials and Methods, Section S4. It was observed that the coarse-graining procedure did not have any influence on the density profiles.
Figure 5.
Comparison of the number density of beads along the major axis of the radius of gyration tensor for various values of the normalization parameter Nf (see Eq. 20 for definition): (a) ON and OFF states at Nf = 0, (b) the OFF state, and (c) the ON state for various values of Nf. To see this figure in color, go online.
We have also compared the density profile corresponding to the ICE-normalized matrix, displayed in Fig. 5 a along with Nf = 0. With the ICE normalization, both states (ON and OFF) show a single peak at the center of mass. The bimodal nature of the ON state is no longer observed. This is a clear prediction that distinguishes the ICE-normalized result from the other results and can be tested in future experiments.
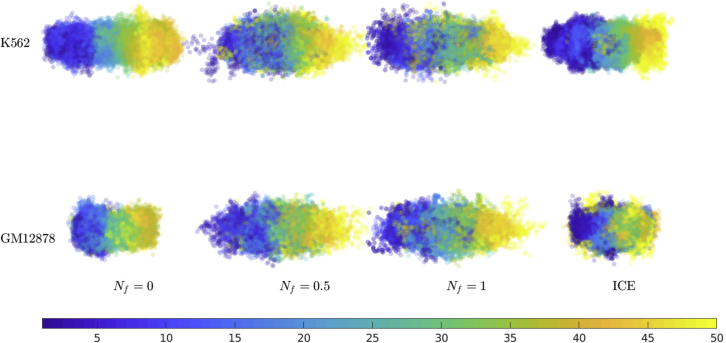
3D conformations
To obtain a snapshot of the 3D structure of the α-globin gene locus, 1000 different configurations from the ensemble were aligned along its major axis and then superimposed on top of each other, as displayed in Fig. 6, for both cell lines at different values of Nf and with the ICE normalization. Each dot represents a bead, and to make them visible, they have been made transparent to some degree. Different colors in the plot represent the bead number along the contour length of the polymer chain. As indicated from the shape functions and the density profiles, the snapshot shows that the structure is highly nonspherical in both cases. In particular, the K562 (ON state) cell line chromatin has a more extended configuration, with slightly higher density away from the center of mass. As can be seen in Fig. 6, the snapshot for Nf = 0 has some differences with snapshots for larger Nf-values. The value of Nf was seen earlier to affect average properties like (Fig. 4). The snapshots in Fig. 6 show a similar behavior as Rg, reflecting the variation for small Nf and saturation for larger Nf.
Figure 6.
Snapshots of 3D configurations, obtained by aligning chains along the major axis of the radius of gyration tensor and superimposing them on top of each other with transparency. Configurations at different values of the normalization parameter Nf (see Eq. 20 for definition) are displayed for cell lines K562 and GM12878. The color assigned to each marker (blue to yellow) represents the bead number along the contour length (bead 1 to bead 50) of the polymer chain. To see this figure in color, go online.
3D spatial distances and contact probabilities
The 3D conformation of the α-globin gene locus has been investigated earlier (36,37). These studies differ from this work in some important respects. Firstly, they assume that the contact counts between any two pairs can be converted to an equilibrium distance between those pairs through a certain predetermined functional form. Secondly, instead of optimizing the interaction strengths to recover the contact counts, their simulations attempt to recover the equilibrium distances that have been derived from contact matrices. It is not clear in these cases whether the experimentally observed contact counts will be recovered by simulations. In this work, no assumptions have been made about the relationship between spatial distance and contact probability for any pair of beads. On the contrary, in this case, we can compute the spatial distances (dμν) that are consistent with the contact probability matrix. Further, no configuration from the ensemble is discarded.
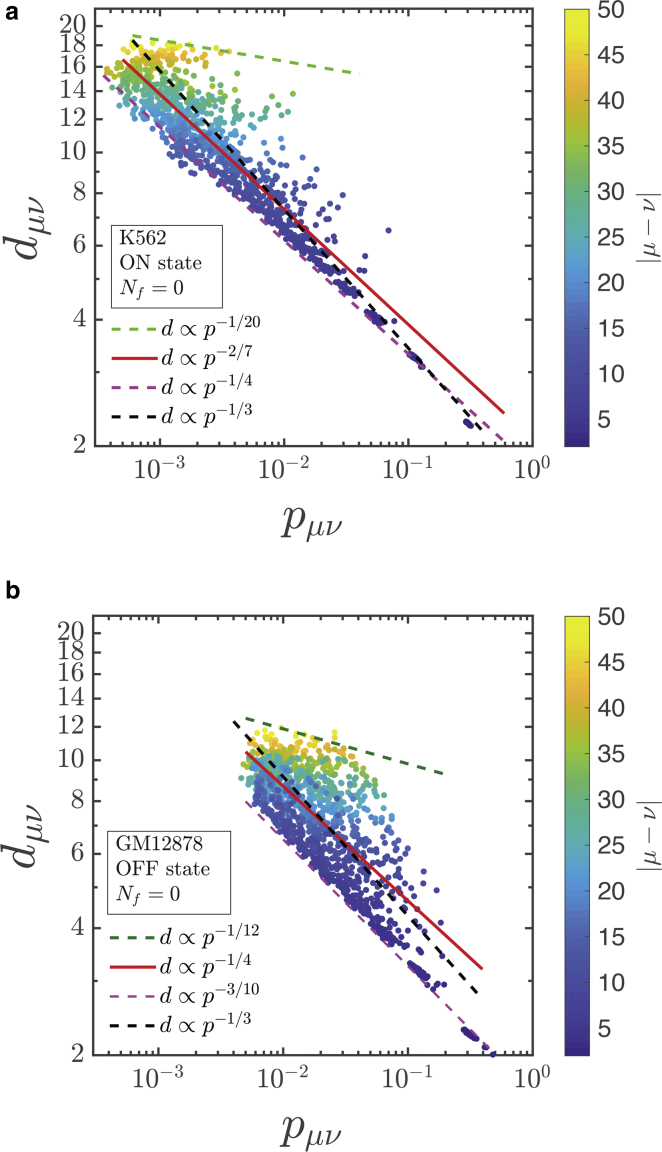
The spatial distances calculated in our work for the contact probabilities in the ON and OFF state are shown in Fig. 7 a for K562 (ON state) and in Fig. 7 b for GM12878 (OFF state) cell lines. Each point in these figures represents the ensemble-averaged 3D distance between a given pair of beads (y axis) having a contact probability as indicated in the x axis. As is immediately apparent, a wide range of 3D distances is possible, unlike what was assumed in earlier studies. It appears that the average 3D distance is not just a function of contact probability pμν (where the interaction between the beads plays a role) but is also a function of the distance along the contour between the beads (|μ − ν|)—the color variation in Fig. 7, a and b indicates the influence of contour length. The red lines in both figures are fitted power laws to the data. In both cases, the exponents are close to −1/4. But the interesting element here is the variability (scatter) in the data, which shows that for a given contact probability value, there can be multiple values of 3D distances with deviations of many units.
Figure 7.
Dependence of mean 3D distances dμν on contact probabilities pμν for (a) K562 (ON state) and (b) GM12878 (OFF state) cell lines, respectively, for Nf = 0. For the K562 (ON state) cell line, the contact probabilities are bounded by power laws dμν ∝ , where τ varies from −1/20 (upper bound) to −1/4 (lower bound), as indicated by the green and magenta dashed lines. Similarly, in the GM12878 (OFF state), τ varies from −1/12 to −3/10. The red line indicates the power law fitted to the simulation data points. The black dashed line represents the analytical relation between the contact probability and a spatial distance for an ideal polymer chain. To see this figure in color, go online.
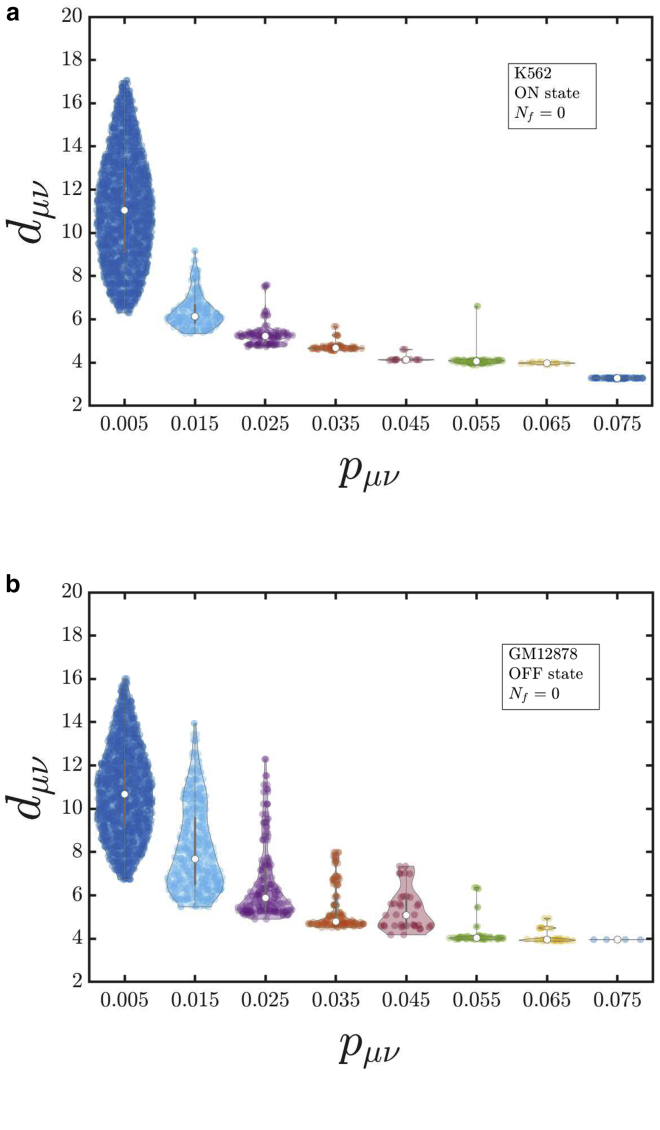
To understand this variability better, we bin the same data and plot them as violin plots that display the mean 3D distance for a given small range of contact probabilities, as shown in Fig. 8, a and b. It is clear that the distribution of points around the mean is very diverse—bimodal in a few cases and with an extended tail in many cases—suggesting that a simple functional form between the mean 3D distance and the contact probability may not be feasible. It must be reiterated here that many previous studies have assumed power-law relations such as dμν ∝ can be used, with exponents τ = −1 (32,33) and τ = −1/2 (35), independent of |μ − ν|. Some groups have also assumed exponential (34) and logarithmic decay of distance with probability (36). As shown above, the results reported here do not support the usage of such simple functional forms. However, for an ideal chain, we know that contact probability p ∝ s−3/2 and the average 3D distance scales as d ∝ s1/2, where s is the contour length between any two polymer beads. Combining these two, we get d ∝ p−1/3. This is shown by the black dashed line in Fig. 7. Clearly, the relation between mean 3D distance and the contact probability is significantly more complex than for a simple ideal chain. The relationship and its variability for Nf = 1 and ICE normalization are discussed in the Supporting Materials and Methods. In these instances, as well, the mean 3D distance is observed to be a function of both the contact probability and contour distance |μ − ν|.
Figure 8.
Violin plots that display the probability distribution of mean 3D distances for selected ranges of contact probabilities in (a) the K562 (ON state) cell lines and (b) the GM12878 (OFF state) cell lines for Nf = 0. To see this figure in color, go online.
Conclusions
The 3D organization of chromatin based on publicly available chromatin conformation capture experimental data has been investigated. Unlike many existing models, our work treats this as an inverse problem in which interactions between different chromatin segments are computed such that the experimentally known contact probabilities are reproduced. A polymer model and an IBD algorithm have been developed for this problem that have the following advantages: 1) they do not assume any a priori relation between spatial distance and contact probability, 2) they optimize the interaction strength between the monomers of the polymer chain to reproduce the target contact probability, and 3) because hydrodynamics interactions are included, they are capable of investigating the dynamics of the chromatin polymer.
The main results of this work are as follows: 1) the IBD method was validated for a bead-spring chain comprising of 45 beads. It was observed that IBD reproduced the contact probability and the interaction strength (within 5% of error), reflecting its reliability. 2) Three different coarse-graining procedures—independent, dependent, and average—were used to map between the experimental and coarse-grained contact matrices. For the gene locus studied in this work (α-globin gene), no significant differences between the three cases was observed, both for the gene extension and the density profile. 3) A procedure for normalizing the contact count matrix was introduced with a parameter Nf varying from 0 to 1 that reflected the two different extreme scenarios for estimating the sample size. For GM12878 (OFF state), the gene extension increases rapidly initially with increasing Nf, whereas for K562 (ON state), on the other hand (which is already in an extended state), there is a very little scope for further extension with increasing Nf. 4) We also simulated the K562 and GM12878 cell line data with ICE normalization. Structural properties such as shape properties, density profile, and 3D configuration show a significant difference between ICE and other normalization technique. 5) Because there is a relationship between the normalization method (value of Nf or ICE) and physically measured properties such as the radius of gyration, it is conceivable that the appropriate normalization method can be inferred from experiments such as FISH, ChIP-Seq, etc. 6) The structural properties of the α-globin gene locus were investigated in terms of shape functions, bead number density distributions, and 3D snapshots. In the ON state (K562), α-globin appears to lack any prominent interactions and exists in an extended structure, whereas in the case of GM12878 (OFF state), the gene appears to be in a folded state. This is also consistent with theory because in the ON state (K562), the transcription factors need to access the gene, whereas the structural status of the OFF state (GM12878) should be to avert the transcription factor, resulting in gene silencing. 7) The density profile along the major axis of the radius of gyration tensor also supports the extended structure in cell line K562 (ON state) and a sharp cluster of monomers at the core of GM12878 (OFF state). 8) The dependency of spatial distance on contact probability has been investigated, and it is shown that the usage of simple functional relationships may not be realistic. 9) No bimodal nature was observed in the density profile of ON state with ICE normalization. Both ON and OFF states show a single peak at the center of mass, indicating a collapsed globule.
Most of the results in this work are predictions that may be tested in suitably designed experiments. We predict that the spatial segmental distance is not only dependent on the contact probability but also on the segment length along the contour. One of the ways to test our prediction is to perform 3D FISH on segment pairs having the same contact probability but different segment lengths. A difference in distance obtained from the FISH experiment will validate the predictions made in this work. Shape properties and density profiles of the α-globin locus are also predicted and can be tested using techniques like super-resolution microscopy and electron microscopy. We require these additional experiments to determine the appropriate normalization. Our work predicts that 3D distances, shape properties, density profile, etc. will depend on the precise nature of normalization. Hence, the appropriate normalization methodology may be determined by comparing our results with future experiments that measure these quantities.
One of the concerns regarding our work could be that this study simulates only a short segment. However, most of the biologically relevant processes happen on the length scale of a gene (or a few genes). Hence, it is essential to zoom in and study the organization and dynamics of short segments. Given that chromatin is organized into small local domains (topologically associated/chromatin domains) having only local interactions predominantly, it may be reasonable to analyze one locus or domain at a time. The IBD algorithm can also be used to study the static and dynamics properties of the whole genome by considering a longer polymer chain. Several sampling techniques can be utilized to sample the phase space efficiently, such as parallel tempering techniques (64). This method can be used to check the validity of the simplest model for a given contact probability matrix. In other words, if a model does not converge to the desired probabilities even after proper sampling, it implies that the model (as represented by the Hamiltonian or the included physics) may require modification, and a more sophisticated model may be required. For instance, we have chosen the simplest model that can reproduce the experimentally observed contact probability map. A lack of convergence (even after proper sampling) may imply the need for adding additional physics into the model. For example, certain far-away contacts may require the addition of nonequilibrium processes like loop extrusion. Because we use Brownian dynamics, our model can be extended to incorporate such nonequilibrium processes.
Because the model has dynamics with hydrodynamics interactions built in, it has the potential to be used to address problems in the future involving dynamics of the 3D chromatin polymer between different chromatin states. Currently, in this model, only chromatin configuration capture data have been considered. However, the model may be extended to incorporate more data (histone modification data, ChIP-Seq data of certain proteins) and address chromatin organization on the length scale of genes in more detail. Recent experiments suggest that 3D chromatin organization is driven by two different dynamic processes, namely phase separation and loop extrusion. Because our model is capable of studying dynamics, the model may be extended to investigate the interplay between different dynamic processes in determining chromatin organization. With the capability of analyzing the 3D configuration along with chromatin dynamics, IBD can complement experimental research and also provide deeper and more useful insights based on the same.
Author Contributions
K.K., B.D., R.P., and J.R.P. designed the research. K.K. wrote code, carried out simulations, and analyzed the data. K.K., B.D., R.P., and J.R.P. wrote the manuscript.
Acknowledgments
We appreciate the funding and support from the IITB-Monash Research Academy and from Science and Engineering Research Board, Department of Science and Technology India via grant number EMR/2016/005965. We gratefully acknowledge the computational resources provided at the NCI National Facility systems at the Australian National University through the National Computational Merit Allocation Scheme supported by the Australian Government, the MonARCH facility maintained by Monash University, and by IIT Bombay.
Editor: Tamar Schlick.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.02.017.
Contributor Information
Ranjith Padinhateeri, Email: ranjithp@iitb.ac.in.
J. Ravi Prakash, Email: ravi.jagadeeshan@monash.edu.
Supporting Material
References
- 1.Alberts B. Sixth Edition. Garland Science, Taylor and Francis Group; New York: 2014. Molecular Biology of the Cell. [Google Scholar]
- 2.Ecker J.R., Bickmore W.A., Segal E. Genomics: ENCODE explained. Nature. 2012;489:52–55. doi: 10.1038/489052a. [DOI] [PubMed] [Google Scholar]
- 3.Larson A.G., Narlikar G.J. The role of phase separation in heterochromatin formation, function, and regulation. Biochemistry. 2018;57:2540–2548. doi: 10.1021/acs.biochem.8b00401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gilbert N., Gilchrist S., Bickmore W.A. Chromatin organization in the mammalian nucleus. Int. Rev. Cytol. 2005;242:283–336. doi: 10.1016/S0074-7696(04)42007-5. [DOI] [PubMed] [Google Scholar]
- 5.Fraser P., Bickmore W. Nuclear organization of the genome and the potential for gene regulation. Nature. 2007;447:413–417. doi: 10.1038/nature05916. [DOI] [PubMed] [Google Scholar]
- 6.Bickmore W.A. The spatial organization of the human genome. Annu. Rev. Genomics Hum. Genet. 2013;14:67–84. doi: 10.1146/annurev-genom-091212-153515. [DOI] [PubMed] [Google Scholar]
- 7.Dekker J., Rippe K., Kleckner N. Capturing chromosome conformation. Science. 2002;295:1306–1311. doi: 10.1126/science.1067799. [DOI] [PubMed] [Google Scholar]
- 8.Simonis M., Klous P., de Laat W. Nuclear organization of active and inactive chromatin domains uncovered by chromosome conformation capture-on-chip (4C) Nat. Genet. 2006;38:1348–1354. doi: 10.1038/ng1896. [DOI] [PubMed] [Google Scholar]
- 9.Dostie J., Richmond T.A., Dekker J. Chromosome Conformation Capture Carbon Copy (5C): a massively parallel solution for mapping interactions between genomic elements. Genome Res. 2006;16:1299–1309. doi: 10.1101/gr.5571506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lieberman-Aiden E., van Berkum N.L., Dekker J. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. 2009;326:289–293. doi: 10.1126/science.1181369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nora E.P., Lajoie B.R., Heard E. Spatial partitioning of the regulatory landscape of the X-inactivation centre. Nature. 2012;485:381–385. doi: 10.1038/nature11049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dixon J.R., Selvaraj S., Ren B. Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature. 2012;485:376–380. doi: 10.1038/nature11082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nora E.P., Dekker J., Heard E. Segmental folding of chromosomes: a basis for structural and regulatory chromosomal neighborhoods? BioEssays. 2013;35:818–828. doi: 10.1002/bies.201300040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rao S.S., Huntley M.H., Aiden E.L. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell. 2014;159:1665–1680. doi: 10.1016/j.cell.2014.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rowley M.J., Corces V.G. Organizational principles of 3D genome architecture. Nat. Rev. Genet. 2018;19:789–800. doi: 10.1038/s41576-018-0060-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mir M., Bickmore W., Narlikar G. Chromatin topology, condensates and gene regulation: shifting paradigms or just a phase? Development. 2019;146:dev182766. doi: 10.1242/dev.182766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sanyal A., Lajoie B.R., Dekker J. The long-range interaction landscape of gene promoters. Nature. 2012;489:109–113. doi: 10.1038/nature11279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schiessel H. The physics of chromatin. J. Phys. Condens. Matter. 2003;15:R699–R774. doi: 10.1088/0953-8984/27/6/060301. [DOI] [PubMed] [Google Scholar]
- 19.Teif V.B., Bohinc K. Condensed DNA: condensing the concepts. Prog. Biophys. Mol. Biol. 2011;105:208–222. doi: 10.1016/j.pbiomolbio.2010.07.002. [DOI] [PubMed] [Google Scholar]
- 20.Ganai N., Sengupta S., Menon G.I. Chromosome positioning from activity-based segregation. Nucleic Acids Res. 2014;42:4145–4159. doi: 10.1093/nar/gkt1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bascom G.D., Myers C.G., Schlick T. Mesoscale modeling reveals formation of an epigenetically driven HOXC gene hub. Proc. Natl. Acad. Sci. USA. 2019;116:4955–4962. doi: 10.1073/pnas.1816424116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dans P.D., Walther J., Orozco M. Multiscale simulation of DNA. Curr. Opin. Struct. Biol. 2016;37:29–45. doi: 10.1016/j.sbi.2015.11.011. [DOI] [PubMed] [Google Scholar]
- 23.Gehlen L.R., Gruenert G., O’Sullivan J.M. Chromosome positioning and the clustering of functionally related loci in yeast is driven by chromosomal interactions. Nucleus. 2012;3:370–383. doi: 10.4161/nucl.20971. [DOI] [PubMed] [Google Scholar]
- 24.Yan J., Kawamura R., Marko J.F. Statistics of loop formation along double helix DNAs. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71:061905. doi: 10.1103/PhysRevE.71.061905. [DOI] [PubMed] [Google Scholar]
- 25.Di Pierro M., Zhang B., Onuchic J.N. Transferable model for chromosome architecture. Proc. Natl. Acad. Sci. USA. 2016;113:12168–12173. doi: 10.1073/pnas.1613607113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mirny L.A. The fractal globule as a model of chromatin architecture in the cell. Chromosome Res. 2011;19:37–51. doi: 10.1007/s10577-010-9177-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bancaud A., Lavelle C., Ellenberg J. A fractal model for nuclear organization: current evidence and biological implications. Nucleic Acids Res. 2012;40:8783–8792. doi: 10.1093/nar/gks586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rosa A., Everaers R. Structure and dynamics of interphase chromosomes. PLoS Comput. Biol. 2008;4:e1000153. doi: 10.1371/journal.pcbi.1000153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Di Pierro M., Cheng R.R., Onuchic J.N. De novo prediction of human chromosome structures: epigenetic marking patterns encode genome architecture. Proc. Natl. Acad. Sci. USA. 2017;114:12126–12131. doi: 10.1073/pnas.1714980114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jost D., Carrivain P., Vaillant C. Modeling epigenome folding: formation and dynamics of topologically associated chromatin domains. Nucleic Acids Res. 2014;42:9553–9561. doi: 10.1093/nar/gku698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gürsoy G., Xu Y., Liang J. Computational construction of 3D chromatin ensembles and prediction of functional interactions of alpha-globin locus from 5C data. Nucleic Acids Res. 2017;45:11547–11558. doi: 10.1093/nar/gkx784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fraser J., Rousseau M., Dostie J. Chromatin conformation signatures of cellular differentiation. Genome Biol. 2009;10:R37. doi: 10.1186/gb-2009-10-4-r37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Duan Z., Andronescu M., Noble W.S. A three-dimensional model of the yeast genome. Nature. 2010;465:363–367. doi: 10.1038/nature08973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tanizawa H., Iwasaki O., Noma K. Mapping of long-range associations throughout the fission yeast genome reveals global genome organization linked to transcriptional regulation. Nucleic Acids Res. 2010;38:8164–8177. doi: 10.1093/nar/gkq955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rousseau M., Fraser J., Blanchette M. Three-dimensional modeling of chromatin structure from interaction frequency data using Markov chain Monte Carlo sampling. BMC Bioinformatics. 2011;12:414. doi: 10.1186/1471-2105-12-414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Baù D., Sanyal A., Marti-Renom M.A. The three-dimensional folding of the α-globin gene domain reveals formation of chromatin globules. Nat. Struct. Mol. Biol. 2011;18:107–114. doi: 10.1038/nsmb.1936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Paulsen J., Sekelja M., Collas P. Chrom3D: three-dimensional genome modeling from Hi-C and nuclear lamin-genome contacts. Genome Biol. 2017;18:21. doi: 10.1186/s13059-016-1146-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Paulsen J., Liyakat Ali T.M., Collas P. Computational 3D genome modeling using Chrom3D. Nat. Protoc. 2018;13:1137–1152. doi: 10.1038/nprot.2018.009. [DOI] [PubMed] [Google Scholar]
- 39.Meluzzi D., Arya G. Recovering ensembles of chromatin conformations from contact probabilities. Nucleic Acids Res. 2013;41:63–75. doi: 10.1093/nar/gks1029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Imakaev M., Fudenberg G., Mirny L.A. Iterative correction of Hi-C data reveals hallmarks of chromosome organization. Nat. Methods. 2012;9:999–1003. doi: 10.1038/nmeth.2148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Cournac A., Marie-Nelly H., Mozziconacci J. Normalization of a chromosomal contact map. BMC Genomics. 2012;13:436. doi: 10.1186/1471-2164-13-436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Knight P.A., Ruiz D. A fast algorithm for matrix balancing. IMA J. Numer. Anal. 2013;33:1029–1047. [Google Scholar]
- 43.Shavit Y., Lio’ P. Combining a wavelet change point and the Bayes factor for analysing chromosomal interaction data. Mol. Biosyst. 2014;10:1576–1585. doi: 10.1039/c4mb00142g. [DOI] [PubMed] [Google Scholar]
- 44.Stansfield J.C., Cresswell K.G., Dozmorov M.G. multiHiCcompare: joint normalization and comparative analysis of complex Hi-C experiments. Bioinformatics. 2019;35:2916–2923. doi: 10.1093/bioinformatics/btz048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hu M., Deng K., Liu J.S. HiCNorm: removing biases in Hi-C data via Poisson regression. Bioinformatics. 2012;28:3131–3133. doi: 10.1093/bioinformatics/bts570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Prakash J.R. Universal dynamics of dilute and semidilute solutions of flexible linear polymers. Curr. Opin. Colloid Interface Sci. 2019;43:63–79. [Google Scholar]
- 47.Soddemann T., Dünweg B., Kremer K. A generic computer model for amphiphilic systems. Eur. Phys. J. E: Soft Matter Biol. Phys. 2001;6:409–419. [Google Scholar]
- 48.Santra A., Kumari K., Prakash J.R. Universality of the collapse transition of sticky polymers. Soft Matter. 2019;15:7876–7887. doi: 10.1039/c9sm01361j. [DOI] [PubMed] [Google Scholar]
- 49.Öttinger H.C. Springer; Berlin: 1996. Stochastic Processes in Polymeric Fluids. [Google Scholar]
- 50.Kuhn W. Über die Gestalt fadenförmiger Moleküle in Lösungen. Kolloid-Zeitschrift. 1934;68:2–15. [Google Scholar]
- 51.Šolc K. Shape of a random-flight chain. J. Chem. Phys. 1971;55:335–344. [Google Scholar]
- 52.Zifferer G. Monte Carlo simulation studies of the size and shape of linear and star-branched polymers embedded in the tetrahedral lattice. Macromol. Theory Simul. 1999;8:433–462. [Google Scholar]
- 53.Haber C., Ruiz S.A., Wirtz D. Shape anisotropy of a single random-walk polymer. Proc. Natl. Acad. Sci. USA. 2000;97:10792–10795. doi: 10.1073/pnas.190320097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Steinhauser M.O. A molecular dynamics study on universal properties of polymer chains in different solvent qualities. Part I. A review of linear chain properties. J. Chem. Phys. 2005;122:094901. doi: 10.1063/1.1846651. [DOI] [PubMed] [Google Scholar]
- 55.Theodorou D.N., Suter U.W. Shape of unperturbed linear polymers: polypropylene. Macromolecules. 1985;18:1206–1214. [Google Scholar]
- 56.Bishop M., Michels J.P.J. Polymer shapes in three dimensions. J. Chem. Phys. 1986;85:5961–5962. [Google Scholar]
- 57.Prabhakar R., Prakash J. Multiplicative separation of the influences of excluded volume, hydrodynamic interactions and finite extensibility on the rheological properties of dilute polymer solutions. J. Non-Newt. Fluid Mech. 2004;116:163–182. [Google Scholar]
- 58.Lyubartsev A.P., Laaksonen A. Calculation of effective interaction potentials from radial distribution functions: a reverse Monte Carlo approach. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1995;52:3730–3737. doi: 10.1103/physreve.52.3730. [DOI] [PubMed] [Google Scholar]
- 59.Lyubartsev A.P., Karttunen M., Laaksonen A. On coarse-graining by the inverse Monte Carlo method: dissipative particle dynamics simulations made to a precise tool in soft matter modeling. Soft Matter. 2002;1:121–137. [Google Scholar]
- 60.Lyubartsev A.P., Naômé A., Laaksonen A. Systematic hierarchical coarse-graining with the inverse Monte Carlo method. J. Chem. Phys. 2015;143:243120. doi: 10.1063/1.4934095. [DOI] [PubMed] [Google Scholar]
- 61.Press W.H., Teukolsky S.A., Flannery B.P. Second Edition. Cambridge University Press; Cambridge: 1992. Numerical Recipes in C. [Google Scholar]
- 62.Fill J.A., Fishkind D.E. The Moore–Penrose generalized inverse for sums of matrices. SIAM J. Matrix Anal. Appl. 2000;21:629–635. [Google Scholar]
- 63.Bird R.B., Curtiss C.F., Hassager O. John Wiley & Sons, Ltd; New York: 1989. Dynamics of Polymeric Liquids. Volume 2: Kinetic Theory. [Google Scholar]
- 64.Bunker A., Dünweg B. Parallel excluded volume tempering for polymer melts. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2001;63:016701. doi: 10.1103/PhysRevE.63.016701. [DOI] [PubMed] [Google Scholar]
- 65.Soysa W.C., Dünweg B., Prakash J.R. Size, shape, and diffusivity of a single Debye-Hückel polyelectrolyte chain in solution. J. Chem. Phys. 2015;143:064906. doi: 10.1063/1.4928458. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.