Quantitative Study of the Chiral Organization of the Phage Genome Induced by the Packaging Motor

Abstract

Molecular motors that translocate DNA are ubiquitous in nature. During morphogenesis of double-stranded DNA bacteriophages, a molecular motor drives the viral genome inside a protein capsid. Several models have been proposed for the three-dimensional geometry of the packaged genome, but very little is known of the signature of the molecular packaging motor. For instance, biophysical experiments show that in some systems, DNA rotates during the packaging reaction, but most current biophysical models fail to incorporate this property. Furthermore, studies including rotation mechanisms have reached contradictory conclusions. In this study, we compare the geometrical signatures imposed by different possible mechanisms for the packaging motors: rotation, revolution, and rotation with revolution. We used a previously proposed kinetic Monte Carlo model of the motor, combined with Brownian dynamics simulations of DNA to simulate deterministic and stochastic motor models. We find that rotation is necessary for the accumulation of DNA writhe and for the chiral organization of the genome. We observe that although in the initial steps of the packaging reaction, the torsional strain of the genome is released by rotation of the molecule, in the later stages, it is released by the accumulation of writhe. We suggest that the molecular motor plays a key role in determining the final structure of the encapsidated genome in bacteriophages.

Significance

The three-dimensional organization of viral genomes determines key functional aspects of viral infection. In double-stranded DNA bacteriophages, the packaging reaction is carried out by a molecular motor that drives the viral genome inside its protein capsid. In this study, we determine the contribution of the packaging motor to the final packaged configuration of the viral genome. Using a previously proposed kinetic Monte Carlo model of the motor, combined with Brownian dynamics simulations of DNA, we find that rotation of the DNA molecule by the motor during the packaging reaction induces chiral packing.

Introduction

Icosahedral bacteriophages are viruses that propagate in bacterial cells and whose genome is packed in a protein capsid with icosahedral symmetry. During bacteriophage morphogenesis and after capsid assembly, the genome is packed inside the capsid by a molecular motor (reviewed in (1)). Once packed, DNA reaches concentrations up to 800 mg ⋅ mL⁻¹ (2), and osmotic pressures of 60 atmospheres (3, 4, 5, 6). Consistent with these measurements, it has been estimated that the packaging motor exerts up to a 50 pN force during the packaging reaction (7,8).

For the last several decades, energy models of viral DNA encapsidation, packaging, and ejection have been actively explored. In 1978, a pioneering article by Riemer and Bloomfield (9) provided the first estimates of the free energy contributions to DNA packaging: the bending energy of the double-stranded genome, the electrostatic energy of interaction between neighboring segments of the DNA molecule, and the free energy due to configurational entropy loss of the confined chain. The work by Tzlil and colleagues (6) provided the first thermodynamic study of the Hamiltonian that encompasses the previously listed energy components. The work of Tzlil et al. (6) and of Klug and Ortiz (10) established some of the main foundations of the energetics models of DNA packaging in bacteriophages. These studies suggest that the DNA molecule is organized following spooling-like trajectories, with an isotropic core near the center of the volume determined by the capsid (11, 12, 13, 14).

In (15), a topological approach was developed to help determine the three-dimensional organization and the biophysical properties of DNA inside the viral capsid. In (16), the same authors proposed that the packaged DNA molecule is chirally organized. To reach this conclusion, following experimental procedures previously outlined in (17, 18, 19, 20), the authors purified DNA particles from bacteriophage P4 tailless mutants and estimated their topological complexity using high-resolution gel electrophoresis and the average crossing number of knots as a proxy for topological complexity (19). Based on gel readings, most knots in these experiments were very complex (i.e., had a large average crossing number), and the observations of knots with low average crossing number (i.e., average crossing number less than 8) were especially informative. In particular, they observed that the four-crossing knot and the five-twist knot were underrepresented when compared with Monte Carlo simulations of closed curves confined to spherical volumes. Inspired by the work in (21), the authors hypothesized that the DNA is chirally organized inside the viral capsid. This hypothesis was confirmed by performing biased Monte Carlo sampling of conformations with high writhe values (informally, writhe measures the quantity and handedness of coils that result from relaxing closed, supercoiled DNA). Further experimental evidence supports this hypothesis. In (20), it was found that DNA molecules with lower molecular weight had a larger knotting probability than heavier ones. This counterintuitive experimental result contradicts simulation results that show that the knotting probability of random chains in confined volumes increases with length (15,22). Simulations of knotting probability estimates incorporating writhe biases (23), on the other hand, showed consistent results with those in (20). A chiral organization of DNA inside the capsid is in agreement with different global organization models and may be a consequence of the interaction between DNA fibers (24,25) or of the geometry imposed by the motor at the time of packaging. The latter is the subject of our study.

Molecular motors of interest in this study are pentameric or hexameric complexes of toroidal shape that thread the DNA molecule through an inner channel (26). Four mechanisms have been proposed for the translocation of the DNA molecule: rotation, revolution, rotation with revolution (see (27) for a review), and a model with neither rotation nor revolution, but instead a mechanism that alternates between stretched and compressed conformations of the DNA molecule (28,29). The rotation with revolution mechanism is shown in Fig. 1. The rotation mechanism has been associated with motors with a small inner channel (∼2 nm) and includes small helicases such as Rho (30) During the translocation reaction, the axis of the DNA molecule is aligned with the center of the inner channel of the motor, allowing for the rotation of the DNA around the DNA’s center axis. This reaction is expected to be accompanied by the formation of compensatory supercoiling domains (31) The revolution mechanism is believed to be a consequence of the fact that diameter of the inner channel is larger than the physical diameter of the DNA, hence allowing for the misalignment of the axis of DNA molecule and the center axis of the inner channel (27,32). Such motors are found in several bacteriophages (see reviews (1,33,34)). The combination of both mechanisms, rotation and revolution, has been proposed as a model for the packaging motor of bacteriophage φ29 (8,32,35,36) and allows for a net gain of rotation of the DNA molecule. Additionally, motors are believed to be stochastic in nature because the activation of their subunits depends on the random binding of ATP molecules (37).

Figure 1.

Model for rotation and revolution of DNA within the packaging motor. The image illustrates (a) counterclockwise (CCW) rotation of the DNA around its axis and CCW revolving of the DNA with respect to the axis going through the center of the motor. The DNA (blue) is translocated in the upward direction, denoted by z, into the viral capsid. (b) The variables ϕ_rev, ϕ_rot, and r_rev measure revolving, rotation, and the distance between the axis of the DNA and the axis of the motor, respectively. CCW rotation and revolution are shown. To see this figure in color, go online.

These observations suggest that, if the packaging of the DNA molecule is driven by a mechanism that includes rotation, then the final configuration of the packaged DNA molecule will accumulate twist, some of which may be released into writhe. Interestingly, some studies addressing the role of the packaging motor and the accumulation of twist have reached contradictory conclusions. For instance, in (38) the authors used a coarse-grained worm-like chain DNA model combined with damped dynamics to show that the rotation of the DNA at the motor during packaging translates into coaxial conformations of the genome (11, 12, 13, 14) and the accumulation of writhe, provided that the DNA end that first enters the capsid (“leading” DNA end) is attached to the interior of the capsid. In 2008, Rollins and colleagues (39) used a similar model but, unlike the previous study, concluded that the torsional forces have negligible effect on packaging.

Motivated by these conflicting results and by the absence of models that incorporate a biophysically motivated packaging reaction, we study here whether packaging motors can induce twist on the DNA molecule and whether the twist translates into a chiral (i.e., nonzero writhe) organization of the packaged genome. To address this question, we extend the model proposed in (32) for the packaging motor and combine it with Brownian dynamics simulations of the DNA molecule inside the viral capsid (38,40). We also extend the timescale trajectories by implementing the algorithms using OpenCL on graphic processing units (GPUs). We consider deterministic and stochastic motors with rotation, revolution, or rotation with revolution mechanisms.

We find both similarities and differences between rotation mechanisms and those that lack rotation. Our results suggest that both models promote the formation of concentric layers with both coiled and folded regions in the external layers. The rotation model, however, uniquely induces the accumulation of writhe on the DNA molecule. Interestingly, our simulations also show that a revolution packaging mechanism without rotation does not significantly contribute to the accumulation of writhe. We therefore suggest that the packaging motor has a distinguishable effect on the final configuration of the DNA molecule inside the bacteriophage capsid and that the chiral organization proposed for P4 bacteriophage is partially accounted for by a rotation mechanism of the motor.

Methods

Simulation of the DNA-packaging motor

We simulated four motor mechanisms: 1) no rotation and no revolution, 2) rotation and no revolution, 3) revolution and no rotation, and 4) rotation with revolution. Each of these models was considered as either deterministic (i.e., constant packaging speed) or stochastic (i.e., motor with variable packaging speed). Mechanisms for deterministic motors have been previously described (25,38,39,41, 42, 43, 44). For the stochastic motor, we implemented a model proposed by Yu and colleagues for bacteriophage φ29 (32). Next, we explain the essential features of the φ29 packaging motor that were considered for the implementation of the model.

The φ29 motor consists of five identical subunits forming a toroidal structure. These subunits interact directly with the DNA molecule in a coordinated fashion to pack the DNA inside the viral capsid (45). Each of the subunits contains a DNA binding domain and a domain that translocates the DNA inside the capsid (46, 47, 48). Upon binding of the ATP to the subunit, a structural change in the packaging subunit occurs, enabling the translocation reaction by ATP hydrolysis (46,49). The motor has a burst and a dwell phase (50). It has been shown that during the burst phase, only four of the five subunits are activated consecutively (45), packaging a total of 10 bp (or 2.5 bp per subunit) (36).

After hydrolysis of ATP the motor then enters a dwell phase, and the DNA stops (and/or slides out (47)) until all subunits are again bound to ATPs, then the burst phase resumes. A schematic of the mechanism is shown in Fig. 1.

In the model, each of the five subunits has three possible chemical states determined by their ATP binding state: T, D, and E for bound with ATP, bound with ADP and empty, respectively. At any given time, DNA is bound to one of the subunits, making the total number of chemical states of the motor to be 5 × 3⁵ = 1215.

In all models considered here, the spatial relationship of the DNA to the molecular motor is described by four variables {z, ϕ_rot, r, ϕ_rev}, where z is the length of the DNA molecule that has passed through the motor, φ_rot is the rotation angle of the DNA molecule at the motor, r is the distance between the axis of the DNA and the center of the motor, and φ_rev is the revolution angle of the DNA molecule around the center of the motor. The values of ϕ_rev and ϕ_rot were defined linearly in terms of z. The variable r was set to 0 nm for simulations without revolving and was fixed at 0.25 nm otherwise.

Changes in the z variable are governed by an energy function that depends on the chemical state of the subunit to which the DNA is attached. The energies associated to each of the chemical states are V_E(z) = 30k_B$\mathcal{T}$ × sin²(πz/10) for state E, V_T(z) = 60k_B$\mathcal{T}$ × sin²(πz/10) for state T, and V_D(z) = 30k_B$\mathcal{T}$ × sin²(π(z − 2.5)/10) for state D, where k_B is Boltzmann’s constant and $\mathcal{T}$ is temperature. To reflect the periodic nature of the reaction, we considered

$$V_{\text{eff}}^j\left(z\right)=V_s\left(z-2.5\times d\right)$$

where s ∈ {E, D, T} and d counts the number of ATP hydrolysis events that push the DNA.

We discretized the z variable to take values of the form 0.5 bp ⋅ n for n ∈ $\mathbb{Z}$ and modeled its movement as a jump process. The transitions rates were chosen to approximate the diffusion of the Fokker-Planck equation, using methods from (51). The value for diffusion was 90 bp² ⋅ ⁻¹ (32).

The action of the motor was implemented using a kinetic Monte Carlo algorithm, whose discrete set of states is given by the product of the chemical state space and the mechanical state space. The transition between states is governed by the master equation:

$$\frac{d{p}_i^j}{dt}=\left[\sum _{j\text{'}\ne j}\left(p_i^{j\text{'}}{k}_i^{j\text{'}\to j}-p_i^j{k}_i^{j\to j\text{'}}\right)\right]+\left(p_{i-1}^j{k}_{i-1\to i}^j-p_i^j{k}_{i\to i-1}^j\right)+\left(p_{i+1}^j{k}_{i+1\to i}^j-p_i^j{k}_{i\to i+1}^j\right).$$

The expression inside the brackets describes the transitions between chemical states, and the two terms outside the brackets describe the transitions between mechanical states. In each of these expressions, $p_i^j$ is the probability that the system is in the mechanical state i and chemical state j, and $k_i^{j\to j\text{'}}$ is the transition rate between chemical states j and j′ for a fixed mechanical state i. The rate constant $k_{i\to i\text{'}}^j$ is defined similarly. Only transitions between “neighboring” states (e.g., states related by only one chemical or mechanical transition that are biochemically valid) are allowed.

The chemical transition rates were also described in (32). Transitioning from E → T, D → T, and E → D depended only on the concentration of reactants in the solution, for instance, k_{E → T} = $k_{E\to T}^0$ ⋅ [ATP]. The other transitions T → E, T → D, and D → E depended on the difference of the increments of the potentials. For instance, k_{T → E} = $k_{T\to E}^0$ ⋅ exp(ΔV_T(z) − ΔV_E(z)). These expressions guarantee the detailed balance condition of the ratios $\left(k_{E\to T}/k_{T\to E}\right)$, $\left(k_{T\to D}/k_{D\to T}\right)$, and $\left(k_{D\to E}/k_{E\to D}\right)$ for different values of z. These base rates were also multiplied by acceleration or inhibition factors that depended on the states of the neighboring subunits. These factors help the model mimic the observed bursting and pausing patterns of the motor (32). In our implementation of the transitions between the burst and dwell phases, we allowed for the possibility that the burst phase could terminate whenever any of the subunits hydrolyzed its ATP before the DNA molecule had reached the subunit. In other words, we allowed for the possibility that fewer power strokes (0–3) occur.

In Yu and colleagues’ work (32), the simulation returned a list of times with associated packaging lengths ${\left\{\left(t_n,z_n\right)\right\}}_{n=1}^N$. Here, we expand the description of the DNA molecule’s conformation to include axial position z, rotation angle ϕ_rot, distance r from the center of the motor portal, and revolving angle ϕ_rev so they can be used as input for the subsequent simulation steps.

Energetics of DNA inside the bacteriophage capsid

We used the discrete implementation of the worm-like chain (WLC) with the addition of the twist degrees of freedom as presented in (38,52, 53, 54). In this coarse-grained model, the nucleic acid is represented as a chain of n beads with coordinates r_i = (x_i, y_i, z_i) for i = 1, …, n connected by n − 1 edges e_i = r_{i + 1} − r_i. As in (41), we allowed consecutive beads to partially overlap to produce a more continuous structure. Additionally, a corresponding unit vector f_i perpendicular to each edge e_i is defined to account for torsional deformation of the DNA molecule.

The model disfavors sharp bends of the DNA axis (measured by bending angles θ_i) and extreme local torsional deformations (measured by twist angles τ_i). To define the twist angles τ_i in terms of r_i, ${\hat{\mathbf{e}}}_i$, (where ${\hat{\mathbf{e}}}_i$ is the normalized vector in the direction of e_i) and f_i, we define for each bead a body-fixed coordinate system Σ_i = $\left({\mathbf{f}}_i,{\mathbf{g}}_i,{\hat{\mathbf{e}}}_i\right)$, where f_i × g_i = ${\hat{\mathbf{e}}}_i$, as described in (32), and where $\hat{\mathbf{v}}$ denotes the normalization of any nonzero vector v, i.e., $\hat{\mathbf{v}}$ = v/||v||. The 3D rotation that maps Σ_i to Σ_{i + 1} can be decomposed into three rotations given by the Euler angles (α_i, β_i, γ_i). The first rotation given by α_i is about ${\hat{\mathbf{e}}}_i$; the second rotation given by γ_i changes the direction of ${\hat{\mathbf{e}}}_i$ to ${\hat{\mathbf{e}}}_{i+1}$ and thus is the same as the bending angle, i.e., γ_i = θ_i; finally, the third rotation given by β_i is about ${\hat{\mathbf{e}}}_{i+1}$. The twist angle τ_i between f_i and f_{i + 1} is calculated as the sum τ_i = α_i + β_i.

If e_i and e_{i + 1} are parallel, then γ_i = 0 and α_i + β_i is the signed angle (right-handed is positive) between f_i and f_{i + 1} about e_i = e_{i + 1} given by

$${\alpha }_i+{\beta }_i=\text{arccos}\left({\mathbf{f}}_i·{\mathbf{f}}_{i+1}\right)·\text{sign}\left(\left({\mathbf{f}}_i\times {\mathbf{f}}_{i+1}\right)·{\mathbf{e}}_i\right)$$

If e_i and e_{i + 1} are not parallel, then

• •the angle α_i is the angle of rotation between f_i and e_{i + 1} × e_i about e_i (i.e., $\text{cos}{\alpha }_i={\mathbf{f}}_i·\widehat{{\mathbf{e}}_{i+1}\times {\mathbf{e}}_i}$), and
• •the angle β_i is the angle of rotation between f_i and e_{i + 1} × e_i about e_{i + 1}, as shown in Fig. 2. Thus, the signed values are

$${\alpha }_i=\text{arccos}\left({\mathbf{f}}_i·\widehat{{\mathbf{e}}_i\times {\mathbf{e}}_{i+1}}\right)·\text{sign}\left(\left({\mathbf{f}}_i\times \widehat{{\mathbf{e}}_i\times {\mathbf{e}}_{i+1}}\right)·{\mathbf{e}}_i\right)$$

and

$${\beta }_i=\text{arccos}\left({\mathbf{f}}_{i+1}·\widehat{{\mathbf{e}}_i\times {\mathbf{e}}_{i+1}}\right)·\text{sign}\left(\left(\widehat{{\mathbf{e}}_i\times {\mathbf{e}}_{i+1}}·{\mathbf{f}}_{i+1}\right)\times {\mathbf{e}}_{i+1}\right)$$

Figure 2.

The twist angle between normal vectors f_i and f_{i + 1} is equal to τ_i = α + β. To see this figure in color, go online.

After having found these values, we calculate τ_i, which because of periodicity is equal to

$${\tau }_i={\alpha }_i+{\beta }_i+2\pi n$$

for some value n. The value n is chosen to minimize Δτ_i with every time step.

The energies are then defined as follows.

• 1)The stretching energy is

$$E_{\text{stretch}}=\frac{1}{2}{k}_{\text{stretch}}\sum _{i=}^{n-2}{\left(\left|{\mathbf{e}}_i\right|-l_0\right)}^2,$$

• where l₀ = 2.4 nm is the resting edge length and k_stretch = 500/$l_0^2{k}_{\text{B}}\mathcal{T}$ (where k_B$\mathcal{T}$ = 4.1 pN ⋅ nm) is chosen arbitrarily high (as in (38)) to approximate the incompressibility of worm-like chains.

• 2)The bending energy is

$$E_{\text{WLC}}=\frac{1}{2}{k}_{\text{WLC}}\sum _{i=1}^{n-2}{\theta }_i^2$$

• where θ_i = arccos$\left({\hat{\mathbf{e}}}_i\cdot {\hat{\mathbf{e}}}_{i+1}\right)$ is the exterior angle between adjacent edges, or bending angle, and k_WLC ≈ 20.67 × k_B$\mathcal{T}$, a value that corresponds to segments of length l₀ and the DNA persistence length of 50 nm (40,55).

• 3)The twist energy is

$$E_{\text{twist}}=\frac{1}{2}{k}_{\text{twist}}\sum _{i=1}^{n-2}{\tau }_i^2$$

• where τ_i is the “twist” angle given by τ_i = α_i + β_i, where α_i is the angle between f_i and e_{i + 1} × e_i and β_i is the angle between f_{i + 1} and e_{i + 1} × e_i, as shown in Fig. 2. The twist energy constant is

$$k_{\text{twist}}=20.0k_{\text{B}}\mathcal{T}=48k_{\text{B}}\mathcal{T}\text{nm}/l_0$$

• and is chosen to match the experimentally derived value 2.0 × 10⁻¹⁹ erg ⋅ cm = 48k_B$\mathcal{T}$ nm for torsional rigidity of DNA (52), scaled for our choice of segment length l₀ = 2.4 nm.

• 4)The repulsion energy exerted by the capsid on the DNA molecule is

$$E_{\text{capsid}}=\sum _i{E}_{\text{capsid}}^i,$$

• where

$$E_{\text{capsid}}^i=k_{\text{capsid}}{\left(\frac{R\left({\mathbf{v}}_i\right)-R_c}{l_0}\right)}^4$$

• if R(v_i) ≥ R_c and 0 otherwise. The constant k_capsid = 20 k_B$\mathcal{T}$ and R(v_i) is the distance of v_i from the center of the capsid. A value of R_c = 22.75 nm would mimic the actual size of the P4 bacteriophage capsid (56); instead, we used R_c = 15 nm, a smaller value, which is believed to capture the qualitative properties of the packaging while saving computational time (38).

• 5)The Debye-Hückel potential for electrostatic interactions is

$$E_{\text{DH}}=k_{\text{DH}}\sum _i\sum _{j>i}\frac{1}{r_{ij}}{e}^{\left(r_{ij}/l_D\right)},$$

• where r_ij is the distance between the centers of beads i and j and k_DH = q²l_Bk_B$\mathcal{T}$, where q is the unit charge per bead and l_B ≈ 0.7 nm is the Bjerrum length for water at room temperature, as used in (38).

• 6)The Lennard-Jones potential is

$$E_{\text{LJ}}=\sum _i\sum _{j>i+3}{E}_{\text{LJ}}^{ij},$$ (1)

• where

$$E_{\text{LJ}}=\frac{1}{12}{k}_{\text{LJ}}\left[{\left(\frac{\sigma }{r_{ij}}\right)}^{12}-2{\left(\frac{\sigma }{r_{ij}}\right)}^6+1\right]$$

• if r_ij < σ and 0 otherwise. In the expression above, k_LJ = 20k_B$\mathcal{T}$ and σ = 2.5 nm is the diameter of the beads, as used in (38). Note that neighboring beads often overlap because the resting edge length l₀ = 2.4 nm is smaller than σ; the Lennard-Jones potential is thus ignored when |i − j| ≤ 3.

Hydrodynamics and the viscosity of the cytoplasm

Hydrodynamic considerations are included in the diffusion tensor. In this study, we considered all hydrodynamic effects to be constant, linear, and local (as done in (38,57)), so that the diffusion tensor D has the form

$$\mathbf{D}=\frac{k_{\text{B}}\mathcal{T}}{6\pi \eta r}{\mathbf{I}}_{3n\times 3n}$$

where η is the viscosity of the solution, r = 1.25 nm is the radius of the beads, and I_{3n × 3n} is the identity matrix of order 3n. The viscosity of water is η = 1.0020 cp at 20°C. Confined water (e.g., one to two molecules thick), however, may exhibit effective viscosities that vary by orders of magnitude (58). We used a high constant elastic viscosity of η = 6 × 10⁴ p in this study, which, to our knowledge, is the first to investigate an effective viscosity of this magnitude for DNA packaging.

Simulation of DNA packaging

We simulated packaging ∼3700 bp of DNA into the capsid in two stages. The length of DNA was chosen to reduce computation time, as was done in (38,57).

We first simulated the action of the motor. For the stochastic motor, we used the kinetic Monte Carlo algorithm described in Simulation of the DNA-Packaging Motor and generated values ${\left\{\left(t_n,z_n\right)\right\}}_{n=1}^N$. These values defined, for every positive value of simulation time t_sim, linearly interpolated values z(t_sim). Additionally, time in the stochastic simulations was scaled to achieve an average packaging rate equal to corresponding simulations that used a deterministic motor. For both motors, the variables that control the rotating and revolving of the DNA—ϕ_rot and ϕ_rev, respectively—satisfy ϕ_rot(t_sim) = c_rot ⋅ z(t_sim) and φ_rev(t_sim) = c_rev ⋅ z(t_sim), where c_rot ∈ $\{0,\pm \frac{7^{\circ }}{2.5\text{bp}}\}$ and c_rev ∈ $\left\{0,\pm \frac{{72}^{\circ }}{2.5\text{bp}}\right\}$ control the rate and direction of the rotating and revolving, the positive direction depicted in Fig. 1 b. In the simulations that involved revolving, the radius of revolution was r = 0.25 nm (32).

Second, the dynamics of the portion of the DNA molecule within the capsid were modeled using Brownian dynamics, which were obtained using

$${\mathbf{x}}_{n+1}={\mathbf{x}}_n+\frac{1}{\mathbf{Z}}\left(-\nabla E\left({\mathbf{x}}_n\right)\right)\Delta t+\sqrt{2\mathbf{D}\Delta t}\mathbf{R}\left(n\right)$$

where x_n is the conformation at step n, Z is the friction coefficient defined by D = k_B$\mathcal{T}$Z⁻¹, and R(n) is Gaussian white noise satisfying $\langle \mathbf{R}\left(n\right)\mathbf{R}\left(m\right)\rangle$ = δ(n − m) for steps n and m. With every iteration, the position of the DNA within the motor is updated. In (38), the Brownian fluctuations during packaging were ignored for two reasons: to focus on the mechanical aspects of the packaging process and to form a basis for future study. We included the fluctuations but scale them by a factor of 1/10 to test whether the results from (38) still hold.

Attenuating the Brownian fluctuations changes statistical properties of the chain, so we tested the implementation of the model using the full fluctuations. With a torsional rigidity of 48k_B$\mathcal{T}$ nm, the root mean-square (rms) twist angle per basepair ${\langle {\tilde{\tau }}^2\rangle }^{1/2}$, where $\tilde{\tau }$ is the twist per basepair, is approximately 4.8° if we ignore the influence of the non-twist-energy terms. This estimate closely agrees with experimental work, which shows sequence-dependent values on the order of 5° (59). In this study, the length of a bead l₀ is longer than that of a basepair l_bp, so to calculate the rms twist angle per basepair, we note that $\langle {\tilde{\tau }}^2\rangle =\langle {\tau }^2\rangle$/(l₀/l_bp).

Simulating the entire packaging process using Brownian dynamics is computationally expensive, so we used the parallel computing platform OpenCL (60) and ran the simulation on GPUs using 32-bit float arithmetic. In general, algorithms optimized for GPU computing can offer an increase of speed of orders of magnitude because of the massive parallelism they offer (61). For this study, the calculation of $\nabla E\left({\mathbf{x}}_n\right)$ was the most costly, but because the calculations can be written to use parallel memory access patterns, we can benefit from using GPUs. Still, the calculation of the nonbonded forces (electrostatic and Lennard-Jones) considers all pairs of beads and so has quadratic computational complexity in the number of beads, so we updated those values once every four time steps. Videos S1 and S2 illustrate the packaging process.

Writhe estimation

We estimated the chirality of the simulated DNA molecule by the writhe of the DNA axis. For a closed curve l in space, the writhe is defined as,

$$\text{Wr}\left(l\right)=\frac{1}{4\pi }\underset{l}{\oint }\underset{l}{\oint }\frac{\left(d{\mathbf{r}}_2\times d{\mathbf{r}}_1\right)·\left({\mathbf{r}}_2-{\mathbf{r}}_1\right)}{{\Vert {\mathbf{r}}_2-{\mathbf{r}}_1^{}\Vert }^3}$$

where r₁ and r₂ are points passing along the curve. We joined the ends of the DNA at points very far from the origin (near “infinity”) to form a closed curve and estimated the writhe using averaged values from method “1a” from (62), first discussed in (63).

A measure of the total torsional deformation of the DNA is given by the twist. This quantity is given by

$$Tw=\frac{1}{2\pi }\sum _{i=1}^{n-2}{\tau }_i,$$

as in (38), where τ_i is the “twist” angle defined above.

Results

Reproducibility of published results

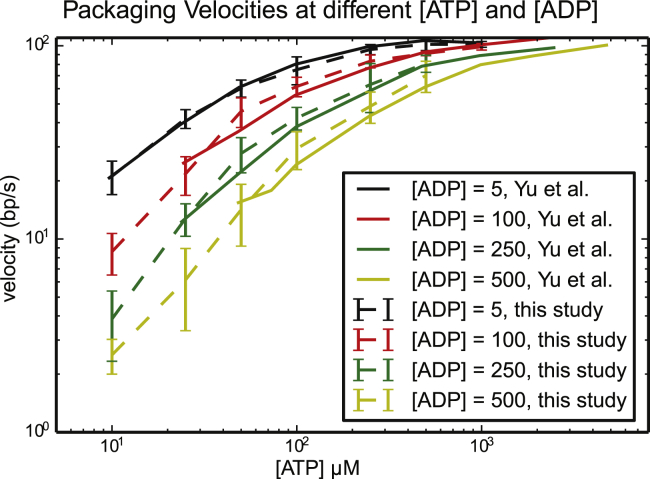
First, we show that the results obtained in our implementation of the stochastic packaging motor are consistent with the results presented by Yu and colleagues (32). Fig. 3 shows the average velocity of packaging for different concentrations of ATP and ADP. The x axis shows the molar concentration of ATP in solution, and the y axis shows the packaging velocity in basepairs per second. Continuous lines are the results published in (32), and dashed lines are the results obtained in this study. The four graphs represent different molar concentrations of ADP, as indicated in the inset. For each fixed concentration of ATP, the graphs show that the velocity of the motor decreases as the molar concentration of ADP increases. This suggests that higher concentrations of ADP outcompete ATP for the binding sites of the protein subunits. Similarly, for any fixed molar concentration of ADP, the packaging velocity increases with the molar concentration of ATP until a saturating concentration is reached. Our results differ slightly from those predicted in (32). This is likely due to minor differences in the implementation of the burst phase of the packaging reaction.

Figure 3.

Stochastic dynamics simulation results of average packaging velocities for various concentrations of ATP and ADP. Each data point is the average of the mean velocities of individual trajectories, with error bars indicating standard deviation of the samples. Data from Yu et al. (32) are included for comparison (solid lines). To see this figure in color, go online.

Twist angle fluctuations match experimental results

Our simulations are consistent with experimental results that show that the rms twist angle per basepair is on the order of 5° (59). Our simulations that include full Brownian fluctuations (discussed in Simulation of DNA Packaging) produced the following rms twist angle per basepair: 4.9° for packaging without rotation and 5.0° for packaging with rotation. In simulations in which the noise was reduced by a factor of 10, the values are lower: 0.50° without rotation and 0.55° with rotation. The theoretical rms values based on the Boltzmann distribution of just the twisting energy are 4.8° for full Brownian fluctuations and 0.48° for one-tenth power Brownian fluctuations. All following results use simulations that include one-tenth power Brownian fluctuations.

Distribution of bending energies is consistent with conformations in equilibrium

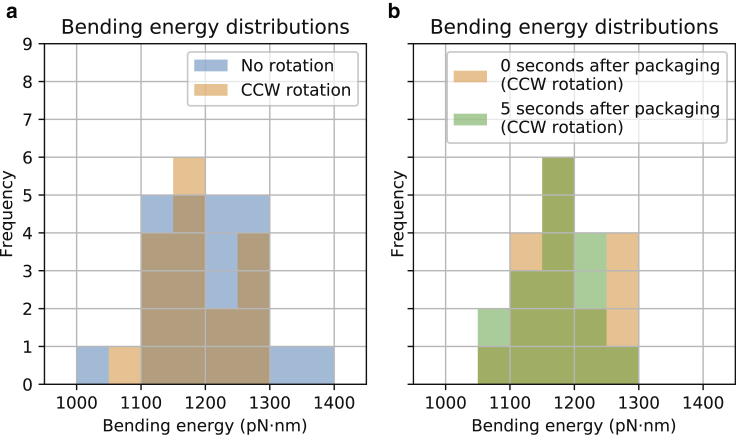
Single-molecule studies show that equilibration of packaged DNA in the phage ϕ29 takes more than 10 minutes (64). It is therefore natural to ask whether the conformations we obtain are at equilibrium or not and whether the rotation mechanism facilitates equilibration. To partially answer these questions, we compared the bending energies at the end of the packaging process for conformations generated with and without rotation. We also compared bending energies for conformations generated with CCW rotation at the time that packaging ended and 5.0 s (in simulation time) after terminating the packaging reaction. Fig. 4 a shows the distributions of bending energy with and without rotation. At the end of the DNA-packaging process, the two models exhibit overall similarity. To determine whether these distributions were significantly different, we performed a t-test. The obtained p-value of 0.55 supports the null hypothesis that there is no difference in the mean bending energy for conformations generated with and without rotation. Finally, adding a modest amount of simulation time had no statistically significant effect on the mean of the bending energy. This was true in both the case of the rotation mechanism (with a p-value of 0.93, Fig. 4 b) and also in the case of no rotation (with a p-value of 0.60, data not shown). This said, the possibility still exists that relaxation with respect to the bending energy occurs on a much larger timescale.

Figure 4.

Histograms of bending energies showing equilibration. (a) A histogram of bending energies at the end of the packaging process for conformations generated with and without rotation of the DNA by the motor is given. The blue (dark) histogram shows the distribution when no rotation was included, and the orange (light) histogram shows it when CCW rotation was included. A t-test comparing the two means showed no statistical difference between the two (p-value = 0.55). (b) A histogram of bending energies for conformations generated with CCW rotation of the DNA by the motor is given. The orange (light) histogram shows the distribution immediately after the DNA packaging ends, and the green (dark) histogram shows it 5 s later. A t-test comparing the means showed no statistical difference between the two (p-value = 0.93). To see this figure in color, go online.

DNA organizes in concentric shells characterized by coiled and folded regions

Examples of the overall patterns observed are shown in the three-dimensional renderings in Fig. 5 and share characteristics with other computational studies (14,38,44,65). The formation of concentric outer layers is likely due to the bending energy, as initially shown by energy minimization studies (14). The spacing between DNA fibers is believed to be mainly driven by electrostatic effects because distances between the outer layers are in the range of 3–5 nm, whereas the other repulsive forces (those from the Lennard-Jones energy term) begin at an interbead distance of σ = 2.5 nm. Furthermore, during the packaging process and as the outer layers are filled, the inner layers start to fill in orientations consistent with electrostatic effects induced by the already-formed layers. The ordering in layers is illustrated in Fig. 5. The graphs at the bottom of Fig. 5 show P(DNA), the “density” of DNA, as a function of R, where R is the distance from the center of the capsid. Given a value R and a sphere of radius R centered at the center of the capsid, P(DNA) is defined as the proportion of the surface area of the sphere that intersects at least one of the beads, which have a radius of σ/2 = 1.25 nm. Both models (with and without rotation) show the characteristic wavelike pattern observed in cryo-electron microscopy reconstructions (13).

Figure 5.

The results of packaging ∼3700 bp of DNA in an R_c = 15 nm capsid without rotation (left column) and with rotation (right column). Rows 1–2 show 3D renderings. Row 1 provides a side view (looking down the x axis), and row 2 provides a bottom view (looking up the z axis, directly at the motor). Color indicates the ordering of packaging: red is packaged first and violet last. Rows 3–4 show cross sections corresponding to the 3D renderings (cutting in the plane parallel to the page). The fifth row shows the “density” of the DNA, P(DNA), as a function of the radial distance from the center, showing concentric shelling with layers spaced 3–4 nm apart. The top left figure shows what might appear to be a self-intersection (the red end with the teal segment), but those vertices have been verified to have a distance greater than σ = 2.5 nm. To see this figure in color, go online.

The outer layers in both examples contain parallel fibers that exhibit both coils as well as folding around tight bends. The formation of these features can be appreciated in the packaging videos (see Videos S1 and S2 ). During the early stages of the packaging process, the DNA begins to form coils, and most torsional strain is alleviated by the rotation of the entire molecule. If there is no rotation of the DNA by the motor, the local accumulation of torsional strain causes the coiling to alternate orientations, especially during the middle stages of packaging. When the motor rotates the DNA, although the DNA coiling may still switch orientations, the DNA mostly forms coils of the orientation that alleviates the torsional strain introduced by the motor. DNA loops caused by the changes in orientation may be restricted in their movement (i.e., when the capsid is partially filled) and flattened, forming the folded regions.

Rotating of the DNA by the motor induces writhing

We simulated packaging reactions under different conditions to determine what aspects of the motor change the writhe of the final configuration of the packed DNA molecule. Specifically, we looked at rotation (no rotation versus clockwise rotation (CW) versus counterclockwise rotation (CCW)), revolution (no revolution versus revolution), and packing mechanism (stochastic versus deterministic). The CW and CCW directions of rotation and revolution are determined by looking down the axis of the motor from within the capsid, as illustrated in Fig. 1 b. We tested all 12 combinations of these characteristics. Results showing the interplay between twist and writhe of the DNA molecule are presented in Fig. 6.

Figure 6.

Writhe (blue) and twist (orange) as a function of time under 12 different sets of parameters for simulations involving a capsid of radius R_c = 15 nm. In each panel, the x axis represents time and the y axis the value of writhe and twist. The top left corner of each graph indicates the mean writhe value with standard deviation (measured at 100 s) and the p-value for the one-sample t-test for the null hypothesis H₀: $\langle Wr\rangle$ = 0. The multiple points represent writhe and twist values measured every 2.5 s from different runs. The left column shows stochastic packaging; the right one shows deterministic (constant packaging speed) packaging. The first two rows show the effect of no rotation, the third and fourth the effect of CCW rotation, and the last two rows the effect of CW rotation. The small effect of revolving the DNA about the axis of the packaging direction as it passes through the motor is shown in alternate rows. For the deterministic motor with neither revolution nor rotation, the writhe value was 0.0 ± 1.6 (12 samples) and with revolution but no rotation was −0.9 ± 2.3 (six samples). The respective values for stochastic motors were −0.7 ± 1.6 (nine samples) and −0.2 ± 1.5 (10 samples). For deterministic motors implementing CCW rotation and no revolution, it was −3.0 ± 2.1 (11 samples), and for those with CCW rotation and revolution, it was −3.2 ± 1.3 (10 samples). For stochastic motors with a CCW rotation and no revolution, it was 3.1 ± 1.6 (14 samples), and for those with CCW rotation and CCW revolution, it was −4.1 ± 1.0 (eight samples). When there is no rotation, the p-values are all larger than 0.1, meaning that the null hypothesis is not rejected. Conversely, rotation during packaging yielded p-values smaller than 0.01, showing that the hypothesis is rejected and that in these cases, there likely exists a writhe bias. To see this figure in color, go online.

Our results suggest that the rotation of the DNA molecule during packaging and the writhe of the packaged chain are highly correlated. We computed the correlation values between the angular velocity of the DNA with its respective orientation (positive or negative, accounting for CW and CCW rotation, respectively) with the writhe values of the packaged chain after 100 s of simulation time. Table 1 shows the results. All correlation values are at least 0.8, and the p-values are smaller than 1 × 10⁻⁶.

Table 1.

Correlation of Rotational Velocity and Writhe

	Stochastic Motor	Deterministic Motor
No revolving	0.86	0.80
CCW revolving	0.91	0.81

Pearson’s r coefficient for the relationship between the angular velocity of the rotation and writhe. The rotation of the packaging motor induces an accumulation of writhe with a sign related to the direction of rotation.

Interestingly, one can see from Fig. 6 that the twist value increases or decreases in mechanisms that include rotation with a sign opposite of that of the corresponding writhe accumulation. This is to be expected because of the way the values for twist and writhe are related for closed DNA chains or chains with spatially fixed ends (66, 67, 68). Additionally, the rate of accumulation of twist increases while that of writhe decreases. This result suggests that the torsional strain induced by the rotation of the DNA molecule at the time of packaging is only released partially; it is released by the rotation of the entire open-ended chain (as suggested in (39)), and it induces coiling of the central axis of the DNA molecule, which translates into writhe (as suggested in (38)), but in decreasing quantities as the movement of the DNA axis becomes ever more restricted as the capsid is filled. Then, after the packaging process is complete and both DNA ends are in the capsid, the accumulated twist is slowly released at both ends (see video of rotation mechanism; in Video S2). Our model captures these phenomena because of the extended simulation time. In these simulations, the twist was quantified as it accumulated as part of the packing process. The natural interplay between twist and writhe causes some twist to convert into writhe, and the amount depends on the properties of the packing reaction. Under natural salt and pH conditions, double-stranded DNA molecules in solution have a constant helical pitch of 10.5 bp per turn. The helical pitch of double-stranded DNA when subjected to high levels of confinement is unknown. However, controlling the helical pitch, and thus the twist, of the chains in our simulations will only exacerbate the accumulation of writhe and strengthen support for the writhe bias observed in all simulations with a rotating packing mechanism (preliminary data; data not shown).

We also evaluated and compared the writhe for configurations obtained for different motor models. Deterministic and stochastic motors cannot be directly compared with confidence because the packaging and rotational rates are slightly different. However, one can compare mechanisms for each of these models. Interestingly, both mechanisms showed very consistent results. First, both models showed that the revolution mechanism in the absence of rotation does not have an appreciable effect on writhe. For instance, the average writhe value for a deterministic motor with revolution and no rotation was −0.9 ± 2.3 (six samples), whereas for a deterministic motor without both revolution and rotation, it was 0.0 ± 1.6 (12 samples). Similar results were obtained for the stochastic motor. Second, revolution of the DNA molecule does not contribute to the final writhe value even in the presence of rotation. For instance, deterministic motors implementing CCW rotation and revolution produced an average writhe value of −3.2 ± 1.3 (10 samples), and those with no revolution accumulated a writhe of −3.0 ± 2.1 (11 samples). For the stochastic motor, the values were −4.1 ± 1.0 (eight samples) and −3.1 ± 1.6 (14 samples). Third, the relative direction of the rotation and revolution did not contribute to the value of the final writhe in a significant manner. For instance, the deterministic motor, with a CW rotation and CCW revolution, gave a writhe of 3.2 ± 2.4 (10 samples), whereas in the model in which both are in the CCW direction, we observe mainly a sign change, −3.2 ± 1.3 (10 samples).

Discussion

A renewed interest in bacteriophages has emerged from the need to develop new approaches to treat bacterial infections (69,70), to implement protein expression systems (e.g., (50)), and to treat infectious diseases caused by these viruses (e.g., (71)). The structural study of bacteriophages is well justified because structure determines function.

Models for the organization of DNA inside icosahedral bacteriophages started in the early 1970s, when Richards and colleagues proposed the ball of yarn model and the coaxial spooling model as two potential packaging geometries for DNA (72). These models were later followed by other models such as the coaxial and longitudinal spooling model (11, 12, 13, 14,73), the spiral-fold model (74), the liquid-crystal model (75,76), and the folded toroid model (76,77). Computer simulations have been key in understanding these models and have provided biophysical arguments favoring some models over others (Table 2). For instance, in (14,43,44), it was shown that concentric spool models are more biophysically meaningful than coaxial models. These works also gave a somewhat unifying view of the different packing models by showing that different arrangements can be reproduced by varying the shape and size of the capsid (43,44,78). More recently, liquid crystalline models have taken center stage in the modeling of DNA in bacteriophage capsids. With the introduction of chromonic liquid crystals in 2012, the work by Klug and Ortiz (10) introduced the concept of the nematic director field to represent the local orientation of DNA segments in the context of DNA packaging and, together with the work by Tzlil et al. (6), to refer to the chromonic structure of encapsidated DNA. From a different perspective, the formation of liquid-crystal phases in condensed DNA was observed in the late 70s by Livolant (79). It was in 2012 that the discovery of toroidal aggregates formed by certain molecular disk-like lyotropic compounds, analogous to those in condensed DNA but with length scales 10⁶ times greater, gave rise to the denomination of chromonic liquid crystals to such materials. In recent work, modeling tools to study chromonic liquid crystals and their application to DNA packaging yielded predictions of the spooling configuration as the minimizer of the total energy, with estimates of the optimal sizes of the isotropic core and the ordered region in the capsid, as well as the inner pressures (80,81). Furthermore, in (81) a numerical algorithm, based on the method of finite elements, was developed and implemented to calculate the previously mechanical features of the packaging and for the design of new viral particles.

Table 2.

Table Reviewing Previously Published Energetic Models

Torsional Stiffness	DNA Effective Diameter	Lennard-Jones	Debye-Hückel	Confinement	Liquid Crystalline	DNA Knotting
Monte Carlo Method
				Arsuaga et al. (15) (quadratic)		Arsuaga et al. (15)
				Arsuaga et al. (quadratic) (16)		Arsuaga et al. (16)
		Comolli et al. (73)	Comolli et al. (73)	Comolli et al. (73) (quartic)
Molecular Mechanics Method
		Kindt et al. (42)		Kindt et al. (42) (quartic)
	Arsuaga et al. (15)		Arsuaga et al. (15)	Arsuaga et al. (15) (quadratic)
		Ali et al. (93)		Ali et al. (93) (Lennard-Jones)
	LaMarque et al. (94)			LaMarque et al. (94) (quadratic)		LaMarque et al. (94)
	Spakowitz et al. (38)	Spakowitz et al. (38)		Spakowitz et al. (38) (quartic)
		Forrey et al. (41)	Forrey et al. (41)	Forrey et al. (41) (Lennard-Jones)
				Locker et al. (quadratic) (95)
	Petrov et al. (78)		Petrov et al. (78)	Petrov et al. (78) (space filling)
Rollins et al. (39)	Rollins et al. (39)			Rollins et al. (39) (quadratic)		Rollins et al. (39)
		Marenduzzo et al. (65)	Marenduzzo et al. (65)	Marenduzzo et al. (65) (quartic)	Marenduzzo et al. (65)	Marenduzzo et al. (65)
		Petrov et al. (96)		Petrov et al. (96) (quadratic)
Córdoba et al. (57)		Córdoba et al. (57)	Córdoba et al. (57)	Córdoba et al. (57) (Weeks-Chandler-Anderson)
this work		this work	this work	this work (quartic)

Stretching and bending energies are omitted because they are considered in all studies. DNA effective diameter accounts for studies in which the effective diameter was explicitly considered. Lennard-Jones accounts for short range electrostatic interactions and stands for its corresponding truncated form; Debye-Hückel stands for long term electrostatic interactions; Confinement accounts for the effects of the capsid.

In the work presented here, we study the effects of the packaging motor on the final organization of the DNA molecule inside the viral capsid. Although the final DNA concentration simulated is lower than that observed in experiments, it is comparable to that reported in previous studies (14,38,40,52,57,73). Two prior studies have investigated the effects of the rotating of the DNA molecule by the packaging motor on the final geometry of the encapsidated DNA, reaching conflicting conclusions (38,39). Both were lacking the implementation of a motor mechanism faithful to biophysical experiments.

Our simulations showed the characteristic shells detected experimentally using cryo-electron microscopy (13,73,82,83). Additionally, simulations from both rotating and nonrotating mechanisms showed coiled domains as well as folded regions in their outer shells. The second result shows there is a strong correlation between rotation and accumulated writhe. This study was motivated by experimental observations that suggest that the DNA molecules is packed inside the bacteriophage capsid in a chiral fashion (16) and by single-molecule experiments of the action of the packaging motor (31,35). In (16), the populations of knots extracted from bacteriophage P4 capsids were characterized and compared with simulated distributions of random knots. This analysis of knots revealed that the four-crossing knot 4₁ was underrepresented in the bacteriophage population. Because this knot is achiral, the authors suggested that the organization inside the bacteriophage capsid is chiral. This hypothesis is also consistent with knot distributions observed in P4 deletion mutants (20,23) and with single-molecule studies that show the presence of compensatory supercoils (31). A testable prediction of this hypothesis is that knots extracted from P4 capsids should all have the same chirality. Two phenomena, not necessarily exclusive, can account for this proposed chiral organization: the interaction of the highly condensed DNA fibers and the geometry imposed on the DNA by the molecular motor.

The first hypothesis was addressed in (24) and in (25). In (24), the authors rigorously showed that if the magnitude of the writhe of a confined knot exceeds the number of times the DNA spooling conformation winds around the central axis, then the knot cannot be achiral; furthermore, the authors proposed a model of random threading of DNA fibers that was consistent with the experimentally observed knot pattern. In 2008, Marenduzzo (25) proposed a different model in which DNA strands had a cholesteric interaction. This model produced coaxially spooled conformations and was also consistent with the distribution of knots extracted from P4 bacteriophages (25). Both models assume reptation of the leading DNA end; in other words, the first DNA that gets packed inside the capsid is able to direct the trajectory of the molecule as it is being packed. This study provides computational evidence that the rotation mechanism of a DNA packaging motor helps to organize the viral genome in a chiral fashion, with the leading DNA end staying close to the capsid wall as it is being pushed into the capsid (see Videos S1 and S2).In this case, knots cannot form while the DNA is being translocated into the capsid, but instead once the DNA is completely packed inside the capsid and the two DNA ends are free to meet.

Modeling of the motor can be further extended by incorporating a feedback mechanism from the DNA molecule to the motor. Our model assumes that the energy stored in the DNA molecule does not affect the force exerted by the motor. This assumption is based on single-molecule observations that show that the packaging of the first 50% of the genome induces very few pauses during the packaging reaction (64), suggesting that there is no feedback mechanism between the DNA molecule inside the capsid and the motor. This independence between energy stored in the DNA molecule and the force exerted by the motor is expected to change at higher concentrations because pauses in the packaging are very frequent as more DNA is packed. Our model can therefore be further improved by allowing forces in the capsid to affect the jump process on the z variable (8,34). Another possibility for the packaging reaction is to model a different mechanism based on the transition of DNA from B to A form, as has been suggested in (28,29,84). Despite these simplifications, we expect that the methods developed here can be used to study the function of other molecular motors. Similarly, the topology of the DNA molecule outside the capsid was not considered in these simulations and may also affect the packaging reaction. Modeling of the DNA inside the capsid needs further development. The physical properties of DNA inside the viral capsid remain mostly unknown, and much work remains to be done to fully characterize it. In our work, we have introduced hydrodynamic interactions that, as in (38), we assume can be modeled using a constant term. This simplification, at least in the early stages of packaging, is also based on the single-molecule data observed in (64). In future studies, we will use a more sophisticated hydrodynamic term that allows longer-range interactions such as those used in (85, 86, 87) and study how the hydrodynamic interactions change as a function of the density of the DNA inside the capsid. As noted in (38), general uncertainty surrounding the effective viscosity makes discussing the timescale difficult, so future work on improving hydrodynamics should include a detailed treatment of viscosity. Additionally, the inclusion of full Brownian fluctuations may help better characterize the packaging process. Although rotation mechanisms with and without revolution do not show differences in the chiral organization of the viral genome, other characteristics may show differences.

Finally, we have postponed the closure of the chains and the determination of the topology of the simulated DNA molecule, for a future study. If both DNA ends are near each other after the packaging process, they can easily anneal, forming a knot inside the capsid. In (88), the two ends of the DNA molecule were near each other and near the capsid, and the authors joined them directly. If the two ends are not very near each other, then the problem is more difficult and requires new mathematical tools. In (89), a probabilistic method to determine the topology of proteins was introduced. In this method, an ensemble of closed molecules is associated to a single protein structure, and the topology of the protein is determined based on the topologies observed in the ensemble. Each of the samples in the ensemble is derived from the original protein backbone by surrounding the protein backbone by a very large sphere and connecting the two ends of the protein to a point in this sphere through two straight lines. This approach was recently generalized to study the linking and entanglement complexity of chromosomes in budding yeast (90). Most recently, a new formalization of entanglement in open curves has been introduced through the concepts of knotoids (91) and knotting probability of an arc diagram (92); whether this will be the correct formulation for biological problems remains to be determined.

Author Contributions

B.C. implemented computer programs, worked on the algorithms and their implementation, and cowrote the manuscript. Z.Z. and B.C. performed simulations, generated data, and cowrote manuscript. C.C. cowrote manuscript and contributed to the energy formulation. J.A. and M.V. conceived and designed study, analyzed data, and cowrote manuscript.

Editor: Wilma Olson.