Abstract
Motivation
Liquid chromatography–mass spectrometry (LC-MS) is a standard method for proteomics and metabolomics analysis of biological samples. Unfortunately, it suffers from various changes in the retention times (RT) of the same compound in different samples, and these must be subsequently corrected (aligned) during data processing. Classic alignment methods such as in the popular XCMS package often assume a single time-warping function for each sample. Thus, the potentially varying RT drift for compounds with different masses in a sample is neglected in these methods. Moreover, the systematic change in RT drift across run order is often not considered by alignment algorithms. Therefore, these methods cannot effectively correct all misalignments. For a large-scale experiment involving many samples, the existence of misalignment becomes inevitable and concerning.
Results
Here, we describe an integrated reference-free profile alignment method, neighbor-wise compound-specific Graphical Time Warping (ncGTW), that can detect misaligned features and align profiles by leveraging expected RT drift structures and compound-specific warping functions. Specifically, ncGTW uses individualized warping functions for different compounds and assigns constraint edges on warping functions of neighboring samples. Validated with both realistic synthetic data and internal quality control samples, ncGTW applied to two large-scale metabolomics LC-MS datasets identifies many misaligned features and successfully realigns them. These features would otherwise be discarded or uncorrected using existing methods. The ncGTW software tool is developed currently as a plug-in to detect and realign misaligned features present in standard XCMS output.
Availability and implementation
An R package of ncGTW is freely available at Bioconductor and https://github.com/ChiungTingWu/ncGTW. A detailed user’s manual and a vignette are provided within the package.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
For proteomics or metabolomics analysis of biological samples, liquid chromatography coupled with mass spectrometry (LC-MS) is a standard method (Mueller et al., 2007; Theodoridis et al., 2008) that produces two-dimensional profiles of constituent compounds over retention time (RT) and mass-to-charge ratio (m/z). The identity and quantity of a particular compound [known (Lu et al., 2008a) or unknown (Vinaixa et al., 2012)] may be inferred by analyzing the associated characteristic peak/curve profile (RT, m/z and intensity information). When analyzing multiple samples, the RT of each compound must be aligned accurately across different samples (Lu et al., 2008b).
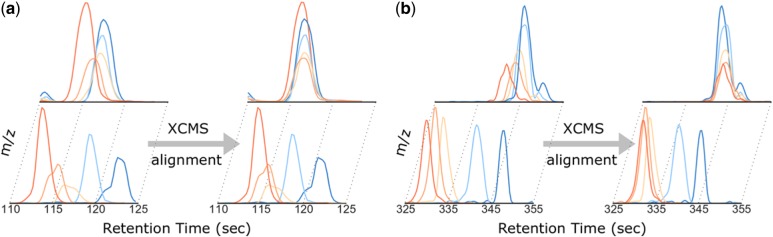
Many software packages for LC-MS data analysis include a tool kit that performs RT alignment, such as XCMS (Smith et al., 2006, 2015). However, due to varying RT drift over different m/z bins in a sample and significant RT drift across distant samples (samples with larger run order difference), often non-linear, accurate RT alignment remains a challenging task (Smith et al., 2015). Unfortunately, classic alignment methods conveniently assume a single warping function across all m/z bins and perform multiple alignment that neglects the run order of each sample (Prakash et al., 2006; Prince and Marcotte, 2006; Zhang et al., 2005). These methods largely ignore the aforementioned two factors, and thus are prone to various types of misalignment. For a large-scale experiment involving many samples, some degree of misalignment for certain features becomes inevitable. For some types of misalignment, an algorithmic effort to mitigate them is to optimize parameter values in complex alignment algorithms. However, current strategies for handling a large number of parameters or features (peaks from the same compound at a single m/z bin with aligned RT across samples) are ad hoc, labor-intensive, subjective and often fail to achieve a desired performance. Furthermore, for misaligned features whose true warping functions are different over different m/z bins, the misalignment cannot be corrected simply by adjusting the parameters of a single warping function (Fig. 1). Moreover, no existing analytics tool includes a systematic way to detect misalignment and thus previously acknowledged misalignment is often undetectable or uncorrected.
Fig. 1.
Examples of the observed misalignments due to single warping function assumption. Five samples over two m/z bins from each dataset are shown here for demonstration, where the upper and lower rows represent two different m/z bins, respectively (see details in Section 2.1). (a) An example from the Rotterdam dataset shows that even with similar RT, the drift of each sample could be significantly different in two m/z bins. Using only a single warping function, XCMS can only align one bin (the upper one) well but not the other one as shown in the right part. (b) A similar example is also observed in MESA dataset
To address the critical problem of the absence of validated methods for misalignment detection and structured alignment, we developed an integrated reference-free profile-based alignment method, neighbor-wise compound-specific Graphical Time Warping (ncGTW), that first detects misaligned features and then aligns affiliated profiles. In contrast to feature-based methods that only align detected peaks, fundamental to the success of our approach is the incorporation of expected RT drift structures across both different m/z bins and distant samples. Specifically, under the GTW framework (Wang et al., 2016), ncGTW uses individualized warping functions for different m/z bins and assigns constraints on warping functions of neighboring samples. Furthermore, ncGTW utilizes a two-stage algorithm to achieve a reference-free alignment, where combinatorial pair-wise alignments are first performed and these aligned profiles are then coordinately aggregated into a pseudo-reference.
The input data to be analyzed by ncGTW include the peak information extracted by XCMS and the raw data profiles corresponding to misaligned features. First, a statistically principled misalignment detection scheme is applied to identify features requiring realignment. Then, each of the two-stage alignment procedures in ncGTW is solved efficiently by network flow-based algorithms (Goldberg et al., 2011). The ncGTW software tool takes full advantage of feature-based alignment methods and is provided currently as a plug-in to XCMS package.
2 Materials and methods
2.1 Datasets
We apply ncGTW pipeline to two large-scale real metabolomics LC-MS datasets, namely the Rotterdam (The Rotterdam Study, The Netherlands) and MESA (The Multi-Ethnic Study of Atherosclerosis, USA) cohorts (Bild et al., 2002; Hofman et al., 2013), first to detect misalignment and then to realign those misaligned features.
Serum lipid profiling datasets were acquired by C8 reversed-phase LC after serum protein precipitation using isopropanol, using protocols adapted from (Sarafian et al., 2014) and (Lewis et al., 2016). LC-MS profiles of the serum samples from the Rotterdam and MESA cohorts were generated using a Waters Acquity Ultra Performance LC system (Waters, Milford, MA, USA) for chromatographic separation and a Xevo G2S Q-TOF (Waters, Milford, MA, USA) for MS detection in positive ionization mode.
The Rotterdam dataset contains 1000 study samples and 44 internal quality control (iQC) samples and the MESA dataset contains 1977 study samples and 335 iQC samples. Each iQC sample is an aliquot of a pool of all the study samples, used to monitor and correct instrument performance in long runs. Because each of these two cohorts contains many samples (>1k), the total time duration on data acquisition would be in the range of weeks—thus, significant RT drift across experiments is expected. Indeed, on the iQC samples, the global warping function assumption made by XCMS is clearly and evidently violated in both Rotterdam (Fig. 1a) and MESA (Fig. 1b) datasets (using five samples from each dataset for demonstration). Moreover, in our observation, we estimate that there are around 3% of features which are misaligned due to the global warping function assumption in each dataset. Given that these two datasets were acquired from different cohorts at different labs with probably different experimental settings, this kind of misalignment may happen in any large dataset, and is not a rare occurrence.
In the subsequent experiments on both iQC and study samples, the major preprocessing steps (peak detection, RT alignment and peak grouping) are done by XCMS, and the ncGTW pipeline uses the default parameter settings.
2.2 Detection of misaligned features
Accurate alignment of RT over a large number of samples remains a challenging task, particularly across distant samples due to significant yet varying RT drift. RT drifts between neighboring samples are small and gradual, even though random RT drifts may occur. More explicitly, the gradual RT drifts among neighboring samples, mainly due to temperature or column age (Benk and Roesli, 2012; Palmblad et al., 2007), can be modeled by the closer or similar run orders (Tengstrand et al., 2014). For a given feature corresponding to a set of peaks detected in several samples (e.g. by XCMS), we assume that the abundances of corresponding compound are independent of sample indices (this is an implication of randomizing the run order—standard practice in analytical science) and alignment relies on sufficient compound abundance in the relevant samples. Thus, for an accurately aligned feature, the samples associated with this feature should be a subset randomly drawn from the entire sample set, including both neighboring and very distant samples in the run-order domain (sample index). In contrast, a misaligned feature often splits into multiple features by the feature detection algorithm with non-ideal parameter setting (Fig. 2). Since most of alignment algorithms tend to group the peaks with similar RT drift together (Smith et al., 2015), regardless of the alignment accuracy, neighboring samples tend to be aligned together due to their similar RT shift. In other words, when a detected feature includes only neighboring samples, it would highly likely constitute a misaligned feature (one of the most common forms of misalignment). Thus, even though the RT drift goes back and forth, and features are misaligned, the neighboring samples would still be grouped into a feature, as shown in Figure 2. Accordingly, we designed a statistically principled approach to detect misaligned features. We associate the null hypothesis with correct alignment, use the range of sample indices within feature as the test statistic, and detect misaligned features by rejecting the null hypothesis.
Fig. 2.
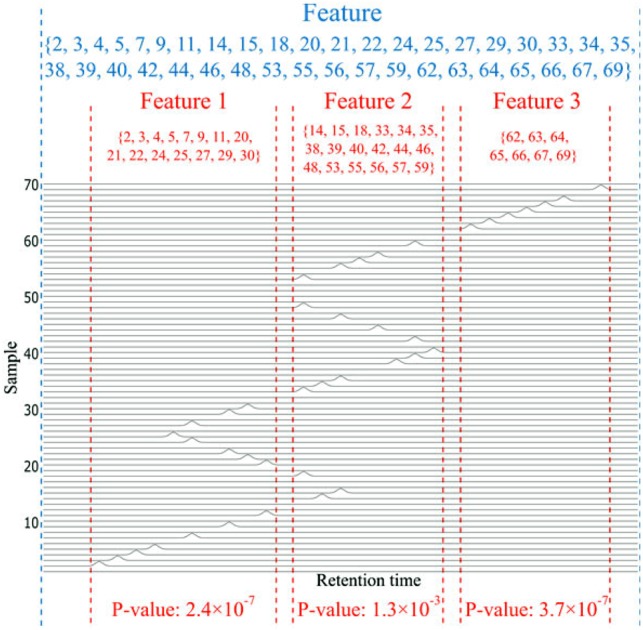
Illustrative example on detecting misaligned features. After initial alignment, among the total 70 samples, relevant peaks are detected only in some samples (the indices in blue), and some of the feature(s) are obviously misaligned. With a lower resolution grouping by XCMS, these peaks are all grouped into one single feature, as shown between the two blue dashed lines. While with higher resolution grouping, this feature is split into three features 1–3 as separated by the red dashed lines. The sample index sets of these features are shown in red, respectively. The P-values of features 1–3 are all smaller than 0.05, thus pass the first criterion. Because the sample index sets of these three features are also disjoint, they pass the second criterion. Accordingly, ncGTW will detect the misalignment and realign the whole blue feature produced by the lower resolution grouping. (Color version of this figure is available at Bioinformatics online.)
For a provisionally aligned feature for which the peak is detected in a total of n samples, as the first criterion, we consider the range of sample indices in the feature as the test statistic, given by:
| (1) |
where is the sample index of the ith sample in the feature, and is the total number of samples. Under the null hypothesis, we assume that follows a discrete uniform distribution. Then, based on order statistics (Arnold et al., 1992), it can be shown that the probability mass function of t is given by:
| (2) |
where t values associated with misalignment will always correspond to very small values under the null hypothesis and the P-values associated with this feature can be estimated by
| (3) |
where is the observed sample index range of the feature. If the P-value of a feature is sufficiently small, reflecting the fact that the alignment only recruits neighboring samples, we can safely reject the null hypothesis and consider this feature as a candidate misaligned feature. The details of the test statistic are given in Supplementary information.
To address the additional layer of complication concerning varying RT drift over different m/z bins, for a candidate misaligned feature, we further check whether there exists neighboring feature(s) in the same m/z bin with sufficiently small P-value, while with disjoint sets of sample indices, and if so, consider these features as needing to be realigned together. The rationale behind this second criterion is that applying the same warping function cross different m/z bins would likely, yet wrongly, split the complete feature of a single compound into several pieces.
In the ncGTW algorithm, these two criteria are combined to detect misaligned features. The initial alignment is performed using the existing XCMS alignment module. After XCMS alignment, two separate grouping results are produced using different RT window parameter values (bandwidth, bw) in the XCMS peak-grouping module (feature detection). More precisely, the lower resolution grouping uses an RT window corresponding to the expected maximal RT drift, while the higher resolution grouping uses an RT window near the RT sampling resolution (the inverse of scan frequency). First, ncGTW algorithm estimates the P-value of each feature using higher resolution grouping result and identifies all features with sufficiently small P-values and disjoint sample subsets. Then, the ncGTW algorithm matches the neighboring features to the corresponding features produced by lower resolution grouping, and considers realigning these features. An illustration of misalignment detection is given in Figure 2.
The true causes for a misaligned feature may be complex and hidden, and may involve multiple yet unknown factors. It may be arguably suspected that the observed misalignment by existing alignment methods is at least partially due to the unstructured cost distributions over neighboring versus distant samples adopted by these methods. The joint optimization may thus be overly influenced by neighboring samples with intrinsically less costs. However, such a biased solution is clearly in conflict with the very purpose of a globally optimal alignment that should be able to simultaneously correct larger and complex RT drift over samples that are widely separated in run order.
2.3 Basic principles of profile-based multiple alignment
Profile-based multiple alignment methods align all profiles in samples to a reference profile , applied on every point in each profile, not just the extracted features. We use to denote the function that maps profile to , commonly referred to warping function. Profile-based multiple alignment methods estimate both and warping functions . One popular method is pair-wise Dynamic Time Warping (DTW) (Sakoe and Chibe, 1978), matching the corresponding points between sample and reference to achieve minimum overall discrepancy while no ‘crossing’ is allowed between links (Fig. 3a). DTW considers alignment as a shortest path problem on a grid where the dots represent all possible point pairs and the edges represent ‘possible path’ in warping function. Specifically, DTW assigns cost to the edges as the intensity distance between the paired points (Fig. 3b). For a sample profile and a reference profile , the optimal warping function corresponds the shortest path, minimizing the cost function:
| (4) |
where is the pointwise distance function, is the th point on , is the th point on and is a dot in the grid.
Fig. 3.
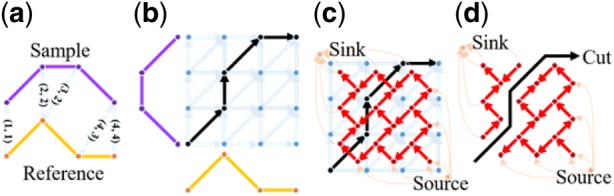
Principle concept of DTW grid and graph. (a) DTW alignment aims to find the pairs of corresponding points over which the maximum profile similarity is achieved. Here the paired corresponding points are (1, 1), (2, 2), (3, 2), (4, 3) and (4, 4) that form the warping function. (b) DTW grid for solving the warping function shown in blue edges and dots, where the cost of each edge is determined by the intensity distance of each point pair. By solving the ‘shortest path’ problem, the warping function is obtained (black path) whose paired corresponding points are reflected in (a). (c) Based on the duality property of planar graph, DTW gird is transformed to DTW graph (red and orange lines and dots), where each red or orange edge crosses one blue edge, and the cost of red or orange edge is the same as the cost of blue edge. Note that orange lines link only the vertices (red dots enclosed by blue lined exterior triangle) to a single source or sink. Then, the shortest path problem becomes a maximum-flow/minimum-cut problem. (d) Solving the alignment problem is to find a ‘cut’ which separates the DTW graph into two parts with the minimum cost, with one part including the source and the other including the sink. The cut with the minimum cost corresponds to the warping function (black path). (Color version of this figure is available at Bioinformatics online.)
Because DTW grid is a planar graph, after converted to the corresponding DTW graph, the shortest path problem is readily converted into an equivalent minimum-cut/maximum-flow problem (Fig. 3c;Wang et al., 2016). The cut with the minimum cost in DTW graph corresponds to the path with the lowest cost in DTW grid (Fig. 3d), thus the alignment problem is solved by any minimum-cut/maximum-flow algorithm.
2.4 Graphical time warping
We have recently developed GTW (Wang et al., 2016) that extends classic DTW to perform multiple alignments with the possibility of incorporating structure information. For example, the run order of samples is one useful type of structure information: samples that are processed at closer time should exhibit similar global drifting.
GTW first converts each DTW grid (shortest path problem) to a DTW graph (minimum-cut/maximum-flow problem). Then additional edges are applied to link the DTW graphs (Fig. 4a) of neighboring samples and form a larger graph—GTW graph. These edges link the vertices with the same position of DTW graphs (Fig. 4b) among neighboring samples (Fig. 4c), and the warping functions in the resulting larger graph are simultaneously estimated by solving the expanded maximum flow problem (Wang et al., 2016). This maximum flow problem is equivalent to finding the warping functions with the minimum cost:
| (5) |
where , is the function measuring the difference between two warping functions and is a hyperparameter. The first term is the summation of DTW cost functions [Eq. (4)] of all samples. The second term is the discrepancy penalty among pairs of warping functions, which incorporates the structure information among samples. (cost of the additional edges) controls the relative contribution of the two terms. When increases, the cut will produce more similar warping functions among neighboring samples. When is close to zero, the warping functions will be similar to those obtained by DTW.
Fig. 4.
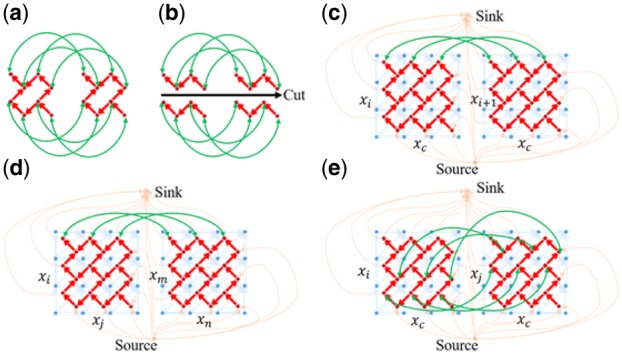
Construction of the various GTW graphs used in the different steps of ncGTW algorithm (Wang et al., 2016). (a) Two small DTW graphs are linked to form a GTW graph via additional ‘connecting’ edges (green lines between the vertices as the same position of two DTW graphs). (b) After adding the green edges, we can solve all warping functions at the same time, with the similarity among warping functions as constraints. The cost on green edges is to control the similarity between warping functions. For example, if the cost is very high, no green edge will be cut and all the warping functions would be the same. (c) GTW graph formed by two linked DTW graphs of two neighboring samples (x_i and x_(i+1)) with a common reference, extendable to all neighboring samples, where the orange lines link vertices to a single source or sink forming a large maximum flow graph, while green edges link the corresponding vertices of two DTW graphs (only edges linking top three vertices are shown here). (d) Part of the graph constructed in Stage 1 of ncGTW without using a common reference, where x_i and x_m are neighboring samples, and x_j and x_n are neighboring samples. (e) Part of the graph constructed in Stage 2 based on all pairwise warping functions obtained in Stage 1, where the warping function Φ_(i→j) guides the links between the corresponding vertices in GTW graphs, with x_c being the virtual reference. (Color version of this figure is available at Bioinformatics online.)
In the application of GTW multiple alignment to real LC-MS data, we have also observed a few drawbacks of this method. Similar to DTW, multiple alignments by GTW requires a common yet ‘ideal’ reference, while in many real-world problems, there is no a priori perfect reference available (e.g. no missing peak and little noise). Moreover, GTW may encounter a post-warping peak-distortion problem.
2.5 Framework of ncGTW algorithm
We developed the ncGTW framework that incorporates structural information, does not require an a priori common reference, and can correct post-alignment peak distortions. As mentioned above, both DTW and GTW align each profile to the specified reference, with the difference that GTW imposes the structural information among warping functions, while DTW aligns separately. Both methods are sensitive to the selection of the reference. Rather than requiring that a common reference be prespecified, ncGTW jointly align all profiles to a virtual reference (), which can be considered as a placeholder in the algorithm and is never estimated. ncGTW utilizes information from two aspects to make the multiple alignment possible: (i) the biological preferences of the shape of warping functions to be estimated ( which aligns profile to ) and (ii) the knowledge of the warping functions between all possible pairs of samples, which in term is estimated utilizing the structural information.
The ncGTW algorithm consists of two key stages. First, by viewing each sample as a reference in a combinatorial network, ncGTW incorporates available sample structure information (in the case of LC-MS data, the run order) and aligns all possible sample pairs in the dataset (without repetition). Then, ncGTW aligns all samples to a virtual reference using the warping point correspondences established in the first stage to make sure and are consistent with estimated in the first stage. The overall flowchart of ncGTW algorithm is given in Figure 5. We will discuss the details of each stage below.
Fig. 5.
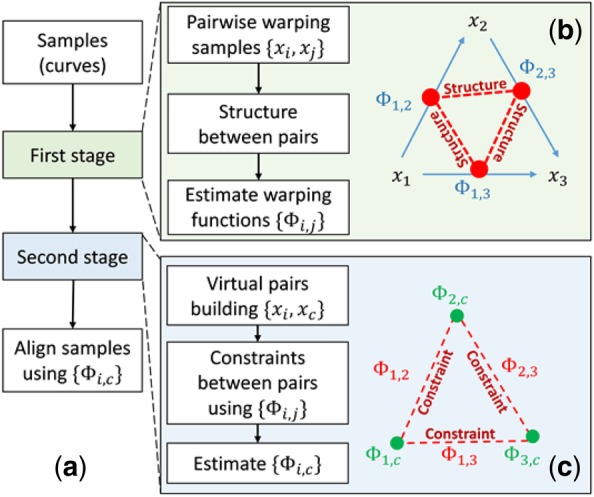
Flowchart of ncGTW algorithm. (a) With two-stage alignment strategy, all input samples (curves) are aligned simultaneously to a virtual reference. (b) Stage 1 of ncGTW with three illustrative samples. First, ncGTW builds a pairwise warping flow map (blue arrows). Then ncGTW incorporates structural information as the constraint and applies to all pairs (pair as red dot and constraint as a red dashed line). Lastly, ncGTW estimates all pairwise warping functions (Φ_(i,j)) jointly with e.g. smoothness constraint on neighboring sample pairs. (c) Stage 2 of ncGTW with three illustrative samples. ncGTW aligns every sample to a common virtual reference x_c, where the warping functions {Φ_(i,j)} obtained in Stage 1 provide warping correspondences and final warping functions {Φ_(i,c)} are calculated by solving the maximum flow problem. (Color version of this figure is available at Bioinformatics online.)
In Stage 1, given the profiles of samples, ncGTW incorporates structural information and simultaneously estimates total warping functions for all distinct sample pairs. Like GTW, instructed by structural information, additional edges are applied to link the vertices at the same position of DTW graphs among neighboring samples (Fig. 4d). Again, this circular multiple alignment can be readily realized by solving a classic maximal flow problem (Supplementary information). Specifically, ncGTW estimates the enumerated pairwise warping functions jointly by minimizing the cost function given by
| (6) |
where , is a hyperparameter, indicates that the warping functions and are associated with neighboring samples ( is the empty set). Eq. (6) may look similar to Eq. (5), but ncGTW estimates the pairwise warping functions, instead of warping functions aligning profiles to the common reference. Similar to in Eq. (5), here is also used for balancing the cost of the first term (the distances between profile pairs after alignment) and second term (the distances between warping functions). All are efficiently obtained by solving an equivalent maximum flow problem.
In Stage 2, ncGTW uses the warping functions as both guidelines and constraints to aggregate the profiles of all samples to a common virtual reference. That is, the need of a reference is bypassed by simultaneously estimating all , thus achieving reference-free multiple alignment. Different from Stage 1, here each DTW graph is constructed between each sample and the virtual reference. Note that the cost of DTW graph edges in this stage has nothing to do with sample profile intensity, so ncGTW does not need a ‘real’ reference but a virtual one as a coordinate. The DTW graphs are ‘fully’ connected in the way that additional edges link all corresponding points of (Fig. 4e, green edges), where the cost of these connecting edges reflecting the distance between the corresponding warping points with respect to virtual reference. Furthermore, ncGTW considers the biological preference of the alignment function to avoid exaggerated distortions of the profiles with unnecessary distortion (expansion and shrink) as well as location shift. Roughly speaking, we hope that after multiple alignment, the information contained in original profiles should not be lost. An example is the so called all-to-one matching (all vertical/horizontal paths), where all the points on a sample align to only one point on the reference, so no information is kept. Thus, a fixed cost is applied to only vertical/horizontal but not diagonal paths in the DTW graphs of , encouraging warping functions with diagonal paths; a completely diagonal warping function means the profile is the same as the original one after alignment. Specifically, ncGTW estimates the final warping functions to virtual reference on all samples jointly by minimizing the cost function given by:
| (7) |
where is the cost measuring the deviation of warping function from diagonal path (one-to-one mapping), is a hyperparameter and is the cost measuring the inconsistency between and given the pairwise warping function (the corresponding points in are aligned to different points on virtual reference c). Likewise, here is the cost of the additional edges, which is for balancing the non-diagonal cost term and the inconsistency term. Overall, the cost function encodes our goal to find the warping functions which are (i) biologically meaningful (without unwanted distortion/displacement, e.g. all to one mapping) and (ii) consistent with pairwise warping functions from Stage 1. Again, all are efficiently obtained by solving an equivalent maximum flow problem and thus the multiple alignment problem (Supplementary information).
Hyperparameters and can be any positive real number. However, we observed that values of or within a certain range may give the same alignment result. That is, they may give the same alignment result as a line segment of the step function. For example, the line segments associated with various and combinations correspond to one of the alignment results (Supplementary information). While the number of total line segments is often unknown, these segments are theoretically searchable. Thus, we iteratively find representative values of and ; in each iteration, a call of ncGTW will be performed to obtain a new value between each neighboring pair of given values. After we search sufficient number of values, a representative value will be found for each line segment and we can pick up the pair of and with the best warping functions .
Practically, the starting and ending points of the first and last segments about and can be found first, and then different values for and can be searched and located where their values are scanned roughly uniformly along line segments. Our experimental result on both Rotterdam and MESA cohorts shows that the alignment performance is highly satisfactory when three values for and one value for are examined on both iQC and study sample data sets. Accordingly, we scan three values for and one value for for each data set as the default setting in our software package. Furthermore, the package allows users to change the search setting on various combinations of and when desirable.
Based on all peak positions within a feature (peak group) after ncGTW realignment with various combinations of and , the best combination of hyperparameter values can be decided. Specifically, the maximum number (K) of all peaks is first determined from the calculated peak numbers across samples, using the relevant information readily provided by XCMS; the peaks are then grouped into K clusters via k-means clustering. If all peaks are well-aligned, the apex RT range in each peak cluster should be small. Accordingly, the optimum hyperparameter values are chosen corresponding to the minimum of the summed RT ranges over all clusters.
2.6 Correction of potential peak distortion
Peak distortion is a potential problem associated with DTW-based alignment, that is, while warping functions are optimally estimated by network flow algorithm, the shape of peaks may be altered. In other words, DTW-based methods do not guarantee one-to-one mapping for the points in the peak area (may be many-to-one or one-to-many), so the peak may become broader or narrower with shape changing. The reason is that DTW-based methods are trying to map the points with similar intensity. When aligning peaks with different shapes, the peak in the sample may be distorted to fit the shape of the peak in the reference. The requirement of maintaining the shape of peaks cannot be easily incorporated into the cost functions of existing methods and ncGTW alike. Therefore, while warping functions are optimally estimated, the shape of peaks may still be altered. To avoid such distortion, based on multiple alignment of all samples, we first extract the information of each peak from XCMS. Within the starting and ending points of each peak, only the apex point will be aligned by the warping function , and the rest of the points are simply shifted by the same amount as the apex. In other words, the whole peak area will be aligned together with shifting the same amount, so the shape of the peak will be the same after alignment. For the samples with peaks undetected by XCMS, we borrow information from samples with detected peaks. The apices on virtual reference aggregated by samples with no missing peaks are first identified, and then a representative peak can be constructed from them. The apex of the representative peak is the median of the locations of the detected apices, and the width is the median of the detected peak widths. The range and apex location of the representative peak is mapped back to each sample with undetected peaks by reversely applying the warping function. Thus, the samples with undetected peaks will be finally aligned without peak distortion. An illustrative experimental result is given in Figure 6(c–d) using the MESA dataset, demonstrating the improved alignment by ncGTW where distorted peaks are effectively corrected.
Fig. 6.
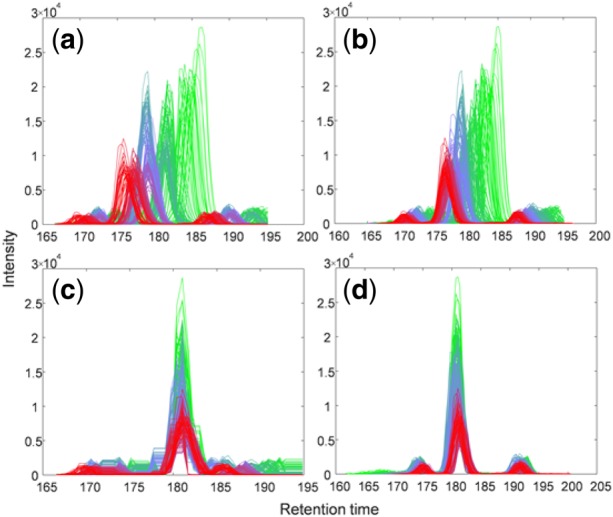
An illustrative experimental result on realignment and peak-distortion correction by ncGTW, where a feature from the MESA dataset was initially misaligned by XCMS. The color mapping (green to blue and blue to red) corresponds to the sample index. (a) Raw LC-MS data associated with the feature of interest (before alignment). (b) The misaligned feature by XCMS that has been correctly detected and reported by the misalignment detection module of ncGTW package. (c) Realignment by ncGTW where apices are well aligned but with observable peak shape distortion. (d) Peak shape distortion is efficiently corrected by the post-processing module of ncGTW package. (Color version of this figure is available at Bioinformatics online.)
2.7 Implementation of ncGTW on a large dataset
For a large dataset, it is very time-consuming to simultaneously align all the samples for a profile-based alignment method. When the sample number is large, the ncGTW graph becomes extremely huge, and it may take hours or even days to solve the maximal flow problem. Thus, in the practical implementation, ncGTW splits the whole dataset into several sub-datasets, and performs alignment on each small dataset. In this way, the numbers of nodes and edges in the graph for each small dataset will decrease significantly comparing with the original graph. Also, since these small datasets are aligned independently, the computation time can be further reduced with parallel computing. After the alignment of each small dataset, we build a ‘super-sample’ for each small dataset. Then, align these super-samples to obtain the warping functions of super-samples. With the warping functions within each small dataset and of the super-samples, we can obtain the final warping functions for each sample. We called this hierarchical alignment process as ‘two-layer ncGTW’. The details about two-layer ncGTW are in Supplementary information.
2.8 Integration of ncGTW into XCMS
The ncGTW R package is developed currently as a complementary plug-in to XCMS tool. The unique features of ncGTW algorithm include misalignment detection, individualized warping function (over m/z bins), incorporation of structural information (run order), reference-free multiple alignment and correction of peak distortion. The functional integration of ncGTW into XCMS also allows ‘iteration’ (or ‘interaction’) between ncGTW and XCMS. For example, information about misaligned features obtained by ncGTW may be used to guide parameter retuning in XCMS. Then, those misaligned features may be realigned by ncGTW and regrouped by XCMS. Moreover, using the correct locations of missing peaks specified by ncGTW warping functions, those missing peaks may be accurately retrieved by the peak-filling procedure in XCMS. The workflow of XCMS-ncGTW pipeline is given in Figure 7.
Fig. 7.
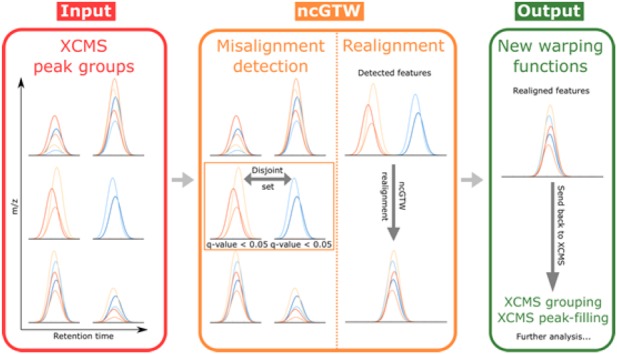
Workflow of ncGTW. As a plug-in to XCMS, ncGTW uses the grouping results provided by XCMS as the inputs (one lower resolution and one higher resolution, as explained in Fig. 2). Then, ncGTW detects all misaligned features using the aforementioned criteria and performs realignment on these features. Lastly, ncGTW calculates final warping functions for each sample that can be sent back to XCMS for re-grouping or peak-filling
3 Results
3.1 Validation of ncGTW multiple alignment using simulated datasets
To test whether our ncGTW can improve multiple alignments by incorporating structural information of various forms, we assess alignment accuracy via realistic simulation studies (Supplementary information). Because the graph representation of structural information about neighboring samples is a unique feature of ncGTW, we consider three different structures including line (samples are profiled continuously), block (samples are profiled in batches) and uniform (no information on how samples are profiled) (Supplementary information), in a set of experiments with 10 simulated samples. Three representative peer methods are selected for comparison including DTW Barycenter Averaging (DBA) (Petitjean et al., 2011), Continuous Profile Model (CPM) (Listgarten et al., 2005) and GTW (Wang et al., 2016). Specifically, DBA iteratively computes the barycenter of each aligned points set to give an average sample as a reference; CPM uses classic hidden Markov model to learn a prototype function for alignment. Since GTW needs a reference, each sample is set as a reference and takes the average of scores in multiple alignments.
In addition to visual inspection, we use two benchmark quantitative measures to assess alignment accuracy, including mean correlation coefficient (MCC) and simplicity (SP; Jiang et al., 2013). MCC is averaged over all aligned sample pairs, and SP is the normalized sum of fourth power over all singular values on data matrix (Supplementary information).
The experimental results are presented in Supplementary information in detail and briefly summarized here. When there are missing peaks in some samples, DBA often misaligns some peaks, independent of specific neighborhood structure. When a selected reference contains missing peaks, GTW often produces many misalignments. CPM performs relatively better than DBA and GTW, while it misaligns several peak groups with block structure of large drift. The proposed ncGTW approach consistently outperforms all three peer methods by aligning all the peaks with the highest scores in all accuracy measures and structures. Table 1 gives the average performance scores of simulation studies.
Table 1.
The average performance scores obtained in the simulation studies with line, block and uniform structure, where ‘Before alignment’ serves as the baseline, MCC and SP represent MCC and SP, respectively, and the range of either score is between 0 and 1 with higher score indicating better performance
| Methods | Scores |
|
|---|---|---|
| MCC | SP | |
| Line structure | ||
| Before alignment | 0.2330 | 0.4202 |
| DBA | 0.5422 | 0.6737 |
| CPM | 0.7894 | 0.8981 |
| GTW | 0.7991 | 0.9592 |
| ncGTW | 0.8366 | 0.9999 |
| Block structure | ||
| Before alignment | 0.1062 | 0.1959 |
| DBA | 0.7767 | 0.8761 |
| CPM | 0.3773 | 0.5078 |
| GTW | 0.8687 | 0.9521 |
| ncGTW | 0.9159 | 0.9998 |
| Uniform structure | ||
| Before alignment | 0.0641 | 0.2341 |
| DBA | 0.3797 | 0.7649 |
| CPM | 0.5651 | 0.8867 |
| GTW | 0.4926 | 0.8447 |
| ncGTW | 0.6953 | 0.9990 |
Note: The best score for each structure is represented in bold.
3.2 Initial test of ncGTW multiple alignment on small-scale real LC-MS dataset
We further conduct similar comparison studies on small-scale real LC-MS datasets of 10 samples (acquired from samples of the MESA cohort) involving line, block and uniform structures. Because no ground truth on correct alignment is available, we opt for visual inspection to assess relative performance. The experimental results are highly consistent with what is observed in simulation studies. DBA and GTW easily misaligned samples with some missing peaks, and CPM failed again on either block structure or samples with significant peak intensity imbalance. In contrast, ncGTW aligned all peaks nicely and consistently under different neighborhood structures. The alignment results are shown in Figure 8 (with line structure), and additional experimental results using other neighboring structures are given in Supplementary information.
Fig. 8.
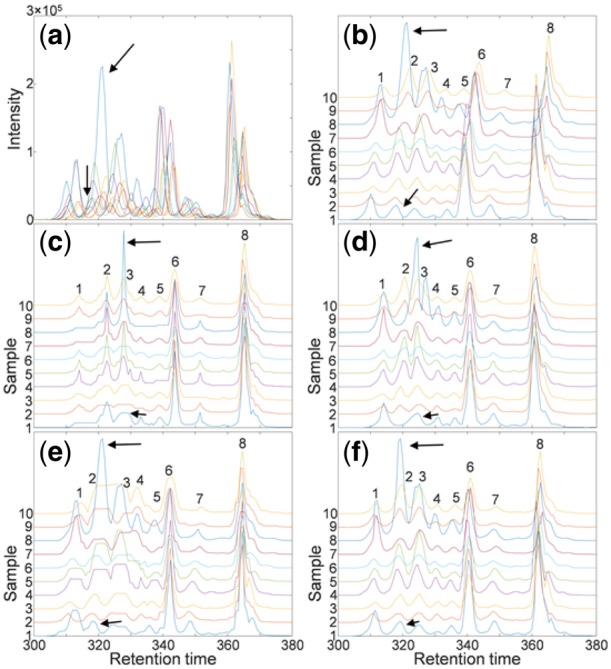
Illustrative realignment successfully performed by ncGTW incorporating ‘line’ structure in small-scale real LC-MS dataset. (a) LC-MS profiles of total ten samples. (b) The same LC-MS profiles but the curves are shifted to separate the curves. The 8 indexed peaks on sample 10 represent there are 8 peak groups. The peaks indicated by arrows in group 2 were misaligned by most peer methods except GTW and ncGTW. (c) The arrow-indicated peaks were wrongly aligned to the third peak group (and all peaks were severely distorted by DBA). (d) The arrow-indicated peaks were misaligned by CPM. (e) The arrow-indicated peaks were well-aligned by GTW while the fourth and fifth peak groups were misaligned. (f) All nine peak groups were correctly and accurately aligned by ncGTW in this challenging case
3.3 Detection of misaligned features
Application of XCMS to the Rotterdam iQC samples alone generates total 1872 features, among which 57 features are detected as potentially misaligned by the misalignment detection module in ncGTW package. With a closer visual inspection (performed independently by two MS experts), 41 features are confirmed as misaligned (true positives, Fig. 6b as an example) and 16 remaining features are considered well-aligned (false positives, see Supplementary Figure S13 as an example). On Rotterdam study samples (excluding iQC samples), XCMS generates total 1689 features, of which 45 features are detected as misaligned. Visual screening identifies 32 true positives and 13 false positives. On MESA iQC samples alone, XCMS generates total 1951 features, of which 61 features are detected as misaligned. Visual inspection identifies 58 true positives and 3 false positives. On MESA study samples (excluding iQC samples), XCMS generates total 1861 features, of which 49 features are detected as misaligned. Visual screening identifies 48 true positives and 1 false positive. All the P-value thresholds of the misalignment detection here are set as 0.05. For the results of different threshold, please refer to Supplementary information. While the false discovery rate is higher than theoretically expected, these false positives are mainly due to signal intensity fluctuation and will be eliminated in a post-realignment step.
3.4 Realignment by ncGTW
We apply the ncGTW tool to realign the features flagged as misaligned in the previous step. While we have applied ncGTW to all study samples to show the scalability, our reports are focused on the results only on iQC samples mainly attributed to the feasibility of performing quantitative assessment. The evaluation criteria are the average pairwise correlation coefficient (Jiang et al., 2013) and the average pairwise total overlapping area (Christin et al., 2008). We use these two benchmark quantitative measures to assess the comparative performances by ncGTW and XCMS.
Comparative experimental results are detailed using two performance measures (Fig. 9), where the features with circles represent true positives and the features with crosses represent the false positives. These comparative experimental results, on both Rotterdam and MESA datasets, consistently show that ncGTW effectively and accurately realigns those misaligned features. Specifically, ncGTW realignment on most true positives achieves much higher performance scores than that of XCMS, and on most false positives, produces comparable performance scores as expected (near the diagonal lines, Fig. 9). Note that the default parameter setting of ncGTW in this step is purposely designed for the true positives, and probably not suitable for the false positives.
Fig. 9.
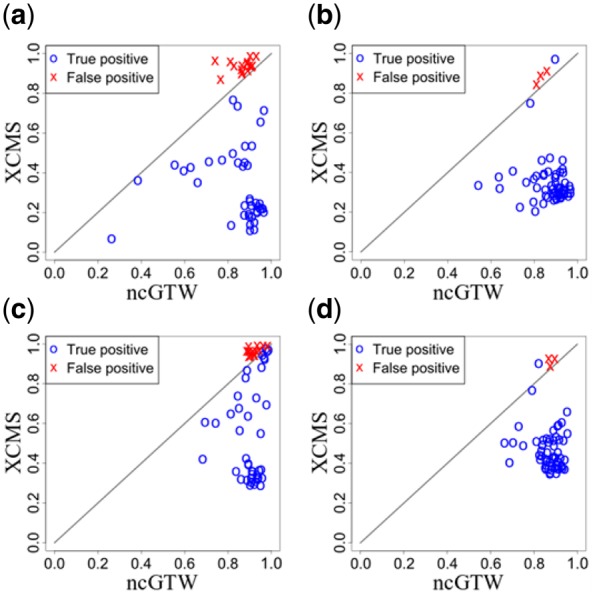
Application of ncGTW realignment method to Rotterdam and MESA datasets, where among the detected misaligned features, the blue circles represent true positives, and the red crosses represent false positives, respectively. (a) The average pairwise correlation coefficients on the Rotterdam dataset. (b) The average pairwise correlation coefficients on the MESA dataset. (c) The average pairwise total overlapping area on the Rotterdam dataset. (d) The average pairwise overlapping area on the MESA dataset. (Color version of this figure is available at Bioinformatics online.)
Experimental results on iQC samples also show that the two performance scores can well separate the true positives and false positives (Fig. 9). Accordingly, via a post-alignment step we use these two performance scores to screen out true positives for further analysis. This strategy is also applicable to handling study samples.
3.5 Evaluation of ncGTW via post-realignment peak-filling performance
Accurate alignment of RT drift has significant impact on the performance of peak-grouping and peak-filling that define the features. In the XCMS pipeline, detected peaks are first grouped into features, and when there are undetected/missing peaks, peak-filling is then performed to retrieve those peaks. In our experiments, the coefficient of variation (CV) of intensity calculated over the samples, with and without ncGTW guided peak-filling, is adopted to assess the beneficial impact of ncGTW realignment (Matuszewski et al., 1998).
Though we proposed that we can screen out the false positives by the two performance scores, we still include the false positives in the peak-filling step to observe the impact of the realignment on them. Post-realignment peak-filling results show that, measured by CV over the iQC sample features, ncGTW realignment consistently reduces the CV as compared with that derived from the initial XCMS alignment in both Rotterdam and MESA datasets (Fig. 10). Note that here again the circles represent the true positives and the crosses represent the false positives. More importantly, post-realignment peak-filling supported by ncGTW has led to the significantly reduction of CV on many ‘hard-to-define’ features, demonstrating the beneficial contribution of ncGTW realignment to improved feature generation.
Fig. 10.
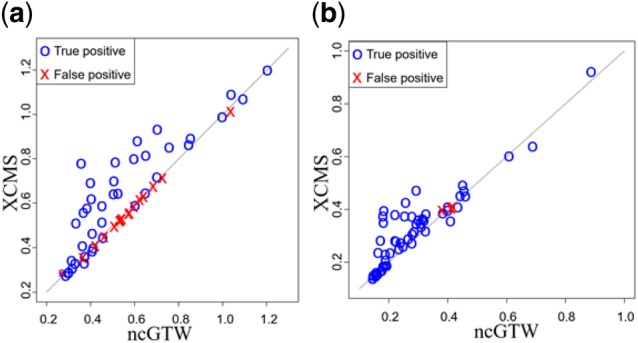
The comparisons of CV with versus without ncGTW realignment after the peak-filling step of XCMS. The blue circles represent the true positives and the red crosses represent the false positives. (a) The CV comparison on Rotterdam dataset. (b) The CV comparison on MESA dataset. (Color version of this figure is available at Bioinformatics online.)
3.6 Biological or clinical importance of the detected misaligned features
When significant misalignment occurs, it is possible that some peaks will be incorrectly assigned to the wrong compound and the information from those peaks comingled with other compounds. In addition, in samples where a peak has been improperly aligned and therefore misclassified, the true compound of interest may appear to be completely absent. These errors may obscure important information about molecular pathways and lead to biased inferences or corrupt statistical analyses concerning relationships between specific compounds and other traits associated with the samples. In Table 2, we provided the detailed annotation for the five features associated with underlying compounds that were initially misaligned in MESA and Rotterdam datasets and later corrected by ncGTW (measured by the reduction in CV values). For the whole list of annotation, please refer to Supplementary Table S9. Indeed, each of these compounds plays important roles in specific and clinically relevant metabolic pathways. For instance, α-tocopherol-glucuronide is a conjugation metabolite of the biological anti-oxidant α-tocopherol (vitamin E); ganglioside GM3 is a phospholipid found predominantly in cell surfaces, and this molecule has important role in cell-to-cell recognition (Lopez and Schnaar, 2009). Phosphatidylinositol is a glycerophospholipid and an important component of cell membranes, found predominantly in the inner surface of the cell membranes (Van Meer et al., 2008); Choline is an important precursor of phosphatidylcholine and sphingomyelin phospholipids, and also the precursor of the neurotransmitter acetylcholine and participates as methyl group donor in several biochemical reactions (Parrish et al., 2008); Lysophosphatidylinositol is a metabolite of phosphatidylinositol resulting from the cleavage of one the two fatty acyl chains by the action of a phospholipase-type A enzyme (Ueda et al., 1993). Given the important biological roles of these compounds, potential misclassification or corruption of the signals concerning these metabolites, due to misalignment, could seriously hinder the ability to understand important aspects of disease biology.
Table 2.
Annotation details on the representative features that are associated with biologically important compounds with their m/z and RT positions, where the improvements in the targeted ncGTW realignment are quantitatively measured by the reduction in CV values
| Dataset | m/z | RT | Metabolite annotation | CV XCMS | CV ncGTW |
|---|---|---|---|---|---|
| MESA | 629.4 | 184.9 | α-Tocopherol-glucuronide | 0.29 | 0.25 |
| MESA | 844.6 | 275.6 | Ganglioside GM3 | 0.39 | 0.29 |
| MESA | 879.5 | 293.8 | Phosphatidylinositol | 0.39 | 0.19 |
| Rotterdam | 104.1 | 24.2 | Choline | 0.66 | 0.51 |
| Rotterdam | 342.3 | 111.5 | Lysophosphatidylinositol | 0.71 | 0.41 |
4 Discussion
Feature-based and profile-based alignment methods are complementary to each other. Because of high efficiency on large datasets, the majority of existing alignment methods are feature-based. However, due to the challenging nature of accurate peak detection particularly, when there are some missing peaks and significant RT drift, misalignment occurs on some features that also causes incorrect peak-grouping and/or peak-filling. Here, we develop the ncGTW method to first detect misaligned features and then to realigned them. One unique advantage of ncGTW is the incorporation of structural information (i.e. run-order) in our multiple alignment method. To the best of our knowledge, most existing alignment methods have overlooked structural information related to experimental design and batch duration. Moreover, the novel design of a reference-free multiple alignment strategy and utility of individualized warping functions across m/z bins all contributed to produce superior performance of ncGTW.
Our approach is built on GTW, a recent extension of DTW to multiple pairs. GTW retains all the desirable properties of DTW such as monotonicity of time shifts and polynomial efficient solution, and yet flexibly models any graph-encoded structure among pairs. However, GTW cannot be directly applied to solve the multiple alignment problems. GTW takes multiple pairs of samples as input and finds alignment for each pair with consistency between pairs considered. The problem considered in this article takes multiple samples as input and aims to find consistent alignment among all samples. Though we can manually specify one certain sample as a reference to construct pairs of samples for input of GTW, to our knowledge, there is no established method that can always help the user to identify which sample is the most suitable one as the reference. Moreover, it is likely that none of the samples contains enough information to serve as a good reference. Thus, ncGTW is a significant improvement of GTW, since ncGTW can model all samples simultaneously and deal with the multiple alignment problems without manually setting a reference.
Currently, there is no consensus method to detect misalignment other than simple visual inspection. Thus, misalignment is often undetected and therefore may not even benefit from the application of (substandard) conventional alignment methods. Specifically designed to address the problem of misalignments complementary to existing alignment software tools, our proposed ncGTW method focuses on correcting only those misaligned features. Toward this objective with high efficiency, the ncGTW package includes a unique functional module that specifically aims to detect misaligned features. We validated ncGTW using both realistic synthetic data and iQC samples. The performance of ncGTW is particularly attractive when processing large-scale datasets consisting of hundreds or thousands of samples, because the RT drifts between distant samples may be significant and warping functions over different m/z bins are not guaranteed to be the same (Fig. 1). Explicit incorporation of the RT structural information by the ncGTW method helps to achieve accurate realignments on misaligned features. While we have only demonstrated ncGTW as a plug-in package to XCMS, in fact, two major functions of the ncGTW tool can serve as a plug-in jointly or independently to other alignment tools as well, and thus have broad applicability, including to other spectral data types beyond LC-MS.
Regarding the peak-distortion problem associated with warping functions, there are at least two potentially effective solutions. First, the peak information provided by XCMS can be utilized by ncGTW to correct peak distortion as discussed in Section 2.6. Second, parameter settings in ncGTW can be adjusted or optimized to reduce the likelihood of peak distortion. Note that the current ncGTW tool package already includes a peak-distortion correction module, and our experiments have also shown that interim peak-distortion correction can help optimize ncGTW parameter settings that will in turn reduce the likelihood of peak distortion.
In our misalignment detection step in Section 3.3, we have observed that the false-positive rate in the Rotterdam dataset is much higher than the theoretical threshold of 0.05. By a closer look at the peak detection results, we found that many peaks were actually missed by XCMS, mainly due to significant yet irregular signal intensity fluctuating over the course of data acquisition as shown in Supplementary Figure S13 with all samples. Considering such relatively higher false-positive rate does not create significant computational burden on ncGTW yet may be uncontrollable, we have opted to first ‘accept’ these false positives and then screen them out at a later stage.
Supplementary Material
Acknowledgement
We thank the anonymous reviewers for their helpful suggestions.
Funding
This work was funded in part by the National Institutes of Health under Grants HL111362-05A1 and HL133932.
Conflict of Interest: none declared.
References
- Arnold B.C. et al. (1992) A First Course in Order Statistics. Siam, Philadelphia, PA. [Google Scholar]
- Benk A.S., Roesli C. (2012) Label-free quantification using MALDI mass spectrometry: considerations and perspectives. Anal. Bioanal. Chem., 404, 1039–1056. [DOI] [PubMed] [Google Scholar]
- Bild D.E. et al. (2002) Multi-ethnic study of atherosclerosis: objectives and design. Am. J. Epidemiol., 156, 871–881. [DOI] [PubMed] [Google Scholar]
- Christin C. et al. (2008) Optimized time alignment algorithm for LC−MS data: correlation optimized warping using component detection algorithm-selected mass chromatograms. Anal. Chem., 80, 7012–7021. [DOI] [PubMed] [Google Scholar]
- Goldberg A.V. et al. (2011) Maximum flows by incremental breadth-first search In: European Symposium on Algorithms. Springer, Berlin, Heidelberg, pp. 457–468. [Google Scholar]
- Hofman A. et al. (2013) The Rotterdam Study: 2014 objectives and design update. Eur. J. Epidemiol., 28, 889–926. [DOI] [PubMed] [Google Scholar]
- Jiang W. et al. (2013) Comparisons of five algorithms for chromatogram alignment. Chromatographia, 76, 1067–1078. [Google Scholar]
- Lewis M.R. et al. (2016) Development and application of ultra-performance liquid chromatography-TOF MS for precision large scale urinary metabolic phenotyping. Anal. Chem., 88, 9004–9013. [DOI] [PubMed] [Google Scholar]
- Listgarten J. et al. (2005) Multiple alignment of continuous time series. Adv. Neural Inf. Process. Syst., 17, 817–824. [Google Scholar]
- Lopez P.H., Schnaar R.L. (2009) Gangliosides in cell recognition and membrane protein regulation. Curr. Opin. Struct. Biol., 19, 549–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu W. et al. (2008a) Analytical strategies for LC-MS-based targeted metabolomics. J. Chromatogr. B Analyt. Technol. Biomed. Life Sci., 871, 236–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu X. et al. (2008b) LC-MS-based metabonomics analysis. J. Chromatogr. B Analyt. Technol. Biomed. Life Sci., 866, 64–76. [DOI] [PubMed] [Google Scholar]
- Matuszewski B. et al. (1998) Matrix effect in quantitative LC/MS/MS analyses of biological fluids: a method for determination of finasteride in human plasma at picogram per milliliter concentrations. Anal. Chem., 70, 882–889. [DOI] [PubMed] [Google Scholar]
- Mueller L.N. et al. (2007) SuperHirn—a novel tool for high resolution LC-MS-based peptide/protein profiling. Proteomics, 7, 3470–3480. [DOI] [PubMed] [Google Scholar]
- Palmblad M. et al. (2007) Chromatographic alignment of LC-MS and LC-MS/MS datasets by genetic algorithm feature extraction. J. Am. Soc. Mass Spectrom., 18, 1835–1843. [DOI] [PubMed] [Google Scholar]
- Parrish W.R. et al. (2008) Modulation of TNF release by choline requires α7 subunit nicotinic acetylcholine receptor-mediated signaling. Mol. Med., 14, 567–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petitjean F. et al. (2011) A global averaging method for dynamic time warping, with applications to clustering. Patt. Recogn., 44, 678–693. [Google Scholar]
- Prakash A. et al. (2006) Signal maps for mass spectrometry-based comparative proteomics. Mol. Cell Proteomics, 5, 423–432. [DOI] [PubMed] [Google Scholar]
- Prince J.T., Marcotte E.M. (2006) Chromatographic alignment of ESI-LC-MS proteomics data sets by ordered bijective interpolated warping. Anal. Chem., 78, 6140–6152. [DOI] [PubMed] [Google Scholar]
- Sakoe H. and Chibe,S. (1978) Dynamic programming algorithm optimization for spoken word recognition IEEE Trans. Acoust. Speech Signal Process., 26, 43–49. [Google Scholar]
- Sarafian M.H. et al. (2014) Objective set of criteria for optimization of sample preparation procedures for ultra-high throughput untargeted blood plasma lipid profiling by ultra performance liquid Chromatography–Mass spectrometry. Anal. Chem., 86, 5766–5774. [DOI] [PubMed] [Google Scholar]
- Smith C.A. et al. (2006) XCMS: processing mass spectrometry data for metabolite profiling using nonlinear peak alignment, matching, and identification. Anal. Chem., 78, 779–787. [DOI] [PubMed] [Google Scholar]
- Smith R. et al. (2015) LC-MS alignment in theory and practice: a comprehensive algorithmic review. Brief Bioinform., 16, 104–117. [DOI] [PubMed] [Google Scholar]
- Tengstrand E. et al. (2014) TracMass 2—a modular suite of tools for processing chromatography-full scan mass spectrometry data. Anal. Chem., 86, 3435–3442. [DOI] [PubMed] [Google Scholar]
- Theodoridis G. et al. (2008) LC-MS-based methodology for global metabolite profiling in metabonomics/metabolomics. Trends Analyt. Chem., 27, 251–260. [Google Scholar]
- Ueda H. et al. (1993) A possible pathway of phosphoinositide metabolism through EDTA-insensitive phospholipase A1 followed by lysophosphoinositide-specific phospholipase C in rat brain. J. Neurochem., 61, 1874–1881. [DOI] [PubMed] [Google Scholar]
- Van Meer G. et al. (2008) Membrane lipids: where they are and how they behave. Nat. Rev. Mol. Cell Biol., 9, 112–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinaixa M. et al. (2012) A guideline to univariate statistical analysis for LC/MS-based untargeted metabolomics-derived data. Metabolites, 2, 775–795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y. et al. (2016) Graphical time warping for joint alignment of multiple curves. Adv. Neural Inf. Process. Syst., 29, 3648–3656. [Google Scholar]
- Zhang X. et al. (2005) Data pre-processing in liquid chromatography-mass spectrometry-based proteomics. Bioinformatics, 21, 4054–4059. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.