PARC: ultrafast and accurate clustering of phenotypic data of millions of single cells

Abstract

Motivation

New single-cell technologies continue to fuel the explosive growth in the scale of heterogeneous single-cell data. However, existing computational methods are inadequately scalable to large datasets and therefore cannot uncover the complex cellular heterogeneity.

Results

We introduce a highly scalable graph-based clustering algorithm PARC—Phenotyping by Accelerated Refined Community-partitioning—for large-scale, high-dimensional single-cell data (>1 million cells). Using large single-cell flow and mass cytometry, RNA-seq and imaging-based biophysical data, we demonstrate that PARC consistently outperforms state-of-the-art clustering algorithms without subsampling of cells, including Phenograph, FlowSOM and Flock, in terms of both speed and ability to robustly detect rare cell populations. For example, PARC can cluster a single-cell dataset of 1.1 million cells within 13 min, compared with >2 h for the next fastest graph-clustering algorithm. Our work presents a scalable algorithm to cope with increasingly large-scale single-cell analysis.

Availability and implementation

https://github.com/ShobiStassen/PARC.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Rapid development in single-cell technologies, notably flow, mass and high-content imaging cytometry, as well as single-cell RNA-sequencing, has revolutionized approaches to measure cellular characteristics, from gene and protein expression to biophysical and morphological phenotypes, at single-cell precision. These advances will help define the diversity of cell types, states and functions and also understand how the phenotypic variability within a heterogeneous population of cells plays a role in tissue development, health and disease.

In recent years, both the depth and the throughput of single-cell measurement have drastically increased, triggering an explosive growth of large-scale single-cell data. Flow cytometry traditionally offers high-throughput measurements (∼10 000–100 000 cells/s) and typically has ∼10 features (cell-surface markers and intracellular proteins). Integrated with high-speed imaging techniques, imaging flow cytometry can now generate a wealth of information at high-throughput given by high-resolution single-cell image-derived phenotypes (Blasi et al., 2016; Caicedo et al., 2017; Lee et al., 2019b). Mass cytometry by time of flight (CyTOF) offers single-cell measurements of millions of cells, with detection of 40 or more proteins for a given experiment (Spitzer and Nolan, 2016), albeit at a lower throughput compared with flow cytometry. Another parallel advance is single-cell RNA-sequencing (scRNA-seq) where droplet-based systems sequence hundreds of cells per second. An example of a large-scale scRNA-seq experiment is the recent ‘Mega-Cell Demonstration’ by 10× Genomics (10× Genomics Datasets, 2017) which features 1.3 million E18 mouse brain cells.

Although the single-cell measurement scale and throughput continue to grow at a staggering rate, such technological advance has outstripped the existing computational capability to handle, process and analyze the resulting heterogeneous single-cell data. New solutions to fill the computational gap will address the sizeable single-cell data backlog and accelerate biological discoveries. Among all computation tasks, unsupervised clustering plays a decisive role in facilitating downstream biological interpretation in single-cell analysis. However, existing methods lack the scalability and data-driven capability required for parsing large and heterogeneous data and thus cannot identify putative cell types in an efficient manner.

Most tools developed for gene expression data become computationally prohibitive when the cell count reaches 10⁵–10⁶ cells. For example, to handle a scRNA-seq dataset of only 6000 cells (of 1572 genes), the popular SC3 and RaceID algorithms take ∼5.6 h, whereas CIDR takes 18 min (Duò et al., 2018). Even Seurat, which is fast on smaller datasets, takes over 1.5 h on a 68 K scRNA-seq dataset of 1000 genes [when bypassing preliminary principal component analysis (PCA)] and often runs into memory allocation errors. In order to digest larger batches of data, the common strategy is to rely on subsampling, which often overlooks rare cell types (e.g. SPADE; Qiu et al., 2011). A handful of other algorithms (that are not specific to transcriptomic data) can operate on larger datasets, for example, FlowSOM (Van Gassen et al., 2015), K-Means and FlowMeans (Aghaeepour et al., 2011). However, they often rely on manual parameter tuning or invoke a number of clusters in advance, which in turn poses challenges to perform unbiased exploration of the unknown complex cellular heterogeneity. In the scenario where it is feasible to perform analysis for a range of predetermined number of clusters and select the result based on the internal clustering evaluation criteria (e.g. Silhouette Index), it is not uncommon that the ‘elbow point’ is a poor reflection of the true underlying structure in the data. A recent benchmarking study of 12 clustering methods on smaller scRNA-seq datasets (Duò et al., 2018) showed that generally no method achieved its best performance at the annotated number of clusters. For instance, in its automated mode, where cluster selection is based on the elbow point of within-cluster-variance, FlowSOM underestimates the number of clusters (as does FlowPeaks; Ge and Sealfon, 2012), typically requiring a ‘generous’ cluster estimate in order to capture annotated populations (Weber and Robinson, 2016).

In light of these challenges, we present PARC—Phenotyping by Accelerated Refined Community-partitioning—a fast, automated, combinatorial graph-based clustering approach that integrates hierarchical graph construction and data-driven graph-pruning with a community-detection algorithm. PARC (i) outperforms existing tools in scalability, without resorting to subsampling of large-scale, high-dimensional single-cell data (>1 million cells); (ii) accelerates the clustering computation by an order of magnitude through automated community-partitioning refinement guided by the data structure itself and (iii) augments the sensitivity and specificity to unbiasedly reveal the cellular heterogeneity, especially rare subsets within large populations.

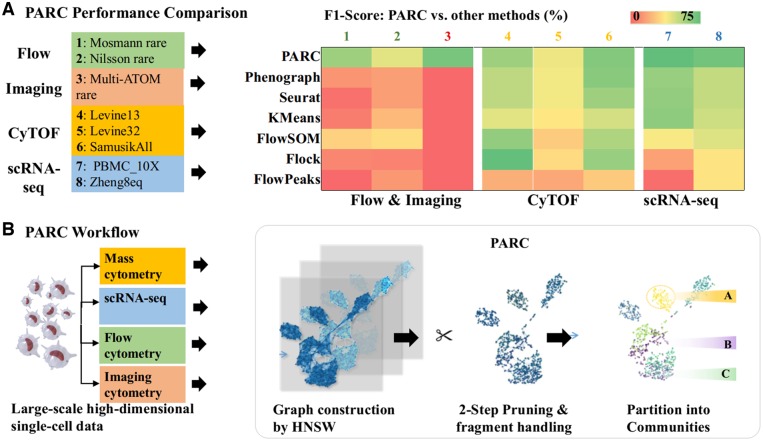
We validate the performance of PARC on large-scale datasets, with respect to speed and accuracy, as well as versatility across a wide range of single-cell data including: mass and flow cytometry, scRNA-seq and imaging cytometry (Fig. 1a and Supplementary Fig. S1). Notably, we demonstrate that PARC can detect subpopulations that were not labeled in the original scRNA-seq datasets of 68 000 peripheral blood mononuclear cells (PBMCs). It also enables data-driven clustering of the entire mouse brain dataset of 1.3 million cells without any downsampling. As a proof of concept, we showcase that PARC correctly infers cell type on a mega-set of multiple lung cancer cell lines (>1 million cells) on the basis of their biophysical attributes derived from multicontrast label-free single-cell images (Lee et al., 2019a, b).

Fig. 1.

(a) Summary of the clustering performance of PARC and other competitive clustering methods on various single-cell datasets, including flow cytometry, mass cytometry (CyTOF), imaging cytometry, and scRNA-seq data. (b) Overview of PARC workflow for large-scale single-cell analysis on multiple types of high-dimensional single-cell data. The enabling features include fast graph construction by HNSW, 2-step data-driven graph refinement and pruning, and accelerated community detection by Leiden algorithm.

2 Materials and methods

PARC employs three major steps to enable scalable and data-driven clustering of single-cell data (Fig. 1b). The first step is an accelerated nearest-neighbor graph construction using hierarchical navigable small world (HNSW) (Malkov and Yashunin, 2016), in which each node is a single cell connected to a neighborhood of its similar cells by a group of edges. The second step is the data-driven pruning of the edges based on the distribution of edge-weights at both the local node-by-node level and the global network level. The last step is a community detection based on Leiden algorithm (Traag et al., 2011) that can efficiently handle singletons (clusters containing one data point) resulting from the pruning. These steps are integrated in such a way that PARCs performance is not determined by each individual step, but the feedback between them. Notably, the pruning procedure in PARC, which reduces the sample size of edges and improves the K-NN graph representation of the underlying data, critically increases the speed and robustness of the subsequent community-detection step. We find that this is particularly advantageous in detecting rare but distinct populations. In Sections 2.1–2.3, we will describe in detail the three modules and their integration.

2.1 HNSW for fast and scalable K-NN search

In the first step, PARC constructs the K-NN graph using HNSW, which offers logarithmic complexity scaling (Malkov and Yashunin, 2016). A small world graph is characterized by long links which bridge different clusters and shorter links which represent inter-cluster connectivity. The HNSW method differs from other navigable small world methods by binning links in hierarchy (i.e. layers) according to their lengths. The search starts at the top layer containing the longest links and traverses the elements until a local minimum is reached. The search then goes to the lower layer (i.e. the layer having shorter links) from the node where the most recent local minimum was detected. Such hierarchical graph structure allows fast graph construction with logarithmic scalability, that is, the construction scales as O(NlogN), whereas each query takes O(logN) time (Malkov and Yashunin, 2016). We note that some tools (e.g. X-Shift Samusik et al., 2016) employ exact neighbor searches whose slightly improved accuracy cannot be justified by their computational overload. Several others incorporate approximate neighbor searches that become time intensive on large-scale data (e.g. Phenograph’s use of Python library Sklearn’s ‘kdtree’ and SCANPY’s UMAP-based neighbor search) (McInnes et al., 2018).

2.2 Graph pruning for effective capture of network structure

The linkages in the K-NN graph impact the clusters found in the modularity optimization algorithm, applied in the third step of PARC, that is, community detection. One common strategy relies on a manually tuned user-defined K value, which does not always yield robust graph representation of the data. Higher K values generally favor preserving larger communities, but compromise the ability to detect rare subpopulations. On the other hand, as we will demonstrate later, lower K values in other clustering methods are only marginally (and inconsistently) better at recovering rare populations but cause fragmentation—complicating the biological discovery.

Another related strategy is to create a weighted graph that aims at revealing the modular structure of the graph. However, current methods (e.g. using Jaccard weight) do not discriminate adequately between links (especially those connected to the rare populations in large-scale datasets), which negatively impacts modularity optimization in the subsequent community-detection algorithm.

In PARC, we pursue a pruning strategy motivated by the observation that the edge-weight statistics in various single-cell datasets commonly exhibit a long-tailed distribution (Fig. 2). In such a skewed distribution, the relative weight difference based on Jaccard similarity (and also Euclidean distance) between the weak and majority edges is diminished due to the fact that the long tail occupies a large portion of the scale. However, this problem, conceivably a result of the ‘curse of dimensionality’, cannot be solved by simply re-weighting the graph using a different metric as it is a direct function of the dimensionality of the data. Consequently, the optimization function employed in the subsequent community-detection step sees the weak (potentially spurious) and majority edges as very similar. The detected subcommunities are thus more susceptible to being merged by spurious links due to the ‘resolution limit’—a common limitation in community detection (Barabasi, 2019)—resulting in undesirable merging of clusters.

Fig. 2.

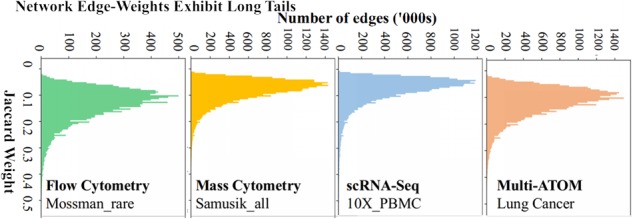
Distributions of graph edge-weights in various SC datasets. The high weight score of important neighbors in the tail, diminishes the difference between weak and majority links negatively impacting the robustness and speed of community detection an issue that could be addressed by graph pruning.

To address the limitations posed by edge-weighting and K-parameter tuning strategies, PARC instead starts with a generous fixed K number (K = 30, see Supplementary Sensitivity Analysis) and implements automated two-step pruning of weak edges guided by the data structure. First, it examines each node locally and removes the weakest neighbors of that particular node based on the Euclidean distance; and second, it re-weights the edges using the Jaccard similarity coefficient and globally removes edges below the median Jaccard-based edge-weight. The local pruning allows us to remove redundant neighbors in very densely connected neighborhoods, whereas the global pruning removes spurious edges that would otherwise persist in more sparsely connected regions.

As a result, the data-driven pruning in PARC has a 2-fold advantage underpinning the clustering performance of PARC. First, it fine tunes the local K value, and thus, overcomes the limitations of manual tuning. In fact, lowering K to reduce runtime becomes less necessary due to the fast graph construction phase. Second, the pruning strategy in PARC results in a refined graph that retains only significant neighbors and thus accelerates the convergence of the optimization algorithm, which empirically scales linearly with the number of edges (see Supplementary Fig. S2 and Supplementary Sensitivity Analysis on the choice of pruning threshold) (Blondel et al., 2008).

2.3 Pruned graph helps shield against resolution limit

Having constructed a network representation of the cells, we apply the Leiden modularity optimization algorithm (Traag et al., 2019). We show that using the pruning strategy described above accelerates clustering time and mitigates the resolution limit issue (whereby smaller clusters are more likely subsumed into larger ones as the network size grows).

Leiden addresses the issue of internally disconnected communities by breaking up clusters into subclusters. However, to control the proliferation of clusters, Leiden only re-assigns refined communities to major communities found in the aggregation step immediately before. This means that once a community is merged into another, it can only be reassigned to any of the existing communities. Thus, substructures may be subsumed into larger communities due to the resolution limit of the quality function which is sensitive to spurious links extending from minor populations to major populations. The effect worsens as the size (or total weight), m, of the network increases, showing why Leiden (without pruning) and the related Phenograph (using Louvain method) are unable to consistently segregate rare yet distinct populations.

To understand the resolution limit issue and how pruning helps to alleviate it, we need to investigate modularity of the graph—a measure of density of links within a community to that between communities. A node is assigned to a community only if the change in modularity is positive. The change in modularity, ΔQ, when assigning node i in community A to community B can be written as (k_i,_in is the sum of weighted links from node i to nodes in community B, k_i is the weighted links incident on node i, Σ_tot is the sum of weighted links incident on B, m is graph weight):

$$\Delta Q=\frac{k_{i,\text{in}}}{m}-\frac{k_i{\sum }_{\text{tot}}}{2m^2}.$$ (1)

If we assign all nodes in community A to B, then the change in modularity is:

$$\Delta Q_{\text{AB}}=\sum _{i\hspace{0.17em}\hspace{0.17em}\text{in} \mathrm{A}}\frac{k_{i,\text{in}}}{m}-\frac{k_i{\sum }_{\text{tot}}}{2m^2}.$$ (2)

For a simplified case of an unweighted graph (or a graph where the weightings are not discriminatory and hence effectively unweighted), we rewrite the change in modularity when merging community A and B as (where k_A and k_B are the total degrees of A and B, and L is the total number of links in the entire network, and l_AB is the number of links between community A and B; Barbasi, 2019):

$$\Delta Q_{\text{AB}}=\frac{l_{\text{AB}}}{L}-\frac{k_{\mathrm{A}}{k}_{\mathrm{B}}}{2L^2}.$$ (3)

Consider the scenario where k_Ak_B/2L < 1, then the change in modularity is positive if there exists even one link between the two communities (l_AB ≥ 1). For the sake of simplicity, let k′=k_A ∼ k_B, then ΔQ is positive when A and B are merged for all k′ ≤ √(2L). Therefore, if the number of links within a small community is below the threshold √(2 L), then a link to another community will result in a merger and the algorithm will struggle to resolve communities below the resolution limit of k′ ≤ √(2L). It is therefore critical to remove artificial or weak links set up in the initial K-NN graph.

The aggressive pruning in PARC generates (for some datasets) several small clusters or singletons which are not necessarily all outliers. Therefore, PARC examines whether these fragments should be assigned to a larger cluster or left as outliers. Fragments (whose population is below a threshold) are assigned to a cluster containing the greatest number of its original neighbors found in the HNSW stage, provided this cluster is above the minimum population threshold. If the cell does not have any neighbors belonging to a larger cluster, then it remains an ‘outlier’ cluster. PARCs efficient handling of fragments overcomes prohibitive runtime bottlenecks such as those experienced by Phenograph (when lowering K) and by Seurat (when increasing pruning) (Fig. 3a and Supplementary Fig. S3). PARCs default threshold for a cluster is a minimum of 10 cells. A more detailed analysis of the acceptable range of parameters and thresholds in terms of impact on accuracy, number of clusters and runtime, is provided in Supplementary Sensitivity Analysis. The analysis shows that pruning not only elevates the accuracy across a wide range of K compared with other methods where K is a (manually) tuned parameter but also extends the range of suitable K values (Supplementary Figs S4 and S5). We also analyze the range of pruning and outlier thresholds (Supplementary Figs S2 and S6) as a guide for users interested in tuning the parameters and show that PARC is robust to reasonable changes. Due to its fast runtime, users can efficiently configure parameters in PARC if they wish.

Fig. 7.

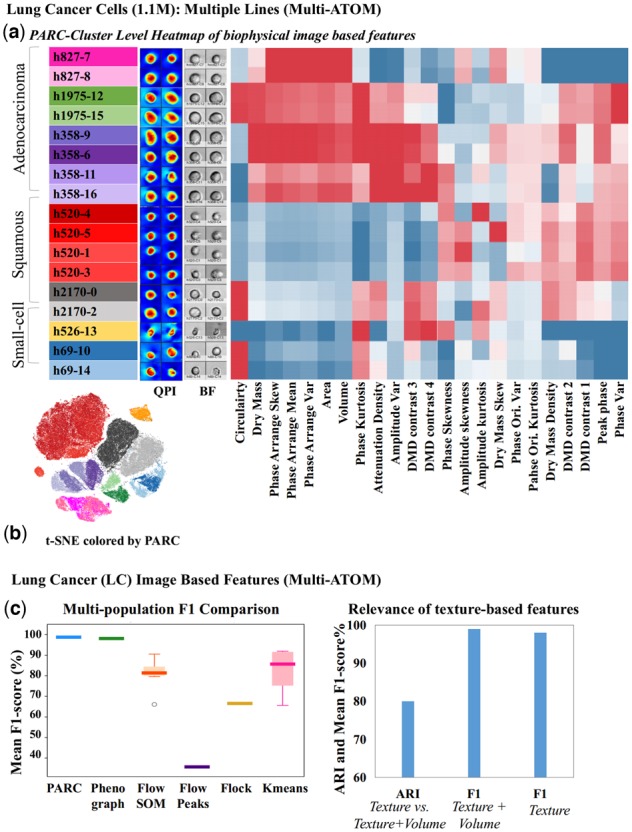
(a) t-SNE visualization of image data clustered by PARC with sample QPI and BF images. (b) Phenotypic profiles of the cell populations clustered by PARC (Table S4 for population composition) based on features related to biophysical characteristics extracted from multi-ATOM images (Supplementary Table S5). Each of the three main lung cancer subtypes, squamous, adenocarcinoma, small-cell lung cancer, shows its characteristic phenotypic profile, with texture-based features further differentiating subtypes/clusters within the cell line. (c) Clustering performance of PARC in comparison to other methods on the lung cancer image datasets (1.1million cells imaged by multi-ATOM). (right) Significance of the label-free sub-cellular texture-based features in distinguishing different cell types.

3 Results

Motivated by the need for a versatile tool to cope with the increasing diversity of large-scale single-cell data types, we tested PARC on a range of annotated single-cell datasets of scRNA-seq, flow cytometry, CyTOF and imaging cytometry, with cell counts spanning three orders of magnitude (from 1000 to 1 300 000 cells). With large-scale clustering being the emphasis, we reviewed and compared PARC with 18 well-known clustering tools benchmarked in Weber and Robinson (2016) as well as to the graph-based method in Seurat. Only six of them are practically scalable on datasets with ∼1 million cells without any subsampling. These six are Phenograph (Levine et al., 2015), FlowSOM (Van Gassen et al., 2015), FlowPeaks (Ge and Sealfon, 2012), Flock (Qian et al., 2010), and K-Means and Seurat (Stuart et al., 2018).

PARCs performance is benchmarked against the six competitive clustering methods and a summary of the results is illustrated in Figure 1a and Supplementary Figure S1. PARC generally outperforms the other methods, especially in revealing minor populations without artificially fragmenting larger populations. We use the unweighted F1-measure calculated with the Hungarian algorithm (suited for realistic, complex data where the ground truth is not absolute but based on correlation or partial manual gating, see Supplementary Materials). In addition, the scores for K-Means and FlowSOM show high variability, strongly depending on the predetermined values of chosen parameters (e.g. K clusters) (Supplementary Fig. S1), which is a drawback for exploratory data with no readily available ground truth. The corresponding adjusted rand index in Supplementary Figure S9 reiterates PARCs competitive performance and confirms that pruning does not artificially generate clusters that reduce the quality of clustering.

In the following sections, we will in greater detail demonstrate the usability of PARC on diverse types of single-cell data: Section 3.1 on flow/mass cytometry data to highlight scalability, Section 3.2 on flow- and imaging cytometry data to highlight rare cell detection, Section 3.3 on transcriptomic data as an enabler for gene analysis on datasets of diverse sample and feature size and Section 3.4 on features derived from imaging cytometry, as a proof of concept of the discriminative power of biophysical properties of cells.

3.1 PARC is scalable on large single-cell cytometry data

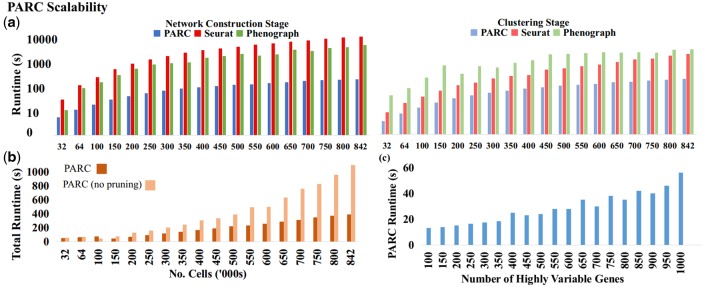
To evaluate how PARC accelerates graph-based clustering, we compare the runtime break-down between the graph-based algorithms PARC, Phenograph and Seurat in terms of network construction and modularity optimization steps in their default settings. We randomly subsample a CyTOF dataset Samusik_all (Samusik et al., 2016): 841 644 replicate-bone-marrow cells from C57BL/6J mice with 39 surface markers. PARCs graph construction and modularity optimization are accelerated (Fig. 3a), leading to a ∼30 factor speedup compared with Phenograph and Seurat. It should be noted that the runtimes reported throughout the article exclude the time taken for preprocessing such as normalization or dimensionality reduction. The reduction in computation time may be attributable to some key steps in PARC, namely (i) the use of HNSW to accelerate the nearest-neighbor search and (ii) the pruning phase which has a knock-on effect to speed up the modularity optimization by reducing the number of edges for a given number of samples (while still maintaining the accuracy as we will show in Section 3.2 and 3.3).

Fig. 3.

(a) Scalability of PARC, Phenograph and Seurat in terms of graph construction and clustering time on random samples of CyTOF data (Samusik_all: 841,644 cells and 39 surface markers). (b) Pruning speeds up PARC by a factor of 2, gains increasing with sample size. (c) PARC scalability with dimensionality on scRNA-seq data (10X_PBMC).

As shown in Figure 3b, pruning becomes more effective in lowering runtime with increasing sample size, marking its significance in clustering acceleration with large-scale SC data. We also tested the scalability of PARC with increasing data dimensionality using the scRNA-seq dataset of human PBMCs (Zheng et al., 2017). We observe a fairly linear scaling in runtime of PARC, even when the dimension goes beyond 500, indicating its ability to scale with high dimensionality (Fig. 3c). The accuracy of results for very high-dimensional inputs (such as count matrices) is examined in Section 3.3. Memory requirements as a function of sample and feature size are shown in Supplementary Figure S10. All performance tests are run on a machine with 126 Gb RAM and eight 3.6 GHz CPUs.

3.2 PARC identifies rare populations in cytometry data

We test the ability of PARC to isolate rare populations first by comparing the accuracy to other methods, and then discussing the role of pruning in uncovering rarer populations and elevating accuracy. As shown in Figure 4a, we run PARC on two flow cytometry datasets (FlowRepository I.D.: FR-FCM-ZZPH) (Weber and Robinson, 2016) and an in-house imaging flow cytometry (Lee et al., 2019b) (see Supplementary Materials for experimental details). We also highlight an example, Levine_13, of multipopulation detection of a mass cytometry dataset. More examples of multipopulation detection are summarized in Figure 1a and Supplementary Figure S1.

Fig. 4.

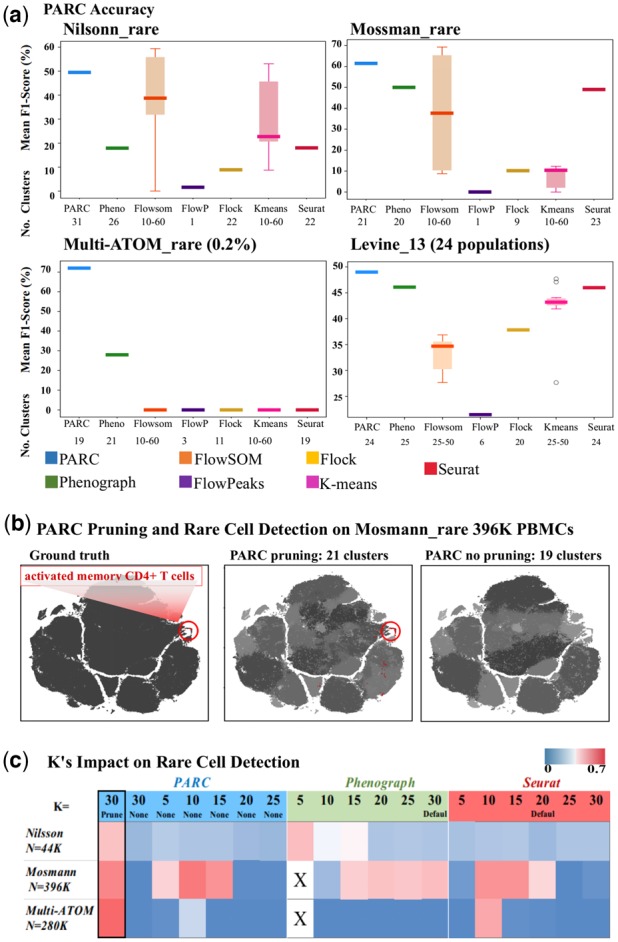
(a) Performance comparison of PARC on 1 multi-population (lower-right, Levine_13) and 3 rare-cell datasets against 6 competitive tools and their corresponding number of clusters. (b) Pruning in PARC enables rare population detection. (left) t-SNE plot colored by 'ground truth' of Mosmann_rare data. PBMCs and activated CD4+ T cells are labeled as black and red (encircled), respectively; (mid) colored by PARC with pruning, the cluster containing majority of rare activated memory T-cells is colored red and other clusters of PBMCs are in shades of grey; (right) colored by PARC without pruning - the rare activated memory T-cells (red) are not detected. (c) Comparison among PARC, Phenograph and Seurat in identifying the rare cell population in 3 datasets: Nilsson_rare, Mosmann_rare, multi-ATOM_rare, with rare populations of 0.08%, 0.03%, and 0.04%. This analysis signifies that simply lowering K in graph construction does not ensure rare-cell detection. X's denote stalled process due to lack of efficient fragmentation handling for low K.

The first dataset, Nilsson_rare (Nilsson et al., 2013), has 44 100 bone marrow cells and 13 surface markers (dimensions), out of which we aim to isolate 358 (0.08% of total population) manually gated hematopoietic stem cells. The second dataset, Mosmann_rare (Mosmann et al., 2014), has 396 400 human peripheral blood cells (14 surface markers), stimulated with influenza antigens. Only 109 (0.03%) of these are manually gated as activated memory CD4 T cells (Fig. 4a,b). The third set, multi-ATOM_rare, has 280 100 digitally mixed cells of 7 lung cancer cell lines with 23 quantitative biophysical features extracted from each label-free single-cell image. There are only 100 (0.04%) randomly subsampled adenocarcinoma cells (H1975). Following the scoring approach of Weber and Robinson (2016), the cluster with the highest F1-score for any cluster containing members of the rare population is reported. The F1-score for the multiple population data is calculated using the Hungarian algorithm (Supplementary Quantification and Statistical Analysis).

We observe that pruning, intended to alleviate the impact of the ‘resolution limit’, allows PARC to outperform other methods in detecting rare populations across these different datasets (Fig. 4a). The F1-score of the rare population obtained using the common large-scale methods (notably FlowSOM and K-Means) are not only lower but sensitive to the user-defined choice of number of clusters {k = 10,15,…60}. In Figure 4b, we plot Mosmann_rare (red for rare cells and gray for non-rare) to visualize how pruning in PARC enables the detection of the small activated memory CD4 T cell population (0.03%), which is otherwise missed if pruning is skipped.

To further evaluate the role of pruning in uncovering rare populations, we consider the performance of PARC with and without pruning, as well as the performance of PARC, Phenograph and Seurat when resorting to lowering the K parameter (number of nearest neighbors) as a potential solution to segregating rare populations (Fig. 4c).

Although the rationale in Phenograph for weighting graph edges is to resolve rare populations by weakening spurious links, we find that the weighted values are not adequately discriminatory and therefore do not enable Phenograph to consistently separate rarer populations. This relates to the discussion in Section 2, where we illustrated how the skewed weight distributions of the graph edges diminish the relative differences of weighted edges.

Consequently, a critical factor in faithfully capturing the network structure is whether or not a link exists. If there exists a link from a small (rare population) to a larger population, it is likely to become integrated into the larger population as a consequence of its edge-weights being non-discriminatory and thus reaching the resolution limit.

To overcome the challenges of recovering rare populations, one might resort to lowering K, but as shown in the heatmap Figure 4c and Supplementary Sensitivity Analysis (Supplementary Fig. S4), this is an ineffective remedy for PARC, Phenograph and Seurat, and also leads to over-fragmentation of clusters that confounds downstream analysis.

In fact, at very low K values (K = 5), Phenograph generates so many singletons and fragments that the process is stalled for 1–2 h in handling these singletons (denoted by ‘X’ in Fig. 4c). In contrast, PARCs statistically driven pruning combined with efficient handling of outliers resulting from pruning seems to be a more reliable approach for the range of benchmarked datasets.

We also note that Seurat, by default, does some pruning at a Jaccard weight of 1/15. We try to optimize Seurat’s performance by conducting a sensitivity analysis of the pruning parameter but find it is not easily tuned. Based on our analysis (Supplementary Fig. S3), we find this is partially due to requiring an absolute Jaccard weight making it difficult to estimate a reasonable value. More importantly, it is challenging to tune the Jaccard threshold parameter because any value that incurs a non-negligible amount of pruning triggers high fragmentation (of thousands of clusters) that Seurat does not efficiently handle, resulting in stalled processes and prohibitive runtime.

3.3 PARC dissects heterogeneous scRNA-seq data

We tested the adaptability of PARC for handling complex single-cell transcriptomic (scRNA-seq) data. We use (i) the gold-standard small-sample size datasets from the recent benchmarking analysis of scRNA-seq clustering tools (Duò et al., 2018) to assess PARC on small (∼1000 cells) datasets with high dimensionality (directly on the counts of filtered genes) as well as their dimensionality reduced counterparts, (ii) the mid-sized annotated 3′ mRNA dataset of 68 000 PBMCs (Zheng et al., 2017) for a more granular analysis and (iii) an exploratory dataset of 1.3 million single cells of the embryonic mouse brain as proof of scalability.

We aim to show that PARC effectively analyzes complex transcriptomic datasets even when the sample size is low but the dimensionality is high. Here, we use four ‘gold-standard’ datasets provided in Duò et al.(2018) (extracted from Bioconductor Library DuoClustering2018) and compare PARC with four clustering tools used in the mentioned study: three of which are the previously benchmarked in Section 2 (FlowSOM, Seurat and KMeans) and the fourth is SC3, which is competitive on smaller data. The gold-standard datasets after filtering for the 10% most highly variable genes (HVG) comprise: Zheng8eq (3798 cells, 1572 HVG), Zheng4uneq (5079 cells, 1644 HVG), Koh (531 cells, 4898 HVG) and Kumar (246 cells, 4516 HVG).

As seen in Figure 8, PARCs accuracy is highly competitive in both the dimensionality reduced case (Fig. 8a) and the case where no dimensionality reduction is applied to the count matrix of filtered genes (Fig. 8b). Although Seurat and SC3 also demonstrate good accuracy on the count matrix inputs, their runtimes are prohibitively long as the dimensionality increases. The runtimes for Seurat and SC3 are 1.5 and 7 h on the 1000 most HVG of the 68 K PBMC dataset, compared with 50 s for PARC, without compromising the accuracy (we find that Seurat has memory allocation errors for some very high-dimensional datasets, Supplementary Fig. S13). As scRNA-seq analyses generally rely on various gene filtering and dimensionality reduction steps to handle the challenges posed by the large number of genes and the issue of dropouts, we also show that PARC remains stable for different types of common preprocessing (following the same filtering steps of Duò et al., 2018) (Supplementary Figs S7 and S8). For instance, on the Zheng8eq dataset (3798 cells), we show that the performance is stable with PCA or UMAP (using first 100 components which corresponds to ∼97% of cumulative variance on all the benchmarked scRNA-seq datasets) on two types of gene filtering, as well as the corresponding filtered count matrices (Supplementary Fig. S8). A comprehensive comparison of all the gold-standard datasets using various preprocessing is provided in the Supplementary Materials.

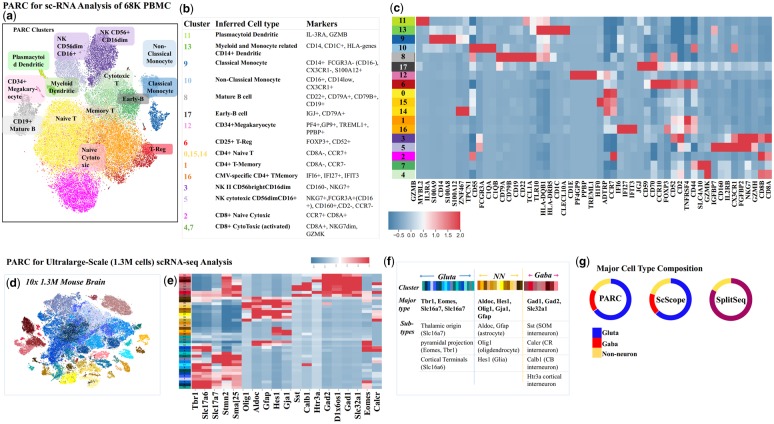
We next consider a mid-size dataset of 68 K PBMCs to show an example of PARC used for detailed analysis. The cells in the mixture are annotated (Zheng et al., 2017) by correlating each cell against the average expression profile of purified populations (Supplementary Fig. S11). We adopt the same preprocessing steps as Zheng et al. which are: filtering out genes based on unique molecular identifier (UMI) count, log normalizing the 1000 most variable genes and subsequently using the first 50 principal components (PCs) generated by PCA applied to the UMI counts (50 PCs corresponds to the inflection point on the scree plot). The issue of ‘dropouts’ is not addressed but partially mitigated by UMI-count-based filtering. We compute log2 fold-changes at the cluster level to infer cell type based on the 10 most differentially expressed genes per cluster (Fig. 6a–c) and plot only 3–5 of these per cluster.

Fig. 6.

(a) t-SNE visualization of 68K PBMCs (Zheng et al. 2017) colored based on PARC clusters, delineates well-known cell subtypes not captured in original annotation (Supplementary Fig. S12, and Table S1 for references of marker genes). (b) table of marker genes (extracted from heatmap) used to infer cell type (c) Heatmap of most differentially (log2-fold) expressed genes in each cluster (d) t-SNE visualization of the entire mouse brain data (1.3M cells). Cluster colors reflect PARC clustering of major neuronal type (Glutamatergic, Gabaergic and non-neuronal) inferred by the marker genes (Allen Brain Atlas and Tasic 2016, Tasic 2018). (e) Mean cluster-level gene expressions of known marker genes and (f) inferred sub-cell types. (g) PARC's major cell-type composition concurs with ScScope and SplitSeq, and prior studies on embryonic mouse brain cells (Table S2).

PARC is a high performer in terms of F1-score (Fig. 5a and b), but more importantly, it identifies subpopulations that were masked by the original manual gating (Fig. 6a–c). This is attributed to the fact that the annotation was mainly given to T-cell subpopulations on a mesoscopic level (e.g. CD4+, CD8+, memory and regulatory T cells) (see the ‘ground truth’ annotation in Supplementary Fig. S11). In contrast, other subtypes of PBMCs (e.g. monocytes, dendritic cells and NK cells) are not annotated by any of their known subtypes. Nevertheless, PARC is able to reveal the clusters showing high expression of CD14 (cluster 9) and CD16 (or FCGR3A) (cluster 10), markers for classical and non-classical monocytes, respectively (Ong, 2018). It also identifies subsets of NK cells as inferred by the expression level of CD160 and CD16 (FCGR3A) (clusters 3 and 5), which is known to be associated to the CD56dim CD16+ cytotoxic NK cell phenotype (cluster 5) (Le Bouteiller et al., 2011). Notably, PARC also detects rare populations of IL-3RA+ (Zhang et al., 2017) plasmacytoid dendritic cells (cluster 11, 0.6%) and megakaryocytes (cluster 12, 0.4%). The marker genes identified for each cluster are summarized in Figure 6b and Supplementary Table S1.

Fig. 5.

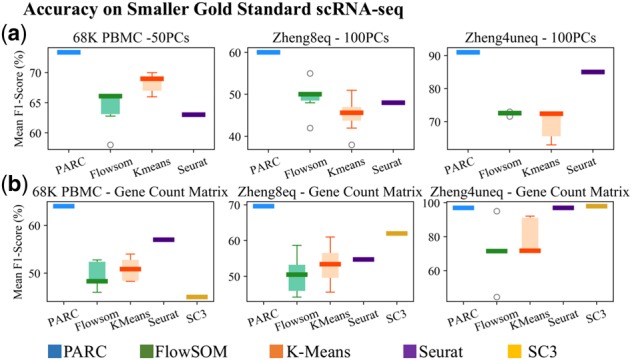
Performance of PARC on scRNA-seq datasets compared to other methods. (a) F1-scores on principal components (PCs) of top 10% highly variable genes (HVG); (b) F1-scores when input is the count matrix of top 10% HVG or 1000 HVG for 68K PBMC shows PARC maintains a high level of accuracy relative to other methods on both types of inputs

We further employ PARC to explore the scRNA-seq dataset of 1 308 421 embryonic mouse neurons. The single-cell transcriptomic profiles were obtained with Cell Ranger 1.2 (10× Genomics Datasets, 2017) and preprocessed in the same manner as the Zheng et al. (2017) dataset using python package SCANPY (Wolf et al., 2018).

Bypassing approaches that downsample data and thus risk losing the original data structure (especially, rare populations; Linderman et al., 2019), PARC completes clustering with a run time of only 15 min on 1.3 million cells (using the first 50 PCs on UMI counts of the 1000 most variable genes found after initial filtering). This is significantly faster than runtimes reported by recent methods that also do not rely on downsampling, that is, ScScope (Deng et al., 2019) and SCANPY (Wolf et al., 2018), with clustering runtimes of 104 and 97 min.

The clusters are annotated by major cell types according to the maximal expression of well-known marker genes from the Allen Brain Atlas and Tasic et al. (2016) (Fig. 6d–g), and have the following composition: GABAergic 18%, Glutamatergic 65% and non-neuronal 17%. The composition concurs with previous studies on embryonic brain cell composition which suggest ∼90% of cells are neuronal (Bandeira et al., 2009), with ∼1 in every five neurons being GABAergic (Sahara et al., 2012). The composition also agrees with the reported fractions by ScScope and SPLiT-Seq (Deng et al., 2019) (Fig. 6g).

Further classification of subtypes is inferred by plotting the average cluster expression for well-known gene markers, thus verifying the segregation of established (non-) neuronal types (Fig. 6g and Supplementary Table S2). Our results thus demonstrate the ability of PARC to enable efficient and effective exploration of the large heterogeneous single-cell datasets.

3.4 PARC clusters 1.1 million label-free single-cell images

An emerging challenge in single-cell analysis is to adapt to the progressively diverse sets of single-cell data generated by the wide range of new single-cell technologies, each with multiple modalities. This becomes a prerequisite for multifaceted single-cell analysis. Apart from the flow/mass cytometry and sequencing technologies, a notable example is high-throughput and high-content single-cell imaging, empowering large-scale image analysis that extracts several features (or phenotypes) representing cell states and types (Caicedo et al., 2017).

In contrast to fluorescence image cellular assay that specifically probes different biomolecular signatures of cellular components and provides functional annotation of genes by morphological similarity (Rohban et al., 2017), a substantial body of work has shown that cellular biophysical properties, extracted from label-free optical imaging (Otto et al., 2015; Tse et al., 2013; Kasprowicz et al., 2017), are effective intrinsic markers for probing cellular rocesses (e.g. cell proliferation, death, differentiation and malignancy). Bypassing the need for costly and time-consuming sample preparation, single-cell biophysical phenotyping could be significant in single-cell analysis especially when other biomolecular assays are not effective.

Here, we test the adaptability of PARC to cluster an in-house niche single-cell image-based dataset which describes the biophysical phenotypic profiles of 1.1 million lung cancer cells [7 cell lines representing three major subtypes: (i) adenocarcinoma, (ii) squamous cell carcinoma and (iii) small cell carcinoma]. The biophysical phenotypes of individual cells were extracted from a recently developed ultrahigh-throughput microfluidic quantitative phase imaging cytometer, multi-ATOM (Lee et al., 2019a), which captures label-free single-cell images at an ultrahigh throughput (>10 000 cells/s) without compromising subcellular resolution. In multi-ATOM, each imaged cell generates three different label-free image contrasts, from which 23 biophysical features are derived, for example, cell size, mass, density, optical opacity and statistical subcellular texture characteristics (see definitions in Supplementary Table S4). After feature Z-score normalization, we apply PARC to cluster a total 1 113 369 single cells.

PARC unambiguously separates (mean-F1 98.8%) between and within the three broad groups of lung cancer cells (Fig. 7a and b). As seen on the heatmap, the three main groups show their characteristic phenotypic profile. We observe subtle differences in some texture features within the same subtype that further differentiate individual cell lines—demonstrating the discriminative power of label-free biophysical phenotypes.

PARC and Phenograph score the highest in terms of accuracy compared with the other methods (Fig. 7c, left), with PARC completing the task in 800 s versus the 7200 for Phenograph using the same computational resources. Seurat is terminated after 5 h with a memory allocation error (at 120 Gb RAM). Furthermore, by running PARC on the randomly selected n = 100 of H1975 cells mixed with an increasing cell count of each of the other six cell lines (multi-ATOM_rare), we demonstrate PARCs consistent performance in rare-population detection based on biophysical features (Fig. 4a and Supplementary Fig. S12).

As an example of image-based phenotypic exploration, we use PARC to investigate the significance of the label-free subcellular texture-based features in distinguishing different cell types. Although cell size and shape are the most conceivable cellular biophysical features, subcellular textures parameterized from label-free imaging are intimately linked to a variety of subcellular spatial characteristics, for example, protein localization (Yan et al., 2018), nucleus architectural changes (e.g. DNA fragmentation, Almassalha et al., 2016; cytoskeletal network, Bon et al., 2014). Hence, they can be harnessed as information-rich single-cell phenotypes. This is evidenced by the negligible drop (1%) in the F1-score when exclusively the texture features (excluding volume, area, circularity and their moments) are input to PARC, compared with the case of using the complete feature set (Fig. 7c (right)). The adjusted rand index between the two sets of clusters (with and without volume features) is 80%, indicating the two sets are well aligned.

4 Discussion

The rapid advancement in bioassay technologies now allows diverse characterization of single cells at an unprecedented throughput and content, creating a need for new computational tools that efficiently handle the scale and complexity of single-cell data. PARC addresses this gap by employing a combinatorial graph-based clustering approach that outperforms other methods not only in speed and scalability but also the ability to accurately capture data structure and detect rare populations.

To deal with large-scale data processing, PARC does not incur prohibitive computational costs nor resort to data downsampling. Instead, PARC is built on three integrated elements: (i) HNSW for accelerated K-NN graph construction, (ii) data-driven two-step graph pruning and (iii) the community-detection Leiden algorithm. Our results show that pruning, guided by the local and global single-cell data structure, refines and improves the data graph representation which in turn accelerates Leiden and alleviates the common problem of the resolution limit in community detection.

We anticipate that the clustering performance can be augmented by incorporating other preprocessing methodologies. For instance, prior to PARC, one could apply correction steps to remove batch effects (MNN by Haghverdi et al., 2018) and imputation strategies for combating noise and dropouts in scRNA-seq data (e.g. scScope, DeepImpute). As PARC does not require prior knowledge of the data, it is easily adaptable to popular single-cell analysis pipelines (e.g. SCANPY, Cell Ranger).

Our results demonstrate that PARC accurately clusters various data types, namely scRNA-seq, flow/mass and imaging cytometry. We thus anticipate that PARCs versatility lends itself to play an important role in emerging techniques that empower integrative characterization of single-cell biochemical/biophysical phenotypes and transcriptional profiles (regarded as single-cell multi-omics; Chappell et al., 2018; Hasin et al., 2017)—the major pursuit to crafting the human cell atlas (Regev et al., 2017). This could offer a deeper mechanistic understanding of biological processes, particularly those driving cellular heterogeneity associated with diseases.

Funding

This work was partially supported by the Research Grants Council of the Hong Kong Special Administrative Region of China [HKU 17259316] and supported by the Collaborative Research Fund [grant number C7047-16G], General Research Fund [17208918, 17209017, 201611159293] and Innovation and Technology Support Programme [ITS/204/18].

Conflict of Interest: none declared.