Optimizing adaptive cancer therapy: dynamic programming and evolutionary game theory

Abstract

Recent clinical trials have shown that adaptive drug therapies can be more efficient than a standard cancer treatment based on a continuous use of maximum tolerated doses (MTD). The adaptive therapy paradigm is not based on a preset schedule; instead, the doses are administered based on the current state of tumour. But the adaptive treatment policies examined so far have been largely ad hoc. We propose a method for systematically optimizing adaptive policies based on an evolutionary game theory model of cancer dynamics. Given a set of treatment objectives, we use the framework of dynamic programming to find the optimal treatment strategies. In particular, we optimize the total drug usage and time to recovery by solving a Hamilton–Jacobi–Bellman equation. We compare MTD-based treatment strategy with optimal adaptive treatment policies and show that the latter can significantly decrease the total amount of drugs prescribed while also increasing the fraction of initial tumour states from which the recovery is possible. We conclude that the use of optimal control theory to improve adaptive policies is a promising concept in cancer treatment and should be integrated into clinical trial design.

1. Background

Intratumoural heterogeneity is increasingly recognized as a cause of metastasis, progression and resistance to therapy [1]. While genetic instability, a hallmark of malignancy [2], can result in this heterogeneity, it is being increasingly understood that eco-evolutionary factors, like selection and clonal interference, can also drive and maintain it [3,4].

While sequencing technologies have enabled increasingly in-depth quantitative understanding of the genetic heterogeneity, relatively little experimental work has sought to directly quantify the eco-evolutionary interactions involved. As more studies come to light showing the efficacy of treatments based on eco-evolutionary trial designs, this lack of quantification is coming into focus.

In line with standard, cell-autonomous growth-based theories, conventional chemotherapy is given to patients at the maximum tolerated doses (MTD): the highest doses that most patients can safely tolerate. Although the MTD-based therapy offers advantages in survival compared to no therapy, cures remain elusive, and side effects can be severe. In addition to the toxicity, it is known that relapse is nearly inevitable due to the emergence of therapeutic resistance: a process driven by Darwinian evolutionary dynamics in which the MTD-based chemotherapy kills off the chemotherapy-sensitive cells, and chemo-refractory cells eventually dominate in the tumour. While it is unknown whether these resistant cells are present before therapy or acquire resistance mutations during therapy, it is the process of variation and selection under standard therapy that drives the inevitable failure in the patient.

Metronomic chemotherapy has been proposed as a possible alternative to the MTD strategy [5–7]. Metronomic chemotherapy is given in an on/off fashion at frequent time intervals according to a set periodic schedule. The idea is to give less overall medication, allowing therapy-sensitive cells to regrow, keeping the tumour sensitive to the therapy, while at the same time mitigating toxicity. This decrease in toxicity has further been postulated to prevent tumour angiogenesis and stimulate resensitization of anticancer immune protection. Frustratingly, the results of clinical trials of metronomic chemotherapy have been ‘variable’ [8] and some of them have not demonstrated significant efficacy [9–11] compared with standard therapy. In recent clinical trials, drug dosage intensity was optimized for a preset schedule, with a positive effect on toxicity [12]. However, the problem of finding an appropriate schedule has not been addressed, even though models suggest that timing is equally important [13,14].

Based on the hypothesis that disease dynamics depend on the evolution of tumour heterogeneity as modulated by competition between subtypes, the idea of using adaptive therapy (AT) has been proposed [15]. AT is much like metronomic therapy, with an important difference: the doses of therapy are administered according to the current state of tumour growth and its anticipated evolutionary changes (trajectory). These can be estimated using direct (e.g. taking biopsies) or indirect (e.g. antigen testing, mathematical modelling) methods. Therefore, unlike the MTD-based or metronomic protocols, AT does not have a preset schedule. The adaptive adjustment of doses and timing also prolongs the period until a tumour becomes chemotherapy-resistant. Recently, the adaptive strategies have shown promise in pre-clinical trials of breast cancer [16] and a phase 2 clinical trial in metastatic castrate-resistant prostate cancer [17].

These two recent successes [16,17] in AT have been based on mathematical modelling of tumour evolution under therapy using a dynamical systems approach based on evolutionary game theory (EGT) [18,19]. This formalism explicitly considers interactions between sub-populations and models their fitness in frequency-dependent terms.¹ EGT has been used to theoretically consider many scenarios in cancer before, including therapy scheduling and timing in prostate cancer [13,17,22–24]; the use of tumour microenvironment targeting therapy in glioblastoma [25]; the trade-off between healthy tissue and cancer in multiple myeloma [26,27]; and drug resistance in general [28–31]. These theoretical studies, combined with the recent empiric realizations, suggest significant opportunities to improve therapy by using this evolutionarily enlightened approach. Nevertheless, therapeutic decisions in general practice are currently not based on this knowledge and continue to use the MTD paradigm.

Even if we make very strong assumptions that an oncologist has perfect information about the current state of a tumour and a faithful mathematical model that can predict its trajectory, it is not clear how he/she should adjust the schedule and doses. Based on a stage of the disease and patient’s needs, the therapy can have different final goals: maximization of patient’s life duration, ensuring the best possible quality of life, decreasing probability of new metastases appearing, decreasing time/cost of the treatment, etc. Unfortunately, an oncologist can usually only focus on one or two of these goals, having some reasonable constraints on the secondary parameters. Thus, an important step toward optimizing AT is to define an objective of the therapy and ‘translate’ it into mathematical language. The next step is to quantify how good each particular strategy is with respect to that chosen objective. Optimizing this objective is a mathematical goal which can be addressed by the tools of optimal control theory.

Optimal control theory, a branch of mathematics typically used in engineering, can be also applied to a wide class of problems arising in oncology [32]. The first such application was due to Swan & Vincent [33], who found the optimal treatment strategy for multiple myeloma with the objective to minimize the total amount of drugs by using the Pontryagin minimum principle (PMP) [34]. Since then, others have used the PMP in different cancer treatment problems: a chemotherapy optimization under evolving drug resistance [35–36], optimal scheduling of a vessel disruptive agent [38], MAPK inhibitors [39] input in cancer treatment, minimizing the amount of drugs prescribed in tumour-immune model [40], finding a compromise between drug toxicity and tumour repression for the myeloma bone disease [41], and many others.

While these approaches have offered benefits in their ability to formally optimize problems written as dynamical systems, the PMP method has several limitations. First, PMP yields only a necessary condition for an optimum, and any locally optimal trajectory of the control system satisfies PMP. Local optimality means that the trajectory is optimal when comparing it with its small perturbations, but there may well be a different trajectory that is even better (globally optimal, compared with all possible trajectories). Secondly, PMP provides a time-dependent (open-loop) control: given an initial state, the method provides an optimal treatment strategy as a function of time—therefore a treating oncologist has to follow it regardless of the changing state of the tumour. However, if the underlying model has been perturbed or includes some noise (like a tumour acquiring mutations, say), the control cannot adapt to these unexpected changes.

A significantly different perspective on control theory is based on the notion of feedback (closed-loop) controls. Using the Hamilton–Jacobi–Bellman (HJB) equations, one can obtain controls that depend on the current state of the dynamical system (current distribution of sub-populations of cancer cells) rather than only the current time [42]. In this case, the treating oncologist’s decisions can be adjusted if something unexpected has happened with the trajectory. Moreover, the HJB equations guarantee that the resulting treatment feedback strategies are globally optimal. Despite these advantages of the HJB, there are only a few treatment optimization studies [43,44] which use this feedback control paradigm.

Here, we apply the HJB approach to compute optimal treatment strategies for a model of lung cancer proposed by Kaznatcheev et al. [20]. In that paper, the authors introduce an evolutionary game (system of replicator-type equations) that models the dynamics of three sub-populations of tumour cells. The article highlights the importance of a good scheduling in the polyclonal regime, when the game has cyclic dynamics. The article has an example of two different scheduling strategies with the same set of initial parameters that lead the system to opposite outcomes: putative recovery, versus putative death of a patient. While several qualitatively different treatment schedules are presented, optimal therapy is not discussed. Given the growing interest in EGT in clinical applications [17] and recent work connecting these models using direct in vitro parametrization [45], we believe the optimization of therapies based on such models will become increasingly important and the HJB-based approach will be used far more often in the future.

2. Methods

We illustrate our approach on a model of cancer evolution that has been proposed in Kaznatcheev et al. [20] and summarized in box 1 with the key steps of derivation included in electronic supplementary material, Section 1S. This model considers interactions between three different sub-populations of cancer cells playing a modified version of the public goods social dilemma: glycoltyic cells (GLY), vascular overproducers (VOP) and cells called defectors (DEF) which use both strategies to ‘cheat’ on the others. While this model is highly simplified, the qualitative aspects of these cell types have been well documented in tumours. GLY cells are anaerobic and produce lactic acid, these are classic ‘Warburg shifted’ cells, and have been implicated in the acid-mediated invasion hypothesis [46]. These cells are largely responsible for local progression and metastasis, and while it has been suggested they can be treated with buffer therapy [47], this has yet to be shown to be clinically actionable; therefore, adaptive dynamics remain a viable approach to control this population. VOP cells spend extra energy to produce HIF-1α, a signalling molecule which drives further production of Vascular Endothelial Growth Factor (VEGF—a protein that works to improve the vasculature), which ultimately benefits both VOP and DEF cells since they require oxygen for aerobic respiration. For this reason, the VOP cells could be targeted by drugs like bevacizumab, which is an anti-body against VEGF. DEF cells, the ‘cheaters’, have analogues in many cancers, and have no cell-autonomous advantages, but instead depend on the ecological interactions with other types for survival. These cells are best targeted by modifying the ecology; e.g. via AT.

Box 1. Mathematical model of cancer sub-population evolution from Kaznatcheev et al. [20].

Transformation/reduction to a 2D system:

Subpopulation proportions:

$(x_G,\hspace{0.17em}{x}_D,\hspace{0.17em}{x}_V)$ for GLY, DEF and VOP, respectively. Note: $x_G+x_D+x_V=1.$

$$\{\begin{array}{c}q=\frac{x_{\mathrm{V}}}{x_{\mathrm{V}}+x_{\mathrm{D}}},\\ p=x_{\mathrm{G}},\end{array}\mathrm{or}\hspace{0.17em}\{\begin{array}{c}{x}_D=(1-q)(1-p),\\ x_G=p,\\ x_V=(1-p)q.\end{array}$$ 2.1

Evolution dynamics in reduced coordinates with control on therapy intensity:

$$\{\begin{array}{c}\dot{q}(t)=q(t)(1-q(t))(\frac{b_v}{n+1}\sum _{k=0}^n{p}^k(t)-c),\\ \dot{p}(t)=p(t)(1-p(t))(\frac{b_a}{n+1}-(b_v-c)q(t)-d(t));\\ q(0)=q_0,p(0)=p_0.\end{array}$$ 2.2

Control and parameters:

• —$d\hspace{0.17em}:\hspace{0.17em}{\mathbb{R}}_{+}\to [0,d_{\max }]$, time-dependent intensity of GLY-targeting therapy;
• —$b_a$, the benefit per unit of acidification;
• —$b_v$, the benefit from the oxygen per unit of vascularization;
• —c, the cost of production VEGF;
• —n, the number of cells in the interaction group.

Conditions for homogeneous regime:

$$\frac{b_a}{n+1}<b_v-c<cn.$$ 2.3

Process terminates as soon as either         Terminal set:

$$\begin{array}{r}\{\begin{array}{c}p(t)<r_b,\hspace{0.17em}\mathrm{if}\hspace{0.17em}\mathrm{therapy}\hspace{0.17em}\mathrm{succeeds};\\ p(t)>1-f_b,\mathrm{if}\hspace{0.17em}\mathrm{therapy}\hspace{0.17em}\mathrm{fails}.\end{array}\mathrm{\Delta }=\{(q,p)\in [0,1]\times [0,1]\hspace{0.17em}:\hspace{0.17em}p<r_b\hspace{0.17em}\mathrm{or}\hspace{0.17em}p>1-f_b\}.\end{array}$$ 2.4

Based on the replicator model from EGT [18,19], transformed into equation (2.2) in box 1, the evolution of the tumour is described by tracking the changing proportions of GLY, VOP and DEF cells in the full population. The patient is viewed as recovered when the GLY proportion falls below some low threshold $r_b$. (Below this recovery barrier, the validity of replicator-based model is harder to justify and we assume that the GLY cells are essentially extinct.) Conversely, we assume that GLY cells suppress other tumour cells and a patient dies if the total proportion of aerobic cells (VOP and DEF sub-populations combined) falls below some low threshold (a failure barrier) $f_b$.

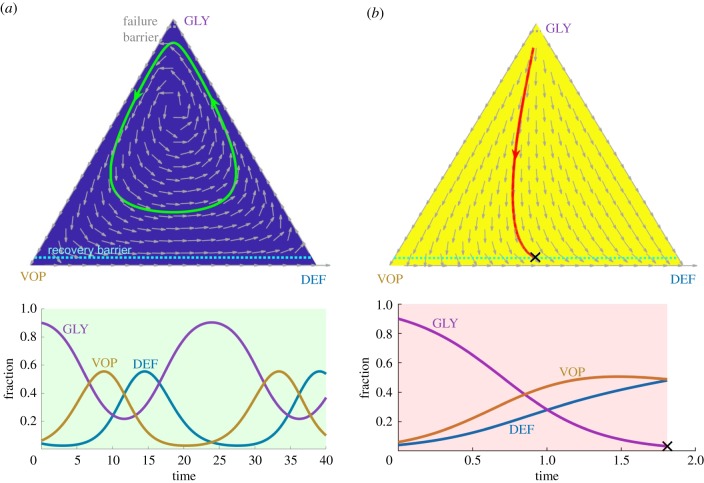
For a range of parameter values (2.3), this model predicts a heterogeneous regime² in cancer evolution with coexistent and oscillating proportions of GLY, VOP and DEF. Without any treatment, these sub-populations follow cyclic dynamics and a patient never recovers (figure 1a).

Figure 1.

A comparison of two possible constant treatment scenarios starting from an initial state $(x_D,x_G,x_V)=(0.04,0.9,0.06)$: (a) without any therapy; (b) with the MTD-based therapy. Top row: phase portraits of corresponding vector fields (shown by grey arrows) on a GLY–VOP–DEF triangle with illustrative trajectories. Blue background and green reference trajectory—no therapy at all. Yellow background and red reference trajectory—MTD-based therapy at all times. Dash light blue and grey lines separate the recovery zone (bottom) and the failure zone (top), respectively. Black cross—termination due to crossing the recovery barrier. Bottom row: evolution of sub-populations with respect to time based on the reference trajectories above. Green time range—no therapy. Pink time range—MTD-based therapy. Note the different scaling of the time axis. (Online version in colour.)

Following section 4.1. in [20], we consider a cell-type-targeting therapy that preferentially penalizes the fitness of GLY cells; see formula (2.2) in box 1. But we emphasize that the same approach can be used to target any cell-type and optimize therapy for any chosen end-condition. During the treatment, a doctor defines the timing of therapy and its intensity. This time-dependent intensity d(t) can vary between 0 (no therapy) and $d_{\max }>0$ (the MTD). Two extreme cases (d(t) = 0 versus $d(t)=d_{\max }$ for all times t) are illustrated in figure 1a,b, respectively.³ In the latter case, GLY cells become extinct and the patient recovers quickly; however, it is natural to ask whether this treatment strategy is optimal in some sense (e.g. would the recovery be much delayed if the patient received therapy less often or at a lower intensity?). In the following section, we will show that the MTD-based treatment can result in an avoidably high cumulative amount of drugs (figure 2c) or might even fail to achieve a recovery in situations where AT-based treatment would have succeeded (figure 4), much like the early results from Zhang et al. in metastatic prostate cancer [17].

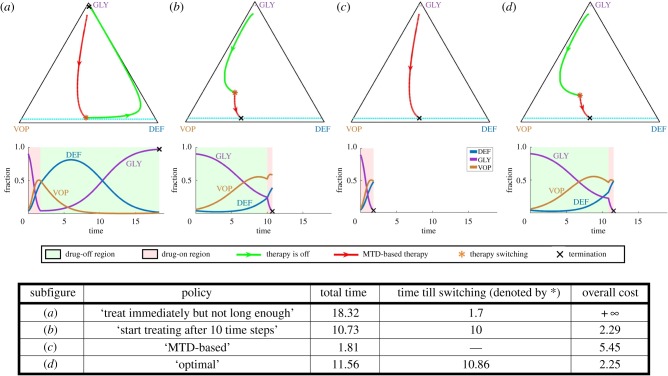
Figure 2.

Importance of optimal scheduling: ensuring recovery and decreasing the cost of treatment. Tumour evolution under four different treatment strategies for the same initial state. A seemingly reasonable treatment strategy may not lead to a recovery; see (a). Even if a patient eventually recovers (as in (b,c)), the overall cost of treatment can be reduced by pursuing a provably optimal policy (d). Top row: tumour evolutionary trajectories under different strategies on a GLY-VOP-DEF triangle. Green part of a trajectory—no therapy is used. Red part of a trajectory—MTD-based (standard) therapy. The moment of switching from one regime to another is denoted by (red *). Dash light blue and grey lines separate the recovery zone and the failure zone, respectively. Black cross—termination due to crossing the failure or recovery barrier. Bottom row: evolution of sub-populations with respect to time based on the reference trajectories above. Green time range—no therapy. Pink time range—MTD-based therapy. (Online version in colour.)

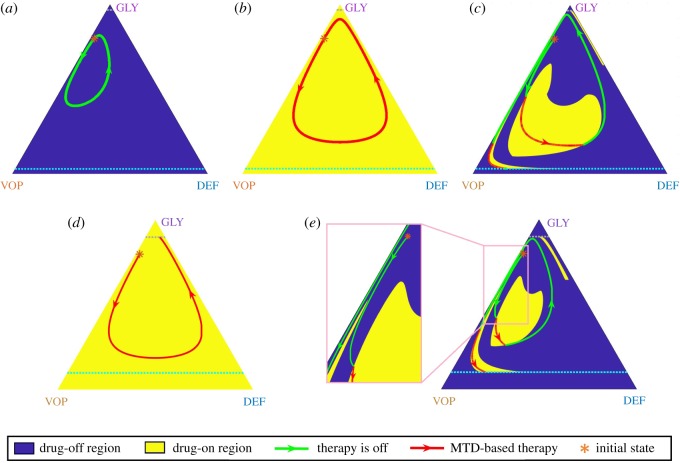
Figure 4.

MTD-based policy versus the optimal (adaptive) policy when the MTD rate is low ($d_{\max }<b_a/(n+1)$). Top row: trajectories under both (a) ‘no therapy’ policy and (b) the MTD-based policy are cyclic and cannot cross either the recovery or the failure barrier from the initial state denoted by (*). Nevertheless, the adaptive/optimal switching leads to a full recovery (c). Bottom row: With a larger failure zone, an MTD-based policy leads to patient’s putative death (d) even though it is still possible to cross the recovery barrier under an adaptive/optimal policy (e). (Online version in colour.)

For the Kaznatcheev et al. tumour model (2.2), a natural objective function to minimize is the total amount of therapy administered over the course of treatment (which in this case could be a surrogate for both toxicity and cost). This can be quantified as $D={\int }_0^T\hspace{0.17em}\text{d}(t)\hspace{0.17em}\text{d}t,$ where the total time of treatment T is dependent on the initial cancer subpopulation fractions and on our chosen therapy policy d( · ). However, this objective is problematic for two reasons. First, the minimum of D is clearly attained without any therapy (taking d(t) ≡ 0 implies D = 0 and T = +∞), even though the dynamics become cyclic and the recovery is never achieved. Second, if we constrain our minimization to only those d( · ) that lead to recovery, an optimal treatment policy does not exist. Instead, there is a sequence of treatment policies that lead to successively smaller d-values but with an unbounded increase in corresponding treatment times T. The idea of such policies is simple: travel along the therapy-free trajectories of figure 1a for most of the time, but use short bursts of therapy only when the drugs are most effective. To approach the optimally small d, one would need to use shorter and shorter bursts, resulting in policies that are hard to implement in practice and would require unrealistically long treatment times T, but would yield a situation like a chronic disease, where while the tumour is never cured, it is always controlled.

In order to get a meaningful optimal policy we will penalize the treatment time by a time penalty σ > 0. The total time spent on the treatment, including time between the doses, is an important factor by itself. Much longer treatment time results in additional costs and lower quality of life for a patient. Therefore, our objective is to minimize the sum of a therapy cost D and a treatment time cost σT, while guaranteeing eventual recovery. For every choice of σ > 0, the resulting treatment policies are thus Pareto-optimal with respect to D and T.

Our method computes the value function, u, which is defined for every starting tumour state as the minimum of $({\int }_0^T\hspace{0.17em}\text{d}(t)\hspace{0.17em}\text{d}\mathrm{t}+\sigma T)$ over the set of treatment policies that lead to recovery. (If recovery is not possible then u = +∞.) Any policy d( · ) that realizes this minimum is called optimal. Due to the structure of this optimization problem, one can show that optimal treatment policies are bang–bang: at any given time t, they either administer drugs at MTD-rate ($d(t)=d_{\max }$) or administer no drugs at all (d(t) = 0); see electronic supplementary material, §2S. For such policies, the objective function becomes a weighted sum of the total therapy time $\tilde{T}$ (when $d(t)\equiv d_{\max }$) and the total treatment time T, with $d_{\max }$ and σ as the corresponding weights. Moreover, this allows for a simple visual representation of any such policy: splitting the full state space into two parts (MTD dynamics versus no-therapy dynamics, shown in yellow and blue, respectively, in all of our figures) and simplifies application of therapy into something familiar to clinicians: on or off.

3. Results

(a). Quantifying the benefits of optimal treatment strategies

We now focus on an optimal control problem summarized in box 2 and based on the example considered in the therapeutic implications section of Kaznatcheev et al. [20]. All model parameter values (d_max = 3, b_a = 2.5, b_v = 2, c = 1, n = 4) correspond to those in [20], except for the recovery and failure barriers⁴ $r_b=f_b={10}^{-1.5}.$ We also use σ = 0.01 to incorporate the time-penalty absent in the original model. In figure 2, we compare the treatment cost (3.3) and treatment time (3.1) of trajectories corresponding to four different treatment strategies starting from the same initial configuration $(x_D,x_G,x_V)=(0.04,0.9,0.06)$. The first two strategies are similar to those modelled in Kaznatcheev et al. [20]: (a) is an example of a bad policy that may cause a failure by stopping the therapy prematurely, while (b) is a good policy based on ad-hoc adjustment of the start time for the therapy. We also illustrate the standard of care ‘MTD-based’ policy (c). Even though both (b) and (c) lead to recovery, neither of these is optimal (with the MTD-based approach resulting in an excessive amount of drugs, captured by the higher cost). The policy minimizing our objective function is found by solving the HJB equation and illustrated in (d).

Box 2. Objective function.

Total treatment (terminal) time:

$$T(q_0,\hspace{0.17em}{p}_0,d(\cdot ))=\text{min}\{t\in {\mathbb{R}}_{+}|(q(t),p(t))\in \mathrm{\Delta },q(0)=q_0,p(0)=p_0\}.$$ 3.1

If the system never gets to the terminal set, we assume that $T(q_0,p_0,d(\cdot ))=+\mathrm{\infty }.$

Terminal cost function is g(q, p):

$$\mathrm{\Delta }\to \{0,+\mathrm{\infty }\}\hspace{0.17em}\text{such that}\hspace{0.17em}g(q,p)=\{\begin{array}{c}+\mathrm{\infty },\hspace{0.17em}\mathrm{if}\hspace{0.17em}\hspace{0.17em}p>1-f_b,\\ 0,\mathrm{otherwise}.\end{array}$$ 3.2

Treatment cost (objective) function:

$$J(q_0,p_0,d(\cdot ))={\int }_0^T(d(s)+\sigma )ds+g(q(T),p(T)),$$ 3.3

where $T:=T(q_0,p_0,d(\cdot ))$ is the terminal time. J is finite if the system (2.2) terminates at the recovery barrier.

Value function

$$u(q_0,p_0)=\underset{d(\cdot )}{\inf }\hspace{0.17em}J(q_0,p_0,d(\cdot ))$$ 3.4

can be found by solving HJB PDE:

$$\underset{d\in [0,d_{\max }]}{min}\{\mathrm{\nabla }u(q,p)\cdot \left(\begin{array}{c}\dot{q}(q,p,d)\\ \dot{p}(q,p,d)\end{array}\right)+d+\sigma \}=0,(q,p)\in ([0,1]\times [0,1])\setminus \mathrm{\Delta }.$$ 3.5

The boundary conditions of HJB equation:

$$\{\begin{array}{c}u(q,p)=0,\mathrm{if}\hspace{0.17em}p<r_b;\\ u(q,p)=+\mathrm{\infty },\text{if}\hspace{0.17em}p>1-f_b.\end{array}$$ 3.6

Once u and $\mathrm{\nabla }u$ are computed, they can be used to obtain the optimal control in feedback form: d* = d(q, p).

The corresponding therapy on/off regions and the resulting vector field are shown in figure 3a. The zoomed version shows that trajectories can be prevented from crossing the failure barrier by using the MTDs just before crossing. In fact, a chattering control (with intermittent and sufficiently frequent use of MTDs) would be sufficient to guarantee this.

Figure 3.

Optimal control in feedback form, the value function, and the pitfalls of PMP. (a) A phase portrait of the optimal system dynamics. The vector field is shown by grey arrows over the optimal drugs-off (blue background) and drugs-on (yellow background) regions. A sample optimal trajectory (in green and red) corresponds to the initial state from figure 2. (b) Computation of the value function u (whose level curves are shown by light blue lines) is used to determine the optimal drugs-on and drugs-off regions (shown in yellow and dark blue, respectively). Optimal trajectories are not unique for initial states on the shockline (where the level curves of u are not smooth). Two such optimal trajectories are shown starting from an asterisk (*). The green-red trajectory takes longer to reach the recovery, but uses less drugs than the red (start-drugs-right-away) trajectory. The cumulative cost is the same for both of them. (c) For initial conditions off the shocklines of u, there can still be multiple locally optimal trajectories. We show an example of two such trajectories starting from a cross marker (×). The risk of applying the PMP method is that it might yield either of them, but only the red (start-drugs-right-away) is globally optimal. (Online version in colour.)

The level sets of u in figure 3b show that value functions need not be smooth. Since the gradient of u is used to determine the optimal course of action (therapy on or off), there can actually be more than one optimal policy for initial states on a shockline (where the gradient is undefined). We show an example of such trajectories (solid green and red lines in figure 3b, both yielding the same cost of 2.764) for an initial point denoted by (*). Non-smoothness of the value function often poses a challenge for methods based on PMP [34] even if the initial state is not on a shockline. For example, perturbing the initial state to a nearby one, denoted by a cross (×) in figure 3c, one sees two locally optimal trajectories and PMP might yield either of these depending on the initial guess. The green one is, however, inferior to the globally optimal red trajectory, which can be always recovered by solving the HJB equation.

The trade-offs between our two optimization objectives (the total administered drugs versus the time to recovery) are further examined in electronic supplementary material, §S5.

(b). ‘Incurable’ states and periodic trajectories under MTD treatment

One might think that, despite being sub-optimal, an aggressive MTD-based strategy is at least always fully reliable and the resulting trajectories are guaranteed to reach the recovery zone from every initial configuration, as shown in figure 2c. Indeed, if $b_a/(n+1)\le d_{\max }$, the MDT-based policy ($d(t)\equiv d_{\max }$) guarantees that $\dot{p}$ is always negative; see equation (2.2). But with $b_a/(n+1)>d_{\max }$ the recovery might not be attained with the constant use of MTDs (even if some other treatment policies are successful!).

Consider, for example, the following set of parameters: $b_a=4$, $b_v=2$, c = 1, n = 4; $r_b=f_b={10}^{-1.5}$; $d_{\max }=0.3$, σ = 0.03 and an initial state $(x_D,x_G,x_V)=(0.02,0.8,0.18)$ denoted by (*) in figure 4. Under these parameters, the MTD-based therapy has a periodic trajectory⁵ (figure 4b). Since the treatment time is infinite, the cost (3.3) of such a policy is +∞. (In reality, this would lead to the emergence of drug resistance and eventual failure, but this biological situation is not modelled in Kaznatcheev et al. [20].)

We can see that neither of two extreme strategies (‘no-drugs-at-all’ in figure 4a and the MTD-based ‘drugs-all-the-time’ in figure 4b) can bring the trajectory to the recovery zone. However, their adaptive combination can still achieve the objective. We show a trajectory corresponding to the optimal policy in figure 4c. With a larger failure zone (e.g. $r_b=f_b={10}^{-1}$), a previously successful MTD-based treatment might even result in death (figure 4d), while the adaptive strategy still leads to recovery (figure 4e).

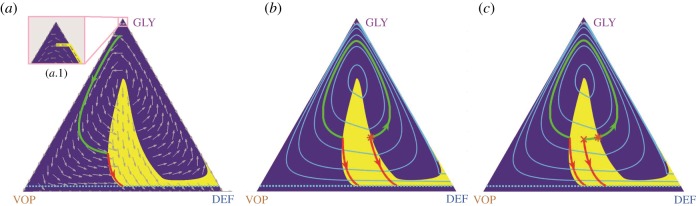
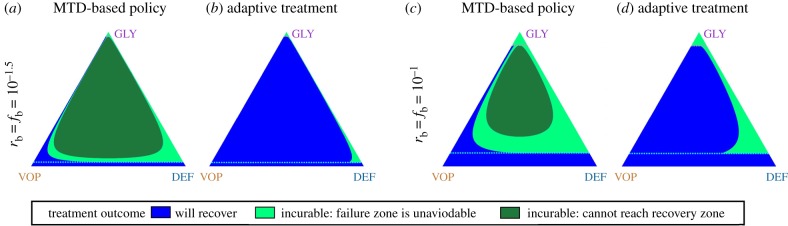
For a fixed treatment policy, we define its corresponding ‘incurable’ area to be a set of states starting from which it is impossible to cross the recovery barrier. For example in figure 4, the incurable area of the MTD-based policy includes the state denoted by (*) (when $r_b=f_b={10}^{-1.5}$ or $r_b=f_b={10}^{-1}$). However, this state is not in the (dramatically smaller) incurable area of the adaptive/optimal policy (figure 5). Of course, the ‘incurable areas’ are also highly dependent on model parameters. In electronic supplementary material, §S6, we show that they can grow due to an increase in the MTD rate $d_{\max }$ or a decrease in vascularization benefits $b_v$.

Figure 5.

(a–d) Comparison of the ‘incurable’ area for the MTD-based policy versus the adaptive policy. Unlike the MTD-based treatment, adaptive policies lead to a patient recover from most initial states even with a small $d_{\max }.$ The blue colour indicates initial states from which the recovery is achievable. The green colours represent initial states from which the recovery is impossible (i.e. the ‘incurable’ area): the light green—trajectories eventually get into the failure zone; the dark green—trajectories are cyclic and cannot cross either the recovery or failure barriers. (Online version in colour.)

Starting from any incurable configuration, one could similarly pose a different control problem of maximizing the time until crossing the failure barrier. While we do not address it here, we note that the HJB approach would be quite suitable to find optimal treatment policies for this problem as well.

4. Discussion

By now, it is widely accepted that cancer is an evolutionary process, and that variation and selection drive the emergence of drug resistance. While this new knowledge is driving cancer research forward, it has largely not yet affected the practice, with the majority of clinical protocols relying on MTD-based approaches, which invariably fail in the setting of most metastatic disease. This is changing with the advent of AT—therapeutic strategies specifically designed with a changing regimen prescribed: one that adapts to an evolving tumour [48].

To optimally design AT protocols, the underling dynamics of the tumour growth and treatment response must be known. While the methods of learning these dynamics are still in their infancy, the last decade has seen a flurry of activity using EGT and other evolutionary models for a range of prescribed dynamics. These works have shown qualitative changes in tumour behaviour in a range of treatment scenarios, and importantly, demonstrated that the sequence [20,49–51] and timing [13,20] of therapy can drastically change the outcomes. As we come closer to the reality of evolutionarily designed therapeutic trials in the mainstream, it is important to develop methods that do not just improve outcomes but aim to formally optimize them.

However, before using any optimization tools, one needs to choose a specific quantifiable criterion for comparing the outcomes. Once that criterion is selected and the underlying mathematical model is sufficiently accurate, the best treatment strategy can be found by the techniques of optimal control theory. In this paper, we show how this can be done for one particular heterogeneous cancer model previously described in Kaznatcheev et al. [20]. We show that the optimal treatment policy can have multiple regimes: always on $d^{\ast }(\cdot )\equiv d_{\max }$, always off d*( · ) ≡ 0, and involving several contiguous treatment periods. For the latter, the challenge is to accurately approximate the on/off ‘switching curves’ in the state space. We show that the definition of optimal treatment policy is heavily dependent on a parameter σ describing the relative importance of minimizing the total amount of drugs versus the total time to recovery. We further show that, for some parameter regimes, there are ‘incurable regions’ in the state space—the starting configurations that will not lead to a recovery regardless of the chosen treatment strategy—suggesting an alternative therapy (or goal) should be considered. Moreover, for some starting configurations, the ‘always on’ treatment might not lead to a recovery even if it is achievable with some on/off hybrid strategies.

Just like any other model, the approach in Kaznatcheev et al. [20] is based on simplifying assumptions (e.g. only the subpopulation fractions are important, and no novel types can arise), which limit its practical applicability. But our message is broader, and we use this specific model primarily to illustrate the general optimization approach applicable to more detailed cancer evolution equations or even in data-driven/equation-free framework.

Of the two main approaches of optimal control theory, the PMP has been much more widely used in cancer treatment research up until now. By contrast, our approach here is based on dynamic programming and the numerical methods for HJB equations. The higher computational cost of these methods is balanced by several important practical considerations. First, they yield a policy in feedback-form and are thus more robust to modelling/measurement errors. Second, they always return the globally optimal treatment strategies and avoid some of the pitfalls well-known for the PMP-based methods (e.g. figure 3b). With the advent of efficient numerical methods, we posit that the HJB equations will be soon playing a larger role in treatment optimization.

There are several obvious directions for extending our approach. First, the ability to optimize outcomes for a range of criteria will open new avenues to quantify physician/patient discussions (on trade-offs and personalized therapy) that have previously been only qualitative. The computation of optimal policies for different values of σ (covered in the electronic supplementary material) can be viewed as a small step in this direction. But there are also many other possible optimization criteria of practical interest. Methods for approximating all Pareto-optimal policies are available [52] but are usually more computationally challenging. For probabilistic cancer evolution models, one can also choose between optimizing different characteristics of the same random quantity (e.g. minimize the average time-to-recovery versus maximizing the probability of recovery in the next year). Finally, one can also use the choice of criterion to promote robustness by systematically treating possible measurement/modelling errors as perturbations chosen by some adversarial player. Such ‘games-against-nature’, as described recently by Stanková et al. [48], can be similarly treated by solving Hamilton–Jacobi–Isaacs equations.

While we believe that our optimization approach will have a major role in design of future clinical trials of AT, the presented version is not yet sufficiently practical. One important limitation is our assumed full knowledge of the system state: the exact subpopulation fractions are needed at every point in time to decide whether to administer the drugs. In practice, one can periodically obtain an approximation of these quantities (e.g. based on a repeat biopsy), but most of the time the decisions must be made based on some less invasive measurements (e.g. based on PSA-levels [17] or on circulating cell-free DNA [53]). A rigorous treatment of such partially observable controlled processes [54] would require a much more detailed model of ‘tumour state’ uncertainties. As an intermediate step, we would recommend validation of such methods in vitro and in vivo, using measured, instead of prescribed games. This is a topic of active interest to our group [45,55], and would be prudent to address before any clinical trials.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

M.G. acknowledges the support from the Institute for Data and Decision Analytics at The Chinese University of Hong Kong, Shenzhen during his visit when this research was completed. J.G.S. would like to thank the NIH Case Comprehensive Cancer Center support grant no. P30CA043703 and the Calabresi Clinical Oncology Research Program, National Cancer Institute Award number K12CA076917. A.V. would like to thank the Simons Foundation for its fellowship support and the National Science Foundation (award DMS-1738010) for supporting development of numerical methods for Hamilton–Jacobi equations. A part of this work was performed during a sabbatical leave at Princeton/ORFE, and A.V. is grateful to ORFE Department for its hospitality.