Numerical modelling of the effect of intermittent upwelling events on plankton blooms

Abstract

In the marine environment, biological processes are strongly affected by oceanic currents, particularly by eddies (vortices) formed by the hydrodynamic flow field. Employing a kinematic flow field coupled to a population dynamical model for plankton growth, we study the impact of an intermittent upwelling of nutrients on triggering harmful algal blooms (HABs). Though it is widely believed that additional nutrients boost the formation of HABs or algal blooms in general, we show that the response of the plankton to nutrient plumes depends crucially on the mesoscale hydrodynamic flow structure. In general, nutrients can either be quickly washed out from the observation area, or can be captured by the vortices in the flow. The occurrence of either scenario depends on the relation between the time scales of the vortex formation and nutrient upwelling as well as the time instants at which upwelling pulses occur and how long they last. We show that these two scenarios result in very different responses in plankton dynamics which makes it very difficult to predict whether nutrient upwelling will lead to a HAB or not. This may in part explain why observational data are sometimes inconclusive in establishing a connection between upwelling events and plankton blooms.

1. Introduction

Coastal regions susceptible to harmful algal bloom (HAB) events are often subjected to upwelling [1]. Due to this upwelling, nutrient-rich deep waters are transported into the euphotic zone and this inflow fosters favourable conditions for the growth of algae [2]. As recent studies note a significant increase of the number of HAB events in the whole world [3–5], it becomes imperative to understand the interplay between the biotic and physical factors that work as their trigger.

Lateral mixing and stirring by the hydrodynamic flow redistributes nutrients and suspended microorganisms, shaping the spatial heterogeneity of the marine ecosystem at different scales [6], leading to plankton blooms, which exhibit a non-uniform distribution in space, referred to as ‘patchines’. This non-uniformity was ubiquitously detected around the globe by satellite imagery [7–10] and by samples along ship transects [11–13]. In a seminal work by Abraham [14], a very simple model of turbulent transport was able to reproduce this spatial heterogeneity in the plankton distribution and its statistical properties, such as spectra. He also observed a difference in phytoplankton and zooplankton patchiness by introducing a long maturation time for the zooplankton species. Subsequent theoretical studies have observed that the ratio between biological and hydrodynamic flow time scales has a non-trivial impact on how plankton is distributed spatially [15,16]. The flow field influences not only the spatial distribution but also the abundance of plankton. Further studies have shown that it is possible to trigger or suppress HABs by tuning the flow to the biological time scales [17,18]. Therefore, the hydrodynamics plays a central role for phytoplankton ecosystems, not only with respect to spatial patterns but also to the inter-specific interactions, establishing so-called fluid dynamical niches, which provide particular growth conditions for certain species [19,20]. Coherent structures of the flow field, such as, for instance, eddies, play an important role influencing the biological processes in the ocean. The recent advances in detecting and tracking eddies in the ocean have shown that they often are long-lived. Notably, they can trap fluid and the whole community of plankton and bacteria inside, which affects the diversity and dominance structure of phytoplankton species observed in the system [20,21]. On the one hand, the species in the almost isolated ecosystem inside the eddy are subjected to competitive pressure. On the other hand, theoretical models speculate that due to this trapping the organisms can also be sheltered inside the eddy from predators or competitors, a mechanism proposed as a possible explanation for the coexistence of species [22–25]. Both effects are a direct result of transport barriers established by the flow field.

The productivity-enhancing effect of coastal upwelling is also shown to be strongly affected by the presence of coherent structures in the flow field [26–28]. The eddies mix and disperse nutrients, while also taking them away from the coastal region. This leads to a decrease in the primary production near the shore, as was recorded for eastern boundary upwelling systems [28]. Furthermore, these nutrients while being transported offshore by the eddies may also trigger the growth of the associated phytoplankton. Theoretical works have shown that eddies, in this case, work as incubators for growth by sustaining favourable environmental conditions. These models emphasize the importance of the role of biological and hydrodynamic time scales in triggering plankton blooms and specifically HABs in this scenario [29–32]. However, these studies have so far only analysed the conditions of an upwelling which is constant in time. Nevertheless, upwelling itself is not a steady process since it depends on winds and seasonality, being therefore highly intermittent. Furthermore, from observations of HABs in nature, it is not always possible to correlate the strength and the duration of an upwelling event and the occurrence and magnitude of HABs. While it was possible to establish such a direct relation for some species (e.g. diatoms of genus Pseudo-nitzschia [33,34] and some dinoflagelates [35]), for others a more complex chain of events appears to be driving the outcome [36]. Moreover, the major challenge consists of finding out how the occurrences of HABs and the episodic upwelling events are associated on a local scale [36,37].

In this work, we analyse the impact of intermittent upwelling events on phytoplankton growth and changes in dominance patterns in the presence of mesoscale hydrodynamic structures for a biological system with three trophic levels. We modify the reaction–advection–diffusion model introduced by Sandulescu et al. [29] for the area around the Canary Islands [29], which couples advection by a vortex street behind an island with a model of plankton dynamics. As in [29] we also choose to ignore the possibility of eddy-induced Ekman pumping, a well-known phenomenon where circulating ocean currents bring nutrients upwards or downwards within the eddies [38,39]. In this way, we can isolate plankton’s response to a single upwelling region, and study the effects of upwelling intermittency. Furthermore, it allows us to simplify to horizontal advection only. In contrast to [29], we analyse here a community that consists of two phytoplankton species competing for a limiting resource and grazed by zooplankton. The population model [40] chosen displays excitability, which arises from the interplay of the fast dynamic time scale of phytoplankton growth (activator) with a slow development of zooplankton (the inhibitor). We chose two scenarios with different plankton communities: (I) where the community structure is shaped only by the availability of nutrients in the environment; (II) where both the grazing pressure and the nutrient availability trigger the bloom formation. First, we show that these two systems exhibit very different spatio-temporal dominance patterns and display distinct and characteristic dynamical response to an upwelling event. Then we show that for both parametrizations even identical pulses of nutrient influx trigger a diverse set of reactions in the plankton dynamics. The variety of possible responses can only be understood by analysing the interplay of different time scales that characterize the system as well as the interplay between the upwelling and mesoscale hydrodynamic structures present in the flow. Our analysis shows that it is impossible to establish a relation between HAB formation and upwelling events by only looking at the respective time series of nutrients and plankton abundances without considering the mesoscale mixing by the ocean flow in the observation region.

The work is organized as follows. First, in §2, we briefly introduce the coupled hydrodynamic–biological model used. In §3.1, we examine how the position and initial time of nutrient parcels initialized at the upwelling region affect the residence time of nutrients in the observation area. In §3.2, we describe the spatio-temporal patterns of plankton for the case without upwelling and in the presence of a single upwelling pulse. Next, in §3.3, we describe how the response of the populations varies considering different initial times for an upwelling pulse. Furthermore, we analyse the chance of HAB formation for upwelling pulses of different duration and strengths. In §3.5, we extend our analysis to the study of the response to a series of irregular (intermittent) upwelling events. We conclude in §4.

2. Model

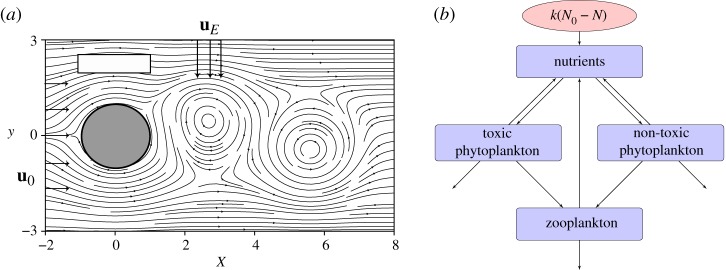
This section describes the modelling framework used in this work. The model consists of a two-dimensional kinematic velocity field coupled to a biological model (figure 1).

Figure 1.

(a) Two-dimensional flow field of the vortex street behind an island. The white rectangular area above the island (grey cylinder) sketches an upwelling region, while the arrows symbolize the Ekman flow u_E perpendicular to the unperturbed flow of strength u₀. (b) Schematic of the biological model.

2.1. Hydrodynamic model

The hydrodynamic model is represented by a two-dimensional kinematic velocity field (u_x, u_y) that flows through a predefined observation region passing by a circular obstacle (of radius r), located at (x₀, y₀) = (0, 0), mimicking an island. The strength of the unperturbed flow velocity u₀ is such that it allows for a periodic formation of vortices in the wake of the island, setting the shedding events at every T/2. In one period, two vortices are released and carried away from the island along the observation region by the main flow u₀, from left to right in figure 1a. These vortices rotate in opposite directions and are characterized by a vortex strength ω. One of them travels slightly above and the other slightly below the axis at y = 0. This kinematic velocity field is generated by a predefined stream function Φ: u_x = ∂Φ/∂y, u_y = −∂Φ/∂x. It is known as an open chaotic flow in the literature; for details see [29,41]. The model has been parametrized to represent one of the islands of the Canarian Archipelago, located in the Eastern Boundary Upwelling System off the African coast, in agreement with [29]. For parameters, see electronic supplementary material. The spatial units throughout the paper are given in units of 25 km (radius of the island).

2.2. Biological model

The biological model used consists of a food web with three trophic levels NPPZ (nutrients, two phytoplankton species and zooplankton) formulated in [40] to describe the formation of HABs. One of the phytoplankton species is considered to be toxic and the other one non-toxic, their concentrations are P_T and P_N, respectively. They compete for a limiting nutrient resource, N, while being grazed by zooplankton, Z (figure 1b). The inter- and intraspecific interactions are described by

$$\begin{array}{rl}\frac{\text{d}N}{\text{d}t}& =k[N_0-N]-g(P_N,P_T)[f_N(N)P_N+f_T(N)P_T]\\ & +r_N{P}_N+r_T{P}_T+\beta h(P_N,P_T)[\lambda (1-\varphi )P_N^2\\ & +\lambda \varphi P_T^2]Z+\gamma \hspace{0.17em}\text{d}Z,\\ \frac{\text{d}{P}_N}{\text{d}t}& ={\theta }_N{f}_N(N)g(P_N,P_T)P_N-r_N{P}_N\\ & -\lambda [1-\varphi ]h(P_N,P_T)P_N^{2}Z-s{P}_N,\\ \frac{\text{d}{P}_T}{\text{d}t}& ={\theta }_T{f}_T(N)g(P_N,P_T)P_T-r_T{P}_T\\ & -\lambda \varphi h(P_N,P_T)P_T^{2}Z-s{P}_T\\ \text{and}\frac{\text{d}Z}{\text{d}t}& =[{\alpha }_N\lambda (1-\varphi )P_N^2+{\alpha }_T\lambda \varphi P_T^2]h(P_N,P_T)Z-\text{d}Z.\end{array}$$ 2.1

The functional responses used are listed in table 1. An important characteristic of this model is that the nutrient uptake by phytoplankton f_N,T(N) (f_N(N) for the non-toxic species and f_T(N) for the toxic species) is given by a Holling Type II functional response, while the grazing of zooplankton h considers a Holling Type III functional response (table 1). Additional effects of interspecific and intraspecific competition are given by the function g, where a/b is the maximum nutrient uptake rate of phytoplankton averaged over the depth of the mixed layer. The rate of loss due to sinking is given by s. The differences between the two groups of phytoplankton can be introduced through different parameters: their nutrient conversion rates θ_N,T, half-saturation constants e_N,T, respiration rates r_N,T, their feeding preference by zooplankton ϕ, and their quality as food for zooplankton expressed by the conversion rates α_N,T. The recycling by bacteria is considered indirectly with factors β and γ for conversion of the dead material back into nutrients.

Table 1.

Functional responses used in equation (2.1).

nutrient uptake by non-toxic species of phytoplankton	fN(N)	$\frac{N}{e_N+N}$
nutrient uptake by toxic species of phytoplankton	fT(N)	$\frac{N}{e_T+N}$
growth rate limitation due to light attenuation	g(PN, PT)	$\frac{a}{b+c{P}_N+c{P}_T}$
feeding rates of the zooplankton	h(PN, PT)	$\frac{1}{({\mu }^2+P_N^2+P_T^2)}$

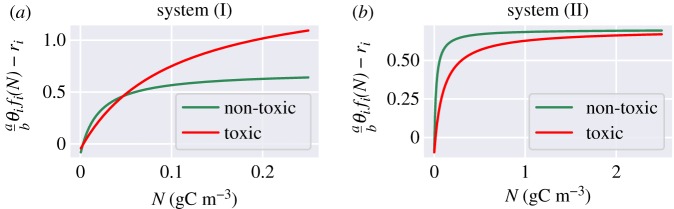
As we will show below the system’s response to nutrient influx from upwelling results from a combination of bottom-up and top-down controls. To be able to analyse how these controls drive HAB formation, we chose two different parametrizations for the population model: system (I), where the community structure and the dominant species result mainly from the availability of nutrients in the environment; system (II), where the grazing preference of zooplankton together with the nutrient availability both establish the resulting community structure. The parameters chosen for the two systems are very similar, with a few differences which emphasize different ecological processes. In system (I), the nutrient conversion rate θ_i and the respiration rates r_i are different for each species (θ_N < θ_T, r_N > r_T), so that the net growth rate per capita of P_T is only larger than the one of P_N for high nutrient concentrations (figure 2a). On the contrary, in system (II), these parameters are set to the same values (θ_N = θ_T, r_N = r_T), for both species. Consequently, in system (II), the abundance of nutrients cannot drive a dominance change (figure 2b), because per capita the net growth rate of P_N is always larger than of P_T. To test the role of grazing, we modify the parametrization of zooplankton in the second system. In order to have a stronger influence of the grazer within the food chain, we boost the abundance of zooplankton by increasing its maximum grazing rate λ and its growth efficiency on the non-toxic species α_N. Finally, we also add in this set-up a strong preference of zooplankton to feed on non-toxic species (ϕ = 0.05), contrarily to system (I) where there is no preference (ϕ = 0.5). With this change, system (II) has a very strong top-down control by design; see electronic supplementary material.

Figure 2.

(a,b) Approximate net-growth rate per capita per day of the two phytoplankton groups (it neglects the self-shading function and the grazing by zooplankton).

As described previously, the model takes into account the vertical influx of nutrients from the deep ocean into the mixed layer where all biological processes take place. The rate of this influx is given by k. This influx of nutrients may occur due to turbulent diffusion (k = k_d) or by vertical transport due to upwelling (k = k_up). Using the vertical diffusion coefficient for the ocean (D_v ∼ 0.1–2.6 m² d⁻¹ [2,42]), we can evaluate k_d in the range of 10⁻² – 10⁻⁴ d⁻¹. Using the measurements of vertical currents, with velocities from 10 to 40 m d⁻¹ [42,43], in the upwelling regions we can estimate k_up of the order of unity; cf. electronic supplementary material.

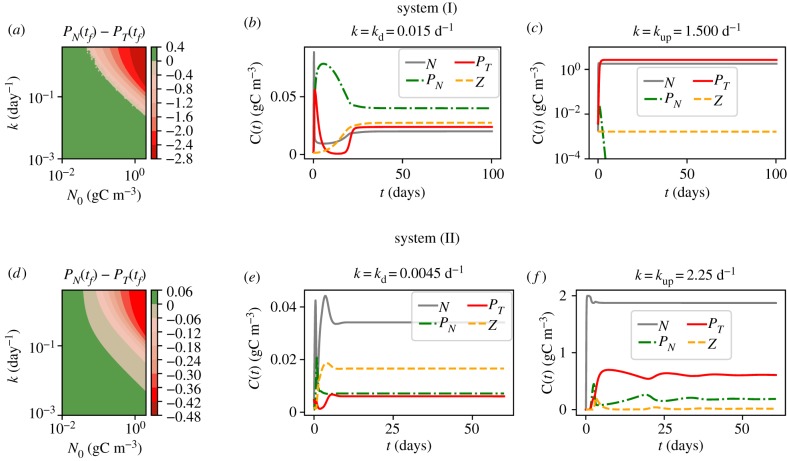
As already mentioned the nutrient influx is regulated by two parameters: the cross thermocline exchange rate k and the nutrient concentration below the thermocline N₀. It is, therefore, compelling to outline here how the coupled effect of these parameters is reflected in the steady-state community structure. These results are summarized in figure 3a,d for systems (I) and (II), respectively. The region of dominance of the toxic species is shown in red, and of the non-toxic in green. In the next simulations, we chose to use N₀ = 2 gC m⁻³ and we also set up two values for the cross thermocline exchange: k_d and k_up representing the conditions without and with upwelling, respectively.

Figure 3.

(a,d) Difference between the concentrations of the non-toxic P_N and toxic P_T species, after 5000 days, for a range of values of the thermocline exchange rate k and of concentrations of nutrients below the thermocline. (b,c,e,f) Time evolution of the biological model for low (b,e) and high (c,f) cross thermocline exchange rates k, for N₀ = 2 gC m⁻³.

Our choice for system (I) corresponds to k_d = 0.015 d⁻¹ and k_up = 1.5 d⁻¹. These values will be used in all further simulations of system (I), unless stated otherwise. The dynamics of the system towards the steady state for diffusive exchange k_d = 0.015 d⁻¹ is shown in figure 3b and leads to a steady state with a dominance of the non-toxic species; see table 2. As explained previously the community structure in system (I) directly reflects the low amount of nutrients of this scenario. Note that for k_d = 0.015 d⁻¹, the presence of zooplankton allows for the coexistence of the two phytoplankton species. On the other hand, for a high nutrient supply k = k_up = 1.5 d⁻¹, the dynamics leads to the dominance of the toxic species and even the extinction of its competitor (figure 3c).

Table 2.

The steady-state values in gC m⁻³ for the systems subjected to k_d or k_up.

	Sys.(I)		Sys.(II)
k (d−1)	0.015	1.5	0.0045	2.25
N	0.02	1.800	0.034	1.873
PN	0.04	<10−4	0.007	0.188
PT	0.024	2.659	0.006	0.608
Z	0.028	0.002	0.016	0.015

The parameters chosen for the further analysis for system (II) are: k_d = 0.0045 d⁻¹ and k_up = 2.25 d⁻¹. Note that a smaller k_d value in this system leads to lower concentrations of phytoplankton in the steady state (table 2). Again we find that with a large input of nutrients the toxic species dominates. However, the main mechanism of how this dominance is achieved differs from the previous case as explained above (figure 2) and explanation to it. Note that we observe here a significant amount of the total biomass concentrated at the higher trophic level, especially for low k. Nevertheless, a low concentration of phytoplankton limits the growth of zooplankton leading to concentration values comparable to that of the first scenario. Another distinction of this set-up is the presence of both species of phytoplankton in the steady state for low as well as high nutrient influx (figure 3e,f).

2.3. Coupled model

The full biological–hydrodynamic model consists of the following reaction–advection–diffusion system of equations:

$$\begin{array}{rl}& \frac{\mathrm{\partial }C}{\mathrm{\partial }t}+\mathit{u}\cdot \mathbf{\nabla }C=F_c+D{\mathrm{\nabla }}^{2}C,\\ & \text{with}\hspace{0.17em}C\in [N,P_N,P_T,Z],\end{array}$$ 2.2

where C(x, y, t) represents the concentration of nutrients or plankton species in space and time, u is the flow field explained in §2.1 and F_c are functions representing the biological interactions among these species, which are given by the right-hand side of equations (2.1). We consider a horizontal turbulent diffusion constant D = 10 m² s⁻¹ that describes the advection by smaller scales in the flow field. Note that our framework focuses on mesoscale advection and does not capture small scale heterogeneities of species’ concentrations within a grid cell (dx = dy = 500 m) nor the interactions between individuals which cannot be described by concentrations. Furthermore, equation (2.1) describes the dynamics as vertically averaged model in the mixed layer while vertical transport is encapsulated in the biological model considering only the vertical exchange of nutrients and the sinking of phytoplankton (cf. §2.2). The influx concentrations at the left boundary are set up as 20% of the steady-state values of table 2. For numerical details, see electronic supplementary material. The code for the simulation reported here can be found in the Github repository: https://github.com/kseniaguseva/Upwelling.

3. Results

3.1. Hydrodynamic time scales

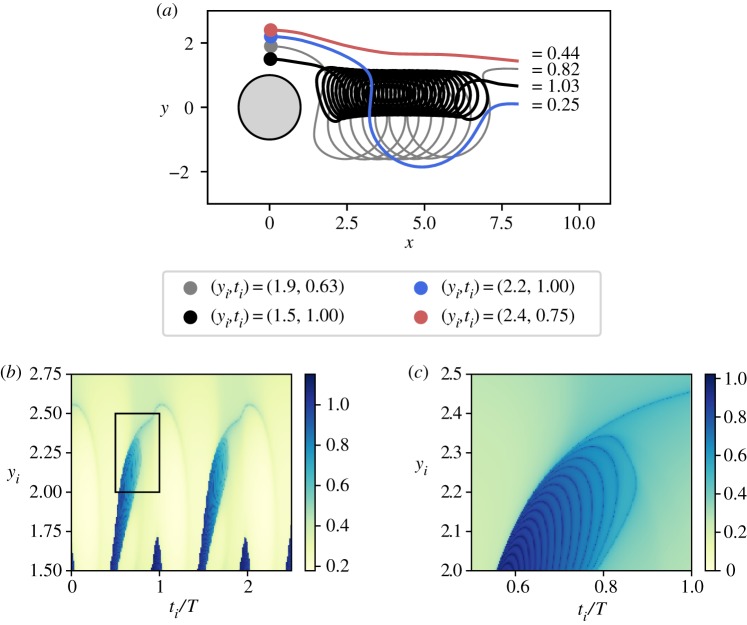
To understand the conditions for HAB formation in the presence of an intermittent upwelling, it is important to analyse the interplay between hydrodynamic and biological time scales. We start the study of this non-trivial coupling by analysing the hydrodynamics that underlies all the biological processes in our system. To that purpose, we follow the motion of non-reacting fluid parcels passively transported by the flow field (tracers). Since we are interested in the impact of upwelling, we compute the residence times of tracers starting in the upwelling region. Furthermore, we want to understand how the residence times of tracers depend on the initial time instant of their release. We measure it by releasing the tracers at a location (x_i, y_i) and by recording the time τ_i when they reach the right boundary at x = 8.

We start by characterizing the possible trajectories that a tracer element can take depending on its release time t_i and its release coordinates (x_i, y_i); see typical trajectories and the respective τ_i in figure 4a. The main difference in τ_i arises from whether the tracer is captured by a vortex in the wake or not: the ones captured into a circular trajectory around the vortex core (black and grey trajectories in figure 4a) spend at least two times longer in the observation area than the ones that are transported more or less straight by the main flow (red and blue trajectories of figure 4a). Figure 4b summarizes our results on residence times of trajectories starting at (x_i = 0, y_i, t_i). The periodicity of the flow can be seen by the repeating patterns shown in figure 4b. The two finger-like structures in the residence times (in blue) correspond to tracers that are captured by the vortices. Another important characteristic of these patterns is their fractality (figure 4c), which directly reflects the influence of the stable and unstable manifolds of the chaotic saddle present in the system [32,41]. Note that although we have chosen to fix x_i at x_i = 0, the results for other release positions within the upwelling region are very similar.

Figure 4.

(a) Typical trajectories of tracers that start in the upwelling region. (b) Residence times of tracers as a function of initial time t_i (in T) and the vertical coordinate y_i. (c) Amplification of the rectangular area of (b).

In summary, when we identify the tracers with nutrients released during upwelling, then the residence time of nutrients in the observation region changes with the position of the upwelling region, the location of release within that region, and the time instant when the nutrients are released. Next, we will investigate the consequences that this effect has on the plankton dynamics.

3.2. Reaction to an upwelling pulse: spatio-temporal patterns

Before we start with the results of this section, we shortly discuss the characteristics of the system in the absence of upwelling. In the absence of upwelling, the spatial distribution of the biological species follows the inhomogeneous nutrient distribution in space. What is observed is an accumulation of nutrients in certain areas, due to the small advective velocities around the island coupled with a constant nutrient influx from below the thermocline (k_d). Subsequently, this high nutrient concentration is captured by the vortices behind the island. This results in a bloom of non-toxic species in these regions in system (I), and a non-toxic bloom followed by the growth of zooplankton in system (II); cf. electronic supplementary material. We define the values of the spatial average over the observation region as 〈C〉, where C stands for N, P_N, P_T or Z. In addition, we will also use a distinct notation for the time average of 〈C〉, established over n periods, for the case without upwelling, defining it as ${⟨C⟩}^{\ast }=(1/nT){\int }_0^{nT}⟨C⟩\hspace{0.17em}\text{d}t$. The values for the two systems are shown in table 3. Note that the main aspects of the growth dynamics of plankton can be understood already from the system without the flow field; see §2.2.

Table 3.

Spatial averages in gC m⁻³ for the system without upwelling. Here, as in §2.2, the two scenarios are characterized by different k_d values.

	Sys.(I)	Sys.(II)
k (d−1)	0.015	0.0045
〈N 〉*	0.025	0.0286
〈PN 〉*	0.042	0.0084
〈PT 〉*	0.019	0.0010
〈Z 〉*	0.005	0.0054

After having analysed the coupled hydrodynamic–biological model, let us characterize the HAB formed in the two systems in the presence of a simple upwelling pulse. We introduce a single upwelling event at 2.5 T, when k_d at the upwelling area is exchanged to k_up. It is kept at this constant value for δ = 0.5 T, when it returns to k_d. For such event, the nutrients can be captured into the lower vortex. Note that as shown in §3.1, the upper vortex can only capture nutrients, if these are released very close to the island, which is not the case for our set-up.

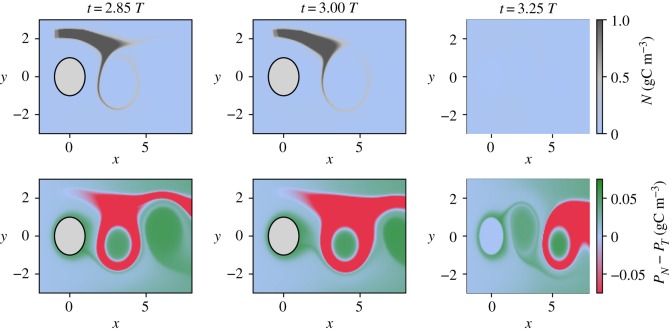
In system (I), the spatio-temporal distribution is simple: the non-toxic species grows in the vortex cores undisturbed by the upwelling event, while the toxic species grows mainly by feeding on nutrients released by the upwelling. Figure 5 illustrates these dominance patterns for three instances of time that follow an upwelling event. Here, we have specifically chosen an upwelling event that triggers a strong dominance change. Note the fast dominance change in the system as a response to the nutrient influx.

Figure 5.

Spatial distribution of the dominance patterns which follow an upwelling event at 2.5 T for system (I).

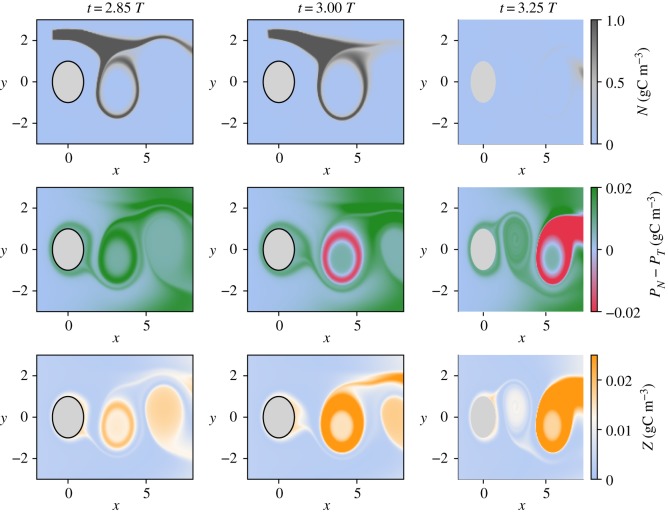
By contrast, in system (II), both phytoplankton species readily grow in response to the nutrients. However, there is a stronger response of the non-toxic species due to its lower half-saturation constant, which allows it to reach high concentration and initiate the growth of zooplankton. However, the zooplankton development is a slow process and it only reaches significant concentrations when the non-toxic bloom is captured by a vortex. It is in this region where the toxic species, with extra nutrients and the presence of zooplankton, can successfully compete with non-toxic species. In fact, the high grazing pressure of zooplankton on the non-toxic species allows for the very localized dominance of the toxic species (figure 6). Note that when the bloom of the toxic species forms, the nutrients brought by the upwelling were already partially consumed.

Figure 6.

Spatial distribution of the dominance patterns which follow an upwelling event at 2.5 T for system (II).

We emphasize that the spatio-temporal dominance patterns that appear in this system in the presence of upwelling in systems (I) and (II) strongly differ. This difference can be explained by the fact that they result from distinct biological mechanisms: bottom up and top down controls. Furthermore, the two set-ups are characterized by different times for achieving the dominance change from the non-toxic to the toxic species as a response to the inflow of nutrients.

3.3. The impact of initial time of the upwelling event

In §3.1, we have illustrated that fluid parcels released at different times, t_i, from the upwelling region can take very distinct paths through the observation area. Some of these paths transport the fluid parcels directly away, describing a quick escape from the observation area, while others consist of spiral trajectories around vortex cores. These latter trajectories, in turn, are characterized by long residence times. In this section, we will connect the advection with the plankton dynamics. Our objective is to answer how these different time scales affect the formation of HABs. Thus, we initialize upwelling pulses starting from different initial times t′, with a predefined duration δ and strength k_up.

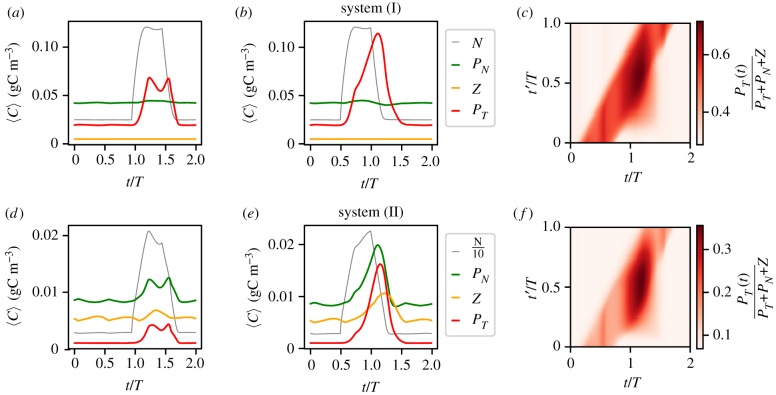
Now we analyse how these upwelling events impact the time series of the spatial averages of the plankton species of our biological model. While in the time series of system (I) only the toxic species exhibits a strong response to the upwelling events, in system (II) we observe, on the contrary, spikes in the growth of both phytoplankton populations and even in the abundance of zooplankton (figure 7a,d). Despite these differences, we observe that in both systems the dynamics of the response of the plankton model to the upwelling event depends on its initial time t′: in both systems, we can have weak or strong responses; see figures 7a,d and 7b,e respectively. This result is summarized in figure 7c,f where the biomass of the toxic species is compared to the total biomass for an event with duration δ = 0.5 T. While for system (I) which is solely nutrient controlled we observe a dominance change for the average concentrations, this behaviour is absent for system (II), which has a strong top down control element. In system (II), we observe only spatially local dominance change which never reaches a dominance of the toxic species in the spatial average. Note the similarity of the diagrams of the two biological systems. The similarity of the response patterns for both systems (I) and (II) with respect to the timing of the response is entirely determined by the hydrodynamics.

Figure 7.

(a,b,d,e) Two possible responses of the population dynamics to the influx of nutrients through upwelling events (δ = 0.5 T) initiated at: (a,d) t′ = 0.95 T and (b,e) t′ = 0.5 T. (c,f ) The time evolution of the relative biomass of the toxic species following upwelling events. The top panels (a–c) represent the results for system (I) and the bottom panels (d–f ) for system (II).

3.4. Impact of the duration and strength of the upwelling event

So far we have seen that the initial time of an upwelling event plays a crucial role for the mechanism of formation of HABs. In this section, we extend our analysis to investigating the effect of the duration and the upwelling strength of randomly initialized upwelling events.

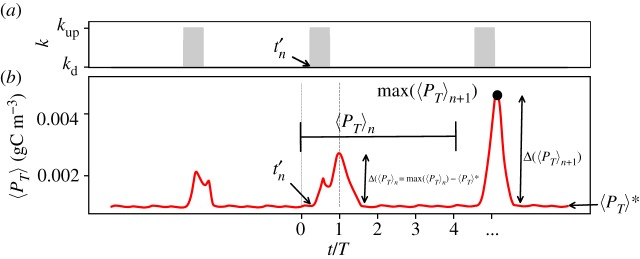
We compose the sequence of upwelling pulses in the following way. The upwelling events are initiated at particular time instants given by 4Tn + t′_n, where n ∈ ${\mathbb{N}}^{\ast }$ and t′_n is chosen randomly for every n from the interval [0, T] (figure 8a). We establish that each sequence is characterized by upwelling events of duration δ and strength k_up. To quantify the effect of the upwelling on the growth of the phytoplankton species, the time series is divided into n intervals: each one of them containing four periods and a single upwelling event. The time series of the average concentration 〈C〉 for each one of these intervals is denoted 〈C〉 _n. Thus, the effect of each upwelling event on the population dynamics is reflected in the maximum, max (〈C〉_n), or by the deviation of maximum concentration from the undisturbed one 〈ΔC 〉 _n = max (〈C〉_n) − 〈C〉 *.

Figure 8.

(a) Time series of the strength of the thermocline exchange rate at the upwelling region; (b) example of a time series of the spatial average of concentration of the toxic species, with blooming events triggered by upwelling.

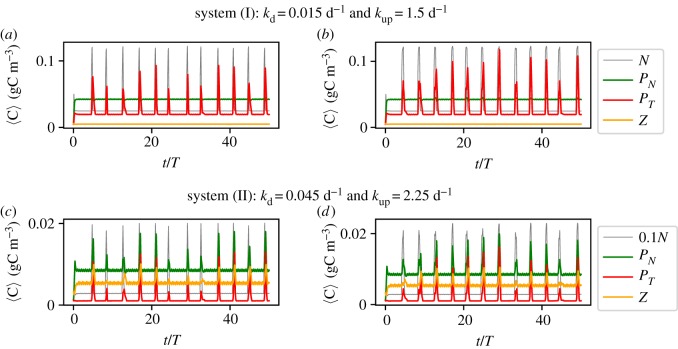
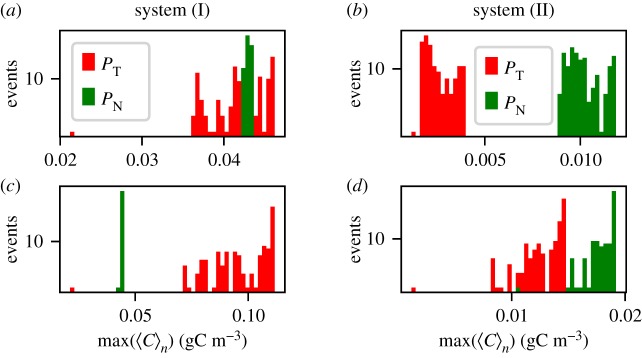
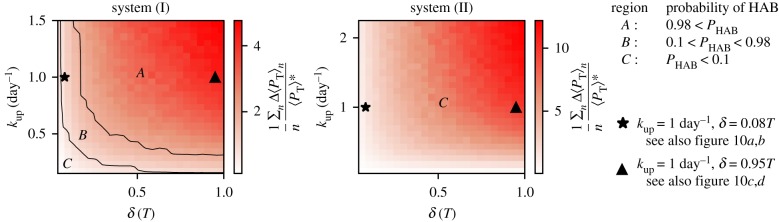
We start our analysis by fixing k_up. In the resulting time series of system (I), see figure 9a,b, the toxic species are the only species that show a response to upwelling in its average values. On the contrary, in system (II), all the species show a bloom-like behaviour; figure 9c,d. It is clear that the average values shown for both of these systems fail to completely describe the complexity of the spatio-temporal dynamics. Nevertheless, part of this complexity is revealed by the variability of different dynamic responses of the biological community to seemingly identical upwelling events (figure 9). Comparing the different responses for the same system with the same duration, we note that it depends crucially on the timing of the upwelling event, how strong the response is going to be. This reveals clearly the importance of the structure of the flow field at the time instant of the upwelling. Additionally, our results reveal that this variability depends on the duration δ, and this relation manifests itself in a similar way for both systems (figure 9). Our results reveal that longer upwelling events are associated with a vigorous growth of the toxic species. For this case, the probability of HABs is large and we observe high peaks in the concentration of the toxic species (large values of Δ〈P_T〉_n). On the other hand, shorter δ values reveal a larger variety of possible outcomes. These results are summarized in the histograms of figure 10 (note the difference of the axes between the upper and the lower panels). The observed behaviour can be explained by taking into account that HAB formation depends on the temporal overlap between the upwelling event and the vortex formation in the wake of the island. Naturally, for larger δ the probability of this overlap is higher and more nutrients are captured to incubate the growth of the toxic species. The strength of upwelling events has a complementary influence. For small values of k_up, the system needs longer upwelling events to release enough nutrients for toxic species to bloom (figure 11). Therefore, each pair of k_up and δ values results in a dynamics with a certain probability of bloom formation, which is strongly influenced by the vortex shedding. The average values of the response of the toxic species $(1/n)\sum _n\mathrm{\Delta }{⟨P_T⟩}_n/{⟨P_T⟩}^{\ast }$, calculated using n = 150 upwelling events, are shown in figure 11. Note the regions with different probabilities of HAB formation P_HAB = P(max (〈P_T〉)_n>max (〈P_N〉_n), A, B and C, showing that the dominance patterns themselves for each pair of these parameters are also related to the biological model chosen.

Figure 9.

Time series of the spatial averages of the concentrations of our biological model 〈C〉 in (a,b) system(I) and (c,d) system (II). The systems are subjected to randomly initiated pulses of upwelling characterized by the duration: (a,c) δ = 0.25 T; (b,d) δ = 0.5 T.

Figure 10.

The distribution of the observed responses of the toxic and non-toxic species to the upwelling pulses, 250 upwelling events distributed over 1000 T for (a,c) system (I) and (b,d) system (II) using: k_up = 1.0 d⁻¹ and (a,b) δ = 0.08 T; (c,d) δ = 0.95 T.

Figure 11.

Responses of the toxic species to upwelling events of different duration δ and strength k_up.

At the end of this section, we want to stress that from an analysis of the time series only, it is especially difficult to establish a causal relation between the upwelling event and the rate of increase of the toxic species. Although an increase in the population of the toxic species always follows the upwelling in our model system, the level of increase in the population varies strongly (figure 10d). This variety of the possible outcomes, however, can be easily explained by coupling the biological model with hydrodynamic mesoscale motion. Therefore, by taking into account the interplay between the initial time of the upwelling event and the formation of vortices in the wake, it is possible to better explain under which conditions the formation of a HAB can be expected.

3.5. Intermittent upwelling events

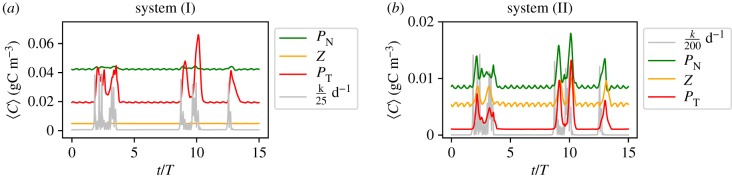
In the previous sections, we have seen that an upwelling pulse, even of the simplest possible profile, can result in a variety of possible outcomes for the plankton growth. The intricate interplay between plankton dynamics and the formation of vortices, or more general mesoscale hydrodynamic structures, results in time series showing responses of different strengths for identical upwelling events. Here, in this section, we analyse the response of our model to upwelling events that follow a time series that displays more complex patterns. The idea here is to mimic a more realistic situation, since upwelling is a wind driven phenomenon and, hence, has an intermittent character. To generate this new time series of upwelling events, we use a dynamical system which displays a special type of intermittent behaviour, known as ‘on–off’ intermittency [44]. Two modes appear in this system: the ‘off’ mode (situation without upwelling) where an observable dwells on very small values for long intervals of time; these intervals are interrupted by seemingly random bursts, characteristic to the ‘on’ mode (upwelling events). Therefore, the thermocline exchange rate at the upwelling region in the ‘off’ mode is k_d and in an ‘on’ mode k_up, which here assumes a set of random values obtained from the dynamical system described in the electronic supplementary material.

Figure 12 shows the response of our two biological systems to an identical time series of intermittent upwelling pulses shown in light grey. For each scenario, the values of k_d and k_up are different; note the difference of magnitude of upwelling events. Note that in this system, there can be several short pulses of different strengths within a single period, furthermore, the events are not isolated but come in small groups. Each group of pulses triggers a different outcome for the toxic population. Furthermore, as can be easily spotted in figure 12, there is a very strong variability between possible responses. Note, for instance, the weak blooming behaviour of the toxic species around t = 2.5 T in contrast to the strong response at t ∼ 10 T. For system (I), we find at t ∼ 2.5 T a rather long bloom with moderate amplitude, while at t ∼ 10 T the bloom exhibits a much higher amplitude. For system (II), we find a similar response, but now not only for the toxic but also for the non-toxic one and the zooplankton reflecting the importance of the grazing pressure in that case.

Figure 12.

Population dynamics in response to intermittent pulses of upwelling.

4. Conclusion

In this work, we have analysed how the competition between two species for a shared limiting resource can be affected by intermittent upwelling events providing an additional input of this resource. We have used a theoretical approach which couples the hydrodynamic flow field with a biological model by means of reaction–advection–diffusion equations. Notably, we have tracked the necessary environmental conditions that trigger a HAB. We were particularly interested in the question of how the interplay of the hydrodynamic time scales as well as the mesoscale hydrodynamic structures, like vortices in the flow, coupled to intermittent upwelling pulses influence the spatio-temporal distribution of dominance patterns of different functional groups of phytoplankton. First, we have characterized the HAB formation in two biological scenarios: the first scenario where the abundance of nutrients is the only factor responsible for the emergence of dominance patterns in the system (bottom-up control); and the second one, where the dominance patterns arise from combination of competition for nutrients and grazing pressure from a higher trophic level (top-down control). Both scenarios are characterized by distinct spatio-temporal inhomogeneous distributions of the phytoplankton groups, which appear as a result of an upwelling event. In the first scenario, the toxic species develops along the whole nutrient plume, while in the second system a bloom is formed in a very localized region namely on a narrow ring around one of the vortices in the wake. The time of the bloom development also differs in these systems: in the first one the response of the toxic species is almost immediate, while in the second one the dominance change occurs while the vortex is advected away from the island. Despite the observed differences in theses two systems, we demonstrate that, in both of them, the decisive factor triggering a bloom or not is the coupling of the upwelling event with the formation of mesoscale vortices. In this scenario, the HAB formation results from the interplay of three time scales: (1) of the vortex formation at the island’s wake, (2) of the upwelling event and (3) of the biological growth. Our analysis shows that identical upwelling events that start in different instances of time may result in a variety of outcomes for the biological community depending on the properties of the flow at the moment of upwelling. The observed response depends on the time interval that nutrients released by upwelling spend in the observation region and consequently the quantity of nutrients captured by the vortices. Therefore, the variability of these possible outcomes depends also on the duration and the strength of the upwelling events. We emphasize that our framework focuses only on the impact of mesoscale vortices and does not capture the small scale heterogeneities within a grid cell. Though in a real oceanographic context smaller hydrodynamic structures do occur, they would not be essential for the interplay between mesoscale hydrodynamic phenomena such as upwelling and vortex formation and their impact on biological growth. However, they could be relevant for other scientific questions, like the effect of turbulence on biological community formation.

In summary, we have observed that HAB formation, independently of the biological set-up, is tightly associated with the transport dynamics of the flow field. From our analysis, we conclude that without taking advection into account, it appears to be difficult to establish a relationship between upwelling events and HABs. For this reason, one cannot expect to find a functional dependence between upwelling events and plankton blooms in general, when only nutrients and plankton abundances are measured and no information about the flow field is available. Such measurements lacking the properties of the flow field will always be difficult to interpret and allow only conclusions when the flow field is simple and does not contain mesoscale hydrodynamic structures.

Data accessibility

The code necessary to reproduce the results reported here can be found in the Github repository: https://github.com/kseniaguseva/Upwelling.

Authors' contributions

K.G. and U.F. conceived the ideas of the research project and drafted the manuscript. The simulation studies were conducted by K.G. Both authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the Volkswagen Foundation (grant no. 88459).