A nonlinear beam model of photomotile structures

Significance

Actuation and propulsion are significant challenges in soft robotics. Supply of power typically requires a cumbersome tether or heavy onboard power source. Further, one typically needs to reset the system. Using theory and numerical simulations, we show, in this work, that this challenge can be overcome by the use of photomechanical materials and actuation by light. We develop a simple modeling framework which reveals how steady illumination from a distance can give rise to cyclic motion. Such motion can be exploited for actuation and propulsion with no need for tether or onboard power source, through the natural but nonlinear/nonlocal coupling between deformation and light absorption.

Abstract

Actuation remains a significant challenge in soft robotics. Actuation by light has important advantages: Objects can be actuated from a distance, distinct frequencies can be used to actuate and control distinct modes with minimal interference, and significant power can be transmitted over long distances through corrosion-free, lightweight fiber optic cables. Photochemical processes that directly convert photons to configurational changes are particularly attractive for actuation. Various works have reported light-induced actuation with liquid crystal elastomers combined with azobenzene photochromes. We present a simple modeling framework and a series of examples that study actuation by light. Of particular interest is the generation of cyclic or periodic motion under steady illumination. We show that this emerges as a result of a coupling between light absorption and deformation. As the structure absorbs light and deforms, the conditions of illumination change, and this, in turn, changes the nature of further deformation. This coupling can be exploited in either closed structures or with structural instabilities to generate cyclic motion.

A major challenge in soft robotics is the integration of sensing, actuation, control, and propulsion. In most soft robotic systems, propulsion and controls are enabled through a physical tether or complex onboard electronics and batteries. A tether simplifies the design but limits the range of motion of the robot, while onboard controls and power supplies can be heavy and can complicate the design (1). Actuation by light through photomechanical processes directly converts photons to deformation and offers an attractive alternative. It can deliver energy remotely. Further, multiple frequencies can be used to actuate and sense different modes. Finally, if a tether is an option, then a significant energy can be delivered through corrosion-free and lightweight fiber optic cables.

A further challenge arises in propulsion where one needs to generate cyclic motion. Since most actuation systems actuate one way, there is a need to reset the system (1). To simplify the control process, it is desirable to do so by inherent response rather than by pulsing of the external source. Actuation by light is again attractive because one can use the directionality of the propagation of light. As the structure absorbs light and deforms, the conditions of illumination change, and this, in turn, changes the nature of further deformation. This coupling can be exploited either in closed structures or with structural instabilities to generate cyclic motion.

These advantages have motivated a recent body of work on developing photomechanical materials (see ref. 2 for an extensive review). Much of this work has focused on incorporating azobenzene photochromes that absorb light and transform between cis and trans configurations into liquid crystal elastomers (LCEs) whose orientational order is coupled to deformation, following the pioneering work of Yu et al. (3). These materials are typically synthesized as thin strips which bend when illuminated with light of appropriate frequency. Further, they can be combined with structural polymers to provide robustness (4).

Various works have demonstrated the ability to generate cyclic motion under steady illumination. Yamada et al. (5) demonstrated that a ring of LCE film containing azobenzene derivatives can roll in the presence of illumination. When wrapped around a series of pulleys, the film can be used as a light-driven plastic motor system. White et al. (6) developed a high-frequency oscillator from a strip which bends under illumination sufficiently to block the light source and reset. Wie et al. (7) produced rolling motion in monolithic polymer films where ultraviolet-visible light transforms the film from flat sheets to spiral ribbons, which then rolls under continuous illumination. Finally, Gelebart et al. (4) created an oscillatory behavior of a doubly clamped LCE film.

Modeling light-mediated actuation is a complex multiphysics process involving three key elements: propagation and absorption of light, chemical transformation and temporal evolution of chromophores between states, and the nonlinear mechanics of structures undergoing large deformations. Corbett and Warner (8) analyzed light absorption and actuation in azobenzene containing LCEs and proposed a geometrical theory of illuminated thin strips (9); this theory assumes that the stress in the strip remains zero, and is only applicable to the special case when the strips are unconstrained. While this model reveals various aspects of photoactuation, it is unable to explain the cyclic behavior in the experiments above, where the constraints applied on the ends of strips, either through boundary conditions (4) or as a closed loop (5), give rise to internal stress.

In this paper, we build on the work of Corbett et al. (9) by coupling it to the mechanics of beams, and derive a fully coupled photoactivated mechanical model for thin illuminated strips which can handle arbitrary boundary conditions. Remarkably, a number of material, physical parameters—time constants of photoactivation and relaxation, penetration depth, the elastic modulus and thickness of the strip, and illumination intensity—collapse into a single nondimensional parameter that governs the behavior. This highlights the flexibility that is available in the choice of material and structure in the development of light-activated structures. Our resulting model is simple and can be solved numerically in real time on any personal computer, while capturing a rich range of behaviors. We use it to address cyclic or periodic motion under steady illumination and reveal the underlying mechanisms. The ability of this simple model to capture complex dynamics of light-illuminated deformation make it a useful tool for the design and control of this novel type of structures.

Photodeformable Elastica

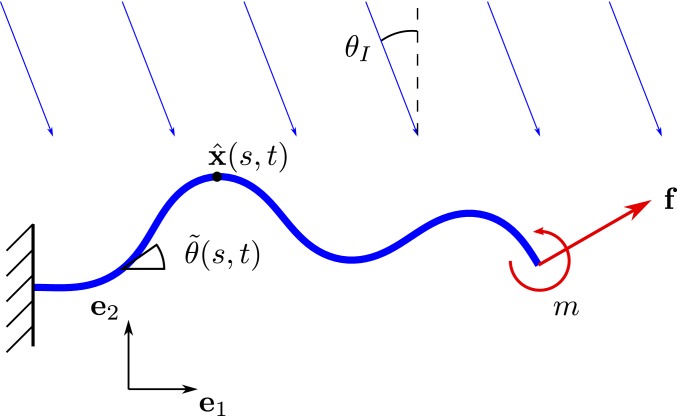
Consider an inextensible beam or a strip (planar elastica) subjected to illumination as shown in Fig. 1. Let $\mathbf{x}\left(s,t\right)$ denote the position of centerline point $s$ at time $t$, and let $\theta \left(s,t\right)$ denote the angle that the tangent to the beam makes with the horizontal axis ${\mathbf{e}}_1$. We assume that the deformation caused by illumination takes place over a significantly slower time scale than the natural periods of vibration of the beam so that we may assume that the beam is at equilibrium at all times. Therefore, at each $t$,

$$\frac{\partial \mathbf{f}}{\partial s}\left(s,t\right)=0,$$ [1]

$$\frac{\partial m}{\partial s}\left(s,t\right)+\left(\hat{\mathbf{t}}\left(s,t\right)\times \mathbf{f}\left(s,t\right)\right)\cdot {\mathbf{e}}_3=0,$$ [2]

where $\hat{\mathbf{t}}\left(\theta \left(s,t\right)\right)=\partial \mathbf{x}/\partial s\left(s,t\right)=\cos \theta \left(s,t\right){\mathbf{e}}_1+\sin \theta \left(s,t\right){\mathbf{e}}_2$ is the unit tangent, $\mathbf{f}\left(s,t\right)$ is the internal force transmitted across a cross-section, and $m\left(s,t\right)$ is the internal moment about ${\mathbf{e}}_3$.

Fig. 1.

Elastica under illumination.

Since we assume that the beam is inextensible and unshearable, the internal force $\mathbf{f}$ is constitutively indeterminate, and we only need to specify a constitutive law for the moment $m$. Following Corbett et al. (9), we assume that the beam is made of an elastic material whose spontaneous or stress-free strain, ${\epsilon }_0$, changes with time depending on the local population of cis molecules. The longitudinal stress at a point at a position $s$ along the length of the beam and $z$ along the depth of the beam and at time $t$ is given by Hooke’s law, $\sigma \left(s,z,t\right)=E\left(\epsilon \left(s,z,t\right)-{\epsilon }_0\left(s,z,t\right)\right)$, where $\epsilon$ is the strain and ${\epsilon }_0$ is the spontaneous strain. The moment is found by integration through the thickness as

$$m\left(s,t\right)={\int }_{-h/2}^{h/2}E\left(\epsilon \left(s,z,t\right)-{\epsilon }_0\left(s,z,t\right)\right)z\mathrm{d}z,$$ [3]

where $h$ is the thickness of the beam and $z=0$ is taken to be the center of the beam. The strain is related to curvature as in classical elastica theory, and the spontaneous strain depends on the built-in curvature ${\kappa }_r$ of the beam (the curvature with no applied load and no illumination) and the concentration $n_c$ of the cis molecules,

$$\epsilon \left(s,z,t\right)=\kappa \left(s,t\right)z,$$ [4]

$${\epsilon }_0\left(s,z,t\right)={\kappa }_r\left(s\right)z-\lambda n_c\left(s,z,t\right),$$ [5]

where $\lambda$ is a constant of proportionality linking the longitudinal strain and concentration of cis molecules.* $\lambda >0$ is when the cis molecules corresponds to an expansion, while $\lambda <0$ corresponds to an induced contraction. This depends on the orientation of the director of the LCE. If the strip is made with directors parallel to the length of the strip [as in the “planar” face of Gelebart et al. (4)], illumination produces a contraction along the length and therefore $\lambda <0$. If, on the other hand, the strip is made with the director along the normal to the strip (as in the “homoetropic” face of Gelebart et al.), illumination causes an elongation along the length of the strip, and therefore $\lambda >0$.

Substituting [4] and [5] into [3], we find the constitutive law in the form

$$m\left(s,t\right)=\frac{E{h}^3}{12}\left(\kappa \left(s,t\right)-{\kappa }_0\left(s,t\right)\right),$$ [6]

where

$${\kappa }_0\left(s,t\right)={\kappa }_r\left(s\right)-\frac{12\lambda }{h^3}{\int }_{-h/2}^{h/2}{n}_c\left(s,z,t\right)z\mathrm{d}z.$$ [7]

It remains to specify the evolution of the spontaneous curvature in the presence of illumination. The concentration of cis molecules is increased by photon absorption, and decreased by thermal decay (9),

$$\frac{\partial n_c}{\partial t}\left(s,z,t\right)=-{\kappa }_1{n}_c\left(s,z,t\right)+\left(1-n_c\left(s,z,t\right)\right){\kappa }_2{\stackrel{\sim }{\alpha }}_1\mathcal{I}\left(s,z,t\right),$$

where $n_c$ is the fraction of activated chromophores, ${\stackrel{\sim }{\alpha }}_1$ is a material constant which measures the efficiency of the production of cis isomers by incident light, and $\mathcal{I}\left(s,z,t\right)$ denotes the illumination, that is, the quantity of photons per unit time arriving at the depth $z$ at time $t$. ${\kappa }_1$ and ${\kappa }_2$ are the thermal decay and the forward isomerization reaction rates, respectively. In typical materials, $n_c\ll 1$ is small (2), so we can simplify the differential equation to

$$\tau \frac{\partial n_c}{\partial t}\left(s,z,t\right)=-n_c\left(s,z,t\right)+{\alpha }_1\mathcal{I}\left(s,z,t\right),$$ [8]

where $\tau =1/{\kappa }_1$ and ${\alpha }_1={\kappa }_2{\stackrel{\sim }{\alpha }}_1/{\kappa }_1$. Further, at any location $s$ along the length of the strip, the intensity diminishes with depth with the number of photons absorbed (9),

$$\frac{\partial \mathcal{I}}{\partial z}=\frac{1-n_c}{d}\mathcal{I}\left(s,z,t\right),$$

where $d$ is the penetration depth. So, when $n_c\ll 1$, the intensity follows Beer’s law,

$$\mathcal{I}\left(s,z,t\right)={\mathcal{I}}_0\left(s,t\right)\exp \left(-\frac{h/2-z}{d}\right),$$ [9]

where $z=h/2$ is the free surface that is illuminated and ${\mathcal{I}}_0$ is the intensity of light on the illuminated surface.† Combining [7]–[9],

$$\begin{array}{cc}\hfill \tau \frac{\partial {\kappa }_0}{\partial t}\left(s,t\right)& =-\frac{12\lambda }{h^3}{\int }_{-h/2}^{h/2}\tau \frac{\partial n_c}{\partial t}\left(s,z,t\right)z\mathrm{d}z\hfill \\ \hfill & =-\left({\kappa }_0\left(s,t\right)-{\kappa }_r\left(s\right)\right)+\alpha {\mathcal{I}}_0\left(s,t\right),\hfill \end{array}$$

where $\alpha =-\frac{12\lambda {\alpha }_1}{h^3}{\int }_{-h/2}^{h/2}\exp \left(-\frac{h/2-z}{d}\right)z\mathrm{d}z$ is an effective (macroscopic) coupling constant. Finally, the absorption of light on the surface depends on light intensity $I_0$ and on the relative orientation of the light and the strip, ${\mathcal{I}}_0\left(s,t\right)=I_{0}f\left(\theta \left(s,t\right)-{\theta }_I\right)$, where ${\theta }_I$ is the angle of illumination. Therefore,

$$\tau \frac{\partial {\kappa }_0}{\partial t}\left(s,t\right)+\left({\kappa }_0\left(s,t\right)-{\kappa }_r\left(s\right)\right)=\alpha I_{0}f\left(\theta \left(s,t\right)-{\theta }_I\right).$$ [10]

The projection function $f$ is chosen as

$$f\left(\varphi \right)=\left\{\begin{array}{cc}\cos \varphi \hspace{1em}\hfill & \text{if}\varphi \in \left(-\pi /2,\pi /2\right),\hfill \\ 0\hspace{1em}\hfill & \text{else}.\hfill \end{array}\right.$$ [11]

This $f$ accounts for self-shadowing in an approximate but effective way: In our examples, the parts of the rods that are exposed to the light source are such that $\varphi \in \left(-\pi /2,\pi /2\right)$, and, in that case, the coefficient $\cos \varphi$ accounts for the reduction in light flux per unit area due to the nonnormal incidence. Regions such that $\varphi \notin \left(-\pi /2,\pi /2\right)$ are considered to be shadowed by other parts of the rod.

Finally, we combine [1], [2], [4], and [6], and nondimensionalize the resulting equation along with [10], introducing the scaled arclength $S=s/l$ (where $l$ is the length of the beam), the scaled time $T=t/\tau$, and the scaled curvature $K=l\kappa$,

$$\begin{array}{l}\hfill \frac{\partial }{\partial S}\left(\frac{\partial \theta }{\partial S}\left(S,T\right)-K_0\left(S,T\right)\right)\\ \hfill -F_x\cos \theta \left(S,T\right)+& F_y\sin \theta \left(S,T\right)=0,\hfill \end{array}$$ [12]

$$\frac{\partial K_0}{\partial T}\left(S,T\right)+\left(K_0\left(S,T\right)-K_r\left(S\right)\right)=\mathrm{\Lambda }f\left(\theta \left(S,T\right)-{\theta }_I\right).$$ [13]

The constants $F_x$ and $F_y$ are Lagrange multipliers that enforce the inextensibility. Remarkably, these equations depend on two parameters only: the angle of illumination ${\theta }_I$ and the dimensionless constant

$$\mathrm{\Lambda }=\alpha l{I}_0=-\frac{12{\kappa }_2{\stackrel{\sim }{\alpha }}_1{\mathcal{I}}_0}{{\kappa }_1{h}^3}{\int }_{-h/2}^{h/2}\exp \left(-\frac{h/2-z}{d}\right)z\mathrm{d}z$$ [14]

that encompasses various material and physical parameters—time constants of photoactivation and relaxation, penetration depth, the elastic modulus and thickness of the strip, and illumination intensity. The fact that so many material and physical parameters collapse into a single nondimensional parameter highlights the flexibility that is available in the choice of material and structure in the development of light-activated structures. Since the dimensionless equations are governed by a single dimensionless parameter $\mathrm{\Lambda }$, we are able to characterize all of the possible behaviors in a given geometry simply by sweeping over $\mathrm{\Lambda }$. Based on the values in Table 1 estimated from literature reports on a glassy azobenzene-functionalized polyimide, we obtain a value of $\left|\mathrm{\Lambda }\right|\approx 2.9$; these values are typical of the materials used in many other experimental works, although not all of them document the material properties in detail.

Table 1.

Estimates of the experimental parameters based on the literature

Parameter	Typical value
$\lambda {\alpha }_1$	$-5.4\times 10^{-5}{\text{m}}^2\cdot {\text{W}}^{-1}$ (11)
$I_0$	$100{\text{W/m}}^2$ (11)
$E$	0.6 GPa to 4 GPa
$h$	$15\hspace{0.17em}\mathrm{\mu }$m (11)
$d$	$0.56\hspace{0.17em}\mathrm{\mu }$m (12)
$w$	1 mm (11)
$l$	15 mm (11)

To predict how the shape of the beam evolves with time, we solve these Eqs. 12 and 13 for $\theta \left(S,T\right)$ using a numerical method described in SI Appendix, section A with specific initial, boundary, and illumination conditions. We remark that, in deriving the equations, we assumed that the material response—the relation between curvature and moment [6], and the relation between illumination and spontaneous curvature [7]—are linear. Yet, the final equations are nonlinear, as evidenced by the presence of the trigonometric terms in [12] and $f$ in [13] due to the presence of finite rotations.

For future reference, we note that the equilibrium Eq. 12 can be derived by the Euler–Lagrange method as the stationarity condition of the energy functional

$$\mathcal{E}\left[\theta \right]={\int }_0^1\frac{1}{2}{\left|\frac{\partial \theta }{\partial S}-K_0\right|}^2\mathrm{d}S.$$ [15]

Rolling Ring

Our first example is motivated by the work of Yamada et al. (5) on a rolling ring and motor, as well as that of Wie et al. (7) on a rolling spiral. We consider a closed, initially circular ring on a rigid horizontal surface, which is illuminated with a steady source at angle ${\theta }_I$. The fact that the ring is closed implies that

$${\int }_0^1\sin \theta \left(S,T\right)\mathrm{d}S={\int }_0^1\cos \theta \left(S,T\right)\mathrm{d}S=0,$$ [16]

as well as $\theta \left(0,T\right)=\theta \left(1,T\right)$. We assume that the ring makes a tangential rolling contact with the horizontal surface so that $X\left(S_c\left(T\right),T\right)=S_c\left(T\right)$, $Y\left(S_c\left(T\right),T\right)=0$, and

$$\theta \left(S_c\left(T\right),T\right)=0,$$ [17]

where $S_c\left(T\right)$ is the point of contact. We determine this point of contact by assuming overall mechanical equilibrium of the ring under gravity so that the center of mass of the ring is always vertically above the point of contact,

$$\begin{array}{cc}\hfill S_c\left(T\right)=X\left(S_c\left(T\right),T\right)& ={\int }_0^{1}X\left(S,T\right)\mathrm{d}S\hfill \\ \hfill & ={\int }_0^1\left({\int }_0^S\cos \theta \left(\stackrel{\sim }{S},T\right)\mathrm{d}\stackrel{\sim }{S}\right)\mathrm{d}S\hfill \\ \hfill & ={\int }_0^1\left(1-S\right)\cos \theta \left(S,T\right)\mathrm{d}S\hfill \\ \hfill & =-{\int }_0^{1}S\cos \theta \left(S,T\right)\mathrm{d}S.\hfill \end{array}$$ [18]

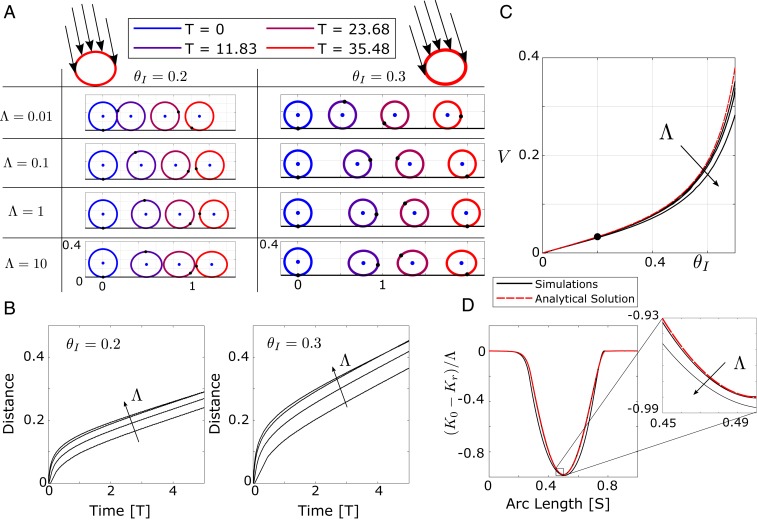
We set $K_r=2\pi$ and $\theta \left(S,0\right)=2\pi S$ corresponding to an initially circular ring and solve Eqs. 12 and 13 subject to the conditions above. Fig. 2A shows snapshots of the ring for various angles and intensity of illumination. In each case, the ring deforms as it is illuminated, in a way which is nonsymmetric with respect to the vertical axis and depends on the angle of illumination. This asymmetry causes the center of mass of the ring to move, which, in turn, causes the ring to roll. Fig. 2B shows the distance traveled by the point of contact as a function of time under various angles and intensity of illumination. After an initial transient, the ring rolls with a steady velocity and has an invariant shape. The steady velocity is plotted as a function of the illumination angle for various illumination intensities in Fig. 2C: It is zero when the illumination is vertical (${\theta }_I=0$), which is a consequence of the symmetry, and increases with increasing angle of illumination ${\theta }_I$. Remarkably, the rolling velocity is practically independent of the intensity of illumination in the range of values of $\mathrm{\Lambda }$ relevant to the experiments and investigated here. To investigate this further, we plot the scaled deviation in spontaneous curvature $\left(K_0-K_r\right)/\mathrm{\Lambda }$ as a function of arclength in Fig. 2D: This quantity appears to be practically independent of the intensity of illumination as well. This shows that the amount of deformation scales linearly with the light intensity, while the profile of deformation (and, hence, the asymmetry and the rolling velocity) is largely independent of the intensity.

Fig. 2.

Rolling ring. (A) Snapshots of an initially circular ring with radius $R=1/\left(2\pi \right)$ subjected to illumination at angle ${\theta }_I$ and of intensity $\mathrm{\Lambda }$ at times $T=\left\{\mathrm{0,11.83},23.68,35.48\right\}$. The point that is initially in contact with the ground is marked with a black dot, while the center of mass is the blue dot. The incident arrows indicate the direction of incoming light. Self-shadowing is taken into account thanks to the choice of $f$ in Eq. 11; this is depicted by the absence of arrows in the lower part of the ring. (B) Distance traveled by the rolling ring vs. time for various intensities $\mathrm{\Lambda }=\left\{0.01,0.1,\mathrm{1,10}\right\}$. Note that a steady velocity is reached in all cases, after an initial transient. (C) Steady-state velocity as a function of illumination angle and intensity $\mathrm{\Lambda }=\left\{0.01,0.1,\mathrm{1,10}\right\}$. The velocity increases when the illumination angle moves away from the vertical, but is relatively insensitive to the intensity of illumination. (D) Scaled change of spontaneous curvature induced by illumination along the beam for ${\theta }_I=0.2$ (indicated by dot in C), for various illumination intensities $\mathrm{\Lambda }=\left\{0.01,0.1,\mathrm{1,10}\right\}$. This quantity appears to be largely insensitive to the intensity of illumination. Simulation data are shown as solid black lines, while the analytical solution given by solving Eq. 29 is shown as a red dashed line. The Inset is at higher magnification.

To understand these features, we analyze steadily rolling solutions, that is, we seek solutions of the form $\theta \left(S,T\right)=\mathrm{\Theta }\left(S-VT\right)$ and aim at identifying the rolling velocity $V$. We set $\omega =2\pi \left(S-VT\right)$, choosing $T=0$ to be a time when the point in contact with the ground is $S=S_c\left(0\right)=0$. This implies

$$\mathrm{\Theta }\left(0\right)=0.$$ [19]

The rolling condition [18] becomes

$$0={\int }_0^{2\pi }\omega \cos \mathrm{\Theta }\left(\omega \right)\mathrm{d}\omega ,$$ [20]

and the evolution Eq. 13 becomes

$$-2\pi V\frac{\mathrm{d}{K}_0}{\mathrm{d}\omega }+\left(K_0-2\pi \right)=\mathrm{\Lambda }f\left(\mathrm{\Theta }-{\theta }_I\right).$$ [21]

We now assume that the shape of the ring is almost circular, so that

$$\mathrm{\Theta }\left(\omega \right)=\omega +{\mathrm{\Theta }}_1\left(\omega \right),\hspace{1em}{K}_0\left(\omega \right)=2\pi +K_1\left(\omega \right),$$ [22]

where $\left|{\mathrm{\Theta }}_1\right|\ll 1$ and $\left|K_1\right|\ll 1$ are treated as perturbations. Keeping only terms linear in ${\mathrm{\Theta }}_1,K_1$, the equilibrium Eq. 12 and closure condition [16] become

$$\begin{array}{c}\hfill 4{\pi }^2{\mathrm{\Theta }}_1^{\prime \prime }\left(\omega \right)-2\pi K_1^{\prime }\left(\omega \right)+F_y\cos \omega -F_x\sin \omega =0,\hfill \\ \hfill {\int }_0^{2\pi }\cos \left(\omega \right){\mathrm{\Theta }}_1\left(\omega \right)\mathrm{d}\omega ={\int }_0^{2\pi }\sin \left(\omega \right){\mathrm{\Theta }}_1\left(\omega \right)\mathrm{d}\omega =0.\hfill \end{array}$$ [23]

Introducing the Fourier transform $\widehat{f}\left(k\right)={\int }_0^{2\pi }f\left(\omega \right)\exp \left(-ik\omega \right)\mathrm{d}\omega$ where $k$ is an integer, we can solve [21] as

$${\widehat{K}}_1\left(k\right)=\frac{\mathrm{\Lambda }{\widehat{f}}_I\left(k\right)}{1-2i\pi kV},$$ [24]

where

$$f_I\left(\omega \right)=f\left(\omega -{\theta }_I\right).$$ [25]

Similarly, we can solve Eq. 23 in Fourier form as

$$\begin{array}{cc}\hfill {\widehat{\mathrm{\Theta }}}_1\left(\pm 1\right)=0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill & \hfill \hspace{1em}\text{for}\left|k\right|=1,\hfill \\ \hfill {\widehat{\mathrm{\Theta }}}_1\left(k\right)=-i\frac{{\widehat{K}}_1\left(k\right)}{2\pi k}\hfill & \hfill \hspace{1em}\text{for}\left|k\right|⩾2.\hfill \end{array}$$ [26]

Note that the first equation in [23] yields $F_x$ and $F_y$ in terms of ${\widehat{\mathrm{\Theta }}}_1\left(\pm 1\right)$ and ${\widehat{K}}_1\left(\pm 1\right)$ as well, but these expressions are not needed.

The horizontal tangency condition [19] reads $0=\mathrm{\Theta }\left(0\right)={\mathrm{\Theta }}_1\left(0\right)=\frac{1}{2\pi }{\sum }_k{\widehat{\mathrm{\Theta }}}_1\left(k\right)$, where the sum runs over all signed integers $k$. Rearranging the terms in the sum and solving for ${\widehat{\mathrm{\Theta }}}_1\left(0\right)$, we find

$${\widehat{\mathrm{\Theta }}}_1\left(0\right)=-2\sum _{k⩾1}\mathfrak{R}{\widehat{\mathrm{\Theta }}}_1\left(k\right),$$ [27]

where we have used ${\widehat{\mathrm{\Theta }}}_1\left(-k\right)+{\widehat{\mathrm{\Theta }}}_1\left(k\right)=\overline{{\widehat{\mathrm{\Theta }}}_1\left(k\right)}+{\widehat{\mathrm{\Theta }}}_1\left(k\right)=2\mathfrak{R}{\widehat{\mathrm{\Theta }}}_1\left(k\right)$, since ${\mathrm{\Theta }}_1\left(\omega \right)$ is a real function. Here, $\overline{z}$ denotes the conjugate of the complex number $z$.

Eqs. 24–27 yield the shape in terms of the known illumination parameter $\mathrm{\Lambda }$ and of the unknown scaled rolling velocity $V$. The latter can be found by linearizing the rolling condition [20] as ${\int }_0^{2\pi }g\left(\omega \right){\mathrm{\Theta }}_1\left(\omega \right)d\omega =0$, where $g\left(\omega \right)=\omega \sin \omega$. Using Parseval’s identity, this can be rewritten as

$$\begin{array}{c}\hfill \frac{1}{2\pi }\sum _kĝ\left(k\right){\widehat{\mathrm{\Theta }}}_1\left(-k\right)=0,\hspace{1em}\hspace{1em}\\ \hfill \text{where}ĝ\left(k\right)=\left\{\begin{array}{cc}-\frac{\pi }{2}\left(2\pi ik+1\right)\hspace{1em}\hfill & \hspace{1em}\text{if}\left|k\right|=1,\hfill \\ \frac{2\pi }{k^2-1}\hspace{1em}\hfill & \text{if}\left|k\right|\ne 1.\hfill \end{array}\right.\end{array}$$ [28]

Inserting [26] and [27] into this equation, we obtain $2{\sum }_{k⩾2}\frac{k^2}{k^2-1}\mathfrak{R}{\widehat{\mathrm{\Theta }}}_1\left(k\right)=0$, which, in view of [24]–[26], yields an implicit equation for the rolling velocity $V$ in terms of the angle of illumination ${\theta }_I$,

$$\begin{array}{c}\hfill \mathrm{\Lambda }\cdot H\left({\theta }_I,V\right)=0\hspace{1em}\\ \hfill \text{where}\hspace{1em}H\left({\theta }_I,V\right)=\sum _{k⩾2}\frac{k}{k^2-1}\mathrm{I}\mathrm{m}\left(\frac{{\widehat{f}}_I\left(k\right)}{1-2i\pi kV}\right).\end{array}$$ [29]

Note that $f_I$, and hence $H$ depends on ${\theta }_I$; see Eq. 25.

When ${\theta }_I=0$, $f_I\left(\omega \right)=f\left(\omega \right)$ is an even function of $\omega$, so that ${\widehat{f}}_0\left(k\right)$ is real; hence $H\left(\mathrm{0,0}\right)=0$. It is also clear from the form of $H\left({\theta }_I,V\right)$ that $\frac{\partial H}{\partial {\theta }_I}$ and $\frac{\partial H}{\partial V}$ are generally nonzero. By the implicit function theorem, we can solve [29] for $V=V\left({\theta }_I\right)$, at least for ${\theta }_I$ that is small enough. We do so numerically; the result is shown in Fig. 2C as the dashed line, and agrees well with the nonlinear simulations. In Fig. 2D, the distribution of natural curvatures predicted by the linear theory is compared to the nonlinear numerical simulations, and a good agreement is obtained as well; the agreement with the linear theory is better and better for lower and lower illuminations, as could be anticipated.

Remarkably, the intensity of illumination $\mathrm{\Lambda }$ factors out in Eq. 29, selecting the rolling velocity, so that $V$ depends on ${\theta }_I$ but not on $\mathrm{\Lambda }$ in this linear theory; this explains why the rolling velocity is largely independent of $\mathrm{\Lambda }$ in the nonlinear simulations.

Waves in Doubly Clamped Beams

The second example we study is motivated by the experiments of Gelebart et al. (4). These experiments were done on a nematic strip possessing a splay director field: The nematic directors are aligned along the length of strip on one surface (called the planar face) and normal to the surface on the opposite face (homeotropic face). The goal is to induce contraction on one face and expansion on the other in order to maximize the magnitude of the photobending coupling $\left|\lambda \right|$. Exposing the planar face to light makes $\lambda <0$, while exposing the homeotropic face to light makes $\lambda >0$. In view of the analysis done in Photodeformable Elastica, $\mathrm{\Lambda }\propto \alpha \propto -\lambda$, so illuminating the planar (respectively, homeotropic) face corresponds to $\mathrm{\Lambda }>0$ (respectively, $\mathrm{\Lambda }<0$) in our model. Illumination, either due to the direct effect or due to temperature rise or both, reduces the nematic order, causing a contraction by ${\left(r/r_0\right)}^{2/3}$ when illuminated on the planar face and an extension by ${\left(r_0/r\right)}^{1/3}$ when illuminated on the homeotropic face, where $r$ (respectively $r_0$) is the anisotropy parameter in the illuminated (respectively ambient) state. Since $r<r_0$, for fixed unscaled illumination intensity $I_0$, we expect the resulting photostrain and spontaneous curvature coefficients $0\le {\mathrm{\Lambda }}_p\approx -2{\mathrm{\Lambda }}_h$, where ${\mathrm{\Lambda }}_p$ is the coefficient when illuminated on the planar side and ${\mathrm{\Lambda }}_h$ is the coefficient when illuminated on the homeotropic side. This distinction between ${\mathrm{\Lambda }}_p$ and ${\mathrm{\Lambda }}_h$ is caused by the small penetration depth only activating the trans to cis isomerization on the illuminated side; therefore, it is only the nematic orientation on the illuminated surface that matters. We study the results of our model first, and compare to the experimental observations next.

We first consider the case $\mathrm{\Lambda }>0$. We take a strip that is flat in the absence of any light or stress, so that $K_r=0$. We use the same scaled quantities as earlier, and the scaled length of the strip is 1. We clamp the two ends at a distance $l_f<1$ from each other, corresponding to boundary conditions

$$\begin{array}{c}\hfill \theta \left(0,T\right)=\theta \left(1,T\right)=0,\\ \hfill \hspace{1em}{\int }_0^1\sin \theta \left(S,T\right)\mathrm{d}S=0,\\ \hfill \hspace{1em}{\int }_0^1\cos \theta \left(S,T\right)\mathrm{d}S=l_f.\end{array}$$ [30]

Since $l_f<1$, the beam buckles, and there are two equivalent fundamental buckled modes, buckled up and down. We choose one of the two states, say, the buckled up state for definiteness, although the results are independent of this choice. We illuminate the strip with a light source that is spatially uniform and at an angle (${\theta }_I\ne 0$) as shown in Fig. 3A. We solve Eqs. 12 and 13 subject to the boundary conditions [30].

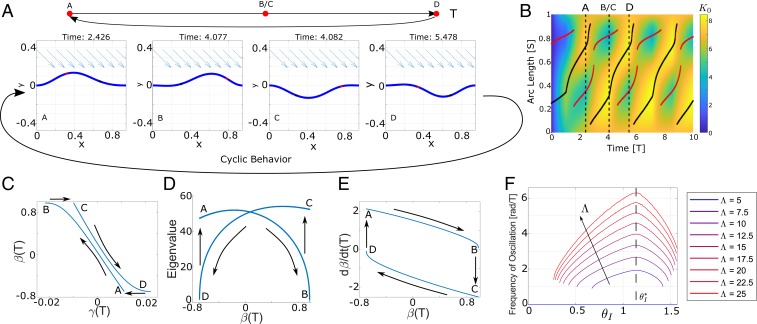
Fig. 3.

Waves in a strip for $\mathrm{\Lambda }>0$. (A) Snapshots of an initially flat strip clamped in a buckled state ($l_f=0.95$) and subjected to illumination with $\mathrm{\Lambda }=10,{\theta }_I=\pi /4$. The arrows indicate the direction of incoming light. After an initial transient, it goes into a periodic motion. (B) Evolution of the light-induced spontaneous curvature $K_0$ of the strip. The peaks are marked with a black curve, and the troughs are marked with a red curve. Note that the evolution becomes periodic but is quite complex, with an alternation of slow (quasi-static) and fast (dynamic) motions. (C) Shape vs. spontaneous curvature descriptors as defined in Eq. 31. (D) Incremental stiffness (lowest eigenvalue of the stiffness matrix) vs. spontaneous curvature descriptor. (E) Phase plot revealing the oscillation cycles after an initial transient. (F) Frequency of flapping as a function of illumination angle for various illumination angles. The angle for maximum flapping frequency (${\theta }_I*$) is shown with the vertical dashed line.

Fig. 3 AE shows a typical simulation result. After an initial transient, we find that the beam goes into a periodic motion alternating between the up and down buckled shapes (Fig. 3A). At the start of the cycle, we have an up-bump at the left side of the strip (state A). Illumination moves it to the right initially rapidly but slows down and becomes very slow as it reaches the right end (B). It then pops into a down-bump located on the left (C). Subsequently, the down-bump moves to the right initially rapidly but slows down and becomes very slow as it reaches the right end (D). It then pops again into an up-bump located on the left of the sample, and the cycle repeats.

The evolution of the light-induced spontaneous curvature as a function of time and position is shown in Fig. 3B. After an initial transient, we see that the spontaneous curvature reaches a steady periodic cycle. This is emphasized in Fig. 3C, which plots one particular Fourier component $\gamma \left(T\right)$ of the deflection against one particular Fourier component $\beta \left(T\right)$ of the natural curvature,

$$\begin{array}{c}\hfill \gamma \left(T\right)={\int }_0^1\sin \left(2\pi S\right)Y\left(S,T\right)\mathrm{d}S,\\ \hfill \hspace{1em}\beta \left(T\right)={\int }_0^1\sin \left(2\pi S\right)K_0\left(S,T\right)\mathrm{d}S.\end{array}$$ [31]

We call these quantities the descriptors of the deformation and curvature, respectively. In Fig. 3, the deformation descriptor appears to vary abruptly during the sudden changes from state B to C, and from D to A, although the curvature descriptor remains unchanged. This suggests that the jumps are snap-through bifurcations, from one equilibrium solution of the elastica to another one. For some fixed time $T$ and spontaneous curvature distribution $K_0\left(S,T\right)$, the equilibrium Eq. 12 may have multiple solutions (equivalently, $\mathcal{E}$ has multiple stationary points). Stable solutions are those for which the second variation is positive definite (SI Appendix, section B). With the aim to confirm the snap-through scenario, we study the lowest eigenvalue associated with the second variation ${\delta }^2\mathcal{E}$ of the energy. It is plotted from the numerical solution, as a function of $\beta$ in Fig. 3D. We see that this eigenvalue is positive at the start of the cycle at A (the solution with the up-bump) but decreases as we go from A to B. The jump at B occurs when the eigenvalue is becoming negative and the solution loses stability. It arrives on another solution C having a down-bump, which appears to be elastically stable, that is, has a positive lowest eigenvalue. Again, the lowest eigenvalue begins to decrease as we go from C to D and passes through zero at D.

This reveals the mechanism of the cyclic motion. At any time, there are two possible solutions, one with an up-bump and one with a down-bump. If the solution with the up-bump has the bump on the right, the solution with the down-bump has the bump on the left, and vice-versa. The evolution of light-induced spontaneous curvature always forces the bump to move to the right, that is, away from the light source. At some point, it loses stability and has to snap to the other solution. The periodic cycles are represented in the phase space $\left(\beta ,\stackrel{·}{\beta }\right)$ in Fig. 3E. Immediately after a snap-through, the evolution speed $\left|\stackrel{·}{\beta }\right|$ is high. As the instability is approached, the magnitude of $\left|\stackrel{·}{\beta }\right|$ decreases until nearly zero. This coincides with the snap-through, and, once the system snaps to the new configuration, $\left|\stackrel{·}{\beta }\right|$ jumps to a large value again, and the other half of the cycle proceeds similarly.

We repeat this calculation for various illumination angles and illumination intensities, and the results are summarized in Fig. 3F. At any given intensity, there is a window of illumination angles at which periodic flapping solutions are observed. Outside of this window, a stationary solution is reached, which can be the up-bump or the down-bump, depending on the initial conditions. Physically, if the illumination is oriented in a direction too shallow to the beam, then the bump moves to the far end and is stable. This explains the lower limit. Similarly, if the illumination is close to being normal to the beam, then the beam finds it difficult to break the symmetry required to induce the periodic motion. This explains the upper limit. The window of periodic behavior becomes wider when the light intensity is increased. Further, at any given orientation, the frequency of the limit cycle increases with intensity; this can be seen from Eq. 10, where an increase of the light intensity in the right-hand side is seen to induce a quicker rate of change $\partial {\kappa }_0/\partial t$ of the curvature.

In Fig. 3F, the angle of incidence ${\theta }_I$ maximizing the flapping frequency is $65.1^{○}$ for $l_f=0.95$, and this angle appears to be virtually independent of the light intensity as long as flapping takes place: It is just a function of $l_f$ in our model. To compare with the observations of ref. 4, we ran additional simulations using the same value $l_f=0.957$ as in the experiments, and found that the maximum frequency is obtained for an angle of incidence ${\theta }_I=65.7^{○}$; this value is similar to the peak at $70^{○}$ in the experiment.

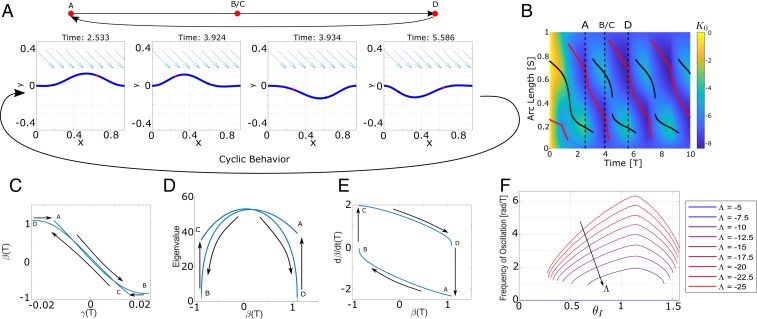
We now turn to the case when $\mathrm{\Lambda }<0$. As can be seen in Fig. 4A, the system again alternates between up and down buckled states. In this case, however, the bulge propagates from right to left, that is, toward the light source, and opposite from the case where $\mathrm{\Lambda }>0$. It can be seen, in Fig. 4 C–E, that the descriptors give different paths through the phase space than when $\mathrm{\Lambda }>0$. This shows that flipping the sign of $\mathrm{\Lambda }$ does not simply amount to reversing the arrow of time. Interestingly, even though the deformation mode differs, the flapping frequency does not change significantly between the positive and negative cases (see Fig. 4F).

Fig. 4.

Waves in a strip for $\mathrm{\Lambda }<0$. Same as in Fig. 3 except with $\mathrm{\Lambda }=-10$.

We now compare the experimental observations of Gelebart et al. (4). After an initial transient, the strip begins a periodic motion with the wave moving from right to left as predicted in Fig. 4, when illuminated on the homeotropic phase ($\mathrm{\Lambda }={\mathrm{\Lambda }}_h<0$). The wave moves from left to right as predicted in Fig. 3, when illuminated on the planar face ($\mathrm{\Lambda }={\mathrm{\Lambda }}_p>0$). They also observed that the frequency of oscillation when illuminating the homeotropic face is lower as compared to the planar face, holding all other parameters fixed. Again, this is consistent with the predictions in Figs. 4F and 3F, since $\left|{\mathrm{\Lambda }}_p\right|>\left|{\mathrm{\Lambda }}_h\right|$ for fixed $I_0$. Further, this wavelike motion is observed only in a finite range of illumination angles, and, for fixed illumination intensity, the range when illuminating the planar side is larger than that of the homeotropic side as predicted, because $\left|{\mathrm{\Lambda }}_p\right|>\left|{\mathrm{\Lambda }}_h\right|$. All of these results are in good agreement with the experimental observations.

Snap-through Instability of Doubly Clamped Beams

The critical event in the emergence of wavelike cyclic behavior is the snap-through instability. We study this instability more closely in our final example, by analyzing the experiments first conducted by Shankar and coworkers (12, 13).

As in the previous example, an initially flat ($K_r=0$) strip of (normalized) length 1 is clamped at both ends so that the end to end distance is $l_f<1$; the beam is subject to the same boundary conditions (Eq. 30). There are two equilibrium conditions, one buckled up, and one buckled down. As before, we start with the buckled up state and shine light on it. There are two differences compared to the geometry of the previous section: We limit attention to normal illumination (${\theta }_I=0$), and use a wide light beam described by a Gaussian distribution of intensity,

$$\mathrm{\Lambda }\left(S,T\right)={\mathrm{\Lambda }}_{max}\hspace{0.17em}g\left(X\left(S,T\right),\mu ,W\right),$$ [32]

where $g\left(X,\mu ,W\right)=\exp \left(-\frac{{\left(X-\mu \right)}^2}{2W^2}\right)$ is a normal distribution centered at $\mu$, with width $W$ and scaled so that the peak value is 1.

We also conduct experiments using 1 mm $\times$ 15 mm $\times$ 50 $\mathrm{\mu }$m beams made of planar nematic liquid crystal network (LCN) films (see Materials and Methods and SI Appendix, section C for details) illuminated using a 365-nm light-emitting diode.

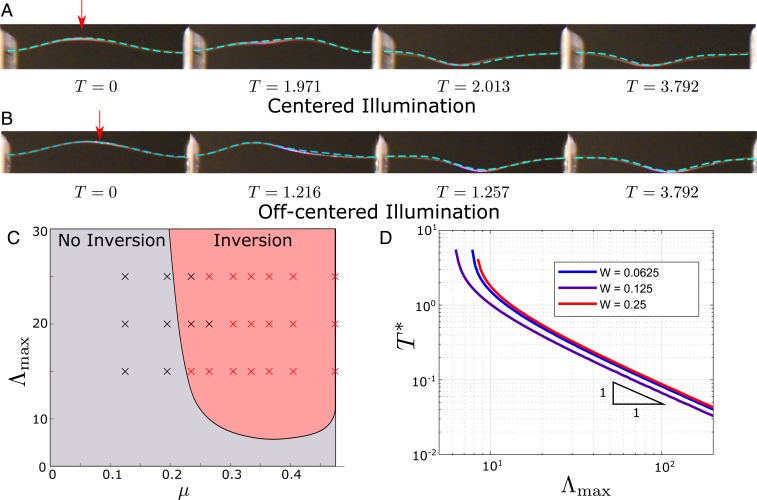
Fig. 5 summarizes our results. First, consider the case when the illumination is centered on the bump ($\mu =l_f/2$) in Fig. 5A. When the light is turned on, the bump flattens out slowly due to photoinduced curvature; after a period of slow deformation, it snaps suddenly at a critical time $T^{*}$ to the down-buckled state. We have verified through eigenvalue analysis as before that the snap-through occurs when the up-bump solution becomes unstable. Continued illumination beyond the time of snap-through does not result in any significant further deformation. Fig. 5B shows the results of the case where the illumination is slightly off the center of the bump ($\mu =0.45$). The overall phenomenon is similar, but the initial slow deformation pushes the bump to the side away from the illumination instead of flattening it. Fig. 5 A and B superposes the results of theoretical computation (cyan dashed line) with images retrieved from the experimental observation, showing excellent agreement.

Fig. 5.

Snap-through of a strip subject to normal illumination. (A and B) Snapshots of an initially flat strip clamped in a buckled state and subjected to illumination with ${\mathrm{\Lambda }}_{max}=10$ and $l_f=0.99$ for two different offsets, (A) $\mu =l_f/2$ and (B) $\mu =0.45$. The red arrows indicate the location of the center of the laser beam. Predictions of the model (cyan) are superimposed onto the experimental observations without any adjustable parameter. Note the two distinct snap-through modes: symmetric with the creation of a flat-top when the light beam is centered, and displacing the peak position when the light beam is not centered. (C) Phase portrait in the illumination vs. offset space, showing the absence or presence of snap-through, for $l_f=0.95$. The background colors and the crosses are the theoretical and experimental results, respectively. (D) Time for snap-through as a function of illumination for $l_f=0.95$ and $\mu =l_f/2$, as predicted by the model.

As the illumination becomes too low, or the offset from center $|l_f/2-\mu |$ is too large, the beam does not snap through. The phase portrait is shown in Fig. 5C along with the experimental observations, again showing good agreement between theory and experiments. At higher illuminations, we see some evidence of photobleaching in the experiments, and we believe that this accounts for the slight discrepancy. The phase portrait also shows that the smallest illumination required for snap-through decreases as the light is moved away from the center (i.e., when $\mu$ decreases from $l_f/2$). In other words, it is easier to snap when the illumination is slightly off center.

Finally, the time it takes for the snap-through to occur as a function of illumination in the centered case is plotted in Fig. 5D. We observe that, for moderate to large illumination (i.e., away from the snap/no-snap boundary), this takes on a power law with an exponent $-1$. Shankar et al. (12) studied this over a very large range of illuminations, and they reported a slope of $-1$, in agreement with our simulations.

Materials and Methods

Planar nematic liquid crystal network films were prepared following the procedure of Gelebart et al. (4) with modification. To synthesize films with a penetration depth of $1.5\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ at an illumination wavelength of $365\hspace{0.17em}\mathrm{n}\mathrm{m}$, a formulation of 9.2:90.8 by weight of 4,4’-Bis(6-acryloyloxyhexyloxy)azobenzene (Azo-6): 1,4-Bis[4-(6-acryloyloxyhexyloxy)benzoyloxy]-2-methylbenzene (RM82) was used, with 2.5 wt % of photoinitiator with respect to the total monomer weight. In a typical sample preparation, 4.6 mg of Azo-6, 45.4 mg of RM82, and 1.25 mg of Iphenylbis(2,4,6-trimethylbenzoyl)phosphine oxide) (Irgacure 819) were melted together in a vial and vortexed repeatedly to ensure mixing. The molten monomer mixture was then infiltrated via capillary action into alignment cells on a hot plate at 100 °C. The alignment cells were prepared by spin-coating Elvamide onto clean glass slides, rubbing the slides with a velvet cloth, and gluing the two Elvamide sides facing each other with epoxy mixed with 15-$\mathrm{\mu }$m glass beads. The filled cells were subsequently cooled to 80 °C, held isothermal for 5 min to induce alignment of the liquid crystalline mesogens, and photopolymerized for 30 min with 405-nm light. Following photopolymerization, samples were postcured at 120 °C for 10 min, and the 15-m-thick LCNs were harvested by cracking open the alignment cells with a razor blade. Finally, beams of 1 mm in width were cut from the film with the nematic director along the long axis of the strip.

Data Availability.

All data needed to evaluate the conclusions in this paper are available in the main text or in SI Appendix.