OrgDyn: feature- and model-based characterization of spatial and temporal organoid dynamics

Abstract

Summary

Organoid model systems recapitulate key features of mammalian tissues and enable high throughput experiments. However, the impact of these experiments may be limited by manual, non-standardized, static or qualitative phenotypic analysis. OrgDyn is an open-source and modular pipeline to quantify organoid shape dynamics using a combination of feature- and model-based approaches on time series of 2D organoid contour images. Our pipeline consists of (i) geometrical and signal processing feature extraction, (ii) dimensionality reduction to differentiate dynamical paths, (iii) time series clustering to identify coherent groups of organoids and (iv) dynamical modeling using point distribution models to explain temporal shape variation. OrgDyn can characterize, cluster and model differences among unique dynamical paths that define diverse final shapes, thus enabling quantitative analysis of the molecular basis of tissue development and disease.

Availability and Implementation

https://github.com/zakih/organoidDynamics (BSD 3-Clause License).

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Our understanding of cell, developmental and cancer biology relies upon the analysis of isolated cells cultured at low density on flat, rigid substrates. Recently, 3D cell culture systems have become more physiologically relevant models for study cell behavior (Cheung et al., 2013; Gencoglu et al., 2017; Nguyen-Ngoc et al., 2012; Nguyen-Ngoc et al., 2015; Padmanaban et al., 2019; Schwartz et al., 2017; Shamir and Ewald, 2014). These systems include 3D cellular spheroids or tumor organoids and 3D matrices in which to grow and visualize cells akin to the way they grow in the human body. To fully realize the potential of these 3D culture models, we urgently need better visualization and analysis methods to handle the large amount of data that results from time-dependent analysis of 3D culture models and subsequent 2D projections.

Conventional approaches to quantify the morphologies of diverse 3D cell samples have either (i) often been limited to qualitative scoring systems, such as binned percentages or categorical scales, (ii) focused on a few spatial descriptors such as distance from centroid (Maeda et al., 2008), Fourier modes (Sánchez-Corrales et al., 2018), membrane extension and retraction (Satulovsky et al., 2008), roundness and hollowness (Åkerfelt et al., 2015) or (iii) developed comprehensive spatial descriptors for non-temporal datasets (Borten et al., 2018).

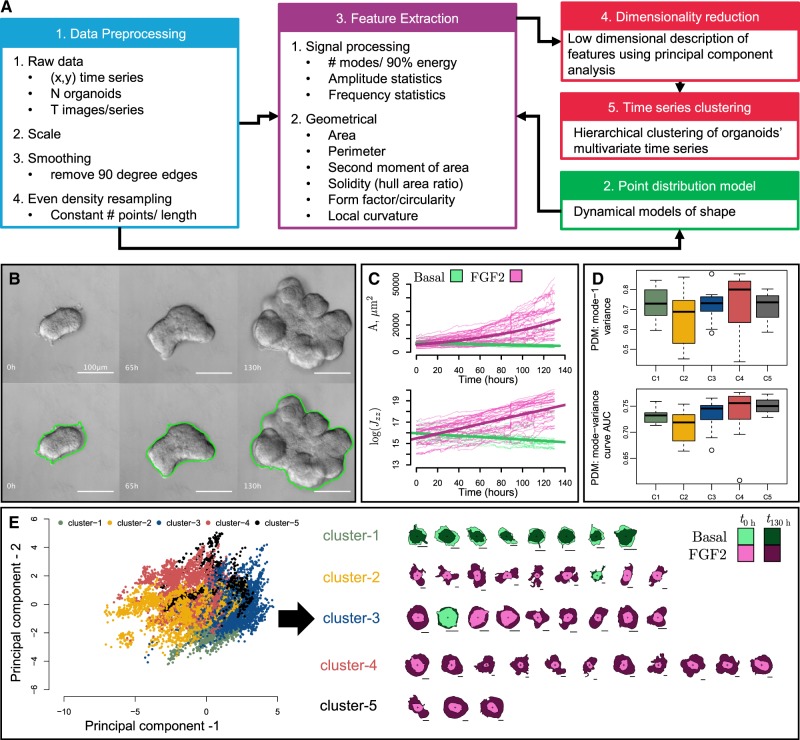
OrgDyn introduces techniques for quantifying the dynamical evolution of organoid morphology by (i) extracting spatio-temporal shape descriptors from time series of 2D organoid contours, (ii) capturing phenotypic spatio-temporal heterogeneity in clusters and (iii) modeling and quantifying dynamical variations (Fig. 1A). At the core of the pipeline are geometrical- and signal processing-based descriptive features of organoid shape, as these are often the focus of shape assessment studies (Borten et al., 2018; Kriegel et al., 2018; Meijering et al., 2012; Meijering, 2012; Pincus and Theriot, 2007; Sánchez-Corrales et al., 2018; Zimmer et al., 2002). We introduce local curvature shape descriptors, and leverage all these features concurrently to increase robustness of spatio-temporal phenotypic analyses. A standardized and intuitive pipeline of organoid morphometric analysis can benefit the experimental community by providing a common path to quantification and form a baseline for future advancements in analytical techniques.

Fig. 1.

OrgDyn tools and example. (A) OrgDyn pipeline. (B) Sample FGF2 treated organoid DIC images and contours using OrgDyn script for ImageJ. (C) Area and polar moment of area time series for FGF2 and basal organoids. (D) PDM metrics for 39 organoids grouped by (E) hierarchical clustering of 39 organoids’ time series in principal component space

2 Materials and methods

The input for OrgDyn is a time series of 2D organoid contours (step 1 in Fig. 1A). Point distribution models (PDM) of each organoid are generated, and metrics of dynamical complexity are calculated (step 2 in Fig. 1A). Ten features are extracted per contour: area A, perimeter P, form factor a_f, solidity a_h, polar moment of area J_zz, fraction of convex f_vex and concave f_cav points, and the number of modes N₉₀, the mean mode amplitude ${\overline{A}}_{90}$ and standard deviation σ₉₀ of mode amplitudes in the 90% discrete Fourier transform of a contour (step 3 in Fig. 1A). Together, these features form multivariate time series for each organoid, and these are cast to principal component (PC) space and then clustered (steps 4 and 5 Fig. 1A). Detailed methods are presented in Supplementary Section 2.

2.1 Numerical implementation

The preprocessing, feature extraction and PDM algorithms are implemented using MATLAB 2017b. Dimensionality reduction and clustering algorithms are implemented in R version 3.4.3.

3 Example

We demonstrate OrgDyn on a 3D culture model of normal mouse mammary development (Ewald et al., 2008; Nguyen-Ngoc et al., 2015) consisting of basal and FGF2-treated organoid groups. The organoids were imaged every 30 min using differential interference contrast (DIC) microscopy for 130 h, creating a time series of contours of each organoid’s boundary (Fig. 1B). Among the 10 features (Fig. 1A, step 3), area and the polar moment of area showed a dramatic difference in the growth trajectories (Fig. 1C). Each contour of an organoid’s time series is cast in reduced PC space in Figure 1E, and connecting together these points creates a reduced dimension time series of each organoid which encompasses the majority of variance in the original features. Clustering the organoids’ PC space time series reveals groups of organoids which have similar dynamical histories. The hierarchical clustering splits cluster-1 from the other clusters first, forming the division between basal and FGF2 types. However, each cluster represents unique phenotypes, and clusters 2–5 are all FGF2 subtypes ranging from the most to least complex morphologies in clusters-2 and cluster-3, respectively (Fig. 1E). Figure 1D shows the PDM metrics grouped by the clusters in Fig. 1E, where the low variance captured by the first mode and AUC of the mode-variance curve confirm that cluster-2 organoids require the greatest number of dynamical modes to capture their evolution. Detailed example is presented in Supplementary Section 3.