Abstract
Although dengue and Zika cocirculation has increased within the past 5 years, very little is known about its epidemiological consequences. To investigate the effect of dengue and Zika cocirculation on the spread of both pathogens, we create a deterministic dengue and Zika coinfection model, the first to incorporate altered infectivity of mosquitoes (due to coinfection). The model also addresses increased infectivity due to antibody-dependent enhancement (ADE) within the human population. Central to our analysis is the derivation and interpretation of the basic reproductive number and invasion reproductive number of both pathogens. In addition, we investigate how model parameters impact the persistence of each disease. Our results identify threshold conditions under which one disease facilitates the spread of the other and show that ADE has a greater impact on disease persistence than altered vector infectivity. This work highlights the importance of ADE and illustrates that while the endemic presence of dengue facilitates the spread of Zika, it is possible for high Zika prevalence to prevent the establishment of dengue.
Keywords: Invasion reproductive number, Copersistence, Zika, Dengue
Introduction
With approximately 50–100 million cases annually, dengue is one of the most prevalent mosquito-borne diseases in the world (World Health Organization 2012). Over 40% of the world’s population live in areas with high risk of dengue transmission and over 100 countries are endemic for the disease (Kumar et al. 2010). Dengue is transmitted to humans mainly through the bite of infected female Aedes aegypti mosquitoes and is caused by one or more viral serotypes of the Flaviviridae family [DENV-1 through 4 are known to infect humans; identification of a fifth, sylvatic serotype termed DENV-5 has been claimed (Mustafa et al. 2015)]. Although this illness is typically self-limiting, with infection by one serotype resulting in lifelong immunity to that specific serotype, severe forms of the disease can cause dengue hemorrhagic fever and dengue shock syndrome (Kumar et al. 2010). Currently, no treatment exists for dengue and only one controversial vaccine () has been licenced. As a result, mosquito control strategies remain the primary method of preventing dengue transmission.
Closely related to dengue is Zika, another disease of international concern. Zika was first discovered in Uganda in 1947 and has since spread across the globe, with outbreaks in Yap Island (2007), French Polynesia (2013), and more recently the Americas (2015) (Gao et al. 2016). The Zika virus (ZIKV) is of the same family as the dengue serotypes and is also transmitted to humans primarily by A. aegypti mosquitoes (although it can also be sexually and vertically transmitted within the human population). While some clinical symptoms of Zika, such as acute fever, nausea, rash, joint pain, and myalgia, are similar to dengue, Zika is unique in that it can cause serious complications in the form of Guillain–Barré syndrome and congenital Zika syndrome (Gao et al. 2016).
Due to having a shared vector, cocirculation of dengue and Zika is common in many geographical regions and increases the likelihood of dengue–Zika coinfections within human and mosquito populations. To date, clinical studies have reported human coinfections in countries such as Colombia, New Caledonia, Nicaragua, and Haiti (Carrillo-Hernández et al. 2018; Dupont-Rouzeyrol et al. 2015; Lovine et al. 2017; Waggoner et al. 2016). However, because of the rapid introduction of Zika into countries that are endemic with dengue, similarities in symptoms between the two diseases, underreporting, and the lack of proper serotesting in developing countries, it is believed that the prevalence of coinfections is higher than currently perceived (Rückert et al. 2017).
In A. aegypti mosquitoes, infection with multiple arboviruses has been shown to affect viral dissemination, transmission, and replication (Abrao and da Fonseca 2016; Magalhaes et al. 2018; Rückert et al. 2017). Researchers in Chaves et al. (2018) reveal that for dengue and Zika specifically, coinfection can impact mosquito infectivity. The results of Chaves et al. (2018) indicate that while the number of dengue virus cDNA copies in coinfected mosquitoes is higher than in monoinfected mosquitoes (up to 12 times higher), Zika cDNA copies are lower in coinfected mosquitoes than in their monoinfected counterparts (6–9 times lower). This suggests that coinfection may cause mosquitoes to be more likely to transmit dengue and less likely to transmit Zika.
Within humans, dengue and Zika can display complex viral interactions in the form of antibody-dependent enhancement (ADE). ADE occurs when antibodies from a previous infection bind to a pathogen in a subsequent infection and, instead of neutralizing the pathogen, increase viral uptake and replication (Whitehead et al. 2007). Many in vitro studies (e.g., Charles and Christofferson 2016; Dejnirattisai et al. 2016; Durbin 2016; Paul et al. 2016) have shown that dengue antibodies cross-react with the ZIKV, increasing Zika infection of cells and production of viral progeny by over 100-fold. The reciprocal effect of ZIKV antibodies increasing dengue virus titers has also been reported (Kawiecki and Christofferson 2016; Stettler et al. 2016). Although these cross-reactive ADE effects have not been confirmed in vivo in humans by field data, they have been observed in vivo in mice (Bardina et al. 2017) and macaques (George et al. 2017). Thus, given the well-known ADE across DENV serotypes and the consistent in vitro results, the potential is clear for immunity to one of the two viruses to enhance transmission of the other virus within the human population.
While many mathematical models have been developed to understand the dynamics of Zika and dengue individually (e.g., Andraud et al. 2012; Braselton and Bakach 2015; Wiratsudakul et al. 2018), only a few have considered both viruses simultaneously. The first two studies to do so also included chikungunya, an arbovirus transmitted by the infamous A. aegypti (Isea and Lonngren 2016; Okuneye et al. 2017), but largely excluded the possibility of coinfection. Isea and Lonngren (2016) focused on analyzing the stability of a nontrivial equilibrium in a system which considers only single transmission of the three viruses. They also introduce a second model that incorporates coinfections within the human population, but its analysis was limited to finding a nontrivial equilibrium. Both models exclude sexual transmission of Zika between humans, coinfection within the mosquito population, and altered infectivity of humans (due to possible ADE) or mosquitoes (due to coinfection). Meanwhile, the model in Okuneye et al. (2017) investigates the impact of a dengue–chikungunya–Zika superinfection hierarchy within humans, where (based on relative incidence data) infection with dengue completely replaces infection with chikungunya or Zika, and infection with chikungunya replaces Zika. Furthermore, the authors include sexual transmission of Zika, assume that dengue vaccination can reduce Zika susceptibility, and consider the possibility of ADE of dengue over Zika (but not ADE of Zika over dengue) by altering the susceptibility of hosts and vectors to Zika, rather than altering Zika infectivity of these populations. Okuneye et al. (2017) found that under this superinfection hierarchy, dengue-induced ADE and dengue vaccination had only minor impacts on Zika transmission.
Another mathematical study considered dengue and Zika coinfection in order to examine the impact of dengue vaccination on a Zika outbreak (Tang et al. 2016). The model captures vaccination indirectly through initial conditions. Every combination of susceptible and infectious populations is given a different infection rate, so in principle the model could accommodate both ADE in humans and altered infectivity of coinfected vectors, but qualitative analysis was limited to computation of the basic reproductive number (the number of secondary infections that a single infected individual can make in a completely susceptible population), and numerical analysis set all the infection rates equal to each other (without units) except the rate at which coinfected mosquitoes infect naive humans (with either virus) and the rate at which Zika-monoinfected mosquitoes infect dengue-recovered humans. Comparison of two graphs verified that when these latter two rates were increased by a factor of 3.6, Zika incidence increased. The study’s main conclusion was that a high mosquito birth rate together with dengue vaccination could increase Zika incidence and cause a Zika outbreak to occur earlier and have a higher peak than observed with low mosquito birth rates.
More recently, Wang and Zhao (2019) published a similar study, with dengue and Zika spreading in a population where the dengue vaccine is available. They assumed perfect vaccine efficacy and found a monotone increase in Zika’s basic reproductive number with increases in vaccination. However, the authors also assumed that mosquitoes cannot be coinfected with Zika and dengue, thus precluding any possibility of considering altered infectivity for coinfected vectors.
We therefore propose a study which simultaneously explores the three facets of what we call the dengue–Zika interplay: coinfection of humans and vectors, altered vector infectivity, and ADE of dengue and Zika. In this article, we develop the first Zika and dengue transmission model that includes coinfection (in humans and mosquitoes), altered vector infectivity, and ADE for both viruses (i.e., viral enhancement of Zika given dengue antibodies and enhancement of dengue given Zika antibodies). The goal of the present study is to better understand the epidemiological consequences of the dengue–Zika interplay. In particular, through a deterministic mathematical model that utilizes a system of nonlinear ordinary differential equations, we seek to answer the following research questions:
How does the endemic presence of dengue affect Zika’s ability to spread in a region?
How does invasion of Zika affect the endemic presence of dengue?
With Zika rapidly spreading across the globe to regions endemic with dengue, examining the complex interactions between the two pathogens is vital to clarifying the public health impact of the cocirculation of both diseases and potentially informing future vaccine development and control strategies.
Model Development
The current study is placed in the context of dengue and Zika cocirculation in El Salvador. The total human population (given in Table 2) represents the calculated at-risk population for Zika in El Salvador during the 2015/2016 outbreak, as described in Shutt et al. (2017). Since Zika and dengue are spread by the same vector and are in similar geographic regions, we assume that this number also represents the population at risk for dengue during that time.
Table 2.
Model parameters
| Symbol | Description (units) | Value | References |
|---|---|---|---|
| Mosquito-to-human dengue infection rate (humans/(mosquito*day)) | 0.25 | Braselton and Bakach (2015) | |
| Mosquito-to-human Zika infection rate (humans/(mosquito*day)) | 0.15 | Manore et al. (2014) | |
| Human-to-mosquito dengue infection rate () | 0.25 | Braselton and Bakach (2015) | |
| Human-to-mosquito Zika infection rate () | 0.15 | Manore et al. (2014) | |
| Zika human sexual transmission rate () | 0.05 | Olawoyin and Kribs (2018) | |
| Dengue recovery rate () | 0.14 | Braselton and Bakach (2015) | |
| Zika recovery rate () | 0.14 | Shutt et al. (2017) | |
| Human birth/death rate () | Braselton and Bakach (2015) | ||
| Mosquito birth/death rate () | 0.07 | Yang et al. (2009) | |
| Modification factor for dengue transmission by coinfected mosquitoes | 12 | Chaves et al. (2018) | |
| Relative likelihood of dengue transmission given prior Zika infection | Inferred from Kawiecki and Christofferson (2016) and Stettler et al. (2016) | ||
| Relative likelihood of Zika transmission given prior dengue infection | Inferred from Charles and Christofferson (2016), Dejnirattisai et al. (2016), Durbin (2016) and Paul et al. (2016) | ||
| Modification factor for Zika transmission by coinfected mosquitoes | 0.11 | Chaves et al. (2018) | |
| Total number of female mosquitoes | 457, 092 | Olawoyin and Kribs (2018) | |
| Total number of humans | 76, 182 | Olawoyin and Kribs (2018) |
A visual representation of the deterministic dengue and Zika coinfection model that we consider is shown in Fig. 1, with the state variables and parameters described in Tables 1 and 2, respectively. In this model, we make the following assumptions:
Human and mosquito populations remain constant.
Only one dengue serotype is cocirculating in the study region [an assumption also made in Isea and Lonngren (2016) and Okuneye et al. (2017)].
There is no disease-induced death in the human population as the case-fatality rate for each disease is low (Moraes et al. 2013; PAHO 2016).
ADE occurs after a person has recovered from a primary infection and is subsequently infected with the other virus. ADE produces an increased viral load.
All humans are equally susceptible to infection by a given virus (and the same for mosquitoes), but humans who have recovered from a primary infection and then become infected with the other virus exhibit altered (increased) infectivity due to ADE.
Any dengue/Zika coinfection in humans and mosquitoes is sequential (i.e., requires two infection events) rather than simultaneous.
Coinfection alters the rate at which mosquitoes transmit dengue/Zika.
Fig. 1.
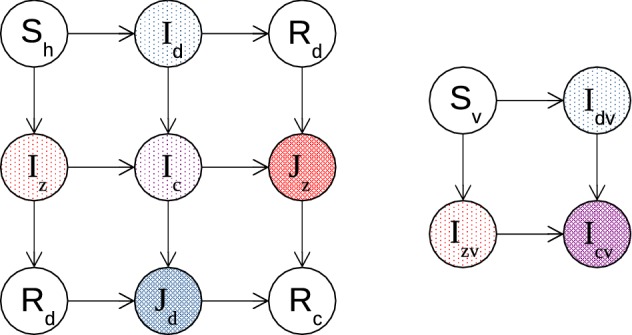
Zika and Dengue Coinfection model schematic: arrows represent changes in infection status (movement between different state variables) among humans (at left) and vectors (at right). Shading indicates infective classes; heavy shading denotes classes with altered infectivity. Note that demographic renewal is not depicted in this diagram
Table 1.
Epidemiological classes
| State variable | Description |
|---|---|
| Dengue and Zika-susceptible humans | |
| Dengue-infected humans | |
| Zika-infected humans | |
| Dengue and Zika-coinfected humans | |
| Dengue-recovered humans | |
| Zika-recovered humans | |
| Dengue-infected humans immune to Zika due to previous exposure | |
| Zika-infected humans immune to Dengue due to previous exposure | |
| Dengue and Zika-recovered humans due to previous exposure to both pathogens | |
| Susceptible female mosquitoes | |
| Dengue-infected female mosquitoes | |
| Zika-infected female mosquitoes | |
| Dengue and Zika-coinfected female mosquitoes |
Humans are born fully susceptible to dengue and Zika at a rate of , where is the natural birth/death rate for humans and is the total human population. Susceptible individuals can become infected with dengue from either a dengue-infected () or coinfected female mosquito (). The mosquito-to-human dengue infection rate is given by . This rate is modified by a factor of to indicate the altered infectivity of coinfected mosquitoes. Once infected with dengue, humans can recover or become coinfected with Zika (by a Zika-infected () or coinfected female mosquito (), or by sexual transmission from a Zika-infected () or coinfected () human) and transition into the or class, respectively. In a similar manner, fully susceptible humans become infected with Zika from a mosquito in the or compartment, or by a human in the or compartment. The mosquito-to-human Zika infection rate is given by and is modified by a factor of for coinfected mosquitoes. Once infected with Zika, humans either recover (with the Zika recovery rate given by ) or become coinfected with dengue through a mosquito in or .
When a coinfected human recovers from dengue, he or she becomes dengue-immune and enters the class. Meanwhile, singly infected humans who recover from dengue join the compartment where they are susceptible to further infection with the ZIKV. For individuals in the class, the rate of ZIKV infection is modified by a factor of which represents the relative Zika infectivity given the effect of ADE. Furthermore, coinfected humans who recover from Zika transition into the class and are immune to ZIKV infection. Once in , an individual’s dengue infectivity is modified by a factor of due to the higher viral load induced by ADE. On the other hand, individuals who recover from a single infection with Zika enter and are susceptible to further infection with dengue. Lastly, individuals immune to dengue or Zika (i.e., those in or ) that undergo subsequent infection with the secondary virus recover and become immune to both diseases ().
In the vector population, mosquitoes are born into the susceptible class () at a rate of , where is the natural birth/death rate for mosquitoes and is the total mosquito population. Susceptible mosquitoes are infected with dengue after feeding on a dengue-infected or coinfected human. In this case, the human-to-mosquito dengue infection rate is given by . Likewise, susceptible mosquitoes can become infected with Zika after feeding on a Zika-infected or coinfected human, with a human-to-mosquito Zika infection rate of . These singly infected mosquitoes can be coinfected with both pathogens after feeding on a human infected with the second virus.
Model Equations
The system of nonlinear differential equations corresponding to the dengue and Zika coinfection model described above is given by (1).
 |
1 |
A majority of the baseline parameter values used for this model were obtained from previously published literary sources as indicated in Table 2. To obtain the Zika and dengue transmission modification factors, we observed the difference in viral cDNA copies between monoinfected and coinfected mosquitoes described in Chaves et al. (2018). Based on this study, the number of dengue virus cDNA copies in coinfected mosquitoes was 1.25–12 times higher than in monoinfected mosquitoes, while ZIKV cDNA copies were 6–9 times lower in coinfected mosquitoes than monoinfected mosquitoes. Assuming that these ranges correspond to the disease transmission capability of coinfected vectors, we use values within the ranges for and . Since the only studies on the effect of ADE on Zika and dengue have been conducted at the cellular level (i.e., comparing viral titers and replication), the direct effect of ADE on dengue or Zika transmission is unknown. However, due to the large rise (up to two orders of magnitude) in viral load caused by ADE, we assume that ADE increases the likelihood of disease transmission and take and to be greater than one.
Under the assumption that human infection with the ZIKV is completely independent of DENV immunity (i.e., ) and that the ability of vectors to transmit Zika is independent of their coinfection with dengue (i.e., ), system (1) simplifies to
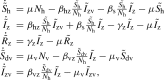 |
2 |
where , , , , and . Since the total human and vector populations, and , respectively, are constant, (2) can be rewritten as
| 3 |
A similar reduction of (1) can be obtained when and. In this case, the model simplifies to (3), with the exception that there is no sexual transmission term, and the z’s in the subscripts of (3) are replaced with d’s.
Equilibrium Points
To find equilibrium values of (1), we set all of the differential equations to zero. Some of the equilibria are detailed in Table 3 and describe scenarios when no disease is present within the population (disease-free equilibrium), or when only one disease is present (dengue-only or Zika-only equilibrium). Although we were unable to find an analytic expression for a copersistence equilibrium, numerical explorations suggest the existence of a stable copersistence equilibrium when both the dengue and Zika invasion reproductive numbers (IRNs) exceed 1. These IRNs are detailed in Sect. 5. Existence criteria for the unique single pathogen equilibria are described in Lemma 1 and Theorem 1.
Table 3.
Equilibrium points
| Equilibrium type | ||||||||
|---|---|---|---|---|---|---|---|---|
| Disease-free | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Dengue-only | 0 | 0 | 0 | |||||
| Zika-only | 0 | 0 | 0 |
In this table, and , where a, b, and c are as described in Sect. 3. In addition, for each equilibrium type
Lemma 1
For (1), a unique dengue-only equilibrium exists iff
The proof of Lemma 1 is in “Appendix.”
Theorem 1
For (1), a unique Zika-only equilibrium exists iff
Proof
As seen in Table 3, all of the nonzero points of the Zika-only equilibrium are expressed in terms of , where is the solution to the quadratic equation . In this equation,
Using the quadratic formula, we have . Since , when , takes the sign of . When , one positive () and one negative () solution are obtained.
Notice that
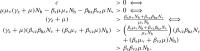 |
By this last inequality, we have . Finally, multiplying by and subtracting on both sides of the inequality, we obtain . This implies that for , . Thus, the only biologically feasible solution for occurs iff and is given by .
Since
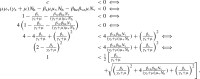 |
this unique Zika-only equilibrium exists iff .
Basic Reproductive Number
To derive the BRN of the ZIKV and DENV coinfection model, we use the next-generation operator method proposed by van den Driessche and Watmough (2002). Evaluating the F and V matrices obtained from this method at the disease-free equilibrium, we have
and
The BRN is the spectral radius of and is given by
The fractions and in are the product of the DENV infection rates and the average time a human or vector remains infected with dengue ( days for vectors and days for humans). The second term under the radical in is similar to and represents vector transmission of Zika. However, also includes sexual transmission of Zika within the human population in the form , where is the sexual transmission rate and is the average duration of infection in humans.
The next-generation operator method ensures the local asymptotic stability of the disease-free state when .
IRNs
Invasion reproductive numbers (Crawford and Kribs 2009; Martcheva 2009; Porco and Blower 1998) for autonomous systems can be derived by extending the next-generation matrix method (van den Driessche and Watmough 2002) to consider any resident (non-invading) infections as non-infectious classes (Mitchell and Kribs 2019). This method establishes conditions for the local asymptotic stability (LAS) of the boundary equilibria: the dengue-endemic equilibrium is LAS when dengue can spread alone but Zika cannot invade it (), and the Zika-endemic equilibrium is LAS when ZIKV can spread alone but dengue cannot invade it (). As noted in Sect. 3, numerical explorations indicate that when both IRNs exceed 1, a copersistence equilibrium is LAS.
Dengue IRN
The dengue IRN, which describes the ability of dengue to spread in a population endemic with Zika, is calculated with , and categorized as the infectious classes. Evaluating the F and V matrices at the Zika-only endemic equilibrium, we obtain
and
Dengue’s IRN is the spectral radius of and is given by , where
and
It is important to note that when , .
Epidemiologically, is the average relative dengue infectivity of mosquitoes in a setting where Zika is resident and is the average relative dengue infectivity of humans within that setting. While the proportion of susceptible mosquitoes that get Zika before dying and the proportion of Zika infectious mosquitoes at the time that dengue arrives have relative dengue infectivity of , the relative dengue infectivity of the proportion of susceptible mosquitoes that die before contracting Zika () is 1.
In the expression, the proportion of susceptible humans who get Zika before dying but recover from Zika prior to getting dengue , the proportion of humans infected with Zika when dengue arrives who recover before getting dengue , and the proportion of humans already recovered from Zika when dengue is introduced () have a relative dengue infectivity of . On the other hand, susceptibles who get Zika but die or get dengue before recovering from Zika , susceptibles who die or get infected with dengue prior to getting Zika , and those currently infected with Zika who die or get dengue before recovering from Zika () all have a relative dengue infectivity of 1.
Zika IRN
The Zika IRN describes the ability of Zika to spread in a population endemic with dengue and is computed in a similar manner as the dengue IRN. However, in this case and are categorized as the infectious classes. Evaluating F and V at the dengue-only endemic equilibrium, we obtain
and
Zika’s IRN is the spectral radius of and is given by
, where
and
Notice that when , . Furthermore, in a similar manner as and , the and expressions describe the relative Zika infectivity of vectors and humans, respectively.
It is worth noting that the four parameters which describe the dengue–Zika interplay do not appear in either virus’s BRN but do appear in the two IRNs, specifically human ADE () through the terms and , and altered infectivity for coinfected vectors () through the terms and .
BRN/IRN Threshold Curves
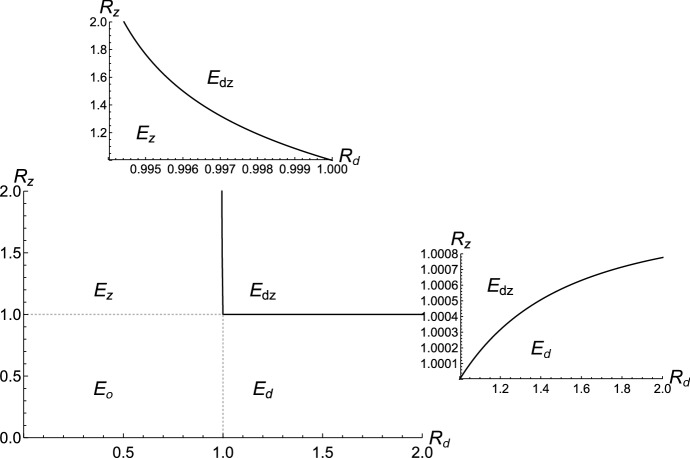
In order to visualize how various aspects of the dengue–Zika interplay impact the persistence of each disease, we plot IRN threshold curves for on the versus axis. As seen in Figs. 2 and 3, this results in four distinct regions of possible model outcomes (extinction of both diseases, , persistence of only dengue, , persistence of only Zika, , and copersistence of both pathogens, ). In these figures, the curve above the line is and the curve to the right of the line is .
Fig. 2.
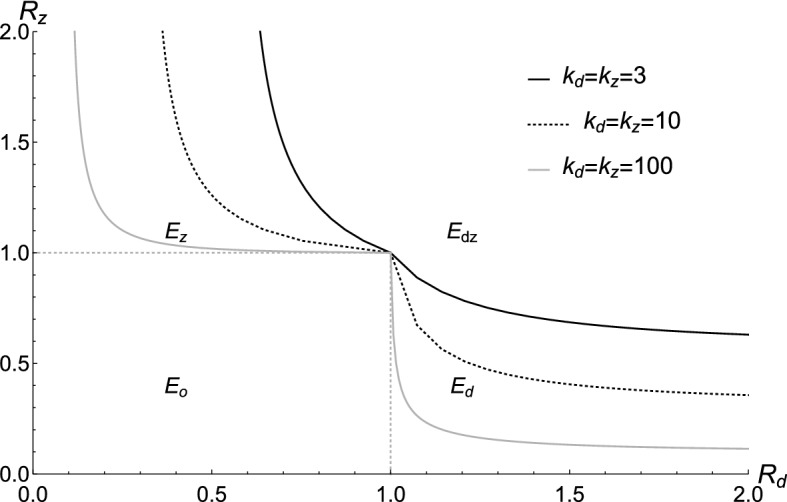
Variations in IRN threshold curves with and . The and parameter values used to generate the IRN threshold curves are as indicated, while other parameter values are kept at their baseline values
Fig. 3.
IRN threshold curves for . To generate this figure, we let and keep other parameters at their baseline values. The miniature figures represent enlarged sections of the (top figure) and (bottom right figure) curves. This graph shows the relatively minimal effect of altered vector infectivity on transmission of the viruses
Figure 2 illustrates that ADE (i.e., ) causes Zika and dengue to benefit from the presence of each other. In particular, due to ADE, the presence of dengue makes it possible for Zika to persist in regions where it would not have been able to persist on its own (i.e., in regions where ). Similarly, this figure shows that the reciprocal effect of Zika presence on dengue is also true with ADE. In fact, as the likelihood of disease transmission by recovered individuals increases across various orders of magnitude, the region widens and makes it easier for dengue and Zika to copersist.
To disentangle the effects of altered infectivity of hosts from that of vectors, we let (while keeping and at their baseline values) and obtain Fig. 3. Since the curves appear to be straight lines, it seems, at first glance, that altered infectivity of vectors does not affect persistence of Zika and dengue. However, after enlarging the IRN threshold curves, it is clear that Zika slightly facilitates the spread of dengue (as seen in the region where dengue is able to invade even though ) while dengue hinders the spread of Zika (as evidenced by the narrow region where Zika is not able to establish itself even though ). This minor impact of and on the persistence of each pathogen can be attributed to the fact that coinfected mosquitoes have a higher likelihood of transmitting dengue and a lower likelihood of transmitting Zika than monoinfected mosquitoes.
A more detailed exploration of how the altered infectivity parameters impact dengue and Zika dynamics is conducted by plotting the and curves on the versus k axis. As shown in Fig. 4, these curves divide the plane into two distinct regions, one where the IRN is greater than the BRN and the other where the IRN is less than the BRN. If Zika-recovered individuals are more than 5.2 times as likely as their Zika-naive counterparts to transmit dengue, the dengue IRN will always be greater than its BRN. On the other hand, any level of ADE (i.e., any ) causes the Zika IRN to be greater than its BRN.
Fig. 4.
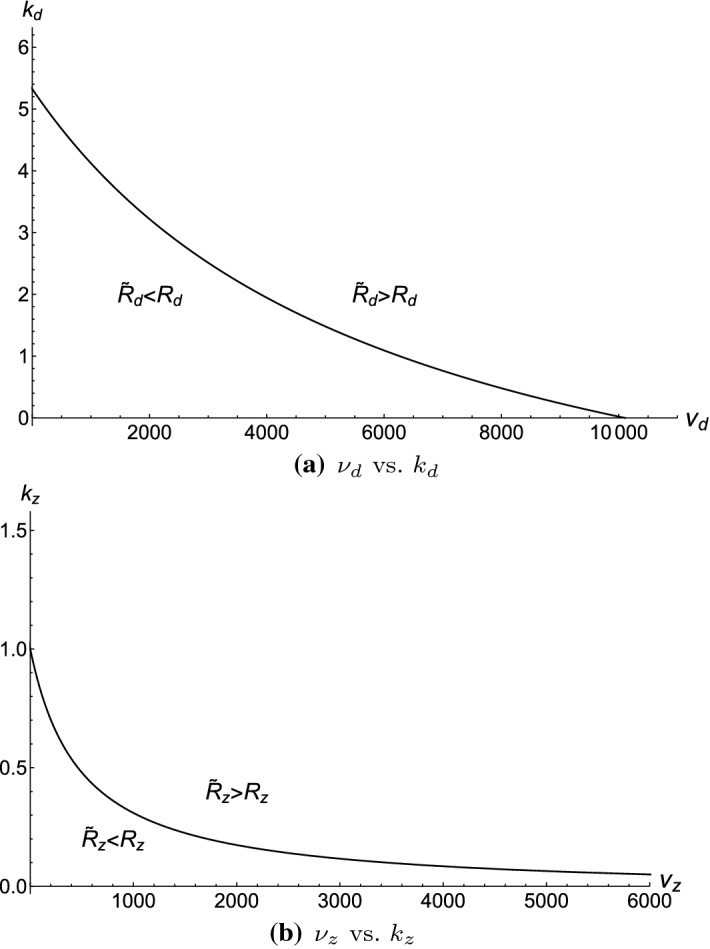
BRN and IRN comparisons on versus k axes
Discussion and Concluding Remarks
Although cocirculation of Zika and dengue is common due to the pathogens’ shared vector, the impact of cocirculation on the presence of each pathogen has not received great mathematical modeling attention. In this study, we develop and analyze the first mathematical model of dengue and Zika that incorporates coinfection in humans and vectors, altered infectivity of coinfected vectors, and ADE. Through various analytical and numerical results, we highlight possible epidemiological consequences inherent in the cocirculation of both diseases.
The results of this work differ from those of the previous mathematical modeling studies to consider dengue and Zika cocirculation. Specifically, our derivation of explicit expressions for the IRNs of the two viruses makes clear the role of each of the two factors (ADE in humans and coinfection in mosquitoes) which we assume to affect the infectivities of both viruses. While the complexity of the model in Isea and Lonngren (2016) prevents the authors from deriving any reproductive numbers, Tang et al. (2016) compute their model’s BRN only, in which neither infectivity-altering factor appears, since the BRN is defined in terms of the disease-free state. The and expressions in our BRN are structurally similar to those in Okuneye et al. (2017) and Wang and Zhao (2019). However, unlike ours, the BRN expressions derived in these latter two papers include both vaccination and ADE parameters, because those studies assume that ADE alters susceptibility, rather than infectivity, including of vaccinated individuals. For them, ADE alters the viruses’ BRNs to the extent that vaccinated individuals are present in the disease-free state. Since ADE increases the viral load during a second infection, until field studies confirm the nature of its effects during transmission, the question of whether the increased viral load increases susceptibility or subsequent infectivity remains open. We consider an increased viral load throughout the course of an infection to affect primarily infectivity.
Our calculation of the IRNs for both diseases therefore permits a more systematic and interpretable study of how ADE and coinfected vectors create a complex and asymmetric interplay between dengue and Zika viruses by changing their infectivities. The expressions for weighted-average infectivities in each IRN show how key parameter values impact them. Through Fig. 4, we see that altered infectivity of hosts has a greater impact on the IRNs than the altered infectivity of vectors. In addition, the and parameters can be used to determine when the presence of one disease makes it easier or harder for the other to spread (i.e., when each pathogen’s IRN will be greater than or less than its BRN). Regardless of the level of ADE, we find that Zika will always spread more easily in dengue-endemic regions than it would on its own. However, this is not the case with dengue. For dengue, the effect of ADE has to be high enough (i.e., ) in order for the presence of Zika to facilitate the establishment of dengue. This allows for interesting scenarios where Zika and dengue will have opposite effects on each other. For example, when and , high dengue propagates the spread of Zika (i.e., ), but high Zika prevalence impedes the invasion of dengue (i.e., ).
In addition to Fig. 4, Figs. 2 and 3 provide valuable insight on how the Zika and dengue viruses affect each other on the population level. With or without altered infectivity of humans, the presence of Zika makes it possible for dengue to persist in a population in which it would not be able to persist by itself. However, our results show that ADE (i.e., ) is essential for Zika to benefit from the presence of dengue. Without ADE, it is possible for Zika’s BRN to be greater than 1, but Zika not be able to successfully invade a population because of the presence of dengue. Both of these results are due to the baseline but values that allow coinfected mosquitoes to be better at transmitting dengue than Zika. Furthermore, as altered host infectivity parameters increase, the region of copersitence of both viruses widens, showing a mutualistic relationship between Zika and dengue due to ADE.
From this research, it is clear that the impact of ADE on the infectivity of hosts plays a crucial role in dengue–Zika dynamics. However, there are no experimental studies that address the epidemiological consequences of ADE, specifically how it affects dengue infectivity of Zika-immune individuals or Zika infectivity of dengue-immune persons. Currently, the studies that address ADE do so on the cellular level, describing its impact on viral titers. We argue that due to the effect of the and parameters on IRN and BRN comparisons and the persistence of Zika and dengue, there is a need for studies that focus on estimating these values. Using experimentally validated and estimates would allow us to draw more concrete conclusions on the population-wide impact of Zika and dengue, which can potentially inform vaccine development efforts.
In future, we plan to extend our study of this dengue–Zika interplay model to consider vaccination and include more than one dengue serotype. Explicitly incorporating potential Zika and dengue vaccines will give a clear picture of the possible impact of vaccinations and whether or not the use of one vaccine can indirectly exacerbate the burden of the other pathogen. In addition, since multiple dengue serotypes typically cocirculate within particular regions (and have been shown to exhibit ADE with each other), it would be beneficial to examine how the presence of more than one dengue serotype with Zika affects the long-term persistence of the various pathogens.
Acknowledgements
The authors acknowledge the National Science Foundation as this material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. 1746052. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Appendix: Proof of Lemma 1
Proof
A brief inspection of the dengue-only equilibrium reveals that this equilibrium point exists (i.e., consists of nonnegative terms) iff . Notice that
 |
Thus, a unique dengue-only equilibrium exists iff .
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Omomayowa Olawoyin, Email: omomayowa.olawoyin@mavs.uta.edu.
Christopher Kribs, Email: kribs@uta.edu.
References
- Abrao E, da Fonseca B. Infection of mosquito cells (c6/36) by dengue-2 virus interferes with subsequent infection by yellow fever virus. Vector-Borne Zoonotic Dis. 2016;16(2):124–130. doi: 10.1089/vbz.2015.1804. [DOI] [PubMed] [Google Scholar]
- Andraud M, Hens N, Marais C, Beutels P. Dynamic epidemiological models for dengue transmission: a systematic review of structural approaches. PLoS ONE. 2012;7(11):e49085. doi: 10.1371/journal.pone.0049085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bardina SV, Bunduc P, Tripathi S, Duehr J, Frere JJ, Brown JA, Nachbagauer R, Foster GA, Krysztof D, Tortorella D, Stramer SL, García-Sastre A, Krammer F, Lim JK. Enhancement of Zika virus pathogenesis by preexisting antiflavivirus immunity. Science. 2017;356(6334):175–180. doi: 10.1126/science.aal4365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braselton J, Bakach L. A survey of mathematical models of dengue fever. J Comput Sci Syst Biol. 2015;8(5):255–267. [Google Scholar]
- Carrillo-Hernández M, Ruiz-Saenz J, Villamizar L, Gómez-Rangel S, Martínez-Gutierrez M. Co-circulation and simultaneous co-infection of dengue, chikungunya, and Zika viruses in patients with febrile syndrome at the Colombian-Venezuelan border. BMC Infect Dis. 2018;18(1):61. doi: 10.1186/s12879-018-2976-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charles A, Christofferson R (2016) Utility of a dengue-derived monoclonal antibody to enhance Zika infection in vitro. PLoS Currents, 8:ecurrents.outbreaks.4ab8bc87c945eb41cd8a49e127082620 [DOI] [PMC free article] [PubMed]
- Chaves B, Orfano A, Nogueira P, Rodrigues N, Campolina T, Nacif-Pimenta R, Pires A, Júnior A, Paz A, Vaz E, et al. Coinfection with Zika virus (ZIKV) and dengue virus results in preferential ZIKV transmission by vector bite to vertebrate host. J Infect Dis. 2018;218(4):563–571. doi: 10.1093/infdis/jiy196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crawford B, Kribs C. The impact of vaccination and coinfection on HPV and cervical cancer. Discrete Contin Dyn Syst Ser B. 2009;12(2):279–304. [Google Scholar]
- Dejnirattisai W, Supasa P, Wongwiwat W, Rouvinski A, Barba-Spaeth G, Duangchinda T, Sakuntabhai A, Cao-Lormeau V-M, Malasit P, Rey F, et al. Dengue virus sero-cross-reactivity drives antibody-dependent enhancement of infection with Zika virus. Nat Immunol. 2016;17(9):1102–1108. doi: 10.1038/ni.3515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupont-Rouzeyrol M, O’Connor O, Calvez E, Daures M, John M, Grangeon J-P, Gourinat A-C. Co-infection with Zika and dengue viruses in 2 patients, New Caledonia, 2014. Emerg Infect Dis. 2015;21(2):381–382. doi: 10.3201/eid2102.141553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durbin A. Dengue antibody and Zika: friend or foe? Trends Immunol. 2016;37(10):635–636. doi: 10.1016/j.it.2016.08.006. [DOI] [PubMed] [Google Scholar]
- Gao D, Lou Y, He D, Porco T, Kuang Y, Chowell G, Ruan S. Prevention and control of Zika as a mosquito-borne and sexually transmitted disease: a mathematical modeling analysis. Sci Rep. 2016;6:28070. doi: 10.1038/srep28070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- George J, Valiant WG, Mattapallil MJ, Walker M, Huang YS, Vanlandingham DL, Misamore J, Greenhouse J, Weiss DE, Verthelyi D, Higgs S, Andersen H, Lewis MG, Mattapallil JJ. Prior exposure to Zika virus significantly enhances peak dengue-2 viremia in rhesus macaques. Sci Rep. 2017;7:10498. doi: 10.1038/s41598-017-10901-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isea R, Lonngren K. A preliminary mathematical model for the dynamic transmission of dengue, chikungunya and Zika. Am J Mod Phys Appl. 2016;3:11–15. [Google Scholar]
- Kawiecki A, Christofferson R. Zika virus-induced antibody response enhances dengue virus serotype 2 replication in vitro. J Infect Dis. 2016;214(9):1357–1360. doi: 10.1093/infdis/jiw377. [DOI] [PubMed] [Google Scholar]
- Kumar K, Singh P, Tomar J, Baijal S. Dengue: epidemiology, prevention and pressing need for vaccine development. Asian Pac J Trop Med. 2010;3(12):997–1000. doi: 10.1016/S1995-7645(11)60017-5. [DOI] [Google Scholar]
- Lovine N, Lednicky J, Cherabuddi K, Crooke H, White S, Loeb J, Cella E, Ciccozzi M, Salemi M, Morris J., Jr Coinfection with Zika and dengue-2 viruses in a traveler returning from Haiti, 2016: clinical presentation and genetic analysis. Clin Infect Dis. 2017;64(1):72–75. doi: 10.1093/cid/ciw667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magalhaes T, Robison A, Young M, Black W, Foy B, Ebel G, Rückert C. Sequential infection of Aedes aegypti mosquitoes with chikungunya virus and Zika virus enhances early Zika virus transmission. Insects. 2018;9(4):177. doi: 10.3390/insects9040177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manore C, Hickmann K, Xu S, Wearing H, Hyman J. Comparing dengue and chikungunya emergence and endemic transmission in A. aegypti and A. albopictus. J Theor Biol. 2014;356:174–191. doi: 10.1016/j.jtbi.2014.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martcheva M. A non-autonomous multi-strain SIS epidemic model. J Biol Dyn. 2009;3(2–3):235–251. doi: 10.1080/17513750802638712. [DOI] [PubMed] [Google Scholar]
- Mitchell C, Kribs C. Invasion reproductive numbers for periodic epidemic systems. Infect Dis Model. 2019;4:124–141. doi: 10.1016/j.idm.2019.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moraes G, de Fátima Duarte E, Duarte E. Determinants of mortality from severe dengue in Brazil: a population-based case-control study. Am J Trop Med Hyg. 2013;88(4):670–676. doi: 10.4269/ajtmh.11-0774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mustafa M, Rasotgi V, Jain S, Gupta V. Discovery of fifth serotype of dengue virus (DENV-5): a new public health dilemma in dengue control. Med J Armed Forces India. 2015;71(1):67–70. doi: 10.1016/j.mjafi.2014.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okuneye K, Velasco-Hernandez J, Gumel A. The “unholy” chikungunya-dengue-Zika trinity: a theoretical analysis. J Biol Syst. 2017;25(04):545–585. doi: 10.1142/S0218339017400046. [DOI] [Google Scholar]
- Olawoyin O, Kribs C. Effects of multiple transmission pathways on Zika dynamics. Infect Dis Model. 2018;3:331–344. doi: 10.1016/j.idm.2018.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- PAHO (2016) Provisional remarks on Zika virus infection in pregnant women: document for health care professionals. http://iris.paho.org/xmlui/handle/123456789/18600. Accessed 18 Oct 2018
- Paul L, Carlin E, Jenkins M, Tan A, Barcellona C, Nicholson C, Michael S, Isern S. Dengue virus antibodies enhance Zika virus infection. Clin Transl Immunol. 2016;5(12):e117. doi: 10.1038/cti.2016.72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porco T, Blower S. Designing HIV vaccination policies: subtypes and cross-immunity. Interfaces. 1998;28(3):167–190. doi: 10.1287/inte.28.3.167. [DOI] [Google Scholar]
- Rückert C, Weger-Lucarelli J, Garcia-Luna S, Young M, Byas A, Murrieta R, Fauver J, Ebel G. Impact of simultaneous exposure to arboviruses on infection and transmission by Aedes aegypti mosquitoes. Nat Commun. 2017;8:15412. doi: 10.1038/ncomms15412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shutt D, Manore C, Pankavich S, Porter A, Del Valle S. Estimating the reproductive number, total outbreak size, and reporting rates for Zika epidemics in South and Central America. Epidemics. 2017;21:63–79. doi: 10.1016/j.epidem.2017.06.005. [DOI] [PubMed] [Google Scholar]
- Stettler K, Beltramello M, Espinosa D, Graham V, Cassotta A, Bianchi S, Vanzetta F, Minola A, Jaconi S, Mele F, et al. Specificity, cross-reactivity and function of antibodies elicited by Zika virus infection. Science. 2016;353(6301):823–826. doi: 10.1126/science.aaf8505. [DOI] [PubMed] [Google Scholar]
- Tang B, Xiao Y, Wu J. Implication of vaccination against dengue for zika outbreak. Sci Rep. 2016;6:35623. doi: 10.1038/srep35623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002;180(1–2):29–48. doi: 10.1016/S0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- Waggoner J, Gresh L, Vargas M, Ballesteros G, Tellez Y, Soda K, Sahoo M, Nuñez A, Balmaseda A, Harris E, et al. Viremia and clinical presentation in Nicaraguan patients infected with Zika virus, chikungunya virus, and dengue virus. Clin Infect Dis. 2016;63(12):1584–1590. doi: 10.1093/cid/ciw589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Zhao H. Dynamics analysis of a Zika-dengue co-infection model with dengue vaccine and antibody-dependent enhancement. Phys A Stat Mech Appl. 2019;522:248–273. doi: 10.1016/j.physa.2019.01.099. [DOI] [Google Scholar]
- Whitehead S, Blaney J, Durbin A, Murphy B. Prospects for a dengue virus vaccine. Nat Rev Microbiol. 2007;5(7):518. doi: 10.1038/nrmicro1690. [DOI] [PubMed] [Google Scholar]
- Wiratsudakul A, Suparit P, Modchang C. Dynamics of Zika virus outbreaks: an overview of mathematical modeling approaches. PeerJ. 2018;6:e4526. doi: 10.7717/peerj.4526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization . Global strategy for dengue prevention and control 2012–2020. Geneva: WHO Library Cataloguing-in-Publication Data; 2012. [Google Scholar]
- Yang H, Macoris M, Galvani K, Andrighetti M, Wanderley D. Assessing the effects of temperature on the population of Aedes aegypti, the vector of dengue. Epidemiol Infect. 2009;137(8):1188–1202. doi: 10.1017/S0950268809002040. [DOI] [PubMed] [Google Scholar]