Oxygen K-edge X-ray Absorption Spectra

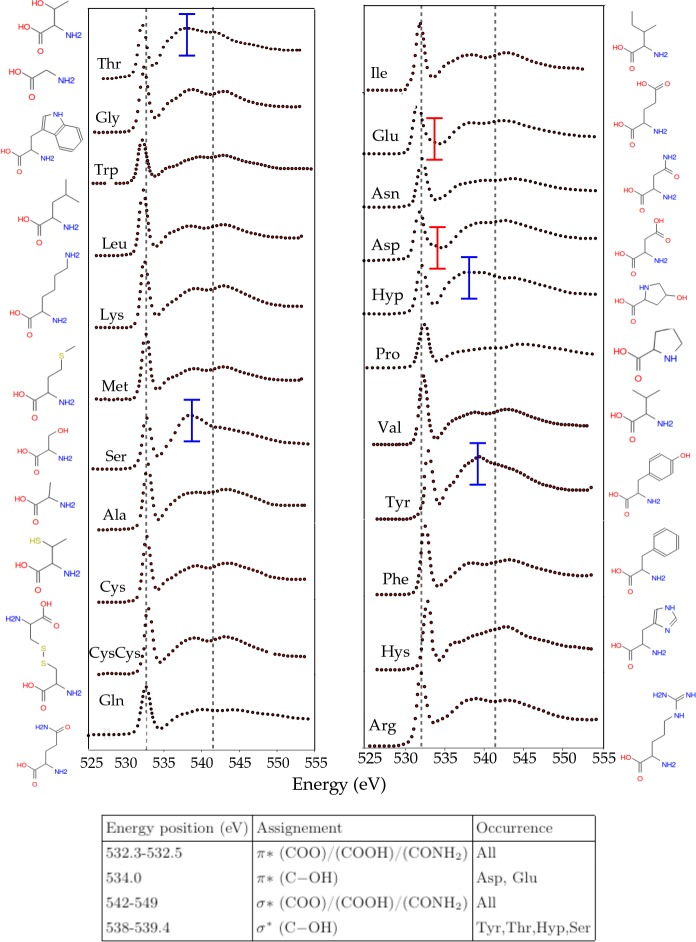
Abstract

We review oxygen K-edge X-ray absorption spectra of both molecules and solids. We start with an overview of the main experimental aspects of oxygen K-edge X-ray absorption measurements including X-ray sources, monochromators, and detection schemes. Many recent oxygen K-edge studies combine X-ray absorption with time and spatially resolved measurements and/or operando conditions. The main theoretical and conceptual approximations for the simulation of oxygen K-edges are discussed in the Theory section. We subsequently discuss oxygen atoms and ions, binary molecules, water, and larger molecules containing oxygen, including biomolecular systems. The largest part of the review deals with the experimental results for solid oxides, starting from s- and p-electron oxides. Examples of theoretical simulations for these oxides are introduced in order to show how accurate a DFT description can be in the case of s and p electron overlap. We discuss the general analysis of the 3d transition metal oxides including discussions of the crystal field effect and the effects and trends in oxidation state and covalency. In addition to the general concepts, we give a systematic overview of the oxygen K-edges element by element, for the s-, p-, d-, and f-electron systems.

1. Introduction

Oxygen is the third most important element in the universe¹ and is the most important element from the earth crust and oceans. From biological processes to industry, the reactivity of oxygen is at the basis of many key chemical reactions. Before dioxygen accumulated in the atmosphere (referred to as the Great Oxygenation Event²), it first reacted with the earth crust minerals to oxidize them and form oxides such as iron oxides.³ The reactivity of oxygen has been the underlying process driving the evolution of early organisms from anaerobic species to aerobic ones via the evolution and development of a complex redox biology.⁴⁻⁶ In more recent time scales, and from a technological point of view, mankind has progressively developed knowledge and control on the oxidation reactions: from combustion reaction producing fire, which was the first source of energy for humankind,^7,8 to modern fuel engines and advanced catalysis,⁹ oxidation is a source of energy; from bloomery to blast furnace,¹⁰ redox processing of metals, which thermodynamics is described in the Ellingham diagrams, led to the development of metallurgy and all its technological improvement across ages along with the ensuing oxidation-aging issues. In short, redox reactions are everywhere in our oxidized world.

Investigating matter from the point of view of the oxygen is thus particularly relevant to determine its role in the atomic and electronic structures and the chemical bonds and resulting reactivity. This is possible using the oxygen K-edge X-ray absorption spectroscopy as an element specific analytical tool.

Already in 1920, Kossel gave an attractive explanation of the X-ray absorption phenomena:^11,12 “.. in Röntgen spectra, we see that the electron cannot make small jumps outside the atom all the neighbor trajectories are already occupied by electrons so it must make a large jump to find a free trajectory, and the absorption occurs only when the frequency is high enough to make it reach the surface of the atom”. Further developments of theory of X-ray absorption in molecules were made by Petersen¹³ followed by the works of Smoluchowski¹⁴ and Kurylenko¹⁵ on the understanding of the absorption of crystals. Starting from the 1960s, a cascade of studies have been published on theory, applications, and techniques of X-ray methodologies, as outlined in the review by Stumm von Bordwehr.¹²

In this review, we discuss the oxygen K-edge X-ray absorption spectra where the oxygen 1s core electron is excited to the lowest empty states. The 1s core electron can be excited by the absorption of a photon in X-ray absorption (XAS), by the scattering of an electron in electron energy loss spectroscopy (EELS) or by the inelastic X-ray scattering (IXS) of a high energy photon. We will systematically describe the oxygen K-edges of atoms, molecules, ions, adsorbates, liquids, and solids and the main experimental and theoretical aspects related to the measurements and the calculation of the oxygen K-edge spectra.

However, an exhaustive review of all published oxygen K-edge spectra is impossible and even beyond necessity. Our choices were dictated by the aim of covering the main families of oxygen based compounds: atoms, molecules, and solids and the whole periodic table of oxides. The review reveals that the application of oxygen K-edge spectroscopy is very variable depending on the research context: from the fingerprint approach to in-depth investigation of the origin of the spectral features based on theoretical calculations, the degree of understanding of all published spectra is very variable. Specifically, some systems have particularly been studied in great detail. For example, we decided to only very briefly discuss the oxygen K-edges of water and of cuprates, where several dedicated reviews exist. The relative size of each sections of this review reflects this heterogeneity. Nonetheless, we have tried to fill gaps in the understanding of O K-edge spectra from the different research fields and provide a unified understanding of the information that can be obtained from this technique.

1.1. Nomenclature

The names of many spectroscopy techniques show some historical variation, and also, some research fields have different names for X-ray absorption spectroscopy. Throughout this review, we will use the term, “Oxygen 1s x-ray-absorption edges of transition-metal oxides”. Instead of “K-edge”, one can use the 1s orbital notation. Some research areas use the term “X-ray absorption near edge structure” (XANES) or “near edge X-ray absorption fine structure” (NEXAFS). We indicate the electron energy loss spectra with EELS and alternative notations include “near edge energy-loss spectroscopy” (ELNES). Finally, inelastic X-ray scattering (IXS) is alternatively indicated with “X-ray Raman scattering” (XRS) or “non-resonant inelastic X-ray scattering” (NIXS).

1.2. Published Reviews and Books

Oxygen K-edge XAS spectra have been reviewed in a number of papers and reviews. The section on 3d transition metal oxides can be seen as an updated version of the 1989 paper “Oxygen 1s x-ray absorption of transition metal oxides”.¹⁶ Chen wrote a detailed review of X-ray absorption spectra of transition metal compounds, including a section on the oxygen K-edge.¹⁷ There have been a number of reviews on the X-ray spectroscopy of water, in particular, the recent reviews by Smith and Saykally¹⁸ and by Nilsson and Petterson.¹⁹ Books on X-ray absorption spectroscopy include NEXAFS spectroscopy by Stohr²⁰ and Core level spectroscopy of Solids.²¹

2. Experimental Section

The oxygen K-edge can be measured with X-ray absorption spectroscopy (XAS), using an X-ray energy larger than the 530 eV excitation energy of an oxygen 1s core electron to an empty state. There are two alternative techniques based on the inelastic scattering of electrons and the inelastic scattering of photons. Electron energy loss spectroscopy (EELS) measures the energy loss of an electron and inelastic X-ray scattering (IXS) the energy loss of an X-ray beam. EELS and IXS are discussed in sections 2.3 and 2.4. An X-ray absorption experiment needs (1) an X-ray source, (2) a monochromator, and (3) a detector, where the sample condition is also an important aspect. In the next section, we briefly introduce some aspects of the experimental conditions.

2.1. Sources for X-ray Absorption Spectroscopy

Historically, XAS was measured with X-ray tubes.¹² X-ray tubes give the largest part of their X-ray emission in the form of intense monochromatic X-ray energies related to the specific core–core X-ray emission channel, for example, the aluminum Kα source at 1486 eV. A second source of X-rays from the tube is the so-called bremsstrahlung. The bremsstrahlung energy loss is due to the slowdown of electrons from the metal in the anode and gives rise to a continuous spectrum of X-rays. Bremsstrahlung is much lower in intensity than the specific X-ray emission lines, but with a source optimized for bremsstrahlung emission, one has enough photons for good X-ray absorption measurements. The 1920 paper from Kossel describes the analysis of the XAS spectral shape.¹¹ Kossel already realized that the X-ray absorption spectral shape was influenced by the valence electrons and the other “external conditions” of the absorbing atom in the surroundings where it was embedded. Using an X-ray tube, Fischer measured a series of oxygen K-edges in 1971 with 0.9 eV resolution.²² To compare X-ray sources, one usually compares the spectral brightness or brilliance of the X-ray beam, which is defined as the number of photons (in a certain bandwidth) per second and per mm² and mrad², where the brilliance of an X-ray tube is 10⁸. Depending on the details of the XAS experiment (for example, whether one measures a gas or a solid), the divergence and the spot size are often not crucial and the X-ray flux is a more important prperty. The flux is defined as the number of photons (in a certain bandwidth) per second. In this review, we will define the term “intensity” as equivalent to flux.

Synchrotron radiation emerged in the 1960s, but a limiting factor for oxygen K-edge XAS measurements was the absence of X-ray monochromators for the 500–600 eV range with good resolution. Synchrotron radiation covers all X-ray energies with a brilliance between 10¹³ and 10¹⁸ photons/s/mm² /mrad², in other words, 10⁵ to 10¹⁰ brighter than an X-ray tube. The X-ray monochromators were improved in the 1970s, and in 1980, Stohr et al. measured the oxygen K-edge spectrum with 2 eV resolution.²³ A big step in experimental resolution was set in the 1980s with the development of the SX700 monochromator by Petersen²⁴ and the DRAGON monochromator by Chen and Sette.²⁵ Both beamlines reached a resolution that was better than the oxygen K-edge lifetime broadening of 0.3 eV, which implies that from this time the experimental resolution of oxygen K-edges was limited not by the experimental resolution, but by the intrinsic lifetime broadening.

More than 95% of all oxygen K-edges are measured with synchrotron radiation sources, but next to the synchrotron and X-ray tubes, a number of additional X-ray sources exist, respectively: (a) plasma sources, (b) high-harmonic generation (HHG) lasers, and (c) X-ray free electron lasers (XFEL). With a plasma source, one is also able to measure soft X-ray spectra.²⁶ Kuhl et al.²⁷ measured an oxygen K-edge spectrum with 2 eV resolution. Soft X-rays can also be generated with HHG laser systems. Most present HHG laser systems operate up to 100 eV, and they are especially used for femtosecond pump–probe experiments. Extensions to the oxygen K-edge at 530 eV are in principle possible on some newly developed sources and/or they are foreseen in the near future.²⁸⁻³² The use of HHG and XFEL lasers for time-resolved experiments is discussed in section 2.6. The oxygen K-edge of cosmic sources is measured with X-ray satellites XMM Newton and Chandra, with a resolution of approximately 2.0 eV.³³

2.2. Detection Techniques

Transmission Detection

X-ray transmission is the most direct technique to measure an oxygen K-edge XAS spectrum and it allows the quantitative detection of the X-ray absorption cross section. The attenuation of 530 eV X-rays is only 100 nm at the oxygen K-edge of solid oxides, implying that one needs thin samples. A transmission measurement is only quantitatively correct if the measured sample is homogeneous in thickness. If thickness variations occur, the spectral shape will appear distorted with essentially the high-intensity peaks appearing flattened. This so-called pinhole effect also plays a role for samples that are inhomogeneous, for example, samples containing nanoparticles or otherwise nanostructured objects that are measured with an area-averaged X-ray probe. Alternative detection methods are based on decay channels of the core–hole. Fluorescence yield (FY) measures the amount of X-rays that are emitted. The energy that is gained by the electron that fills the core–hole can also be used to emit another electron in the Auger process. In the further relaxation of the core–hole, more electrons can be emitted and electron yield (EY) also measures the total amount of emitted electrons.

Fluorescence Yield Detection

The core–hole is filled with an electron from another shell and the energy can be emitted as an X-ray. Detecting the fluorescent X-rays after radiative core–hole decay can yield a method that is proportional to the XAS spectral shape. In total fluorescence yield (TFY) detection, one detects all emitted X-ray photons, from all elements present in the sample. Assuming that all nonresonant photoionization provides a constant background, the TFY measures the XAS spectral shape. However, spectral distortions can occur due to saturation and self-absorption effects, because usually the X-ray emission (being off-resonance) has a larger probing depth than the penetration depth of the X-ray at the edge.³⁴⁻³⁶ While scanning through an absorption edge, the X-ray penetration depth varies due to the XAS spectrum, and if there is no background absorption, the observed spectral shape would be highly distorted. If the background X-ray absorption dominates, the X-ray penetration depth is constant over the edge and no saturation occurs. In other words, TFY can only be used for materials where the observed element is dilute. We note that if the concentration of the absorbing element is very low, the FY from the other elements might dominate the signal, and the specific FY from the dilute element will have low signal-to-noise. Bulk oxides are too concentrated and their TFY spectra appear highly saturated. In addition to saturation effects, there can be effects due to self-absorption, in other words, the reabsorption of the emitted X-ray emission. Again, this effect is only significant for concentrated samples.³⁷ Saturation and self-absorption effects are angle-dependent, which also offers a method to quantify the saturation effects. In the case of the oxygen K-edge, there are no spectral modifications due to state-dependent decay.³⁸⁻⁴⁰

Instead of TFY, only a limited energy range of the X-ray emission can be detected. Such a partial fluorescence yield (PFY) method can have an advantage if the X-ray emission signal is dominated by another element. As such, PFY measurements allow the detection of XAS spectra of very low concentrations, down to the 100 ppm range.⁴¹ A special type of PFY is inverse PFY (IPFY). In this method, one detects the FY of a different element than the element from which the XAS spectrum is measured, where one can prove that in IPFY measurements no saturation effects can occur.⁴²

Electron Yield Detection

In total electron yield (TEY), electrons that escape from the sample are detected in electron analyzers. This can include the integrated signal from energy-dispersive detectors or, in the case of conductive samples, the current measurement to the sample. If the energy of the electrons is selected, one speaks of partial electron yield (PEY) or with the detection of a specific decay channel also of Auger electron yield.⁴³ A special property of electron yield is that the electrons have an escape depth that is on the order of a few nanometers, much shorter than the X-ray penetration depth, implying that in most cases the TEY signal is not saturated.^44,45 Thus, electron yield detection turns XAS into a surface-sensitive probe. This can be used to enhance the signal from the surface and near-surface part of the sample. The surface sensitivity also implies that the measured signal is not exactly equal to the bulk signal. In the case of surface oxidation or surface modification, the electron yield signal is different from the XAS spectrum of the bulk system. Even for a perfect surface in a single crystal, the TEY signal will be different from the bulk because the atoms in the top layer at the surface have different surroundings and corresponding electronic structure. Due to the probing depth of only 4 nm, the top layer contributes significantly (10%) to the total spectral shape. In addition, most crystals show surface reconstructions that extend a few layers into the crystal. This makes the TEY measurements usually affected by surface-induced effects to some extend.

If TEY is measured under a gas atmosphere, conversion electron yield (CEY) appears as an additional option.⁴⁶ In a gas atmosphere, the electrons emitted from the sample create ions that are counted, and as such, the CEY method effectively measures the XAS spectral shape. Often, two detectors are used that measure respectively the gas phase and the sample surface plus gas phase, allowing both signals to be differentiated.⁴⁷ The conversion of electrons to ions can be dependent on the electron kinetic energy and the molecules in the gas phase, which implies that CEY should be well calibrated during the experiments. Another type of CEY is applied in liquids. One can measure the XAS spectrum of a surface that is in contact with a liquid, by detecting the ions that are generated in the liquid by the escaping electrons, also known as the ion-current detection.⁴⁸ In general, these CEY methods should always be well calibrated and tested to check their linearity with the XAS cross section.

Ion Yield Detection

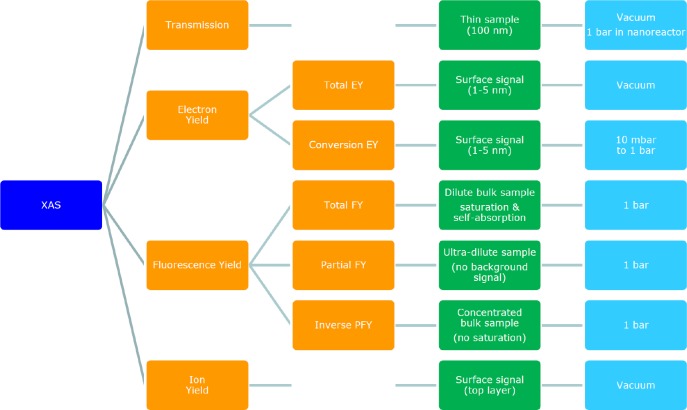
Ion yield detection (IY) is different from the ions measured in CEY methods described above. In ion yield, one measures a specific ion with a mass spectrometer while scanning through the XAS spectrum. Himpsel et al. used IY to measure the surface of a CaF₂ crystal.⁴⁹ IY is a common technique in gas phase experiments, where it is linked to photofragmentation detection. The oxygen K-edge can be measured by detecting various possible ionic fragments that are produced by the XAS process.⁵⁰ IY has been applied to the oxygen K-edge by Hayakawa et al., who measured a series of cerium oxide clusters.⁵¹Figure 1 gives an overview of the detection techniques of X-ray absorption spectroscopy, including transmission, electron yield, fluorescence yield, and ion yield methods.

Figure 1.

Overview of the detection techniques of X-ray absorption spectroscopy, including transmission, electron yield, fluorescence yield, and ion yield methods. Sample measurement details are given in green and the pressure in blue.

2.3. Inelastic X-ray Scattering

Inelastic X-ray scattering (IXS), also known as X-ray Raman Scattering (XRS), measures the inelastic scattering of hard X-rays, not resonant with a core level. IXS is a low-intensity experiment, implying that an intense synchrotron or XFEL beamline is required. The oxygen K-edge can be measured with IXS by detecting the 530 eV energy loss. By changing the scattering angle of the IXS experiment, one can modify the momentum transfer. An important application of q-dependent measurements is the change of the ratio between dipole and quadrupole transitions. Pylkanen et al. applied q-dependent IXS to the oxygen K-edge of a series of alcohols.⁵² The advantage of the hard X-rays used in IXS is that one can measure the oxygen K-edge under extreme conditions, for example, high pressure.⁵³ High pressure studies include the study of the phases of supercritical and solid phases of H₂O⁵⁴ and studies regarding the nature of the high pressure phases of silicates.⁵⁵ A review of high pressure publications until 2016 is given by Sternemann and Wilke.⁵³

2.4. Electron Energy Loss Spectroscopy

Electron energy loss spectroscopy (EELS) is usually measured with transmission electron microscope (TEM), but historically some dedicated EELS machines have also been used, for example, the EELS experiments performed by the group of Fink.⁵⁶ The resolution of EELS in dedicated electron microscopes is 0.3 eV or better since the 1990s.⁵⁷ As a rule, EELS is performed with an electron beam with an energy above 100 keV. The high energy and low momentum transfer effectively turns the 1/e Coulomb operator in inelastic electron scattering into an effective optical operator. Studies using low-energy (100 eV) electrons, for example, resonant EELS at electron energies equal to core level binding energies, are mainly limited to metal edges and to valence excitations.^58,59 Using a 100 keV electron beam at low scattering angle, one can approximate the EELS spectrum with the dipole approximation. Under these approximations (high primary energy, low scattering angle), EELS becomes essentially equivalent to X-ray absorption. In EELS, one can tune the dipole/quadrupole ratio by changing the scattering angle. In the remainder of the manuscript, we will treat EELS spectra conceptually equally to XAS spectra. TEM-EELS has the advantage that one can reach atomic resolution, allowing the measurement of an oxygen K-edge of one atom (or better one atomic column) through a sample.

2.5. In Situ Experiments

Oxygen K-edge XAS is usually performed in vacuum. Soft X-rays have a penetration depth through air on the order of 1 cm. In principle, this is long enough to perform transmission or X-ray fluorescence experiments. From 1988, Fischer et al. performed a series of in situ TFY experiments at pressures up to 100 mbar.⁶⁰ Using nanoreactors in a scanning transmission X-ray microscopy (STXM), the oxygen K-edge of Fe₃O₄ supported on SiO₂ has been studied at 1 bar under Fischer–Tropsch conditions.⁶¹ More examples of STXM experiments are given in the section on X-ray microscopy.

A more popular approach is to use electron yield detection. Because TEY is surface sensitive and TFY is bulk sensitive, their comparison can be very useful. TFY and TEY were compared to study the changes of propylene on the surface of Ag/Y zeolites. The use of both TFY and TEY nicely separates the behavior of the surface and the bulk.⁶² Traditionally, in situ TEY measurements are performed in combination with X-ray photoemission and the XPS detector makes it difficult to go above 10 mbar pressure. A series of 1 to 10 mbar in situ oxygen K-edge studies have been performed on so-called near-ambient pressure photoemission beamlines.⁶³ This allows the study of the surface of heterogeneous catalysts under working conditions in a flowthrough reactor. An example of an oxygen K-edge study that has been performed is the methanol oxidation to formaldehyde over copper metal.

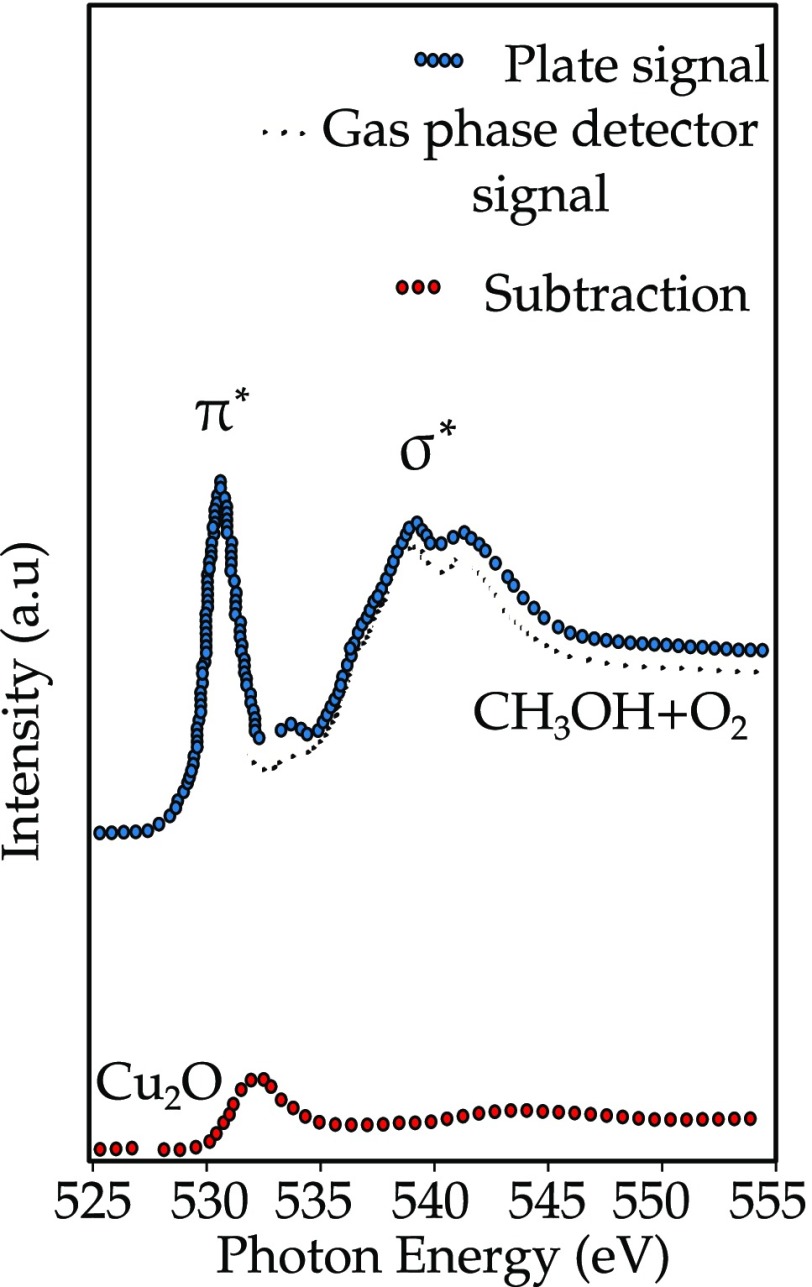
Figure 2 shows the oxygen K-edge of a mixture of methanol and oxygen at 0.52 mbar that reacts on a Cu foil at 520 K. The spectral shapes are a combination of O₂, CH₃OH, and the Cu₂O surface species. The system uses one detector that measures the gas phase and a second detector that measures the combination of the surface and the gas phase. Using the difference between the two detectors, the surface signal can be revealed. Experiments can be performed at different gas mixtures, pressures, and temperatures, as has been described in a number of applications.⁶³⁻⁶⁷ A series of detailed in situ oxygen K-edge studies has been applied to vanadium oxides, under different gas atmospheres and with different loadings of the vanadium. The analysis of the oxygen K-edge, in combination with DFT studies allows the distinction between separate vanadia, silica, and interface contributions.^68,69 A more recent development is to use CEY detection up to pressures of 3 bar.⁷⁰

Figure 2.

Oxygen K-edge of a mixture of methanol and oxygen at 0.52 mbar that reacts on a Cu foil at 520 K. The detectors near the surface detect the signal from the gas phase and the surface; the detector far from the surface detects the pure gas phase spectrum.⁴⁷

2.6. Time-Resolved XAS

One can combine oxygen K-edge XAS with time-resolved measurements. An overview of the recent developments for time-resolved X-ray experiments with synchrotron sources, X-ray FELs, and high harmonic sources is given in the review by Kraus et al.⁷¹ Cavalleri et al. measured the time evolution of the oxygen K-edge of VO₂ using a laser-sliced synchrotron beam with a time resolution of 500 fs, from which new information on the photoinduced metal–insulator transition in VO₂ was found.⁷² The LCLS X-ray FEL was used to study the changes in the excited-state electronic structure of the nucleobase thymine, by using the changes in the oxygen K-edge.⁷³ A number of fs oxygen K-edge XFEL studies have been performed on adsorbates, for example, CO on Ru(0001).^74,75 Femtosecond XFEL studies focusing on the oxygen 1s X-ray emission channel have also been performed on water.^76,77 As mentioned above, HHG sources have reached the oxygen K-edge energy and femto- and attosecond oxygen K-edge spectra are foreseen in the near future.²⁸⁻³¹

2.7. X-ray and Electron Spectromicroscopy

Before discussing some X-ray microscopy options, first, transmission electron microscopes (TEM) will be briefly discussed. With TEM, one can measure core levels below 1000 eV with atomic resolution (down to 0.1 nm);^78,79 for example, Muller et al. studied the Si:SiO₂ interface, indicating a different electronic structure of oxygen at the interface.⁸⁰ Egoavil et al. studied La₂CoMnO₆ films on SrTiO₃(111) substrates.⁸¹ They use cobalt and manganese EELS to determine the site specific valence, in combination with the oxygen K-edge based EELS maps. Zhou et al. studied ZrO₂-(La,Sr)MnO₃ thin films using the atomic EELS contrast of several elements, including the oxygen K-edge.⁸² The methods used to derive the atomic resolution images are explained by Wang et al.,⁸³ who used the oxygen K-edge of SrTiO₃ as an example.

With scanning transmission X-ray microscopy (STXM) one can measure the oxygen K-edge with spatial resolution. Such STXM-XAS experiments are analogous to STEM-EELS, with the difference being that with TEM one can reach 0.1 nm resolution and with TXM 10 nm. On the other hand, STXM allows for thicker samples and operando conditions.⁸⁴ De Smit et al. used the oxygen K-edge STXM data to provide a thickness profile of their Fe₃O₄/SiO₂ catalyst sample, while the metal edges were used to probe their spatial variation and valence.⁶¹ The literature is rich with oxygen K-edge studies performed with STXM microscopes, but a full overview of the performance of this technique goes beyond the scope of this review. Sharma et al. studied the oxygen K-edge spectra in graphene and graphene oxide with a STXM microscope.⁸⁵ The STXM microscopes can also be used to select a specific small oxide material, and for example, Ward et al. studied the oxygen K-edge of uranium minerals,⁸⁶ while a series of rare earth oxides have also been studied with a STXM.⁸⁷

An alternative X-ray microscopic technique is X-ray photoelectron emission microscopy (PEEM). In X-ray PEEM, one measures the emitted electron with an electron microscopic lens system. X-ray PEEM is mainly used to study magnetic structure, using either magnetic linear dichroism (MLD) or magnetic circular dichroism (MCD). Kinoshita et al. studied the magnetic domain structure of a NiO(100), comparing the X-ray PEEM images measured at the oxygen K-edge with the nickel L edge.⁸⁸ Oxygen K-edge PEEM was also used to study polymer mixtures.⁸⁹

2.8. Using the Oxygen K-edge as Resonance

Resonance studies include the use of the oxygen K-edge in resonant photoemission spectroscopy (RPES) and resonant inelastic X-ray scattering (RIXS). In addition, one could perform X-ray scattering at the oxygen K-edge and resonant EELS with electron sources. The oxygen K-edge of solid samples does not contain excitonic states, which turns the two-dimensional RIXS plane essentially in a convolution of the oxygen K-edge and the nonresonant 1s2p X-ray emission spectrum.⁹⁰ The oxygen K-edge is particularly used as a resonator for the iridates. Because the Ir 2p edge lies in the hard X-ray range, it has low resolution. The soft X-ray oxygen K-edge then adds improved resolution to study the electronic structure. This has been used for Ba₂IrO₄⁹¹ and SrIrO₄,⁹² where the magnon dispersion is measured. The oxygen K-edge RIXS spectra are also used to study the core–hole clock mechanism, in which it is reasoned that by changing the excitation energy, one change the ratio between resonant and normal decay channels. An example is the study on the oxygen K-edge RIXS of alcohols.⁹³

3. Theory

In oxygen K-edge X-ray absorption, an X-ray with 530 eV energy excites the initial state of the system to a final state, where the initial and final states are many-body (or total energy) states of the system. The X-ray absorption process is calculated with the Fermi golden rule using the many-body initial and final state wave functions Ψ_i and Ψ_f:

1

ϵ̂·R is the transition operator that we have approximated as the dipole operator. δ indicates a δ-function including E_fi, the energy difference between the states Ψ_i and Ψ_f. The goal is the computation of the dipole matrix elements and the transition energies where different approximations can be adopted.

3.1. Density Functional Theory (DFT)

Independent Particle Approximation

The main point of the independent particle approximation is the decoupling of the dynamics of the many-body system in a single-particle description. The Hamiltonian can be rewritten with a term that mimics the interaction of the electrons with the average field that they feel and contains the kinetic energy of the electron and the potential energy of the electron in the field of the nuclei. With each independent electron is associated a spatial function and a corresponding energy eigenvalue, obtained by solving the Schrödinger equation with this Hamiltonian. The independent particle approximation is also called the single-particle approximation and the corresponding Hamiltonian the one-electron Hamiltonian.

Within the independent particle approximation, it is possible to replace the many-body quantities in the Fermi golden rule with single-particle energies, since the excitation process is described by the promotion of an electron from an occupied to an unoccupied orbital (or single-particle state):

2

The many-body eigenstates and upper case operators on the left side of the equation are substituted by the lower case effective single-particle states.⁹⁴ In the remainder of this manuscript, we will use the term “single-particle state” as equivalent to the term “orbital”. We note that this change from the many-body description to a single-particle description involves two coupled approximations: (1) the description of the ground state in the independent particle approximation and (2) the description of the final state in the independent particle approximation. We note that in the case of 2p L_2,3 X-ray absorption of transition metal systems, the 2p core–hole in the final state has large electron–electron interactions with the 3d valence electrons that create the so-called multiplet effects. In the case of oxygen K-edges, we are dealing with a 1s core–hole and (exchange) interaction with the valence electrons smaller than 1 meV which can be ignored.

Transition energies can be computed with the Delta Kohn–Sham (ΔKS) method.^95,96 The idea behind the ΔKS method is that the transition energies can be calculated as the difference between a ground-state energy, computed with a self-consistent field calculation, and an ionized and excited-state energy, obtained through a restricted open shell calculation. The procedure introduces an occupation number constrained in the 1s oxygen KS orbital, justified by its localized character. The nonorthogonal matrix elements between the Kohn–Sham ground-state determinant and each excited-state determinant are used in order to obtain the oscillator strength.⁹⁷ With the ΔKS scheme, two calculations are needed, one for the ground state and another one for the excited state. Good agreement with experimental results have been obtained in the calculation of small molecules and metal adsorbate cluster oxygen K-edges in terms of excitation energies⁹⁸ and trends in oscillator strengths⁹⁹ where the energy underestimation from the TD-DFT scheme is improved.¹⁰⁰

Only one calculation is needed in an approximate procedure that is called the Slater transition state,¹⁰¹ even if different calculations are needed for each excited state. This procedure consists of the estimation of the excitation energy as orbital energy differences between two levels of variationally determined states, which are defined as the transition state, with only one-half electron excited.^101,102 The Slater transition state provides an estimation of the excitation energy with a correction to second order in the change of occupation. The formula describes a state where half an electron has been removed from the initial state ψ_i and placed in the final state ψ_f. It is important to notice that the number of electrons is conserved. The ground-state energy can be expressed as a Taylor expansion to the second order in the occupation numbers.

Once we have the two energies, the transition energy can be computed as a difference between them. Viewed as a balanced compromise between initial and final states, the transition-state orbitals can be used to represent both states, which reduce the evaluation of transition moments to single-electron transitions without affecting the other occupied orbitals.¹⁰² The evaluation of the oscillator strengths becomes simplified since the same orbitals are used to describe the final and initial states. The weakness of the method is that one has to compute an X-ray absorption excitation for each state. An approximation to the Slater transition-state scheme that circumvents the state-by-state calculations required is the transition potential approach formulated by Triguero et al.¹⁰³ The approximation consists of removing half an electron from the oxygen 1s core level and to obtain all the possible excited states with only one global diagonalization from the potential generated by the core with the half-occupied core–hole. The complete spectrum evaluation in transition potential density functional theory (TP-DFT) consists of the calculation of the matrix elements between the orbitals corresponding to the 1s and the unoccupied orbitals since the initial and final states have the same orthogonal basis set.¹⁰² It has been demonstrated that excitation energies computed in the TP-DFT framework require relaxation effects to be taken into account up to the second order.¹⁰¹ Since the TP-DFT calculations can be considered as approximations to the Slater transition-state scheme, the use of the half core–hole is theoretically justified. Extensions of the TP-DFT method, particularly suited when excitonic effects are strong, are the full core–hole (FCH)¹⁰⁴ and the excited core–hole (XCH).¹⁰⁵ A correct description of the core–hole is one of the most challenging tasks of XAS simulations.

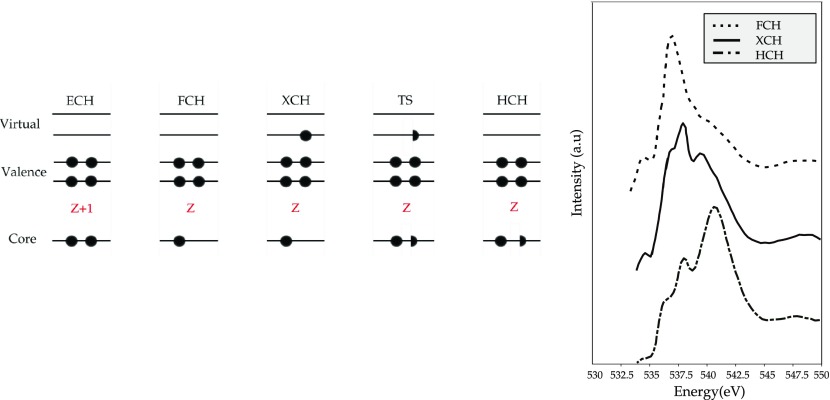
In Figure 3, some of the approximation schemes for the core–hole are indicated. The Z+1 approximation, also called the empty core–hole (ECH) approximation, introduces the core–hole as an additional nuclear charge. The equivalent core–hole approximation is justified, since for electrons in the external shells, a deep core–hole is felt as a positive charge.^108,109 On an oxygen 1s core excited spectrum, oxygen is replaced by fluorine, but because of the high electronegativity of the latter, a charge transfer could be induced in the neighboring atoms with a subsequent increase in the p-population of the excited core causing a distortion in the spectral shape.¹¹⁰ Its applicability can be questioned also if the system has shallow core–holes.¹¹¹ In the exchange core–hole (XCH) approach, the potential of the first fully core excited state determines all the excited-state orbitals. A strong approximation is made in the XCH procedure since the orbitals computed for one specific final state are supposed to describe the initial and final states, and no information about the initial ground states is present in the orbitals used.^102,105 The FCH method is similar to the XCH: the core electron is ionized, which creates a hole in the core level, but in this case, the impact of the excited electron on the core–hole is neglected.¹¹⁰ The DFT-based methods cited above can, in principle, be applied to atoms, molecules, and condensed phases. All these one-electron calculations approximate the particle hole and the correlation effects.

Figure 3.

(Left) XAS final-state approximations: (a) Z+1 equiv core–hole, (b) full core–hole, (c) excited core–hole, (d) Slater transition state, (e) transition state approximation.¹⁰⁶ (Right) The FCH, XCH, and HCH approximations applied to liquid H₂O.¹⁰⁷

3.2. DFT in Solids

If one deals with solids, the Fermi Golden Rule is usually rewritten as

3

where M is the one-electron transition matrix element, and ρ is the empty density of states. All electronic structure schemes can in principle be used in order to generate the density of states (DOS) and within a conceptual DFT framework; many routes can be used to evaluate the empty DOS and the XAS spectral shape. The specific methods can be divided into the following:

• real space multiple scattering methods (FEFF¹¹²)

• real space wave function method (ADF,¹¹³ ORCA¹¹⁴)

• reciprocal space band structure methods (Wien2K,¹¹⁵ Quantumespresso¹¹⁶)

We refer to the websites and original references of the methods indicated for details. The majority of solid-state X-ray absorption calculations have been performed with local density approximation of the density functional theory. A large number of specific procedures have been developed to solve the one-electron Schrödinger equation.

Using a linear method, different routines can be used to solve the band structure problem. The two main schemes both make use of the variational principle for the one-electron Hamiltonian, and their difference lies in the formulation of the trial functions: linear combinations of energy independent augmented plane waves (LAPW) or muffin-tin orbitals (LMTO). The strength of these procedures is the use of the variational principle to solve the Schrödinger equation with energy independent basis functions, so that the secular equations become linear in energy.¹¹⁷

A plane wave basis set with a pseudopotential approximation has been introduced to model the interaction between ions and valence electrons.¹¹⁸ The pseudopotential neglects the inner core electrons and their strong potential due to the attraction to the nuclei. All electron descriptions of the system involve a strong orthogonal constraint between all the core and valence orbitals. The orthogonality relation presumes strong oscillations of the valence orbitals in the vicinity of the nucleus, as indicated in Figure 4. These oscillations, which require a large number of plane waves to be described, can be neglected in the pseudopotential framework, where the orthogonality relation is no longer valid, and only a reduced number of plane waves is needed to describe the correct behavior of the valence wave functions. The pseudopotential is then constructed for an initial DFT calculation for an isolated atom: a core radius r_c should then be chosen and the valence wave functions are adapted to it in order to remove the nodal structure; these are the pseudo-wavefunctions. The pseudopotential approximation has been widely employed to model the oxygen K-edge XAS in many different systems, and satisfactory agreement with experiment has been reached.

Figure 4.

Representation of pseudo-wavefunction and pseudopotential. The pseudo-wavefunctions are smoother than the real wave function near the nuclei (where r_c is the core radius), so the number of plane waves required is reduced.

3.3. Core–Hole Effects in Solids

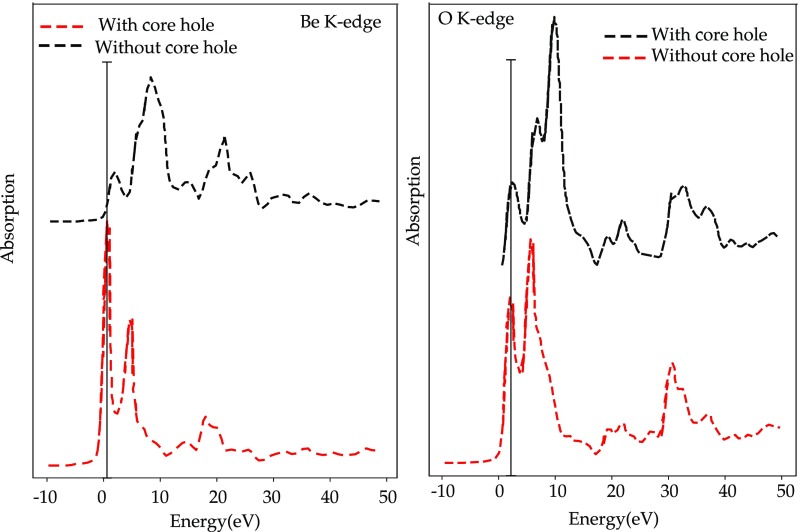
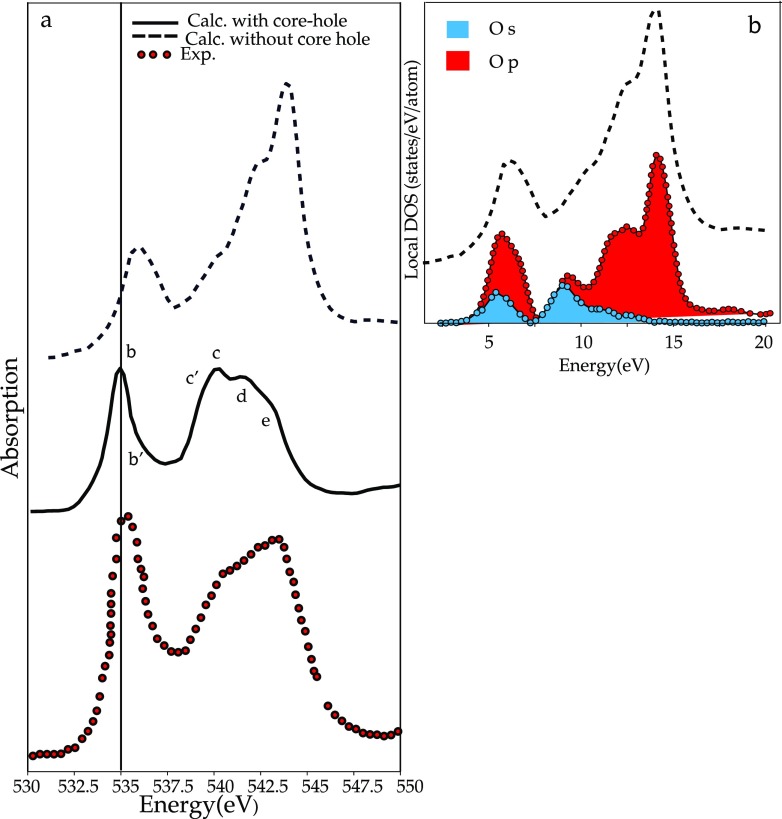
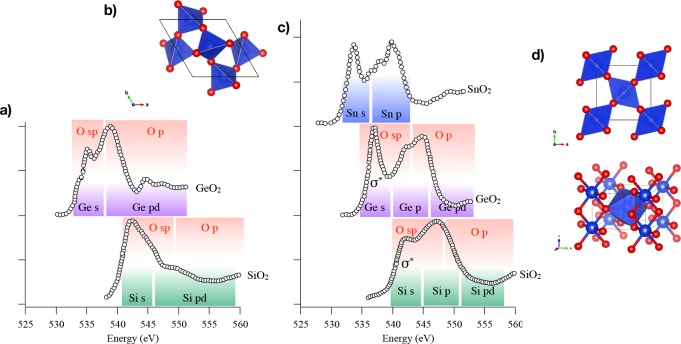
It has been demonstrated that the core–hole effects are stronger for spectra arising from elements in an ionic or covalent compound with lower electronegativity.¹¹⁹ In Figure 5, the theoretical results for the ionic compound BeO are compared for both the metal and the oxygen edge with and without the core–hole. The presence of the core–hole alters both spectra, but in the oxygen case, the modifications to the spectral shape are less significant. Although core–hole effects have to be taken into account in order to have a good agreement with experiment, omitting any treatment of the core–hole usually results in a shift of the threshold to higher energies and modified peak intensities in the low energy part of the spectra.¹¹⁹ In Figure 6, the oxygen K-edge spectra of GeO₂ with and without the core–hole is compared to the experiment. In this case, the relative intensities of some peaks are better reproduced without the inclusion of the core–hole. This is evidence that the core–hole potential, in the adopted supercell approach, is too attractive.^120,121 If one compares the spectra without the inclusion of the core–hole with the ground-state DOS calculations, one can show that in some systems a ground-state calculation can give features consistent with experiment¹²⁰ and provide information to explain the features in terms of orbital hybridization.¹²²

Figure 5.

(Left) Beryllium K-edge of BeO calculated with and without core–hole. (Left) Oxygen K-edge of BeO calculated with and without core–hole.¹¹⁹

Figure 6.

(a) Theoretical GeO₂ oxygen K-edge with and without core–hole compared with experiment. (b) Theoretical oxygen K-edge XAS without core–hole compared with a ground-state oxygen DOS calculation.¹²⁰

3.4. Beyond the One Particle Approximation

We have seen that the one-body DFT calculations successfully describe the oxygen K-edges of delocalized systems. However, they lack accuracy in the description of partly localized and atomic edges, where many-body and multiplet effects are important. This encouraged the push to go beyond the single-particle picture with the inclusion of many-body effects. After the first attempts made by Zangwill and Soven¹²³ and Zaanen et al.¹²⁴ to overcome the single-particle description, nowadays the most widely used schemes are the Bethe Salpeter equations (BSE)¹²⁵ and the time dependent density functional theory (TD-DFT)¹²⁶ based methods. When Runge and Gross¹²⁷ proposed the TD-DFT scheme to compute spectra, it became very popular for molecules, but its implementation for solid systems is more recent.¹²⁸ The TD-DFT description of the X-ray absorption cross section enriched with the core–hole contribution is also called the adiabatic local-density approximation. In this framework, the exchange correlation kernel depends only on the density in the ground state (t = 0). The potential generated by the kernel is local in space and time, and it is exactly this feature that produces an unsatisfactory long-range behavior in solids.^126,129 Another obstacle to the correct description of solids with TD-DFT is linked to the inability of the latter to reproduce bound excitations¹²⁸ that leads to failure of the core–hole effect description. Many attempts^130−132 have been made in order to make TD-DFT suitable for the description of the photoabsorbtion process in extended system, since it would be desirable in terms of simplicity,¹²⁶ that is, two-point equations are required in TD-DFT instead of the four-point equations in BSE.

The Bethe-Salpeter equation (BSE)¹³³ represents the equation of motion of a particle–hole state, as for example a photoexcited electron to the conduction band from the 1s oxygen orbital. The BSE description of X-ray absorption includes single-particle terms that describe the quasi-particle energies of the core–hole and the excited photoelectron, together with the interaction between them. The interaction between the electron–hole pair has two terms: the Coulomb interaction, which includes adiabatic screening of the core–hole, and an unscreened exchange term.¹³⁴ BSE calculations are considerably heavy in terms of computational cost and usually they have been limited to systems of restricted dimension. A BSE calculation consists of the following steps: (i) determine the ground-state electronic structure, (ii) correct the quasiparticle energies by adding a GW self-energy, (iii) evaluate the screening response to the core–hole, and (iv) determine the excitation spectrum of the BSE Hamiltonian. Liang et al. reported the oxygen K-edge spectra of several transition metal oxides obtained through the BSE procedure and they showed the accuracy of the method in predicting the excitonic character of some peaks. The reproduction of the correct excitonic features of the spectra is ensured in BSE by the screened Coulomb interaction W, present in the interaction kernel, that acts on the electron–hole matrices and introduces a long-range coupling between the electron and the hole wave functions.¹³⁵

An overview of the calculation procedures is given in Figure 7.

Figure 7.

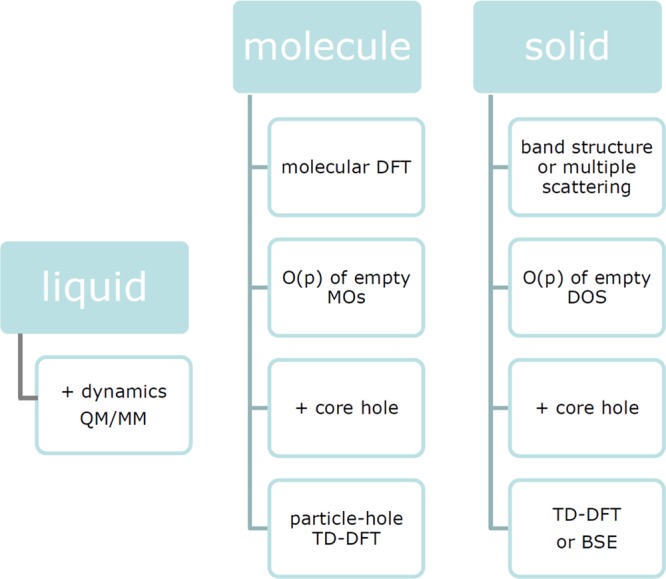
Oxygen K-edge spectra can in the first approximation be calculated from DFT codes, where molecules are usually calculated from molecular DFT codes and solids with band structure codes or multiple scattering. The oxygen p-contribution to the MOs or the oxygen p-projected DOS can be compared with the oxygen K-edge spectral shape, where matrix elements are also included. As a next step, the core–hole effect can be included, where many different procedures have been used both for molecules and for solids. In the case of solids, one has to perform a supercell calculation to prevent the core–hole from interacting with each other. Formally, the correct way to calculate the oxygen K-edges is to apply electron–hole excitation schemes such as TD-DFT or BSE, where the complexity of the calculations necessitates approximations. In systems where the dynamics of the system is important (including liquids), the calculations must be combined with molecular dynamics calculations. For example, a series of atomic positions can be determined and their X-ray absorption spectra added. Because of the 300 meV lifetime broadening, (in most cases) the effects of multiplets, orbital polarization, and magnetic exchange are not visible. Vibrations are visible in the case of (small) molecules.

3.5. Charge Transfer Multiplet Calculations

Van Elp and Tanaka calculate the oxygen K-edge spectra of transition metal ions from a charge transfer multiplet model.¹³⁶ The charge transfer multiplet model has been successfully applied to the metal L_2,3-edges (2p XAS) of transition metal ions,²¹ which makes it interesting to check its applicability to the oxygen K-edges of the same systems. There are however a number of differences between the metal L_2,3-edge and the oxygen K-edge; in particular, the metal L_2,3-edge creates excitonic states that are dominated by large 2p3d interactions (multiplet effects) and a large 2p core–hole spin orbit coupling. These interactions are absent for the oxygen K-edge, and only the dd-electron correlations remain. The exchange interaction of the dd-electrons is treated in spin-polarized DFT calculations, leaving out only the orbital polarization. In other words, the charge transfer multiplet calculations include the orbital polarization, but they do not include the band structure effects due to the crystal structure. Because the oxygen K-edge is broadened by the 300 meV lifetime broadening, we do not expect that the orbital polarization effects will be visible.

3.6. Post Hartree–Fock Methods

Excitations from core orbitals to empty molecular orbitals cannot be computed with Hartree–Fock because of some serious difficulties:¹³⁷

• convergence achievement

• variational collapse¹³⁸

• correlation effects

Post Hartree–Fock schemes have been investigated in order to overcome these difficulties. Approaches based on the coupled cluster hierarchy have been developed by Coriani¹³⁹ and Nooijen¹⁴⁰ using a linear response approach and an equation of motion, respectively. These methods yield a very good description of the initial and final state wave functions, but because of the high computational cost, their applicability is limited to small molecular systems.

Asmuruf and Besley proposed a second-order perturbative approximation to the coupled cluster with single and double excitation (CCSD) based on a single configuration interaction (CIS). The methodology provides results equivalent to TD-DFT for the valence excitations, but because of the inclusion of the exact Hartree–Fock exchange, better performance is obtained in the core excitation treatment.¹⁴¹ Additional methods include the symmetry-adapted cluster configuration interaction (SAC–CI)¹⁴² and multiconfigurational self-consistent field schemes.¹⁴³ The applicability of these methods is limited to small systems since the choice of a relevant active space including local and nonlocal orbitals yields large calculations.¹⁴⁴

4. Atoms and Molecules

Energy States of Open-Shell Systems

The description of the energy states of open-shell systems needs a description of the coupling of their angular momenta to describe the many electron states. The L, S, and J quantum numbers of the multielectron state are indicated with a so-called term symbol that is written as ^2S+1L_J. The 2p⁴ configuration of an oxygen atom has the term symbols ³P, ¹D, and ¹S, where the orbital quantum is indicated with letters: L = 0 is written as S(harp), L = 1 as P(rincipal), L = 2 as D(iffuse), and L = 3 as F(undamental). The ³P state is split by the 2p spin–orbit coupling into, respectively, ³P₀, ³P₁, and ³P₂ states, using the rule that J runs from |L – S| to L + S in steps of 1. The Hunds rules determine the state with the lowest energy, respectively, the state with (1) the largest S, (2) the largest L, and (3) the largest J, where in case a shell is less than half-filled, the lowest J is the ground state due to the inverted effect of the spin–orbit coupling. This makes the ³P state the ground state. The ¹D has an energy of 2.0 eV above the ground state and the excitation energy of the ¹S state is 5.5 eV. The 2p spin–orbit splitting is small and the energy difference between the ³P₂ ground state and the ³P₁ state is only 25 meV.

4.1. Oxygen Atom

Atomic oxygen has a total of eight electrons with the electronic configuration 1s²2s²2p⁴. The 2p orbitals are partially filled and there are different ways to arrange the electrons in the 2p orbitals. Figure 7 shows the oxygen K-edge of atomic oxygen on a logarithmic scale. In the first peak at 528 eV, a 1s electron fills one of the two 2p holes and the final state configuration is 1s¹2s²2p⁵. This configuration has two open shells, i.e., 1s¹2p⁵. The term symbols of such a configuration can be found from the multiplication of the term symbols from the individual shells, in this case, ²S times ²P, yielding respectively, ¹P and ³P. In oxygen, these states are split by 2.5 eV. Including the 2p spin–orbit coupling yields the ³P₀, ³P₁, and ³P₂ states. This implies that from the ³P₂ Hunds rule ground state, one can reach three final states, respectively, the ¹P₁, ³P₁, and ³P₂ states. The ³P₁ and ³P₂ states are separated by only 40 meV and appear as one peak in the experiment. The ¹P₁ state, which is 2.5 eV higher in energy, is not visible due to its low relative intensity of 10^–5. The result is that the excitation from the 1s to the 2p state has effectively one visible peak as shown in Figure 7 at 528 eV.

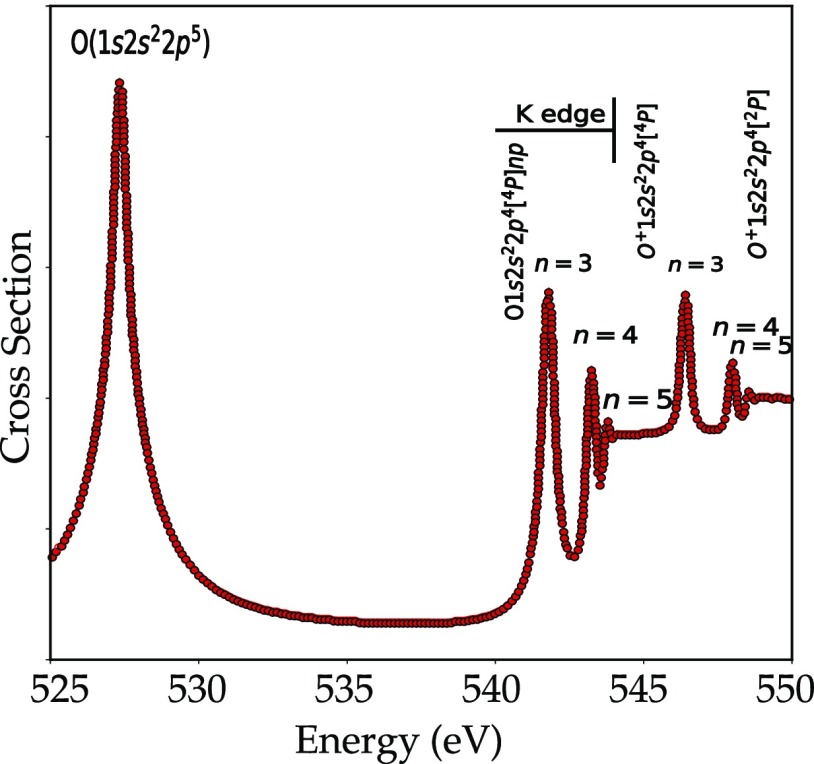
The ionization energy of the oxygen atom relates to the excitation of the 1s electron into a free electron. In fact, there are two ionization energies depending on the relative orientations of the spins of the excited core electron and the two holes in the 2p states. This yields, respectively, states with S = 2 or S = 4, as indicated in Figure 8 at 545 and 548 eV.¹⁴⁶ The peaks in between the edge and the ionization energy above 540 eV are assigned to transitions from the 2p⁴ ground state to the 1s¹2p⁴(np) states, where n can take the values 3, 4, 5, etc., the so-called Rydberg states. The 1s¹2p⁴ configuration is split into multiplets by the 1s2p exchange, the 2p2p electron–electron interactions, and the small 2p spin–orbit coupling. The term symbols are, respectively, ²S, ²P, ²D, and ⁴P, from which only the ²P and ⁴P states gain detectable intensity. The ²P and ⁴P states are split by 3.5 eV, and this yields two series of Rydberg states as given numerically in Table 1.¹⁴⁷

Figure 8.

Experimental atomic oxygen K-edge X-ray absorption spectrum from ref (145). The 1s to 2p transition is visible at 527 eV. The Rydberg states are visible above 540 eV.

Table 1. Comparison of Experimental and Theoretical Energies and Relative Intensities of the Two Rydberg Series Converging to the ⁴P and ²P Limit of Atomic Oxygen¹⁴⁷.

configuration	energy expt (eV)	energy theory (eV)	relative intensity expt	relative intensity theory
1s2s22p5(3P)	527.8	528.1	100	100
1s2s22p4(4P)3p	541.3	542.2	6.2	5.1
1s2s22p4(4P)4p	542.6	543.8	1.6	1.9
1s2s22p4(4P)5p	543.2	544.3	0.36	1.1
1s2s22p4(2P)3p	545.6	545.6	5.4	2.0
1s2s22p4(2P)4p	547.2	547.2	1.9	0.5
1s2s22p4(2P)5p	547.7	547.8	0.36	0.24

The 1s2p peak and the Rydberg peaks in the oxygen K-edge of the oxygen atom have been calculated by Petrini and Araujo.¹⁴⁸ The analysis of the resonant Auger spectra gives a more complete understanding of the nature of the states in the oxygen K-edge XAS.¹⁴⁹

4.2. Oxygen Ions

When oxygen is ionized, the ground state changes from 2p⁴ to 2p³, yielding a new ground-state symmetry as indicated in Table 2. Because the positive charge of the O¹⁺ ion, it costs more energy to excite its 1s core electron. The energy shift from a neutral oxygen atom to a O¹⁺ ion is 4.5 eV. Table 2 makes use of data on oxygen ions from X-ray satellites such as the Chandra X-ray observatory and XMM Newton. These X-ray satellites are able to detect the oxygen K-edge XAS spectrum with around 200 meV resolution.¹⁴⁶ Oxygen is often studied, as it plays a key role in the understanding of the chemical evolution of the Universe.¹⁵⁰ If the oxygen atom is ionized to a O¹⁺ ion, the oxygen 1s binding energy increases due to the decrease of the valence electrons.¹⁵¹ The O²⁺ and O³⁺ ions have an XAS spectrum containing three peaks. Due to their less-than-half-filled configuration and related Hunds rule ground state with minimum J, three final states have similar intensity.

Table 2. Theoretical 1s2p Excitation Energies of Oxygen Ions^a.

ion	configuration	symmetry	1s2p (eV)
O	2s22p4	3P	528.8
O1+	2s22p3	4S	533.3
O2+	2s22p2	3P	537.2
O3+	2s22p1	2P	545.8
O4+	2s2	1S	554.6
O5+	2s1	2S	562.3

^aThe Hunds rule ground state is given along with the symmetries of the main peaks in the final state¹⁵¹.

Photoionization and photoabsorption cross sections used to model important astrophysical processes have been provided first by theory,¹⁵² as at that time, limited experimental reliable data were available. Early theoretical photoionization cross sections are computed by means of Hartree–Slater wave functions¹⁵³ and Dirac–Slater wave functions.¹⁵⁴ Pradhan et al.¹⁵¹ calculated the resonant transition energies and the resonance oscillator strengths from the ground state of different oxygen ions (of astrophysical importance) by means of the Breit–Pauli R-matrix method. Photoabsorption cross sections have been calculated with the R-matrix approaches¹⁵⁵ and multiconfigurational methods (MCHF¹⁵⁶ and MDHF¹⁴⁹). McLaughlin et al.¹⁵⁷ reported photoabsorption cross sections obtained with RMPS and high-resolution experimental measurements.

4.3. Binary Molecules CO, NO, and O₂

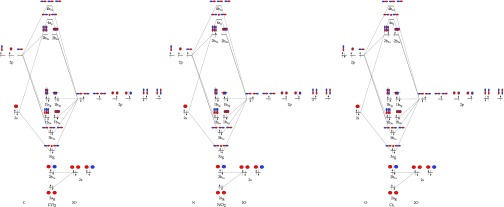
In CO, NO, and O₂ molecules, there are, respectively, 14, 15, and 16 electrons that can be placed into the molecular orbitals. The orbitals in molecules can be constructed from the combination of the atomic orbitals. Figure 9 shows the molecular orbitals of O₂, CO, and NO.

Figure 9.

Molecular orbital diagram of CO, NO, and O₂. The three MO energy schemes are equivalent, where in the case of O₂, the order of the bonding σ_2p and π_2p states is inverted due to a decreased influence of the 2s states. The antibonding orbital π_2p^* is filled with, respectively, 0, 1, and 2 electrons, creating the triplet ground state for O₂.

The 1s orbitals of O₂ are not overlapping with the neighboring orbitals and retain their atomic character. The 2s and 2p orbitals of O₂ overlap with the neighboring 2s and 2p orbitals and have σ bonding and antibonding orbitals. The 2p orbitals of O₂ also have π overlap with the neighboring 2p orbitals. The antibonding π_2p^* molecular orbitals contain two paired electrons, and the antibonding σ_2p are empty. At higher energies, one can find the molecular orbitals due to 3s, 3p, and 3d atomic orbitals. The molecular orbitals of NO are equivalent with one electron in the antibonding orbital π_2p^*, and CO has zero electrons in the antibonding orbital π_2p. Because for CO, NO, and O₂ molecules there are two partly empty 2p states, one expects two peaks in the XAS spectrum corresponding, respectively, to transitions to the π* and σ* states.

O₂

The π_2p^* orbital in O₂ is doubly degenerate and half filled, implying that different electronic states can be obtained depending on the electronic configuration. There are three different states, respectively, ³Σ_g, ¹Δ_g, and ¹Σ_g corresponding to different arrangements of these electrons in the C₂ point group symmetry. The ground state of molecular oxygen is the triplet state ³Σ_g. The oxygen K-edge spectrum of O₂ has been extensively studied.^{158,158−171} The strong first resonance in the oxygen K-edge absorption spectrum (E_edge) at 531 eV (O 1s → π*) has been analyzed, and the vibrational structure has been resolved.¹⁷⁰ The ionization energy E_ion of O₂ is found at approximately 547 eV, and like for the oxygen atom, it is split into a quartet and a doublet state depending on the coupling of the core electron spin to the valence spins, indicated in Figure 10.

Figure 10.

(a) Oxygen K-edge of O₂ from ref (158) including a high-resolution inset of the Rydberg states. (b) Energy level diagram and allowed transitions, including the ionization potential for spin up and down indicated as ²Σ and ⁴Σ. The exchange splitting arises from differences in the magnetic exchange interactions in the final states yielding the experimental peaks B and C.¹⁷²

The challenging part of the assignment of the peaks in the O₂ absorption spectrum is the region between 535 and 545 eV. In this region, we expect the 2pσ* peaks but also the Rydberg states. The 1s → σ* resonance is split into two features converging to the ⁴Σ^– and ²Σ^– ionization thresholds at 543.39 and 544.43 eV.^{162,169,171,173} Kosugi et al. reported symmetry-resolved oxygen K-edge spectra where two σ features with different intensities are assigned to the bound-state transitions 2pσ*.^158,174 The solid-state oxygen K-edge spectra of O₂ show no strong quenching or broadening of these peaks.¹⁷⁵ This suggests that the peaks cannot be assigned to Rydberg states, because the Rydberg states will behave differently in the solid state, due to strong intermolecular overlap of the extended 3p and 4p states.

Wurth at al.¹⁷² reported an exchange splitting of 4 eV and assigned the σ* resonance to the spin up and spin down transitions 1σ_g → 3σ_u^*.¹⁷² Ruckman et al. studied the O₂ gas-phase spectrum in comparison with the oxygen K-edge of the alkali metal superoxides, and they reported an experimental exchange splitting value of 0.4 eV,¹⁷⁶ with both components located in peak B. The exchange splitting value that can be found in the literature spans a broad range, and this can be ascribed to the theoretical difficulties in treating the Coulomb and exchange interaction in the core–hole excited states.¹⁷⁷ These two different interpretations of the absorption interaction lead to different conclusions. By comparison of the adsorbed O₂ and gas phase, the changes in the peak positions and intensities are interpreted either as quenching of the exchange splitting¹⁷² or as the consequence of the Rydberg nature of peak C in free O₂.¹⁷⁶ The analysis of the de-excitation spectra helps the separation between σ* and Rydberg core excited states. The de-excitation spectra excited at feature C can be understood from the decay of one or more Rydberg states, whereas the de-excitation spectra for the chosen excitation energies within feature B are associated with the decay of the 2pσ* state. Under pressure, O₂ condenses to a liquid, and at 5.5 GPa, it solidifies to a solid. As a function of pressure, several solid O₂ phases exist.¹⁷⁸ The oxygen K-edges of the liquid and solid O₂ phases show that as a function of pressure the π* and the σ* peaks move to higher energy, consistent with a decreasing O–O interatomic distance. In addition, the π* loses intensity due to the increased interaction between the O₂ molecules leading to a singlet ground state for the ϵ (O₂)₄ phase.¹⁷⁸

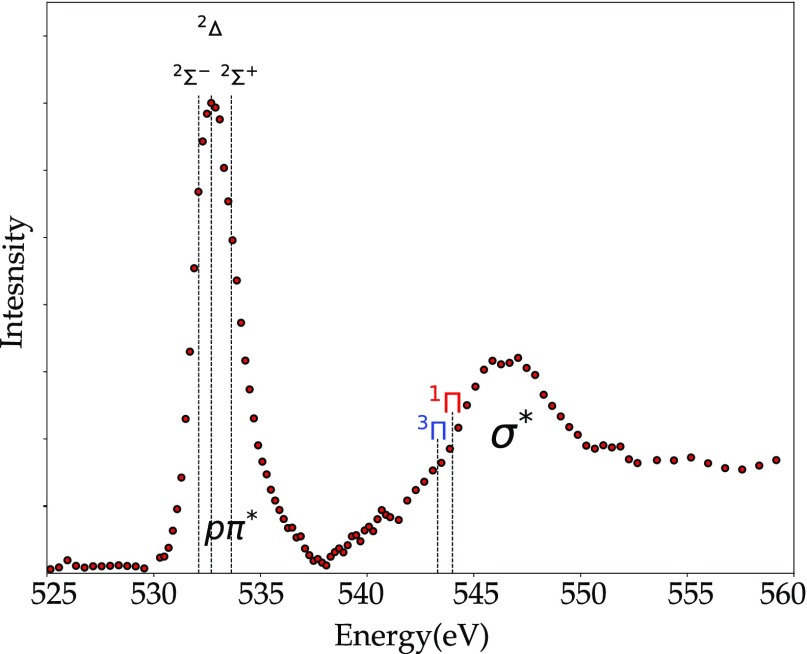
NO

The electronic configuration of NO is equivalent to that of O₂ with only one electron in the 2p_π orbital, resulting in a ground-state symmetry with term symbol ²Π. Figure 11 shows the oxygen K-edge spectrum of NO, which is similar to that of O₂. The π* peak at 532.55 eV followed by the σ* peak at 546 eV. Because NO is an open-shell molecule, the excitation of the inner 1s_σ electron in the oxygen K-edge results in the coupling between the unpaired electron spins of the core and valence shells.¹⁷⁹ This implies that the π* peak at 532.7 eV is split into three states, respectively, ²Σ^–, ²Δ, and ²Σ⁺.^158,179

Figure 11.

Oxygen K-edge spectrum of NO where the ionization limits are indicated as ¹Π and ³Π.¹⁸⁰ The three theoretical components (²Σ^–, ²Δ, and ²Σ⁺) in the 1s2p peak at 532.7 eV are indicated.

The core–valence interactions also yield two ionization thresholds (Δ = ∓1/2) ³Π and ¹Π.¹⁸¹ The symmetry-resolved spectra confirm their bound-state transition character. The atomic population analysis¹⁸² and photoelectron measurements¹⁸³ find that the 2pπ* orbitals have an high percentage of nitrogen character. Auger decay investigations suggest that the three doublets state gives the highest contribution to the high energy autoionizing lines observed in the oxygen K Auger spectrum.¹⁸⁴ The feature with a maximum around 540 eV has been assigned to Rydberg transitions with quantum number n = 3, while the σ resonances are observed above the ionization threshold.^158,179 Three series (ns, np, and nd) of Rydberg states are found.¹⁸¹

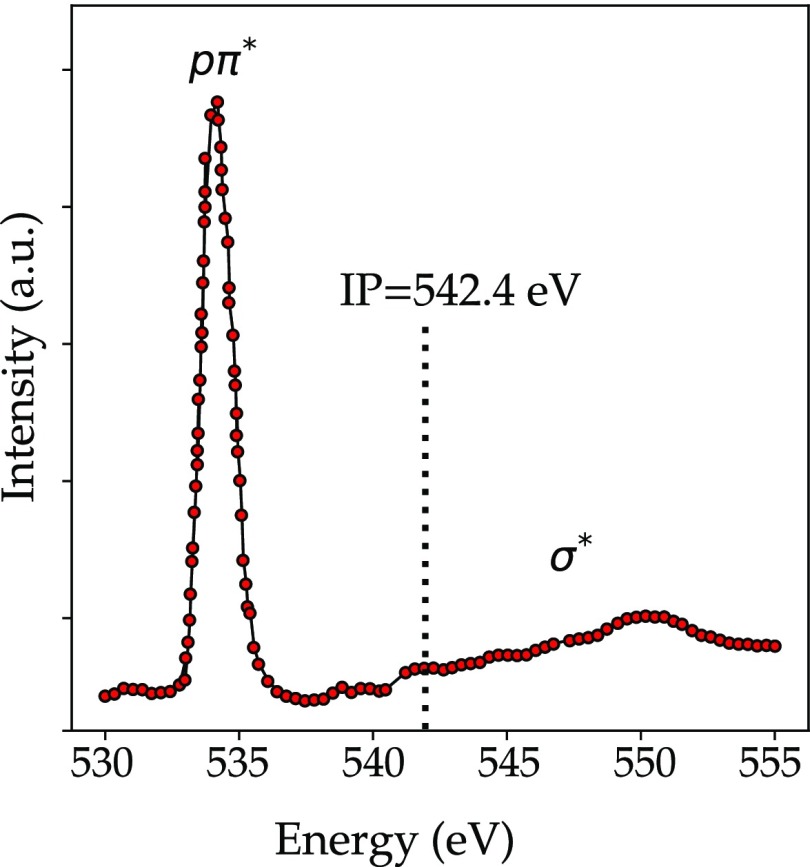
CO

Carbon monoxide (CO) has a singlet ground state, where there are no electrons in antibonding orbitals. The molecule has a closed-shell configuration, and its ground state is a totally symmetric singlet ¹Σ⁺. In Figure 12, the CO oxygen K-edge spectra is reported. The first feature in the oxygen K-edge is the bound excitation into an antibonding π* orbital that can be vibrationally resolved.^170,181 In addition, for CO the σ shape resonance appears above the ionization threshold. The two higher energy peaks are assigned to 3sσ and 3pπ Rydberg excitations. The features in the continuum have been interpreted as the l = 3 shape resonance enhancement in the σ channel¹⁸⁵ or as a transition to the quasi-bound σ*.¹⁸⁶

Figure 12.

Oxygen K-edge spectrum of CO where the ionization potential (IP) is indicated.¹⁷⁴

In Table 3, we compare the excitation energies to the 2pπ* peak in CO, NO, and O₂. The excitation energy increases from O₂ to CO, indicating that it becomes more difficult to excite the 1s core electron to the 2pπ* state. The nitrogen K-edge shifts down in going from N₂ to NO. An increase in the excitation energy was also seen for the change from oxygen atoms to ions. Extrapolating this to NO indicates that the oxygen atom in NO is more positive than in O₂, with the N atom being more negative. In CO, the oxygen atom is even more positive.

Table 3. Energy Position of the 2pπ* Peak of Binary Molecules and Ions.

2pπ* peak energy
	energy (eV)	ref
O2–	529.0	(176)
O2	530.8	(158)
O2+	533.2	(187)
NO	532.7	(158)
CO	534.2	(170)
CO+	533.8	(188)

Ions of Two Atom Oxides

Lindblad measured the oxygen K-edge of a O₂⁺ and CO⁺ molecules. The 2pπ* peak shifts to higher energy in O₂, in agreement with its positive charge implying a higher excitation energy.¹⁸⁷ Ruckman et al. measured the oxygen K-edge spectra of the alkali superoxide KO₂.¹⁷⁶ These systems can be considered to contain K⁺ and O₂^– ions and the oxygen K-edge of KO₂ can be interpreted as that of O₂^–. The 2pπ* peak shifts to lower energy in O₂^–. The removal of a valence electron in the CO molecule will create a vacancy in the 5σ orbital, implying that the first peak corresponds to transitions into this orbital. The peak at 533.8 eV is the 2pπ* peak that has shifted to lower energy from 534.2 eV in CO,¹⁸⁸ with the corresponding carbon 2pπ* peak shifting 2.6 eV to higher energy. This indicates that the positive charge of the CO⁺ ion is mainly at the carbon site.

4.4. Molecules with Three Atoms

Renner Teller Effect

The breakdown of the adiabatic approximation in triatomic molecules is called the Renner Teller effect. The experimental manifestation of this effect is an irregular vibrational structure of the spectra that reflects the coupling of two electronic states in the bent nuclear conformations which were degenerate at the linear molecular geometry. The Renner Teller effect is a consequence of the electrostatic interaction between two components of an electronic state with a nonzero angular momentum.

In this section, we discuss some molecular systems with three atoms. The general interpretation of the oxygen K-edge remains similar to the binary molecules, that is, one observes the lowest empty orbitals, and at higher excitation energies, they are mixed with Rydberg states. Figure 13 shows the molecular orbitals of O₃, CO₂, and NO₂.

Figure 13.

Molecular orbital diagrams of CO₂, NO₂, and O₃. The MO schemes are equivalent to the difference that the number of electrons in the 2pπ* orbital is respectively 0, 1, and 2.

O₃

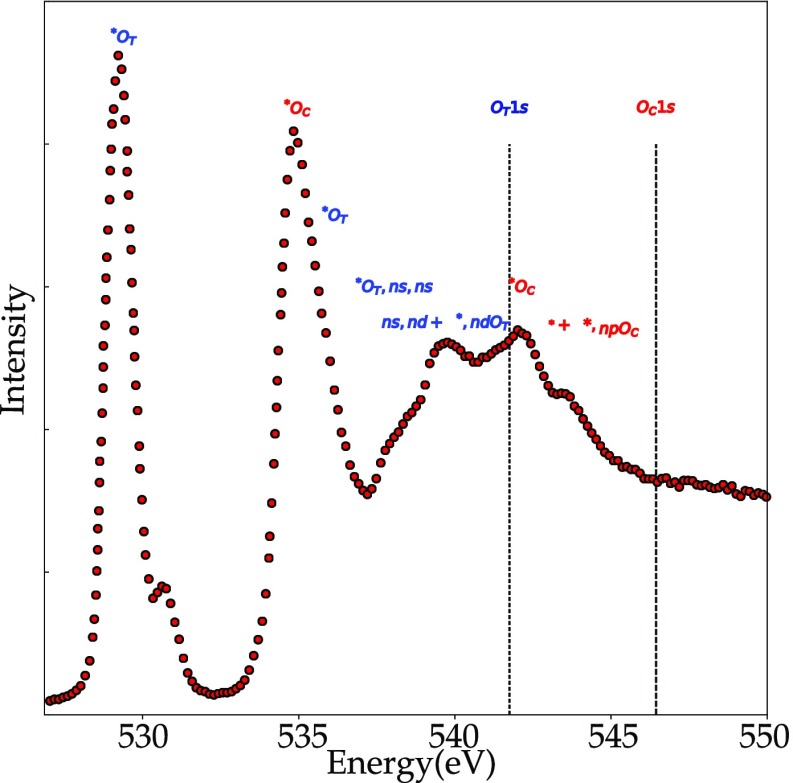
Ozone, O₃, is a bent molecule with a central oxygen atom and two equivalent end oxygens. This creates a new situation compared to O₂, because it is now possible to excite a 1s core electron from two different oxygen atoms. The molecular orbitals of O₃ can be divided into π orbitals and σ orbitals. The π orbitals are for bonding, nonbonding, and antibonding combinations, with only the 2pπ* antibonding orbital empty. At higher energy, there are two 2pσ* antibonding orbitals. The O₃ oxygen K-edge spectrum shown in Figure 14 shows two sharp peaks appear at 529 and 536 eV.¹⁸⁹ The first sharp peak has been ascribed to the transition from the 1s electron of the terminal oxygen to the 2pπ*. The second sharp peak at 536 eV is ascribed to transitions from the 1s electron of the central oxygen to the 2pπ*. Note that both the peaks at, respectively, 529 and 536 eV originate from the same molecular orbital, but still they appear at 7 eV difference in their excitation energy because the terminal oxygen atoms are much lower in energy. In other words, the central oxygen atom is more positively charged. The complete analysis shows that the second peak also has some intensity from transitions into the 2pσ* antibonding orbitals for the terminal oxygens. The peaks at 540 to 545 eV are due to transitions into the (mixed) 2pσ* antibonding orbitals and to Rydberg transitions. To summarize, it is interesting to compare the assignments for the oxygen atom and the O₂ and O₃ molecules:

• The oxygen atom only has the main 2p peak and at higher energy the Rydberg states.

• The O₂ molecule has different chemical states, respectively, the 2pπ* and 2pσ* peaks.

• The O₃ molecule has different oxygen atoms, respectively, at the center and at the edge of the O₃ molecule, yielding different peaks related to the same 2pπ* orbital due to different core–hole potentials.

Figure 14.

Oxygen K-edge TIY spectrum of ozone.¹⁸⁹ The peaks at 529 and 536 eV are excitations into the same 2pπ* state, from, respectively, the terminal O_T and the center oxygens O_C. Note that the small peak at 531 eV is due to the presence of some O₂.

NO₂

Nitrogen dioxide is a bent molecule with a central nitrogen atom and two equivalent end oxygens; in other words, it has a similar structure to O₃. This implies also that the molecular orbitals of NO₂ are similar to those of O₃ and the π orbitals form bonding, nonbonding, and antibonding combinations. Because there is one electron less, the nonbonding π orbital contains only one electron. The oxygen K-edge of NO₂ contains two sharp peaks, respectively, related to the nonbonding and antibonding π orbitals. At higher energy, we observe broad structures due to the σ orbitals and Rydberg states. It is interesting to note that both NO₂ and O₃ have two π related peaks, but for NO₂, they relate to two different orbitals, while for O₃, they relate to the same orbital but a 1s core–hole on two different oxygen atoms, center, respectively, end.

CO₂

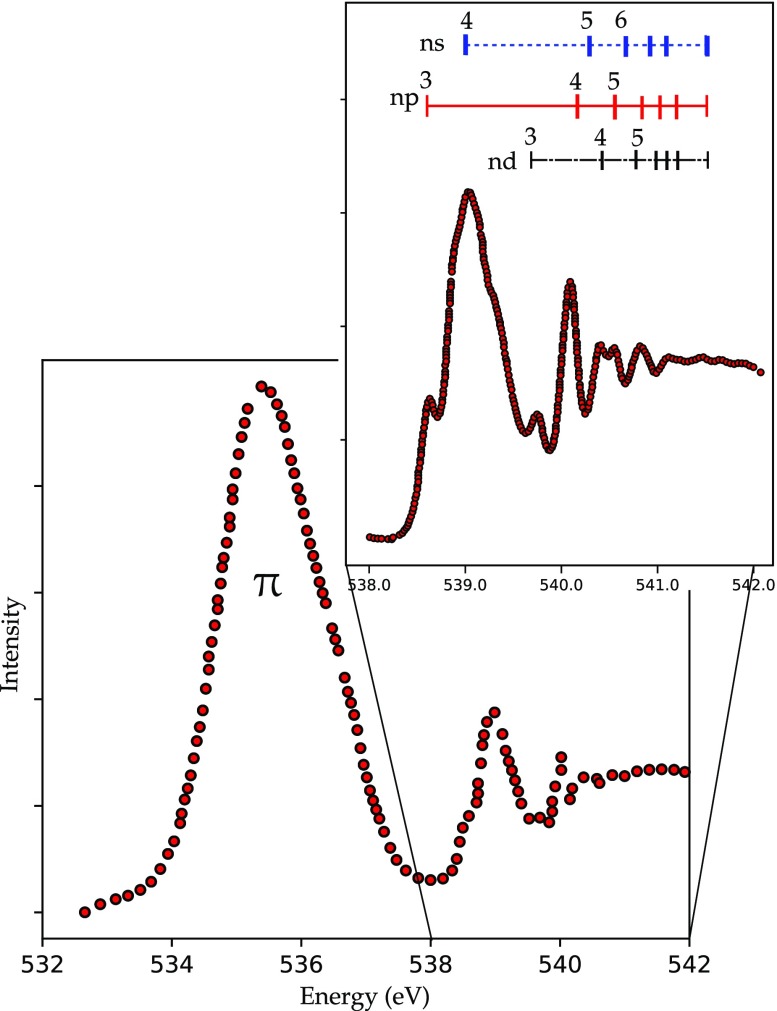
Carbon dioxide is a linear molecule with the bonding and nonbonding 2p orbitals occupied. It is a closed shell system that has a ground-state term symbol ¹Σ_g⁺. The lowest three empty states are, respectively, the double degenerate 2pπ* state, followed by two antibonding 2pσ* states. The 2pπ* state is doubly degenerate, but upon the oxygen K shell excitation, the equilibrium bond angle is changed and the degeneracy is removed by the Renner Teller effect.^179,190 Because of the energy lowering resulting from bending the structure, the 2π_u splits in two components. The first peak in Figure 15 corresponds to the promotion of an oxygen core electron to the two component of the lowest empty molecular orbital 2π_u.

Figure 15.

Oxygen K-edge spectrum of CO₂ from ref (191). The 2pπ* state is seen at 535 eV. Above 538 eV, the 2pσ* and the Rydberg states are visible.

This peak presents a large fwhm compared to the elastic peak,¹⁷⁹ which suggests that not only the excitation from the K shell to the 2π orbital contributes to this peak but also the lowest 1sσ_u → 3sσ_g Rydberg transition with antibonding valence character.¹⁹¹ This hypothesis is supported by the fact that this transition is optically allowed. The peaks in the higher energy part of the spectrum can be assigned to Rydberg transitions.¹⁹¹ Thus, all the pπ, pσ, and σ transitions are allowed. This can lead to the conclusion that a mixing of the valence state with the σ* antibonding resonance occurs.¹⁹⁰ Shieh et al. study the oxygen K-edge of CO₂ under pressure.¹⁹² The pπ peak disappears at 37 GPa and it is replaced by two structures at, respectively, 532 and 540 eV. At pressures above 37 GPa, CO₂ does not exist as separate molecules, but has polymerized. There are several options for the condensed phase of CO₂, with the phase where carbon is fourfold coordinated can best explain the observed spectral changes.¹⁹²

4.5. Atomic Adsorption

Molecules adsorbed on a surface change their electronic structure, and the oxygen K-edge is a useful tool to study the adsorption processes of oxygen-containing molecules. The adsorption phenomena of small molecules are particularly important as the fundamental steps in catalytic processes.

The interaction of oxygen atoms with a surface is strong due to the bonding of the oxygen 2p orbitals with the metal orbitals near the Fermi level. Three 2p orbitals are involved in the surface chemical bond with an adsorbing atom. The interaction with the 2p_z orbital has σ symmetry with respect to the surface. The 2p_x and 2p_y orbitals are parallel to the surface and can only interact with the surface s atomic orbitals in high coordination sites. This bonding interaction contributes significantly to the total surface bond energy, implying that bonding to high coordination sites is favored. The 2p orbitals form bonding and antibonding orbitals with the metal orbitals.

Figure 16 shows the oxygen K-edge of oxygen adsorbed on a Cu(100) surface (points) compared with the energy-shifted copper 2p XAS spectrum of copper metal. The atomic energy of the 2p orbital is below the Fermi level, implying that the antibonding combinations will have mainly metal character. The oxygen K-edge in a first approximation maps the empty metal states, slightly shifted to higher energy due to the antibonding character. From this analysis, one would expect that if an oxygen atom is adsorbed on a copper surface, in the first approximation the oxygen K-edge will map the empty metal states, and as such it will look similar to the copper 2p XAS spectrum that maps the empty copper s states.

Figure 16.

Oxygen K-edge of oxygen adsorbed on a Cu(100) surface (points)¹⁹³ compared with the Cu L₃-edge shifted by 401 eV.¹⁹⁴

4.6. Molecular Adsorption

X-ray absorption of the adsorption of molecules to surfaces has been discussed in detail in the book Chemical bonding at surfaces and interfaces by Nilsson, Pettersson, and Norskov.¹⁹⁵ The adsoption of oxygen-containing molecules to a surface is weaker than that of oxygen atoms. In a molecule, the atom that binds to the surface is still bonded to other atoms from the molecule. The adsorbed atom divides its bonding strength between the molecule and the surface, with the consequence of weaker bonding than an isolated oxygen atom. One can distinguish physisorption and chemisorption. In chemisorption, there is a chemical bond between the molecule and the surface, while in physisorption, the molecule is attached to the surface without a chemical bond, for example, via van der Waals interactions.

Linear Dichroism

Linear dichroism or polarization dependent X-ray absorption concerns the difference in XAS spectral shape of a system as a function of its angle with respect to the X-rays. At a bending magnet beamline, the X-ray is linearly polarized in the plane of the synchrotron. This implies that the X-ray excites the electric dipoles that are aligned in this plane. Assuming a planar molecule lying on a flat surface, one can excite the planar bonds if the X-ray polarization vector lies in this plane. The bonds perpendicular to the plane are excited when the sample is turned with the electric vector perpendicular to the molecular plane. This yields two polarization dependent spectra, and the difference spectrum is the linear dichroism spectrum. If the symmetry of the system is broken by a magnetic field, there will also be linear dichroism, which then is called magnetic linear dichroism (MLD).

CO on Metal Surfaces

The bonding of CO on Ni(100) was studied in detail in 1982 by Stöhr and Jaeger.¹⁹⁶ One observes the transitions to the 2π* orbital at 534.0 eV and to the σ* orbital at 550.0 eV. In the free CO molecule, these excitation energies are, respectively, 534.2 and 550.9 eV (see Table 3), implying that the 2π* excitation energy does not shift, while the σ* orbital shifts by 0.9 eV. Thus, the energy difference between the 2π* and the σ* orbitals is reduced from 16.8 eV in free CO to 16.0 eV in CO/Ni(100). This energy reduction can be ascribed to the shift to higher energy by the antibonding combination of the 2π* orbital and the Ni 3d orbitals. Figure 17 shows an angular dependence. At normal incidence, the 2π* peak is strong because the electric field is aligned with the 2π* resonance. At grazing incidence, the electric field is parallel to the CO axis, hence perpendicular to the 2π* orbital, and the 2π* resonance is small. The argument is reversed for the σ* orbital that has the highest intensity when the electric field is parallel to the CO axis. This angular dependent effect, also known as linear dichroism, indicates the bonding orientation of the adsorbed molecule. Tillborg et al. studied the oxygen K-edge XAS spectra of CO adsorbed on three different sites on a Ni(100) surface, respectively, hollow sites, bridge sites, and on-top sites. The energy position and relative intensity of the oxygen K-edge indicates the difference in chemical bonding.¹⁹⁷

Figure 17.

Oxygen K-edge of CO on Ni(100).¹⁹⁶ The 2π* orbital is visible at 534.0 eV and the σ* orbital at 550.0 eV.

4.7. Analysis of Catalytic Reactions

The information on the adsorbed species can be used in the analysis of oxygen K-edges of catalytic reactions. One can study the oxygen K-edge XAS spectra under in situ conditions. The most common approach uses conversion electron yield; i.e., the excited electrons ionize the gas phase and the resulting ionized ions are detected. Often, these experiments are performed in so-called near-ambient-pressure XPS setups, implying that the gas pressure is in the millibar range,⁴⁷ but one could also use 1 bar pressures in dedicated in situ XAS reactors. Knop-gericke et al. studied methanol oxidation to formaldehyde over copper metal.⁴⁷ One detector tracks the oxygen components in the gas phase, and a second detector tracks the oxygen components of the surface and gas phase combined, allowing the determination of the surface species by subtracting the pure gas phase spectrum. The oxygen K-edge as a function of temperature indicates a transition from Cu₂O at 540 K to a species that is described as adsorbed oxygen atoms that mainly interact with the copper s states. The different oxygen species are then correlated with the catalytic reactions.⁴⁷

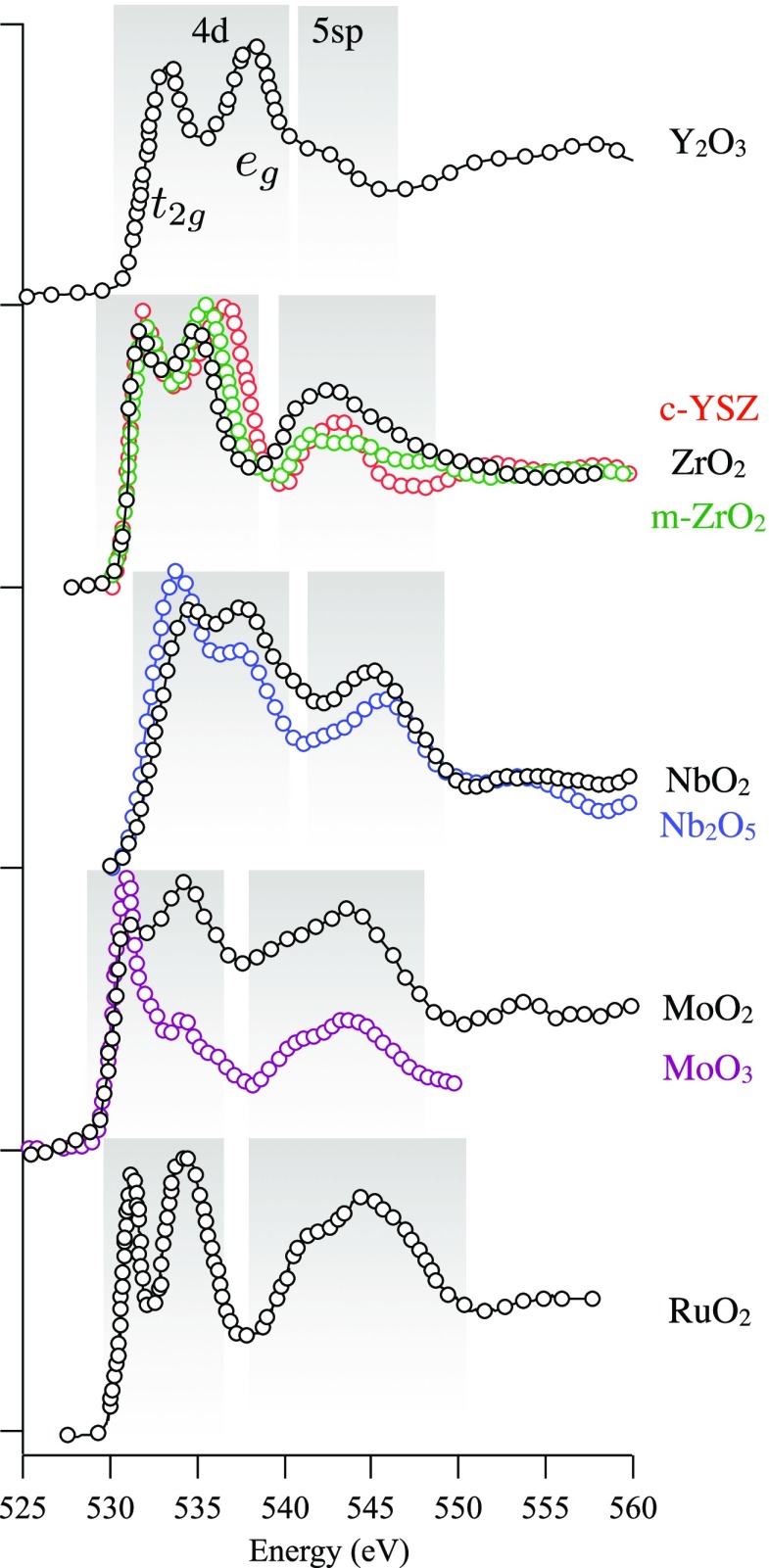
Pfeifer et al. performed a detailed study on the comparison between amorphous and crystalline rutile IrO₂, which is important regarding its behavior as electrocatalyst for the oxygen evolution reaction.¹⁹⁸ The rutile phase is a pure Ir⁴⁺ O^2– oxide and the oxygen K-edge shows two peaks: a sharp peak at 530 eV related to the empty Ir 5d states and a broad peak at 533 eV due to the sp band. The amorphous IrO_x shows additional fine structure in the 5d spectral region, which in the paper is assigned to partial reduction to Ir³⁺, due to the formation of Ir vacancies. In our opinion, a shift to lower energy in the oxygen K-edge should be related to an oxidation to Ir⁵⁺; in other words, the Ir vacancy creates Ir⁵⁺ sites at neighboring positions, which causes a shift to lower binding energy.

Tesch et al. studied the behavior of MnO_x electrocatalysts as a function of the potential.¹⁹⁹ The oxygen K-edge of the MnO_x system changes as a function of the potential, which is analyzed as a change in the Mn–O hybridization. In our opinion, what is visible in the oxygen K-edge is mainly the change of the ratio of MnO_x and nafion/graphene background, and the oxygen K-edge related to the MnO_x species remains the same for all potentials.

5. Liquids and Solutions

5.1. Water

H₂O is studied in the gas, liquid, and solid phases. In this section, we briefly discuss all the states of water. The oxygen K-edge of water is a very active research field and we do not intend to cover all developments but instead focus only on the basic components in the analysis. Readers are referred to recent reviews on the X-ray spectroscopy of water, in particular, the recent reviews by Smith and Saykally¹⁸ and by Nilsson and Petterson.¹⁹

Gas-phase H₂O is a bent molecule with five occupied orbitals. The highest occupied molecular orbital is a nonbonding 1b₁ orbital derived from the oxygen 2p_x orbital without contributions from the hydrogen 1s orbital; in other words, it is the “lone pair”. At lower energy, the orbitals are, respectively, from highest to lowest energy the 3a₁, 1b₂, and 2a₁ molecular orbitals with contributions from hydrogen 1s and oxygen 2s and 2p orbitals, i.e., participating in the O–H bond. The two lowest unoccupied molecular orbitals are the O–H 4a₁ and 2b₂ antibonding orbitals.

Water molecules in liquid and solid phases show two different types of O–H interactions: (1) covalent intramolecular O–H bonding and (2) weak intermolecular hydrogen bonds.²⁰⁰ The study of the oxygen K-edge allows the investigation of the unoccupied states; most importantly, the antibonding O–H molecular orbitals and their character that is sensible to the H-bonding network around the probed oxygen atom. The oxygen K-edge spectrum of water is considered as being formed by three regions: the pre-edge region at 535 eV, the main edge region around 537 eV, and the post-edge region at 541 eV. These regions go through modifications depending on the water phase. In Figure 18, the oxygen K-edge spectra of ice-, liquid-, and gas-phase water are compared.

Figure 18.

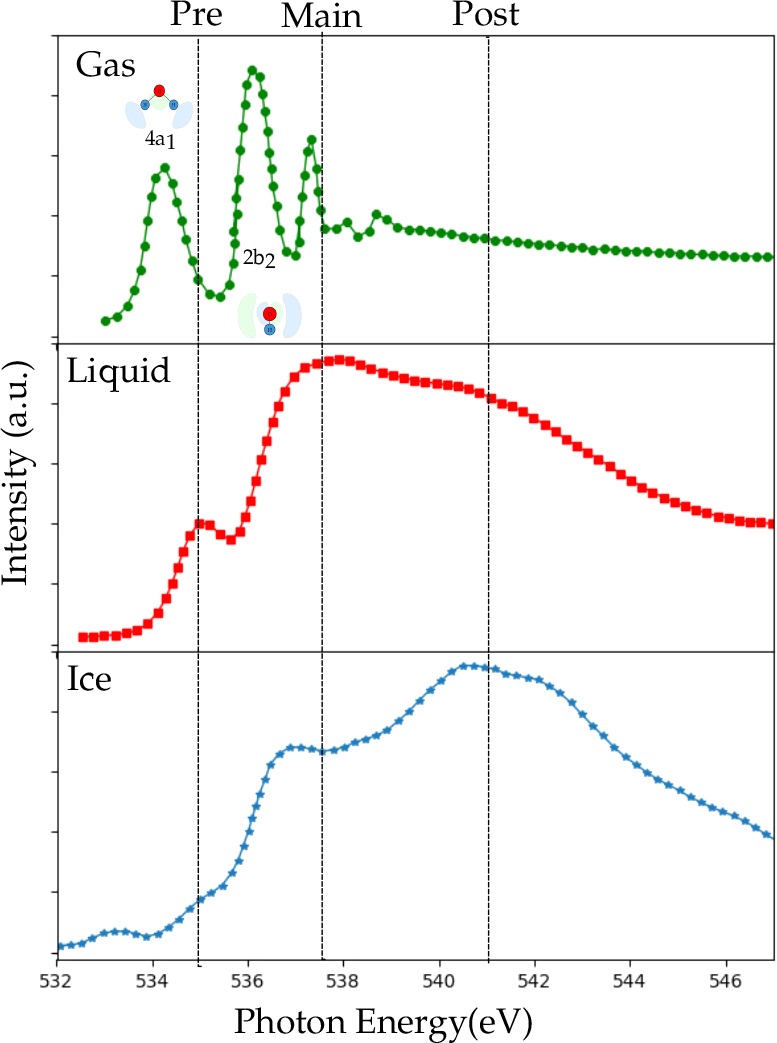
X-ray absorption spectra of gas-phase water, liquid water at 299 K, and ice grown on BaF₂ at 144 K.²⁰¹

The gas-phase spectrum shows the antibonding orbitals in the molecular MO scheme. In the case of the liquid state, the pre-edge has been ascribed to the presence of broken H-bonds by computational and experimental studies,²⁰² and the main edge region has been ascribed to interstitial water molecules.¹⁴⁴ The post-edge region contains features that consist of states delocalized trough the H-network and results from a tetrahedral ice-like coordination.⁵² Cavalleri et al. investigated the spectral change for the pre- and main edge going from the free molecule to the pentamer. They highlighted the role of the H-bond directionality on the spectral shape: the unoccupied antibonding O–H orbitals, in gas phase, are polarized toward the hydrogen, so they have a strong sensitivity to additional H-bonds.²⁰³ The features that constitute the post-edge region have been related to states that are localized along the H-bond. These states give rise to the conduction band in the ice phase with a strong intensity due to the fact that both OH groups are involved in donor hydrogen bonds.²⁰⁴ The three different regions of the water spectra are affected by several factors such as a change in temperature, different solvents, and isotope effects. Heating the liquid will cause the post-edge region to lose intensity, while the pre-edge and the main edge will increase their intensity. The study of Wernet et al.²⁰⁵ gave rise to a huge debate on the local structure of liquid water at different temperatures. It has been concluded that the spectrum of liquid water is composed of two different species: a species with two hydrogen-bonded configurations with one strong donor and one strong acceptor bond donating H-bond and a second species that is more symmetric with a tetrahedral-like coordination close to the ice coordination. By increasing the temperature, the water structure diverges from the tetrahedral-like coordination.

In addition, different solvents such as benzene, acetonitrile, and chloroform²⁰⁶ can be seen as hydrogen bonding network perturbations that allow symmetrical bonding and promote ice-like structures with a consequent increase in the post-edge structure. Fuchs at al.^207,208 observed a significant isotope influence on the spectra of liquid water: the pre-edge peak shows a blue shift in the D₂O spectra due to the different zero point energies of the ground states and a reduced intensity in the pre-edge region of the deuterated species due to smaller distortion of the bonding network.

5.2. Bio-Organic Molecules

The general interpretation of the oxygen K-edges of large molecules is similar to the small molecules discussed above. The peaks in the oxygen K-edge are analyzed in terms of the lowest empty orbitals, where in the case of two or more nonequivalent oxygen atoms in a molecule, the individual spectra of the oxygen atoms are added, taking into account that there can be different excitation energies into the same orbital. A large number of oxygen K-edge spectra is given in the COREX database.²⁰⁹

XAS studies of bio-organic molecules are difficult due to the risk of beam damage.²¹⁰ The main degradation processes that can occur when measuring the oxygen K-edge can be grouped as:²¹⁰ (a) dehydrogenation due to the O–H group, (b) dehydration, i.e., the loss of water molecules because of the C–OH bond, (c) decarboxylation (loss of molecular CO₂), and (d) decarbonylation, the loss of molecular CO. Zubachius et al.²¹⁰ investigated the radiation induced modification in the oxygen K-edge spectra of cysteine (Figure 19). The spectral shape is less affected by the beam damage than the intensity; the spectra recorded after 17 min of exposure have an intensity of 1 order of magnitude lower than that of the pristine system. This implies that at least 90% of the oxygen present in the molecule has been detached as H₂O or CO₂. Radiation damage can manifest itself in the oxygen K-edge measurements also as perturbation of the supramolecular structure.^211,212 Panajotović et al. investigated the radiation damage on phospholipidic membranes, and they tested the impact of different incidence modes on the spectra: many broken σ bonds, especially in normal mode, and new features appeared.²¹³ Other common chemical modifications induced by ionizing radiation are the formation of free radicals,^214,215 where the reduction product is usually formed by the addition of an electron to the carbonyl oxygen of the carboxyl group^{214,216−218}and mass loss phenomena,^219,220 depending on factors such as the initial mass, the dose rate, and the area of irradiation.²¹⁹

Figure 19.

(a) Time evolution of the oxygen K-edge spectra of cysteine at time zero and after 17 min without any rescaling.²¹⁰ (b) Oxygen K-edge of DPPC at grazing incidence (GI) and normal incidence (NI) before and after the irradiation.²¹³

Amino Acids, Polypeptides, and Proteins

The measurement of the oxygen K-edge XAS in amino acids is a powerful tool, since oxygen can be in different bonding environments, and different chemical shifts for each oxygen in amino acids are observed.²²¹

In Figure 20, the oxygen K-edge spectra of all 22 amino acids are reported.²²² The spectra show a dominant peak that has been assigned to the π* resonance followed by the σ* resonance at higher energy. In the aspartic acid spectra, a peak around 534.0–534.5 eV, with an energy difference from the main peak of 1.5 eV has been reported and assigned to the 1s → π* excitation of the OH oxygen in the carboxy group.^221−223 In addition, the glutamic acid shows a similar feature.²²² From the hydroxyl group of serine, threonine, and hydroxyproline, a σ* (O–C) transition occurs in the range ∼538–540 eV.²²² A probable contribution from residual water is expected in the energy range 537–540 eV.^222,224

Figure 20.

Experimental oxygen K-edge spectra of the 22 amino acids and their molecular formulas.²²² In the table, the peak positions together with their assignments are reported.

Even if isolated amino acids in the gas phase are always neutral, in solution any change in pH can bear dramatic changes in their charge state, as they can exist as cations at low pH values, charge neutral zwitterions at intermediate pH values, and anions in basic solutions. The addition or removal of a proton affects the local symmetry of the electric field surrounding the terminal oxygen,²²⁴ so the energy levels of molecular orbitals at the carboxylic group would be modified by any pH change.

In Figure 21, the spectra in solution of glycine at different pH values is reported. The terminal carboxyl group of glycine is protonated in an acid environment, so a lift of the degeneracy CO double bond and a feature around 535 eV due to the C–O bond is expected. The strong background from the aqueous solution cannot be easily subtracted and makes the attempt to identify further resonances difficult.²²⁴

Figure 21.

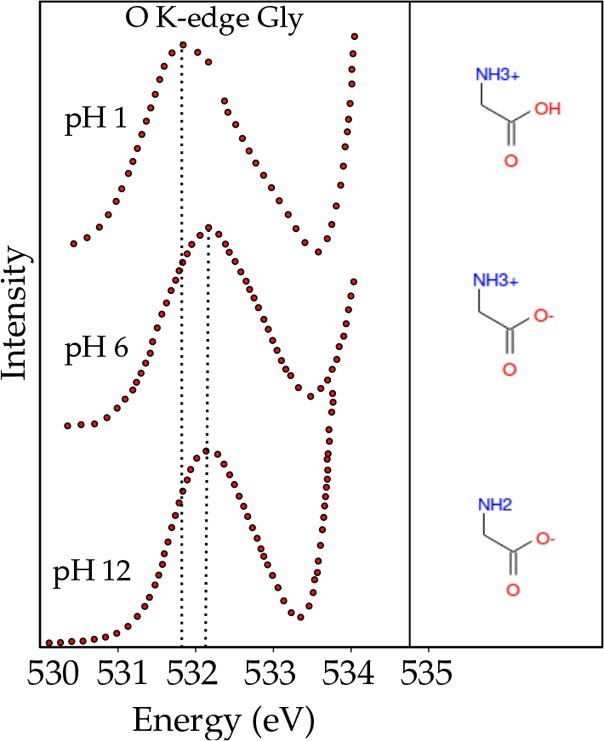
Oxygen K-edge spectra of 0.6 M glycine (aq) as a function of pH. A small red shift is observed for the acidic solution, which has been illustrated by a dotted line through the center of each peak. This shift is caused by the protonation of the carboxylate subgroup at low pH, and the resultant breaking of the degeneracy in the O 1s → π_CO^* transition.²²⁴

DNA Components

In Figure 22, the oxygen K-edge XAS spectra of uracil (U), thymine (T), cytosine (C), and guanine (G) are reported.²²⁵ The bases show a strong feature around 532 eV arising from the carbonyl group (π_CO^*), and a σ* resonance above 535 eV, thymine shows a splitting of the π* main resonance due to an energy differnce of the two C=O bonds.^226−228

Figure 22.

(a) Oxygen K-edge spectra of uracil, thymine, cytosine, and guanine together with their molecular structure and the peak assignment.²²⁵ (b) Effect on the oxygen K-edge spectra from adding sugar and phosphate groups of DNA to thymine.²²⁶

In addition, the uracil spectra has a splitting in the first π* peak, but less pronounced; the stronger blue shift of the π₂* of thymine is related to the substitution effect of the methyl group. DNA is built up by nucleobases attached to ribose sugar and phosphate groups. The way the sugar and the phosphate group affect the spectra of the oxygen K-edge of thymine is shown in Figure 22. With the addition of sugar and phosphate, the spectrum acquires features characteristic of the phosphate group as the enhancement of the σ*(C–O) structure.^225,226 The small peak in the π* region comes only from the base.²²⁵

6. Solid Oxides of s- and p-Elements

6.1. Alkali Metal Oxides

The alkali metals lithium, sodium, potassium, rubidium, and cesium form a number of different oxides. Taking lithium as an example, lithium forms, respectively, the oxide Li₂O, the peroxide Li₂O₂, and the superoxide LiO₂. The superoxide MO₂ can be considered as a M⁺ ion combined with a negatively charged oxygen molecule O₂^–. The molecular orbitals of O₂^– are similar to those of O₂ with one more electron occupying the antibonding π* orbital leaving only one hole. The extra charge on the oxygen molecule makes it easier to excite a 1s core electron to the empty orbitals. Figure 23 shows the spectra of superoxide MO₂ (M = Li, K, Cs) compared to the molecular O₂.¹⁷⁶ The spectra of the superoxides show a first peak assigned to the π* orbital and two peaks assigned the σ* orbital and the ionization potential. The three features shift toward lower energy for the different superoxides.¹⁷⁶ Pedio et al. also measured the superoxide KO₂.²²⁹ The experimental spectrum is equivalent to that shown in Figure 23, though with a π* peak at 531.0 eV instead of 529.0 eV. Kang et al. reproduce the oxygen K-edge of KO₂ from band structure calculations using Wien2K.²³⁰

Figure 23.

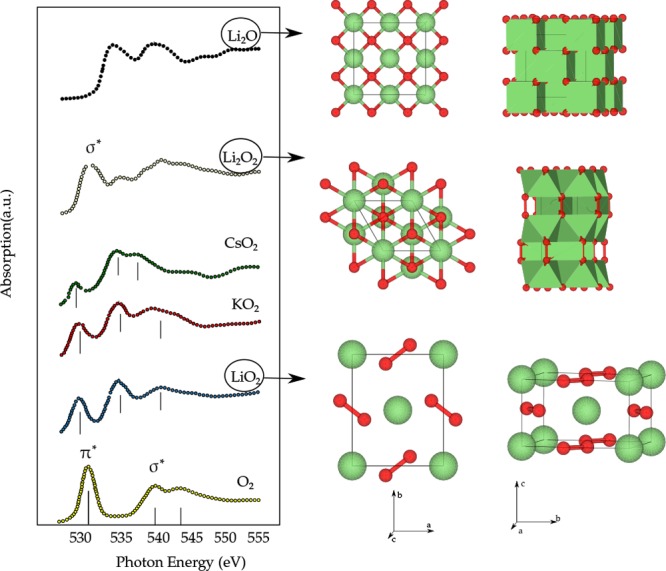
Oxygen K-edge spectra of the oxide Li₂O, the peroxide Li₂O₂,²³¹ and the superoxides LiO₂, CsO₂, and KO₂¹⁷⁶ compared to O₂. The σ and π character of the antibonding states are indicated.

The M₂O oxides (M = Li, Na, K, Rb) crystallize in the cubic antifluorite structure; Cs₂O crystallizes in hexagonal anti-CdCl₂ structure. Alkaline ions occur mainly as cations M⁺ and have rather weak bonds. Lithium oxides are an important compounds of many battery systems. This includes lithium–air batteries, where the reactions between lithium and oxygen play an important role. The reversible oxidation of lithium at the anode and reduction of oxygen at the cathode are important parameters that influence the energy capacity of the battery system. Li₂O and Li₂O₂ have been studied as key components forming at the solid electrolyte interphase in lithium batteries, and their evolution was studied with the oxygen K-edge by Qiao et al.²³¹Figure 23 shows the spectra of Li₂O and Li₂O₂. Li₂O₂ shows a first peak assigned to the σ* orbital of the O–O bond. It is found that both Li₂O₂ and Li₂CO₃ evolve toward Li₂O under the soft X-ray irradiation, where Li₂CO₃ is very sensitive.²³¹

6.2. Alkaline Earth Oxides

Alkaline earth metals combined with oxygen form binary oxides with a rock salt structure and a well ordered surface. Figure 24 shows the oxygen K-edge of the alkaline earth oxides MgO, CaO, SrO, and BaO, from refs (232−236).

Figure 24.

Oxygen K-edge spectra of alkaline earth oxides showing discrepancies between the experiments: MgO,^{232,234,235,237} CaO,^232−235 SrO,^232,234,235 and BaO.^232,234,236

Figure 24 shows some discrepancies between the experimental data^232,234 for CaO, SrO, and BaO. The discrepancies between the different sets of data can be linked to the high reactivity of the alkaline earth metal oxide surfaces. The surfaces of these materials, when exposed to air, are covered with CO₂, water, and, in some cases, dioxygen.²³⁸ No details on how the materials were handled prior to the measurements have been reported;^232,234 hence, possible surface contamination cannot be ruled out. In the experimental spectra reported by Nakai²³² and McLeod,²³⁴ the absorption threshold from CaO to BaO does not change significantly, while the MgO spectrum shows a red shift of about 4 eV with respect to the oxides with the heavier metals. Significant changes can be observed in the near-edge structure going from MgO to BaO: the intensity of the first peak increases from MgO to SrO and the shape of the first peak changes from CaO to BaO.

Mizoguchi et al.²³⁹ analyzed the oxygen K-edge of MgO trough band structure calculations. The first feature at 532 eV is assigned to the Mg 3s band and the main structure 537–540 eV is assigned to the magnesium 3p band. In the MgO experimental spectra by Lindner,²³⁷ a small peak around 532 eV appears in the MgO oxygen K-edge, and a theoretical study from Pascual et al.²⁴⁰ has shown that a small peak with oxygen 2p character 1.5 eV below the ionization edge is present in the MgO, and they attribute its origin to the 1s–3p_z transition polarized out of the plane, in contrast to the assignment to the 3s band.

Fronzoni et al.²⁴¹ reported the TD-DFT oxygen K-edge XAS spectra of MgO, CaO, SrO, and BaO by means of cluster models. They compare the theoretical results with the experimental ones^232,235 and tried to reproduce the experimental trend, where the intensity of the first peak increases when the atomic number Z increases. Their computed spectra match well with the experimental oxygen K-edges. The change in the pre-edge features from MgO to BaO is correlated with a different composition of the low-lying metal orbitals and the metal–oxygen interaction. In an ionic model, the transition in the pre-edge region 1s–2p is weak; its strength rises when the covalent character increases from MgO to BaO. While the participation of 3d orbitals from magnesium in the bonding with oxygen has been ruled out because of their high energy position,^241,242 the participation of d orbitals is important for the heavier alkaline earth oxides.²⁴³

The electronic structure of solid oxides differs from that of molecules, which have molecular orbitals with fixed energy. In a solid, the electronic states form bands that continuously span a certain energy range, which is due to the presence of translational symmetry in crystalline solids. Because of the translation symmetry, it is conceptually and computationally easier to describe solids in reciprocal space. In band structure calculations, the electronic states are described as a series of bands that are given as a function of their (q) wave-vector in the Brillouin zone. The oxygen 1s core state is localized, implying that it has the same energy in for all q-vectors. Because the X-ray photon has negligible momentum, X-ray absorption is effectively a vertical transition in the band structure. This implies that the oxygen K-edge spectrum integrates the band structure to the density-of-states. Because the oxygen 1s core state is localized at oxygen, the local density-of-states is visible, and because of the dipole selection rule, only oxygen projected states of p-symmetry have nonzero matrix elements. In other words, an oxygen K-edge of a solid maps the oxygen p-projected density-of-states. Assuming constant matrix elements and neglecting the final state core–hole, the ground-state calculated oxygen p-projected density-of-states can be compared with the oxygen K-edge. In section 3 on Theory, we discussed the core–hole effects.

6.3. General Considerations of p-Element Oxides

Solid oxides of p-electron element systems form insulators that can be well described by band structure calculations. One of the major issues in the study of p-element oxides is the determination of the geometric structure of the solid. While the average crystalline structure can be determined by X-ray diffraction, variations of the local environment of each atom in the solid can be studied with X-ray absorption using EXAFS, where the EXAFS experiments are usually performed on the hard X-ray cation XAS spectra. Furthermore, amorphous materials do not have a periodic structure and XAS is a key method to determine the local structure of the atoms. The high covalency of the cation-oxygen bond has been a motivation for the investigation of the geometric and electronic structures from the oxygen point of view.

The oxygen 2p orbitals form bonding and antibonding bands with the cation ns and np orbitals. The oxygen K-edge maps the empty states and as such shows the (oxygen 2p character of the) cation combined sp bands. Figure 25 compares the spectra of quartz and rutile polymorphs of SiO₂ and GeO₂ and rutile SnO₂. The spectra show the dependence of the oxygen K-edge on the crystalline structure, the bond angles, and the resulting consequences for the mixing of the oxygen 2p orbitals with the ns, np, and nd orbitals. In the quartz structure, the cation is in fourfold tetrahedral coordination and the oxygen is twofold coordinated. In the rutile structure, the cation is in sixfold elongated octahedral coordination and the oxygen is threefold coordinated.

Figure 25.

(a) Oxygen K-edge spectra of SiO₂²⁴⁴ and GeO₂²⁴⁵ in the quartz structure (b) and (c) oxygen K-edge spectra of SiO₂,²⁴⁴ GeO₂,²⁴⁵ and SnO₂²⁴⁶ in the rutile structure (d). The natures of the final states are assigned based on the DOS calculations.

The multiple scattering calculations,^247,248 later confirmed by band structure calculations,²⁴⁹ have allowed the assignment of the oxygen K-edge features in α-quartz SiO₂: the main intense peak at the edge is assigned to the oxygen 2sp hybridized with silicon 3s followed by features assigned to transitions to oxygen 2p hybridized with silicon 3pd states split by the crystal field. We note that the cation tetrahedral coordination allows the cation pd state mixing. The spectral shape of quartz-GeO₂ is drastically different as a consequence of the different cation–O–cation bond angle (from 143.7° in SiO₂ to 130° in GeO₂) on the orbital overlap.²⁵⁰ However, in both cases, the general final state assignment is similar for SiO₂ and GeO₂.

Contrary to the quartz compounds, the oxygen K-edge spectra of SiO₂, GeO₂, and SnO₂ in rutile structure, Figure 25c shows similar shapes: a first sharp peak followed by a broader structured feature. In the case of SiO₂, these features are not as well separated as in GeO₂ and SnO₂. According to the calculated p-DOS,^250,251 the first sharp feature corresponds to the oxygen 2sp antibonding σ* states hybridized with the empty cation ns states (Si: n = 3, Ge: n = 4, and Sn: n = 5). The strong intensity of this feature is related to the strong bonding of the oxygen in a threefold planar coordination. This can be described with a orbital view: in this geometry, the hybrid sp² orbitals of oxygen point at the cation s orbitals in a strong covalent σ bonding. The following broad feature is assigned to oxygen 2sp states and oxygen 2p states hybridized with the cation np states. For germanium and Sn, the contribution at higher energy from (n – 1)d states is also found. The p-DOS calculations shows that the missing mixing of the cation p and d states as not allowed in the octahedral symmetry. The spectra of the rutile compounds shift to low energy along the series in agreement with the decrease of their respective band gaps.

In the following sections, we first discuss the most studied p-element compounds: borate, carbonate, aluminate, silicate, and germanate crystals and glasses. Then, we review briefly the other p-element compounds, including p-electron heavy metals.

6.4. Overview of p-Element Oxides

6.4.1. Boron Oxides

Boron and borate oxides are formed by two different structural units depending on the nature and content of alkali cations and/or the temperature and pressure conditions: planar BO₃ triangles or BO₄ tetrahedrons. The coordination of oxygen can be twofold bridging oxygens or onefold coordinated nonbridging oxygens. In glasses, the addition of alkalis induces the transformation from BO₃ to BO₄ and a higher connectivity between the boron units. Further increase of the alkali content induces the depolymerization of the glass or crystal network.²⁵²

The determination of the boron and oxygen coordination is thus a critical parameter to understand the properties of borate crystals and glasses in various temperature and pressure conditions. For these systems, the low penetration depth of soft-X-rays and surface sensitivity have been a serious limitation for their investigation, especially because of their particular hygroscopicity. IXS has been used as a good solution to circumvent these limitations. Lelong et al. have investigated of the oxygen K-edge XAS via IXS in a series of crystalline lithium borates²⁵³ and in comparison with glasses.²⁵²Figure 26 shows the oxygen K-edge of selected boron oxides. The spectra show two main features: the first 5 eV of the oxygen K-edge spectra is assigned to π* overlap between oxygen 2p and boron 2p, while the next 10 eV range is assigned to σ* O–B overlap. DFT calculations have further distinguished the contribution of bridging and nonbridging oxygens according to the energy position of the π*-peak, which shifts to lower energy in the case of nonbridging oxygens as observed when comparing amorphous B₂O₃ and Li₃BO₃. Comparison between crystals and glasses has allowed a further understanding of the structural variations in lithium borate glasses with the chemical composition. Lee et al. have studied v-B₂O₃ glass at high pressure using IXS up to 8.4 GPa. Figure 26 shows the decrease of the π*-peak related to boroxol rings, i.e., planar structure formed by three BO₃ units, upon increasing the pressure together with the increase of the boron coordination from three- to fourfold suggesting that the unpaired Op orbital gets involved in forming a σ* bond with another boron resulting in a threefold oxygen.²⁵⁴

Figure 26.

Oxygen K-edge spectra of amorphous B₂O₃ at 1 bar²⁵³ and 8.4 GPa, LiBO₂,²⁵³ Li₂B₄O₇,²⁵³ and Li₃BO₃,²⁵³ with the fraction of BO₃ units and nonbridging oxygens indicated. Nonbridging orbitals induce a shift of the π* feature to lower energy and the conversion from BO₃ to BO₄ induces the decrease of its intensity.

6.4.2. Carbonates

Carbonates are important compounds for the carbon cycle. Carbonate rocks result from the mineralization of the CO₂ from the atmosphere. Figure 27 shows the oxygen K-edge of BaCO₃, Li₂CO₃, CaCO₃, and Na₂CO₃. The oxygen K-edge XAS spectra of carbonate compounds are dominated by the oxygen antibonding states from the CO₃^–2 units, similarly to the BO₃ units for boron (see above). These planar triangular units favor the formation of in-plane σ covalent bonds involving sp² mixing. The first intense and sharp peak is assigned to the π* antibonding state from the C=O bonds resulting from out-of-plane π bonds involving only p states. The second part of the spectra corresponds to the σ* antibonding state.

Figure 27.

Oxygen K-edge spectra of carbonates: BaCO₃,²³⁶ Li₂CO₃,¹⁷⁶ CaCO₃,²⁵⁵ and Na₂CO₃,²⁵⁶ all showing the π* antibonding state from the C=O bonds of the CO₃^–2 units.

Calcium carbonate, CaCO₃, is an important biomineral occurring in shells and corals. CaCO₃ occurs in three different structures, calcite, aragonite, and vaterite; in addition, there are hydrated and amorphous structures. DeVol et al. studied the oxygen K-edge of these forms of CaCO₃, using the polarization dependence of single crystals.²⁵⁵ The experiments are simulated with FEFF calculations. Despite similar isotropic spectral shapes, the oxygen K-edge polarization dependence varies with the crystal structure of the polymorph. The polarization dependent contrast is used to study natural species (shells and tunic spicules) with X-ray spectral microscopy. De Clermont Gallerande et al. analyzed the monopole and dipole contributions to the oxygen K-edge spectra of Li₂CO₃ measured with IXS, separating the π and σ antibonding states. The oxygen K-edge of Na₂Si₂O₅ shows a sharp peak at 533 eV that is assigned to Na₂CO₃ adsorbed at the surface.²⁵⁷ Na₂CO₃ and NaHCO₃ have been measured by Espinal et al.²⁵⁶ They are used as references to study the interaction of CO₂ with amine groups. Recently, the oxygen K-edge of barium carbonates and nitrates have been studied, in comparison with the binary oxide. Karshoglu et al. measured the oxygen K-edge of BaO, Ba(OH)₂, BaCO₃, and Ba(NO₃)₂, prepared in situ as thin films.²⁵⁸

6.4.3. Aluminum Oxides

Aluminum is the third most abundant element of the earth crust²⁵⁹ after oxygen and silicon and is present as trivalent cations in various biological and mineralogical forms. The oxygen K-edge values of α-Al₂O₃ (corundum structure), MgO, and MgAl₂O₄ (spinel structure) are compared with their calculated projected DOS by Kostlmeier et al.²⁶⁰ Kaneko et al. study the difference between the oxygen K-edge of the center of a Al₂O₃ grain with the grain boundary.²⁶¹ The features correspond to the antibonding oxygen states hybridized with aluminum 3s, p, and sp states.²⁶² Henderson et al. studied the oxygen K-edge of a series of crystalline calcium aluminates²⁶³ followed by the study of a series of CaO–Al₂O₃–SiO₂ mixed glasses.²⁶² The oxygen K-edge spectra of the glasses reveal the contribution of both calcium and aluminum hybridized states and the coordination change of calcium as well as the degree of polymerization of AlO₄ tetrahedral units. The oxygen K-edges of Cu–Al–O thin films have been compared with copper oxide and Al₂O₃ references.²⁶⁴ The oxygen K-edge of crystalline α-Al₂O₃ has been compared for different shapes.²⁶⁵

6.4.4. Silicon Oxides

SiO₂ is the first most abundant oxide of the earth crust²⁵⁹ mainly as part of the mineral species like silica and silicates. Oxygen K-edge has been used to investigate the atomic structure of crystalline and amorphous silica and silicates. Marcelli et al. showed the sensitivity of the oxygen K-edge on the Si–O–Si bond angle in glasses,²⁶⁶ which stimulated intense efforts to the development of accurate modeling of the oxygen K-edge using multiple scattering approaches^247,266,267 and later followed by band structure calculations.^244,249 The experimental oxygen K-edge spectra of silica crystal polymorphs were investigated by Wu et al.²⁴⁷ The influence of the chemical composition of silicate glasses on the structure was investigated.^{245,268−270} The interpretation of the spectra is more complex when considering silicate glasses with also calcium, aluminum, and titanium. The oxygen K-edge spectra reveal the bonding with the different cations but is also influenced by the coordination geometry changes. Another important aspect of glass structure is the degree of polymerization of the glass network. The addition of alkali cations to amorphous SiO₂ induces the depolymerization of the SiO₄ network and formation of nonbridging oxygens (O bond to a single Si). It has been shown with the support of full multiple scattering calculations that the threshold of the oxygen K-edge is dominated by the presence of the nonbridging oxygens in silicates,²⁷¹ similarly to the case of borates.

The multiple scattering calculations,^247,248 and later DFT calculations,²⁴⁹ have allowed reproducing the experimental data. Multiple scattering calculations on clusters of different sizes have allowed the contribution of the multiple scattering to the features due to medium range order. The effect of the core–hole has been discussed in these studies. While it is shown to be very important for the silicon K-edge,²⁵¹ the contribution to the oxygen K-edge has been described as small by Wu et al.,²⁴⁸ but it was shown to be non-negligible by Taillefumier et al.²⁴⁹ These authors highlighted that some cautions should be used to compare the calculated oxygen K-edge and the oxygen 2p pDOS, in reference to the work of Mo et al.²⁴⁴ which presented strong disagreement between the oxygen K-edge spectrum and pDOS calculations. While Mo et al. assigned this mismatch to the energy dependence of the dipole matrix element, Taillefumier et al. have pointed out the influence of the region used for the angular momentum projection.²⁴⁹

6.4.5. Germanium Oxides

The oxygen K-edge of crystalline and amorphous germanates have been investigated to obtain structural information.

Based on the study of crystalline references, oxygen K-edge has been used to determine the coordination of germanium in amorphous systems. The similarity of the oxygen K-edge of amorphous and crystalline (quartz) GeO₂ confirmed the twofold coordination of oxygen and the fourfold coordination of germanium in both cases as well as similar angles between the GeO₄ tetrahedrons.

Fivefold germanium is observed in the alkali germanate glasses but only in compositions at the germanate anomaly maximum and beyond. It was confirmed that there is no formation of sixfold coordinated germanium within the glass before the germanate anomaly maximum.²⁴⁵ No study of oxygen K-edges in germanates has reported the contribution from nonbridging oxygens, even for high-alkali content glasses, although these are expected. Such an interpretation is indeed subject to great caution because of the surface sensitivity of XAS, but here, IXS could provide an alternative interesting probe. By comparison with the crystal references, Lelong et al. demonstrated with IXS measured oxygen K-edge the formation of the fivefold coordinated germanium at the intermediate high pressure (5 GPa) from amorphous germania and the formation of sixfold coordinated germanium at the highest pressure (18 GPa).²⁷² McLeod et al. used oxygen K-edge in light of calculations with Wien2k to study the oxygen vacancies in GeO_x nanoparticles as electrodes for lithium storage.²⁷³

6.4.6. Other p-Element Oxides

Zinc Oxides

ZnO is a common semiconductor oxide. The oxygen K-edge of the hexagonal wurtzite polymorph has been measured by McLeod et al.²³⁴Figure 28 shows the oxygen K-edge spectrum of ZnO. Because all 3d orbitals are full, the spectrum reveals only the oxygen 2p states hybridized with the 4sp states of the Zn. Guo et al.²⁷⁴ compare the bulk spectrum with a thin film and nanorods. ZnO doped with transition metal ions (Fe, Co) yields so-called dilute magnetic semiconductors. These systems have ferromagnetic order above room temperature and the combination of charge and spin degrees of freedom makes them useful for devices. Figure 28 shows that the doping with iron induces the presence of additional empty 3d states at the onset of the oxygen K-edge. Furthermore, the features observed for pure ZnO are broadened, probably due to the distortion of the crystal lattice. The oxygen K-edge of ZnO doped with iron and with cobalt mainly show the same spectral shape as pure ZnO with an additional peak due to the Fe–O and Co–O interaction.^275−277 The oxygen K-edges of the [Cd,Zn]O mixed oxides are discussed in the section on cadmium oxides.

Figure 28.

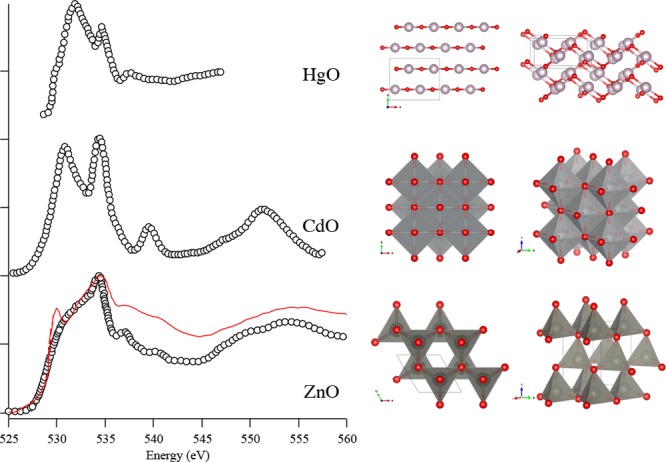
Oxygen K-edge spectra of ZnO (wurtzite) compared to Fe:ZnO (red),²⁷⁵ CdO (rock salt),²⁷⁸ and HgO (orthorhombic, montroydite).²³⁴ Similarities in the spectrum shape and assignment are highlighted despite the differences in the crystal structures.

Phosphates

Calcium phosphates are the main component of human bone. The materials include tricalcium phosphate Ca₃(PO₄)₂ and hydroxyapatite Ca₅(PO₄)₃OH. Rajendran et al. compare the calcium phosphate materials plus CaCO₃ and CaO with the oxygen K-edges from the bones of sheep, deer, chicken, etc.²⁷⁹ They use TEY and FY to differentiate between surface and bulk; they find that the surface of dried bone has a larger proportion of carbonate than the interior that is mainly made up of phosphates. The phosphate systems with transition metal ions, (LiFePO₄, LiNiPO₄, etc.) are discussed in the sections of the respective transition metal ions.

Gallium Oxides

The gallium oxide Ga₂O₃ exists in five polymorphs (α to ϵ). The β-Ga₂O₃ trigonal structure has recently got much attention in relation to possible optoelectronic as well as catalytic properties.²⁸⁰ The oxygen K-edge of β-Ga₂O₃ has been calculated with the FDMNES code by Hegde et al.²⁸⁰ Interestingly, they do not find any significant difference between a calculation with and without core–hole. The oxygen K-edge of β-Ga₂O₃ has also been published by Cocchi et al.²⁸¹ who find that their BSE calculation gives an accurate agreement with the experiment, in contrast to the calculation without core–hole.

Cadmium Oxides

CdO is a rock salt structured semiconductor. The oxygen K-edge spectrum is measured by Demchenko et al.²⁸² McLeod et al. compare the oxygen K-edge with Wien2K calculations.²³⁴ The bulk spectrum of CdO is compared with thin films that are measured both with electron yield and with fluorescence yield. Detert et al. measured the oxygen K-edges of the [Cd,Zn]O mixed oxides for different ratios of cadmium and zinc.²⁷⁸ The phase transition between wurtzite ZnO and rock salt CdO is visible in the oxygen K-edge between 62% and 75% CdO. Figure 28 compares the spectra of ZnO and CdO.

Indium Oxides

Indium oxide In₂O₃ (cubic polymorph) is compared to the other 5s⁰ oxides by McLeod et al. as reproduced in Figure 29. The oxygen K-edges of the cubic, rhombohedral, and orthorhombic In₂O₃ polymorphs have been measured by de Boer et al.²⁸³ All polymorphs give similar oxygen K-edge spectra with a first intense sharp peak assigned to the oxygen 2p states hybridized to the cation empty 5s states and then a variable second broad feature corresponding to the metal 5p states. They calculated the spectra with Wien2K with and without core–hole potential. The final state calculations accurately reproduce the observed spectral shapes.

Figure 29.

Oxygen K-edge spectra of (a) 5s⁰ oxides (In₂O₃, SnO₂, Sb₂O₅) and (b) 5s² oxides (SnO, Sb₂O₃, TeO₂). Data are reproduced from ref (234) for all but TeO₂.²⁸⁴ The cation contributions to the oxygen 2sp antibonding states are given according to the p-DOS calculations from McLeod et al.²⁴⁶

Tin Oxides

Cassiterite SnO₂ has a rutile structure and is the common ore for tin. The oxygen K-edge is shown in Figure 29. It is shifted to lower energies but shows a similar shape to that of GeO₂ and SiO₂. This allows transposing the feature assignment from the germanium and silicon well studied systems: the first intense peak corresponds to the oxygen 2p hybridized with the σ* of the Sn 5s states and the higher energy features correspond to the Sn p and pd bands. The monoxide α-SnO has a PbO structure. Upon heating, it converts to an intermediate tin oxide SnO_x, before converting to SnO₂. The EELS oxygen K-edges of the three different oxides SnO, SnO_x, and SnO₂ have been measured by Moreno et al.²⁸⁵ The oxygen K-edge of the intermediate SnO_x phase has a shape that can be constructed from a linear combination of SnO and SnO₂. Kurganskii measured the oxygen K-edge of SnO₂ and then calculated the spectrum with Wien2K.²⁸⁶ A Wien2K calculation was performed with a core–hole potential, but the agreement with experiment is not very good. We note that the oxygen K-edge of SnO₂ is different as measured with EELS and with XAS. The EELS spectrum has two leading sharp peaks and the XAS spectrum only one. A possible explanation is that the EELS spectrum contains SnO that has its first peak at exactly the same energy. Kronawitter et al. studied the interface between SnO₂ and TiO₂.²⁸⁷ Their SnO₂ spectra are measured with TEY XAS and agree with the spectra from Kurganskii.

Antimony Oxides

The oxygen K-edge of antimony oxides, shown in Figure 29, were studied as part of a broader investigation of chemical bonding and hybridization in 5p binary oxides by McLeod et al.²⁴⁶ The authors further compare 5s⁰ oxides (In₂O₃, SnO₂, Sb₂O₅) with 5s² oxides (SnO, Sb₂O₃, TeO₂). Comparison of DOS and spectra calculations performed with Wien2k with experimental spectra reveals that in general the hybridization between oxygen 2p states and cations states decreases with increasing cation atomic number. In the 5s² oxides, the first relatively broad feature of the oxygen K-edge is due to the antibonding oxygen 2p bands mixed with the cation 5p, while in the 5s⁰ oxides, the cation 5p band is shifted to high energy and the first sharp feature is due to the empty cation 5s band mixed with the oxygen 2p.

Tellurium Oxides

TeO₂ is an important building block for telluride glasses used for nonlinear optics such as in optical fiber amplification. The oxygen K-edge of TeO₂ measured by Jiang et al. with EELS²⁸⁴ is shown in Figure 29. The authors compare the spectrum with a number of different FEFF calculations. The core–hole calculation gives equivalent results to the Z+1 calculation. To improve the correlation with experiment, a Z+2 approximation is used, but the agreement obtained is still not very good. McLeod et al. have compared the Wien2k calculated oxygen 2p DOS with the experimental spectra. The projected DOS reveal that the first peak in the TeO₂ oxygen K-edge spectrum is dominated by oxygen 2p antibonding states hybridized with Te 5p, and the second peak is dominated by oxygen 2p states hybridized with tellurium 4d.

Mercury Oxides

Mercury is the third element of the group. Mercury oxide is a II–VI-type semiconductor. Divalent mercury ions have full 5d orbitals and 6s⁰ and 6p⁰ valence electronic configuration. The oxygen K-edge of mercury oxide HgO, whose structure consists of chains of Hg–O in the montroydite form (orthorhombic), has been compared with Wien2K calculations.²³⁴Figure 28 compares the spectral shape of HgO with CdO and ZnO. As the cation increases in mass, the core–hole has a decreasing effect on the local conduction band probed by XAS measurements. There is close agreement between the measured XAS and the calculated DOS for HgO.

Lead Oxides

Qamar studied four different types of PbO samples: α-PbO or litharge, the red tetragonal polymorph; β-PbO or massicot, the yellow orthorhombic polymorph; amorphous PbO; and polycrystalline PbO.²⁸⁸ They compare the experiments with Wien2K DFT calculations with and without the core–hole potential. Oxygen K-edges of lead oxides for lead acid batteries were published by Moseley et al.²⁸⁹ The oxygen K-edge of BaPbO₃ has been measured in comparison with calculations with and without core–hole.²⁹⁰ The whole series of Ba(Pb,Bi)O₃ perovskites has been measured as a function of the bismuth doping. A gradual change from BaPbO₃ to BaBiO₃ is observed experimentally (Figure 30). Mastelaro et al. used the oxygen K-edge to determine the hybridization between lead 6p and oxygen 2p orbitals in Pb_1–xLa_xTiO₃ compounds.²⁹¹ The lead 6p peak appears in between the two titanium 3d bands. A similar approach with the support of FEFF calculations was used in to study the ferroelectric Pb_1–xBa_xZr_0.65Ti_0.35O₃ compounds.²⁹²

Figure 30.

Oxygen K-edge spectra of BaBiO₃ and the BaPbO₃.²⁹⁰

Bismuth Oxides

Torruella et al. studied monoclinic α-Bi₂O₃ with EELS.²⁹³ They compared the spectral changes of a pellet with powder and nanowires, in particular, the effect of defects on the spectral shape. BaBiO₃ and the Ba(Pb,Bi)O₃ perovskite systems have been discussed in the section on lead. BiFeO₃ and BiVO₄ are discussed in the sections on the transition metal ions.

7. Solid Oxides of d- and f-Elements

Solid oxides from d- and f-elements are different from the s- and p-elements because of the presence of d- and/or f-electrons that have a stronger localization. One consequence of this localization is that normal DFT calculations, either band structure or multiple scattering, tend to lead to incomplete descriptions of the electronic structure.

In the discussion of the s and p oxides, we have used the identity of the DFT calculated empty states with the XAS spectral shape. Band theory²⁹⁴ fails to describe the detailed electronic and magnetic order of 3d transition metal oxides, because it neglects the strong local interactions between the 3d electrons. The conduction electrons are in bands with mainly 3d character from the transition metal ion and the relatively small overlap between the 3d orbitals of the metal and the p orbitals of the oxygen makes the energy bands narrow, with bandwidths of 1 to 2 eV.²⁹⁵ The repulsive interaction between 3d electrons leads to localization and the formation of nonconducting states.

The strongly correlated nature of the 3d electrons causes the 2p XAS spectra of the 3d metals to be dominated by local interactions, implying that the 2p XAS spectral shape has no direct correspondence to the empty states. The main reasons are the strong 2p3d electron–electron interactions (multiplet effects) and the 2p spin–orbit coupling. As discussed in the theory section, for the oxygen K-edge spectra these correlation effects are less important. There are no multiplet effects, no core–hole spin–orbit coupling, and the core–hole sits on oxygen, while the strongly correlated 3d states are localized on the metal sites. It turns out to be the case that (within the 0.3 eV resolution as given by the lifetime broadening) the empty states as calculated by LDA+U combined with core–hole methods are still relatively close to the experimental results. The interpretation is schematically indicated in Figure 31.

Figure 31.

Interpretation of the oxygen K-edge XAS spectrum of a 3d transition metal oxide. The oxygen 1s core state is given in green at 530 eV binding energy. The occupied oxygen 2s and 2p bands are given as a combination of oxygen (green) and metal (red). The empty states are given with striped colors: The ratio of t_2g and e_g states is 6:4, but the oxygen contribution (in green) is equivalent. At higher energy, the metal 4sp band is given. The experimental spectrum of TiO₂ is given as example.

7.1. General Considerations of 3d-Element Oxides

7.1.1. Effects of Crystal Field, Exchange, and Covalency

We first discuss the general analysis of the oxygen K-edges of 3d transition metal oxides. The crystal field splitting and the exchange splitting are analyzed, and we look at the influence of the covalency on the trend of the 3d series and also on the effect of the covalency on the spectral shape. Next, we discuss binary oxides and their trends in the spectra as a function of oxidation state.

Crystal Field Splitting

There is a close relation between the energy difference separating the two peaks of the 3d band and the ligand field splitting. In the case of 3d⁰ systems and high-spin 3d⁵ systems, there is no additional effect due to exchange, and the relation between the peak distance and 10Dq should hold exactly. In binary oxides, the crystal field splitting is approximately 0.6 eV times the formal valence, which would imply a crystal field of 1.2 eV in MnO and 2.4 eV in TiO₂, where the actual values can be different by ∼0.2 eV. Comparing the peak distance to the 10Dq value as determined from optical dd-excitations, one finds that the oxygen K-edge spectra yield a 10% shorter energy distance.²⁹⁶ The final state core–hole localizes the oxygen 2p states, thereby decreasing the overlap with the metal 3d states. We note that this reduction is less than for the metal 2p XAS spectra that have a final state 10Dq value that is reduced by ∼20% via a similar core–hole localization effect.²⁹⁷

Exchange Splitting

In systems with a finite spin, there is a splitting between the spin-up and spin-down sub-bands. For example, high-spin octahedral 3d³ systems have three spin-up t_2g electrons in their ground state. This creates an exchange splitting between the empty high-spin and low-spin states. The exchange splitting can be approximated as the number of unpaired spins times 0.6 eV. This implies that in the case of Cr₂O₃ both the exchange splitting and the crystal field are approximately 1.8 eV.

Covalency and the Trend of the 3d Series

Looking at the oxygen K-edge of binary 3d oxides where the metal ions have an octahedral surroundings, one finds a similar shape of the empty states due to interaction of the metal 4s and 4p and oxygen 2p states. The lowest energy states are the oxygen 2p states that are hybridized with the empty 3d states. Assuming an equal hybridization for all systems, the intensity of the 3d band yields the number of empty 3d states. Analysis shows that one finds approximately a linear relation between the intensity of the 3d band and the number of empty 3d states,¹⁶ where the 3d band intensity is normalized to the intensity of the 4sp band. Suntivich et al. found for a series of perovskites that the covalency is not constant but becomes larger through the 3D series.²⁹⁸ While filling the 3d band, the energy position of the 3d states with respect to the oxygen 2p states decreases, thereby increasing their overlap. In addition, the average metal–oxygen distance gets shorter, implying that both the O 2p–M 4sp and the O 2p–M 3d interactions will increase. The average metal–oxygen distance varies between different oxide systems; for example, M₂O₃ corundum has larger metal–oxygen distances than LaMO₃ perovskites. This variation can cause differences in the intensity of the 3d part of the spectrum even for the same element, valence, and spin-state.

Covalency and Spectral Shape

The covalency can be further analyzed by including the difference between the hybridization of the t_2g and the e_g states in octahedral symmetry. The e_g states point directly to the oxygen atoms and have σ overlap. The t_2g states point in between the oxygen atoms and have π overlap with the oxygen 2p states. Effectively, this yields a difference in the hopping terms of 2:1, which implies a difference in hybridization of 4:1 for each O 2p–M 3d overlap. Additional factors for the intensity ratio are the fact that the π bonding is possible with two O 2p orbitals and σ overlap with one O 2p orbital. In the case of 3d⁰ systems (TiO₂), there are six t_2g and four e_g states. The total (relative) intensity ratio for the t_2g/e_g band is 1/4 × 2/1 × 6/4 = 12/16. This implies that one expects a 3:4 integrated intensity ratio for the t_2g to e_g band, which is close to the observed ratio for TiO₂ and MnO. Figure 32 shows the effects of degeneracy and overlap on the t_2g and e_g peaks of a 3d⁰-system. In the case of 3d¹ systems, one can assume that the exchange splitting is smaller than the crystal field splitting, and with this assumption, the t_2g:e_g band ratio is 10:16.

Figure 32.

Intensity of the t_2g and e_g peaks of a 3d⁰-system due to degeneracy, number of overlaps, and overlap strengths.

The 3d³ system has an exchange splitting that is 1.5–2.0 eV, which implies that the spin-down t_2g band overlaps with the spin-up e_g band, which complicates the two-band t_2g:e_g analysis. Figure 33 shows the effects of exchange splitting, degeneracy, and overlap on the t_2g and e_g peaks of a 3d³-system.

Figure 33.

Intensity of the t_2g and e_g peaks of a 3d³-system due to the exchange splitting, degeneracy, the number of overlaps, and the overlap strengths.

7.1.2. Binary Oxides and Oxidation State Trends

We first discuss the trends of the oxygen K-edge through the 3d series on three series of binary oxides, respectively, the rock salt MO oxides, the corundum M₂O₃ oxides, and the rutile MO₂ oxides.

Figure 34 shows the divalent 3d transition metal oxides with a rock salt structure. Respectively given are 3d³ VO, 3d⁵ MnO, 3d⁶ FeO, 3d⁷ CoO, and 3d⁸ NiO, where these divalent 3d transition metal oxides are always high-spin. They all have a crystal field splitting of approximately 1.2 eV. The lowest energy peaks relates to the empty 3d states, and the peaks around 540 eV relate the metal 4s and 4p band. Rock salt has a typical sharp band structure peak around 545 eV. In the case of MnO, the empty 3d states are at relatively high energy at 534 eV and they overlap with the 4s and 4p structures. MnO has a 3d⁵ configuration, and in principle, one would expect two 3d peaks split by the crystal field. Because of the small crystal field splitting of 1.2 eV, compared with the band widths, the splitting is not visible in the spectral shape. FeO has a 3d⁶ configuration, and similarly to MnO, the crystal field splitting is too small to be visible. In the case of CoO, one could see the fine structure in the 3d peak, and the first small feature could be assigned to the empty t_2g state. NiO has a 3d⁸ configuration spin-down e_g band is empty, which yields a sharp 3d peak.

Figure 34.

Oxygen K-edge of the 3d monoxides VO,²⁹⁹ MnO,³⁰⁰ FeO,³⁰¹ CoO,³⁰² and NiO:³⁰² below 535 eV, the 3d band related peaks; and from 536 to 543 eV, the metal 4sp band.

Figure 35 shows the trivalent 3d transition metal oxides with a corundum structure. Respectively given are 3d¹ Ti₂O₃, 3d² V₂O₃, 3d³ Cr₂O₃, 3d⁴ Mn₂O₃, 3d⁵ Fe₂O₃, and 3d⁶ Co₂O₃. All trivalent 3d transition metal oxides have a crystal field splitting of 1.8 eV and are high-spin, except Co₂O₃ that is low-spin. The 3d¹ system Ti₂O₃ has two peaks in the 3d part split by the crystal field. Trivalent oxides have a crystal field splitting of 1.8 to 2.0 eV, clearly visible in the oxygen K-edges.At 540–545 eV, the structure related to the metal 4s and 4p bands is visible. The 3d² system V₂O₃ has a similar spectral shape. In the case of the 3d³ system Cr₂O₃, the exchange splitting between spin-up and spin-down states is similar in size to the crystal, yielding a first intense peak related to a combination of the spin-down t_2g and spin-up e_g band. The 3d⁴ system Mn₂O₃ is a Jahn–Teller system due to its half-filled spin-up e_g state. The combination of (i) the octahedral crystal field, (ii) the exchange splitting, and (iii) the Jahn–Teller distortion yields a broad 3d-related feature. The 3d⁵ system Fe₂O₃ has a half-filled 3d band and shows two peaks split by the crystal field splitting. The 3d⁶ system Co₂O₃ is low-spin and has a filled t_2g band, hence a single sharp peak related to the empty e_g band.

Figure 35.

Oxygen K-edge of the corundum oxides Ti₂O₃,¹⁶ V₂O₃,¹⁶ Cr₂O₃,¹⁶ Mn₂O₃,³⁰³ Fe₂O₃,¹⁶ and Co₂O₃:³⁰⁴ Below 535 eV, the 3d band related peaks; and from 536 to 545 eV, the metal 4sp band.

Figure 36 shows the tetravalent 3d transition metal oxides with a rutile structure. Respectively given are 3d⁰ TiO₂, 3d¹ VO₂, 3d² CrO₂, and 3d³ MnO₂, where these tetravalent 3d transition metal oxides have a crystal field splitting of 2.4 eV. TiO₂ shows two peaks split by the crystal field splitting, and the VO₂ spectrum is similar, but due to the presence of the vanadium L_2,3-edge at 720 eV, the oxygen K-edge of VO₂ sits on a background of the tail of this spectrum. The 3d² system CrO₂ is a well-known half-metal. The relatively large exchange splitting yields a first spin-up t_2g band, while the other sub-bands are all part of the second structure. The 3d³ system MnO₂ has a similar spectrum to Cr₂O₃, with the first peak a mixture of the spin-down t_2g and spin-up e_g band.

Figure 36.

Oxygen K-edge of the rutile oxides TiO₂,³⁰² VO₂,²⁹⁹ CrO₂,³⁰⁵ and MnO₂:³⁰⁰ Below 535 eV, the 3d band related peaks; and from 536 to 547 eV, the metal 4sp band.

The comparison of the three common valences 2+, 3+, and 4+ gives rise to the following observations:

Intensity of the 3d Part

The 3d part of the spectrum has more intensity for high-valence oxides. The reason is that the covalency increases when the valence is increased from 2+ to 3+ and 4+. Increased covalence implies more oxygen character in the metal 3d band and, as such, more intensity in the 3d part of the oxygen K-edge. Due to the increased covalency, the 4sp part of the spectrum will also gain intensity, but this effect is smaller than for the 3d part, because the 4s and 4p orbitals are already delocalized and gain less overlap than the 3d orbitals.

Excitation Energy

The excitation energy of the metal L_2,3-edges shifts to higher energy with increased valence. The simplest approximation is that it is due to the increased (effective) charge on the metal site, implying a larger energy needed to excite a core electron. In contrast, the energy position of the oxygen K-edge does not always shift in the same direction by changing the formal charge of the metal ion. Depending on the specific metal ion, the oxygen K-edge shifts to lower energy, to higher energy, or remains at the same energy.

Looking at the experimental data, there is no shift observed for the valence changes Ti³⁺/Ti⁴⁺, V³⁺/V⁴⁺/V⁵⁺, and Mn³⁺/Mn⁴⁺. In some cases, the increase in valence opens a sub-band that was occupied with the lower valence, with the result that the oxygen K-edge shifts to lower excitation energy. This happens for the octahedral 3d³, 3d⁵, and 3d⁸ systems, including Ni²⁺/Ni³⁺ and Fe³⁺/Fe⁴⁺. These two examples also contain a negative Δ ion (i.e., a system where the charge transfer energy (Δ) is smaller than zero, implying a significant amount of holes on the oxygen ions). A negative Δ is a second reason for a shift to lower energy, and the couple Cu²⁺/Cu³⁺ shows a shift to lower energy, although no new sub-band becomes available in the low-spin negative ΔCu³⁺ oxides. Finally, a change of spin-state from high-spin to low-spin can cause a positive shift as visible for Co²⁺/Co³⁺ (in cases where the Co³⁺ system is low-spin). In conclusion, we state that there is no uniform rule regarding the shift of the excitation energy with valence. A last point of warning is that the energy calibration of many oxygen K-edges is not uniform throughout the literature.

Crystal Field

As mentioned above, the crystal field in octahedral high-spin oxides follows the approximate rule that it is equal to 0.6 eV times the formal valence, implying a crystal field of 1.2 eV for 2+ oxides, 1.8 eV for 3+ oxides, and 2.4 eV for 4+ oxides. The exchange splitting for 3d oxides is approximately 0.6 eV per paired spin-couple. Taken together, these numbers imply that divalent oxides are always high-spin, tetravalent oxides are always low-spin, and trivalent oxides have both options, where Mn³⁺, Co³⁺, and Ni³⁺ are in many oxides close to a high-spin–low-spin transition point.

7.1.3. Perovskites

Perovskites have a general formula ABO₃ where A is a larger cation than B, and they are arranged in the ideally cubic structure illustrated in Figure 37a. Almost all metallic elements from the periodic table are stable in this structure. Depending on the chemical formulation, distortions from the ideal cubic structure might happen. Another related family of materials are the layered perovskites, which contain layers of perovskite-like arrangement of MO₆ metal cation units. One simple example is A₂BO₄, the structure of which is illustrated in Figure 37b. Depending on the chemical composition, substitution of various elements allows tuning of the electron or hole doping in the structure and the resulting properties. Perovskite and layered perovskite materials are intensively studied from their chemical³⁰⁶ (heterogeneous catalysis, surface chemistry) and physical properties (electric, magnetic, and optical properties). The layered structure results in enhanced electron mobility and can give rise to specific properties such as superconductivity.

Figure 37.

(a) Crystal structure of cubic perovskite with the ABO₃ formula. (b) Crystal structure of layered perovskite with the A₂BO₄ formula. A: green ; B: orange, O: red.

Oxygen K-edge spectra have been largely used to probe the M–O chemical bonding or the metal valence and spin state, although it often requires complementary measurements such as the metal L_2,3-edges. Suntivich et al. performed a systematic analysis of the chemical bonding of LaTMO₃ systems based on the oxygen K-edge,²⁹⁸ for the transition metals Cr, Mn, Fe, Co, and Ni. The oxygen K-edge spectra of the series extended with the other 3d metals from complementary references is shown in Figure 38. The perovskite spectra show a similar general shape with a first single or double peak corresponding to the oxygen 2p states hybridized with the metal 3d states. The shape of this features is correlated to the valency and spin state of the transition metal ion. At 535 eV, one finds the oxygen 2p states hybridized with the lanthanide 5d states followed by the oxygen 2p states hybridized with the metal 4sp states.

Figure 38.

Oxygen K-edge spectra of LaMO₃ perovskite systems for the transition metals Ti,³⁰⁷ V,³⁰⁸ Cr,²⁹⁸ Mn,²⁹⁸ Fe,²⁹⁸ Co,²⁹⁸ Ni,²⁹⁸ and Cu.³⁰⁹ (H.S.: high spin; L.S.: low spin).

Covalency in d⁰ Tetrahedral Oxyanions

The isoelectronic d⁰ metal cations from groups 6 and 7 (Cr, Mo, W, Mn, Tc, Re) form tetrahedral oxyanions MO₄^n–. The investigation of this series allows probing the metal–oxygen bond covalency trends. A first comparative study of the oxyanions MO₄ (M = Ti, V, Cr, Mn) was done by Brydson et al.³¹⁰ who proposed a rationalization of the observed trends in both metal L_2,3-edge and oxygen K-edge. Minasian et al. performed this comparative study, including the radioactive Tc compound, using oxygen K-edges with three different detection methods, respectively, transmission XAS in a STXM, TFY XAS, and IXS, and compared the experiments with TD-DFT calculations.³¹¹ In an earlier study, Bradley et al. had also compared the oxygen K-edge spectra obtained from different methods.³¹²Figure 39 shows the oxygen K-edge spectra of the series. The first two peaks in the spectra are, respectively, the transition to the empty e and t₂ states, split by approximately 2.0 eV in all six systems. The excitation energy of the first peak is the lowest in the 3d systems, followed by 4d and 5d. In addition, the Mn, Tc, and Re oxyanions have lower excitation energies than their Cr, Mo, and W analogs. There is a linear relation between the first peak in the oxygen K-edge and the first optical excitation energy, i.e., from the highest occupied state to the empty e states. Minasian et al. demonstrated that the e (π overlap) mixing increases from group 6 to 7 and down the periods, while the t₂ symmetry (π + σ overlap) mixing is rather constant. TD-DFT simulations of spectra are in good agreement with the experimental spectra.

Figure 39.

Oxygen K-edge spectra of the oxyanions MO₄^n– with M = Cr, Mo, W, Mn, Tc, and Re.³¹¹

7.2. Overview of the 3d Oxides

In the following sections, the 3d transition metal oxides are discussed by element.

7.2.1. Titanium Oxides

Most titanium oxides have a valency of 4+, implying an empty 3d band. They are insulators with a band gap between the oxygen 2p band and the titanium 3d band. The binary oxide TiO₂ occurs in three different crystal structures, respectively, rutile, anatase, and brookite. Its oxygen K-edge has been measured many times.^{16,232,296,313−318} Ti⁴⁺ forms perovskite structures with Ba²⁺, Ca²⁺, and Sr²⁺. SrTiO₃ is a commonly used support material for thin film oxides. Figure 40 shows the oxygen K-edge of the perovskites SrTiO₃ and LaTiO₃. The 3d peaks in the oxygen K-edge are essentially given by the valency of titanium, 4+ for SrTiO₃ and 3+ for LaTiO₃. Because the coordination in the perovskites is close to octahedral, the e_g band is relatively wide.

Figure 40.

Oxygen K-edge of LaTiO₃³¹⁹ and SrTiO₃³⁰⁷ perovskites. The titanium 3d, lanthanum 5d/strontium 4d, and titanium 4sp related peaks are indicated.

The published oxygen K-edges of SrTiO₃ show some variation in the intensity of the e_g-peak.^{296,317,320,321} The oxygen K-edges of CaTiO₃³¹⁶ and BaTiO₃³¹⁸ are equivalent to that of SrTiO₃. The best resolution oxygen K-edge of SrTiO₃ is given by Palina et al.³⁰⁷ Palina et al. compared pure SrTiO₃ with TiO₂-terminated SrTiO₃ and thin films/interfaces with LaAlO₃. They claim that for the conducting samples, a new peak is visible at 540.5 eV due to “molecular-like oxygen”, related to the concentration of electronic defects.

The trivalent titanium oxides Ti₂O₃^16,316 and LaTiO₃³²⁰ have a 3d¹ ground state. Haverkort et al. performed a detailed analysis of the ground state³²² based on the titanium L-edge. They found that the ground state is affected by the crystal field distortion and the 3d spin–orbit coupling. Such details cannot be found from the oxygen K-edge due to the lack of final state interactions. Fujimori et al. studied the effects of doping from the oxygen K-edge spectra of a series of (La,Sr)TiO₃ systems.³¹⁹ While electron doping creates a pre-peak for the late transition metal ions such as in the cuprates, this is not the case for the Ti³⁺/Ti⁴⁺ system. The first t_2g peak in the oxygen K-edge has approximately the same energy for LaTiO₃ and SrTiO₃, which is related to the large covalency of the titanium systems and the fact that the Hubbard U is smaller than the charge transfer energy.

7.2.2. Vanadium Oxides

The vanadium 2p XAS edge sits at 515 eV, which implies that the oxygen K-edge of vanadium oxides is found in the tail of the vanadium L_2,3-edge. This complicates the analysis, as the background of the vanadium L_2,3-edge must be subtracted. In the 1989 paper on transition metal oxides, the spectrum of V₂O₃ and VO₂ has been included.¹⁶ A systematic study of the oxygen K-edges of vanadium oxides has been published by Abbate et al.³²³ They compared the spectra of V₂O₃, VO₂, and V₂O₅ with the projected DOS calculated with the LSW method. Goering et al. measured V₂O₃, VO₂, V₂O₅, and also the mixed valent oxide V₆O₁₃. They measured a strong angular dependence in the oxygen K-edge of V₂O₅.³²⁴ Hebert et al. measured the VO, V₂O₃, VO₂, and V₂O₅ oxides with EELS and performed Wien97 calculations of the vanadium oxides.²⁹⁹ In the calculations, the core–hole was not included.

V₂O₃ has a 3d² ground state with a partly filled spin-up t_2g shell; it has two phase transitions at approximately 150 and 250 K. Below 150 kV₂O₃ is an antiferromagnetic insulator; between 150 and 250 K a (paramagnetic) metal and above 250 K an insulator again. Park et al. performed detailed vanadium L_2,3 XAS and linear dichroism for three different phases of V₂O₃ as a function of temperature.³²⁵ This revealed the details of the electronic ground states. The oxygen K-edges measured by Park can be found in a paper by Huang et al.³²⁶ The first peak related to the transition to the t_2g-up state is relatively low in intensity,^299,324,326 much lower than the 3d² system CrO₂ (see below). The increased valence of Cr⁴⁺ drastically increases the overlap of the t_2g states with the oxygen states.

VO₂ has a 3d¹ ground state with a partly filled spin-up t_2g shell; it has a metal–insulator transition, and the differences in the electronic structure below and above the phase transition have been studied with the oxygen K-edge.³²⁷ In the insulating phase, the t_2g band is split into two sub-bands. Abe et al. measured the VO₂ phase transition with EELS.³²⁸ Room temperature spectra of VO₂ have also been published by van Aken et al.,³¹⁶ and Liang et al. performed detailed calculations that are discussed in the theory section.³²¹

V₂O₅ has a 3d⁰ ground state and is a semiconductor with a band gap between the oxygen 2p band and the vanadium 3d band. γ-V₂O₅ has two different vanadium surroundings and five differently coordinated oxygen atoms. The spectrum is different from α-V₂O₅ but well reproduced from DFT calculations.³²⁹ Maganas et al. calculated the oxygen K-edge of V₂O₅ using a cluster-based calculation. The important feature in their calculation is that they also calculated the vanadium L-edge using a restricted open shell configuration interaction with singles (ROCIS) method.³³⁰

Lithium-doped vanadium oxides are potential battery materials. The oxygen K-edges of Li_1+xV₃O₈ oxides have been measured by Choi et al.³³¹ The spectra revealed that the insertion of lithium affects the V–O bonds and induces a change in bonding geometry. Willinger et al. measured the oxygen K-edge of the vanadium phosphate VOPO₄.³³² The V⁴⁺ ions sit in a distorted octahedral site. The 3d-part of the spectrum looks similar to V₂O₅, and at higher energy, the oxygen K-edge is dominated by phosphor–oxygen bonds. The oxygen K-edge of vanadium bronzes have been measured with XAS and with EELS.³³³ The Na_0.33V₂O₅ spectrum is calculated with Wien2K calculations without core–hole. The AlV₂O₄ spinel system is measured with EELS and compared with Wien2K calculations. In contrast to the binary oxides, no separate 3d-related features are observed.³³⁴ Bismuth vanadate, BiVO₄, is used as an anode in photoelectrochemical water splitting. The oxygen K-edge of BiVO₄ is different from that of V₂O₅.³³⁵ Mixed oxides with other transition metal ions include the (V,Cr)O₂ systems.³³⁶ For a full overview of all systems, we refer to the XASEELS database, where all oxygen K-edge spectra are collected.³³⁷

7.2.3. Chromium Oxides

Chromium exists in a large number of valences, from 3d⁴ 2+ to 3d⁰ 6+. In 1971, Fischer measured the oxygen K-edge spectra of Cr₂O₃, CrO₃, Na₂CrO₄, and K₂Cr₂O₇ using a laboratory X-ray source.²² We compare them below, system by system, with more recent data.

The divalent binary oxide CrO does not exist as bulk material. It has been made as a thin film, and its Cr L_2,3 XAS spectrum has been measured but not its oxygen K-edge spectrum.³³⁸ Cr₂O₃ has a 3d³ ground state forming an antiferromagnetic ground state. For every Cr³⁺ ion, the t_2g shell is half-filled. The crystal field splitting is equivalent to the exchange splitting yielding a two-peak 3d-part of the spectrum with the first peak being a combination of spin-up e_g and spin-down t_2g states. The oxygen K-edge of Cr₂O₃ has been published in a number of papers.^{16,22,302,313,316,339−341}Figure 41 reproduces four published Cr₂O₃ spectra. Qualitatively, the spectral shapes look equivalent, and some variation is caused by the different experimental resolutions. The second peak/shoulder of the 3d part of the spectrum shows intensity variations, and the energy calibration of the Cr₂O₃ spectrum is different in every publication, depending on the specific calibration method used.

Figure 41.

Oxygen K-edge of Cr₂O₃. (a) ref (339); (b) ref (302); (c) ref (340); (d) ref (341) There is variation visible in the spectral shape and especially in the energy calibration.

Docherty measured a series of spinel spectra, including MgCr₂O₄ and ZnCr₂O₄, that all contain Cr³⁺. The 3d part of the measured spectra looks essentially like Cr₂O₃.³⁴² At higher energies, the peaks resemble the delocalized electrons of the spinel crystal structure. Remarkably, LaCrO₃, containing Cr³⁺ and 3d³, looks completely different from Cr₂O₃.²⁹⁸ From local considerations, one would expect every distorted, octahedral Cr³⁺ to look similar to the two peaks observed for Cr₂O₃. We do not have an explanation for the LaCrO₃ spectrum. The 10% Sr-doped LaCrO₃ spectrum measured by Sarma et al.³⁴³ is different from Cr₂O₃, where we note that the two published LaCrO₃ oxygen K-edges are different from each other.

CrO₂ has a rutile structure where Cr⁴⁺ occupies a distorted octahedon and has a 3d² ground state with a partly filled spin-up t_2g shell, making it a half-metallic ferromagnet. The oxygen K-edge of CrO₂ has been measured by several groups.^{326,339,340,344} Goering et al.³⁴⁴ compared the XMCD spectrum with the spin-polarized DOS. A similar calculation was performed by Kanchana.³⁰⁵ Both calculations simulate the oxygen 1s XAS accurately, but fail to simulate the Cr L_2,3 XMCD, due to their large multiplet effects. Koide et al. calculated the angular-dependent XMCD, and they find that it is important to include spin–orbit coupling,³⁴⁵ i.e., the spin–orbit coupling on the nearest-neighbor Cr atoms is the main contributor to the oxygen K-edge MCD spectral shape. Huang et al.³²⁶ measured the linear dichroism of CrO₂ on TiO₂(100). They showed that the first peak is the almost purely t_2g spin-up state, confirming the half-metallic ferromagnetic state.

CrO₃ has a 3d⁰ ground state; it is a strong oxidizer, and it is known for its carcinogenic properties. The high valence of chromium shifts the oxygen K-edge to lower excitation energy by 3 eV with respect to Cr₂O₃.^22,341 The tetrahedral 3d⁰ ion Cr⁶⁺ complex is measured as PbCrO₄³¹⁰ and as Na₂CrO₄³¹¹ which both give similar spectral shapes. This is an important reference material for the study of Cr⁶⁺-based paintings.³⁴⁶ Oxyanions can undergo condensation reaction, as is the case for chromate ions forming dichromate ions. The binuclear [Cr₂O₇]^2– complex has been measured by Diaz et al.,³⁴⁰ and the spectrum is compared to the spectrum of the simple oxyanion in Figure 39. The shape is strongly altered with the broadening and shifting to lower energies of the two first peaks. This can be related to the strong distortion of the CrO₄ tetrahedra in the dichromate species and increase of three of the four Cr–O bond lengths should explain the decrease of the ligand field.

Applications of chromium include catalysts, paints, and steel compositions. CrO₂ and Cr₂O₃ supported on titania are used for the selective catalytic reduction of nitric oxide by ammonia. The shapes of the oxygen K-edge of CrO₂ and Cr₂O₃ films on TiO₂ were compared with bulk references, suggesting that new chromium oxide phases are not present in the bulk.³³⁹ Lopez et al. studied a series of stainless steels, comparing their chromium, iron, and nickel L_2,3-edges and oxygen K-edges. The spectra confirmed that in all cases the passive film was formed by Cr₂O₃.^347,348

Mixed oxides with other transition metal ions include the (V,Cr)O₂ systems,³³⁶ CuCr₂O₄ spinel,³⁴⁹ (Li,Ti)CrO₇,³⁴⁰ (Mg,Cr,Fe)₃O₄ spinel systems,³⁵⁰ and (Cu,Ni,Co)Cr₂O₄.³⁴² For a full overview of all systems, we refer to the XASEELS database.³³⁷

7.2.4. Manganese Oxides

Manganese exists in a large number of valences, from 3d⁵ 2+ to 3d⁰ 7+. MnO has a 3d⁵ ground state with the spin-up t_2g and e_g states occupied. The oxygen K-edge of MnO has been published in a number of papers.^{232,300,303,351−357} MnO is sensitive to the X-ray and electron beams of the XAS and EELS measurements, and MnO is also sometimes modified by defects; some MnO samples are deliberately doped with defects, for example, the MnO(1%Li) sample.³⁵² Gilbert et al.³⁰³ studied the sample damage effects, and the corrected XAS spectrum is equivalent to the EELS spectrum of Kurata et al.³⁵³ In the first approximation, the oxygen K-edge will show two peaks respectively related to the empty t_2g and empty e_g states. As discussed in the introduction of the 3d oxides, the intensity of the two peaks is expected to be 3:4. What is special in MnO is that the excitation energy is high because of the high ionicity of MnO, i.e., a large charge transfer energy Δ. In addition, MnO is a rock salt octahedral system that yields a sharp first peak at 539 eV due to the empty manganese 4sp states. The combination of the two effects means that the 3d part of the spectrum is not well separated from the 4sp part of the spectrum.

Mn₂O₃ has a 3d⁴ antiferromagnetic ground state. For every Mn³⁺ ion, the spin-up t_2g states are occupied. The e_g state is half-occupied, creating a Jahn–Teller ground state implying significant site distortions. The oxygen K-edge of Mn₂O₃ has been published in a number of papers^{303,351,353,355,356} The oxygen K-edge has three peaks that can be assigned respectively to e_g-up, t_2g-down, and e_g-down. Mn₃O₄ has two octahedral Mn³⁺ sites and one tetrahedral Mn²⁺ site. The oxygen K-edge can in the first approximation be described as the Mn₂O₃ spectrum where the second peak is related to the tetrahedral Mn²⁺ site. We note that there is some variation in the observed spectral shapes of Mn₃O₄.^{303,351,353,357}

MnO₂ has a rutile structure where Mn⁴⁺ occupies distorted octahedral sites and has a 3d³ antiferromagnetic ground state. For every Mn⁴⁺ ion, the spin-up t_2g states are occupied. The MnO₂ spectrum has two peaks related to the 3d part of the spectrum.^{16,300,303,351,355−358} The first peak is a combination of the spin-up e_g-states and the spin-down t_2g-states. The second peak is related to the spin-down e_g-states. The oxygen K-edge spectra of MnO, Mn₃O₄, Mn₂O₃, and MnO₂ have been calculated with FEFF7, yielding not very accurate simulations of the general shape.²³³ More accurate FEFF calculations were performed by Gilbert et al.³⁰³ They also remeasured the manganese oxides and carefully corrected for beam damage effects. The calculations essentially confirmed the exchange plus crystal field picture for the 3d-part of the spectrum and further explain the higher-energy spectral shape.

The tetrahedral Mn⁷⁺ permanganate MnO₄^– ion has a 3d⁰ ground state and has been measured as KMnO₄.^303,311 Kurata et al. have measured the 3d¹ equivalent BaMnO₄.³⁵³ However, the spectral shape is very close to that of MnO₂, and although the authors did not mention it, it is possible that the data correspond to a photoreduced compound. Minasian et al.³¹¹ measured the oxygen K-edge spectrum of KMnO₄ with three different detection methods, respectively, transmission XAS in a STXM, TFY XAS, and IXS and compared the calculations with TD-DFT calculations. They compared a series of MO₄^x– anions and performed a detailed analysis on the trends in their chemical bonding.

Suntivich et al. performed a detailed analysis of the chemical bonding of LaTMO₃ systems based on the oxygen K-edge,²⁹⁸ for the transition metals Cr, Mn, Fe, Co, and Ni. The LaMnO₃ contains the 3d⁴ Mn³⁺ cation. The oxygen K-edge spectrum has three distinct features, related mainly to, respectively, the manganese 3d states, the lanthanum 5d states, and the manganese 4sp states. The equivalent oxygen K-edge (Figure 42) of LaMnO₃ has also been measured by Abbate et al.³⁵⁹ and Lafuerza et al.,³⁶⁰ and the PrMnO₃ by Toulemonde et al.³⁶¹ The (La,Sr)MnO₃ perovskites show a transition from Mn³⁺ in LaMnO₃ to Mn⁴⁺ in SrMnO₃.³⁵⁹ Changing lanthanum for Sr replaces the lanthanum 5d states for the strontium 4d states, while the manganese 3d states change from Mn³⁺ 3d⁴ to Mn⁴⁺ 3d³, thereby increasing the intensity of the first structure in the oxygen K-edge. Lafuerza et al.³⁶⁰ studied the doping of the manganese sites in LaMnO₃ with gallium. The La(Mn,Ga)O₃ system shows in the first approximation a gradual decrease of the Mn³⁺ signal, where both features in the 3d band decrease and the manganese 4p band is replaced by a gallium band. The (Pr,Ca)MnO₃ system studied by Toulemonde et al.³⁶¹ shows a similar change as the (La,Sr)MnO₃ perovskites; the 3d part of the PrMnO₃ spectrum is similar to that of LaMnO₃, and CaMnO₃ is similar to SrMnO₃. Galdi et al. performed a detailed oxygen K-edge study of LaMnO₃/SrMnO₃ multilayers.³⁶² Their spectra for superlattices (SrMnO₃)_n/(LaMnO₃)_2n mainly showed the lanthanum 5d states and no strontium 4d states. Mixed oxides with other transition metal ions include the La(Mn,Co)O₃ perovskites³⁶³ and Ba₃Ti₂MnO₉.³⁶⁴

Figure 42.

Oxygen K-edge of LaMnO₃²⁹⁸ and SrMnO₃.³⁵⁹ The peaks are caused by the Mn 3d states, the La and Sr 5d/4d states, and the Mn 4sp states, as indicated.

Figure 43 compares the oxygen K-edge XAS spectra of MnO with a series of (Li,Mn)O_x oxides, respectively, 3d⁴ Li₂MnO₃, mixed-valent 3d³/3d⁴ LiMn₂O₄, and 3d³ LiMnO₂.³⁵² The Li₂MnO₃ spectrum is similar to that of MnO₂, and the spectra of the two 3d⁴ systems Mn₂O₃ and LiMnO₂ are also similar. The LiMn₂O₄ oxide was also measured by Risch et al.³⁵⁷ Mixed oxides with other transition metal ions include the Li(Mn,Ni)O₂ battery systems,³⁶⁵ La(Mn,Co)O₃ perovskites,³⁶³ and Ba₃Ti₂MnO₉³⁶⁴ For a full overview of all systems, we refer to the XASEELS database.³³⁷

Figure 43.

Oxygen K-edge of MnO, LiMnO₂, LiMn₂O₄, Li₂MnO₃. The 3d⁵ oxide MnO contains impurities from Mn³⁺ visible in the intensity before 529 eV. The 3d⁴ oxide LiMnO₂ has a broad 3d part due to a combination of the octahedral crystal field, exchange, and the Jahn–Teller distortion. The 3d³ oxide Li₂MnO₃ has a first peak related to a combination of spin-up e_g and spin-down t_2g states. LiMn₂O₄ is a mixed valence Mn³⁺/Mn⁴⁺ oxide, and in the first approximation its 3d part is a combination of the spectra of Mn³⁺ and Mn⁴⁺ sites.

7.2.5. Iron Oxides

Iron oxides are among the most abundant materials on earth, in particular, Fe₂O₃ and Fe₃O₄. Iron oxides have valences 3d⁶ 2+ and 3d⁵ 3+. Fe⁴⁺ and higher valences are uncommon for iron oxide materials. FeO has a 3d⁶ ground state; it is known to be intrinsically unstable with regard to its stoichiometry. The oxygen K-edge of FeO has been often measured since the first measurement by Grunes in 1982.^{57,232,301,313,316} All spectra show a first peak related to the iron 3d states, that depending on the experimental resolution, have some structure.

Fe₂O₃ has a 3d⁵ ground state and appears in several crystal structures, the most common being the corundum α-Fe₂O₃ structure.^{16,57,301,302,316,321,351,366} Fe₂O₃ is a half-filled antiferromagnet, and the first two peaks directly relate to, respectively, the spin-down t_2g and e_g states. The oxygen K-edge of γ-Fe₂O₃ looks similar, with some differences at higher energy due to the different crystal structure.⁵⁷

The (La,Sr)FeO₃ perovskites show a transition from Fe³⁺ in LaFeO₃ to Fe⁴⁺ in SrFeO₃.³⁵⁹ The oxygen K-edge of LaFeO₃ is compared to that of SrFeO₃ in Figure 44. We observed the t_2g and e_g peaks, followed by the lanthanum 5d states.^298,367 The change from Fe³⁺ to Fe⁴⁺ is osberved in the increase of the first feature intensity. The spectrum of Wu et al. looks similar, but the e_g peak has lower intensity.³⁶⁸ All formally Fe⁴⁺ spectra, SrFeO₃^359,369 and BaFeO₃,³⁶⁹ look different from each other. The polarization dependent oxygen K-edges of thin films BiFe₃ have been studied by Zhenget al.³⁷⁰ Mixed iron oxides with other transition metal ions include the (La,Sr)(Co,Fe)O₃,³⁷¹ Sr(Ti,Fe)O₃,³⁷² (Co,Fe,B)SiO₂,³⁶⁶ (Ba,Sr)(Co,Fe)O₃,³⁶⁹ and FeTiO₃.³¹⁶ For a full overview of all systems, we refer to the XASEELS database.³³⁷

Figure 44.

Oxygen K-edge of LaFeO₃²⁹⁸ and SrFeO₃³⁵⁹ perovskite. The peaks are, respectively, caused by the Fe 3d states, the La and Sr 5d/4d states, and the Fe 4sp states, as indicated.

7.2.6. Cobalt Oxides

CoO has a 3d⁷ ground state that is always high-spin in oxides. Octahedral Co²⁺ has a ⁴T_1g ground state that is split by the 3d spin–orbit coupling. The oxygen K-edge of CoO has two peaks split by the crystal field, respectively, related to the empty t_2g state and the empty e_g state.^{302,354,366,367,373−375} At higher energy is found the typical double structure of the rock salt crystal.

Co³⁺ has a 3d⁶ ground state; in oxides, the crystal field is similar in magnitude to the exchange splitting, implying that Co³⁺ occurs as (t_2g⁶) low-spin and as (t_2ge_g²) high-spin oxides. The oxygen K-edge of Co₂O₃ has a sharp single peak at the edge indicating a low-spin Co³⁺ ground state.³⁰⁴ Co₃O₄ is a spinel with tetrahedral Co²⁺ and octahedral Co³⁺ sites³⁷³ Because the Co³⁺ site is more covalent, it has more oxygen character, and the oxygen K-edge of Co₃O₄ is dominated by the low-spin Co³⁺ features. The peaks of the tetrahedral Co²⁺ site are superimposed.

The oxygen K-edge of lithium-doped CoO and its end member LiCoO₂ have been often studied in relation to charge doping in CoO and in particular related to battery research.^{373,374,376−378} LiCoO₂ is a low-spin system with a similar spectral shape to that of Co₂O₃, i.e., a sharp peak related to the empty e_g states, followed by the cobalt 4sp band. Doping CoO with lithium gives oxygen K-edges that can be approximated as a mixture of CoO and LiCoO₂.³⁷³

In the prevoskite LaCoO₃, the 3d⁶ Co³⁺ undergoes a spin transition from low-spin at low temperature to mainly high-spin above 500 K. The t_2g⁶ low-spin system EuCoO₃ has the 3d peak related to the empty e_g states at 529.5 eV with a tail to higher energy.³⁷⁹ The t_2ge_g² high-spin system Sr₂CoO₃Cl contains CoO₅ pyramids and has its first t_2g peak at 528.5 eV and a second smaller e_g peak at 530.5 eV.³⁷⁹ The phase transition in LaCoO₃ was studied by Abbate et al.³⁸⁰ The transition from the low-spin one-peak spectrum to a broader spectrum is observed, but there is little peak shift and the spectral change is not very clear. Similar LaCoO₃ spectra have been measured,^298,375 but as these data are obtained at room temperature, they are a mixture between low-spin and high-spin. Simbock and co-workers studied the coexistence of low-spin and high-spin ions in LaCoO₃ systems of a series of catalytically active systems. They correlate the oxygen K-edge derived electronic parameters with reaction rates.³⁸¹

The low-spin (t_2g⁵) Co⁴⁺ system SrCoO₃ shifts to lower energy with respect to low-spin Co³⁺ oxides, and a small shoulder is visible at low energy related to the empty t_2g state.³⁷⁵ The (La,Sr)(Li,Co)O₃ system studied by Hu et al. contains 40% Co⁴⁺, and the spectral shape is a combination of the low-spin Co³⁺ and Co⁴⁺ peaks.^367,375 Harvey et al. also measured the Co⁴⁺ oxides SrCoO₃ and BaCoO₃,³⁶⁹ but their observed spectral shapes look different, with significant Co³⁺ contribution, in addition to large carbonate peaks that make the spectrum complex to analyze above 532 eV. The (La,Sr)CoO₃ system was studied by Moodenbaugh et al. and by Hu et al.^367,382 They concluded that already at 10% strontium doping the Co³⁺ switches to high-spin, modifying the whole spectral shape. The (partial) change in spin state of Co³⁺ and Co⁴⁺ s,ites makes the comparison of the oxygen K-edge spectra of Co³⁺ and Co⁴⁺ systems very complex to analyze on their own, without other information such as the cobalt L_2,3-edge.

Mixed cobalt oxides with other transition metal ions include the (La,Sr)(Co,Fe)O₃,³⁷¹ (Ba,Sr)(Co,Fe)O₃,³⁶⁹ and (Co,Ni)₂O₃.³⁰⁴ For a full overview of all systems we refer to the XASEELS database.³³⁷

7.2.7. Nickel Oxides

NiO has a 3d⁸ ground state with two e_g holes. The oxygen K-edge of NiO is one of the most published oxygen K-edge spectra, whereas in this review, we limit the citations to the papers that focus on the spectral shape.^{16,232,302,313,316,354,375,383−388} A full overview of all published NiO spectra is given in the XASEELS database.³³⁷ The NiO spectrum has been measured over a long energy range by Zschech et al.,³⁸⁵ where they focused on the self-absorption effects in FY detection. We refer to the experimental section for further discussion of FY detection.

The 3d⁷ Ni³⁺ system Nd₂Li_0.5Ni_0.5O₄ is considered to be a low-spin system based on its Ni L_2,3-edge. The oxygen K-edge shows a shift of 2.6 eV with respect to NiO with a sharp peak at the edge related to the three empty e_g states.^375,387,389 Suntivich et al. measured LaNiO₃ and a series of rare-earth (RE) RENiO₃ oxides.²⁹⁸ The oxygen K-edge looks similar in all RENiO₃ oxides and shows an intense sharp peak at the edge similar also to the Nd₂Li_0.5Ni_0.5O₄ system and suggesting a low-spin state for all systems. This is in contrast to the Ni L_2,3-edge that shows a change from low-spin to high-spin, for example, in the case of EuNiO₃.³⁹⁰ The layered perovskite (Nd,Sr)₂NiO₄ shows a different oxygen K-edge compared with the Nd₂Li_0.5Ni_0.5O₄ system, likely due to a partial high-spin ground state.³⁷⁵ Similar oxygen K-edge spectra are measured for La₂NiO₄ containing 3d⁸ Ni²⁺.³⁹¹ Hu et al. measured the polarization dependent oxygen K-edge of the Ni²⁺ oxide Y₂BaNiO₅.³⁹² Upon doping, the yttrium sites with calcium and Ni³⁺ state are found.³⁹²

7.2.8. Copper Oxides

CuO has a 3d⁹ ground state with one e_g hole. CuO has a rather complex crystal structure with low symmetry. The oxygen K-edge of CuO has a sharp peak at the edge related to the empty e_g state.^{16,232,313,316,387,393,394} At higher energy, the spectrum appears quite different from all other rock salt divalent transition metal oxides, related to its monoclinic crystal structure. The CuO spectral shape has been calculated by Jiang et al.³⁹⁴

The oxygen K-edge of Cu₂O was measured by Stohr et al. in 1980.²³ They measured the spectrum over an energy range of 400 eV. Jiang et al. calculated the oxygen K-edge of Cu₂O in good agreement with experiments.^393,394 Hu et al. measured the oxygen K-edge RIXS of Cu₂O.³⁹⁵ The oxygen K-edge spectrum of the formally Cu³⁺ oxide LaLi_0.5Cu_0.5O₃ has been studied by Hu et al.^387,389

There are many papers on the cuprate systems, and full coverage falls outside the scope of this review. We focus on the main papers that show the experimental data. The oxygen K-edges measured with XAS and EELS up to 1994 have been reviewed by Fink et al.³⁹⁶ The study on the effect of Sr-doping in the layered perovskite La₂CuO₄ has been studied with oxygen K-edges using EELS³⁹⁷ and XAS.³⁹⁸ La₂CuO₄ has a Cu²⁺ related peak at 530.5 eV. Upon doping with Sr, part of the copper is changed to Cu³⁺ with a peak at 528.5 eV, where the 528.5 eV peak shifts slightly down upon increased doping and the 530.5 eV peak shifts slightly up. Recent contributions on the oxygen K-edge of cuprates include RIXS studies³⁹⁹ and the measurement of layer specific spectra using a STEM EELS study.⁴⁰⁰

7.3. General Considerations of the 4d and 5d Oxides

The crystal field splitting in 4d oxides is larger than for 3d oxides, typically around 3.5 eV for octahedral sites. This implies that 4d oxides always are in a low-spin ground state. Figure 45 shows a selection of oxygen K-edge spectra for 4d oxides. Most oxides are not magnetic, implying that the assignment of the peaks is essentially the same for all 4d oxides in octahedral symmetry: respectively (a) the 4d t_2g states, (b) the 4d e_g states, and (c) the empty sp bands of the metal ion. Mixed oxides have the empty states of the other cation superimposed.

Figure 45.

Oxygen K-edge spectra of Y₂O₃,⁴⁰¹ tetragonal,⁴⁰² and monoclinic⁴⁰³ (m-) ZrO₂ and cubic yttrium stabilized zirconia⁴⁰³ (c-YSZ), NbO₂ and Nb₂O₅,⁴⁰⁴ MoO₃⁴⁰⁵ and MoO₂,⁴⁰⁶ and RuO₂.⁴⁰⁷ Visible are, respectively, the t_2g states, the e_g states, and the empty sp bands of the metal ion.

7.4. Overview of the 4d and 5d Oxides

7.4.1. 4d Transition Metal Oxides

Yttrium Oxides

Yttria, Y₂O₃, is a wide-gap semiconductor with a band gap of 5.6 eV. It has a cubic crystal structure where Y cations are sixfold coordinated in distorted octahedrons. The oxygen K-edge of Y₂O₃ (Figure 45) shows two main features corresponding to the crystal field split 4d states with the t_2g peak at 533 eV and the e_g peak at 538 eV, implying a crystal field of 5.0 eV. We note that there is an energy spread of 3.0 eV in the energy calibration of the first peak in the publications.^{401,403,408−410} Similar variations in calibration occur in many other oxygen K-edge spectra.

Zirconium Oxides

The most common oxide of zirconium is ZrO₂, which is also known as zirconia. ZrO₂ occurs in three phases, cubic, tetragonal, and monoclinic, and one can use an impurity element to stabilize one of those phases. The oxygen K-edge of ZrO₂ (Figure 45) shows subtle differences between the different polymorphs. It mainly contains the 4d t_2g peak at 532.4 eV and the 4d e_g peak at 535.5 eV, implying a crystal field of 3.1 eV.^{402,403,411−416} Several investigations of the oxygen K-edges in ZrO₂ and yttrium stabilized zirconia (YSZ) samples with varying compositions have been reported demonstrating that the spectra are very sensitive to local crystalline structure and dopant content. For example, ytrria stabilized zirconia ZrO₂[Y] is an important ceramic material^403,417 used in dental crowns and nonmetal knife blades. Recently, a number of other dopants were studied in relation to the photocatalytic properties of ZrO₂, including ZrO₂[Ce]^414,416 and ZrO₂[Cu].⁴¹⁵

Niobium Oxides

Niobium has three oxides, respectively, divalent 4d³ in the cubic NbO, tetravalent 4d¹ in the tetragonal NbO₂, and pentavalent 4d⁰ Nb₂O₅. Nb₂O₅ and also Nb₃O₇(OH) nanostructures are promising materials in the field of photoelectrodes in dye-sensitized solar cells and photoelectrochemical cells.⁴¹⁸ Olszta et al. compared the oxygen K-edges of the three oxides.⁴⁰⁴Figure 45 shows the spectra of NbO₂ and Nb₂O₅. The crystal field splitting of the first two peaks corresponding to the 4d states is further reduced compared to Y and Zr oxides. The first peak of the oxygen K-edges shifts from 533.5 eV (Nb₂O₅) to 534.3 eV (NbO₂) and 535.1 eV (NbO), as determined by our measurements on the published spectra. The shifts are inverted at the Nb M₃ edge, i.e., respectively, 365.9 eV (Nb₂O₅) to 364.6 eV (NbO₂) and 362.8 eV (NbO). Note that the relative shifts are larger for the Nb M₃ edge than for the oxygen K-edge, related to the larger core–hole effect for the Nb 3p core–holes. Soriano et al. compared the Nb₂O₅ spectrum to the other 3d⁰, 4d⁰, and 5d⁰ oxides.⁴⁰² The 5d⁰ oxide KNbO₃ has its first peak at 531.1 eV,⁴¹⁹ at lower energy than Nb₂O₅ (531.6 eV,⁴⁰² respectively, 533.3 eV⁴⁰⁴). The crystal field is also 0.5 eV larger for KNbO₃.

Molybdenum Oxides

Molybdenum has two binary oxides, 4d⁰ MoO₃ and 4d² MoO₂. MoO₂ has a distorted rutile structure. The oxygen K-edge of MoO₂, shown in Figure 45, has peaks related to the empty 4d states, but there is significant variation in the published spectra.^{406,420−422} Thakur et al. compared TEY and TFY spectra with high resolution,⁴²¹ and they observed three peaks within the 4d band that they assigned to a distortion of the octahedral site. The three features were also observed by Khyzhun et al.⁴²⁰ Wang et al. studied the reduction of MoO₃ to MoO₂ in the electron beam during an EELS experiment.⁴⁰⁶ Possibly all MoO₂ spectra contain some admixture of MoO₃, but as the peaks essentially overlap, it is difficult to determine such mixing quantitatively.

The 4d⁰ system MoO₃ is used as an oxidation catalyst. Its oxygen K-edge spectrum is compared to MoO₂ in Figure 45. Schlogl et al. measured the oxygen K-edge of a single crystal MoO₃, which they compared with a partly reduced sample MoO_2.8.⁴²³ The other published MoO₃ spectra are all similar to this reduced spectrum.^{405,406,422,424} Wu et al. measured their MoO₃ sample both with electron yield and with ion yield. In ion yield, one detects the O⁺ ions that escape from the sample upon X-ray irradiation. Ion yield is an extremely surface sensitive technique and measures only oxygen atoms in the surface layer of the system.⁴⁰⁵ Several papers discuss oxygen K-edge spectra of mixed oxides, for example, the (Mo,Fe) mixed oxides in relation to magnetism⁴²¹ and the (Mo,V) mixed oxides in relation to catalysis.⁴²³

Technetium Oxides

Minasian et al. studied a series of d⁰ tetrahedral oxyanions of 3d, 4d, and 5d metal ions, including the pertechnetate TcO₄^– anion.³¹¹ They simulated all oxygen K-edge spectra with TD-DFT and obtained good agreement with the experimental spectra. The first two peaks in the spectra are, respectively, the transition to the empty e and t₂ states, split by approximately 2.0 eV in all six systems. The excitation energy of the first peak is lowest in the 3d systems, followed by 4d and 5d. In addition, the Mn, Tc, and Re oxyanions have lower excitation energies than their Cr, Mo, and W analogs. There is a linear relation between the first peak energy position in the oxygen K-edge and the first optical excitation energy, i.e., from the highest MO to the empty e states.³¹¹

Ruthenium Oxides

The 4d⁴ system RuO₂ has a rutile structure. Its oxygen K-edge, Figure 45, has a sharp peak related to the t_2g states followed by a broader peak related to the e_g states.^407,425,426 The oxygen K-edge of RuO₂ bears much resemblance to the other rutile oxides such as TiO₂ and IrO₂ (see 5d element section). Tsai et al. studied RuO₂ nanorods for field emission applications.⁴⁰⁷

Ruthenates are systems that contain the RuO₆ octahedrons combined with other cations, mainly Sr and Ca. The most studied material is Sr₂RuO₄ and is a layered perovskite with a structure similar to that of (La,Sr)₂CuO₄, which also shares the superconducting properties with the copper analogs, though with critical temperature of less than 1 K. In 1996, Schmidt et al. measured the angular dependence of Sr₂RuO₄ single crystals.⁴²⁷Figure 46 shows the angular dependence of the oxygen K-edge spectrum of Sr₂RuO₄. The first two peaks at 528.5 and 529.5 are assigned to empty 4d t_2g states, where the first peak is related to the apical oxygen and the second to the in-plane oxygen. The following two peaks at 531 and 533.5 eV are related to 4d e_g states and have higher intensity in the out-of-plane direction.

Figure 46.

Oxygen K-edge of Sr₂RuO₄ layered perovskite⁴²⁷ with the incident electrical field parallel to the layer (ε_ab) and perpendicular to the layer (ε_c). The contributions from the apical and in-plane oxygens are highlighted.

This assignment is essentially reproduced in later experiments on Sr₂RuO₄ and Ca₂RuO₄.^{425,428−431} Fatuzzi et al. performed an elegant experiment to distinguish the three 2p orbitals x, y, and z, from a combination of angular and polarization dependence. They performed a RIXS experiment on Sr₂RuO₄ and Ca₂RuO₄ and analyzed the low-energy excitations as a combination of the crystal field splitting of the t_2g states and the effect of the 4d spin–orbit coupling.⁴³⁰ One can make more complex layered oxides from combinations of Sr and Ru. By keeping the valence of Ru at 4+, the series includes several combinations of SrO with RuO₂, i.e., (SrO)_x(RuO₂)_y, including SrRuO₃, Sr₂RuO₄, Sr3Ru₂O₇, and Sr₄Ru₃O₁₀, where a range of magnetic and superconducting properties are found in these systems. The oxygen K-edges of the Sr₂RuO₄, Sr₃Ru₂O₇, and Sr₄Ru₃O₁₀ ruthenates have been measured by Malvestuto et al.⁴²⁹ In addition, one can change the valence of Ru and make the Ru⁵⁺ system Sr₄Ru₂O₉ for which Hu et al. measured the oxygen K-edge.⁴²⁵ Chikamatsu et al. compared the Sr₂RuO₄ system with the oxyfluoride system Sr₂RuO₃F₂. The oxygen K-edge spectra, in relation to other core and valence band spectroscopies, indicate that the Ru⁴⁺ in Sr₂RuO₃F₂ is in a high-spin ground state, in contrast to the low-spin Sr₂RuO₄ systems.⁴³¹

Palladium Oxides

Palladium is an important catalyst, for which the reactivity is enhanced by fabricating nanosized metallic particles. The oxidation of the surface of the nanoparticles motivates their study with microscopy and spectroscopy. Sun et al. studied a Pd/Al₂O₃ system.⁴³² They measured the oxygen K-edge of the Pd nanoparticles with EELS and observed an oxygen K-edge that is different from the reference PdO. To interpret the experimental data obtained on nanoparticles, the oxygen K-edge of PdO was calculated for three crystal structures by Mogi et al.⁴³³ They used Wien2K calculations and reproduced the main features of the experimental spectrum.

Silver Oxides

Metallic silver is importantly used for its surface reactivity, and several studies investigated the absorbed oxygen reactivity on the metal surface, in particular, for ethylene epoxidation.^434−436 The oxygen K-edge of Ag₂O shows a first intense peak corresponding the O 2p states hybridized with the Ag 4d states followed by the O 2p/Ag 5sp bands. Comparison with absorbed oxygen atoms reveal that the nucleophilic species bind differently from the electrophilic species at the silver surface. Ruzankin et al. studied the ethylene epoxidation on the silver surface. They observed several features in the oxygen K-edge that were simulated with an Ag₂O molecule.⁴³⁶ Another oxygen K-edge spectrum has been published for silver foil that was treated with C₂H₄ and O₂ at 470 K.⁴³⁴

7.4.2. 5d Transition Metal Oxides

Hafnium Oxides

Hafnium oxide HfO₂ is an important material in the semiconductor industry due to its high dielectric constant k. These so-called high k materials are used to replace a silicon dioxide layer of a device, which is important for further miniaturization of microelectronic components. Soriano et al. compared HfO₂ with its 3d and 4d analogs TiO₂ and ZrO₂.⁴⁰² Unlike TiO₂, HfO₂ presents the same crystal structures and polymorphs as zirconia. The oxygen K-edge spectrum of HfO₂ is shown in Figure 47 along with its analogs from group IVb. The two first features correspond to the metal 5d bands, and the higher energy features correspond to the 6sp states. The crystal field splitting and the total dispersion of the metal d band increase from Ti to Zr to Hf revealing larger interactions caused by larger nd orbitals. The absorption threshold shifts to higher energies in the series in agreement with the larger band gaps for the oxides of the heavier elements. Since 2003, there have been a series of publications that studied the interface of HfO₂ with Si.^437−441 In addition to HfO₂, the oxygen K-edge has been measured to be of amorphous HfSiO⁴⁴¹ and HfSiON.⁴⁴²

Figure 47.

Oxygen K-edge of HfO₂ compared to its 3d and 4d analogs TiO₂ (rutile) and ZrO₂⁴⁰² and to IrO2⁴⁰⁷ (rutile).

Tantalum Oxides

The tantalum oxides Ta₂O₅ are important materials for memory resistors in memory devices. Kumar et al. studied the oxygen K-edge spectrum of Ta₂O₅ in such devices with a 30 nm resolved STXM experiment.⁴⁴³ The oxygen K-edge of the tantalum oxide Ta₂O₅ has two peaks at the edge, related to, respectively, the Ta 5d t_2g and e_g states.^402,443,444

Tungsten Oxides

Tungsten oxide WO₃ is a 5d⁰ W⁶⁺ system that occurs in a number of crystal structures. Purans et al. studied six different tungsten oxides. Figure 48 shows the spectrum of monoclinic WO₃. All spectra have a sharp first peak related to the empty t_2g states. The second structure related to the empty e_g states overlaps with the structure related to the tungsten s and p empty states.^419,424,445 Oxygen K-edge spectra have been published for films and nanorods,^446−450 and γ-WO₃ is doped with Na to form sodium–tungsten bronze, where the sodium atoms occupy a fraction of the 12-coordinate interstitial A-sites in the WO₆ octahedra framework. The oxygen K-edge of Na_xWO₃ shows a similar first peak as WO₃ related to the t_2g states. The region between 535 and 545 eV shows a different spectral shape, which is related to the differences in crystal structure despite the same octahedral environment for W ions.^424,445,449 The Na₂WO₄ system has a quite different structure from the bronzes. This system contains tetrahedral complexes of the tungsten oxyanion WO₄^2–. Its oxygen K-edge has two sharp peaks related to, respectively, the t₂ and the e empty states.³¹¹

Figure 48.

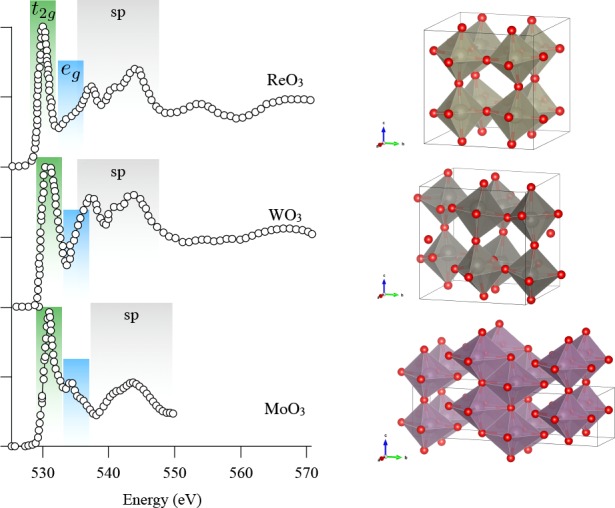
Oxygen K-edge spectra of monoclinic WO₃ and cubic ReO₃ compared to MoO₃ (orthorhombic) with the assignment of the spectral features.⁴²⁴

Rhenium Oxides

Rhenium oxide ReO₃ has a similar structure to that of perovskites and contains Re⁶⁺ 5d¹ ions. Purans et al. measured its oxygen K-edge spectrum^419,445 and investigated the effect of the distortion of the ReO₆ octahedron on the spectrum. The spectrum is shown in Figure 48 together with monoclinic WO₃. The ReO₃ spectrum bears much resemblance to the WO₃ and MoO₃ oxygen K-edge. The Re⁷⁺ system NaReO₄ contains Re in tetrahedral surroundings, and its oxygen K-edge is similar to that of the other tetrahedral oxyanion complexes.³¹¹ The oxygen K-edge of the series of oxyanion is discussed and compared in section 7.2 on 3d metal oxides.

Iridium Oxides

The iridium oxide IrO₂ contains Ir⁴⁺ 5d⁵ ions and has a rutile structure. The oxygen K-edge spectrum is shown in Figure 47 where it is compared to TiO₂ rutile and HfO₂. The shape is very similar to the spectrum of TiO₂ revealing the effect of the rutile crystal structure. It contains a small first peak related to the single hole in the t_2g state followed by a large peak related to the e_g states.^{198,407,424,451} Kim et al. measured an epitaxial IrO₂ film on TiO₂. They observe that the sharp t_2g peak has a very strong angular dependence with almost all intensity being related to the σ direction. This observation implies that this empty t_2g state lacks involvement of an Ir d_xy orbital, which in turn implies that despite the importance of the 5d spin–orbit coupling in IrO₂, the J_eff = 1/2 state (as observed in the iridates, see below) does not form in IrO₂. The IrO₂ oxide-based systems are often studied in relation to the oxygen evolution reaction. Pfeifer et al. showed the difference between the crystalline rutile IrO₂ and amorphous IrO₂. In amorphous IrO₂, the sharp t_2g peak at 529 eV is broadened into a double structure with a new feature at 528 eV.¹⁹⁸ These two features are in two later papers assigned to, respectively, O^2– and O^– character.^452,453

Within the context on transition metal ions, a more usual assignment would be to assign the new peak at lower energy to a higher valence of the iridium, similar to the assignments in the doped cuprates, and others. When Ir in IrO₂ is partly oxidized to Ir⁵⁺, the peaks in the oxygen K-edge will shift to lower energy. The ground state of high valent ions will have strong covalence, and part of the hole character will be on oxygen, especially for so-called negative charge transfer ions such as Cu³⁺ and Fe⁴⁺, but to relate this to O^– is in our view not the best model. In conclusion, we follow a different assignment for the operando oxygen K-edge spectra of IrO₂ systems and assign the first peak to the creation of Ir⁵⁺ ions.

The iridates are an important group of strongly correlated iridium oxides with electron correlation properties that are governed by the combination of a large 5d spin–orbit coupling and the on-site electron correlation U. The oxygen K-edges of the SrIrO₃, Sr₂IrO₄, and Sr₃Ir₂O₇ have been measured on single crystal systems.^454,455Figure 49 compares the angular dependence of the t_2g peak in SrIrO₃ versus Sr₂IrO₄ and indicates the difference between the 3D system and the layered system: similarly to the ruthenium layered perovskites, the oxygens are all equivalent in the 3D perovskite; the out-of plane oxygens pointing at the layer can be distinguished from the in-plane oxygens.

Figure 49.

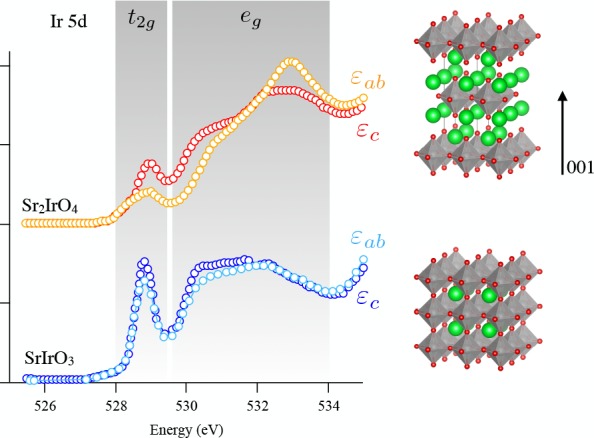
Oxygen K-edge spectra of Sr₂IrO₄ layered perovskite compared the SrIrO₃ perovskite with the incident electrical field parallel to the layer ε_ab and perpendicular to the layer ε_c.⁴⁵⁴

Platinum Oxides

As another noble metal, platinum is largely used as a metal for its surface reactivity. Oxygen K-edge spectroscopy has been used to investigate oxygen interaction with platinum metal surface or interface or the oxides formed. Platinum occurs in different oxide forms: tetragonal and cubic PtO, Pt₃O₄, α-PtO₂, and β-PtO₂. α-PtO₂ has been measured by Srot et al.⁴¹⁷ in the context of Pt/yttrium-stabilized zirconia for oxygen electrode reaction. They compare the spectrum with a number of calculations for the other oxides. Guinel et al. studied Pt nanoparticles on carbon nanotubes and they concluded that platinum occurs as Pt₃O₄ oxide nanoparticles.⁴⁵⁶

7.5. General Considerations of the 4f Oxides

The systems with an open 4f shell are known under the names rare earths and lanthanides. Lanthanide atoms have 3 electrons in the 5d, 6s, and 6p mixed states and their configuration can be written as 4f^N(5d6s6p)³. The 4f orbitals of the lanthanides are localized, while the 5d, 6s, and 6p orbitals form bonds with oxygen. This results in their main trivalent oxidation state, where the delocalized electrons fill the oxygen 2p valence band. The localized 4f-states are positioned in between the occupied oxygen 2p valence and the empty mixed 5d, 6s, and 6p bands.

Altman et al. studied the oxygen K-edge of the complete series of lanthanide sesquioxides Ln₂O₃ (Ln = La to Lu) with STXM and attempted to rationalize the observed spectroscopic variations in relation with the electronic structure of the Ln³⁺ ions. Two different structures were studied: the hexagonal phases where the Ln³⁺ ion is sevenfold coordinated and the cubic phase where the Ln³⁺ ion is sixfold coordinated.⁸⁷ The oxygen K-edges of six compounds of this series are shown in Figure 50. Starting from the assignment of the transitions observed for Lu³⁺ in which the 4f is full, the authors assigned the transitions between 532 and 540 eV to oxygen 2p mixed with lanthanide 5d and 6p states. The 5d states are split by the crystal field and the authors distinguished the 5dπ contribution around 532 eV and the 5dσ contribution around 538 eV. The authors analyzed the variation of the intensity and position of the 5d and 6p states to deduce the contribution of 4f states in the assignment of the oxygen K-edge XAS peaks in the other lanthanide compounds using a configuration interaction approach. They discussed the observed abrupt changes in the spectra in terms of orbital hybridization between oxygen 2p and lanthanide 5d in relation to the chemical reactivity of these oxides.

Figure 50.

(a) Oxygen K-edge spectra of the Ln₂O₃ oxides digitized from ref (87); (b) the corresponding qualitative energy band diagrams.

A following study of the Ce, Pr, and Tb dioxides (cubic fluorite structure, eightfold coordinated Ln⁴⁺ ions) by Minasian et al.⁴⁵⁷ revealed drastic changes in the oxygen K-edge spectra (Figure 51) as compared to the trivalent oxides with the contribution of an intense peak around 530 eV. This feature is assigned to transitions to the oxygen 2p states mixed with the 4f states in light of DOS calculated with VASP. It is followed by the crystal field split 5d states. Minasian et al. showed that the orbital mixing between lanthanide 4f and oxygen 2p increases in the order TbO₂ to CeO₂ to PrO₂.

Figure 51.

(a) Oxygen K-edge spectra of the cubic CeO₂, PrO₂, and TbO₂ with the corresponding band assignment in (b) cubic fluorite structure (oxygen atoms in red and lanthanide atoms in yellow) and (c) the corresponding schematic DOS adapted from ref (457).

Below, the oxygen K-edge studies of lanthanum and cerium oxides are specifically reviewed.

7.5.1. Lanthanum Oxides

La₂O₃ forms cubic and hexagonal crystal structures, where the hexagonal La₂O₃ is often studied with respect to its high-k dielectric constant. Calmels et al.⁴⁵⁸ measured the oxygen K-edge of cubic and hexagonal La₂O₃. They compared the experiments with both FEFF and Wien2K calculations and reached good agreement. Figure 52 shows the oxygen K-edge spectra of both polymorphs. Cubic La₂O₃ (sixfold coordinated La) shows two distinct peaks at 532.4 and 536.8 eV, that relate to the oxygen character of the La e_g and t_2g symmetry 5d states, but also containing 6s and 6p character. At higher energies, no clear peaks are visible. Hexagonal La₂O₃ shows a similar spectrum characterized by two features although broader and less distinct than in the cubic case. In both cases, the contribution of the hybridized 4f states was not ruled out by the authors.^87,458 4f oxides are hygroscopic and tend to form hydroxides in air. The oxygen K-edge of La(OH)₃ was measured and calculated by Calmels et al.⁴⁵⁸

Figure 52.

Oxygen K-edge spectrum of cubic La₂O₃⁴⁵⁸ and hexagonal La₂O₃.⁸⁷

Lanthanum is present in a series of perovskites, including LaMnO₃ and LaCoO₃, and the layered perovskites including La₂CuO₄. These 3d transition metal oxide systems have been discussed in the 3d section, as the leading peaks at the edge are the partly empty 3d states of the transition metal ion. The lanthanum 5d band is always visible at in the 530–540 eV energy range. Jeong et al.⁴⁵⁹ studied the decomposition of La₂CuO₄ into La₂O₃ and other oxides with TEM. By comparison to the reference spectra, their spectra showed that the decomposition product was hexagonal La₂O₃.

7.5.2. Cerium Oxides

Ce₂O₃ is the cerium analog of La₂O₃ and it has a 4f¹ configuration. The oxygen K-edge of Ce₂O₃ is shown in Figure 50 and is similar to that of La₂O₃. It is dominated by the 5d, 6s, and 6p states.^87,460,461 Xu et al. studied mixtures of Ce₂O₃ and CeO₂ and the occurrence of a small peak before the Ce₂O₃ peaks was assigned to CeO₂ impurities.⁴⁶⁰

In CeO₂, Ce⁴⁺ has 4f⁰5d⁰ electronic configuration. The oxygen K-edge of cubic CeO₂ has been often measured both with XAS and with EELS.^460−466 The spectrum is shown in Figure 51. The presence of a strong 4f-related peak highlights the non-negligible hybridization between oxygen 2p and Ce 4f orbitals. The crystal field in cerium dioxide splits the 5d states, but the splitting of the 4f states is not observed in agreement with the small overlap between the f orbitals and the ligands in lanthanides. The crystal field splitting of the 5d states is 4.3 eV for CeO₂. Mullins et al. reported spectra for cerium oxides thin films used as an important component in automotive exhaust catalysts.⁴⁶⁷ Wang et al. studied the mixture of cerium and terbium oxides.⁴⁶⁵ Garvie and Buseck showed that CeO₂ changes to Ce₂O₃ in the electron beam.⁴⁶¹

7.6. General Considerations of the 5f Oxides

With their relatively delocalized 5f valence electrons, actinides show a rich molecular chemistry, with oxidation states spanning from 3+ to 7+. In particular, actinides in high oxidation states 5+ and 6+ can occur as a linear trans-dioxo actinyl cation, with two short highly covalent An=O bonds. These bonds are often considered as chemically inert. The actinyl cation forms bipyramidal polyhedra by bonding various number of equatorial ligands. Oxygen K-edge XAS is used to provide insights into the fundamental understanding of the participation of 5f and 6d orbitals to chemical bonding. Figure 53 presents the spectra of the light actinide dioxides: UO₂, NpO₂, and PuO₂, all in the cubic fluorite structure.

Figure 53.

Oxygen K-edge spectra of UO₂,⁴⁷¹NpO₂,⁴⁷² and PuO₂.⁴⁷²

In light of DFT+U calculations, Modin et al. used oxygen K-edge XAS to compare the nature of the conduction band of these compounds.⁴⁶⁸ The oxygen K-edge XAS spectra of the three actinides show a first peak assigned to oxygen 2p states hybridized with An 5f and two peaks assigned to hybridized An 6d–O 2p bands split by crystal field. Differences in the XAS spectra arise from the relative position of the empty 5f and 6d bands. While in UO₂, the 5f and first 6d(e_g) band overlap, it appears that when changing from U to Np to Pu, the 5f band is lowered in energy and separates from the first 6d(e_g) band, in agreement with the increase of the number of 5f electrons from 2 in U⁴⁺ to 4 in Pu⁴⁺. Oxygen K-edge spectroscopy was used to probe the oxidation state of Pu in the PuO₂ single crystal.⁴⁶⁹ Oxygen K-edge XANES measured with STXM was applied to the characterization of sonochemical Pu colloids.⁴⁷⁰ The spatial resolution offered by the STXM technique enabled discovery of the contribution of the hydrolyzed species in hydrolytic colloids compared with sonochemical colloids.

7.6.1. Uranium Oxides

Thanks to its early discovery and high relative abundance, in addition to the relatively low activity of its radioisotopes, uranium is the most studied and best known actinide element. Understanding fully its chemical reactivity is of relevance for industrial, environmental, and health purposes. Efforts have been dedicated to determine the contribution of the 5f and 6p valence electrons to the chemical bonds. We discuss first the binary oxide UO₂ and subsequently the U⁶⁺ uranyl molecular complexes.

UO₂ is an important compound for nuclear fuel processing as well as a reference compound for the study of the fundamental physics of f electrons. The determination of the nature of the bottom of the conduction band is another important step in the physics of UO₂. Although known to be a Mott-Hubbard insulator, several studies aimed at discriminating between the f-f or f-d type. This information is relevant to understand the poor thermal conductivity of UO₂ as well as test the first-principle theoretical band structure predictions. Both are critical for the management of nuclear power plants. However, experimental proof is required to validate the first-principle calculations.

UO₂ formally has 5f²6d⁰ electronic configuration where U⁴⁺ is in a cubic site with eight equivalent U–O bonds. The crystal field in uranium splits the 6d states by 4.8 eV.⁴⁶³ The oxygen K-edge of UO₂ (Figure 53) analyzed by multiple-scattering and LSDA+U calculations^463,464 provided proof of the f-f type Mott-Hubbard insulator. The oxygen K-edge XAS spectra have been calculated with LDA+U calculations.⁴⁶⁸

The oxygen K-edge XAS has been used to study the evolution of UO₂-based nuclear fuel under irradiation. An early study of UO₂ pellets implanted with Mo ions used the low penetration depth of oxygen K-edge XAS⁴⁷¹ to probe the oxidation state of uranium at the implanted surface. The observation of a low energy resonance after annealing was assigned to the presence of interstitial oxygens and the hyperstoichiometric nature of the surface. The thesis of Pizzi⁴⁷³ on the influence of the partial pressure of oxygen on the oxidation state of uranium in UO₂ used the oxygen K-edge to investigate the contribution of oxidized phases. Pizzi highlighted the difference between oxygen K-edge data obtained in TEY vs TFY modes: the TEY data from Wu et al. contain the contribution of an oxidized layer, which is absent in the data measured in TFY.

In ambient conditions, uranium is most stable in its oxidized U⁶⁺ uranyl state and tends to form strongly covalent linear trans-dioxo uranyl species. Understanding the electronic structure of the uranyl species has been the subject of many investigations to determine its reactivity. Denning et al. used linear polarized X-rays to distinguish between σ (parallel to the uranyl bond) and π (perpendicular to the uranyl bond) orbital symmetry of the antibonding orbitals of the uranyl in a Cs₂UO₂Cl₄ single crystals, which contains oxygen ligands only in the uranyl species (Figure 54). Comparison of the parallel and perpendicular polarized spectra with the molecular orbital diagram of the uranyl cation calculated by DFT with the ADF code, allows assignment of the three main peaks of the oxygen K-edge XAS spectrum to 3π_u(5f_π), 5σ_u(5f_σ), 4σ_g(6d_σ), and 2π_g(6d_π).⁴⁷² A following study of these antibonding valence states of U⁶⁺ was performed on Ba₂ZnUO₆ where all oxygen in the U coordination sphere are equivalents. Experimental spectrum was compared to FDMNES calculations using the finite-difference method.⁴⁷⁴ Then, Fillaux et al. studied specifically the effect of the equatorial ligands on the trans-dioxo bonds using nonoxygen equatorial ligands.⁴⁷⁵ Oxygen K-edge spectra were calculated with FDMNES, and the finite-difference method where the electronic configuration was obtained from Mulliken population analysis performed with ADF. Polarized calculations enable distinguishing the antibonding π* from the σ* orbitals, and pDOS calculations allow assigning the transitions to the 5f and 6d. The intensity of oxygen K-edge XANES features can be used as a fingerprint for the hybridization strength. Fillaux et al. showed that the nature of the equatorial ligands strongly modifies the relative energies of the antibonding molecular orbitals.

Figure 54.

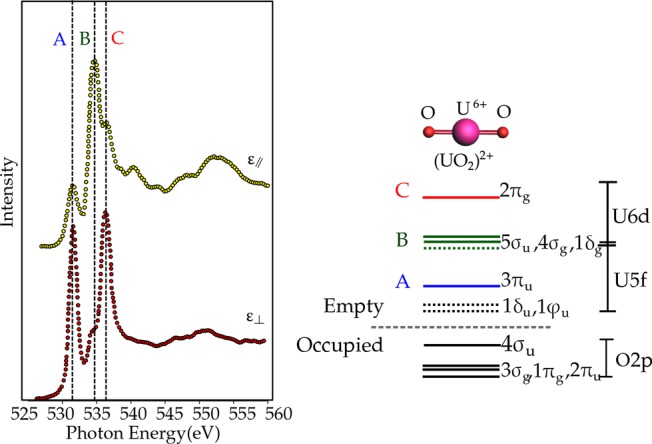
Polarized oxygen K-edge spectrum of the uranyl UO₂²⁺ species in Cs₂UO₂Cl₄ single crystal.⁴⁷² The σ and π characters of the probed states are revealed with the incident light polarization respectively parallel and perpendicular to the uranyl bond.

In the field of geochemistry, Ward et al. published a compilation of oxygen K-edge data of common uranyl-bearing minerals, including carbonates, oxyhydroxides, phosphates, and silicates. All spectra present a first sharp peak assigned to the 3π_u(5f_π) of the uranyl and other features at higher energy depending on the compound. The authors showed that the uranyl compounds can be distinguished based on their oxygen K-edge spectra. This opens perspectives for mineral identification using STXM.⁸⁶

8. Outlook

In this review, we have discussed the general analysis of the oxygen K-edge X-ray absorption spectra of atoms, molecules, and solids. An important experimental fact is that the oxygen K-edge spectrum is broadened by the oxygen 1s core–hole lifetime broadening of 300 meV. Since 1987, the resolution of most synchrotron beamlines is superior to this resolution, and this is also the case for most EELS measurements. This implies that the published oxygen K-edges essentially did not change in resolution over the last 30 years.

We have reviewed the theoretical analysis and simulations of oxygen K-edges. In principle, the procedure to calculate oxygen K-edges is known, and in the first approximation, the oxygen K-edge corresponds to the empty oxygen p-projected states. More detailed calculations calculate the electron–hole excitations with TD-DFT or BSE. Some open issues remain in the interpretation of oxygen K-edges, in particular, (a) the best procedure to describe the core–hole effect, (b) the accurate calculation of the exact excitation energies, and (c) the (calculational) best way to describe dynamics.

Experimental progress is made in the combination of oxygen K-edges with (i) time-resolution with femtosecond resolution, (ii) spatial resolution both with X-rays and electrons, (iii) operando conditions, and (iv) resonant experiments such as RIXS, which we briefly discuss with regard to their possible future developments.

Time

Concerning the future of time-resolved oxygen K-edge measurements, there is much progress in the development of HHG sources and XFEL sources with femtosecond time-resolution.^77,476−485 We expect that in the near future it will become possible to measure the pump–probe excited-state oxygen K-edges with good statistics and well-determined femtosecond time-resolution. Such measurements of the femtosecond dynamics of oxides will be important for the fundamental studies on strongly correlated oxides as well as for the study of the fundamental steps in chemical reactions.

Space

Electron microscopes have atomic resolution, and one can expect further detailed study of the oxygen K-edge spectra with atomic resolution of thin film oxides. X-ray microscopes will likely improve to better than 5 nm resolution, allowing the measurement of oxygen K-edges of systems that cannot be measured with electron microscopes. Combining X-ray microscopy with transmission, fluorescence yield, and electron yield, one can specifically study (a) the surface of active systems and (b) the distribution and chemical nature of dilute species.^61,486

Operando

With the further development of nanotechnology, one can expect that the design of dedicated reactor cells for active systems will improve, allowing the study of the oxygen K-edge of active systems. This includes the important applications in the fields of batteries and (electro)(photo)catalysis. An issue that will remain to complicate operando studies is the constant struggle with X-ray induced effects. A way to avoid X-ray induced effects is to constantly replace samples. For example, liquid jet design is developing quickly, allowing the measurement of sensitive systems.^477,487

Resonance

We expect that many new experiments will become possible using resonant experiments, including RIXS, resonant elastic scattering, and resonant diffraction. The experimental resolution and the detection efficiency of RIXS beamlines are constantly improving. This will allow a new level of RIXS experiments, in combination with time and/or spatial resolution. The time-resolved RIXS and spatially resolved RIXS experiments are expected to bring much new information on the detailed (dynamics of) the electronic structure.^399,488,489

In conclusion, there is a very interesting future for oxygen K-edge X-ray absorption spectra, not so much in the progress of their specific spectral shapes (as limited by the 1s lifetime), but rather in the combination of oxygen K-edges with time-resolved, spatially resolved, operando, and resonant experiments.

Biographies

Federica Frati received her bachelor in chemistry in 2014 from Perugia University, where she did undergraduate research under the direction of Professor F. Tarantelli and Leonardo Belpassi. She obtained her master degree with Professor Mauro Stener and Remco W.A. Havenith at Trieste University in 2016. She is currently a PhD candidate of the Department of Inorganic Chemistry and Catalysis at Utrecht University. Her primary research efforts are directed toward oxygen K-edge modeling in molecular and solid systems.

Myrtille Hunault is a beamline scientist at the SOLEIL synchrotron, France. She graduated from both the ESPCI ParisTech and the University Pierre and Marie-Curie in Paris, France, in 2011. She received her PhD in material chemistry in 2014 for the spectroscopic study of the colors of ancient glasses. After a 1-year postdoctoral fellowship to study the colors of the 15th century rose of the Sainte-Chapelle of Paris, she then went for a second postdoctoral fellowship in the Chemistry Department of Utrecht University to work on the fundamentals of X-ray spectroscopy of metal oxides. Since 2017, she has been working at the SOLEIL synchrotron, France. Her research focuses on the speciation and coloring role of transition metals and actinide ions in oxides, using optical and X-ray spectroscopies and theoretical calculations.

Frank de Groot is Professor of X-ray spectroscopy at the Chemistry department of Utrecht University. He received his MSc degree in Chemistry from Nijmegen University in 1986 and a PhD in Chemistry from Nijmegen University in 1991. He then went on to the LURE synchrotron in Orsay, France, and in 1995 to a KNAW academic research position at Groningen University. Since 1999, he has been working in the Chemistry Department of Utrecht University. His research is focused on X-ray spectroscopy for the study of the electronic and magnetic structure of condensed matter, in particular, for transition metal oxides and heterogeneous catalysts under working conditions.

The authors declare no competing financial interest.