A hydrodynamic analog of Friedel oscillations

We report a new classical analog of electron scattering from an impurity on a metal surface.

Abstract

We present a macroscopic analog of an open quantum system, achieved with a classical pilot-wave system. Friedel oscillations are the angstrom-scale statistical signature of an impurity on a metal surface, concentric circular modulations in the probability density function of the surrounding electron sea. We consider a millimetric drop, propelled by its own wave field along the surface of a vibrating liquid bath, interacting with a submerged circular well. An ensemble of drop trajectories displays a statistical signature in the vicinity of the well that is strikingly similar to Friedel oscillations. The droplet trajectories reveal the dynamical roots of the emergent statistics. Our study elucidates a new mechanism for emergent quantum-like statistics in pilot-wave hydrodynamics and so suggests new directions for the nascent field of hydrodynamic quantum analogs.

INTRODUCTION

A millimetric liquid drop may self-propel along the surface of a vibrated liquid bath through a resonant interaction with its own wave field. This coupled wave-particle object, henceforth termed as a Couder walker after its discoverer (1, 2), extends the range of classical mechanics to include certain features previously thought to be exclusive to quantum systems (3). Quantum-like behavior has been reported primarily in effectively “closed” systems, wherein the drop’s spatial domain is limited by either applied forces (4–7) or bounding geometry (8–10). In particular, this hydrodynamic pilot-wave system has been shown to exhibit wavelike statistics and mode superposition effects (8, 9) notably similar to those arising in quantum corrals (11, 12). A requirement for the emergence of quantization and quantum-like statistics is that the “memory” time (13), as dictates the longevity of the drop’s guiding or “pilot” wave field, exceeds the time taken for the drop to cross its domain; thus, the drop continually navigates its self-excited wave field. Wavelike statistics emerge in these closed settings when the drop dynamics becomes chaotic, and the drop switches intermittently between weakly unstable periodic orbital states (14).

The distinction between closed and open systems is also fundamental at the quantum level. While “particle-in-a-box” models (11, 12) may qualitatively describe the statistical behavior of closed systems, they have no predictive power for resonance widths or standing-wave patterns in open systems (15). Friedel oscillations (11, 16, 17) result from single electron-impurity scattering interactions on a metal surface, and are manifest as localized, spatially decaying, wavelike modulations in the probability density of the electron sea surrounding the atomic impurity. Sufficiently far from the impurity, the charge carriers are undisturbed, and the electron sea is homogeneous; thus, Friedel oscillations may be viewed as arising in an open quantum system. Here, we combine experiments and simulations to demonstrate that hydrodynamic pilot-wave dynamics around a topographical defect may lead to analogous statistical behavior. The localized wavelike statistics are rationalized in terms of a wave-mediated scattering mechanism that is markedly different from that arising in closed hydrodynamic analogs (4–6, 8, 9). Notably, no such interaction mechanism has been elucidated in the related quantum system (11, 16, 17), where the microscopic impurities are modeled in terms of scattering potentials (15).

RESULTS

We consider the interaction between a walking drop and a topographical defect in the form of a submerged circular well at the bottom of the vibrating liquid bath (Fig. 1A and movie S1). The plan view and schematic cross section of the bath are shown in Fig. 1B. The drop, with radius R = 0.39 ± 0.01 mm, and bath are both composed of 20-cSt silicon oil. The bath is vibrated vertically at forcing acceleration Γ(t) = γcos (2πft), where f = 70 Hz is the oscillation frequency. We define the Faraday threshold γ_F as the critical vibrational acceleration above which Faraday waves (18) appear above the well. In all experiments γ < γ_F, so no waves exist in the absence of the drop. The bath depth beyond the well is h = 1.6 ± 0.03 mm, and the well diameter and depth are D = 13 ± 0.1 mm and H = 6.2 ± 0.03 mm, respectively. A submerged star-shaped wave damper around the border of the bath serves as a passive launcher that continuously redirects the drop toward the well (Fig. 1B). See the “Experiments” section for further experimental detail.

Fig. 1. Walker dynamics in the vicinity of a circular well.

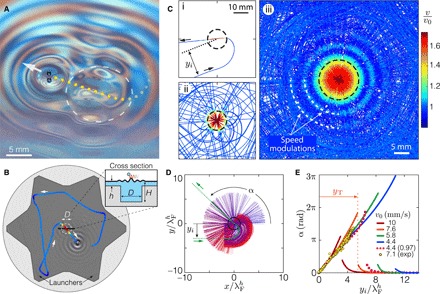
(A) Oblique view of a walking drop passing over a submerged circular well (dashed line) (see movie S1). (B) Plan view and schematic cross section of the experimental setup. (C) Walker trajectories with γ/γ_F = 0.990 and free-walking speed v₀ = 7.1 mm s⁻¹. The arrows denote the direction of motion and trajectories are color coded according to drop speed. A total of 449 trajectories were collected, culminating in speed modulations shown in (iii) (see movie S2). (D) Experimental trajectories colored according to their impact parameter y_i. These trajectories are obtained by rotating those shown in (C, iii) until the drop’s initial direction is parallel to the x axis. α then denotes the scattering angle. (E) Scattering angle α versus impact parameters y_i for experimental (yellow dots) and simulated (solid lines) trajectories with walkers of different size and speed at γ/γ_F = 0.990. The dotted magenta line corresponds to the same drop as the blue solid line but at a lower memory, γ/γ_F = 0.970.

The experiment is performed at a forcing acceleration γ/γ_F = 0.990 ± 0.002, where γ_F ≃ 3.820g. Notably, ${\mathrm{\gamma }}_{\mathrm{F}}^H<{\mathrm{\gamma }}_{\mathrm{F}}<{\mathrm{\gamma }}_{\mathrm{F}}^h$, where ${\mathrm{\gamma }}_{\mathrm{F}}^H\simeq 3.325g$ and ${\mathrm{\gamma }}_{\mathrm{F}}^h\simeq 4.050g$ are the Faraday thresholds of uniform baths of depth H, and h, respectively. Decaying quasi-monochromatic Faraday waves with wavelength λ_F are excited by the impacting drop. We note that the Faraday wavelengths corresponding to the shallow ${\mathrm{\lambda }}_{\mathrm{F}}^h=5.19$ mm and deep ${\mathrm{\lambda }}_{\mathrm{F}}^H=5.27$ mm regions are only marginally different. The wave-induced horizontal force on the drop is F(x_p, t) ∼ −mg∇η∣_x=xp, where m is the drop mass and ∇η∣_x=xp is the surface height gradient evaluated at x_p(t), the point of impact (2, 19). In the absence of the well and boundary interactions, the drop executes rectilinear motion at the free-walking speed v₀ = 7.1 mm s⁻¹. While spatiotemporal damping of the wave field has been shown to play a role in certain settings (20–22), to leading order one may treat the waves as decaying exponentially ∼e^−t/T_M, with a characteristic time scale T_M = T_d/(1 − γ/γ_F), the memory time of the system (13). Here, T_d is the local wave-decay time in the absence of vibration (13, 19), and γ_F is the local Faraday threshold. Because of its influence on both the Faraday threshold and wave-decay rate, the well may be seen to act as a region of high excitability.

Figure 1C shows the walker trajectories in the vicinity of the submerged well (see movie S2). Initially, the drop approaches the well along a straight path with some offset relative to the well center, the so-called impact parameter y_i. The drop then spirals in toward the well as if acted upon by an attractive force. In particular, the drop approaches the well at constant speed v along a unique Archimedean spiral of the form r = a + bθ (see fig. S2). An expression for the effective well-induced force, F_w, acting on the drop during the incoming phase may be inferred (23) (see text S1) and found to be

$${\mathbf{F}}_{\mathrm{w}}=m(1+\frac{{\stackrel{.}{r}}^2}{v^2})\stackrel{.}{\mathrm{\Theta }}\times v$$ (1)

where $\stackrel{.}{\mathrm{\Theta }}=(v_{\mathrm{\theta }}/r){\widehat{\mathbf{e}}}_{\mathbf{z}}$ is the instantaneous angular velocity of the drop around the well center and ${\widehat{\mathbf{e}}}_{\mathbf{z}}$ is the vertical unit vector. Note that F_w is a lift force, orthogonal to the direction of drop motion. After passing through the well, the drop departs radially along a rectilinear path offset by an angle α relative to its incident path, henceforth the scattering angle. The walker accelerates significantly when passing above the well due to the local generation of relatively high-amplitude waves; however, its vertical motion is largely unaffected (see movie S1). A total of 449 trajectories were collected, the superposition of which yields Fig. 1C, iii.

In Fig. 1D, the experimental trajectories are characterized in terms of y_i and α. The well evidently acts as a scatterer. The scattering angle α may be expressed in terms of the impact parameter y_i, which determines when the walker locks onto the spiral, and the spiral slope b = dr/dθ, as α ∼ y_i/b. To explore further such walker-well interactions, we complement our experiments with simulations based on the quasi-potential model of Faria (24), according to which the influence of stepwise variable bottom topography is captured through its effect on the local wave speed (see the “Numerical simulations” section). The resulting trajectories (see fig. S1) are virtually identical to those arising in our experiments. Figure 1E shows the relation between y_i and α in both the experiments and simulations. Excellent quantitative agreement is observed. The simulations further demonstrate that the well-induced attraction is spatially limited: α increases monotonically with y_i up to a critical tethering length y_T, beyond which the walker is not drawn into the well (Fig. 1E). We use the simulations to examine the influence of γ/γ_F and drop size 0.353 ≤ R ≤ 0.425 mm, the latter corresponding to drop speeds in the range 4.4 ≤ v₀ ≤ 10 mm s⁻¹ at γ/γ_F = 0.990 (see Table 1). For a given γ/γ_F, smaller, slower drops lead to larger y_T and α. For a given drop speed, decreasing γ/γ_F reduces the tethering length y_T, but has a negligible effect on the scattering angle α (Fig. 1E).

Table 1. Range of drops considered in our study.

The values reported for γ/γ_F = 0.990 are from experimental observations with h = 1.6 mm. The case with γ/γ_F = 0.970 corresponds to our simulations in which the impact phase φ was adjusted to match v₀, and so drop inertia, for the smallest drop. This adjustment allowed us to assess the role of memory on the range of interaction, independent of drop inertia (see Fig. 1E).

R (mm)	γ/γF	v0 (mm/s)	φ/2π
0.355	0.990	4.4	0.259
0.375	•	5.8	0.266
0.390	•	7.1	0.269
0.400	•	7.6	0.277
0.425	•	10.0	0.286
0.355	0.970	4.4	0.268

The superposition of all the experimental trajectories reveals a pattern of evenly spaced, concentric speed modulations in the vicinity of the well (Fig. 1C, iii). We now turn our attention to rationalizing the origin and discussing the statistical implications of such a spatially dependent speed distribution. We split the trajectories at their point of nearest approach to the well center into incoming (Fig. 2A) and outgoing (Fig. 2B) phases. While the speed along the incoming spiral phase is constant and equal to v₀ beyond the well (Fig. 2A), the straight outgoing trajectories display speed oscillations (Fig. 2B), which are also evident in the simulations (Fig. 2, D and E). Comparing the speed pattern (Fig. 2B) with the Faraday wave mode of the well (Fig. 2C) reveals their spatial correlation: The wavelength of the speed modulations is λ_F. Note that these speed modulations are not the result of the walker moving over externally imposed Faraday waves; rather, they reflect self-excited wave-mediated forces generated by the resonant interaction between the walker and the well. Note that the relative amplitude of the speed modulations increases for slower drops, while the wavelength of oscillation remains fixed at ${\mathrm{\lambda }}_{\mathrm{F}}^h$. Figure 2 (D and E) shows the trajectories for the slowest drop simulated (previously shown in Fig. 1E and fig. S1), in which speed oscillations are enhanced by ∼50% relative to those observed in the experiments. Figure 2 (F and G) demonstrates that, for a given drop, the instantaneous speed data v(r) for all the trajectories collapse onto the same curve, indicating the insensitivity of the statistical behavior to the initial conditions.

Fig. 2. Emergent statistical behavior.

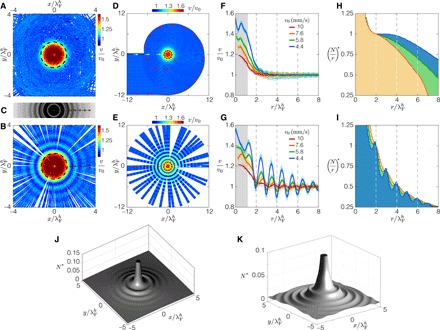
Top view illustrating the experimental (A) incoming and (B) outgoing drop trajectories, color coded according to speed v. Trajectories are obtained by splitting those shown in Fig. 1G at the point nearest the well center (dashed line). Concentric speed modulations appear in the outgoing phase. (C) Faraday waves observed above the well at threshold γ = γ_F. Note the spatial correspondence between the Faraday wave extrema and the speed modulations evident in (B). (D) Incoming and (E) outgoing trajectories, color coded according to speed, corresponding to the slowest walker with γ/γ_F = 0.990 in Fig. 1F. Red arrows identify the outermost trajectory crossing the well. White arrows indicate the trajectory with a radial approach. Dependence of the normalized speed v on radius r for (F) incoming and (G) outgoing walkers of different size and speed. The gray area denotes the well’s extent. (H and I) Histograms of the drop’s radial position corresponding to the data shown in (F) and (G). The bin size is ${\mathrm{\lambda }}_{\mathrm{F}}^h/13$. The histograms have been normalized by their respective height at $r/{\mathrm{\lambda }}_{\mathrm{F}}^h=2$, corresponding to the first speed minimum outside the well observed in (G). (J and K) Two-dimensional histograms (normalized by the histogram height at the center of the well) resulting from the experimental (B) and simulated (E) outgoing trajectories. Asterisks denote normalized quantities.

The wavelike statistical behavior in the vicinity of the well is most evident in the histogram of the walker position. The data shown in Fig. 2 (F and G) result in the position histograms presented in Fig. 2 (H and I). The statistical modulations, originating in the outgoing phase (Fig. 2I), have the same spacing, λ_F, as the speed oscillations but are out of phase: Speed minima correspond to peaks in the histogram. The relative size of the statistical modulations is, thus, prescribed by the amplitude of the speed oscillations; hence, slower drops have more pronounced statistical modulations. The different decay rates apparent in Fig. 2H arise because the well has a larger range of influence on slower drops. A three-dimensional (3D) rendering of the experimental and simulated histograms is presented in Fig. 2 (J and K), which bears a notable resemblance to the Friedel oscillations around a magnetic impurity (11, 16, 17). We note that the amplitude of the walker’s histogram modulations, relative to the histogram height at the center of the well, is ∼0.8% (Fig. 2K), comparable to that in the quantum experiment, ∼1.5% (11).

We proceed by detailing the wave-mediated drop-well interaction mechanism through examination of the wave field (Fig. 3, A and B, and movies S3 and S4). Of particular interest is the well-induced, or “anomalous,” wave field $\mathrm{\xi }(\mathit{x},t)=\mathrm{\eta }-\overline{\mathrm{\eta }}$ (Fig. 3C and movie S5), obtained by subtracting from the simulated wave field η(x, t) (Fig. 3B) that of the drop following the same path in the absence of the well, $\overline{\mathrm{\eta }}(\mathit{x},t)$ (as we deduce via simulation). The scattering properties of the well are related to the emergence of a beam-like structure (25) in the anomalous wave field during the incoming phase (Fig. 3C, ii). This beam spans the drop and the well and so rotates around the well while sliding in the radial direction. Note that the drop always resides in one of the beam troughs, which is consistent with the constancy of its speed during the incoming phase. Decreasing γ/γ_F reduces the tethering length y_T by reducing the characteristic extent of the wave field (19). The dependence of the scattering angle on drop size (Fig. 1E) may be rationalized in terms of the fundamental wave slopes at the drop position by noting that α ∼ y_i/b ∼ y_i(dθ/dr) ∼ (y_i/r)(v_θ/v_r) ∼ ∇_θη/∇_rη. Since the contribution to the azimuthal gradient from the well-induced wave field is negligible ${\nabla }_{\mathrm{\theta }}\overline{\mathrm{\eta }}\gg {\nabla }_{\mathrm{\theta }}\mathrm{\xi }$, it follows that $\mathrm{\alpha }\sim {\nabla }_{\mathrm{\theta }}\overline{\mathrm{\eta }}/{\nabla }_r\mathrm{\eta }$ . Moreover, since v₀ is proportional to ${\nabla }_{\mathrm{\theta }}\overline{\mathrm{\eta }}$, our scaling correctly indicates that larger, faster drops scatter more. The localized wavelike statistics are rooted in the resonant amplification (by ∼30%) of the concentric waves excited when the drop crosses the well (Fig. 3C, iii). These resonant waves are spatially fixed and have a decay time $T_{\mathrm{M}}^H\sim 2.5$ s, significantly larger than both the wave-decay time in the shallow region $T_{\mathrm{M}}^h\sim 0.6$ s and the characteristic crest crossing time λ_F/v₀ ∼ 0.7 s. The speed oscillations described in Fig. 2 are the result of the drop navigating this relatively persistent localized wave pattern as it exits the well (Fig. 3C, iv and v). A 3D visualization of the anomalous wave field is presented in Fig. 4, including the complete time series of the perturbation at the drop location.

Fig. 3. Wave-mediated interaction.

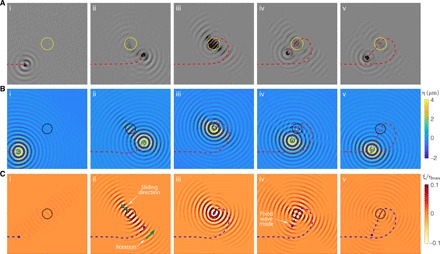
(A) Experimental and (B) simulated walker wave field η during its interaction with a submerged well (solid circle). Snapshots illustrate the walker (i) approaching the well in straight-line motion, (ii) spiraling inward, (iii) exciting localized large-amplitude waves as it crosses the well, and (iv and v) exiting the well along a straight trajectory. (C) Well-induced wave perturbation $\mathrm{\xi }=\mathrm{\eta }-\overline{\mathrm{\eta }}$ (normalized by the instantaneous maximum wave amplitude η_max = max ∣η∣) obtained by subtracting from the wave field η shown in (B) the computed wave field $\overline{\mathrm{\eta }}$ of a drop following the same trajectory in the absence of the well. A sliding beam-like wave mode emerges as the drop spirals inward (ii). Along the outgoing trajectory, the drop crosses a spatially fixed wave field centered on the well (iv). The resulting speed variations give rise to the wavelike statistics evident in Fig. 2. The simulated walker corresponds to γ/γ_F = 0.990, v₀ = 4.4 mm s⁻¹, and $y_i/{\mathrm{\lambda }}_{\mathrm{F}}^h=6$. See movies S3 to S5.

Fig. 4. Well-induced wave perturbation deduced from simulations.

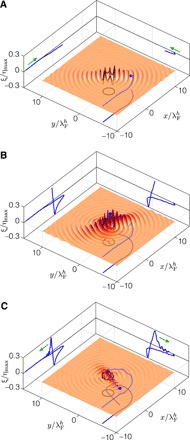
3D visualization of the well-induced wave perturbation as the drop (A) spirals inward, (B) crosses the well, and (C) exits in a rectilinear fashion. Solid blue lines projected onto the vertical (xz and yz) planes illustrate the evolution of the perturbation amplitude beneath the drop. The drop approaches the well in an ever-deepening trough and then exits radially across a field of waves centered on the well. The simulated walker corresponds to that shown in Fig. 3 (B and C). See movie S5.

DISCUSSION

The differences between the quantum (11, 12, 16, 17) and hydrodynamic (3) systems are vast: The typical defect size and particle speed in the macroscopic ex shows the trajectories for the slowest periment are ∼10⁸ larger and ~10⁷ slower than those in their microscopic counterpart. Nevertheless, we have demonstrated remarkable similarities. We have shown that a self-propelling walking drop interacting with a submerged well, a topographical defect in the medium, may lead to particle scattering and localized wavelike statistics. These two effects may be rationalized in terms of the markedly distinct dynamics arising in the incoming and outgoing phases. The scattering angle is set during the incoming trajectory, in which the drop is deviated by a wave-mediated lift force induced by the well. While distant walkers are only weakly deviated, those sufficiently close are drawn into the well along an Archimedean spiral, whose origins lie in a shifting beam-like wave perturbation between the drop and well. The drop speed along the incoming spiral trajectory is nearly constant; thus, the incoming phase does not contribute to the emergent statistical behavior. As the walking drop crosses the well, it resonates with the wave-mode of the well, generating a standing wave field that persists as the walker exits the well, leading to the modulations in drop speed responsible for the axially symmetric statistical signature. Consideration of an ensemble of drop trajectories reveals that our hydrodynamic pilot-wave system displays localized wavelike statistics in the particle position histogram strongly reminiscent of Friedel oscillations (11, 16, 17). The decaying oscillations have half the Fermi (or de Broglie) wavelength in the quantum system, and the Faraday wavelength λ_F in the hydrodynamic system, as corresponds to the wavelength of the drop’s pilot wave.

In previous studies of closed hydrodynamic pilot-wave systems, the emergence of quantum-like statistics has relied on chaotic switching between unstable periodic orbits (4, 6–10, 26). In the open system considered here, they emerge because of oscillations in the droplet speed prompted by its interaction with the well, which acts as a localized region of high excitability. While perturbation-induced speed oscillations have been reported in previous experimental (27) and theoretical (28) investigations, their potential importance for the emergent statistics has not previously been recognized. Our study demonstrates that such speed oscillations may provide an alternative route for the emergence of quantum-like statistical behavior in classical systems. It thus motivates a revisitation of the corral experiments (8–10), where the origins of the emergent statistics remain unclear (29–31), but a strong correlation between the speed map and the position histogram is apparent. Our study further suggests myriad new directions for the field of hydrodynamics quantum analogs (14). In particular, our work invites analog studies of related wave-mediated phenomena associated with charge carrier mobility, including Anderson localization (32) and Mott transitions (33).

MATERIALS AND METHODS

Experiments

The drop and bath are both composed of 20-cSt silicon oil with density ρ = 950 kg m⁻³, viscosity ν = 20.9 cSt, and surface tension σ = 20.6 mN m⁻¹. The drop, with radius R = 0.39 ± 0.01 mm, is created using a piezoelectric drop generator (34). The bath is vibrated vertically with a Data Physics V55 electromagnetic shaker and a PA300E amplifier. A spatially uniform vibration with an acceleration amplitude γ that is constant to within ±0.002g, where g is the gravitational acceleration, is achieved by using the vibrating setup detailed elsewhere (35). Decaying quasi-monochromatic subharmonic Faraday waves, with wavelength λ_F = 2π/k_F prescribed by the standard capillary-gravity dispersion relation ${\mathrm{\omega }}_{\mathrm{F}}^2=(g{k}_{\mathrm{F}}+\mathrm{\sigma }{k}_{\mathrm{F}}^3/\mathrm{\rho })\text{tan}h k_{\mathrm{F}}h$, are excited by the impacting drop, where ω_F = πf and k_F are the Faraday frequency and wave number, respectively.

The bath depth beyond the well h = 1.6 ± 0.03 mm is chosen to ensure that the walker respond to variations in bottom topography (9). The well diameter D = 13 ± 0.1 mm is chosen to ensure that the Faraday waves emerging at threshold γ = γ_F are concentric (Fig. 2C). The well depth H = 6.2 ± 0.03 mm is sufficiently large with respect to k_F that the well corresponds to the so-called deep-fluid regime, i.e., tanh k_FH ≃ 1. The resulting walker motion is characterized by the synchronous (2,1) walking mode (27) in both the deep and shallow regions. A total of 6 hours of experimental data was recorded, acquired in 1-hour intervals to minimize temperature-induced drifts in γ_F, which were limited to ±0.01g.

The liquid height above the star-shaped wave damper is 0.2 ± 0.1 mm. The distance between the region of interest around the well and the innermost part of the launcher is sufficiently large ($\sim 6{\mathrm{\lambda }}_{\mathrm{F}}^h$) with respect to the wave damping length (22) that boundary effects play a negligible role on the walker-well interactions. The time that the drop takes to revisit the well, typically ∼50 ± 20 s, is much longer than the relevant memory time T_M ∼ 2.5 s; thus, only memory effects related to the current well-walker interaction are significant. The bath is sealed with a transparent acrylic lid to shield the system from air currents. The walker motion is recorded from above with a charge-coupled device camera at 20 frames/s and tracked with an in-house particle-tracking algorithm. The wave field (Fig. 3A) is visualized by placing a semireflective mirror at 45^∘ between the camera and the bath, and lighting horizontally with a diffuse-light lamp. Bright regions then correspond to horizontal portions of the surface, dark regions to areas of large slope (36).

Numerical simulations

Our simulations are performed with the model developed by Faria (24) to account for variable bottom topography, which builds on the linearized quasi-potential, weakly viscous flow model developed by Milewski et al. (37). Faria (24) reduces the problem to the free surface η(x, t) by treating changes in topography through their influence on the local wave speed. Specifically, the wave problem becomes

$${\mathrm{\varphi }}_t=-G(t)\mathrm{\eta }+\frac{\mathrm{\sigma }}{\mathrm{\rho }}{\nabla }^2\mathrm{\eta }+2{\mathrm{\nu }}_{\mathrm{e}}{\nabla }^2\mathrm{\varphi }-\frac{1}{\mathrm{\rho }}{P}_{\mathrm{D}}(\mathit{x}-{\mathit{x}}_p(t),t)$$ (2)

$${\mathrm{\eta }}_t=-\nabla ·[b(\mathit{x})\nabla \mathrm{\varphi }]+2{\mathrm{\nu }}_{\mathrm{e}}{\nabla }^2\mathrm{\eta }$$ (3)

where ϕ(x, t) denotes the velocity potential u = ∇ ϕ in the bath, G(t) = g + γcos (2πft − φ) the effective gravity in the bath’s frame of reference, φ the drop’s impact phase, ν_e = 0.861ν the effective kinematic viscosity (chosen to match the experimental stability threshold γ_F) (19), and x_p(t) the drop’s horizontal position. The wave-drop coupling is modeled by treating the drop as an instantaneous excess point-pressure P_D in the dynamic surface condition (19, 37). Changes in bottom topography are modeled by approximating the vertical gradient of the velocity potential as ϕ_z ≈ − ∇ · [(b(x) ∇ ϕ], where b(x) is an effective depth chosen to ensure the correct the dispersion relation of Faraday waves in both the shallow and deep regions, according to

$$b(\mathit{x})=\{\begin{array}{cc}\text{tanh} (k_{{\mathrm{F}}_H}H)/k_{{\mathrm{F}}_H},& \text{for} x\in W\\ \text{tanh} (k_{{\mathrm{F}}_h}h)/k_{{\mathrm{F}}_h},& \text{for} x\notin W\end{array}$$ (4)

where W denotes the well region, and k_FH and k_Fh the most unstable wave numbers in the deep and shallow regions, respectively, computed as detailed by Milewski et al. (37).

The local gradient of the resulting wave field ∇η∣_x=xp determines the lateral force exerted on the drop at impact. The drop’s trajectory is thus described through

$$m\frac{d^2{\mathit{x}}_p}{{\mathrm{dt}}^2}+(c_4\sqrt{\frac{\mathrm{\rho }R}{\mathrm{\sigma }}}F(t)+6\mathrm{\pi R}{\mathrm{\mu }}_{\text{air}})\frac{d{\mathit{x}}_p}{\mathrm{dt}}={-F(t)\nabla \mathrm{\eta }\mid }_{x=x_p}$$ (5)

where μ_air = 1.8 × 10⁻⁵ Pa·s is the dynamic viscosity of air, and c₄ = 0.17 is the coefficient of tangential restitution (19). The drop bounces in synchrony with the Faraday waves, and the impacts thus take place at t = nT_F, where T_F = 2/f is the Faraday period. Assuming instantaneous impacts, the force becomes $F(t)=\mathit{mg}{\sum }_{n=0}^{\infty }\mathrm{\delta }(t/T_{\mathrm{F}}-n)$, where δ is the delta function. Last, the penetration depth of the drop is assumed to be infinitesimally small relative to the Faraday wavelength. The drop pressure thus becomes $P_{\mathrm{D}}(\mathit{x}-{\mathit{x}}_p,t)=(F(t)/{\mathrm{\lambda }}_{\mathrm{F}}^2)\mathrm{\delta }((\mathit{x}-{\mathit{x}}_p)/{\mathrm{\lambda }}_{\mathrm{F}})$, which vanishes when the drop is not in contact with the bath (24).

The model is solved numerically using a pseudospectral method in space, periodic boundary conditions, and a fourth-order Runge-Kutta scheme for the time integration (24). The simulations are performed on a square domain of size $48{\mathrm{\lambda }}_{\mathrm{F}}^h\times 48{\mathrm{\lambda }}_{\mathrm{F}}^h$, discretized with 512 × 512 points. Numerical tests were performed to ensure that the domain size and spatial resolution were adequate to render discretization-independent results. Simulations with a larger domain size but the same resolution ($64{\mathrm{\lambda }}_{\mathrm{F}}^h\times 64{\mathrm{\lambda }}_{\mathrm{F}}^h$, 682 × 682) and same domain size but a finer resolution ($48{\mathrm{\lambda }}_{\mathrm{F}}^h\times 48{\mathrm{\lambda }}_{\mathrm{F}}^h$, 768 × 768) produced results that were virtually indistinguishable from those reported in the main text. In all the simulations presented, a uniform distribution of impact parameters y_i is considered, with resolution $\mathrm{\Delta }{y}_i/{\mathrm{\lambda }}_{\mathrm{F}}^h=0.25$.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/20/eaay9234/DC1