Significance
Owing to internal homeostatic mechanisms, cellular traits may experience long periods of stable selective pressures. Nonetheless, drift and mutation still conspire to generate significant variation in mean phenotypes among phylogenetic lineages. Provided there are classes of mutations with sufficiently small effects, even in the face of constant selection, variation in genetic effective population sizes will result in gradients of mean phenotypes with respect to organism size across the tree of life. Mutation is an important determinant of such patterns, even in the absence of directional bias. Thus, a substantial amount of variation in cellular features may be a simple consequence of lineage-specific differences in the power of drift rather than a reflection of adaptive divergence.
Keywords: cellular evolution, evolutionary theory, optimal phenotype, mutation bias, random genetic drift
Abstract
Owing to internal homeostatic mechanisms, cellular traits may experience long periods of stable selective pressures, during which the stochastic forces of drift and mutation conspire to generate variation. However, even in the face of invariant selection, the drift barrier defined by the genetic effective population size, which is negatively associated with organism size, can have a substantial influence on the location and dispersion of the long-term steady-state distribution of mean phenotypes. In addition, for multilocus traits, the multiplicity of alternative, functionally equivalent states can draw mean phenotypes away from selective optima, even in the absence of mutation bias. Using a framework for traits with an additive genetic basis, it is shown that 1) optimal phenotypic states may be only rarely achieved; 2) gradients of mean phenotypes with respect to organism size (i.e., allometric relationships) are likely to be molded by differences in the power of random genetic drift across the tree of life; and 3) for any particular set of population-genetic conditions, significant variation in mean phenotypes may exist among lineages exposed to identical selection pressures. These results provide a potentially useful framework for understanding numerous aspects of cellular diversification and illustrate the risks of interpreting such variation in a purely adaptive framework.
The field of theoretical population genetics typically considers the evolutionary behavior of alleles in a generic way, usually assigning general selection coefficients and mutation rates to alternative alleles. This platform has been enormously successful at elucidating the combined roles of selection, mutation, and drift in the evolutionary dynamics of single loci and quantitative traits (1, 2). Nonetheless, there remains a disconnect between theory, the underlying biology of specific traits, and the constraints on key population-genetic parameters that exist in different molecular, cellular, or phylogenetic contexts. Often, a continuous distribution of mutational effects is assumed such that any phenotype is viewed as being accessible, but with no explicit connections with actual biological features.
The details appear to matter in a number of contexts. For example, many aspects of cell biology are effectively manifest in a digital rather than an analog manner. Transcription-factor binding sites (typically no more than 12 bp in length) can be defined in terms of the number of matches to the preferred motifs of their cognate transcription factors (3, 4). MicroRNA-binding site interactions and protein–protein interfaces can be viewed in a similar manner (5). Posttranslational modifications such as phosphorylation and ubiquitinylation (involved in many signal-transduction and protein-disposal pathways) can be described in terms of a small number of modified sites per protein (6). The numbers of carbon atoms and double bonds in the fatty-acid tails of lipids (generally fewer than 20 and 6, respectively) influence membrane width and fluidity (7), and some have argued that specific amino acids or nucleotides may be selected for on the basis of numbers of carbon, nitrogen, or sulfur atoms (8, 9). Many other examples could be given.
The restriction of simple molecular traits to discontinuous values may have unique evolutionary consequences. For example, the optimum energy of molecular binding or transfer for a particular trait may be unattainable unless it coincides with an integer multiple of the underlying granularity. If this is not the case, two allelic states straddling the optimum may have nearly the same fitness, resulting in an essentially neutral process of molecular evolution combined with a permanent state of suboptimal fitness. In addition, if certain suboptimal allelic states are more accessible by mutation, this can compete with the ability of selection to promote higher-fitness states. As is discussed below, this is virtually always the case, even in the absence of mutation bias.
The theory developed below has two central goals. First, given the common view that all phenotypic variation can be explained in terms of adaptation, it is desirable to consider the degree to which phylogenetic lineages are free to diverge under a regime of invariant selection pressure. Here, results will be given on the extent to which expected mean phenotypes are subject to scaling relationships (e.g., with organism size and/or population size) associated with the power of random genetic drift (the drift barrier) and on the degree to which populations exposed to identical forces of mutation, selection, and drift are free to wander across mean-phenotype space. Second, because the primary forces of evolution, most notably the mutation rate and random genetic drift, are nonindependent across the tree of life (10), consideration will be given to how such covariation influences patterns of variation.
General Theory
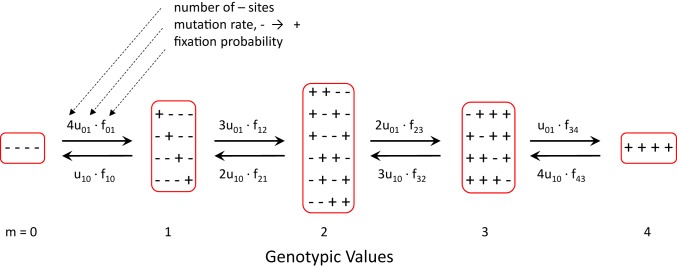
We start with a simple model with equivalent sites (factors), each with two alternative allelic states, and , contributing positively and negatively to the trait (Fig. 1). Under this model, for all but the two most extreme genotypes, a multiplicity of functionally equivalent classes exists with respect to the number of positive alleles, , defined by the binomial coefficients. As an example, for the case of , there are five genotypic classes (, 1, 2, 3, 4, and 5), with multiplicities 1, 4, 6, 4, and 1, respectively (Fig. 1). With equivalent fitness for all members (haplotypes) within a particular class, this variation in multiplicity of states plays an important role in determining the long-term evolutionary distribution of alternative classes. The site-specific per-generation mutation rates from the to the state, and vice versa, are defined as and , respectively. Unless stated otherwise, a haploid, nonrecombining population will be assumed. The absolute population size consists of individuals, so that a de novo mutation has initial frequency . However, the effective population size, , which is generally no greater than and often considerably smaller, governs the magnitude of random genetic drift and as discussed below is defined by the remaining features of the population-genetic environment (including the mutation bias and the strength of selection).
Fig. 1.
Schematic for the transition rates between adjacent classes under the sequential-fixation model for the case of sites. This schematic readily generalizes to any value of . and are the mutation rates from to allelic states, and vice versa, and is the probability of fixation of a newly arisen mutation to allele from a background of , defined as SI Appendix, Eq. S5. The number of alleles in a class is denoted by , and except for the two extreme classes ( and ), there are multiple equivalent genotypic states within each class of genotypic values.
This type of biallelic model has been widely exploited in theoretical studies of the genetic structure of quantitative (multilocus) traits (2), including cell-biological features (4, 5). Most quantitative-genetic theory on such systems has focused on the equilibrium within-population variation under selection–mutation balance in infinite-sized populations. However, in finite populations, the stochasticity of mutation and drift ensures that genotype distributions are not fixed. Instead, the mean genotype is expected to wander over time within limits dictated by the strength of selection and the structure of the underlying genetic system. The goal here is to determine the long-term probability distribution of genotypic means defined by the joint forces of selection, mutation, and random genetic drift. Justification of this quasi–steady-state view derives from the fact that many internal cellular traits have functions (and cytoplasmic environments) that likely remain relatively stable for millions of years (even in the face of a changing external environment).
A Single Biallelic Locus.
As a point of departure, the case of a single locus with reversible mutation will highlight several key points and provide a useful backdrop for the evaluation of more complex traits. Allele A (denoted as state 1 below) is taken to have a fractional selective advantage over allele a (denoted as state 0). For this limiting case, previous work provides an exact solution for the equilibrium mean frequencies of alleles (SI Appendix). However, because the final expression is a bit cumbersome mathematically, it is common in population genetics to use one of two alternative approximations.
One extreme view is that drift is weak enough relative to mutation and selection that the population can be treated as effectively infinite in size, yielding SI Appendix, Eqs. S3a and S3b. A second approach assumes a situation in which, relative to the power of drift, mutation rates are low enough and the strength of selection high enough that polymorphisms are almost never present, with fixation of alternative monomorphic states being the norm, and the long-term mean frequency of the beneficial allele being
| [1] |
where is the strength of selection scaled to drift, and is the ratio of mutation rates. Under this weak-mutation/strong-selection scenario, referred to below as the sequential-fixation model, the equilibrium distribution depends only on the product of the two ratios of rates, not on the absolute values of their components. Although the concern here is with the long-term probabilities of alternative states at a particular locus, Eq. 1 was derived previously to describe the genome-wide expected frequencies of codons for particular amino acids (11, 12). Note that under neutrality (), all three approaches yield identical results, with the mean frequency of the A allele being the neutral expectation .
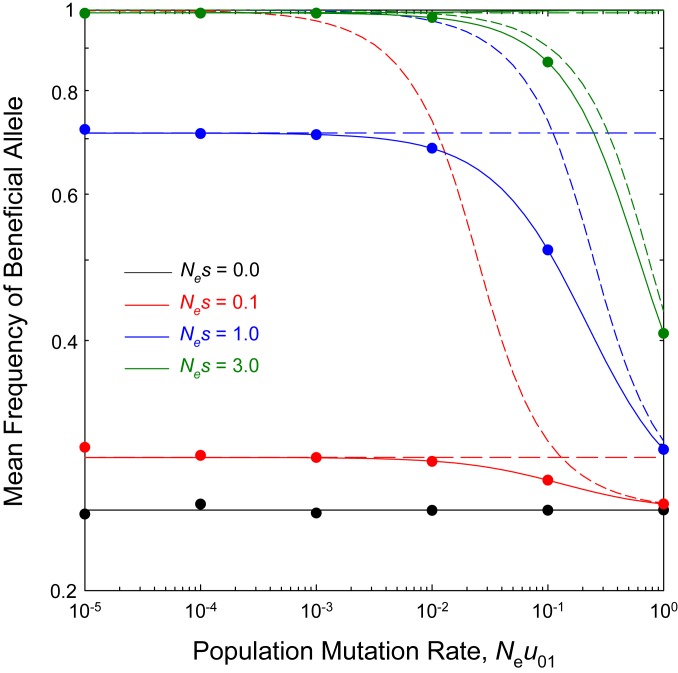
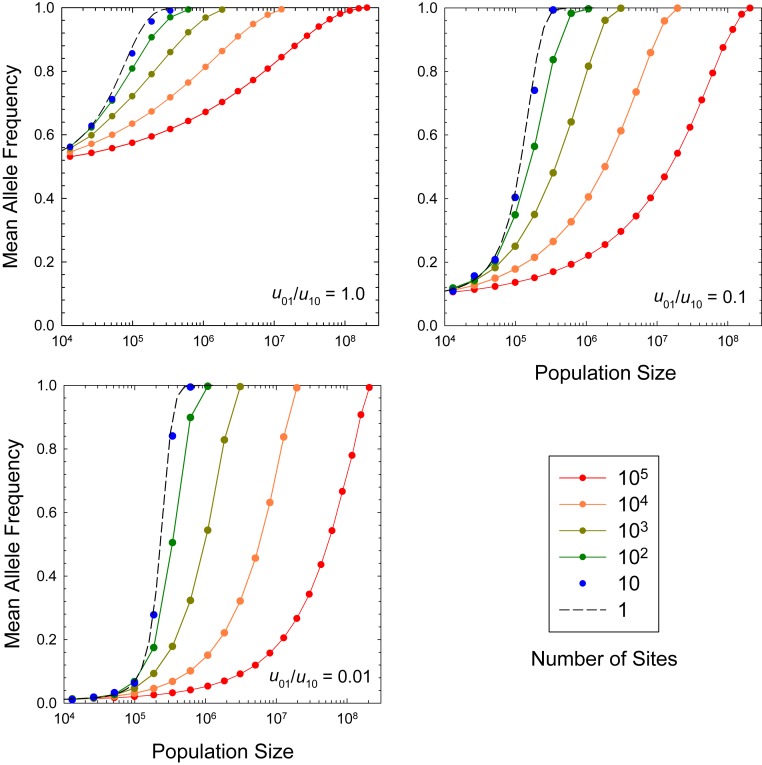
Although the deterministic and sequential models have very different implications for the standing levels of variation within populations, often in comparative biology, just a single genome will be sampled per taxon, rendering the matter of within-population variation moot. Thus, it is desirable to know the domains in which these two approximations (if either) provide the most reasonable approximation of actual long-term mean allele frequencies. Comparison with the general analytical solution, SI Appendix, Eq. S2, allows several general conclusions. First, the sequential model begins to substantially overestimate the frequency of the beneficial allele once exceeds 0.01 (Fig. 2). These deviations are particularly large when outside the realm of effective neutrality, i.e., for . Second, for weak to moderately strong selection (), a critical point near separates domains in which the sequential vs. deterministic model fits the data more closely. At this crossover point, both of the simple models overestimate the actual mean frequency of the beneficial allele, often substantially so. Third, the predictions of the deterministic model converge on the results of the general model once the number of beneficial mutations () entering the population exceeds 1.0 per generation. As the population-wide mutation rates ( and ) increase beyond this point, mutation pressure begins to overwhelm both selection and drift, and the asymptotic frequency of the beneficial allele converges on the neutral expectation, .
Fig. 2.
Average beneficial allele frequency (long-term average) for a single-locus model, under the general model (SI Appendix, Eq. S2, solid lines), the infinite population size model (SI Appendix, Eqs. S3a and S3b, short-dashed lines), and the sequential-fixation model (Eq. 1, long-dashed lines). Results from Wright–Fisher simulations are given as solid points for the case in which the actual and effective population sizes are equal (). The mutation rate of beneficial to deleterious alleles () is three times the reciprocal rate (as would be the approximate case for a single optimal nucleotide at a site). The infinite population size results use the selection coefficient inferred by the constant product for each curve, so that in this case scales inversely with .
Two other points are illustrated in Fig. 2. First, in the presence of mutation bias, there can exist a wide range of population sizes in which the most common allelic state does not match the optimal state; e.g., . Second, situations may be common in which there is ample phylogenetic variation in allelic state despite the constancy of selection. For example, in the domain of the sequential model, when the directional forces of mutation and selection balance such that , the mean frequencies of the alternative allelic states will be equal to 0.5. In the absence of knowledge on mutation bias, such cases could easily be misinterpreted as implying neutral genotypes, when in fact the population is under persistent selection in the opposite direction of mutation bias.
Two Sites.
Proceeding to more complex traits, it becomes necessary to specify a function relating the genotypic states to fitness. Although the concepts developed hereafter are general with respect to the form of the fitness function, here we will assume a Gaussian (bell-shaped) function such that individuals in genotypic class have fitness
| [2] |
where is the optimum phenotypic value, and is a measure of the width of the fitness function (analogous to the SD of a normal distribution). Selection is purely directional if or , and neutrality is approached as . Although is confined to integer values, need not be, and if is outside of the range, the optimum is unattainable.
As a central goal is to determine the relationship between the expected genotype distribution and the effective population size (), it is desirable to perform analyses with realistic parameter values for and the mutation rate. Across the tree of life, generally falls in the range of to , and the mutation rate per nucleotide site scales negatively with the power of (10, 13). Thus, the following analyses were performed under the assumption of a deleterious-mutation rate per site (which might be a cluster of adjacent nucleotides) of at , such that , which is approximately 10 times the known rate per nucleotide site. As implied above and shown further below, provided the mutation rates are sufficiently low, it turns out that this scaling has no effect on the equilibrium distribution, which depends only on the ratio . Unless stated otherwise, the beneficial rate () is set to of the former one.
With two sites, there are three possible genotypic classes, , with the phenotypically equivalent and states being lumped into the class. For reasons described in Moderately Complex Traits, the long-term equilibrium frequencies are given by
| [3] |
where the normalization constant is equal to the reciprocal of the sum of the terms to the right of for to 2, and the binomial term takes on values of for . The indexed selection coefficients, , are measures of the class-specific deviations of fitness from some reference genotype (e.g., the class with the highest fitness, in which case , or class 0); the specific reference does not matter, as it cancels out through the normalization constant. The mean phenotype
| [4] |
reduces to in the case of neutrality. (Throughout, is used to indicate an equilibrium frequency and to denote a mean, in this case of , the number of + alleles.)
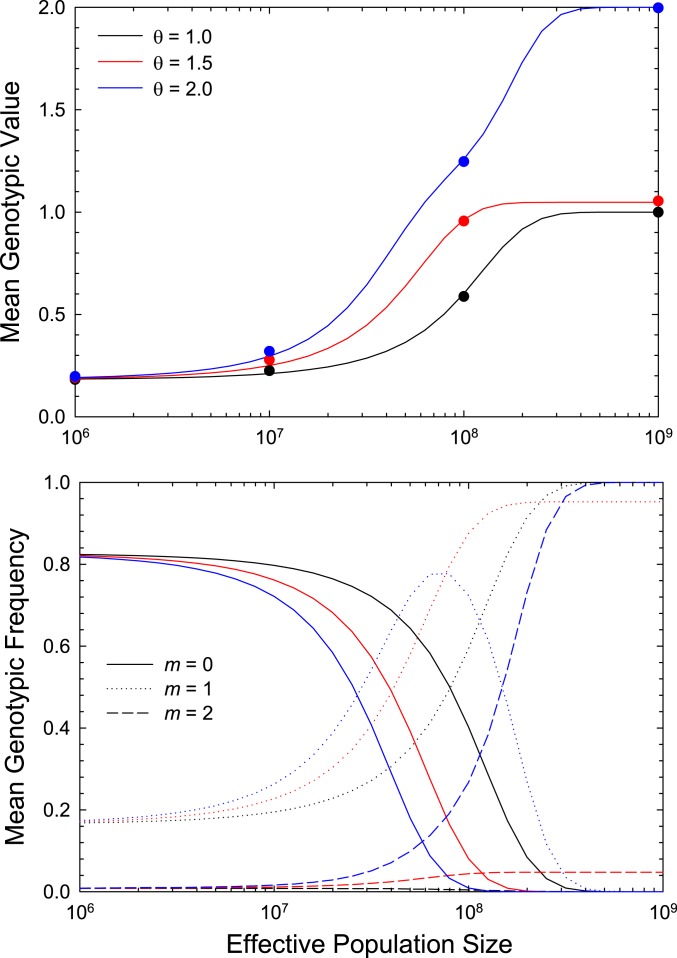
This expansion to a second site introduces complexities not encountered with the one-site model, all of which can be understood by reference to Eq. 3. First, for the case of , where the optimum is straddled by the class 1 and 2 genotypes, the genotypic mean () never reaches the optimum, even at very large , and instead remains much closer to (Fig. 3). This bias results because although the class 1 and 2 genotypes have equivalent fitness, mutation pressure toward alleles weights the frequency of class 1 by a factor of (the 2 being the multiplicity of this class), but class 2 by the smaller factor of .
Fig. 3.
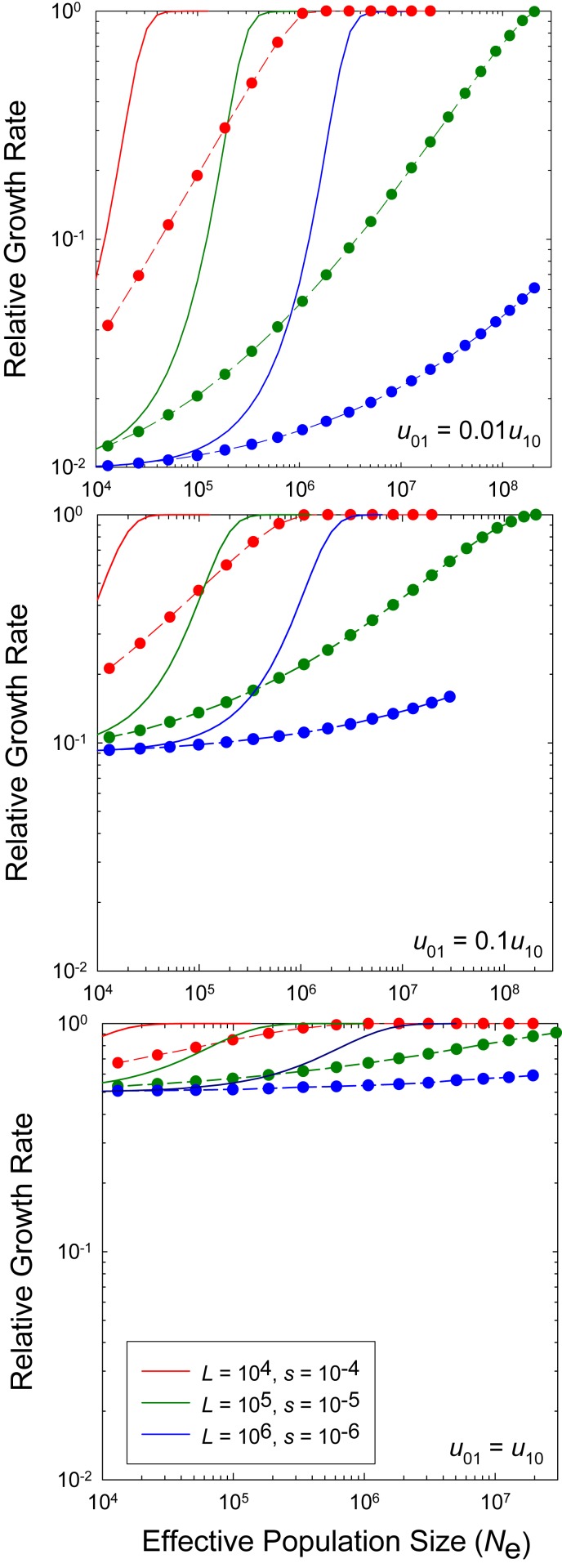
The response of the long-term mean genotypic state (number of + alleles, Upper) and the underlying mean class frequencies (Lower) over a gradient of effective population sizes for a two-locus, two-allele model. The mutation rate to beneficial alleles is 10% of that to deleterious alleles. Results are given for three phenotypic optima, with the width of the fitness function . In Lower panel, for each color-coded optimum, the mean frequencies of the three genotypic classes (0, 1, 2) are given as solid, dotted, and dashed lines, and for each sum to 1.0. Data points in Upper panel were obtained by computer simulations of a Wright–Fisher model, showing the near perfect agreement with the sequential-model approximation.
Second, for the case in which (pure directional selection), there is a progressive succession of the prevailing genotype classes with increasing . When is sufficiently low to impose effective neutrality, class 0 predominates owing to the mutation bias toward alleles. With increasing , selection becomes more effective at promoting class 1, but there remains effective mutation pressure against class 2. Finally, with very large , selection becomes efficient enough to drive class 2 to near fixation, thereby decreasing the incidence of class 1. These results show that, in the face of a constant pattern and strength of selection, the genotypic mean can exhibit a considerable gradient with owing entirely to changes in the power of drift and also that appreciable incidences of all three genotypic classes can be expected over time in lineages with intermediate .
Moderately Complex Traits.
We now turn to the general case of arbitrary , starting with the sequential-fixation view that mutations are rare enough that evolution proceeds in an essentially stepwise manner, with incremental changes being restricted to adjacent states. The absolute flux rates between adjacent genotypic classes are then equal to the products of the expressions on the arrows in Fig. 1, where the numerical coefficients depend on the numbers of and sites within each class. Because the absolute population size influences all mutational flux rates in the same way, it is omitted as a prefactor, but both and influence the equilibrium solution via the fixation probabilities, defined as SI Appendix, Eq. S5.
This linear sequential model has a relatively simple solution. Provided there are nonzero connections between all adjacent states, the steady-state frequencies are proportional to the products of all of the coefficients pointing upwardly and downwardly toward the state of interest. Prior results (4) lead to Eq. 3, which shows that the equilibrium frequencies of the alternative genotypes are functions of three factors: 1) the multiplicity of configurations, as defined by the binomial coefficients; 2) the ratio of mutation rates; and 3) the strength of selection scaled by the power of random genetic drift. All other things being equal, the within-class multiplicity magnifies the likelihood of residing in such a state. However, for , the net effect of the multiplicity is further modified by the mutation bias term, .
Under neutrality (denoted by ), for all , and Eq. 3 simplifies to a binomial distribution
| [5] |
with being the expected frequency of alleles at each site. In this case, the long-term mean and variance of the trait are and , respectively. Comparison of Eqs. 3 and 5 shows that the steady-state probabilities of genotypes under selection are simple transformations of the neutral expectations, with each class being weighted by the exponential function of the scaled strength of selection , with ,
| [6] |
Provided is not overly close to 0.0 or 1.0, the neutral distribution is approximately normal, and if , the steady-state distribution of mean phenotypes with selection will also approach normality, with mean
| [7a] |
and variance
| [7b] |
where (14). Under these conditions, the grand mean is the average of the expectations under mutation and selection alone, with each component weighted by the inverse of the variance under the relevant conditions.
As , which implies a flatter fitness function, the mean and variance converge on the expectations for a purely neutral process, and . As , which implies a flattened distribution under mutation and drift alone, the mean and variance converge on the expectations for a purely selection-driven process, and . The pivot point separating these two domains is , showing that an -fold increase in the width of the fitness function shifts the critical point to an -fold larger .
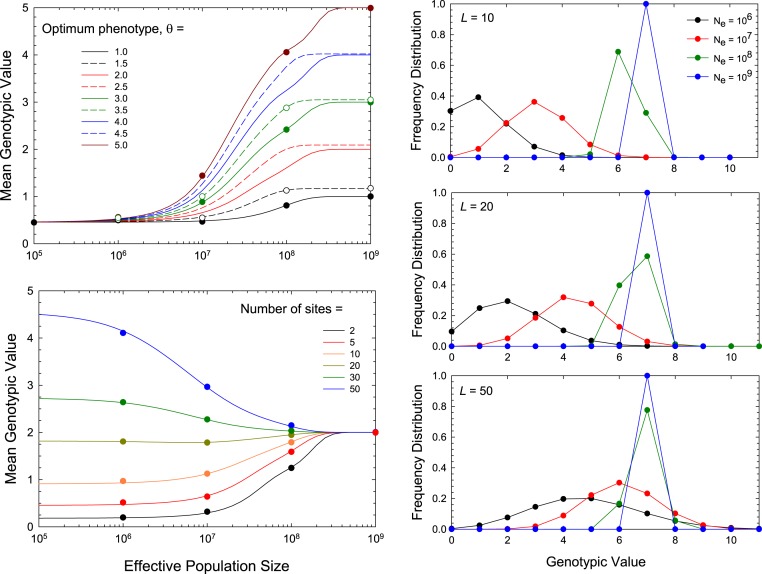
Eq. 6 predicts the steady-state distribution of the most recently fixed state, and one must acknowledge that some small amount of polymorphism exists in the time intervals between fixation. Thus, it is desirable to know how closely the preceding expressions represent the true sampling probabilities when polymorphism is allowed for. To evaluate this issue, extensive Wright–Fisher simulations were carried out, with recursive episodes of selection, mutation, and drift, for long enough periods to achieve highly precise estimates of the distributions of means to compare with the analytical expectations for (SI Appendix). Because violations of the sequential model will be a function of the absolute number of mutations entering the population per generation, it is essential to perform such evaluations with realistic parameter estimates for and the mutation rate, and the scaling relationship between the mutation rate and noted above was adhered to. The consistency of the simulation results with the analytical approximations, even with as high as 50 (Fig. 4, Left), justifies the use of Eq. 6 up to this level of granularity.
Fig. 4.
(Left) Response of the mean genotypic value to change in the effective population size, for the case in which the fitness function has width , and the ratio of mutation rates is . (Upper Left) The effects of increasing the optimum phenotype (), for the case in which there are sites. (Lower Left) The effects of increasing the number of sites from to 50, for the case in which the optimum phenotype is . In both panels, the color-coded plotted points were obtained by computer simulations of a Wright–Fisher model, showing the near perfect agreement with the sequential-model approximation. (Right) Equilibrium genotype distributions (number of alleles) for situations in which (Top), 20 (Middle), and 50 (Bottom), with optimum genotypic value and width of the fitness function . Results from Eq. 6 are given for four effective population sizes.
This expansion to larger numbers of sites again shows significant scaling of mean genotypic values with for a wide range of conditions, upholding the conclusion that situations exist in which the optimal phenotype is rarely achieved even in very large populations (Fig. 4, Left). Moreover, for fixed selection and mutation functions, the direction of scaling of the mean genotype with depends on the complexity of the underlying trait (). If the genotypic mean in the absence of selection () exceeds the genotypic optimum, there will be negative scaling of with , regardless of the direction of mutation bias. In addition, there will always be an intermediate level of , such that the mean under neutrality fortuitously equals the selective optimum, i.e., , at which point there is no response of the mean phenotype to . Finally, for particular population-genetic environments, multiple genotypic classes often have appreciable expected frequencies, and depending on the direction of mutation bias, these can be both above and below the optimum (Fig. 4, Right).
Large Numbers of Loci.
When large numbers of loci contribute to a trait, the total number of mutations entering the population per generation will often exceed 0.01, violating the conditions necessary for the sequential model to closely approximate the steady-state distribution. One such example is the cellular growth rate, which likely depends on essentially every nucleotide in the genome in some way, e.g., the simple bioenergetic cost of a nucleotide pair (15). As a first-order generalization, one expects natural selection to relentlessly promote an organism’s ability to convert energy and other limiting resources into biomass, and persistent directional selection may apply to many other traits such as catalytic rates and error minimization. To analyze the evolution of traits under such selective conditions, an exponential fitness function with independent mutational effects was evaluated,
| [8] |
where is the number of beneficial alleles in the genome.
For random genetic drift to impose a significant barrier to the evolution of such a trait, there must be a substantial pool of deleterious mutations with small enough effects that they can drift to fixation in species with small , and this process will be further facilitated if mutations are biased in the negative direction. Numerous lines of evidence are consistent with both conditions. First, studies of serially bottlenecked mutation-accumulation (MA) lines across diverse species consistently reveal a slow per-generation decline in growth rate and other fitness traits, in accordance with a strong bias of mutations toward deleterious effects (16, 17). Statistical inferences based on the distribution of MA-line performance imply highly skewed distributions of fitness effects, with the modes for both deleterious and beneficial mutations indistinguishable from zero and the bulk of the distributions having absolute effects (18–20). Second, indirect inferences derived from studies on the site-frequency spectra of segregating alleles commonly suggest that 10 to 40% of mutations in diverse organisms have deleterious effects smaller than , with the mode of this pool again being near (if not at) 0.0 (21–25). There are theoretical reasons for expecting this to be the case (26), and as many of these studies focus only on the nonsynonymous sites in protein-coding genes, the true distribution of effects can be expected to be even more skewed toward near-zero values. Third, bioenergetic considerations of the costs of small nucleotide insertions, which typically comprise of de novo mutations (27), imply fractional reductions in fitness typically far below (15). Thus, the existence of large pools of mutations with deleterious effects small enough to allow fixation in some lineages but large enough to ensure removal by selection in others is not in doubt.
These observations allow some simple qualitative statements about the limits to selection. Sites with effects () smaller than will be highly susceptible to the vagaries of genetic drift and have expected deleterious-allele frequencies near . This quantity depends only on the mutation-rate ratio (), not on the absolute mutation rate. In contrast, when , selection overwhelms drift, and the expected frequency of deleterious alleles is approximately , which is near zero when the strength of selection greatly exceeds that of mutation. The central issue is then the degree to which specific classes of deleterious alleles move from the domain of accumulation by mutation pressure to the domain of effective purging by selection as the population size increases. A complication that emerges with large is that the effective population size () is often orders of magnitude below the actual population size () owing to selective interference between simultaneously segregating mutations, which greatly elevates the level of required for the effective purging of mildly deleterious alleles.
Although the ultimate goal is to derive analytical expressions for the distribution of mean phenotypes in this large- domain, the system is sufficiently complex that it is necessary to perform Wright–Fisher simulations to determine the degree of validity of any equations that emerge. For these analyses, for each , it was assumed initially that , which is roughly consistent with the empirical observation that the frequency of mutation types is a decreasing function of the selective effects. Each set of simulations involved a single fixed value of : , ; , ; and , . Example outcomes of the grand means are given in Fig. 5, along with the limiting expectations for single sites (from SI Appendix, Eq. S2, which assumes no background interference from linkage disequilibrium). These results highlight the expectations noted above—at sufficiently small , the mean frequency of alleles converges on the neutral expectation, whereas at large , it converges on frequencies close to 1.0. Notably, however, the gradient in the mean frequency of alleles is much shallower in the case of multiple linked loci than in the ideal single-locus case, particularly when is small.
Fig. 5.
The equilibrium mean frequency of + alleles (i.e., relative to the maximum possible value, ) as a function of the absolute population size. Results are given for three different levels of mutation bias for three numbers of loci () with equivalent additive effects on the growth rate and multiplicative effects on fitness. Absolute mutation rates are defined by the empirical scaling relationship noted in the text. Analytical results (solid lines) are given for the case of free recombination, and simulation results (dashed lines and data points) for the case of complete linkage. Throughout, , the inverse of the number of factors contributing to the trait.
The key remaining challenge is to obtain an approximate analytical expression for the equilibrium behavior in Fig. 5. As outlined in SI Appendix, despite some intriguing relationships, a solution from first principles has not been obtained. Nonetheless, the general scaling behavior in Fig. 5 suggests a formula of the form
| [9] |
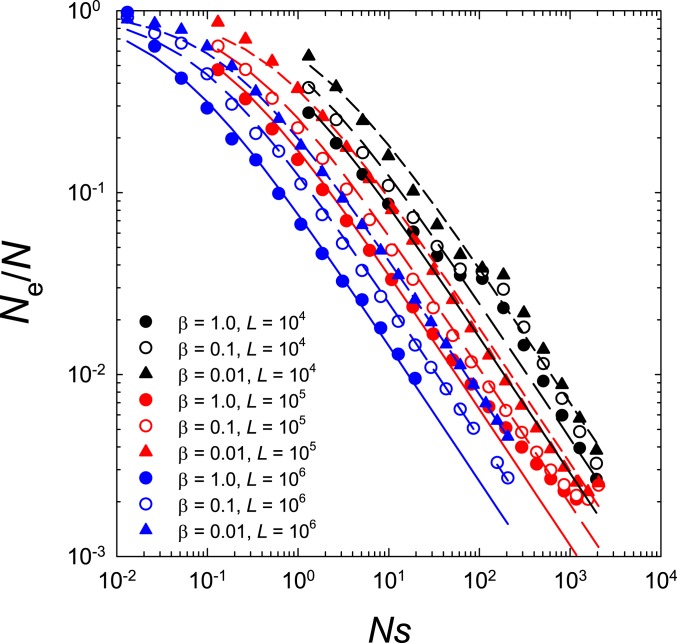
where is a function of and . For Eq. 9 to yield appropriate behavior, must asymptotically approach 0 and 1 in the limits of large and small . A simple expression that allows for such behavior, , is attractive because this yields the known result for the sequential model in which selection operates on a set of single sites without selective interference (Eq. 1), and Charlesworth (ref. 28, equation A13) suggested this as a solution. However, whereas Eq. 1 yields correct results in the limits of and , the predictions are too high at intermediate . The likely reason for the poor fit in this region of parameter space is that the genetic effective population size () can be substantially lower than , owing to parallel selection operating on multiple polymorphic sites.
To gain insight into this matter, Eq. 1 can be rearranged to yield the effective population size necessary to yield the mean frequency of alleles, , observed with computer simulations,
| [10] |
As can be seen in Fig. 6, there appear to be three central determinants of using this formulation. First, provided the strength of selection is at least , scales negatively with the power of , reflecting the increased involvement of selective interference. Second, increases weakly as the incidence of beneficial mutations declines, scaling negatively with the power of , presumably reflecting the reduced competition among simultaneously segregating beneficial mutations. Third, there is a further depression in with increasing , presumably reflecting more background variation in fitness resulting from elevated numbers of simultaneously segregating polymorphisms.
Fig. 6.
Depression in the effective population size as a function of , , and . Points are estimates from the average behavior in simulations, whereas the solid lines map the expected behavior based on Eq. 11. As noted in the text, is varied by keeping the deleterious mutation rate constant (although varying at each population size) and modifying .
Regrettably, it has not been possible to derive an analytical expression encapsulating these three scaling relationships. However, by inspection, all three can be included in a single expression,
| [11] |
which is consistent with observations for the full range of parameter space (Fig. 6), except for and , in which case the population behaves nearly deterministically and is of minor significance. The key scaled selection parameter in Eq. 1, , can then be approximated by multiplying Eq. 11 by , and provided , this reduces further to
| [12] |
Together, Eqs. 11 and 12 show that provided is not too small, then scales only slowly with and the mutation bias , with the key parameter being . The effect of increasing the number of sites is also nonlinear, with a 100-fold increase in decreasing only by a factor of . Finally, decreasing by a factor of 100 increases by a factor , showing that the bulk of the interference in promoting beneficial genotypes derives from simultaneously segregating beneficial alleles.
With Eq. 11 in hand, it then becomes possible to express the equilibrium expectation for the mean fraction of sites occupied by favorable alleles by substituting for in Eq. 1. This yields predictions that are generally within 10% of simulated values for the full range of parameter space and that are particularly accurate with large numbers of loci with small individual selective effects (SI Appendix, Fig. S2). Thus, although there must be additional second-order terms involved, Eq. 11 appears to capture the collective effects of selective interference, at least in the context of mutations with equal effects.
Notably, although the preceding analyses relied on a particular scaling of the mutation rate with , the evolved genotypic mean appears to depend only on the mutational bias . In addition, results for a wide range of indicate that the approximate scalings indicated in Eqs. 11 and 12 are not a peculiarity of the use of in the preceding analyses (SI Appendix, Fig. S3). Finally, although the exact scaling relationships are different, a similarly derived expression for the case of a half-Gaussian fitness function is given in SI Appendix.
These results also provide an interesting contrast to the “infinitesimal” model widely used in quantitative genetics (2, 29). Under this model, the genotypic values of traits are assumed to be influenced by alleles with infinitesimally small effects distributed over an infinite number of loci, such that the mean phenotypes of traits evolve with effectively no change in allele frequencies at individual loci. Despite its mathematical elegance, this model is inconsistent with the fact that all traits are encoded by finite numbers of genetic loci (bounded by the size of the genome) and more notably has the puzzling feature that directional selection is possible despite all allelic effects being miniscule. In contrast, the results in Fig. 5 show that with finite numbers of loci, subdivision of total fitness into increasingly fine contributions progressively diminishes the ability of directional selection to advance a mean phenotype, as expected under the principles of effective neutrality, illustrating the limitations of the mathematically convenient infinitesimal model.
Effects of Recombination.
To this point, the chromosomal segments being modeled have been assumed to be nonrecombining. Given the population sizes employed here, the introduction of recombination into the simulations would be extremely demanding computationally, but an argument introduced by Good et al. (30) provides a simple way to address the matter qualitatively. They demonstrated that the overall behavior of a recombining system with multiple sites simultaneously segregating can be treated by subdividing the genome into blocks that are effectively nonrecombining on the timescale of the coalescent.
From a prior survey (31), we know that the average recombination rate between adjacent bases () is in the range of to for unicellular eukaryotes and to for multicellular species. The exact numbers depend on the overall genome size and numbers of chromosomes, as there is generally on the order of one crossover per chromosome arm. The mean time to coalescence of alleles within a population is on the order of (haploids) to (diploids) generations, so over this duration the expected number of recombination events within a span of length is to . Thus, because is commonly in the range of to for unicellular eukaryotes (10, 13), a span as small as 2 bp will have a high probability of experiencing at least one recombination event in the coalescence time for individual alleles, suggesting that Eq. 1 might serve as a reasonable description of the expected allele frequency in many obligately sexual unicellular populations. However, most unicellular species primarily reproduce asexually, and allowing for recombination every generations would expand the average linkage-block length by a factor of . With in multicellular species generally falling in the range of to , nonrecombining block lengths may commonly fall in the range of to bp in such organisms.
Following these rough guidelines, results of simulations with a range of segment lengths () are given in Fig. 7. For the mutation rates employed herein, and the exponential fitness model, mean allele frequencies are very close to those for the single-site expectations (Eq. 1) when , and those for are only moderately smaller. With increasing block lengths, however, the effects of linkage become increasingly substantial. With , a transition from the neutral expectation to near fixation occurs over a 10-fold range of , whereas with this transition unfolds over a four orders-of-magnitude range of . This is consistent with the gradual three orders-of-magnitude reduction in with increasing noted in Fig. 6. The key point here is that because linkage-block lengths are expected to decline with increasing , in actual comparative analyses of different species, the scaling of the drift barrier with is expected to be a hybrid of the kinds of functions shown in Fig. 7.
Fig. 7.
Expected frequencies of beneficial alleles as a function of and length of the chromosomal segment (in number of sites), for the case in which . Dots are results from computer simulations, whereas the dashed line is the single-site expectation given by SI Appendix, Eq. S2.
Discussion
Although much of population genetics is focused on standing levels of genetic variation and the impact on short-term responses to selection (2), comparative biology is generally concerned with the divergence of mean phenotypes among phylogenetic lineages. There is, therefore, a need for theory focused more on such long timescales (32, 33). The approach taken here starts with the assumption that the forces of mutation, drift, and selection remain relatively constant over long periods of time (tens to hundreds of millions of years), a feasible scenario for many intracellular traits. Even if the steady-state assumption is not fulfilled in every respect, the results still provide insight into the relative likelihoods of lineages wandering into alternative phenotypic states under a given set of population-genetic conditions (34), and the suggested approach can be readily modified to allow for additional factors such as fluctuating selection or alternative mutation functions. This framework of jointly accounting for the forces of selection, mutation, and drift is similar in spirit to the steady-state distributions of allele frequencies at single diallelic loci developed by Wright (35) and provides a conceptual contrast to the common approach among empiricists of simply assuming that the strength of selection is so overwhelming that observed mean phenotypes must precisely reflect optima dictated by the forces of natural selection.
The results here illustrate the riskiness of such an optimization approach. Mutation can cause mean phenotypes to deviate from the optimum in substantial and often unexpected ways that are not simply a function of the magnitude of mutation bias. Rather, when alternative, functionally equivalent underlying genotypes exist for a trait, the multiplicity of certain intermediate combinations can result in a mutational pull of the mean phenotype away from the optimum. This effect becomes especially significant when the phenotypic optimum is far from the expected mean under mutation alone and even more so if the level of multiplicity for the optimum is relatively small relative to other phenotypic states. Such effects can extend to populations with the largest known effective sizes, and, as noted previously (14), cases may even exist in which the selection gradient is sufficiently strong that the equilibrium mean-phenotype distribution can have two peaks, one driven by selection and the other by mutation.
With an increased understanding of the rates and molecular spectra of mutation, the approximate bounds on , and the relationships between these two (10, 13), for cell biological features with well-understood genetic bases, this framework now provides a foundation for exploring the consequences of alternative selection functions for the scaling and diversification of cellular features with lineage-specific estimates of . The challenge for future empirical work will be to obtain estimates of the key functional parameters, which minimally reduce to: 1) , the number of sites (loci) encoding the trait; 2) the ratio of forward to reverse mutations rates, ; 3) , the effective population size; and 4) the mapping of genotypic values to a fitness function. With a focus on Gaussian stabilizing selection, there are just two fitness-function parameters: 1) , the phenotypic optimum, and 2) , the width of the fitness function; and with an exponential fitness function, there is just one parameter.
Notably, the direction and magnitude by which genotypic means scale with are not simply functions of the pattern of selection and mutation bias, but are also influenced by the granularity of the system (i.e., the number of loci). The latter dictates the null distribution of genotypes in the absence of selection, with the selection function (scaled by the power of drift) then transforming the baseline distribution in a multiplicative manner. Expected gradients of genotypic means with respect to can be positive or negative, depending on whether there is an excess or a deficit of mutational accessibility relative to the optimum state. One of the most striking examples consistent with this drift-barrier hypothesis is the negative scaling of the mutation rate per nucleotide site with observed across the tree of life (10). Although the exact results will vary depending on the distribution of fitness effects associated with mutations for particular traits, the kinds of results illustrated in Fig. 6 suggest that for traits under persistent directional selection (such as growth rate), power-law scalings with exponents at least as extreme as 0.20 can be expected in large comparative studies. This raises challenges for fields such as evolutionary and physiological ecology that simply assume that such relationships are consequences of biophysical constraints.
Finally, it is worth noting that because of the degrees of freedom in systems like those illustrated above, isolated species can diverge to nonoverlapping underlying genetic constitutions despite residing in the same functional class. Consider, for example, a four-factor trait with initial state . If each of two descendant species experiences a transition, there is a 50% chance that this will involve different factors, leading to and configurations. Single independent reverse mutations in both lineages have a joint probability of converting these two states back to the class containing two sites but with nonoverlapping states and , implying a 1/9 chance of complete divergence. As becomes larger, the probability of divergent states (in the face of constant selection) increases rapidly owing to the increased degrees of freedom in the overall system.
As one example of such a scenario, consider the phosphorylation of particular amino acid residues on proteins, which commonly plays a role in modifying activity level. Phosphorylation sites are typically clustered on the surface of a protein or in disordered regions, and the critical feature may simply be the acquisition of an adequate local charge. Comparative studies in yeasts and mammals indicate that many phosphorylated serines and threonines are under purifying selection to retain their phosphosite status (6, 36–38). Nonetheless, a large fraction of phosphosites appears free to vary among species in terms of status and location (39–42). For example, only of all Saccharomyces cerevisiae phosphorylation sites appear to have been conserved across the entire yeast lineage (dating back million y), and even when the same phosphorylatable residue is present in two moderately related species, their phosphorylation status may differ. In addition, Asp and Glu residues, which are naturally charged negatively, serve as potential replacements for their phosphorylatable counterparts; i.e., phosphosites often evolve from phosphomimetic Asp and Glu sites and vice versa (43–45). Taken together, these observations suggest a scenario whereby the degree of a protein’s phosphorylation is under stabilizing selection for an appropriate charge, with the specific locations of many of the affected residues free to wander in an effectively neutral fashion (6, 46). That is, the number of phosphorylated residues on individual proteins appears to operate as a sort of quantitative trait under stabilizing selection, but with enough degrees of freedom that there can be considerable turnover of the specific phosphosites.
Aside from the need for a formal derivation of the expected distributions of mean phenotypes that fully account for the distinction between and for the case of large , several things remain to be done to achieve a fuller understanding of the ways in which the drift barrier scales with population size and directional mutation bias. First, although the preceding expressions focus on the expected value of the mean phenotype, there can be considerable drift around the grand mean, so formal expressions for the temporal variance (or among-population variance) of the mean are desirable. This is a potentially significant issue for comparative studies based on small numbers of taxa, as the stochastic variance of means among taxa might be inappropriately assumed to reflect underlying adaptive differences. Second, there is a need to generalize the theory to allow for a distribution of mutational effects, in contrast to the fixed-effects approach taken herein. On the one hand, increasing the variance of mutational effects, while keeping the mean constant, should prolong the gradient of the response of the mean phenotype to population-size change as the fractions of mutations in the smallest populations that are subject to selection and in the largest populations that are subject to drift increase. On the other hand, greater variance in the fitness effects of alleles may increase the efficiency of selective discrimination among simultaneously segregating mutations, thereby reducing the depression of relative to . Finally, as noted above, there is a need for a more direct analysis of the role of recombination than that provided herein, particularly in combination with variable mutational effects.
Supplementary Material
Acknowledgments
This research was supported by the Multidisciplinary University Research Initiative Awards W911NF-09-1-0444 and W911NF-14-1-0411 from the US Army Research Office, NIH Award R35-GM122566-01, and NSF Award MCB-1518060. I thank G. Bolstad, T. Hansen, K. Jain, and B. Trickovic for helpful comments.
Footnotes
The author declares no competing interest.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2000446117/-/DCSupplemental.
References
- 1.Charlesworth B., Charlesworth D., Elements of Evolutionary Genetics (Freeman W. H., 2010). [Google Scholar]
- 2.Walsh J. B., Lynch M., Evolution and Selection of Quantitative Traits (Oxford University Press, 2018). [Google Scholar]
- 3.Berg J., Willmann S., Lässig M., Adaptive evolution of transcription factor binding sites. BMC Evol. Biol. 4, 42 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lynch M., Hagner K., Evolutionary meandering of intermolecular interactions along the drift barrier. Proc. Natl. Acad. Sci. U.S.A. 112, E30–E38 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lynch M., Evolutionary diversification of the multimeric states of proteins. Proc. Natl. Acad. Sci. U.S.A. 110, E2821–E2828 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Landry C. R., Freschi L., Zarin T., Moses A. M., Turnover of protein phosphorylation evolving under stabilizing selection. Front. Genet. 5, 245 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rawicz W., Olbrich K. C., McIntosh T., Needham D., Evans E., Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79, 328–339 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Baudouin-Cornu P., Surdin-Kerjan Y., Marliére P., Thomas D., Molecular evolution of protein atomic composition. Science 293, 297–300 (2001). [DOI] [PubMed] [Google Scholar]
- 9.Acquisti C., Kumar S., Elser J. J., Signatures of nitrogen limitation in the elemental composition of the proteins involved in the metabolic apparatus. Proc. Biol. Sci. 276, 2605–2610 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lynch M., et al. , Genetic drift, selection, and evolution of the mutation rate. Nat. Rev. Genet. 17, 704–714 (2016). [DOI] [PubMed] [Google Scholar]
- 11.Li W. H., Models of nearly neutral mutations with particular implications for non-random usage of synonymous codons. J. Mol. Evol. 24, 337–345 (1987). [DOI] [PubMed] [Google Scholar]
- 12.Bulmer M., The selection-mutation-drift theory of synonymous codon usage. Genetics 129, 897–907 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Long H., et al. , Evolutionary determinants of genome-wide nucleotide composition. Nature Ecol. Evol. 2, 237–240 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lynch M., Phylogenetic diversification of cell biological features. Elife 7, e34820 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lynch M., Marinov G. K., The bioenergetic costs of a gene. Proc. Natl. Acad. Sci. U.S.A. 112, 15690–15695 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lynch M., et al. , Spontaneous deleterious mutation. Evolution 53, 645–663 (1999). [DOI] [PubMed] [Google Scholar]
- 17.Baer C. F., Miyamoto M. M., Denver D. R., Mutation rate variation in multicellular eukaryotes: Causes and consequences. Nat. Rev. Genet. 8, 619–631 (2007). [DOI] [PubMed] [Google Scholar]
- 18.Keightley P. D., The distribution of mutation effects on viability in Drosophila melanogaster. Genetics 138, 1315–1322 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Robert L., et al. , Mutation dynamics and fitness effects followed in single cells. Science 359, 1283–1286 (2018). [DOI] [PubMed] [Google Scholar]
- 20.Böndel K. B., et al. , Inferring the distribution of fitness effects of spontaneous mutations in Chlamydomonas reinhardtii. PLoS Biol. 17, e3000192 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Keightley P. D., Eyre-Walker A., Joint inference of the distribution of fitness effects of deleterious mutations and population demography based on nucleotide polymorphism frequencies. Genetics 177, 2251–2261 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bataillon T., Bailey S. F., Effects of new mutations on fitness: Insights from models and data. Ann. N. Y. Acad. Sci. 1320, 76–92 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huber C. D., Kim B. Y., Marsden C. D., Lohmueller K. E., Determining the factors driving selective effects of new nonsynonymous mutations. Proc. Natl. Acad. Sci. U.S.A. 114, 4465–4470 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kim B. Y., Huber C. D., Lohmueller K. E., Inference of the distribution of selection coefficients for new nonsynonymous mutations using large samples. Genetics 206, 345–361 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lynch M., Ackerman M., Spitze K., Ye Z., Maruki T., Population genomics of Daphnia pulex. Genetics 206, 315–332 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rice D. P., Good B. H., Desai M. M., The evolutionarily stable distribution of fitness effects. Genetics 200, 321–329 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sung W., et al. , Evolution of the insertion-deletion mutation rate across the tree of life. G3 6, 2583–2591 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Charlesworth B., Stabilizing selection, purifying selection, and mutational bias in finite populations. Genetics 194, 955–971 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bulmer M., The effect of selection on genetic variability. Am. Nat. 105, 201–211 (1971). [Google Scholar]
- 30.Good B. H., Walczak A. M., Neher R. A., Desai M. M., Genetic diversity in the interference selection limit. PLoS Genet. 10, e1004222 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lynch M., Bobay L.-M., Catania F., Gout J.-F., Rho M., The repatterning of eukaryotic genomes by random genetic drift. Annu. Rev. Genom. Hum. Genet. 12, 347–366 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lande R., Natural selection and random genetic drift in phenotypic evolution. Evolution 30, 314–334 (1976). [DOI] [PubMed] [Google Scholar]
- 33.Bürger R., Lande R., On the distribution of the mean and variance of a quantitative trait under mutation-selection-drift balance. Genetics 138, 901–912 (1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.McCandlish D. M., Long-term evolution on complex fitness landscapes when mutation is weak. Heredity 121, 449–465 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wright S., Evolution and the Genetics of Populations. The Theory of Gene Frequencies (University of Chicago Press, 1969), vol. 2. [Google Scholar]
- 36.Nguyen Ba A. N., Moses A. M., Evolution of characterized phosphorylation sites in budding yeast. Mol. Biol. Evol. 27, 2027–2037 (2010). [DOI] [PubMed] [Google Scholar]
- 37.Gray V. E., Kumar S., Rampant purifying selection conserves positions with posttranslational modifications in human proteins. Mol. Biol. Evol. 28, 1565–1568 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Levy E. D., Michnick S. W., Landry C. R., Protein abundance is key to distinguish promiscuous from functional phosphorylation based on evolutionary information. Philos. Trans. R. Soc. Lond. B Biol. Sci. 367, 2594–2606 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Moses A. M., Liku M. E., Li J. J., Durbin R., Regulatory evolution in proteins by turnover and lineage-specific changes of cyclin-dependent kinase consensus sites. Proc. Natl. Acad. Sci. U.S.A. 104, 17713–17718 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Holt L. J., et al. , Global analysis of Cdk1 substrate phosphorylation sites provides insights into evolution. Science 325, 1682–1686 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Freschi L., Osseni M., Landry C. R., Functional divergence and evolutionary turnover in mammalian phosphoproteomes. PLoS Genet. 10, e1004062 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Studer R. A., et al. , Evolution of protein phosphorylation across 18 fungal species. Science 354, 229–232 (2016). [DOI] [PubMed] [Google Scholar]
- 43.Kurmangaliyev Y. Z., Goland A., Gelfand M. S., Evolutionary patterns of phosphorylated serines. Biol. Direct 6, 8 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pearlman S. M., Serber Z., Ferrell J. E. Jr, A mechanism for the evolution of phosphorylation sites. Cell 147, 934–946 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Diss G., Freschi L., Landry C. R., Where do phosphosites come from and where do they go after gene duplication? Int. J. Evol. Biol. 2012, 843167 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lienhard G. E., Non-functional phosphorylations? Trends Biochem. Sci. 33, 351–352 (2008). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.