Competitive pricing of substitute products under supply disruption

Abstract

There has been an increased interest in optimizing pricing and sourcing decisions under supplier competition with supply disruptions. In this paper, we conduct an analytical game-theoretical study to examine the effects of supply capacity disruption timing on pricing decisions for substitute products in a two-supplier one-retailer supply chain setting. We investigate whether the timing of a disruption may significantly impact the optimal pricing strategy of the retailer. We derive the optimal pricing strategy and ordering levels with both disruption timing and product substitution. By exploring both the Nash and Stackelberg games, we find that the order quantity with the disrupted supplier depends on price leadership and it tends to increase when the non-disrupted supplier is the leader. Moreover, the equilibrium market retail prices are higher under higher levels of disruption for the Nash game, compared to the Stackelberg game. We also uncover that the non-disrupted supplier can always charge the highest wholesale price if a disruption occurs before orders are received. This highlights the critical role of order timing. The insights can help operations managers to proper design risk mitigation ordering strategies and re-design the supply contracts in the presence of product substitution under supply disruptions.

1. Introduction

Retailers frequently rely on suppliers that are prone to disruptions. In this setting, retailers face the common problem to adjust their pricing and ordering decisions in response to the prevailing supply uncertainty. This is particularly relevant when multiple suppliers offer competing substitute goods when the wholesale price needs to be decided. Our study deals with one specific aspect of this decision-making environment, posing the following research question: how retailers should account for the timing of disruptions at the competing suppliers of substitutable products when making pricing and ordering decisions?

Our main analysis is based on three stylized facts, which we motivate in the following. First, despite the complexity of supply chains (SCs), one can distinguish a dyadic supplier-retailer structure as one of the most common ones in the analysis. There is a growing body of research that studies the impact of a supply disruption to pricing and ordering at retailers [e.g.; [3], [9], [11], [15], [20], [26], [51], [67]], specifically in SCs for beverages, fresh produce, etc. Severe disruptions typically result in supply shortages at the retailer for the disrupted product and retailers employ demand management (such as pricing) and supply management (e.g., placing emergency orders or managing inventory) strategies to mitigate this temporary disruption [19], [27], [29], [36], [38], [41], [42], [43], [46], [58]. For instance, retailers sourcing fresh produce, such as fresh fruits and vegetables, in large quantities from multiple competing suppliers may face supply loss due to crop failures or food contamination. Recently, there was a case of supply disruption of romaine lettuce to retailers and restaurants due to contamination with Shiga-toxin producing E. coli bacteria [47]. A food-safety recall was issued by the Centers for Disease Control and Prevention [6]. This recall led to an increase in the demand and prices of other lettuce produce, and the price of iceberg lettuce increased from $36 before the supply disruption to around $60 (each carton) after the disruption. In addition, several retailers and restaurants such as Panera Bread [40] managed their lettuce supply by intermittently ordering from the suppliers which were not part of the CDC recall notice. During that time, romaine lettuce was still available for sale, however, the product sales were reduced by about 38% (total $7.5 million) in the week ending on November 24, 2018, as compared to the week before that. In conclusion, the supply disruption of romaine lettuce led to an increase in the price and demand of other (substitute) lettuce produce. This disruption also led to a decrease in the sales of (in-stock/ on-shelf) romaine lettuce at the retailers.

We argue that our findings can help explain the firms’ pricing behavior under supply disruptions and provide recommendations to enhance their operations. In particular, we explain the role of product substitution in pricing and sourcing strategies of competing suppliers who work with a common retailer. Considering different constellations of ordering decisions and disruption timing, we propose a method to analyze the existing pricing-ordering policies in the disrupted supply cases and to derive the optimal ones. Factoring the timing of disruption in pricing has a clear practical motivation. Knowing whether a disruption takes place between two orders or after both orders can help a retailer because they can control the pricing decisions when disruption happens. Finally, we include disruption severity and price leadership in our analysis and uncover equilibrium pricing strategies.

Second, the supplier-retailer pricing decisions may not always entail direct competition between products, however, the suppliers of substitutable products are more likely to compete based on prices when there is supply disruption. Thus, supply shortages for food and beverage products, usually short-term, can lead to an increase in retail prices, procurement costs, and the demand for substitute products from alternate suppliers. Besides food and beverage businesses, other businesses resort to managing demand, when facing supply disruption, by offering available substitute products to their customers. For example, facing supply disruption of silicone, a material used to manufacture tires through vulcanization, a company called Ace Products and Consulting LLC used devulcanized silicone as a substitute of silicone [5]. Their CEO, Erick Sharp, stated in 2018: “If we can offset 10% of it (silicone demand), anything helps at this point, especially when you’re trying to equal the price back out.” In this paper, we focus on competitive pricing as a demand management tool that can be used to match supply and demand for substitute products in the event of short-term supply shortages.

Third, we consider the information available to the players regarding the supply disruption. An important determinant in the reliable/unreliable sourcing literature is the information available about the disruption, and more specifically, the availability of information to some players and the non-availability of this information to other players. Gümüş et al. [21], Teunter et al. [49], Yang et al. [59], [60], Yang and Babich [61], and Zhu [68] assume a lack of visibility regarding the disruption risk of a supplier and study different scenarios of information availability/unavailability among the players. Their findings imply, for example, that optimal pricing and ordering profiles can be efficiently derived when considering competing suppliers in different scenarios of information availability/unavailability.

We draw on several theoretical foundations to address the real-world challenges due to supply disruption as described above. The area of supply disruption risk mitigation and recovery is mainly shaped by problems of reliable/unreliable and primary/backup suppliers [[23], [28], [33], [36], [50], [54], [61], [63], [64], to name a few]. Most studies consider how changes to some operational parameters (e.g., capacity disruptions) impact sourcing and customer performance. There is a strong and growing literature in the given area, with methodologies grounded in the newsboy problem extensions and game theory. Typically, a two-stage sourcing system is considered where a single product can be sourced from both unreliable (less expensive) and reliable (more expensive) suppliers [12], [50]. In this problem domain, competition, pricing, and contracting issues have been the research focus [for e.g., [4], [66]], resolving the trade-off between supply reliability vs costs. While studies have established the salience of optimal pricing and ordering policies in single product cases, including supplier portfolio diversification, little attention has been directed to substitutable products sold by competing suppliers.

The reviewed research shows a diversity of knowledge and findings of supplier disruption risk management in the SC. At the same time, new practical cases motivate researchers to extend existing modeling frameworks. In particular, the issues of product substitution in the case of disruption can be considered as an interesting research avenue. Even if the power imbalance with substituable products was studied in literature [for e.g., 17], the inclusion of product substitution effects on the pricing and ordering decisions under supply disruption was considered only in a few recent papers [7], [37], [51]. Our literature analysis provides evidence that supply disruptions may lead to price fluctuations due to supply shortages. For example, the devastating shortage of flu vaccinations that occurred in the US in 2004, which was caused by bacterial pollution, led to an increase in the vaccination price from $60 to $800 [64]. The earthquake in Japan also resulted in the increasing prices for products affected by the natural disaster [18], [34]. While natural disasters may cause supply interruption and the resulting price fluctuations, in other settings, the opposite effect can be observed when the price increases cause supply interruptions. For example, French discounter E. Leclerc had refused to accept Coca-Cola’s price increases request in 2018 which left several stores without the product for several weeks [39]. Leclerc had to allegedly contact another source to acquire the popular drinks.

One of these new cases that we observed in person, was encountered in spring 2017 when a leading beverage producer’s distribution center was disrupted and remained out of operation for about three months leading to supply shortage to its retailers1 The resulting supply shortage was partially mitigated at most retailers by sourcing the product from a competing supplier. This spurred our initial motivation to extend the existing body of knowledge with regards to product substitution issues. Such questions have arisen as pricing strategy sensitivity to disruption among competitors at one supplier, or the impact of disruption on retailer’s ordering behavior and the price policy of non-disrupted suppliers who know about their competitor’s disruptions has become more apparent. Should non-disrupted suppliers charge a higher (or lower) wholesale price to capitalize on the lost supply? Does a retailer always loses money because of a potential loss in supply and a potential increase in the wholesale prices? The literature is scarce in answering these significant questions, specifically, the effects of disruption timing, the sequence of ordering decisions by suppliers and bi-directional product substitution.

More recently, due to the Coronavirus COVID-19 pandemic outbreak there have been widespread supply disruptions. Supply availability in most SCs has been drastically reduced and led to massive demand mismatches even for products with relatively stable demand [31], [32] such as meat products in the United States [65] and CO₂ for beverage production [57]. The analysis and insights from our paper can be utilized by SC managers to mitigate the impacts of supply uncertainty due to the pandemic in the short term by placing appropriate emergency orders and setting retail prices accordingly.

A comprehensive literature analysis led us to three papers that consider both supply disruptions and product substitution [51], utilized product substitution as one parallel policy for supplier disruption risk mitigation in terms of demand switching [37]; explored downward substitutable products (i.e., only higher-grade products can be substituted for lower-grade ones); and Chakraborty et al. [7], who studied a system with two competing manufacturers and a common retailer, which is similar to our study, but they considered complete information about capacity disruption. Meanwhile, the literature highlights the importance of sourcing re-configuration as an important dimension to withstand the disruptions and adapt [2], [8], [35], [50]. None of these studies, though, have formally and rigorously quantified the optimal pricing and ordering configuration by adapting the sourcing decisions. Moreover, the impact of supply disruption timing has not been explicitly specified. In contrast to these studies, we do not consider the demand switching effect, but the supply switching perspective of product substitution, bi-directionally substitutable products, and incomplete information about supply disruptions. Such a perspective appears to be more relevant in a practical decision environment, relative to inherent problems in adapting the pricing and ordering decisions on the changes in the supplier base [9], [25], [34], [56].

Our model makes the following significant contributions to the literature. First and principally, we study for the first time the effects of customers’ substitution behavior due to a supply disruption on the pricing strategies of competing suppliers who work with a common retailer. Specifically, we study competing suppliers who deliver substitute products to a retailer, and the effects of supply disruption timing on pricing decisions for substitute products in a two-supplier, one-retailer SC setting. We hypothesize that the timing of disruption may significantly impact the optimal pricing and ordering decisions at the retailer. We prove the existence of an equilibrium pricing strategy and ordering levels, and conceptualize a novel model setting that captures both disruption timing and product substitution.

Given the aforementioned model settings, we construct a model that combines a novel problem setting to comprehensively investigate the impact of product substitution in the presence of a supply disruption. Such a combination is unique in the literature and captures some of the complexities of sourcing decisions in practice. It considers the timing of disruptions, pricing, and sourcing decisions and product substitution, all of which as a whole may generate significantly different results as compared to previous research. We show that the associations of disruption timing and severity and price leadership with the optimal pricing and ordering configuration can be efficiently deciphered by our approach. We examine the equilibrium pricing strategies of the suppliers and the retail prices and investigate different problem settings regarding the timing of disruption and price leadership in the supply chain.

The rest of this study is organized as follows. Section 2 analyzes the recent literature. Section 3 is devoted to benchmark modeling of the considered problem setting. In Section 4, the disruptions are modeled with the consideration of their differing scale and timing, as well as the SC leadership. Analytical and numerical analyses along with extensions incorporating the likelihood of disruption and timing are presented in Section 5 and Section 6, respectively. The managerial insights are generated in Section 7. Section 8 concludes the paper by summarizing the main insights, limitations of this study, and outlining future research avenues.

2. Literature review

This paper builds on and contributes to several streams of research in operations management (OM). First, it relates to supply reliability [15], [30]. In the literature, Tomlin [50] and Chopra et al. [12] study a sourcing system where a single product can be sourced from both unreliable and reliable suppliers. Their findings highlight how costs, capacity (limited or unlimited), and volume flexibility affect the optimal selection of contingency policies, such as risk mitigation inventory and capacity flexibility. Serel [44] explores a supply chain system with one retailer, a manufacturer, and an unreliable supplier under the extended newsboy problem setting. The author shows the existence of a Nash equilibrium under the competitive pricing game setting. He also reveals that in a Stackelberg game led by the manufacturer, the retailer is expected to earn a higher profit when excess demand is backordered. Note that a similar scenario with a two-product system is studied by Tomlin and Wang [53]. Chen et al. [8] extend [50] and [12] to investigate a periodic-review inventory system with stochastic demand and limited backup supplier capacity. He et al. [25] show that supply reliability thresholds play a critical role in buyer procurement strategy choices. Ang et al. [2] find that a manufacturer’s optimal sourcing strategy depends on the degree of overlap of suppliers in the supply network.

Second, some prior studies explore the presence of multiple competing suppliers with reliability concerns. For instance, Babich et al. [4] study a supply chain system with two competing suppliers and one retailer and consider the supplier default risk. The authors find that a low supplier default correlation would dampen competition among suppliers, and increase the equilibrium wholesale prices. Li et al. [35] analyze how pricing power affects a firm’s decisions to source from two unreliable suppliers. The authors prove that a supplier can win larger orders by increasing their reliability. Chen and Yang [9] consider a supply chain system with two suppliers and one retailer where the production of the primary supplier has a random yield, and the shortage can be compensated by the backup supplier. The authors generate insights by comparing different gaming structures, namely the buyer-Stackelberg model and the supplier-Stackelberg model. Hu and Kostamis [28] investigate a supply chain with one reliable supplier and one unreliable supplier. They show that the total order quantity and its allocation between the two suppliers are independent decisions. Gupta et al. [22] study the implications of a contingent sourcing strategy under competition and the probable occurrence of supply disruption. The authors highlight the importance of backup cost and customer sensitivity.

Third, a few studies have considered both pricing and sourcing decisions. For example, under a common reliable/unreliable supplier setting, Li et al. [36] analyze a committed pricing scenario, where the firm makes the pricing decision before the supply uncertainty is resolved. The authors also explore the responsive pricing scenario, where the firm’s pricing decision is made after the supply uncertainty is resolved. Assuming a commonly used linear price-dependent demand function, Kumar et al. [34] examine the retailer’s pricing decisions and sourcing strategies under disruption risk with retail competition. The authors explore price adjustment and splitting orders strategies in the presence of expensive and reliable, cheaper and unreliable suppliers. This paper also follows this line of research and considers both pricing and sourcing decisions but with different focal points and model settings.

As a remark, several published papers in the literature have considered both supply disruptions and product substitution. To be specific, Tomlin [51] compares three policies for supplier disruption risk mitigation. Among them, one policy is on product substitution. Note that, different from Tomlin [51], we do not consider the demand switching effect, but we focus on the supply switching perspective of product substitution. Lu et al. [37] study a common single period system where two substitute products can be sourced from a reliable and expensive supplier or an unreliable and cheaper supplier. The products in their study are downward substitutable (i.e., only higher-grade products can substitute for lower- grade ones). The author proves that product substitution increases the expected marginal benefit of dual sourcing for the higher-grade product. Different from Lu et al. [37], we consider bi-directionally substitutable products. Chakraborty et al. [7] study a system with two competing manufacturers and a common retailer. The authors formulate a newsboy problem-based model to determine the optimal price and quantity and study the non-cooperative games in the supply chain.

Observe that some prior studies point out the importance of full and incomplete information in analyzing sourcing disruption risk. For instance, Tomlin [52] studies the impact of supply learning when suppliers are unreliable using a Bayesian approach. Gümüş et al. [21] assume a lack of visibility regarding the disruption risk of a supplier. They consider a system with a buyer and two competing suppliers in a typical setting and analyze issues and effects of supplier selection based on price and quantity guarantees. Wakolbinger and Cruz [55] consider strategic information sharing and risk-sharing contracts for supply disruption risks. Zhu [68] study four different scenarios of disruption source and information availability. Other studies considering information asymmetry are presented by Yang et al. [59], [60], Yang and Babich [61]. Note that this paper does not explicitly consider information asymmetry and hence are different from them.

Other important related studies on supply risk management include Hu et al. [29] who explore the role of capacity restoration to deal with supply disruptions, Chen [10] who examines how beliefs and supply disruptions affect operations efficiency, Tang et al. [48] who study supply disruptions with the considerations of reliability of the supply process, Gao et al. [20] who investigate supply risk management, Dong et al. [15] who study production disruptions and how insurance can be used to help, and Hwang et al. [30] who reveal how the commonly used wholesale pricing contract performs well in the supply chain with supply disruptions.

Overall, this paper relates to the above-reviewed literature as it also focuses on exploring supply disruptions through an analytical approach. In fact, it can be treated as an extension of various prior studies by investigating the impacts of product substitution on supplier disruption risk mitigation in the following problem setting:

• 1.The system consists of one retailer and two suppliers, and the retailer aims to maximize its profits by adjusting pricing policies. Product substitution (between two products supplied by the respective suppliers) is considered whereby products are bi-directionally substitutable. Different timing in relation to the ordering decisions and disruption in the supply chain is examined. Price leadership in the supply chain is considered.
• 2.The linear price-dependent demand function is applied, which has been widely used in the OM literature, such as Deo and Corbett [14], Anderson and Bao [1], Shang et al. [45], Ha et al. [24], and Kumar et al. [34].
• 3.Supply disruptions risk can be modeled using different modeling approaches including random yield, all-or-nothing supply, and stochastic capacity. In this paper, for analytical tractability as well as fitness to our scope, we use the random yield modeling approach [9], [13], [62] in our study, i.e., in this model, the quantity received by a buyer is a random fraction of the quantity ordered from the disrupted supplier.

Last but not least, from the extant literature and observed industrial practices, there is no doubt that facing supply disruptions, both substitute products and timing of ordering are critically important. However, the issue is under-explored in the literature. As such, this paper fills this important gap. To the best of our knowledge, the model constructed in this paper and the specific problems have not yet been examined in the literature.

3. Model

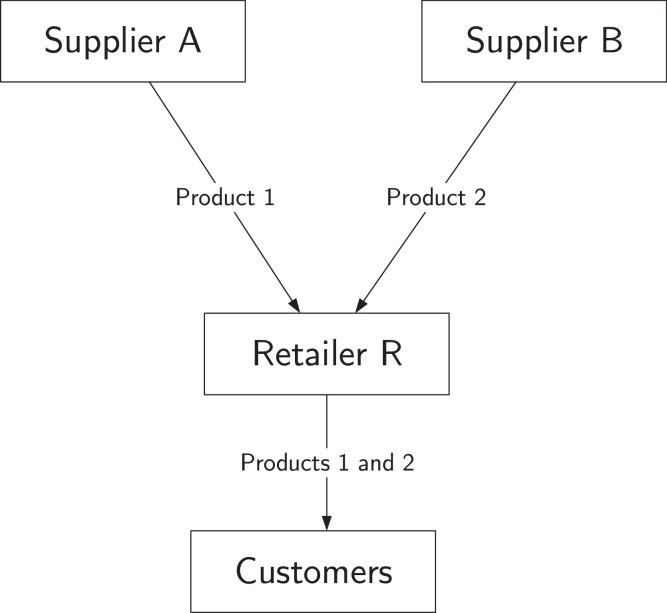
We study a supply chain (SC) (Fig. 1 ) with a common retailer (R), who sources products 1 and 2 (e.g., two beverage products), from two competing suppliers, A and B, respectively. R sells these products to customers in a market, where the customers choose to buy either product 1 or 2 based on the prices at the retailer and their own product preferences. The aggregate demands for the products are given by:

$$D_1(p_1,p_2)={\alpha }_1-{\beta }_{11}{p}_1+{\beta }_{12}{p}_2,\text{and}{D}_2(p_1,p_2)={\alpha }_2+{\beta }_{21}{p}_1-{\beta }_{22}{p}_2,$$

where α_i is the market potential for product i, and β_ii and β_ij are the price elasticity and cross-price elasticity of product i. Considering ${\beta }_{11}={\beta }_1>0,{\beta }_{21}={\beta }_2>0,{\beta }_{12}={\beta }_{21}=1>0,$ and β_i ≥ 1, i ∈ {1, 2}. The last assumption indicates that the own-price elasticity of each product (β_i) is greater than the cross-price elasticity (1), i.e., the change in price of a product has a significantly higher impact on its demand as compared to the change in price of the substitute product. Also, the assumption β_i ≥ 1 ensures concavity of the profit functions. This results in simplified aggregate demands of:

$$\begin{array}{ccc}\hfill D_1(p_1,p_2)& =& {\alpha }_1-{\beta }_1{p}_1+p_2,\text{and}{D}_2(p_1,p_2)={\alpha }_2+p_1-{\beta }_2{p}_2.\hfill \\ & \end{array}$$ (1)

R purchases product 1 from A and product 2 from B at unit wholesale prices w ₁ and w ₂, respectively. These wholesale prices include transportation costs. The costs per unit of supplying (includes their procurement costs) the products for suppliers A and B are c ₁ and c ₂, respectively. The pricing decisions in the SC involve setting the wholesale prices by suppliers A and B and the retail prices by the retailer R. The retail prices are market clearing, i.e, they are set such that demand consumes all available supply. In other words, there is no surplus or deficit inventory at R after the market demand for the products is realized. This feature is important as we focus on pricing as a demand management tool to match supply and demand, as a result, the retailer sets market clearing retail prices.

Fig. 1.

Supply chain structure.

First, we present a benchmark case analysis where there is no disruption of supply. Based on the timing of the pricing decisions, there are two possible scenarios for the benchmark case. In the first scenario, the suppliers set the wholesale prices at the same time (or at different times), i.e., R can place orders to A and B simultaneously (or at different times), and in the second scenario, one of the suppliers leads the other supplier in setting the wholesale price. These two scenarios are presented in Fig. 2 : case a) both suppliers are jointly (wholesale) price-leaders; case b) where supplier A or B is the price-leader, respectively. We do not discuss a scenario where R leads with the setting of the retail prices, and then the suppliers subsequently set the wholesale prices; because in this particular setting, A and B can simply set the wholesale prices on par with the retail prices and extract all the profits from R. We analyze the aforementioned scenarios in the following subsections.

Fig. 2.

Possible benchmark cases with suppliers as price-leaders.

3.1. Analysis without supply disruption - both suppliers lead

We solve the game (case (a) in Fig. 2) as a two-stage game: in the first stage, A and B simultaneously set the wholesale prices w ₁ and w ₂, respectively, and receive orders from R. This is a Nash game between A and B. We refer to this game as the benchmark Nash game and use the subscript “n” where applicable. In the second stage, R sets the market clearing prices p ₁ and p ₂ for the products. We solve this game by using the backward induction method, i.e., by solving the optimal centralized prices $p_1^{*}(w_1,w_2)$ and $p_2^{*}(w_1,w_2)$ for the second stage, and then using those prices to determine the equilibrium wholesale prices $w_1^e$ and $w_2^e$ in the first stage. Let us now derive the optimal centralized prices for R given the wholesale prices (w ₁, w ₂).2 The objective function for retailer R is given by: ${\Pi }_{R,n}^{*}(w_1,w_2)={\max }_{(p_1,p_2)}{\Pi }_{R,n}(p_1,p_2;w_1,w_2),\text{where}{\Pi }_{R,n}(p_1,p_2;w_1,w_2)=(p_1-w_1)({\alpha }_1-{\beta }_1{p}_1+p_2)+(p_2-w_2)({\alpha }_2+p_1-{\beta }_2{p}_2).$

Lemma 1

Π_{R, n}(p ₁, p ₂; w ₁, w ₂) is jointly concave in p ₁ and p ₂ for the given wholesale price contracts (w ₁, w ₂).

From Lemma 1, we obtain the centralized equilibrium prices under the Nash game by solving the first order conditions such that: $p_{1,n}^{*}(p_2;w_1,w_2)={\displaystyle \frac{{\alpha }_1+2p_2+{\beta }_1{w}_1-w_2}{2{\beta }_1}},$ and $p_{2,n}^{*}(p_1;w_1,w_2)={\displaystyle \frac{{\alpha }_2+2p_1+{\beta }_2{w}_2-w_1}{2{\beta }_2}}$. We then obtain the optimal centralized prices only as functions of (w ₁, w ₂), i.e., $p_{1,n}^{*}(w_1,w_2)$ and $p_{2,n}^{*}(w_1,w_2)$ as:

$$\begin{array}{ccc}\hfill p_{1,n}^{*}\left(w_1\right)& =& {\displaystyle \frac{{\alpha }_1{\beta }_2+{\alpha }_2}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_1}{2}},\text{and}\hfill \\ \hfill p_{2,n}^{*}\left(w_2\right)& =& {\displaystyle \frac{{\alpha }_2{\beta }_1+{\alpha }_1}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_2}{2}}.\hfill \end{array}$$ (2)

Lemma 2

The centralized retail price $p_{i,n}^{*}\left(w_i\right)$ is increasing in wholesale price w_i, market sizes (α ₁, α ₂), and decreasing in the product’s own price elasticity β_i and the other product’s price elasticity ${\beta }_{-i}$ .

Now, we solve the first stage of the game, where A and B set w ₁ and w ₂, respectively. The objectives for A and B are: ${\max }_{w_1}(w_1-c_1)D_1(p_1,p_2)$ and ${\max }_{w_2}(w_2-c_2)D_2(p_1,p_2),$ respectively. We have Lemma 3.

Lemma 3

Each supplier’s profit is concave in its own wholesale price and linearly increases in the other supplier’s wholesale price.

From Lemma 3 and (2), we obtain the Nash equilibrium wholesale prices $(w_{1,n}^e,w_{2,n}^e)$. We can determine the best responses of A and B: $w_1\left(w_2\right)={\displaystyle \frac{{\alpha }_1+w_2}{2{\beta }_1}}+{\displaystyle \frac{c_1}{2}},$ and $w_2\left(w_1\right)={\displaystyle \frac{{\alpha }_2+w_1}{2{\beta }_2}}+{\displaystyle \frac{c_2}{2}}$.

The Nash equilibrium is obtained by solving these two best responses simultaneously as follows:

$$\begin{array}{ccc}\hfill w_{1,n}^e& =& {\displaystyle \frac{{\alpha }_2+{\beta }_2(2({\alpha }_1+{\beta }_1{c}_1)+c_2)}{4{\beta }_1{\beta }_2-1}},\text{and}\hfill \\ \hfill w_{2,n}^e& =& {\displaystyle \frac{{\alpha }_1+{\beta }_1(c_1+2({\alpha }_2+{\beta }_2{c}_2))}{4{\beta }_1{\beta }_2-1}}.\hfill \end{array}$$ (3)

We assume that $w_{1,n}^e>c_i$. Therefore, we have: ${\alpha }_{-i}+2{\beta }_{-i}{\alpha }_i+{\beta }_{-i}{c}_{-i}+c_i>2{\beta }_1{\beta }_2{c}_i,$ for $i=\{1,2\}$.

From (2) and (3), we can obtain the equilibrium centralized retail prices $p_{i,n}^e:=p_{i,n}^{*}\left(w_{i,n}^e\right)$ in closed form:

$$\begin{array}{ccc}\hfill p_{1,n}^e& =& \frac{{\alpha }_1{\beta }_2+{\alpha }_2}{2({\beta }_1{\beta }_2-1)}+{\displaystyle \frac{w_1^e}{2}}={\displaystyle \frac{{\alpha }_1{\beta }_2+{\alpha }_2}{2({\beta }_1{\beta }_2-1)}}\hfill \\ & & +{\displaystyle \frac{{\alpha }_2+{\beta }_2(2({\alpha }_1+{\beta }_1{c}_1)+c_2)}{2(4{\beta }_1{\beta }_2-1)}},\text{and}\hfill \\ \hfill p_{2,n}^e& =& {\displaystyle \frac{{\alpha }_2{\beta }_1+{\alpha }_1}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_2^e}{2}}={\displaystyle \frac{{\alpha }_2{\beta }_1+{\alpha }_1}{2({\beta }_1{\beta }_2-1)}}\hfill \\ & & +\frac{{\alpha }_1+{\beta }_1(2({\alpha }_2+{\beta }_2{c}_2)+c_1)}{2(4{\beta }_1{\beta }_2-1)}.\hfill \end{array}$$ (4)

To avoid trivial cases, we have $p_{i,n}^e>w_{i,n}^e,$ i.e., ${\displaystyle \frac{{\alpha }_i{\beta }_{-i}+{\alpha }_{-i}}{{\beta }_1{\beta }_2-1}}>{\displaystyle \frac{{\alpha }_{-i}+{\beta }_{-i}(2({\alpha }_i+{\beta }_i{c}_i)+c_{-i})}{4{\beta }_1{\beta }_2-1}},$ for $i=\{1,2\}$.

Finally, using the retail prices from (4), we can fully obtain the quantities ordered $(q_{1,n}^e,q_{2,n}^e)$ by the retailer R, and the profits realized by R, A, and B to complete the analysis for the benchmark case.

$$q_{1,n}^e={\alpha }_1-{\beta }_1{p}_{1,n}^e+p_{2,n}^e,\text{and}{q}_{2,n}^e={\alpha }_2-{\beta }_2{p}_{2,n}^e+p_{1,n}^e.$$ (5)

Proposition 1

i) Equilibrium wholesale prices $w_{i,n}^e$ and retail prices $p_{i,n}^e$ are decreasing in the price sensitivity parameters β_i and ${\beta }_{-i}$ . ii) $w_{i,n}^e\ge w_{-i,n}^e$ if ${\displaystyle \frac{{\alpha }_i-{\beta }_i{c}_i}{2{\beta }_i-1}}\ge {\displaystyle \frac{{\alpha }_{-i}-{\beta }_{-i}{c}_{-i}}{2{\beta }_{-i}-1}},$ and $p_{i,n}^e\ge p_{-i,n}^e$ if ${\displaystyle \frac{{\alpha }_i-{\beta }_i{c}_i}{2{\beta }_i-1}}\ge {\displaystyle \frac{{\alpha }_{-i}-{\beta }_{-i}{c}_{-i}}{2{\beta }_{-i}-1}}$ and ${\displaystyle \frac{{\alpha }_i}{{\beta }_i-1}}\ge {\displaystyle \frac{{\alpha }_{-i}}{{\beta }_{-i}-1}}$ .

Proposition 1. i) states that both the wholesale and retail prices decrease when demand elasticity of either one of the products increases. This price decrease is driven by competition between the suppliers to sell to their common retailer. In order to induce demand for a product with higher elasticity, the market price must be lowered, which results in lower retail prices. Consequently, the upstream wholesale price must also go down for the same product. However, due to price competition between the suppliers, the other supplier must reduce the wholesale price of its own product as well to compete. In the Nash game, a supplier can set a higher wholesale price than its competitor if the supplier has a larger customer base (α_i), a lower cost c_i or customer’s are less sensitive to it’s price (an indication of product loyalty) β_i as compared to the same parameters for the competing supplier. This result is summarized in Proposition 1. ii)

3.2. Analysis without supply disruption - supplier A leads or supplier B leads

We now study case (b) as presented in Fig. 2, where one of the suppliers leads the other in receiving orders from R. Note that we study the scenario when A leads: results will be symmetric for the scenario when supplier B leads. This is a Stackelberg game between A and B, where A is the leader and B is the follower. We use subscript ‘s_A’ to represent expressions when A leads the SC, and ‘s_B’ when B leads the SC. We solve the game as a three-stage game: in the first stage, the wholesale price w ₁ is determined by A, who then receives an order for product 1 from R. This stage is followed by B setting w ₂ and receiving an order from R in the second stage. In the third (final) stage, R sets the market clearing prices p ₁ and p ₂ for the products. The analysis for the third stage is similar to the analysis in Section 3.1. Specifically, the second stage presented in Section 3.1 is identical to the third stage in this case, and therefore, the expressions for the optimal centralized retail prices are identical to (2).

Now, we solve the second stage, where w ₂ is set by B as:

$$w_{2,s_A}^{*}\left(w_1\right)=\arg \underset{w_2}{\max }(w_2-c_2)D_2(p_{1,s_A}(w_1,w_2),p_{2,s_A}(w_1,w_2)),$$

where $p_{1,s_A}$ and $p_{2,s_A}$ are obtained from (2). It is easy to see that Lemma 3 will continue to hold in this scenario. Therefore, there are unique $w_{2,s_A}\left(w_1\right)={\displaystyle \frac{{\alpha }_2+w_1}{2{\beta }_2}}+{\displaystyle \frac{c_2}{2}}$ and $w_{1,s_A}\left(w_2\right)$. We find the equilibrium wholesale price $w_{1,s_A}^e$ in the first stage by solving $w_{1,s_A}^e=\arg {\max }_{w_1}(w_1-c_1)D_1(p_{1,s_A}\left(w_1\right),p_{2,s_A}\left(w_1\right))$ as follows:

$$\begin{array}{ccc}\hfill w_{1,s_A}^e& =& {\displaystyle \frac{2{\alpha }_1{\beta }_2+{\alpha }_2+{\beta }_2{c}_2}{2(2{\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_1}{2}},\text{and}\hfill \\ \hfill w_{2,s_A}^e& =& {\displaystyle \frac{1}{4}}({\displaystyle \frac{{\alpha }_2+c_1}{{\beta }_2}}+{\displaystyle \frac{2({\alpha }_1+{\alpha }_2{\beta }_1)+c_2}{2{\beta }_1{\beta }_2-1}})+{\displaystyle \frac{c_2}{2}}.\hfill \end{array}$$ (6)

From (2) and (6), we derive $p_{i,s_A}^e:=p_{i,s_A}^{*}(w_1^e,w_2^e)$ in closed form.

$$\begin{array}{ccc}\hfill p_{1,s_A}^e& =& {\displaystyle \frac{{\alpha }_1{\beta }_2+{\alpha }_2}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_1^e}{2}}={\displaystyle \frac{{\alpha }_1{\beta }_2+{\alpha }_2}{2({\beta }_1{\beta }_2-1)}}\hfill \\ & & +{\displaystyle \frac{2{\alpha }_1{\beta }_2+{\alpha }_2+{\beta }_2{c}_2}{4(2{\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_1}{4}},\text{and}\hfill \\ \hfill p_{2,s_A}^e& =& {\displaystyle \frac{{\alpha }_2{\beta }_1+{\alpha }_1}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_2^e}{2}}={\displaystyle \frac{{\alpha }_2{\beta }_1+{\alpha }_1}{2({\beta }_1{\beta }_2-1)}}\hfill \\ & & +{\displaystyle \frac{1}{8}}({\displaystyle \frac{{\alpha }_2+c_1}{{\beta }_2}}+{\displaystyle \frac{2({\alpha }_1+{\alpha }_2{\beta }_1)+c_2}{2{\beta }_1{\beta }_2-1}})+{\displaystyle \frac{c_2}{4}}.\hfill \end{array}$$ (7)

Finally, using the wholesale and retail prices from (6) and (7), we obtain the quantities ordered $(q_{1,s_A}^e,q_{2,s_A}^e)$ by R, and the profits realized by R, A, and B to complete the analysis for the benchmark cases. We present the equilibrium retail prices and the wholesale prices when B leads the SC by symmetry, i.e., by simply switching the indices “1 and 2” with “2 and 1”, respectively, in the above analysis. The equilibrium wholesales price for A and B when B leads are:

$$\begin{array}{ccc}\hfill w_{1,s_B}^e& =& {\displaystyle \frac{1}{4}}({\displaystyle \frac{{\alpha }_1+c_2}{{\beta }_1}}+{\displaystyle \frac{2({\alpha }_2+{\alpha }_1{\beta }_2)+c_1}{2{\beta }_1{\beta }_2-1}})+{\displaystyle \frac{c_1}{2}},\text{and}\hfill \\ \hfill w_{2,s_B}^e& =& {\displaystyle \frac{2{\alpha }_2{\beta }_1+{\alpha }_1+{\beta }_1{c}_1}{2(2{\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{2}},\hfill \end{array}$$ (8)

and the equilibrium centralized retail prices $p_{i,s_B}^e$ in closed form are:

$$\begin{array}{ccc}\hfill p_{1,s_B}^e& =& {\displaystyle \frac{{\alpha }_1{\beta }_2+{\alpha }_2}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_1^e}{2}}={\displaystyle \frac{{\alpha }_1{\beta }_2+{\alpha }_2}{2({\beta }_1{\beta }_2-1)}}\hfill \\ & & +{\displaystyle \frac{1}{8}}({\displaystyle \frac{{\alpha }_1+c_2}{{\beta }_1}}+{\displaystyle \frac{2({\alpha }_2+{\alpha }_1{\beta }_2)+c_1}{2{\beta }_1{\beta }_2-1}})+{\displaystyle \frac{c_1}{4}},\text{and}\hfill \\ \hfill p_{2,s_B}^e& =& {\displaystyle \frac{{\alpha }_2{\beta }_1+{\alpha }_1}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_2^e}{2}}={\displaystyle \frac{{\alpha }_2{\beta }_1+{\alpha }_1}{2({\beta }_1{\beta }_2-1)}}\hfill \\ & & +{\displaystyle \frac{2{\alpha }_2{\beta }_1+{\alpha }_1+{\beta }_1{c}_1}{4(2{\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{4}}.\hfill \end{array}$$ (9)

Comparisons of equilibrium wholesale and retail prices, order quantities, and profits

We now compare the wholesale and retail prices, order quantities, and profits across the benchmark cases. In the Nash game, there is a higher competition between suppliers A and B as compared to the Stackelberg gaming cases when A or B leads the SC. A higher degree of competition between the suppliers leads to lower wholesale prices and consequently lower retail prices. This result is presented below as Theorem 1. i). Interestingly, we note that lower prices do not always result in larger order quantities, and only the follower in the SC receives a larger order quantity as compared to the order quantity in the Nash game as outlined in Theorem 1. ii). This occurs because a price decrease or increase by the leading supplier can be easily followed by the other supplier by a price reduction or increment, respectively. Hence the second mover gains an advantage by being able to respond to the price of the competing supplier; this observation is in confirmation with the economics literature on price competition e.g. [16]. Theorem 1. iii) observes that the retailer benefits from a higher competition (Nash) between A and B and earns a higher profit. Theorem 1. iv) indicates that the follower in the Stackelberg game always earns a higher profit as compared to its profit in the Nash game, as it receives a larger order quantity and sells at a higher wholesale price as compared to the Nash alternative. This result is interesting, as in a typical Stackelberg game, the leader of SC is known to have the first-mover advantage, but our result shows the other way round. Theorem 1. v) presents the upper bound on the increase in profit of supplier A as the Stackelberg leader of the pricing game. Both suppliers set a higher wholesale price and earn a higher profit as compared to the profit, while only B receives a larger order as compared to the order quantity under the Nash game. A is able to earn a higher profit with a smaller order size by increasing w_A but there is an upper bound on the increase in profit given by 9/8 or an increase of 12.5%.

Theorem 1

i) The equilibrium wholesale and retail product prices for the Stackelberg game are higher than the corresponding wholesale and retail prices for the Nash game: $\{w_{i,s_A}^e,w_{i,s_B}^e\}>w_{i,n}^e$ and $\{p_{i,s_A}^e,p_{i,s_B}^e\}>p_{i,n}^e$ for $i=1,2$ . ii) The equilibrium order quantity for the product ordered first is lower, i.e., $q_{1,s_A}^e<q_{1,n}^e<q_{1,s_B}^e,$ whereas order quantity for the product ordered second is higher $q_{2,s_A}^e>q_{2,n}^e>q_{2,s_B}^e$ than the corresponding order quantities in Nash equilibrium. iii) The retailer’s profit is higher when orders are placed simultaneously than when the orders are placed separately, i.e., ${\Pi }_s^{R,e}<{\Pi }_n^{R,e}$ . iv) Comparing the profits under the Nash equilibrium, supplier B earns a higher profit as a follower of supplier A, i.e., ${\Pi }_{s_A}^{B,e}>{\Pi }_n^{B,e}$ . v) Supplier A, as the leader, always earns a higher profit under the Stackelberg game with an upper bound of $1<{\Pi }_{s_A}^{A,e}/{\Pi }_n^{A,e}\le 9/8$ .

4. Analysis with supply disruption

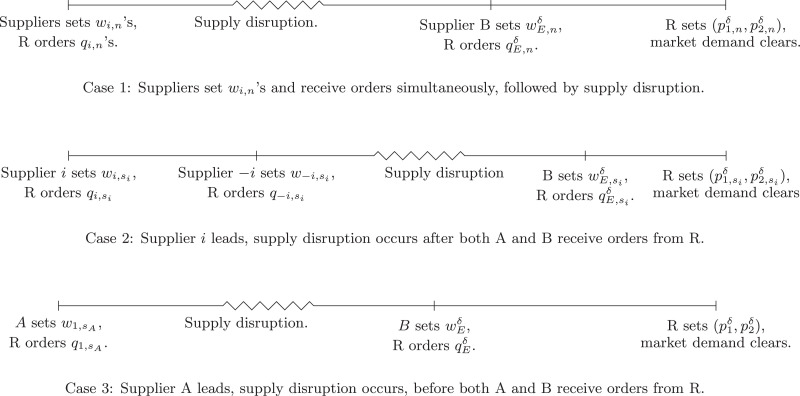
Under the framework shown in Section 3, we now introduce the scenarios with supply disruption (Fig. 3 ). In the event of a disruption, supplier A cannot supply the entire ordered quantity to R. This modeling feature is motivated by the example of a beverage supplier in Moscow. Once upon a time, when its beverage supply was disrupted, it could only supply a portion from its supply capacity. In addition, we assume that the disruption occurs after A has received the order from R and, due to disruption, A can supply only a fraction δ ∈ [0, 1] of the undisrupted order quantity. In the special case when $\delta =0,$ A cannot supply any quantity to R. This special case reflects the scenarios when food products such as lettuce were recalled by the CDC in the United States, and this recall was limited to only suppliers from a particular geographic location [6]. In the above examples, supply disruption information was public knowledge (i.e., news and public announcements). Thus, in our study, we also assume that the extent of supply disruption is common knowledge to A, B, and R. Subsequently, all decisions before the disruption in the SC are identical to the corresponding decisions in the benchmark cases.

Fig. 3.

Possible sequence of events based on the timings of the orders by R with the suppliers, and the supply disruption at A.

In order to analyze the impact brought by the timing of the disruption, we discuss three scenarios which are based on the timing of the disruption and price-leadership in the market, as presented in Fig. 3. In the first case, both suppliers simultaneously receive orders from R, then disruption occurs at A, and R places an emergency order with quantity q_E to B at a wholesale price w_E. Finally, the retailer sets the market prices and demand is realized. When one supplier leads the other, the disruption at A can occur after the other supplier receives the order (Case 2) or before the other supplier receives the order (Case 3). In the first two scenarios, there are always two orders with B: a regular order placed before the disruption and an emergency order placed after the disruption. In Case 3, R places only a single emergency order with B at the wholesale price w_E of quantity q_E. In the following subsections, we analyze and discuss the three cases in detail. It is easy to see in Case 1 and Case 2 that A and B receive orders identical to the equilibrium order quantities in benchmark Cases a) and b), respectively. In Case 3, A receives an order quantity identical to the equilibrium quantity in Case 2 when A is the leader. This information is useful for the analysis and comparisons.

4.1. Case 1: Suppliers lead simultaneously

We follow the steps similar to those in Section 3.1 and solve the game as a three-stage game. For the first stage, the regular wholesale prices $(w_{1,n}^e,w_{2,n}^e)$ and the order quantities $(q_{1,n}^e,q_{2,n}^e)$ are identical to the equilibrium wholesale prices as given by (3) and the order quantities in benchmark case a), respectively. This is because the supply disruption occurs after all these decisions are realized in stage 1. We need to derive the equilibrium emergency order quantity q_E, the corresponding wholesale price w_E, and the equilibrium retail prices (p ₁, p ₂). Using the backward induction method, we solve the last stage first and derive the optimal centralized prices for R, given the regular wholesale prices $(w_1,w_2)=(w_{1,n}^e,w_{2,n}^e)$ and the supply constraint on A: $q_1=\delta q_{1,n}^e,\delta \in [0,1)$. The quantity of product 1 received by R is given by $\delta q_{1,n}^e$. Since market prices are set to be market clearing, we have: $\delta q_{1,n}^e=D_1(p_1,p_2)={\alpha }_1-{\beta }_1{p}_1+p_2$. Therefore, the objective function for retailer R is given by:

$$\begin{array}{ccc}& & \underset{(p_1,p_2)}{\max }(p_1-w_1)\delta q_{1,n}^e+p_2({\alpha }_2+p_1-{\beta }_2{p}_2)\hfill \\ & & -w_{2,n}^e{q}_{2,n}^e-w_E({\alpha }_2+p_1-{\beta }_2{p}_2-q_{2,n}^e).\hfill \end{array}$$

Due to the additional constraint $\delta q_{1,n}^e={\alpha }_1-{\beta }_1{p}_1+p_2,$ the objective function for R can be reduced to only one variable p ₁ as:

$$\begin{array}{ccc}& & \underset{p_1}{\max }(p_1-w_1)\delta q_{1,n}^e+(\delta q_{1,n}^e-{\alpha }_1+{\beta }_1{p}_1)\hfill \\ & & ({\alpha }_2+p_1-{\beta }_2(\delta q_{1,n}^e-{\alpha }_1+{\beta }_1{p}_1))-w_{2,n}^e{q}_{2,n}^e\hfill \\ & & -w_E({\alpha }_2+p_1-{\beta }_2(\delta q_{1,n}^e-{\alpha }_1+{\beta }_1{p}_1)-q_{2,n}^e).\hfill \end{array}$$ (10)

It is easy to see from the second order condition that the retailer’s objective function is concave in p ₁ (and p ₂), and thus we obtain the unique maximizer directly from the first order condition:

$$\begin{array}{ccc}\hfill p_{1,n}^{*}\left(w_{E,n}\right)& =& {\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2{\beta }_1({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{2({\alpha }_1-\delta q_{1,n}^e)+w_{E,n}}{2{\beta }_1}},\text{and}\hfill \\ \hfill p_{2,n}^{*}\left(w_{E,n}\right)& =& {\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_{E,n}}{2}}.\hfill \end{array}$$ (11)

Using the centralized prices in (11), we solve the equilibrium wholesale price decision by B in the second stage. Supplier B’s objective for the emergency order is: ${\max }_{w_E}(w_E-c_2)q_E\left(w_E\right)={\max }_{w_E}(w_E-c_2)({\alpha }_2+p_1^{*}\left(w_E\right)-{\beta }_2{p}_2^{*}\left(w_E\right)-q_{2,n}^e),$ as $q_E\left(w_E\right)={\alpha }_2+p_{1,n}^{*}\left(w_E\right)-{\beta }_2{p}_{2,n}^{*}\left(w_E\right)-q_{2,n}^e$. From the first order condition, we obtain:

$$w_{E,n}^e={\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1-2\delta q_{1,n}^e-2{\beta }_1{q}_{2,n}^e}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{2}}.$$ (12)

Note that the order quantities $(q_{1,n}^e,q_{2,n}^e)$ are those derived in the benchmark case in Section 3.1. We can derive the retail prices in closed form by substituting $w_{E,n}=w_{E,n}^e$ from above in the expressions for $p_{1,n}^{*}\left(w_{E,n}\right)$ and $p_{2,n}^{*}\left(w_{E,n}\right)$ in (7).

$$\begin{array}{ccc}\hfill p_{1,n}^{\delta ,e}& =& {\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2{\beta }_1({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{2({\alpha }_1-\delta q_{1,n}^e)+w_{E,n}^e}{2{\beta }_1}}\hfill \\ & =& {\displaystyle \frac{3({\alpha }_1+{\alpha }_2{\beta }_1)-2\delta q_{1,n}^e-2{\beta }_1{q}_{2,n}^e}{4{\beta }_1({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{{\alpha }_1-\delta q_{1,n}^e}{{\beta }_1}}+{\displaystyle \frac{c_2}{4{\beta }_1}},\hfill \\ \hfill p_{2,n}^{\delta ,e}& =& {\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_{E,n}^e}{2}}={\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2({\beta }_1{\beta }_2-1)}}\hfill \\ & & +{\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1-2\delta q_{1,n}^e-2{\beta }_1{q}_{2,n}^e}{4({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{4}}\hfill \\ & =& {\displaystyle \frac{3({\alpha }_1+{\alpha }_2{\beta }_1)-2\delta q_{1,n}^e-2{\beta }_1{q}_{2,n}^e}{4({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{4}}.\hfill \end{array}$$ (13)

This completes the analysis for Case 1.

4.2. Case 2: Supply disruption after placing orders to suppliers

In Case 2, when the supply disruption occurs, both suppliers have received the purchase orders from R. We have two cases based on price leadership in the SC. We analyze and present both the cases - i) A leads the SC, and ii) B leads. From Theorem 1, we note the differences in equilibrium prices and profits due to the difference in price leadership. Specifically, the Stackelberg follower in the benchmark case has a second mover advantage and earns a higher profit as compared to the profit earned under Nash game or when it acts as the Stackelberg leader. In addition, through our analysis, we wish to examine the difference in the impact of disruption at the preferred supplier (with whom R places an order first) versus disruption at the not-preferred supplier (with whom R places an order subsequently).

The analysis is similar to the previous analysis in the benchmark case (3.2) and the analysis of the case when supply disruption occurs after purchase orders are placed simultaneously to A and B (4.1). Specifically, the wholesale prices set by A and B before the supply disruption will follow the wholesale prices in (6), and the analysis for the final stage where R sets the market prices following (10). Next, we discuss the two cases of price-leadership in detail.

4.2.1. A leads the supply chain

Supplier A is the leader and B is the follower in receiving the purchase orders from R. After the purchase orders are received, there is a supply disruption at A; the wholesale prices w ₁, and w ₁ are identical to the prices in the benchmark case (6). Because of the supply disruption, R places an emergency order to B. As a result of this additional order, R's objective function while setting the retail prices is identical to (10), and thereby, the centralized prices $(p_1^{*}\left(w_E\right),p_2^{*}\left(w_E\right))$ have expressions identical to (11). Therefore,

$$\begin{array}{ccc}\hfill p_1^{*}\left(w_{E,s_A}\right)& =& {\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2{\beta }_1({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{2({\alpha }_1-\delta q_{1,s_A}^e)+w_{E,s_A}}{2{\beta }_1}},\text{and}\hfill \\ \hfill p_2^{*}\left(w_{E,s_A}\right)& =& {\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_{E,s_A}}{2}}.\hfill \end{array}$$ (14)

Note that (11) and (14) are algebraically similar except for the order quantity before disruption and the emergency order quantity. Thus, we can argue that the expression for the emergency wholesale price will be similar to (12), where $q_{1,s_A}^e$ and $q_{2,s_A}^e$ are the equilibrium order quantities, as they were in the benchmark case 2 (Section 3.2). Therefore, we have

$$w_{E,s_A}^e={\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1-2\delta q_{1,s_A}^e-2{\beta }_1{q}_{2,s_A}^e}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{2}}.$$ (15)

We can derive the retail prices in closed form by substituting $w_E=w_E^e$ from above in the expressions for $p_1^{*}\left(w_{E,s_A}\right)$ and $p_2^{*}\left(w_{E,s_A}\right)$ in (14).

$$\begin{array}{ccc}\hfill p_{1,s_A}^{\delta ,e}& =& {\displaystyle \frac{3({\alpha }_1+{\alpha }_2{\beta }_1)-2\delta q_{1,s_A}^e-2{\beta }_1{q}_{2,s_A}^e}{4{\beta }_1({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{{\alpha }_1-\delta q_{1,s_A}^e}{{\beta }_1}}+{\displaystyle \frac{c_2}{4{\beta }_1}},\hfill \\ \hfill p_{2,s_A}^{\delta ,e}& =& {\displaystyle \frac{3({\alpha }_1+{\alpha }_2{\beta }_1)-2\delta q_{1,s_A}^e-2{\beta }_1{q}_{2,s_A}^e}{4({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{4}}.\hfill \end{array}$$ (16)

The case where B leads the supply chain is identical to that where A leads the supply chain due to symmetry, just replace A with B and vice-versa in the associated expressions.

4.3. Case 3: Supply disruption occurs before all orders to suppliers

In this scenario, the supply disruption occurs before all orders are received by the suppliers, i.e., supply disruption occurs after A receives an order from R but before B receives an order. Thus, A leads the SC, and since B has not yet received an order, R places a single emergency order to B. As in the benchmark case b) where supplier A leads, in the first stage, A charges the same wholesale price, as presented in (6). R orders the corresponding quantity of product 1 ($q_1^e$) as in Section 3.2 but receives only $\delta q_{1,s_A}^e$ because of the supply disruption. We obtain the equilibrium wholesale price w_E charged by B for the emergency order. The retail prices are obtained using the backward-induction method. In the last stage, R’s objective function is to determine optimal retail prices: ${\max }_{(p_1,p_2)}(p_1-w_1)\delta q_{1,s_A}^e+(p_2-w_E)({\alpha }_2-{\beta }_2{p}_2+p_1),$ where $\delta q_{1,s_A}^e=D_1(p_1,p_2)={\alpha }_1-{\beta }_1{p}_1+p_2$. We can express the dual variable objective function in terms of a single variable p ₁ (or p ₂) as follows:

$$\begin{array}{ccc}& & \underset{p_1}{\max }(p_1-w_1)\delta q_{1,s_A}^e+(\delta q_{1,s_A}^e-{\alpha }_1+{\beta }_1{p}_1-w_E)\hfill \\ & & ({\alpha }_2-{\beta }_2(\delta q_{1,s_A}^e-{\alpha }_1+{\beta }_1{p}_1)+p_1).\hfill \end{array}$$

The above objective function is concave in p ₁, and we can simply use the first order condition to derive $p_1^{*}\left(w_E\right)$ and then $p_2^{*}\left(w_E\right)$ as:

$$\begin{array}{ccc}\hfill p_1^{*}\left(w_E\right)& =& {\displaystyle \frac{(2{\beta }_1{\beta }_2-1){\alpha }_1+{\alpha }_2{\beta }_1+(w_E-2\delta q_{1,s_A}^e)({\beta }_1{\beta }_2-1)}{2{\beta }_1({\beta }_1{\beta }_2-1)}}\hfill \\ & =& {\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2{\beta }_1({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_E+2({\alpha }_1-\delta q_{1,s_A}^e)}{2{\beta }_1}},\hfill \\ \hfill p_2^{*}\left(w_E\right)& =& {\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1+w_E({\beta }_1{\beta }_2-1)}{2({\beta }_1{\beta }_2-1)}}={\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_E}{2}}.\hfill \end{array}$$ (17)

Using expressions for $p_1^{*}\left(w_E\right)$ and $p_2^{*}\left(w_E\right)$ in (17), we can solve the equilibrium emergency wholesale price charged by the supplier B whose objective is: ${\max }_{w_E}(w_E-c_2)({\alpha }_2-{\beta }_2{p}_2^{*}\left(w_E\right)+p_1^{*}\left(w_E\right))$. The equilibrium wholesale price for B is:

$$w_E^{\delta ,e}={\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1-2\delta q_{1,s_A}^e}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{2}}.$$ (18)

From (17) and (18), the equilibrium retail prices are:

$$\begin{array}{ccc}\hfill p_1^{\delta ,e}& =& {\displaystyle \frac{3({\alpha }_1+{\alpha }_2{\beta }_1)-2\delta q_{1,s_A}^e}{4{\beta }_1({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{4({\alpha }_1-\delta q_{1,s_A}^e)+c_2}{{\beta }_1}},\text{and}\hfill \\ \hfill p_2^{\delta ,e}& =& {\displaystyle \frac{3({\alpha }_1+{\alpha }_2{\beta }_1)-2\delta q_{1,s_A}^e}{4({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{4}}.\hfill \end{array}$$ (19)

5. Analytical and numerical comparisons

In this section, we quantify the impacts of price leadership and supply disruption on wholesale prices (Section 5.1), retail prices (Section 5.2), and profits (Section 5.3). The comparisons of equilibrium wholesale and retail prices, and profits for the retailer and suppliers based on price leadership are not immediate from the above analysis. Thus, we discuss them in more detail in this section. For the cases when analytical results cannot be found, we resort to numerical analysis to quantify and illustrate the important results found in this paper.

We specify the model parameters for numerical analysis as follows. The base model parameters are ${\alpha }_1={\alpha }_2=1,$ ${\beta }_1={\beta }_2=2,$ $c_1=c_2=0.33,$ $\delta =0.25$. These specific values of model parameters have been adopted from Kumar et al. [34] for numerical analysis (except for ${\beta }_1={\beta }_2=2$ and $\delta =0.25$). We generate scenarios by systematically varying the model parameters to generate relevant scenarios from the base scenario. Our results are robust and valid for a wider range of model parameters than those presented in the paper, for brevity.

5.1. Impact of the timing of disruption on wholesale prices

In order to quantify the impact of price leadership, we analytically compare the equilibrium wholesale prices across the three cases presented in Section 4, i.e., we compare (12), (15), and (18). It is reasonable to argue that supplier B charges more for an emergency order as the level of disruption at supplier A increases. We would expect that the higher emergency order’s wholesale price, the higher the retail price will be.

Lemma 4

When A leads, we have: $w_{E,s_A}^e>w_{E,n}^e$ only if $\delta \in ({\displaystyle \frac{{\beta }_1{\beta }_2}{2{\beta }_1{\beta }_2-1}},1)$ . However, when B leads, we have: $w_{E,s_B}^e>w_{E,n}^e,\forall \delta \in [0,1)$ .

Lemma 4 outlines the comparison between the emergency wholesale prices based on price leadership in the SC. Specifically, Lemma 4 notes that supplier A charges a higher equilibrium emergency wholesale price than what it will charge in the corresponding Nash game, but only for low levels of disruption when A leads the SC. However, when B leads the SC, the equilibrium emergency wholesale price is always higher than the corresponding price that will be charged in the Nash game. This result is surprising: the equilibrium wholesale prices charged by A and B are both higher than their Nash gaming counterparts in the Stackelberg games for the benchmark cases, as shown in Theorem 1. i). Therefore, intuitively the emergency wholesale prices must also be higher than the Nash game counterpart. However, this occurs only when B leads the SC. This result is driven by Theorem 1. ii) which posits that the quantity ordered to supplier A is lower when A leads the SC than when B leads the SC. Consequently, if there is a low level of disruption, then the supply R loses from A is not high, and B can charge a higher emergency wholesale price for the smaller quantity of product 2 ordered by R. However, when B leads the SC, the impact of disruption is high. This is because the quantity ($q_{1,s_B}^e$) ordered with supplier A is higher compared to the quantity ordered in the corresponding Nash game, ($q_{1,n}^e$), resulting in a higher emergency wholesale price.

Lemma 5

Under disruption, the equilibrium emergency order price before both suppliers receive orders is higher compared to the emergency order price after both suppliers receive orders, i.e., $w_E^e>\{w_{E,n}^e,w_{E,s_A}^e,w_{E,s_B}^e\}$ . Additionally, we have: $w_E^e>w_{E,s_B}^e>w_{E,n}^e\forall \delta ,$ and $w_E^e>w_{E,s_B}^e>w_{E,n}^e>w_{E,s_A}^e\forall \delta \in [0,{\displaystyle \frac{{\beta }_1{\beta }_2}{2{\beta }_1{\beta }_2-1}})$ .

Lemma 5 extends the result in Lemma 4 by including a comparison with the emergency wholesale price in Case 3. It is interesting to observe that supplier B is always able to charge the highest wholesale price if the disruption occurs before any orders are received. This highlights how the timing of supply disruption coupled with price leadership impacts the wholesale price for the emergency order.

Compared to the emergency wholesale price charged when R simultaneously places orders to A and B, the emergency wholesale price charged by B is only lower when R first places an order to A if there is a high level of disruption, specifically $\delta \in [0,{\displaystyle \frac{{\beta }_1{\beta }_2}{2{\beta }_1{\beta }_2-1}})$. This result is derived from Lemma 4, presented below as Theorem 2, and captures the role played by timing of the disruption and ordering in determining wholesale prices. Generally, compared to the Stackelberg game, the Nash game leads to lower wholesale prices in the market because of the greater level of competition between the suppliers. In Theorem 1. i), we have already observed this well-known phenomenon in the benchmark cases.

Theorem 2

When disruption is more serious (δ is low), the equilibrium emergency order’s wholesale price when A leads the SC is lower compared to the emergency order’s wholesale price in the corresponding Nash game, i.e., $w_{E,s_A}^e<w_{E,n}^e$ if $\delta \in [0,{\displaystyle \frac{{\beta }_1{\beta }_2}{2{\beta }_1{\beta }_2-1}})$ .

In Theorem 2, note that when supplier A’s supply disruption is serious, i.e., the quantity supplied to R is very low as compared to original order quantity to A, the emergency order’s wholesale price charged by B is higher even when A leads the SC as compared to the emergency wholesale price for the Nash game. Observe from Lemma 4 that this order relationship between the wholesale prices does not hold when the supply disruption is not too serious (i.e., $\delta \in \left[{\displaystyle \frac{{\beta }_1{\beta }_2}{2{\beta }_1{\beta }_2-1}}\right),1)$. The reason for this interesting observation can be explained using Theorem 1. ii). We know that, in the Nash game, the equilibrium order quantity $q_{2,n}^e$ ($q_{1,n}^e$) is lower (higher) compared to the order quantity $q_{2,s_A}^e$ ($q_{1,s_A}^e$) in the Stackelberg game. When the level of disruption is high (δ is low) and $q_1^e$ is high, A fulfills a much smaller quantity of the original order for product 1. Consequently, R would place a larger order to B for product 2 and thus, B charges a higher emergency price in the Nash game since $q_{1,n}^e>q_{1,s_A}^e$. This effect is further pronounced by the fact that the initial order $q_{2,n}^e<q_{2,s_A}^e$ is lower in the Nash game where both suppliers lack price leadership. Overall, the theorem provides insights into the influence of the sequence of ordering and disruption on the pricing behavior of the emergency supplier. Thus, when a retailer is working with a supplier facing disruption, it is better to order first with them only when the disruption is serious to secure a better emergency order wholesale contract price.

Proposition 2

The equilibrium emergency order’s wholesale price and the equilibrium retail prices decrease as the level of disruption decreases.

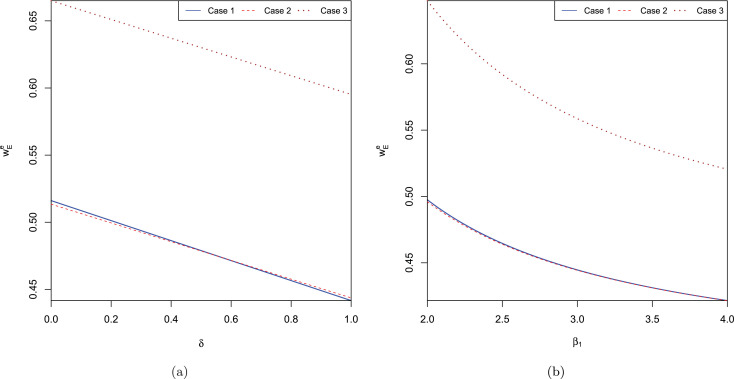
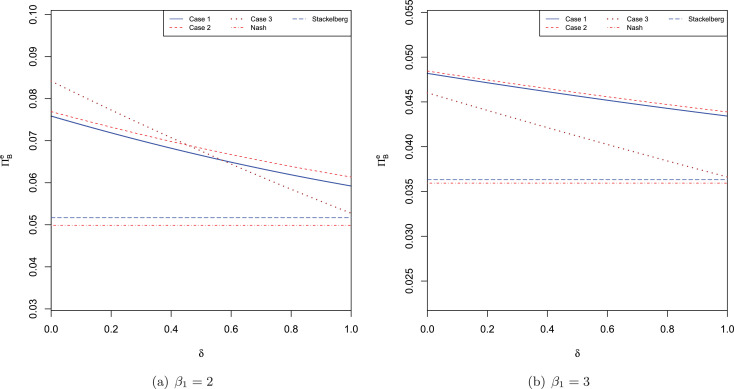
Proposition 2, illustrated below in Fig. 4 (a), formalizes the argument that both the wholesale price and retail price increase as the level of disruption increases. The greater the disruption, the more supplier B charges for the emergency order, and consequently, R sets a higher retail price. Moreover, Proposition 1. i) continues to apply to the emergency wholesale prices, i.e, $w_E^e$ decreases in the product price elasticity β ₁ and β ₂ (Fig. 4 (b)).

Fig. 4.

Variation of the equilibrium emergency wholesale price $w_E^e$ with δ and β₁.

5.2. Impact of the timing of disruption on retail prices

Now we study the impact of price leadership and supply disruption on the equilibrium retail prices. Intuitively, the retail prices should be directly affected by the emergency wholesale price, as noted in (11). Subsequently, similar to Lemmas 4 and 5, we obtain the order relationships between the equilibrium retail prices. Lemma 6 presents results similar to Lemmas 4 and 5, but the level of supply disruption is even lower (due to the double marginalization effect in the SC) for $p_{1,s_A}^{\delta ,e}>p_{1,n}^{\delta ,e}$. The arguments for Lemmas 4 and 5 continue to apply to Lemma 6.

Lemma 6

i) $p_{1,s_A}^{\delta ,e}>p_{1,n}^{\delta ,e}$ if $\delta \in ({\displaystyle \frac{4{\beta }_1{\beta }_2}{{(2{\beta }_1{\beta }_2-1)}^2}},1)$ .

ii) $p_1^{\delta ,e}>p_{1,s_B}^{\delta ,e}>p_{1,n}^{\delta ,e}$ . Also, if $\delta \in [0,{\displaystyle \frac{4{\beta }_1{\beta }_2}{{(2{\beta }_1{\beta }_2-1)}^2}}),$ we have $p_1^{\delta ,e}>p_{1,s_B}^{\delta ,e}>p_{1,n}^{\delta ,e}>p_{1,s_A}^{\delta ,e}$ .

iii) The equilibrium retail price for the undisrupted product follows: $p_2^{\delta ,e}>p_{2,s_B}^{\delta ,e}>p_{2,n}^{\delta ,e}\forall \delta ,$ and $p_2^{\delta ,e}>p_{2,s_B}^{\delta ,e}>p_{2,n}^{\delta ,e}>p_{2,s_A}^{\delta ,e}\forall \delta \in [0,{\displaystyle \frac{{\beta }_1{\beta }_2}{2{\beta }_1{\beta }_2-1}})$ .

The equilibrium market retail prices charged by R to customers are higher under more serious disruption for the Nash game when both suppliers receive orders simultaneously, as compared to the corresponding retail prices in the Stackelberg game. Again, the arguments for Theorem 2 and (11) can be used jointly to explain this interesting phenomenon. The retail prices for the products are directly proportional to the emergency wholesale price for products across all cases. This result, based on the timing of ordering and the level of disruption, is presented in Theorems 3. i) and 3. ii).

Theorem 3

i) When the significance of disruption is high (i.e., δ is low), the equilibrium retail price for the disrupted product is lower when A leads, compared to the equilibrium retail price in the Nash game, i.e., $p_{1,s_A}^{\delta ,e}<p_{1,n}^{\delta ,e}$ if $\delta \in [0,{\displaystyle \frac{4{\beta }_1{\beta }_2}{{(2{\beta }_1{\beta }_2-1)}^2}})$ . ii) When the significance of disruption is high (δ is low), the equilibrium retail price for the undisrupted product is lower when A leads, compared to the equilibrium retail price in the Nash game, i.e., $p_{2,s_A}^{\delta ,e}<p_{2,n}^{\delta ,e}$ if $\delta \in [0,{\displaystyle \frac{{\beta }_1{\beta }_2}{2{\beta }_1{\beta }_2-1}})$ .

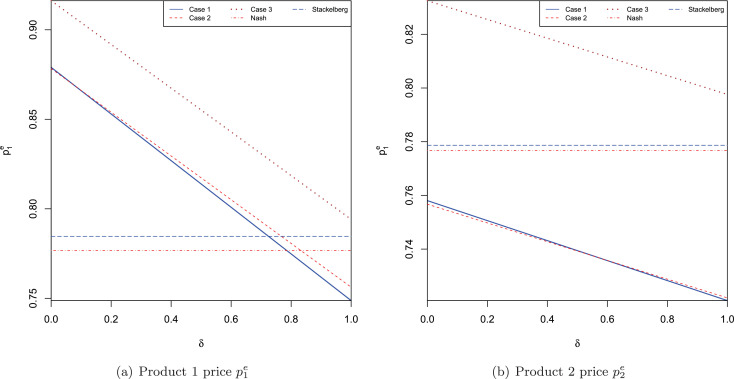
Let ${\delta }_1:={\displaystyle \frac{{\beta }_1{\beta }_2}{2{\beta }_1{\beta }_2-1}}$ and ${\delta }_2:={\displaystyle \frac{4{\beta }_1{\beta }_2}{{(2{\beta }_1{\beta }_2-1)}^2}}$. Theorems 2 and 3. ii) are valid in the region δ ∈ [0, δ ₁), while Theorem 3. i) is restricted to δ ∈ [0, δ ₂). All the theorems are valid in the region [0, min {δ ₁, δ ₂}). Comparing δ ₁ and δ ₂, we see that δ ₁ > δ ₂ if β ₁ β ₂ > 5/2. We know that β_i > 1 and thus β ₁ β ₂ > 1. Therefore δ ₁ ≤ δ ₂ if β ₁ β ₂ ∈ (1, 5/2]. In the region δ ∈ (min {δ ₁, δ ₂}, max {δ ₁, δ ₂}), Theorem 3. i) is not valid and we have $p_{1,s_A}^{\delta ,e}>p_{1,n}^{\delta ,e}$. This relationship of equilibrium retail prices with δ is shown in Fig. 5 .Comparison of order quantities: Almost immediately, we obtain the following order relationship, presented in Corollary 1: for the disrupted product from Theorem 1. ii), since the order quantity fulfilled by supplier A under disruption is a fraction δ of the equilibrium order quantities without any disruption, we have: $q_{1,s_A}^{\delta ,e}:=\delta q_{1,s_A}^e,q_{1,n}^{\delta ,e}:=\delta q_{1,n}^e,q_{1,s_B}^{\delta ,e}:=\delta q_{1,s_B}^e$.

Corollary 1

$q_{1,s_A}^{\delta ,e}<q_{1,n}^{\delta ,e}<q_{1,s_B}^{\delta ,e}$ .

Fig. 5.

Variation of the equilibrium retail prices with δ.

From Corollary 1, we know that, if everything else is the same, A delivers the maximum order quantity when B leads the SC, and the disruption occurs after both suppliers receive orders from R. On the other hand, A delivers the least quantity to R when A receives the first order from R. Due to the market clearing assumption, order quantities for the products are identical to market demand; consequently, the same relationship holds for the demand for product 1.

Next, we consider the total order quantity or the total demand for product 2. It is straightforward to obtain the relationship between the regular order quantities (orders before disruption) as $q_{2,s_A}^{\delta ,e}>q_{2,n}^{\delta ,e}>q_{2,s_B}^{\delta ,e}$. However, the emergency order quantity depends on the market prices and the regular order quantity. We know $D_2^e=q_2^e+q_E^e={\alpha }_2-{\beta }_2{p}_2^e+p_1^e$ (we have dropped the case dependent subscripts for simplicity).

We know that the centralized retail prices under disruption satisfy (11) in all cases, and we compare them in Proposition 3.

Proposition 3

$D_2^{\delta ,e}<D_{2,s_B}^{\delta ,e}<D_{2,n}^{\delta ,e},\forall \delta$ and if $\delta \in [0,{\displaystyle \frac{{\beta }_1{\beta }_2}{2{\beta }_1{\beta }_2-1}})$ then $D_{2,n}^{\delta ,e}<D_{2,s_A}^{\delta ,e}$ .

The relationship shown in Proposition 3 is not surprising and follows the same relationship as in the benchmark case. Further insights can be gained by comparing emergency order quantities across different cases. We defer this and the comparison of profits across different cases to the next Section 5.3.

5.3. Impact of the timing of disruption on profits

In the following, we explore and discuss the impact of price leadership and supply disruption on the profits earned by all SC members. We conduct these comparative studies exclusively through numerical studies as comparing the profit expressions across different cases is not direct. Although our findings are valid for a wider range of parameters, we discuss and present findings with respect to (w.r.t.) the base model parameters.

5.3.1. Supplier A profit

Supplier A’s equilibrium profit in the different disruption cases is obtained as a fraction δ of the corresponding profit in the benchmark case. For instance, in Case 1, ${\Pi }_{A,n}^{\delta ,e}=\delta {\Pi }_{A,n}^e$. As a consequence, the order relationship for A’s profit as presented in Theorem 1. v) continues to apply in different cases of disruption.

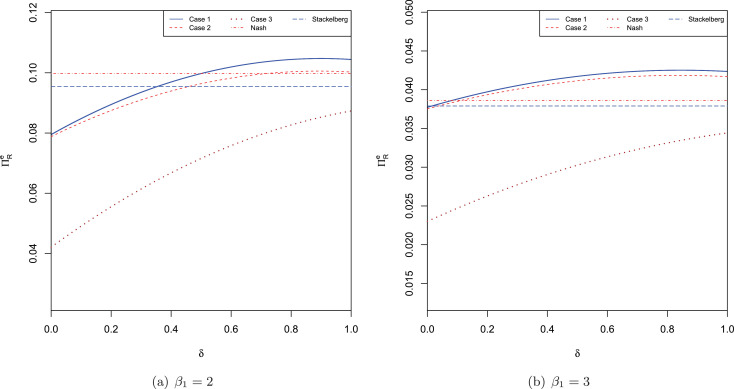
The profits for supplier B and retailer R can have different values because of the emergency order and its impact on market prices. Figs. 6 and 7 show the variation in profits for B and R, respectively w.r.t. δ.

Fig. 6.

Variation of supplier B’s profit with δ for different values of product1’s price elasticity β₁. The horizontal lines are the benchmark profits.

Fig. 7.

Variation of retailer R’s profit with δ for different values of product1’s price elasticity β₁. The horizontal lines are the benchmark profits.

5.3.2. Supplier B profit

From Fig. 6, we observe that B always earns the highest profit when there is an extreme disruption ($\delta =0$). When the sequence of events follows Case 2, B generally earns the highest profit compared to all other cases (including the benchmark case). However, in Fig. 6 a, we observe that when product 1 has a lower price elasticity and the level of disruption is low, B earns a higher profit in Case 3 as compared to Case 2. Interestingly, with low price elasticity for product 1, we observe that B can earn a low profit similar to what’s possible in the benchmark cases. This is because customers do not switch to product 2 when the disruption level is low (i.e., supply disruption is not significantly high).

5.3.3. Retailer’s profit

The retailer earns the highest profit when the suppliers decide the wholesale prices simultaneously in a Nash game as in Case 1. When product1’s price elasticity is low, the retailer earns a higher profit when there is no disruption; however, when customers are more price elastic, e.g., ${\beta }_1=3$ as in Fig. 7 b, the retailer earns a higher profit when A leads (Case 1) and there is a low level of disruption. This is because the retailer gets a better (lowest) equilibrium wholesale price from competing suppliers (as shown in Lemma 5) in Case 1 and is able to sell more product in the market (see Proposition 3). More interestingly, the retailer can benefit due to a supply disruption at A and earns a higher profit such as in Case 1 and in Case 2 (for higher β ₁) when the supply disruption occurs after placing orders with the suppliers. A retailer always earns a lower profit when the disruption occurs prior to placing the orders. In conclusion, a retailer’s profit significantly depends on the timing of disruption.

6. Extensions with likelihood of disruption and its timing

In this section, first, we extend our model to include the likelihood (uncertainty) of disruption given by θ, where θ ∈ [0, 1] is the probability that a supply disruption will occur at A. Inclusion of this additional parameter further generalizes the model and we show that our key results continue to hold. To preserve space, we only present the analysis for the case when both suppliers receive orders simultaneously (Nash game) as the analysis for the other cases is similar.

6.1. Suppliers lead simultaneously

Fig. 8 shows the sequence of events when there is no disruption (above) and when there is a supply disruption at A (below). Wholesale prices $w_{i,n}^{\theta }$ and order quantities $q_{i,n}^{\theta }$ are decided prior to the disruption while the retail prices are set post the disruption. We notate them differently as $p_{i,n}^{\theta }$ and $p_{i,n}^{\delta ,\theta }$ without and with disruption, respectively. Supplier B sets $w_{E,n}^{\delta ,\theta }$ and R places an order $q_{E,n}^{\delta ,\theta }$ post disruption. Therefore, we solve separately for $p_{i,n}^{\theta }$ and $p_{i,n}^{\delta ,\theta }$ which are set in the last stage of the game for both the scenarios. First, we consider the scenario without disruption: the analysis for optimal retail prices $p_{i,n}^{\theta ,*}(w_{1,n}^{\theta },w_{2,n}^{\theta })$ is identical to the analysis in Section 3.1 and the optimal retail prices satisfy (2). Additionally, the equilibrium order quantities are given by $q_{1,n}^{\theta ,e}={\alpha }_1-{\beta }_1{p}_{1,n}^{\theta ,e}+p_{2,n}^{\theta ,e}$ and $q_{2,n}^{\theta ,e}={\alpha }_2-{\beta }_2{p}_{2,n}^{\theta ,e}+p_{1,n}^{\theta ,e},$ respectively, with suppliers A and B.

Fig. 8.

Sequence of events when the supply disruption at A occurs with likelihood θ.

When there is disruption, the retailer orders the same quantity $q_{i,n}^{\theta ,e}$ at wholesale price $w_{i,n}^{\theta ,e}$ but receives only $\delta q_{1,n}^e$ from A. This helps us to express the expected profits for A and B, respectively as follows:

$$\begin{array}{ccc}\hfill \text{E}\left[{\Pi }_A\right]\left(w_{1,n}\right)& =& (w_{1,n}-c_1)[\theta \left(\delta q_{1,n}^e\right)+(1-\theta )q_{1,n}^e]\hfill \\ & =& (w_{1,n}-c_1)q_{1,n}^e[1-\theta (1-\delta \left)\right],\hfill \\ \hfill \text{E}\left[{\Pi }_B\right]\left(w_{2,n}\right)& =& (w_{2,n}-c_2)[\theta \left(q_{2,n}^e\right)+(1-\theta )q_{2,n}^e]\hfill \\ & =& (w_{2,n}-c_2)q_{2,n}^e.\hfill \end{array}$$ (20)

From the profit expression of A above, in (20) we note the similarity with Case 3.1; as the profit shrinks by $[1-\theta (1-\delta \left)\right]$ due to disruption. Consequently, the equilibrium wholesale prices (and order quantities) observed in the corresponding benchmark case continue to hold, i.e., we have identical wholesale and retail prices $w_{i,n}^{\theta ,e}=w_{i,n}^e,$ $p_{i,n}^{\theta ,e}=p_{i,n}^e,$ and order quantities $q_{i,n}^{\theta ,e}=q_{i,n}^e$ as presented in (3).

Next, we solve for the equilibrium emergency wholesale price $w_{E,n}^{\delta ,e}$ and retail prices $(p_{1,n}^{\theta ,\delta ,e},p_{2,n}^{\theta ,\delta ,e})$ in the event of disruption. Due to disruption, A delivers a quantity $\delta q_{1,n}^{\theta ,e}$ and B delivers $q_{2,n}^{\theta ,e}+q_{E,n}\theta ,\delta$. Using the backward induction method, we derive the optimal centralized prices for R. The objective function for retailer R is:

$$\begin{array}{ccc}& & \underset{(p_1,p_2)}{\max }(p_1-w_1^{\theta ,e})\delta q_{1,n}^{\theta ,e}+p_2({\alpha }_2+p_1-{\beta }_2{p}_2)-w_{2,n}^{\theta ,e}{q}_{2,n}^{\theta ,e}\hfill \\ & & -w_E^{\theta ,\delta }({\alpha }_2+p_1-{\beta }_2{p}_2-q_{2,n}^{\theta ,e}).\hfill \end{array}$$

Due to the additional constraint $\delta q_{1,n}^{\theta ,e}={\alpha }_1-{\beta }_1{p}_1+p_2,$ the objective function can be reduced to only one variable p ₁ which makes the objective identical to (10) and thus the unique maximizer satisfies (11). Supplier B’s decision for the emergency wholesale price is identical to (12). Note again that the order quantities $(q_{1,n}^{\theta ,e},q_{2,n}^{\theta ,e})$ are identical to those derived in Section 3.1, therefore, we can derive the retail prices in closed form as follows:

$$\begin{array}{ccc}\hfill p_{1,n}^{\delta ,e}& =& {\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2{\beta }_1({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{2({\alpha }_1-\delta q_{1,n}^e)+w_{E,n}^e}{2{\beta }_1}}\hfill \\ & =& {\displaystyle \frac{3({\alpha }_1+{\alpha }_2{\beta }_1)-2\delta q_{1,n}^e-2{\beta }_1{q}_{2,n}^e}{4{\beta }_1({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{{\alpha }_1-\delta q_{1,n}^e}{{\beta }_1}}+{\displaystyle \frac{c_2}{4{\beta }_1}},\hfill \\ \hfill p_{2,n}^{\delta ,e}& =& {\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{w_{E,n}^e}{2}}={\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1}{2({\beta }_1{\beta }_2-1)}}\hfill \\ & & +{\displaystyle \frac{{\alpha }_1+{\alpha }_2{\beta }_1-2\delta q_{1,n}^e-2{\beta }_1{q}_{2,n}^e}{4({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{4}}\hfill \\ & =& {\displaystyle \frac{3({\alpha }_1+{\alpha }_2{\beta }_1)-2\delta q_{1,n}^e-2{\beta }_1{q}_{2,n}^e}{4({\beta }_1{\beta }_2-1)}}+{\displaystyle \frac{c_2}{4}}.\hfill \end{array}$$ (21)

This completes the analysis for Case 1 with the additional parameter θ. We note that the analysis is almost identical to that in Section 4.1 except that the profit expression for A changes by a fraction $[1-\theta (1-\delta \left)\right]$. Analysis for Case 2 and Case 3 will be similar by including θ.

6.2. Uncertainty in disruption timing

Now, we discuss another scenario where a retailer places order(s) with the suppliers and the disruption timing is uncertain, i.e., the disruption occurs immediately after only one of the orders is placed or after both the orders are placed with known probabilities. Therefore, by definition this scenario precludes the case with the Nash game between A and B. We only consider the case when A leads the SC by setting the wholesale price for product 1, R ordering from A and afterwards there are two possibilities: disruption occurs immediately or occurs after R places an order with B. These two scenarios are presented as Cases 3 and 2, respectively in Fig. 3. The ordering and pricing decisions that take place after the uncertainty about the disruption is resolved are identical to the decisions in the deterministic cases presented in Section 4, and the only difference arises for the two decisions that always occur before disruption which is the wholesale price set by A and the corresponding order quantity by R. It is easy to see that the quantity delivered by A in both cases is the same, i.e., a fraction δ of the original order quantity. The objective function of retailer A does not depend on the probabilities for disruption timing and the results from Section 4 will continue to hold. This result is expected and consistent with the analysis with disruption timing.

7. Managerial insights

There has been an increased interest in optimizing pricing and sourcing decision under supplier competition considering greater levels of uncertainty and disruption risks, much of it focusing on designing resilient and efficient supplier portfolios. While the development of optimal pricing and ordering configuration within a supplier base is desirable and indeed critical for some firms, exploiting these capabilities to achieve targeted performance outcomes through efficient adaptation at the demand side is becoming increasingly important. One of these adaptations is product substitution, and its timing. We have developed in this paper a game-theoretical study to decipher the effects of capacity disruption timing on pricing decisions for substitute products in a two-supplier, one-retailer SC setting.

The results of this research provide twofold managerial insights. First, we have uncovered the role of price leadership in supplier competition for cases of substitute products and supply disruptions. Second, we have revealed differences and commonalities in emergency pricing strategies depending on the timing and scale of disruptions. Pricing managers must factor the disruption timing in the pricing decisions when a supply disruption occurs. Table 1 summarizes the major results of this study. These results are structured according to the impacts brought by the timing of the disruption, the price-leadership in the market, and the scale of disruptions.

Table 1.

Major results of this study.

Scale of disruption /	Price leadership
Timing of disruption	The disrupted supplier (A) leads	The non-disrupted supplier (B) leads
	Supplier B charges a higher equilibrium emergency order’s wholesale price than the corresponding price charged in the Nash game.	The equilibrium emergency order’s wholesale price is higher than the corresponding price charged in the Nash game.
Low disruption level	The quantity ordered with supplier A is lower. B can charge a higher emergency order’s wholesale price for the smaller quantity of product 2 ordered by retailer.	The quantity ordered with supplier A is higher.
	The equilibrium retail prices for both the disrupted and non-disrupted products are lower compared to the equilibrium retail price in the Nash game.	The equilibrium emergency order’s wholesale price is higher than the corresponding price charged in the Nash game.
High disruption level	The equilibrium emergency order’s wholesale price is lower compared to the emergency order's wholesale price in the Nash game.	The order quantity with supplier A is higher compared to the corresponding order quantity in the Nash game, resulting in a higher emergency order’s wholesale price.
Timing of disruption	The emergency order’s wholesale price charged by B is lower when the retailer places orders to A first, as compared to the emergency order’s wholesale price when the retailer simultaneously places orders to both A and B.

We have considered cases where (i) both suppliers simultaneously receive orders from the retailer and then disruption occurs at one of the suppliers, and the retailer places an emergency order to the other supplier, (ii) one of the suppliers leads the other supplier and the disruption occurs after the non-disrupted supplier receives the order or before the non-disrupted supplier receives the order. In the first case, there are always two orders with the non-disrupted supplier, i.e., a regular order which is launched before the disruption, and an emergency order placed after the disruption. In the second case, the retailer places only a single emergency order with the non-disrupted supplier.

Our results offer solutions for decision-makers not only at the level of immediate reaction to disruptions but also at a higher level of developing a contingent sourcing strategy. On one hand, the solutions to a series of games presented in our study allow for creating evidence for SC managers regarding the disruption impacts on the profitability. On the other hand, our results can be used to re-consider a retailer’s supply structure in terms of internal competition and product substitutability as well as to re-design the contracts used within the supplier base. Such results can be of special use for firms that have made their decisions neglecting possibilities of a disruption.

Some generalized observations for all the investigated cases can be made. First, the non-disrupted supplier tends to charge more for the emergency order as the scale of the disruption increases, depending on the price leadership model. Second, when the non-disrupted supplier is the price leader, the quantity ordered with the disrupted supplier increases. Third, the equilibrium market retail prices charged by the retailer to customers are higher when the disruption is more severe for the Nash game when both suppliers simultaneously receive orders, as compared to the corresponding retail prices under the Stackelberg game. Fourth, it is interesting to note that the non-disrupted supplier is always able to charge the highest wholesale price if the disruption occurs before they receive any orders compared to all other cases. This result highlights the impact that the timing of a supply disruption has on the emergency order’s wholesale price.

The taxonomy developed in Table 1 depicts that the timing of disruption may significantly impact the optimal pricing and ordering configuration at the retailer. Our model specifies the existence of optimal pricing strategy and ordering levels and conceptualizes a unique decision-support setting with both disruption timing and product substitution. It allows us to identify different combinations of disruption severity, timing, and the price leadership to derive recommendations on when and how to adapt price and quantity levels in case of disruption in the supplier base. Moreover, our findings show the proposition that the associations of the disruption timing and severity, and price leadership with the optimal pricing and ordering configuration can be efficiently deciphered by our approach. This highlights the major implications of our findings.

The findings of our study can help explain and improve the firms’ operations in a generalized setting. First, a non-disrupted supplier can benefit from a disruption at the competitor especially in case of promotion actions. The non-disrupted supplier can quickly arrange a promotion action with the retailer. On the contrary, the organization of future promotion actions would be problematic for the disrupted supplier since this might be too risky for the retailer. Any disruption during the promotional period has a very high impact on the retailers. Second, reductions in sales impact both the suppliers and retailers. A disruption weakens the negotiation positions of the supplier to increase purchasing prices in the future since the retailer can refer to lost sales and low delivery performance in the past. Third, the game results can help analyze the company operations from a medium-term perspective (1–12 months) in terms of market competitiveness and efficiency improvement.

8. Conclusions

We studied in this paper the effects of a supply disruption on price-setting decisions for substitute products in a two-supplier, one-retailer SC context. Our study was motivated by the pricing-setting behavior of two beverage producing and supplying companies, who are known to be engaged in price competition. One of the companies was not able to fulfill all product orders for its retailers because of a crash in their distribution center; their end consumers were able to switch to the other beverage product during this period of disruption.

We developed an analytical game-theoretical model to examine the equilibrium pricing strategies of the suppliers and the retail prices in the event of such a supply disruption. To generate insights, we investigated different problem settings in terms of the timing of the disruption in relation to the ordering decisions and price leadership in the SC. We characterized the industry conditions under which the product substitution is most likely to have positive effects on a firm’s operations when coping with supply disruptions.

Two significant contributions emerge. First, our results can be of value for the development of managerial recommendations on pricing strategies in the case of two competing suppliers with bi-directional, substitutable products subject to conditions of supply capacity disruption and considering the timing of disruptions in relation to ordering decisions in the supply chain. Second, we showed that timing of disruption may significantly impact the optimal pricing and ordering configuration at the retailer when suppliers compete and their products are substitutable in the market. We conceptualized a unique model setting with considerations of both disruption timing and product substitution and showed that the associations of the disruption timing and severity, and price leadership with the optimal pricing and ordering configuration can be efficiently deciphered by our approach. The insights developed can guide operations managers to design effective risk mitigation ordering strategies, re-design the supplier contracts, and utilize the product substitution option when deciding the optimal pricing and ordering levels.

The usage of Stackelberg games provided some counterintuitive results, especially compared to the Nash games. In particular, we observed that the quantity ordered with the disrupted supplier depends on the price leadership. More specifically, those quantities tend to increase when the non-disrupted supplier is the price leader. Another interesting insight is that the equilibrium market retail prices charged by the retailer to customers are higher under higher levels of disruption for the Nash game when both suppliers simultaneously receive orders, as compared to the corresponding retail prices in the Stackelberg game. Finally, it is interesting to observe that the non-disrupted supplier is always able to charge the highest wholesale price if the disruption occurs before orders are received; the timing of disruption impacts the emergency order’s wholesale price.

The results gained can be used as managerial recommendations on pricing strategies for scenarios with two competing suppliers with bi-directional substitutable products in the presence of supply capacity disruption and considering the timing of disruptions. Despite the possibility of generalizing the results, the model applied herein is limited in some ways. First, the demand function is deterministic. Even if the usage of such a function can be justified by other studies in the area, this is certainly a restriction in the application of the model to cases with stochastic demand. Second, we assumed full information availability in this study. This can be justified by the fact that serious disruptions usually become quickly known in markets with few competitors, as in the situational context of our cases. At the same time, there are certainly other problem settings for which a lack of visibility in the SC must be considered. The third limitation is a restriction of our results to some specific products for which operational changes in prices are possible. In practice, this holds true for products which are purchased on a tender basis, e.g., imported fruits and vegetables, regional meat and poultry, or fish. Finally, an important factor which is not explicitly included in our model is the ordering/delivery frequency. In case of frequent deliveries (2–3 times per week), one plausible application of our findings is the price adjustments by a retailer for the next price negotiation cycle, and not for the next order. The distribution of order timings in relation to the disruption can be considered in regards to the most critical orders, for instance, for products that are under promotion by the retailer to stimulate demand.

These limitations point to several possible future research avenues. First, this study can be extended by investigating other forms of demand function. Second, information unavailability can be included in future analysis. The present study discusses extensions with likelihood of disruption/timing, and another possible extension of the present study is to include an explicit belief of the firms of a likelihood of disruption/timing and to model this explicitly. Another direction of future research is to analyze different constellations of timings when the disruption occurs and when the retailer realizes the disruption. Furthermore, some additional restrictions in regard to limited supply capacities could be considered. For example, one could examine gradual ramp-ups of supply capacities along with uncertain demand disruptions as posed by the COVID-19 pandemic context.

CRediT authorship contribution statement

Varun Gupta: Methodology, Software, Writing - original draft. Dmitry Ivanov: Conceptualization, Writing - review & editing. Tsan-Ming Choi: Writing - review & editing.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/

Supplementary Data S2

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/