Increased variability but intact integration during visual navigation in Autism Spectrum Disorder

Significance

Recent computationally focused theories of Autism Spectrum Disorder (ASD) have postulated that the pathological condition is broadly defined by anomalies in either the width of sensory likelihoods (i.e., the reliability of incoming sensory information) and/or the strength and flexibility of priors (i.e., contextual information)—the two components forming Bayes’ Rule. Furthermore, many consider that the process of integration is impaired in ASD. Here, we use an ecologically valid and data-rich navigation task to fit Bayesian likelihoods and priors as well as examine how self-velocity estimates are integrated into self-position in control and ASD subjects. Results suggest that priors and integration are intact in ASD; instead, their variability is heightened.

Abstract

Autism Spectrum Disorder (ASD) is a common neurodevelopmental disturbance afflicting a variety of functions. The recent computational focus suggesting aberrant Bayesian inference in ASD has yielded promising but conflicting results in attempting to explain a wide variety of phenotypes by canonical computations. Here, we used a naturalistic visual path integration task that combines continuous action with active sensing and allows tracking of subjects’ dynamic belief states. Both groups showed a previously documented bias pattern by overshooting the radial distance and angular eccentricity of targets. For both control and ASD groups, these errors were driven by misestimated velocity signals due to a nonuniform speed prior rather than imperfect integration. We tracked participants’ beliefs and found no difference in the speed prior, but there was heightened variability in the ASD group. Both end point variance and trajectory irregularities correlated with ASD symptom severity. With feedback, variance was reduced, and ASD performance approached that of controls. These findings highlight the need for both more naturalistic tasks and a broader computational perspective to understand the ASD phenotype and pathology.

Autism Spectrum Disorder (ASD) is a heterogeneous neurodevelopmental disorder with high prevalence (1). In response to its pervasiveness, researchers have recently turned their attention to computational and normative tools attempting to identify canonical computations underlying ASD symptomatology (2, 3). A promising candidate family is that of probabilistic inference (4), and indeed, a large number of Bayesian accounts of ASD have recently been put forward—positing an anomaly in the strength of Bayesian priors (5, 6), the abnormal updating of these priors (7, 8), the aberrant precision in sensory representations (9–12), and the atypical weighting of sensory prediction error (6, 13, 14).

Unfortunately, as for many other aspects of the ASD phenotype and pathology, there is yet no clear consensus. Remarkably, both attenuated (15, 16) and intact (12, 17, 18) priors have been reported as well as normal (19) and abnormal (7, 8) updating of these priors. These conflicting results may partially be due to a lack of quantification. Many studies have based their conclusions on a loose link to “reduced top-down modulation of sensory processing,” “difficulties in accessing underlying statistical rules in an unstable context,” or “impairment in predictive abilities” without any quantitative fit of the inference/predictive process (16–28). A handful of studies has provided Bayesian model simulations (11, 15, 16), and Karvelis et al. (12) have computationally disentangled individuals’ likelihoods and priors yet did so in a group of healthy individuals with differing levels of autistic traits. In this latter study, the authors reported no correlation between autistic traits and the shape of the prior distribution.

In addition to a lack of quantification, another contributing factor to conflicting conclusions may be the widespread use of constrained and data-poor tasks defined by binary behavioral outcomes. Separating perception from action, for example, is a laboratory construct that has little to do with the challenges of everyday experiences. Furthermore, binary outcome tasks offer few data points to allow firm exploitation of complex computations, like fitting likelihoods and priors. We argue that to understand the dynamic neural processes that mediate natural behavior—and deficits thereof—we must study recurrent neural computations by using continuous time behavioral outcomes where actions influence sensory inflow—particularly when crucial variables cannot be directly observed such that the observer must draw inferences about those latent variables, such as is often the case in ecological behaviors.

Here, we used a virtual reality navigation task that allows exploitation of brain computation in the naturalistic setting of continuous action and active sensing as well as dynamic online inference about latent, task-relevant variables (29, 30). More specifically, we use a virtual navigation task that required control and ASD participants to use a joystick to actively acquire memorized targets by integrating visual motion cues (optic flow). This task not only is more natural in terms of the dynamic, closed loop interactions between sensory inflow, internal beliefs, and actions but also, requires the continuous integration of visual motion cues—a process previously reported to be abnormal in ASD (31–33) but recently suggested to reflect heightened sensitivity to noise (11). Furthermore, our navigate-to-target task provides a rich and continuous dataset (i.e., two-dimensional movement trajectories extending for ∼5 s per trial) permitting the tracking of belief states (29, 30, 34) and efficient fitting of different components forming Bayesian computations (i.e., priors and likelihood functions).

Results

We asked ASD (n = 14) and matched control (n = 25) (Methods has details) adolescents to use a joystick to virtually navigate toward and stop at the location of a briefly presented visual cue, a “firefly.” No landmarks were presented, only ground-plane triangular elements providing optic flow cues (Fig. 1A). In the second half of trials, participants were instructed in the task via feedback in the form of concentric circles indicating the location of the target and a colored arrow (green if “rewarded” and red if “unrewarded” in Fig. 1B). The portion of space rewarded was adaptively manipulated to become more restrictive with improved task performance (Methods). Targets were distributed randomly and uniformly (Fig. 1C) within a range of r = 1 to 6 m (r, radial distance) and θ = ±42.5° (θ, angular eccentricity) of visual angle relative to where the subject was stationed at the beginning of the trial. This radial distance is within the regime where humans are known to overshoot targets (29) (undershooting appears at and beyond ∼20 m). Indeed, visualizing exemplar target locations and trial trajectories (Fig. 1C) during the block without feedback suggests that participants explored a larger space than that required by target locations. To further depict this trend, we expressed participants’ responses in polar coordinates (Fig. 1D), with an eccentricity from vertical (angular response, $\stackrel{\sim }{\theta }$) and a radial distance $\left(\stackrel{\sim }{r}\right)$. In the example presented in Fig. 1 D, Left, the error vector points radially outward and away from straight ahead. This pattern was consistent across trials for this particular subject as shown in the vector field of errors (Fig. 1 D, Right). This profile of errors implies consistent overshooting in terms of both absolute distance traveled and angular rotation. We initially focus on performance and impact of feedback on path integration for control subjects. Then, we assess baseline performance and the impact of feedback in individuals with ASD compared with neurotypical individuals.

Fig. 1.

Experimental protocol and normal performance. (A) Participants use a joystick to navigate to a flashed target (yellow disk or firefly) using optic flow generated by ground-plane triangles. (B) Example trajectory of a participant approaching the unseen target. In the feedback block, after participants have made their response, concentric circles and either a green (if rewarded) or red (if unrewarded) arrow appears indicating the true location of the target. (C) Distribution of targets (C, Left) and example trajectories from one experimental block (C, Right). (D, Left) Target and end points expressed in polar coordinates (angular distance: θ; radial distance: r). (D, Right) Errors of the example trajectories. (E–H) Scatter plots of radial and angular distance responses (y axis) as a function of the respective target distance (x axis) for a representative subject (control subject #3) shown separately without and with feedback. Individual dots are single trials. Solid lines: linear regression; dashed lines: identity lines. (I–L) Scatter plots of regression slopes (1 = no bias; <1 = undershooting; >1 = overshooting) for all participants individually (gray dots) and population average (error bars: ±SEM).

Typical Performance and Impact of Feedback.

To quantitatively assess the apparent underestimation in self-velocity (and thus, the overshooting in final position) during path integration, we separately compared the radial and angular error by performing a linear regression between target positions $\left(r,\theta \right)$ and responses $\left(\stackrel{\sim }{r},\stackrel{\sim }{\theta }\right)$. Fig. 1 E and F shows these regressions in the radial and angular dimensions, respectively, for an exemplar control individual during the block without feedback. The linear fits account relatively well for the pattern of responses observed (radial: R² = 0.54; angular: R² = 0.92) while also evidencing considerable variability across trials, particularly in the radial dimension (in Fig. 1E, individual dots are single trials). Furthermore, these data suggest that bias during path integration is multiplicative: the greater the distance traveled, the greater the error as indicated by regression slopes over 1 (slope = 1 reflects no bias; radial: $\stackrel{\sim }{r}$ vs. $r$ slope = 1.51; angular: $\stackrel{\sim }{\theta }$ vs. $\theta$ slope = 1.78). There is no notable distance-independent bias, which would have been expressed as regressions with nonzero intercepts. Fig. 1 G and H illustrates the relationship between target location and responses in the block with feedback (same participant as in Fig. 1 E and F), showing improvement in terms of both accuracy ($\stackrel{\sim }{r}$ vs. $r$ slope = 0.99; $\stackrel{\sim }{\theta }$ vs. $\theta$ slope = 1.14) and precision of end points (radial: R² = 0.77; angular: R² = 0.98) compared with the block without feedback (permutation tests; all P < 0.05).

The above findings were consistent across subjects as illustrated in Fig. 1 I and J. In the absence of feedback, both radial (mean ± SEM: 1.10 ± 0.06; P = 0.045) and angular (1.49 ± 0.05; P = 1.50 × 10⁻¹⁴) overshooting biases were appreciable. Similar to Lakshminarasimhan et al. (29), the effect size was four to five times greater in the angular (50%) than radial (10%) dimension (78 vs. 19% in ref. 29). All subjects show angular overestimation, while not all show radial overestimation.

The introduction of feedback completely eliminated overshooting in radial distance (0.97 ± 0.02; P = 0.6) (Fig. 1I) and reduced but did not completely eliminate the angular bias (1.09 ± 0.02; P = 5.51 × 10⁻⁸) (Fig. 1J). Interestingly, providing feedback at the end of each trial increased not only accuracy but also, precision (feedback – without feedback; ΔR² radial = 0.09 ± 0.02; P = 4.25 × 10⁻⁴; ΔR² angular = 0.01 ± 0.004; P = 0.003) (Fig. 1 K and L). Furthermore, the introduction of feedback drove participants to faster trajectories both in the radial (F = 125.0; P < 0.001) and in the angular (F = 24.0; P < 0.001) dimensions and in turn, to shorter duration trials (from 5.42 ± 0.05 s without feedback to 3.70 ± 0.05 s with feedback; F = 98.22; P < 0.001) (SI Appendix, Fig. S1). This strategy was seemingly adaptive given the positive association between trial duration and nonsystematic end point errors (“residual variance”) (SI Appendix, Fig. S2).

Path Integration Improves with Feedback Due to a Reduction in Self-Motion Uncertainty.

To further understand the root cause of participants’ overshooting of the target and most importantly, the driving, latent mechanism behind their improvement during trial-to-trial feedback, we instantiated two dynamic Bayesian observer models (first introduced in ref. 29). Both models assume that subjects maintain estimates of both the mean and uncertainty associated with their location and steer toward the target to maximize reward on each trial (29) (Methods). The trajectories generated by each model correspond to the subject’s beliefs about their distance to target throughout the trial. Thus, these models are fitted to the whole movement trajectory for each trial by maximizing the overlap between the posterior distribution over believed position and the target region at the end of each trial (Methods).

The first model hypothesizes that participants overshoot targets because they misestimate their speed due to a nonuniform prior that biases velocity estimates. In contrast, sensory evidence accumulation (path integration) is assumed to be lossless (SI Appendix, Fig. S3A) (35–38). The inference of velocity estimates from optic flow signals depends on the shape of the observer’s prior distribution for velocity (Fig. 2A, solid black lines) ($a_v$ and $a_w$ defining the exponential decay of the radial and angular velocity components, respectively), which is combined with a likelihood function (Methods; Fig. 2A, dashed black lines) ($b_v$ and $b_w$ defining the linear relationship between velocity and the variance of the radial and angular likelihood, respectively) to generate the final posterior estimate of velocity (Fig. 2A, green). Unlike ref. 29, here the exponents dictating the shape of the prior distribution ($a_v$ and $a_w$) were allowed to be negative or positive (allowing for both under- and overestimation) given that participants are overall accurate during the feedback condition, and even in the block without feedback, a subset of participants did not radially overshoot targets.

Fig. 2.

Speed prior dynamic Bayesian Observer Model of path integration. (A) Biases in path integration originate from an underestimation of velocity modeled as a posterior (in green) based on a prior for speeds (black solid lines) and a likelihood distribution (black dashed lines). The likelihood width is taken to scale with velocity as shown by the superimposed gray likelihoods increasing with width. This velocity posterior is then integrated into an estimate of position. Improvement in performance may be due to either the prior relaxing (Lower Left) or the scaling of likelihood width becoming shallower. (B) Extraction of the parameters best accounting for participant trajectories suggests that the prior does not change with feedback (FB) vs. without feedback (woFB), but instead, the scaling of the likelihood width with velocity becomes shallower. *P ≤ 0.001.

The second “leaky integration” model (SI Appendix, Fig. S3B) hypothesizes that estimates of velocity are correct, and instead, biases are due to imperfect integration of velocity into position estimates (39–41). This assumes a flat prior $\left(a_v=a_w=0\right)$ but a leaky integration. Integration is dictated by two independent leak time constants ${\tau }_d$ and ${\tau }_{\phi }$ that specify the timescale over which radial and angular velocities are integrated. This leaky integration model was refuted for neurotypical individuals in ref. 29 but has been included here to compare between ASD and controls given that one of the many ASD hypotheses claims deficient integration in this conditions (42–44).

Both the speed prior and leaky integrator models have four free parameters: parameters $b_v$ and $b_w$ expressing how fast the squared spread (i.e., variance) of the likelihood functions scales with the magnitude of linear and angular velocity measurements and either $a_v$ and $a_w$ (for the speed prior model) or ${\tau }_d$ and ${\tau }_{\phi }$ (for the leaky integrator model). To gauge the quality of model fits, we reasoned that a good behavioral model ought to believe that the participants should stop where they did stop. In other words, the model fit should reflect that participants stopped where they believed to be overlapping with the target (29). Equivalently, if the model accounts well for participant’s beliefs, its position estimate should be concentrated near the true target. To evaluate this, we used the best-fit model parameters for each subject to reconstruct the subjects’ believed end position. There was no residual bias (i.e., bias after accounting for the subject’s best-fit parameters) prior to or after feedback and in either the radial or angular dimension when utilizing the speed prior model (“residual” bias contrast to a slope of 1—no bias—all P > 0.10) (SI Appendix, Fig. S3A). On the other hand, under the architecture of leaky integration, all contrasts showed significant residual biases (all P < 0.02) (SI Appendix, Fig. S3B). A quantitative comparison of log likelihood ratios contrasting goodness of model fits concurred in supporting that overall the speed prior model accounted best for observed trajectories (∼1.21 times better than the leaky integration model; P = 1.5 × 10⁻⁸; ∼1.35 times in ref. 29).

Given that the speed prior model (Fig. 2A) accounted best for the observed data (in the conditions both with and without feedback), there are two putative mechanisms leading to enhanced performance in the block with feedback. The first is that, during the block with feedback, the exponential prior for speed relaxes and becomes closer to a uniform prior (Fig. 2 A, Lower Left). The second is that the scaling of the variance of the likelihood distribution with velocity becomes shallower (Fig. 2 A, Lower Right). To distinguish between these possibilities, we extracted the latent parameters of the best-fit model for each participant, which were then compared across feedback conditions. As shown in Fig. 2 B, Upper, there was no change with feedback in the exponent characterizing the prior for speed in either the radial (Δradial = 0.002 ± 0.002; P = 0.2) or angular (Δangular = − 0.01 ± 0.014; P = 0.71) dimension. Of note, however, while the angular exponent was on average (i.e., taking into account the block both with and without feedback) significantly smaller than zero (−0.10 ± 0.02; P = 1.0 × 10⁻⁷), the radial one was not (−2.75 × 10⁻⁴ ± 0.001; P = 0.81), suggesting that the greater bias exhibited by participants in the angular than radial dimension in the block without feedback is driven by a stronger prior in the former dimension.

On the other hand, the scaling of the likelihood variance with velocity decreased with feedback both in the radial (Δradial = − 9.69 ± 2.0; P = 9.9 × 10⁻⁵) and in the angular (Δangular = − 3.81 ± 0.96; P = 7.30 × 10⁻⁴) dimensions (Fig. 2 B, Lower). Together, the modeling results indicate that biases in path integration originate chiefly from biases in velocity estimates that are then appropriately integrated into position estimates. However, the improvement in path integration accuracy during feedback is driven by a reduction in the scaling of uncertainty with velocity and not a change in the prior.

Abnormal Uncertainty Prior to Feedback in Autism.

Next, we assess path integration abilities in individuals with ASD and examine whether feedback improves their performance using a strategy akin to that employed by neurotypical individuals. We start with a model-independent quantification of the behavior and end with a direct comparison of latent variables given Bayesian model fits.

Prior to feedback, the clinical group showed marked overshooting of targets both in the radial ($\stackrel{\sim }{r}$ vs. $r$ slope = 1.10 ± 0.08; P = 0.048) and in the angular ($\stackrel{\sim }{\theta }$ vs. $\theta$ slope = 1.52 ± 0.07; P = 1.3 × 10⁻⁵) dimensions. The magnitude of this bias was not different from that of neurotypical controls (all P > 0.73) (SI Appendix, Fig. S4, y axis). Providing feedback at the conclusion of each trajectory improved their performance (feedback – without feedback; Δradial = −0.12 ± 0.08; P = 0.021; Δangular = −0.40 ± 0.07; P = 2.2 × 10⁻⁴), and the magnitude of this enhancement was similar across control and ASD groups (all P > 0.92) (SI Appendix, Fig. S4). A direct comparison of bias prior to and after feedback across the distinct experimental groups suggested that feedback afforded benefit of equal magnitude across groups both in the radial (interaction term; P = 0.95) and angular (P = 0.92) dimensions. Similar to the control subjects, during feedback individuals with ASD shortened their trial duration (P = 7.69 × 10⁻⁹) by increasing radial (P = 2.71 × 10⁷) and angular velocities (P = 0.01) (SI Appendix, Fig. S1). In fact, they employed this same strategy to a greater extent than control subjects (interaction terms; all P < 0.045). Furthermore, the trial-to-trial dynamics with which feedback improved end point accuracy within these groups was ostensibly also similar as suggested by the fact that the outer boundary of the “rewarded zone” decreased at the same rate (SI Appendix, Fig. S5).

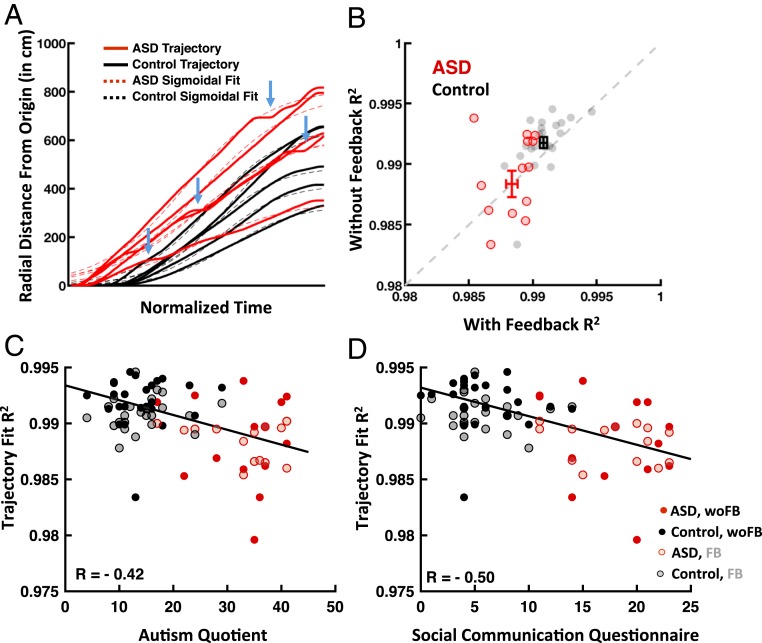
Contrary to the similarity in performance when average responses were considered, indexing of dispersion tendencies suggested that at baseline (i.e., prior to feedback) individuals with ASD exhibited a heightened degree of variability with respect to control individuals. Namely, prior to feedback, trial-to-trial variance in radial end points as captured by R² values of the linear regression fits was larger in ASD than control individuals (P = 1.3 × 10⁻⁶) (Fig. 3A). The introduction of feedback reduced uncertainty to a greater degree in ASD than controls (interaction term; P < 0.001) such that it eliminated the deficit shown by the clinical group relative to controls (P = 0.61). A similar analysis contrasting the variability of angular responses during the no feedback block did not detect a significant difference between groups (P = 0.36) (Fig. 3B), possibly due to a ceiling effect (77/78 R² values > 0.92). To circumvent this problem, we also quantify uncertainty as the SD of a select group of trials split into equally sized quartiles based on target distance. This analysis showed that, prior to feedback, end point responses of ASD individuals were more variable than those of control participants (Fig. 3 C and D) both in the radial (P = 0.030) and in the angular (P = 0.048) dimensions. Furthermore, uncertainty scaled with target distance (both P < 0.001), a scaling that was exacerbated in ASD participants for the radial dimension (P = 0.028). With feedback, variability was overall reduced (both in the radial and in the angular dimensions; P < 0.001), yet this reduction in variance was greater in ASD than control subjects (interaction terms; both P < 0.039) and ultimately, equated the uncertainty expressed by the clinical and control groups after feedback (P = 0.32) (Fig. 3 C and D). Importantly, the correlation between increasing uncertainty and increasing target distance—and the greater scaling of the latter with the former in the ASD group—was also true when conducting partial correlations accounting for response distance, trial duration, movement duration, reaction time, and mean movement velocity (P < 0.05) (SI Appendix, Fig. S2). In addition to target distance, trial duration and mean velocity of movements (both in the radial and angular dimensions) also showed positive correlations (P < 0.05) with variance, even when accounting for the rest of variables (SI Appendix, Fig. S2). Thus, the greater variance shown by ASD subjects seemingly spanned from perceptual (e.g., target distance) to motor (e.g., steering velocity) variables.

Fig. 3.

Increased uncertainty in autism. (A and B) Goodness of fit (R²) of linear regression between response vs. target distance (from plots as in Fig. 1 E–H) for ASD (red) and control (black) subjects without and with feedback. Data are shown for individual subjects and group averages (±SEM). (C and D) SD of the end point responses within specific target distance bins (x axis) in the radial (C) and angular (D) dimension. (E and F) Variance of the likelihood function (computed from the speed prior model fit). (G and H) Radial R² correlates inversely with ASD symptomatology prior to feedback (solid colors and dashed lines): the larger the end point variability, the higher participants scored on the AQ and the SCQ. Single dots are individual participants. **P ≤ 0.01; ***P ≤ 0.001.

As in the case with the control individuals, we leveraged the full extent of movement trajectories in two dimensions to track belief states by fitting the two abovementioned dynamic Bayesian Observer Models: one hypothesizing a prior for speeds leading to inaccurate velocity estimates and the other hypothesizing an imperfect process of integration. As for the control subjects, the model that accounted best for participants’ trajectories was the speed prior (SI Appendix, Fig. S3) (∼1.22 times more likely than the leaky integration model according to log likelihood ratios; P = 7.86 × 10⁻¹⁰). Furthermore, there was no overall difference in the goodness of model fit between the ASD and control subjects (P = 0.2), and a particular model (speed prior or leaky integration) did not fit better one group of participants than the other (P = 0.43). These results refute that ASD individuals are poorer than controls in integrating visual velocity signals over time (ref. 11 has a similar conclusion using a passive visual motion integration task). Importantly, the best-fit estimated speed prior was equal in ASD and control groups both before (linear, P = 0.61; angular, P = 0.13) and after feedback (linear: P = 0.42; angular: P = 0.89; interaction terms: all P > 0.159) (SI Appendix, Fig. S6). In contrast and as expected given the R² results, the best-fit parameters of the scaling of the radial likelihood variance with velocity reflected a steeper dependence (i.e., uncertainty grew faster with velocity) in ASD than controls (P = 0.01) (Fig. 3E). With feedback, the scaling of the radial likelihood width with speed decreased to a greater extent in ASD than control subjects (interaction terms; P < 0.012); thus, the difference in radial likelihood scaling between ASD and controls disappeared after feedback (P = 0.64). While generally, the scaling of the angular likelihood with velocity also decreased with feedback in the ASD group (P = 2.93 × 10⁻⁵), it did not do so differently than for controls (interaction term = 0.809) (Fig. 3F).

What is perhaps most notable is that the degree of trial-to-trial variability in radial end points before feedback not only was different across experimental groups but also, showed strong correlations with ASD symptomatology. The Autism Quotient (AQ) (45), measuring symptoms of autism spectrum in healthy populations, and the Social Communication Questionnaire (SCQ) (46), measuring communication skills and social functioning symptomatology, both negatively correlated with the R² values of the linear regression between radial targets and responses prior to feedback (radial R² and AQ: r = − 0.64; P = 9.52 × 10⁻⁶; radial R² and SCQ: r = − 0.68; P = 1.5 × 10⁻⁶) (Fig. 3 G and H). Further supporting the association between greater variability and ASD symptomatology, the scaling of radial uncertainty with velocity extracted from the best-fit speed prior model also showed a positive correlation with both the AQ (r = 0.53; P = 4.63 × 10⁻⁴) and the SCQ (r = 0.55; P = 2.27 × 10⁻⁴) (SI Appendix, Fig. S6). These findings suggest that worsened symptomatology is associated with heightened variability in responses. We did not attempt further correlational analyses between behavioral observations and subdomains of the clinical scales given the moderate data sample, large number of potential combinations, and potential for false positives.

The observed differences in uncertainty between ASD and control groups as well as the correlation of this variability with ASD symptomatology were also apparent under a more fine-grained inspection of the trajectories themselves. Namely, as expected given the fact that trials begin and end with null velocities, radial distance from origin as a function of time was very well described by sigmoidal functions (r = 0.99 ± 6.34 × 10⁻⁴) (Methods and Fig. 4A). These trajectories, however, were smoother in control than ASD individuals (P = 0.001) (Fig. 4A shows a handful of example trajectories in control and ASD participants, with blue arrows indicating moment of jerkiness; SI Appendix). Notably, unlike end point variability, the quality of this fit did not change with feedback for either group (P = 0.13) (Fig. 4B). However, importantly, the smoothness of movement trajectories in virtual reality scaled with ASD symptomatology: higher AQ (r = −0.42; P = 0.007) (Fig. 4C) and SCQ (r = −0.50; P = 8.63 × 10⁻⁴) (Fig. 4D) scores were associated with larger deviations from perfectly sigmoidal trajectories both prior to and after feedback.

Fig. 4.

Trajectory smoothness correlates inversely with ASD symptomatology. (A) Radial distance from the origin as a function of time (solid lines) was fit with a sigmoidal function (dashed lines); shown for a handful of example trajectories from control (black) and ASD (red) individuals. Blue arrows mark examples of jerkiness in ASD trajectories. (B) Scatter plot of R² of the sigmoidal fit with and without feedback for ASD (red) and control (black) individuals (also shown are means ± SEM). (C and D) The R² values of sigmoidal fits correlated with both the AQ and SCQ, suggesting that the smoother participants’ trajectory, the lower they scored on ASD-related symptomatology. With feedback, FB; without feedback, (woFB).

Discussion

Using a dynamic action–perception integration task, we found that on average ASD and control populations performed similarly, showing comparable biases (target overshooting) (29) in the absence of feedback. Similarly, both groups were also able to ameliorate their performance given feedback at the end of each trial. The initial bias seemingly stemmed from a speed prior (29, 36, 38) biasing estimates of self-velocity and not from the leaky integration of velocity into position estimates (39–41). Thus, the first conclusion of this work is that, contrary to what has been suggested in some previous literature (42, 47), individuals with ASD do not seem to be particularly poor integrators, at least not within the cadre of a naturalistic task wherein the integration is across a sustained time period on the order of 5 to 6 s. This finding is in line with Giovannini et al. (48), who demonstrated no difference between children with ASD and control individuals in blindly navigating toward a briefly presented target using nothing but proprioceptive and kinematic information (as opposed to visual flow here). This finding is also in line with Zaidel et al. (11), who demonstrated that both visual motion integration and the (maximum likelihood estimation) (49) integration of visual and vestibular signals into a multisensory estimate of self-motion were optimal and no different across control and ASD individuals. Overall, the current findings question theories of ASD emphasizing marked deficits in information integration (42, 49–51).

By fitting a dynamic Bayesian observer model across the entire trajectory, we were able to track participants’ belief states (34) and estimate likelihood functions and priors. The second conclusion of this work is that, contrary to the hypoprior hypothesis of ASD (5), results showed no difference in the prior for self-motion speeds in either the radial or angular dimension and either before or after feedback. Thus, the present findings augmented the observation of Karvelis et al. (12) that autistic traits do not relate to the overall shape of the prior distribution by demonstrating an analogous lack of such a relation in a clinical group (i.e., individuals with autism) as opposed to a healthy population with differing levels of ASD traits. By contrast, these results contradict the hypothesis that hypopriors can indeed represent a global property of ASD. Importantly, these results do not argue against the hierarchical Bayesian framework for ASD; rather, they simply demonstrate that a canonical signature of ASD cannot be found in the rather simplistic hypoprior explanation.

On the other hand, results revealed heightened variability in the clinical population. Namely, whether uncertainty was quantified as the fitted width of likelihood functions in the Bayesian model, by summary statistics (i.e., R²), or by examining the finer-grain detail of trajectories, we found that individuals with ASD were more variable than their neurotypical counterparts. Furthermore, we found that, across multiple task variables (i.e., target distance and movement velocity), variability scaled quicker in ASD than in controls. Importantly, the variability of path integration end points (quantified by either R² or likelihood widths within a dynamic Bayesian Observer Model) as well as the degree to which movement trajectories deviated from smooth sigmoids were all associated with increased severity in ASD symptomatology as measured by both the AQ and SCQ scores.

Given the closed loop nature of our task, this heightened variability can reflect either a decreased ability to generate consistent motor responses and/or an impairment in filtering out noise on the sensory side. The former is in line with known deficits in motor inhibition (52) and visuospatial working memory (53) in ASD but is likely not the sole cause given that variability also scaled with target distance even after accounting for movement variables. The latter explanation is in line with findings from simpler, open loop perceptual tasks (11, 32, 54–56). More broadly, as illustrated by the current task, sensory and motor computations in the natural environment are not independent processes as actions change the nature of the incoming sensory evidence (i.e., active sensing). Thus, the behavioral effects observed here likely reflect an agglomeration of more specific deficits yet likely reflect these deficits as they are expressed in everyday life.

From a mechanistic standpoint, widespread deficits in precision could emanate from a deficit in a global, brain-wide computation. One such canonical computation is divisive normalization (57), where neural firing is contextualized by a normalizing pool, effectively leading to a filtering operation. In fact, using neural network simulations, Rosenberg et al. (3) demonstrated that anomalies in divisive normalization could account for an array of visual perception consequences reported in ASD, and more recently, Coen-Cagli and Solomon (58) showed that neurons that are more strongly normalized fire more reliably. These putative widespread deficits in canonical computations would express across the ASD phenotype, yet it is also possible to imagine how a decreased ability to cope with uncertainty could lead to specific phenotypes, such as repetitive behaviors (52), by increasing the frequency with which one samples from the environment. We speculate that deficits in sensory encoding (59) lead to increased uncertainty and the need to more frequently sample from the environment.

An alternative but not necessarily mutually exclusive explanation is that the increased variability in path trajectories and end points does not reflect a heightened sensitivity to noise at the stage of encoding or more variable motor output but rather, an increased volatility of belief states. Specifically, it has recently been proposed that the core abnormality in ASD may reside in perceptual aberrations due to an imbalance in predictive coding (13, 14). According to this hypothesis, individuals with ASD overestimate their sensory prediction errors such that the world seems more volatile than it is. This expansion of the original hypoprior hypothesis to predictive coding (7) not only is qualitatively consistent with previous experimental findings but also, has been recently supported experimentally by Lawson et al. (7), who showed that adults with ASD overestimate volatility in the face of environmental change. This comes at the expense of learning to build stable expectations that lead to adaptive surprise, and thus, this leads to overreacting to environmental change and being disproportionately receptive to sensory input. According to this framework, wrongfully precise prediction errors during inference would urge new learning that results in “noise” as it is unlikely to repeat. Given the naturalistic, closed loop action/perception/prediction nature of our task, where actions (driven by prediction errors) influence sensory inflow, such erroneous learning due to overestimated sensory prediction errors would lead to increased variability in actions as observed here. With feedback, ASD performance matched that of control individuals, likely because feedback provided a veridical precision for sensory prediction errors. Thus, the present findings, which do not support the hypoprior hypothesis, are qualitatively consistent with the sensory prediction error hypothesis.

While normative computational frameworks are certainly well positioned to account for the panoply of cognitive and perceptual abnormalities present in ASD, the recently promoted Bayesian approaches (7, 10, 12, 21) are only a narrow view of a larger and more complex story. Notably, whether priors are weak (5) or too volatile (7, 8), these theories emphasize anomalies that act exclusively at the decoding level—but this is but a small component of brain computation. To our knowledge, other aspects of statistical inference have so far been ignored: that is, how likelihood functions are constrained by priors (i.e., efficient coding) (60). Our closed loop task involves both encoding and decoding in an intertwined, naturalistic way, which may adhere better to ASD symptomatology of everyday experiences. We argue for the use of more naturalistic, dynamic tasks (e.g., where sensory processing, perceptual inference, and actions/decisions are not artificially segregated in laboratory tasks) and normative modeling to understand how the neural computation in individuals with ASD has gone awry.

Collectively, both studies that have explicitly fitted priors and likelihoods in individuals with differing levels of ASD traits (12) or in a clinical ASD group (present study) have demonstrated that the source of the computation that has gone awry in ASD is not the prior. Instead, broader aberrant learning and inference may be the core components of maladaptive cognition within the condition. Maladaptive inference in ASD can arise from alterations in one of several core components (beyond priors and likelihoods of an extremely simplified Bayesian model) that span a multidimensional computational space (13). Establishing the mapping between this multidimensional computational space and specific deficits within the ASD phenotype will be an important endeavor moving forward. The hypothesized fundamental mechanism affected in ASD, hierarchical Bayesian learning, is much broader than just the simple equation argued in recent publications (Posterior = Prior × Likelihood). Sensory encoding, efficient coding (where the prior is an inherent component of sensory encoding) (60), and action-oriented predictive coding (61–63) all constitute critical components of cognitive computations that must be quantitatively explored in ASD. Although not exhaustive, the space of possibilities for how the phenotypic and clinical variability of ASD patients could arise from different impairments of hierarchical Bayesian inference is multidimensional. In other words, different autistic phenotypes could arise from different impairments in the computation of multiple key variables, which may qualitatively (but erroneously) appear as priors and likelihoods. A few years ago, a computational perspective on autism was rare. Now, it is growing in appeal. However, we should not underestimate the complexity of both the brain and the ASD phenotype, particularly in light of the highly constrained experimental tasks and models that we use.

Methods

Participants.

Thirty-nine subjects completed the firefly catching task. Fourteen were individuals diagnosed within the ASD (n = 14; mean ± SD; age = 14.5 ± 2.1 y; AQ = 32.7 ± 7.3; SCQ = 17.8 ± 4.2) by expert clinicians. The rest were age-matched neurotypical individuals (control; n = 25; mean ± SD; age = 14.8 ± 2.14 y; AQ = 14.0 ± 5.5; SCQ = 5.6 ± 3.2). Participants had normal or corrected to normal vision and no history of musculoskeletal or neurological disorders. Prior to partaking in the study, all participants completed the AQ (45) and the SCQ (46). The Institutional Review Board at Baylor College and Medicine approved this study, and all participants gave their written informed consent and/or assent.

Materials and Procedures.

Participants were tasked with virtually navigating to the location of a briefly presented target (i.e., the firefly) via an analog joystick with two degrees of freedom (linear and angular speed). Participants were seated facing a large projection screen (width × height: 149 × 127 cm) positioned 67.5 cm in depth with respect to their eyes and wore a seatbelt in order to restrain trunk movements. Visual stimuli were rendered as a red–green anaglyph, and subjects wore goggles fitted with Kodak Wratten filters (red #29 and green #61) to view the stimulus. The virtual world comprised a ground plane in which textural elements were isosceles triangles (base × height = 8.5 × 18.5 cm) that were randomly positioned and reoriented at the end of their lifetime (lifetime = 250 ms; floor density = 2.5 elements per 1 m²) (Fig. 1A). This floor texture had a limited lifetime and was reoriented at each presentation in order to allow them to provide optic flow information but not serve as landmarks. The ground plane was circular with a radius of 70 m (near and far clipping planes at 5 and 4,000 cm, respectively), and the subject was positioned at the center of this virtual world at the beginning of each trial. On each trial, the target was a circle of radius 20 cm in which luminance was matched to the ground texture elements, blinked at 5 Hz, and appeared at a random location between θ = ±42.5° of visual angle and at a distance of r = 1 to 6 m relative to where the subject was stationed at the beginning of the trial. After 1 s, the target disappeared, which cued subjects that they could use the joystick to navigate to the location of the target. The maximum linear and angular speeds were limited to $v_{max}=2\text{m}/\text{s}$ and $w_{max}=90°/\text{s}$, respectively. On arriving at the location where they thought the firefly was present, participants pressed a button to indicate their response.

The experiment consisted of two blocks, with each block consisting of 150 trials. In the second block, participants were given visual feedback. This feedback was in the form of a bull’s-eye pattern rendered on the virtual floor (Fig. 1B). This pattern consisted of six concentric circles, with the radius of the outermost circle being continuously scaled (up or down by 5%) according to the one-up, two-down staircase procedure. Additionally, an arrowhead indicating the target location was presented on the ground with either green or red color depending on whether the participant’s final response was within or outside the outermost rewarded concentric circle (Fig. 1B). The two blocks of trials (without and with feedback) were separated by at least a 5-min rest.

All stimuli were generated and rendered using C++ Open Graphics Library (OpenGL) by continuously repositioning the camera based on joystick inputs to update the visual scene at 60 Hz. The camera was positioned at a height of 1 m above the ground plane. Spike2 software (Cambridge Electronic Design Ltd.) was used to record and store the subject’s linear and angular velocities $\left(\stackrel{\sim }{r},\stackrel{\sim }{\theta }\right)$, target locations (r, θ), and all event markers for offline analysis at a sampling rate of 833.3 Hz. Further details of the experimental setup and task can be found in Lakshminarasimhan et al. (29).

Data Analyses.

The location of randomly presented targets (Fig. 1 C, Left), participants’ trajectory (Fig. 1 C, Right), and final position responses were expressed in polar coordinates as a radial distance (target = r; response = $\stackrel{\sim }{r}$) and an angular eccentricity (target = θ; response = $\stackrel{\sim }{\theta }$; arbitrarily, straight ahead = 0°) (Fig. 1C). When visualizing responses as a function of target location (Fig. 1 D, Right), it was apparent that a linear model with multiplicative gain scaling accounted well for the observed data (Results and Fig. 1D) (error was greater at the farthest locations tested). Thus, we used the slopes of the corresponding linear regressions as a measure of bias. Note that in this schema a slope of one indicates no bias, while slopes larger than one indicate overshooting (either in radial distance or angle). For each subject, we extract R² values of the linear fit of radial/angular target vs. response as an indication of trial-to-trial variability. Lastly, virtual path trajectories were fit with a sigmoidal function (given that participants started and ended their trajectories at velocity v = 0; parameters dictating the location and steepness of the nonlinearity were left as free parameters, and the saturation points were taken to be the minimum and maximum observed in data). Trajectories were down sampled to 83.33 Hz prior to sigmoidal fitting.

Dynamic Bayesian Observer Model.

To account for the pattern of behavioral results, we considered an observer model composed of a Bayesian estimator that uses noisy measurements $m_v$ and $m_w$ to decode linear and angular self-motion velocities $v$ and $w$. These internal velocity beliefs were then temporally integrated to dynamically update the subject’s position in the virtual world. We parameterized the model by making the following three assumptions. First, we chose an exponential function to describe the priors over both linear and angular velocities: $p\left(v\right)=e^{a_{v\left|v\right|}}$ and $p\left(w\right)=e^{a_{w\left|w\right|}}$. Second, likelihood functions $p\left(m_v|v\right)$ and $p\left(m_w|w\right)$ were assumed to be Gaussian, centered on the respective measurements $m_v$ and $m_w$. That is, likelihoods were unbiased. The variance of these likelihood functions scales proportional to the magnitude of velocity measurements: $Var\left(m_v\right)=b_v\left|m_v\right|$ and $Var\left(m_w\right)=b_w\left|m_w\right|$. Under these conditions, it can be shown that the means and variances of the maximum a posteriori estimates $\widehat{v}$ and $\widehat{w}$ are given by (29, 36)

$$E\left[\widehat{v}\text{|}{m}_v\right]=\left(1+a_v{b}_v\right)m_v$$ [1]

$$Var\left[\widehat{v}\text{|}{m}_v\right]={\left(1+a_v{b}_v\right)}^{2}Var\left(m_v\right)$$ [2]

and correspondingly for $\widehat{w}$. A flat prior corresponds to an exponent of zero, yielding an unbiased estimate, while negative/positive values of the exponents would result in under-/overestimation of the speeds.

The third and final building block of the model pertains to the integrator computing position from velocity. We assume that the integrative process is dictated by two independent leak time constants ${\tau }_d$ and ${\tau }_{\phi }$ that specify the timescales of integration of estimated linear and angular speeds to compute distance $\left(d\right)$ and heading $\left(\phi \right)$. In turn,

$$\dot{d}=-\frac{d\left(t\right)}{{\tau }_d}+\widehat{v}\left(t\right)$$ [3]

$$\dot{\phi }=-\frac{\phi \left(t\right)}{{\tau }_{\phi }}+\widehat{w}\left(t\right).$$ [4]

The average distance and heading at each time point can be determined by convolving the mean velocity estimates with exponential kernel $E\left[\widehat{d}\left(t\right)\right]=e^{-t/{\tau }_d}\cdot E\left[\widehat{v}\left(t\right)\right]$ and $E\left[\widehat{\phi }\left(t\right)\right]=e^{-t/{\tau }_{\phi }}\cdot E\left[\widehat{w}\left(t\right)\right]$, where the expectations are taken over the corresponding posterior probability distributions. Likewise, if the noise in the velocity measurements is temporally uncorrelated, the variance of the distance and heading estimates can be expressed in terms of the variances of the velocity estimates: $Var\left[\widehat{d}\left(t\right)\right]=e^{-t/{\tau }_d}\cdot Var\left[\widehat{v}\left(t\right)\right]$ and $Var\left[\widehat{\phi }\left(t\right)\right]=e^{-t/{\tau }_{\phi }}\cdot Var\left[\widehat{w}\left(t\right)\right]$. Hence, in this case, both mean and variance of the integrated estimates will share the same temporal dynamics. Note that the mean estimates $E\left[\widehat{d}\left(t\right)\right]$ and $E\left[\widehat{\phi }\left(t\right)\right]$ will be accurate with large time constants but will be misestimated if these constants are comparable with travel time, $t$. Since position is determined jointly by the time course of distance and heading, it follows that the subject’s mean estimate of their linear and angular positions $\widehat{r}$ and $\widehat{\theta }$ will also be different from their veridical values when $\tau \approx t$.

Model Fitting.

In a prior study, our group (29) demonstrated that a slow-speed prior model (i.e., with negative $a_v$ and $a_w$ exponents) with perfect integration (${\tau }_d$ and ${\tau }_{\phi }$ set to infinity) best accounted for overshooting observed in this path integration task. Different from Lakshminarasimhan et al. (29), however, we allow for $a_v$ and $a_w$ to be either negative or positive (or zero; flat prior). In addition, as many (16, 42, 47, 64) claim that individuals with ASD are poor integrators, we also fit a leaky integrator model, where the prior was held flat $\left(a_v=a_w=0\right)$, yet ${\tau }_d$ and ${\tau }_{\phi }$ were free parameters. Both the slow-speed prior model and the leaky integrator model have four free parameters: width parameters $b_v$ and $b_w$ expressing how fast the spread of the likelihood functions scale with the magnitude of linear and angular velocity measurements and either $a_v$ and $a_w$ (for the speed prior model) or ${\tau }_d$ and ${\tau }_{\phi }$ (for the leaky integrator model).

Since subjects’ position estimates are probabilistic, we fit model parameters by taking both mean and uncertainty of position into account; this was done by maximizing the expected reward: that is, the probability that the subjects believed themselves to be within the target at the end of each trial. The fitting procedure is a maximum likelihood procedure, and model parameters were optimized utilizing MATLAB’s fmincon function, constraining time constants (where applicable) and likelihood widths to be nonnegative and by initializing a total of 100 random seeds. Further detail is in Lakshminarasimhan et al. (29).

Data Availability.

Data and code have been made available at https://osf.io/chtjb/.