Noncollinear phases in moiré magnets

Significance

Moiré patterns, which result when two or more two-dimensional materials with incommensurate or rotated lattices are layered together, create controllable electronic bands that have recently been shown to induce a tremendous wealth of physical phenomena. Here we initiate the theoretical study of moiré patterns’ influence on magnetic states of localized spins. We construct a general formalism using continuum field theory and present thorough analyses in twisted bilayers of antiferromagnets and also ferromagnets, which are within the experimental reach of Van der Waals materials. Two-dimensional magnets, well known for their strong intrinsic spin fluctuations, may serve as a new platform for moiré effects and open the door to a large class of novel phenomena that were once unimaginable.

Abstract

We introduce a general framework to study moiré structures of two-dimensional Van der Waals magnets using continuum field theory. The formalism eliminates quasiperiodicity and allows a full understanding of magnetic structures and their excitations. In particular, we analyze in detail twisted bilayers of Néel antiferromagnets on the honeycomb lattice. A rich phase diagram with noncollinear twisted phases is obtained, and spin waves are further calculated. Direct extensions to zigzag antiferromagnets and ferromagnets are also presented. We anticipate the results and formalism demonstrated to lead to a broad range of applications to both fundamental research and experiments.

The wealth of new phenomena revealed in incommensurate layered structures of graphene and other two-dimensional (2D) semiconductors and semimetals have sparked major efforts in the study of electronic physics atop moiré patterns. The materials from which these structures are made, Van der Waals (VdW) solids, come in many varieties, inspiring a nascent field going well beyond graphene (1). In particular, a growing family of VdW magnets are being explored both for their magnetism directly as well as for the interplay of that magnetism with electronics (2). Two-dimensional magnets are of particular interest for the fluctuation effects inherent to them. For example, the Mermin–Wagner theorem (3) proves that a strictly 2D magnet with Heisenberg or XY symmetry cannot show long-range order at any nonzero temperature. Exotic quantum phases of magnets, e.g., quantum spin liquids, are widely expected to be more prevalent in two dimensions (4).

In this paper, we introduce a framework to study moiré structures of 2D magnets, under assumptions which are widely applicable and achievable in VdW systems. We present a general methodology to derive continuum models for incommensurate/twisted/strained multilayers including the effects of interlayer coupling, obviating the need to consider thousands or tens of thousands of lattice sites/spins with complicated local environments. We illustrate the method with detailed calculations for the case of a twisted bilayer of two-sublattice Néel antiferromagnets on the honeycomb lattice, a situation realized in ${\mathrm{M}\mathrm{n}\mathrm{P}\mathrm{S}}_3$ and ${\mathrm{M}\mathrm{n}\mathrm{P}\mathrm{S}\mathrm{e}}_3$, and also discuss applications to honeycomb lattice antiferromagnets with zigzag magnetic order [as in ${\mathrm{F}\mathrm{e}\mathrm{P}\mathrm{S}}_3$, ${\mathrm{C}\mathrm{o}\mathrm{P}\mathrm{S}}_3$, and ${\mathrm{N}\mathrm{i}\mathrm{P}\mathrm{S}}_3$; see ref. 5 for a review] and to the honeycomb lattice ferromagnet ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$ (6). We show that twisting these magnets leads to controllable emergent noncollinear spin textures (despite the fact that the parent materials all exhibit collinear ordering) and a rich spectrum of magnonic subbands.

Now we turn to the exposition of the problem and approach, which we illustrate as we go for the simplest case of a two-sublattice Néel order on the honeycomb lattice. First, we detail the assumptions under which a continuum description is possible. We consider structures built from 2D magnets with long-range magnetic order at zero temperature and assume that the interlayer exchange interactions $\sim J\prime$ are weak compared to the intralayer exchange $J$, i.e., $J\prime \ll J$. Additionally, we assume that the lattice in each layer may be regarded as a deformed version of a parent structure shared by all layers. Each layer $l$ is described by a displacement field ${\mathit{u}}_l\left(\mathit{x}\right)$ in Eulerian coordinates:

$${\mathit{u}}_l\left({\mathit{x}}_l\right)={\mathit{x}}_l-{\mathit{x}}_l^{\left(0\right)},$$ [1]

where ${\mathit{x}}_l$ and ${\mathit{x}}_l^{\left(0\right)}$ are the deformed and original positions, respectively, of points in layer $l$. The displacement field of each layer need not be uniform or small, but its gradients should be small, i.e., $\left|{\partial }_{\mu }{u}_{l,\nu }\right|\ll 1$. For uniform layers, this allows any long-period moiré structure, i.e., for which the period of the moiré pattern is large compared to the magnetic unit cell. For two identical but twisted layers, it corresponds to the case of a small twist angle, $\theta \ll \pi$. This construction is directly analogous to the procedure to build the continuum model of twisted bilayer graphene (7) following the recent derivation in ref. 8 which is valid under nearly identical assumptions.

In this situation the interlayer couplings and the displacement gradients are small perturbations on the intrinsic magnetism of the layers and therefore have significant effects only at low energies. This allows a continuum representation of the magnetism of each layer in terms of its low-energy modes: space–time fluctuations of the order parameters. The order parameter of the two-sublattice antiferromagnet is a Néel vector ${\mathit{N}}_l$ with fixed length $\left|{\mathit{N}}_l\right|=1$, and its low-energy dynamics for an isolated undeformed layer is described by the nonlinear sigma model with the Lagrange density

$${\mathcal{L}}_0\left[{\mathit{N}}_l\right]=\frac{\rho }{2v^2}{\left({\partial }_t{\mathit{N}}_l\right)}^2-\frac{\rho }{2}{\left(\nabla {\mathit{N}}_l\right)}^2+d{\left(N_l^z\right)}^2,$$ [2]

where $\rho \sim J$ is the spin stiffness, $v$ is the spin-wave velocity, and $d$ is a uniaxial anisotropy with $d>0$ signifying Ising-like and $d<0$ XY-like antiferromagnetism. For ${\mathrm{M}\mathrm{n}\mathrm{P}\mathrm{S}}_3$, there is weak Ising-like anisotropy (9) so $0<d\ll J/A_{\mathrm{u}.\mathrm{c}.}$ ($A_{\mathrm{u}.\mathrm{c}.}$ is the area of the 2D unit cell). Such smallness (but not the sign) of the anisotropy is common for third row transition metal magnets.

Next we consider the first-order effects of displacement gradients upon the intralayer terms in Eq. 2. As in ref. 8, such terms arise from pure geometry, i.e., carrying out the coordinate transformation from ${\mathit{x}}_l^{\left(0\right)}$ to ${\mathit{x}}_l$ defined in Eq. 1, and from strain-induced changes in energetics. Taking them together, the leading corrections to Eq. 2 are

$$\begin{array}{cc}\hfill {\mathcal{L}}_1\left[{\mathit{N}}_l,{\mathit{u}}_l\right]& =\rho \left({\epsilon }_{l,xx}+{\epsilon }_{l,yy}\right)\left[\frac{{\delta }_1}{v^2}{\left({\partial }_t{\mathit{N}}_l\right)}^2-{\delta }_2{\left(\nabla {\mathit{N}}_l\right)}^2\right]\hfill \\ \hfill & +{\delta }_3{\epsilon }_{l,\mu \nu }{\partial }_{\mu }{\mathit{N}}_l\cdot {\partial }_{\nu }{\mathit{N}}_l,\hfill \end{array}$$ [3]

where ${\delta }_{\mathrm{1,2,3}}$ are dimensionless $O\left(1\right)$ constants and ${\epsilon }_{l,\mu \nu }=\left({\partial }_{\mu }{u}_{l,\nu }+{\partial }_{\nu }{u}_{l,\mu }\right)/2$ is the strain field in layer $l$. For simplicity we assumed that spin-orbit effects (e.g., anisotropy $d$) are small and hence that deformation terms in Eq. 3 are SU(2) invariant: anisotropic deformation terms must be small in both spin-orbit coupling and in displacement gradients and hence are neglected.

Next we turn to the interlayer coupling terms. By locality and translational symmetry, it is generally of the form

$${\mathcal{L}}_2\left[{\mathit{N}}_1,{\mathit{N}}_2,{\mathit{u}}_1-{\mathit{u}}_2\right]=J\prime \left[{\mathit{u}}_1-{\mathit{u}}_2\right]{\mathit{N}}_1\cdot {\mathit{N}}_2,$$ [4]

where $J\prime \left[\mathit{u}\right]$ is a function with the periodicity of the undeformed Bravais lattice. Due to the smallness of $J\prime$, we neglect corrections proportional to displacement gradients in Eq. 4. Generally, $J\prime \left[\mathit{u}\right]$ can be expanded in a Fourier series and well approximated by a small number of harmonics. We obtain a specific form by considering local coupling of the spin densities in the two layers. Using the symmetries of the honeycomb lattice, the minimal Fourier expansion of the spin density ${\mathcal{S}}_l$ of a single layer contains the three minimal reciprocal lattice vectors ${\mathit{b}}_a$,

$${\mathcal{S}}_l\left(\mathit{x}\right)=n_0{\mathit{N}}_l\sum _{a=1}^3\sin \left({\mathit{b}}_a\cdot {\mathit{x}}^{\left(0\right)}\right)=n_0{\mathit{N}}_l\sum _{a=1}^3\sin \left[{\mathit{b}}_a\cdot \left(\mathit{x}-{\mathit{u}}_l\right)\right],$$ [5]

where $n_0$ measures the size of the ordered moment, and we define the origin $\mathit{x}=\mathbf{0}$ at the center of a hexagon. Taking the product ${\mathcal{S}}_1\cdot {\mathcal{S}}_2$ and applying trigonometric identities to extract the terms which vary slowly on the lattice scale (rapidly varying components do not contribute at low energy) gives the form of Eq. 4, with

$$J\prime \left[\mathit{u}\right]=J\prime \sum _{a=1}^3\cos \left({\mathit{b}}_a\cdot \mathit{u}\right),$$ [6]

where the constant $J\prime$ is proportional to the interlayer exchange and $n_0^2$. Physically, Eq. 6 captures the fact that, e.g., for intrinsically ferromagnetic exchange $J\prime >0$, the preferred relative orientation of the A sublattice spins of the two layers is parallel for AA stacking but antiparallel for AB and BA stackings.

The full Lagrange density $\mathcal{L}={\sum }_{l=\mathrm{1,2}}\left({\mathcal{L}}_0\left[{\mathit{N}}_l\right]+{\mathcal{L}}_1\left[{\mathit{N}}_l,{\mathit{u}}_l\right]\right)+{\mathcal{L}}_2\left[{\mathit{N}}_1,{\mathit{N}}_2,{\mathit{u}}_1-{\mathit{u}}_2\right]$ captures the low-energy physics of a bilayer with arbitrary deformations of the two layers. We now specialize to the case of a rigid twist of the two layers by a relative angle $\theta$: ${\mathit{u}}_1=-{\mathit{u}}_2=\frac{\theta }{2}\widehat{\mathit{z}}\times \mathit{x}$. In this case the strain vanishes, and one finds the full Lagrangian is

$$\mathcal{L}=\sum _l\frac{\rho }{2v^2}{\left({\partial }_t{\mathit{N}}_l\right)}^2-{\mathcal{H}}_{\mathrm{c}\mathrm{l}},$$ [7]

where

$${\mathcal{H}}_{\mathrm{c}\mathrm{l}}=\sum _l\left[\frac{\rho }{2}{\left(\nabla {\mathit{N}}_l\right)}^2-d{\left(N_l^z\right)}^2\right]-J\prime \mathrm{\Phi }\left(\mathit{x}\right){\mathit{N}}_1\cdot {\mathit{N}}_2$$ [8]

is the classical energy density. Here the coupling function

$$\mathrm{\Phi }\left(\mathit{x}\right)=\sum _{a=1}^3\cos \left({\mathit{q}}_a\cdot \mathit{x}\right),$$ [9]

and ${\mathit{q}}_a=\theta \widehat{\mathit{z}}\times {\mathit{b}}_a$ are the reciprocal lattice vectors of the moiré superlattice.

Eqs. 7–9 form the basis for an analysis of the magnetic structure on the moiré scale, as well as for the magnon excitations above them. The magnetic ground state is obtained as the variational minimum of ${\mathcal{H}}_{\mathrm{c}\mathrm{l}}\left[{\mathit{N}}_1,{\mathit{N}}_2\right]$. Owing to the sign change of $\mathrm{\Phi }\left(\mathit{x}\right)$, the problem is frustrated: the Néel vectors of the two layers wish to be parallel in some regions and antiparallel in others, forcing them to develop gradients within the plane—the representation in the continuum of incompletely satisfied in-plane bonds. We find that the optimal classical solution is coplanar but not necessarily collinear (see SI Appendix for a complete weak coupling analysis), and without loss of generality we can take the spins to lie in the x–z plane: ${\mathit{N}}_l^{\mathrm{c}\mathrm{l}}=\sin {\varphi }_l\widehat{\mathit{x}}+\cos {\varphi }_l\widehat{\mathit{z}}$. The formulae are simplified by forming symmetric and antisymmetric combinations, ${\varphi }_s={\varphi }_1+{\varphi }_2$ and ${\varphi }_a={\varphi }_1-{\varphi }_2$, and adopting dimensionless coordinates $\mathsf{x}=q_m\mathit{x}$, with $q_m=\left|{\mathit{q}}_a\right|$ the moiré wavevector. Then the dimensionless energy density ${\mathsf{H}}_{\mathrm{c}\mathrm{l}}={\mathcal{H}}_{\mathrm{c}\mathrm{l}}/\left(\frac{1}{2}\rho q_m^2\right)$ becomes, up to an additive constant,

$$\begin{array}{l}\hfill {\mathsf{H}}_{\mathrm{c}\mathrm{l}}=\frac{1}{2}\left(|{\nabla }_{\mathsf{x}}{\varphi }_s{|}^2+|{\nabla }_{\mathsf{x}}{\varphi }_a{|}^2\right)-\left(\alpha \widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)+\beta \cos {\varphi }_s\right)\cos {\varphi }_a.\\ \hfill \end{array}$$ [10]

Here we have introduced the dimensionless parameters

$$\alpha =\frac{2J\prime }{\rho q_m^2},\beta =\frac{2d}{\rho q_m^2},$$ [11]

and $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)={\sum }_{a=1}^3\cos \left({\widehat{\mathit{q}}}_a\cdot \mathsf{x}\right)$, where ${\widehat{\mathit{q}}}_a={\mathit{q}}_a/q_m$ are unit vectors. We can obtain partial differential equations for the phase angles by applying calculus of variations to Eq. 10:

$${\nabla }_{\mathsf{x}}^2{\varphi }_s=\beta \cos {\varphi }_a\sin {\varphi }_s,$$ [12]

$${\nabla }_{\mathsf{x}}^2{\varphi }_a=\left(\beta \cos {\varphi }_s+\alpha \widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)\right)\sin {\varphi }_a.$$ [13]

We must find the solutions of the saddle point equations which minimize the integral of ${\mathsf{H}}_{cl}$. There is always a trivial solution with ${\varphi }_s={\varphi }_a=0,\pi$, which corresponds to the Ising limit of aligned or counteraligned spins. Nontrivial solutions with potentially lower energies will be discussed in different limits below. We first focus on the case of $\beta >0$, i.e., the Ising-like anisotropy.

For $\alpha ,\beta \ll 1$, corresponding to large angles, the gradient terms in the Hamiltonian dominate and the solution is nearly constant. Perturbation theory with fixed $\delta =\beta /{\alpha }^2$ gives a nontrivial solution

$$\begin{array}{cc}\hfill {\varphi }_s& =\pi ,\hfill \\ \hfill {\varphi }_a& ={\varphi }_a^{\left(0\right)}-\alpha \hspace{0.17em}\sin {\varphi }_a^{\left(0\right)}\left(\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)-{\mathrm{\Phi }}_0\right)+O\left({\alpha }^2,\beta \right),\hfill \end{array}$$ [14]

with $\cos {\varphi }_a^{\left(0\right)}=-\frac{2}{3}\hspace{0.17em}\delta$, and where ${\mathrm{\Phi }}_0$ is a constant given in SI Appendix, Section C. In this twisted solution, $\cos {\varphi }_a$ tends to imitate the sign of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$, to gain energy from the potential term. This change of ${\varphi }_a$, however, will need to be balanced against the energy penalty due to the kinetic term. Comparing the energy of the twisted solution with that of the trivial one, we see that the former has a lower energy for $\delta <\frac{3}{2}$, i.e., whenever it exists. In this limit, at $\delta =\frac{3}{2}$, the system undergoes a continuous transition to the collinear phase. More details can be found in SI Appendix.

For small twist angles, on the other hand, $\alpha \gg 1$. In this limit, we first consider small values of $\beta$; the potential term $\alpha \widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$ in Eq. 10 dominates, and the energy is minimized by choosing ${\varphi }_a=0$ or $\pi$ almost everywhere, such that $\cos {\varphi }_a=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left[\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)\right]$, which means the order parameter vectors in the two layers are locally parallel or antiparallel. At small values of $\beta$, ${\varphi }_s$ prefers to take a constant value, and since the total area with negative $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$ is larger than the positive area, ${\varphi }_s=\pi$ is chosen; this solution lies in the same phase as that of the twisted solution found for $\alpha \ll 1$ above, that also showed the property ${\varphi }_s=\pi$; we call this phase twisted-s. The twisted-s solution obviously breaks the U(1) symmetry of spin rotations about the $z$ axis of spin space, but it retains an Ising symmetry under interchanging layers and reflecting spin $N^z\to -N^z$. One may check that $\phi ={\varphi }_s-\pi$ is odd under this symmetry.

Interestingly, however, one can further check that in the same limit of $\alpha \gg 1$, above some order 1 value of $\beta$, another twisted solution becomes more energetically favored. It belongs to what we call a twisted-a phase, where ${\varphi }_s$ is no longer constant and actually shows a twisted pattern similar to that of ${\varphi }_a$, such that $\cos {\varphi }_s$ exhibits spatial variations following those of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$ (see SI Appendix for details). This implies a nonzero value for $\phi$ so that the twisted-a phase spontaneously breaks the aforementioned Ising symmetry. The value of $\phi \hspace{0.17em}\ne \hspace{0.17em}0$ increases smoothly from zero on entering the twisted-a phase from the twisted-s one, consistent with the expected continuous behavior of an Ising transition (treated at mean-field level by the saddle point analysis).

Finally, we study the $\alpha ,\beta \gg 1$ limit, where the twisted-a solution is the lowest energy nontrivial solution. It requires ${\varphi }_s$ to take the values 0 or $\pi$ almost everywhere along with ${\varphi }_a$, such that $\cos {\varphi }_s$ matches the sign of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$; this means simply that the vectors ${\mathit{N}}_l$ align or counteralign along the $\pm \widehat{\mathit{z}}$ axis almost everywhere. The order parameter rotations occur in a narrow domain wall centered on the zeros of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$, i.e., forming a closed almost circular loop in the middle of the unit cell. This domain wall costs an amount of energy proportional to its length; as a result of this energy penalty, the twisted-a phase gives way to the collinear phase when the energy gain from the twist is exceeded by the domain wall energy. In order to study this competition, we assume that such transition occurs when $\beta \gg \alpha$, which we later check is self-consistent. The widths ${\mathsf{w}}_a$ and ${\mathsf{w}}_s$ (in dimensionless distance normal to the domain wall) over which ${\varphi }_a$ and ${\varphi }_s$ wind are determined by the balance of the gradient terms and the corresponding potential terms. This gives ${\mathsf{w}}_{a/s}\sim 1/\sqrt{\beta }$ in this limit and an energy cost per unit length of the wall of $\mathsf{E}\sim \sqrt{\beta }$. Now the bulk energy gain of the twisted state is simply proportional to $\alpha$, so we obtain the result that the twist collapses when $\sqrt{\beta }\gtrsim \alpha$. This treatment is valid since under these conditions $\beta /\alpha \gtrsim \alpha \gg 1$ (we did not determine the multiplicative order 1 constant in this inequality). Note that the transition between the collinear and twisted-a phase is a level crossing between two distinct and disconnected saddle points; consequently it corresponds to a first-order transition, and the first derivatives of the energy are discontinuous across this boundary. A tricritical point separates the two continuous transitions from this first-order one.

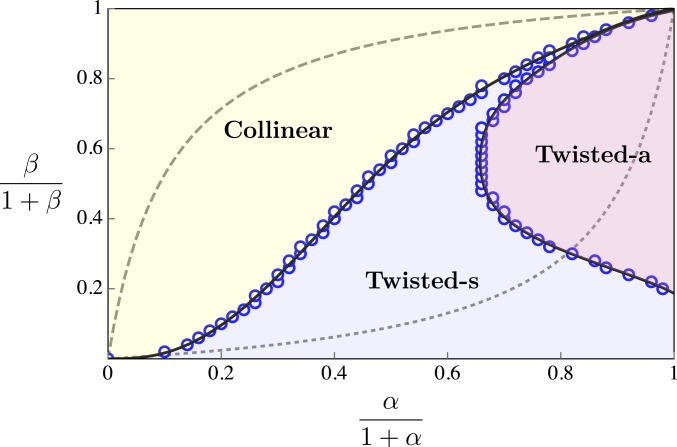
To summarize, we find three different phases for $\beta >0$, two of which correspond to twisted configurations. The transition between the two twisted phases happens at some $\beta$ of order 1, when the phase boundary is crossed in the large $\alpha$ limit; the twisted phases collapse on the other hand when $\beta >\frac{3}{2}{\alpha }^2$ in the $\alpha ,\beta \ll 1$ limit (twisted-s to Ising transition) and when $\beta \gtrsim {\alpha }^2$ in the $\alpha ,\beta \gg 1$ limit (twisted-a to Ising transition). We sketch a phase diagram in Fig. 1 based on the numerical solutions to Eq. 12, Eq. 13, which is consistent with and in fact interpolates between the perturbative and strong-coupling analyses above. The dashed and dotted lines in Fig. 1 show examples of paths with a fixed ratio $\beta /\alpha =d/J\prime$; this ratio is determined by the material, but one can tune the twisting angle $\theta$ to move along the lines and consequently enter/leave different phases. Remarkably, for a fixed $d/J\prime$, the twisted-a state is always stabilized for sufficiently small $\theta$; this can be understood by noting that $\beta /\alpha$ is invariant when $\theta$ changes as mentioned above, and thus, decreasing the twist angle increases $\alpha$ linearly with $\beta$ forming a straight line in the $\alpha -\beta$ plane (different from the axes in Fig. 1), but the twisted-a phase, when $\alpha ,\beta \gg 1$, is separated from the collinear phase by a $\beta \sim {\alpha }^2$ relation and from the twisted-s phase by $\beta \sim \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}$. Thus, the above mentioned straight line lies between these two phase boundaries at sufficiently small $\theta$. Plots of the real space configurations of the ground states in the two twisted solutions are presented in Fig. 2 A and B.

Fig. 1.

The phase diagram with respect to the normalized dimensionless parameters $\alpha /\left(1+\alpha \right)$ and $\beta /\left(1+\beta \right)$. In the collinear phase, the Néel vectors of the two layers are constant and either aligned or counteraligned. The characteristics of the twisted phases are most obvious when the potential term plays the dominant role: in the twisted-s phase, ${\varphi }_s=\pi$, while the sign of $\cos {\varphi }_a$ exhibits modulations resembling those of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$ (see Fig. 2A). In the twisted-a phase, on the other hand, the signs of both $\cos {\varphi }_s$ and $\cos {\varphi }_a$ follow that of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$. The twisted-s phase terminates at $\left(0.88,0.94\right)$ near the right top corner of the diagram. The dashed line shows $\beta =10\alpha$, while the dotted line corresponds to $\beta =0.1\alpha$. For $\beta =\alpha$, the corresponding line would be the diagonal one connecting the left bottom and right top corners.

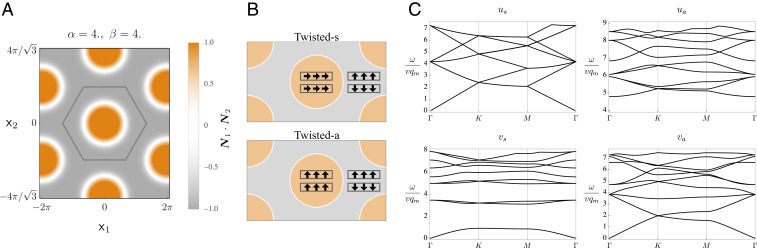
Fig. 2.

Real space configurations and spin wave plots in twisted antiferromagnets. (A) Spatial configurations of ${\mathit{N}}_1\cdot {\mathit{N}}_2=\cos {\varphi }_a$. It can be seen that $\cos {\varphi }_a$ is either $+1$ or $-1$ almost everywhere, based on the sign of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$; indeed, the choice of $\alpha =4,\beta =4$ corresponds to a solution in which the potential term plays the dominant role and that lies in the twisted-a phase; the same quantity, i.e., $\cos {\varphi }_a$, looks very similar if $\beta$ is lowered even into the twisted-s phase while keeping $\alpha$ fixed. (B) A schematic diagram of the spatial dependence of the orientation of the Néel vectors (not actual spins) in the two layers in the strong coupling limit. A vertical (horizontal) arrow denotes out-of-plane (in-plane) orientation; the brown and gray areas show regions with positive and negative values for $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$. The main difference is that in the brown region, the twisted-s phase shows in plane orientation, and the twisted-a phase shows out-of-plane orientation. (C) The lowest 10 magnon bands at $\alpha =2$ for the four branches, in the isotropic case ($d=0$) of two coupled two-sublattice antiferromagnets.

Once the minimum energy saddle point is obtained, the full Lagrangian allows for calculation of the magnon spectrum. We define

$${\mathit{N}}_l=\sqrt{1-u_l^2-v_l^2}{\mathit{N}}_l^{\mathrm{c}\mathrm{l}}\left(\mathsf{x}\right)+u_l{\mathit{u}}_l\left(\mathsf{x}\right)+v_l{\mathit{v}}_l\left(\mathsf{x}\right),$$ [15]

where ${\mathit{u}}_l=\cos {\varphi }_l\left(\mathsf{x}\right)\widehat{\mathit{x}}-\sin {\varphi }_l\left(\mathsf{x}\right)\widehat{\mathit{z}}$ and ${\mathit{v}}_l=\widehat{\mathit{y}}$ complete a spatially dependent orthonormal basis such that $\widehat{\mathit{u}}\times \widehat{\mathit{v}}={\mathit{N}}_l^{\mathrm{c}\mathrm{l}}$ at every $\mathit{x}$. The fluctuations about the classical solution are described by space–time-dependent fields $u_l\left(\mathsf{x},t\right),v_l\left(\mathsf{x},t\right)$. Inserting Eq. 15 into Eq. 7, expanding to quadratic order in the fluctuations, and finding the Euler–Lagrange equations for $u_{s/a}=u_1\pm u_2,v_{s/a}=v_1\pm v_2$, one obtains linear wave equations for four branches of excitations. For simplicity, we present the results for $d=\beta =0$ (see SI Appendix for the general result), in which case the four modes decouple immediately,

$$\begin{array}{l}\hfill -{\partial }_t^2{u}_{s/a}=v^2{q}_m^2{\widehat{\mathsf{D}}}_{u,s/a}{u}_{s,a},-{\partial }_t^2{v}_{s/a}=v^2{q}_m^2{\widehat{\mathsf{D}}}_{v,s/a}{v}_{s,a},\\ \hfill \end{array}$$ [16]

with the linear operators

$$\begin{array}{ll}\hfill {\widehat{\mathsf{D}}}_{u,s}=& -{\nabla }_{\mathsf{x}}^2,\hfill \\ \hfill {\widehat{\mathsf{D}}}_{u,a}=& -{\nabla }_{\mathsf{x}}^2+\alpha \widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)\cos {\varphi }_a,\hfill \\ \hfill {\widehat{\mathsf{D}}}_{v,s}=& -{\nabla }_{\mathsf{x}}^2-\frac{1}{4}|{\nabla }_{\mathsf{x}}{\varphi }_a{|}^2-\frac{\alpha }{2}\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)\left(1-\cos {\varphi }_a\right),\hfill \\ \hfill {\widehat{\mathsf{D}}}_{v,a}=& -{\nabla }_{\mathsf{x}}^2-\frac{1}{4}|{\nabla }_{\mathsf{x}}{\varphi }_a{|}^2+\frac{\alpha }{2}\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)\left(1+\cos {\varphi }_a\right).\hfill \end{array}$$ [17]

Taking $u_{s/a}\left(\mathsf{x},t\right)=e^{i\omega t}{u}_{s/a}\left(\mathsf{x}\right)$, we obtain eigenvalue problems such that the magnon frequencies are ($v{q}_m$ multiplied by) the square roots of the eigenvalues of the $\widehat{\mathsf{D}}$ operators. These eigenvalue problems have the form of continuum nonrelativistic Schrödinger–Bloch problems and therefore can be solved using the Bloch ansatz to find an infinite series of magnon bands. When $\alpha$ is large, the potential terms in the above equations become alternated deep wells and hard walls, which confine the magnons to either of the two domains. This leads to the flattening of magnon bands in branches $u_a$ and $v_s$. Fig. 2C shows the lowest magnon bands when $\alpha$ is at intermediate value. There are three gapless Goldstone modes in the $u_s$, $v_s$, and $v_a$ branches, which correspond to the three generators of the $O\left(3\right)$ group.

Finally, we comment on the case of $d<0$ in brief, where the anisotropy term favors the spins to lie in the XY plane. The corresponding equations of motion resemble those of the isotropic case, i.e., ${\varphi }_s$ tends to be uniform everywhere, while $\cos {\varphi }_a$ imitates the sign of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$ due to the interlayer exchange, leading to twisted configurations. More details can be found in SI Appendix.

Zigzag Antiferromagnet

Having described the case of the Néel antiferromagnet in detail, we give further results more succinctly for other types of 2D magnets. The materials ${\mathrm{F}\mathrm{e}\mathrm{P}\mathrm{S}}_3$, ${\mathrm{C}\mathrm{o}\mathrm{P}\mathrm{S}}_3$, and ${\mathrm{N}\mathrm{i}\mathrm{P}\mathrm{S}}_3$ all have the same lattice structure as ${\mathrm{M}\mathrm{n}\mathrm{P}\mathrm{S}}_3$ but exhibit zigzag magnetic order. It is a collinear magnetic order which doubles the unit cell. There are three possible ordering wavevectors: the M points at the centers of the edges of the moiré Brillouin zone, which are half reciprocal lattice vectors, ${\mathit{b}}_a/2$, with $a=\mathrm{1,2,3}$. The spin density (analogous to Eq. 5) therefore contains three order parameter “flavors,” ${\mathit{N}}_a$:

$${\mathcal{S}}_l\left(\mathit{x}\right)=n_0\sum _{a=\mathrm{1,2,3}}{\mathit{N}}_{l,a}\sin \left[\frac{1}{2}{\mathit{b}}_a\cdot \left(\mathit{x}-{\mathit{u}}_l\right)\right].$$ [18]

Here in a zigzag state, just a single one of the three ${\mathit{N}}_a$ vectors is nonzero: this describes three possible spatial orientations of the zigzag chains of aligned spins. Proceeding as before, we obtain the effective classical Hamiltonian in the form

$${\mathcal{H}}_{\mathrm{c}\mathrm{l}}^{\mathrm{z}\mathrm{i}\mathrm{g}-\mathrm{z}\mathrm{a}\mathrm{g}}=\sum _{a,l}\left[\frac{\rho }{2}{\left(\nabla {\mathit{N}}_{a,l}\right)}^2+\frac{\stackrel{\sim }{\rho }}{2}{\left({\widehat{\mathit{q}}}_a\cdot \nabla {\mathit{N}}_{a,l}\right)}^2\right]$$ [19]

$$+\sum _{l}V\left[{\mathit{N}}_{1,l},{\mathit{N}}_{2,l},{\mathit{N}}_{3,l}\right]-\frac{J\prime }{2}\sum _a{\mathit{N}}_{a,1}\cdot {\mathit{N}}_{a,2}\cos \left(\frac{{\mathit{q}}_a\cdot \mathit{x}}{2}\right).$$

Here $\rho ,\stackrel{\sim }{\rho }$ are two stiffness constants, and $V$ is a potential which may be taken in the form

$$\begin{array}{ll}\hfill V\left[{\mathit{N}}_1,{\mathit{N}}_2,{\mathit{N}}_3\right]& =u{\left(\sum _a|N_a{|}^2-1\right)}^2+v\sum _{a>b}\left|N_a{|}^2\right|N_b{|}^2\hfill \\ \hfill & -d\sum _a{\left(N_a^z\right)}^2,\hfill \end{array}$$ [20]

with $u,v>0$ to model the energetic preference for a single nonzero stripe orientation and $d$ as before to tune anisotropy.

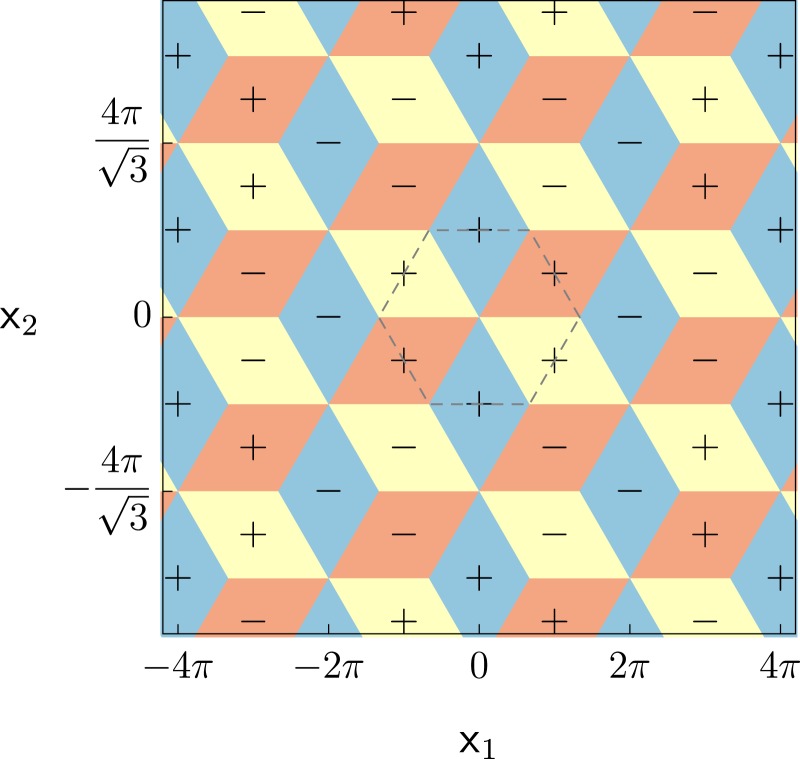
Eq. 19 gives a continuum model to determine the magnetic ordering texture for arbitrary twist angles. The most important difference from the two-sublattice antiferromagnet is that here each spatial harmonic couples to a single flavor, while in the former case, Eq. 18, the single flavor of order parameter couples to the sum of harmonics. While we do not present a general solution, we note immediate consequences in the strong coupling limit, $J\prime \gg \rho q_m^2,\stackrel{\sim }{\rho }{q}_m^2$. In this situation, for each $\mathit{x}$ we must choose the largest harmonic, i.e., the $a$ which maximizes $\left|\cos \left(\frac{{\mathit{q}}_a\cdot \mathit{x}}{2}\right)\right|$, and then take ${\mathit{N}}_{a,1}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left[J\prime \cos \left(\frac{{\mathit{q}}_a\cdot \mathit{x}}{2}\right)\right]{\mathit{N}}_{a,2}$ and ${\mathit{N}}_{a\prime ,l}=0$ for $a\prime \hspace{0.17em}\ne \hspace{0.17em}a$. Remarkably, the result is a tiling of six possible zig-zag domains which evokes a dice lattice, as shown in Fig. 3. Narrow domain walls separate these regions.

Fig. 3.

The real space tiling with six possible domains which appear in a twisted bilayer of zigzag antiferromagnets in the strong coupling (small angle) limit. The colors show which flavor of the order parameter is nonzero in each domain, while the $\pm$ signs label the relative sign between the order parameter in the two layers. The dashed hexagon shows a moiré structural unit cell.

Twisted Ferromagnet

Naïvely, twisting a homobilayer of ferromagnets is relatively innocuous. However, experiments and theory (10–16) for ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$ have indicated that the interlayer exchange has a strength and sign that depends upon the displacement between neighboring layers. This can be directly incorporated into a continuum model following our methodology.

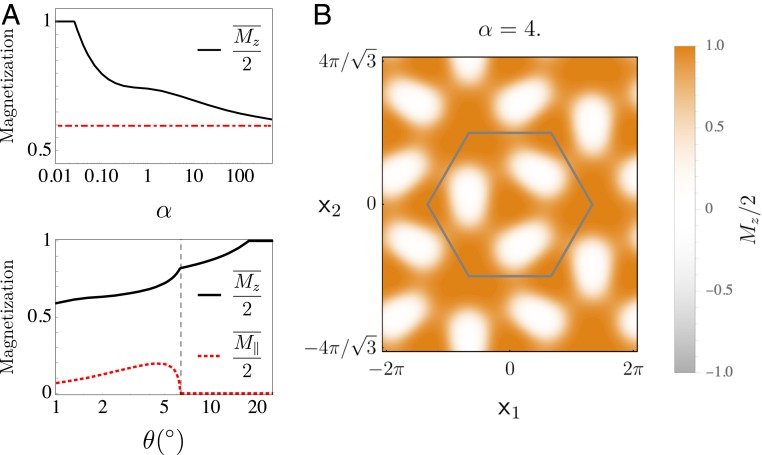
To this end, for a general twisted bilayer of a ferromagnetic material with the above property, one can use the energy functional shown in Eq. 8 with minimal modifications: 1) the Néel vectors ${\mathit{N}}_l$ should be everywhere replaced by the uniform magnetization ${\mathit{M}}_l$ since in fact each layer is ferromagnetic within itself and 2) the function $\mathrm{\Phi }\left({\mathit{u}}_1-{\mathit{u}}_2\right)$ takes a more complicated form. Assuming a small twist angle, the latter may be determined from the dependence of the interlayer exchange of untwisted layers on a uniform interlayer displacement. For the case of ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$, we have extracted the stacking dependent interlayer exchange data from the first principle calculations in ref. 14. Similar to the case of twisted antiferromagnets, a variational analysis of Eq. 8 can be performed, which leads to the same set of Euler–Lagrange equations, i.e., Eqs. 12 and 13. In order to simplify the analysis, we will only consider an infinitesimal $\beta$ here; its effect is to fix the value of ${\varphi }_s=0$ for ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$ as discussed in SI Appendix. The effects of nonzero $\beta$ can also be studied in a way similar to the previous case. The mathematical problem is then to obtain the functional form of ${\varphi }_a\left(\mathit{x}\right)$ and its dependence upon $\alpha$. In the ferromagnetic case, the Fourier expansion of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$ generally has a nonzero constant term, which dominates the solution at small $\alpha$. In the case of ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$, the constant term is small and ferromagnetic; thus, ${\varphi }_a=0$ is chosen for small $\alpha$. However, if other harmonics of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$ are strong enough, a twisted solution starts to appear at a finite value of $\alpha$ with a lower energy. As in the antiferromagnetic case, $\cos {\varphi }_a$ shows spatial modulations imitating the changes of $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)$ in this twisted solution. This property of the twisted solution is most visible in the large $\alpha$ limit, where the kinetic energy penalty is least important: one observes then domains with $\cos {\varphi }_a=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left[\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)\right]$, separated by narrow domain walls. For a detailed analysis of the above statements in the case of ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$, see SI Appendix. A plot of the average magnetization in the system is shown in Fig. 4A with a transition from collinear to twisted phase at finite $\alpha$. Unlike the antiferromagnets discussed above, there is a finite interval of twist angles where the collinear phase exists even with infinitesimal anisotropy parameter $\beta$. Also a plot of the spatial configuration of a twisted solution is presented in Fig. 4B; it shows that there are large regions in real space with maximal magnetization while at the same time there are also other regions exhibiting close to zero magnetization.

Fig. 4.

Phase diagrams and a real space configuration plot in twisted bilayers of the ferromagnet ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$. (A) (Top) The average value of the $z$ component of the sum of the two layers’ spins for ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$, when the anisotropy parameter is taken to be positive and infinitesimal. A continuous transition from the collinear phase to the twisted phase occurs at $\alpha =0.025$. This phase is analogous to the twisted-s phase discussed previously. The total area in which $\widehat{\mathrm{\Phi }}\left(\mathsf{x}\right)>0$ is shown with a dashed red line here as the limiting value of $\frac{\overline{M_z}}{2}$ for very large $\alpha$. (Bottom) The average value of the $z$ and in-plane components of the total magnetization calculated with physical parameters chosen as discussed in the main text for ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$. In particular, the anisotropy is nonzero here. At $\theta =17.5^{○}$, a transition from collinear to twisted-s phase occurs at which point $\overline{M_z}$ starts to be nonzero. Moreover, a transition to the twisted-a phase occurs at $\theta =6.4^{○}$, which exhibits itself in $\overline{M_{\parallel }}$ starting to be nonzero for smaller angles. (B) Spatial profile of local magnetization $\frac{M_z}{2}=\frac{1}{2}\left(M_{1,z}+M_{2,z}\right)$ for a twisted solution in ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$. The anisotropy parameter is taken to be positive and infinitesimal. There are large regions in real space with a net magnetization, while other regions have vanishingly small net magnetization.

Conclusion

In this work, we have considered moiré 2D magnets and in particular the twisted bilayers of VdW magnetic materials. We have developed a low-energy formalism in the continuum and studied in detail three different examples of twisted bilayers: antiferromagnetic, zigzag antiferromagnetic, and ferromagnetic. Remarkably, a rich phase diagram is obtained as one varies the twist angle and material parameters; there are interesting twisted ground state solutions comprising long-wavelength noncollinear magnetic textures. Such spatial patterns can potentially be observed in experiments, where the twist angle control adds to the tunability of the system. Furthermore, at small twist angles in the noncollinear phases, certain spin waves also exhibit interesting features such as flattening dispersion curves.

Material-wise, ${\mathrm{M}\mathrm{n}\mathrm{P}\mathrm{S}}_3$ has $\beta \approx 4.54\alpha$, and the system is in the collinear phase for generic twist angles. The ratio can be derived using $d={\mathrm{\Delta }}^2/\left(12J{A}_{\text{u.c.}}\right)$ and $J\prime =J_{\text{exp}}^{\prime }{S}^2/\left(2A_{\text{u.c.}}\right)$, where the intralayer exchange $J$, interlayer coupling $J_{\text{exp}}^{\prime }$, and the magnon gap $\mathrm{\Delta }$ are extracted from ref. 9. On the other hand, for ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$, we have derived $\beta \approx 0.62\alpha$ using the intralayer exchange and anisotropy parameter as given in ref. 17 and the interlayer exchange data as given in ref. 14. A plot of average magnetization for ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$ in the perpendicular and parallel directions for which the above parameters are used is presented in Fig. 4A, Bottom; it can be seen that at large angles, the system is in the collinear phase, but the twisted-s phase (${\varphi }_s=0$) starts to be preferred at $\theta =17.5^{○}$; upon further decreasing the angle, starting at $\theta =6.4^{○}$, the twisted-a phase becomes the ground state (see the legend of Fig. 4 for details). This shows that in a twisted bilayer of ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$, it is reasonable to expect both of the twisted phases to be realized in experimentally accessible settings.

The present methodology can be utilized with minimal modifications in further analyses of other moiré systems in the vast collection of possible bilayer magnetic materials. For example, here we have mainly presented the examples of homobilayers, but interesting phenomena can also arise for heterobilayers of VdW magnets, such as the stacking of ferromagnets on antiferromagnets (18). The magnetic properties of general moiré systems as well as their interplay with the electronic/transport properties could be the subject of future studies. Given the extremely fruitful research done in the field of moiré electronic systems, one can anticipate that the magnetic moiré systems could play the role of a new platform where novel exciting physics could be pursued.

Materials and Methods

In this section, we explain our numerical manipulations.

In order to find the ground states, one needs to solve Eqs. 12 and 13 simultaneously. We have done so by two different methods: The first method is solving the equations in real space by the use of overdamped dynamics, i.e., adding fictitious time derivatives of ${\varphi }_a$ and ${\varphi }_s$ to the equations and running the time evolution; a final configuration with zero time derivative ensures that the equations are satisfied. The second method is solving the equations in the Fourier representation iteratively by starting from a well-chosen simple guess; most of the time, ${\varphi }_a\left(\mathsf{x}\right)={\varphi }_s\left(\mathsf{x}\right)=\pi /2$ is a suitable initial seed. The results from the above two approaches agree completely

In Fig. 1, the phase boundaries can be extracted by observing the changes of behavior of $\cos {\varphi }_s$ and $\cos {\varphi }_a$. We first solve Eqs. 12 and 13 for various combinations of $\alpha$ and $\beta$ and plot the corresponding functions $\cos {\varphi }_s$ and $\cos {\varphi }_a$ in real space. In the collinear phase, both are constant. Fixing $\beta$ while increasing $\alpha$ from zero, $\cos {\varphi }_a$ will begin to have spatial variations at the phase boundary between the collinear and the twisted-s phase. On the other hand, if one fixes $\alpha$ while increasing $\beta$ from zero, the $\cos {\varphi }_s$ will start from a constant in the twisted-s phase and begin to have spatial variations once it crosses the phase boundary and enters the twisted-a phase. Similar reasoning works for finding the phase boundaries in the case of ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$, i.e., results presented in Fig. 4A.

As for Fig. 2C, the spin waves are obtained from the Bloch ansatz $u_{s/a}\left(\mathsf{x}\right)={û}_{s/a}\left(\mathsf{x}\right)e^{i\mathsf{k}\cdot \mathsf{x}}$ and similarly for $v_{s/a}$. The variables in Eq. 17 thus become ${û}_{s/a}$ and ${\widehat{v}}_{s/a}$ with the substitutions ${\nabla }_{\mathsf{x}}^2\to {\left({\nabla }_{\mathsf{x}}+i\mathsf{k}\right)}^2$ and $-{\partial }_t^2\to {\omega }^2$. Discretizing the moiré unit cell, the linear operators become large matrices and can subsequently be diagonalized using Mathematica to find the magnon bands.

The interlayer exchange for ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$ is extracted from figure 2b of ref. 14, where the dependence upon displacement is presented along two special lines. The interlayer exchange is a periodic function with the same period as that of the monolayer lattice; thus, a Fourier series for the interlayer exchange (a constant along with the lowest five harmonics) in the 2D space is assumed which induces one-dimensional functions on the above two special lines. One can fix the Fourier coefficients by comparing these induced forms with the given functions in the above reference. The Euler–Lagrange equations for ${\mathrm{C}\mathrm{r}\mathrm{I}}_3$ are solved using the same methods described above.

Data Availability.

No data, materials, or protocols are needed to reproduce the results presented in this paper. All codes are available upon request.