Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Apr 20;11(10):3828–3834. doi: 10.1021/acs.jpclett.0c00527

Combining SchNet and SHARC: The SchNarc Machine Learning Approach for Excited-State Dynamics

Julia Westermayr †, Michael Gastegger ‡,*, Philipp Marquetand †,¶,§,*
PMCID: PMC7246974  PMID: 32311258

Abstract

graphic file with name jz0c00527_0004.jpg

In recent years, deep learning has become a part of our everyday life and is revolutionizing quantum chemistry as well. In this work, we show how deep learning can be used to advance the research field of photochemistry by learning all important properties—multiple energies, forces, and different couplings—for photodynamics simulations. We simplify such simulations substantially by (i) a phase-free training skipping costly preprocessing of raw quantum chemistry data; (ii) rotationally covariant nonadiabatic couplings, which can either be trained or (iii) alternatively be approximated from only ML potentials, their gradients, and Hessians; and (iv) incorporating spin–orbit couplings. As the deep-learning method, we employ SchNet with its automatically determined representation of molecular structures and extend it for multiple electronic states. In combination with the molecular dynamics program SHARC, our approach termed SchNarc is tested on two polyatomic molecules and paves the way toward efficient photodynamics simulations of complex systems.

Excited-state dynamics simulations are powerful tools to predict, understand, and explain photoinduced processes, especially in combination with experimental studies. Examples of photoinduced processes range from photosynthesis, DNA photodamage as the starting point of skin cancer, to processes that enable our vision.1−5 As they are part of our everyday lives, their understanding can help to unravel fundamental processes of nature and to advance several research fields, such as photovoltaics,6,7 photocatalysis,8 or photosensitive drug design.9

Because the full quantum mechanical treatment of molecules remains challenging, exact quantum dynamics simulations are limited to systems containing only a couple of atoms, even if fitted potential energy surfaces (PESs) are used.10−26 In order to treat larger systems in full dimensions, i.e., systems with up to hundreds of atoms, and on long time scales, i.e., in the range of several 100 ps, excited-state machine learning (ML) molecular dynamics (MD), where the ML model is trained on quantum chemistry data, has evolved as a promising tool in the last couple of years.27−33

Such nonadiabatic MLMD simulations are in many senses analogous to excited-state ab initio molecular dynamics simulations. The only difference is that the costly electronic structure calculations are mostly replaced by an ML model, providing quantum properties like the PESs and the corresponding forces. The nuclei are assumed to move classically on those PESs. This mixed quantum–classical dynamics approach allows for a very fast on-the-fly evaluation of the necessary properties at the geometries visited during the dynamics simulations.

In order to account for nonadiabatic effects, i.e., transitions from one state to another, further approximations have to be introduced.34 One method, which is frequently used to account for such transitions, is the surface-hopping method originally developed by Tully.35 A popular extension for this method including not only nonadiabatic couplings (NACs) but also other couplings, e.g., spin–orbit couplings (SOCs), is the SHARC (surface hopping including arbitrary couplings) approach.36−38 Importantly, NACs, also called derivative couplings, are used to determine the hopping directions and probabilities between states of the same spin multiplicity.36,37,39−41 The NAC vector (denoted as CNAC) between two states, i and j, can be computed as39,42,43

graphic file with name jz0c00527_m001.jpg 1

where the second-order derivatives are neglected. As a further difficulty, NACs are often missing from quantum chemistry implementations and hopping probabilities and directions are thus often approximated.44−52 SOCs (denoted as CSOC) are present between states of different spin multiplicity

graphic file with name jz0c00527_m002.jpg 2

and determine the rate of intersystem crossing. They are obtained as off-diagonal elements of the Hamiltonian matrix in standard electronic-structure calculations.37,53

Most of the recent studies involving ML dynamics deal with ground-state MD simulations, see e.g. refs (54−78), where one of the most promising ML models is SchNet,79,80 a deep continuous-filter convolutional-layer neural network. In contrast to popular ML models like RuNNer,64 n2p2,81 TensorMol,82 ANI,63 or the DeePMD model83 that require hand-crafted molecular descriptors, SchNet belongs to the class of message-passing neural networks.84 Other examples of such networks are the DTNN,85 PhysNet,86 or HIP-NN.87 The advantage is that the descriptors of molecules are automatically designed by a deep neural network and are based on the provided data set. In this way, the descriptors are tailored to the encountered chemical environments. Thus, we choose SchNet as a convenient platform for our developments.

An arising difficulty compared to ground-state energies and properties is that for the excited states not only one, but several PESs as well as the couplings between them have to be taken into account. Only a small but quickly increasing number of studies deal with the treatment of excited states and their properties using ML.15−28,31,33,88

In addition to the higher dimensionality that can be tackled with ML,89,90 the learning of couplings proves challenging because properties resulting from electronic wave functions of two different states, Ψi and Ψj, have their sign dependent on the phase of the wave functions.32,33,91,92 Because the wave function phase is not uniquely defined in quantum chemistry calculations, random phase jumps occur, leading to sign jumps of the coupling values along a reaction path. Hence, the couplings can not be learned directly as obtained from a quantum chemistry calculation. An option is to use a phase correction algorithm to preprocess data and remove these random phase jumps. Assuming that the effect of the Berry phase remains minor on the training set, smooth properties are obtained that are learnable by ML models.32 However, this approach is expensive and many quantum chemistry reference computations are necessary to generate the training set. In cases of large polyatomic molecules with many close-lying energetic states, this approach might even be infeasible.

The aim of this Letter is to provide a framework to carry out efficient excited-state MLMD simulations and to combine two popular methods for this purpose: the SHARC approach for photodynamics with states of different multiplicity and SchNet to efficiently and accurately fit potential energies and other molecular properties. We call this combination the SchNarc approach and adapted SchNet for the treatment of excited-state potentials, their forces, and couplings for this purpose. The SchNarc approach can overcome the current limitations of existing MLMD simulations for excited states by allowing (i) a phase-free training to omit the costly preprocessing of raw quantum chemistry data and, to treat (ii) rotationally covariant NACs, which can either be trained or (iii) alternatively be approximated from only ML potentials, their gradients, and Hessians, and to treat (iv) SOCs. When using the phase-free training in combination with the approximated NACs, the costs required for the training set generation can be reduced substantially. Further, each data point can be computed in parallel, which is not possible when phase correction is needed. With all these methodological advances, the SchNarc ML approach simplifies accelerated nonadiabatic dynamics simulations, broadening the range of possible users and the scope of systems, in order to make long time scales accessible.

To validate our developments, the surface hopping dynamics of two molecules, showing slow and ultrafast excited-state dynamics, are investigated. The first molecule is CH2NH2+, of which we take a phase-corrected training set from ref (32). Using the same level of theory (MR-CISD(6,4)/aug-cc-pVDZ) with the program COLUMBUS,93 the training set is recomputed without applying phase correction to train ML models also on raw data obtained directly from quantum chemistry programs. This training set should be used to validate our phase-free training approach. The ML models are trained on energies, gradients, and NACs for three singlet states using 3000 data points.

Slow photoinduced processes are present in thioformaldehyde, CSH2.94 The training set is built up of 4703 data points with two singlet states and two triplet states after initial sampling of normal modes and adaptive sampling with simple multilayer feed-forward neural networks according to the scheme described in ref (32). This scheme applied for the training set generation is based on an uncertainty measure. Two (or more) ML models are trained and dynamics simulations are performed. At each time step, the predictions of the different ML models are compared. Whenever the error between the models exceeds a manually defined threshold, the molecular geometry visited at this time step is recomputed with quantum chemistry and the data added to the training set. Our previously proposed network32 was used for this purpose because the training set was generated before SchNarc was developed. The sampling procedure is largely independent of the network architecture used and could therefore also be carried out with SchNarc but has not been tested here. The program MOLPRO95 is used for the reference calculations with CASSCF(6,5)/def2-SVP.

The main novelty of the phase-free training is that it removes the influence of the arbitrary phase during the learning process of an ML model. It can be applied to any existing ML model capable of treating excited states and any existing data set for excited states eliminating an expensive and time-consuming phase correction preprocessing. The chosen ML model here is SchNet, for which the new loss function termed phase-less loss function is implemented and tested using the methylenimmonium cation, CH2NH2+. The phase-less loss is based on the standard L2 loss, but here, the squared error of the predicted properties is computed 2NS–1 times, with NS being the total number of states. The value of each property, LP (i.e., LSOC and LNAC), that enters the loss function is the minimum function of all possible squared errors εPk:

graphic file with name jz0c00527_m003.jpg 3

with

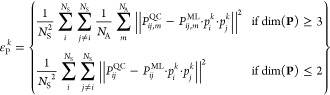graphic file with name jz0c00527_m004.jpg 4

for vectorial and nonvectorial properties, respectively. The error εPk for a specific phase is computed as the mean squared error of a property P from quantum chemistry (index QC) and machine learning (index ML). The property P couples different states, indicated by i and j. Because the wave function of each of the states can have an arbitrary phase, the property Pij that couples state i and j has to be multiplied with a product of the phases for these states, pi·pj. The phases for all states together form a vector p with entries of either +1 and −1. Which of the 2NS–1 possible combinations for p is chosen is indicated by the index k, also defined in eq 3. The possible combination that gives the lowest error enters the loss function. This is done for all samples inside of the training set and can be seen as an internal ML-based phase correction. Because of the continuity of ML fitted functions, the sign of properties is consistent for predictions. Note that the relative signs within one vector remain and must be predicted correctly for successful training.

The overall loss function in this work is a combination of such phase-less loss functions and mean squared errors for all properties with a trade-off factor to account for their relative magnitude. The relative magnitude of each property is defined by a manually set trade-off factor (a detailed description of the implementation is given in the Supporting Information).

Results are given in Figure 1, which shows the population schemes of CH2NH2+ obtained after excitation to the second excited singlet state, S2. The populations obtained from quantum chemistry are shown by dotted lines. SchNarc models are illustrated using solid lines. Panels A and C are obtained from SchNarc models trained on a data set that is not phase-corrected; that is, it contains couplings that can randomly switch their sign. Those are compared to populations obtained from models trained on phase-corrected data (panels B and D). As can be seen, the L2 loss function, as used in the upper plots, leads to an accurate ML model to reproduce ultrafast transitions only in the case of phase-corrected data (panel B), whereas this loss can not be used when trained on raw quantum chemistry data (panel A). In comparison, a SchNarc simulation with an ML model that applies the phase-less loss function is successful in reproducing the populations for both training sets (panels C and D).

Figure 1.

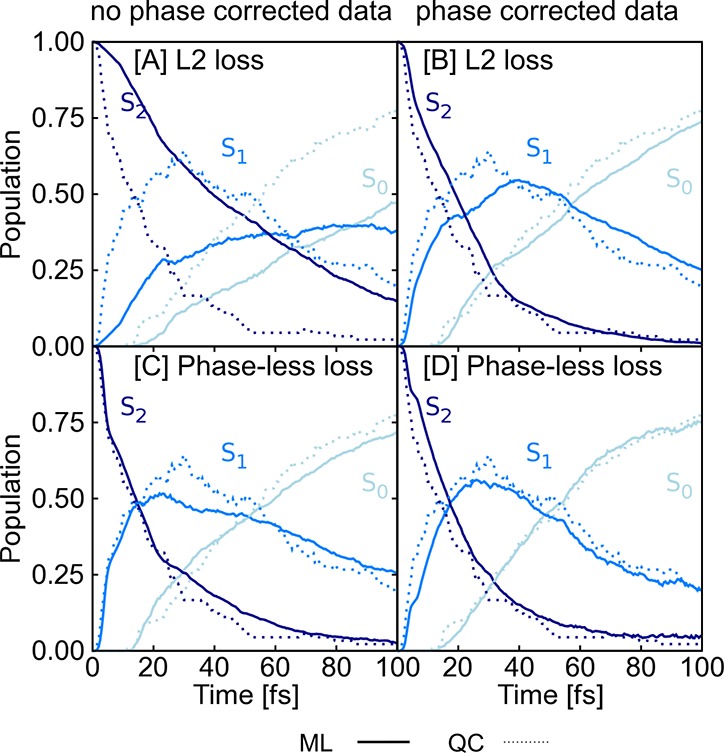
Figure 1

Open in a new tab

Populations obtained from 90 QC (MR-CISD(6,4)/aug-cc-pVDZ) trajectories are shown by dotted lines and are compared to populations resulting from 1000 trajectories initially excited to the S2 obtained from SchNet (solid lines) that is trained on (A) not phase-corrected data and takes the L2 norm as loss function; (B) a similar SchNet model, but trained on phase-corrected data; (C) a SchNet model trained on not phase-corrected data, but using the new phase-less loss function; and (D) a SchNet model trained on phase-corrected data using the new phase-less loss function.

In those simulations, the NACs are multiplied with the corresponding energy gaps, i.e., C̃ijNAC = Cij ·ΔEij, to get rid of singularities.21,33 These smooth couplings C̃ijNAC are not directly learned, but rather constructed as the derivative of a virtual property, analogously to forces that are predicted as derivatives of an energy-ML model. The virtual property is the multidimensional antiderivative of the rightmost expression in eq 1, 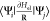Inline graphic (a derivation is given in the Supporting Information). Compared to previous ML models for NACs,29,30,32,33 where NACs are learned and predicted as direct outputs or even single values, this approach provides rotational and translational covariance, which has recently been achieved in a similar way for the electronic friction tensor.96

However, even without the need of preprocessing the training set, the costly computations of NAC vectors for the training set generation remain. Approximations of NACs exist and often involve the computation of the squared energy-gap Hessian.11,97−101 Their use in dynamics simulations is rather impracticable with quantum chemistry methods, especially in the case of complex systems, because of the expenses of computing second-order derivatives.

Here, we take advantage of the efficiency for second-order derivative computation from ML models with respect to atomic coordinates to obtain the Hessians of the fitted PESs:

graphic file with name jz0c00527_m006.jpg 5

with R being the atomic coordinates of a molecular system. Note that Hessians are also employed in quantum dynamics simulations,102,103 which might open further applications for our implementation.

The squared energy-gap Hessian can be further obtained as the sum of two symmetric dyads, which define the branching space.101 Hence, this Hessian can be employed to obtain the symmetric dyad of the smooth NACs via11,104

graphic file with name jz0c00527_m007.jpg 6

After singular value decomposition, the hopping direction can be computed as the eigenvector, vij, of the largest nonzero eigenvalue101,104,105 with the corresponding eigenvalue, λij, as the squared magnitude of the ML smooth coupling, C̃ijNAC. The final approximated NAC vectors, Cij, between two states are then

graphic file with name jz0c00527_m008.jpg 7

The approximated NAC vectors can be employed in the vicinity of a conical intersection; otherwise, the output becomes too noisy. For the latter reason, we define thresholds of 0.5 and 1.0 eV for the energy gaps to compute approximated NACs between coupled singlet–singlet states and triplet–triplet states, respectively. It is worth mentioning that the ML models slightly overestimate the energy gaps at a conical intersection,32 because ML PESs, in contrast to quantum chemical PESs, are smooth everywhere and can reproduce the cones present in such critical regions only to a certain extent. In ref (105), approximated NACs were applied for a 1D system, and their usefulness in combination with ML was already anticipated.

We turn this idea into reality and show ML excited-state dynamics with approximated NACs for the methylenimmonium cation, CH2NH2+, as presented before, and thioformaldehyde, CSH2. A detailed analysis on the reference computations, the ab initio methods applied, as well as information on the timing of the Hessian evaluation are given in the Supporting Information in sections S2 and S3.1, respectively. The quality of the approximated NACs that is further compared to learned NACs is assessed using a linear vibronic coupling model of sulfur dioxide. The results are given in the Supporting Information in section S4.1 in Figures S1–S3 and support the validity of this approximation. Scatter plots and scans along a reaction coordinate of CH2NH2+ and CSH2 are further computed for energies, gradients, and couplings (and approximated NACs for CH2NH2+) in sections S4.2 (Figures S4 and S5) and S4.3 (Figures S6 and S7), respectively. Computed normal modes from ML Hessians are compared to reference values in Tables S3–S5 and show their accuracy. None of the data points from the ab initio MD simulations, to which we compare our SchNarc models, are included in the training sets, and thus, the dynamics simulations can be seen as an additional test.

The populations of CH2NH2+ are given in Figure 2. The reference population (panel A) is compared to SchNarc simulations trained on energies and gradients (panel B). As is visible, CH2NH2+ serves as a test system for ultrafast population transfer after photoexcitation. Transitions from the second excited singlet state back to the ground state take place within 100 fs,32,106 which can be reproduced only with accurate NACs.33 Those transitions can be reproduced with SchNarc using also the approximated NACs.

Figure 2.

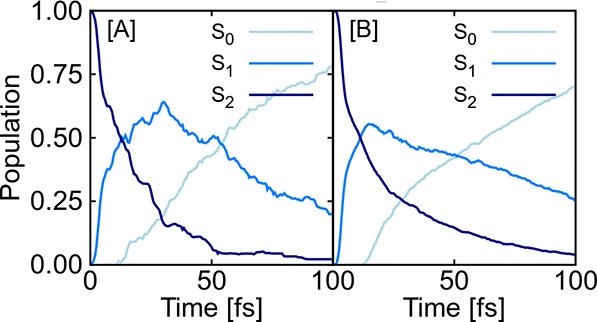
Figure 2

Open in a new tab

Quantum populations of the methylenimmonium cation obtained from (A) 90 trajectories using MR-CISD/aug-cc-pVDZ (QC) and (B) 1000 trajectories using SchNarc (ML). ML models are trained only on energies and gradients, and NACs are approximated from energies, gradients, and Hessians of ML models; this is in contrast to results from Figure 1, where ML models are also trained on NACs.

The application of the NAC approximation is further tested on CSH2, showing slow population transfer. This model also includes triplet states; thus, SOCs are additionally treated with SchNarc. To the best of our knowledge, for the first time, SOCs are trained with ML as directly obtained from quantum chemistry. The population curves are given in Figure 3, where panel A gives the reference population for 3000 fs and panel B the SchNarc populations. In contrast to the methylenimmonium cation, the CSH2 molecule serves as a test system for slow populations transfer and shows intersystem crossing strongly dependent on the accuracy of the underlying potentials.94 Inaccurate ML models would thus be unable to reproduce the reference dynamics. Also the slow population can be reproduced accurately, which proves the validity of the ML approach.

Figure 3.

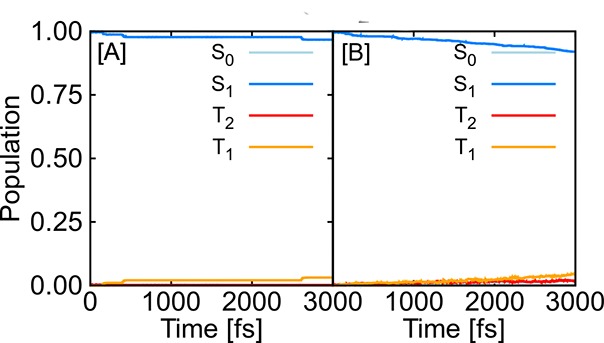
Figure 3

Open in a new tab

Quantum populations of populations up to 3000 fs of the thioformaldehyde molecule obtained from (A) 100 trajectories using CASSCF(6,5)/def2-SVP (QC) and (B) 9590 trajectories using SchNarc (ML).

In summary, the SchNarc framework combines the SHARC37 approach for surface hopping and the SchNet80 approach for ML and introduces several methodological developments, which simplify the use of nonadiabatic ML dynamics substantially. SchNarc takes advantage of SchNet’s automatic generation of representations for the molecular structure and extends it to excited states. The training of ML models is facilitated by using the phase-less loss and the NAC approximation, avoiding quantum chemical NAC calculations at all. Thus, photodynamics simulations are possible based on solely ML PESs, their derivatives, and SOCs. Furthermore, this method allows for an efficient computation of the Hessians of all the excited states at each time step. Hence, SchNarc allows for efficient nonadiabatic dynamics simulations of excited states and light-induced processes including internal conversion and intersystem crossing.

Acknowledgments

This work was financially supported by the AustrianScience Fund, W 1232 (MolTag), the uni:docs program of the University of Vienna (J.W.) and the European Union Horizon 2020 research and innovation program under the Marie Sklodowska-Curie Grant Agreement No. 792572 (M.G.). Part of the work has been performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme; in particular, the authors gratefully acknowledge the support of Univ.-Prof. Dr. Klaus-Robert Müller for hosting the visit of J.W. at the Technical University of Berlin and the computer resources and technical support provided by HLRS Stuttgart. The computational results presented have been achieved in part using the Vienna Scientific Cluster (VSC). P.M. thanks the University of Vienna for continuous support, also in the frame of the research platform ViRAPID. J.W. and P.M. are grateful for an NVIDIA Hardware Grant and thank Sebastian Mai for helpful discussions concerning the phase-free training algorithm.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c00527.

  • SchNet for excited states, training sets and reference computations, nonadiabatic couplings, and quality of ML models (PDF)

  • Calculated frequencies and normal modes of SO2, CH2NH2+, and CSH2 with ML (readable with standard programs for quantum chemistry) (ZIP)

The authors declare no competing financial interest.

Notes

The data sets are partly available32 and are partly made available on github.com/schnarc. The molecular geometries and corresponding properties are saved in a database format provided by the atomic simulation environment.107

Notes

All code developed in this work are made available on github.com/schnarc.

Supplementary Material

jz0c00527_si_001.pdf (2.4MB, pdf)
jz0c00527_si_002.zip (3.5KB, zip)

References

  1. Cerullo G.; Polli D.; Lanzani G.; De Silvestri S.; Hashimoto H.; Cogdell R. J. Photosynthetic Light Harvesting by Carotenoids: Detection of an Intermediate Excited State. Science 2002, 298, 2395–2398. 10.1126/science.1074685. [DOI] [PubMed] [Google Scholar]
  2. Schultz T.; Samoylova E.; Radloff W.; Hertel I. V.; Sobolewski A. L.; Domcke W. Efficient Deactivation of a Model Base Pair via Excited-State Hydrogen Transfer. Science 2004, 306, 1765–1768. 10.1126/science.1104038. [DOI] [PubMed] [Google Scholar]
  3. Schreier W. J.; Schrader T. E.; Koller F. O.; Gilch P.; Crespo-Hernández C. E.; Swaminathan V. N.; Carell T.; Zinth W.; Kohler B. Thymine Dimerization in DNA Is an Ultrafast Photoreaction. Science 2007, 315, 625–629. 10.1126/science.1135428. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Rauer C.; Nogueira J. J.; Marquetand P.; González L. Cyclobutane Thymine Photodimerization Mechanism Revealed by Nonadiabatic Molecular Dynamics. J. Am. Chem. Soc. 2016, 138, 15911–15916. 10.1021/jacs.6b06701. [DOI] [PubMed] [Google Scholar]
  5. Romero E.; Novoderezhkin V. I.; van Grondelle R. Quantum Design of Photosynthesis for Bio-Inspired Solar-Energy Conversion. Nature 2017, 543, 355–365. 10.1038/nature22012. [DOI] [PubMed] [Google Scholar]
  6. Mathew S.; Yella A.; Gao P.; Humphry-Baker R.; Curchod B. F. E.; Ashari-Astani N.; Tavernelli I.; Rothlisberger U.; Nazeeruddin M. K.; Grätzel M. Dye-Sensitized Solar Cells with 13% Efficiency Achieved Through the Molecular Engineering of Porphyrin Sensitizers. Nat. Chem. 2014, 6, 242–247. 10.1038/nchem.1861. [DOI] [PubMed] [Google Scholar]
  7. Bartók A. P.; De S.; Poelking C.; Bernstein N.; Kermode J. R.; Csányi G.; Ceriotti M. Machine Learning Unifies the Modeling of Materials and Molecules. Sci. Adv. 2017, 3, e1701816. 10.1126/sciadv.1701816. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Sanchez-Lengeling B.; Aspuru-Guzik A. Inverse Molecular Design Using Machine Learning: Generative Models for Matter Engineering. Science 2018, 361, 360–365. 10.1126/science.aat2663. [DOI] [PubMed] [Google Scholar]
  9. Ahmad I.; Ahmed S.; Anwar Z.; Sheraz M. A.; Sikorski M. Photostability and Photostabilization of Drugs and Drug Products. Int. J. Photoenergy 2016, 2016, 1–19. 10.1155/2016/8135608. [DOI] [Google Scholar]
  10. Köuppel H.; Domcke W.; Cederbaum L. S. Multimode molecular dynamics beyond the Born-Oppenheimer approximation. Adv. Chem. Phys. 2007, 57, 59–246. 10.1002/9780470142813.ch2. [DOI] [Google Scholar]
  11. Köppel H.; Gronki J.; Mahapatra S. Construction Scheme for Regularized Diabatic States. J. Chem. Phys. 2001, 115, 2377–2388. 10.1063/1.1383986. [DOI] [Google Scholar]
  12. Worth G. A.; Cederbaum L. S. Beyond Born-Oppenheimer: Molecular Dynamics Through a Conical Intersection. Annu. Rev. Phys. Chem. 2004, 55, 127–158. 10.1146/annurev.physchem.55.091602.094335. [DOI] [PubMed] [Google Scholar]
  13. Bowman J. M.; Carrington T.; Meyer H. Variational Quantum Approaches for Computing Vibrational Energies of Polyatomic Molecules. Mol. Phys. 2008, 106, 2145–2182. 10.1080/00268970802258609. [DOI] [Google Scholar]
  14. Meyer H.-D.; Gatti F.; Worth G. A.. Multidimensional Quantum Dynamics; Wiley-VCH Verlag GmbH & Co. KGaA, 2009. [Google Scholar]
  15. Alborzpour J. P.; Tew D. P.; Habershon S. Efficient and Accurate Evaluation of Potential Energy Matrix Elements for Quantum Dynamics Using Gaussian Process Regression. J. Chem. Phys. 2016, 145, 174112. 10.1063/1.4964902. [DOI] [PubMed] [Google Scholar]
  16. Richings G. W.; Habershon S. Direct grid-Based Quantum Dynamics on Propagated Diabatic Potential Energy Surfaces. Chem. Phys. Lett. 2017, 683, 228–233. 10.1016/j.cplett.2017.01.063. [DOI] [Google Scholar]
  17. Liu F.; Du L.; Zhang D.; Gao J. Direct Learning Hidden Excited State Interaction Patterns from ab initio Dynamics and Its Implication as Alternative Molecular Mechanism Models. Sci. Rep. 2017, 7, 8737. 10.1038/s41598-017-09347-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Richings G. W.; Habershon S. MCTDH On-the-Fly: Efficient Grid-Based Quantum Dynamics Without Pre-Computed Potential Energy Surfaces. J. Chem. Phys. 2018, 148, 134116. 10.1063/1.5024869. [DOI] [PubMed] [Google Scholar]
  19. Williams D. M. G.; Eisfeld W. Neural Network Diabatization: A New Ansatz for Accurate High-Dimensional Coupled Potential Energy Surfaces. J. Chem. Phys. 2018, 149, 204106. 10.1063/1.5053664. [DOI] [PubMed] [Google Scholar]
  20. Xie C.; Zhu X.; Yarkony D. R.; Guo H. Permutation Invariant Polynomial Neural Network Approach to Fitting Potential Energy Surfaces. IV. Coupled Diabatic Potential Energy Matrices. J. Chem. Phys. 2018, 149, 144107. 10.1063/1.5054310. [DOI] [PubMed] [Google Scholar]
  21. Guan Y.; Zhang D. H.; Guo H.; Yarkony D. R. Representation of Coupled Adiabatic Potential Energy Surfaces Using Neural Network Based Quasi-Diabatic Hamiltonians: 1,2 2A’ States of LiFH. Phys. Chem. Chem. Phys. 2019, 21, 14205–14213. 10.1039/C8CP06598E. [DOI] [PubMed] [Google Scholar]
  22. Richings G. W.; Robertson C.; Habershon S. Improved On-the-Fly MCTDH Simulations with Many-Body-Potential Tensor Decomposition and Projection Diabatization. J. Chem. Theory Comput. 2019, 15, 857–870. 10.1021/acs.jctc.8b00819. [DOI] [PubMed] [Google Scholar]
  23. Polyak I.; Richings G. W.; Habershon S.; Knowles P. J. Direct Quantum Dynamics Using Variational Gaussian Wavepackets and Gaussian Process Regression. J. Chem. Phys. 2019, 150, 041101 10.1063/1.5086358. [DOI] [PubMed] [Google Scholar]
  24. Guan Y.; Guo H.; Yarkony D. R. Neural Network Based Quasi-Diabatic Hamiltonians with Symmetry Adaptation and a Correct Description of Conical Intersections. J. Chem. Phys. 2019, 150, 214101. 10.1063/1.5099106. [DOI] [PubMed] [Google Scholar]
  25. Wang Y.; Xie C.; Guo H.; Yarkony D. R. A Quasi-Diabatic Representation of the 1,21A States of Methylamine. J. Phys. Chem. A 2019, 123, 5231–5241. 10.1021/acs.jpca.9b03801. [DOI] [PubMed] [Google Scholar]
  26. Guan Y.; Guo H.; Yarkony D. R. Extending the Representation of Multistate Coupled Potential Energy Surfaces to Include Properties Operators Using Neural Networks: Application to the 1,21A States of Ammonia. J. Chem. Theory Comput. 2020, 16, 302–313. 10.1021/acs.jctc.9b00898. [DOI] [PubMed] [Google Scholar]
  27. Behler J.; Reuter K.; Scheffler M. Nonadiabatic Effects in the Dissociation of Oxygen Molecules at the Al(111) Surface. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 115421. 10.1103/PhysRevB.77.115421. [DOI] [Google Scholar]
  28. Carbogno C.; Behler J.; Reuter K.; Groß A. Signatures of Nonadiabatic O2 Dissociation at Al(111): First-Principles Fewest-Switches Study. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 035410 10.1103/PhysRevB.81.035410. [DOI] [Google Scholar]
  29. Hu D.; Xie Y.; Li X.; Li L.; Lan Z. Inclusion of Machine Learning Kernel Ridge Regression Potential Energy Surfaces in On-the-Fly Nonadiabatic Molecular Dynamics Simulation. J. Phys. Chem. Lett. 2018, 9, 2725–2732. 10.1021/acs.jpclett.8b00684. [DOI] [PubMed] [Google Scholar]
  30. Dral P. O.; Barbatti M.; Thiel W. Nonadiabatic Excited-State Dynamics with Machine Learning. J. Phys. Chem. Lett. 2018, 9, 5660–5663. 10.1021/acs.jpclett.8b02469. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Chen W.-K.; Liu X.-Y.; Fang W.-H.; Dral P. O.; Cui G. Deep Learning for Nonadiabatic Excited-State Dynamics. J. Phys. Chem. Lett. 2018, 9, 6702–6708. 10.1021/acs.jpclett.8b03026. [DOI] [PubMed] [Google Scholar]
  32. Westermayr J.; Gastegger M.; Menger M. F. S. J.; Mai S.; González L.; Marquetand P. Machine Learning Enables Long Time Scale Molecular Photodynamics Simulations. Chem. Sci. 2019, 10, 8100–8107. 10.1039/C9SC01742A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Westermayr J.; Faber F.; Christensen A. S.; von Lilienfeld A.; Marquetand P.. Neural Networks and Kernel Ridge Regression for Excited States Dynamics of CH2NH2+: From Single-State to Multi-State Representations and Multi-Property Machine Learning Models. Mach. Learn.: Sci. Technol. 2020, in press, 10.1088/2632-2153/ab88d0. [DOI] [Google Scholar]
  34. Ibele L. M.; Nicolson A.; Curchod B. F. E.. Excited-State Dynamics of Molecules with Classically Driven Trajectories and Gaussians. Mol. Phys. 2019, 1. 10.1080/00268976.2019.1665199. [DOI] [Google Scholar]
  35. Tully J. C. Molecular Dynamics with Electronic Transitions. J. Chem. Phys. 1990, 93, 1061–1071. 10.1063/1.459170. [DOI] [Google Scholar]
  36. Richter M.; Marquetand P.; González-Vázquez J.; Sola I.; González L. SHARC: Ab Initio Molecular Dynamics with Surface Hopping in the Adiabatic Representation Including Arbitrary Couplings. J. Chem. Theory Comput. 2011, 7, 1253–1258. 10.1021/ct1007394. [DOI] [PubMed] [Google Scholar]
  37. Mai S.; Marquetand P.; González L. Nonadiabatic Dynamics: The SHARC Approach. WIREs Comput. Mol. Sci. 2018, 8, e1370 10.1002/wcms.1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Mai S.; Richter M.; Ruckenbauer M.; Oppel M.; Marquetand P.; González L.. SHARC2.0: Surface Hopping Including Arbitrary Couplings – Program Package for Non-Adiabatic Dynamics. sharc-md.org, 2018.
  39. Doltsinis N. L.Molecular Dynamics Beyond the Born-Oppenheimer Approximation: Mixed Quantum-Classical Approaches; NIC Series; John von Neumann Institute for Computing, 2006. [Google Scholar]
  40. Ha J.-K.; Lee I. S.; Min S. K. Surface Hopping Dynamics beyond Nonadiabatic Couplings for Quantum Coherence. J. Phys. Chem. Lett. 2018, 9, 1097–1104. 10.1021/acs.jpclett.8b00060. [DOI] [PubMed] [Google Scholar]
  41. Mai S.; González L.. Molecular Photochemistry: Recent Developments in Theory. Angew. Chem., Int. Ed. in press. 2020 10.1002/anie.201916381 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Baer M. Introduction to the Theory of Electronic Non-Adiabatic Coupling Terms in Molecular Systems. Phys. Rep. 2002, 358, 75–142. 10.1016/S0370-1573(01)00052-7. [DOI] [Google Scholar]
  43. Lischka H.; Dallos M.; Szalay P. G.; Yarkony D. R.; Shepard R. Analytic Evaluation of Nonadiabatic Coupling Terms at the MR-CI Level. I. Formalism. J. Chem. Phys. 2004, 120, 7322–7329. 10.1063/1.1668615. [DOI] [PubMed] [Google Scholar]
  44. Rubbmark J. R.; Kash M. M.; Littman M. G.; Kleppner D. Dynamical Effects at Avoided Level Crossings: A Study of the Landau-Zener Effect Using Rydberg Atoms. Phys. Rev. A: At., Mol., Opt. Phys. 1981, 23, 3107–3117. 10.1103/PhysRevA.23.3107. [DOI] [Google Scholar]
  45. Hagedorn G. A. Proof of the Landau-Zener Formula in an Adiabatic Limit with Small Eigenvalue Gaps. Commun. Math. Phys. 1991, 136, 433–449. 10.1007/BF02099068. [DOI] [Google Scholar]
  46. Wittig C. The Landau-Zener Formula. J. Phys. Chem. B 2005, 109, 8428–8430. 10.1021/jp040627u. [DOI] [PubMed] [Google Scholar]
  47. Nakamura H.Nonadiabatic Transition: Concepts, Basic Theories and Applications, 2nd edition; World Scientific: Singapore, 2012. 10.1142/8009. [DOI] [Google Scholar]
  48. Zhu C.; Kamisaka H.; Nakamura H. Significant Improvement of the Trajectory Surface Hopping Method by the Zhu–Nakamura Theory. J. Chem. Phys. 2001, 115, 11036–11039. 10.1063/1.1421070. [DOI] [Google Scholar]
  49. Zhu C.; Kamisaka H.; Nakamura H. New Implementation of the Trajectory Surface Hopping Method with Use of the Zhu–Nakamura Theory. II. Application to the Charge Transfer Processes in the 3D DH2+ System. J. Chem. Phys. 2002, 116, 3234–3247. 10.1063/1.1446032. [DOI] [Google Scholar]
  50. Kondorskiy A.; Nakamura H. Semiclassical Theory of Electronically Nonadiabatic Chemical Dynamics: Incorporation of the Zhu–Nakamura Theory into the Frozen Gaussian Propagation Method. J. Chem. Phys. 2004, 120, 8937–8954. 10.1063/1.1687679. [DOI] [PubMed] [Google Scholar]
  51. Oloyede P.; Mil’nikov G.; Nakamura H. Generalized Trajectory Surface Hopping Method Based on the Zhu-Nakamura Theory. J. Chem. Phys. 2006, 124, 144110. 10.1063/1.2187978. [DOI] [PubMed] [Google Scholar]
  52. Ishida T.; Nanbu S.; Nakamura H. Clarification of Nonadiabatic Chemical Dynamics by the Zhu-Nakamura Theory of Nonadiabatic Transition: From Tri-Atomic Systems to Reactions in Solutions. Int. Rev. Phys. Chem. 2017, 36, 229–285. 10.1080/0144235X.2017.1293399. [DOI] [Google Scholar]
  53. Granucci G.; Persico M.; Spighi G. Surface Hopping Trajectory Simulations with Spin-Orbit and Dynamical Couplings. J. Chem. Phys. 2012, 137, 22A501. 10.1063/1.4707737. [DOI] [PubMed] [Google Scholar]
  54. Bartók A. P.; Payne M. C.; Kondor R.; Csányi G. Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett. 2010, 104, 136403. 10.1103/PhysRevLett.104.136403. [DOI] [PubMed] [Google Scholar]
  55. Li Z.; Kermode J. R.; De Vita A. Molecular Dynamics with On-the-Fly Machine Learning of Quantum-Mechanical Forces. Phys. Rev. Lett. 2015, 114, 096405 10.1103/PhysRevLett.114.096405. [DOI] [PubMed] [Google Scholar]
  56. Gastegger M.; Marquetand P. High-Dimensional Neural Network Potentials for Organic Reactions and an Improved Training Algorithm. J. Chem. Theory Comput. 2015, 11, 2187–2198. 10.1021/acs.jctc.5b00211. [DOI] [PubMed] [Google Scholar]
  57. Rupp M. Machine Learning for Quantum Mechanics in a Nutshell. Int. J. Quantum Chem. 2015, 115, 1058–1073. 10.1002/qua.24954. [DOI] [Google Scholar]
  58. Behler J. Perspective: Machine Learning Potentials for Atomistic Simulations. J. Chem. Phys. 2016, 145, 170901. 10.1063/1.4966192. [DOI] [PubMed] [Google Scholar]
  59. Gastegger M.; Kauffmann C.; Behler J.; Marquetand P. Comparing the Accuracy of High-Dimensional Neural Network Potentials and the Systematic Molecular Fragmentation Method: A benchmark Study for All-Trans Alkanes. J. Chem. Phys. 2016, 144, 194110. 10.1063/1.4950815. [DOI] [PubMed] [Google Scholar]
  60. Gastegger M.; Behler J.; Marquetand P. Machine Learning Molecular Dynamics for the Simulation of Infrared Spectra. Chem. Sci. 2017, 8, 6924–6935. 10.1039/C7SC02267K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Deringer V. L.; Csányi G. Machine learning based interatomic potential for amorphous carbon. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 95, 094203 10.1103/PhysRevB.95.094203. [DOI] [Google Scholar]
  62. Botu V.; Batra R.; Chapman J.; Ramprasad R. Machine Learning Force Fields: Construction, Validation, and Outlook. J. Phys. Chem. C 2017, 121, 511–522. 10.1021/acs.jpcc.6b10908. [DOI] [Google Scholar]
  63. Smith J. S.; Isayev O.; Roitberg A. E. ANI-1: An Extensible Neural Network Potential with DFT Accuracy at Force Field Computational Cost. Chem. Sci. 2017, 8, 3192–3203. 10.1039/C6SC05720A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Behler J. First Principles Neural Network Potentials for Reactive Simulations of Large Molecular and Condensed Systems. Angew. Chem., Int. Ed. 2017, 56, 12828–12840. 10.1002/anie.201703114. [DOI] [PubMed] [Google Scholar]
  65. Zong H.; Pilania G.; Ding X.; Ackland G. J.; Lookman T. Developing an Interatomic Potential for Martensitic Phase Transformations in Zirconium by Machine Learning. npj Comput. Mater. 2018, 4, 48. 10.1038/s41524-018-0103-x. [DOI] [Google Scholar]
  66. Bartók A. P.; Kermode J.; Bernstein N.; Csányi G. Machine Learning a General-Purpose Interatomic Potential for Silicon. Phys. Rev. X 2018, 8, 041048 10.1103/PhysRevX.8.041048. [DOI] [Google Scholar]
  67. Chmiela S.; Sauceda H. E.; Müller K.-R.; Tkatchenko A. Towards Exact Molecular Dynamics Simulations with Machine-Learned Force Fields. Nat. Commun. 2018, 9, 3887. 10.1038/s41467-018-06169-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Imbalzano G.; Anelli A.; Giofré D.; Klees S.; Behler J.; Ceriotti M. Automatic Selection of Atomic Fingerprints and Reference Configurations for Machine-Learning Potentials. J. Chem. Phys. 2018, 148, 241730. 10.1063/1.5024611. [DOI] [PubMed] [Google Scholar]
  69. Zhang L.; Han J.; Wang H.; Saidi W. A.; Car R.; Weinan E.. End-to-end Symmetry Preserving Inter-atomic Potential Energy Model for Finite and Extended Systems. Proceedings of the 32Nd International Conference on Neural Information Processing Systems; United States, 2018.
  70. Zhang L.; Han J.; Wang H.; Car R.; E W. Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics. Phys. Rev. Lett. 2018, 120, 143001. 10.1103/PhysRevLett.120.143001. [DOI] [PubMed] [Google Scholar]
  71. Chan H.; Narayanan B.; Cherukara M. J.; Sen F. G.; Sasikumar K.; Gray S. K.; Chan M. K. Y.; Sankaranarayanan S. K. R. S. Machine Learning Classical Interatomic Potentials for Molecular Dynamics from First-Principles Training Data. J. Phys. Chem. C 2019, 123, 6941–6957. 10.1021/acs.jpcc.8b09917. [DOI] [Google Scholar]
  72. Christensen A. S.; Faber F. A.; von Lilienfeld O. A. Operators in Quantum Machine Learning: Response Properties in Chemical Space. J. Chem. Phys. 2019, 150, 064105 10.1063/1.5053562. [DOI] [PubMed] [Google Scholar]
  73. Wang H.; Yang W. Toward Building Protein Force Fields by Residue-Based Systematic Molecular Fragmentation and Neural Network. J. Chem. Theory Comput. 2019, 15, 1409–1417. 10.1021/acs.jctc.8b00895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Chmiela S.; Sauceda H. E.; Poltavsky I.; Müller K.-R.; Tkatchenko A. sGDML: Constructing Accurate and Data Efficient Molecular Force Fields Using Machine Learning. Comput. Phys. Commun. 2019, 240, 38–45. 10.1016/j.cpc.2019.02.007. [DOI] [Google Scholar]
  75. Carleo G.; Cirac I.; Cranmer K.; Daudet L.; Schuld M.; Tishby N.; Vogt-Maranto L.; Zdeborová L. Machine Learning and the Physical Sciences. Rev. Mod. Phys. 2019, 91, 045002 10.1103/RevModPhys.91.045002. [DOI] [Google Scholar]
  76. Krems R. V. Bayesian Machine Learning for Quantum Molecular Dynamics. Phys. Chem. Chem. Phys. 2019, 21, 13392–13410. 10.1039/C9CP01883B. [DOI] [PubMed] [Google Scholar]
  77. Deringer V. L.; Caro M. A.; Csányi G. Machine Learning Interatomic Potentials as Emerging Tools for Materials Science. Adv. Mater. 2019, 31, 1902765. 10.1002/adma.201902765. [DOI] [PubMed] [Google Scholar]
  78. Schütt K. T.; Gastegger M.; Tkatchenko A.; Müller K.-R.; Maurer R. J. Unifying Machine Learning and Quantum Chemistry with a Deep Neural Network for Molecular Wavefunctions. Nat. Commun. 2019, 10, 5024. 10.1038/s41467-019-12875-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Schütt K. T.; Sauceda H. E.; Kindermans P.-J.; Tkatchenko A.; Müller K.-R. SchNet – A Deep Learning Architecture for Molecules and Materials. J. Chem. Phys. 2018, 148, 241722. 10.1063/1.5019779. [DOI] [PubMed] [Google Scholar]
  80. Schütt K. T.; Kessel P.; Gastegger M.; Nicoli K. A.; Tkatchenko A.; Müller K.-R. SchNetPack: A Deep Learning Toolbox For Atomistic Systems. J. Chem. Theory Comput. 2019, 15, 448–455. 10.1021/acs.jctc.8b00908. [DOI] [PubMed] [Google Scholar]
  81. Singraber A.; Morawietz T.; Behler J.; Dellago C. Parallel Multistream Training of High-Dimensional Neural Network Potentials. J. Chem. Theory Comput. 2019, 15, 3075–3092. 10.1021/acs.jctc.8b01092. [DOI] [PubMed] [Google Scholar]
  82. Yao K.; Herr J. E.; Toth D.; Mckintyre R.; Parkhill J. The TensorMol-0.1 Model Chemistry: A Neural Network Augmented with Long-Range Physics. Chem. Sci. 2018, 9, 2261–2269. 10.1039/C7SC04934J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  83. Wang H.; Zhang L.; Han J.; E W. DeePMD-kit: A Deep Learning Package for Many-Body Potential Energy Representation and Molecular Dynamics. Comput. Phys. Commun. 2018, 228, 178–184. 10.1016/j.cpc.2018.03.016. [DOI] [Google Scholar]
  84. Gilmer J.; Schoenholz S. S.; Riley P. F.; Vinyals O.; Dahl G. E.. Neural Message Passing for Quantum Chemistry. Proceedings of the 34th International Conference on Machine Learning; International Convention Centre, Sydney, Australia, 2017; pp 1263–1272.
  85. Schütt K. T.; Arbabzadah F.; Chmiela S.; Müller K. R.; Tkatchenko A. Quantum-Chemical Insights from Deep Tensor Neural Networks. Nat. Commun. 2017, 8, 13890. 10.1038/ncomms13890. [DOI] [PMC free article] [PubMed] [Google Scholar]
  86. Unke O. T.; Meuwly M. PhysNet: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges. J. Chem. Theory Comput. 2019, 15, 3678–3693. 10.1021/acs.jctc.9b00181. [DOI] [PubMed] [Google Scholar]
  87. Lubbers N.; Smith J. S.; Barros K. Hierarchical Modeling of Molecular Energies Using a Deep Neural Network. J. Chem. Phys. 2018, 148, 241715. 10.1063/1.5011181. [DOI] [PubMed] [Google Scholar]
  88. Häse F.; Valleau S.; Pyzer-Knapp E.; Aspuru-Guzik A. Machine Learning Exciton Dynamics. Chem. Sci. 2016, 7, 5139–5147. 10.1039/C5SC04786B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  89. Ramakrishnan R.; von Lilienfeld O. A. Many Molecular Properties from One Kernel in Chemical Space. Chimia 2015, 69, 182–186. 10.2533/chimia.2015.182. [DOI] [PubMed] [Google Scholar]
  90. Zubatyuk R.; Smith J. S.; Leszczynski J.; Isayev O. Accurate and Transferable Multitask Prediction of Chemical Properties with an Atoms-in-Molecules Neural Network. Sci. Adv. 2019, 5, eaav6490. 10.1126/sciadv.aav6490. [DOI] [PMC free article] [PubMed] [Google Scholar]
  91. Akimov A. V. A Simple Phase Correction Makes a Big Difference in Nonadiabatic Molecular Dynamics. J. Phys. Chem. Lett. 2018, 9, 6096–6102. 10.1021/acs.jpclett.8b02826. [DOI] [PubMed] [Google Scholar]
  92. Bellonzi N.; Medders G. R.; Epifanovsky E.; Subotnik J. E. Configuration Interaction Singles with Spin-Orbit Coupling: Constructing Spin-Adiabatic States and their Analytical Nuclear Gradients. J. Chem. Phys. 2019, 150, 014106 10.1063/1.5045484. [DOI] [PubMed] [Google Scholar]
  93. Lischka H.; et al. High-Level Multireference Methods in the Quantum-Chemistry Program System COLUMBUS: Analytic MR-CISD and MR-AQCC Gradients and MR-AQCC-LRT for Excited States, GUGA Spin-Orbit CI and Parallel CI Density. Phys. Chem. Chem. Phys. 2001, 3, 664–673. 10.1039/b008063m. [DOI] [Google Scholar]
  94. Mai S.; Atkins A. J.; Plasser F.; González L. The Influence of the Electronic Structure Method on Intersystem Crossing Dynamics. The Case of Thioformaldehyde. J. Chem. Theory Comput. 2019, 15, 3470–3480. 10.1021/acs.jctc.9b00282. [DOI] [PubMed] [Google Scholar]
  95. Werner H.-J.et al. 2012; see http://www.molpro.net.
  96. Zhang Y.; Maurer R. J.; Jiang B. Symmetry-Adapted High Dimensional Neural Network Representation of Electronic Friction Tensor of Adsorbates on Metals. J. Phys. Chem. C 2020, 124, 186–195. 10.1021/acs.jpcc.9b09965. [DOI] [Google Scholar]
  97. Thiel A.; Köppel H. Proposal and Numerical Test of a Simple Diabatization Scheme. J. Chem. Phys. 1999, 110, 9371–9383. 10.1063/1.478902. [DOI] [Google Scholar]
  98. Köppel H.; Schubert B. The Concept of Regularized Diabatic States for a General Conical Intersection. Mol. Phys. 2006, 104, 1069–1079. 10.1080/00268970500417937. [DOI] [Google Scholar]
  99. Maeda S.; Ohno K.; Morokuma K. Updated Branching Plane for Finding Conical Intersections without Coupling Derivative Vectors. J. Chem. Theory Comput. 2010, 6, 1538–1545. 10.1021/ct1000268. [DOI] [PubMed] [Google Scholar]
  100. Kammeraad J. A.; Zimmerman P. M. Estimating the Derivative Coupling Vector Using Gradients. J. Phys. Chem. Lett. 2016, 7, 5074–5079. 10.1021/acs.jpclett.6b02501. [DOI] [PubMed] [Google Scholar]
  101. Gonon B.; Perveaux A.; Gatti F.; Lauvergnat D.; Lasorne B. On the Applicability of a Wavefunction-Free, Energy-Based Procedure for Generating First-Order Non-Adiabatic Couplings Around Conical Intersections. J. Chem. Phys. 2017, 147, 114114. 10.1063/1.4991635. [DOI] [PubMed] [Google Scholar]
  102. Frankcombe T. J. Using Hessian Update Formulae to Construct Modified Shepard Interpolated Potential Energy Surfaces: Application to Vibrating Surface Atoms. J. Chem. Phys. 2014, 140, 114108. 10.1063/1.4868637. [DOI] [PubMed] [Google Scholar]
  103. Richings G.; Polyak I.; Spinlove K.; Worth G.; Burghardt I.; Lasorne B. Quantum dynamics simulations using Gaussian wavepackets: the vMCG method. Int. Rev. Phys. Chem. 2015, 34, 269–308. 10.1080/0144235X.2015.1051354. [DOI] [Google Scholar]
  104. An H.; Baeck K. K. Practical and Reliable Approximation of Nonadiabatic Coupling Terms between Triplet Electronic States Using Only Adiabatic Potential Energies. Chem. Phys. Lett. 2018, 696, 100–105. 10.1016/j.cplett.2018.02.036. [DOI] [Google Scholar]
  105. Baeck K. K.; An H. Practical Approximation of the Non-Adiabatic Coupling Terms for Same-Symmetry Interstate Crossings by Using Adiabatic Potential Energies Only. J. Chem. Phys. 2017, 146, 064107 10.1063/1.4975323. [DOI] [PubMed] [Google Scholar]
  106. Barbatti M.; Aquino A. J. A.; Lischka H. Ultrafast Two-Step Process in the Non-Adiabatic Relaxation of the CH2NH2 Molecule. Mol. Phys. 2006, 104, 1053–1060. 10.1080/00268970500417945. [DOI] [Google Scholar]
  107. Hjorth Larsen A.; et al. The Atomic Simulation Environment—a Python Library for Working with Atoms. J. Phys.: Condens. Matter 2017, 29, 273002. 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz0c00527_si_001.pdf (2.4MB, pdf)
jz0c00527_si_002.zip (3.5KB, zip)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES