The Influence of Parametric Uncertainty on Projections of Forest Land Use, Carbon, and Markets

Abstract

This paper uses Monte Carlo methods and regression analysis to assess the role of uncertainty in yield function and land supply elasticity parameters on land use, carbon, and market outcomes in a long-term dynamic model of the global forest sector. The results suggest that parametric uncertainty has little influence on projected future timber prices and global output, but it does have important implications for regional projections of outputs. A wide range of outcomes are possible for timber outputs, depending on growth and elasticity parameters. Timber output in the U.S., for instance, could change by −67 to +98 million m³ per year by 2060. Despite uncertainty in the parameters, our analysis suggests that the temperate zone may sequester +30 to +79 Pg C by 2060 and +58 to +114 Pg C by 2090 while the tropics are projected to store −35 to +70 Pg C and −33 to +73 Pg C for the same time periods, respectively. Attributional analysis shows that uncertainty in the parameters regulating forest growth has a more important impact on projections of future carbon storage than uncertainty in the land supply elasticity parameters. Moreover, the results suggest that understanding growth parameters in regions with large current carbon stocks is most important for making future projections of carbon storage.

1. Introduction

Dynamic optimization modeling has emerged in literature as a key analytical tool to project future resource conditions, management changes, or economic outcomes (e.g., prices) in forestry systems. For example, Sedjo and Lyon (1990), Adams et al. (1996), Adams et al. (1999), Sohngen and Mendelsohn (1998 and 2003), and Sohngen et al. (1999) developed dynamic optimization approaches to project future forest stocks in the U.S. or globally. These approaches all assumed that the parameters in the underlying model are deterministic, even though there may be important underlying uncertainty. Forestry models, for instance, parameterize the biological growth of forests over time, but many factors make these parameters uncertain, including the methods by which the original data was collected, and the application of values estimated for specific sites to cover entire regions.

While forestry models have become more sophisticated and widely used to project future forest conditions and carbon outcomes under assumed baseline economic, policy, and environmental conditions, there is still a great deal of variation in future projections for key regions, including the U.S. (Latta et al., 2018; Tian et al., 2018; Wear and Coulston, 2015). The variations may arise from methodological differences in the models, but they may also arise from differences in assumptions about key parameters, such as forest growth and land supply. Historically, carbon outcomes across the world have been influenced by two important drivers most affected by these parametric assumptions: land use change and forest regrowth (Smith et al., 2014). It is natural to anticipate that these factors will continue to be important for future carbon outcomes; therefore, it is useful to examine the extent to which uncertainty in underlying forest yield growth or land supply parameters can affect the variation in future forest sector projections.

To address questions about the effect of parameter uncertainty on timber market and forest stock projections, we conduct a Monte Carlo analysis with a global dynamic optimization model of timber markets, the Global Timber Model (see Tian et al., 2018; Daigneault et al., 2008; Sohngen et al., 1999). Monte Carlo analysis is well suited to our question, which focuses on the role of uncertainty in key model parameters on important model outcomes. Many dynamic forestry models have a large set of parameters that describe forest yields in different regions. These parameters are typically estimated or collected directly through forest inventories and thus are subject to uncertainty, particularly when estimates from field studies are aggregated and used across larger regions. While sensitivity analysis can provide important insights, it may ignore potential interactions between underlying parameters, making it difficult for attributional analysis that seeks to evaluate the relative influence of a given model parameter on uncertainty ranges for key model outputs. Furthermore, partial factorial experimental designs and response surface regressions are often not feasible with large-scale optimization models in which there are hundreds or thousands of spatially-varying parameters that would need to be varied and interacted.

Monte Carlo techniques provide a way to test the effects of uncertainty in the underlying parameters on the model outcomes by evaluating different parameters drawn from a distribution of each yield function and running the model multiple times with different sets of randomly drawn parameters. Monte Carlo techniques have been widely applied by static land use and management models (Hertel et al., 2010; Plevin, 2010; Laborde and Valin, 2012; Valin, 2015). However, few studies have published results from parametric uncertainty analysis using intertemporal optimization methods and models of land use sectors. This limited literature is due, in part, to the computational complexity of intertemporal optimization models. Dynamic models of land use systems are typically large, computationally complex, and require relatively long solve times, thus limiting the ability to run hundreds or thousands of simulations using random parameter draws, as is typically required for a Monte Carlo simulation analysis. With computational processing advances, emerging grid computing techniques, and increasing access to super computers, such techniques will be easier to employ in the future.

Monte Carlo methods may be useful for characterizing the influence of parameter uncertainty on several key variables. Forest yields, for instance, are among the most important components of dynamic forestry models, determining timber volume and growth rates, as well as influencing harvesting and investment decisions made by land managers. Because forest management involves supervising large capital assets over time, under- or over-estimating the growth in these capital assets can have potentially large effects on future projections of timber prices, regional harvesting rates, managed forest area, and carbon fluxes.

This paper presents an analysis of parametric uncertainty on projected land use and market-related output from a baseline simulation of a model of the global forest sector, the Global Timber Model, with recent updates described in Kim et al. (2018). We assess uncertainty over parameters of the yield functions and the land rental function (i.e., land supply elasticity) and employ regression methods to run an attributional stochastic analysis with the purpose of investigating the relative importance of these parameters on key projected outcomes of carbon and timber harvests. Yield growth parameters are a key component of any representation of forest resource systems and represent both the rate of growth over time that a particular forest type in a particular region will experience, as well as the system’s stocking density (or carrying capacity) per-unit area. Land rental functions play an important role in our modeling framework because they control the amount of land used by the forestry sector in competition with agriculture. Specifically, land rental functions recognize the opportunity cost of shifting land into forestry in terms of lost agricultural rents. As more land is brought into forestry in response to changing market conditions, land rental functions ensure higher marginal costs of further afforestation. This analysis provides baseline uncertainty ranges in key model outputs, including projected forest area, prices, production, carbon stocks, and factors explaining intensive margin investments. Furthermore, we present a detailed discussion on how specific parameter sets relate to the magnitude of uncertainty implied by model outputs.

This paper makes several contributions to the literature by offering an assessment of the relative influence of parameters that drive forest land supply and productivity in structural economic models on projections of forest markets and associated environmental outputs (carbon stocks). There is a growing literature that projects forest carbon stocks across a wide range of socioeconomic, policy, and environmental change scenarios. This literature reports a range of possible forest carbon futures using different modeling frameworks that represent forest resources at different spatial and temporal scales (Wear and Coulston, 2015; Nepal et al., 2015; Tian et al., 2018; Latta et al., 2018; Kim et al., 2018; Forsell et al., 2016). However, these studies focus on the variability in forest carbon projections across discrete alternative future scenarios in which policy, environmental, or macroeconomic inputs are varied.

The sensitivity analysis approach differs from the goals of this paper, which seeks to evaluate the influence of specific data and parameter inputs on modeled projections. In a similar recent analysis, Buongiorno and Johnston. (2018) analyze parameter uncertainty using the Global Forest Products Model (GFPM), a detailed recursive dynamic and partial equilibrium model covering multiple forest product markets. The Buongiorno study focuses on economic parameters such as demand elasticities in driving future projections and finds wide variation in future forest market conditions. Our study, in contrast, focuses on parameters related to forest productivity and land supply/costs using an intertemporal model of the global forest sector with a large set of simulation scenarios.

In this manuscript we first present an assessment of uncertainty in future baseline market and land use trends driven by uncertainty in important physical and market parameters. Using a Monte Carlo analysis, we show that future market and land use results are sensitive to these parameter assumptions. Globally, timber prices are not substantially influenced by parametric uncertainty, but timber outputs for several species can be heavily affected, as can global carbon storage. Thus, while timber outputs and forest carbon stock projections remain relatively stable and do not vary substantially across our simulations, we find large regional variation in projected forest carbon stocks. This result hints at a difficulty individual countries may have in developing robust baseline projections of forest carbon stocks without considering systematic feedback across the global market system.

Second, we conduct an attributional analysis that suggests that results are more sensitive to uncertainty in the parameters influencing the timber yield compared to uncertainty in land supply elasticity. This is particularly true for measuring carbon stocks, with uncertainty in the carrying capacity and growth rates of trees having implications for the size of carbon stocks. This finding has important implications for the value of inventory-based forest yield growth used in projections modeling contexts; since uncertainty in stocking density is a primary driver of the variability in projected forest carbon outcomes, this supports additional measurement and field sampling to reduce the uncertainty around physical forest yield attributes. This attributional analysis provides important information to policy makers that can help them better allocate resources to research on the more influential parameters.

2. Methods

In this section, we describe the methodological background of the analysis. First we provide a brief description of the Global Timber Model (GTM), including key assumptions and components, and references to recent model documentation. Then, we present a description of the attributional regression analysis, which we use to assess the relative importance of model parameters on variables of interest.

2.1. The Global Timber Model (GTM)

The Global Timber Model (GTM) has been widely used for policy analysis in forestry, addressing conservation policy (Sohngen et al., 1999), climate change (Sohngen et al., 2001; Tian et al., 2016; Sohngen and Tian, 2016), carbon sequestration (Sohngen and Mendelsohn, 2003; Tavoni et al., 2007), exchange rates (Daigneault et al., 2008), and biomass energy (Daigneault et al., 2012). The model is a dynamic optimization model that maximizes the present value of consumers’ plus producers’ surplus by harvesting forests and determining optimal levels of timber investments and regeneration, subject to a set of constraints that describe the growth of forests over time. Foresters in the model are assumed to be forward-looking, taking future prices into account when they determine both when to harvest trees and how intensively to regenerate forests.

The version of GTM applied in this analysis includes heterogeneous forest product demand, consistent with the versions of the model applied in Baker et al. (2017 and 2018), Kim et al. (2018), and Tian et al. (2018). Demand for pulpwood and sawtimber are represented separately, building on the single-product demand structure presented in Daigneault et al. (2012). This disaggregated demand structure recognizes that forest resources are often managed differently to supply pulpwood and sawtimber, thus GTM allocates harvests endogenously to pulpwood and sawtimber markets. As market, policy, or environmental factors evolve, the relative proportion of harvests allocated to pulpwood and sawtimber markets can change (that is, we do not assume a fixed proportion of harvests allocated to separate end uses). We also allow a portion of forest biomass (pulpwood or sawtimber) to be allocated to bioenergy use, but this proportion must be exogenously defined. Additional information on the version of the GTM applied for this analysis, including a technical appendix that lists structural equations, parameters, variables, and key assumptions, can be found in Kim et al. (2018).

One important set of model inputs are the forest biomass yield functions, which are used directly in the uncertainty analysis. Yield is assumed in the model to have the following functional form:

$$Y_{a,t}^i=e^{\left({\delta }_i-{\pi }_i/a\right)}$$ (1)

The yield function in (1) measures the volume of timber available for markets in land class i and age class a at time t. For the United States, for instance, the U.S. Forest Service collects data on forested plots throughout the country at regular intervals. The term δ_i measures the carrying capacity of the site, and π_i accounts for forest growth. Both are parameters of the yield function, which can be estimated with data on age classes and biomass per hectare.

Yield functions estimated this way contain some uncertainty in the parameters based on a number of factors, such as differences in the quality of sites, historical disturbance regimes on those sites (which have influenced biomass levels when measured), and climate factors. As yield functions are based on aggregate forest inventory data and empirical yield functions, there is uncertainty in growth estimates and projections as yield functions are represented at the mean and do not capture heterogeneity that exists within the inventory data. In models that are forward-looking, uncertainty over yield parameters can have large potential consequences for a range of management decisions, including harvests, timberland area managed, and regeneration intensity.

There is even greater uncertainty on yield function parameters in regions outside of the U.S. where the quality of data is not as substantial as in the U.S. In these cases, yield function data in the GTM is obtained using data from relatively few sites, or from studies done in similar forests. Thus, in most regions of the world, there is considerable uncertainty about both the rate of growth of trees and the maximum amount of biomass that can be stored on a site.

To account for uncertainty in the forest growth function parameters, we assume the parameters of the yield function, δ_i and π_i, are stochastic and follow triangular distributions (Equations 2a and 2b). Triangular distributions are popular empirical distributions when observational data are limited since parameters can be estimated from a small sample. There are several published studies in the forest modeling literature that have used triangular distributions to represent forest yield growth assumptions or various demand-side parameters in Monte Carlo studies, including McKenney et al. (2004) and Buongiorno and Johnston. (2018). Furthermore, triangular distributions have been applied to other large-scale modeling studies, including Valin (2015) and Plevin (2010). Given this precedent and the limited amount of forest inventory data available in certain regions, the use of triangular distributions is justified in this analysis.

$${\delta }_i\sim randTriangle(low,mid,high)$$ (2a)

$${\pi }_i\sim randTriangle(low,mid,high)$$ (2b)

The δ_i parameter controls the overall size of the stock of biomass on a site, with larger δ implying larger overall levels of biomass. The π_i parameter accounts for the rate of growth of forests over time. In a triangular distribution, the low value is the inverse of the normal cumulative distribution at probability 2%, and the high value is the inverse of the normal cumulative distribution at probability 98%. The mean value for the triangular distribution is taken from the yield functions that are used in the GTM (many of which were estimated using data from the underlying regions) and the standard deviation from estimates in Kim and Sohngen (2009). Thus, the underlying GTM yield function parameters represent the mid-point of the triangular distribution.

The land supply function for each timber type, i, is shown in equation (3):

$$\sum _{a=1}^A{X}_{a,t}^i=A_t^i{\left(L_t\right)}^{(1/\gamma )}{\left(R_t^i\right)}^{{\eta }_i}$$ (3)

Equation (3) is a constant elasticity function that sets the total area of land in forests in each timber type i, calculated as the sum of the area of land in each age class, $X_{a,t}^i$, as a function of the rental rate, $R_t^i$. $A_t^i$ is a slope parameter that changes over time to reflect shifts in the demand for land in the agricultural sector. As $A_t^i$ increases, so do forestry rents, or the opportunity costs of bringing a marginal unit of land into forestry at the expense of alternative uses such as cropland. L_t is the ratio of the current aggregate area of global forests to the initial aggregate area of forests globally. The parameter η_i is the own-price elasticity of supply, and γ is the price elasticity of global forestland supply. In the deterministic model, η_i is 0.3 in each region, meaning that if rents increase by 10%, the area of forestland will increase by 3%. We also set γ to 0.3 in the deterministic model, so that if the area of forests globally increases by 10%, it takes about a 30% increase in rents in any given region to maintain the same forestland area. Thus, if the aggregate area of forests globally is increasing (i.e., L_t > 1), it becomes costlier to maintain forestland in all regions. Although we do not directly model agricultural markets, this is consistent with the effects of rising output prices in the agricultural sector and rising opportunity costs associated with scarcity in that sector.

Given differences in productivity levels in forests and agriculture across regions, one might expect that the elasticity parameter, η_i, would vary from region to region. Unfortunately, information is not available from enough regions around the world to know what the elasticity parameter is with high statistical confidence. For the baseline model, we have assumed that it is the same in all regions as it is in the U.S., 0.3. Standard errors for all regions are also based on the U.S. due to data shortcomings on forests in many parts of the world. While having regionally specific data and standard errors would be ideal, the use of distributions based on U.S. data across other regions in the model is reasonable if heterogeneity in regions outside the U.S. is similar.

The parameter draws for the Monte Carlo analysis for the land supply elasticity parameters were assumed to follow a triangular distribution, using data from Kim and Sohngen (2009). As above, the low value is the inverse of the normal cumulative distribution at probability 2%; the high value is the inverse of the normal cumulative distribution at probability 98%.We assumed that environmental risks are uncorrelated, so increases or decreases in forest growth are randomly distributed across our forest types, which are distributed across different regions covered in the model. If these risks were correlated—that is, entire continents experienced the same set of shocks—then one might expect larger uncertainty bounds for global prices with shifts in productivity in one direction for important forest product exporting regions. We acknowledge that a potential consequence of this approach is that random draws could result in a range of positive and negative deviations from the mean for yield growth parameters that would essentially cancel each other out at a global scale. However, GTM represents a large number of distinct forest types, with heterogeneity in regional age class distributions and harvest/management costs. This combined with the large market shares of global pulpwood and sawtimber held by a relatively small number of forest types globally, minimizes the potential bias that could result from simultaneous random parameter draws across different forest types.

We also have not accounted for the effects of climate change in this analysis. Other studies have considered climate change impacts (e.g., Tian et al., 2016, 2018). It is also important to note that we have not accounted for demand shocks in this assessment, and demand shocks could cause prices to shift outside the ranges projected. However, other recent studies have evaluated market and forest management changes under alternative demand scenarios using the GTM, including Kim et al. (in press), Tian et al. (2018), and Baker et al. (2017).

Within the model, there are 211 land classes with individual yield functions (i.e., i = 211); thus, there are 211 α’s and β’s. Land supply functions only apply to accessible forest types and various accessible, semi-accessible, and inaccessible forests in the tropics where semi-accessible lands are more fungible with accessible areas. Thus, there are fewer σ’s in the model (111).

For the analysis, we ran 300 independent draws of each of these parameters from the triangular distributions using the Ohio Supercomputer Center. Some stochastic parameter combinations induced infeasible model solutions, so we ended up with 273 unique optimal solutions over the 300 simulations.

2.2. Attributional Analysis of Stochastic Parameters

In this analysis, a spatial weighting procedure is applied to assess the relative importance of the GTM’s stochastic parameters on projections of cumulative stored carbon, as well as sawtimber and pulpwood harvests under different baseline simulations. As will be shown below, there is relatively large uncertainty in carbon outcomes in carbon-intensive regions like Brazil, but it is not clear if the uncertainty is derived from the parameters of the growth function (i.e., Equation 1) or the parameters of the land supply function (i.e., Equation 3). Understanding which set of parameters has the largest impact on timber output or carbon may be most important in regions with potentially large land use changes. For the attributional analysis, we use regression analysis to assess the influence of parameter choice on market and carbon outputs by region.

We start by estimating regression equations for each forest land class in the model. The dependent variables in the regression equations are cumulative projected sawtimber harvests, pulpwood harvests, and carbon stocks in the 2050 and 2090 simulation periods, all represented at the land class level. Explanatory variables in the regression models include a constant term, plus estimated coefficient values for δi and π_i, the own-price elasticity in the rental function for each land class, and the global land supply elasticity. For the sawtimber and pulpwood equations, we include observations for each decade up to 2050 in one set of regressions and up to 2090 in another. We average the output across the decades, and we include decadal fixed effects to account for time-varying cumulative changes in management and harvest not explained by the variation in stochastic parameters. The carbon stock regressions use only data for the two specific time periods since carbon is cumulative. Regression results for all land classes, for the 2050 and 2090 periods are provided in Online Appendix A.

These land class specific regressions provide useful information, but for interpretation we aggregate the results to the regional level using a spatial weighting procedure. Using the land class specific parameters, we compute the average regional effect of a given stochastic parameter as:

$$Regiona{l}_{-}Effec{t}_n=\sum _{m=1}^L{w}_m\ast {\beta }_{mn}$$

where m = 1, …, L are forest types for a given region, as noted before

n = stochastic parameters as previously defined

w_m = forest land class m weight and is computed as $w_m=\frac{{\sum }_{t=1}^T{A}_{mt}}{{\sum }_{t=1}^T{\sum }_{m=1}^L{A}_{mt}}$,

where A_mt is the area of forest land class m in time t

β_mn = estimated coefficient value for forest type m and stochastic parameter n

This aggregation allows us to differentiate net regional implications of a change in the stochastic parameters without placing too much emphasis on a given forest type. We start by assessing the weighted regression results for sawtimber and pulpwood outputs for 2090. The δ_m parameter, as noted above, accounts for the overall size of the stock of biomass on a site, with larger δ_m implying larger overall levels of biomass. It is expected that this parameter will be positive, such that increases in δ_m will increase sawtimber outputs by increasing supply.

3. Results

This section provides an overview of key results from the analysis, including baseline projections generated by the GTM framework of relevant market and environmental variables. Following this are the results of the attributional analysis, which shed light on the relative influence of stochastic parameters on regional pulpwood and sawtimber harvests and forest carbon sequestration.

3.1. Results of the GTM Framework

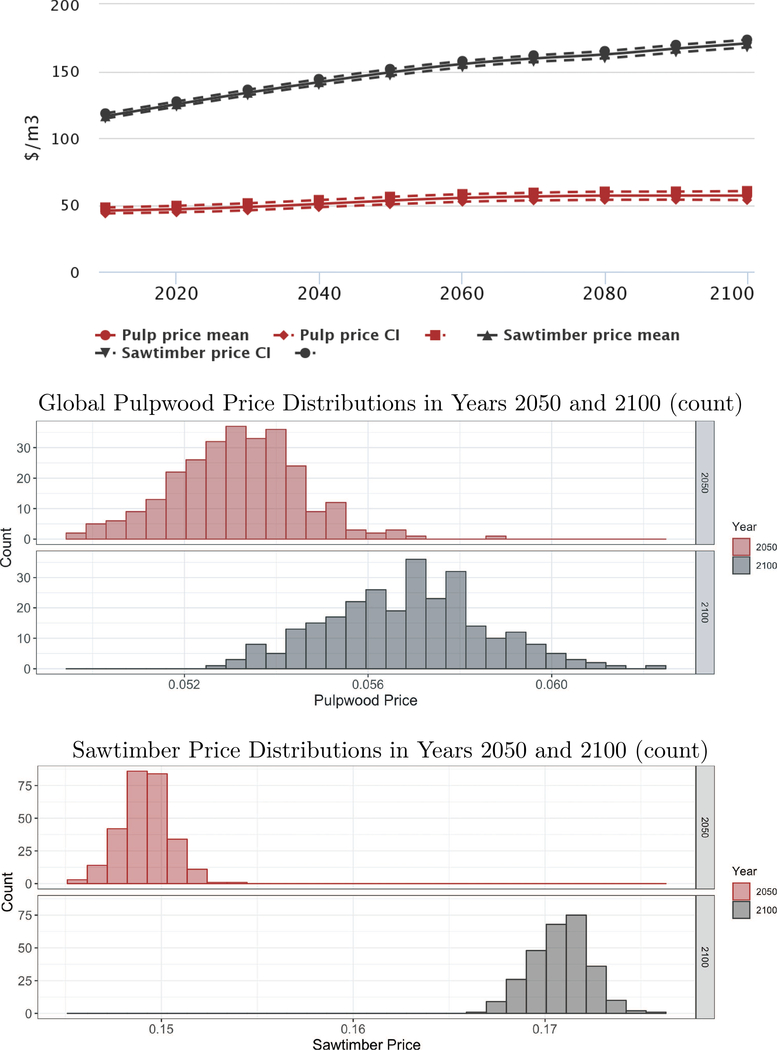
Results from this analysis show the effects of input parameter uncertainty on a number of model outcomes by examining the sample averages and the 95% uncertainty intervals from the Monte Carlo simulations. The baseline income and population projections assume demand growth of 2%–3% early in the century, followed by slower growth later in the century. This results in relatively modest overall price growth in the model (Figure 1). Prices for sawtimber are around three times those of pulpwood, which is consistent with observed price differentials (Howard and Kwameka, 2016). Sawtimber prices rise more rapidly over the century, as expected, given that sawtimber is used for more valuable outputs and the marginal costs of extracting additional sawtimber are higher than the marginal costs of extracting additional pulpwood. Pulpwood is undifferentiated and thus can be used for a wider range of products, including pulp or bioenergy. The uncertainty bounds on prices are small, especially with regards to sawtimber prices where the bounds represent less than 3.5% of mean sawtimber price through 2100. The uncertainty bounds are higher for pulpwood prices where the corresponding figure is 12% of mean pulpwood prices in 2100. This relatively modest variation is also expected. Wood outputs from various regions are highly substitutable in the demand function, meaning that different regions compete based on relative costs and timber availability to meet forest product demand globally. Thus, parametric deviations in supply through the yield functions or rental functions will have little impact on aggregate quantity supplied.

Figure 1:

Global Sawtimber and Pulpwood Price Projections, US$/m³ (Average, and 95% Uncertainty Interval Bounds – value at the 2.5 and 97.5 percentiles)

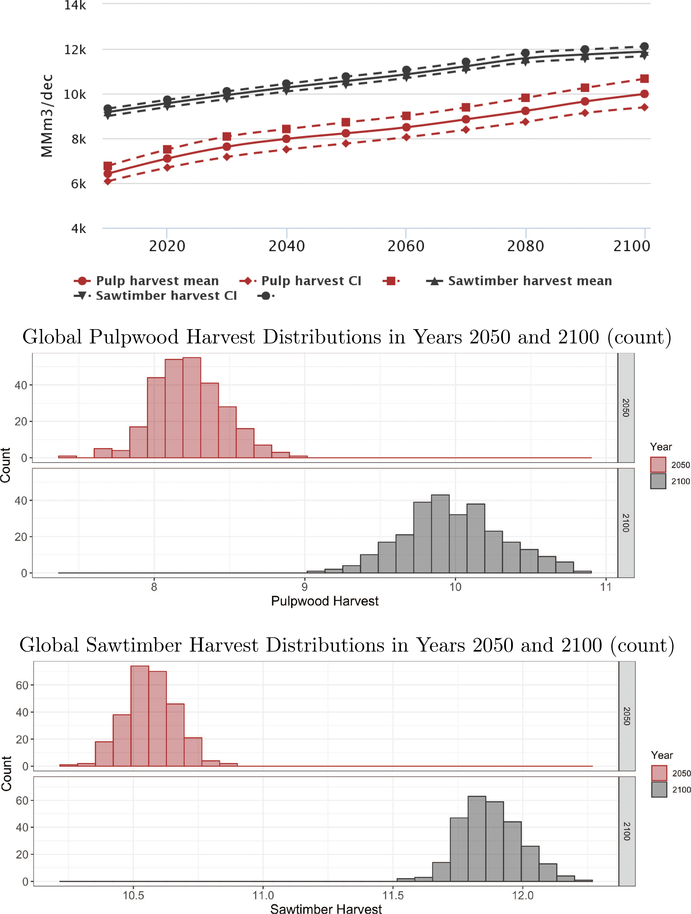
Global sawtimber and pulpwood production increases over the century, with pulpwood output increasing slightly more rapidly over time. Figure 2 shows projected pulpwood production, 95% uncertainty bounds for the projections presented in the top figure of the panel and histograms representing the distribution of outcomes across the Monte Carlo simulations for the 2050 and 2090 simulation periods. The 95% uncertainty bounds for pulpwood outputs are larger than the uncertainty bounds for sawtimber. Pulpwood is the lower value output, and some pulpwood cannot substitute into sawtimber markets. Hence, smaller deviations in parametric assumptions about forest growth will have larger effects on production and prices of pulpwood. The distribution of outcomes does not change much over time other than an outward shift in the mean.

Figure 2:

Global Sawtimber and Pulpwood Production Projections, million m³/decade (Average, and 95% Uncertainty Interval Bounds – value at the 2.5 and 97.5 percentiles)

On average, outputs increase in both the temperate and tropical zones, although the largest projected increases in pulpwood outputs occur in the tropics by 2050 and 2090 (Table 1). The analysis suggests some potential for a reduction in pulpwood production in the temperate zone over the century, with the largest reductions in Canada, where the 95% uncertainty interval encompasses lower pulpwood outputs in the future. These results suggest that the projected decline in comparative advantage for producing pulpwood in Canada over the century is fairly robust to uncertainty in forest growth rates and land supply elasticity. By 2090, the tropics experience a potentially large increase in pulpwood output, driven mostly by increased output in Brazil. Much of this expansion in Brazil is driven by increased productivity and harvest outputs from intensive margin investment in fast-growing plantations in Brazil.

Table 1:

Change in pulpwood output per year in 2050 and 2090 compared to 2010, 95% uncertainty interval in parentheses.

	2050	2090
	Change in output (million m3/yr)
Temperate
U.S.	−4.7 (−57.6, 57)	115.7 (43.1, 190)
China	46.1 (16.9, 75.3)	56.1 (24.6, 88.1)
Canada	−24.4 (−38.3, −8.7)	−25.8 (−38.4, −9.9)
Russia	0.5 (−27.2, 28.5)	5.2 (−25.7, 35.7)
EU	13.4 (−29.9, 53.6)	−4.5 (−50.5, 38.4)
Oceania	−1.2 (−12.7, 10.6)	10.3 (−4.3, 26.3)
Japan	2.3 (−1.9, 6.3)	−0.9 (−5.5, 3.1)
East Asia	11.4 (8.1, 14.7)	6 (0.4, 13.5)
Total Temperate	43.4 (−142.6, 237.3)	162.1 (−56.3, 385.2)
Tropical
Brazil	94.5 (37, 151.4)	119.3 (31.4, 203.2)
Rest of South America	3.9 (−14.6, 19.4)	−4.3 (−19.9, 12.6)
Central America	1.4 (−2.6, 5.4)	2.1 (−4.1, 8.4)
South Asia	−5.3 (−9.7, 0)	−6 (−9.6, −2.4)
Subsaharan Africa	1.9 (−13.4, 16.3)	−16.6 (−34.1, 0.2)
SE Asia	51.3 (27.1, 74)	71.4 (34.9, 108.1)
Africa/ME	−1.1 (−2.6, 0.4)	−1.4 (−3.2, 0.6)
Total Tropical	146.6 (21.2, 266.9)	164.5 (−4.6, 330.7)
Total	190 (−121.4, 504.2)	326.6 (−60.9, 715.9)

Sawtimber output is projected to increase in much of the temperate region, except for Canada and Russia (Table 2). A key reason for lower projected harvest levels in Canada and Russia is the relatively high cost of accessing land in those regions, combined with the relatively low productivity of forests. Investments in other regions with faster growth rates have greater net impact on markets. This result is robust across the uncertainty ranges in growth parameters and land supply elasticity, suggesting high potential for declining comparative advantage in timber production in boreal regions. In contrast, temperate regions in the U.S., China, and Europe are projected to experience increased sawtimber output over the century. Tropical regions also see gains in outputs, but the increases are relatively modest in comparison.

Table 2:

Change in sawtimber output per year in 2050 and 2090 compared to 2010, 95% uncertainty interval in parentheses.

	2050	2090
	Change in output (million m3/yr)
Temperate
U.S.	9.5 (−10.2, 40.9)	75.3 (55.3, 110.6)
China	34.6 (29.9, 39.3)	50.5 (45.1, 56.5)
Canada	−31.8 (−48.4, −17.2)	−4.8 (−24.1, 16.4)
Russia	−29.1 (−38.3, −20.8)	−35 (−44.5, −26.2)
EU	80.3 (50.6, 107.1)	100.4 (68.1, 128.8)
Oceania	2.2 (−1, 5.2)	−0.2 (−8.1, 6.1)
Japan	13.8 (11.4, 16.1)	17.3 (14.6, 20.3)
East Asia	1.5 (1.2, 1.8)	1.6 (1.3, 1.9)
Total Temperate	81 (−4.8, 172.4)	205.1 (107.7, 314.4)
Tropical
Brazil	14.6 (7.4, 22.3)	19.2 (11.7, 26.8)
Rest of South America	8.1 (−3.8, 19.8)	6.4 (−5, 17.8)
Central America	2.9 (2.1, 3.8)	3.8 (2.7, 4.8)
South Asia	4 (0.6, 7.4)	9.1 (4.7, 13.6)
Subsaharan Africa	8.2 (1.9, 14.6)	4.9 (−4.3, 12.6)
SE Asia	22 (12, 32)	23.4 (13.2, 33)
Africa/ME	1.1 (0.3, 2)	1.7 (0.9, 2.6)
Total Tropical	60.9 (20.5, 101.9)	68.5 (23.9, 111.2)
Total	141.9 (15.7, 274.3)	273.6 (131.6, 425.6)

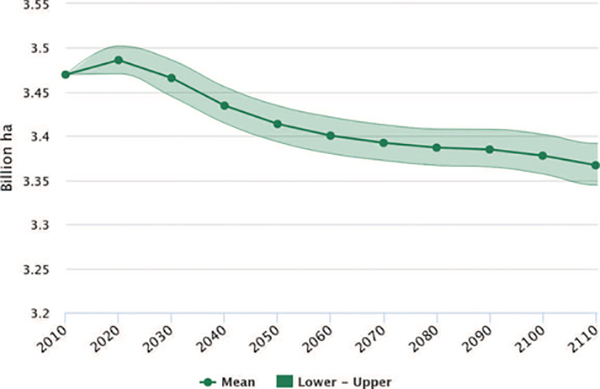
Global forest area is projected to increase initially in the Monte Carlo analysis, albeit modestly (Figure 2). Over the projection period to 2100, the total forest area declines by around 100 million ha. The 95% uncertainty interval is about 1.5% of the total forest area, suggesting that yield and land supply elasticity have little effect on global land area in forests. Globally, the aggregate change in forestland area is influenced mostly by assumptions about the underlying factors driving land use change, such as the demand for land to be used in the agricultural sector.

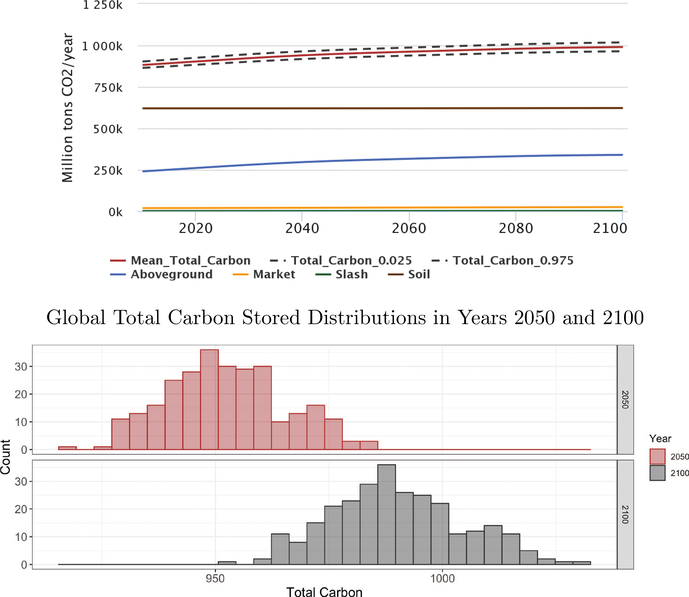
Examining carbon, total carbon storage increases in the baseline (Figure 3). Total forest carbon includes aboveground carbon, market carbon, carbon stored in slash, and soil carbon. While the bulk of carbon in forests is stored in soil components belowground (regional percentage ranges from 40% to 83% with an average of 66%), the largest change in carbon occurs in the aboveground portion. The 95% uncertainty range (bounded by the 2.5 and 97.5 percentile value) for above ground C represents around 8% of the average above ground carbon. The 95% range for total carbon storage is relatively small (+/− 2.5%), in part because the soil component is assumed to be fixed across regions and forest types, sawtimber harvests do not vary extensively (thus market carbon remains consistent), and we do not assign uncertainty to the parameters determining the soil component (a large portion relative to the total). Although not obvious in the figure, the lower bound on the 95% uncertainty range is slightly closer to the mean than the upper bound, suggesting that outliers, or large deviations from the mean, are more likely to occur in the positive direction (i.e., more carbon in the system, not less).

Figure 3: Global forest area (billion hectares).

* The solid line represents the mean value while the lower and upper limits depict the value at the 2.5 and 97.5 percentiles (uncertainty interval bounds), respectively.

Total carbon gains over the long-term projection period range from −5.0 to 149.1 Pg C by 2050 and 24.8 to 186.6 Pg C by 2090 (Table 3). The potential carbon gains range from +3.3% to nearly +23% by 2090 relative to 2010 levels. The gains are largest in Brazil and Russia. In Brazil, the increase amounts to a 16% increase by 2090, and in Russia it amounts to a 24% increase. However, in these two regions, uncertainty over parameters leads to fairly large uncertainty bounds on potential future carbon in 2050 and 2090. In our model, Brazil increases carbon storage on average while at the same time losing land to deforestation because regeneration and growth on existing forests outweighs the losses due to deforestation. This outcome, however, is heavily influenced by uncertainty in parameters in Brazil, given the relatively large potential for carbon losses shown by the 95% uncertainty range. Interestingly, in other tropical regions in our model, namely Rest of South America and SE Asia, deforestation occurs rapidly enough to negate any carbon benefits associated with regrowth.

Table 3:

Average change in total carbon between 2010 and the year given, with the minimum and maximum changes based on the 95% uncertainty intervals in parentheses.

	2050	2090
	Change in Carbon Stored (Pg C)
Temperate
U.S.	2.7 (1.3, 4.2)	5.7 (4.2, 7.2)
China	6.8 (5.5, 8.2)	10.8 (9.2, 12.6)
Canada	1.9 (−1.9, 5.8)	2.9 (−0.9, 6.8)
Russia	35.5 (23.1, 48.5)	56.1 (40.8, 72)
EU	3.4 (−0.1, 6.9)	4 (0.5, 7.4)
Oceania	2.8 (1.5, 4)	4.9 (3.5, 6.4)
Japan	0.7 (0.4, 1.1)	0.8 (0.5, 1.2)
East Asia	0.2 (0.1, 0.3)	0.1 (0, 0.2)
Total Temperate	54 (29.9, 79)	85.3 (57.8, 113.8)
Tropical
Brazil	20.3 (−14.4, 55.5)	25.7 (−9.6, 62.3)
Rest of SA	−2 (−8.2, 3.9)	−3.8 (−9.7, 1.8)
Central America	0.2 (−0.6, 0.9)	0.2 (−0.6, 0.9)
South Asia	−0.1 (−0.7, 0.4)	−0.1 (−0.7, 0.4)
Subsaharan Africa	1.6 (−2.3, 5.5)	1 (−2.9, 4.8)
SE Asia	−2.3 (−8.5, 3.6)	−3.4 (−9.2, 2.3)
Africa/ME	0 (−0.2, 0.3)	0 (−0.3, 0.3)
Total Tropical	17.7 (−34.9, 70.1)	19.6 (−33, 72.8)
Total	71.7 (−5.0, 149.1)	104.9 (24.8, 186.6)

The large increase in forest carbon stocks in Russia largely occurs in forests remaining forests in eastern Russia (i.e., Siberia). In this region, carbon stocks increase substantially over time, mainly as currently young forests increase in age. Importantly, we do not include land rents for many of these forests, so the uncertainty analysis has no effect on land use in this region (that is, land use is constant over time in many Russian forests in the far East). One factor that could influence forest stocks in this region that we have not explicitly modeled is forest fires. We do incorporate forest fires through the net yield functions used in the model, but this may understate the effects of fire on the carbon cycle.

3.2. Results of the Attributional Analysis

For the most part, the parameter δ_m, or total potential biomass on a given site, is positive for sawtimber and pulpwood (Tables 4a and 4b). For sawtimber there is one exception, SE Asia. To determine why SE Asia appears to differ, we look at the regression results for the individual land classes (see Online Appendix A). For SE Asia, the parameter on δ_m for the fast-growing tropical forests, and the two plantation types, is negative. This result is primarily driven by a shift in the distribution of outputs in these types from sawtimber to pulpwood as δ_m increases. Thus, as the stocking capacity increases for this forest type, the production portfolio shifts towards pulpwood. The δ_m parameter for these three forest land classes turns out to be positive in regressions where pulpwood harvest is the dependent variable. This result holds for most other individual forest types, particularly the fast-growing plantation types: as δ_m increases, output shifts towards pulpwood types.

Table 4a:

Weighted parameter estimates for sawtimber output, averaged 2010–2090 (n = 277).

Region	Delta (δ)	Pi (π)	Own-price elasticity	World Elasticity
Africa/Middle East	142.07	(8.07)	60.80	(16.14)
Brazil	12.31	1.24	(26.86)	(7.54)
Canada	112.20	(1.48)	34.94	(29.81)
Central America	32.04	(0.86)	14.79	(2.13)
China	26.38	(0.32)	3.12	10.10
EU Annex I countries	80.95	(1.50)	10.10	6.48
EU non-annex I countries	69.73	(0.80)	14.98	8.58
East Asia	278.89	(4.49)	154.23	(98.77)
Japan	59.39	(1.50)	51.03	(6.15)
Oceania	41.56	(0.20)	2.92	(14.67)
Rest of South America	39.58	0.17	(6.59)	(13.75)
Russia	16.99	(0.24)	(7.58)	8.49
SE Asia	(6.54)	0.80	(16.66)	(6.84)
Sub-Saharan Africa	28.62	(0.22)	(33.36)	(13.72)
South Asia	96.47	(2.65)	47.53	(16.45)
United States	44.71	(0.45)	14.86	(16.58)

Table 4b:

Weighted parameter estimates for pulpwood output, averaged 2010–2090 (n = 277).

Region	Delta (δ)	Pi (π)	Own-price elasticity	Global Elasticity
Africa/Middle East	14.66	(0.88)	5.90	(2.33)
Brazil	28.00	(0.47)	6.43	(7.89)
Canada	9.60	(0.16)	(0.28)	(0.91)
Central America	2.86	(0.20)	1.66	(0.21)
China	28.92	(0.63)	3.99	(3.60)
EU Annex I countries	113.85	(2.34)	10.63	0.48
EU non-annex I countries	51.11	(0.57)	7.64	1.61
East Asia	19.76	(0.34)	10.30	(9.66)
Japan	55.61	(1.56)	73.27	(20.00)
Oceania	(0.89)	(0.04)	(1.34)	2.43
Rest of South America	0.39	(0.06)	0.53	0.07
Russia	2.41	(0.02)	0.10	(0.08)
SE Asia	(1.68)	(0.01)	0.79	1.41
Sub-Saharan Africa	(0.09)	(0.04)	1.58	(0.27)
South Asia	1.40	(0.02)	0.17	(0.16)
United States	6.31	(0.19)	6.63	0.63

The parameter π controls the rate of growth of timber, with an increase in π signifying a lower growth rate, all else equal. For an industrially managed forest, an increase in π will lead to an increase in the rotation age and vice-versa. More importantly, an increase in π will reduce the annual supply of timber (and vice-versa) from an industrially managed forest. If all stocks in a country were managed industrially, then one would expect that an increase in π would reduce supply from the country (and vice-versa). In general, higher π leads to a reduced supply of sawtimber (Table 1), a result that makes sense given the effect that π is expected to have. In all regions, an increase in π leads to a reduction in pulpwood output (Table 2).

There are three exceptions for the sawtimber results—Brazil, Rest of South America, and SE Asia—where higher π leads to an increase in sawtimber output. This result for those regions is driven largely by the effects of changes in π on the fast-growing plantation types in those regions. For those types, an increase in π causes output to shift toward sawtimber and away from pulpwood. Thus, factors that slow growth in these fast-growing plantation types will encourage more output to be used in sawtimber and less in pulpwood within the specific types, and because these types are a relatively large proportion of pulpwood output within those regions, they affect the regional calculations. This effect is consistent across the parameter on π for many of the short-rotation nonindigenous species in the model, although it only affects the regional weighted parameter for the three regions mentioned above.

The own-price elasticity parameter (the parameter on land class-specific land supply elasticity) is positive in most regions in the weighted regressions for sawtimber (Table 4a) and pulpwood (Table 4b) outputs. In most cases, higher own-price elasticity on the land supply function shifts the land supply function out and allows more land to enter the forest type at any given rental value. The parameter on own-price elasticity is negative in the weighted sawtimber outputs for several regions. In Brazil, the negative parameter is driven by the results for the two plantation types (see Online Appendix). For many of the plantation types in various regions, higher own-price elasticity results in lower sawtimber output. As with δ and π discussed above, for many of the same forest types, the own-price elasticity parameter is positive in the pulpwood results. This suggests that higher land supply elasticity shifts harvesting towards pulpwood and away from sawtimber in the faster growing plantation types. The own-price elasticity parameter is also negative in the weighted results for Russia. As with the fast-growing types, the parameter has the opposite sign for pulpwood, implying an adjustment from sawtimber towards pulpwood in Russia as land supply elasticity increases.

The impact of the global land supply parameter (γ in Equation 3 above) is generally negative in the weighted sawtimber output results (Table 4a). The global land supply function shifts all rental functions in the model inward or outward, depending on whether total global forestland is greater or less than the initial forest area. In general, global forestland falls over time as agricultural demands drive more land out of forests and into agriculture, so the variable L_t in Equation 3 above is less than 1. As the global area of agricultural land expands and forestland declines, the global rental function shifts outward (the value $L_t^{(1/\gamma )}$ decreases), meaning that it takes a lower forestland rent in any region to maintain any given land area in forests. When L_t < 1, an increase in γ means that $L_t^{(1/\gamma )}$ is bigger, such that with greater elasticity (i.e., larger γ), it takes a larger rent to hold the same area of land in forests. In scenarios where global forestland area is declining over time, or an increase in the global land supply elasticity parameter, it will be costlier to hold land in forests; thus, one would expect that an increase in the global elasticity will lower timber outputs and carbon sequestration and vice versa.

The weighted parameter estimates for total carbon change and land carbon change by 2090 generally meet expectations (Tables 5a and 5b). The parameter estimates on δ are positive, as expected, with one exception in Japan. Thus, in general, higher δ leads to higher overall biomass and higher levels of carbon, all else equal. The parameter estimates on π are negative for all regions, as higher π is associated with slower growth and hence less carbon. The parameter on own-price elasticity is positive in most regions in the weighted regressions. In general, an increase in own-price elasticity will cause the rental function to decline, thus reducing rents and increasing the land in forests. Two exceptions occur in inaccessible types in the Rest of South America and Sub Saharan Africa. The parameter on global elasticity is negative. As noted above, this occurs because of the functional form used in Equation (3) and the fact that total forest area is declining over time. Hence, higher elasticity values will increase rents for any given land area in forests, and make land more expensive. This will cause the model to hold less land in forests if the elasticity value is higher, thus decreasing total carbon storage.

Table 5a:

Weighted parameter estimates for total carbon, cumulative change by 2090 (n = 277).

Region	Delta (δ)	Pi (π)	Own-price elasticity	Global Elasticity
Africa/Middle East	1434.70	(21.94)	787.02	(485.47)
Brazil	399210.35	(3407.94)	63926.82	(62828.47)
Canada	4833.41	(36.27)	2078.57	(873.64)
Central America	5545.67	(47.79)	1533.86	(1295.37)
China	3729.99	(43.20)	3654.70	(l386.8o)
EU Annex I countries	4296.97	(60.11)	4044.20	(2415.60)
EU non-annex I countries	1804.80	(23.38)	1966.23	(1214.95)
East Asia	378.17	(7.06)	632.03	(494.51)
Japan	(36.76)	(15.31)	3671.55	(898.54)
Oceania	3858.66	(32.08)	264.90	(46.48)
Rest of South America	36548.33	(814.69)	(4195.14)	(15723.55)
Russia	66237.85	(487.52)	3027.87	(2388.63)
SE Asia	20384.59	(298.69)	2215.27	(7322.43)
Sub-Saharan Africa	39445.55	(438.40)	(2280.91)	(12838.06)
South Asia	1109.49	(40.42)	1771.02	(1660.85)
United States	841.33	(15.95)	2014.63	(308.33)

Table 5b:

Weighted Parameter Estimates for Land Carbon, Cumulative Change by 2090 (n = 277).

Region	Delta (δ)	Pi (π)	Own-price elasticity	Global Elasticity
Africa/Middle East	1420.70	(21.80)	783.40	(483.20)
Brazil	399020.40	(3406.50)	63922.00	(62830.50)
Canada	4680.60	(34.50)	2013.20	(823.70)
Central America	5533.90	(47.70)	1530.90	(1294.40)
China	3592.80	(40.70)	3571.60	(1342.50)
EU Annex I countries	3675.30	(51.30)	3803.30	(2323.00)
EU non-annex I countries	1708.00	(22.30)	1947.30	(1229.30)
East Asia	363.20	(6.80)	553.00	(453.10)
Japan	(137.30)	(12.80)	3490.90	(860.00)
Oceania	3821.80	(31.50)	258.20	(38.20)
Rest of South America	36306.50	(812.20)	(4197.70)	(15725.70)
Russia	65846.30	(484.20)	3023.90	(2393.00)
SE Asia	20199.50	(296.50)	2246.40	(7301.40)
Sub-Saharan Africa	39312.90	(437.40)	(2282.10)	(12839.70)
South Asia	1060.30	(39.50)	1732.60	(1626.90)
United States	615.90	(10.30)	1659.70	(295.70)

4. Discussion

This study uses Monte Carlo methods to assess how uncertainty in key parameters in the GTM potentially affects projected market outcomes, focusing on timber prices, outputs, and carbon. The parameters we include as uncertain are the yield function parameters and the land supply elasticity parameters, following other recent applications of this modeling framework and similar studies (Kim, 2010; Choi et al., 2011; Kim, 2016). The results suggest that timber prices, timber outputs, and carbon are all expected to increase over time, consistent with other recent studies that applied the same or similar versions of this modeling framework (Baker et al., 2017, 2018; Kim et al., 2018; Tian et al. (2018), 2016; Favero et al. 2017). Various ecosystem services from forests, namely timber outputs and carbon, are projected to change significantly in the future, and the aggregate changes are influenced by uncertainty in key underlying parameters.

The baseline projects that sawtimber prices increase at 0.4% per year through 2090 and pulpwood prices increase 0.2% per year. These increases suggest continuing scarcity for wood products in the future, although the rates of growth are slower than historical price increases of the past century (Haynes, 2009). Price growth is lowest for pulpwood given that a wider variety of forest types and tree sizes can be used to produce pulpwood. In contrast, sawtimber is a higher valued use and has fewer types that can be used to produce it. All Monte Carlo scenario projections imply rising prices both for sawtimber and pulpwood, and the range across the various scenarios is fairly narrow. This makes sense given our assumption that parameter draws are taken from a triangular distribution and that wood from various regions is relatively fungible within a global demand system. That is, while some regions enjoy faster forest growth due to the parameter draws, other regions have slower forest growth. These changes are all random, so that increases are offset by decreases elsewhere.

Although global harvests are projected to increase over time, not all regions share in the gains. Some regions, the north in particular, are projected to experience reductions in timber output. For example, sawtimber and pulpwood outputs are expected to decline in Canada by 2050, although sawtimber outputs are projected to rebound modestly by 2090. Sawtimber and pulpwood outputs decline in Russia over the entire century. These reductions in output are a result of the relatively high costs of accessing timber and harvesting it in these regions, and the slow growth in pulpwood and sawtimber prices. Rather than building road infrastructure to remote places, investors place resources in harvesting timber in more productive temperate and subtropical regions. This result is consistent across the range of parameter draws. Pulpwood outputs in the tropics also tend to fall, with the exception of Brazil, which experiences strong increases in pulpwood outputs by 2090. This growth is driven by rising stocks and harvests in second growth forests.

Total carbon stored in the world’s forests is projected to increase by 71.7 Pg C by 2050 and 104.9 Pg C by 2090. The 95% uncertainty interval includes the possibility that global storage declines in 2050 relative to 2010 levels, but by 2100, the model indicates carbon storage increases with 95% confidence. Brazil and Russia experience the largest gains in absolute terms, although the 95% uncertainty interval in Brazil includes the likelihood of a reduction in total C storage by 2050 and 2090. For the most part, other temperate regions also experience growth in carbon storage, while a number of tropical regions experience reductions. The largest reductions are projected to occur in SE Asia as a result of deforestation losses.

The regression results provide insights into the specific factors affecting sawtimber, pulpwood and carbon outputs. As expected, factors that increase biomass on forest sites are expected to increase output of both sawtimber and pulpwood and vice-versa. There are some exceptions to this general rule in some of the regions because shifts in carrying capacity also encourage a shift in the proportion of timber allocated to pulpwood versus sawtimber. This effect is species specific. Similarly, an increase in the rate of growth of a species leads to an increase in both sawtimber and pulpwood output (the parameter π is negative). The result is reversed in some regions for sawtimber due to a reallocation of output towards pulpwood.

Changes in the parameters have less ambiguous impacts on carbon storage. Higher carrying capacity increases carbon storage, as does faster growth. Similarly, an increase in own-price land supply elasticity increases carbon storage, and an increase in the parameter for global land supply elasticity reduces carbon storage. Based on the individual parameter estimates for each forest type, we calculate the marginal impact of changes in carrying capacity (δ_m), growth rates (π_m), and the elasticity parameter in the rental function (η_m) on carbon storage in each region (Table 6). Changes in carrying capacity have the largest effect on total carbon storage, followed by changes in the growth rate of forests. The effects of deviations in the carrying capacity parameter have their biggest impact in Brazil, followed by Russia. The effects of deviations in carrying capacity are large in Brazil and Russia because these regions also contain a large portion of the world’s existing carbon. Interestingly, the 10% increase in carrying capacity increases carbon by less than 10%. The largest changes in carbon occur in Brazil, SE Asia, and Sub-Saharan Africa. In contrast, changes in elasticity have a relatively modest effect on carbon.

Table 6:

Effect of a 10% change in each parameter on regional total carbon storage in 2090 in million tons C and as a % of the average baseline projection by 2090.

Region	Delta (δ) (%)	Pi (π) (%)	Own-price elasticity	Global Elasticity
	Million tons C
Africa/Middle East	0.3, (3.8%)	0.2, (3.1%)	0.05, (0.7%)	−0.09, (−1.1%)
Brazil	49.0, (8.2%)	25.7, (4.4%)	2.82, (0.5%)	−5.18, (−0.9%)
Canada	4.1, (2.3%)	2.4, (1.3%)	0.37, (0.2%)	−0.53, (−0.3%)
Central America	1.1, (5.8%)	0.6, (3.2%)	0.12, (0.6%)	−0.20, (−1.1%)
China	2.3, (3.9%)	1.8, (3.0%)	0.42, (0.7%)	−0.57, (−1.0%)
EU Annex I	2.5, (4.3%)	2.6, (4.5%)	0.70, (1.2%)	−1.16, (−2.0%)
EU non-annex I	0.4, (4.0%)	0.5, (4.6%)	0.13, (1.3%)	−0.21, (−2.2%)
East Asia	0.1, (1.7%)	0.1, (2.3%)	0.03, (0.9%)	−0.05, (−1.6%)
Japan	−0.1, (−0.1%)	0.1, (1.8%)	0.20, (2.9%)	−0.24, (−3.6%)
Oceania	1.5, (3.7%)	0.6, (1.6%)	0.10, (0.3%)	−0.13, (−0.3%)
Rest of SA	5.6, (5.8%)	7.6, (7.7%)	−0.12, (−0.1%)	−0.62, (−0.7%)
Russia	17.4, (4.0%)	13.8, (3.2%)	0.36, (0.1%)	−0.61, (−0.1%)
SE Asia	6.7, (6.6%)	5.9, (5.9%)	0.17, (0.2%)	−0.90, (−0.9%)
Sub-Saharan Africa	7.8, (7.1%)	5.3, (4.8%)	−0.11, (−0.1%)	−0.64, (−0.6%)
South Asia	0.2, (2.2%)	0.4, (3.7%)	0.11, (1.0%)	−0.19, (−1.7%)
United States	1.5, (2.2%)	1.4, (2.2%)	0.48, (0.7%)	−0.55, (−0.8%)

The focus of this uncertainty analysis is on key model parameters related to forest yield growth, carrying capacity, and the relative costs of moving new land into forests, which are all critical ingredients for projecting future biomass availability and carbon stocks. It is important to note, however, that other model parameters were held at their base value for this analysis and were not part of the Monte Carlo analysis, including demand elasticity parameters for pulpwood and sawtimber. Our justification for omitting key parameters from the Monte Carlo experiment is that introducing too many random parameters would confound the interpretation of the analysis. Restricting the random parameter sets to just those that are related to physical growth rates and the economic decision to expand or contract forest land supply offers a tractable set of parameters for conducting attributional analysis and exploring heterogeneity in the relative importance of specific parameters across regions and time.

However, to illustrate the relative importance of demand elasticities on projected forest market and management outcomes, we ran two additional sensitivity scenarios with alternative elasticity assumptions while holding all other parameter values at their mean levels. In the first case, demand elasticities are divided by one half (from an assumed value of −1 to −0.5). Less elastic demand results in approximately 6% more carbon storage globally by 2050 (relative to the mean parameter value baseline scenario). This elasticity change results in more investment and increased growing stocks, which increases carbon accumulation. In the second case, elasticities are more elastic (doubled from −1.0 to −2.0), which has the opposite effect and reduces projected carbon by approximately 4% in 2050.

We include an attributional analysis to assess relative importance of increased biomass and rates of growth of each species on sawtimber and pulpwood outputs. Results from this attributional analysis show that increased biomass and higher rates of growth on forest sites increase output of both sawtimber and pulpwood and vice-versa. However, there are some exceptions based on a tendency in some regions to reallocate output towards pulpwood with higher rates of growth or biomass capacity. We further gauge the relative importance of the biomass and growth rate parameters as well as land supply elasticities on carbon output. Our results are unambiguous: higher biomass carrying capacity increases carbon storage, as does faster growth. Similarly, an increase in own-price land supply elasticity increases carbon storage and an increase in the parameter for global land supply elasticity reduces carbon storage.

When considering the attributional analysis, we find that carbon storage is most sensitive to uncertainty in biological growth parameters. Perhaps surprisingly, uncertainty in land supply elasticity has a fairly small impact upon the carbon storage. One reason for this is that many forests, including a large portion of carbon storage, are far from the extensive frontier (e.g., the agriculture and forestry interface) and will not experience land use change over the projection period. Changes in the physical growth parameters have an important effect because they impact relatively large land areas simultaneously, and for some region and forest type combinations, modest increases in growth rates or stock density parameters can result in meaningful changes in carbon storage.

There are a few limitations of this analysis worth mentioning. First, given the lack of publicly available forest inventory data in most regions of the world, we apply triangular distribution assumptions to reflect uncertainty in forest growth parameters that are broadly consistent with parameter distributions empirically estimated for U.S. forest types. This approach ignores regional heterogeneity in the underlying uncertainty of physical yield attributes but represents a reasonable alternative for developing regional parameter distributions in the absence of available inventory data. Second, as previously discussed, parameters are drawn randomly across regions and forest types, and thus we do not account for systemic risks or the possibility that forest yield growth changes (or general uncertainty) could be similar in direction across forest types within a large region such as the United States or Brazil. Finally, this analysis only includes a limited number of the GTM’s parameters in the Monte Carlo analysis, which could ignore important interactions between physical growth parameters and other economic inputs such as demand elasticities. To address this, results from a sensitivity analysis are provided that illustrate the importance of demand-side elements in projected forest carbon outcomes, but deviations in demand elasticities are not interacted with stochastic yield growth and land supply parameters for full attributional analysis.

Nevertheless, while the literature is full of sensitivity analyses that evaluate the impact of adjusting some set of model inputs or policy-related constraints, few studies have applied Monte Carlo techniques to evaluate the relative importance of stochastic model parameters on endogenous variable outputs using integrated intertemporal models of economic and resource management systems. This is partly due to computational complexity and the difficulty in addressing key scenario design issues (e.g., choosing which parameters to be stochastic). This analysis seeks to add to this literature by applying Monte Carlo techniques to a global intertemporal model of forest resources and markets. Our results show relatively modest uncertainty ranges for projected model outcomes, which suggests that the global forestry sector is relatively resilient to local deviations in physical growth or land supply assumptions. Finally, attributional analysis reveals that the relative influence of physical growth parameters is likely a more important determinant of future forest carbon stocks than economic parameters that influence the amount of forest land in the system.

5. Conclusion

Numerous models have now been used to project future market and biomass outcomes for forests. When confronted with uncertainty associated with the underlying parameters used in the models, the modelers have typically resorted to sensitivity analysis to assess how the results are influenced by shifts in important parameters. More recently, modelers have been using Monte Carlo techniques to more fully characterize the influence of parameter uncertainty on model outcomes. While Monte Carlo techniques can be applied in a straightforward way with static or recursive models, their application to dynamic models, particularly in forestry, has been limited because of the computational burdens. This paper addresses the computational issue by using a super computer to conduct a Monte Carlo analysis with a global dynamic optimization model of timber markets through 2020. Given the importance of forests in the global carbon cycle, it is useful to better understand the sensitivity of market outcomes (e.g., prices, outputs) and carbon, to important input parameters, such as the biomass yield functions and land supply.

The results of the paper suggest that aggregate trends are not significantly affected by uncertainty in the underlying parameters for forest yield or land rents. Prices are expected to increase modestly both for sawtimber and pulpwood, consistent with results presented in Tian et al. (2018), another detailed baseline assessment, and Kim et al. (2018), but the uncertainty bounds for both prices are very small. The results also suggest that the distribution of timber outputs and carbon fluxes is sensitive to uncertainty in the underlying set of parameters. Projected sawtimber and pulpwood prices both trend upwards, with the fastest rate of increase in sawtimber (0.4% per year versus 0.2% per year). Nonetheless, future prices are projected to increase over the next century at only a fraction of the rate of the last century (e.g., Sohngen and Haynes, 1994; Haynes, 2009). The 95% uncertainty interval on global prices is relatively narrow for both sawtimber and pulpwood. Despite the modest price increases, we project that sawtimber and pulpwood outputs both increase by around 320–350 m³ per year. The increases in pulpwood are perhaps surprising given concerns about reductions in harvests due to declining pulpwood demands (e.g., Latta et al., 2015), but we have maintained relatively robust demand growth in our model simulations to account for other similar demands, such as fuelwood and bioenergy.

Despite the potential increase in aggregate global output, the results suggest that timber harvests could decline in some regions in the future. Canada, for instance, is projected to experience a reduction in pulpwood and total timber harvests by 2050 and continuing through the end of the century. Similarly, Russia is expected to experience a reduction in timber harvests. Based on the uncertainty bounds, there is relatively high potential for pulpwood harvests to decline both by the middle of the century and the end of the century globally, although the average change is positive. The largest share of these reductions occurs in temperature and boreal regions. Others have suggested that pulpwood harvests could be declining due to demand side factors (Latta et al., 2015), and these results suggest that there is a concern about the competitiveness of pulpwood production in many regions even if demand remains somewhat strong over time.

Global carbon storage is expected to increase by 71.7 Pg C (−5.0 to 149.1) by 2050 and 104.9 Pg C (24.8 to 186.6) by 2090. Most regions are expected to experience an increase in carbon storage, with the biggest increases on average occurring in Russia and Brazil. The lower bound in Russia remains well above 0 both in 2050 and 2090. In the tropics, there is more potential for carbon losses over time, due largely to continuing deforestation trends there and the interaction of deforestation with uncertainty in land supply elasticity.

Overall, our results provide evidence that future global forest carbon stock trends are robust to uncertainty surrounding yield growth assumptions and economic parameters related to land supply. However, we find substantial variation across regions, indicating a need for increased investment in local inventory assessments and monitoring to inform global systems models and improve national- or regional-scale projections of forest carbon futures.

Figure 4:

Global carbon storage, and storage in components, including aboveground, soil, slash, and marketed products (Million tons CO₂).